Абсолютная температура Калькулятор | Вычислить Абсолютная температура
✖Тепло из низкотемпературного резервуара — это тепло материала при более низкой температуре.ⓘ Тепло из низкотемпературного резервуара [Qlow] | АттоджоульМиллиарда баррелей нефтяного эквивалентаБританская тепловая единица (IT)Британская тепловая единица (th)Калорийность (ИТ)Калорийность (питательная)Калорийность (тыс.)сантиджоульCHUдекаджоульДециджоульДин СантиметрЭлектрон-вольтЭргЭкзаджоульФемтоджоульфут-фунтГигагерцГигаджоульГигатонныеГигаватт-часГрамм-сила-сантиметрграмм-сила-метрХартри энергия гектоджоульГерцЛошадиная сила (метрическая) ЧассилочасДюйм-фунтДжоульКельвинКилокалория (IT)Килокалория (й)килоэлектрон вольтКилограммКилограмм тротилаКилограмм-сила-сантиметрКилограмм-сила-метркилоджоульKilopond Meterкиловатт-часкиловатт-секундаМБТУ (ИТ)Мега БТЕ (ИТ)Мегаэлектрон-Вольтмегаджоульмегатоннамегаватт-часмикроджоульМиллиджоульММБТУ (ИТ)наноджоульНьютон-метрУнция-сила-дюймПетаджоульПикоджоульПланка Энергияфунт-сила футафунт силы дюймпостоянная РидбергаТерагерцТераджоультермтерм (EC)Therm (США)Тон (взрывчатые вещества)Тон-час (Охлаждение)Тонна нефтяного эквивалентаБлок Единая атомная массаВатт-часДжоуль | +10% -10% | |
✖Тепло из высокотемпературного резервуара – это тепло, поступающее в тело при более высокой температуре. | АттоджоульМиллиарда баррелей нефтяного эквивалентаБританская тепловая единица (IT)Британская тепловая единица (th)Калорийность (ИТ)Калорийность (питательная)Калорийность (тыс.)сантиджоульCHUдекаджоульДециджоульДин СантиметрЭлектрон-вольтЭргЭкзаджоульФемтоджоульфут-фунтГигагерцГигаджоульГигатонныеГигаватт-часГрамм-сила-сантиметрграмм-сила-метрХартри энергия гектоджоульГерцЛошадиная сила (метрическая) ЧассилочасДюйм-фунтДжоульКельвинКилокалория (IT)Килокалория (й)килоэлектрон вольтКилограммКилограмм тротилаКилограмм-сила-сантиметрКилограмм-сила-метркилоджоульKilopond Meterкиловатт-часкиловатт-секундаМБТУ (ИТ)Мега БТЕ (ИТ)Мегаэлектрон-Вольтмегаджоульмегатоннамегаватт-часмикроджоульМиллиджоульММБТУ (ИТ)наноджоульНьютон-метрУнция-сила-дюймПетаджоульПикоджоульПланка Энергияфунт-сила футафунт силы дюймпостоянная РидбергаТерагерцТераджоультермтерм (EC)Therm (США)Тон (взрывчатые вещества)Тон-час (Охлаждение)Тонна нефтяного эквивалентаБлок Единая атомная массаВатт-часДжоуль | +10% -10% |
|
✖Абсолютная температура — это температура, измеряемая по шкале Кельвина, где ноль — это абсолютный нуль. |
⎘ копия |
👎
Формула
сбросить
👍
Абсолютная температура Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Тепло из низкотемпературного резервуара: 200 Джоуль —> 200 Джоуль Конверсия не требуется
Тепло из высокотемпературного резервуара: 800 Джоуль —> 800 Джоуль Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
0. 25 —> Конверсия не требуется
25 —> Конверсия не требуется
< 10+ Термодинамические свойства Калькуляторы
< 10+ Температура Калькуляторы
Абсолютная температура формула
Абсолютная температура = Тепло из низкотемпературного резервуара/Тепло из высокотемпературного резервуара
Tabs = Qlow/QHigh
Что такое абсолютная температура?
Абсолютная температура, также называемая термодинамической температурой, — это температура объекта по шкале, где 0 принимается за абсолютный ноль.
Share
Copied!
Физика. 10 класс. Основы молекулярно-кинетической теории. Урок 5.
Физика. 10 класс. Основы молекулярно-кинетической теории.
UCOZ Реклама
Российская академия образования
Институт общего среднего образования РАО
Центр дистанционного образования «Эйдос»
Материалы 2-го Всероссийского конкурса
Физика. 10 класс.
Урок 5.
Температура. Абсолютная шкала температур.
Молекулярно-кинетическая теория позволяет нам понять, что представляет собой физическая сущность такого сложного понятия, как температура. Когда соприкасаются два тела (или несколько тел), между ними происходит теплообмен. Если система тел изолирована (т.е. не взаимодействует с окружающими телами и внешней средой), теплообмен будет длиться до тех пор, пока температуры тел не выравняются и не установится тепловое равновесие.
Тепловым или термодинамическим равновесием называют такое состояние, при котором все макроскопические параметры в системе сколь угодно долго остаются неизменными.Это означает, что в системе не меняются объем и давление, не изменяются агрегатные состояния вещества, концентрации веществ. Но микроскопические процессы внутри тела не прекращаются и при тепловом равновесии: меняются положения молекул, их скорости при столкновениях. В системе тел, находящейся в состоянии термодинамического равновесия, объемы и давления могут быть различными, а температуры обязательно одинаковы. Таким образом, температура характеризует состояние термодинамического равновесия изолированной системы тел.
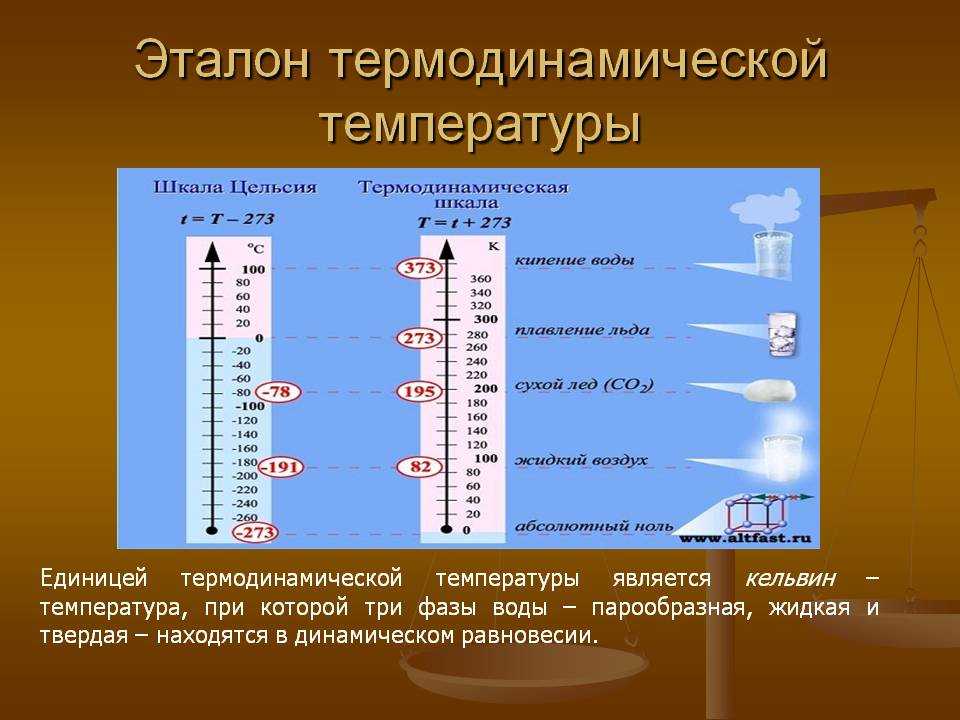
Для измерения температуры служат специальные приборы — термометры. Их действие основано на том факте, что при изменении температуры, изменяются и другие физические параметры тела, например, такие, как давление и объем.В 1787 году Ж. Шарль из эксперимента установил прямую пропорциональную зависимость давления газа от температуры. Из опытов следовало, что при одинаковом нагревании давление любых газов изменяется одинаково. Использование этого экспериментального факта легло в основу создания газового термометра. Если использовать температурную шкалу Цельсия, то экспериментально установленный Шарлем закон имеет вид: P = Po(1+at), где Рo — давление газа при температуре 0oС, a — установленный из опытов температурный коэффициент давления газа. Можно преобразовать формулу, выражающую зависимость давления от температуры, используя абсолютную температурную шкалу (Т), предложенную Кельвином: P=T· const. (T=t + 273 K). Измеряемая по шкале Цельсия температура может быть как положительной, так и отрицательной, в то время как абсолютная температура всегда неотрицательна. Наименьшая температура по абсолютной шкале — это абсолютный нуль. При такой температуре P=0, что согласно МКТ возможно, если средняя кинетическая энергия молекулы равна нулю.
Таким образом, при абсолютном нуле температуры прекращается тепловое движение частиц вещества. Ниже этой температуры быть уже не может. Эта температура приблизительно равна — 273oС. Единица абсолютной температуры называется кельвином (K).
Опытным путем было установлено, что при постоянном объеме и температуре давление газа прямо пропорционально его концентрации. Объединяя экспериментально полученные зависимости давления от температуры и концентрации, получаем уравнение: р = nkT, где — k коэффициент пропорциональности — постоянная Больцмана. Постоянная Больцмана связывает температуру со средней кинетической энергией движения молекул в веществе. Это одна из наиболее важных постоянных в МКТ. Температура прямо пропорциональна средней кинетической энергии теплового движения частиц вещества. Следовательно, температуру можно назвать мерой средней кинетической энергии частиц, характеризующей интенсивность теплового движения молекул. Этот вывод хорошо согласуется с экспериментальными данными, показывающими увеличение скорости частиц вещества с ростом температуры.Рассуждения, которые мы проводили для выяснения физической сущности температуры, относятся к идеальному газу. Однако выводы, полученные нами, справедливы не только для идеального, но и для реальных газов. Справедливы они и для жидкостей и твердых тел. В любом состоянии температура вещества характеризует интенсивность теплового движения его частиц.
Иллюстрации и основные итоги.
Решите задачу 3. Найти среднюю квадратичную скорость молекулы водорода при температуре 27oС.
© Всероссийский конкурс «Дистанционный учитель года»,
2000
© Львовский Марк Бениаминович, 2000
http://www.eidos.ru/dist_teacher/index.htm
E-mail: [email protected]
Абсолютная температура
Вы наверняка знакомы с понятием температуры. Количество тепла или холода тела (живого и неживого) можно измерить с помощью термометра. Интересно отметить, что температура, которая не может понизиться дальше, называется абсолютной температурой. Также известная как термодинамическая температура, количество тепла измеряется с помощью шкалы Кельвина.
Также известная как термодинамическая температура, количество тепла измеряется с помощью шкалы Кельвина.
Абсолютная температура равна -273,15 градуса Цельсия. Нижняя точка шкалы Кельвина равна нулю, как и на других шкалах, измеряющих температуру. Существует небольшая разница между нулем по шкале Кельвина и другими шкалами. Эта конкретная температура описывается как абсолютный ноль, когда материя, достигшая этой температуры, почти не движется, и тело не может стать холоднее. Это крайняя форма холода, известная ученым до сих пор.
Объяснение температуры
Что ж, температура не является формой энергии, как думают многие. Вместо этого вы можете определить его как измерение кинетической энергии внутри крошечной частицы, такой как атом или молекула. Простое описание чего-либо как горячего или холодного не приводит к тому, что человеческий мозг создает яркий образ. Вам понадобится точка отсчета, чтобы сравнить уровень жара или холода. Метеорологические сводки часто раскрываются с помощью двух колонок. Один отображает температуру или количество тепла в атмосфере, тогда как другой показывает уровень влажности. Поэтому жарко и влажно — это не то, что вы можете точно измерить. Вы имеете в виду, как человек чувствует себя в такой среде. Абсолютная температура — это то, что люди не замечают, когда они следуют стандартной рутине.
Один отображает температуру или количество тепла в атмосфере, тогда как другой показывает уровень влажности. Поэтому жарко и влажно — это не то, что вы можете точно измерить. Вы имеете в виду, как человек чувствует себя в такой среде. Абсолютная температура — это то, что люди не замечают, когда они следуют стандартной рутине.
Связь между кинетической энергией и температурой
Энергия движущегося тела определяется как кинетическая энергия. Эта энергия находится во всем, что нас окружает. Вы даже найдете его в плотных, твердых неживых объектах, где молекулы плотно упакованы. Средняя кинетическая энергия всех молекул известна как их температура. Скорость молекулярного движения увеличивается, когда рассматриваемый объект/вещество поглощает тепло. Увеличение скорости молекул также увеличивает кинетическую энергию. Молекулы разделяются, поскольку каждая стремится удалиться от другой. Постоянное повышение температуры может привести к плавлению твердого тела и переходу его в жидкое состояние. Точно так же жидкость может изменить свое состояние и в конце концов превратиться в газ. Запасенная энергия, которая используется для движения молекул внутри вещества, повышается при температуре, поскольку его вибрационное движение продолжает расти.
Точно так же жидкость может изменить свое состояние и в конце концов превратиться в газ. Запасенная энергия, которая используется для движения молекул внутри вещества, повышается при температуре, поскольку его вибрационное движение продолжает расти.
Что такое абсолютный нуль температуры?
Самый простой способ определить температуру абсолютного нуля — это указать ее как самую низкую возможную температуру, которую можно найти на Земле. Для его определения принято использовать шкалу Кельвина. Абсолютная температура стоит на нуле по этой шкале. Вы можете уточнить его, переведя в -273 градуса по Цельсию или -460 градусов по Фаренгейту. Абсолютная температура также не поддерживает никакого тепла.
Все микроскопические частицы в идеальном кристалле останутся неподвижными при этой температуре. Идея действительно кажется фантастической, и многим трудно поверить в эту теорию из-за отсутствия практических доказательств. Однако абсолютный ноль или абсолютная температура теоретически существуют. Ученые, работающие над температурой термодинамики, пытались достичь абсолютного нуля. Результаты пока неубедительны. Внедрение криокулеров, а также рефрижераторов разбавления привело к тому, что в настоящее время температура близка к нулю.
Ученые, работающие над температурой термодинамики, пытались достичь абсолютного нуля. Результаты пока неубедительны. Внедрение криокулеров, а также рефрижераторов разбавления привело к тому, что в настоящее время температура близка к нулю.
Как измеряется абсолютная температура?
Абсолютная температура обозначается как К, для ее измерения используется шкала Кельвина. Показания шкалы начинаются с отметки -273,15 °C, что соответствует абсолютному нулю. На данный момент температура не имеет практического применения, но ученые используют ее для изучения законов термодинамики и подтверждения свойств, обнаруживаемых идеальными газами. Вы также можете использовать шкалу Ренкина в качестве альтернативы шкале Кельвина. Он используется редко, поскольку на сегодняшний день предпочтительным стандартом для измерения абсолютного нуля является Кельвин. Интересно отметить тот факт, что соотношение между двумя абсолютными температурами, рассчитанными по двум разным шкалам, остается одинаковым независимо от типа используемой шкалы.
Вы можете пойти дальше и изучить этот аспект температуры более подробно, ознакомившись с определением этого стандарта, приведенным в формуле распределения Максвелла–Больцмана. Вы также найдете ссылки, упомянутые в статистике Ферми-Дирака и статистике Бозе-Эйнштейна. Единица kT, используемая вместе с числами, представляет постоянную Больцмана (k) и температуру (T).
Температурные шкалы
В настоящее время для измерения температуры используются три основные шкалы. Кельвин используется для измерения абсолютной температуры с абсолютным нулем, равным нулю на шкале. Вы найдете несколько других менее известных весов, используемых для различных целей. Среди них выделяются: —
- Ноль на шкале Ренкина равен абсолютному нулю, как и на шкале Кельвина. Разница температур в 1 градус Ренкина равна 1 градусу F
- Шкала Делиля имеет обратную зависимость. Более высокие градусы холоднее, а более низкие температуры теплее
Вы сможете понять, как работает каждая шкала, взглянув на сравнительную таблицу ниже:-

 ⓘ Тепло из высокотемпературного резервуара [QHigh]
ⓘ Тепло из высокотемпературного резервуара [QHigh] ⓘ Абсолютная температура [Tabs]
ⓘ Абсолютная температура [Tabs]
 00
00 9839
9839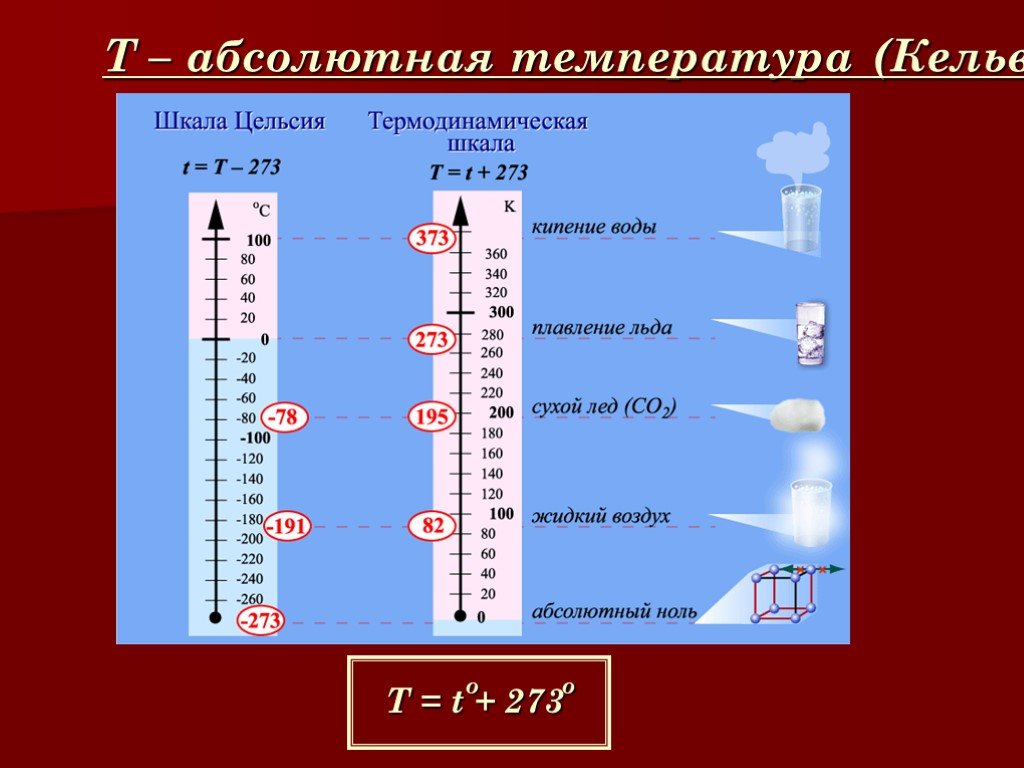
 Таким образом, должна существовать некоторая функция эмпирической температуры, которую можно определить независимо от материала. Эта температура называется абсолютной температурой. Обратите внимание, что, поскольку \(Q_1 < Q_2\), мы имеем \(|f(θ_1)| < |f(θ_2)|\), если \(θ_1 < θ_2\). Таким образом, \(|f|\) должна быть возрастающей функцией эмпирической температуры. Далее, мы не можем иметь \(f(θ_1) = 0\) для некоторой температуры \(θ_1\). Для этого потребуется \(Q_1 = 0\). Соответствующий двигатель будет брать некоторое количество тепла \(Q_2\) из более горячего резервуара и полностью преобразовывать его в работу, что противоречит утверждению Кельвина. Это означает, что мы должны считать f либо всегда положительным, либо всегда отрицательным для всех \(0\). Обычно мы принимаем это как положительное. Конкретный вид функции определяет шкалу температуры. Самый простой — взять линейную функцию эмпирических температур (как это определено обычными термометрами). Сегодня мы принимаем это за
Таким образом, должна существовать некоторая функция эмпирической температуры, которую можно определить независимо от материала. Эта температура называется абсолютной температурой. Обратите внимание, что, поскольку \(Q_1 < Q_2\), мы имеем \(|f(θ_1)| < |f(θ_2)|\), если \(θ_1 < θ_2\). Таким образом, \(|f|\) должна быть возрастающей функцией эмпирической температуры. Далее, мы не можем иметь \(f(θ_1) = 0\) для некоторой температуры \(θ_1\). Для этого потребуется \(Q_1 = 0\). Соответствующий двигатель будет брать некоторое количество тепла \(Q_2\) из более горячего резервуара и полностью преобразовывать его в работу, что противоречит утверждению Кельвина. Это означает, что мы должны считать f либо всегда положительным, либо всегда отрицательным для всех \(0\). Обычно мы принимаем это как положительное. Конкретный вид функции определяет шкалу температуры. Самый простой — взять линейную функцию эмпирических температур (как это определено обычными термометрами). Сегодня мы принимаем это за
 Если делать такие деления все тоньше и тоньше, ошибка аппроксимации цикла серией замкнутых циклов Карно будет стремиться к нулю по мере того, как число циклов Карно стремится к бесконечности. Поскольку вдоль адиабатики изменение \(Q\) равно нулю, мы можем использовать результат из уравнения \ref{3.4.11} выше, чтобы написать
Если делать такие деления все тоньше и тоньше, ошибка аппроксимации цикла серией замкнутых циклов Карно будет стремиться к нулю по мере того, как число циклов Карно стремится к бесконечности. Поскольку вдоль адиабатики изменение \(Q\) равно нулю, мы можем использовать результат из уравнения \ref{3.4.11} выше, чтобы написать Это функция состояния, заданная в терминах термодинамических переменных.
Это функция состояния, заданная в терминах термодинамических переменных. Для последнего шага \(dQ_{rev} = T dS\). Таким образом, комбинация поглощает количество тепла, равное \(dQ_{irr} -T dS\) без изменения состояния. Если это положительно, это должно быть полностью преобразовано в работу. Однако это нарушило бы второй закон. Следовательно, у нас должно быть
Для последнего шага \(dQ_{rev} = T dS\). Таким образом, комбинация поглощает количество тепла, равное \(dQ_{irr} -T dS\) без изменения состояния. Если это положительно, это должно быть полностью преобразовано в работу. Однако это нарушило бы второй закон. Следовательно, у нас должно быть Для любого процесса мы можем сказать, что
Для любого процесса мы можем сказать, что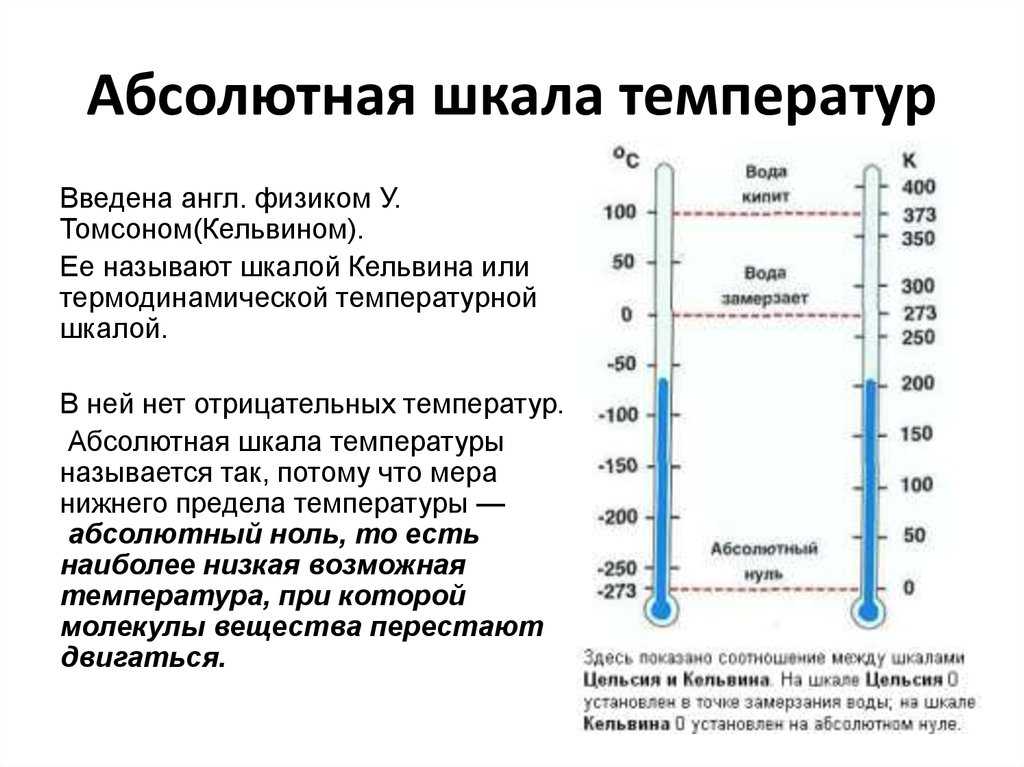 д.
д.