Абсолютная термодинамическая шкала: Абсолютная термодинамическая температура | это… Что такое Абсолютная термодинамическая температура?

Температура и ее измерение. Абсолютный нуль температуры. Термодинамическая шкала температур.

Температу́ра (от лат. temperatura — надлежащее смешение, нормальное состояние) — скалярная физическая величина, характеризующая приходящуюся на одну степень свободы среднюю кинетическую энергию частиц макроскопической системы, находящейся в состояниитермодинамического равновесия.

В Международной системе единиц (СИ) термодинамическая температура входит в состав семи основных единиц и выражается в кельвинах. В состав производных величин СИ, имеющих специальное название, входит температура Цельсия, измеряемая в градусах Цельсия^[1]. На практике часто применяют градусы Цельсия из-за исторической привязки к важным характеристикам воды — температуре таяния льда (0 °C) и температуре кипения (100 °C). Это удобно, так как большинство климатических процессов, процессов в живой природе и т.  д. связаны с этим диапазоном

Абсолю́тный нуль температу́ры (реже — абсолютный ноль температуры) — минимальный предел температуры, которую может иметь физическое тело. Абсолютный нуль служит началом отсчёта абсолютной температурной шкалы, например, шкалы Кельвина. В 1954 X Генеральная конференция по мерам и весам установила термодинамическую температурную шкалу с одной реперной точкой — тройной точкой воды, температура которой принята 273,16 К (точно), что соответствует 0,01 °C, так что по шкалеЦельсия абсолютному нулю соответствует температура −273,15 °C ^[1].

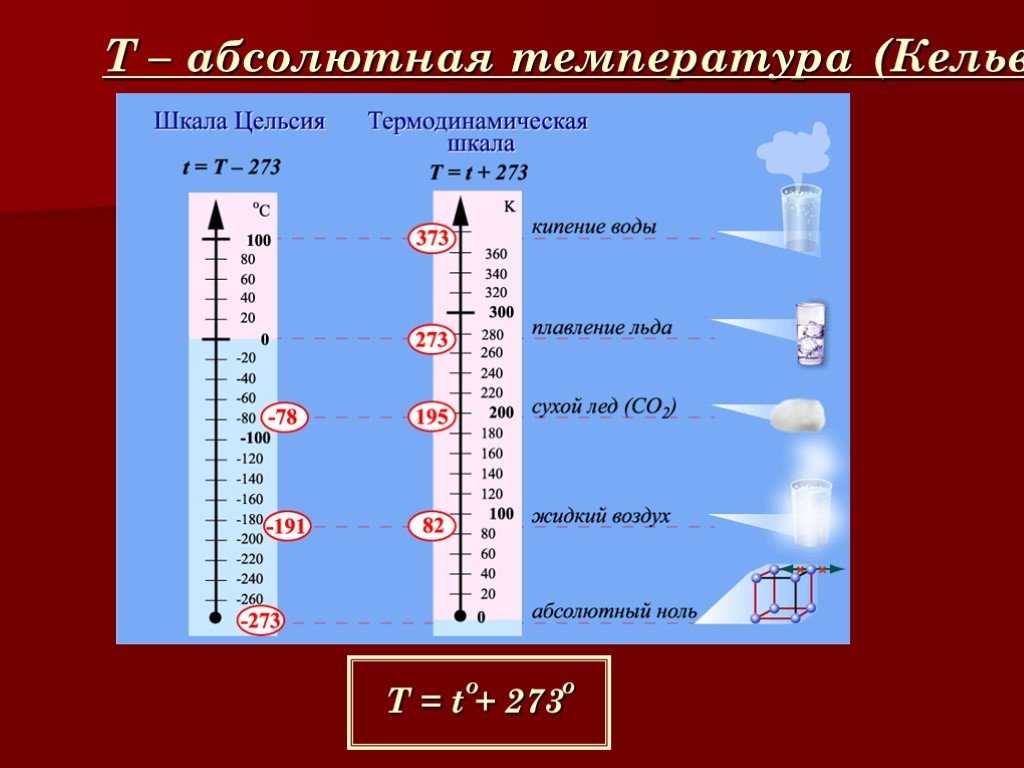
В рамках применимости термодинамики абсолютный нуль на практике недостижим. Его существование и положение на температурной шкале следует из экстраполяции наблюдаемых физических явлений, при этом такая экстраполяция показывает, что при абсолютном нуле энергия теплового движения молекул и атомов вещества должна быть равна нулю, то есть хаотическое движение частиц прекращается, и они образуют упорядоченную структуру, занимая чёткое положение в узлах 

кристаллической решётки (жидкий гелийсоставляет исключение)

ТЕРМОДИНАМИЧЕСКАЯ ТЕМПЕРАТУРНАЯ шкала(Кельвина шкала) — абсолютная шкала температур, не зависящая от свойств термометрического вещества (началоотсчета — абсолютный нуль температуры). Построение термодинамической температурной шкалы основано на втором начале термодинамики и, в частности, на независимости кпд Карно цикла от природы рабочего тела.Единица термодинамической температуры — кельвин (К) — определяется как 1/273,16 часть термодинамической температуры тройной точки воды.

По значению удельного электрического сопротивления полупроводникизанимают промежуточное место между хорошими проводниками и диэлектриками. К числу полупроводников относятся многие химические элементы (германий, кремний, селен, теллур, мышьяк и др.), огромное количество сплавов и химических соединений. Почти все неорганические вещества окружающего нас мира – полупроводники. Самым распространенным в природе полупроводником является кремний, составляющий около 30 % земной коры. Качественное отличие полупроводников от металлов проявляется прежде всего в зависимости удельного сопротивления от температуры. С понижением температуры сопротивление металлов падает (см.

 рис. 4.12.4). У полупроводников, напротив, с понижением температуры сопротивление возрастает и вблизи абсолютного нуля они практически становятся изоляторами (рис. 4.13.1).

Билет №15

29. Газовые законы. Уравнение состояния идеального газа. Молярная газовая постоянная.

Уравнение состояния

 идеального газа (иногда уравнениеКлапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением,молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

где  — давление,  — молярный объём,  — универсальная газовая постоянная  — абсолютная температура,К.

•    2. Молярная газовая постоянная. Для одного моля любого газа при нормальных условиях имеем:        p = 1 атм = 1,013·10⁵ Па,        V = 22,4 л = 0,0224 м³,        t = 0°C или T = 273 К. Вычислим произведение давления на объем, деленное на температуру:                  Полученное значение, отнесенное к одному молю, называется 

  молярной газовой постоянной:          Установим ее связь с другими константами.         Запишем уравнение Клапейрона:  Для одного моля вещества количество молекул равно числу Авогадро, а объем, занимаемый газом при нормальных условиях, равен молярному объему, тогда можно записать:  Но в левой части стоит величина, равная молярной газовой постоянной, поэтому:   

30. Электрическая проводимость полупроводников. Полупроводниковые приборы.

Полупроводники — это вещества, удельное сопротивление которых убывает с повышением температуры, наличием примесей, изменением освещенности. По этим свойствам они разительно отличаются от металлов. Обычно к полупроводникам относятся кристаллы, в которых для освобождения электрона требуется энергия не более 1,5—2 эВ. Типичными полупроводниками являются кристаллы германия и кремния, в которых атомы объединены ковалентной связью.

 

При температуре, близкой к абсолютному нулю, полупроводник ведет себя как абсолютный непроводник, потому что в нем нет свободных электронов. Если повышения температуры нет, связь валентных электронов с атомными ядрами ослабевает и некоторые из них вследствие теплового движения могут покидать свои атомы. Вырвавшийся из межатомной связи электрон становится свободным (на рис. 1, б — черная точка), а там, где он был до этого, образуется пустое место. Это пустое место в межатомной связи полупроводника условно называют дыркой (на рис. 1 ,б — разорвавшаяся линия электрона). Чем выше температура полупроводника, тем больше в нем появляется свободных электронов и дырок. Таким образом, образование в массе полупроводника дырки связано с уходом из оболочки атома валентного электрона, а возникновение дырки соответствует появлению положительного электрического заряда, равного отрицательному заряду электрона.

Билет №16

31. Температура – мера средней кинетической энергии хаотического движения молекул.

32. Магнитное поле, особый вид материи.

Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающиемагнитным моментом, независимо от состояния их движения^[1], магнитная составляющая электромагнитного поля^[2]

Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты).

Магнитное поле можно назвать особым видом материи^[7], посредством которого осуществляется взаимодействие между движущимися заряженными частицами или телами, обладающими

магнитным моментом.

Магнитные поля являются необходимым (в контексте специальной теории относительности) следствием существования электрических полей.

Вместе, магнитное и электрическое поля образуют электромагнитное поле, проявлениями которого являются, в частности, свет и все другие электромагнитные волны.

Билет №17

Термодинамическая шкала температур

Еще в 1848 г. В. Томсон отметил, что теоремой Карно можно воспользоваться, чтобы построить рациональную температурную шкалу, которая не зависит от особенностей термометрического вещества и устройства термометра.

Поэтому прежде чем перейти непосредственно к рассмотрению термодинамической шкалы температур, сформулируем теорему, которая называется теоремой Карно:

Здесь надо подчеркнуть, что речь идет не о том, что все обратимые машины имеют равный КПД, а о том, что все обратимые машины, работающие по циклу Карно, имеют равный КПД при одних и тех же заданных температурах нагревателя и холодильника. Мы эту теорему доказывать не будем, так как доказательство довольно простое и встречается во всех учебниках по термодинамике. Кроме того, в предыдущих главах была получена формула для расчета КПД цикла Карно, при выводе которой не делалось никаких ограничений по веществу рабочего тела и по конструкции теплового двигателя, при этом мы получили, что КПД цикла Карно зависит только от температур нагревателя и холодильника.

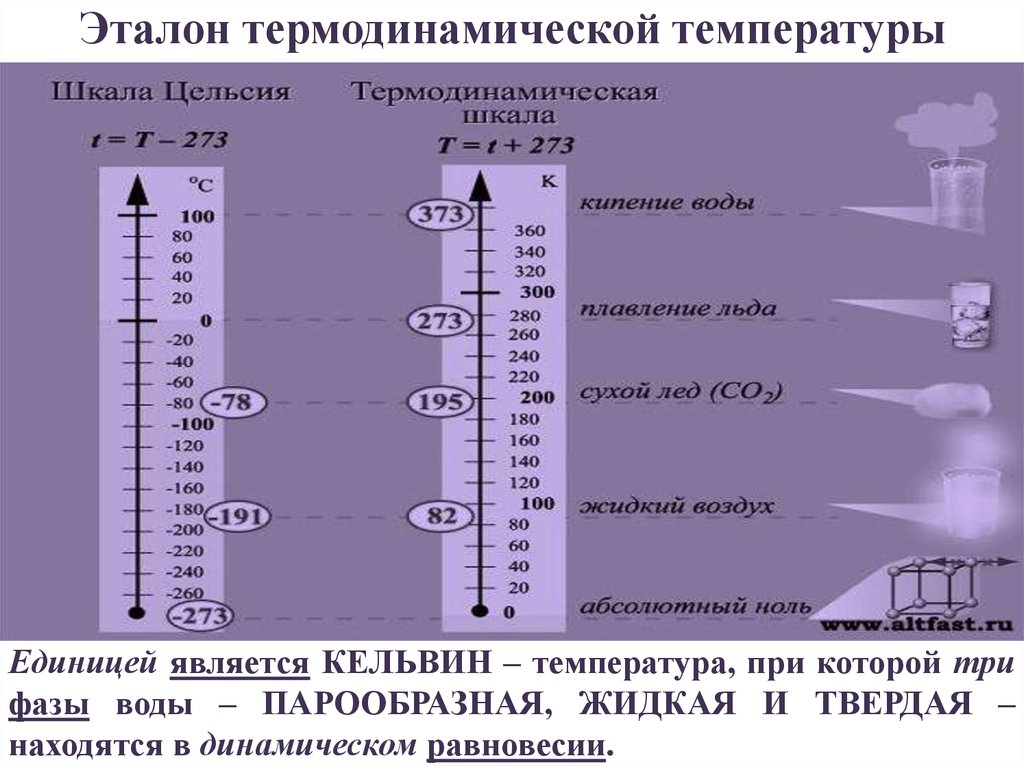
КПД ($\eta $) тепловой машины можно рассчитать по формуле:

\[\eta =1-\frac{Q_{ch}}{Q_n}\ \left(1\right),\]

где $Q_n$ — количество теплоты, полученное рабочим телом от нагревателя, $Q_{ch}$- количество теплоты, отданное рабочим телом холодильнику. Так как $\eta $ имеет одинаковые значения для всех тепловых машин, работающих по обратимому циклу Карно с температурой нагревателя и температурой холодильника. Обозначим временно величины этих температур ${\theta }_1\ и\ {\theta }_2,$ то для отношение $\frac{Q_{ch}}{Q_n}$ можно записать:

\[\frac{Q_{ch}}{Q_n}=f\left({\theta }_1\ ,\ {\theta }_2\right)\left(2\right),\]

где $f\left({\theta }_1\ ,\ {\theta }_2\right)$ — функция температур холодильника и нагревателя, универсальная для всех циклов Карно. Покажем, что $f\left({\theta }_1\ ,\ {\theta }_2\right)$ можно представить в виде:

\[f\left({\theta }_1\ ,\ {\theta }_2\right)=\frac{\varphi \left({\theta }_1\right)}{\varphi \left({\theta }_2\right)}\ \left(3\right),\]

где $\varphi \left(\theta \right)$ — универсальная функция от температуры.

Рассмотрим две обратимые машины (рис.1). Холодильник одной машины — нагреватель для другой. Допустим, что вторая машина отбирает от нагревателя с температурой ${\theta }_2$- столько тепла, сколько отдает ему первая машина (${Qch}_2={Qn}_2$). Исходя из (2), для каждой машины запишем:

\[\frac{Q_{ch3}}{Q_{n1}}=f\left({\theta }_1\ ,\ {\theta }_2\right)\left(4\right),\] \[\frac{Q_{ch4}}{Q_{ch3}}=f\left({\theta }_2\ ,\ {\theta }_3\right)\left(5\right).\]

Если рассмотреть машину на рис.1 как единую с тепловым резервуаром температуры (${\theta }_1$) и холодильником с температурой (${\theta }_3$), то получим:

\[\frac{Q_{ch4}}{Q_{n1}}=f\left({\theta }_1\ ,\ {\theta }_3\right)\left(6\right).\]

Рис. 1

Разделим (6) на (4), имеем:

\[\frac{Q_{ch4}}{Q_{ch3}}=\frac{f\left({\theta }_1\ ,\ {\theta }_3\right)}{f\left({\theta }_1\ ,\ {\theta }_2\right)}=\frac{Q_{n2}}{Q_{ch3}}\left(7\right). \]

Сравниваем (7) и (5), получаем:

\[f\left({\theta }_2\ ,\ {\theta }_3\right)=\frac{f\left({\theta }_1\ ,\ {\theta }_3\right)}{f\left({\theta }_1\ ,\ {\theta }_2\right)}\ \left(8\right).\]

Уравнение (8) связывает температуры, связывает все температуры${\ \theta }_1\ ,\ {\theta }_2,\ {\theta }_3.$ Решим, что ${\ \theta }_1$ постоянна, получим, что функция $f\left({\theta }_1\ ,\ \theta \right)$ — функция одной переменной $\theta $. Обозначим эту функцию $\varphi (\theta )$, тогда уравнение (8) примет вид:

\[f\left({\theta }_2\ ,\ {\theta }_3\right)=\frac{\varphi \left({\theta }_3\ \right)}{\varphi \left({\theta }_2\ \right)}\ \left(9\right),\]

или

\[f\left({\theta }_1\ ,\ {\theta }_2\right)=\frac{\varphi \left({\theta }_2\ \right)}{\varphi \left({\theta }_1\ \right)}\ \left(10\right),\]

Что совпадает с тем, что мы хотели доказать, то есть с выражением (3).

Функция $\varphi \left(\theta \ \right)$ зависит только от температуры. Поэтому ее значение можно использовать для характеристики температуры соответствующего тела, то есть полагать температуру равной $\varphi $, где $\varphi =\varphi \left(\theta \ \right).$ В таком случае уравнение (4) примет вид:

\[\frac{Q_{ch3}}{Q_{n1}}=\frac{{\varphi }_2}{{\varphi }_1}\ \left(11\right).\]

Соотношение (11) ложится в основу термодинамической шкалы температур. Ее преимущество — независимость от выбора рабочего тела в цикле Карно, которое используют для измерения температуры.

Величину $\varphi $ принимают за меру температуры тела и называют абсолютной термодинамической температурой. В примерах мы покажем, что она совпадает с используемой нами ранее с абсолютной температурой T по шкале идеального газового термометра. В выражении (11) мы видим отношение двух термодинамических температур. Чтобы определить температуру одного тела можно:

Абсолютная термодинамическая температура не может быть отрицательной.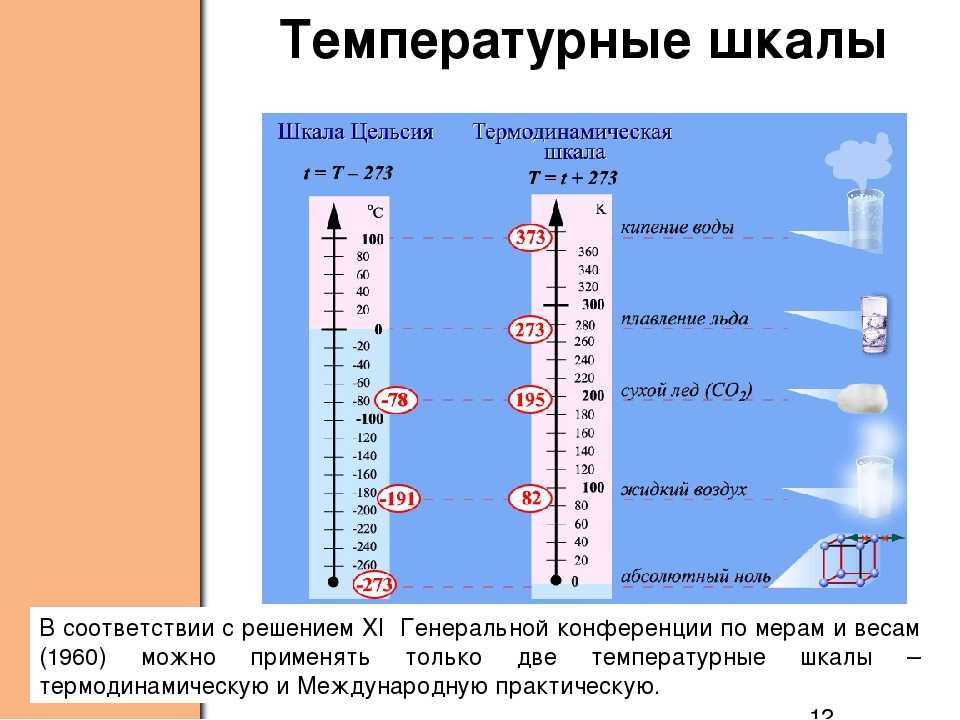 Самая низкая температура, которую допускает второе начало термодинамики: T=0K. Абсолютная термодинамическая шкала температур тождественна с абсолютной шкалой.

температура — Разница между абсолютной термодинамической шкалой и ИТС-90

спросил 8 лет, 3 месяца назад

Изменено 8 лет, 2 месяца назад

Просмотрено 2к раз

$\begingroup$

Чем отличается абсолютная термодинамическая шкала температур от практической температурной шкалы: ИТС-90?

• температура

$\endgroup$

$\begingroup$

Абсолютная термодинамическая шкала температур — это шкала, фиксируемая абсолютным нулем и (по крайней мере, для кельвинов, я не уверен насчет шкалы Ренкина) тройной точкой воды, где абсолютный ноль определяется как 0 К, а тройная точка воды определяется как 273,16 К.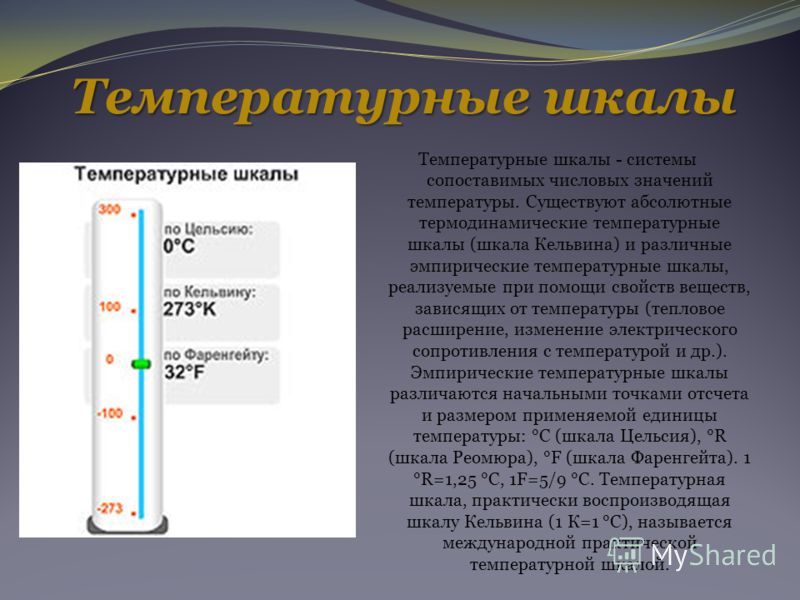 Остальная часть шкалы представляет собой прямую линию от нуля до 273,16 К до бесконечности. Однако эта шкала опирается только на две определенные точки (только одна из которых может быть фактически измерена, а абсолютный нуль устанавливается из термодинамических соотношений).

При практическом использовании, для целей калибровки термометров и т.п., это не очень большой масштаб, поскольку две точки калибровки могут находиться далеко от области температур, которую нужно измерить. Обычный способ справиться с этим — использовать другие контрольные точки вне фактического определения. Чтобы разные люди делали это максимально последовательно, ИТС-90 создавался как практическая реализация абсолютной шкалы, задающая дополнительные опорные точки (все фазовые переходы) на определенные значения, интерполируя между ними для получения других значений. Технически это не шкала сама по себе, а просто стандарт для калибровки температур, максимально приближенных к абсолютной шкале. Убедившись, что все используют одни и те же опорные точки, измерения могут быть более последовательными, чем если бы опорные точки выбирались произвольно и, возможно, им присваивались разные значения.

Например, если кто-то хочет сделать термометр для общего лабораторного использования, можно выбрать тройную точку ртути, тройную точку воды и точку плавления галлия из стандарта ITS-90 в качестве эталонных точек, зная, что другие термометры в этом диапазоне, соответствующие стандарту, также будут откалиброваны таким образом, вместо того, чтобы выбирать, скажем, точки плавления и кипения воды, что увеличивает вероятность согласованных измерений с другими термометрами.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Определение термодинамической температуры в физике.

(существительное)

Температура определяется в терминах законов термодинамики, а не свойств реального материала: выражается в кельвинах.

• Обзор нулевого закона

  • Нулевой закон оправдывает использование термодинамической температуры , определяемой как общая температура трех указанных систем, находящихся в равновесии.
  • Этот вывод может показаться очевидным, потому что все три имеют одинаковую температуру , но нулевой закон лежит в основе термодинамики .
  • Нулевой закон оправдывает использование термодинамической температуры : общая «метка», которую разделяют три системы в приведенном выше определении, определяется как температура систем.
  • Термометры на самом деле измеряют свою температуру , а не температуру объекта, который они измеряют.
  • Обсудите, как работает нулевой закон термодинамики оправдывает использование термодинамического температурного

• Абсолютная температура

  • Абсолютная температура является наиболее часто используемой термодинамической температурной единицей и является стандартной единицей температуры .
  • Термодинамический температура является абсолютной мерой температуры .
  • Это один из основных параметров термодинамики и кинетическая теория газов.
  • Термодинамическая температура является «абсолютной» шкалой, поскольку она является мерой фундаментального свойства, лежащего в основе температуры : ее нуль или нулевая точка («абсолютный ноль») — это температура , при которой частицы составляют материю иметь минимальное движение и не может стать холоднее.
  • Используя шкалу абсолютной температуры (система Кельвина), которая является наиболее часто используемой термодинамическая температура , мы показали, что средняя поступательная кинетическая энергия (КЭ) частицы в газе имеет простую зависимость от температуры :

• Шкала Кельвина

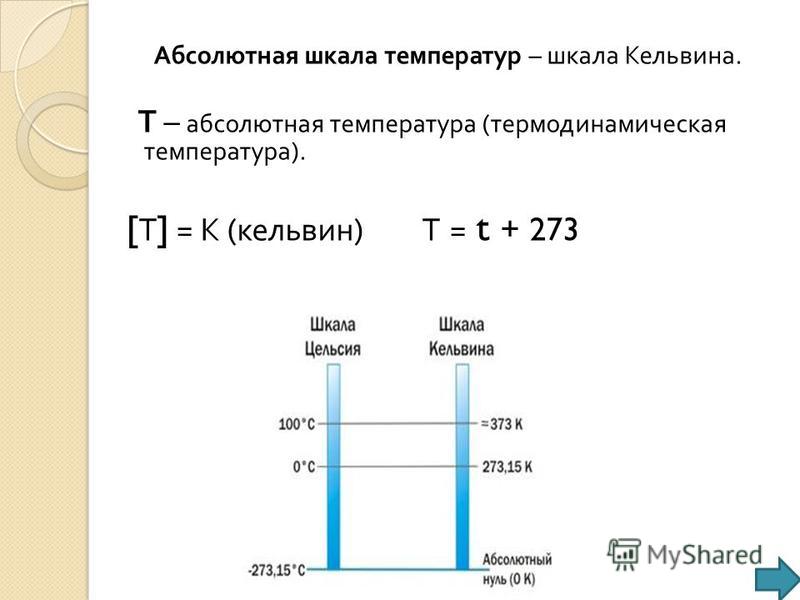
  • Кельвин — единица измерения температуры ; нулевой точкой шкалы Кельвина является абсолютный ноль, самая низкая возможная температура .
  • Шкала Кельвина является абсолютной, термодинамической температура шкала с использованием абсолютного нуля в качестве нулевой точки.
  • В классическом описании термодинамики абсолютным нулем является температура , при которой прекращается всякое тепловое движение.
  • Кельвин определяется как доля 1/273,16 от термодинамической температуры тройной точки воды (ровно 0,01°C или 32,018°F).
  • Краткое введение в температура и температура 9Весы 0067 для студентов, изучающих теплофизику или термодинамику .

• Абсолютный ноль

  • Абсолютный ноль — самая холодная возможная температура ; формально это температура , при которой энтропия достигает минимального значения.
  • Абсолютный ноль — это самая холодная возможная температура .
  • Однако в интерпретации классической термодинамики кинетическая энергия может быть равна нулю, а тепловая энергия вещества обращается в нуль.
  • Нулевая точка термодинамической температурной шкалы, такой как шкала Кельвина, устанавливается на абсолютный ноль.
  • Краткое введение в температурные и температурные весы для студентов, изучающих теплофизику или термодинамику .

• Нулевой закон термодинамики

  • Нулевой закон термодинамики утверждает, что системы, находящиеся в тепловом равновесии, находятся в одном и том же температура .
  • Есть несколько способов сформулировать Нулевой Закон Термодинамики , но самый простой из них следующий: системы, находящиеся в тепловом равновесии, существуют при одной и той же температуре .
  • Нулевой закон термодинамики означает, что температуру стоит измерять, потому что она показывает, будет ли тепло перемещаться между объектами.
  • Температура не упоминается явно, но подразумевается, что температура существует.
  • Системы A, B и C имеют одинаковую температуру .

• Шкала Цельсия

  • Цельсий или градус Цельсия — это шкала и единица измерения температуры .
  • Это один из наиболее часто используемых температурных блоков .
  • Это определение также точно связывает шкалу Цельсия со шкалой Кельвина, которая определяет базовую единицу СИ термодинамического температура и который использует символ K.
  • Помимо выражения конкретных температур по шкале (например, «Галлий плавится при 29,7646 ° C» и « температура снаружи составляет 23 градуса Цельсия»), градус Цельсия также подходит для выражения температурных интервалов — различий между температурами или их неопределенностями (например,
  • Краткое введение в температура и температура 9Весы 0067 для студентов, изучающих теплофизику или термодинамику .

• Изотермические процессы

  • Изотермический процесс представляет собой изменение термодинамической системы, при котором температура остается постоянной.
  • Изотермический процесс – это изменение системы, при котором температура остается постоянной: ΔT = 0,
  • В термодинамике работа, необходимая для перехода газа из состояния A в состояние B, равна просто
  • Также стоит отметить, что для многих систем, если температура поддерживается постоянной, внутренняя энергия системы также постоянна, и поэтому $\Delta U = 0$.
  • Из первого начала термодинамики следует, что $Q =-W$ для этого самого изотермического процесса.

• Второй закон

  • Второй закон термодинамики гласит, что теплопередача происходит самопроизвольно только от высших к низшим температура тел.
  • Второй закон термодинамики касается направления самопроизвольных процессов.
  • Например, теплота включает передачу энергии от более высокой к более низкой температуре .
  • Закон, запрещающий эти процессы, называется вторым законом термодинамики .
  • Второй закон термодинамики (первое выражение): Теплопередача происходит самопроизвольно от более высоких к более низким температуры тела но никогда самопроизвольно в обратном направлении.

• Термодинамика

  • Черное тело, конечно, характеризуется одной температурой , $T$.
  • Обычно используются три характеристики температуры : яркость температура , эффективная температура и цвет температура .
  • Яркость температура определяется путем приравнивания яркости или интенсивности астрофизического источника к интенсивности черного тела и решения для температура соответствующего черного тела.
  • В каком режиме начинает нарушаться линейная зависимость между яркостью температурой и интенсивностью?
  • Наконец, эффективная температура — это температура абсолютно черного тела, которое излучает на своей поверхности тот же поток, что и источник, т.