Глава 15. Работа газа в циклическом процессе. Тепловые двигатели. Цикл Карно
В программу школьного курса физики входит ряд вопросов, связанных с тепловыми двигателями. Школьник должен знать основные принципы работы теплового двигателя, понимать определение коэффициента полезного действия (КПД) циклического процесса, уметь находить эту величину в простейших случаях, знать, что такое цикл Карно и его КПД.
Тепловым двигателем (или тепловой машиной) называется процесс, в результате которого внутренняя энергия какого-то тела превращается в механическую работу. Тело, внутренняя энергия которого превращается двигателем в работу, называется нагревателем двигателя. Механическая работа в тепловых машинах совершается газом, который принято называть рабочим телом (или рабочим веществом) тепловой машины. При расширении рабочее тело и совершает полезную работу.
Для того чтобы сделать процесс работы двигателя циклическим, необходимо еще одно тело, температура которого меньше температуры нагревателя и которое называется холодильником двигателя.
зависимости давления от объема, причем со знаком «плюс», если цикл проходится по часовой стрелке, и «минус» — если против.
Таким образом, двигатель превращает в механическую работу не всю энергию, взятую у нагревателя, а только ее часть; остальная часть этой энергии используется не для совершения работы, а передается холодильнику, т.е. фактически теряется для совершения работы. Поэтому величиной, характеризующей эффективность работы двигателя, является отношение
(15.1) |
где — работа, совершаемая газом в течение цикла, — количество теплоты, полученное газом от нагревателя за цикл. Отношение (15.1) показывает, какую часть количества теплоты, полученного у нагревателя, двигатель превращает в работу и называется коэффициентом полезного действия (КПД) двигателя.
Если в течение цикла рабочее тело двигателя отдает холодильнику количество теплоты (эта величина по своему смыслу положительна), то для работы газа справедливо соотношение . Поэтому существует ряд других форм записи формулы (15.1) для КПД двигателя
(15. |
Французский физик и инженер С. Карно доказал, что максимальным КПД среди всех процессов, использующих некоторое тело с температурой в качестве нагревателя, и некоторое другое тело с температурой ( ) в качестве холодильника, обладает процесс, состоящий из двух изотерм (при температурах нагревателя и холодильника ) и двух адиабат (см. рисунок).
Изотермам на графике отвечают участки графика 1-2 (при температуре нагревателя ) и 3-4 (при температуре холодильника ), адиабатам — участки графика 2-3 и 4-1. Этот процесс называется циклом Карно. КПД цикла Карно равен
(15.3) |
Теперь рассмотрим задачи. В задаче 15.1.1 необходимо использовать то обстоятельство, что работа газа в циклическом процессе численно равна площади цикла на графике зависимости давления от объема, причем со знаком «плюс», если цикл проходится по часовой стрелке, и «минус» — если против. Поэтому во втором цикле работа газа положительна, в третьем отрицательна. Первый цикл состоит из двух циклов, один из которых проходится по, второй — против часовой стрелки, причем, как следует из графика 1, площади этих циклов равны. Поэтому работа газа за цикл в процессе 1 равна нулю (правильный ответ — 2).
Поэтому во втором цикле работа газа положительна, в третьем отрицательна. Первый цикл состоит из двух циклов, один из которых проходится по, второй — против часовой стрелки, причем, как следует из графика 1, площади этих циклов равны. Поэтому работа газа за цикл в процессе 1 равна нулю (правильный ответ — 2).
Поскольку в результате совершения циклического процесса газ возвращается в первоначальное состояние (
Применяя в задаче 15.1.3 первый закон термодинамики ко всему циклическому процессу и учитывая, что изменение внутренней энергии газа равно нулю (см. предыдущую задачу), заключаем, что (ответ 3).
Поскольку работа газа численно равна площади цикла на диаграмме «давление-объем», то работа газа в процессе в задаче 15.1.4 равна (ответ 1). Аналогично в задаче 15.1.5 газ за цикл совершает работу (ответ 1).
Работа газа в любом процессе равна сумме работ на отдельных участках процесса. Поскольку процесс 2-3 в задаче 15.1.6 — изохорический, то работа газа в этом процессе равна нулю. Поэтому (ответ 3).
Поскольку процесс 2-3 в задаче 15.1.6 — изохорический, то работа газа в этом процессе равна нулю. Поэтому (ответ 3).
По определению КПД показывает, какую часть количества теплоты, полученного у нагревателя, двигатель превращает в работу ( задача 15.1.7 — ответ 4).
Работа двигателя за цикл равна разности количеств теплоты, полученного от нагревателя и отданного холодильнику : . Поэтому КПД цикла есть
(задача 15.1.8 — ответ 3).
По формуле (15.3) находим КПД цикла Карно в задаче 15.1.9
(ответ 2).
Пусть температура нагревателя первоначального цикла Карно равна , температура холодильника (задача 15.1.10). Тогда по формуле (15.3) для КПД первоначального цикла имеем
Отсюда находим . Поэтому для КПД нового цикла Карно получаем
Поэтому для КПД нового цикла Карно получаем
(ответ 2).
В задаче 15.2.1 формулы (2), (3) и (4) представляют собой разные варианты записи определения КПД теплового двигателя (см. формулы (15.1) и (15.2)). Поэтому не определяет КПД двигателя только формула 1. (ответ 1).
Мощностью двигателя называется работа, совершенная двигателем в единицу времени. Поскольку работа двигателя равна разности полученного от нагревателя и отданного холодильнику количеств теплоты, имеем для мощности двигателя в задаче 15.2.2
(ответ 3).
По формуле (15.2) имеем для КПД двигателя в задаче 15.2.3
где — количество теплоты, полученное от нагревателя, — количество теплоты, отданное холодильнику (правильный ответ — 2).
Для нахождения КПД теплового двигателя в задаче 15.2.4 удобно использовать последнюю из формул (15.2). Имеем
где — работа газа, — количество теплоты, отданное холодильнику. Поэтому правильный ответ в задаче — 3.
Пусть газ совершает за цикл работу (задача 15.2.5). Поскольку количество теплоты, полученное от нагревателя равно ( — количество теплоты, отданное холодильнику), и работа составляет 20 % от этой величины, то для работы справедливо соотношение = 0,2 ( + 100). Отсюда находим = 25 Дж (ответ 1).
Поскольку работа теплового двигателя в задаче 15.2.6 равна 100 Дж при КПД двигателя 25 %, то двигатель получает от нагревателя количество теплоты 400 Дж. Поэтому он отдает холодильнику 300 Дж теплоты в течение цикла (ответ
В задаче 15.2.7 газ получает или отдает теплоту только в процессах 1-2 и 3-1 (процесс 2-3 по условию адиабатический). |
Цикл, данный в задаче 15.2.8, состоит из двух изотерм 2-3 и 4-1 и двух изохор 1-2 и 3-4. Работа газа в изохорических процессах равна нулю. Сравним работы газа в изотермических процессах. Для этого удобно построить график зависимости давления от объема в рассматриваемом процессе, поскольку работа газа есть площадь под этим графиком. График зависимости давления от объема для заданного в условии процесса приведен на рисунке. Поскольку изотерме 2-3 соответствует бóльшая температура, чем изотерме 4-1, то она будет расположена выше на графике . Объем газа в процессе 2-3 увеличивается, в процессе 4-1 уменьшается. Таким образом, график процесса на графике проходится по часовой стрелке, и, следовательно, работа газа за цикл положительна (ответ 1). |
Для сравнения работ газа на различных участках процесса в задаче 15.2.9 построим график зависимости давления от объема. Этот график представлен на рисунке. Из рисунка следует, что работы газа в процессах 1-2 и 3-4 одинаковы по модулю (этим работам отвечают площади прямоугольников, «залитых» на рисунке светлой и темной «заливкой»). Работе газа на участке 4-1 отвечает площадь под графиком 4-1, которая меньше площади под графиком 1-2. Работе газа на участке 2-3 отвечает площадь под кривой 2-3 на рисунке, которая заведомо больше площади «залитых» прямоугольников. Поэтому в процессе 2-3 газ и совершает наибольшую по абсолютной величине (среди рассматриваемых процессов) работу (ответ
Согласно определению коэффициент полезного действия представляет отношение работы газа за цикл к количеству теплоты , полученному от нагревателя . Как следует из данного в условии задачи 15.2.10 графика, и в процессе 1-2-4-1 и в процессе 1-2-3-1 газ получает теплоту только на участке 1-2. Поэтому количество теплоты, полученное газом от нагревателя в процессах
1-2-4-1 и 1-2-3-1 одинаково. А вот работа газа в процессе 1-2-4-1 вдвое меньше (так площадь треугольника 1-2-4 как вдвое меньше площади треугольника 1-2-4-1). Поэтому коэффициент полезного действия процесса 1-2-4-1 вдвое меньше коэффициента полезного действия процесса 1-2-3-1 (ответ 1).
Поэтому количество теплоты, полученное газом от нагревателя в процессах
1-2-4-1 и 1-2-3-1 одинаково. А вот работа газа в процессе 1-2-4-1 вдвое меньше (так площадь треугольника 1-2-4 как вдвое меньше площади треугольника 1-2-4-1). Поэтому коэффициент полезного действия процесса 1-2-4-1 вдвое меньше коэффициента полезного действия процесса 1-2-3-1 (ответ 1).
Энергетическое образование
1. Общие сведения
Паровые машины. В середине XVII века были сделаны первые попытки перехода к машинному производству, потребовавшие создания двигателей, не зависящих от местных источников энергии (воды, ветра и пр.). Первым двигателем, в котором использовалось тепловая энергия химического топлива стала пароатмосферная машина, изготовленная по проектам французского физика Дени Папена и английского механика Томаса Севери. Эта машина была лишена возможности непосредственно служить механическим приводом, к ней «прилагалось в комплект» водяное мельничное колесо (по-современному говоря, водяная турбина), которое вращала вода, выжимаемая паром из котла паровой машины в резервуар водонапорной башни. Котел то подогревался паром, то охлаждался водой: машина действовала периодически.
Котел то подогревался паром, то охлаждался водой: машина действовала периодически.
В 1763 году русский механик Иван Иванович Ползунов изготовил по собственному проекту стационарную паровую машину непрерывного действия. В ней были сдвоены два цилиндра, поочерёдно заполнявшиеся паром, и также подающими воду на башню, но — постоянно.
К 1784 году английский механик Джеймс Уатт создал более совершенную паровую машину, названную универсальным паровым двигателем. Уатт с детства работал подручным на машине конструкции Севери. В его задачу входило постоянно переключать краны подачи пара и воды на котел. Эта однообразная работа изрядно надоела изобретателю и побудила изобрести как поршень двойного хода, так и автоматическую клапанную коробку (потом и центробежный предохранитель). В машине был предусмотрен в цилиндре жесткий поршень, по обе стороны которого поочередно подавался пар. Все происходило в автоматическом режиме и непрерывно. Поршень вращал через кривошипно—шатунную систему маховик, обеспечивающий плавность хода. Паровая машина могла теперь стать приводом различных механизмов и перестала быть привязана к водонапорной башне.
Паровая машина могла теперь стать приводом различных механизмов и перестала быть привязана к водонапорной башне.
Элементы, придуманные Уаттом, входили в той или иной форме во все паровые машины. Паровые машины совершенствовали и применяли для решения различных технических задач: привода станков, судов, экипажей для перевозки людей по дорогам, локомотивов на железных дорогах. К 1880 году суммарная мощность всех работавших паровых машин превысила 26 млн кВт (35 млн л.с.).
Локомотив.Цикл Карно — идеальный термодинамический цикл. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадают соответственно с максимальной и минимальной температурами цикла Карно. Цикл Карно назван в честь французского физика Сади Карно, который впервые его исследовал в 1824 году. Одним из важных свойств цикла Карно является его обратимость: он может быть проведён как в прямом, так и в обратном направлении, при этом энтропия адиабатически изолированной (без теплообмена с окружающей средой) системы не меняется.
В 1816 шотландец Роберт Стирлинг предложил двигатель внешнего сгорания, называемый сейчас его именем Двигатель Стирлинга. В этом двигателе рабочее тело (воздух или иной газ) заключен в герметичный объём. Здесь осуществлен цикл по типу цикла Севери («до-Уаттовского»), но нагрев рабочего тела и его охлаждение производятся в различных объёмах машины и сквозь стенки рабочих камер. Природа нагревателя и охладителя для цикла не имеют значения, а потому он может работать даже в космосе и от любого источника тепла. КПД созданных сейчас стирлингов невелик. Теоретически он должен раза в 2 превышать КПД для ДВС, а практически — это примерно одинаковые величины. Но у стирлингов есть ряд других преимуществ, которые способствовали развитию исследований в этом направлении.
Двигатели внешнего сгорания — класс двигателей, где источник тепла или процесс сгорания топлива отделены от рабочего тела. К этому классу относятся паровые машины, паровые турбины, двигатели Стирлинга, газовые турбины внешнего сгорания, а также другие типы двигателей. Долгое время были неоправданно забыты, в последнее время находят всё большее применение, в основном из-за таких своих особенностей как возможность использования любых источников тепла (например, солнечной или ядерной энергии), нетребовательность к виду топлива.
Долгое время были неоправданно забыты, в последнее время находят всё большее применение, в основном из-за таких своих особенностей как возможность использования любых источников тепла (например, солнечной или ядерной энергии), нетребовательность к виду топлива.
Двигатель внутреннего сгорания. Проект первого двигателя внутреннего сгорания (ДВС) принадлежит известному изобретателю часового анкера Христиану Гюйгенсу и предложен ещё в XVII веке. Интересно, что в качестве топлива предполагалось использовать порох, а сама идея была подсказана артиллерийским орудием. Все попытки Дениса Папена (упомянутого выше, как создатель первой паровой машины) построить машину на таком принципе, успехом не увенчались. Первый надёжно работавший ДВС сконструировал в 1860 году французский инженер Эжен Ленуар. Двигатель Ленуара работал на газовом топливе. Спустя 16 лет немецкий конструктор Николас Отто создал более совершенный 4-тактный газовый двигатель. В этом же 1876 году шотландский инженер Дугальд Кларк испытал первый удачный 2-тактный двигатель. Совершенствованием ДВС занимались многие инженеры и механики. Так, в 1883 году немецкий инженер Карл Бенц изготовил использованный им в дальнейшем 2-тактный ДВС. В 1897 году его соотечественник и тоже инженер Рудольф Дизель предложил ДВС с воспламенением рабочей смеси в цилиндре от сжатия воздуха, названный впоследствии дизелем. В XX веке ДВС стал основным двигателем в автомобильном транспорте. В 70-х годах почти 80 % суммарной мощности всех существовавших ДВС приходилось на транспортные машины (автомобили, трактора и пр.). Параллельно шло совершенствование гидротурбин, применявшихся на гидроэлектростанциях. Их мощность в 70-х годах XX века превысила 600 МВт.
Совершенствованием ДВС занимались многие инженеры и механики. Так, в 1883 году немецкий инженер Карл Бенц изготовил использованный им в дальнейшем 2-тактный ДВС. В 1897 году его соотечественник и тоже инженер Рудольф Дизель предложил ДВС с воспламенением рабочей смеси в цилиндре от сжатия воздуха, названный впоследствии дизелем. В XX веке ДВС стал основным двигателем в автомобильном транспорте. В 70-х годах почти 80 % суммарной мощности всех существовавших ДВС приходилось на транспортные машины (автомобили, трактора и пр.). Параллельно шло совершенствование гидротурбин, применявшихся на гидроэлектростанциях. Их мощность в 70-х годах XX века превысила 600 МВт.
Поршневые двигатели — камерой сгорания является цилиндр, где химическая энергия топлива превращается в механическую энергию, которая из возвратно-поступательного движения поршня превращается во вращательную с помощью кривошипно-шатунного механизма.
Бензиновые двигатели — смесь топлива с воздухом готовится в карбюраторе и далее во впускном коллекторе, или во впускном коллекторе при помощи распыляющих форсунок (механических или электрических), далее смесь подаётся в цилиндр, сжимается, а затем поджигается при помощи искры, проскакивающей между электродами свечи. Основная характерная особенность топливо-воздушной смеси в этом случае — её гомогенизированность. Чем более однородной по составу является смесь, тем более качественно идёт процесс сгорания.
Основная характерная особенность топливо-воздушной смеси в этом случае — её гомогенизированность. Чем более однородной по составу является смесь, тем более качественно идёт процесс сгорания.
Дизельные двигатели — специальное дизельное топливо впрыскивается в цилиндр под высоким давлением. Горючая смесь образуется (и сразу же сгорает) непосредственно в цилиндре по мере впрыска порции топлива. Воспламенение смеси происходит под действием высокой температуры воздуха, подвергшегося сжатию в цилиндре.
Дизельные двигатель.Роторно-поршневой двигатель внутреннего сгорания, конструкция которого разработана в 1957 году инженером компании NSU Вальтером Фройде, ему же принадлежала идея этой конструкции. Двигатель разрабатывался в соавторстве с Феликсом Ванкелем, работавшим над другой конструкцией роторно-поршневого двигателя.
Роторно-поршневой двигатель.Реактивный двигатель — тепловой реактивный двигатель, в качестве рабочего тела которого используется атмосферный воздух, нагреваемый за счёт химической реакции окисления горючего кислородом, содержащимся в самом рабочем теле. Реактивные двигатели используются, как правило, для приведения в движение воздушных летательных аппаратов.
Реактивные двигатели используются, как правило, для приведения в движение воздушных летательных аппаратов.
Газотурбинный двигатель — тепловой двигатель, в котором газ сжимается и нагревается, а затем энергия сжатого и нагретого газа преобразуется в механическую работу на валу газовой турбины. В отличие от поршневого двигателя, в газотурбинном двигателе процессы происходят в потоке движущегося газа.
В первой половине XX века. создали новые типы первичных двигателей: газовые турбины, реактивные двигатели, а в 50-х и ядерные силовые установки. Процесс совершенствования и изобретения первичных двигателей продолжается.
Тепловые двигатели
Тепловые двигатели Тепловой двигатель обычно использует энергию, полученную в виде тепла, для выполнения работы, а затем выбрасывает тепло, которое не может быть использовано для выполнения работы. Термодинамика – это наука о взаимосвязях между теплом и работой.
| Индекс Концепции тепловых двигателей | ||||
| Назад |
| Диаграммы давления-объема (PV) являются основным инструментом визуализации для
изучение тепловых двигателей.
| Индекс Концепции фотоэлектрических диаграмм Концепции тепловых двигателей | ||
| Назад |

 2)
2) Поэтому данное в условии задачи количество теплоты является количеством теплоты, полученным от нагревателя в течение цикла, — количеством теплоты, отданном холодильнику. Поэтому работа газа равна (ответ 1).
Поэтому данное в условии задачи количество теплоты является количеством теплоты, полученным от нагревателя в течение цикла, — количеством теплоты, отданном холодильнику. Поэтому работа газа равна (ответ 1).
 Первый закон и второй закон термодинамики ограничивают работу тепловой машины. Первый закон представляет собой применение закона сохранения энергии к системе, а второй устанавливает пределы возможного КПД машины и определяет направление потока энергии.
Первый закон и второй закон термодинамики ограничивают работу тепловой машины. Первый закон представляет собой применение закона сохранения энергии к системе, а второй устанавливает пределы возможного КПД машины и определяет направление потока энергии. Поскольку двигатели обычно используют газ в качестве
рабочего вещества, закон идеального газа связывает диаграмму PV с
температуры, так что три существенные переменные состояния газа
можно проследить по циклу двигателя. Так как работа совершается только тогда, когда
объем газа изменяется, диаграмма дает наглядную интерпретацию
работа выполнена. Поскольку внутренняя энергия идеального газа зависит от его
температура, диаграмма PV вместе с температурами, рассчитанными по закону идеального газа, определяют изменения внутренней энергии газа
так что количество подведенного тепла можно оценить из первого закона термодинамики. Таким образом, диаграмма PV обеспечивает основу для анализа любой тепловой машины, которая
использует газ в качестве рабочего тела.
Поскольку двигатели обычно используют газ в качестве
рабочего вещества, закон идеального газа связывает диаграмму PV с
температуры, так что три существенные переменные состояния газа
можно проследить по циклу двигателя. Так как работа совершается только тогда, когда
объем газа изменяется, диаграмма дает наглядную интерпретацию
работа выполнена. Поскольку внутренняя энергия идеального газа зависит от его
температура, диаграмма PV вместе с температурами, рассчитанными по закону идеального газа, определяют изменения внутренней энергии газа
так что количество подведенного тепла можно оценить из первого закона термодинамики. Таким образом, диаграмма PV обеспечивает основу для анализа любой тепловой машины, которая
использует газ в качестве рабочего тела.
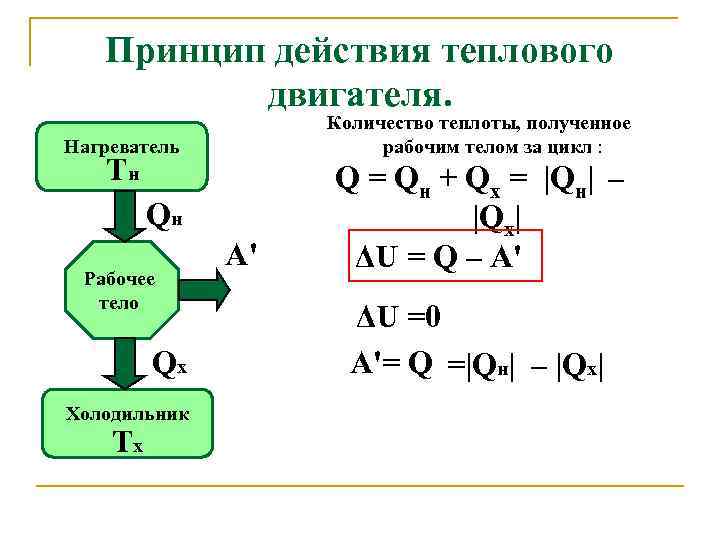 Двигатель берет энергию из горячего резервуара и использует часть ее для выполнения работы, но второй закон термодинамики ограничивает его выбросом части энергии в холодный резервуар. В случае автомобильного двигателя горячим резервуаром является горящее топливо, а холодным резервуаром является среда, в которую выбрасываются продукты сгорания.
Двигатель берет энергию из горячего резервуара и использует часть ее для выполнения работы, но второй закон термодинамики ограничивает его выбросом части энергии в холодный резервуар. В случае автомобильного двигателя горячим резервуаром является горящее топливо, а холодным резервуаром является среда, в которую выбрасываются продукты сгорания. Росснагель Дж., Докинс С.Т., Толацци К.Н., Абах О., Лутц Э., Шмидт-Калер Ф., Сингер К. .,
Одноатомная тепловая машина. Наука
352,
325–329 (2016). [PubMed] [Google Scholar]
Росснагель Дж., Докинс С.Т., Толацци К.Н., Абах О., Лутц Э., Шмидт-Калер Ф., Сингер К. .,
Одноатомная тепловая машина. Наука
352,
325–329 (2016). [PubMed] [Google Scholar]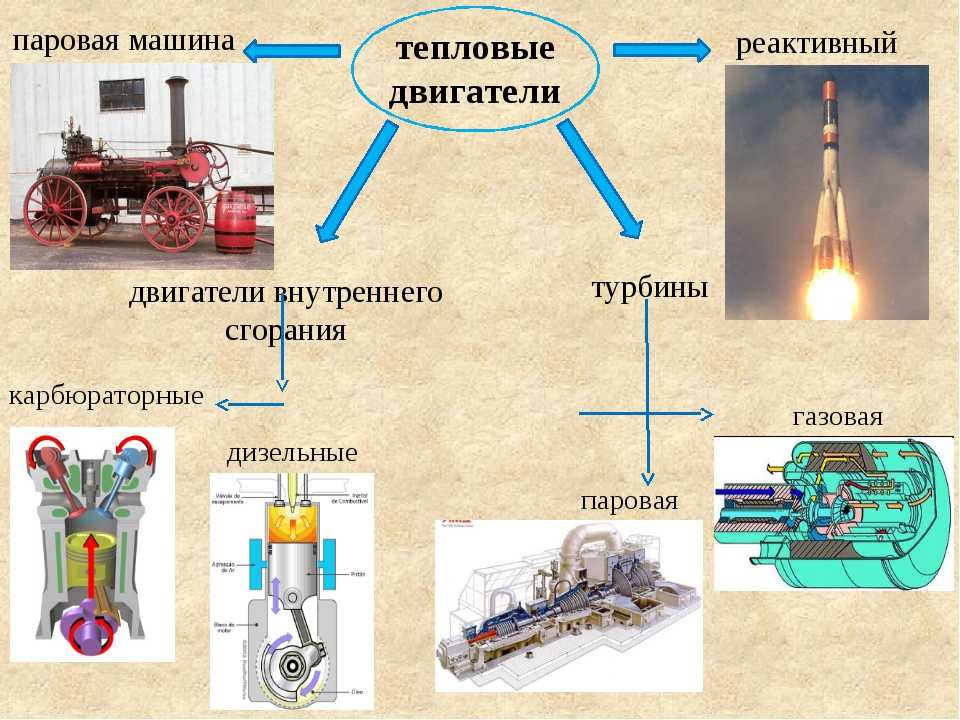 Серра-Гарсия М., Фоэр А., Молерон М., Лайдон Дж., Чонг С., Дарайо С.,
Механическая автономная стохастическая тепловая машина. физ. Преподобный Летт.
117,
010602 (2016). [PubMed] [Google Scholar]
Серра-Гарсия М., Фоэр А., Молерон М., Лайдон Дж., Чонг С., Дарайо С.,
Механическая автономная стохастическая тепловая машина. физ. Преподобный Летт.
117,
010602 (2016). [PubMed] [Google Scholar] , Жорж А.,
Термоэлектрическая тепловая машина с ультрахолодными атомами. Наука
342,
713–715 (2013). [PubMed] [Google Scholar]
, Жорж А.,
Термоэлектрическая тепловая машина с ультрахолодными атомами. Наука
342,
713–715 (2013). [PubMed] [Google Scholar] , Сафави-Наейни А. Х., Хилл Дж. Т., Краузе А., Гроблахер С., Аспельмейер М., Пейнтер О.,
Лазерное охлаждение наномеханического генератора до его квантового основного состояния. Природа
478,
89–92 (2011). [PubMed] [Google Scholar]
, Сафави-Наейни А. Х., Хилл Дж. Т., Краузе А., Гроблахер С., Аспельмейер М., Пейнтер О.,
Лазерное охлаждение наномеханического генератора до его квантового основного состояния. Природа
478,
89–92 (2011). [PubMed] [Google Scholar]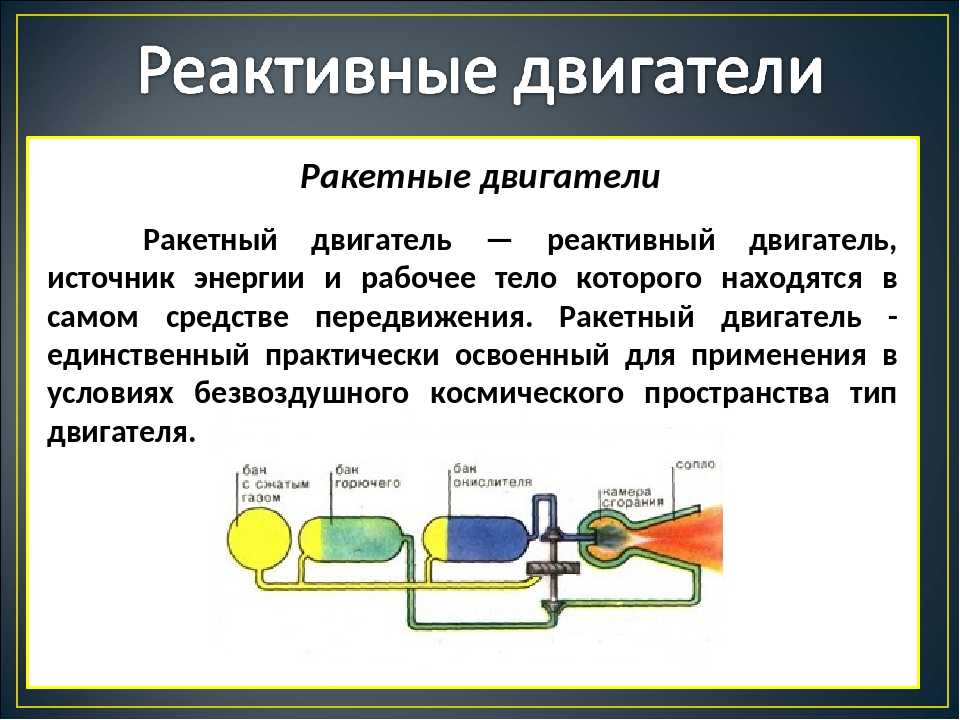 ,
Оптомеханический звонок. физ. Преподобный Летт.
121,
220404 (2018). [PubMed] [Академия Google]
,
Оптомеханический звонок. физ. Преподобный Летт.
121,
220404 (2018). [PubMed] [Академия Google]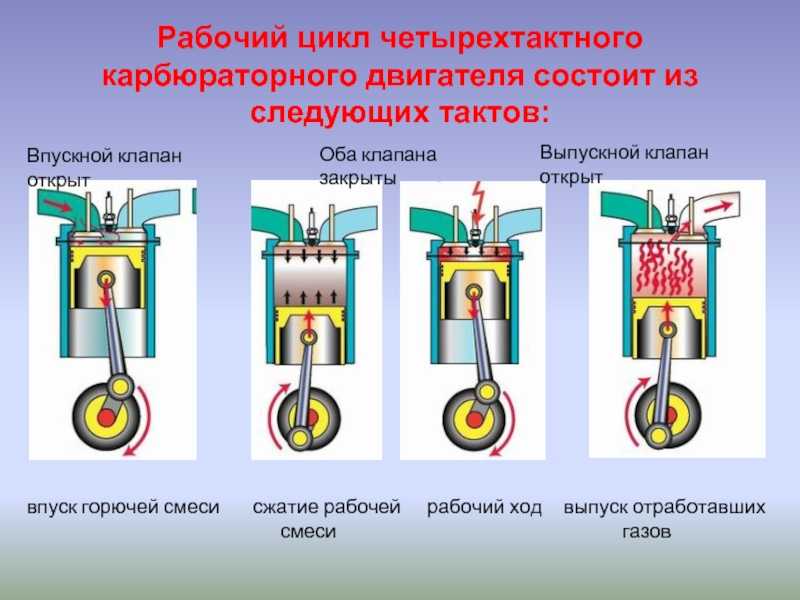 [Google Scholar]
[Google Scholar]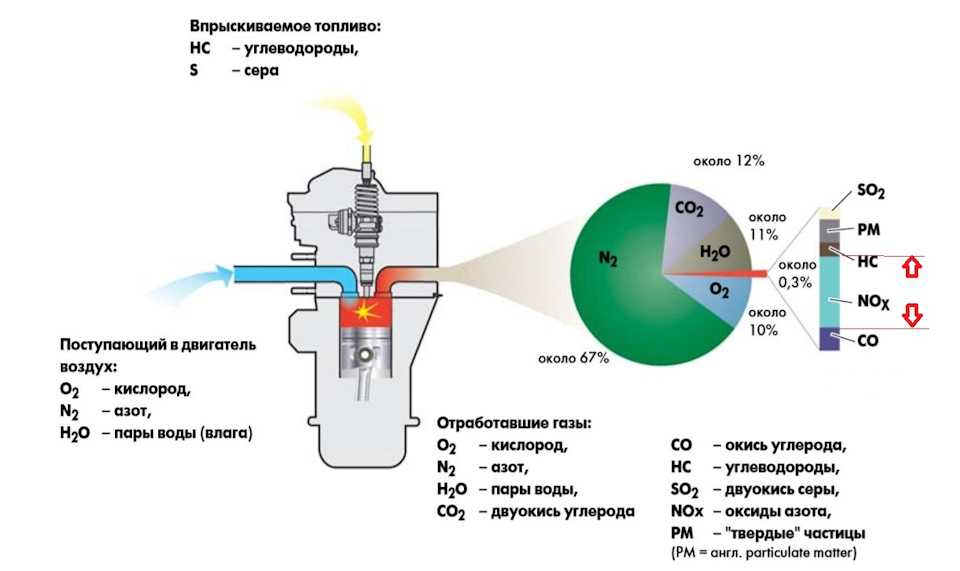 Нац. коммун.
11,
4656 (2020). [Бесплатная статья PMC] [PubMed] [Google Scholar]
Нац. коммун.
11,
4656 (2020). [Бесплатная статья PMC] [PubMed] [Google Scholar] ,
Обратимое извлечение работы в гибридной оптико-механической системе. New J. Phys.
17,
055018 (2015). [Google Scholar]
,
Обратимое извлечение работы в гибридной оптико-механической системе. New J. Phys.
17,
055018 (2015). [Google Scholar] New J. Phys.
20,
083024 (2018). [Google Scholar]
New J. Phys.
20,
083024 (2018). [Google Scholar] New J. Phys.
19,
123037 (2017). [Google Scholar]
New J. Phys.
19,
123037 (2017). [Google Scholar] , Seitner M.J., Krenn P., Kotthaus J.P., Weig E.M.,
Неадиабатическая динамика двух сильно связанных мод наномеханического резонатора. физ. Преподобный Летт.
109,
037205 (2012). [PubMed] [Google Scholar]
, Seitner M.J., Krenn P., Kotthaus J.P., Weig E.M.,
Неадиабатическая динамика двух сильно связанных мод наномеханического резонатора. физ. Преподобный Летт.
109,
037205 (2012). [PubMed] [Google Scholar]