Что называют средней скоростью: Мгновенная и средняя скорость

Содержание

Мгновенная и средняя скорость

Если материальная точка находится в движении, то ее координаты подвергаются изменениям. Этот процесс может происходить быстро или медленно.

Определение 1

Величина, которая характеризует быстроту изменения положения координаты, называется скоростью.

Определение 2

Средняя скорость – это векторная величина, численно равная перемещению в единицу времени, и сонаправленная с вектором перемещения υ=∆r∆t; υ↑↑∆r.

Рисунок 1. Средняя скорость сонаправлена перемещению

Модуль средней скорости по пути равняется υ=S∆t.

Мгновенная скорость точки. Формулы

Мгновенная скорость характеризует движение в определенный момент времени. Выражение «скорость тела в данный момент времени» считается не корректным, но применимым при математических расчетах.

Определение 3

Мгновенной скоростью называют предел, к которому стремится средняя скорость υ при стремлении промежутка времени ∆t к 0:

υ=lim∆t∆r∆t=drdt=r˙.

Направление вектора υ идет по касательной к криволинейной траектории, потому как бесконечно малое перемещение dr совпадает с бесконечно малым элементом траектории ds.

Рисунок 2. Вектор мгновенной скорости υ

Имеющееся выражение υ=lim∆t∆r∆t=drdt=r˙ в декартовых координатах идентично ниже предложенным уравнениям:

υx=dxdt=x˙υy=dydt=y˙υz=dzdt=z˙.

Перемещение и мгновенная скорость

Запись модуля вектора υ примет вид:

υ=υ=υx2+υy2+υz2=x2+y2+z2.

Чтобы перейти от декартовых прямоугольных координат к криволинейным, применяют правила дифференцирования сложных функций. Если радиус-вектор r является функцией криволинейных координат r=rq1, q2, q3, тогда значение скорости запишется как:

υ=drdt=∑i=13∂r∂qi∂qi∂r=∑i=13∂r∂qiq˙i.

Рисунок 3. Перемещение и мгновенная скорость в системах криволинейных координат

При сферических координатах предположим, что q1=r; q2=φ; q3=θ, то получим υ, представленную в такой форме:

υ=υrer+υφeφ+υθφθ, где υr=r˙; υφ=rφ˙sin θ; υθ=rθ˙; r˙=drdt; φ˙=dφdt; θ˙=dθdt; υ=r1+φ2sin2θ+θ2.

Определение 4

Мгновенной скоростью называют значение производной от функции перемещения по времени в заданный момент, связанной с элементарным перемещением соотношением dr=υ(t)dt

Пример 1

Дан закон прямолинейного движения точки x(t)=0,15t2-2t+8. Определить ее мгновенную скорость через 10 секунд после начала движения.

Решение

Мгновенной скоростью принято называть первую производную радиус-вектора по времени. Тогда ее запись примет вид:

υ(t)=x˙(t)=0.3t-2; υ(10)=0.3×10-2=1 м/с.

Ответ: 1 м/с.

Пример 2

Движение материальной точки задается уравнением x=4t-0,05t2. Вычислить момент времени tост, когда точка прекратит движение, и ее среднюю путевую скорость υ.

Решение

Вычислим уравнение мгновенной скорости, подставим числовые выражения:

υ(t)=x˙(t)=4-0,1t.

4-0,1t=0;tост=40 с;υ0=υ(0)=4;υ=∆υ∆t=0-440-0=0,1 м/с.

Ответ: заданная точка остановится по прошествии 40 секунд; значение средней скорости равняется 0,1 м/с.

Автор: Роман Адамчук

Преподаватель физики

Прямолинейное неравномерное движение. Средняя скорость

Как вы понимаете, в жизни практически невозможно встретить тело, движущееся точно равномерно. Поэтому мы с вами переходим к изучению более сложных видов движения. Рассмотрим простой пример. Пусть автомобиль, который едет из Москвы в Санкт-Петербург по прямой, за 10 ч проезжает 600 км (рис. 50). Будем считать автомобиль точечным телом, так как его размеры по сравнению с пройденным расстоянием пренебрежимо малы. Понятно, что за время своего движения автомобиль многократно разгонялся и тормозил и даже стоял перед светофорами. В результате движение автомобиля было неравномерным. Поэтому определение скорости равномерного прямолинейного движения здесь применять нельзя.

Для таких случаев вводят понятие «средняя путевая скорость». В рассмотренном примере за время t = 10 ч автомобиль проехал путь s = 600 км. Средняя путевая скорость автомобиля при этом равна

v_ср.п = s/t = 600 км / 10 ч = 60 км/ч.

Средней путевой скоростью тела называют физическую величину, равную отношению пути, пройденного телом за рассматриваемый промежуток времени, к длительности этого промежутка.

v_ср.п = s/t

Обратим внимание на то, что путь s не имеет направления и является скалярной неотрицательной величиной. Поэтому и средняя путевая скорость v

ср.п всегда является скалярной неотрицательной величиной. Она не имеет направления, а следовательно, не является вектором.

Средняя путевая скорость v_ср.п – скалярная неотрицательная величина.

Теперь рассмотрим определение еще одной физической величины, которая связана не с путем, пройденным телом, а с его перемещением за рассматриваемый промежуток времени.
Введем систему отсчета так, как показано на рис. 50. В результате мы найдем, что за время t = 10 ч автомобиль совершил перемещение Δx в положительном направлении оси X, модуль которого |Δx| = 600 км.

Средней скоростью тела за промежуток времени t называют физическую величину, равную отношению перемещения Δx, совершенного телом, к длительности этого промежутка времени.

v_ср = Δx/t

Поскольку перемещение Δx является вектором, то средняя скорость – тоже вектор. Направление средней скорости vср совпадает с направлением перемещения Δx.

Чтобы лучше понять, чем отличаются друг от друга средняя скорость и средняя путевая скорость, обратимся к рис. 51. Пусть автомобиль, выехавший из Москвы в Санкт-Петербург, находился в пути 10 ч. При этом, проехав 400 км в сторону Санкт-Петербурга, он повернул обратно и проехал 200 км в сторону Москвы. Ясно, что путь, пройденный автомобилем за 10 ч, равен (400 + 200) км = 600 км. Значение перемещения автомобиля за то же время равно (400 — 200) км = 200 км. Используя данные определения, найдем среднюю путевую скорость и значение средней скорости автомобиля за 10 ч движения:

v_ср.п = s/t = 600 км / 10 ч = 60 км/ч;
v_ср

= Δx/t = 200 км / 10 ч = 20 км/ч.

Итоги

Средняя путевая скорость – это физическая величина, равная отношению пути, пройденного телом за рассматриваемый промежуток времени, к длительности этого промежутка.

v_ср.п = s/t

Средняя путевая скорость – скалярная неотрицательная величина.

Средняя скорость тела за промежуток времени t – это физическая величина, равная отношению перемещения Δx, совершенного телом, к длительности этого промежутка времени.

v_ср = Δx/t

Средняя скорость – вектор. Она направлена туда, куда направлено перемещение тела за рассматриваемый промежуток времени.

Если тело все время движется в одном направлении, то модуль средней скорости равен средней путевой скорости. Если же в процессе своего движения тело меняет направление движения, то модуль средней скорости меньше средней путевой скорости.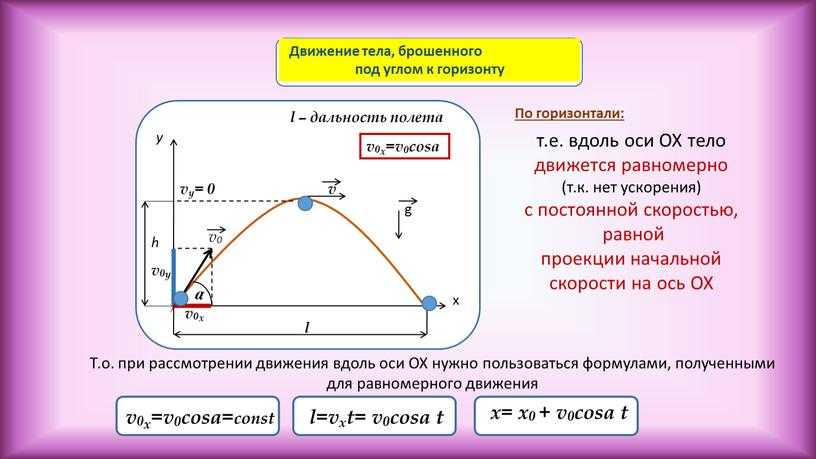

Вопросы

Дайте определение средней скорости и средней путевой скорости. Какая из этих величин является векторной? Почему средняя путевая скорость не может быть отрицательной?
Чему равно значение средней скорости за промежуток времени, в течение которого перемещение тела было равно нулю? Всегда ли будет равна нулю средняя путевая скорость за этот же промежуток времени? Приведите примеры.

Упражнения

1. Пусть автомобиль проехал за первый час 90 км в положительном направлении оси X, а за второй час – 70 км в противоположном направлении.
Определите среднюю путевую скорость автомобиля и значение его средней скорости: а) за первый час; б) за второй час; в) за первые два часа движения.
Объясните, почему эти скорости отличаются друг от друга.

2.Представьте себе, что вы выехали на автомобиле со стоянки, находящейся рядом с вашим домом, в 8 часов утра. В 17 часов вечера вы вернули автомобиль на прежнее место.

За день вы проехали путь s = 380 км, при этом в течение промежутка времени от 10 до 12 часов дня вы ехали по прямолинейной трассе строго на север с постоянной скоростью 60 км/ч. Ответьте на вопросы:
а) чему была равна ваша средняя путевая скорость за время с 8 часов утра до 17 часов вечера?
б) какова была ваша средняя скорость за интервалы времени: с 8 до 17 часов; с 10 до 12 часов?

3. Определите значение средней скорости и среднюю путевую скорость за промежуток времени от момента времени t₀ = 0 до момента времени t₂ = 7 с для тела, график движения которого приведен на рис. 47.

4. А) Измерьте шагами свой путь от дома до школы и время движения. Переведите это расстояние в метры, а время в секунды. Считайте, что длина одного шага приблизительно равна 0,6 м. Вычислите свою среднюю путевую скорость. Проделайте тот же путь на велосипеде и по результатам измерений найдите среднюю путевую скорость.

Б) Используя карту местности, найдите расстояние по прямой от дома до школы, чтобы затем рассчитать среднюю скорость при движении пешком и на велосипеде.

Средняя скорость

Повседневное представление о скорости возникает, когда мы рассматриваем, насколько быстро или медленно движется тело. Каким-то образом мы связываем перемещение тела со временем нахождения в таком перемещении. В этом разделе мы собираемся определить, что в физике понимается под средней скоростью и ее разницей со средней скоростью.

Средняя скорость тела, движущегося из точки P ₁ в точку P ₂ определяется как отношение пройденное расстояние и соответствующее истекшее время . Он задается выражением:

Vср = ∆s∆t= s2-s1t2 — t1

где:

Vср: Средняя скорость на исследуемом интервале. Единицей измерения в Международной системе (СИ) является метр в секунду (м/с)
∆s : Пройденное расстояние за рассматриваемый интервал. Измерено по траектории . Единица измерения в Международная система (СИ) — метр (м)
∆t : Время , затраченное телом на путь от P ₁ до P ₂ . Единицей измерения в Международной системе (СИ) является секунда (с)
s ₁ , s ₂ : Путь, пройденный телом по траектории от начала движения до P ₁ 8 _{0 (s 1_{)0014 , а с начала движения P ₂ (s ₂ ) . Единицей измерения в Международной системе (СИ) является метр (м)}}

.
T ₁ , T ₂ : Время , в котором тело встречается в начальной точке P ₁ и в последней точке P ₂ соответственно. Единицей измерения в Международной системе (СИ) является секунда (с)

Средняя скорость — это скалярная величина , в отличие от средней скорости, которая является вектором. Единицей измерения в Международной системе (СИ) средней скорости является метр в секунду (м/с) . С другой стороны, в отличие от средней скорости, которая зависела от векторов начального и конечного положения движения, средняя скорость зависит от пройденного пути по траектории. Следовательно, тело в движении всегда будет иметь среднюю скорость больше 0 . В общем случае Vср≥vaср→ выполняется, и оба значения будут одинаковыми в случае прямолинейного движения без изменения направления.

Экспериментируйте и учитесь

Данные

Средняя скорость

График показывает траекторию движения тела, его начальное и конечное положения и расстояние, пройденное между двумя точками (Δs).

Перетащите точки ближе или дальше друг от друга и наблюдайте, как пройденное расстояние соответственно уменьшается или увеличивается. Кроме того, вы можете изменить время, затрачиваемое телом на переход из одной точки в другую (Δt), и заметить изменение средней скорости.

Что произойдет, если не менять позицию, а уменьшить время?

Пример

Тело делает полный круг радиусом 4 метра за 1,5 секунды. Рассчитайте:

а) среднюю скорость.
б) средняя скорость.

Решение

Теперь… ¡Проверь себя!

Какова ваша «средняя скорость» в жизни, здоровье и работе?

У меня есть друг по имени Натан Барри, который недавно закончил писать три книги всего за 9 месяцев.

Как он это сделал?

Следуя простой стратегии. Он писал по 1000 слов в день. (Это примерно 2-3 страницы.) И он делал это каждый день в течение 253 дней подряд.

А теперь сравните эту стратегию с классическим образом писателя, который неделями прячется в хижине и пишет как сумасшедший, чтобы закончить свою книгу.

У маньяка в салоне высокая «максималка» — может 20, а то и 30 страниц в день. Но через несколько недель в таком неустойчивом темпе либо книга закончена, либо автор.

Для сравнения, максимальная скорость Натана никогда не достигала пикового уровня сумасшедшего писателя в салоне. Однако в течение года или двух его средняя скорость была намного выше.

Этот урок выходит далеко за рамки письма.

Например, каждый может почувствовать прилив вдохновения, отправиться в спортзал и выложиться на одной тренировке. Это максимальная скорость. Мы тратим много времени, зацикливаясь на этом. Насколько тяжелой была твоя тренировка? Насколько вы мотивированы? Как быстро вы его толкаете?

Но что, если бы вы усреднили все свои дни в прошлом месяце? Сколько из этих дней включали тренировки? Как насчет последних трех месяцев? Или последний год? Какова была ваша средняя скорость ?

Посмотрите на это так, и вы поймете, например, что неделю болели и пару раз прогуливали спортзал после долгого рабочего дня, а также были в дороге две недели . Внезапно вы понимаете, что ваша максимальная скорость время от времени может быть высокой, но ваша средняя скорость намного ниже, чем вы думаете.

Насколько я могу судить, этот принцип применим к вашим привычкам на работе, привычкам в еде, привычкам в отношениях и практически ко всем другим сферам вашей жизни.

Удивительная вещь о средней скорости

Вот удивительная вещь о средней скорости: Средней скорости не нужно много времени, чтобы давать невероятные результаты.

Так часто мы тратим впустую свое время и энергию, думая, что нам нужны монументальные усилия, чтобы достичь чего-то значительного. Мы говорим себе, что нам нужно усилить мотивацию и желание. Мы считаем, что нам нужно работать усерднее, чем всем остальным.

Но когда вы смотрите на людей, которые действительно добиваются успехов, вы видите нечто иное. Натан писал по 1000 слов в день, каждый день. А девять месяцев спустя? Три книги готовы. Ни в коем случае он не обязательно работал усерднее , чем все остальные. Нет ничего сексуального или шокирующего в том, чтобы писать по 2 или 3 страницы в день. Натан просто был более последовательным, чем все остальные, и в результате его средняя скорость за эти 253 дня была намного выше, чем у большинства людей.

Конечно, из всего этого следует естественный вопрос: «Как увеличить среднюю скорость?»

Давайте поговорим об этом сейчас.

Градация привычек: как увеличить среднюю скорость

Недавно мне рассказали об идее «градации привычек». То есть перейти от вашей текущей привычки на один уровень выше. По сути, градация привычки заключается в увеличении средней скорости.

Вот несколько примеров…

Если ваша средняя скорость составляет три здоровых приема пищи в неделю, можете ли вы «перевести» ее на один здоровый прием пищи в день?
Если ваша средняя скорость тренируется два раза в месяц, можете ли вы «повысить» ее до одного раза в неделю?
Если ваша работа сумасшедшая, и вы разговариваете со своими старыми друзьями по телефону только раз в три месяца, можете ли вы запланировать эти звонки в свой календарь и «перевести» эту привычку на один раз в месяц?

Вы поняли. Градация привычки заключается в рассмотрении ваших целей и вашей текущей средней скорости, а также в размышлениях о том, как вы можете увеличить свою производительность хотя бы немного на постоянной основе.

Я думал о том, как я мог бы применить это сам.

Последние восемь месяцев я публикую новую статью каждый понедельник и каждый четверг в обязательном порядке. Теперь я подумываю о том, чтобы «вывести» эту привычку на новый уровень.

Например, я мог бы следовать стратегии Натана и писать по 1000 слов в день. Предположительно, это позволило бы мне продолжать писать по две статьи в неделю, одновременно работая над другими полезными вещами — например, над собственной книгой.

Куда идти дальше

Мы все имеем среднюю скорость, когда дело доходит до наших привычек. И если мы будем честными с самими собой, эта средняя скорость может быть намного ниже, чем нам хотелось бы.

По правде говоря, каждый может замотивироваться и подтолкнуть себя на один день, но очень немногие удерживают постоянные усилия каждую неделю в обязательном порядке.

Главное не осуждать себя и не чувствовать себя виноватым из-за того, что средняя скорость ниже, чем хотелось бы.