Дифференциал функции
- Понятие и геометрический смысл дифференциала
- О разных формах записи дифференциала
- Свойства дифференциала
- Применение дифференциала в приближенных вычислениях
- Абсолютная и относительная погрешности приближенных вычислений
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Определение. Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.
Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента).
Это записывается так:
или
или же
Геометрический смысл дифференциала. Дифференциал функции y = f(x) равен приращению ординаты касательной S, проведённой к графику этой функции в точке M( рисунок).
рисунок).
Почему дифференциал можно использовать в приближенных вычислениях?
Дифференциал, является главной, линейной относительно частью приращения функции; чем меньше , тем большую долю приращения составляет эта часть. В этом можно убедиться, мысленно передвигая перпендикуляр, опущенный из точки P (см. рисунок) к оси Ox, ближе к началу координат. Поэтому при малых значениях (и при ) приращение функции можно приближенно заменить его главной частью , т.е.
Дифференциал функции в точке x и обозначают
или
Следовательно,
(1)
или
, (2)поскольку дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной.
Замечание. Нужно помнить, что если x – исходное значение аргумента, а — наращенное значение, то производная в выражении дифференциала берётся в исходной точке x ; в формуле (1) этого не видно из записи.
Дифференциал функции можно записать в другой форме:
(3)
или
(4)
Пример 1. Найти дифференциалы функций:
1) ;
2) ;
3) ;
4) .
Решение. Применяя формулы дифференцироивания степенной и логарифмической функций из таблицы производных, а также формулу (4), находим:
1) ;
2) ;
3) ;
4) .
Найти дифференциалы самостоятельно, а затем посмотреть решения
Пример 2. Найти дифференциал функции
в точке x = 2,
1) выделив линейную часть;
2) по формуле.
Пример 3. Найти дифференциал функции
в точке x.
Пример 4. Найти дифференциал функции
в точках x = 0 и x = 1.
Посмотреть правильные решения примеров 2, 3, 4.
В основном же задачи на дифференциалы — это более сложные, чем рассмотренные выше для разминки, поэтому стоит посетить страницу с решением задач на дифференциалы сложных функций. Скорее всего, вызывающие у вас трудности задачи именно к таким и относятся.
В этом и следующем параграфах каждую из функций будем считать дифференцируемой при всех рассматриваемых значениях её аргументов.
Дифференциал обладает свойствами, аналогичными свойствам производной:
(С – постоянная величина) (5)
(6)
(7)
(8)
(9)
Формулы (5) – (9) получаются из соответствующих формул для производной умножением обеих частей каждого равенства на .
Одно из особеннейших свойств дифференциала — инвариантность формы дифференциала в случае сложных функций.
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Производная, дифференциал и их применение
Установленное во втором параграфе приближенное равенство
или
(10)
позволяет использовать дифференциал для приближенных вычислений значений функции.
Запишем приближенное равенство более подробно. Так как
а
то
или
(11)
Пример 5. Пользуясь понятием дифференциала, вычислить приближенно ln 1,01.
Решение. Число ln 1,01 является одним из значений функции y = ln x .
Положим
тогда
Следовательно,
что является очень хорошим приближением: табличное значение ln 1,01 = 0,0100.
Пример 6. Пользуясь понятием дифференциала, вычислить приближенно
Решение. Число
является одним из значений функции
Так как производная этой функции
то формула (11) примет вид
Полагая
и
получаем
(табличное значение
).
Вычислить приближенно самостоятельно, а затем посмотреть решение
 Вычислить приближенно:
Вычислить приближенно:
1) ;
2) .
Посмотреть правильное решение и ответ.
Пользуясь приближенным значением числа, нужно иметь возможность судить о степени его точности. С этой целью вычисляют его абсолютную и относительную погрешности.
Абсолютная погрешность приближенного числа равна абсолютной величине разности между точным числом и его приближенным значением:
(12)
Относительной погрешностью приближенного числа называется отношение абсолютной погрешности этого числа к абсолютной величине соответствующего точного числа:
(13)
Если точное число неизвестно, то
(14)
Иногда, прежде чем применить формулу (11), требуется предварительно преобразовать исходную величину. Как правило, это делается в двух целях.
Пример 8. Пользуясь понятием дифференциала, вычислить приближенно . Оценить точность полученного результата.
Решение. Рассмотрим функцию
Её производная равна
а формула (11) примет вид
В данном случае было бы нерационально вычислять приближенно следующим образом:
так как значение
не является малым по сравнению со значением производной в точке
Здесь удобно предварительно вынести из под корня некоторое число, например 4/3. Тогда
Теперь, полагая
получим
Умножая на 4/3, находим
Принимая табличное значение корня
за точное число, оценим по формулам (12) и (13) абсолютную и относительную погрешности приближенного значения:
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Производная, дифференциал и их применение
Весь блок «Производная»
- Что такое производная
- Найти производную: алгоритм и примеры решений
- Производные произведения и частного функций
- Производная суммы дробей со степенями и корнями
- Производные простых тригонометрических функций
- Производная сложной функции
- Дифференциал функции
- Дифференциал сложной функции, инвариантность формы дифференциала
- Правило Лопиталя
- Частные производные
Поделиться с друзьями
Дифференциал | это.
 .. Что такое Дифференциал? I Дифференциа́л (от лат. differentia — разность, различие)
.. Что такое Дифференциал? I Дифференциа́л (от лат. differentia — разность, различие)в математике, главная линейная часть приращения функции. Если функция y = f (x) одного переменного х имеет при х = х0 производную, то приращение
Δy = f (x0 + Δx) — f (x0)
функции f (x) можно представить в виде
Δ
где член R бесконечно мал по сравнению с Δх. Первый член
dy = f’ (x0) Δх
в этом разложении и называется дифференциалом функции f (x) в точке x0. Из этой формулы видно, что дифференциал dy линейно зависит от приращения независимого переменного Δx, а равенство
Δy = dy + R
показывает, в каком смысле Д. dy является главной частью приращения Δy.
dy является главной частью приращения Δy.
Подробнее о Д. функций одного и нескольких переменных см. Дифференциальное исчисление.
Обобщение понятия дифференциала. Обобщение понятия Д. на вектор-функции, начало которому положили в начале 20 в. французские математики Р. Гато и М. Фреше, позволяет лучше выяснить смысл понятия «дифференциал» для функций нескольких переменных, а в применении к Функционалам приводит к понятию вариации, лежащему в основе вариационного исчисления (См. Вариационное исчисление).
Важную роль в этом обобщении играет понятие линейной функции (линейного отображения). Функция L (x) векторного аргумента х называется линейной, если она непрерывна и удовлетворяет равенству
L (x’ + х «) = L (x’) + L (x «)
для любых х’ и х « из области определения. Линейная функция n-мерного аргумента х = {x1,. .., xn} всегда имеет вид
.., xn} всегда имеет вид
L (x) = a1x1 +… + anxn,
где a1,…, an — постоянные. Приращение
ΔL = L (x + h) — L (x)
линейной функции L (x) имеет вид
ΔL = L (h),
т. е. зависит только от векторного приращения h, и притом линейно. Функция f (x) называется дифференцируемой при значении аргумента х, если её приращение Δf = f (x + h) — f (x), рассматриваемое как функция от h, имеет главную линейную часть L (h), т. е. выражается в виде
Δf = L (h) + R (h),
где остаток R (h) при h → 0 бесконечно мал по сравнению с h. Главная линейная часть L (h) приращения Δf и называется дифференциалом df функции f в точке x. При этом в зависимости от того, в каком смысле понимается бесконечная малость R (h) по сравнению с h, различают слабый дифференциал, или дифференциал Гато, и сильный дифференциал, или дифференциал Фреше. Если существует сильный Д., то существует и слабый Д., равный сильному Д. Слабый Д. может существовать и тогда, когда сильный не существует.
Главная линейная часть L (h) приращения Δf и называется дифференциалом df функции f в точке x. При этом в зависимости от того, в каком смысле понимается бесконечная малость R (h) по сравнению с h, различают слабый дифференциал, или дифференциал Гато, и сильный дифференциал, или дифференциал Фреше. Если существует сильный Д., то существует и слабый Д., равный сильному Д. Слабый Д. может существовать и тогда, когда сильный не существует.
В случае f (x) ≡ x из общего определения следует, что df = h, т. е. можно приращение h считать Д. аргумента x и обозначать dx.
Если сделать теперь переменной точку x, в которой определяется Д. df, то он будет функцией двух переменных:
df (x; h).
Далее, считая h = h1 постоянным, можно найти Д. от дифференциала df (x; h1) как главную часть приращения
от дифференциала df (x; h1) как главную часть приращения
df (x + h2; h1) — df (x; h1),
где h2 — некоторое второе, не связанное с h1 приращение x. Получаемый таким образом второй дифференциал d2f = d2f (x; h1, h2) является функцией трёх векторных аргументов x, h1 и h2, линейной по каждому из двух последних аргументов. Если d2f непрерывно зависит от x, то он симметричен относительно h1 и h2:
d2f (x; h1, h2) = d2f (x; h2, h1).
Аналогично определяется дифференциал dnf = dnf (x; h1,…, hn) любого порядка n.
В вариационном исчислении сам векторный аргумент x является функцией x (t), а дифференциалы df и d2f функционала f [x (t)] называются его первой и второй вариациями и обозначаются δf и δ2f.
Всюду выше речь шла об обобщении понятия Д. на числовые функции векторного аргумента. Существует обобщение понятия Д. и на случай вектор-функций, принимающих значения в банаховых пространствах.
Лит.: Ильин В. А., Позняк Э. Г., Основы математического анализа, 2 изд., М., 1967; Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 2 изд., М., 1968; Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд. , т. 1, М., 1969; Кудрявцев Л. Д., Математический анализ, т. 1, М., 1970; Рудин У., Основы математического анализа, пер. с англ., М., 1966; Дьедонне Ж., Основы современного анализа, пер. с англ., М., 1964.
, т. 1, М., 1969; Кудрявцев Л. Д., Математический анализ, т. 1, М., 1970; Рудин У., Основы математического анализа, пер. с англ., М., 1966; Дьедонне Ж., Основы современного анализа, пер. с англ., М., 1964.
А. Н. Колмогоров.
II Дифференциа́лДифференциальный механизм в приводе ведущих колёс автомобиля, трактора или др. транспортных машин. Д. обеспечивает вращение ведущих колёс с разными относительными скоростями при прохождении кривых участков пути.
Дифференциал вашего автомобиля? Какова его цель?
Перейти к основному содержанию 1404 Мейн-стрит
Направления
Орегон-Сити, Орегон 97045
- Позвоните или напишите в отдел продаж: 503-656-0612
- Служба: 503-656-0612
- Запчасти: 503-656-0612
Больше, чем автосалон
Скрыть Показать
Что такое дифференциал автомобиля? Между ведущими колесами вашего нового Subaru находится коробка передач. Если это полноприводная система, то у вас почти всегда будет передний и задний дифференциал. Эта коробка передач работает с трансмиссией вашего автомобиля, чтобы передавать мощность от двигателя на ось колеса, что стабилизирует поворот вашего автомобиля. Когда вы поворачиваете, для лучшего сцепления вам нужно, чтобы внешние колеса вращались быстрее, чем внутренние, и для этого в дифференциале используются шестерни. Вот почему так важно проводить техническое обслуживание вашего автомобиля в нашем сервисном центре, включая замену жидкости дифференциала каждые 30 000–60 000 миль пробега.
Автомобили Subaru имеют разные дифференциалы для разных моделей, все они предназначены для улучшения сцепления с дорогой, поворотливости и общей безопасности. Эти системы включают вязкостной центральный дифференциал (VCD), активное разделение крутящего момента (ATS), переменное распределение крутящего момента (VTD) и центральный дифференциал, управляемый водителем (DCCD).
Вискомуфта межосевого дифференциала (VCD) обеспечивает распределение крутящего момента между передними и задними колесами в соотношении 50/50. Тормоза используются для уменьшения проскальзывания и улучшения крутящего момента колеса, посылая сигналы торможения вращающейся шине. Если ось начинает пробуксовывать, вискомуфта передает крутящий момент на колесо с большим сцеплением, будь то переднее или заднее. Эта система VCD включена в модели с механической коробкой передач, такие как Crosstrek, Impreza и Forester.
Активное разделение крутящего момента (ATS) имеет разделение крутящего момента 60/40 для передней и задней части. Эта система на самом деле отличается, потому что она включает в себя многодисковый центральный пакет сцепления, а не дифференциал, который допускает проскальзывание и всегда частично включен. Быть «активным» означает, что он постоянно ищет больше, чем просто проскальзывание колес, но также получает информацию от всех доступных датчиков и определяет, может ли быть потеря сцепления с дорогой, и обеспечивает корректировку.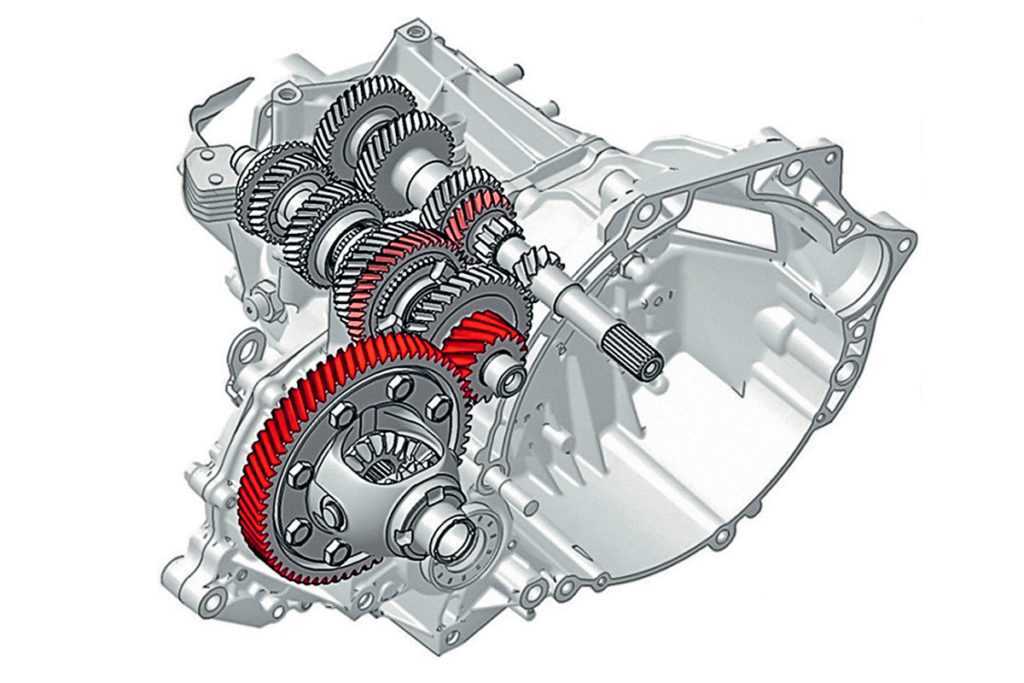 Вы найдете это на таких моделях, как Legacy и Outback.
Вы найдете это на таких моделях, как Legacy и Outback.
Что касается Variable Torque Distribution (VTD) , который доступен только в некоторых автомобилях Subaru, таких как WRX, предназначен для автомобилей, которым необходимо быстро разгоняться. Между передними и задними колесами имеется разделение 45/55, что дает вам лучшее сцепление с задним концом, а электронная гидравлическая раздаточная муфта блокирует колеса, которые в этом нуждаются.
Наконец, управляемый водителем межосевой дифференциал (DCCD) , исключительно в STI, представляет собой невероятно сложную систему, которая включает не только дифференциал повышенного трения, но и электронный дифференциал. Есть 41/59разделены на перед и зад. Модуль управления многодисковым сцеплением и трансмиссией вносил коррективы на основе данных датчиков, но водитель также может контролировать происходящее. Независимо от того, с каким сценарием вы столкнулись, у вас есть все, что вам нужно, чтобы обеспечить правильное сцепление с любыми колесами, которые в этом нуждаются.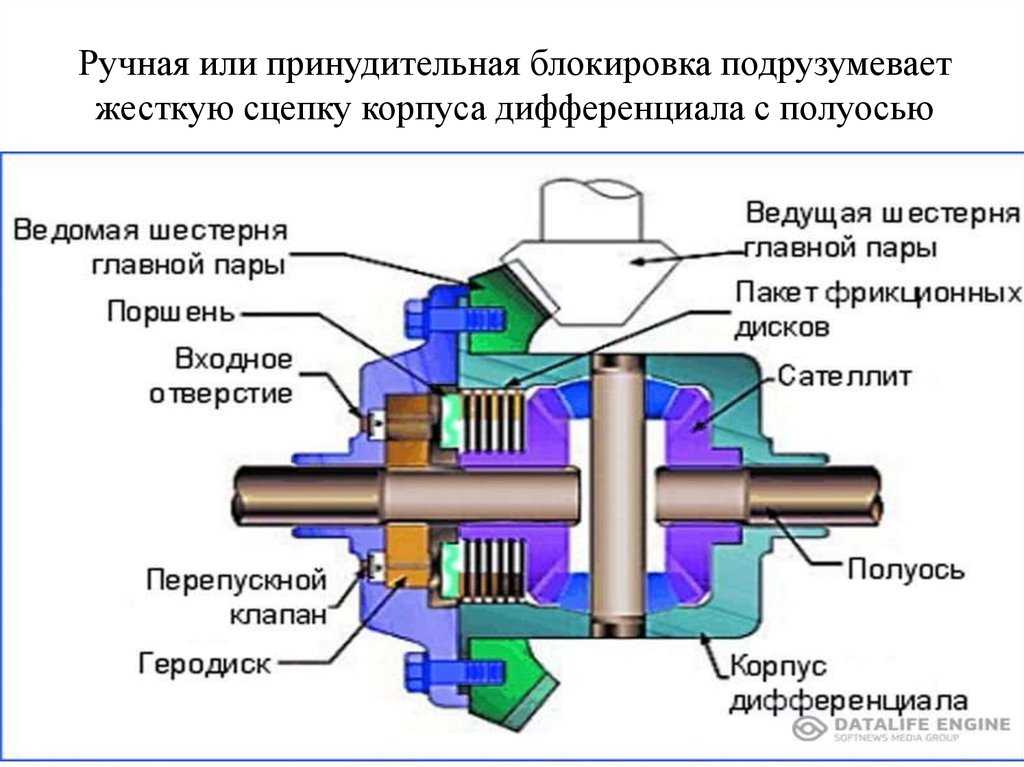
Категории: Сервис, запчасти
Метки: сертифицированный сервис Subaru в Орегон-Сити, Subaru AWD, запчасти Subaru, дифференциал, ремонт автомобилей
- Запросить дополнительную информацию
Поиск по блогу
Политика конфиденциальности
Подпишитесь на наш блог
- RSS 2.0
- Видео — RSS 2.0
Популярные теги
Автосервис новые модели субару Ремонт машин Новый Субару Новости Субару сервис субару субару новые модели Subaru для продажи в Орегон-Сити будущие модели субару сертифицированный сервис Subaru в Орегон-Сити новый инвентарь Модели Субару 2023 года Зимнее вождение Обслуживание шин субару импреза Субару Кросстрек Новые шины субару форестер субару аутбэк Предстоящие модели Subaru 2022 года модельный ряд субару Субару Легаси Субару Восхождение Зеленый Продам оригинальные запчасти Субару Новый автомобиль Новая модель Субару Модели Субару 2022 года Новости сертифицированный сервисный центр Subaru)
Фейсбук Твиттер Ютуб; ;
Tech Talk — Что такое дифференциалы? • Скручивание автомобилей
Когда мы думаем об основных элементах трансмиссии автомобиля, двигатель, коробка передач и ведущие колеса являются нашими первыми и часто единственными мыслями как критическими элементами, отвечающими за управление автомобилем. Но есть меньшая мысль об устройстве, которое играет большую, большую роль — дифференциал. Дифференциал играет большую роль не только во всем процессе трансмиссии, но и в управлении транспортным средством. В конце концов, сила — ничто, если вы не можете ее использовать.
Но есть меньшая мысль об устройстве, которое играет большую, большую роль — дифференциал. Дифференциал играет большую роль не только во всем процессе трансмиссии, но и в управлении транспортным средством. В конце концов, сила — ничто, если вы не можете ее использовать.
Но что такое дифференциал? Как это работает? Какую пользу он приносит автомобилю, и есть ли недостатки? Читайте дальше…
Что такое дифференциал и для чего он нужен?
Дифференциал представляет собой узел, состоящий из нескольких различных типов шестерен, который находится между коробкой передач и ведущими валами ведомых колес. Его физическое положение обычно находится на оси ведущих колес — по крайней мере, в самой базовой конфигурации — по сути, разделяя ведущую ось на две части. Он выполняет три основные функции:
- Направляет крутящий момент на ведущие колеса, часто преобразовывая крутящий момент под углом 90°
- Он действует как редуктор конечной передачи, регулируя скорость вращения в последний раз, прежде чем вращение достигнет ведущих колес.

- Однако третья и основная функция дифференциала, от которой он и получил свое название, заключается в том, что он позволяет двум ведущим колесам на одной оси вращаться с разными скоростями.
Эта последняя функция чрезвычайно важна для эксплуатации транспортного средства и управления им. При движении по прямой колеса, левое и правое, проходят одинаковое расстояние и вращаются с одинаковой скоростью. Однако при повороте автомобиля внутреннее и внешнее колеса проходят разные расстояния.
Рассмотрим приведенный ниже пример схемы:
Если колеса автомобиля находятся на расстоянии 1,5 метра друг от друга (от центра до центра каждой шины), и автомобиль движется по кругу постоянного радиуса – в этом примере 1,5 метра на внутреннем колесе — внешнее колесо движется по кругу с радиусом 3,0 метра. Окружность двух пройденных кругов — общее расстояние путей внутреннего и внешнего колес — можно рассчитать по математической формуле: Окружность = 2 x π x радиус
Расстояние, пройденное внутренним колесом, составляет 9,4 метра, а внутреннее колесо проходит 18,8 метра. Внешнему колесу необходимо преодолеть большее расстояние — в данном случае удвоенное расстояние — за то же время, которое требуется внутреннему колесу, чтобы преодолеть более короткое расстояние. Для этого внешнее колесо должно вращаться быстрее, чем внутреннее. Вот где дифференциал вступает в игру.
Внешнему колесу необходимо преодолеть большее расстояние — в данном случае удвоенное расстояние — за то же время, которое требуется внутреннему колесу, чтобы преодолеть более короткое расстояние. Для этого внешнее колесо должно вращаться быстрее, чем внутреннее. Вот где дифференциал вступает в игру.
Как работает дифференциал?
Стандартный дифференциал, часто называемый открытым дифференциалом , является наиболее простым и распространенным типом дифференциала. Он состоит из четырех основных компонентов:
- Шестерня на входном валу
- Зубчатый венец
- Зубчатая передача/ шестерни
- Боковые шестерни, соединенные с валами ведущих колес
Шестерня входит в зацепление с зубчатым венцом, преобразуя крутящий момент под углом 90° в передачу мощности на ведущие колеса. Крестовина крепится к зубчатому венцу и вращается вместе с ним, в свою очередь вращая боковые шестерни и ведомые колеса. На прямой крестовина находится в фиксированном положении и оба колеса вращаются с одинаковой скоростью. Однако при повороте крестовина может вращаться вокруг своей оси — процесс, при котором одна боковая шестерня вращается быстрее, а другая замедляется. Это позволяет колесам вращаться независимо друг от друга, и каждая сторона транспортного средства движется с разной скоростью. По сути, это простейшая форма векторизации крутящего момента — тема, которую мы вскоре обсудим в другом выпуске Tech Talk.
На прямой крестовина находится в фиксированном положении и оба колеса вращаются с одинаковой скоростью. Однако при повороте крестовина может вращаться вокруг своей оси — процесс, при котором одна боковая шестерня вращается быстрее, а другая замедляется. Это позволяет колесам вращаться независимо друг от друга, и каждая сторона транспортного средства движется с разной скоростью. По сути, это простейшая форма векторизации крутящего момента — тема, которую мы вскоре обсудим в другом выпуске Tech Talk.
В приведенном ниже видео просто показаны основы дифференциала:
Но открытый дифференциал, являющийся простейшим по своей конструкции типом, имеет несколько недостатков.
Недостатки открытого дифференциала…
Основной принцип открытого дифференциала отдает предпочтение колесу с наименьшим сопротивлением, что позволяет ему вращаться быстрее. В принципе, это звучит хорошо — и в идеальном мире, в пределах повседневного использования, это было бы хорошо — вот почему многие пригородные автомобили используют открытые дифференциалы. Но в сценариях, когда одному колесу не хватает сцепления с поверхностью, это может стать проблемой.
Если одно колесо начнет проскальзывать – из-за дождя, льда или даже рыхлого песка – открытый дифференциал позволит проскальзывающему колесу свободно вращаться, а другое колесо вообще лишит привода. Такая же ситуация может возникнуть при прохождении поворотов на высокой скорости, когда отдельные колеса могут потерять сцепление с дорогой из-за дорожного покрытия или дроссельной заслонки. В таких ситуациях управление и даже поступательный импульс затруднены, а реакции на управление не такие острые и прямые, как необходимо.
Однако существуют разные типы различий, некоторые из которых созданы для решения этой проблемы. Они известны как дифференциалы повышенного трения и являются лишь одним из многочисленных типов дифференциалов.
Какие еще типы дифференциалов существуют?
Дифференциал повышенного трения (LSD) — это наиболее распространенный альтернативный тип дифференциала, который часто используется в высокопроизводительных автомобилях для улучшения управляемости и общего уровня сцепления с дорогой. Внутри группы ЛСД есть два основных подраздела:
- Механический LSD — в механических LSD используется подпружиненная система на выходных валах, которая реагирует на центростремительную силу (силу, действующую по прямой линии от центра вращения). Они допускают проскальзывание и разные скорости колес до определенного момента, но когда скорость одного колеса сильно отличается от скорости другого, включается пружинная система, частично или полностью блокирующая дифференциал.
 Эта система накладывает ограничения на принцип наименьшего сопротивления, допуская это только до определенного момента. Механические LSD нашли хорошее применение во многих автомобилях, например, в Renault Megane RS, для улучшения управляемости.
Эта система накладывает ограничения на принцип наименьшего сопротивления, допуская это только до определенного момента. Механические LSD нашли хорошее применение во многих автомобилях, например, в Renault Megane RS, для улучшения управляемости. - Электронный LSD — Электронный LSD, или e-diff , использует компьютерные датчики, определяющие скорость вращения колес. Когда обнаруживается, что одно колесо вращается слишком быстро по отношению как к скорости движения (км/ч или миль/ч), так и к скорости другого ведущего колеса, компьютер запускает электронный привод, который либо частично, либо полностью блокирует дифференциал, регулируя индивидуальное колесо. скорость соответственно. Volkswagen Golf GTI особенно использовал электронный дифференциал, начиная с Golf 7 GTI Performance Pack.
Блокируемые дифференциалы — еще один распространенный тип дифференциалов, чаще встречающийся на внедорожниках, таких как Jeep Wrangler и Mercedes-Benz G-Class. Это традиционно открытые дифференциалы, но с возможностью блокировки дифференциала для распределения фиксированного крутящего момента на любое колесо. В грязных условиях они обеспечивают постоянный привод каждого колеса, что обеспечивает максимальное сцепление на скользких поверхностях. Блокируемые дифференциалы могут быть как с механическим, так и с электронным управлением.
Это традиционно открытые дифференциалы, но с возможностью блокировки дифференциала для распределения фиксированного крутящего момента на любое колесо. В грязных условиях они обеспечивают постоянный привод каждого колеса, что обеспечивает максимальное сцепление на скользких поверхностях. Блокируемые дифференциалы могут быть как с механическим, так и с электронным управлением.
Mercedes-Benz G-Класса оснащен тремя переключателями для блокировки дифференциалов
Межосевые дифференциалы — это тип дифференциала, который традиционно используется как в полноприводных автомобилях, так и в полноприводных (AWD). Там, где дифференциалы традиционно используются для распределения крутящего момента между колесами на одной ведущей оси, центральные дифференциалы позволяют распределять крутящий момент между передней и задней осями. Межосевые дифференциалы обычно встречаются в двух основных вариантах:
- В полноприводных автомобилях центральный дифференциал часто позволяет полностью отключить переднюю или заднюю ось, что снижает расход топлива и общий износ.
 Неведущая ось может быть повторно включена – как правило, в состоянии покоя – при пересечении пересеченной местности, требующей дополнительных ведущих колес. Это чаще всего встречается в бакки / пикапах и внедорожниках 4 × 4.
Неведущая ось может быть повторно включена – как правило, в состоянии покоя – при пересечении пересеченной местности, требующей дополнительных ведущих колес. Это чаще всего встречается в бакки / пикапах и внедорожниках 4 × 4.
Заключение
Хотя базовая концепция дифференциала может быть довольно простой, многочисленные различные типы дифференциалов были разработаны для того, чтобы адаптировать базовую конструкцию к текущим потребностям. В то время как все современные автомобили имеют по крайней мере один дифференциал, нередко можно найти высокопроизводительные или внедорожные автомобили с двумя или даже тремя дифференциалами. Хотя все они могут выполнять разные функции, их основная функция остается неизменной — позволять распределять крутящий момент в различной степени либо спереди назад, либо из стороны в сторону.
Обязательно следите за нами в социальных сетях, чтобы не пропустить наш следующий сегмент Tech Talk: Что такое Torque Vectoring? Скоро…
Автор: Roger Biermann
2.
