Если есть категория с как получить в: Как получить категорию B, если есть C или на трактор?

Содержание

«Как получить категорию А, если есть Б и С?» — Яндекс Кью

Как получить Права Категории А или А1 при наличии В

Водительское удостоверение категории В является самой распространенной категорией водительских прав. Данная категория разрешает управлять легковыми автомобилями общей массой 3.5 тонны и с количеством пассажирских мест до 8. Легковые автомобили все больше и больше заполоняют дороги городов, образовывая пробки и затрудняя, замедляя передвижение. Открытие категории А – выход из сложившейся ситуации. Законодательство Украины упрощает открытие младшей категории, если есть старшая, с условием подтверждённого стажа вождения более 1го года. В данной статье мы поговорим про разницу мотоциклетных категорий, и про то как открыть категорию А или А1, при наличии старшей категории.

Разница категорий А и А1

Чтобы понять, как получить права категории А или А1 при наличии В, сначала нужно разобраться, какая именно из двух существующих мотоциклетных категории вам подойдет лучше.

До 2013го года существовала только категория А, позволяющая управлять 2х колесными транспортными средствами – мотоциклами. На все маломощные ТС (мопеды, скутера, мотороллеры) водительское удостоверение не требовалось. Но в связи с увеличением таких средств передвижения на дорогах общего пользования в 2013м году появились права категории А1.

На чем можно ездить с категорией А? В чем отличие от категории А1?

— с категорией А1 разрешается управление мопедами, мотороллерами, скутерами с объемом двигателя до 50 куб см, или мощностью электродвигателя до 4 кВт;

— категория А подразумевает управление двухколесными ТС, мотоциклами, также мопедами, скутерами и мотороллерами, если их объем двигателя превышает 50 кубическим сантиметров, а мощность электромотора выше 4 кВт.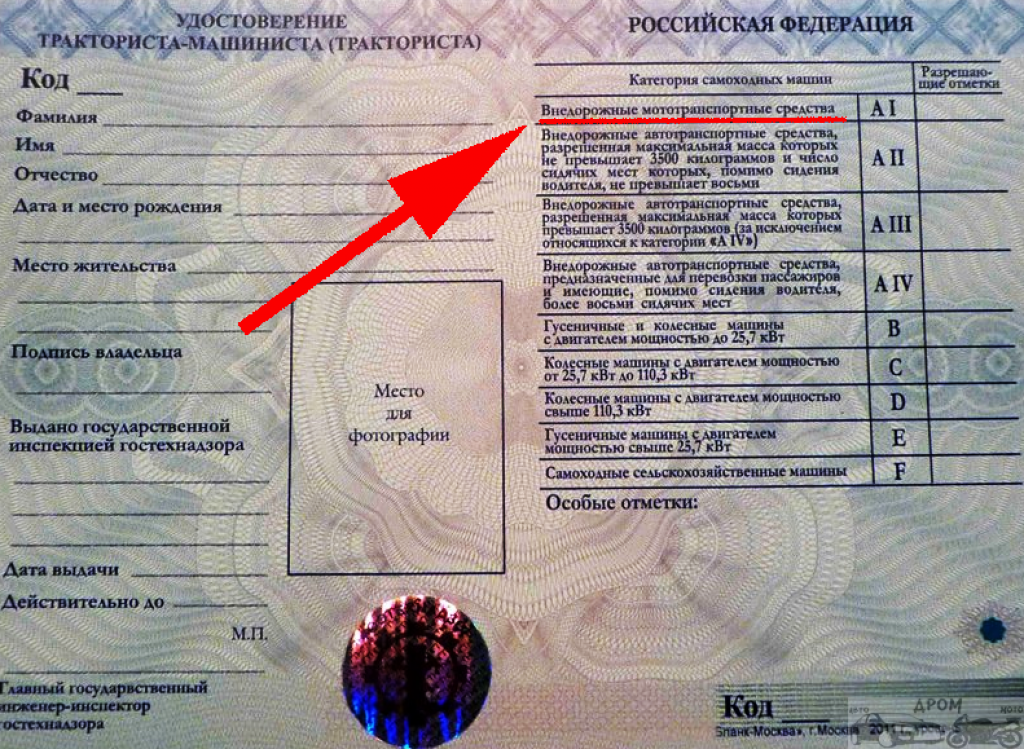

Курсы вождения на мотоцикле доступны для всех желающих с 16-ти лет. Есть одно исключение, даже при наличии открытой категории А, мотоциклом с двигателем от 350 см3 разрешено управлять только с 18-ти лет.

Открытие категории А, если есть Б

Разобравшись с существующими мотоциклетными категориями можно смело переходить к нашей основной теме. Владельцам старшей категории В (Б), при желании открыть одну из младших категорий, при наличии стажа от 1го года, сдавать второй раз теорию не нужно! Сдача экзамена в сервисном центре МВД заключается только в сдаче практической части. Для открытия младшей категории необходимо сделать следующее:

— собрать пакет документов, пройти медкомиссию;

— обратиться в СЦ МВД (сервисный центр МВД) для допуска к экзамену;

— подготовиться к практическому экзамену, путем посещения автошколы и докатки необходимого количества часов.

Автошкола «Антарес» в городе Павлоград предоставляет возможность докатки и открытия младшей категории по самым приемлемы ценам.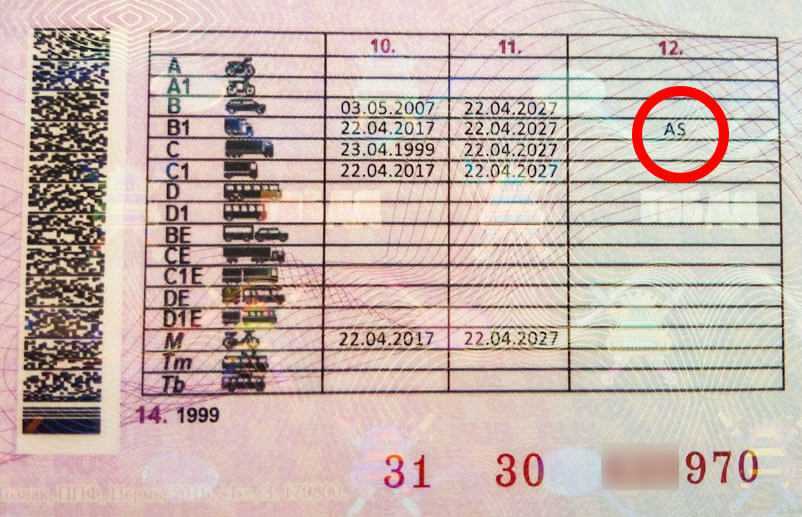 Перейдя по данной ссылке, вы узнаете сколько стоит сдать на права на мотоцикл и сможете ознакомиться со всеми услугами нашей автошколы.

Нужно ли сдавать теорию на категории А, если есть категория Б, мы узнали, а как обстоят дела с практикой?

Сдача практического экзамена в сервисном центре МВД на младшую категорию

Как указывалось выше, сдача практической части обязательна. После докатки необходимого количества часов в автошколе с инструктором, вы получаете соответствующий документ, допуск к экзамену в СЦ МВД. И после этого, если подтверждённый стаж на старшей категории больше 1го года, сдаете практическую часть непосредственно в сервисном центре.

Некоторые поступают иначе. Открывают сразу 2 категории, что не запрещено законом.

Одновременное открытие двух категорий

К примеру, одновременное открытие категории В (Б) и категории А1 в Украине, не запрещается, а местами даже поощряется. В таких случаях обучение происходит следующим образом. Во время обучения автошкола проводит лекционные занятия по старшей категории, а практику – сразу для двух. В таком случае ученик должен понимать, что времени, потраченного в автошколе, будет больше, чем при открытии одной категории, и отнестись к этому необходимо с полной серьезностью.

Что касается экзаменационной части в СЦ МВД – там проходит все по такой же схеме. Теорию вы сдаете 1 раз по старшей категории, после чего приступаете к двум практическим экзаменам на соответствующих видах транспорта.

Автошкола «Антарес» в городе Павлоград приглашает всех желающих обучиться вождению на любом виде транспорта. Наша школа вождения имеет аккредитацию на все виды категорий. Также, при наличии категории В, у нас вы сможете выучиться на права категории А, по ценам радующим глаз. Набор в новые группы проходит регулярно! Наши двери всегда открыты!

Наверх

Как определить новую категорию в теории категорий?

Почему для морфизма выбрали «гомоморфизмы групп»?

Понятие категории должно охватывать три вещи:

Объекты, что бы это ни значило;
Морфизмы между этими объектами, то есть то, как мы перемещаемся между объектами, что бы это ни значило;
Композиция морфизмов, т. е. как соединить морфизмы в новый морфизм;

Мы также хотим, чтобы композиция была ассоциативной, потому что это свойство присутствует почти везде. И мы также хотим, чтобы у каждого объекта был особый «тождественный» морфизм, который, кажется, есть почти везде.

Итак, учитывая группу как объект, выбор морфизма невелик. Это может быть просто функция, но тогда мы просто рассматриваем групповую категорию как заданную категорию. Это может быть просто абстрактная «стрелка», но тогда нам придется вручную определять каждую и как их составить, проблематично. Плюс какой смысл? Так какой еще у нас есть выбор? Групповые гомоморфизмы возникают естественным образом.

Обратите внимание на важную вещь: понятие группы и группового гомоморфизма было изобретено первым, и только потом кто-то понял, что оно подходит для языка теории категорий. Я почти уверен, что то же самое можно сказать почти о каждой категории.

Почему сами группы являются объектами, а не элементами группы, как это является вашей общей точкой отсчета в теоретико-множественной перспективе?

Вы можете определять объекты по своему усмотрению. Но для такой категории, объекты которой являются элементами некоторой группы, какими могут быть морфизмы между этими элементами? Кажется, что нет естественного способа определить их. Что не значит, что это невозможно. Самое главное, однако, что некоторые категории более популярны, чем другие по простой причине: полезность.

Здесь вы много узнаете о категориях топологических пространств, групп, модулей, колец и т. д. просто потому, что эти понятия полезны и имеют много общих свойств, которые можно описать на языке теории категорий.

Почему они придумали все эти ярлыки, такие как « мономорфизмы в группе «, и как они придумали все остальные утверждения? и т.д.

Я не совсем уверен, откуда берутся имена, это лингвистический вопрос. Но для идей это часто следующий процесс. Рассмотрим пример мономорфизма. В теории групп мономорфизм определяется как инъективный гомоморфизм групп. Аналогично для множества, модулей и т. д. Как же теперь выразить это свойство на языке теории категорий? Потому что инъективные функции/гомоморфизмы кажутся полезными. И определяются аналогично. Проблема в том, что эти определения основаны на элементах множества, группы, модуля и т. д. Но в категориях у нас нет элементов. У нас есть только объекты, морфизмы и композиция. Так это бесполезно? Не обязательно, требуется некоторый навык, чтобы выразить такое свойство в этих терминах, и иногда это можно сделать, иногда нет. Это не автоматический процесс и требует некоторого воображения.

Обратите внимание, что категориальное определение «мономорфизма» не обязательно совпадает с «инъективным отображением». Есть несколько категорий, в которых эти понятия расходятся, например. в категории всех делимых групп и гомоморфизмов групп есть категоричные мономорфизмы, не являющиеся инъективными.

Вы просто рисуете категориальные «объекты» из шляпы, а затем выбираете произвольную функцию (я полагаю, гомоморфизм) в качестве морфизма?

Нет. Обычно эти объекты и морфизмы естественным образом встречаются вместе. Топологические пространства естественным образом сопровождаются непрерывными отображениями.

Группы естественно возникают с групповыми гомоморфизмами. Векторные пространства естественным образом появляются вместе с линейными картами. Поэтому обычно вы берете некоторые математические структуры и функции между теми структурами, которые сохраняют эту структуру.

Однако обратите внимание, что существуют, возможно, более сложные (и абстрактные) категории, которые по-прежнему полезны. Примечательным примером является рассмотрение частично упорядоченного множества $(X,\leq)$ как категории, объекты которой являются элементами множества, и существует уникальный абстрактный морфизм (стрелка) $x\to y$ тогда и только тогда, когда $x\ leq y$ в $X$. Затем эту идею можно использовать, например, в так называемой теории пучков.

Как мы узнаем, являются ли два объекта в категории одинаковыми или нет?

О выборе экзистенциальных воплощений

Предположим, что мы выбрали одноэлементный элемент $\{a\}$ из $\mathbf{Set}$. И предположим, что мы выбрали одноэлементный $\{b\}$ из $\mathbf{Set}$.
Как мы можем знать, выбрали ли мы один и тот же синглтон или нет?

Если вы имеете в виду обычное равенство ($=$), когда говорите «один и тот же» ¹ , то вы не можете этого знать.

Сравните следующий тесно связанный вопрос: допустим, у нас есть $\exists x \in \mathbb{N}. x \ \text{even}$ в качестве лежащего поблизости предположения. Если мы воспользуемся обычными правилами исчисления естественной дедукции, то теперь мы можем применить правило «экзистенциального исключения» к а) получению новой переменной, скажем, $y$, и к б) получению утверждения $y\ \text{even}$ как новое предположение. Давайте снова применим исключение к тому же оператору, чтобы снова получить другую новую переменную $z$ и новое предположение $z\ \text{even}$. Можем ли мы сделать вывод, что $y = z$? Нет мы не можем.

Можно утверждать, что вы сделали то же самое в своем вопросе. Вы предположили, что $\exists w. \{w\} \in \mathbf{Set}$ и создал его дважды, используя новые переменные $a$, $b$.

Точно так же, если мы ссылаемся на синглтон $\{a\}$, то как мы можем ссылаться на него во второй раз и убедиться, что это действительно тот же синглтон?

Такие же вопросы возникают и у тривиальных групп. Предположим, я выбираю две тривиальные группы. Как я узнаю, выбрал ли я один и тот же дважды или нет?

Опять же, нельзя. Сравните с $\exists G \in \mathbf{Grp}. G\ \text{тривиальный}$.

Обратите внимание, что все части теории категорий инвариантны относительно изоморфизмов . ² Это означает, что не имеет значения, «какую новую переменную» вы выберете, если они гарантированно изоморфны. Действительно, все тривиальные группы изоморфны, так что вы можете применить экзистенциальное исключение к $\exists G \in \mathbf{Grp}. G\ \text{тривиальные}$ столько раз, сколько пожелаете, и вставьте все полученные свежие переменные в произвольные места и в произвольном порядке в любые места, ожидающие тривиальных групп.

Инвариантность относительно изоморфизмов гарантирует вам, что это не имеет значения.

Равенство в математике и ZF

Позвольте мне объяснить часть того, что такое равенство в обычной математике, за исключением более сложных тем, таких как теория гомотопических типов. Осмелюсь сказать, что все знаки равенства, которые вы видели до сих пор, являются знаком равенства логики первого порядка (FOL). Обычно предполагаемая теория множеств ZF также является теорией над FOL . Это означает, что мы берем FOL в качестве базовой логики и добавляем аксиомы ZF в наш контекст предположений.

Если два выражения $\varphi$ и $\psi$ равны структурно равно (от POV уровня meta к FOL), то мы можем вывести $\varphi = \psi$ в рамках логики. С другой стороны, если они , а не структурно равны, то, как правило, мы застреваем без дополнительных аксиом в нашей теории ВОЛС. Рассмотрим следующее равенство, которое определенно должно быть верным, верно? $$\{a \in \mathbb{Z} \ |\ a\ \text{четный}\} = \{a \in \mathbb{Z} \ |\ (a+1)\ \text{нечетный}\ }$$

Но LHS и RHS не структурно равны. К счастью, если мы предполагаем работать в ZF, мы можем призвать на помощь аксиому экстенсиональности ZF. Он предлагает свести равенство множеств к принадлежности к множествам: $$\forall x\ y.\ (\forall z. z \in x \Leftrightarrow z \in y) \Rightarrow x = y$$

Затем, в свою очередь, отношение принадлежности часто сводится к равенству объектов внутри множества. Допустим, мы просим $c \in \{a, b, c, d\}$. Эквивалентно мы можем спросить, является ли $c=a \vee c=b \vee c=c \vee c=d$. В этом духе мы можем сказать, что аксиома экстенсиональности сводит равенство множеств даже к равенству членов этих множеств.

Почему мы не можем распространить равенство на изоморфизмы (легко)

Теперь вы можете спросить, почему мы не делаем то же самое, скажем, с изоморфными группами:

$$\forall \\text{groups } G\ H.\ (G \ \text{изоморфен}\ H) \Rightarrow G = H$$

И причина в том, что эта аксиома — при использовании в нашем обычном контексте теории множеств ZF — сразу же приводит к противоречиям. Чтобы показать одно легкое противоречие, обозначим базовое множество группы $G$ через $\mathcal{U}(G)$. Тогда мы можем написать следующее истинное утверждение:

Пусть $G$ — группа слагаемых целых чисел. Пусть $x \in \mathcal{U}(G)$. Тогда $x \in \mathcal{U}(G)$.

Теперь выберем группу, изоморфную $G$, скажем, группу, порожденную некоторым фиксированным $a$, т. е. $H := \langle a \rangle$. Основная теория групп говорит нам, что группы $G$ и $H$ изоморфны. Следовательно, по нашей предварительной аксиоме мы получили бы $G = H$. Это, в свою очередь, в контексте FOL и обычных правил естественной дедукции означает, что мы можем взять любое истинное утверждение и заменить вхождения $G$ на $H$ — даже только в некоторых местах. 9я\ |\ я \in \mathbb{Z}\}$.

(Кстати, в более простом примере использовалось бы кодирование групп как кортежей базового набора, оператор и доказательства групповых аксиом. Тогда из $G = H$ мы могли бы сразу вывести противоречие $ \mathcal{U}(G) = \mathcal{U}(H)$.