Из чего состоит дифференциал: устройство, неисправности и методика выбора |

Что собой представляет дифференциал

Дифференциал является весьма интересным механическим устройством, известным людям с глубокой древности.

Сравнительно недавно считалось, что впервые механизм, работавший согласно принципу дифференциала применялся в антикитерском механизме, являющем собой весьма интересную находку, поднятую с морского дня. Это не что иное, как своеобразный древнейший калькулятор, предназначенный для осуществления астрономических вычислений. Несмотря на свою древность, идея дифференциала получила истинное признание лишь после появления автомашин.

Что представляет собой дифференциал и каково его назначение

В машине дифференциал является особым механизмом , который распределяет угловые скорости и момент вращения на колёса от основной передачи. Это необходимо для того, чтобы автотранспорт нормально поворачивался, при этом не нарушая равномерность сцепления колёс. При попытке развернуть движущуюся повозку с жёсткой осью вы непременно столкнётесь с тем, что колесо, располагающееся внутри радиуса, начинает пробуксовывать.

В то же время колесо, располагающееся на наружной дуге, которое должно двигаться на порядок быстрее, утрачивает сцепление с поверхностью. Проще говоря, оказывается, что крайне проблематично совершать поворот с парой колёс, насаженных на единую ось. Остаётся лишь выразить сочувствие несчастным лошадям, которым приходится таскать неповоротливые телеги.

Но автомобиль – не телега и в том числе потому, что при совершении им поворотов активируется дифференциал, распределяющий скорость вращения таким образом, чтобы колёса замедлялись внутри дуги поворота и ускорялись в 3 раза при движении по внешней дуге. Это происходит исключительно благодаря механическому распределению момента вращения, без участия со стороны водителя.

Место расположения дифференциала

ПОДРОБНЕЕ ПРО ⇒ ДИФФЕРЕНЦИАЛЫ ⇐ ЧИТАЙТЕ В ИСТОЧНИКЕ

Месторасположения дифференциала диктуется используемым в авто типом привода:

• В полноприводных машинах наряду с полным приводом устанавливается в раздаточной коробке межосевой дифференциал (распределяющий усилия между задней и передней осями) и межколёсные на каждую из осей;
• В автомашинах с задним приводом монтируется в заднем мосту на оси ведущей;
• Переднеприводные автомашины оборудованы передним дифференциалом, располагающимся в коробке передач;
• Для подключаемого полного привода не требуется межосевого распределителя, в данных авто на каждую ось монтируют межосевой дифференциал.

Дифференциал ставится на ведущую ось потому, что его назначением является распределение момента вращения, поступающего от двигателя, а, следовательно, на оси ведущей.

Особенности устройства и принцип работы

В техническом плане дифференциал обладает весьма простой конструкцией, которая при этом способна выдерживать существенные нагрузки.

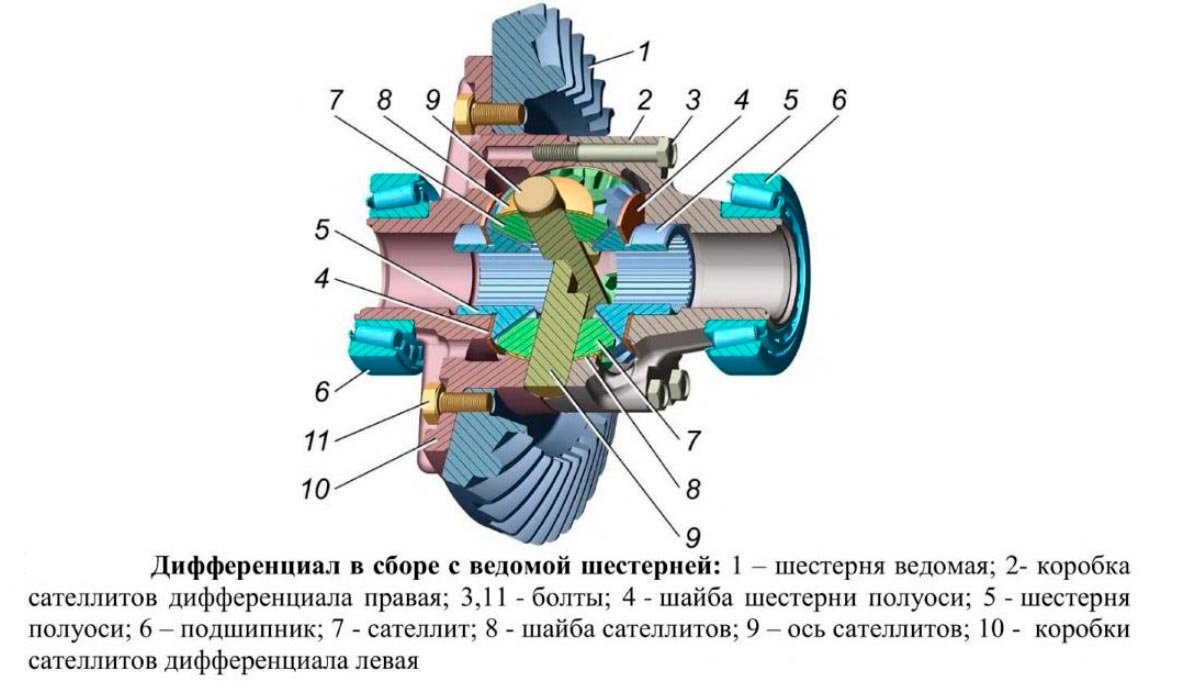
По типу он являет собой редуктор планетарный, снабжённый полным набором необходимых составляющих. Он состоит из:

• Шестерней полуосей, соединённых с сателлитами и не контактирующих с прочими составляющими дифференциала;
• Сателлитов, закреплённых в «чашке» ведомой шестерни, из-за чего они вращаются одновременно;
• Ведомой шестерни, связанной с шестерёнками-сателлитами и основной передачей;
• Шестерни основной передачи, подающей на дифференциал вращение от КПП.

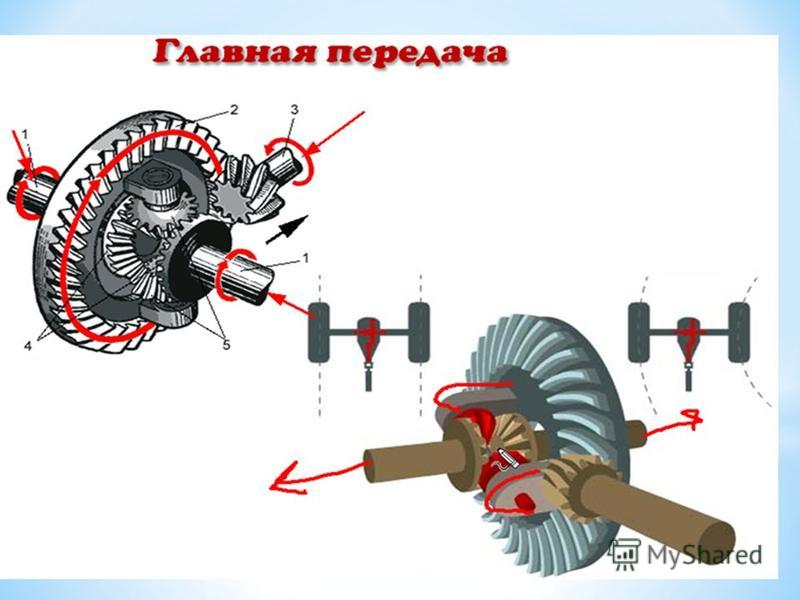
Принцип работы

Дифференциал функционирует следующим образом:

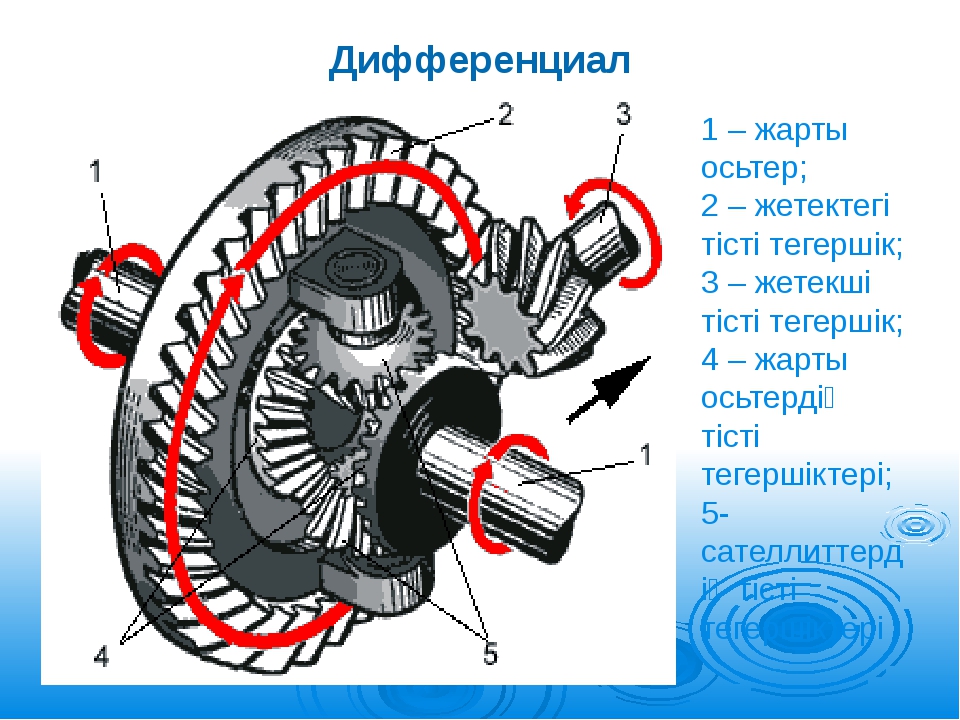
1. От КПП отходит валик основной передачи, от которого вращение поступает на шестерёнку ведомую;
2. Шестерёнка ведущая вместе со скреплённой с ней «чашей» (водилом) принимают крутящий момент;
3. При вращении «чаша» и шестерёнка ведома активизируют движение шестерёнок-сателлитов;
4. Сателлиты передают вращение на полуоси;
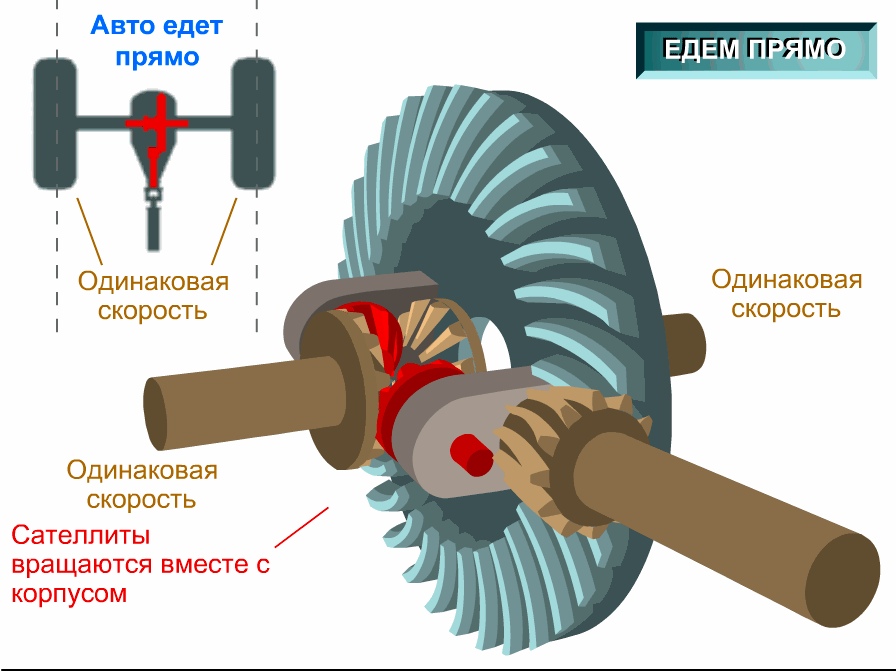
5. Если нагрузка на оси равномерна (при движении автомашины по прямым дорогам с равномерным покрытием) то вращение сателлитов не происходит.
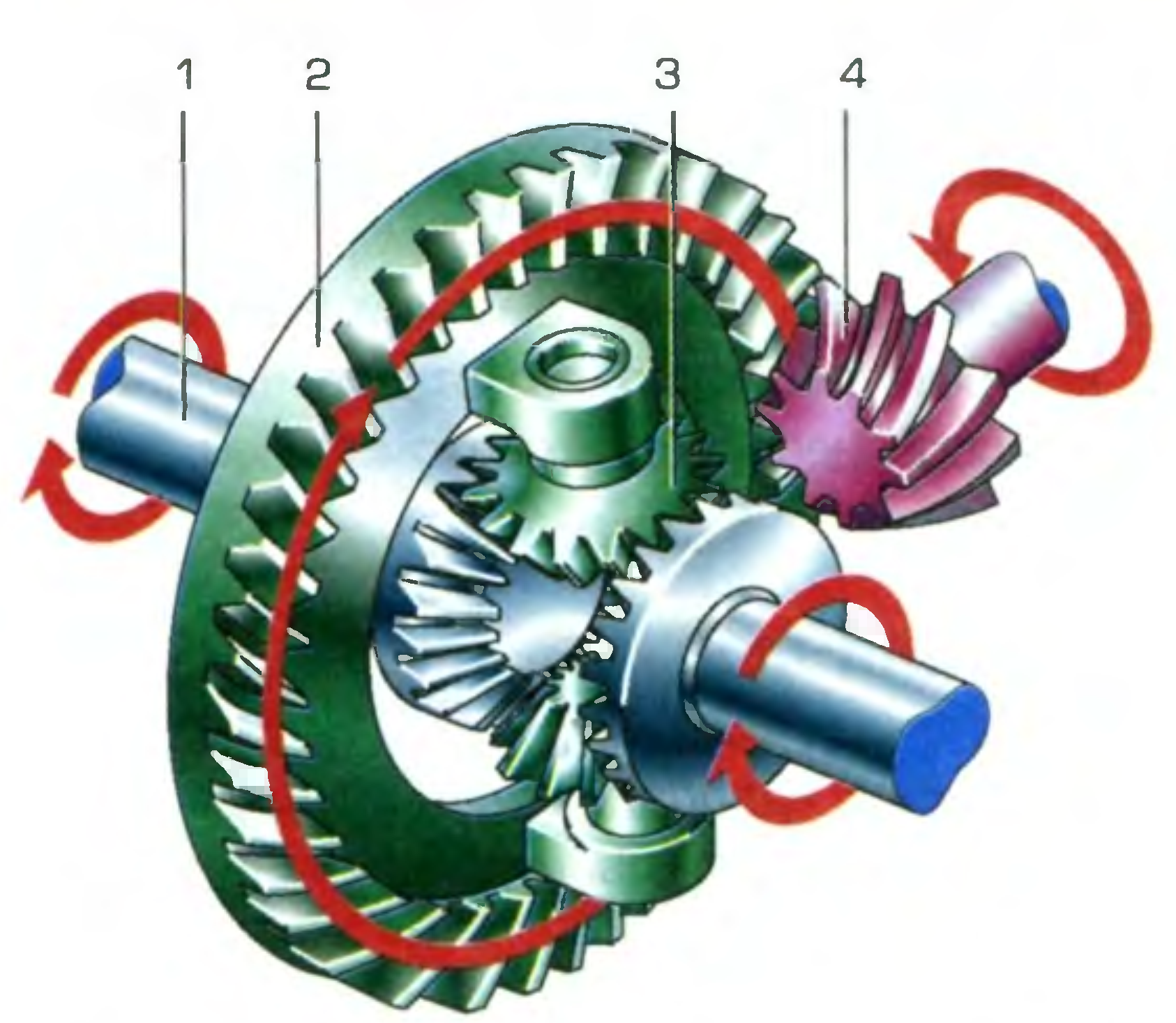   Функционирует исключительно ведомая шестерёнка, в чьей чаше крепятся сателлиты. Вместе с ней они описывают обороты, не осуществляя при этом вращений вокруг собственной оси. Момент вращения, таким образом, поровну на все оси.
6. При повороте автомашины, когда одно колесо должно замедлить движение, в то время, как второе – ускорить его, сателлиты приводятся в движение. Коническая зубчатая передача при вращении ускоряют одну полуось и замедляют другую. Проще говоря, они осуществляют перераспределение момента вращения в требуемой пропорции без потери усилий.
7. В случае пробуксовки 1-го колеса активируется блокировочный механизм, без использования которого на колесо, вращающееся быстрее, пришлось бы потратить без остатка весь момент вращения. Без применения авто останавливается в случае попадания хоть одного колеса на любую скользкую поверхность.

Плюсы и минусы

Главный плюс дифференциала заключается в том, что он позволяет осуществлять повороты. Каждое колесо на ведущей оси оперативно, автоматически подстраивается под особенности дорожной ситуации, без какого либо участия со стороны водителя. Это в десятки раз повышает маневренность и безопасность машины. На сегодняшний день различные конструкции дифференциала применяются на всех автомашинах.

Другое достоинство заключается в высоком уровне надёжности узла. Планетарной передаче под силу выдерживать существенные нагрузки. В то же время конструктивные особенности некоторых разновидностей дифференциала способствуют повышению их уровня мощности и износостойкости.

Ключевым минусом дифференциалом является необходимость применения блокировочного механизма для того, чтобы машина могла двигаться как по трудным дорогам, так и по льду. Все типы блокировки должны применяться в обязательном порядке. Следовательно, создаётся вспомогательный механизм, который с течением времени может сломаться.

Помимо того, следует помнить о необходимости контроля за состоянием узла. Это дополнительный узел, в котором следует периодически менять масло, хотя и не слишком часто, а также следить за износом всех элементов конструкции. Надо отметить, что большинство владельцев автомашин забывают о важности данной процедуры.

Разновидности дифференциалов

С течением времени данный аппарат активно совершенствовался и изменялся. На сегодняшний день в автомобилестроении активно применяются всевозможные разновидности дифференциалов, исходя из тех нагрузок, на которые рассчитано авто, для каких дорог оно предназначено и какие цели ставил перед собой конструктор.

• Согласно распределению усилий на полуоси дифференциал может быть несимметричным и симметричным. В последнем случае шестерни имеют равное количество зубцов, что позволяет симметрично распределить вращения. Если количество зубцов неравное, то распределение усилий происходит несимметричным образом, что крайне выгодно внедорожникам высокого уровня проходимости.
• Согласно конструктивным особенностям различают три типа дифференциалов: червячный, цилиндрический и конический. Название диктуется типом передачи, применяемым для осуществления вращения полуосей. На сегодняшний день наибольшей популярностью пользуются модели конического типа.

Разновидности блокировки дифференциала

Блокировочная система была создана для внедорожников, для которых пробуксовка любого из колёс может привести к остановке авто.

ПОДРОБНЕЕ ПРО БЛОКИРОВКИ ДИФФЕРЕНЦИАЛА

Различают три главных типа блокировки:

1. Электронная блокировка. Являет собой имитацию функционирования дифференциала. Электроблокировка применяется в антипробуксовочных электросистемах. В случае необходимости тормоз замедляет буксующее колесо. После этого усилие перераспределяется дифференциалом, увеличивая нагрузку на 2-ю полуось, характеризующуюся лучшим сцеплением с дорожным полотном.
2. Самоблокировка либо автоблокировка. Это система, облегчающая процесс управления машиной, избавляя тем самым водителя от необходимости лично блокировать дифференциал. Данный тип также именуется дифференциалом повышенного трения.
3. Ручная блокировка дифференциала. Данная система предполагает самостоятельное включение и выключение водителем блокировки согласно собственному усмотрению. Возле места водителя располагается клавиша либо рычаг управления блокировкой, посредством которых осуществляется принудительная остановка процесса вращения сателлитов вокруг собственной оси. Работа дифференциала фактически начинается так же, как и во время движения по прямой, равномерно распределяя усилие на обе оси. В процессе этого происходит существенное ухудшение управляемости, поскольку крайне проблематично осуществлять повороты, если дифференциал заблокирован.

Различают два типа самоблокирующихся дифференциалов:

1. Speed Sensitive. Блокировка осуществляется посредством вискомуфты, срабатывающей тогда, когда одна полуось движется быстрее другой.
2. Torque. Блокировка, активизирующаяся от разницы момента крутящего момента на полуосях. Во время пробуксовки активируются гасители скорости, которые подтормаживают полуось, которая вращается быстрее другой.

В современных автомашинах применяется несколько разновидностей дифференциалов:

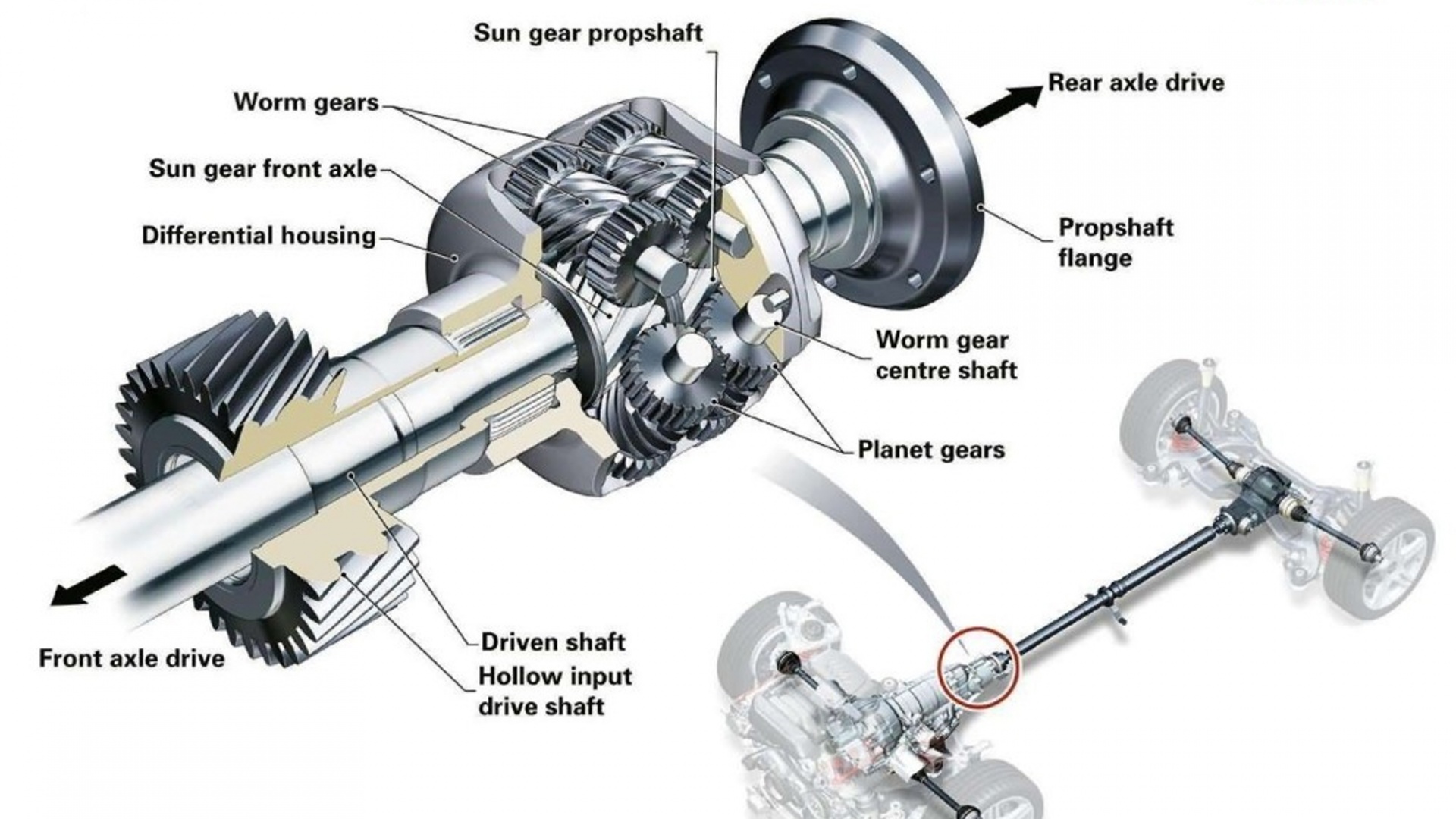
• Torsen. Это коническо-червячный, комбенированный механизм. Благодаря своей высокой надёжности и мощности он применяется для езды в условиях крайнего бездорожья.
• Кулачковая (полная) блокировка. Предполагает ручную блокировку из салона авто. Довольно неудобен, но, не смотря на это, данный вид продолжает использоваться на всех внедорожных автомобилях. Помимо того существует довольно много сторонников данного способа блокировки.
• Дисковая блокировка. Являет собой конструкцию с несколькими дисками, муфтами и коническими шестернями. В случае разности в скорости вращения полуосей стыки между шестернями разъединяются, и происходит блокировка системы, вследствие чего скорость вращения полуосей выравнивается.
• Вискомуфта. Данное блокировочное устройство базируется на использовании жидкости с переменной влажностью. Уровень вязкости данной жидкости зависит от скорости её перемещения (соотношения скорости вращения правой и левой полуосей). Вплоть до 100-процентной блокировки контактных блоков дисков. Вискомуфту монтируют на легковые автомашины и кроссоверы. Она не подходит для использования в условиях крайнего бездорожья.
• Квайф. Это наиболее простая конструкция. Её ключевая особенность заключается в применении нескольких пар сателлитов, которые сцепляются друг с другом. Возникающая сила трения заставляет механизм автоматически подстраиваться под дорожные условия, осуществлять грамотное распределение момента вращения во время пробуксовки и поворотов.

Итог

На сегодняшний день дифференциал применяется абсолютно на всех автомашинах, что является свидетельством его незаменимости. Для большинства владельцев авто не имеет значения что именно располагается под днищем их «железного коня». Тонкости и нюансы данного узла интересуют разве что любителей автомобилей и езды по суровому бездорожью. Однако чем качественнее работает этот узел, тем безопаснее и увереннее может чувствовать себя автовладелец при совершении манёвров на дороге.

Сайт источник vaznetaz.RU

Дифференциал

	Главная > Учебные материалы > Математика:  Дифференциал
	1.Понятие дифференциала. 2.Свойства дифференциала. 3.Дифференциал сложной функции. 4.Приближенные вычисления с помощью дифференциала.
	9 10 11 12 13 14 15 16 17
	1. Понятие дифференциала.    Допустим функция y=f(x) определена на промежутке Х и дифференцируема в некоторой окресности точки xϵX, т.е. существует производная y’. Согласно теореме о связи бесконечно малых величин с пределами функции запишем:
	из рисунка 1 видно, что угол β равен сумме двух углов: ϕ и γ. tg ϕ = f'(x) в точке М, tg β — tg ϕ = а(∆x) представляет собой бесконечно малую величину, зависящую от ∆x.    ∆y/∆x = f'(x) + а(∆x)    где а(∆x) — бесконечно малая величина при ∆х →0, откуда    ∆y = f'(x)∆x + а(∆x)∆x из формулы можно увидеть, что приращение функции ∆y состоит из двух слагаемых: линейного относительно ∆x и нелинейного. Таким образом, дифференциалом функции называется главная, линейная часть приращения функции относительно ∆x, равная произведению производной на приращение независимой переменной.     dy =f'(x) ∆x или dy = f'(x) dx
	2. Геометрический смысл дифференциала.    Допустим задана функция y = f(x). Возьмем произвольную точку М(x,y). Дадим переменной x приращение ∆x. Тогда функция получит приращение ∆y = f(x+∆x) — f(x). (см.рис. 1). Проведем касательную к кривой y = f(x) в точке М, которая образует угол ϕ с положительным направлением оси Ох, т.е f'(x) = tg ϕ. Из прямоугольного треугольника МAB AB = MB · tg ϕ = ∆x tg ϕ = f’ (x)∆x т.е. dy = AB. Можно сказать что, дифференциал функции есть приращение ординаты касательной, проведенной к графику функции y = f(x) в данной точке, когда х получает приращение ∆x.		Рис 1. Геометрический смысл дифференциала.
	3. Свойства дифференциала.    Дифференциал имеет следующие свойства.    1. dc=0    2. d(cu)= c du    3. d(u+v)=du+dv          4. d(uv)=v du + u dv          5. d(u/v) = (v du — u dv) / v²
	3.Дифференциал сложной функции.    Дифференциал функции dy = f'(x) dx. Рассмотрим функцию y = f(u), где f(u) является сложной функцией, т.е. y = f(g(x)). Если функции y = f(u) и u = g(x) — дифференцируемые функции от своих аргументов, то производная сложной функции равна:    dy = f'(x) dx = f'(u) · u’dx = f'(u) du.    т.е. dy = f'(u) du
	4. Приближенные вычисления с помощью дифференциала.
	Из формулы ∆y = f'(x)∆x + а(∆x)∆x можно увидеть, что приращение функции приблизительно равно ее дифференциалу, т.к. величина а(∆x)∆x бесконечно малая. Именно поэтому, при достаточно малых значениях ∆x можно считать, что ∆y≈ dy т.е. f(x+∆x)≈f(x)+f ‘(x)∆x. Данная формула тем точнее, чем меньше значение ∆x. Это приближенное равенство можно применить в приближенных вычислениях.
	Пример:
	9 10 11 12 13 14 15 16 17

предназначение, методы и их особенности

На чтение 7 мин. Просмотров 4.7k.

Блокирование дифференциала – отличный метод улучшения возможностей для проходимости вашего автомобиля на бездорожье. Выбор лучшего варианта, а также его осознанное использование – вот ключ к успеху!

Автомобилям, которые постоянно передвигаются по бездорожью, всегда не хватает проходимости. Существует большое количество различных вариантов, которые могут помочь решить эту проблему, но самым правильным и полезным считается блокировка дифференциала. Если у машины есть межосевой дифференциал, то на нем, как правило, устанавливаются определенные блокировки, которые помогают преодолевать сложные дорожные условия. В большинстве случаев эта операция производится только для заднего моста, так как для переднего моста это не так эффективно и оправданно.

Необходимо отметить, что применять блокировку необходимо не всегда, ведь она влияет на поведение автомобиля и имеет свои плюсы и минусы. Для того чтобы выяснить целесообразность таких изменений, необходимо четко понимать как это работает, какие механизмы используются, а также разобраться в самой сути этих действий, то есть к чему приведет блокирование силового привода.

Смысл блокирования дифференциала в обеспечении вращение колес с разной скоростью, чтобы обороты колес одной оси различались, в зависимости от потребностей.

Когда автомобиль передвигается по бездорожью без блокировки, то по конструкции шасси какая-то полуось будет прокручиваться. Решается это путем блокировки, в чем и есть ее главное достоинство. Устанавливается такой механизм на внедорожниках и используется только на плохих участках дороги.

Свободный дифференциал работает по следующей схеме: когда колеса на одной оси начинают прокручиваться, то другое получает больший момент для преодоления препятствия. Когда же применяется блокировка дифференциала, то на колесо с лучшим зацепом начинает подаваться больший крутящий момент. Для того чтобы применить этот механизм, необходимо:

1. Ограничить движение сателлитов;
2. Приварить часть дифференциала к полуоси.

Типы блокировок

Выделяют различные типы блокирования силового привода автомобиля.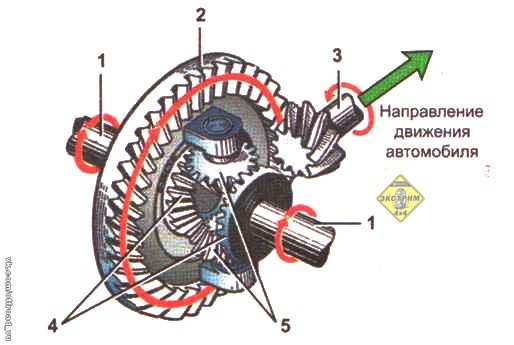 Если имеет место полная блокировка, то это означает полноценное сцепление различных элементов дифференциала, что позволяет перемещать полностью крутящий момент на одно из колес, имеющее максимальный зацеп.

Дифференциал

Что касается частичной блокировкой, то она предполагает ограничение передачи крутящего момента на разные полуоси с разным сцеплением.

Чтобы определить, какой момент необходим на каждое колесо, используется коэффициент блокировки. То есть, данный показатель помогает выяснить, какой крутящий момент необходимо передавать на колесо с хорошим зацепом и на то, которое прокручивается. Если коэффициент будет определяться неправильно, то это может привести к определенным поломкам.

Блокировку можно устанавливать либо на межосевых, либо на межколесных дифференциалах. Блокировать переднюю ось на полноприводной машине нет необходимости, так как это значительно снизит его управляемость на обычных дорогах.

Бывают несколько вариантов блокирования: автоматическое и принудительное. Последнее может включаться и выключаться водителем самостоятельно при необходимости, а поэтому она иногда называется ручной. В то же время автоматический вариант производится с применением определенных механизмов, которые называются самоблокирующимися дифференциалами.

Ручная блокировка

Ручная блокировка силового привода предполагает использование кулачковой муфты, то есть соединяет части дифференциала и полуоси. Для того чтобы ее включать или выключать применяется специальный механизм. Это может быть пневматический, механический, гидравлический или электрический привод.

Механический привод работает за счет определенной системы из тросов и рычагов, движение которых либо включает, либо выключает блокировку. Электрический вариант работает за счет специального двигателя, а активация происходит путем нажатия на кнопку в салоне. Что касается гидравлического и пневматического приводов, то здесь главными механизмами считаются цилиндры и пневмокамеры соответственно.

Такой тип блокировки необходим, если автомобиль используется как на бездорожье, так и на обычных дорогах. Крайне важно после преодоления препятствий выключать эту систему для избегания поломок и для комфортного передвижения.

дифференциал блокировка

Автоматическая блокировка

Когда речь идет об автоматической блокировке, которая основывается на дифференциале повышенного трения, это можно назвать неким компромиссом, так как реализуется он за счет сочетания работы полной блокировки и свободного дифференциала. Свободные дифференциалы бывают нескольких типов:

• Когда блокировка происходит при разном крутящем моменте на колесах;
• Когда блокировка происходит при отличии угловых скоростей полуосей.

Что касается первого типа, то он применяется на червячном дифференциале. Второй тип включает в себя механизмы с вязкостной муфтой, а также дисковый и электронно-блокирующийся дифференциал.

Дисковый дифференциал

Дисковый дифференциал – это симметричный механизм, которые включает в себя несколько групп фрикционных дисков.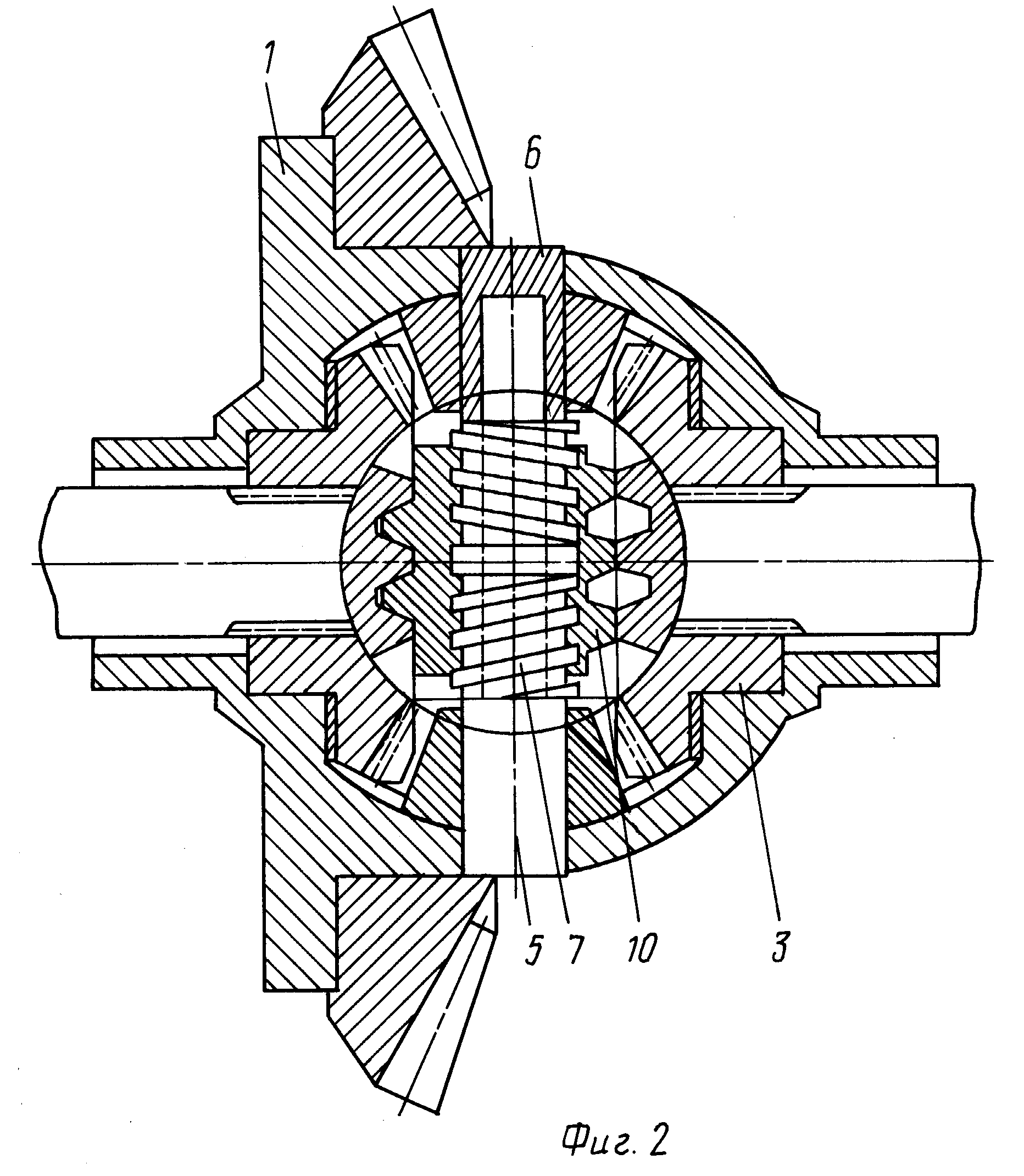 Одна группа соединяется с внешней частью дифференциала, а вторая связывается с полуосью. Работа этой системы обеспечивается за счет трения от разной скорости.

Дисковый дифференциал

Если автомобиль двигается прямо, то весь механизм работает как единое целое, с одинаковой частотой вращения. Когда какое-то колесо начинает двигаться быстрее, то фрикционные диски соответственно ускоряются и за счет силы трения крутящий момент на колесе с хорошим сцеплением увеличивается. Таким образом, дифференциал в некоторой мере блокируется и препятствие преодолевается.

Если в механизме используются пружины, то сжатие группы дисков будет постоянным, а если применяется гидравлический привод – она будет меняться в зависимости от ситуации.

Вязкостная муфта

Вязкостная муфта

Следующий тип – вязкостная муфта. Этот механизм состоит из группы перфорированных дисков, которые крепятся к самому дифференциалу и к валу привода. Они хранятся в специальном приспособлении, которое внутри имеет вязкое наполнение.

Когда вал привода и дифференциал имеет одинаковые обороты, то группа дисков вращается как один сплошной элемент. Когда же вал привода ускоряется, то какое-то количество перфорированных дисков также ускоряется, перемешивая жидкость и, таким образом, блокируя дифференциал. Вал, с другой стороны, получает больший крутящий момент. Когда скорость снова стабилизируется, то муфта автоматически выключается.

Вязкостная муфта используется либо в качестве блокировки межосевого дифференциала, либо как элемент автоматически подключаемого полного привода. Недостатком этого варианта считается склонность к перегреву, а также конфликтность с ABS. Поэтому в современных автомобилях такая система не применяется.

Электронный дифференциал является частью системы, которая препятствует пробуксовке. Когда колесо начинает прокручиваться, оно замедляется, а тяга передается на колесо с хорошим зацепом.

Червячный дифференциал

Когда имеет место разница между скоростью вращения на корпусе дифференциала и на приводном вале, может использоваться червячный дифференциал.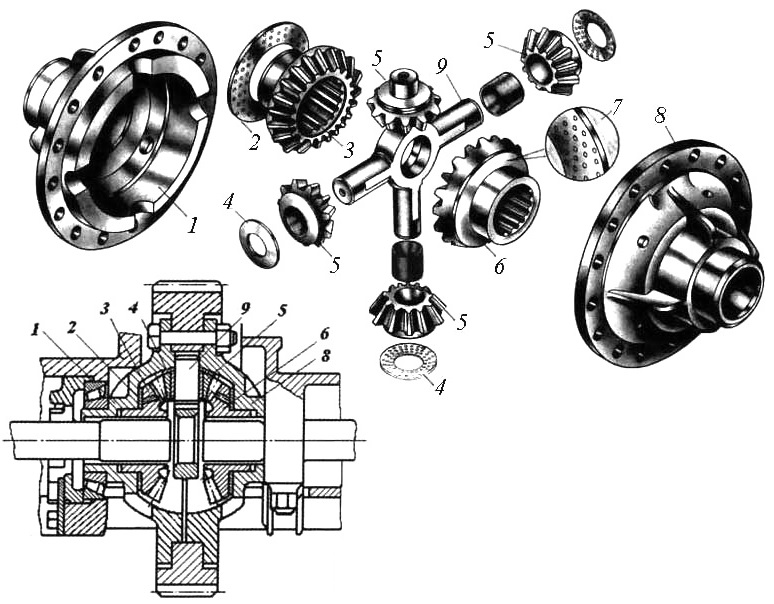 Когда колесо начинает прокручиваться и терять крутящий момент, он переходит на колесо, которое имеет хороший зацеп за счет блокировки. Она частичная и ее уровень определяется на основе количества потерянного момента.

Среди механизмов такого типа наиболее популярными считаются Torsenи Quaife, которые являются редукторами из червячных шестеренок. Червячная шестерня может влиять на остальные шестерни, но при этом оставаться независимой от них. Такое явление называют расклиниванием, и служит оно для блокировки. Такого типа дифференциалы могут использоваться как для межосевых, так и для межколесных блокировок.

Червячный дифференциал

Недостатки блокировки дифференциала

Несмотря на все положительные качества этого механизма, имеют место и некоторые минусы.

Когда автомобиль двигается по бездорожью, он очень часто может сталкиваться с искривленной траекторией. В таком случае, колеса начинают вращаться с разной скоростью, так как проходят разный путь за одинаковое время.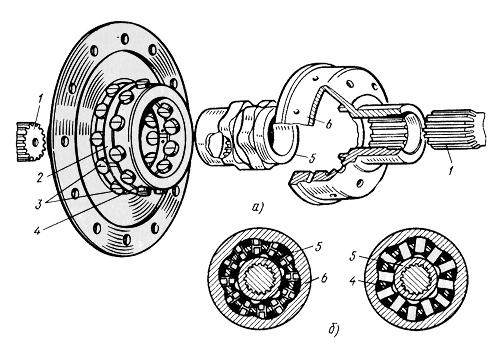 Например, при движении по кривой небольшого радиуса, внешнее колесо проходит больший путь, чем внутреннее. Для того чтобы внешнее колесо вращалось быстрее применяется межколесный дифференциал, который распределяет обороты по необходимости.

Когда же применяется блокировка, колеса соединяются и двигаются с одинаковой скоростью. Из-за этого внутреннее колесо будет буксовать, забирая максимально тягу, а внешнее будет прокручиваться. Такая ситуация на бездорожье может привести к тому, что будет вырыта колея, ухудшиться сцепление и преодолеть препятствие будет сложно. Поэтому при передвижении по небольшим кривым блокировку лучше отключать, если есть возможность.

Блокировка дифференциала – это очень распространенный метод повышения эффективности передвижения по бездорожью.

Однако, его необходимо использовать только в определенный случаях, иначе это приведет только к ухудшению проходимости или даже к поломке.

Дифференциал функции

Если функция дифференцируема в точке, то её приращение можно представить в виде суммы двух слагаемых

, где

. Эти слагаемые являются бесконечно малыми функциями при .Первое слагаемое линейно относительно ,второе является бесконечно малой более высокого порядка, чем .Действительно,

.

Таким образом второе слагаемое при быстрее стремится к нулю и при нахождении приращения функцииглавную роль играет первое слагаемоеили (так как).

Определение. Главная часть приращения функции в точке , линейная относительно,называется дифференциалом функции в этой точке и обозначается dy или df(x)

. (2)

Таким образом, можно сделать вывод: дифференциал независимой переменной совпадает с её приращением, то есть .

Соотношение (2) теперь принимает вид

(3)

Замечание. Формулу (3) для краткости часто записывают в виде

(4)

Геометрический смысл дифференциала

Рис. 2

Рассмотрим график дифференцируемой функции . Точкиипринадлежат графику функции. В точкеМ проведена касательная К к графику функции, угол которой с положительным направлением оси обозначим через. Проведем прямыеMN параллельно оси Ox и параллельно осиOy. Приращение функции равно длине отрезка . Из прямоугольного треугольника, в котором, получим

.

Изложенные выше рассуждения позволяют сделать вывод:

Дифференциал функции в точке изображается приращением ординаты касательной к графику этой функции в соответствующей её точке.

Связь дифференциала с производной

Рассмотрим формулу (4)

.

Разделим обе части этого равенства на dx , тогда

.

Таким образом, производная функции равна отношению её дифференциала к дифференциалу независимой переменной.

Часто это отношение рассматривается просто как символ, обозначающий производную функцииу по аргументу х.

Удобными обозначениями производной также являются:

, и так далее.

Употребляются также записи

, ,

особенно удобные, когда берется производная от сложного выражения.

2. Дифференциал суммы, произведения и частного.

Так как дифференциал получается из производной умножением её на дифференциал независимой переменной, то, зная производные основных элементарных функций, а также правила для отыскания производных, можно прийти к аналогичным правилам для отыскания дифференциалов.

1⁰. Дифференциал постоянной равен нулю

.

2⁰. Дифференциал алгебраической суммы конечного числа дифференцируемых функций равен алгебраической сумме дифференциалов этих функций

.

3⁰. Дифференциал произведения двух дифференцируемых функций равен сумме произведений первой функции на дифференциал второй и второй функции на дифференциал первой

.

Следствие. Постоянный множитель можно выносить за знак дифференциала

.

Пример. Найти дифференциал функции .

Решение.Запишем данную функцию в виде

,

тогда получим

.

.

4. Функции, заданные параметрически, их дифференцирование.

Определение. Функция называется заданной параметрически, если обе переменныех и у определяются каждая в отдельности как однозначные функции от одной и той же вспомогательной переменной – параметра t:

где t изменяется в пределах .

Замечание. Параметрическое задание функций широко применяется в теоретической механике, где параметр t обозначает время, а уравнения представляют собой законы изменения проекций движущейся точкина осии.

Замечание. Приведем параметрические уравнения окружности и эллипса.

а) Окружность с центром в начале координат и радиусом r имеет параметрические уравнения:

где .

б) Запишем параметрические уравнения для эллипса:

где .

Исключив параметр t из параметрических уравнений рассматриваемых линий, можно прийти к их каноническим уравнениям.

Теорема. Если функция у от аргумента х задана параметрически уравнениями , гдеидифференцируемые поt функции и , то

.

Пример. Найти производную функции у от х , заданной параметрическими уравнениями.

Решение. .

Дифференциал (математика) — Википедия

Материал из Википедии — свободной энциклопедии

Дифференциа́л (от лат. differentia «разность, различие») — линейная часть приращения функции.

Обозначения

Обычно дифференциал функции f{\displaystyle f} обозначается df{\displaystyle df}. Некоторые авторы предпочитают обозначать df{\displaystyle {\rm {d}}f} шрифтом прямого начертания, желая подчеркнуть, что дифференциал является оператором.

Дифференциал в точке x0{\displaystyle x_{0}} обозначается dx0f{\displaystyle d_{x_{0}}f}, а иногда dfx0{\displaystyle df_{x_{0}}} или df[x0]{\displaystyle df[x_{0}]}, а также df{\displaystyle df}, если значение x0{\displaystyle x_{0}} ясно из контекста.

Соответственно, значение дифференциала в точке x0{\displaystyle x_{0}} от h{\displaystyle h} может обозначаться как dx0f(h){\displaystyle d_{x_{0}}f(h)}, а иногда dfx0(h){\displaystyle df_{x_{0}}(h)} или df[x0](h){\displaystyle df[x_{0}](h)}, а также df(h){\displaystyle df(h)}, если значение x0{\displaystyle x_{0}} ясно из контекста.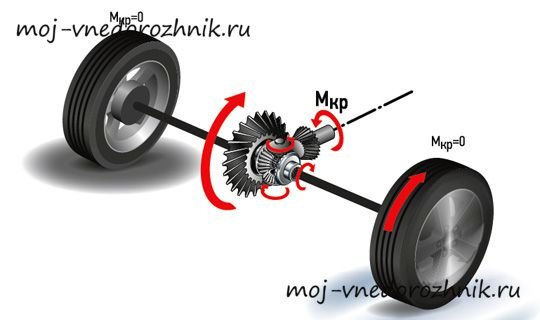

Использование знака дифференциала

Определения

Для функций

Дифференциал функции f:R→R{\displaystyle f\colon \mathbb {R} \to \mathbb {R} } в точке x0∈R{\displaystyle x_{0}\in \mathbb {R} } может быть определён как линейная функция

dx0f(h)=f′(x0)h,{\displaystyle d_{x_{0}}f(h)=f'(x_{0})h,}

где f′(x0){\displaystyle f'(x_{0})} обозначает производную f{\displaystyle f} в точке x0{\displaystyle x_{0}}, а h{\displaystyle h} — приращение аргумента при переходе от x0{\displaystyle x_{0}} к x0+h{\displaystyle x_{0}+h}.

Таким образом df{\displaystyle df} есть функция двух аргументов df:(x0,h)↦dx0f(h){\displaystyle df\colon (x_{0},h)\mapsto d_{x_{0}}f(h)}.

Дифференциал может быть определён напрямую, то есть, без привлечения определения производной, как функция dx0f(h){\displaystyle d_{x_{0}}f(h)}, линейно зависящая от h{\displaystyle h}, и для которой верно следующее соотношение

dx0f(h)=f(x0+h)−f(x0)+o(h).{\displaystyle d_{x_{0}}f(h)=f(x_{0}+h)-f(x_{0})+o(h). {m}}.

Свойства

История

Термин «дифференциал» введён Лейбницем. Изначально dx{\displaystyle dx} применялось для обозначения «бесконечно малой» — величины, которая меньше всякой конечной величины и всё же не равна нулю. Подобный взгляд оказался неудобным в большинстве разделов математики за исключением нестандартного анализа.

Вариации и обобщения

Понятие дифференциала содержит в себе больше, чем просто дифференциал функции или отображения. Его можно обобщать получая различные важные объекты в функциональном анализе, дифференциальной геометрии, теории меры, нестандартном анализе, алгебраической геометрии и так далее.

Литература

• Г. М. Фихтенгольц «Курс дифференциального и интегрального исчисления»

Дифференциальные уравнения — основные понятия

Онлайн-заметки Павла

Ноты Быстрая навигация Скачать

• Перейти к
• Ноты
• Задачи практики и задания еще не написаны. Пока позволяет время, я работаю над ними, однако у меня нет того количества свободного времени, которое я имел раньше, поэтому пройдет некоторое время, прежде чем здесь что-нибудь появится.
• Показать / Скрыть
• Показать все решения / шаги / и т. Д.
• Скрыть все решения / шаги / и т. Д.

• Разделы
• Введение в DE второго порядка
• Настоящие и отчетливые корни
• Разделы
• DE Первого Ордена
• Преобразования Лапласа
• Классы
• Алгебра
• Исчисление I
• Исчисление II
• Исчисление III
• Дифференциальные уравнения
• Дополнительно
• Алгебра и триггерный обзор
• Распространенные математические ошибки
• Праймер для комплексных чисел
• Как изучать математику
• Шпаргалки и таблицы
• Разное
• Свяжитесь со мной
• Справка и настройка MathJax
• Мои студенты

• Заметки Загрузки
• Полная книга
• Текущая глава
• Текущий раздел
• Practice Problems Загрузок
• Проблем пока не написано.
• Проблемы с назначением Загрузок
• Проблем пока не написано.
• Прочие товары
• Получить URL для загружаемых элементов

• Распечатать страницу в текущем виде (по умолчанию)
• Показать все решения / шаги и распечатать страницу
• Скрыть все решения / шаги и распечатать страницу

• Дом
• Классы
• Алгебра
  • Предварительные мероприятия
    • Целочисленные экспоненты
    • Рациональные экспоненты
    • Радикалы
    • Полиномы
    • Факторинговые многочлены
    • Рациональные выражения
    • Комплексные числа
  • Решение уравнений и неравенств
    • Решения и наборы решений
    • Линейные уравнения
    • Приложения линейных уравнений
    • Уравнения с более чем одной переменной
    • Квадратные уравнения — Часть I
    • Квадратные уравнения — Часть II
    • Квадратные уравнения: сводка
    • Приложения квадратных уравнений
    • Уравнения, сводимые к квадратичным в форме
    • Уравнения с радикалами
    • Линейные неравенства
    • Полиномиальные неравенства

Что такое дифференциальная ассоциация?

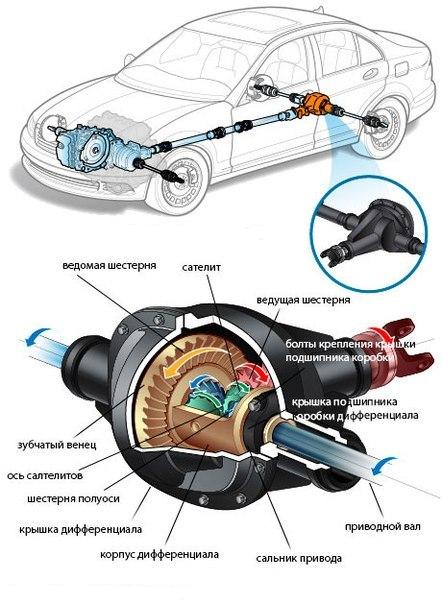Дифференциальная ассоциация — это теория преступного и правонарушительного поведения, разработанная в 1930-х годах американским социологом Эдвином Сазерлендом. Его главный принцип заключается в том, что преступление — это выученное поведение. Несовершеннолетний учится преступному поведению, живя в среде, где другие люди относятся к преступному поведению более благосклонно, чем следуют закону. В отличие от теорий, которые объясняют преступность внутренней предрасположенностью или преступным характером, дифференциальная ассоциация определяет его как процесс обучения.

Человек с руками на бедрах

Согласно теории дифференциальной ассоциации, все преступное поведение изучается, и нет никаких биологических или генетических оснований для преступного поведения.Изучение такого поведения происходит в группе, уже осведомленной о преступном поведении и вовлеченной в нее. Обучение включает в себя, как совершать преступления, и все объяснения для этого. Преступное поведение подкрепляется тем, что о нем отзываются положительно. Уважение социальных норм, таких как следование закону, вызывает у группы неуважение.

Теория дифференциальной ассоциации Сазерленда утверждает, что люди совершают преступное поведение не только потому, что их социальное окружение состоит из других, которые так поступают, но и из-за их относительной изоляции от тех, кто этого не делает.В зависимости от состава окружения человека дифференциальные ассоциации могут иметь разную степень продолжительности, важности или серьезности. Изучение преступного поведения включает в себя те же процессы, что и любое обучение. Чем дольше длится обучение, тем более укорененным оно становится. Это особенно верно при отсутствии какого-либо значительного воздействия некриминального поведения.

Теория дифференциальной ассоциации расходилась с другими теориями, которые утверждали, что преступность была результатом общих экономических факторов или психологических недостатков, которые могут вызвать бедность.Сазерленд не считал, что бедность обычно является единственной причиной преступного поведения, потому что это убеждение игнорировало преступления белых воротничков. Он также считал, что криминальная статистика искажена из-за этого упущения. Он считал, что теории о том, что преступление основано исключительно на классовой принадлежности, не подтверждаются.

Теория дифференциальных ассоциаций подвергалась критике как слишком общая и за то, что она не дает определения того языка, который делает преступное поведение приемлемым среди группы. Его также упрекали в том, что он не принимает во внимание такие вещи, как свобода воли или объясняет отдельные примеры преступного поведения отдельных лиц. Тем не менее, некоторые из основных принципов теории дифференциальных ассоциаций все еще используются сегодня и включены в другие теории преступного поведения. Кроме того, некоторые теоретики полагают, что маловероятно, чтобы какая-либо одна теория могла объяснить все условия и факторы, приводящие к преступному поведению.

Дифференциальные уравнения — Введение

Дифференциальное уравнение — это уравнение с функцией и одной или несколькими производными:

Пример: уравнение с функцией y и ее производная dy dx

Решение

Мы решаем , когда обнаруживаем функцию y (или набор функций y).

Есть много «уловок» для решения дифференциальных уравнений (, если их можно решить!).

Но сначала: почему?

Почему полезны дифференциальные уравнения?

В нашем мире все меняется, и , описывающий, как они меняются, часто заканчивается дифференциальным уравнением:

Пример: кролики!

Чем больше у нас будет кроликов, тем больше у нас будет кроликов.

Тогда эти кролики вырастут и тоже родят детей! Население будет расти все быстрее и быстрее.

Важными частями этого являются:

• население N в любое время т
• темп роста р
• Скорость изменения населения dN dt

Подумайте о dN dt как о «насколько меняется население с изменением времени в любой момент времени».

Представим, что темп роста r равен 0. 01 новых кроликов в неделю на каждого текущего кролика.

Когда популяция составляет 1000 , скорость изменения dN dt составляет 1000 × 0,01 = 10 новых кроликов в неделю.

Но это верно только для определенного времени и не включает тот факт, что население постоянно увеличивается. Чем больше популяция, тем больше у нас кроликов!

При населении 2000 мы получаем 2000 × 0.01 = 20 новых кроликов в неделю и т. Д.

Так что лучше сказать, что скорость изменения (в любой момент) — это скорость роста, умноженная на численность населения в этот момент:

dN dt = rN

И это дифференциальное уравнение , потому что оно имеет функцию N (t) и ее производную.

А какая мощная математика! Это короткое уравнение гласит, что «скорость изменения населения с течением времени равна скорости роста, умноженной на численность населения».

Дифференциальные уравнения могут описывать, как меняется население, как движется тепло, как вибрируют пружины, как распадается радиоактивный материал и многое другое. Это очень естественный способ описания многих вещей во Вселенной.

Что с ними делать?

Само по себе дифференциальное уравнение — прекрасный способ выразить что-либо, но его сложно использовать.

Итак, мы пытаемся решить их, превратив дифференциальное уравнение в более простое уравнение без дифференциальных битов, чтобы мы могли выполнять вычисления, строить графики, предсказывать будущее и так далее.

Пример: Сложные проценты

Деньги приносят проценты. Проценты могут быть начислены в определенное время, например, ежегодно, ежемесячно и т. Д., И добавлены к исходной сумме.

Это называется сложным процентом.

Но когда он начисляется непрерывно , тогда в любое время проценты добавляются пропорционально текущей стоимости ссуды (или инвестиций).

И по мере роста ссуды проценты по ней увеличиваются.

Используя t для времени, r для процентной ставки и V для текущей стоимости кредита:

dV dt = rV

И вот что интересно: это то же самое уравнение, которое мы получили с кроликами! Просто у него разные буквы.Итак, математика показывает нам, что эти две вещи ведут себя одинаково.

Решение

Дифференциальное уравнение говорит об этом хорошо, но его трудно использовать.

Но не волнуйтесь, это можно решить (с помощью специального метода, называемого разделением переменных), и в результате получится:

V = Pe ^rt

Где P — принципал (первоначальный заем), а e — число Эйлера.

Таким образом, непрерывно начисляемый заем в размере 1000 долларов США на 2 года с процентной ставкой 10% становится:

V = 1000 × e ^{(2 × 0.1)}

В = 1000 × 1,2 2140 . ..

V = 1221,40 $ (с точностью до цента)

Итак, дифференциальные уравнения хороши для описания вещей, но их нужно решать, чтобы быть полезными.

Дополнительные примеры дифференциальных уравнений

Уравнение Ферхюльста

Пример: снова кролики!

Помните наше дифференциальное уравнение роста:

dN dt = rN

Что ж, этот рост не может продолжаться вечно, потому что у них скоро закончится доступная еда.

Итак, давайте улучшим его, включив:

• максимальное население, которое может содержать еда тыс.

Парень по имени Ферхюльст во всем разобрался и получил это дифференциальное уравнение:

dN dt = rN (1 − N / k)

Уравнение Ферхюльста

Простое гармоническое движение

В физике простое гармоническое движение — это тип периодического движения, в котором восстанавливающая сила прямо пропорциональна смещению. Примером этого является груз на пружине.

Пример: пружина и груз

К пружине прикреплен груз:

• вес опускается под действием силы тяжести,
• по мере того, как пружина растягивается, ее натяжение увеличивается,
• вес замедляется,
• , затем натяжение пружины возвращает ее вверх,
• , затем он снова и снова падает, вверх и вниз.

Опишите это математически!

Гиря тянется вниз под действием силы тяжести, и мы знаем из Второго закона Ньютона, что сила равна массе, умноженной на ускорение:

F = m a

А ускорение — это вторая производная положения по времени, поэтому:

F = m d ² x dt ²

Пружина подтягивает ее вверх в зависимости от того, насколько она растянута ( k — жесткость пружины, а x — степень ее растяжения): F = -kx

Две силы всегда равны:

м d ² x dt ² = −kx

У нас есть дифференциальное уравнение!

Имеет функцию x (t) и вторую производную d ² x дт ²

Примечание: мы не включили «демпфирование» (замедление отскоков из-за трения), которое немного сложнее, но вы можете поиграть с ним здесь (нажмите играть ):

Создание дифференциального уравнения является первым важным шагом. Но нам также нужно решить , чтобы узнать, как, например, пружина со временем подпрыгивает вверх и вниз.

Классифицируйте, прежде чем пытаться решить

Так как же нам решить их?

Это не всегда просто!

За прошедшие годы мудрые люди разработали специальных метода для решения некоторых типов дифференциальных уравнений.

Итак, нам нужно знать , что это за тип дифференциального уравнения.

Это как путешествие: разные виды транспорта решили, как добраться до определенных мест. Это рядом, так что мы можем просто гулять? Есть дорога, по которой мы можем взять машину? Или это в другой галактике, и мы просто еще не можем туда добраться?

Итак, давайте сначала классифицируем дифференциальное уравнение .

Обычное или частичное

Первая основная группа:

• «Обычные дифференциальные уравнения» (ODE) содержат одиночный i

.