Измерение физических величин — Лабораторный практикум
В ходе выполнения лабораторных работ Вы будете производить различные измерения.
ИЗМЕРЕНИЕ- нахождение значения физической величины опытным путем с применением технических средств.
- Прямое измерение- значение интересующей нас физической величины мы видим непосредственно на приборе (время мы можем измерить, например, секундомером, диаметр- микрометром и т.п.).
- Косвенное измерение- значение величины находится как функция других величин (например, среднюю скорость мы определяем как отношение расстояния, которое проходит тело ко времени прохождения этого расстояния, где время и расстояние мы измеряем непосредственно).
Истинное значение X измеряемой величины найти практически невозможно. Это связано с ограниченностью возможностей измерительных приборов и наличием факторов, искажающих их показания. Речь может идти о нахождении приближенного значения Xсв искомой величины и определении ошибки, погрешности, разности между оценкой и точным значением измеряемой величины:
∆X=|X-X
В полную ошибку свой вклад вносят ошибки- приборные и отсчета. Прибор, которым были проведены измерения, в силу своего несовершенства, непременно поучаствует в отклонении результата от истинного.
Способ задания пределов допускаемой основной
абсолютной погрешности прибора определяется зависимостью погрешности
от значения измеряемой величины. Если абсолютная погрешность измерительного
прибора не зависит от измеряемой величины, то погрешность называется аддитивной
и ее предел может быть выражен одним числом. Источники аддитивной погрешности –
трение в опорах, неточность отсчета, дрейф, наводки, вибрации и другие факторы.
От этой погрешности зависит наименьшее значение величины, которое может быть
измерено прибором. Каждому такому прибору соответствует его максимально допустимая стандартом приборная погрешность ∆X пр=δ либо класс точности прибора k.
Эти величины часто указываются на самом приборе.
В случае указания класса точности приборную погрешность вычисляют так:

Класс точности характеризует точность электроизмерительных и ряда других приборов. Класс точности- это число, равное выраженному в процентах отношению предельной абсолютной погрешности прибора к предельному значению шкалы прибора. Для электроизмерительных приборов бывают классы точности 0,02; 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0. Если погрешность прибора неизвестна, то ее можно оценочно принять равной половине цены деления шкалы.
Погрешность отсчета учитывают в том случае, когда показания прибора приходится округлять. Интервалы округления зависят от условий конкретного опыта. В учебных лабораториях погрешность отсчета берут не меньше половины цены деления прибора. Целую цену деления берут в том случае, когда:
- стрелка прибора движется скачками;
- стрелка колеблется около некоторого значения;
- наш прибор индикаторный.
Если погрешность прибора зависит от измеряемой величины, то она называется мультипликативной. Мультипликативная погрешность прямо пропорциональна значению измеряемой величины Х. Источники мультипликативной погрешности – действие влияющих величин на параметры элементов и узлов средств измерений. Для приборов, аддитивная составляющая погрешности которых преобладает над мультипликативной, класс точности выражается одним числом. К таким приборам относится большинство аналоговых стрелочных приборов.
Класс точности средств измерения, у которых аддитивная и мультипликативная составляющие основной погрешности соизмеримы, обозначается двумя числами, разделенными косой чертой: c/d. Причем класс точности должен удовлетворять условию c/d>1. К приборам, класс точности которых выражается дробью, относятся цифровые показывающие приборы.
Мультипликативная погрешность прямо пропорциональна значению измеряемой величины Х. Источники мультипликативной погрешности – действие влияющих величин на параметры элементов и узлов средств измерений. Для приборов, аддитивная составляющая погрешности которых преобладает над мультипликативной, класс точности выражается одним числом. К таким приборам относится большинство аналоговых стрелочных приборов.
Класс точности средств измерения, у которых аддитивная и мультипликативная составляющие основной погрешности соизмеримы, обозначается двумя числами, разделенными косой чертой: c/d. Причем класс точности должен удовлетворять условию c/d>1. К приборам, класс точности которых выражается дробью, относятся цифровые показывающие приборы.
Приборная ошибка и ошибка отсчета считаются систематическими, т.е. повторяющимися от опыта к опыту в ряду измерений. К систематическим ошибками относят ошибки, которые искажают результат в определенную сторону и имеющие закономерный характер.
Кроме систематических ошибок следует учесть и случайные ошибки. Причины и источники их появления могут быть различными. Влияния отдельных факторов в ходе эксперимента могут изменятся от измерения к измерению. Учесть их по отдельности не представляется возможным. Однако теория вероятностей позволяет оценить величину случайных ошибок.
Результат измерений следует записывать с указанием доверительной вероятности в интервальной форме.
Следует упомянуть еще один вид погрешности- промах. Это такой результат, который отличается от прочих при одинаковых условиях измерения. Причина получения такого результата кроется в субъективности понятия «одинаковые условия измерения». Экспериментатор не может контролировать одинаковость всех параметров, определяющих условия измерения. «Удачное» влияние таких неучтенных параметров может дать результат весьма существенно отличающийся от ожидаемого значения. Такие измерения исключают из дальнейших расчетов, но оставляют в записях и на графиках тоже отображают.
«Удачное» влияние таких неучтенных параметров может дать результат весьма существенно отличающийся от ожидаемого значения. Такие измерения исключают из дальнейших расчетов, но оставляют в записях и на графиках тоже отображают.
Относительная погрешность определяется как отношение абсолютной погрешности измеряемой величины к значению измеряемой величины. Относительная погрешность показывает, какова доля ошибки в единице определенной нами физической величины. Поэтому по полученному результату всегда есть смысл оценить относительную погрешность.
Абсолютные ,относительные и приведенные погрешности измерений
Абсолютная погрешность – это разница между измеренной датчиком величиной Хизм и действительным значением Хд этой величины.
Действительное значение Хд измеряемой величины это найденное экспериментально значение измеряемой величины максимально близкое к ее истинному значению. Говоря простым языком действительное значение Хд это значение, измеренное эталонным прибором, или сгенерированное калибратором или задатчиком высокого класса точности. Абсолютная погрешность выражается в тех же единицах измерения, что и измеряемая величина (например, в м3/ч, мА, МПа и т.п.). Так как измеренная величина может оказаться как больше, так и меньше ее действительного значения, то погрешность измерения может быть как со знаком плюс (показания прибора завышены), так и со знаком минус (прибор занижает).
Абсолютная погрешность выражается в тех же единицах измерения, что и измеряемая величина (например, в м3/ч, мА, МПа и т.п.). Так как измеренная величина может оказаться как больше, так и меньше ее действительного значения, то погрешность измерения может быть как со знаком плюс (показания прибора завышены), так и со знаком минус (прибор занижает).
См.Абсолютная погрешность микрокомпьютерного расходомера скоростемера МКРС
Относительная погрешность – это отношение абсолютной погрешности измерения Δ к действительному значению Хд измеряемой величины.
Относительная погрешность выражается в процентах, либо является безразмерной величиной, а также может принимать как положительные, так и отрицательные значения.
См.Относительная погрешность ультразвукового уровнемера ЭХО-АС-01
Приведенная погрешность – это отношение абсолютной погрешности измерения Δ к нормирующему значению Хn, постоянному во всем диапазоне измерения или его части.
Нормирующее значение Хn зависит от типа шкалы датчика КИП:
- Если шкала датчика односторонняя и нижний предел измерения равен нулю (например, шкала датчика от 0 до 150 м3/ч), то Хn принимается равным верхнему пределу измерения (в нашем случае Хn = 150 м3/ч).

- Если шкала датчика односторонняя, но нижний предел измерения не равен нулю (например, шкала датчика от 30 до 150 м3/ч), то Хn принимается равным разности верхнего и нижнего пределов измерения (в нашем случае Хn = 150-30 = 120 м3/ч).
- Если шкала датчика двухсторонняя (например, от -50 до +150 ˚С), то Хn равно ширине диапазона измерения датчика (в нашем случае Хn = 50+150 = 200 ˚С).
Довольно часто в описании на тот или иной датчик указывается не только диапазон измерения, например, от 0 до 50 мг/м3, но и диапазон показаний, например, от 0 до 100 мг/м3. Приведенная погрешность в этом случае нормируется к концу диапазона измерения, то есть к 50 мг/м3, а в диапазоне показаний от 50 до 100 мг/м3 погрешность измерения датчика не определена вовсе – фактически датчик может показать все что угодно и иметь любую погрешность измерения. Диапазон измерения датчика может быть разбит на несколько измерительных поддиапазонов, для каждого из которых может быть определена своя погрешность как по величине, так и по форме представления. При этом при поверке таких датчиков для каждого поддиапазона могут применяться свои образцовые средства измерения, перечень которых указан в методике поверки на данный прибор.
Диапазон измерения датчика может быть разбит на несколько измерительных поддиапазонов, для каждого из которых может быть определена своя погрешность как по величине, так и по форме представления. При этом при поверке таких датчиков для каждого поддиапазона могут применяться свои образцовые средства измерения, перечень которых указан в методике поверки на данный прибор.
погрешности измерений
2.2. Погрешности измерений
Ни одно измерение не выполняется идеально точно, всегда по различным причинам существует погрешность, т.е. отклонение результата измерения от истинного значения измеряемой величины. Причиной погрешности может стать несовершенство методики измерения, используемых средств измерений, органов чувств человека-оператора, а также влияние внешних условий.
Все погрешности, не связанные с грубыми
ошибками (промахами, возникающими вследствие недосмотра экспериментатора или
неисправности аппаратуры), имеют случайную и систематическую составляющие.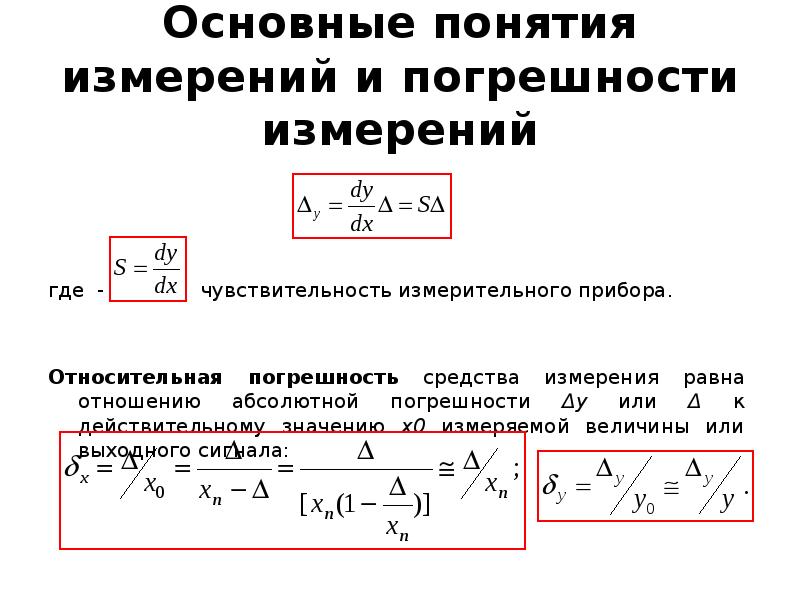
Систематические погрешности остаются постоянными по величине и знаку или закономерно изменяются при повторных измерениях одной и той же величины. Систематические погрешности разделяются на методические (несовершенство метода измерений; в том числе влияние средств измерения на объект, свойство которого измеряется), инструментальные (зависящие от погрешности применяемых средств измерений), внешние (обусловленные влиянием условий проведения измерений) и субъективные (обусловленные индивидуальными особенностями оператора).
Различают абсолютную и относительную погрешность измерения.
Под абсолютной погрешностью измерения понимают разность между полученным в ходе измерения и истинным значением физической величины:
(2. 1)
1)
Без сравнения с измеряемой величиной абсолютная погрешность ничего не говорит о качестве измерения. Одна и та же погрешность в 1 мм при измерении длины комнаты не играет роли, при измерении длины тетради уже может быть существенна, а при измерении диаметра проволоки совершенно недопустима.
Поэтому вводят относительную погрешность, показывающую, какую часть абсолютная погрешность составляет от истинного значения измеряемой величины.
(2.2)
Относительная погрешность обычно выражается в
процентах.
Результат измерения величины принято записывать в виде:
xизм ± Dх, d=…%.
При записи абсолютной погрешности ее величину округляют до двух значащих цифр, если первая их них является единицей, и до одной значащей цифры во всех остальных случаях. При записи измеренного значения величины последней должна указываться цифра того десятичного разряда, который использован при указании погрешности.
Из формул (2.1) и (2.2) следует, что для нахождения погрешностей измерений необходимо знать истинное значение измеряемой величины. Поэтому этими формулами можно пользоваться только в тех редких случаях, когда проводятся измерения констант, значения которых заранее известны. Цель же измерений, как правило, состоит в том, чтобы найти не известное значение физической величины. Поэтому на практике погрешности измерений не вычисляются, а оцениваются.
В частности, относительную погрешность находят как отношение абсолютной погрешности не к истинному, а к измеренному значению величины:
(2. 3)
3)
Способы оценки абсолютной погрешности разные для прямых и косвенных измерений.
Максимальную абсолютную погрешность при прямых измерениях находят как сумму абсолютной инструментальной погрешности и абсолютной погрешности отсчета: Dх=Dхприб + Dхотсч (2.4)
Погрешность отсчета является случайной и устраняется при многократных измерениях. Если же проводится одно измерение, она обычно принимается равной половине цены деления шкалы измерительного прибора.
Обратимся теперь к анализу погрешностей
средств измерения. В зависимости от условий применения средств измерения
различают основную и дополнительную погрешности. Основная погрешность
– это погрешность средств измерений, используемых при нормальных условиях; дополнительная погрешность – это погрешность средств измерений,
возникающая в результате отклонения значения одной или более влияющих
величин от нормального значения.
Способ задания пределов допускаемой основной абсолютной погрешности измерительных средств определяется зависимостью погрешности от значения измеряемой величины. Если абсолютная погрешность измерительного прибора не зависит от измеряемой величины, то погрешность называется аддитивной и ее предел может быть выражен одним числом:
Dхмакс приб = ± а (2.5)
Зона погрешности в этом случае ограничена двумя прямыми линиями, параллельными оси абсцисс (рис.2.1а). Источники аддитивной погрешности – трение в опорах, неточность отсчета, дрейф, наводки, вибрации и другие факторы. От этой погрешности зависит наименьшее значение величины, которое может быть измерено прибором.
Если погрешность прибора зависит от измеряемой
величины, то она называется мультипликативной и предел допускаемой
абсолютной погрешности выражается формулой
Dхмакс
приб =
±
(а + вх),
(2. 6)
6)
где в – постоянная величина, вх – предельное значение мультипликативной погрешности, а – предельное значение аддитивной погрешности.
Таким образом, мультипликативная погрешность прямо пропорциональна значению измеряемой величины х. Источники мультипликативной погрешности – действие влияющих величин на параметры элементов и узлов средств измерений. Зона погрешности при наличии аддитивной и мультипликативной составляющей показана на рисунке 2.1 б.
Инструментальная погрешность электроизмерительных приборов определяется их классом точности. Класс точности (максимальная приведенная погрешность) – это отношение максимальной абсолютной погрешности прибора к пределу измерения величины (полному значению шкалы). Его, как и относительную погрешность, выражают в процентах. Класс точности показывает, сколько процентов максимальная инструментальная погрешность составляет от всей шкалы прибора:
(2. 7)
7)
ГОСТом установлено 8 классов точности измерительных приборов: 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0. Зная класс точности прибора и предельное значение измеряемой величины, можно определить абсолютную и относительную инструментальную погрешность измерения:
(2.8)
(2.9)
Из формулы (2.9) видно, что чем ближе значение
измеряемой величины к пределу измерения, тем меньше относительная
инструментальная погрешность.
У приборов, аддитивная составляющая погрешности которых преобладает над мультипликативной, класс точности выражается одним числом. К таким приборам относится большинство аналоговых стрелочных приборов. Относительная инструментальная погрешность в этом случае находится просто по формуле (2.9).
Класс точности средств измерения, у которых аддитивная и мультипликативная составляющие основной погрешности соизмеримы, обозначается двумя числами, разделенными косой чертой: c/d. Причем класс точности должен удовлетворять условию c/d>l. К приборам, класс точности которых выражается дробью, относятся цифровые показывающие приборы. Их максимальная относительная погрешность определяется по формуле:
(2.10)
Для сравнения
погрешностей измерения цифровых и стрелочных измерительных приборов
постройте самостоятельно график зависимости относительной погрешности
измерения постоянного напряжения от его величины приборами АВО-63 и Щ4313 на
пределе 2В.
Класс точности или максимальная инструментальная погрешность приборов обычно приводится в его паспорте. Для менее точных приборов, если в паспорте ничего не указано, максимальная инструментальная погрешность принимается равной половине цены или цене деления шкалы.
Для прямых измерений сначала оценивается абсолютная погрешность, а затем относительная. При оценке погрешности косвенных измерений величины поступают следующим образом. Сначала находят абсолютные погрешности величин, полученных в ходе прямых измерений. Затем вычисляют относительную погрешность исследуемой величины, пользуясь для этого одной из формул, приведенных в таблице «расчет погрешностей». Формула относительной погрешности зависит от того, по какой формуле находят значение измеряемой величины. И только после этого находят абсолютную погрешность измеряемой величины, выражая ее из формулы (2.3).
Примеры расчета неопределенности измерений — Profilab.by
Примеры расчета неопределенности измерений
Оценивание неопределенности измерений (количественных величин) – одна из важных задач, стоящих перед каждой лабораторией. Требование к оцениванию неопределенности измерений заложено в межгосударственном стандарте ГОСТ ISO/IEC 17025-2019, а также политике ILAC-G17:2002.
Требование к оцениванию неопределенности измерений заложено в межгосударственном стандарте ГОСТ ISO/IEC 17025-2019, а также политике ILAC-G17:2002.
Чтобы получить предварительную информацию по теме Неопределенность измерений, посмотрите, пожалуйста, наше обучающее видео:
Международное метрологическое сообщество давно уже разработало и приняло основные принципы концепции неопределенности, закрепив их в серии международных документов JCGM (Joint Committee for Guides in Metrology), а также документах ISO/IEC Guide 98. Разработано много дополнительных руководств по различных подходам оценивания неопределенности измерений в конкретных областях испытаний/измерений (EA, EURACHEM, Nordtest, EUROLAB и т.д.).
ОНЛАЙН-КАЛЬКУЛЯТОР
Расчет составляющей неопределенности измерений из-за построения градуировочного графика
ПОДРОБНЕЕ
Несмотря на хорошо разработанные и представленные в документах свободного доступа теоретические принципы и подходы оценивания, и даже наличия конкретных примеров, у специалистов лабораторий все еще остаются вопросы по практической реализации этих принципов и подходов для измерений, проводимых в их лаборатории.
Ближайшие семинары:
«Валидация/верификация методик выполнения измерений в рамках одной лаборатории. Метрологическая прослеживаемость измерений» — 5-6 мая (онлайн)
Подтверждение прослеживаемости своих измерений и валидация методов измерений являются одними из требований ГОСТ ISO/IEC 17025-2019. Не смотря на то, что лаборатории имеют большой опыт, все еще остаются вопросы, связанные с практической реализацией прослеживаемости измерений и процедуры валидации…
ПОДРОБНЕЕ
«Неопределенность измерения величин: основные принципы и подходы к оцениванию (при проведении химических и био-аналитических измерений)» — 26-27 мая (онлайн)
Оценивание неопределенности измерения является одним из требований ГОСТ ISO/IEC 17025-2019…
ПОДРОБНЕЕ
«Неопределенность измерений, обусловленная отбором проб: оценивание составляющей неопределенности измерений» — 9 июня (онлайн)
Отбор проб является одним из важных этапов реализации испытаний. Репрезентативность отобранной пробы напрямую влияет на достоверность заключений, которые делаются на основании результата измерений, и вносит вклад в суммарную стандартную неопределенность измерений…
Репрезентативность отобранной пробы напрямую влияет на достоверность заключений, которые делаются на основании результата измерений, и вносит вклад в суммарную стандартную неопределенность измерений…
ПОДРОБНЕЕ
С целью наглядного представления основных принципов концепции неопределенности измерений и подхода моделирования предлагаем Вашему вниманию решение нескольких несложных, но часто встречающейся в практике многих испытательных лабораторий, задач:
Пример 1. Оценивание неопределенности измерений массовой доли влаги
Пример 2. Оценивание неопределенности измерений сопротивления изоляции
Пример 3. Оценивание неопределенности измерений коэффициента поправки титрованного раствора
Пример 4. Оценивание неопределенности измерений pH воды
Пример 5. Оценивание неопределенности измерений относительного удлинения эластичного герметика
Пример 6.
 Оценивание неопределенности измерений прочности бетона на растяжение при изгибе
Оценивание неопределенности измерений прочности бетона на растяжение при изгибеПример 7. Оценивание неопределенности измерений твердости по Бриннелю
Пример 1. Оценивание неопределенности измерений массовой доли влаги
Исходные данные:
- Объект измерений – углекислый барий
- Измеряемая величина – массовая доля влаги
- Единицы измерений – процент (%)
- Методика выполнения измерения – ГОСТ 2149-75 «Барий углекислый технический. Технические условия»
- Метод измерений – метод высушивания пробы до постоянной массы
Этап 1. Составление функции измерений
Функция измерений для измеряемой величины составляется на основании принципа измерений, заложенного в методе измерений, и описанного для реализации в методике выполнения измерений.
Массовую долю влаги бария углекислого Х в процентах вычисляют на основании ГОСТ 2149 (п. 3.5) в соответствии с функцией измерений:
3.5) в соответствии с функцией измерений:
где Хi – массовая доля влаги i-ой пробы углекислого бария, %;
m1 – масса стаканчика для взвешивания с навеской до высушивания, г;
m2 – масса стаканчика для взвешивания с навеской после высушивания, г;
m – масса навески углекислого бария, г;
mcт – масса стаканчика для взвешивания, г;
i – номер параллельной пробы, i = 1, 2;
F – поправочный множитель, учитывающий допускаемое расхождение между параллельными определениями.
Разработка/Валидация МЕТОДИК
Выполним работы по разработке Методик измерений
ПОДРОБНЕЕ ОБ УСЛУГЕ
МЕТОДИКИ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ
В комплекте с автоматизированным расчетом
ПОДРОБНЕЕ ОБ УСЛУГЕ
Этап 2.
 Анализ входных величин
Анализ входных величин1) Масса стаканчика для взвешивания с навеской до высушивания, m1
Масса стаканчика для взвешивания с навеской до высушивания определяется путем взвешивания на весах лабораторных AV264C. При измерении влажности двух проб бария углекислого были получены следующие значения входной величины:
- для первой пробы m1(1) = 41,0055 г,
- для второй пробы m1(2) = 41,3842 г.
Неопределенность, связанную с величиной m1, оцениваем, используя данные производителя на весы. В паспорте на весы лабораторные AV264C для диапазона измерений до 50 г указаны пределы погрешности взвешивания ± 0,001 г. Поскольку значение дано без доверительной вероятности, принимаем прямоугольное распределение значений погрешности взвешивания в этих границах. Стандартная неопределенность массы стаканчика для взвешивания с навеской до высушивания m1 оценивается по типу В и составляет:
2) Масса стаканчика для взвешивания, mcт
Масса стаканчика для взвешивания определяется путем взвешивания на весах лабораторных AV264C. При измерении влажности двух проб бария углекислого были получены следующие значения входной величины:
При измерении влажности двух проб бария углекислого были получены следующие значения входной величины:
- для первой пробы mст(1) = 21,0034 г,
- для второй пробы mст(2) = 21,3822 г.
Неопределенность массы стаканчика для взвешивания после высушивания обусловлена двумя факторами:
- погрешностью взвешивания стаканчика на весах;
- возможными отклонениями массы стаканчика после высушивания вследствие нечеткого определения в методике выполнения измерений момента, в который масса стаканчика после высушивания будет являться постоянной величиной.
Стандартная неопределенность u1(mcт), связанная с погрешностью взвешивания, оценивается на основании данных производителя на весы лабораторные AV264C, определяется аналогично неопределенности величины m1 и составляет u1(mcт) = 0,00058 г.
Стандартную неопределенность u2(mcт), обусловленную отклонениями массы стаканчика для взвешивания после высушивания, можно определить на основании информации о том, что разность между двумя последующими взвешиваниями стаканчика для взвешивания после сушки не должна превышать 0,002 г (принято лабораторией, поскольку ГОСТ 2149-75 четко не устанавливает момент, в который масса стаканчика после высушивания будет являться постоянной величиной). Это значение можно рассматривать как 95-% доверительный интервал для разности двух оценок величины, распределенной по нормальному закону распределения (предел повторяемости по СТБ ИСО 5725-6). Стандартная неопределенность u2(mcт) будет равна стандартному отклонению, рассчитанному на основании указанного интервала по типу В по формуле:
Это значение можно рассматривать как 95-% доверительный интервал для разности двух оценок величины, распределенной по нормальному закону распределения (предел повторяемости по СТБ ИСО 5725-6). Стандартная неопределенность u2(mcт) будет равна стандартному отклонению, рассчитанному на основании указанного интервала по типу В по формуле:
Суммарную стандартную неопределенность величины mcт находим путем суммирования квадратов стандартных неопределенностей перечисленных выше двух вкладов:
3) Масса стаканчика для взвешивания с навеской после высушивания, m2
Масса стаканчика для взвешивания с навеской после высушивания определяется путем взвешивания на весах лабораторных AV264C. При измерении влажности двух проб бария углекислого были получены следующие значения входной величины:
- для первой пробы m2(1) = 40,9850 г,
- для второй пробы m2(2) = 41,3638 г.

Неопределенность массы стаканчика для взвешивания с навеской после высушивания обусловлена двумя факторами:
- погрешностью взвешивания пробы на весах;
- возможными отклонениями массы пробы после высушивания вследствие нечеткого определения в методе испытаний момента, в который масса пробы после высушивания будет являться постоянной величиной.
Стандартная неопределенность u1(m2), связанная с погрешностью взвешивания, оценивается на основании данных производителя на весы лабораторные AV264C, определяется аналогично неопределенности величины m2 и составляет u1(m2) = 0,00058 г.
Стандартную неопределенность u2(m2), обусловленную отклонениями массы стаканчика для взвешивания с навеской после высушивания, можно определить на основании информации о том, что разность между двумя последующими взвешиваниями стаканчика для взвешивания с навеской пробы бария углекислого после сушки не должна превышать 0,002 г (принято лабораторией, поскольку ГОСТ 2149-75 четко не устанавливает момент, в который масса пробы после высушивания будет являться постоянной величиной). Это значение можно рассматривать как 95-% доверительный интервал для разности двух оценок величины, распределенной по нормальному закону распределения (предел повторяемости по СТБ ИСО 5725-6). Стандартная неопределенность u2(m2) будет равна стандартному отклонению, рассчитанному на основании указанного интервала по типу В по формуле:
Это значение можно рассматривать как 95-% доверительный интервал для разности двух оценок величины, распределенной по нормальному закону распределения (предел повторяемости по СТБ ИСО 5725-6). Стандартная неопределенность u2(m2) будет равна стандартному отклонению, рассчитанному на основании указанного интервала по типу В по формуле:
Суммарную стандартную неопределенность величины m2 находим путем суммирования квадратов стандартных неопределенностей перечисленных выше двух вкладов:
4) Поправочный множитель, учитывающий допускаемое расхождение между параллельными определениями, F
Значение оценки величины принимается равным единице: F = 1.
Стандартная неопределенность поправочного множителя рассчитывается на основании информации о допускаемом расхождении между параллельными определениями влажности, приведенными в ГОСТ 2149-75 (п.3.5.2). Приведенное допускаемое относительное расхождение составляет r = 20 % и рассматривается как 95-% доверительный интервал для разности двух оценок величины, распределенной по нормальному закону распределения. Стандартная неопределенность поправочного множителя будет равна стандартному отклонению, рассчитанному на основании указанного интервала, с учетом того, что за результат измерения принимают среднее арифметические определений двух параллельных проб, по типу В по формуле:
Стандартная неопределенность поправочного множителя будет равна стандартному отклонению, рассчитанному на основании указанного интервала, с учетом того, что за результат измерения принимают среднее арифметические определений двух параллельных проб, по типу В по формуле:
Этап 3. Анализ корреляций
Все входные величины рассматриваются как некоррелированные, поскольку получены независимо друг от друга в различных экспериментах.
ОБУЧЕНИЕ ПРОЦЕДУРЕ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ (химия и аналитика)
Семинар: «Неопределенность измерения величин: основные принципы и подходы к оцениванию»
ПОДРОБНЕЕ О СЕМИНАРЕ
ОБУЧЕНИЕ ПРОЦЕДУРЕ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ (прямые методы измерений)
Семинар: «Неопределенность измерения величин: основные принципы и подходы к оцениванию»
ПОДРОБНЕЕ О СЕМИНАРЕ
Этап 4. Измеренное значение величины
Массовая доля влаги i-ой пробы углекислого бария рассчитывается по формуле (2):
Расхождение между результатами измерений двух параллельных проб не превышает допускаемого значения, установленного в ГОСТ 2149-75 (п. 3.5.2):
3.5.2):
Массовая доля влаги бария углекислого Х в процентах вычисляется в соответствии с функцией измерений (1):
Измеренное значение (оценку измеряемой величины) округляют до четырех знаков после запятой (принято лабораторией, поскольку ГОСТ 2149-75 четко не устанавливает требования к округлению результата измерения).
Этап 5. Суммарная стандартная неопределенность
Стандартную неопределенность измеряемой величины Х получаем по закону распространения неопределенностей путем суммирования квадратов произведений стандартных неопределенностей всех влияющих величин, входящих в функции измерений (1) и (2), на соответствующие коэффициенты чувствительности:
где коэффициенты чувствительности рассчитываются как частные производные функции измерений по входным величинам:
Примечание – Для вычисления коэффициентов чувствительности можно использовать либо минимальные значения масс, полученные при измерении массовой доли влаги i-ой пробы бария углекислого, либо результаты измерений масс, полученные на определенной пробе бария углекислого. В данном примере коэффициенты чувствительности рассчитываются на основании результатов измерений масс для первой пробы.
В данном примере коэффициенты чувствительности рассчитываются на основании результатов измерений масс для первой пробы.
Суммарная стандартная неопределенность составит
Этап 6. Бюджет неопределенности
В таблице представлен бюджет неопределенности для измеряемой величины.
Вклад в неопределенность от j-ой входной величины рассчитывается как произведение стандартной неопределенности этой величины на соответствующий коэффициент чувствительности.
Этап 7. Расширенная неопределенность
Расширенную неопределенность U получаем умножением суммарной стандартной неопределенности на коэффициент охвата k, который выбирается равным 2 при уровне доверия приблизительно 95 % в предположении нормального распределения вероятностей измеряемой величины:
Этап 8. Представление результата измерения
Результат измерения массовой доли влаги углекислого бария представляют в виде:
«Массовая доля влаги бария углекислого составила (0,1022 ± 0,0150) %, где число, следующее за знаком ±, является численным значением расширенной неопределенности, которая получена умножением суммарной стандартной неопределенности на коэффициент охвата k = 2, основанный на предполагаемом нормальном распределении, и определяет интервал, соответствующий вероятности охвата приблизительно 95 %».
Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, Вы можете задать их нашим специалистам посредством обратной связи или по телефонам, указанным в контактных данных на сайте.
Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.
УЗНАТЬ СТОИМОСТЬ РАЗРАБОТКИ МЕТОДИКИ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ…
Пример 2. Оценивание неопределенности измерений сопротивления изоляции
Исходные данные:
- Объект измерений – кабель силовой АВБбШв
- Измеряемая величина – сопротивления изоляции
- Единицы измерений – МОм
- Измерение сопротивления изоляции выполняется методом непосредственной оценки с помощью мегаомметра Е6-24
Измерения проведены в диапазоне измерений мегаомметра Е6-24 от 100 до 999 МОм при температуре окружающего воздуха 22 °С и относительной влажности воздуха 65 %.
Этап 1. Составление функции измерений
Сопротивление изоляции определяется в соответствии со следующей функцией измерений
где R – сопротивление изоляции, МОм;
Rind – среднее арифметическое повторных измерений сопротивления изоляции, МОм;
FΔ – поправка, учитывающая допускаемую основную погрешность измерения сопротивления мегаомметра Е6-24, МОм;
Fс – поправка, учитывающая единицу младшего разряда, выдаваемых мегаомметром Е6-24 показаний сопротивления, МОм.
Примечание – В функции измерений не учитываются поправки FΔt и FΔφ на дополнительные погрешности измерения сопротивления мегаомметра Е6-24, вызванные отклонением соответственно температуры и влажности окружающей среды от нормальных условий в рабочем диапазоне. Поправки будут вводиться только в случае, если измеренные значения температуры и/или относительной влажности окружающей среды находятся в рабочем диапазоне, но выходят за диапазон нормальных условий эксплуатации мегаомметра Е6-24 (значения нормальных и рабочих условий эксплуатации указаны в руководстве по эксплуатации мегаомметра Е6-24).
Этап 2. Анализ входных величин
1) Среднее арифметическое повторных измерений сопротивления изоляции Rind, МОм.
При проведении измерений сопротивления изоляции кабеля силового АВБбШв получены следующие результаты повторных измерений: R1 = 124 МОм; R2 = 131 МОм; R3 = 137 МОм.
Значение оценки величины Rind определяется по формуле
где Ri – результат i-го повторного измерения сопротивления изоляции, определяемый как показание, снимаемое с дисплея мегаомметра Е6-24, МОм;
n – количество повторных измерений, n = 3.
Стандартная неопределенность измерений величины Rind, МОм, рассчитывается в предположении нормального распределения вероятностей по формуле
2) Поправка, учитывающая допускаемую основную погрешность измерения сопротивления мегаомметра Е6-24, FΔ
Значение оценки величины FΔ принимается равным 0,0 МОм.
Стандартная неопределенность u(FΔ), МОм, оценивается на основании информации о пределах допускаемой основной абсолютной погрешности измерения сопротивления мегаомметра Е6-24 ± Δ, МОм. В предположении прямоугольного распределения вероятностей значений погрешности в границах ± Δ определяется по формуле
Примечание — согласно [1] пределы допускаемой основной погрешности измерения сопротивления приведены в виде ± (% + е.м.р.) т. е. для получения пределов абсолютной погрешности измерения Δ нужно воспользоваться формулой
где δ» – допускаемая относительная погрешность измерения сопротивления, которая принимается равной первому числу, стоящему в [1] в записи пределов допускаемой основной погрешности измерения сопротивления, %;
100 – коэффициент перехода от долей к процентам, %;
m – второе число стоящее в [1] в записи пределов допускаемой основной погрешности измерения сопротивления, определяющее количество единиц младшего разряда;
с – единица младшего разряда выдаваемого мегаомметром Е6-24 показания сопротивления, МОм.
3) Поправка, учитывающая единицу младшего разряда выдаваемых мегаомметром Е6-24 показаний сопротивления, Fс
Значение оценки величины Fc принимается равным 0,0 МОм.
Стандартная неопределенность u(Fc), МОм, определяется на основании информации о единице младшего разряда выдаваемого мегаомметром Е6-24 показания сопротивления c = 1 МОм (для диапазона измерений мегаомметра Е6-24 от 100 до 999 МОм). В предположении прямоугольного распределения вероятностей значений величины c в границах ± c/2 определяется по формуле
Этап 3. Анализ корреляций
Все величины, входящие в функцию измерений (1), рассматриваются как некоррелированные.
Этап 4. Оценка измеряемой величины
Значение оценки величины R, МОм, «сопротивление изоляции» рассчитывается по формуле (1)
Значение сопротивления изоляции (МОм) округляют до одного знака после запятой.
Этап 5. Суммарная стандартная неопределенность
Суммарная стандартная неопределенность измерений сопротивления изоляции силового кабеля u(R), МОм, определяется по формуле
Процентные вклады неопределенностей влияющих величин в суммарную стандартную неопределенность u(R) определяются по формулам
Этап 6. Бюджет неопределенности
Бюджет неопределенности измерений сопротивления изоляции силового кабеля представлен в таблице 1.
Таблица 1 – Бюджет неопределенности измерений сопротивления изоляции силового кабеля
Этап 7. Расширенная неопределенность
Расширенная неопределенность измерений сопротивления изоляции силового кабеля U(R), МОм, определяется для вероятности 95 % в предположении распределения Стьюдента по формуле
где коэффициент охвата k = 2,26, выбирается в зависимости от числа эффективных степеней свободы veff, которое рассчитывается по формуле
Этап 8.
 Результат измерения
Результат измеренияСопротивление изоляции силового кабеля АВБбШв составило
(130,7 ± 12,5) МОм (k = 2,26, veff = 9,14, Р = 95 %).
Библиография
[1] РЛПА 411218.001 РЭ Руководство по эксплуатации. Мегаомметры Е6-24, E6-24/1 и E6-24/2.
Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, Вы можете задать их нашим специалистам посредством обратной связи или по телефонам, указанным в контактных данных на сайте.
Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.
УЗНАТЬ СТОИМОСТЬ РАЗРАБОТКИ МЕТОДИКИ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ…
Пример 3. Оценивание неопределенности измерений коэффициента поправки титрованного раствора
Исходные данные:
- Объект измерений – раствор серной кислоты концентрации моль/дм3
- Измеряемая величина – коэффициента поправки 0,1 моль/дм3 раствора серной кислоты
- Единицы измерений – безразмерная величина
- Методика измерений – ГОСТ 25794.
 1 83 «Реактивы. Методы приготовления титрованных растворов для кислотно-основного титрования»
1 83 «Реактивы. Методы приготовления титрованных растворов для кислотно-основного титрования» - Метод измерений – титриметрический по безводному углекислому натрию
Этап 1. Составление функции измерений
Значение оценки коэффициента поправки 0,1 моль/дм3 раствора серной кислоты Ki, при единичном определении рассчитывается по формуле:
где m – масса навески безводного углекислого натрия, г;
P – чистота реактива безводного углекислого натрия, P = 1;
M – молярная масса эквивалента безводного углекислого натрия, г/моль;
с – заданная молярная концентрация серной кислоты в 0,1 моль/дм3 растворе серной кислоты, с = 0,1 моль/дм3, рассматривается как постоянная и не учитывается при расчете неопределенности измерений коэффициента K;
V – объем 0,1 моль/дм3 раствора серной кислоты, израсходованный на титрование, см3.
1000 – коэффициент перехода единицы измерения объема см3 в дм3.
Значение оценки коэффициента K вычисляется как среднее арифметическое трех повторных определений коэффициента поправки раствора серной кислоты по формуле:
где F – поправочный коэффициент, учитывающий расхождение между результатами повторных определений коэффициента поправки раствора серной кислоты, F = 1.
Расхождение между результатами трех повторных определений коэффициента поправки раствора серной кислоты не должно превышать значения 0,001, установленного ГОСТ 25794.1 (п. 1.11).
Этап 2. Анализ входных величин
2.1 Масса навески безводного углекислого натрия, m
Значение массы навески безводного углекислого натрия, m, г, определяется как разность показаний весов при взвешивании стаканчика с навеской установочного вещества и пустого стаканчика. При выполнении измерения были получены следующие значения выходной величины для трех повторных определений коэффициента поправки: m1 = 0,1648 г; m2 = 0,1643 г; m3 = 0,1649 г.
При выполнении измерения были получены следующие значения выходной величины для трех повторных определений коэффициента поправки: m1 = 0,1648 г; m2 = 0,1643 г; m3 = 0,1649 г.
Стандартная неопределенность измерений массы навески установочного вещества, u(m), г, оценивается на основании информации о пределах допускаемой погрешности используемых весов ВСЛ-200/0,1А ± Δm = ± 0,001 г в диапазоне измерений от 0,01 до 50 г, и дискретности отсчета весов d = 0,0001 г, установленных в технической документации на весы. В предположении прямоугольного распределения вероятностей значений погрешности и дискретности в границах ± Δm и ± d/2 соответственно и учитывая двойное взвешивание (пустого стаканчика и стаканчика с навеской установочного вещества) стандартная неопределенность u(m) рассчитывается по формуле:
2.2 Чистота реактива безводного углекислого натрия, P
Значение оценки величины P принимается равным 1.
Стандартная неопределенность измерений степени чистоты реактива углекислого натрия u(P) оценивается на основании информации о том, что согласно ГОСТ 83-79 «Реактивы. Натрий углекислый. Технические условия» массовая доля углекислого натрия в реактиве безводного углекислого натрия составляет не менее 99,8 %. Неопределенность измерений u(P) рассчитывается исходя из отклонения значения чистоты реактива от 1 в предположении прямоугольного распределения величины Р в границах ± (1 – 0,998) по формуле:
2.3 Молярная масса эквивалента безводного углекислого натрия, M
Значение оценки величины M, г/моль, определяется как произведение фактора эквивалентности безводного углекислого натрия fэ = 1/2 на молярную массу установочного вещества M0, г/моль, по формуле:
где молярная масса безводного углекислого натрия (Na2CO3) рассчитывается на основании значений атомных масс натрия, углерода и кислорода A, взятых из таблиц атомных масс IUPAC (//www. sbcs.qmul.ac.uk/iupac/AtWt/), и количества атомов этих элементов в молекуле безводного углекислого натрия n (ANa ≈ 22,98976928, Aс = 12,011, A0 = 15,999, nNa= 2, nс = 1, n0 = 3):
sbcs.qmul.ac.uk/iupac/AtWt/), и количества атомов этих элементов в молекуле безводного углекислого натрия n (ANa ≈ 22,98976928, Aс = 12,011, A0 = 15,999, nNa= 2, nс = 1, n0 = 3):
Стандартная неопределенность измерений молярной массы эквивалента безводного углекислого натрия, u(M), г/моль, определяется на основании возможных разбросов значений атомных масс углерода и кислорода ΔА = Amax – Amin и неопределенности последней цифры атомной массы натрия ΔA, а также количества атомов этих элементов в молекуле безводного углекислого натрия n. Данные по разбросам значений атомных масс углерода и кислорода и неопределенности последней цифры атомной массы натрия выбираются из таблиц атомных масс IUPAC (//www.sbcs.qmul.ac.uk/iupac/AtWt/). Стандартная неопределенность значений атомных масс химических элементов рассчитывается в предположении прямоугольного распределения вероятностей атомных масс элементов в границах ± ΔА/2 (для углерода и кислорода) и в границах ± ΔA (для натрия). Неопределенность для вклада атомов одного элемента рассчитывается умножением стандартной неопределенности атомной массы элемента на количество атомов элемента. Стандартная неопределенность измерений молярной массы эквивалента безводного углекислого натрия, u(M), г/моль, определяется по формуле:
2.4 Объем раствора серной кислоты, израсходованный на титрование, V
Значение оценки величины V, см3, определяется по шкале бюретки номинальной вместимостью 25 см3 2-го класса точности по ГОСТ 29251-91 «Посуда лабораторная стеклянная. Бюретки. Часть 1. Общие требования». При выполнении измерения были получены следующие значения выходной величины для трех повторных определений коэффициента поправки: V1= 31,1 см3; V2= 31,0 см3; V3= 31,1 см3.
Стандартная неопределенность измерений объема 0,1 моль/дм3 раствора серной кислоты, израсходованного на титрование, u(V), см3, состоит из следующих основных вкладов:
- стандартная неопределенность, обусловленная погрешностью измерения объема сливаемой жидкости используемой бюретки, u(VΔ), см3;
- стандартная неопределенность, обусловленная ценой наименьшего деления шкалы используемой бюретки, u(Vc), см3;
- стандартная неопределенность, обусловленная отличием температуры, при которой проводятся измерения, от температуры, при которой нормируется погрешность измерения объема сливаемой жидкости бюретки, u(Vt), см3.
Стандартная неопределенность u(VΔ), см3, рассчитывается на основании информации о пределах погрешности измерения сливаемой жидкости бюреткой ± ΔV = 0,1 см3, установленных ГОСТ 29251 в предположении треугольного распределения погрешности в установленных пределах по формуле:
Стандартная неопределенность u(Vc), см3, рассчитывается на основании информации о цене наименьшего деления шкалы используемой бюретки см3, в предположении прямоугольного распределения вероятностей цены деления в пределах ± dV/2 по формуле:
Стандартная неопределенность u(Vt), см3, рассчитывается в предположении прямоугольного распределения исходя из возможных пределов изменения объема жидкости при условии колебания температуры в лаборатории при измерении в пределах (20 ± 5) °С (Δt = 5 °С) и коэффициента объемного расширения жидкости kV, ºС-1, равного 0,00021 ºС-1 для воды (основное вещество в растворе) по формуле:
Примечание – Для оценивания стандартной неопределенности u(Vt) используется измеренное значение объема раствора серной кислоты, пошедшего на титрование, полученное для первой навески безводного углекислого натрия.
Суммарная стандартная неопределенность измерений объема 0,1 моль/дм3 раствора серной кислоты, израсходованного на титрование, u(V), см3 вычисляется путем суммирования стандартных неопределенностей перечисленных выше вкладов по формуле:
2.5 Поправочный коэффициент, учитывающий расхождение между результатами повторных определений коэффициента поправки раствора серной кислоты, F
Значение оценки величины F принимается равным 1.
Стандартная неопределенность измерений поправочного коэффициента, учитывающего расхождение между результатами повторных определений коэффициента поправки раствора серной кислоты, u(F), определяется на основании установленного ГОСТ 25794.1 (п. 1.11) допускаемого расхождения между результатами повторных определений коэффициента поправки r = 0,001, которое рассматривается как предел повторяемости согласно СТБ ИСО 5725-6-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике». С учетом того, что за результат измерения принимается среднее арифметическое трех определений, стандартная неопределенность u(F) определяется по формуле:
Этап 3. Анализ корреляций
Все входные величины рассматриваются как некоррелированные, поскольку получены независимо друг от друга в различных экспериментах.
Этап 4. Оценка измеряемой величины
Значения коэффициента поправки раствора серной кислоты при i-ом определении согласно формуле (1) составляют:
Максимальное расхождение между результатами трех определений не превышает допускаемого значения, установленного ГОСТ 25794.1:
Значение коэффициента поправки раствора серной кислоты определяется по формуле (2) на основании результатов параллельных определений, которые рассчитываются по формуле (1):
Коэффициент поправки вычисляют с точностью до четвертого десятичного знака. Полученное значение коэффициента поправки раствора серной кислоты удовлетворяет требованию ГОСТ 25794.1 (п. 1.11) о том, что значение коэффициента поправки должно соответствовать диапазону .
Этап 5. Суммарная стандартная неопределенность
Суммарная стандартная неопределенность измерений коэффициента поправки K определяется по закону распространения неопределенностей путем суммирования относительных стандартных неопределенностей всех влияющих величин, входящих в функции измерений (1) и (2), по формуле:
Примечание — Для оценивания суммарной стандартной неопределенности u(K) используются значения оценок влияющих величин (измеренные значения), полученные для первой навески безводного углекислого натрия.
Значения относительных стандартных неопределенностей влияющих величин рассчитываются как отношение стандартной неопределенности влияющей величины к значению оценки влияющей величины.
Значения процентных вкладов неопределенностей влияющих величин в суммарную стандартную неопределенность рассчитываются как умноженное на 100 % отношение квадрата относительной стандартной неопределенности влияющей величины к квадрату относительной суммарной стандартной неопределенности.
Этап 6. Бюджет неопределенности
В таблице представлен бюджет неопределенности измерений коэффициента поправки серной кислоты.
Этап 7. Расширенная неопределенность
Расширенная неопределенность измерений коэффициента поправки серной кислоты, U(K), получается умножением суммарной стандартной неопределенности, u(K), на коэффициент охвата k, который выбирается равным 2 при уровне доверия приблизительно 95 % в предположении нормального распределения вероятностей измеряемой величины:
Этап 8. Результат измерения
Коэффициент поправки раствора серной кислоты концентрации c(H2SO4) = 0,1 моль/дм3 составляет (1,0001 ± 0,0108), где число, следующее за знаком ±, является численным значением расширенной неопределенности, которая получена умножением суммарной стандартной неопределенности на коэффициент охвата k = 2, основанный на предполагаемом нормальном распределении, и определяет интервал, соответствующий вероятности охвата приблизительно 95 %.
Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, Вы можете задать их нашим специалистам посредством обратной связи или по телефонам, указанным в контактных данных на сайте.
Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.
УЗНАТЬ СТОИМОСТЬ РАЗРАБОТКИ МЕТОДИКИ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ…
Пример 4. Оценивание неопределенности измерений pH воды
Измерительная задача
Метод основан на измерении разности потенциалов гальванического элемента с использованием соответствующего рН-метра. Измерения проводят рН-метром/иономером ИТАН. Перед измерением пробы воды про-водится двухточечная калибровка по буферным растворам. Температура пробы питьевой воды и температура буферных растворов измеряется термодатчиком, встроенным в рН-метр. рН-метр автоматически учитывает разность температур буферных растворов и пробы питьевой воды в выдаваемых показаниях.
Этап 1. Составление функции измерений
Измеряемой величиной является рН пробы питьевой воды, ед. рН, которая определяется согласно функции измерений:
где рНизм – показания рН-метра, ед. рН;
δкал – поправка на погрешность калибровки рН-метра, ед. рН;
δсх – поправка на повторяемость измерений, ед. рН.
Измеренное значение величины округляют до одного десятичного знака.
Результаты измерений
Температура пробы питьевой воды, измеренная термодатчиком рН-метра, составила 10 °С. При измерении пробы питьевой воды с цифрового дисплея рН-метра было снято показание рН равное 6,52 ед. рН.
Этап 2. Анализ входных величин
2.1 Показания рН-метра (рНизм)
Показание рН-метра составило рНизм = 6,52 ед. рН.
Стандартная неопределенность величины рНизм рассчитывается на основании информации о пределах основной допускаемой абсолютной погрешности рН-метра в предположении прямоугольного распределения вероятностей. В паспорте на рН-метр/иономер ИТАН указаны пределы основной допускаемой абсолютной погрешности измерения рН (измерительным преобразователем в комплекте с электродной системой в растворах с температурой от 10 °С до 60 °С) ± Δ = ± 0,050 ед. рН. Стандартная неопределенность величины рНизм рассчитывается по формуле:
Примечание – Неопределенностью измерений, обусловленной разрешающей способностью цифрового дисплея рН-метра пренебрегаем, поскольку данная составляющая неопределенности значительно ниже составляющей, обусловленной основной допускаемой абсолютной погрешностью рН-метра.
2.2 Поправка на погрешность калибровки рН-метра (δкал)
Поправка на погрешность калибровки рН-метра оценивается значением «нуль»
δкал = 0 ед. рН.
Стандартная неопределенность измерений величины δкал рассчитывается на основании информации о допускаемом отклонении значений рН, при проверке калибровки, от значений рН буферных растворов в контрольных точках ± Δк = ± 0,03 ед. рН. Стандартная неопределенность величины δкал рассчитывается в предположении прямо-угольного распределения вероятностей в указанных границах по формуле:
Примечание – Неопределенностью измерений рН буферных растворов пренебрегаем, т.к. значения расширенных неопределенностей измерений рН буферных растворов не превышают 1/3 от допускаемого отклонения Δк.
2.3 Поправка на повторяемость измерений (δсх)
Поправка на повторяемость измерений рН оценивается значением «нуль» δсх = 0 ед. рН.
Стандартная неопределенность измерений величины δсх рассчитывается на основании информации о стандартном отклонении повторяемости в предположении нормального распределения вероятностей. Для питьевой воды в диапазоне рН от 6,35 до 6,46 ед. рН при межлабораторном исследовании метода измерений рН было установлено значение стандартного отклонения повторяемости σr = 0,011 ед. рН. В лаборатории при внедрении метода измерений установленное значение показателя повторяемости было подтверждено и распространено на диапазон измерений, содержащий измеренное значение рН в исследуемой пробе питьевой воды. Стандартная неопределенность величины δсх рассчитывается по формуле:
Этап 3. Анализ корреляций
Все входные величины рассматриваются как некоррелированные.
Этап 4. Измеренное значение величины
рН пробы питьевой воды будет оцениваться в соответствии с выражением (1) и составит:
Этап 5. Суммарная стандартная неопределенность
Суммарная стандартная неопределенность измерений величины рН рассчитывается по формуле:
Коэффициенты чувствительности для всех влияющих величин, входящих в функцию измерений (1), будут равны 1.
Этап 6. Бюджет неопределенности
В таблице представлен бюджет неопределенности для измеряемой величины и произведены соответствующие расчеты для нахождения ее стандартной неопределенности.
Таблица – Бюджет неопределенности для рН пробы питьевой воды
Этап 7. Расширенная неопределенность
Расширенная неопределенность U получается умножением суммарной стандартной неопределенности на коэффициент охвата k, который выбирается равным 2 при уровне доверия 95 % в предположении нормального распределения вероятностей измеряемой величины:
Этап 8. Представление результата измерения
Результат измерения записывается в виде:
«рН пробы воды составила (6,5 ± 0,1) ед. рН, k = 2, P = 95 %».
Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, Вы можете задать их нашим специалистам посредством обратной связи или по телефонам, указанным в контактных данных на сайте.
Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.
УЗНАТЬ СТОИМОСТЬ РАЗРАБОТКИ МЕТОДИКИ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ…
Пример 5. Оценивание неопределенности измерений относительного удлинения эластичного герметика
Измерительная задача
Относительное удлинение герметика полиуретанового определяется по ГОСТ 21751-76 «Герметики. Метод определения условной прочности относительного удлинения при разрыве и относительной остаточной деформации после разрыва» с применением разрывной машины РМ-30-1 методом растяжения образцов с постоянной скоростью при заданной температуре до разрыва с последующим измерением геометрических параметров образца. Длина рабочего участка образца до и после приложения нагрузки измеряется линейкой металлической по ГОСТ 427-75 с пределом измерений 300 мм и ценой деления 1 мм.
Образцы герметика для испытаний типа 1 вырезают длиной (115 ± 1) мм специальным ножом согласно ГОСТ 21751 (пп. 1.3, 2.1-2.4). Общее количество испытываемых образцов – 5. Испытания проводят при температуре окружающего воздуха (20 ± 3) ºС и относительной влажности (65 ± 5) %.
Этап 1. Составление функции измерений
Относительное удлинение каждого испытываемого образца, εрi, в процентах рассчитывается на основании функции измерений:
где lpi – длина рабочего участка образца в момент разрыва, мм;
l0 – первоначальная длина рабочего участка образца, мм.
Относительное удлинение герметика полиуретанового рассчитывается как среднее арифметическое относительных удлинений, εрi, полученных для каждого из испытываемых образцов:
где – среднее арифметическое измерений относительного удлинения пяти образцах, %;
t – количество испытанных образцов герметика;
Fr – поправка на рассеяние результатов измерений относительных удлинений, полученных на всех испытанных образцах, %.
Результат измерения округляется до целых чисел.
Результаты измерений
При определении относительного удлинение герметика полиуретанового было испытано 5 образцов. Результаты испытаний представлены в таблице 1.
Таблица 1 – Результаты испытаний образов герметика полиуретанового на относительное удлинение
Этап 2. Анализ входных величин
2.1 Среднее арифметическое измерений относительного удлинения пяти образцах ()
Значение оценки рассчитывается по формуле
Возможное рассеяние результатов измерений относительного удлинения на пяти единичных образцах герметика учитывается через влияющую величину F.
2.2 Первоначальная длина рабочего участка образца (l0i)
Тип оценивания неопределенности: В
Вид распределения: трапецеидальное
Значение оценки: получают путем снятия показаний со шкалы линейки при прямых измерениях длины рабочего участка образца до проведения испытаний, мм; значения для каждого образца представлены в таблице 1
Стандартная неопределенность: u(l0i) = 0,294 мм
Неопределенность, связанная с величиной l0i, оценивается на основании информации о допускаемом отклонении от номинальных значений длины шкалы используемой линейки с пределом измерений 300 мм ±Δl = ±0,10 мм и цене деления линейки d = 1 мм. Поскольку значения приведено без вероятности, принимаем прямоугольное распределение значений погрешности линейки и ошибки оператора при снятии показаний со шкалы линейки в соответствующих границах. Стандартная неопределенность оценивается по типу В и составляет:
2.3 Длина рабочего участка образца в момент разрыва (lpi)
Вид распределения: трапецеидальное
Значение оценки: получают путем снятия показаний со шкалы линейки при прямых измерениях длины рабочего участка образца после проведения испытаний, мм; значения для каждого образца представлены в таблице 1
Стандартная неопределенность: u(lpi) = 0,294 мм
Неопределенность, связанная с величиной lpi, оценивается на основании информации о допускаемом отклонении от номинальных значений длины шкалы используемой линейки с пределом измерений 300 мм ±Δl = ±0,10 мм и цене деления линейки d = 1 мм. Поскольку значения приведено без вероятности, принимаем прямоугольное распределение значений погрешности линейки и ошибки оператора при снятии показаний со шкалы линейки в соответствующих границах. Стандартная неопределенность оценивается по типу В и составляет:
2.4 Поправка на рассеяние результатов измерений относительных удлинений, полученных на всех испытанных образцах (Fr )
Тип оценивания неопределенности: А
Вид распределения: нормальное
Значение оценки: Fr = 0,0 %
Стандартная неопределенность: u(Fr) = 22,80 %
Стандартная неопределенность поправки рассчитывается как стандартное отклонение среднего арифметического измерений относительного удлинения пяти образцах по типу А в предположении нормального распределения и составляет:
Этап 3. Анализ корреляций
Все входные величины рассматриваются как некоррелированные.
Этап 4. Измеренное значение величины
Оценка измеряемой величины – относительное удлинение герметика, εр, в процентах, рассчитывается по формуле (1) используя полученные в Этапе 2 значения оценок входных величин:
Этап 5. Суммарная стандартная неопределенность
Стандартную неопределенность измеряемой величины εр, %, рассчитываем по закону распространения неопределенностей путем суммирования квадратов произведений стандартных неопределенностей влияющих величин, входящих в функции измерений (1) и (2), на соответствующие коэффициенты чувствительности:
Коэффициенты чувствительности рассчитываются как частные производные функции измерений (1) по входным величинам:
Примечание – Для расчета коэффициентов чувствительности используются значения параметров, полученные при испытаниях первого образца герметика.
Вклад в неопределенность от j-ой входной величины рассчитывается как произведение стандартной неопределенности этой величины на соответствующий коэффициент чувствительности. Процентный вклад рассчитывается как отношение квадрата вклада входной величины к квадрату суммарной стандартной неопределенности (выражается в процентах):
Этап 6. Бюджет неопределенности
Бюджет неопределенности для относительного удлинения герметика представлен в таблице 3.
Таблица 3 – Бюджет неопределенности для относительного удлинения
Этап 7. Расширенная неопределенность
Расширенную неопределенность U получаем умножением суммарной стандартной неопределенности на коэффициент охвата k. Поскольку в бюджете неопределенности доминирует составляющая, распределенная по нормальному закону распределения и рассчитанная на малом объеме экспериментальных данных (менее 10), то значение коэффициента охвата выбирается в предположении распределения Стьюдента для измеряемой величины как квантиль распределения Стьюдента при вероятности 95 % и числе эффективных степеней свободы, которые рассчитываются по формуле Уэлча-Саттертуэта
Значение коэффициента охвата принимается равным k = 2,57. Расширенная неопределенность будет рассчитываться по формуле:
Этап 8. Представление результата измерения
Результат измерения представляют в виде:
«Относительное удлинение герметика полиуретанового составило (580 ±63) %, где число, следующее за знаком ±, является численным значением расширенной неопределенности, которая получена умножением суммарной стандартной неопределенности на коэффициент охвата k = 2,78, основанный на предполагаемом распределении Стьюдента и числе эффективных степеней свободы νeff = 5, и определяет интервал, соответствующий вероятности охвата 95 %».
Библиография
ГОСТ 21751-76 Герметики. Метод определения условной прочности относительного удлинения при разрыве и относительной остаточной деформации после разрыва
ГОСТ 427-75 Линейки измерительные металлические. Технические условия
Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, Вы можете задать их нашим специалистам посредством обратной связи или по телефонам, указанным в контактных данных на сайте.
Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.
УЗНАТЬ СТОИМОСТЬ РАЗРАБОТКИ МЕТОДИКИ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ…
Пример 6. Оценивание неопределенности измерений прочности бетона на растяжение при изгибе
Измерительная задача
Прочность на растяжение при изгибе бетона класса прочности на растяжение при изгибе Вtb3,6 определяется по ГОСТ 10180-2012 «Бетоны. Методы определения прочности по контрольным образцам» путем разрушающих кратковременных статических испытаний специально изготовленных контрольных образцов бетона. В качестве контрольных образцов используются изготовленные согласно ГОСТ 10180 (п. 4) образцы бетона в форме призмы квадратного сечения 100×100×400 мм. Количество контрольных образцов в серии – три.
Испытания контрольных образцов на прочность на растяжение при изгибе проводят на универсальной испытательной машине C093-03A. Линейные размеры образцов измеряют линейкой металлической по ГОСТ 427-75 с пределом измерений 500 мм и ценой деления 1 мм.
Этап 1. Составление функции измерений
Прочность бетона на растяжение при изгибе для i-го образца в серии Rtb,i, МПа, вычисляется в соответствии со следующей функцией измерений:
где δ – масштабный коэффициент для приведения прочности бетона к прочности бетона в образцах базовых размера и формы;
Fi – разрушающая нагрузка для i-го контрольного образца, Н;
ai – ширина поперечного сечения призмы для i-го контрольного образца, мм;
bi – высота поперечного сечения призмы для i-го контрольного образца, мм;
l – расстояние между опорами, мм.
Прочность бетона на растяжение при изгибе Rtb, МПа, вычисляется в соответствии со следующей функцией измерений:
где Fr – поправочный коэффициент, учитывающий расхождение между результатами измерений прочности n образцов, Fr = 1;
n – количество образцов в серии, n = 3.
Измеренное значение прочности бетона на растяжение при изгибе округляется с точностью до 0,01 МПа.
Результаты измерений
При проведении испытаний трех контрольных образцов бетона на растяжение при изгибе были получены значения параметров, представленные в таблице 1.
Таблица 1 – Результаты испытаний контрольных образцов бетона на прочность на растяжение при изгибе
Этап 2. Анализ входных величин
2.1 Масштабный коэффициент для приведения прочности бетона к прочности бетона в образцах базовых размера и формы (δ)
Значение оценки выбирается согласно ГОСТ 10180 (таблица 1) и составляет δ = 0,92.
Величина рассматривается как постоянная.
2.2 Разрушающая нагрузка для i-го контрольного образца (Fi)
Значение оценки величины Fi для каждого контрольного образца определяется по шкале отсчетного устройства испытательной машины и представлено в таблице 1
Тип оценивания неопределенности: В
Вид распределения: трапецеидальное
Стандартная неопределенность: u(F) = 164,04 Н
Неопределенность, связанная с величиной F, оценивается на основании информации о пределах допускаемой относительной погрешности показания силы ± δF = ± 1 % и цене деления шкалы стрелочного индикатора d = 500 Н. Поскольку значения приведены без вероятности, принимаем прямоугольное распределение значений погрешности показаний силы и ошибки оператора при снятии показаний со шкалы индикатора в соответствующих границах. Стандартная неопределенность оценивается по типу В и составляет:
Примечание – Для расчета стандартной неопределенности разрушающей нагрузки используется значение параметра, полученное при испытаниях первого контрольного образца.
2.3 Ширина поперечного сечения призмы для i-го контрольного образца (ai)
Значение оценки величины аi для каждого контрольного образца определяется по шкале линейки металлической и представлено в таблице 1
Тип оценивания неопределенности: В
Вид распределения: трапецеидальное
Стандартная неопределенность: u(а) = 0,301 мм
Неопределенность, связанная с величиной а, оценивается на основании информации о допускаемом отклонении от номинальных значений длины шкалы используемой линейки с пределом измерений 500 мм ±Δl = ±0,15 мм и цене деления линейки dl = 1 мм. Поскольку значения приведено без вероятности, принимаем прямоугольное распределение значений погрешности линейки и ошибки оператора при снятии показаний со шкалы линейки в соответствующих границах. Стандартная неопределенность оценивается по типу В и составляет:
2.4 Высота поперечного сечения призмы для i-го контрольного образца (bi)
Значение оценки величины bi для каждого контрольного образца определяется по шкале линейки металлической и представлено в таблице 1
Тип оценивания неопределенности: В
Вид распределения: трапецеидальное
Стандартная неопределенность: u(b) = 0,301 мм
Неопределенность, связанная с величиной b, оценивается на основании информации о допускаемом отклонении от номинальных значений длины шкалы используемой линейки с пределом измерений 500 мм ±Δl = ±0,15 мм и цене деления линейки dl = 1 мм. Поскольку значения приведено без вероятности, принимаем прямоугольное распределение значений погрешности линейки и ошибки оператора при снятии показаний со шкалы линейки в соответствующих границах. Стандартная неопределенность оценивается по типу В и составляет:
2.5 Расстояние между опорами (l)
Значение оценки величины l = 300 мм и определяется по шкале линейки металлической
Тип оценивания неопределенности: В
Вид распределения: трапецеидальное
Стандартная неопределенность: u(l) = 0,301 мм
Неопределенность, связанная с величиной l, оценивается на основании информации о допускаемом отклонении от номинальных значений длины шкалы используемой линейки с пределом измерений 500 мм ±Δl = ±0,15 мм и цене деления линейки dl = 1 мм. Поскольку значения приведено без вероятности, принимаем прямоугольное распределение значений погрешности линейки и ошибки оператора при снятии показаний со шкалы линейки в соответствующих границах. Стандартная неопределенность оценивается по типу В и составляет:
2.6 Поправочный коэффициент, учитывающий расхождение между результатами измерений прочности n образцов (Fr)
Значение оценки: Fr = 1
Тип оценивания неопределенности: B
Вид распределения: нормальное
Стандартная неопределенность: u(Fr) = 0,06
Стандартная неопределенность поправки рассчитывается на основании среднего внутрисерийного коэффициента вариации прочности бетона, установленного в лаборатории согласно ГОСТ 10180 (Приложение А) и равного 6 %. Стандартная неопределенность оценивается по типу В в предположении нормального распределения и составляет:
Примечание – Для использования в расчетах установленного в лаборатории среднего внутрисерийного коэффициента вариации следует проверить соответствие реального разброса результатов измерений прочности бетона на растяжение при изгибе, полученного на испытанных контрольных образцах, установленному среднему внутрисерийному коэффициенту вариации используя положения СТБ ИСО 5725-6 и следующее неравенство:
где f(n) – коэффициент критического размаха, выбирается в зависимости от количества контрольных образцов в серии n по СТБ ИСО 5725-6 (таблица 1).
Для нашего примера f(n=3) = 3,3 и неравенство (8) выполняется:
Этап 3. Анализ корреляций
При измерении величин а и b, близких по измеренным значением, присутствуют корреляционные эффекты, связанные с применением одного средства измерений (линейки металлической) в одной точке диапазона измерений (узком диапазоне измерений) и вызванные погрешностью применяемого средства измерений. Однако, учитывая, что вклад этой составляющей в стандартные неопределенности величин а и b незначителен (в процентном выражении составляет 8,3 %), существующей корреляцией пренебрегаем и не учитываем при расчете суммарной стандартной неопределенности измеряемой величины: прочности бетона на растяжение при изгибе.
Все остальные входные величины рассматриваются как некоррелированные.
Этап 4. Измеренное значение величины
Оценка измеряемой величины – прочности бетона на растяжение при изгибе, Rtb, МПа, рассчитывается по формуле (2) используя полученные в таблице 1 значения оценок входных величин:
Этап 5. Суммарная стандартная неопределенность
Стандартную неопределенность измеряемой величины Rtb, МПа, рассчитываем по закону распространения неопределенностей путем суммирования квадратов относительных стандартных неопределенностей влияющих величин, входящих в функции измерений (1) и (2):
и составляет для нашего примера
Примечание – Для расчета относительных стандартных неопределенностей входных величин используются значения величин, полученные для первого контрольного образца.
Значения процентных вкладов неопределенностей влияющих величин в суммарную стандартную неопределенность рассчитываются как умноженное на 100 % квадрат отношения относительной стандартной неопределенности влияющей величины к относительной суммарной стандартной неопределенности:
Этап 6. Бюджет неопределенности
Бюджет неопределенности для прочности бетона на растяжение при изгибе представлен в таблице 3.
Таблица 3 – Бюджет неопределенности для прочности бетона на растяжение при изгибе
Этап 7. Расширенная неопределенность
Расширенную неопределенность U получаем умножением суммарной стандартной неопределенности на коэффициент охвата k = 2 в предположении нормального распределения при уровне доверия приблизительно 95 %:
Этап 8. Представление результата измерения
Результат измерения представляют в виде:
«Прочность бетона на растяжение при изгибе бетона класса прочности на растяжение при изгибе Вtb3,6 составила (3,65 0,45) МПа, где число, следующее за знаком ±, является численным значением расширенной неопределенности, которая получена умножением суммарной стандартной неопределенности на коэффициент охвата k = 2, основанный на предполагаемом нормальном распределении, и определяет интервал, соответствующий вероятности охвата приблизительно 95 %».
Библиография
ГОСТ 10180-2012 Бетоны. Методы определения прочности по контрольным образцам
ГОСТ 427-75 Линейки измерительные металлические. Технические условия
СТБ ИСО 5725-6-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике
Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, Вы можете задать их нашим специалистам посредством обратной связи или по телефонам, указанным в контактных данных на сайте.
Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.
УЗНАТЬ СТОИМОСТЬ РАЗРАБОТКИ МЕТОДИКИ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ…
Пример 7. Оценивание неопределенности измерений твердости по Бриннелю
Измерительная задача
Измерение твердости трубопровода из Стали 10Г2СД по шкале Бриннеля выполняется твердомером ТКМ-459
Условия проведения измерений:
- температура окружающего воздуха +15 ºС;
- относительная влажность 60 %;
- толщина контролируемого участка детали 10 мм;
- шероховатость поверхности, на которой производится измерение Rа 1,2.
Этап 1. Составление функции измерений
Измеряемой величиной является твердость контролируемого участка объекта контроля по шкале Бринелля, Н, которая определяется как:
где Низм – показания твердомера, НВ;
δт – поправка на погрешность твердомера, НВ;
δр – поправка на разрешающую способность дисплея твердомера, НВ.
Результаты измерений
На контролируемом участке были получены следующие единичные результаты наблюдения твердости по шкале Бринелля:
h2 = 180 НВ
h3 = 184 НВ
h4 = 175 НВ
h5 = 172 НВ
H5 = 183 НВ
Этап 2. Анализ входных величин
2.1 Показания твердомера (Низм)
Показания твердомера оцениваются как среднее арифметическое из 5 единичных результатов наблюдений твердости контролируемого участка объекта контроля по формуле:
Стандартная неопределенность величины Низм рассчитывается как среднее квадратическое отклонение среднего арифметического из 5 единичных результатов наблюдений по формуле:
Примечание – Данная составляющая может не учитываться, если отклонение максимального единичного показания твердости от минимального не превышает предела основной допускаемой погрешности твердомера.
2.2 Поправка на погрешность твердомера (δт)
Поправка на погрешность твердомера оценивается значением «нуль». В паспорте на твердомер установлены пределы абсолютной погрешности ± Δ = ± 15 НВ при измерении по шкале Бринелля (НВ). Стандартная неопределенность поправки определяется по типу В на основании установленных пределов абсолютной погрешности твердомера в предположении прямоугольного закона распределения: 2.3 Поправка на разрешающую способность дисплея твердомера (δр)
Поправка на разрешающую способность дисплея твердомера оценивается значением «нуль». Стандартная неопределенность поправки определяется через величину единицы наименьшего разряда дисплея (а = 1 НВ).
Стандартная неопределенность поправки на разрешающую способность дисплея твердо-мера оценивается по типу В в предположении прямоугольного распределения из выражения:
Этап 3. Анализ корреляций
Все входные величины рассматриваются как некоррелированные.
Этап 4. Измеренное значение величины
Твердость контролируемого участка трубопровода будет оцениваться в соответствии с выражением (1) и составит:
Этап 5. Суммарная стандартная неопределенность
Суммарная стандартная неопределенность, приписываемая результату измерения Н, рас-считывается по формуле:
Коэффициенты чувствительности для всех влияющих величин, входящих в функцию измерений (1), будут равны 1.
Этап 6. Бюджет неопределенности
В таблице представлен бюджет неопределенности для измеряемой величины и произведены соответствующие расчеты для нахождения ее стандартной неопределенности.
Таблица – Бюджет неопределенности для твердости по шкале Бриннеля Н
Этап 7. Расширенная неопределенность
Суммарное распределение измеряемой величины предполагаем прямоугольным (по-скольку доминирует составляющая неопределенности от величины δт, процентный вклад составляет более 90 %). Коэффициент охвата для уровня доверия 95 % принимается равным k = 1,65. Расширенную неопределенность рассчитываем по формуле:
Этап 8. Представление результата измерения
Результат измерения записывается в виде:
«Твердость по Бринеллю контролируемого участка трубопровода из Стали 10Г2СД со-ставила (180 ± 15) НВ, k = 1,65, P = 95 %».
Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, Вы можете задать их нашим специалистам посредством обратной связи или по телефонам, указанным в контактных данных на сайте.
Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.
УЗНАТЬ СТОИМОСТЬ РАЗРАБОТКИ МЕТОДИКИ ОЦЕНИВАНИЯ НЕОПРЕДЕЛЕННОСТИ…
ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
ПОГРЕШНОСТИ ИЗМЕРЕНИЙКак выполнить и оформить лабораторную работу
Общие указания
Погрешности измерений
О численных расчетах
Правила построения графиков
В лабораторном практикуме студенты вначале знакомятся с основными приемами проведения физических измерений и правилами обработки результатов. При этом должны быть выработаны определенные навыки, что является предпосылкой дальнейшей успешной работы в лаборатории. Целью лабораторного практикума является более глубокое осознание студентами физических явлений и законов. Эта задача может быть успешно решена только в том случае, если лабораторные работы выполняются с достаточным пониманием сущности исследуемых явлений. Поэтому домашняя подготовка к выполнению лабораторной работы является одним из важнейших этапов.
Подготовка к работе. При подготовке к работе рекомендуется придерживаться следующего плана.
- Прочитайте название работы и выясните смысл всех непонятных слов.
- Прочитайте описание работы от начала до конца, не задерживаясь на выводе формул. Задача первого прочтения состоит в том, чтобы выяснить, какой физический закон или явление изучается в данной работе и каким методом проводится исследование.
- Прочитайте по учебнику материал, относящийся к данной работе. Разберите вывод формул по методическому пособию. Найдите ответы на контрольные вопросы, приведенные в конце описания работы.
- Разберите по методическому пособию принцип устройства и работы приборов, которые предполагается использовать в работе.
- Выясните, какие физические величины и с какой точностью будут непосредственно измеряться и каковы их размерности.
- Начертите в лабораторном журнале принципиальную схему эксперимента и таблицы, в которые будут заноситься результаты измерений.
- Продумайте, какой окончательный результат должен быть получен в данной лабораторной работе.
Выполнение работы. При выполнении работы вначале следует ознакомиться с приборами. Нужно установить их соответствие описанию, выполнить рекомендованную в описании прибора последовательность действий по подготовке прибора к работе, убедиться в том, что при изменении положений органов управления возникают ожидаемые изменения параметров, определить цену деления шкалы прибора и его систематическую погрешность, выяснить, как изменить множитель шкалы (если это возможно), попробовать сделать пробный отсчет. Далее следует провести предварительный опыт с тем, чтобы пронаблюдать качественно изучаемое явление, оценить, в каких пределах находятся измеряемые величины. После проведенной подготовки можно приступать к измерениям. Следует помнить, что всякое измерение, если только это возможно сделать, должно выполняться больше, чем один раз.
Производимые по приборам отсчеты записываются в лабораторный журнал сразу же после выполнения отсчета в том виде как они считаны со шкалы прибора — без каких-либо пересчетов на множитель шкалы или систему единиц. Естественно, что единицы измерений и множитель шкалы должны быть записаны в заголовке соответствующей таблицы с результатами измерений. При измерениях, выполняемых при помощи осциллографа, отсчет следует делать непосредственно по шкале осциллографа, установив предварительно подходящий размер изображения. Картинка, срисованная с экрана, может быть использована только в качестве иллюстрации или для качественного анализа. Все записи при выполнении лабораторной работы должны вестись исключительно в лабораторном журнале. Лабораторный журнал является одновременно и черновиком, и чистовиком. Его следует вести самым аккуратнейшим образом. Здесь и только здесь производятся все записи при выполнении лабораторной работы, в том числе прикидочные расчеты и предварительные результаты. Все исправления в журнале должны делаться так, чтобы предыдущий результат оставался читаемым. Рядом с исправлением следует указывать, в чем состоит причина исправления. Лабораторный журнал является тем единственным документом, на основании которого затем делается отчет о выполненной работе. Поэтому журнал следует приносить на все занятия, как при выполнении работы, так и при сдаче отчета.
Оформление отчета. На титульном листе отчета указывается название работы и фамилия автора отчета. В начале отчета формулируется цель работы и/или физический закон (явление), исследованный в работе. Обязательно приводится схема установки (не рисунок!), на которой выполнялась работа. В механике- это кинематическая схема, на которой видны все перемещения частей устройства, в электричестве- принципиальная схема, в оптике- схема расположения оптических элементов и ход лучей и т.д. В соответствующих таблицах приводятся результаты непосредственных измерений, причем все таблицы должны быть озаглавлены (например, “Таблица 1. Результаты измерения массы тела студента до и после обеда”). Приводятся все расчетные формулы (без вывода) как в символьном виде, так и с подставленными числами. Приводится вывод формул для расчета погрешностей и сам расчет. В конце каждого упражнения записывается окончательный результат, полученный в данном упражнении. К отчету прикладываются необходимые графики. На каждом графике должно быть указано, к какому упражнению он относится, и что на графике изображено. В конце отчета формулируются выводы. В выводах должны быть проанализированы полученные результаты и дано заключение об их согласии с теоретическими зависимостями.
ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
Основной задачей физического эксперимента является измерение численных значений наблюдаемых физических величин. Измерением называется операция сравнения величины исследуемого объекта с величиной единичного объекта. Так, например, за единицу длины принят метр, и в результате измерения длины некоторого отрезка определяется, сколько метров содержится в этом отрезке.
Принято различать прямые и косвенные измерения. При прямом измерении производится непосредственное сравнение величины измеряемого объекта с величиной единичного объекта. В результате искомая величина находится прямо по показаниям измерительного прибора, например, сила тока — по отклонению стрелки амперметра, вес — по растяжению пружинных весов и т.д. Однако гораздо чаще измерения проводят косвенно, например, площадь прямоугольника определяют по измерению длин его сторон, электрическое сопротивление — по измерениям силы тока и напряжения и т.д. Во всех этих случаях искомое значение измеряемой величины получается путем соответствующих расчетов.
Результат всякого измерения всегда содержит некоторую погрешность. Поэтому в задачу измерений входит не только нахождение самой величины, но также и оценка допущенной при измерении погрешности. Напомним, что абсолютной погрешностью приближенного числа называется разность между этим числом и его точным значением, причем ни точное значение, ни абсолютная погрешность принципиально неизвестны и подлежат оценке по результатам измерений. Относительной погрешностью приближенного числа называется отношение абсолютной погрешности приближенного числа к самому этому числу. Если оценка погрешности результата физического измерения не сделана, то можно считать, что измеряемая величина вообще неизвестна, поскольку погрешность может, вообще говоря, быть того же порядка, что и сама измеряемая величина или даже больше. В этом состоит отличие физических измерений от бытовых или технических, в которых в результате практического опыта заранее известно, что выбранный измерительный инструмент обеспечивает приемлемую точность, а влияние случайных факторов на результат измерений пренебрежимо мало по сравнению с ценой деления применяемого прибора.
Погрешности физических измерений принято подразделять на систематические, случайные и грубые. Систематические погрешности вызываются факторами, действующими одинаковым образом при многократном повторении одних и тех же измерений. Систематические погрешности скрыты в неточности самого инструмента и неучтенных факторах при разработке метода измерений. Обычно величина систематической погрешности прибора указывается в его техническом паспорте. Что же касается метода измерений, то здесь все зависит от квалификации экспериментатора. Хотя суммарная систематическая погрешность во всех измерениях, проводимых в рамках данного эксперимента, будет приводить всегда либо к увеличению, либо к уменьшению правильного результата, знак этой погрешности неизвестен. Поэтому на эту погрешность нельзя внести поправку, а приходится приписывать эту погрешность окончательному результату измерений.
Случайные погрешности обязаны своим происхождением ряду причин, действие которых неодинаково в каждом опыте и не может быть учтено. Они имеют различные значения даже для измерений, выполненных одинаковым образом, то есть носят случайный характер. Допустим, что сделано n повторных измерений одной и той же величины. Если они выполнены одним и тем же методом, в одинаковых условиях и с одинаковой степенью тщательности, то такие измерения называются равноточными.
| Пусть минимальный интервал значений измеряемой величины, через который ведутся отсчеты (цена деления прибора), будет h, а среднее арифметическое всех результатов измерений пусть будет < x> . Обозначим через ki число тех результатов, которые отклонились от среднего < x> на величину Δx= ih. Отложив по оси абсцисс величину абсолютных погрешностей Δx, а по оси ординат значения k, получим ступенчатый график, называемый гистограммой (рис.1). |
Если устремить число измерений к бесконечности, а интервал h — к нулю, то гистограмма переходит в пределе в непрерывную кривую, которая является кривой распределения погрешностей. При некоторых условиях, которые обычно выполняются при проведении измерений, эта кривая представляет собой график функции Гаусса, имеющей следующий вид:
Рис. 2 |
где параметр σ определяет ширину распределения. Несколько кривых Гаусса для разных значений параметра σ показаны на рис.2. |
Третий тип погрешностей, с которыми приходится иметь дело — грубые погрешности или промахи. Под грубой погрешностью измерения понимается погрешность, существенно превышающая ожидаемую при данных условиях. Она может быть сделана вследствие неправильного применения прибора, неверной записи показаний прибора, ошибочно прочитанного отсчета, неучета множителя шкалы и т.п.
Вычисление погрешностей. В дальнейшем будем предполагать, что
1) грубые погрешности исключены;
2) поправки, которые следовало определить (например, смещение нулевого деления шкалы), вычислены и внесены в окончательные результаты;
3) все систематические погрешности известны (с точностью до знака).
В этом случае результаты измерений оказываются все же не свободными от случайных погрешностей. Если случайная погрешность окажется меньше систематической, то, очевидно, нет смысла пытаться уменьшить величину случайной погрешности — все равно результаты измерений не станут значительно лучше и, желая получить большую точность, нужно искать пути к уменьшению систематической погрешности. Наоборот, если случайная погрешность больше систематической, то именно случайную погрешность нужно уменьшить в первую очередь и добиться того, чтобы случайная погрешность стала меньше систематической, с тем чтобы последняя опять определяла окончательную погрешность результата. На практике обычно уменьшают случайную погрешность до тех пор, пока она не станет сравнимой по величине с систематической погрешностью. Как будет видно из дальнейшего, случайная погрешность уменьшается при увеличении числа измерений.
Поскольку из-за наличия случайных погрешностей результаты измерений по своей природе представляют собой тоже случайные величины, истинного значения xист измеряемой величины указать нельзя. Однако можно установить некоторый интервал значений измеряемой величины вблизи полученного в результате измерений значения xизм, в котором с определенной вероятностью содержится xист. Тогда результат измерений можно представить в следующем виде:
| (2) |
где Δx—погрешность измерений. Вследствие случайного характера погрешности точно определить ее величину невозможно. В противном случае найденную погрешность можно было бы ввести в результат измерения в качестве поправки и получить истинное значение xист.. Задача наилучшей оценки значения xист и определения пределов интервала (2) по результатам измерений является предметом математической статистики. Воспользуемся некоторыми ее результатами.
Пусть проведено n измерений величины x. Тогда за лучшую оценку истинного значения результата измерений принимается среднее арифметическое значение
| (3) |
где xi — результат i -го измерения.
Для оценки случайной погрешности измерения существует несколько способов. Наиболее распространена оценка с помощью стандартной или средней квадратичной погрешности σ (ее часто называют стандартной погрешностью или стандартом измерений).
Средней квадратичной погрешностью называется величина
| (4) |
где n — число наблюдений.
Если число наблюдений очень велико, то подверженная случайным колебаниям величина Snстремится к постоянному значению σ:
.
Именно этот предел и входит в качестве параметра σ в распределение Гаусса (1). Квадрат этой величины называется дисперсией измерений. В действительности, по результатам измерений всегда вычисляется не σ , а ее приближенное значение Sn, которое, вообще говоря, тем ближе к σ, чем больше n.
Все сказанное выше о погрешностях относится к погрешностям отдельного измерения. Однако важнее знать, насколько может уклоняться от истинного значения x среднее арифметическое < x> , полученное по формуле (3) для n повторных равноточных измерений. Теория показывает, что средняя квадратичная погрешность среднего арифметического S равна средней квадратичной погрешности отдельного результата измерений Sn, деленной на корень квадратный из числа измерений n, то есть
| (5) |
Это фундаментальный закон возрастания точности при росте числа наблюдений.
Пусть α означает вероятность того, что результат измерений отличается от истинного на величину, не большую, чем Δx. Вероятность α в этом случае носит название доверительной вероятности, а интервал значений измеряемой величины oт < x> — Δx до < x> +Δx называется доверительным интервалом.
Определим доверительный интервал. Чем большим будет установлен этот интервал, тем с большей вероятностью xистпопадаетв этот интервал. С другой стороны, более широкий интервал дает меньшую информацию относительно величины xист. Если ограничиться учетом только случайных погрешностей, то при небольшом числе измерений n для уровня доверительной вероятности a полуширина доверительного интервала (2) равна
| (6) |
где tα,n— коэффициент Стьюдента.
Таблица 1. Коэффициенты Стьюдента.
| Смысл понятий «доверительный интервал» и «доверительная вероятность» состоит в следующем: пусть α =0.95, тогда можно утверждать с надежностью 95%, что истинное значение величины xист не отличается от оценки (3) больше, чем на ±Δxсл.Значения коэффициентов tα ,n в зависимости от α и n табулированы (см. табл. Чтобы окончательно установить границы доверительного интервала необходимо расширить его с учетом систематической погрешности Δxсист. Систематическая погрешность, как правило, указана в паспорте или на шкале прибора, а в простейших случаях может быть принята равной половине цены деления младшего разряда шкалы. Обычно (хотя, строго говоря, и неверно) суммарная погрешность определяется как корень квадратный из суммы квадратов случайной и систематической погрешностей: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (7) |
Определенная согласно (7) величина Δx является абсолютной погрешностью. Очевидно, что при одном и том же значении Δx результат может оказаться достаточно точным при измерении некоторой большой величины, тогда как при измерении малой величины его точность будет недостаточной. Например, пусть имеется возможность измерять линейные размеры с погрешностью Δx=1 мм. Ясно, что это заведомо превышает необходимую точность при измерении, скажем, размеров комнаты, но измерение окажется слишком грубым при определении толщины монеты. Таким образом, становится понятной необходимость введения относительной погрешности, которая определяется как
| (8) |
и выражается, обычно, в процентах. Как видно, выражение (8) позволяет оценить величину погрешности по отношению к самой измеряемой величине. Очевидно, что в тех случаях, когда измеряемая величина представляет собой условное число, например, астрономическое время в данный момент (но не интервал времени между двумя событиями), пространственная координата (но не расстояние между двумя точками) и т.п., определение относительной погрешности смысла не имеет. Действительно, точность определения текущего времени по одним и тем же часам одинакова и в 12 часов, и в 1 час.
Рассмотрим теперь случай, когда при повторении измерений в одних и тех же условиях устойчиво получаются одинаковые значения x=x0. В этом случае систематическая погрешность настолько превышает случайную, что влияние случайной погрешности полностью маскируется. Истинное значение x отнюдь не равно x0. Оно, по-прежнему, остается неизвестным, и для него можно записать x=x0±Δx, причем погрешность Δx определяется в данном случае воспроизводящимися от опыта к опыту ошибками, связанными с неточностью измерительных приборов или метода измерений. Такую погрешность Δx, как отмечалось, называют систематической. Для более точного определения физической величины x в данном случае необходимо изменить постановку самого опыта: взять прибор более высокого класса точности, улучшить методику измерений и т.п.
Класс точности прибора (приведенная погрешность) — это выраженная в процентах относительная погрешность, которую дает данный прибор при измерении им наибольшего значения измеряемой величины, указанной на шкале прибора. Тогда абсолютная погрешность оказывается одинаковой по всей шкале прибора. Например, пусть имеется амперметр класса 1,5 со шкалой 20 А. При измерении им любого значения тока абсолютная погрешность будет равна 0,015·20 = 0,3 А. Нетрудно видеть, что при измерениях в конце шкалы относительная погрешность оказывается меньше, приближаясь к приведенной. Класс точности обычно указывается на шкале прибора соответствующей цифрой. Если на шкале такого обозначения нет, то данный прибор внеклассный, и его приведенная погрешность более 4%.
Рассмотрим, каким образом оценить случайную погрешность косвенно измеряемой величины y, которая является функцией некоторого числа m непосредственно измеряемых величин xi, т.е.
| (9) |
Само среднее значение <y> можно найти из известной функциональной зависимости (9), подставляя в качестве аргументов усредненные по всем проведенным опытам значения непосредственно измеренных величин < xi> . Соответствующие вычисления показывают, что абсолютная погрешность Δy в этом случае определяется по формуле
| (10) |
где обозначает так называемую частную производную.
Частная производная — это такая производная, которая вычисляется от функции f по аргументу xi , притом как все остальные аргументы считаются постоянными.
Относительная погрешность для косвенно измеряемой величины y определяется как
| (11) |
Формулу (10) применяют в тех случаях, когда в зависимости (9) измеряемые величины xiвходят, в основном, в виде слагаемых, а формула (11) оказывается особенно удобной тогда, когда правая часть (9) представляет собой произведение величин xi . Учитывая простую связь между абсолютной и относительной погрешностями δ =Δy/< y> , легко по известной величине Δy вычислить δ и наоборот. Рассмотрим применение формул (10) и (11) на примере. Пусть функциональная зависимость косвенно измеряемой величины y от непосредственно измеряемых величин xi имеет следующий простой вид:
.
Поскольку функция y представляет собой сумму двух слагаемых, находим частные производные
и подставляем их в формулу (10):
,
причем абсолютные погрешности Δx1 и Δx2 должны быть предварительно определены, как указано выше, по формулам (4) — (7).
Пусть теперь функциональная зависимость косвенно измеряемой величины y от непосредственно измеряемых величин xi имеет следующий вид:
.
В этом случае для определения погрешности косвенно измеряемой величины y воспользуемся формулой (11). Для этого сначала найдем логарифм, а затем — частные производные:
Подставляя в (11), найдем
.
Нетрудно видеть, что предварительное логарифмирование существенно упростило вид частных производных. Измеряемая величина y, вообще говоря, имеет какую-то размерность. Брать логарифм от размерной величины конечно же нельзя. Чтобы устранить некорректность, достаточно разделить y на постоянную, равную единице данной размерности (если y — длина, то разделим на 1 м). После логарифмирования получится дополнительное слагаемое, которое все равно исчезнет при взятии частных производных (производная от постоянной равна нулю), поэтому наличие такого слагаемого обычно подразумевается.
При обработке результатов измерений предлагается следующий порядок операций.
При прямых (непосредственных) измерениях
1. Вычисляется среднее из n измерений:
.
2. Определяется среднеквадратичная погрешность среднего арифметического:
.
3. Задается доверительная вероятность α и определяется коэффициент Стьюдента tα,n для заданного α и числа произведенных измерений n по табл. 1.
4. Находится полуширина доверительного интервала (абсолютная погрешность результата измерений):
| , где Δ xсл = tα,nS. |
5. Оценивается относительная погрешность результата измерений
6. Окончательный результат записывается в виде
x=< x> ±Δ x.
При косвенных измерениях
1. Для каждой серии измерений величин, входящих в определение искомой величины, производится обработка в описанной выше последовательности. При этом для всех измеряемых величин задают одно и то же значение доверительной вероятности a .
2. Оценивается точность результата косвенных измерений по формуле (10) либо (11), где производные вычисляются при средних значениях величин.
3. Определяется относительная погрешность результата серии косвенных измерений.
4. Окончательный результат записывается в виде
y=< y> ± Δy, где < y> =f(< x1>, < x2>,…,< xm>).
Возможен и другой подход к оценке погрешности результата косвенного измерения. Вместо определения искомой величины через средние значения < xi>как
< y> =f(< x1>, < x2>,…,< xm>)
можно для каждого выполненного опыта вычислить
а затем найти < y> как среднее арифметическое согласно (3) и далее абсолютную погрешность Δy по формулам (4)- (6). Оба способа дают близкие результаты.
О ЧИСЛЕННЫХ РАСЧЕТАХ
При вычислениях на микрокалькуляторе в ответе автоматически получается столько цифр, сколько их вмещается на индикаторе микрокалькулятора. При этом создается впечатление об избыточной точности результата. В то же время результаты измерений являются приближенными числами. Напомним (см., например, М.Я.Выгодский, Справочник по элементарной математике), что для приближенных чисел отличают запись 2,4 от 2,40, запись 0,02 от 0,0200 и т.д. Запись 2,4 означает, что верны только цифры целых и десятых, истинное же значение числа может быть, например, 2,43 или 2,38. Запись 2,40 означает, что верны и сотые доли, истинное число может быть 2,403 или 2,398, но не 2,421 и не 2,382. То же отличие проводится и для целых чисел. Запись 382 означает, что все цифры верны. Если же за последнюю цифру ручаться нельзя, то число округляется, но записывается не в виде 380, а в виде 38·10. Запись же 380 означает, что последняя цифра (ноль) верна. Если в числе 4720 верны лишь первые две цифры, его нужно записать в виде 47·102 или 4,7·103. В тех случаях, когда численные значения физических величин много больше либо много меньше единицы, их принято записывать в виде числа между 1 и 10, умноженного на соответствующую степень десяти.
Число знаков в окончательном результате устанавливается по следующим правилам. Сначала ограничивается число значащих цифр погрешности. Значащими цифрами называются все верные цифры числа кроме нулей, стоящих впереди числа. Например, в числе 0,00385 три значащие цифры, в числе 0,03085 четыре значащие цифры, в числе 2500 — четыре, в числе 2,5·103— две. Погрешность записывается всегда с одной или двумя значащими цифрами. При этом руководствуются следующими соображениями.
Величина случайной погрешности, полученная из обработки результатов некоторого числа измерений, сама является случайным числом, т.е., если проделать это же число измерений еще раз, то, вообще говоря, будет получен не только другой результат для измеряемой величины, но и другая оценка для погрешности. Поскольку погрешность оказывается случайным числом, то, пользуясь законами математической статистики, можно и для нее найти доверительный интервал. Соответствующие расчеты показывают, что даже при довольно большом числе измерений этот доверительный интервал оказывается весьма широким, т.е. величина погрешности оценивается достаточно грубо. Так при 10 измерениях относительная погрешность у погрешности превышает 30%. Поэтому для нее следует приводить две значащие цифры, если первая из них 1 или 2, и одну значащую цифру, если она равна или больше 3. Это правило легко понять, если учесть, что 30% от 2 составляет 0,6, а от 4 уже 1,2. Таким образом, если погрешность выражается, например, числом, начинающимся с цифры 4, то это число содержит неточность (1,2), превышающую единицу первого разряда.
После того, как погрешность записана, значение результата должно быть округлено таким образом, чтобы его последняя значащая цифра была того же разряда, что и у погрешности. Пример правильного представления окончательного результата:
t=(18.7± 1.2)·102с.
ПРАВИЛА ПОСТРОЕНИЯ ГРАФИКОВ
Графики строятся на миллиметровой бумаге, на которую прежде всего наносятся координатные оси. На концах осей указываются откладываемые физические величины и их размерности. Затем на оси наносят масштабные деления так, чтобы расстояние между делениями составляло 1, 2, 5 единиц (или 0.1, 0.2, 0.5, или 10, 20, 50 и т.д.). Обычно порядок масштаба, т.е. 10±nвыносится на конец оси. Например, для пути, пройденного телом, вместо 1000, 1100, 1200 и т.д. метров около масштабных делений пишут 1.0, 1.1, 1.2, а в конце оси физическую величину обозначают как S, 103 м или S·10—3, м. Точка пересечения осей не обязательно должна соответствовать нулю по каждой из осей. Начало отсчета по осям и масштабы следует выбирать так, чтобы график занял всю координатную плоскость. После построения осей на миллиметровку наносят экспериментальные точки. Их обозначают маленькими кружками, квадратиками и т.д. Если на одной координатной плоскости строится несколько графиков, то для точек выбираются разные обозначения. Затем от каждой точки вверх, вниз и вправо, влево откладывают отрезки, соответствующие погрешностям точек в масштабах осей. Если погрешность по одной из осей (или по обеим осям) оказывается слишком малой, то предполагается, что она отображается на графике размером самой точки.
Экспериментальные точки, как правило, не соединяются между собой ни отрезками прямой, ни произвольной кривой. Вместо этого строится теоретический график той функции (линейной, квадратичной, экспоненциальной, тригонометрической и т.д.), которая отражает проявляющуюся в данном опыте известную или предполагаемую физическую закономерность, выраженную в виде соответствующей формулы. В лабораторном практикуме встречаются два случая: проведение теоретического графика преследует цель извлечения из эксперимента неизвестных параметров функции (тангенса угла наклона прямой, показателя экспоненты и т.д.) либо делается сравнение предсказаний теории с результатами эксперимента.
В первом случае график соответствующей функции проводится «на глаз» так, чтобы он проходил по всем областям погрешности возможно ближе к экспериментальным точкам. Существуют математические методы, позволяющие провести теоретическую кривую через экспериментальные точки в определенном смысле наилучшим образом. При проведении графика «на глаз» рекомендуется пользоваться зрительным ощущением равенства нулю суммы положительных и отрицательных отклонений точек от проводимой кривой.
Во втором случае график строится по результатам расчетов, причем расчетные значения находятся не только для тех точек, которые были получены в опыте, а с некоторым шагом по всей области измерений для получения плавной кривой. Нанесение на миллиметровку результатов расчетов в виде точек является рабочим моментом — после проведения теоретической кривой эти точки с графика убираются. Если в расчетную формулу входит уже определенный (или заранее известный) экспериментальный параметр, то расчеты проводятся как со средним значением параметра, так и с его максимальным и минимальным (в пределах погрешности) значениями. На графике в этом случае изображается кривая, полученная со средним значением параметра, и полоса, ограниченная двумя расчетными кривыми для максимального и минимального значений параметра.
Правила построения графиков рассмотрим на следующем примере. Предположим, что в опыте исследовался закон движения некоторого тела. Тело двигалось прямолинейно, и задачей опыта было измерение расстояния, которое тело проходит за различные промежутки времени. После проведения некоторого числа опытов и обработки результатов измерений были найдены средние значения измеряемых величин и их погрешности. Требуется изобразить результаты опыта, представленные в табл. 2, в виде графика и найти из графика скорость тела, предполагая, что движение равномерное.
Таблица 2. Зависимость пути, пройденного телом, от времени
| Номер опыта | t,с | Dt,с | S, см | DS, см |
| 1 | 35.5 | 1.0 | 97 | 6 |
| 2 | 40.0 | 1.0 | 99 | 9 |
| 3 | 45.0 | 1.0 | 108 | 9 |
| 4 | 50.0 | 1.0 | 139 | 11 |
| 5 | 55.0 | 1.0 | 146 | 12 |
Последовательность операций
- Строим оси координат и устанавливаем на них шкалы, исходя из интервалов изменения измеренных величин. Начало оси абсцисс (время) берем при t=30 с, а начало оси ординат (расстояние) — при S=80 см. Размечаем ось абсцисс с шагом 10 с, а ось ординат с шагом 20 см.
- Наносим на координатную плоскость точки, представленные в таблице. Для каждой точки откладываем влево и вправо погрешность Δt в масштабе оси абсцисс, а вверх и вниз — погрешность ΔS в масштабе оси ординат.
- Исходя из предположения о равномерном движении, т.е. о линейной зависимости S(t)=v0t, проводим прямую с таким расчетом, чтобы она наилучшим образом проходила через все измеренные точки. При проведении прямой учитываем, что в данном опыте при t=0 путь S=0 независимо от скорости, т.е. согласно теоретической формуле продолжение прямой должно проходить через точку (0,0), которая находится за пределами рабочего участка координатной плоскости. Так как скорость v=dS/dt, а производная геометрически представляется тангенсом угла наклона касательной к графику функции, то для равномерного движения тангенс угла наклона прямой дает скорость v0. Находить из графика следует именно тангенс, т. е. отношение противолежащего катета к прилежащему, взятых в масштабных единицах соответствующих осей. Очевидно, что угол наклона прямой зависит от выбора масштаба на осях. Поэтому измерение угла с последующим определением его тангенса смысла не имеет.
- Для оценки погрешности проводим через экспериментальные точки еще две прямые — с максимальным и минимальным наклоном в пределах погрешностей большинства точек и с учетом того, что продолжения этих прямых должны пересекать точку (0,0). Определяем тангенс угла наклона этих прямых и устанавливаем интервал, в пределах которого находится искомая величина (скорость).
Окончательный результат построений показан на рис.3.
Рис. 3
Следует заметить, что графическая обработка опытных данных не столь строга, как аналитическая, зато она проста и наглядна.
В тех случаях, когда диапазон изменений измеряемой величины превышает порядок, при построении графика обычно применяют логарифмический масштаб. Для построения логарифмической шкалы по оси от начальной точки в некотором масштабе откладываются отрезки, равные десятичным логарифмам ряда чисел. Если отложен lga, то около соответствующей точки ставится пометка a. Около начальной точки должна стоять пометка 1 (lg1=0). Таким образом, на логарифмической шкале расстояние от пометки 1 до пометки a равно в выбранном масштабе lga. Так как lg(10a)=1+ lga, то пометки на логарифмической шкале на участке от 10 до 100 будут в точности соответствовать пометкам на участке от 1 до 10. Это же рассуждение может быть проведено и для других участков шкалы. Поэтому, для изображения чисел от 1 до 100 на логарифмической оси требуется увеличить длину оси всего в два раза по сравнению с осью, размеченной от 1 до 10. Пусть, например, на оси длиной 10 см требуется отобразить числа от 1 до 100. Тогда на одну декаду будет приходиться 5 см. Соответственно пометка 2 должна стоять на расстоянии lg2·5=1.5см от начала оси, пометка 3 — на расстоянии lg3·5=2.4 см, а пометка 30 — на расстоянии lg30·5=7.4 см. На рис.4 приведен пример участка оси с логарифмической шкалой.
Рис. 4
РЕКОМЕНДОВАННАЯ ЛИТЕРАТУРА
- Зайдель А.Н. Погрешности измерений физических величин. — Л.: Наука, 1985.
- Тэйлор Дж. Введение в теорию ошибок. — М.: Мир, 1985.
- Руководство к лабораторным занятиям по физике. Под ред. Л.Л.Гольдина. — М.: Наука, 1973
[на главную страницу]
Сайт управляется системой uCoz
Управление погрешностью измерений физической величины в микропроцессорном датчике Текст научной статьи по специальности «Физика»
Никишин Владимир Владимирович — e-mail: [email protected]; кафедра технической экспертизы и управления качеством; к.т.н.; доцент.
Eliseeva Maria Alexsandrovna — Sevastopol National University; e-mail: [email protected]; 33, Universitetskaya street, Sevastopol, 299053, Russia; phone: +78692713041; the department technical expertise and quality management; postgraduate student.
Nikishin Vladimir Vladimirovich — e-mail: [email protected]; the department technical expertise and quality management; cand. of eng. sc.; associate professor.
УДК 681.3.01
С.И. Клевцов, Е.В. Удод
УПРАВЛЕНИЕ ПОГРЕШНОСТЬЮ ИЗМЕРЕНИЙ ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ В МИКРОПРОЦЕССОРНОМ ДАТЧИКЕ
Повышение точности измерений физической величины за счет схемотехнических или алгоритмических методов практически всегда приводит к увеличению стоимости датчика, часто, весьма значительному. При этом не всегда необходимость достижения высоких показателей точности технически и экономически обоснована. Для управления погрешностью измерений, в том числе достижения низких ее значений, предлагается использовать метод построения пространственной мультисегментной характеристики преобразования на основе линейных и нелинейных пространственных элементов. На основе анализа особенностей метода рассматриваются версии построения характеристики преобразования, определяющие пути оптимизации погрешности измерений. Модель пространственной характеристики преобразования, формируемая на основе ранее упомянутого метода, максимально адаптирована к особенностям конфигурации функции преобразования первичного измерительного преобразователя, фактически повторяя ее пространственную форму с учетом нелинейности, дрейфа нуля, влияния внешних факторов, включая температуру. Это обеспечивает низкую погрешность вычисления физической величины и ее адаптацию для потребностей конкретной задачи измерений. Исследование эффективности метода мультисегментной аппроксимации характеристики преобразования для управления погрешностью и повышения точности измерений физических величин проводилась на основе экспериментальное данных, полученных в процессе градуировки при различных значениях температуры термоанемометрических измерителей скорости потока жидкости. Полученные результаты показывают, что максимальная приведенная погрешность измерения скорости потока жидкости с помощью термоанемометра с использованием мультисегментной пространственной характеристики преобразования не превышает ~ 0,45 % при произвольной температуре, зафиксированной при проведении измерений. Анализ возможных путей оптимизации погрешностей измерения также проводился с использованием данных испытаний тензометрических датчиков давления. При использовании нелинейного пространственного элемента погрешность измерений датчика давления не превысила ~ 0,3 % в заданном диапазоне температур.
Управление погрешностью; термоанемометрический измеритель; датчик давления; пространственная мультисегментная характеристика преобразования.
S.I. Klevtsov, E.V. Udod
IMPROVE ACCURACY MEASUREMENT OF PHYSICAL QUANTITIES USING THE MODEL MULTI-SEGMENT SPATIAL CHARACTERISTICS CONVERSION IN SMART SENSORS
Improving the accuracy of measurements of the physical quantity due to hardware or algorithmic methods almost always leads to an increase in the cost of the sensor, often quite significant. It is not always necessary to achieve high levels of accuracy of technically and economically
justified. Existing mathematical and algorithmic methods for improving the accuracy of measurements Smart Sensors are ineffective in solving the problem of management error because it does not allow the use of different functional relationships to the approximation of arbitrary functions of individual elements of a real transformation in the space of its domain. The task of control the measurement error in the model of multi-segment space conversion characteristic is achieved through the combined use of linear and nonlinear spatial elements, as well as change the size and placement of the segments in the space conversion function definition of the primary device. To control the measurement error, including achieving low values it is proposed to use a method of constructing a multisegment spatial conversion characteristics based on linear and nonlinear spatial elements. On the basis of analysis of the features of the method are considered version build conversion characteristic defining ways to optimize the measurement error. The model of the spatial characteristics of the transformation that is formed on the basis of the previously mentioned method, the most adapted to the characteristics of the configuration of the conversion function transducer actually repeating its spatial form based on linearity, zero drift, the effect of external factors, including temperature. It provides a low error of calculation ofphysical size and its adaptation to the needs of specific measurement tasks. Research of efficiency of multi-segment approximation method to control the characteristics of conversion error and improve the accuracy of measurements of physical quantities was based on experimental data obtained in the process of calibration at different temperatures hot-wire flow meter of liquid. These results indicate that the maximum percentage error measure flow rate of fluid through a multi-segment thermal anemometer using spatial characteristics to be less than ~ 0.45 % at an arbitrary temperature, fixed during measurements. Analysis of possible ways to optimize the measurement errors are also performed using test data strain gauge pressure sensors. When using non-linear spatial element of the pressure sensor measurement error does not exceed about 0.3 % in a predetermined temperature range.
Control the measurement error; thermoanemometric a measuring instrument; pressure sensor; the spatial multisegment characteristic of transformation.
Введение. Спрос на высокоточные приборы измерения медленно меняющихся физических величин растет в связи с развитием сферы услуг и промышленного производства, с развитием различных отраслей страны. Область применения датчиков физических величин достаточно широка — системы автоматического контроля, регулирования и управления сложными техническими объектами и технологическими процессами, где необходимо обеспечение непрерывного измерения различных величин [1-4]. В последние годы уделяется большое внимание производству микропроцессорных датчиков с повышенными точностными характеристиками [1, 3, 4]. Часто более точное измерение физической величины, например, давления позволяет сократить убытки при расчете газа или нефти в нефтегазовой промышленности, повысить качество продукции металлургической и химической промышленности [1, 2].
Повышение точности и достоверности определения значений физических величин представляет собой одну из важных задач совершенствования математических и алгоритмических методов обработки данных в микропроцессорных датчиках [1, 3-6]. Используемые методы и алгоритмы должны обеспечивать учет влияния различных дестабилизирующих факторов на результаты измерений, таких как, например, температура [1, 3, 4].
Достижение низкой погрешности измерения физической величины в микропроцессорном датчике базируется на использовании модели его характеристики преобразования, адаптированной к особенностям поведения функции преобразования первичного преобразователя [1, 4, 6, 7]. Для микропроцессорного датчика необходимо построить такую модель характеристики преобразования, которая бы повторяла пространственную форму реальной характеристики настолько точно, насколько это необходимо, исходя из потребностей решаемых датчиком задач.
Для обработки сигналов, поступающих с чувствительного элемента, в микропроцессорном датчике физических величин используются различные модели его характеристики преобразования, которые базируются на пространственном представлении функции преобразования первичного преобразователя [7-18].
Наиболее простой моделью характеристики датчика, широко используемой для градуировки датчика, является кусочно-линейная пространственная аппроксимация [8-12]. Сложные модели обеспечивают большую точность измерений, однако платой за это повышение является увеличение стоимости градуировки в связи с большим объемом необходимых исходных данных, что ограничивает их широкое применение [13-18].
Однако, повышение точности измерений физической величины за счет схемотехнических или алгоритмических методов практически всегда приводит к увеличению стоимости датчика, часто, весьма значительному. При этом не всегда необходимость достижения очень высоких показателей точности обоснована с технических и экономических позиций.
В связи с этим актуальна проблема управления точностью измерения физической величины в микропроцессорном датчике для достижения погрешности, определяемой текущими целями решаемой задачи.
Однако возможности управления погрешностью измерений в перечисленных выше моделях ограничены, поскольку для них характерно использование единого представления характеристики для всей области изменения полезного сигнала и внешних факторов [1, 4, 10].
Постановка задачи. В данной работе рассматривается подход к управлению погрешностью на основе использования модели пространственной мультисег-ментной характеристики преобразования микропроцессорного датчика, на основе которого возможно достижение заданной точности измерений, достаточной для решаемой датчиком задачи в рамках конкретной области применения.
При этом, снижается стоимость градуировки датчика, стоимость измерений и достигается погрешность измерения физической величины не выше предельно допустимой, обеспечивающая в полном объеме функции датчика в составе технического объекта.
В работе анализируются полученные результаты и даются рекомендации по использованию подхода.
Использование модели пространственной мультисегментной характеристики преобразования для управления погрешностью измерений. Для снижения и управления погрешностью определения физических величин предлагается использовать метод мультисегментной аппроксимации характеристики преобразования микропроцессорного датчика [19, 20, 21].
В рамках предлагаемого метода реальная характеристика преобразования заменяется системой локальных поверхностей так, чтобы они в совокупности повторяли ее пространственную конфигурацию. Тип аппроксимирующей локальной поверхности определяется многими факторами, такими как, например, точностные характеристики, объем и полнота исходных данных, требуемая скорость вычислений и другими.
В основе метода лежат следующие основные положения [1, 4, 20, 21]:
Модель пространственной характеристики преобразования должна быть максимально адаптирована к особенностям конфигурации функции преобразования первичного измерительного преобразователя. В этом случае характеристика фактически повторяет пространственную форму функции преобразования с учетом нелинейности, дрейфа нуля, влияния внешних факторов, например, температуры, преобразований сигналов в аналоговом интерфейсе датчика.
Пространственная аппроксимация характеристики датчика должна удовлетворять заданным требованиям, основными из которых являются достижения заданной погрешности аппроксимации во всех диапазонах измерения физической величины и изменения внешних воздействующих факторов, а также требования к
допустимому уровню сложности вычислений. Погрешность аппроксимации пространственной градуировочной характеристики может корректироваться в зависимости от решаемых датчиком задач.
Пространственная аппроксимация характеристики преобразования представляет собой систему локальных линейных и (или) нелинейных пространственных элементов, — сегментов.
Функции, описывающие пространственную форму сегментов, могут быть различными и существенно отличаться по типу, например, часть сегментов описывается линейными выражениями, а часть — нелинейными (полиномом). Тип функциональной зависимости определяется многими факторами, такими как, достижение заданной погрешности аппроксимации, объем и полнота исходных данных, требуемая скорость вычислений и другими.
Сшивка сегментов на границе раздела их областей определения не производится, что значительно снижает сложность алгоритма. Пространственная конфигурация краев сегментов на границах областей их определения должна обеспечивать достижение заданной погрешности аппроксимации характеристики преобразования при выборе любого из сегментов в процессе проведения измерений. То есть отдельные сегменты характеристики могут перекрывать друг друга без ухода погрешности за пределы заданной допустимой зоны
Исследование эффективности модели для управления погрешностью измерений. Исследование эффективности метода мультисегментной аппроксимации характеристики преобразования по снижению и управлению погрешностью измерений проводилась на основе экспериментальное данных, полученных в процессе градуировки термоанемометрических измерителей (ТА) скорости потока жидкости и датчиков давления при различных значениях температуры.
В первом случае испытания проводились для двух однотипных термоанемометрических измерителей скорости потока жидкости (№1 и №2) в диапазонах скоростей потоков (ориентировочно) от 1,46 м/с до 11,5 м/с для первого образца и от 1,79 м/с до 15,00 м/с для другого образца при 4-х значениях температуры для первого образца (Т ~ 23-25°С, ~ 30°С, ~ 38-39°С, ~ 45-47°С) и 6-ти значениях температуры для второго образца (Т ~ 21-23°С, ~ 25°С, ~ 30-31°С ~ 35-36°С, ~ 40-41°С, ~ 45-47°С ).
Использование метода мультисегментной аппроксимации характеристики преобразования на основе моделей линейных или нелинейных пространственных элементов для вычислений значений скорости потока жидкости проводилось с учетом температуры.
Представленные данные испытаний характеризуются значительной нелинейностью при задаваемой температуре, которая изменялась в небольшом диапазоне величин относительно некоторого среднего значения. Диапазон отклонений температуры (разница между верхним и нижним значениями при задаваемом значении температуры) достигали значений в 1-2°С.
Нелинейность наблюдается на всем диапазоне изменения скорости потока жидкости.
Зависимость электрического сигнала канала измерения скорости потока Uta ТА от температуры также имеет нелинейный характер. При увеличении температуры для одних и тех же значениях скорости потока выходной сигнал Uta уменьшается, что на графиках (рис. 1, 2) выглядит как «сползание» характеристики, то есть сдвиг в область более низких значений измеряемого электрического сигнала.
Кроме того, реальная характеристика преобразования ТА представляет вогнутую поверхность в системе параметров VxUtaxT, которая имеет особенность, -это вогнутая поверхность относительно области определения UtaxT , границы поверхности не параллельны относительно оси 0Т (рис. 3).
Рис. 1. Изменение сигнала ТА №1 в зависимости от скорости потока жидкости
при различных температурах
Рис. 2. Изменение сигнала ТА №2 в зависимости от скорости потока жидкости
при различных температурах
Рис. 3. Характеристика преобразования ТА №1 в пространстве Ухи(ахТ, построенная по результатам испытаний
Пространственную мультисегментную характеристику преобразования (МСХП) для ТА формировали на основе данных испытаний следующим образом: ♦ по параметру иа значения выбирались для каждой задаваемой температуры из ряда значений через один, начиная со значения, соответствующего наименьшей скорости потока жидкости;
♦ не выбранные для построения градуировочной характеристики значения использовались для оценки точности измерений скорости потока жидкости с помощью МСХП.
Количество сегментов по оси температур ОТ — 3, по оси 0иа — 3, т.е. всего девять сегментов.
Коэффициенты аппроксимации МСХД определяли методом наименьших квадратов для каждого сегмента с использованием экспериментальных точек, принадлежащих области определения сегмента.
На рис. 4, 5 представлены графики абсолютной величины приведенной погрешности (в процентах к диапазону измеряемой скорости движения жидкости) вычисления значений скорости движения жидкости для ТА №1 и ТА №2 с использованием нелинейных пространственных элементов МСХП при задаваемых температурах.
Следует отметить, что погрешность аппроксимации в данном случае значительно ниже 0,01 %, что позволяет не учитывать ее при измерениях.
та (В)
Рис.
Е<)25 2
| 0.2 К 0.15-
с 0 ‘Г
0(15 ?.4
Рис. 5. Графики изменения абсолютного значения приведенной погрешности вычисления скорости потока жидкости с помощью мультисегментной характеристики преобразования ТА №2
На рис. 6, 7 представлены в пространстве параметров УхЦахТ графики абсолютной величины приведенной погрешности (в процентах к диапазону измеряемой скорости движения жидкости) вычисления значений скорости движения жидкости для ТА №1 и ТА №2 с использованием нелинейных пространственных элементов МСХП при задаваемых температурах.
Рис. 6. График изменения абсолютного значения приведенной погрешности вычисления скорости потока жидкости с помощью мультисегментной характеристики преобразования ТА №1 в пространстве параметров УхП^хТ
I На (В)
Рис. 7. График изменения абсолютного значения приведенной погрешности вычисления скорости потока жидкости с помощью мультисегментной характеристики преобразования ТА №2 в пространстве параметров Ух~ишхТ
Таким образом, погрешность измерения скорости потока жидкости с помощью термоанемометра с использованием мультисегментной пространственной характеристики преобразования позволяет получить результат с максимальной приведенной погрешность ~ 0,45 % при произвольной температуре, зафиксированной при проведении измерений.
Оценка эффективности метода для решения задачи управления погрешностью осуществлялась на основе градуировочных испытаний датчиков давления. Учитывая особенности метода мультисегментной пространственной характеристики преобразования, можно определить способы управления погрешностью измерений контролируемой физической величины.
На точность измерения давления с помощью метода мультисегментной аппроксимации ПГХ непосредственно влияет выбор размеров пространственных элементов в области определения Р*Т.
Для оценки влияния размеров пространственных элементов на погрешность вычисления значений давления с использованием рассматриваемых моделей воспользуемся данными градуировочных температурных испытаний чувствительного элемента тензорезисторного типа.
Испытания проводились по следующей схеме:
♦ температура изменялась от -40 оС до +80 оС с шагом 5 оС, давление от 0 до 600 КПа с шагом 60 КПа;
♦ при каждом фиксированном значении температуры давление изменялось от нижнего значения до верхнего предела и обратно. Количество циклов изменений давления при заданной температуре — 4. Таким образом, фиксировался гистерезис реальной функции преобразования чувствительного элемента.
Рассмотрим влияние размеров линейных и нелинейных пространственных элементов отдельно по оси давлений и оси температур.
Для оценки влияния размеров ЛПЭ и НПЭ по давлению вычисление давления проводилось с использованием пространственной градуировочной характеристики, построенной на базисе экспериментальных точек с шагом по температуре 5оС для двух вариантов шага по давлению, — 300 кПа и 120 кПа.
Графики максимальных значений относительных приведённых погрешностей вычислений значений давления при использовании ЛПЭ и НПЭ для различных температур для шага по давлению 120 КПа и 300 КПа, приведены соответственно на рис. 8, 9.
Из анализа рисунков следует, что уменьшение величины локального пространственного элемента по давлению в 2,5 раза привело к снижению погрешности вычислений значений давления в 1,7-1,8 раза, в результате чего максимальная погрешность определения давления при использовании ЛПЭ составила 0,12 %, а НПЭ — 0,1 %.
«« 60 [211 [«(I 2-Ю 300 «II 480 540 600
Даолсшю (КПл)
Рис. 8. Максимальные значения относительной приведённой погрешности вычислений значений давления при использовании ЛПЭ
Рис. 9. Максимальные значения относительной приведённой погрешности вычислений значений давления при использовании НПЭ
Для оценки влияния размеров ЛПЭ и НПЭ по температуре вычисление давления проводилось с использованием пространственной градуировочной характеристики, построенной на базисе экспериментальных точек с шагом по давлению 60 кПа для трех вариантов шага по температуре, — 20 оС, 15 оС и 10 оС.
Для оценки влияния на точность вычисления давления размеров локальных пространственных элементов по температуре приведём на рис. 10, 11 максимальные значения относительных приведённых погрешностей вычислений значений давления при использовании ЛПЭ и НПЭ соответственно.
Рис. 10. Максимальные значения относительной приведённой погрешности вычислений значений давления при использовании ЛПЭ для различных температур
Рис. 11. Максимальные значения относительной приведённой погрешности вычислений значений давления при использовании НПЭ для различных температур
Из анализа рисунков следует, что уменьшение размера локального пространственного элемента по температуре сильно влияет на точность вычислений значений давления. Так при уменьшении размеров локальных пространственных элементов с 20 оС до 10 оС, происходит снижение погрешности вычислений значений давления в 1,7-1,8 раза, при уменьшении с 10 оС до 5 оС даже при больших размерах локальных пространственных элементов по давлению приводит к снижении погрешность примерно в 4 раза.
0.77
0
-40 -30 -20 -10 0 10 20 30 40 50 60 70 80 Температура (°Г)
Кроме того, результаты моделирования показывают, что уменьшение размеров пространственных элементов по температуре более существенно снижают погрешность вычислений, чем изменение размеров пространственных элементов по давлению.
Выводы. Анализ показывает, что использование модели мультисегментной пространственной характеристики преобразования позволяет достичь очень низких погрешностей измерений за счет высокой точности аппроксимации реальной функции преобразования первичного измерительного преобразователя с одновременным учетом влияния на измерения внешних и внутренних дестабилизирующих факторов во всем диапазоне их изменений.
Расчет скорости потока жидкости с помощью термоанемометра с использованием данной модели в наилучшем случае позволил получить результат с максимальной приведенной погрешность ~ 0,45 % при произвольной температуре, зафиксированной при проведении измерений [3]. Для измерения давления в наилучшем случае максимальная приведенная погрешность составляет ~ 0,1 % [1, 4, 20, 21]. Подобная точность измерений трудно достижима при использовании известных моделей функций преобразования, поскольку погрешности аппроксимации только термометров в термоанемометре изменяются в диапазоне 1,8-3,1 % [3]. А, например, погрешность аппроксимации для датчика давления в случае мультисегментной модели может составлять величину в диапазоне 0,01-0,03 [1, 4, 20, 21], что позволяет не учитывать эту погрешность при расчетах.
Существующие математические и алгоритмические методы повышения точности измерений в микропроцессорных датчиках малоэффективны при решении задачи управления погрешностью, поскольку не позволяют применять различные функциональные зависимости к аппроксимации произвольных отдельных элементов реальной функции преобразования в пространстве ее области определения [7-18].
Анализ результатов моделирования показал, что задача управления погрешностью измерений в рамках модели мультисегментной пространственной характеристики преобразования решается с помощью комплексного использования линейных и нелинейных пространственных элементов, а также изменения размеров и размещения сегментов в пространстве определения функции преобразования первичного преобразователя. При этом необходимо учитывать, что погрешность вычислений значений давления с компенсацией температурного влияния на основе линейного пространственного элемента менее чувствительна к погрешности исходных данных, чем модель на основе параболического пространственного элемента, но при погрешностях менее 0,5 % точность вычислений значений давления при использовании НПЭ будет выше, чем при использовании ЛПЭ за счёт более низкой методической погрешности.
Отношение погрешности вычислений значений давления к погрешности исходных данных при одинаковых абсолютных значениях погрешности на канале давления и температуры при использовании ЛПЭ и НПЭ примерно равно 1,5-1,6. Чувствительность модели ПГХ при использовании ЛПЭ к погрешности на канале температуры ниже, чем чувствительность к погрешности на канале температуры при использовании НПЭ.
В заключении можно отметить, что использование метода мультисегмент-ных пространственных характеристик преобразования в микропроцессорных датчиках может обеспечить не только высокую точность измерений в широком диапазоне изменения измеряемых физических величин и внешних влияющих факторов, но и эффективное управление погрешностью измерений при оптимизации затрат на калибровку. Полученные результаты могут быть полезны при создании программно-алгоритмического обеспечения микропроцессорных датчиков физических величин.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Научно-технические, технологические и практические основы конструирования датчи-ковой аппаратуры для измерений физических величин в 5-ти т. Т. 1. Датчиковая аппаратура давлений: монография. — М.: ГОУ ВПО МГУЛ, 2010. — 579 с.
2. Васильев Н.К. Учет природного газа на объектах магистральных газопроводов. — Л.: Недра, 1990. — 128 с.
3. Пьявченко О.Н., Зори А.А., Клевцов С.И., Кузнецов Д.Н. Информационно-измерительные системы определения параметров газожидкостных потоков: монография. — Таганрог: Изд-во ЮФУ, 2013. — 244 с.
4. Пьявченко О.Н., Клевцов С.И., Мокров Е.А., Панич А.Е., Пьявченко А.О., Удод Е.В., Федоров А.Г. Прецизионные интеллектуальные тензометрические датчики давления. Методы, модели, алгоритмы и архитектуры / Под ред. О.Н. Пьявченко. — Ростов-на-Дону: Изд-во ЮФУ, 2009. — 152 с.
5. Anton Bakker, Johan Huijsing High-Accuracy CMOS Smart Temperature Sensors — Springer Science & Business Media, 2013 — 121 с. — URL: https://books.google.ru/books ?id=ZhjTBwAAQBAJ&printsec=frontcover&hl=ru#v=onepage&q&f=false
6. Spiridonov E.I., Markov A.V. Calibration productivity increase of pressure measuring devices under high accuracy requirements // The Third International Conference on Problem of PHYSICAL METROLOGY. Abstracts. Saint Petersburg, Russia 15-19 June, 1998. — P. 144.
7. Клевцов С.И., Линьков В.С., Веретельников Ю.А., Кузьминов В.Г. Погрешности вычисления давления в интеллектуальном датчике при матрично-полиномиальной аппроксимации его градуировочной характеристики // Известия ТРТУ. — 2004. — № 2 (37). — С. 30-48.
8. Бобровников Н.Р., Яркин С.В., Гридин Ю.Н., Стрыгин В.Д., Чертов Е.Д. Математическое обеспечение микропроцессорных преобразователей аналоговых пневматических сигналов // Приборы и системы. Управление, контроль, диагностика. — 2002. — № 2. — С. 36-39.
9. Мухатаев Н.А. Алгоритм линеаризации и температурной компенсации характеристик преобразователей // Материалы третьей научно-практической конференции «Перспективные системы и задачи управления». — Т. 2. — Таганрог, ТТИ ЮФУ. — 2008. — С. 74-76.
10. Клевцов С.И. Модели и методы построения прецизионных градуировочных характеристик интеллектуальных датчиков давления // Известия ТРТУ. — 2007. — № 3 (75). — С. 110-118.
11. Гутников В.С. Тенденции развития электронных измерительных преобразователей для датчиков // Приборы и системы управления. — 1990. — № 10. — С. 32-35.
12. Gorbunov S. F., Tsypin B.V. Linearization of calibration characteristics of capacitance pressure sensors // Measurement Techniques. — 2011. — Vol. 53, No. 10. — P.1113-1117.
13. Bluemm C. Weiss R. Weigel R. Brenk D. Correcting nonlinearity and temperature influence of sensors through B-spline modeling // Industrial Electronics (ISIE). 2010. IEEE International Symposium. 4-7 July 2010. — P. 3356-3361.
14. Patra J.C. Chakraborty G. Meher P.K. Neural-Network-Based Robust Linearization and Compensation Technique for Sensors Under Nonlinear Environmental Influences // IEEE Transactions on Circuits and Systems I: Regular Papers. — 2008. — Vol. 55, Issue 5. — P.1316-1327.
15. Bartkovjak J., Karovicova M. Approximation by Rational Functions // Measurement Science Review. — 2001. — Vol. 1, No. 1. — P. 63-65.
16. Hillea P., Hohlera R., Stracka H. A Linearisation and Compensation Method for Integrated Sensors // Sensors and Actuators A: Physical. — 1994. — Vol. 44, Issue 2. — P. 95-102
17. Попов А.Е., Лазуков А.В. Использование двухпараметрических математических моделей для аппроксимации функций преобразования давления // Вестник ЮУрГУ. Серия Компьютерные технологии, управление, радиоэлектроника. — 2008. — Вып. 7, № 3. — С. 38-40.
18. Шапонич Д., Жигич А. Коррекция пьезорезистивного датчика давления с использованием микроконтроллера // Приборы и техника эксперимента. — 2001. — № 1. — С. 54-60.
19. Клевцов С.И., Удод Е.В. Пространственная плоскостная модель градуировочной характеристики интеллектуального датчика давления // Известия ЮФУ. Технические науки.
— 2005. — Т. 45, № 1. — С. 99-107.
20. Клевцов CM. Мультисегментная пространственная аппроксимация градуировочной характеристики микропроцессорного датчика // Метрология. — 2011. — № 7. — С. 26-36.
21. Клевцов С.И. Формирование мультисегментной модели градуировочной характеристики интеллектуального датчика // Известия ЮФУ. Технические науки. — 2008. — № 11 (88).
— С. 8-11.
Статью рекомендовал к опубликованию д.т.н., профессор П.Г. Михайлов.
Клевцов Сергей Иванович — Южный федеральный университет; e-mail: [email protected]; 347900, г. Таганрог, ул. Петровская, 81; тел.: 88634328025; к.т.н.; доцент.
Удод Евгений Васильевич — e-mail: [email protected]; к.т.н.; доцент.
Klevtsov Sergey Ivanovich — Southern Federal University; e-mail: [email protected]; 81, Petrovsky, Taganrog, 347900, Russia; phone: +78634328025; cand. of eng. sc; associate professor.
Udod Eugene Vasilyevich — e-mail: [email protected]; cand. of eng. sc; associate professor.
УДК 519.6:004.383
М.И. Ледовской, Е.С. Синютин
АЛГОРИТМ ИНТЕГРИРОВАНИЯ ПОРОЖДАЮЩИХ УРАВНЕНИЙ ДЛЯ ВЫЧИСЛЕНИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
Рассмотрена задача создания энергоэффективного алгоритма для вычисления элементарных функций в беспроводных сенсорных системах, где энергопотребление обеспечивается за счет накопления энергии из окружающей среды. В основу алгоритма положен таблично-алгоритмический метод вычисления функций и способ определения поправки путем интегрирования порождающих уравнений, описывающих поведение функции между ближайшим табличным и заданным значением аргумента. Предложена оригинальная реализация способа интегрирования порождающих уравнений. Процесс интегрирования развертывается по двоичным разрядам аргумента, а также используется переменный шаг, равный весу текущего разряда аргумента. На примере функций sin(x), cos(x) исследована возможность использования подходящих методов интегрирования: методов Эйлера 1-го и 2-го порядка, метода Рун-ге-Кутта 4-го порядка, из которых выбран метод Эйлера 2-го порядка. Получена зависимость методической погрешности алгоритма от порядка метода интегрирования и номера разряда аргумента. Определен шаг таблицы значений функций для рассмотренных методов интегрирования. Приведено сравнение предлагаемого алгоритма с методом линейной интерполяции и алгоритмом CORDIC. По сравнению с алгоритмом CORDIC число выполняемых циклов в среднем уменьшается в два раза. По сравнению с методом линейной интерполяции в несколько раз уменьшается количество табличных значений функций. Например, для функции cos(x) количество табличных значений уменьшается в 16раз. При этом набор операций алгоритма ограничивается простыми операциями сложения (вычитания) и сдвига. Приведены результаты экспериментального анализа методической, инструментальной и полной погрешности алгоритма в системе MATLAB. В условиях ограниченной разрядности микроконтроллера и вычислений с фиксированной точкой погрешность алгоритма принимает допустимые значения, соизмеримые с погрешностью округления данных. Результаты настоящей статьи могут найти применение при разработке алгоритмического и программного обеспечения для беспроводных сенсорных модулей на базе микроконтроллеров, а также других видов встраиваемых систем с низким энергопотреблением.
Встраиваемые системы; вычисление функций; таблично-алгоритмический метод; алгоритм CORDIC; алгоритм численного интегрирования.
M.I. Ledovskoy, E.S. Sinyutin
ALGORITHM OF INTEGRATION OF THE GENERATING EQUATIONS FOR THE CALCULATION OF ELEMENTARY FUNCTIONS
In the present paper the task of creation of algorithm with low consumption of energy for a calculation of elementary functions in wireless touch systems where energy consumption is ensured at the expense of accumulation of energy from environment is considered. In an algorithm basis the tabular-algorithmic method of functions evaluation and a mode of definition of the correction is supposed by a path of integration of the generating equations describing behavior of
Изменения и оценка погрешностей измерений
ИЗМЕРЕНИЯ И ОЦЕНКА ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ
ФИЗИЧЕСКИХ ВЕЛИЧИН.
1. ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ.
1.1 ЧТО ЗНАЧИТ – ИЗМЕРИТЬ ВЕЛИЧИНУ?
От других наук физика отличается тем, что при изучении свойств материи и её изменений вводятся физические величины, которые можно измерять и выражать числами. Для обозначения при письме каждой физической величины используется символ – буква алфавита. Благодаря этому ход явлений и связи явлений выражаются математическими соотношениями (формулами) между введенными величинами. Самые важные соотношения между величинами называются законами природы.
ИЗМЕРИТЬ ФИЗИЧЕСКУЮ ВЕЛИЧИНУ – это значит с использованием технических средств (средств измерения) найти опытным путем значение физической величины, а также степень её приближения к истинному значению, которое в принципе неизвестно.
Для измерения физической величины необходимо ввести единицу величины и определить способ, при помощи которого можно сравнивать численные значения данной физической величины у разных тел или в различных процессах.
1.2. ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН.
Общепринятой в настоящее время является Международная система единиц (СИ). Она строится на семи основных единицах:
— единица длины – метр.
— единица массы – килограмм.
— единица времени – секунда.
— единица силы электрического тока – Ампер.
— единица температуры – Кельвин.
— единица силы света – кандела.
— единица количества вещества – моль.
Для обеспечения единства физических измерений созданы международные эталоны каждой из основных единиц СИ.
ЗНАЧЕНИЕ ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ – это произведение отвлеченного числа на принятую для данной физической величины единицу измерения.
ПРИМЕР. Масса тела 5 кг.
Физический смысл данного выражения можно раскрыть двояко.
а) Это означает следующее:
— «5 кг» – это значение массы тела.
— «5» – отвлеченное число, показывающее, во сколько раз масса данного тела больше массы эталона, у которого масса тела 1 кг
б) Иначе:
— «5» — числовое значение физической величины.
— «кг» — единица массы.
2. ИЗМЕРЕНИЕ ФИЗИЧЕСКИХ ВЕЛИЧИН.
2.1. ТОЧНОСТЬ ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН.
Истинное значение измеряемой величины определить невозможно прежде всего потому, что ограничено воспроизведение эталона единицы физической величины, т.е. сам эталон не абсолютен. Например, точность изготовления эталона массы составляет 2 · 10 – 9 кг. Скорость света, являющаяся основой для создания эталонов метра и секунды, также измерена с некоторой погрешностью. По последним данным, истинное значение скорости находится с точностью: С = (299 792 458 ± 1, 2) м /с.
Истинное значение измеряемой величины неизвестно и не может быть найдено в конкретном сколь угодно точном эксперименте.
Нельзя определить и абсолютную погрешность измерения в виде алгебраической разности:
∆ абсолют. Х = Х изм. – Х где Х – истинное значение,
Х изм. – результат измерения.
Физическая величина измеряется в единицах физической величины, записывается с наименованием.
2.2. ГРАНИЦА АБСОЛЮТНОЙ И ОТНОСИТЕЛЬНОЙ ПОГРЕШНОСТИ.
В каждом измерении, в принципе, возможно определить так называемую границу абсолютной погрешности. Если при выполнении опыта его результат получен Х изм., то можно представить его графически в виде интервала (рис.1).
Рис. 1
Соответствующая запись такова:
Х изм — ∆ Х < Х изм < Х изм — ∆ Х
Х = Х изм ± ∆ Х
Граница абсолютной погрешности – это половина
длины интервала 2 ∆Х, достоверно содержащего
истинное значение измеряемой величины.
Граница абсолютной погрешности всегда положительное число.
Граница абсолютной погрешности не в полной мере характеризует измерение.
ПРИМЕР. Измерили размеры крышки стола, получили:
— длина крышки (100 ± 1) см
— толщина крышки (2 ± 1) см
Граница абсолютной погрешности измерения в этих двух случаях одинакова (1 см), но интуитивно угадываем, что в первом случае качество измерения выше.
Качество измерения характеризуется понятием границы относительной погрешности.
Границей относительной погрешности называется отношение границы абсолютной погрешности к значению измеряемой величины. Выражается числом без наименования или в процентах:
∆ Х ∆Х
ξ = ——- или ξ = ——- · 100 %
Х изм Х изм
2.3. ВИДЫ ИЗМЕРЕНИЙ.
Способ определения значения измеряемой физической величины и граница абсолютной погрешности зависят от вида измерений. Измерения могут быть прямыми, косвенными и совместными.
Измерения, в которых результат находится непосредственно в процессе считывания со шкалы прибора, называются прямыми.
Измерения, в которых результат определяется на основе расчетов, называют косвенными.
Измерения двух или нескольких неодноимённых величин, производимые одновременно с целью нахождения функциональной зависимости между ними, называют совместными.
2.4. МЕРЫ.
Кроме измерительных приборов, используют так называемые меры.
Мера – это тело или устройство, служащее для воспроизведения одного или нескольких известных значений данной величины.
Меры бывают однозначные и многозначные.
К однозначным мерам относятся гири и наборы гирь, наборы грузов по механике, наборы сопротивлений наборы конденсаторов.
К многозначным мерам относятся линейки, измерительные цилиндры, мензурки, амперметры, вольтметры.
Номинальное значение меры – значение данной физической величины, обозначенное на мере или её футляре (от латинского «nominalis» – именной). Например, на каждой гире обозначено её номинальное значение в килограммах, граммах или миллиграммах.
3. ТРЕБОВАНИЯ К ЗАПИСЯМ ПРИ ОБРАБОТКЕ ИЗМЕРЕНИЙ.
Процесс измерения сопровождается вычислениями. Правильная организация вычислений связана с учетом абсолютных и относительных погрешностей. Принципиальная особенность вычислений состоит в том, что приходится работать с приближенными числами.
3.1. ВЕРНАЯ ЦИФРА.
В физике пользуются понятием «верная цифра» в узком смысле: цифра п-го разряда называется верной, если абсолютная погрешность не превосходит половины единицы этого разряда.
ПРИМЕР. Если по таблице плотностей для газа азота плотность равна 1,25 кг/м 3, то цифра 5 в разряде сотых верная. Следовательно, граница погрешности числа 1,25 равна 0,005 кг/м 3. Также построена подпрограмма по округлению чисел микрокалькулятора.
3.2. ЗНАЧАЩАЯ ЦИФРА.
Значащими цифрами называются все верные цифры в записи числа, кроме нулей, стоящих перед первой, отличной от нуля, цифрой.
ПРИМЕР. В числе 0, 00060 = 6,0 · 10 – 4 две значащие цифры.
Число значащих цифр и десятичных знаков связано с относительными и абсолютными погрешностями. Число десятичных знаков определяет абсолютную погрешность приближенного числа. Количество значащих цифр определяет относительную погрешность числа.
ПРИМЕР. Число Х = 25,6 записано верными цифрами. Это значит, что
Х = 25,60 ± 0,05.
0,05
Следовательно, относительная погрешность ξ х = ———-
25,60
Относительная погрешность не зависит от положения запятой.
3.3. ЗАПИСЬ РЕЗУЛЬТАТА ВЫЧИСЛЕНИЯ.
Результат измерений и расчетов не должен записываться с бόльшим числом десятичных знаков, чем их имеется в абсолютной погрешности.
ПРИМЕР. При вычислении скорости тела, брошенного под углом к горизонту, получили с помощью микрокалькулятора результат 0,560325035 м/с. Это означает, что скорость измерена с погрешностью 0,0000000005 м/с = 5 · 10 – 10 м/с и это абсурдно, т.к. реальная погрешность значительно выше. Чтобы не делать таких ошибок, при округлении числа цифры в разрядах за верными цифрами отбрасываются, т.к. они не являются верными.
В приведенном примере результат нужно записать (0,56 ± 0,**) м/с.
3.4. ПРАВИЛА ОКРУГЛЕНИЯ ГРАНИЦЫ АБСОЛЮТНОЙ ПОГРЕШНОСТИ.
Чаще всего погрешность записывается с одной значащей цифрой. Первая слева цифра погрешности определяет сомнительную цифру результата. Вторая цифра погрешности обычно не вносит существенных изменений в результат.
При записи приближенного значения достаточно одной значащей цифры в погрешности, т.к. число записывается не более чем с одной сомнительной цифрой.
ПРИМЕР № 1. Было получено число (27,47 ± 0,18) м. Округляем погрешность до одной значащей цифры (∆ = 0,2 м), округляем приближенное значение до десятых и записываем результат следующим образом: (27,5 ± 0,2) м.
ПРИМЕР № 2. Вместо записи (5391 ± 28) м при округлении погрешности до одной значащей цифры с избытком получим (5391 ± 30) м. Это означает, что цифра десятков в числе 5391 сомнительна, а цифра единиц неверна. Правильная запись результата такова (5390 ± 30) м.
ПРИМЕР № 3. При записи (5398 ± 30) м верной будет запись (5400 ± 30) м.
ПРИМЕР №4. Можно отступить от основного правила округления погрешности с избытком до одной значащей цифры, если вторая цифра 5, её можно оставить и записать результат (73,48 ± 0.25) м.
Особое внимание следует обращать на использование нуля в качестве значащей цифры.
ПРИМЕР № 1. Запись (2,4 ± 0,08) м нарушает правило об одинаковом числе знаков в числе и его погрешности. Правильная запись такова (2,40 ± 0,08) м.
ПРИМЕР № 2. При измерении длины отрезка получен результат (72 ± 0,5) см. Если результат записать так 720 мм, то в числе 720 нуль значащий, а абсолютная погрешность равна 0,5 мм, тогда как в действительности погрешность измерения длины отрезка равна 0,5 см, т.е. в 10 раз больше. Таким образом, нуль в числе 720 не является значащим. Именно поэтому необходимо пользоваться стандартной формой записи числа с наименованием в системе СИ: 7,2 · 10 – 1 м.
При сложении приближенных значений границы абсолютных погрешностей складываются арифметически.
ПРИМЕР. По формуле Ф = а + в + с + … запишем: ∆Ф = ∆а + ∆в + ∆с + …
При арифметическом сложении погрешностей можно пренебречь малыми слагаемыми, которые не превышают (1/3 ÷ 1/4) от максимальных. Это правило называют правилом ничтожных погрешностей и его учет значительно упрощает вычислительную работу при оценке погрешностей.
Относительная ошибка: определение, формула, примеры
Определения статистики> Относительная ошибка
Содержание :
Относительная погрешность как показатель точности
Относительная погрешность (RE) — при использовании в качестве меры точности — это отношение абсолютной погрешности измерения к выполняемому измерению. Другими словами, этот тип ошибки связан с размером измеряемого объекта. RE выражается в процентах и не имеет единиц измерения.
В качестве формулы это:
Например, предположим, что два человека измеряют ковер метровой палкой. Один человек измеряет длину, а другой — ширину. Стрелка измерителя имеет точность в пределах 1 мм, что означает абсолютную погрешность & pm; 0,001 м.
- Длина коврика составляет 3,215 метра. RE = 0,001 м / 3,215 м = 0,0003%.
- Ширина ковра измеряется в 4.075 метров. RE = 0,001 м / 4,075 м = 0,0002%.
Хотя абсолютная погрешность 0,001 м одинакова для каждого из них, относительная погрешность для ширины меньше.
Различных единиц
Относительная ошибка очень полезна, когда вы хотите иметь возможность сравнивать вещи, которые измеряются в разных единицах. Например, вы измеряете рост и вес собаки. Рост собаки составил 84 см с абсолютной погрешностью & pm; 3 см. Вес собаки 35 фунтов с абсолютной погрешностью & pm; 1 фунт.Что точнее?
Ответ можно найти, вычислив относительные ошибки для обоих:
- RE высота = 3 см / 84 см = 0,04%
- RE Вес = 1 фунт / 35 фунтов = 0,03%
Более точное измерение веса.
Относительная погрешность как мера точности
В девяти случаях из десяти RE является мерой точности, как в приведенных выше примерах. Однако этот же термин может (сбивающе с толку) также использоваться для описания точности; В частности, насколько точное измерение сравнивается с истинным значением.Вы можете найти RE с точностью только в том случае, если знаете фактическое «истинное» измерение — это трудно сделать, если вы не измеряете по атомным часам. Формула:
Например, если ваши весы для ванной весят вас в 165 фунтов, но вы знаете, что ваше «истинное» измерение (по данным кабинета врача) составляет 172 фунта, тогда:
RE точность = (165 фунтов / 172 фунта) * 100% = 0,96
При выражении в процентах (т.е. 96%), это также называется процентной ошибкой.
Если вы не знаете «истинного» измерения, вы можете использовать первое определение — точность — в качестве замены.
Список литературы
Агрести А. (1990) Анализ категориальных данных. Джон Вили и сыновья, Нью-Йорк.
Гоник, Л. (1993). Мультяшный справочник по статистике. HarperPerennial.
Vogt, W.P. (2005). Словарь статистики и методологии: нетехническое руководство для социальных наук. МУДРЕЦ.
Wheelan, C. (2014). Голая статистика.W. W. Norton & Company
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .
АНАЛИЗ ОШИБОК:
АНАЛИЗ ОШИБОК:
1) Как ошибки складываются :
Независимые и коррелированные ошибки влияют на результирующую ошибку в расчете по-разному.Для Например, вы измерили одну сторону металлического квадрата и обнаружили, что быть 1,001 дюйм. Кроме того, вы обнаружите, что погрешность этого измерения составляет 0,001 дюйма. Чтобы найти площадь, умножаем ширину (W) и длину (L). Площадь тогда
Д x Ш = (1,001 дюйм) x (1,001 дюйм) = 1,002001 дюйм 2 который округляется до 1,002 в 2 . Это дает ошибку 0,002, если нам дано, что квадрат был точно сверхточная сторона 1 дюйм.
Это пример коррелированной ошибки (или не независимая ошибка), поскольку ошибки в L и W одинаковы. Ошибка в L коррелирует с ошибкой в W. Теперь предположим, что мы сделали самостоятельное определение ширины и длины отдельно с погрешностью 0,001 в каждом. В этом случае, когда два выполняются независимые измерения погрешности независимых или некоррелированный . Поэтому погрешность результата (площади) вычисляется иначе следующим образом (правило 1 ниже).Сначала найдите относительную погрешность (погрешность / количество) в каждом из количества, которые входят в расчет, относительная погрешность в ширине составляет 0,001 / 1,001 = 0,00099900. Результирующий относительная погрешность
Относительная ошибка в области =
Следовательно, абсолютная ошибка (относительная ошибка) x (количество) = 0,0014128 x 1,002001 = 0,001415627. который округляется до 0,001.
Следовательно, площадь равна 1,002 в 2 0.001in. 2 .
Это показывает, что случайные относительные ошибки не просто добавляют арифметически, скорее, они объединяются правилом среднеквадратичной суммы (пифагорейское теорема). Подведем итоги некоторых правила, которые применяются к объединению ошибок при сложении (или вычитании), умножении (или разделение) различных количеств. Этот Тема также известна как распространение ошибок.
2. Распространение ошибки для особых случаев:
Пусть σ x обозначает ошибку в величине x.Далее предположим, что две величины x и y и их ошибки σ x и σ y равны измеряется независимо. В таком случае относительные и процентные ошибки определены как
Относительная ошибка = σ x / x, ошибка в процентах = 100 (σ x / x)
- Умножение или деление на постоянную .
Результирующая абсолютная ошибка также умножается или делится.
- Умножение или деление, относительная ошибка .
- Дополнение или вычитание : в этом случае абсолютные ошибки подчиняются пифагорову теорема. Если a и b постоянные,
Если имеется более двух измеренных величин, вы можете расширить выражения, указанные выше, добавив больше терминов под квадратным корнем знак.
- Квадрат или куб измерения:
Относительная погрешность может быть рассчитано от
, где а — постоянная.
Пример 1:
Определите погрешность площади прямоугольника, если длина l = 1,5 0,1 см и ширина 0,420,03 см. Используя правило умножения,
Пример 2:
Площадь круга пропорциональна квадрату радиус.Если радиус определяется как r = 10,0 0,3 см, какова погрешность в районе?
ТРЕБУЕТСЯ КОРРЕКЦИЯ (см. Примечания к лекциям) !!
Следовательно,
Погрешности измерений — Chemistry LibreTexts
- Последнее обновление
- Сохранить как PDF
- Введение
- Систематические vs.Случайная ошибка
Все измерения имеют некоторую неопределенность независимо от точности и точности. Это вызвано двумя факторами: ограничениями измерительного прибора (систематическая ошибка) и навыками экспериментатора, проводящего измерения (случайная ошибка).
Введение
Градуированная бюретка на Рисунке 1 содержит определенное количество воды (с желтым красителем), которое необходимо измерить. Количество воды составляет от 19 до 20 мл согласно отмеченным линиям.Проверив, где находится дно мениска, по десяти меньшим линиям, количество воды составляет от 19,8 мл до 20 мл. Следующим шагом является оценка погрешности между 19,8 и 20 мл. Делая примерное предположение, уровень меньше 20 мл, но больше 19,8 мл. Затем мы сообщаем, что измеренное количество составляет примерно 19,9 мл. Градуированный цилиндр сам по себе может быть искажен так, что градуированные отметки будут содержать неточности, и показания будут немного отличаться от фактического объема имеющейся жидкости.
Рис. 1 : Мениск в бюретке с цветной водой. «20,00 мл» — правильное измерение глубины. Щелкните здесь, чтобы получить более полное описание использования бюретки, включая правильное чтение. Рисунок использован с разрешения Википедии.
Систематическая и случайная ошибка
На приведенной ниже диаграмме показано различие между систематическими и случайными ошибками.
Рисунок 2: Систематические и случайные ошибки.Рисунок использован с разрешения Дэвида ДиБиасе (штат Пенсильвания, США).
Систематические ошибки: Когда мы используем инструменты, предназначенные для измерения, мы предполагаем, что они правильные и точные, однако измерительные инструменты не всегда подходят. Фактически, у них есть естественные ошибки, которые называются систематическими ошибками . Систематические ошибки имеют тенденцию быть последовательными по величине и / или направлению. Если величина и направление ошибки известны, точность может быть улучшена с помощью аддитивных или пропорциональных поправок. Аддитивная коррекция включает добавление или вычитание постоянного поправочного коэффициента для каждого измерения; Пропорциональная коррекция включает в себя умножение измерения (-ий) на константу.
Случайная ошибка с: Иногда называемая человеческой ошибкой, случайная ошибка определяется навыками или способностью экспериментатора проводить эксперимент и считывать научные измерения. Эти ошибки случайны, поскольку полученные результаты могут быть слишком высокими или низкими. Часто случайная ошибка определяет точность эксперимента или ограничивает точность.Например, если бы мы измеряли время оборота стабильно вращающегося поворотного устройства, случайная ошибка была бы временем реакции. Время нашей реакции может меняться из-за задержки в запуске (недооценка фактического результата) или задержки в остановке (завышение фактического результата). В отличие от систематических ошибок случайные ошибки различаются по величине и направлению. Однако можно вычислить среднее значение набора измеренных положений, и это среднее значение, вероятно, будет более точным, чем большинство измерений.
- Так как Том должен полагаться на прибор для измерения оптической плотности, а он обеспечивает постоянно разные измерения, это пример систематической ошибки.
- Большая часть отклонений Клэр во времени, вероятно, может быть отнесена к случайным ошибкам, таким как усталость после нескольких кругов, непостоянство в форме плавания, небольшое отклонение от времени при запуске и остановке секундомера или бесчисленное множество других мелких факторов, которые изменяют время круга. В гораздо меньшей степени сам секундомер может иметь ошибки отсчета времени, приводящие к систематической ошибке.
- Процентная погрешность исследователя составляет около 0,62%.
- Это известно как ошибка множителя или коэффициента масштабирования.
- Это называется ошибкой установки смещения или нуля.
- Ошибка Сьюзен в процентах составляет -7,62%. Эта процентная погрешность отрицательна, потому что измеренное значение на ниже принятого значения на . В задаче 7 процент ошибки был положительным, потому что он был на выше, чем на , чем принятое значение.
- Сначала необходимо взвесить сам стакан.После определения веса вы добавляете графит в стакан и взвешиваете его. Получив этот вес, вы вычитаете вес графита плюс стакан минус вес стакана.
Абсолютная и относительная ошибка: определение и формула — практический класс [видео 2021 года]
Считается, что инструменты измерения в определенной степени точны. Предположим, что измерительная лента, которую Дэн использовал для измерения своей новой половицы, была с точностью до 1 дюйма.Это означает, что существует 1-дюймовый диапазон или «окно» вокруг измерения, в котором действительно может быть найдено истинное значение. Судя по измеренному значению, это полдюйма с каждой стороны. Дэн измерил новую половицу на 36 дюймов в длину, но истинная длина могла быть от 35,5 до 36,5 дюймов. В этом случае половица была на самом деле на более длинном конце. Мы говорим, что размер 36 ± 0,5 дюйма.
Абсолютная ошибка
Есть два типа ошибок, на которые влияет точность измерительных инструментов.Абсолютная ошибка определяется как абсолютное значение (или величина) разницы между измеренным значением и истинным значением. Таким образом, пусть:
- e a = абсолютная ошибка
- x м = измеренное значение
- x t = истинное значение
Формула для вычисления абсолютной ошибки:
e a = | x м — x t |
Есть только одна загвоздка — мы обычно не знаем, каково истинное значение.В этом случае нам просто нужно подумать о точности измерительного инструмента. В качестве примера возьмем сантиметровую ленту Дэна. Он имеет точность до 1 дюйма, что означает, что истинное значение любого измерения может быть на полдюйма меньше или на полдюйма больше фактического измерения. Максимально возможная разница между измеренным значением и его истинным значением составляет полдюйма. Следовательно, абсолютная погрешность составляет 0,5 дюйма.
Относительная ошибка
Есть другой тип ошибки, на которую влияет точность измерительных инструментов.Относительная ошибка определяется как абсолютная ошибка относительно размера измерения. Все, что вам нужно сделать, это разделить абсолютную ошибку на измеренное значение. В дополнение к переменным let:
Тогда формула для вычисления относительной ошибки:
В ситуации Дэна абсолютная ошибка составляет 0,5 дюйма, и он измерил половицу на длине 36 дюймов, поэтому относительная погрешность составляет:
e r = 0,5 дюйма / 36 дюймов = 0,014 (округлено до ближайшей тысячной)
В относительной ошибке нет единиц измерения, поскольку они сокращаются во время вычисления.Относительная ошибка — это пропорция, поэтому мы также можем выразить ее в процентах, умножив относительную ошибку на 100%, например:
e r = 0,014 * 100% = 1,4%
Мы можем сказать, что абсолютная погрешность составляет 1,4% от измеренного значения.
Сравнение относительных ошибок
Относительная ошибка зависит как от абсолютной ошибки, так и от измеренного значения. Давайте посмотрим, что происходит, когда вы измеряете два объекта разных размеров одним и тем же измерительным инструментом.Скажем, Дэн использовал ту же рулетку, чтобы измерить ширину половицы на 6 дюймов. Абсолютная погрешность все еще составляет 0,5 дюйма. Что такое относительная ошибка? Это:
e r = 0,5 дюйма / 6 дюймов = 0,083 (округлено до тысячных долей)
Его также можно выразить в процентах следующим образом:
e r = 0,083 * 100% = 8,3%
Относительная погрешность больше, когда измеряемый размер мал.Это имеет смысл, потому что абсолютная погрешность в полдюйма имеет большое значение, когда вы измеряете что-то длиной всего 6 дюймов по сравнению с длиной 36 дюймов.
Что происходит с относительной погрешностью, когда вы выполняете одно и то же измерение с помощью двух разных измерительных инструментов? Давайте сравним измерительную ленту Дэна с точностью до 1 дюйма с линейкой с точностью до 0,5 дюйма (что означает, что абсолютная погрешность составляет 0,25 дюйма). В качестве примера мы будем использовать ширину паркетной доски. И измерительная лента, и линейка говорят, что длина половицы составляет 6 дюймов.Рассчитаем относительные погрешности:
- Измерительная лента : e r = 0,5 дюйма / 6 дюймов = 0,083 * 100% = 8,3%
- Линейка : e r = 0,25 дюйма / 6 дюймов = 0,042 * 100% = 4,2%
Относительная погрешность при использовании линейки меньше относительной погрешности при использовании измерительной ленты, поскольку абсолютная погрешность линейки меньше абсолютной погрешности измерительной ленты.
Итоги урока
Давайте рассмотрим. Абсолютная погрешность определяется как абсолютное значение разницы между измеренным значением и истинным значением измерения и обычно дается как максимально возможная погрешность с учетом степени точности измерительного инструмента. Абсолютная погрешность имеет те же единицы, что и измерения. Относительная ошибка определяется как абсолютная ошибка относительно размера измерения и зависит как от абсолютной ошибки, так и от измеренного значения. Относительная погрешность велика, когда измеренное значение мало или когда велика абсолютная погрешность.Относительная погрешность не имеет единиц.
F. Неопределенность в процентах :: Физика
Неопределенность измеренного значения также может быть представлена в процентах или в виде простого отношения (относительная неопределенность). Процент неопределенности знаком. Вычисляется как:
Неопределенность в процентах можно интерпретировать как описание неопределенности, которая возникла бы, если бы измеренное значение было 100 единиц. Аналогичная величина — относительная неопределенность (или дробная неопределенность).Его проще вычислить, и его вычисляют по формуле:
Относительную неопределенность можно интерпретировать как описание неопределенности, которая возникла бы, если бы измеренное значение было всего лишь одной единицей. С этими двумя новыми представлениями о неопределенности мы должны быть осторожны в устной и письменной речи, чтобы наша аудитория понимала, какое из них используется. В следующем списке описывается допустимое использование.
- Абсолютная неопределенность: это простая неопределенность самого значения, как мы обсуждали ее до сих пор.Этот термин используется, когда нам нужно отличить эту неопределенность от относительной или процентной неопределенности. Если нет шанса на путаницу, мы все равно можем просто сказать «неопределенность», имея в виду абсолютную неопределенность. Абсолютная неопределенность имеет те же единицы, что и значение. Таким образом, это: 3,8 см ± 0,1 см.
- Относительная неопределенность: это простое отношение неопределенности к заявленному значению. Относительная погрешность как отношение одинаковых величин не имеет единиц измерения. На самом деле не существует специального символа или обозначения для относительной неопределенности, поэтому вы должны четко дать понять, когда вы сообщаете об относительной неопределенности.2,95 кг ± 0,043 (относительная погрешность)
- Процент погрешности: это просто относительная погрешность, умноженная на 100. Поскольку процентная погрешность также является отношением аналогичных величин, она также не имеет единиц измерения. К счастью, для процентной погрешности (%) существует специальное обозначение, поэтому ее легко распознать в письменном виде. 2,95 кг ± 4,3%
Обратите внимание, что относительные погрешности и погрешности в процентах можно указывать в виде двух цифр. Это сделано для предотвращения ошибок округления при обратном преобразовании в абсолютную неопределенность.
Погрешность в процентах имеет большое значение при сравнении относительной точности различных измерений. Например, если мы ограничимся точностью до 0,1 процента, мы узнаем, что длина метровой палки — 1 мм, длина моста — 1 метр, длина моста — 1 метр, а расстояние до Солнца (93 миллиона миль) — не лучше 93 000 миль. . Таким образом, давая результат измерения, нужно иметь достаточно цифр, чтобы показать точность измерения, не больше и не меньше, и, кроме того, следует указывать A.D. или процентная погрешность. Для трех приведенных выше примеров следует написать:
1,000 ± 0,001 метра (или 1,000 метров ± 0,1%)
1000 ± 1 метр (или 1000 метров ± 0,1%)
(93,00 ± 0,09) x 10 6 миль (или 93,00 x 10 6 миль ± 0,1%)
Последнее обновление 19 ноября 2014 г.
Систематическая ошибка — обзор
Нарушение измеряемой системы в результате измерения является распространенным источником систематической ошибки.Если бы мы начали со стакана с горячей водой и хотели бы измерить ее температуру с помощью ртутного стеклянного термометра, тогда мы бы взяли термометр, который изначально должен был иметь комнатную температуру, и погрузили его в воду. Поступая таким образом, мы вводим относительно холодную массу (термометр) в горячую воду, и между водой и термометром происходит теплопередача. Эта теплопередача снизит температуру воды. Хотя снижение температуры в этом случае будет настолько незначительным, что его нельзя будет обнаружить из-за ограниченной разрешающей способности измерения такого термометра, эффект конечен и четко устанавливает принцип, согласно которому почти во всех ситуациях измерения процесс измерения нарушает работу системы. и изменяет значения измеряемых физических величин.
Особенно важным примером этого является диафрагма. Его помещают в трубу, по которой проходит жидкость, для измерения скорости потока, которая является функцией давления, измеряемого по обе стороны от диафрагмы. Эта процедура измерения вызывает постоянную потерю давления в текущей жидкости. Нарушение измеряемой системы часто может быть очень значительным.
Таким образом, как правило, процесс измерения всегда мешает измеряемой системе. Величина помехи варьируется от одной измерительной системы к другой и зависит, в частности, от типа инструмента, используемого для измерения.Способы минимизации помех в измеряемых системах являются важным аспектом при проектировании приборов. Однако для этого необходимо точное понимание механизмов нарушения работы системы.
Измерения в электрических цепях
При анализе нарушений в системе во время измерений в электрических цепях теорема Тевенина (см. Приложение 2) часто оказывается очень полезной. Например, рассмотрим схему, показанную на рис. 3.1a, в которой напряжение на резисторе R 5 должно быть измерено вольтметром с сопротивлением R m .Здесь R m действует как шунтирующее сопротивление на R 5 , уменьшая сопротивление между точками AB и тем самым нарушая цепь. Следовательно, напряжение E m , измеренное измерителем, не является значением напряжения E o , которое существовало до измерения. Степень нарушения можно оценить, рассчитав напряжение холостого хода E o и сравнив его с E m .
Рисунок 3.1. Анализ нагрузки цепи: (a) Схема, в которой необходимо измерить напряжение на R 5 ; (б) Эквивалентная схема по теореме Тевенина; (c) Схема, используемая для нахождения эквивалентного одиночного сопротивления R AB .
Теорема Тевенина позволяет заменить схему рис. 3.1a, состоящую из двух источников напряжения и пяти резисторов, эквивалентной схемой, содержащей одно сопротивление и один источник напряжения, как показано на рис. 3.1b. Для определения эквивалентного одиночного сопротивления цепи по теореме Тевенина все источники напряжения представлены только их внутренним сопротивлением, которое может быть приближено к нулю, как показано на рис. 3.1c. Анализ проводится путем расчета эквивалентных сопротивлений секций цепи и их наращивания до тех пор, пока не будет получено требуемое эквивалентное сопротивление всей цепи. Начиная с C и D , цепь слева от C и D состоит из последовательной пары сопротивлений ( R, , 1, и R, , 2 ), параллельных R 3 , а эквивалентное сопротивление можно записать как:
1RCD = 1R1 + R2 + 1R3orRCD = (R1 + R2) R3R1 + R2 + R3
Теперь перейдем к A и B, цепь слева состоит из пара последовательных сопротивлений ( R CD и R 4 ) параллельно с R 5 .Сопротивление эквивалентной цепи R AB , таким образом, можно записать как:
1RAB = 1RCD + R4 + 1R5orRAB = (R4 + RCD) R5R4 + RCD + R5
Подставляя для R CD используя полученное ранее выражение, получаем:
(3.1) RAB = [(R1 + R2) R3R1 + R2 + R3 + R4] R5 (R1 + R2) R3R1 + R2 + R3 + R4 + R5
Определение I в качестве тока, протекающего в цепи при подключении к нему измерительного прибора, мы можем записать: I = EoRAB + Rm, а измеренное измерителем напряжение тогда будет выражено как Em = RmEoRAB + Rm.
При отсутствии измерительного прибора и его сопротивления R m , напряжение на AB будет источником напряжения эквивалентной цепи, значение которого составляет E o . Таким образом, результат измерения заключается в уменьшении напряжения на AB на соотношение, определяемое следующим образом:
(3.2) EmEo = RmRAB + Rm
Таким образом, очевидно, что по мере увеличения R m отношение E м / E o приближается к единице, показывая, что стратегия проектирования должна заключаться в том, чтобы сделать R м как можно более высоким, чтобы свести к минимуму нарушение измеряемого система.(Обратите внимание, что мы не вычисляли значение E o , так как это не требуется при количественной оценке эффекта R m .)
Пример 3.1
Предположим, что компоненты схемы, представленные на рис. 3.1а, имеют следующие значения: R 1 = 400 Ом; R 2 = 600 Ом; R 3 = 1000 Ом, R 4 = 500 Ом; R 5 = 1000 Ом.Напряжение на AB измеряется вольтметром с внутренним сопротивлением 9500 Ом. Какая погрешность измерения вызвана сопротивлением измерительного прибора?
Решение
Продолжая, применяя теорему Тевенина, чтобы найти схему, эквивалентную схеме на рис. 3.1a, в форме, показанной на рис. 3.1b, и подставляя данные значения компонентов в уравнение для R AB (Ур. 3.1), получаем:
RAB = [(10002/2000) +500] 1000 (10002/2000) + 500 + 1000 = 100022000 = 500 Ом
Из уравнения.(3.2) имеем:
EmEo = RmRAB + Rm
Погрешность измерения определяется как ( E o — E m ): Eo − Em = Eo
( 1 − RmRAB + Rm)
Подставляем значения: Eo − Em = Eo
(1−950010000) = 0,95Eo
Таким образом, погрешность измеренного значения составляет 5%.
Здесь интересно отметить ограничения, которые существуют, когда предпринимаются практические попытки достичь высокого внутреннего сопротивления в конструкции вольтметра с подвижной катушкой.Такой инструмент состоит из катушки с указателем, установленной в фиксированном магнитном поле. Когда ток течет через катушку, взаимодействие между генерируемым полем и фиксированным полем заставляет указатель, который он несет, поворачиваться пропорционально приложенному току (см. Главу 10 для получения дополнительной информации). Самый простой способ увеличить входной импеданс (сопротивление) измерителя — это либо увеличить количество витков в катушке, либо построить такое же количество витков катушки из материала с более высоким сопротивлением.Однако любое из этих решений уменьшает ток, протекающий в катушке, давая меньший магнитный момент и, таким образом, уменьшая чувствительность измерения прибора (то есть при заданном приложенном напряжении мы получаем меньшее отклонение стрелки). Эту проблему можно преодолеть, изменив жесткость пружины удерживающих пружин инструмента, так что для поворота стрелки на заданную величину требуется меньший крутящий момент. Однако это снижает жесткость инструмента, а также требует улучшенной конструкции шарнира для уменьшения трения.Это подчеркивает очень важный, но утомительный принцип в конструкции инструментов: любая попытка улучшить характеристики инструмента в одном отношении обычно снижает производительность в другом аспекте. Это неизбежный факт жизни с пассивными приборами, такими как упомянутый тип вольтметра, и часто является причиной использования альтернативных активных приборов, таких как цифровые вольтметры, где включение вспомогательного источника питания значительно улучшает производительность.
Подобные ошибки из-за загрузки системы также возникают, когда амперметр вставлен для измерения тока, протекающего в ответвлении цепи.Например, рассмотрим схему, показанную на рис. 3.2a, в которой ток, протекающий в ветви схемы, обозначенной A-B, измеряется амперметром с сопротивлением R m . Здесь R m действует как резистор последовательно с резистором R 5 в ветви A-B, тем самым увеличивая сопротивление между точками AB и тем самым нарушая цепь. Следовательно, текущее значение I m , измеренное счетчиком, не является значением текущего I o , существовавшего до измерения.Степень нарушения может быть оценена путем расчета тока холостого хода I или и сравнения его с I m .
Рисунок 3.2. Анализ нагрузки цепи: а) цепь, в которой необходимо измерить ток, протекающий в ветви A-B цепи; (b) Схема, в которой все источники напряжения представлены их приблизительно нулевым сопротивлением; (c) Эквивалентная схема по теореме Тевенина.
Теорема Тевенина снова является полезным инструментом для анализа эффекта вставки амперметра.Чтобы применить теорему Тевенина, источники напряжения представлены просто их внутренним сопротивлением, которое может быть приближено к нулю, как показано на рис. 3.2b. Это позволяет заменить схему на рис. 3.2a, состоящую из двух источников напряжения и пяти резисторов, эквивалентной схемой, содержащей только два сопротивления и один источник напряжения, как показано на рис. 3.2c. Анализ проводится путем расчета эквивалентных сопротивлений секций цепи и их наращивания до тех пор, пока не будет получено требуемое эквивалентное сопротивление всей цепи.Начиная с C и D, цепь слева от C и D состоит из последовательной пары сопротивлений ( R 1 и R 2 ), параллельных R 3 и эквивалентных сопротивление можно записать как:
1RCD = 1R1 + R2 + 1R3orRCD = (R1 + R2) R3R1 + R2 + R3
Ток, протекающий между A и B, можно просто вычислить по закону Ома как: I = ERCB + RCD
Когда амперметр не в цепи, R CB = R 4 + R 5 и I = I 0 , где I 0 — нормальный (без нагрузки) текущий ток.
Следовательно,
I0 = ER4 + R5 + [(R1 + R2) R3R1 + R2 + R3] = E [R1 + R2 + R3] [R4 + R5] [R1 + R2 + R3] + [(R1 + R2 ) R3]
С амперметром в цепи, R CB = R 4 + R 5 + R м и I = I м , где I м — измеренный ток.
Следовательно,
Im = ER4 + R5 + Rm + [(R1 + R2) R3R1 + R2 + R3] = E [R1 + R2 + R3] [R4 + R5 + Rm] [R1 + R2 + R3] + [ (R1 + R2) R3]
Погрешность измерения определяется соотношением I м / I 0 .
(3.3) ImI0 = [R4 + R5] [R1 + R2 + R3] + [(R1 + R2) R3] [R4 + R5 + Rm] [R1 + R2 + R3] + [(R1 + R2) R3 ]
Пример 3.2
Предположим, что компоненты схемы, показанной на рис. 3.2a, имеют следующие значения: R 1 = 250 Ом; R 2 = 750 Ом; R 3 = 1000 Ом, R 4 = 500 Ом; R 5 = 500 Ом. Ток между A и B измеряется амперметром с внутренним сопротивлением 50 Ом.Какая погрешность измерения вызвана сопротивлением измерительного прибора?
Решение
Подставив значения параметров в уравнение. (3.3):
ImI0 = [R4 + R5] [R1 + R2 + R3] + [(R1 + R2) R3] [R4 + R5 + Rm] [R1 + R2 + R3] + [(R1 + R2) R3] = [1000] [2000] + [1000 × 1000] [1050] [1000] + [1000 × 1000] = 30003100 = 0,968
Ошибка 1 — I м / I 0 = 1–0,968 = 0,032 или 3,2%.
Таким образом, погрешность измерения тока равна 3.2%.
Мостовые схемы для измерения значений сопротивления — еще один пример необходимости тщательного проектирования измерительной системы. Импеданс прибора, измеряющего выходное напряжение моста, должен быть очень большим по сравнению с сопротивлениями компонентов в мостовой схеме. В противном случае измерительный прибор нагружает цепь и потребляет ток от нее. Более подробно это обсуждается в главе 6.
Анализ ошибок (без исчисления)
| m | 0.07 г | ||
| = | = 0,002, или, если хотите, 0,2% | ||
| M | 34,6 г |
Выбор выражения относительного ошибки «как есть» (в виде дробей) или в процентах. Я предпочитаю работать с ними как дроби в расчетах, избегая необходимости постоянно умножаем на 100.Зачем делать ненужную работу?
Но при выражении окончательных результатов часто имеет смысл выразите относительную неопределенность в процентах. Это легко сделать, просто умножьте относительную погрешность на 100. Это 0,2%.
3. Абсолютная или относительная форма; который использовать.
При выборе формы необходимо руководствоваться здравым смыслом и здравым смыслом. использовать для представления ошибки при заявлении результата . Рассмотрим измерение температуры с помощью термометра, который, как известно, надежен для ± 0.5 градусов Цельсия. Имеет ли смысл сказать, что это причины погрешность измерения температуры кипения воды 0,5% (100 градусов) но колоссальная погрешность в 10% при измерении холодной воды при температура 5 градусов? Конечно нет! [А что, если температуры были выражены в градусах Кельвина? Казалось бы снизить процент ошибок до незначительности!] Ошибки и расхождения, выраженные в процентах, не имеют смысла для некоторых типов измерений. Иногда это связано с характером измерительный прибор, иногда характер измеряемого само количество или способ его определения.
Бывают также случаи, когда абсолютные ошибки неуместны и поэтому ошибки должны быть выражены в относительной форме.
Иногда как абсолютная, так и относительная погрешность необходимо для полной характеристики погрешности измерителя. Для Например, если пластиковая измерительная линейка с возрастом равномерно сжимается, эффект может быть выражена в виде определяемой ошибки в процентах. Если половина миллиметра были стерты с нулевого конца палки, и это не было замечено или компенсировано, это лучше всего выразить как абсолютная определенная ошибка.Очевидно, обе ошибки могут присутствовать в конкретной метрической палке. Производитель вольтметра (или другой электросчетчик) обычно дает свои гарантированные пределы ошибка как постоянная определенная ошибка плюс `процент ‘ ошибка.
Как относительная, так и дробная формы ошибки могут появляться в промежуточные алгебраические шаги при выводе уравнений ошибок. [Этот обсуждается в разделе H ниже.] Это просто вычислительный артефакта, и не имеет отношения к вопросу о том, какая форма имеет смысл для сообщения размера и характера ошибки в данные и результаты.
G. ВАЖНОСТЬ ПОВТОРНЫХ ИЗМЕРЕНИЙ
Одного измерения количества недостаточно, чтобы передать какие-либо информация о качестве измерения. Вам может понадобиться сделайте повторные измерения, чтобы узнать, насколько стабильно измерения есть.Если вы ранее выполняли этот тип измерения, с тем же инструмента, и определили неопределенность этого конкретного измерительный инструмент и процесс, вы можете обратиться к своему опыту оценить неопределенность.В некоторых случаях вы можете знать из прошлого опыт, что измерение — шкала ограничена , что в том, что его неопределенность меньше, чем наименьшее приращение, которое вы можете прочитать на шкале прибора. Такое измерение даст то же значение точно для повторных измерений одной и той же величины. Если вы знаете (из непосредственного опыта), что это масштаб ограничено, затем укажите его неопределенность как наименьшее приращение, которое вы можно читать по шкале.
Студентам этого курса не обязательно становиться экспертами в области штрафов. детали статистической теории. Но они должны быть постоянно в курсе экспериментальных ошибок и сделайте все необходимое, чтобы выяснить насколько они влияют на результаты. Следует позаботиться о том, чтобы свести к минимуму ошибки. Размеры экспериментальных ошибок как в данных, так и в результатах должны определяться, когда это возможно, и количественно оцениваться выражая их как средние отклонения. [В некоторых случаях здравый смысл экспериментальное исследование может предоставить информацию об ошибках без использования сложной математики.]
Студент должен понимать, что полный рассказ об экспериментальном ошибки здесь не приводились, но будут выявлены позже. курсы и более продвинутые лабораторные работы.
H. РАСПРОСТРАНЕНИЕ ОПРЕДЕЛЕННЫХ ОШИБОК
Важность оценки ошибок данных обусловлена тем, что ошибки данных распространяются через вычисления, чтобы произвести ошибки в результатах. Это размер влияния ошибок данных на результаты, что является наиболее важным. Необходимо приложить все усилия для определения разумных оценок ошибок для каждого важного экспериментальный результат.Мы проиллюстрируем, как распространяются ошибки, сначала обсудив, как найти количество ошибок в результатах по учитывая, как ошибки данных распространяются через простые математические операции. Сначала рассмотрим случай детерминированных ошибок : те которые знали знак. Таким образом мы обнаружим определенные полезные правила для распространения ошибок, тогда мы сможем изменить правила, применяемые к другим мерам погрешности, а также к неопределенным ошибки.
Здесь мы разрабатываем математические правила для «конечные разности», алгебра чисел, имеют относительно небольшие вариации. Конечная различия — это отклонения от «истинных значений», вызванные экспериментальные ошибки.
Этот метод основан на фундаментальном принципе. В любом расчете мы хотим знать, сколько ошибка в одной входной переменной повлияет на результат вывода. В сложных расчетах, таких как в метеорологическом прогнозировании погоды компьютеры позволяют нам делать это непосредственно с каждой из многих входных переменных, что-то никто бы никогда не попытался «вручную».Это метод «грубой силы», но он необходим. В этой лаборатории уравнения будут намного проще и обычно уступают место алгебре и нескольким простым правилам.Предположим, что экспериментальный результат вычисляется из суммы две величины данных A и B. Для этого обсуждения мы будем использовать a и b для представления ошибок в A и B соответственно. Данные количества написаны так, чтобы явно показать ошибки:
(A + a) и (B + b)Мы допускаем, что a и b могут быть либо положительными, либо отрицательный, при этом знаки находятся в символах «а» и «б».»Но мы должны подчеркнуть что мы здесь рассматриваем случай, когда знаки a и b определимы, и мы знаем, что это за знаки (положительные или отрицательные).
Результат сложения A и B для получения R выражается как уравнение: R = A + B. С явно включенными ошибками, это написано:
(А + а) + (В + б) = (А + В) + (а + б)Результат с явной ошибкой r: (R + r):
(R + r) = (A + B) + (a + b)Следовательно, ошибка R равна: r = a + b.
Мы заключаем, что определенная ошибка в сумме двух величин — это всего лишь сумма ошибок в этих количествах. Вы можете легко потренироваться сам случай, когда результат рассчитывается из разница двух величин. В этом случае определенная ошибка в результатом будет разница в ошибках. Обобщение:
- Правило сумм для детерминированных ошибок. Когда добавляются два количества, их детерминированные ошибки добавляют.
- Правило разницы для определенных ошибок. Когда вычитаются две величины, их определенные ошибки вычитаются.
(R + r) = (A + a) (B + b) = AB + aB + Ab + ab или: r = aB + Ab + abЭто не выглядит многообещающим для переделки по простому правилу. Тем не мение, когда мы выражаем ошибки в относительной форме , вещи выглядишь лучше.Если ошибка a мала относительно A, а b мала относительно B, то (ab) заведомо мала относительно AB, а также мал по сравнению с (aB) и (Ab). Поэтому мы пренебречь термином (ab) (выбросить), так как нас интересует только по ошибке оценивается до одной или двух значащих цифр. Сейчас мы выразить относительную ошибку в R как
Это дает нам очень простое правило:
r aB + bA a b = = + R AB A B
- Правило продукта для определенных ошибок.Когда две величины перемножаются, их относительных детерминированных ошибок доп.
А + А (А + а) В А (В + б) – – r B + b B (B + b) B B (B + b) = = R A / B A / B
(A + a) B — A (B + b) (а) Б — А (б) а б = ≈ ≈ – A (B + B) AB A B
Приближение, сделанное на предпоследнем шаге, заключалось в пренебрежении b в знаменателе, который действителен, если относительные ошибки небольшой.Итак, результат:
Следствием правила продукта является следующее:Правило частного для определенных ошибок. Когда две величины разделены, относительная определенная ошибка частного — это относительная определенная ошибка числителя минус относительная определенная ошибка знаменателя.
Одним из примеров практического использования определенных ошибок является случай исправления результата, когда вы обнаруживаете, после завершения длительных измерений и вычислений, что в одном или нескольких измерениях была определенная ошибка. Возможно, шкала или метр были неправильно откалиброваны. Вы обнаруживаете это и определяете размер и знак ошибки в этом измерительном инструменте.Вместо того, чтобы повторять все измерения, вы можете составить уравнение определяемой ошибки и использовать свои знания об ошибке неправильной калибровки для исправления результата. Как вы увидите в следующих разделах, обычно вам все равно придется составлять уравнение ошибки, так почему бы не использовать его для исправления обнаруженной ошибки, вместо того, чтобы повторять все вычисления?Правило мощности для определенных ошибок. Когда количество Q возводится в степень, P, относительная определенная ошибка в результате P умноженная на относительная определенная ошибка в Q.Это также верно для отрицательных степени, то есть относительная определенная ошибка в квадратном корне из Q составляет половину относительной детерминированной ошибки в Q.
I. РАСПРОСТРАНЕНИЕ НЕОПРЕДЕЛЕННЫХ ОШИБОК
Неопределенные ошибки имеют неизвестный знак. Если их распределение симметрично относительно среднего, тогда они несмещены относительно знака.Также, если неопределенные ошибки в разных величины не зависят друг от друга, их знаки имеют тенденции компенсировать друг друга в вычислениях. [11]Когда нас интересуют только пределы ошибки (или максимальная погрешность) мы должны предположить «наихудшую» комбинацию знаков. В случае вычитание, A — B, происходит наихудшее отклонение ответа когда ошибки либо + a и -b, либо -a и + b. В любом случае, максимальная ошибка будет (a + b).
В случае отношения A / B наихудшее отклонение ответ возникает, когда ошибки имеют противоположный знак, либо + a, и -b или -a и + b. В любом случае максимальный размер родственника ошибка будет (a / A + b / B).
Результаты операций сложения и умножения таковы: так же, как прежде. Таким образом, максимально неопределенных ошибки распространяются по следующим правилам:
Следствие правила продукта следующее:Правило сложения и вычитания для неопределенных ошибок.Абсолютно неопределенный ошибки доп. Произведение и правило частного для неопределенных ошибок. Относительные неопределенные ошибки Добавлять.
Эти правила применяют только при объединении независимых ошибки, то есть отдельные ошибки, не зависящие от каждого другое по размеру или знаку.Правило мощности для неопределенных ошибок. Когда количество Q возводится в степень, P, относительная ошибка в результате P умноженная на относительную ошибку в Q. Это также верно для отрицательных степеней, то есть относительной ошибки в квадратный корень из Q составляет половину относительной ошибки в Q.
Можно показать (но не здесь), что эти правила также применяются достаточно хорошо для ошибок, выраженных в виде средних отклонений. В одним из недостатков этого является то, что оценки ошибок, сделанные таким образом, все еще чрезмерно консервативны в том, что они не полностью учитывают склонность терминов ошибок, связанных с независимыми ошибками, к компенсировать друг друга.Однако это будет незначительное исправление небольшое значение в нашей работе в этом курсе.
Правила распространения ошибок могут быть получены для других математических операции по мере необходимости. Например, правила для ошибок в триггере функции могут быть получены с использованием триггерных идентификаторов, используя приближения: sin ß = ß и cos ß = 1, действительно, когда ß мало. Правила для экспонент могут быть выведены также.
Когда математические операции комбинируются, правила могут быть последовательно применяется к каждой операции, и уравнение может быть алгебраически полученный [12], который выражает ошибку в результате с точки зрения ошибок в данных.Такое уравнение всегда можно составить в стандартную форму , в которой каждый источник ошибок появляется в единственный срок. Пусть x представляет ошибку в x, y ошибку в y и т. Д. Тогда ошибка r в любом результате R, вычисленная любой комбинацией даны математические операции над значениями данных X, Y, Z и т. д. по:
r = (c x ) x + (c y ) y + (c z ) z … и т. д.Это всегда можно алгебраически изменить на:
r / R = {C x } (x / X + {C y } (y / Y) + {C z } (z / Z)… так далее.Коэффициенты (c x ) и {C x } и т. Д. в каждом семестре чрезвычайно важно, потому что они, наряду с размерами ошибок, определить, насколько каждая ошибка влияет на результат. Родственник размер членов этого уравнения показывает нам относительную важность источников ошибок. Дело не в относительном размере ошибок (x, y и т. д.), но относительный размер ошибок, который говорит нам их относительная важность.
Если это уравнение ошибки было получено из определенная ошибка правила, относительные ошибки в приведенных выше могут иметь + или — приметы. Коэффициенты также могут иметь знаки + или -, поэтому члены сами могут иметь знаки + или -. Следовательно, возможно условия, чтобы компенсировать друг друга.
Если это уравнение ошибки было получено из неопределенного значения ошибка правила, содержащиеся в нем меры погрешности по своей сути положительны.Коэффициенты также окажутся положительными, поэтому члены не могут компенсировать друг друга.
Удобно знать, что уравнение неопределенной ошибки может можно получить непосредственно из уравнения детерминированной ошибки, просто выбирая наихудший случай, т. е. принимая абсолютное значение каждый семестр. Это заставляет все термины быть положительными. Этот шаг сделано только после , уравнение с определенными ошибками полностью выведен в стандартном виде.
Уравнение ошибок в стандартной форме — один из самых полезных инструментов. для экспериментального дизайна и анализа. Он должен быть выведен (в алгебраическая форма) еще до начала эксперимента, как руководство к экспериментальная стратегия. Он может показать, какие источники ошибок преобладают, и которые незначительны, тем самым экономя время, которое можно потратить возня с неважными соображениями. Это может подсказать, как влияние источников ошибок может быть минимизировано соответствующим выбором размеров переменных.Он может сказать вам, насколько хорошо инструмент, необходимый для достижения желаемой точности в полученные результаты.
Учащийся, который пренебрегает выводом и использованием этого уравнения, может потратить весь лабораторный период с использованием инструментов, стратегии или ценностей недостаточно для требований эксперимента. И он может закончить вверх без малейшего представления почему результаты не такие хороши, какими должны были быть.
Заключительный комментарий для тех, кто хочет использовать стандартные отклонения в качестве неопределенные меры погрешности: поскольку стандартное отклонение получено из среднего квадратов отклонений , уравнение (7) необходимо изменить — каждый член уравнения (обе стороны) должен в квадрате:
(r / R) = (C x ) 2 (x / X) + (C y ) 2 (y / Y) + (C z ) 2 (z / Z)Это правило приводится здесь без доказательства.
J. ПРИМЕРЫ
Пример 1: Студент находит постоянное ускорение медленного движущийся объект с секундомером. Используемое уравнение: s = (1/2) при 2 . Время измеряется секундомером, расстояние — метровой палкой.s = 2 ± 0,005 метра. Это 0,25%. t = 4,2 ± 0,2 секунды. Это 4,8%.Что такое ускорение и его расчетная погрешность?
Мы будем использовать заглавные буквы для измеряемых величин, строчные буквы для их ошибок.Решите уравнение для получения результата: a. А = 2С / Т 2 . Его уравнение неопределенной ошибки:
Фактор 2 во временном термине заставляет этот термин доминировать, так как применение Правило для ошибок в величинах, возведенных в степень, приводит к ошибке 4,8% во время удвоения, что дает ошибку более 9,5% в T 2 . Ошибка 1/4 процента из-за измерения расстояния явно ничтожно мало по сравнению с 9.5% погрешность из-за измерения времени, итак результат (ускорение) записывается: A = 0,23 ± 0,02 м / с 2 .а т с - = 2 - + - А Т С
Пример 2: Результат рассчитывается по формуле R = (G + H) / Z, значения данных:
G = 20 ± 0,5
H = 16 ± 0,5
Z = 106 ± 1,0
Символ ± указывает на неопределенность этих ошибок. Расчет R требует как сложения, так и деления, и дает значение R = 3.40. Для расчета погрешности требуется как правило сложения и умножения, применяемые последовательно, в том же порядке, что и операции, выполняемые при вычислении самого R.
Правило сложения гласит, что абсолютные ошибки в G и H складываются, поэтому погрешность в числителе 1,0 / 36 = 0,28.
Правило деления требует, чтобы мы использовали относительно (дробные ошибки). Относительная погрешность числителя равна 1,0 / 36 = 0,028.Относительная погрешность знаменателя равна 1,0 / 106 = 0,0094. Относительная погрешность в знаменателе добавляется к числителю, чтобы получить 0,0374, что является относительной погрешностью в р.
Если требуется абсолютная ошибка в R, это (0,0374) R = 0,0136. Результат с ошибкой может быть выражен как:
Пример 3: Напишите уравнение с определенным значением ошибки например 1.
Мы выполняем те же действия, но представляем ошибки символически.Пусть N представляет числитель, N = G + H. Определенная ошибка в N тогда g + h. Относительная погрешность числителя (g + h) / N. Относительная погрешность знаменателя равна z / Z. Относительная ошибка в R тогда:
Это уравнение имеет стандартную форму ; каждая ошибка, g, h и z появляется в только один член , этот член, представляющий вклад этой ошибки в ошибку в R.р г + ч з г з - = ————— - - = ——— + ——— - - R G + H Z G + H G + H Z r G g H h z - = ——— - + ——— - - - R G + H G G + H H Z
Пример 4: Выведите уравнение неопределенной ошибки для этого та же формула, R = (G + H) / Z.
Вот где окупается наша предыдущая работа. Посмотрите на уравнение детерминированной ошибки из примера 3 и перепишите его. для наихудшего случая знаков сроков. Это эквивалентно превращению всех терминов в стандарта сформировать уравнение положительное:
Пример 5: Пример 2 доработки, на этот раз с использованием неопределенной ошибки уравнение, полученное в примере 4.r G g H h z - = ——— - + ——— - + - R G + H G G + H H Z
Ввод значений:
Это меньше 4%.г 20 0,5 16 0,5 1 - = ————— ——— + ———————— +—— Р 20 + 16 20 20 + 16 16 106 г 20 0,5 16 0,5 1 - = —— ——— + —— ——— + ——— 36 20 36 16 106 рэнд р - = 0,555 (0,025) + 0,5 (0,031) + 0,0094 р р - = 0,014 + 0,014 + 0,0094 = 0,0374 р
Пример 6: Результат R вычисляется по формуле R = (G + H) / Z, с теми же значениями данных, что и в предыдущем примере.После завершения эксперимента обнаруживается, что значение Z было на 0,05 слишком мало из-за систематической ошибки измерительный инструмент. Результат был получен путем усреднения больших объемов данных, и задача пересчета поправки к каждому значению устрашающе. Но это не обязательно Используйте эту информацию, чтобы исправить результат.
Посмотрите на определенное уравнение ошибки :
-0.Ошибка 05 по Z представляет собой относительную ошибку -0,05 / 106. в Z. Предполагая нулевую определенную ошибку в G и H, мы имеем:r G g H h z - = ——— - + ——— - - - R G + H G G + H H Z
r / R = — (z / Z) = — (- 0,05 / 106)
Итак: r = (0,05 / 106) (0,338) = 0,0001594
Пример 7: Необходимо получить плотность длинного медного стержня. Его длина измеряется метровой палкой, диаметр — микрометром. штангенциркуль и его масса с электронными весами.
L = 60,0 ± 0.1 см (0,17%) D = 0,632 ± 0,002 см (0,32%) [Таким образом, ошибка в D 2 составляет 0,64%] m = 16,2 ± 0,1 г (0,006%)Площадь поперечного сечения πr 2 = πD 2 /4. Таким образом, плотность равна = m / v = 4m / LπD 2 . Относительная погрешность результата (плотности) должна быть не более (0,17% + 0,64% + 0,006% = 0,816%) или около 0,8%. Это написано:
плотность = 8,606 ± 0,07 г / см 3
Справочник дает 8.87 г / см 3 как плотность меди. Экспериментальное расхождение составляет 0,26, что указывает на то, что что-то не так. Студент, взявший эти данные, возможно, ошибся при измерении. Может быть, это была не чистая медь, а медный сплав. Если это ошибка при измерении, измерение диаметра является наиболее эффективным. скорее всего подозреваю.
К. ЦЕЛИ ЛАБОРАТОРНОЙ РАБОТЫ
Хороший способ завершить эту главу — подумать о том, что цели студентов в лаборатории должны быть.Первокурсник лаборатория , а не , как исследовательская лаборатория, но мы надеемся что студент узнает о некоторых проблемах, методы, инструменты и цели исследователей-физиков.Эксперименты в лаборатории первокурсников делятся на несколько категорий. В каждом случай ниже, мы указываем, за что должен отвечать студент быть.
1. Для измерения фундаментальной физической величины.
Студент разрабатывает экспериментальную стратегию для получения максимальной точный результат на имеющемся оборудовании.Студент должен понимать работу оборудования и исследовать присущих эксперименту неопределенностей достаточно полно, чтобы утверждать пределы погрешности данных и результатов с уверенностью, что «истинные» ценности (если бы они были известны) не лежали бы за пределами заявленные пределы погрешности.
2. Подтвердить или проверить известный закон или принцип.
В этом случае недостаточно сказать «Закон был (или не был) проверено.»Экспериментатор должен указать, какой погрешностью ограничивает проверка выполняется, и для каких ограничений диапазона данных, условия эксперимента и т. д. Слишком легко сделать чрезмерные обобщения. Студент в лаборатории для первокурсников не проверяет закон, скажем, F = ma, для — все возможных случаев, в которых может применяться этот закон. В ученик вероятно, исследовал закон в более ограниченном случае гравитационная сила у поверхности земли, действующая на небольшой масса, падающая с расстояния одного-двух метров.Студент следует указать эти ограничения. Не следует широко утверждать «проверили закон Ньютона». Еще хуже было бы заявить чтобы «доказать закон Ньютона».
3. Исследовать явление, чтобы сформулировать закон или отношение, которое лучше всего его описывает.
Здесь недостаточно найти закон, который «работает», но показать, что найденный вами закон лучше отражает данные, чем другие законы, которые вы можете проверить.Например, у вас может быть график экспериментальные данные, которые «выглядят» как некоторая степень x. Вы найдете мощность, которая кажется подходящей. Другой студент говорит, что это «похоже» на экспоненциальная функция от x. Экспоненциальная кривая испытана и кажется подходить. Итак, какое соотношение «правильное» или «лучшее»? Вы можете быть в состоянии чтобы показать, что один из них лучше соответствует данным. Один может быть более физически значимым в контексте более крупного картина установленных законов и теории физики.Но может быть так ни один из них не является явно лучшим представлением данных. В в этом случае вам следует изменить эксперимент таким образом, чтобы он может окончательно решить между двумя конкурирующими гипотезами.
Читатель вашего отчета очень внимательно рассмотрит «результаты». и выводы «, в котором представлены ваши претензии по результат эксперимента. Читатель также будет смотреть, вы обосновали свои претензии конкретной ссылкой на данные вы взяли в эксперименте.Ваши претензии должны быть подтверждены данные и должны быть разумными (в пределах ограничений эксперимент). Это проверка вашего понимания эксперимента, вашего суждения при оценке результатов, и вашего умение общаться.
L. ЗАКЛЮЧЕНИЕ
Анализ ошибок — это не деятельность «постфактум»; это пронизывает весь экспериментальный процесс от дизайна эксперимента до сбор данных для окончательного анализа результатов. И это не «нарезанный» метод или набор рецептов для «расчета ошибки.»Хотя существуют статистические математические критерии, которые лежат в основе всего процесса, глубокое понимание и суждение и здравый смысл должен быть задействован в эксперименте, чтобы правильно оценить динамическое взаимодействие источников ошибок. В экспериментатор должен понимать физику, имеющую отношение к эксперимент, чтобы сделать это должным образом. Экспериментатор должен упражнение здравый смысл и здравый смысл в выборе экспериментальных стратегий для улучшить результаты, и в выборе методов определения эффекта экспериментальных неопределенностей.Когда анализ ошибок рассматривается как «бездумный» расчетный процесс, грубейшие ошибки анализа и может произойти интерпретация.ПРИЛОЖЕНИЕ I. МЕРЫ НЕОПРЕДЕЛЕННОСТИ
Размер экспериментальной неопределенности в наборе измерений может выражаться несколькими способами, в зависимости от того, насколько «консервативно» ты хочешь быть.1. Пределы погрешности.
Попытка указать весь диапазон, в котором все замеры будут врать.На практике один указывает диапазон в пределах в которых лежат измеренные значения.
2. Среднее отклонение.
Среднее отклонение набора измерений от его среднее значение находится путем суммирования отклонений n измерений, затем разделив сумму на (n-1). Эта мера описывает «разброс» набора измерений.
Когда кто-то хочет сделать выводы о том, насколько далеко оценочное среднее может отклоняться от «истинного» среднего значения родительского распределения, используйте среднее отклонение от среднего значения .К вычислите его, сложите отклонения n измерений, затем разделите эту сумму на n (n-1) 1/2 . Эта мера выражает качество вашей оценки среднего. Это мера, которую мы неопределенность назовем (или ошибкой) в среднем.
Это последнее определение автоматически включает два математических исправления, необходимые для того, чтобы сделать выводы о родителях распределение из конечной выборки данных, и одно для исправления Дело в том, что вы использовали только малый образец .
3. Стандартное отклонение.
Стандартное отклонение стало «стандартным» методом для выражая неуверенность, потому что это подтверждается развитая математическая модель. К сожалению, это только уместно, когда экспериментатор (а) имеет большие выборки данных, и (б) знает, что распределение данных действительно гауссово, или почти гауссовский. Поэтому его редко используют в лаборатории для первокурсников. оправдано — что-то вроде того, как кувалдой раскололи грецкий орех.
ПРИЛОЖЕНИЕ II. РАСЧЕТЫ С ПОМОЩЬЮ СТАНДАРТНЫХ ОТКЛОНЕНИЙ
Правила распространения ошибок для элементарных алгебраических операции могут быть пересмотрены для применения, когда стандартные отклонения используется в качестве меры ошибки для случайных (неопределенных) ошибок:- При добавлении независимо измеренных величин или вычтенный, стандартное отклонение результата — это квадратный корень из суммы квадратов стандартных отклонений величин.
- При перемножении независимо измеренных величин или разделенное, относительное (дробное или процентное) стандартное отклонение результата — квадратный корень из суммы квадратов относительные стандартные отклонения величин.
При использовании стандартных отклонений правила сложения средних отклонения модифицируются следующим образом: вместо простого суммирования меры ошибок, вы возводите их в квадрат, суммируете квадраты и затем берете квадратный корень из суммы.Это называется «квадратурным суммированием».
Стандартные отклонения лучше? Слишком много элементарных лаборатория в руководствах подчеркивается, что стандартное отклонение является единственным стандартным способом экспресс меры погрешности. Однако из стандартных статистическая теория, согласно которой при очень небольшом количестве измерений сами оценки ошибок будут иметь низкую точность. Неопределенность из оценка ошибки, сделанная из n частей данных, составляет
100 процентов [2 (n-1)] 1/2
Таким образом, нам пришлось бы усреднить 51 независимое значение, чтобы получить ошибку 10%. в определении ошибки.Нам потребуется 5000 измерений чтобы получить погрешность, оцените до 1%. Если бы было всего 10 измерений сделано, погрешность стандартного отклонения составляет около 24%. Вот почему мы постоянно подчеркивали, что оценки ошибок 1 или 2 значащих цифр достаточно, когда выборки данных небольшие.
Это лишь одна из причин, почему использование стандартного отклонения в элементарная лаборатория редко бывает оправданной. Как часто нужно принимать больше, чем несколько измерений каждой величины? Можно ли вообще взять достаточно измерений, чтобы определить характер ошибки распределение? Это гауссово или что-то еще? Обычно один не знает.Если он не близок к гауссовскому, весь аппарат обычных правил статистической ошибки для стандартного отклонения должны быть модифицированным. Но правила максимальной погрешности, пределов погрешности и средняя ошибка достаточно консервативна и надежна, чтобы все еще можно надежно использовать даже для небольших образцов.
Однако, когда три или более разных количества вносят вклад в В результате более реалистичная мера ошибки получается при использовании метод «сложения в квадратуре», описанный в начале этого раздел.
Точно так же, как это плохой тон — отображать более значимые цифры, чем оправдано, или претендовать на большее значение для результатов, чем подтверждено экспериментом, поэтому использовать статистические методы и меры погрешности для выражения результатов когда данные не подтверждают эти меры погрешности или математические правила, используемые для их получения. Это подразумевает большее качество значение для результатов, чем может иметь место, и граничит с научное мошенничество.
ПРИЛОЖЕНИЕ III. ВАЖНОСТЬ НЕЗАВИСИМОСТИ ПРИ ИСПОЛЬЗОВАНИИ АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ РАСПРОСТРАНЕНИЯ ОШИБОК
Алгебраические правила для распространения неопределенных ошибок являются одним из способов вывести правильные уравнения ошибок, но должны использоваться с осторожностью. Вот пример, иллюстрирующий ловушку, которую вы должны избегать.Студент хочет вычислить уравнение ошибки для эффективного сопротивления R, из двух резисторов X и Y, в параллели. Уравнение для параллельных резисторов:
Студент решает это для R, получая:1 1 1 - = - + - R X Y
Ошибка знаменателя по правилу сумм равна x + y.Продолжать, мы должны использовать правило частного, которое требует относительных ошибка меры. Таким образом, студент переводит ошибку в знаменателе в относительная форма, (x + y) / (X + Y). Остальное касается продуктов и частных, так что относительная определенная ошибка в R оказывается равной быть:XY R = ————— X + Y
Следующий шаг требует некоторой алгебры, чтобы преобразовать это в стандартный формы, но давайте не будем тратить усилия, потому что это уравнение уже неверно!г х у х + у - = - + - - ————— R X Y X + Y
Почему? Уравнение11 имеет X и Y в числителе и знаменатель. Следовательно, числитель и знаменатель не являются независимый . Правило частного недействительно, если числитель и знаменатель не независимы.
Чтобы избежать этой ошибки, делайте все, что необходимо для алгебры. переставьте исходное уравнение так, чтобы применение правил никогда не потребует объединение ошибок для независимых величин. Фактически, форма уравнения 10 является идеальной отправной точкой для всех его операций (+ и /) связаны с независимыми величинами.
Чтобы сделать это правильно, начните с уравнения. 10 (в которых каждый количество появляется только один раз, и нет никаких сомнений в том, что каждый операция независимая). Относительная ошибка в 1 / X определяется правило частного (0 — x / X), которое просто -x / X. Ошибка в 1 / X составляет следовательно (-x / X) (1 / X) = -x / X 2 . Точно так же ошибка в y — это -y / Y 2 , а в r — -r / R 2 . Наконец, используя правило сложения ошибок, результат:
2 2 2 Р Х Х Y Y X X Y Y R X Y Или, используя уравнение.11, правая часть может быть выражена через только измеренные величины.2 2 r x y r R x R r R x R y —— = —— + ——, или - = - - + - -, или r = - - + - -
R X + Y X X + Y Yг Y x X y - = ——— - + ——— -
УПРАЖНЕНИЯ
В следующих ситуациях учитывайте здравый смысл. физические принципы, чтобы определить, какой из них наиболее осмысленный способ описания ошибки: как абсолютное ошибка или дробная ошибка, неопределенная ошибка или определенная ошибка, точная мера или точный один.Подтвердите свои ответы, изложив свои доводы.(1) Партия пластиковых измерительных стержней изготовлена точно, но через год после выхода с завода пластик изрядно сжался равномерно в среднем на 2 мм.
(2) Острие ножей механических весов (используемых для взвешивания объекты) затупились.
(3) Регулировочный винт быстрого / медленного действия в прецизионном механическом секундомере. неправильно настроен.
(4) Опоры конического подшипника в механическом электрическом вольтметр ослабли, так что стрелка подшипника очень свободно ограниченный.
(5) Влияние (небольшое) сопротивления воздуха на измерение ускорение свободного падения в эксперименте с падающим телом.
(6) (a) Влияние неконтролируемой и неизмеряемой лаборатории температура на тонком механическом инструменте, который делает измерения ежедневно в течение многих месяцев. (б) Влияние температуры на приборе, если эксперимент длился 60 секунд.
(7) Влияние сопротивления воздуха на период маятника.
(8) Влияние очень нечистого спирта, используемого в качестве жидкости в определение плотности твердого тела по принципу Архимеда. [The твердое вещество взвешивается при погружении в жидкость и формула для результат содержит плотность жидкости.]
В следующей группе упражнений примите следующие данные: A = 10, B = 2, C = 5, D = 20. В каждом случае формула для результат, R. Вычислите числовое значение R. Найдите определите уравнение ошибки в каждом случае, а затем используйте его для ответьте на заданный конкретный вопрос.
(9) Уравнение: R = (C — B) / A. Используйте уравнение детерминированной ошибки, чтобы найти, каким было бы значение R, если бы B было на самом деле 2,1 из 2. Проверьте свой ответ прямым подсчетом.
Подсказка: Фактически не записывая всю определенную ошибку уравнение, мы можем записать член этого уравнения, который дает вклад из-за ошибки в B.r c - b a - = ————— - - - R C - B A
только из-за ошибки в B.r -B b - = ————— -, R C - B B
(10) Уравнение: R = (C / A) — C — 5. Используйте уравнение ошибки, чтобы найти R, если C был изменен на 4.7. Проверьте ответ прямым подсчетом.
(11) Уравнение: R = (D 2 C 2 ) -3 / (D — А) 2 . Найдите, как R меняется, если D меняется на 22, A меняется до 12 и C меняется на 5.3 (все сразу).
(12) Уравнение: R = D sin [(A — C) / 3B]. Найдите, как R меняется, если C увеличивается на 2%. Помните, что аргументы триггерных функций всегда в радианах .
(13) Уравнение: R = exp [(C — B) / D] Найдите, как R изменяется, если B уменьшается на 2% и D увеличивается на 4 единицы. Это стандартное обозначение: exp (x) означает то же, что и e x . Здесь е — это, конечно, база натуральные логарифмы.
Эта последняя группа вопросов носит более общий характер и требует внимательного отношения к ней. мысль и анализ всех возможностей.Обязательно учтите это в самом общем контексте, учитывая все возможные меры погрешности: неопределенные, определенные, относительные и абсолютный. Утверждения могут быть верными для одного типа ошибок. мера и ложь для других. Если да, укажите это в своем отвечать.
(14) Студент говорит: «Когда два измерения математически вместе, ошибка в результате всегда больше, чем ошибка любого из измерений ». Обсудите это утверждение. критически.
(15) Другой студент говорит: «Когда два измерения имеют ошибку 2%, и они используются в уравнении для вычисления результата, результат будет иметь ошибку 4% ». Обсуди критически.
(16) Еще один студент говорит: «Когда несколько измерений используется для расчета результата, ошибка в результате никогда не может быть меньше, чем ошибка худшего измерения ». Обсуди, критически.
(17) Еще один студент говорит: «Когда используются несколько измерений вычислить результат, а погрешность единицы в 10 раз больше как следующий худший, вы можете пренебречь всем, кроме худшего один в уравнении распространения ошибки.»Обсуди критически.
КОНЕЦ
1. Некоторые из лучших способов анализа ошибок:- Янг, Хью Д. Статистическая обработка экспериментальных Данные. Макгроу-Хилл 1962.
- Baird, D. C. Эксперименты, введение в теория измерений и план экспериментов. . Второе издание. Прентис-Холл, 1988.
- Тейлор, Джон Р. Введение в анализ ошибок. Книги университетских наук, 1962.
- Майнерс, Гарри Ф., Эппенштейн и Мур. Лаборатория Физика. Wiley, 1969 год.
- Swartz, Clifford E. Используемая математика, в течение первых двух лет колледж науки. Прентис-Холл, 1973 г. Американский институт Physics, 1996. В главе 1 обсуждается анализ ошибок на уровне подходит для первокурсника.
- Шварц, Клиффорд Э. и Томас Майнер. Преподавание вводное
Физика, Справочник. Американский институт физики, 1977.
В главе 2 этой ценной книги рассказывается об анализе ошибок.
что полностью соответствует моей философии по данному вопросу.
В нем рассматриваются три уровня обработки ошибок.
- Значимые цифры — первое приближение к анализу ошибок. (Но такой, который не подходит для лабораторных работ по физике в бакалавриате.)
- Абсолютные и процентные ошибки — второе приближение к ошибке анализ.Это уровень, который мы подробно обсуждали выше. Шварц и Майнер говорит: «[Эти] правила … часто бывают удовлетворительными. вводные лабораторные работы, это единственные действующие правила.
- Кривые распределения данных — третье приближение к анализу ошибок.
Это включает использование стандартных отклонений в качестве меры ошибки и
правила их совмещения. Я не могу удержаться от цитаты из этой книги:
Использование этого третьего приближения к анализу ошибок оправдано только при соблюдении определенных экспериментальных условий и требований.Если формализм применяется вслепую, как это часто бывает, можно требовать высокой точности когда его вообще нет. Ситуация усугубляется легким наличие статистических программ на многих ручных калькуляторах. Просто введите несколько чисел, нажмите клавиши и стандартные отклонения и корреляции упадет до 10 незначительных цифр.
3. Величина количества — это его размер безотносительно к его величине. алгебраический знак.
4. Среднее отклонение правильнее было бы назвать «средним абсолютное отклонение «или» среднее абсолютное отклонение «, поскольку это среднее абсолютных значений отклонений, а не сами отклонения.[Среднее значение отклонений симметричной распределение будет нулевым.]
5. В статистическом исследовании неопределенностей слова «средний» и «означает» не используются как полные синонимы. Когда ссылаясь на среднее значение набора из данных измерений, всегда используется слово «средний», а не «средний». При обращении к в других процессах усреднения слово «среднее» предпочтительнее. Возможно, это различие в использовании призвано избежать создания неуклюжего имени. как «среднее отклонение от среднего».»
6. См. Лабораторная физика Майнерса, Эппенсейна и Мура. для получения более подробной информации о среднем отклонении и других показателях дисперсии.
7. Это относительно новое обозначение средних значений, на мой взгляд, более аккуратное. и легче читается, чем старые обозначения ставить черту над В.
8. Хорошее обсуждение см. В Laboratory Physics by Майнерс, Эппенштейн и Мур. Там (на стр.36) вы найдете параллельный расчет среднего отклонения и стандарта отклонение, и обсуждение того, как они сравниваются как меры ошибка.
9. Гауссово распределение, иногда называемое «нормальной кривой» ошибки »имеет уравнение:
f (X) = C e где2 - [(X -
) / 2 с]
10. См. Meiners et. др., которые комментируют: «Это означает, что для многих целей, мы можем использовать среднее отклонение … вместо стандартное отклонение. Это преимущество, потому что средний отклонение вычислить легче, чем стандартное отклонение ».
11.Независимые ошибки — это те, для которых ошибка одного индивидуальное измерение не зависит от ошибок в других измерения. Никакая ошибка не влияет на другие или математически определяется из других.
12. Вместо этого можно использовать исчисление.
Этот документ принадлежит доктору Дональду Э. Симанеку, © 1996, 2017. Университет Лок-Хейвена, Лок-Хейвен, Пенсильвания, 17745. Коммерческое использование запрещено без разрешения автора. Документ может быть свободно используется инструкторами и бесплатно распространяется среди студентов, поэтому пока включено это уведомление об авторских правах.
Отзывы и предложения по дополнениям и улучшениям приветствуются по адресу адрес, показанный справа.
