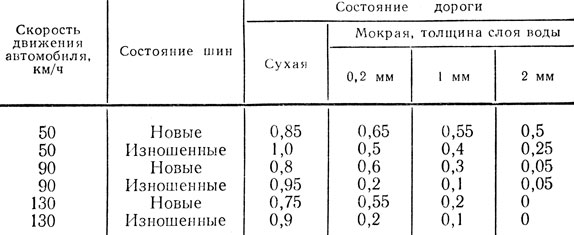
Коэффициент сцепления шин с дорогой и факторы, влияющие на него
Направление ветра, скорость, давление в шинах – все эти факторы имеют особое значение для гонщиков-профессионалов, так как определяют собой поведение автомобиля на дороге. Для простых водителей основным фактором является коэффициент сцепления шин с дорогой, характеризующийся степенью скользкости дорожного покрытия.
Оглавление:
- От чего зависит коэффициент сцепления шин?
- Как предотвратить заносы и скольжения?
- Причины плохого сцепления с дорогой
- Как проверить скользкость дороги?
От чего зависит коэффициент сцепления шин?
Дорожное покрытие однозначно влияет на поведение автомобиля на дороге. Грунтовка, плиты, брусчатка вызывают тряску. Однако подобные покрытия встречаются значительно реже, чем асфальт. Поэтому главными причинами, определяющими коэффициент сцепления, являются погодные условия: грязь, лед, слякоть, температура и другие.
На коэффициент сцепления колеса с дорогой сильно влияет конструкция шины и тип рисунка протектораВсегда нужно знать, на что обращать внимание и как действовать в определенных обстоятельствах. Вот несколько основных факторов, приводящих к появлению скользкого дорожного покрытия на отдельных участках.
Вот несколько основных факторов, приводящих к появлению скользкого дорожного покрытия на отдельных участках.
- Лужи. Главной опасностью на дороге в дождливую погоду является аквапланирование. Оно характеризуется полной или частичной потерей сцепления шин с дорогой при контакте с водой. Даже в сильный гололед оно отчасти остается, но в случае с водой сцепления почти нет. Маслянистые участки дороги. Разлитые нефтепродукты делают дорогу скользкой.
- Заносы из снега или песка. Подобные явления возникают по причине гидрометеорологических бедствий, поэтому еще и сопровождаются плохой видимостью. Очевидно, что в такую погоду лучше не садиться за руль.
- Грунтовая дорога. На таких поверхностях при малейшем контакте с водой образуется грязь, которая налипает на шины. Выезд с грунтовой дороги обычно очень скользкий и колёса очень плохо сцепляются с дорожным покрытием.
- Частичный гололед. После сильных заморозков на дорогах появляется лед, но позже не весь он тает равномерно.
 Тени от деревьев, построек препятствуют таянию. Соответственно, в таких местах дороги значительно уменьшается сцепление.
Тени от деревьев, построек препятствуют таянию. Соответственно, в таких местах дороги значительно уменьшается сцепление.
Как предотвратить заносы и скольжения?
Лучше сторониться вышеуказанных мест на проезжей части либо снижать скорость при езде по ним. Особенно опасно проезжать по подобным местам только одной стороной машины. Это чревато заносом из-за разности коэффициентов сцепления с дорогой. Но иногда невозможно проехать иначе, в таком случае необходимо придерживаться следующих рекомендаций:
- Избегать резких поворотов руля, изменений скорости движения, то есть плавно использовать педали тормоза и газа, стараясь придерживаться максимально прямой траектории движения.
- Для безопасного движения на поворотах рекомендуется ехать внутренней парой колес по области с плохим сцеплением, а внешней парой держаться сухой поверхности.
Причины плохого сцепления с дорогой
Плохое сцепление на всей дороге может обуславливаться следующими причинами.
- Гололед. Данное погодное явление бывает тяжело заметить на дороге, поэтому при температуре воздуха около ноля лучше почаще проверять поверхность на наличие обледенения. В такие дни рекомендуется выбирать маршрут с интенсивным движением, так как это способствует более быстрому таянию льда.
- Дождь. Начало небольшого, на первый взгляд безобидного дождя может послужить причиной возникновения проблем на дороге. На сухой поверхности скапливается множество пыли, грязи, капель нефтяных и масляных отходов от автомобилей. С началом дождя на асфальте образуется небольшая пленка, которая бывает такой же скользкой, как легкое обледенение. При такой погоде лучше придерживаться тех же правил управления автомобилем, как и при гололеде.
- Снег. В период заморозков на дорогах с большим движением образуется слякоть, которая препятствует сцеплению.
- Булыжная дорога в дождь. Булыжная дорога в смоченном состоянии особенно опасна для проезда из-за особенностей материала изготовления.

- Жаркая погода. В зной на асфальте выступает тончайшая маслянистая пленка вяжущего вещества, которая влияет на поведение автомобиля.
- Опавшие листья. Ковер из мокрых листьев очень скользкий, лучше объезжать подобные места или быть предельно осторожным.
Таблица. Значения коэффициента сцепления шин с различными дорожными покрытиями.
Дорожное покрытие | Состояние дорожного покрытия | |
сухое | мокрое | |
| Асфальт, бетон | 0,7—0,8 | 0,45—0,55 |
| Песчаная дорога | 0,7—0,8 | 0,6—0,65 |
| Щебеночное покрытие | 0,6—0,7 | 0,4—0,5 |
| Грунтовая дорога | 0,5—0,6 | 0,4—0,5 |
| Булыжник и брусчатка | 0,5—0,55 | — |
| Дорога, покрытая снегом | 0,2—0,4 | |
| Снежная укатанная дорога | 0,2—0,25 | |
| Гололед | 0,2—0,25 | |
Как проверить скользкость дороги?
На небольшой скорости можно слегка притормозить либо резко надавить на газ, почти сразу отпустив педаль.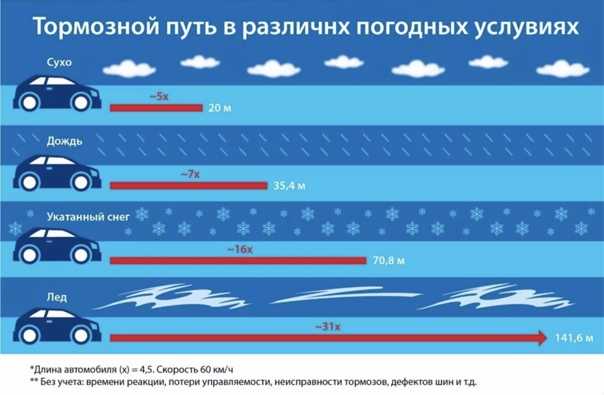 Чтобы определить коэффициент сцепления более точно, нужно давить на газ множество раз, на каждый увеличивая резкость нажатия. Если приводные колеса начнут буксовать, это будет указывать на то, что дорога скользкая, и чем раньше они забуксуют, тем выше степень опасности.
Чтобы определить коэффициент сцепления более точно, нужно давить на газ множество раз, на каждый увеличивая резкость нажатия. Если приводные колеса начнут буксовать, это будет указывать на то, что дорога скользкая, и чем раньше они забуксуют, тем выше степень опасности.
Многие ошибочно полагают, что реагировать на опасные участки дороги нужно только по мере необходимости. На самом же деле, чтобы максимально обезопасить себя, нужно вести машину равномерно, независимо от дорожных условий.
Двигаться без резких движений, всегда контролировать руль, не выжимать сцепление в моменты торможения. Изменять скорость лучше только на ровной, прямой дороге. Если придерживаться данных рекомендаций, это значительно повысит устойчивость на дорогах в любых условиях и снизит вероятность заноса.
От чего зависит сцепление шин с дорогой? Часть 1
Дорогие друзья! Два года назад я написал статью «Сцепление шин с дорогой не зависит от площади пятна контакта?», и она вызвала бурную реакцию аудитории. Статья до сих пор находится в блоге, и на ее странице много комментариев, вопросов, споров, рассуждений. Кто-то, прочитав, поблагодарил меня за развенчивание мифов и простое, доступное объяснение физики процесса. Кто-то, наоборот, раскритиковал за излишнюю упрощенность и ограниченность моих рассуждений и аргументов.
Статья до сих пор находится в блоге, и на ее странице много комментариев, вопросов, споров, рассуждений. Кто-то, прочитав, поблагодарил меня за развенчивание мифов и простое, доступное объяснение физики процесса. Кто-то, наоборот, раскритиковал за излишнюю упрощенность и ограниченность моих рассуждений и аргументов.
За два года, что прошли с момента написания этой статьи, я поучаствовал во многих дискуссиях на эту тему, познакомился с новой литературой, пообщался с другими физиками (сам я – тоже физик по специальности), гонщиками и кое-что переосмыслил. Суть моих размышлений не поменялась, они стали более систематизированы и поменялись формулировки. Вот их я и изложу ниже. Поехали.
Сила трения покоя: закон Амонтона-Кулона
Снова вернусь к школьной физике. Напомню, школьная физика и классическая механика достаточно точно описывают повседневные явления. Пока речь не заходит об очень маленьких масштабах или релятивистких скоростях, классическая механика отлично работает. Более того, в какие бы научные труды о сцеплении шин с дорогой я не заглядывал, я видел в них много страшных зубодробящих формул, интегралов, рядов, но в конце концов все сводилось к одной простой школьной формуле, которая называется законом Амонтона-Кулона:
Более того, в какие бы научные труды о сцеплении шин с дорогой я не заглядывал, я видел в них много страшных зубодробящих формул, интегралов, рядов, но в конце концов все сводилось к одной простой школьной формуле, которая называется законом Амонтона-Кулона:
F = µN = µmg (1)
где µ — коэффициент сцепления, N – сила, прижимающие одно тело к другому (в данном случае, вес шины плюс вес части автомобиля, приходящейся на эту шину), m — масса тела (шины и части автомобиля, приходящейся на эту шину), g — ускорение свободного падения.
То есть сила трения пропорциональна силе, прижимающей одно тело к другому, и коэффициенту трения. В самом простом случае эта сила — вес и представляет собой силу тяжести, то есть произведение массы тела на ускорение свободного падения. И тогда сила трения покоя пропорциональна коэффициенту трения, массе тела и ускорению свободного падения.
Сила трения покоя – она же сила сцепления
Автомобиль движется благодаря силе трения покоя в области контакта шины с дорожным полотном, а не силе трения качения, как иногда думают. Сила трения качения – следствие деформации шины. Она наоборот тормозит движение автомобиля. А пятно контакта шины с дорогой покоится относительно дороги в случае качения шины. Конечно, во время качения в пятне контакта всегда присутствуют элементы протектора, проскальзывающие относительно дороги, но в случае равномерного прямолинейного движения автомобиля в первом приближении их можно не учитывать и считать силу трения силой трения покоя или еще ее называют силой сцепления шины с дорогой, а коэффициент трения покоя – коэффициентом сцепления. При торможении большая часть элементов протектора может скользить вдоль дорожного полотна. В этом случае вращение колеса (и следовательно автомобиль) тормозится силой трения скольжения. Стоит отметить, что обычно сила трения скольжения меньше силы трения покоя.
Перераспределение веса авто между шинами и сцепление с дорогой
Теперь разберем, что есть что в формуле Амонтона-Кулона. Ускорение свободного падения постоянно, его из обсуждения исключаем. Масса в целом тоже постоянна. Конечно, вес автомобиля распределен между 4 шинами, и при изменении скорости и/или траектории движения распределение веса может существенно меняться: какие-то шины разгружаются, а какие-то нагружаются дополнительно.
Перераспределение веса автомобиля между шинами тоже косвенно влияет на их сцепление с дорогой. Скажем, при торможении вес машины частично смещается с задней оси на переднюю, следовательно, сила прижатия задних шин к дороге уменьшается и поэтому сила их сцепления с дорогой ухудшается. Это повышает вероятность заноса автомобиля, но на тормозной путь не влияет, потому что сила сцепления передних колес с дорогой увеличивается из-за перераспределенной нагрузки. Если на одних и тех же шинах будут тормозить Porsche 911 и Porsche Cayenne, у последнего вследствие большей высоты смещение веса с задних шин на передние будет в большей степени, и Cayenne больше рискует попасть в занос.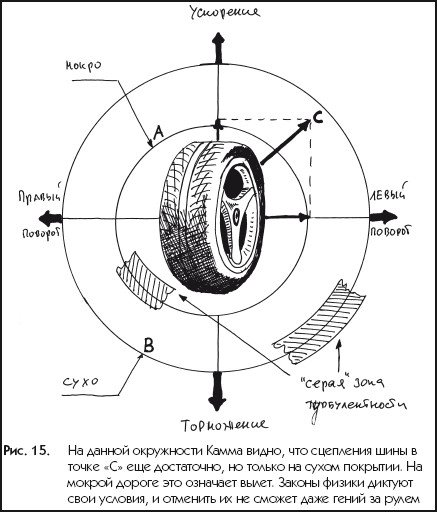 Но тормозной путь от этого меньше не станет. То, что Cayenne тяжелее – тоже не влияет, об этом читайте статью «Тормозной путь не зависит от массы авто?». Поворачивать Cayenne будет конечно же хуже 911-го и на меньших скоростях – как раз из-за более высокого центра тяжести и большего смещения веса и больших кренов.
Но тормозной путь от этого меньше не станет. То, что Cayenne тяжелее – тоже не влияет, об этом читайте статью «Тормозной путь не зависит от массы авто?». Поворачивать Cayenne будет конечно же хуже 911-го и на меньших скоростях – как раз из-за более высокого центра тяжести и большего смещения веса и больших кренов.
Кроме того, на перераспределение веса влияет манера вождения. При аккуратном вождении, когда водитель избегает резких поворотов, перестроений, ускорений и торможений (читай, чем меньше нажата педаль тормоза или чем на меньший угол поворачивается руль), запас сцепления шин с дорогой максимален, то есть шины находятся «максимально далеко» от перехода в состояние полного скольжения и, как следствие, управление автомобилем максимально безопасно. Во-вторых, одно и то же перемещение педалей или руля можно совершить по-разному: быстро, резко или по нарастающей, прогрессивно. Резкое нажатие на педаль или поворот руля приведет к соответствующему резкому перераспределению веса с одних шин на другие, и это чревато их срывом в скольжение и сходом с траектории движения.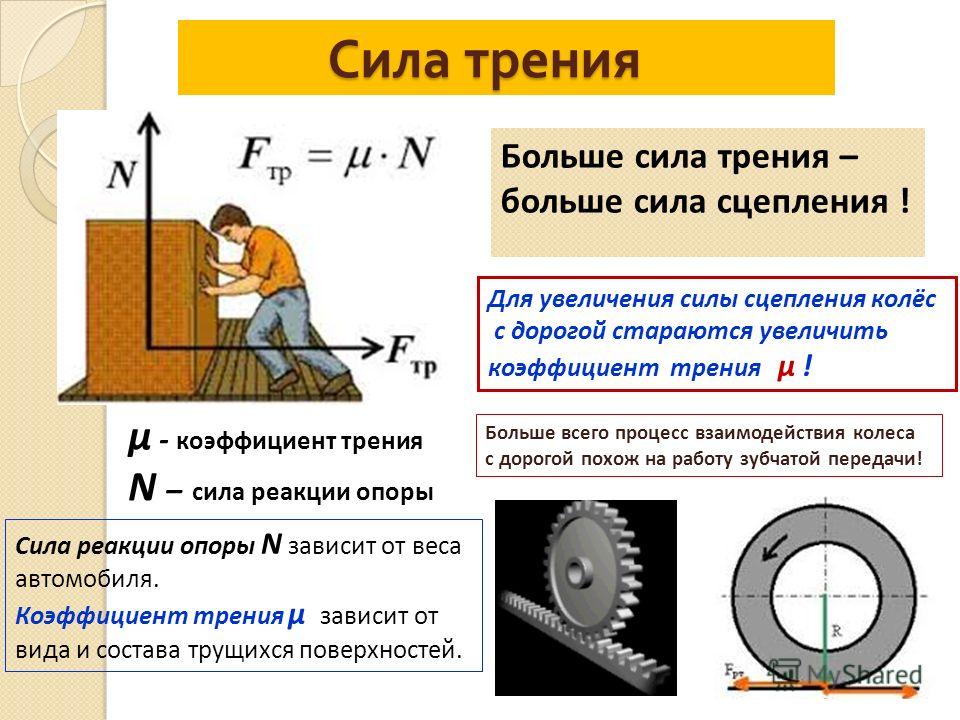 Постепенное же воздействие на органы управления приводит к столь же плавному перераспределению веса, что позволяет шинам цепляться за дорогу без риска скольжения и потери управляемости или устойчивости автомобиля. Убедиться в этом на практике вы можете на курсах контраварийной подготовки водителей, например, при выполнения упражнения «экстренный объезд препятствия».
Постепенное же воздействие на органы управления приводит к столь же плавному перераспределению веса, что позволяет шинам цепляться за дорогу без риска скольжения и потери управляемости или устойчивости автомобиля. Убедиться в этом на практике вы можете на курсах контраварийной подготовки водителей, например, при выполнения упражнения «экстренный объезд препятствия».
Практические рекомендации
1. Если вы хотите водить машину по дорогам общего пользования безопасно, а по гоночному треку быстро, перемещайте органы управления (руль, педали газа и тормоза) плавно и постепенно.
Теперь поговорим о том, что в самой шине влияет на ее сцепление.
Коэффициент сцепления шины с дорогой
Остается последний параметр в формуле силы трения Амонтона-Кулона – коэффициент сцепления µ, который, в первую очередь, зависит от природы соприкасающихся поверхностей. Самый показательный пример – сцепление резины с асфальтом куда лучше, чем той же резины со снегом и тем более льдом, несмотря на разные механизмы трения между шиной и этими тремя покрытиями.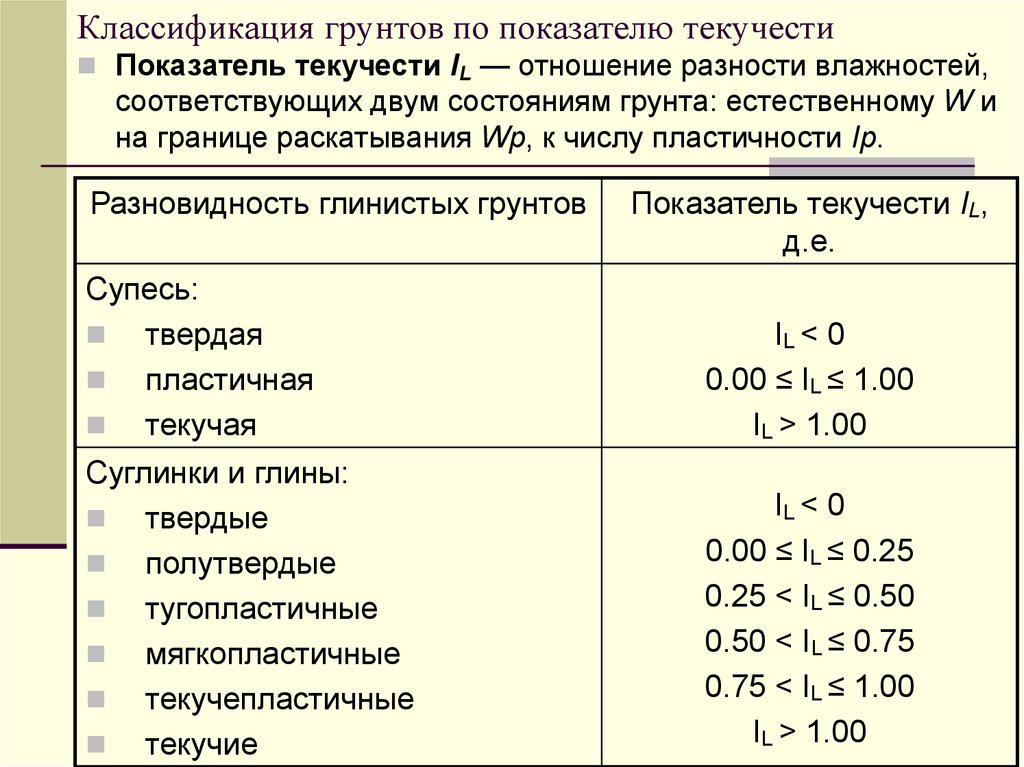 А при одном и том же дорожном покрытии коэффициент сцепления будет зависеть уже от состава резины и конструкции протектора. Например, на зимних шинах автомобиль куда лучше держит скользкую дорогу, чем на летних. И главное отличие зимних и летних шин – именно разный состав резины и конструкция протектора.
А при одном и том же дорожном покрытии коэффициент сцепления будет зависеть уже от состава резины и конструкции протектора. Например, на зимних шинах автомобиль куда лучше держит скользкую дорогу, чем на летних. И главное отличие зимних и летних шин – именно разный состав резины и конструкция протектора.
А если вы когда-нибудь смотрели по телевизору Формулу 1, наверняка слышали о разных типах шин и разных составах: «мягкий состав, сверхмягкий состав, жесткий состав». Именно это и оказывает ключевое влияние на коэффициент сцепления, даже в Формуле 1.
Так что же, все? Больше ничего не влияет? И что, этот коэффициент сцепления постоянен? Влияет, и как раз потому, что коэффициент сцепления не является постоянным и зависит от некоторых факторов. Но для начала расскажу о пресловутой площади пятна контакта.
Влияет ли площадь пятна контакта на сцепление шины с дорогой?
На всякий случай напомню, что такое пятно контакта. При контакте с плоским дорожным покрытием ВСЯ шина деформируется, сминаясь и становясь плоской в зоне контакта. Эту зону и называют пятном контакта. Пятно контакта имеет площадь, примерно равную размеру ладони. Обыватели часто думают, что чем больше площадь пятна контакта, тем лучше сцепление шины с дорогой. И еще многие думают, что чем шире шина, тем больше площадь пятна контакта. А следовательно, думают, что чем шире шина, тем лучше ее сцепление с дорогой. Ниже я расскажу обо всем этом по порядку.
Эту зону и называют пятном контакта. Пятно контакта имеет площадь, примерно равную размеру ладони. Обыватели часто думают, что чем больше площадь пятна контакта, тем лучше сцепление шины с дорогой. И еще многие думают, что чем шире шина, тем больше площадь пятна контакта. А следовательно, думают, что чем шире шина, тем лучше ее сцепление с дорогой. Ниже я расскажу обо всем этом по порядку.
Как видно из формулы Амонтона-Кулона, площадь пятна контакта в силу трения не входит. Почему? Ведь, казалось бы, чем больше площадь, тем больше элементов шины участвует в зацеплении и тем больше сила трения. С одной стороны – да, а с другой – чем больше площадь соприкосновения, тем меньше давление шины на дорогу. Выходит баш на баш, и площадь не играет никакой роли. Теперь объясню то же самое на языке физики.
Чтобы было понятнее, куда же делась площадь, можно формулу Амонтона-Кулона (1) переписать иначе, с учетом площади пятна контакта и отразить влияние пятна на давление. Все просто: давление тела на опору или, в нашем случае, шины на асфальт равно весу тела (шины), деленному на площадь контакта:
P = N/S = mg/S (2)
где P — давление шины на дорогу, N = mg — все тот же вес шины.
Тогда отсюда можно выразить вес через давление:
N = PS (3)
Теперь, если подставить эту формулу в закон Амонтона-Кулона, получим:
F = µPS (4)
Или, выражаясь человеческим языком, сила сцепления шины с дорогой пропорциональна коэффициенту сцепления, давлению шины на дорогу и площади пятна контакта. Это именно то, как воспринимает силу сцепления большинство людей. Но здесь зарыта собака – в том, что давление напрямую зависит от площади пятна контакта и обратно пропорционально ему. Об этом нам говорит формула (2). Подставляя сюда выражение для давления, получим:
F = µmgS/S (5)
Тогда площадь мы успешно сокращаем и приходим к закону Амонтона-Кулона (1) и силе сцепления, не зависящей от площади пятна контакта.
Влияние адгезии на коэффициент сцепления
Многие интуитивно полагают, что механизм трения резины объясняется адгезией — её приклеиванием к дорожному покрытию: чем больше площадь соприкосновения, тем больше приклеивание и тем больше сцепление. При этом приклеивание, вроде бы, не очень зависит от прижимающей силы. Действительно, тот же скотч липнет к гладким чистым поверхностям без всякого усилия, обеспечивая великолепное сцепление. Ключевое слово тут – гладкие чистые поверхности. Если поверхность шероховатая и грязная, как асфальт, то скотч будет держать гораздо хуже. На этом эффекте основан принцип защиты поверхностей в городской среде от наклеивания объявлений. И скотч, и объявления не держатся на неровных поверхностях потому, что реальная площадь контакта гораздо меньше площади самого скотча или бумаги. Если материал текучий и его контакт с неровной поверхностью сохраняется достаточно долго, то склеивание будет возможно. Обычная резина – материал мягкий, но не текучий, а времена ее контакта с дорожным полотном довольно малы. В результате, вкладом прилипания в формирование коэффициента трения можно пренебречь. Для желающих разобраться в вопросе самостоятельно, я могу порекомендовать ознакомиться с теориями Гринвуда-Вильямсона и Джонсона-Кендалла-Робертса и последующим развитием теории механики контактного взаимодействия.
В результате, вкладом прилипания в формирование коэффициента трения можно пренебречь. Для желающих разобраться в вопросе самостоятельно, я могу порекомендовать ознакомиться с теориями Гринвуда-Вильямсона и Джонсона-Кендалла-Робертса и последующим развитием теории механики контактного взаимодействия.
Что же касается езды по гоночному треку на спортивных и гоночных шинах, там эффект прилипания шины к поверхности трека может быть более заметным. Отчасти это связано со специфическим составом резины протектора и отчасти – с более высокой температурой, до которой прогреваются шины при гоночной езде. Этот эффект и объясняет, почему коэффициент сцепления гоночных шин может быть заметно больше 1 (у шин в Формуле 1 – около 1,8).
И вот как такой коэффициент сцепления сказывается на практике:
Тормозной путь гоночного болида F1 со скорости 140 км/ч оказался короче на 32 метра, чем обычного дорожного автомобиля, 48 метров против 80, то есть в 1,66 раза короче. Во столько же раз коэффициент сцепления гоночной шины в этом видео больше, чем у дорожной.
Во столько же раз коэффициент сцепления гоночной шины в этом видео больше, чем у дорожной.
Влияние аэродинамической прижимной силы на силу сцепления
Не стоит путать эффект прилипания шин к поверхности трека с эффектом аэродинамической прижимной силы, благодаря которой пилоты Формулы 1 при торможениях, ускорениях и поворотах могут испытывать перегрузки, в несколько раз превышающие величину ускорения свободного падения. А болиды, соответственно, иметь в несколько раз большую динамику торможения и скорость прохождения поворотов, чем обычные дорожные машины. То есть в повороте боковое ускорение величиной 4g (где g – ускорение свободного падения) болиды развивают не за счет прилипания шины и коэффициента сцепления, якобы, в 4 раза большего, чем у дорожных шин, а за счет большой прижимной силы, которая создается антикрыльями на большой скорости и в несколько раз превышает силу тяжести болида.
Увеличенное пятно контакта – спущенные шины
Из практики, площадь пятна контакта можно увеличить, уменьшив давление в шинах. Если спустить шины до 1 атмосферы, то при норме в 2 атмосферы это вдвое меньшее давление и вдвое большая площадь пятна контакта. Так что же, ездовые характеристики машины улучшатся в 2 раза? Конечно же нет и, более того, они ухудшатся. Хотя… тормозной путь уменьшится, но не из-за увеличившегося пятна контакта, а из-за увеличившейся силы трения качения вследствие более мягкой шины и большей ее деформации. А ускорение не станет лучше и будет только хуже – все из-за той же силы трения качения. Ну а в поворотах… машина будет вести себя, как будто водитель сильно пьян 🙂 В общем, не делайте этого – не спускайте шины без необходимости, и, кстати, об этой необходимости…
Если спустить шины до 1 атмосферы, то при норме в 2 атмосферы это вдвое меньшее давление и вдвое большая площадь пятна контакта. Так что же, ездовые характеристики машины улучшатся в 2 раза? Конечно же нет и, более того, они ухудшатся. Хотя… тормозной путь уменьшится, но не из-за увеличившегося пятна контакта, а из-за увеличившейся силы трения качения вследствие более мягкой шины и большей ее деформации. А ускорение не станет лучше и будет только хуже – все из-за той же силы трения качения. Ну а в поворотах… машина будет вести себя, как будто водитель сильно пьян 🙂 В общем, не делайте этого – не спускайте шины без необходимости, и, кстати, об этой необходимости…
Увеличение площади пятна контакта за счет спускания шин реально может помочь, если нужно проехать через какие-то рыхлые, зыбучие места. За счет большей площади контакта с поверхностью уменьшится давление шин на поверхность, а значит, и риск провалиться или увязнуть.
Увеличим ширину шин в 10 раз и спасем мир от ДТП?
Обратный пример, узкие шины мотоцикла не делают его более медленным, чем машина, и, более того, он заметно быстрее ее. Быстрее он по другим причинам, но значительно меньшая ширина шины негативного влияния точно не оказывает.
Быстрее он по другим причинам, но значительно меньшая ширина шины негативного влияния точно не оказывает.
И еще идея – а давайте увеличим ширину шины в 10 раз и тем самым увеличим сцепление в 10 раз, и раз и навсегда решим все проблемы зимней езды, а на асфальте машина вообще будет останавливаться, как вкопанная! И всем всегда будет хватать тормозного пути! Что, вам не нравится эта идея? Правильно, если б все было так просто, это бы давно уже сделали…
В итоге:
увеличение площади пятна контакта => увеличение количества элементов шины, участвующих в зацеплении, и одновременно уменьшение давления шины на дорогу => оба эффекта компенсируют друг друга в равной степени => сцепление шины с дорогой не меняется
Влияет ли ширина шины на площадь пятна контакта?
Более того, увеличив ширину шины, хоть в 10 раз, мы не увеличим площадь пятна контакта, а лишь изменим его форму. Пока вы не закидали меня тухлыми помидорами после этой фразы, я попробую успеть доказать ее :)))
Вспомним, что такое давление – это сила (в нашем случае – сила тяжести, прижимная сила), приходящаяся на единицу площади. Об этом нам говорит формула (2), продублирую ее:
Об этом нам говорит формула (2), продублирую ее:
P = N/S = mg/S (2)
где m – масса тела (шины и части машины, приходящейся на эту шину), а S – площадь соприкосновения тел, то есть, в нашем случае площадь пятна контакта.
Отсюда площадь пятна контакта равна
S = mg/P (6)
То есть площадь пятна контакта шины с дорогой тем больше, чем больше вес машины, приходящийся на эту шину, и чем хуже она накачана. И, конечно, на площадь влияет и жесткость боковин шины. Чем жестче боковины, тем меньше деформируется шина и тем меньше деформируется шина при уменьшении давления воздуха в ней. Хороший пример – современные шины с усиленными боковинами Run Flat, которые даже будучи полностью спущенными могут довезти автомобиль до места назначения, не особо проседая. От ширины шины площадь пятна контакта при одном и том же давлении и одной и той же нагрузке не зависит (в первом приближении).
От ширины шины площадь пятна контакта при одном и том же давлении и одной и той же нагрузке не зависит (в первом приближении).
Ширина шины влияет на форму пятна контакта
Прекрасно! А куда же делась ширина шины??? Очень просто, и тут опять работает принцип «баш на баш». Пятно контакта – следствие деформации шины, которая, в свою очередь, возникает вследствие приложенной сверху силы, то есть cилы тяжести самой шины и автомобиля. Чем шире шина, тем шире пятно контакта, что, казалось бы, должно увеличить площадь пятна. С другой стороны, чем шире шина, тем меньшее давление она оказывает на дорогу и тем меньше деформируется. В итоге, при увеличении ширины профиля шины мы имеем ту же площадь пятна контакта, но более вытянутую по ширине и узкую его форму.
В одном из серьезных научных трудов, который попался мне на глаза за последнее время (Автомобильные шины, диски и ободья, Евзович В.Е., Райбман П.Г.), авторы привели результат эксперимента с тремя шинами, две из которых были одной и той же модели, но разного диаметра ширины:
205/55 R16 с площадью отпечатка 173*143 мм = 247,39 см2
225/45 R17 с площадью отпечатка 185*134 мм = 247,90 см2
Как видим, у более широкой шины пятно более вытянутое и узкое, чем у более узкой шины. При этом в квадратных сантиметрах площадь пятна контакта практически одна и та же.
При этом в квадратных сантиметрах площадь пятна контакта практически одна и та же.
То есть, да, при одном и том же давлении у широкой шины пятно контакта по площади больше, чем у узкой. Но насколько? В данном примере на десятые доли процента, а вообще – максимум на несколько процентов. Теоретически, мы можем поставить на машину вместо шин с шириной профиля 195 мм шины с профилем, скажем, 245 мм. Но на практике это недопустимо по требованиям завода-изготовителя автомобиля. В любом случае, как я писал выше, площадь пятна контакта непосредственно не влияет на силу сцепления, поэтому ни эти доли процента, ни большее увеличение площади (например, за счет снижения давления в шине) погоды нам не сделают.
В итоге:
увеличиваем ширину профиля шины => увеличиваем ширину пятна контакта и одновременно уменьшаем давление шины на дорогу и деформацию шины в зоне контакта => уменьшаем длину пятна контакта => изменяется форма пятна контакта, но не меняется его итоговая площадь (меняется незначительно)
А увеличить площадь пятна контакта можно либо уменьшив давление воздуха в шине, либо увеличив нагрузку на шину сверху.
Сила сцепления шины с дорогой. Итоги
Итак, ширина шины напрямую не влияет на ее сцепление с дорогой по двум причинам:
а) площадь пятна контакта не влияет на сцепление
б) ширина шины не влияет на площадь пятна контакта
Я бы сказал, сила трения имеет «двойную защиту» от ширины шины :)))
Однако ширина шины все же косвенно влияет на силу сцепления, и независимость площади пятна контакта от ширины никак не мешает этому влиянию. Обо всем этом – ниже.
В итоге, сцепление шины с дорогой зависит от:
1) веса, приходящегося на шину, от развесовки автомобиля и динамического перераспределения веса, а значит, и от конструктивных его особенностей – высоты центра тяжести, колесной базы, колеи, подвески, жесткости кузова. Обсуждение этих моментов – отдельная тема и выходит за рамки этой серии статей.
2) коэффициента сцепления (трения покоя). А он, в свою очередь, много от чего зависит, но не от площади пятна контакта! 🙂 Вот параметры, влияющие на величину коэффициента сцепления шины с дорогой, известные мне из университетского курса физики, специальной литературы и из водительского и инструкторского опыта:
- тип и качество дорожного покрытия
- состав резины протектора
- температура шины
- скорость движения автомобиля
- проскальзывание шины
- увод шины
Обо всем этом я подробно напишу в следующих статьях. Кроме того, все эти вопросы мы подробно обсуждаем на курсе безопасного вождения «МВА для водителя: Мастерство Вождения Автомбиля». Конкретно в следующей статье — о влиянии дорожного покрытия, типа протектора шины, рисунка протектора и степени его износа на коэффициент сцепления, а также о зависимости коэффициента сцепления от температуры шины.
Кроме того, все эти вопросы мы подробно обсуждаем на курсе безопасного вождения «МВА для водителя: Мастерство Вождения Автомбиля». Конкретно в следующей статье — о влиянии дорожного покрытия, типа протектора шины, рисунка протектора и степени его износа на коэффициент сцепления, а также о зависимости коэффициента сцепления от температуры шины.
Продолжение следует…
Коэффициент сцепления шин с дорогой: на что влияет.
Автомобильная шина отвечает за безопасность движения. В зависимости от покрытия подбирают варианты резины, обладающие наилучшим сцеплением в конкретных условиях. При выборе нужно учитывать коэффициент сцепления шины с дорогой.
Что такое индекс сцепления шин с дорогой
Одним из важнейших параметров любой авторезины является коэффициент сцепления шины. Он показывает силу, которая противостоит скольжению колеса относительно дорожного покрытия. При этом, параметр равняется силе трения, которая возникает в пятне контакта покрышки с дорогой.
Для дорог с грунтовым или другим неустойчивым покрытием, показатель уровня сцепления может отличаться.
На автошине маркируется словом Traction. Рядом с этим словом проставляется буква, соответствующая конкретному индексу. Всего используется три варианта показателей:
- A – показывает самый лучший уровень для шины этого класса;
- B – средний показатель.
- C – минимально допустимый параметр.
Иногда встречается обозначение «AA». Оно характерно больше для спортивных покрышек, говорит об улучшенном коэффициенте сцепления.
Как измеряется коэффициент шины с дорогой
Стоит разобраться, как рассчитывается и измеряется индекс сцепления шины, обычно он показывается в виде коэффициента. Замеры производятся в строгом соответствии с регламентом, определенным:
- ГОСТ 30413–96;
- ГОСТ Р 50597-93;
- ОДН 218.0.006-2002.
Перед началом работы требуется проверить уровень сцепления самой дороги. Для этого замеряется этот параметр с помощью динамометрического прибора, обязательно перед этим асфальт смачивается.
Непосредственно шина тестируется следующим образом.
- Покрышка накачивается до давления 1,65 кг/см2. Но, если тестируются типы шин с другими требованиями, давление может отличаться.
- Накаченная автошина монтируется на прицеп, имеющий смонтированное измерительное оборудование. Общая масса прицепа 984 кг, соответственно на одну покрышку приходится нагрузка в 492 кг.
- Для проведения теста прицеп буксируют по мокрому асфальту со скоростью 65 км/ч. Далее резко тормозят до блокировки колеса прицепа. В этот момент и замеряют коэффициент сцепления.
Окончательные данные получаются путем расчетов, где учитываются параметры конкретного асфальта, замеренные перед тестом.
В зависимости от многих показателей, таких как загрязненность, температура и прочее, асфальт может оказывать разное влияние на коэффициент сцепления шины.
Как рисунок протектора влияет на индекс сцепления
На практике очень большое значение на индекс сцепления оказывает протектор. Именно от него во многом зависит, насколько будет эффективна шина в сложных дорожных условиях. Рассмотрим несколько примеров.
- Если на улице дождь, дорога будет мокрая. При этом, на асфальте постоянно находится небольшое количество воды. Этого вполне достаточно для эффекта аквапланирования, и снижения сцепления. От того, насколько эффективно будет отводиться вода из пятна контакта, напрямую будет зависеть коэффициент сцепления. Наличие водоотводящих канавок на протекторе значительно улучшает качество работы автошины.
- Ламели, на протекторе также усиливают сцепление. Особенно это проявляется на снегу, обледенелой дороге. Там также образуется пленка воды, ламели эффективно ее отводят, также помогают протекторным блокам плотнее прилегать к покрытию.
- На качество сцепления оказывает влияние и размер блоков протектора.
 Тут нужно учитывать особенности дорожного покрытия, в одних случаях лучший показатель будет у крупных «шашек», в других лучше поведут себя мелкие шины.
Тут нужно учитывать особенности дорожного покрытия, в одних случаях лучший показатель будет у крупных «шашек», в других лучше поведут себя мелкие шины.
Нужно учитывать, что коэффициент сцепления замеряется в сравнении с определенным типом шин и протектора. Для дождевой резины и шин, созданных для сухой дороги, показатель «A» будет разным в условиях, например, дождя.
Как ширина профиля влияет на сцепление шины с дорогой
Среди водителей ходит ошибочное мнение, что ширина покрышки влияет на качество сцепления. Считается, что при большей ширине увеличивается площадь контакта, это и улучшает эффективность сцепления. Это неверно.
Чем шире площадь контакта, тем меньше давление, которое оказывает колесо на квадратный сантиметр дороги. Соответственно сила трения снижается, и сцепление уменьшается.
Уменьшение показателя незначительно. Можно просто его не учитывать, считая, что ширина ската не оказывает влияния на сцепление.
Влияние температуры на сцепление
Температура покрытия оказывает значительное влияние на сцепление. Резина становится мягче или жестче при изменении температурного режима. Тут еще нужно учитывать, что шина сама нагревается при движении.
Резина становится мягче или жестче при изменении температурного режима. Тут еще нужно учитывать, что шина сама нагревается при движении.
В общих чертах можно сказать, что для зимней авторезины, при понижении температуры от +5° до -15° коэффициент будет увеличиваться, а при более низких температурах уменьшаться. Для летней резины схожий процесс будет наблюдаться при увеличении температуры до +30°, после чего показатель станет снижаться.
Коэффициент сцепления шины важный параметр, оказывающий влияние на безопасность движения. Он указывается на боковине каждой покрышке, но водителю нужно помнить, что на практике сцепление отличается от полученных на тестах результатов.
Сцепление шин — Racecar Engineering
Как только мы поймем, как работает резина, нам нужно понять, как создается сцепление шин. ПРЕДОСТАВЛЕНИЕ: XPB Сцепление определяется как коэффициент трения между поверхностью шины и поверхностью гоночной трассы.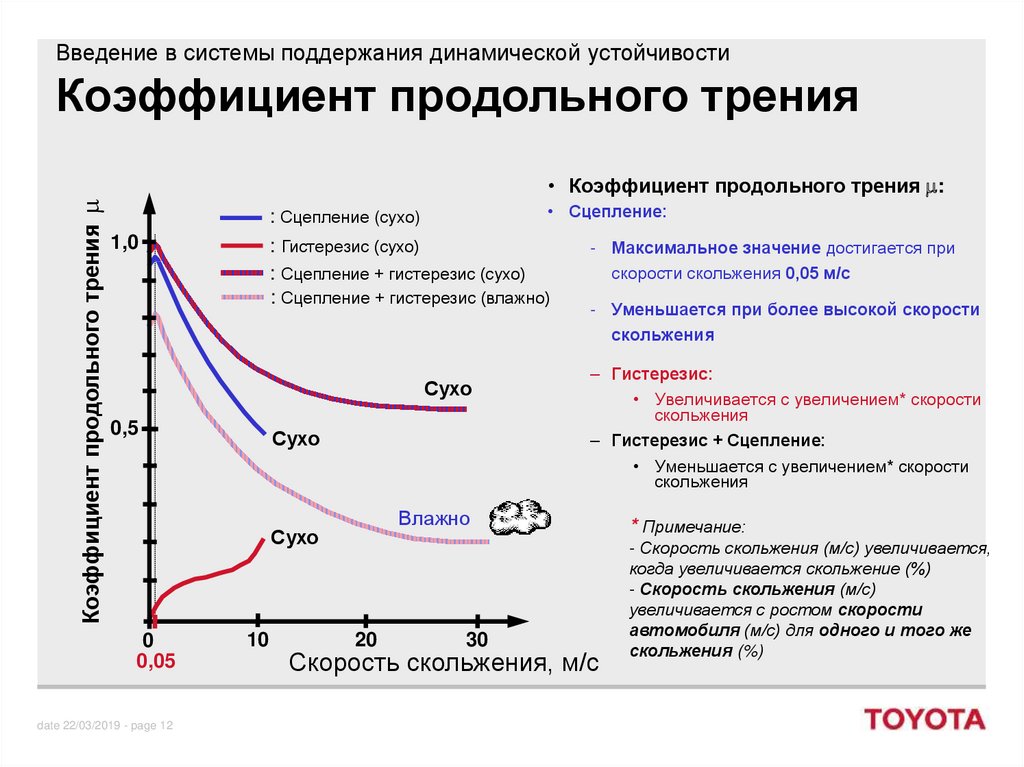 Это трение зависит от множества факторов, включая шероховатость трассы, а также тип, температуру и, следовательно, поведение резины шины. Эти факторы в конечном итоге влияют на деформируемость и вязкость резины шины, которые наряду с гистерезисом шины являются ключевыми факторами в обеспечении сцепления с дорогой.
Это трение зависит от множества факторов, включая шероховатость трассы, а также тип, температуру и, следовательно, поведение резины шины. Эти факторы в конечном итоге влияют на деформируемость и вязкость резины шины, которые наряду с гистерезисом шины являются ключевыми факторами в обеспечении сцепления с дорогой.
Шина создает сцепление за счет двух типов механизмов напряжения:
- Вдавливание
- Молекулярная адгезия
Здесь резиновый материал возбуждается неровностями дорожного покрытия. Поскольку резина шин является вязкоупругой, она искажается и адаптируется к текстуре дорожного покрытия при скольжении по нему. Поэтому при наезде на неровность дороги блок протектора деформируется, но из-за гистерезиса резины не сразу возвращается к исходной форме. Эта асимметричная деформация резины создает силу реакции, противодействующую проскальзыванию, другими словами, создает силу трения (сцепления).
Мишлен. (2001). Шина – сцепление. [Онлайн]. Доступно по адресу: http://www.dimnp.unipi.it/guiggiani-m/Michelin_Tire_Grip.pdf (дата обращения: 01.02.20)
Шина – сцепление. [Онлайн]. Доступно по адресу: http://www.dimnp.unipi.it/guiggiani-m/Michelin_Tire_Grip.pdf (дата обращения: 01.02.20)Мы можем визуализировать углубление, используя аналогию с пружиной и демпфером, описанную в разделе «Как работает резина шины». . Когда резина ударяется о неровность, пружина и демпфер сжимаются, но вязкость масла внутри демпфера сопротивляется смещению, что приводит к выделению тепла. После удара, когда нагрузка снята, накопленное в демпфере сопротивление толкает поршень назад, но не в исходное положение. Гистерезис демпфера и потеря энергии в виде тепла приводят к асимметричной деформации резины, которая создает тангенциальную силу X , как показано на схеме выше.
Вмятина возникает, когда резина шины контактирует с неровностями дороги размером от нескольких миллиметров (макротекстура) до нескольких микрон (микротекстура), и таким образом сохраняется сцепление на мокрой дороге.
Молекулярная адгезия Здесь происходит молекулярное взаимодействие на границе между резиной шины и поверхностью дороги, которое создает сцепление. По сути, молекулярные цепи резины образуют связи (или связи Ван-дер-Ваальса) с дорожным покрытием 9.0003 (1) . По мере того, как шина продолжает скользить по поверхности, эти цепи растягиваются, и вязкость резины (показана на примере поршня в аналогии с пружиной и демпфером) сопротивляется деформации, создавая силу трения X (сцепление), которая препятствует проскальзыванию (2) . Затем связь разрывается (3) и снова формируется дальше. Таким образом, молекулярные цепи каучука следуют этому циклу растяжения и разрыва, что создает вязкоупругую работу. Эта работа фактически умножает количество энергии связи на коэффициент, который зависит от температуры резины и скорости проскальзывания.
По сути, молекулярные цепи резины образуют связи (или связи Ван-дер-Ваальса) с дорожным покрытием 9.0003 (1) . По мере того, как шина продолжает скользить по поверхности, эти цепи растягиваются, и вязкость резины (показана на примере поршня в аналогии с пружиной и демпфером) сопротивляется деформации, создавая силу трения X (сцепление), которая препятствует проскальзыванию (2) . Затем связь разрывается (3) и снова формируется дальше. Таким образом, молекулярные цепи каучука следуют этому циклу растяжения и разрыва, что создает вязкоупругую работу. Эта работа фактически умножает количество энергии связи на коэффициент, который зависит от температуры резины и скорости проскальзывания.
Молекулярная адгезия является причиной того, что шина откладывает резину на гоночной трассе. Молекулярные связи могут либо оторваться от гусеницы (как объяснялось выше), либо оторваться от шины, и в этом случае молекулы каучука эффективно отрываются от шины и остаются на поверхности гусеницы.
Молекулярные связи могут либо оторваться от гусеницы (как объяснялось выше), либо оторваться от шины, и в этом случае молекулы каучука эффективно отрываются от шины и остаются на поверхности гусеницы.
Эти куски резины могут либо откладываться на гоночной трассе, что увеличивает сцепление с трассой, поскольку в этом случае шины контактируют с резиной на трассе, а не только на трассе. Или, если температура высока и состав шины ухудшается, резина может откладываться в виде больших шариков, которые разлетаются по гоночной трассе, что снижает сцепление с дорогой.
Молекулярная адгезия — это механизм износа шин, приводящий к отложению резины или шарикам в автономном режиме. КРЕДИТ: XPBКлючевой момент
Захват создается за счет
1) Вдавливания и 2) Молекулярной адгезии . Оба эти механизма зависят от гистерезиса, деформируемости и вязкости каучука. Вмятина — это место, где неровности трассы воздействуют на резину шины. В то время как молекулярная адгезия — это то, где происходит взаимодействие между резиной шины и гоночной трассой.
- БИРКИ
- Сцепление для шин
- Резина для шин
Джемма Хаттон — Заместитель редактора
Джемма имеет степень бакалавра технических наук в области машиностроения в Университете Бата и степень магистра в области передовых инженеров в области автоспорта в Университете Крэнфилда. Она работала на трассе в BTCC, GT и F1 в качестве инженера по шинам в Pirelli, а затем в Manor F1. Она пишет для Racecar с 2010 года, используя свой инженерный опыт для изучения современных технологий автоспорта.
Динамика шин — Racecar Engineering
Теперь мы понимаем, как создается сцепление шин, следующий вопрос: как это влияет на динамику шины? ПРЕДОСТАВЛЕНИЕ: XPBДиаграмма, иллюстрирующая угол скольжения. Балквилл, Дж. (2017) Performance Vehicle Dynamics Угол скольжения Чтобы полностью понять динамику шин, первое, что вам нужно понять, это угол скольжения. Он определяется как угол (в градусах), образованный между фактическим направлением движения колеса и «указывающим» направлением колеса (перпендикулярно оси вращения). Есть всегда угол между ними, когда гоночный автомобиль испытывает боковое ускорение.
Он определяется как угол (в градусах), образованный между фактическим направлением движения колеса и «указывающим» направлением колеса (перпендикулярно оси вращения). Есть всегда угол между ними, когда гоночный автомобиль испытывает боковое ускорение.
На приведенной выше диаграмме показано, как элементы в пятне контакта смещены в соответствии с направлением движения. Затем эти элементы возвращаются в нейтральное состояние по направлению к задней части пятна контакта по мере уменьшения силы реакции.
Избыточная поворачиваемость — это когда угол увода задних шин больше, чем угол увода передних шин в повороте. ПРЕДОСТАВЛЕНИЕ: XPBТипичная тенденция зависимости угла скольжения от поперечной силы — явный пик поперечной силы можно увидеть примерно при шести градусах угла скольжения. Балквилл, Дж. (2017) Performance Vehicle Dynamics Всякий раз, когда вводится угол увода, пятно контакта деформируется, поскольку на шину действуют боковые силы. Эта деформация вызывает напряжение (удлинение) в молекулярной структуре резины шины. Кроме того, эластичность резиновой смеси противостоит этому напряжению, которое создает силу, перпендикулярную оси вращения. Этот цикл растяжения-расслабления, который шина повторяет при каждом обороте, также создает внутреннее трение и, следовательно, тепло внутри шины; увеличение сцепления шин. Это увеличивается до тех пор, пока резина шины не переработается, и сцепление резко не уменьшится, что также известно как «обрыв».
Кроме того, эластичность резиновой смеси противостоит этому напряжению, которое создает силу, перпендикулярную оси вращения. Этот цикл растяжения-расслабления, который шина повторяет при каждом обороте, также создает внутреннее трение и, следовательно, тепло внутри шины; увеличение сцепления шин. Это увеличивается до тех пор, пока резина шины не переработается, и сцепление резко не уменьшится, что также известно как «обрыв».
Фундаментальная мера способности шины к сцеплению в поперечном направлении известна как жесткость на поворотах. Это выражается как сила, создаваемая на градус угла скольжения (Н/°). При заданном угле увода шина с более высокой жесткостью на поворотах будет производить большее поперечное ускорение, и это ключевой показатель производительности любой шины.
Коэффициент скольжения Понятие угла скольжения применяется только при описании производства поперечной силы. В продольном смысле это известно как коэффициент скольжения. Коэффициент скольжения аналогичен углу скольжения, но измеряется не угловым смещением, а относится к величине проскальзывания шины относительно условий скольжения. Например, коэффициент скольжения, равный 0, означает, что шина свободно катится, а коэффициент, равный 1, означает, что шина потеряла сцепление с дорогой. Общей тенденцией, наблюдаемой в шинах, является пик продольной силы при коэффициенте скольжения около 0,3–0,4.
В продольном смысле это известно как коэффициент скольжения. Коэффициент скольжения аналогичен углу скольжения, но измеряется не угловым смещением, а относится к величине проскальзывания шины относительно условий скольжения. Например, коэффициент скольжения, равный 0, означает, что шина свободно катится, а коэффициент, равный 1, означает, что шина потеряла сцепление с дорогой. Общей тенденцией, наблюдаемой в шинах, является пик продольной силы при коэффициенте скольжения около 0,3–0,4.
Последним фундаментальным принципом динамики шин, который необходимо понять, является круг трения или диаграмма g-g. Круг трения графически иллюстрирует пределы шины, генерирующей одновременно продольное и поперечное ускорение, и позволяет понять, как транспортное средство движется относительно этого.
В действительности диаграмма g-g напоминает эллипс, а не идеальный круг, но из этого можно извлечь урок: очевидно, что водитель не может рассчитывать на такой же уровень бокового ускорения, генерируемого в чистом повороте, в то время как требуется ускорение/торможение, и наоборот.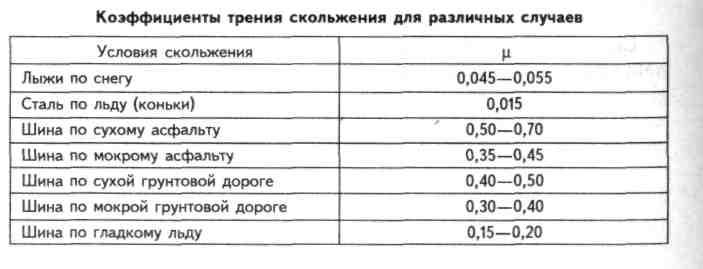 В практическом смысле это означает, что нельзя тормозить или ускоряться при попытке достичь максимальной скорости прохождения поворотов. Точно так же не следует вводить боковое ускорение при попытке достичь максимального усилия торможения или ускорения, иначе можно ожидать потери сцепления с дорогой.
В практическом смысле это означает, что нельзя тормозить или ускоряться при попытке достичь максимальной скорости прохождения поворотов. Точно так же не следует вводить боковое ускорение при попытке достичь максимального усилия торможения или ускорения, иначе можно ожидать потери сцепления с дорогой.
Такие методы, как «торможение по следу», появились именно для того, чтобы максимизировать усилие трения шины и обеспечить максимально возможное нахождение гоночного автомобиля на «крае» круга трения.
Круг трения или gg-биграмма суперкара V8. ПРЕДОСТАВЛЕНИЕ: ChassisSim Коэффициент трения — «Mu» График CoF в зависимости от силы реакции, показывающий непропорциональность их соотношения. Эти данные взяты с одноместного автомобиля FSAE. Балквилл, Дж. (2017) Performance Vehicle DynamicsКоэффициент трения (CoF), иногда называемый mu (μ), связывает силу трения с силой реакции между двумя контактирующими объектами.
Важно понимать, что CoF не увеличивается пропорционально увеличению силы реакции (вертикальной нагрузки на шину).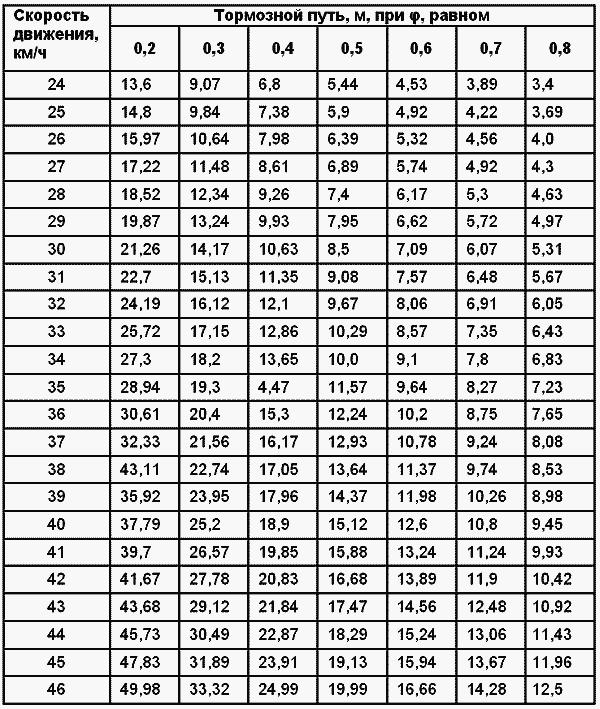 Другими словами, удвоение силы реакции не удваивает CoF и, следовательно, не удваивает уровень сцепления шины с дорогой.
Другими словами, удвоение силы реакции не удваивает CoF и, следовательно, не удваивает уровень сцепления шины с дорогой.
Это становится важным для динамики гоночного автомобиля для понимания уровней сцепления, когда сила реакции неравномерно распределяется между левой и правой или передней и задней частью автомобиля из-за переноса веса.
Представьте себе пятно контакта в виде матрицы дискретных элементов. Более широкая шина снижает контактное давление на каждом элементе для данной массы автомобиля, что увеличивает коэффициент трения. При этом каждый элемент шины способен генерировать чуть меньшую силу, но этот баланс перевешивается наличием большего количества элементов (площадь контакта). Результатом является чистое увеличение сцепления шин. Это также объясняет, почему в автоспорте часто используются самые большие шины в поисках производительности.
Внешние факторы, влияющие на сцепление На уровень сцепления влияют не только внутренние факторы, присущие конкретной шине, такие как резиновая смесь и конструкция. Есть также ряд внешних факторов, которые также влияют на CoF между шиной и дорогой. Следует понимать, что они влияют на определенные динамические характеристики шины в гоночном автомобиле через шину.
Есть также ряд внешних факторов, которые также влияют на CoF между шиной и дорогой. Следует понимать, что они влияют на определенные динамические характеристики шины в гоночном автомобиле через шину.
Температура резиновой смеси шины влияет на сцепление, увеличивая соответствие и проникновение пиков и впадин на дороге в пятно контакта. Это также увеличивает скорость химической реакции между резиной шины и асфальтом, но только до определенного момента, после которого шина «сойдет» и уровень сцепления с дорогой уменьшится.
Давление накачивания Из-за гибкости резины шин давление накачивания вызывает деформацию контактной поверхности в диапазоне от вогнутого профиля (низкое давление) до выпуклого профиля (высокое давление). Это влияет на площадь поверхности пятна контакта. Где-то посередине находится плоский профиль, обеспечивающий максимальную площадь контакта и оптимальное сцепление. Это цель динамиста.
Где-то посередине находится плоский профиль, обеспечивающий максимальную площадь контакта и оптимальное сцепление. Это цель динамиста.
Интересно, что иногда, если команды борются за температуру шин, они повышают давление в шинах, что приводит к выпуклому профилю и очень узкому пятну контакта. Это пятно контакта нагревается быстрее, а затем распространяется на остальную часть шины, повышая ее общую температуру.
Однако важно понимать свойства газа в том смысле, что для заданного объема, если температура увеличивается, то растет и давление, что приводит к комбинированному эффекту как снижения адгезии, так и уменьшения площади пятна контакта.
Состояние гусеницыНа уровень сцепления влияют такие переменные, как шероховатость поверхности гусеницы, мокрая гусеница, пыльная гусеница.
Шероховатость поверхности может быть описана микро- и макрошероховатостью. Michelin. (2001). Шина – сцепление. [Онлайн]. Доступно по адресу: http://www. dimnp.unipi.it/guiggiani-m/Michelin_Tire_Grip.pdf (Проверено 27 января 2020 г.)
dimnp.unipi.it/guiggiani-m/Michelin_Tire_Grip.pdf (Проверено 27 января 2020 г.)В целом, при поиске максимальной жесткости на поворотах CoF всегда должен быть максимальным. Вот почему колеса, шасси подвески и настройка являются жизненно важными инструментами, которые могут помочь настроить сцепление шин. Все эти и другие темы будут раскрыты в нашей новой серии статей о динамике гоночных автомобилей.
Джахи Кэмпбелл-Бреннан — участник
https://www.waveydynamics.com
Джахи — высококвалифицированный инженер, который руководит собственной консультационной компанией Wavey Dynamics, которая специализируется на динамике транспортных средств, гоночной технике, трансмиссии и аэродинамике в автоспорте и автомобилестроении.
Оценка коэффициента сцепления с дорогой в различных дорожных условиях на основе динамики торможения автомобиля | Китайский журнал машиностроения
- Оригинальный артикул
- Открытый доступ
- Опубликовано:
- You-Qun Zhao 1 ,
- Hai-Qing Li 1 ,
- Fen Lin 1 ,
- Jian Wang 2 &
- jian Wang 2 & 9012 …
- 11111111111111111111111111111111111111111111111111111111111111111111119.
Китайский журнал машиностроения том 30 , страницы 982–990 (2017)Цитировать эту статью
34 тыс. обращений
29 цитирований
2 Альтметрика
Сведения о показателях
Abstract
Точная оценка коэффициента сцепления с дорогой в системе управления активной безопасностью становится все более важной.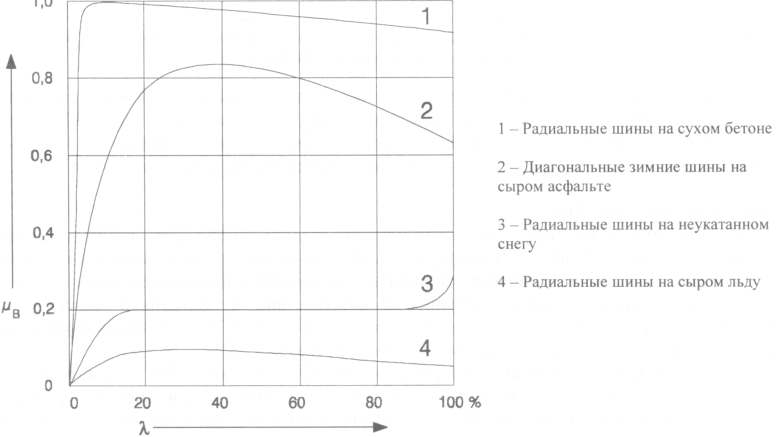 В большинстве предыдущих исследований по оценке сцепления с дорожным покрытием использовалась только продольная или поперечная динамика транспортного средства и часто игнорировалась передача нагрузки, что приводило к неточным результатам фактического коэффициента сцепления с дорожным покрытием. Предложен новый метод, учитывающий передачу нагрузки на переднюю и заднюю оси для оценки коэффициента сцепления с дорожным покрытием на основе динамической модели торможения двухколесного транспортного средства. Техника управления режимом скольжения используется для создания идеального регулятора тормозного момента, целью которого является контроль фактического коэффициента проскальзывания передних и задних колес, отслеживая идеальный коэффициент проскальзывания колес. Чтобы устранить проблему вибрации контроллера скользящего режима, для проектирования поверхности скользящего режима используется интегральная поверхность переключения. Линейный наблюдатель расширенного состояния второго порядка предназначен для наблюдения за коэффициентом сцепления с дорогой на основе скорости вращения колес и тормозного момента передних и задних колес.
В большинстве предыдущих исследований по оценке сцепления с дорожным покрытием использовалась только продольная или поперечная динамика транспортного средства и часто игнорировалась передача нагрузки, что приводило к неточным результатам фактического коэффициента сцепления с дорожным покрытием. Предложен новый метод, учитывающий передачу нагрузки на переднюю и заднюю оси для оценки коэффициента сцепления с дорожным покрытием на основе динамической модели торможения двухколесного транспортного средства. Техника управления режимом скольжения используется для создания идеального регулятора тормозного момента, целью которого является контроль фактического коэффициента проскальзывания передних и задних колес, отслеживая идеальный коэффициент проскальзывания колес. Чтобы устранить проблему вибрации контроллера скользящего режима, для проектирования поверхности скользящего режима используется интегральная поверхность переключения. Линейный наблюдатель расширенного состояния второго порядка предназначен для наблюдения за коэффициентом сцепления с дорогой на основе скорости вращения колес и тормозного момента передних и задних колес.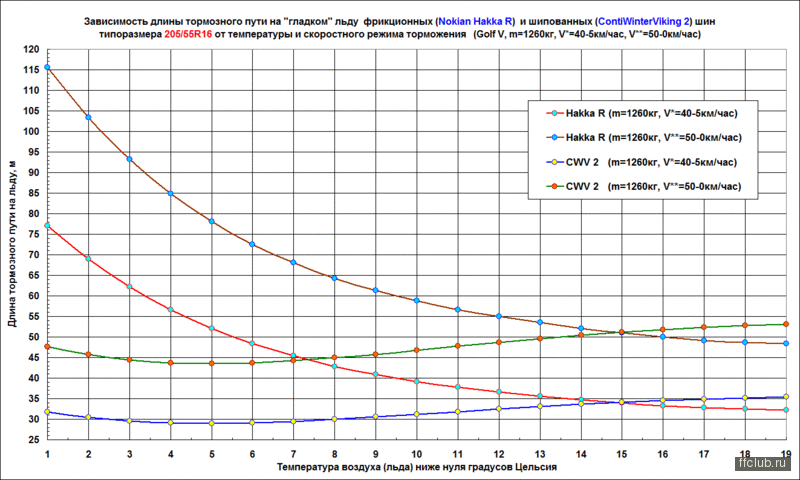 Предлагаемые схемы оценки коэффициента сцепления с дорогой оцениваются путем моделирования в ADAMS/Car. Результаты показывают, что оценочные значения могут хорошо совпадать с фактическими значениями в различных дорожных условиях. Наблюдатель может точно в режиме реального времени оценить коэффициент сцепления с дорожным покрытием и противостоять внешнему возмущению. Предлагаемое исследование обеспечивает новый метод оценки коэффициента сцепления с дорогой с высокой надежностью и большей точностью.
Предлагаемые схемы оценки коэффициента сцепления с дорогой оцениваются путем моделирования в ADAMS/Car. Результаты показывают, что оценочные значения могут хорошо совпадать с фактическими значениями в различных дорожных условиях. Наблюдатель может точно в режиме реального времени оценить коэффициент сцепления с дорожным покрытием и противостоять внешнему возмущению. Предлагаемое исследование обеспечивает новый метод оценки коэффициента сцепления с дорогой с высокой надежностью и большей точностью.
Введение
Это мощное средство для повышения безопасности вождения и устойчивости автомобиля с помощью систем активной безопасности, таких как предотвращение аварийных столкновений (ECA), активное переднее рулевое управление (AFS), антиблокировочная тормозная система (ABS), прямой момент рыскания. контроль (DYC) и противобуксовочная система (TCS) [1,2,3,4,5,6]. Они хорошо работают только с силами в шинах в пределах предела трения, что означает, что знание коэффициента сцепления с дорогой может улучшить работу систем. Например, в процессе рулевого управления боковая сила на шину ограничивается коэффициентом сцепления с дорогой. Транспортное средство может занести, если транспортное средство резко поворачивается на относительно высокой скорости из-за ограничения поперечной силы на шину. Если бы активная система управления могла оценить ограничение трения в момент, когда водитель начинает рулить и предпринимает меры по снижению скорости, поперечная динамика транспортного средства была бы улучшена [4]. При торможении колес в различных дорожных условиях мы, как правило, не можем получить в реальном времени значение коэффициента сцепления с дорогой, что приводит к нестабильности всего процесса управления [7, 8]. Таким образом, коэффициент сцепления с дорогой имеет важное значение в конструкции электронной системы управления шасси транспортного средства. Точная оценка коэффициента сцепления с дорожным покрытием может способствовать совершенствованию системы активной безопасности и повышению эффективности работы систем безопасности транспортных средств.
Например, в процессе рулевого управления боковая сила на шину ограничивается коэффициентом сцепления с дорогой. Транспортное средство может занести, если транспортное средство резко поворачивается на относительно высокой скорости из-за ограничения поперечной силы на шину. Если бы активная система управления могла оценить ограничение трения в момент, когда водитель начинает рулить и предпринимает меры по снижению скорости, поперечная динамика транспортного средства была бы улучшена [4]. При торможении колес в различных дорожных условиях мы, как правило, не можем получить в реальном времени значение коэффициента сцепления с дорогой, что приводит к нестабильности всего процесса управления [7, 8]. Таким образом, коэффициент сцепления с дорогой имеет важное значение в конструкции электронной системы управления шасси транспортного средства. Точная оценка коэффициента сцепления с дорожным покрытием может способствовать совершенствованию системы активной безопасности и повышению эффективности работы систем безопасности транспортных средств.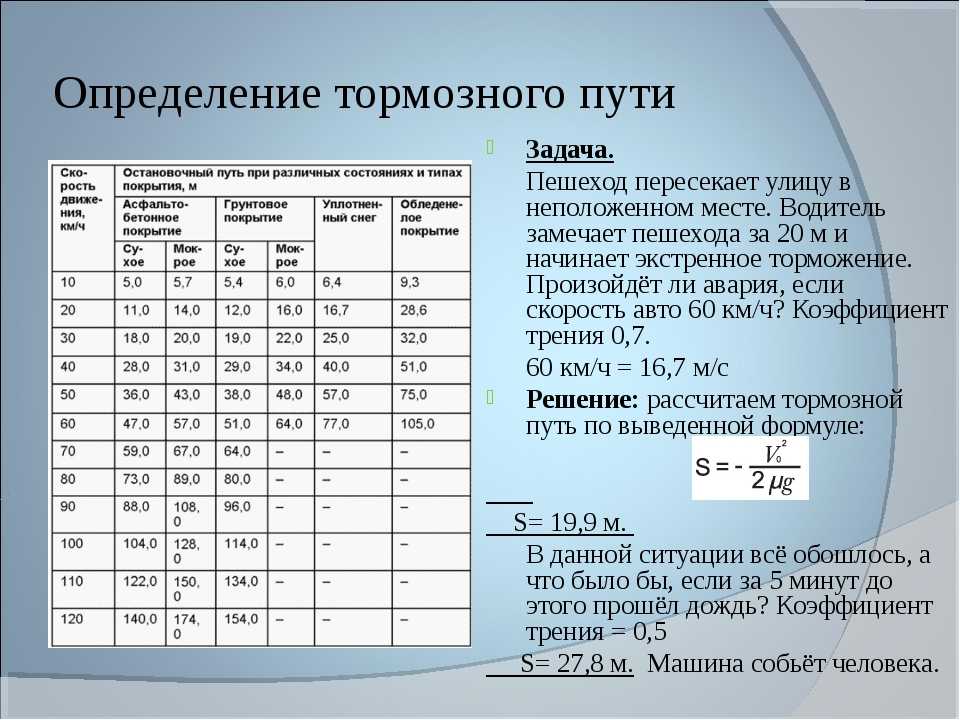 Система активной безопасности может автоматически корректировать стратегию управления в соответствии с изменением дорожных покрытий в отношении свойств трения, что может максимизировать функционирование системы управления.
Система активной безопасности может автоматически корректировать стратегию управления в соответствии с изменением дорожных покрытий в отношении свойств трения, что может максимизировать функционирование системы управления.
В последние годы для получения коэффициента сцепления с дорогой многие ученые предложили различные методы оценки [8,9,10,11,12,13,14,15,16,17,18,19,20,21]. Среди них отечественные ученые, особенно Лян Л.И. и их коллективы, использовали метод слияния сигналов [8, 9], метод двойного кубатурного фильтра Калмана [10] и наблюдатель [11] для оценки коэффициента сцепления с дорогой. Вообще говоря, они в основном подразделяются на две группы: методы, основанные на использовании специальных датчиков [12,13,14], и методы, основанные на динамике транспортного средства, также известные как основанные на причине и на основе следствия [15]. Метод причины использовался оптическими датчиками для измерения поглощения и рассеяния света на дороге в соответствии с формой дорожного покрытия и физическими свойствами. Этот метод выглядит простым и прямым, но имеет практическую проблему стоимости, что ограничивает его использование в серийных автомобилях. Метод, основанный на эффектах, был представлен путем измерения соответствующего отклика модели динамики транспортного средства и применения расширенной фильтрации Калмана или другого алгоритма для получения его значения. Модель динамики транспортного средства включала как продольную, так и поперечную динамику [16, 17]. Основные особенности этих методов позволяют в полной мере использовать бортовые датчики и снизить затраты, что широко используется.
Этот метод выглядит простым и прямым, но имеет практическую проблему стоимости, что ограничивает его использование в серийных автомобилях. Метод, основанный на эффектах, был представлен путем измерения соответствующего отклика модели динамики транспортного средства и применения расширенной фильтрации Калмана или другого алгоритма для получения его значения. Модель динамики транспортного средства включала как продольную, так и поперечную динамику [16, 17]. Основные особенности этих методов позволяют в полной мере использовать бортовые датчики и снизить затраты, что широко используется.
Два очень похожих исследования [18, 19] использовали фильтр Калмана (KF) для оценки продольной силы транспортного средства сначала, а затем с помощью рекурсивного метода наименьших квадратов (RLS) и изменения CUSUM для оценки коэффициента сцепления с дорогой. Венцель и др. [20] сообщил о другом методе двойного расширенного фильтра Калмана (DEKF) для оценки коэффициента сцепления с дорогой. Сравнение алгоритма фильтра Калмана и расширенного алгоритма фильтрации Калмана, Ref. [21] разработали наблюдатель расширенного состояния (ESO) с помощью модели динамики 1/4 шины для торможения для оценки коэффициента сцепления с дорогой. Этот метод может обеспечить высокую точность вычислений и не требует решения якобиана.
[21] разработали наблюдатель расширенного состояния (ESO) с помощью модели динамики 1/4 шины для торможения для оценки коэффициента сцепления с дорогой. Этот метод может обеспечить высокую точность вычислений и не требует решения якобиана.
В данной статье с учетом передачи нагрузки на переднюю и заднюю оси построена динамическая модель торможения двухколесного транспортного средства. Метод управления режимом скольжения был использован для создания идеального регулятора тормозного момента, целью которого является управление фактическим коэффициентом проскальзывания передних и задних колес, отслеживая идеальный коэффициент проскальзывания колес. Чтобы устранить проблему вибрации контроллера скользящего режима, для проектирования поверхности скользящего режима была использована интегральная поверхность переключения. Коэффициент сцепления с дорогой можно наблюдать в линейном расширенном состоянии второго порядка на основе скорости вращения колес и тормозного момента передних и задних колес. По сравнению с обсуждаемой статьей, этот метод учитывал влияние передачи осевой нагрузки на оценку коэффициента сцепления с дорогой. Он имеет как меньшее количество учитываемых параметров, так и более высокую вычислительную эффективность.
По сравнению с обсуждаемой статьей, этот метод учитывал влияние передачи осевой нагрузки на оценку коэффициента сцепления с дорогой. Он имеет как меньшее количество учитываемых параметров, так и более высокую вычислительную эффективность.
Модель динамики торможения транспортного средства
Модель полного транспортного средства
Допущения для модели транспортного средства следующие: (1) пренебрегать влиянием уклона дороги; (2) не учитывать передачу нагрузки боковыми ускорениями; (3) Влиянием сопротивления воздуха и сопротивления качению шины пренебрегают; (4) Не обращайте внимания на влияние системы трансмиссии, системы рулевого управления и подвески на транспортное средство. Модель автомобиля, представленная здесь, представляет собой модель двухколесного автомобиля с эскизом, приведенным на рис. 1.
Рис. 1Модель двухколесного транспортного средства. ч ф , ч r —Высота автомобиля спереди, сзади по неподрессоренной массе, л ф , л r ψ —Расстояние между центром тяжести и передней и задней осями, F з ф , ф z r — Вертикальные силы передней и задней шин транспортного средства, м ж, м r —Передняя, задняя неподрессоренные массы, х —Водоизмещение в процессе, м s —Подрессоренная масса автомобиля, ч s — Высота подрессоренной массы автомобиля
Изображение в натуральную величину
Из рис. 1 продольное и рысканье тела можно описать соответственно уравнениями (1)–(4) следующим образом:
1 продольное и рысканье тела можно описать соответственно уравнениями (1)–(4) следующим образом:
$$\dot{x} = V,$$
(1)
$$\dot{V} = — g\frac{{\mu (\lambda_ {\text{f}} )m_{1} + \mu (\lambda_{\text{r}} )m_{2} }}{{m — \mu (\lambda_{\text{f}} )m_ {3} + \mu (\lambda_{\text{r}} )m_{3} }},$$
(2)
$$\dot{\omega}_{\text{f}} = \frac{1}{{2J _{\text{f}} }}( — T_{\text{bf}} + \mu (\lambda _{\text{f}} )m_{1} R_{{{\ omega }}} g — \mu (\lambda_{\text{f}} )m_{3} R_{{{\omega }}} \ddot{x}),$$
(3)
$$\dot{\omega}_{\text{r}} = \frac{1}{{2J _{\text{r}}}}( — T_{\text{br} } + \mu (\lambda_{\text{r}} )m_{2} R_{{{\omega }}} g + \mu (\lambda_{\text{r}} )m_{3} R_{{ {\omega }}} \ddot{x}),$$
(4)
, где
$$m_{1} = \frac{{l_{\text{r}}}}{{l_{ \text{f}} + l_{\text{r}} }}m\;,\;m_{2} = \frac{{l_{\text{f}} }}{{l_{\text{f }} + l _ {\ text {r}} }} m \ ;, \; m_ {3} = \ frac {{m _ {\ text {f}} h _ {\ text {f}} + m _ {\ text { s}} h _ {\ text {s}} + m _ {\ text {r}} h _ {\ text {r}} }} {{l _ {\ text {f}} + l _ {\ text {r}}} },$$
где µ ( λ f ) и µ ( λ r ) – коэффициент сцепления передних и задних колес с дорогой, m – полная масса автомобиля, V – продольная скорость автомобиля, T бф и Т br — тормозной момент передних и задних колес, Дж f и J r – моменты инерции передних и задних колес, ω f и ω r — угловая скорость передних и задних колес, R ω — радиус качения колеса.
Полноприводная модель
Усилие на шину настолько важно, что влияет на точность моделирования. Модель шины должна отражать влияние вертикальной силы шины на продольные и поперечные силы, а также взаимодействие продольных и поперечных сил. Для прогнозирования продольной силы транспортного средства в условиях торможения модель Буркхардта вводится путем теоретического деформационного и имитационного анализа на основе модели Magic Formula [22, 23]. Он обеспечивает коэффициент трения шины-дороги \(\mu\) в зависимости от проскальзывания колеса \(\лямбда\) и скорости автомобиля \(V\). Уравнение можно описать как
$$\mu (\lambda ,V) = \left( {C_{1} (1 — \exp (C_{2} \lambda )) — C_{3} \lambda )} \right)\exp ( — C_{4} \lambda V),$$
(5)
где C 1 , С 2 и С 3 – характеристические параметры сцепления шин; С 4 – параметр влияния скорости автомобиля на сцепление и находится в пределах 0,02–0,04. В таблице 1 показаны параметры модели трения для различных дорожных условий.
В таблице 1 показаны параметры модели трения для различных дорожных условий.
Полная таблица
На рис. 2 показана зависимость коэффициента сцепления с дорогой от коэффициента скольжения при различных дорожных условиях.
Рис. 2Зависимость коэффициента сцепления с дорогой от коэффициента скольжения
Изображение полного размера
Как видно из рисунка, модель шины Burckhardt хорошо описывает нелинейный закон изменения коэффициента сцепления с дорогой в зависимости от скорости проскальзывания колеса. .
Конструкция контроллера тормозного момента
Конструкция тормозного момента
Коэффициент продольного скольжения передних и задних колес можно описать как.
$$\lambda_{\text{f}} = \frac{{V — \omega_{\text{f}} R_{\omega}}}}{V},$$
(6)
$ $\lambda_{\text{r}} = \frac{{V — \omega_{\text{r}} R_{\omega } }}{V},$$
(7)
, где λ f и λ r обозначает соответственно коэффициент продольного скольжения переднего и заднего колеса и производную от него по времени соответственно.
$$\dot{\lambda}_{\text{f}} = \frac{{\dot{V}(1 — \lambda_{\text{f}} ) — \dot{\omega}_{ \text{f}} R_{\omega} }}{V},$$
(8)
$$\dot{\lambda}_{\text{r}} = \frac{{\dot{ V}(1 — \lambda_{\text{r}}) — \dot{\omega}_{\text{r}} R_{\omega}}}}{V}.$$
(9)
Подставляя уравнения. (8), (9) в уравнение динамики автомобиля, тогда
$$\dot{V} = f_{2} (\lambda_{\text{f}} ,\lambda_{\text{r}} ),$ $
(10)
$ $ \ dot {\ lambda} _ {\ text {f}} = \ frac {{f_ {2} (\ lambda _ {\ text {f}} , \ lambda _ {\ text { r}} )(1 — \lambda_{\text{f}} ) — R_{\omega} f_{3} (\lambda_{\text{f}} ,\lambda_{\text{r}} ) + u_ {\text{f}} }}{V}, $$
(11)
$$\dot{\lambda}_{\text{r}} = \frac{{f_{2} (\lambda_{\text{f}} ,\lambda_{\text{r }} )(1 — \lambda_{\text{r}} ) — R_{\omega} f_{4} (\lambda_{\text{f}} ,\lambda_{\text{r}} ) + u_{ \text{r}} }}{V},$$
(12)
где
$$f_{2} (\lambda_{\text{f}} ,\lambda_{\text{r}} ) = — g \ frac {{\ mu (\ lambda _ {\ text {f}} ) m_ {1} + \ mu (\ lambda _ {\ text {r}} ) m_ {2} }} {{m — \ mu (\lambda_{\text{f}} )m_{3} + \mu (\lambda_{\text{r}} )m_{3} }},$$
$$f_{3} (\lambda_ {\ text {f}} , \ lambda _ {\ text {r}} ) = \ frac {1} {{2J _ {\ text {f}} }} (\ mu (\ lambda _ {\ text {f}} ) m_{1} R_{\omega } g — \mu (\lambda _{\text{f}} )m_{3} R_{\omega } f_{2} ),$$
$$f_{4} (\lambda_{\text{f}} ,\lambda_{\text{r}} ) = \frac{1}{{2J _{\text{r}} }}(\mu (\lambda_{r} )m_{2} R_{\omega} g + \mu (\lambda_{\text{r}} )m_{3} R_{\omega} f_{2} ),$$
$$u_{\text{f}} = \frac{{T_{\text{bf}} R_{\omega} }}{{2J _{\text{f}}}},\;\;\;\ ;u_{\text{r}} = \frac{{T_{\text{br}} R_{\omega } }}{{2J_{\text{r}} }}. { + } ), $ $ 9{ + } } \right\}.$$
{ + } ), $ $ 9{ + } } \right\}.$$
(26)
Определить разницу между фактическим и заданным коэффициентом скольжения передних и задних колес как поверхность переключения режима скольжения. Уравнения могут быть описаны как
$$S_{1} = \tilde{\lambda}_{\text{f}} = \lambda_{\text{f}} — \lambda_{\text{fd}} , $$
(27)
$$S_{2} = \tilde{\lambda}_{\text{r}} = \lambda_{\text{r}} — \lambda_{\text{rd}} ,$$
(28)
где λ f и λ r обозначает фактический коэффициент скольжения передних и задних колес соответственно, λ fd и λ rd обозначает целевой коэффициент скольжения передних и задних колес соответственно. Для достижения эквивалентного управляющего крутящего момента производная уравнений. (27), (28) по времени равны соответственно
$$T_{{{\text{eq}} . {\text{bf}}}} = \frac{{2J _{\text{f}} }}{{R_{{{\omega }}} }}\left[ {\dot{\lambda}_{\ text{fd}} V — \hat{f}_{2} (\lambda_{\text{f}} ,\lambda_{\text{r}} )(1 — \lambda_{\text{f}} ) + R_{{{\omega }}} \шляпа{f}_{3} (\lambda_{\text{f}} ,\lambda_{\text{r}} )} \right],$$
{\text{bf}}}} = \frac{{2J _{\text{f}} }}{{R_{{{\omega }}} }}\left[ {\dot{\lambda}_{\ text{fd}} V — \hat{f}_{2} (\lambda_{\text{f}} ,\lambda_{\text{r}} )(1 — \lambda_{\text{f}} ) + R_{{{\omega }}} \шляпа{f}_{3} (\lambda_{\text{f}} ,\lambda_{\text{r}} )} \right],$$
(29)
$$T_{{{\text{экв}} . {\text{br}}}} = \frac{{2J _{\text{r}} }}{{R_{{{\omega }}} }}\left[ {\dot{\lambda}_{\ text{rd}} V — \hat{f}_{2} (\lambda_{\text{f}} ,\lambda_{\text{r}} )(1 — \lambda_{\text{r}} ) + R_{{{\omega }}} \шляпа{f}_{4} (\lambda_{\text{f}} ,\lambda_{\text{r}} )} \right],$$
( 30)
Тормозной момент передних и задних колес определяется как
$$T_{\text{b}} = T_{{{\text{eq}} . {\text{b}}}} — k\text{знак} (S).$$
(31)
По условиям доступности поверхности переключения должно выполняться неравенство следующего вида:
$$S\dot{S} \le 0.$$
(32)
Определяется идеальный тормозной момент передних и задних колес как
$$T_{\text{bf}} = \frac{{2J_{\text{f}} }}{{R_{{{\omega }}} }}\left[ \begin{align} & \dot{\lambda}_{\text{fd}} V — \hat{f}_{2} (\lambda_{\text{f}} ,\lambda_{\text{r}} )(1 — \ lambda _ {\ text {f}} ) + R_ {{{\ omega }}} \ hat {f} _ {3} (\ lambda _ {\ text {f}} , \ lambda _ {\ text {r}} ) \ \ & — (F _ {\ text {f}} (\ lambda _ {\ text {f}}, \ lambda _ {\ text {r}}) + \ eta_ {1} ) \ text {sign} (S_ {1} ) \\ \end{align} \right],$$
(33)
$$T_{\text{br}} = \frac{{2J_{\text{r}} }}{{R_{{{\omega }}} }}\left[ \begin {выровнено} & \dot{\lambda}_{\text{rd}} V — \hat{f}_{2} (\lambda_{\text{f}} ,\lambda_{\text{r}} ) (1 — \lambda_{\text{r}} ) + R_{{{\omega }}} \hat{f}_{4} (\lambda_{\text{f}} ,\lambda_{\text{r }} ) \\ & — (F _ {\ text {r}} (\ lambda _ {\ text {f}} , \ lambda _ {\ text {r}} ) + \ eta_ {2} ) \ text {sign} ( S_{2} ) \\ \end{align} \right]. $$
$$
(34)
Соответственно
$$F_{\text{f}} (\lambda_{\text{f}} ,\ lambda_{\text{r}} ) = F_{2} (1 — \lambda_{\text{f}} ) + R_{{{\omega }}} F_{3} , $$
$$F_{\text{r}} (\lambda_{\text{f}} ,\lambda_{\text{r}} ) = F_{2} (1 — \lambda_{\text{r}} ) + R_{{{\omega }}} F_{4} ,$$
, где η 1 , η 2 — положительные константы.
Устранение вибраций
Явление вибраций является одним из нежелательных эффектов управления в скользящем режиме. Для устранения явлений дребезга при скользящем режиме управления была использована насыщенная функция sat( S / φ ) и переработан регулятор скользящего режима с использованием интегральной поверхности переключения, чтобы сделать закон управления плавным [24]. Определение интегральной поверхности переключения как
$$S_{1} = \lambda_{\text{f}} — \lambda_{\text{fd}} + \xi_{1} \int {(\lambda_{\text{f }} — \lambda_{\text{fd}} } ){\text{d}}t,$$
(35)
$$S_{2} = \lambda_{\text{r}} — \ lambda _ {\ text {rd}} + \ xi_ {2} \ int {(\ lambda _ {\ text {r}} — \ lambda _ {\ text {rd}} } ) {\ text {d}} t, $ $
(36)
где ξ 1 и ξ 2 — константа.
Используя метод интегральной поверхности переключения, идеальный тормозной момент передних и задних колес определяется выражением
$$\begin{aligned} T_{\text{bf}} = \hfill \\ \;\ ;\;\;\frac{{2J _{\text{f}} }}{{R_{{{\omega }}} }}\left[ \begin{aligned} & (\dot{\lambda }_{ \text{fd}} — \xi_{1} \tilde{\lambda }_{\text{f}} )V — \шляпа{f}_{2} (\lambda_{\text{f}} ,\ lambda _ {\ text {r}} ) (1 — \ lambda _ {\ text {f}} ) + R_ {{{\ omega }}} \ hat {f} _ {3} (\ lambda _ {\ text {f} } ,\lambda_{\text{r}} ) \hfill \\ & — (F_{\text{f}} (\lambda_{\text{f}} ,\lambda_{\text{r}} ) + \ eta_ {1}) \ text {sat} \ left ( {\ frac {{\ tilde {\ lambda} _ {\ text {f}} + \ xi_ {1} \ int {\ tilde {\ lambda} _ {\ text{f}} {\text{d}}t}}}{{\varphi_{1} }}} \right) \hfill \\ \end{aligned} \right], \hfill \\ \end{aligned }$$
(37)
$$\begin{align} T_{\text{br}} = \hfill \\ \;\;\;\frac{{2J _{\text{r}}}}{{R_ {{{\omega }}} }}\left[ \begin{align} & (\dot{\lambda}_{\text{rd}} — \xi_{2} \tilde{\lambda}_{\text {r}} )V — \шляпа{f}_{2} (\lambda_{\text{f}} ,\lambda_{\text{r}} )(1 — \lambda_{\text{r}} ) + R_{{{\omega}}} \шляпа{f}_{4} (\lambda_{\text{f}} ,\lambda_{\text{r}} ) \\ & — (F_{\text{ r}} (\ lambda _ {\ text {f}}, \ lambda _ {\ text {r}}) + \ eta_ {2}) \ text {sat} \ left ( {\ frac {{\ tilde {\ lambda} _{\text{r}} + \xi_{2} \int {\tilde{\lambda}_{\text{r}} {\text{d}}t}}}{{\varphi_{2}} }} \right) \\ \end{aligned} \right], \hfill \\ \end{aligned}$$
(38)
где φ 1 и φ 2 константа, φ 1 и φ 2 — толщина пограничного слоя, которая изменяется для использования пропускной способности системы. Как получить значения, представленные Ref. [23].
Как получить значения, представленные Ref. [23].
Датчик коэффициента сцепления с дорогой Конструкция
Линейный наблюдатель в расширенном состоянии может расширить неопределенность и модель управляемого объекта с неизвестным возмущением в новое наблюдение состояния, и это очень подходит для задач оценки коэффициента сцепления с дорогой, которые имеют только измеренный выходной сигнал и управляющий вход [25, 26]. Используя наблюдатель линейного расширенного состояния, можно наблюдать коэффициент сцепления с дорогой, где коэффициент трения между шиной и дорогой является выходом линейного расширенного состояния второго порядка, а угловая скорость и тормозной момент передних и задних колес — входными данными.
По разделу 2.1 модели динамики торможения двухколесного транспортного средства можно получить
$$\left\{ \begin{aligned} \dot{\omega }_{\text{f}} = \frac{1}{{ 2J_{\text{f}} }}( — T_{\text{bf}} + \mu (\lambda_{\text{f}} )m_{1} R_{{{\omega }}} g — \ mu (\ lambda _ {\ text {f}}) m_ {3} R_ {{{\ omega }}} \ ddot {x}) \ ;, \ hfill \\ \ dot {\ omega} _ {\ text {r }} = \frac{1}{{2J _{\text{r}} }}( — T_{\text{br}} + \mu (\lambda_{\text{r}} )m_{2} R_{ {{\omega}}} g + \mu (\lambda_{\text{r}} )m_{3} R_{{{\omega}}} \ddot{x})\;. \hfill \\ \end{выровнено} \right.$$
\hfill \\ \end{выровнено} \right.$$
(39)
Переписать уравнение (39), затем
$$\left\{ \begin{aligned} \dot{\omega }_{\text{f}} = \frac{1}{{2J_{f} }}\mu (\ lambda_{\text{f}} )(m_{1} R_{{{\omega }}} g — m_{3} R_{{{\omega }}} \ddot{x}) + \frac{ — 1 }{{2J_{\text{f}}}}T_{\text{bf}} \;, \hfill \\ \dot{\omega}_{\text{r}} = \frac{1}{{ 2J_{r} }}\mu (\lambda_{\text{r}} )(m_{2} R_{{{\omega }}} g + m_{3} R_{{{\omega }}} \ddot {x}) + \frac{ — 1}{{2J _{\text{r}} }}T_{\text{br}} \;. \hfill \\ \end{выровнено} \right.$$
(40)
Содержит член коэффициента сцепления с дорожным покрытием уравнения. (40) рассматривались как возмущение системы, а для переменных состояния разложения системы определялось
$$\begin{aligned} \omega_{\text{f}} = x_{1} ,\;\ ;\frac{1}{{2J _{\text{f}} }}\mu (\lambda _{\text{f}} )(m_{1} R_{{{\omega }}} g — m_{3 } R_{{{\omega }}} \ddot{x}) = x_{2} ,\;\;\omega_{\text{r}} = x_{3} ,\, \hfill \\ \frac{ — 1}{{2J_{\text{f}}}} = b_{1} ,\;\frac{1}{{2J_{\text{r}} }}\mu (\lambda_{\text{r }} )(m_{2} R_{{{\omega }}} g + m_{3} R_{{{\omega }}} \ddot{x}) = x_{4} ,\;\frac{ — 1}{{2J_{\text{r}}}} = b_{2} ,\; \hfill \\ T_{\text{bf}} = u_{1} ,\;\;T_{\text{br}} = u_{2} . \hfill \\ \end{выровнено}$$
\hfill \\ \end{выровнено}$$
Переписывание уравнения. (40) в систему двух рядов интегратора соответственно задаются как
$$\left\{ \begin{aligned} \dot{x}_{1} = x_{2} + b_{1} u_{1} \;, \hfill \\ y_{1} = x_{1} \;. \hfill \\ \end{align} \right.$$
(41)
$$\left\{ \begin{aligned} \dot{x}_{3} = x_{4} + b_{2 } u_{2} , \hfill \\ y_{2} = x_{3} \;. \hfill \\ \end{aligned} \right.$$
(42)
Используя систему рядов интегратора уравнения. (41) например, линейный наблюдатель расширенного состояния второго порядка был спроектирован следующим образом для наблюдения 9{2} \;\;, \hfill \\ z_{1} (k + 1) = z_{1} (k) + h\left[ {z_{2} (k) — \beta_{01} e( k) + b_{0} u_{1} (k)} \right], \hfill \\ & z_{2} (k + 1) = z_{2} (k) + h\left[ { — \beta_ {02} e(k)} \right], \hfill \\ \end{aligned} \right.$$
(43)
, где ω 0 — полоса пропускания линейного расширенного наблюдателя по назначению полюсов, u 1 и у 1 — входной сигнал, соответственно z 1 и z 2 — это выходной сигнал линейного наблюдателя расширенного состояния, который представляет собой наблюдения x 1 и х 2 , б 0 — расчетное значение усиления управления b 1 . Из того, что обсуждалось выше, наблюдения x 3 и x 4 можно также сформулировать как уравнение. (42).
Из того, что обсуждалось выше, наблюдения x 3 и x 4 можно также сформулировать как уравнение. (42).
Чтобы оценить коэффициент сцепления с дорогой, подставив уравнение (40) в уравнение. (41) линейный наблюдатель расширенного состояния был подробно построен следующим образом:
$$\left\{ \begin{aligned} & \omega_{f} = z_{1} , \hfill \\ & \frac{1 }{{2J_{\text{f}} }}\mu (\lambda_{\text{f}} )(m_{1} R_{{{\omega }}} g — m_{3} R_{{{ \omega }}} \ddot{x}) = z_{2} , \hfill \\ \end{align} \right.$$
(44)
где z 1 и z 2 — это наблюдения x 1 (угловая скорость переднего колеса) и x 2 (содержат коэффициент сцепления с дорогой). Вероятно,
$$\left\{ \begin{aligned} & \omega_{\text{r}} = z_{3} , \hfill \\ & \frac{1}{{2J _{\text{r} } }}\mu (\lambda_{\text{r}} )(m_{2} R_{{{\omega }}} g + m_{3} R_{{{\omega }}} \ddot{x} ) = z_{4} , \hfill \\ \end{aligned} \right. $$
$$
(45)
где z 3 и z 4 — это наблюдения x 3 (скорость заднего колеса) и x 4 . Объединение уравнений. (44), (45), коэффициент сцепления передних и задних колес с дорогой можно сформулировать как
$$\left\{ \begin{aligned} \mu (\lambda_{\text{f}} ) = \frac{ {2J_{\text{f}} z_{2}}}{{m_{1} R_{{{\omega }}} g — m_{3} R_{{{\omega }}} \ddot{x} }}, \hfill \\ \mu (\lambda_{\text{r}} ) = \frac{{2J _{\text{r}} z_{4}}}{{m_{2} R_{{{\ omega }}} g + m_{3} R_{{{\omega }}} \ddot{x}}}\;. \hfill \\ \end{выровнено} \right.$$
(46)
Если расчетная схема заднего колеса одинакова с передним колесом, расчетную схему заднего колеса показывать не нужно.
Результаты симуляции
В этом разделе выполняется ряд симуляций в программном обеспечении для моделирования ADAMS/Car, имитирующих транспортное средство в среде виртуального моделирования для анализа и оценки схемы оценки, предложенной в этой статье. В то время как для оценки коэффициента сцепления с дорогой установите параметры модели транспортного средства в моделировании следующим образом: м = 1500 кг, м с = 1285 кг, м f = 96 кг, м р = 119 кг, л f = 1,186 м, л r = 1,258 м, ч ж = 0,3 м, ч р = 0,3 м, р ω = 0,326 м, Дж f = 1,7 кг м 2 , J r = 1,7 кг·м 2 . Полная модель транспортного средства в ADAMS/Car показана на рис. 3. С помощью компилятора road builder в ADAMS/Car была построена тестовая среда для дороги с различным коэффициентом трения, и предложенный метод оценки коэффициента сцепления с дорогой был протестирован в созданной виртуальной среде.
В то время как для оценки коэффициента сцепления с дорогой установите параметры модели транспортного средства в моделировании следующим образом: м = 1500 кг, м с = 1285 кг, м f = 96 кг, м р = 119 кг, л f = 1,186 м, л r = 1,258 м, ч ж = 0,3 м, ч р = 0,3 м, р ω = 0,326 м, Дж f = 1,7 кг м 2 , J r = 1,7 кг·м 2 . Полная модель транспортного средства в ADAMS/Car показана на рис. 3. С помощью компилятора road builder в ADAMS/Car была построена тестовая среда для дороги с различным коэффициентом трения, и предложенный метод оценки коэффициента сцепления с дорогой был протестирован в созданной виртуальной среде. .
.
Тестовая модель автомобиля в целом в ADAMS/Car
Увеличенное изображение
Метод оценки построен на основе данных о тормозном моменте и датчике скорости вращения колеса. Из того, что обсуждалось выше, блок-схема схемы оценки коэффициента сцепления переднего колеса с дорогой показана на рис. 4.
Дорожное покрытие с высоким коэффициентом трения
Идеальный регулятор тормозного момента может в полной мере использовать коэффициент сцепления с дорогой при торможении автомобиля. Тормозной момент передних и задних колес показан на рис. 5 при высоком коэффициенте трения 0,8 и начальной продольной скорости 30 м/с.
Рис. 5Тормозной момент передних и задних колес µ = 0,8
Изображение в полный размер и задние колеса. Как видно из рисунка, расчетный коэффициент сцепления передних и задних колес с дорогой очень близок к реальным значениям коэффициента сцепления с дорогой. Наибольшая разница между оценочными и реальными значениями возникает около 0,3 с назад. Также видно, что значения коэффициента сцепления с дорожным покрытием для передних колес лучше, чем для задних колес. Однако при торможении транспортного средства сигнал скорости вращения колеса смешивается с шумом измерения и предполагается, что это независимый белый гауссовский процесс с нулевым средним значением.
Наибольшая разница между оценочными и реальными значениями возникает около 0,3 с назад. Также видно, что значения коэффициента сцепления с дорожным покрытием для передних колес лучше, чем для задних колес. Однако при торможении транспортного средства сигнал скорости вращения колеса смешивается с шумом измерения и предполагается, что это независимый белый гауссовский процесс с нулевым средним значением.
Оценка коэффициента сцепления с дорогой µ = 0,8
Изображение в натуральную величину
На рис. 7 показан расчетный коэффициент сцепления с дорогой с учетом шумовых помех. Замечено, что линейный наблюдатель в расширенном состоянии оценил коэффициент сцепления с дорогой с шумовыми помехами также очень близко к реальным значениям и точно с высокой устойчивостью.
Рис. 7Расчетный коэффициент сцепления с дорогой с учетом шумовых помех µ = 0,8
Изображение полного размера
Поверхность дороги с низким коэффициентом трения
На рис.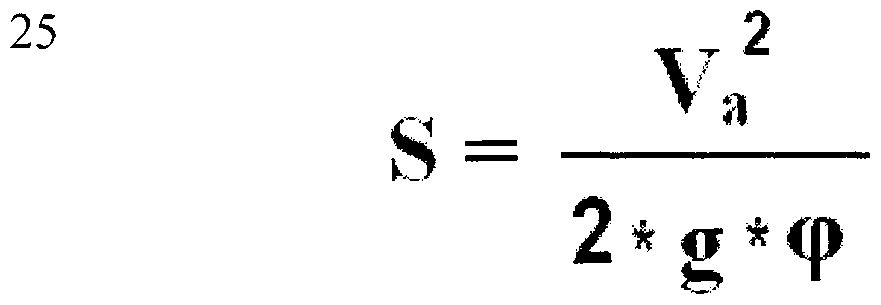 8 показан тормозной момент передних и задних колес, возникающий при низком коэффициенте трения 0,2 и начальной продольной скорости 30 м/с. Расчетные значения и реальные значения сцепления с дорожным покрытием представлены на рис. 9, что указывает на то, что предложенный оценщик хорошо работает на дорожном покрытии с низким коэффициентом трения, а на рис. 10 показан оценочный коэффициент сцепления с дорожным покрытием с шумовыми помехами соответственно.
8 показан тормозной момент передних и задних колес, возникающий при низком коэффициенте трения 0,2 и начальной продольной скорости 30 м/с. Расчетные значения и реальные значения сцепления с дорожным покрытием представлены на рис. 9, что указывает на то, что предложенный оценщик хорошо работает на дорожном покрытии с низким коэффициентом трения, а на рис. 10 показан оценочный коэффициент сцепления с дорожным покрытием с шумовыми помехами соответственно.
Тормозный крутящий момент передних и задних дисков µ = 0,2
Полноразмерное изображение
Рис.Оценка коэффициента во фрикционной форме µ = 0,2
. 10
Расчетный коэффициент сцепления с дорогой с учетом шумовых помех µ = 0,2
Изображение в полный размер
Легко видеть, что предложенный линейный наблюдатель в расширенном состоянии может оценить коэффициент сцепления с дорогой с хорошей точностью по сравнению с измерениями в торможение автомобиля на одиночном дорожном покрытии с высоким или низким коэффициентом трения. Даже в условиях шумовых помех он также может эффективно оценивать коэффициент сцепления с дорогой. Однако значения оценки коэффициента сцепления с дорожным покрытием при использовании передних колес лучше, чем при использовании задних колес.
Даже в условиях шумовых помех он также может эффективно оценивать коэффициент сцепления с дорогой. Однако значения оценки коэффициента сцепления с дорожным покрытием при использовании передних колес лучше, чем при использовании задних колес.
Далее подробно рассматривается моделирование дорожных условий с неравномерным коэффициентом трения.
Дорога с коэффициентом трения при неровностях
Для оценки коэффициента сцепления на дорогах с неровным трением разработано дорожное покрытие с коэффициентами трения в диапазоне от высокого к низкому и от низкого к высокому.
Тормозной момент передних и задних колес показан на рис. 11(а) при коэффициентах трения в диапазоне от 0,8 до 0,2 и начальной продольной скорости 30 м/с. Где от 0 до 2 с транспортные средства движутся по дорожному покрытию с высоким коэффициентом трения и от 2 до 7 с по дорожному покрытию с низким коэффициентом трения. Аналогично, тормозной момент передних и задних колес, проводимый при коэффициентах трения в диапазоне от 0,2 до 0,8, показан на рис. 11б. Где от 0 до 2 с транспортные средства движутся по дорожному покрытию с низким коэффициентом трения и от 2 до 5 с по дорожному покрытию с высоким коэффициентом трения. Соответственно, изменения расчетного коэффициента сцепления с дорожным покрытием в идеальном состоянии с учетом шумовых помех представлены на рис. 12.
11б. Где от 0 до 2 с транспортные средства движутся по дорожному покрытию с низким коэффициентом трения и от 2 до 5 с по дорожному покрытию с высоким коэффициентом трения. Соответственно, изменения расчетного коэффициента сцепления с дорожным покрытием в идеальном состоянии с учетом шумовых помех представлены на рис. 12.
Тормозной момент передних и задних колес
Изображение полного размера
Рис. 12Сравнение смоделированного и расчетного коэффициента сцепления с дорогой
Изображение полного размера в идеальном состоянии (рис. 12(а), (в)) или измерении с шумовыми помехами (рис. 12(б), (г)) близко к эталонным значениям, а расчетные значения менее подвержены влиянию шумовых помех.
Несмотря на то, что дорожные коэффициенты сильно изменяются, результаты моделирования показывают, что предложенный метод оценки по-прежнему может точно оценивать коэффициент сцепления с дорожным покрытием с высокой надежностью, которая может противостоять внешним возмущениям.
Выводы
- (1)
В соответствии с динамикой торможения транспортного средства представлен линейный наблюдатель расширенного состояния для оценки коэффициента сцепления с дорогой, который имеет хорошую точность при движении транспортного средства по дороге с различным коэффициентом трения.
- (2)
Использование метода функции насыщения и интегральной поверхности переключения может устранить вибрацию управления скользящим режимом.
- (3)
Результаты моделирования с использованием значений оценки коэффициента сцепления с дорогой для передних колес лучше, чем для задних колес.
- (4)
Предлагаемый метод обладает высокой устойчивостью к различным дорожным условиям, что позволяет противостоять внешним возмущениям.

История изменений
28 июля 2017 г.
Опубликовано исправление к этой статье.
Каталожные номера
Р. Изерманн, Р. Маннале, К. Шмитт. Системы предотвращения столкновений PRORETA: Анализ ситуации и управление вмешательством. Инженерная практика управления , 2012, 20(11): 1236–1246.
J Wu, Y Q Zhao, X W Ji и др. Обобщенная внутренняя модель надежного управления для активного вмешательства переднего рулевого управления. Китайский журнал машиностроения , 2015, 28(2): 285–293.
J Wu, Y H Liu, F B Wang и др. Исследование активного рулевого управления автомобиля на основе надежного внутреннего управления моделью с двумя степенями свободы. Китайский журнал машиностроения , 2016, 29(4): 1-8.
«>Л. Ли, С. Ран, К. Ву и др. Новый корректирующий алгоритм на основе нечеткой логики для систем контроля тяги на неровных дорогах с низким коэффициентом трения. Динамика систем автомобиля , 2015, 53 (6): 711–733.
М. Канг, Л. Ли, Х. Ли и др. Координированное управление тягой автомобиля на основе крутящего момента двигателя и тормозного давления в сложных дорожных условиях. Динамика систем автомобиля , 2012, 50 (9): 1473–1494.
H Z Li, L Li, L He и др. ПИД плюс метод нечеткой логики для управления крутящим моментом в системе контроля тяги. Международный журнал автомобильных технологий , 2012, 13(3): 441–450.

Л. Л. И., К. Ян, Г. Цзя и др. Комплексная оценка коэффициента сцепления шины с дорогой на основе метода слияния сигналов при выполнении сложных операций маневрирования. Механические системы и обработка сигналов , 2015, 56(3): 259–276.
J Song, C Yang, H Z Li и др. Оценка коэффициента сцепления с дорогой на основе объединения данных мультисенсоров для системы AYC. Qinghua Daxue Xuebao/Journal of Tsinghua University , 2009, 49(5): 715–718. (на китайском)
G Li, RC Xie, S Y Wei, et al. Оценка состояния автомобиля и коэффициента сцепления с дорогой на основе двойного кубатурного фильтра Калмана. Наука Китая: технологические науки , 2015, 45(4): 403–414. (на китайском языке)
C Yang, L Li, J Song и др. Алгоритм оценки коэффициента сцепления с дорогой на основе наблюдателя усилия на шинах. Китайское машиностроение , 2009, 20(7): 873–876.
 (на китайском языке)
(на китайском языке)Дж. О. Хан, Р. Раджамани, Л. Александр. Определение коэффициента сцепления шины с дорогой в режиме реального времени на основе GPS. IEEE Transactions on Control Systems Technology , 2002, 10(3): 331–343.
Г. Эрдоган, Л. Александр, Р. Раджамани. Измерение несвязанных боковых прогибов каркаса с помощью беспроводного пьезоэлектрического датчика и оценка коэффициента сцепления шин с дорогой // ASME 2010 Dynamic Systems and Control Conference , Кембридж, Массачусетс, США, 12–15 сентября 2010 г.: 541–548.
Г. Эрдоган, Л. Александр, Р. Раджамани. Оценка коэффициента трения шины о дорогу с помощью нового беспроводного пьезоэлектрического датчика шины. IEEE Sensors Journal , 2011, 11(2): 267–279.
ZP Yu, JL Zuo, LJ Zhang. Краткий обзор состояния разработки методов оценки коэффициента сцепления шин с дорогой.
 Автомобильная техника , 2006, 28(6): 546–549. (на китайском языке)
Автомобильная техника , 2006, 28(6): 546–549. (на китайском языке)K Enisz, I Szalay, G Kohlrusz, et al. Оценка коэффициента сцепления шины с дорогой на основе расширенного фильтра Калмана с дискретным временем. Труды Института инженеров-механиков, часть D: журнал автомобильной инженерии , 2015, 229(9): 1158–1168.
К. Эниш, Д. Фодор, И. Салай и др. Улучшение систем активной безопасности с помощью расширенного фильтра Калмана, основанного на оценке коэффициента сцепления шины с дорогой // 2014 IEEE International Electric Vehicle Conference, Флоренция, Италия, 11-19 декабря 2014 г.: 1–5.
Y Q Zhao, F Lin. Оценка коэффициента сцепления с дорожным покрытием на основе виртуального эксперимента. Журнал Цзилиньского университета: Инженерно-технологический выпуск , 2011, 41(2): 309–315. (на китайском языке)
Ф Линь, К Хуанг.
 Фильтр Калмана без запаха для оценки коэффициента сцепления с дорогой. Журнал Харбинского технологического института , 2013, 45(7): 115–120. (на китайском языке)
Фильтр Калмана без запаха для оценки коэффициента сцепления с дорогой. Журнал Харбинского технологического института , 2013, 45(7): 115–120. (на китайском языке)Т. А. Вензел, К. Дж. Бернхэм, М. В. Бланделл и др. Двойной расширенный фильтр Калмана для оценки состояния и параметров автомобиля. Динамика систем автомобиля , 2006, 44 (2): 153–171.
Ф. Г. Ян, Ю. Б. Ли, Дж. Х. Руан и др. Оценка коэффициента сцепления шины с дорогой в режиме реального времени на основе расширенного наблюдателя. Труды Китайского общества сельскохозяйственной техники , 2010 г., 41 (8): 6–9. (на китайском языке)
Л Рэй. Нелинейная оценка силы шины и идентификация сцепления с дорогой: моделирование и эксперименты. Automatica , 1997, 33 (10): 1819–1833.
Харифи А., Агаголзаде А., Ализаде Г. и др. Разработка регулятора скользящего режима для управления проскальзыванием антиблокировочной системы тормозов.

Дж. Чен, Дж. Сонг, Л. Ли и др. Новый метод предварительного контроля устойчивости динамики транспортного средства, основанный на критической стабильной скорости во время переходного маневрирования рулевым управлением. Китайский журнал машиностроения , 2016, 29(3): 475-485.

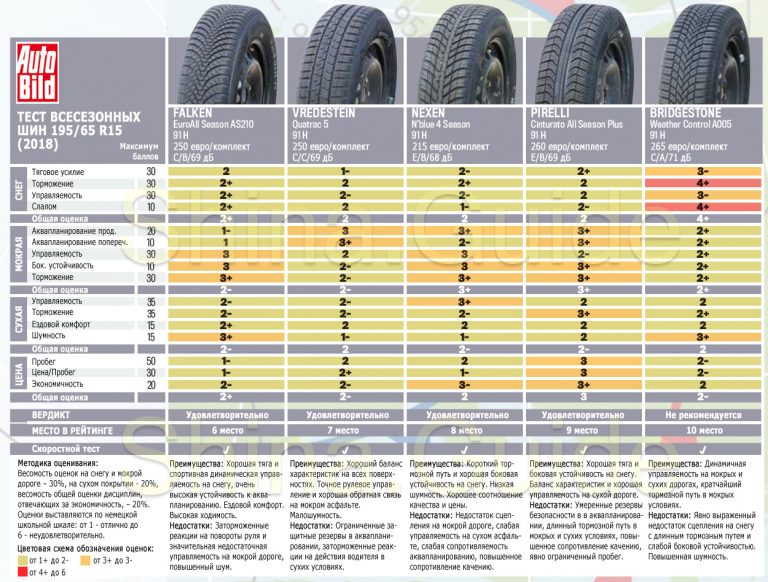 Тени от деревьев, построек препятствуют таянию. Соответственно, в таких местах дороги значительно уменьшается сцепление.
Тени от деревьев, построек препятствуют таянию. Соответственно, в таких местах дороги значительно уменьшается сцепление.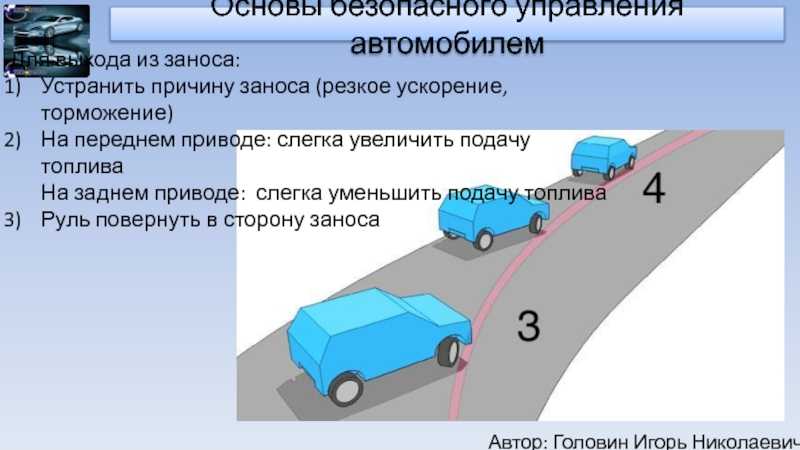


 Тут нужно учитывать особенности дорожного покрытия, в одних случаях лучший показатель будет у крупных «шашек», в других лучше поведут себя мелкие шины.
Тут нужно учитывать особенности дорожного покрытия, в одних случаях лучший показатель будет у крупных «шашек», в других лучше поведут себя мелкие шины.

 (на китайском языке)
(на китайском языке) Автомобильная техника , 2006, 28(6): 546–549. (на китайском языке)
Автомобильная техника , 2006, 28(6): 546–549. (на китайском языке)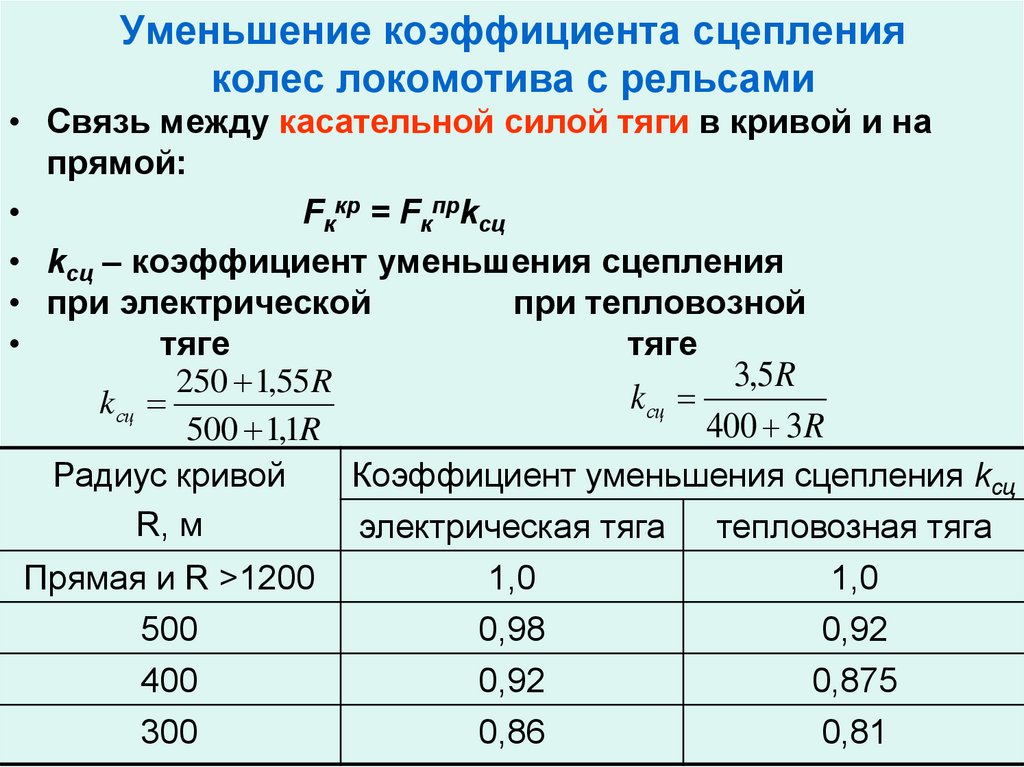 Фильтр Калмана без запаха для оценки коэффициента сцепления с дорогой. Журнал Харбинского технологического института , 2013, 45(7): 115–120. (на китайском языке)
Фильтр Калмана без запаха для оценки коэффициента сцепления с дорогой. Журнал Харбинского технологического института , 2013, 45(7): 115–120. (на китайском языке)