Крутильные колебания: . . , “ ”, . -. -. . . . ., 11:1 (2019), 50–58

Содержание

КРУТИЛЬНЫЕ КОЛЕБАНИЯ — это… Что такое КРУТИЛЬНЫЕ КОЛЕБАНИЯ?

— механич. колебания, при к-рых упругие элементы испытывают деформации сдвига. Имеют место в разл. машинах с вращающимися валами: в поршневых двигателях, турбинах, генераторах, редукторах, трансмиссиях транспортных машин.

К. к. возникают в результате неравномерности периодич. момента как движущих сил, так и сил сопротивления. Неравномерность крутящего момента вызывает неравномерность изменения угловой скорости вала, т. е. то ускорение, то замедление вращения. Обычно вал представляет собой чередование участков с малой массой и упругой податливостью с более жёсткими участками, на к-рых закреплены значит. массы. В каждом сечении вала будет своя степень неравномерности вращения, поскольку в одинаковый промежуток времени массы проходят разные углы и, следовательно, движутся с разными скоростями, что создаёт переменное кручение вала и динамич. знакопеременные напряжения, гл.

обр. касательные.

При совпадении частот собств. колебаний системы с частотой периодич. крутящего момента движущих сил и сил сопротивления возникают резонансные колебания. В этом случае повышается уровень динамич. переменных напряжений; возрастает акустич. шум, излучаемый работающей машиной. Динамич. знакопеременные напряжения при неправильно выбранных (заниженных) размерах вала, недостаточной прочности его материала и возникновении резонанса могут превысить предел выносливости, что приведёт к усталости материала вала и его разрушению.

При расчёте К. к. валов машин часто пользуются расчётной схемой с двумя дисками, соединёнными упругим стержнем, работающим на кручение. В этом случае собств. частота


где I1 — момент инерции 1-го диска, I2 — момент инерции 2-го диска, С -крутильная жёсткость стержня, Для круглого стержня диаметром

d и длиной l С где G — модуль сдвига. Более сложные расчётные схемы содержат большее число дисков, соединённых стержнями и образующих последоват. цепи, а иногда — разветвлённые и кольцевые цепи. Расчёт собств. частот форм и вынужденных К. к. по этим расчётным схемам производится на ЭВМ.

Др. примером К. к. является крутильный маятник, к-рый представляет собой диск, закреплённый на одном конце стержня, работающего на кручение и жёстко заделанного др. концом. Собств. частота такого маятника где I — момент инерции диска. Приборы с использованием крутильного маятника применяют для определения модуля упругости при сдвиге, коэф. внутр. трения твёрдых материалов при сдвиге, коэф. вязкости жидкости.

К. к. возникают в разнообразных упругих системах; в нек-рых случаях возможны совместные колебания с разл. видами деформации элементов системы, напр. изгибно-крутильные колебания. Так, при определ. условиях полёта под действием аэродинамич. сил иногда возникают самовозбуждающиеся изгибно-крутильные колебания крыла самолёта (т.

н. флаттер), к-рые могут вызывать разрушение крыла.

Лит.: Ден-Гартог Д. П., Механические колебания, пер. с англ., М., 1960; Маслов Г. С., Расчёты колебаний валов. Справочник, 2 изд., М., 1980; Вибрации в технике. Справочник, под ред. В. В. Болотина, т. 1, М., 1978; Силовые передачи транспортных машин, Л., 1982. А. В. Синев.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.

Крутильные колебания

Крутильные колебания – это вращательное движение тела, подвешенного на упругой нити (стальной проволоке), вокруг вертикальной оси, выражающееся в его попеременном отклонении в ту и другую сторону от положения равновесия. Силовая величина, характеризующая динамику такого движения, является следствием деформации нити.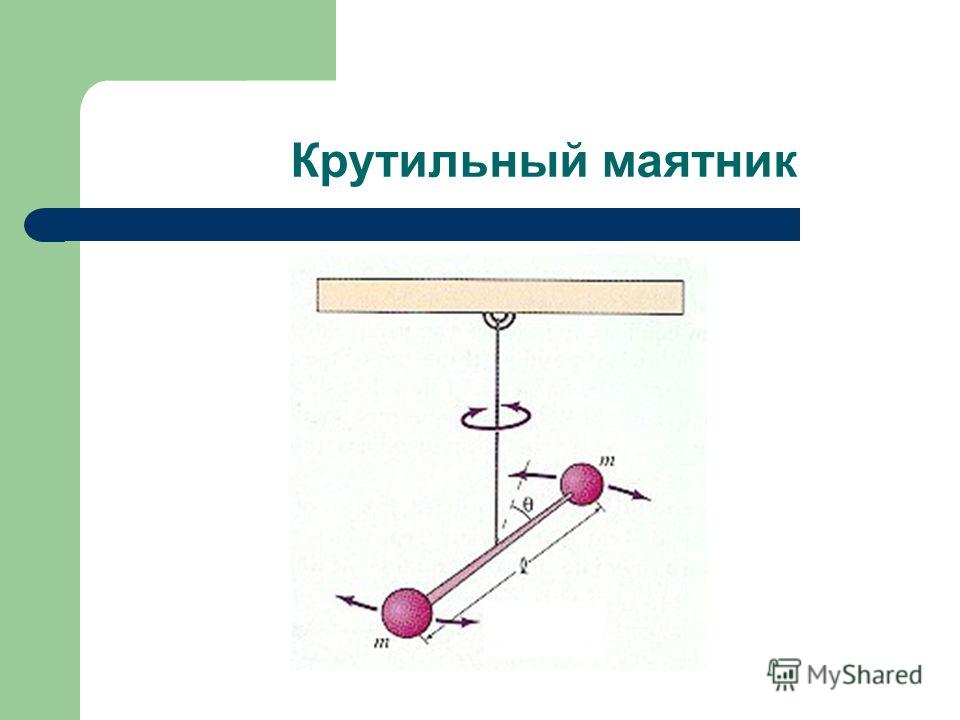 Деформация – это изменение формы и размеров тела под действием приложенных к нему сил. Если после прекращения действия силы тело принимает первоначальные размеры и форму, то деформация называется упругой. Существует несколько видов деформации тел: растяжение, сжатие,

5

кручение, сдвиг, изгиб. При этом внутри деформированного тела возникает противодействующая сила, равная по величине деформирующей силе и называемая упругой силой. Величина упругой силы Fупр., возникающей при малых деформациях любого вида, прямо пропорциональна величине деформации

x, то есть изменению размеров тела, что в общем виде выражается соотношением:

Fупр.= – kх (10)

где k – коэффициент пропорциональности, называемый коэффициентом упругости. Соотношение (10) называется законом Гука. Знак минус указывает на противоположные направления упругой силы и величины деформации.

При закручивании нити с подвешенным телом на некоторый угол φ (рис. 1) возникающее в нити противодействие представляет собой момент силы М, значение модуля которого пропорционально углу φ, а направление, как и при любой деформации, противоположно ей, т.е. углу закручивания:

М = –Dφ (11)

Здесь:D – модуль кручения (коэффициент упругости), характеризующий упругие свойства нити.

Для вращательного движения тела второй закон Ньютона записывается в виде:

М = Jε (12)

где J – момент инерции тела, ε = d2φ/dt2 – угловое ускорение, М – суммарный момент сил, в данном случае представляющий собой момент упругой силы, которая возникает при закручивании упругой нити (проволоки) на угол φ. Подставляя в это уравнение выражение для момента упругой силы (11), мы получим линейное дифференциальное уравнение второго порядка, описывающее движение тела при крутильных колебаниях:

J (d2φ/dt2) + Dφ = 0 (13)

Решение этого уравнения имеет вид:

φ = φ0sin(ω

t + φo) (14)

где φ – угол поворота тела в момент времени t, φ0 – максимальный угол поворота тела при колебаниях (амплитуда колебаний), φo – начальная фаза колебаний, а коэффициент при t, составляющий ω = (D/J)1/2, – циклическая (или круговая) частота колебаний. Поскольку, с другой стороны,

6

циклическая частота колебаний, по определению, равна 2π/T (T – период колебаний), то можно записать равенство:

ω = (D/J)1/2 = 2π/T (15)

откуда следует уравнение, связывающее период крутильных колебаний с моментом инерции тела, подвешенного на упругой нити, и модулем кручения нити:

T = 2π(J/D)1/2 (16)

Описание установки и метода измерений:

Для определения моментов инерции твердых тел в работе используется установка, показанная на рис. 2.

На основании 1 расположен электронный блок 2 с миллисекундомером и счетчиком полных колебаний, а также укреплена колонка 3, на которой находятся три кронштейна 4, 5, 6. Кронштейны 4 и 6 имеют зажимы для подвеса рамки на упругих стальных нитях 7. Рамка представляет собой две балки 8, соединенных стержнями 9. На стержнях с помощью цанговых зажимов 10 закрепляется в нужном положении подвижная балка

11,

7

которая позволяет (путем закручивания винта 12) укреплять в рамке исследуемые тела 13, значительно отличающиеся по внешним размерам. На стальной плите, прикрепленной к кронштейну 5, располагаются соединенные с электронный блоком электромагнит 14 и фотоэлектрический датчик 15, а также угловая шкала (на рисунке не показана), которая служит для задания амплитудного значения угла закручивания.

Работа на установке проводится в следующем порядке:

  1. Закрепить электромагнит в положении, которое соответствует определенному углу закручивания рамки (задается преподавателем).

  2. Если требуется заданием, укрепить в рамке исследуемое тело. Для этого:

а) ослабить зажимы 10;

б) передвигая подвижную балку 11, зажать тело между коническим выступом нижней балки и конусом винта 12, затянуть зажимы 10;

в) окончательно укрепить тело, закручивая винт 12.

  1. Включить питающее напряжение нажатием клавиши «Сеть». При этом должны светиться лампочки фотоэлектрического датчика и индикатора секундомера.

  2. Нажать клавишу «Сброс» для обнуления индикатора секундомера, генерирования сигнала разрешения на измерение и включения обмотки электромагнита.

  3. Повернуть рамку прибора так, чтобы в отклоненном состоянии она была зафиксирована электромагнитом.

  4. Нажать клавишу «Пуск». Нажатие этой клавиши запускает секундомер и отключает электромагнит. Рамка при этом отпускается и начинает совершать крутильные колебания, которые подсчитываются в электронном блоке посредством сигналов, поступающих от фотоэлектрического датчика

    15.

  5. После совершения рамкой определенного числа колебаний систему остановить нажатием кнопки «Стоп». Индикаторы электронного блока указывают число N совершенных колебаний и общее время t, за которое они были совершены.

Задание 1. Определение модуля кручения.

При использовании установки крутильных колебаний для определения моментов инерции твердых тел необходимо знать величину модуля кручения D нитей подвеса 7 рамки. Поскольку упругие свойства

8

материала при кручении зависят от многих факторов, то значение модуля D определяют экспериментально. В настоящей работе используется динамический метод измерения модуля кручения, основанный на зависимости периода Т крутильных колебаний рамки, подвешенного на проволоке, от упругих свойств материала проволоки.

Согласно уравнению (16), период колебаний Т зависит как от модуля кручения D, так и от момента инерции J системы, совершающей колебания. Поэтому измерения проводят с помощью эталонных тел, моменты инерции которых Jт известны, или легко рассчитываются. Система, совершающая колебания, включает в себя эталонное тело и рамку, моментом инерции Jр которой нельзя пренебречь. Так как эталонное тело и рамка совершают вращательное движение вокруг одной и той же оси, то, согласно уравнению (9), их моменты инерции суммируются:

J = Jр + Jт (17)

Если выразить момент инерции из уравнения (16), то:

J = Jр + Jт =Т2D/(42) (18)

Поскольку момент инерции рамки Jр неизвестен, измерения проводят в два этапа, используя два различных эталонных тела с моментами инерции Jт1 и Jт2. В этом случае мы имеем систему двух уравнений:

Jр + Jт1 = Т12 D/(42) (19а)

Jр + Jт2 = Т22 D/(42) (19б)

Вычитая одно из другого, получаем выражение для модуля кручения, не содержащее неизвестных (или не определяемых в эксперименте) параметров:

D = 42(Jт1 – Jт2)/(Т12 – Т22) (20)

Измерения проводятся следующим образом:

  1. Взять первое эталонное тело – один из двух дисков. Измерить штангенциркулем его толщину l и диаметр. Получить значение радиуса диска r. Взвесить диск на технических весах, или принять известное

9

значение его массы m (может быть указано на диске или на установке). По формуле (4) рассчитать момент инерции диска Jт1 и занести это значение в таблицу 1.

  1. Провести операции согласно пунктам 1-7 порядка работы на установке (см. раздел «Описание установки и метода измерений»). Полученные значения N и t для первого тела занести в таблицу 1.

  2. Еще два раза определить N и t (операции по пунктам 4-7 порядка работы на установке) и занести их в те же колонки.

  3. Рассчитать значения периодов колебаний T1 как отношение t/N и их среднее значение T1ср. Занести их в таблицу 1.

  4. Повторить предыдущие операции (1-4) для другого диска, занося значения Jт2, N, t, T2 и T2ср в таблицу 1 («Второе тело»).

  5. Используя полученные значения Jт1 , Jт2 , Т1 и Т2 , по формуле (20) рассчитать и занести в таблицу 1 значение модуля кручения D.

  6. Методом косвенных измерений найти абсолютную и относительную погрешности измерений.

Таблица 1.

№ п/п

Первое тело

Второе тело

D, Нм

Jт1, кг·м2

N

t, с

T1 , с

T1ср , с

Jт2, кг·м2

N

t, с

T2 , с

T2ср , с

1

2

3

Задание 2.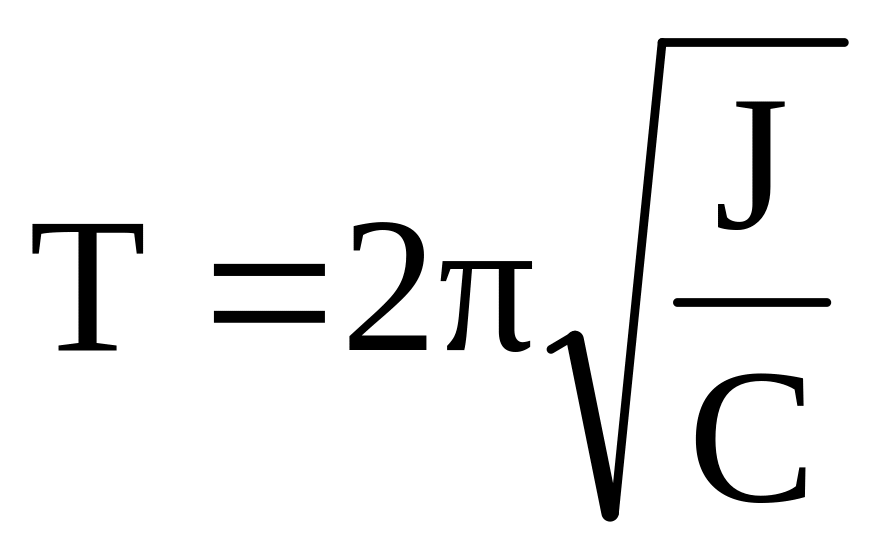 Определение момента инерции пустой рамки.

  1. Освободить рамку от дополнительных тел и три раза определить значения N и t для пустой рамки (аналогично тому, как это делалось в предыдущем задании для рамки с телом) и занести их в таблицу 2.

10

  1. Определить три значения периода колебаний пустой рамки T0, рассчитать их среднее значение T0ср и занести эти данные в таблицу 2.

  2. Тремя способами определить значение момента инерции пустой рамки:

а) используя полученное значение периода колебаний T0ср и значение D из таблицы 1, рассчитать Jр0 по формуле, аналогичной формуле (18):

Jр0 = (Т0ср)2D/(42)

б) используя значения Jт1, Т1 и D из таблицы 1, рассчитать Jр1 по формуле, полученной из формулы (19а):

Jр1 = Т12 D/(42) – Jт1

в) используя значения Jт2, Т2 и D из таблицы 1, рассчитать Jр2 по формуле, полученной из формулы (19б):

Jр2 = Т22 D/(42) – Jт2

  1. Сравнить полученные значения Jр0, Jр1 и Jр2; рассчитать из них среднее значение момента инерции пустой рамки Jр-ср и занести его в таблицу 2.

  2. Вычислить абсолютную и относительную погрешности.

Таблица 2.

№ п/п

N

t , с

T0 , с

T0ср , с

Jр0 , кг·м2

Jр1 , кг·м2

Jр2 , кг·м2

Jр-ср , кг·м2

1

2

3

Задание 3. Определение момента инерции тела.

  1. Закрепить исследуемое тело – прямоугольный параллелепипед – в рамке, совместив с осью вращения одну из главных осей инерции данного тела. Три раза определить N и t (так же, как это делалось в предыдущих заданиях) и занести эти значения, а также соответствующие им значения T = t/N, для оси № I в таблицу 3.

11

  1. Повторить проделанные операции для двух других главных осей инерции исследуемого тела. Полученные значения N, t и T для оси № II и для оси № III занести в таблицу 3.

  2. Для всех трех осей из трех значений периода колебаний рамки с телом T рассчитать их средние значения Tср и занести эти данные в таблицу 3.

  3. Рассчитать и занести в таблицу 3 значения моментов инерции рамки с исследуемым телом J, рассчитанные по формуле (18): J = (Тср)2D/(42)

  4. Используя полученное ранее среднее значение момента инерции рамки Јр‑ср (таблица 2), из соотношения Јт = Ј – Јр‑ср определить значения моментов инерции тела Јт относительно трех его главных осей инерции и занести эти значения в таблицу 3.

Таблица 3.

№ оси

№ п/п

N

t, с

T, с

Tср , с

J, кг·м2

Jт, кг·м2

1

I

2

3

4

II

5

6

7

III

8

9

12

Контрольные вопросы для подготовки к работе:

  1. Какая величина называется моментом инерции материальной точки и твердого тела?

  2. По какому закону происходят крутильные колебания?

  3. Что такое модуль кручения и от чего он зависит?

  4. Какие величины измеряют в данной работе, какие вычисляются и по каким формулам?

Контрольные вопросы для защиты работы:

  1. Что такое момент инерции и каков физический смысл этой величины?

  2. Каковы единицы измерения момента инерции?

  3. Что называется упругой деформацией?

  4. Вывести формулу для определения модуля кручения.

  5. Какова природа крутильных колебаний и по какому закону они происходят?

  6. Что называется моментом импульса тела? Как он направлен?

  7. В чем состоит теорема Штейнера?

  8. Написать формулу периода крутильных колебаний.

УЧЕБНОЕ ИЗДАНИЕ

Макаров Игорь Евгеньевич, д.х.н. профессор

Юрик Тамара Константиновна, к.х.н. доцент

Крутильные колебания — для чего нужен гаситель?

Крутильные колебания или вибрации возникают в процессе вращения коленчатого вала из-за его неравномерной по разные стороны формы и маховика. В этой статье мы поговорим о том, откуда они возникают, чем опасны, и расскажем об устройстве, снижающим воздействие этих вибраций – гаситель крутильных колебаний.

Что такое крутильные колебания?

Любой маховик двигателя имеет определенную массу, которая не в полной мере сочетается с коленчатым валом мотора. При вращении коленвала, маховик, обладая большой массой, начнет колебаться, что приводит к появлению определенных вибраций не только на нем, но и на валу. Частота и амплитуда колебаний будет напрямую зависеть от массы маховика, а также его радиуса. Чем больше расстояние от края до центра и больше масса маховика, тем выше эта частота колебаний.

При уменьшении воздействия, которое прилагается от поршней и шатунов, уменьшаются и вибрации. Логично предположить, что если не прилагать большую нагрузку на коленвал, от этих вибраций можно избавиться, однако мы не в состоянии постоянно снижать нагрузку на вал, так как автомобиль все время находится в движении. Данный вид колебаний, получаемых при воздействии на маховик внешних сил, называется вынужденным.

Опасным явлением, в которое могут перерасти колебания – это резонанс. В процессе вращения маховика, он находится в механической связи с первичным валом коробки передач. Вал КПП также имеет небольшую величину вибраций, которая взаимно передается на маховик коленвала. Если эти колебания совпадают, это приводит к резонансу – пропорциональному повышению колебаний обоих механических элементов и, как следствие, к разрушению обоих валов.

Гаситель крутильных колебаний

Как вы поняли, совпадение частот этих вибраций совершенно не допустимо, именно поэтому в трансмиссии автомобиля предусмотрено специальное устройство – демпфер. Он устанавливается на диске сцепления автомобиля и имеет специальную конструкцию. Задача демпфера заключается в создании самой упругой связи диска сцепления с его небольшой ступицей на коленчатом валу.

Демпфер представляет собой пружины цилиндрической формы, которые по кругу устанавливаются на всей внутренней окружности диска сцепления. Пружины гасителя обеспечивают защиту трансмиссии автомобиля от совпадения частот колебаний маховика и сцепления на больших оборотах вращения коленвала. Однако, такое устройство не способно обеспечить надежную защиту при низких частотах колебаний. Специально для этого служить другое устройство, которое называется поглотитель низкочастотных колебаний.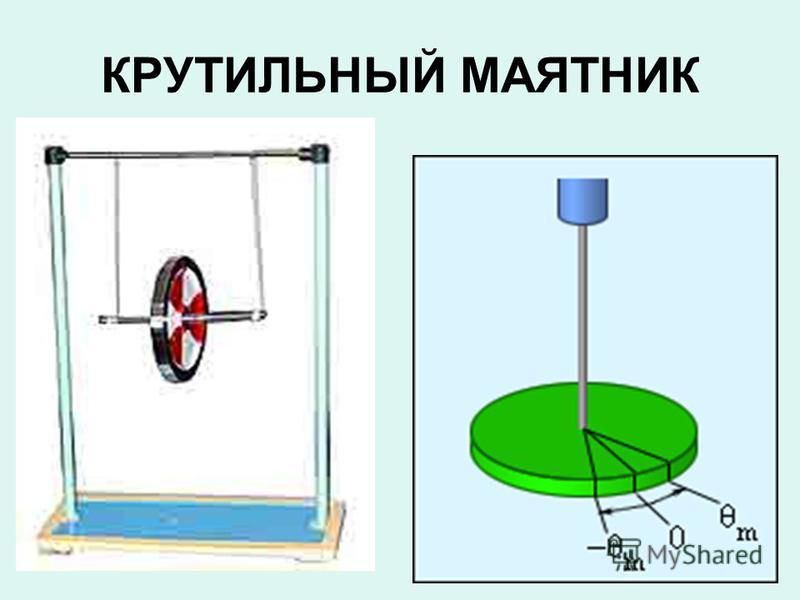

В грузовых же автомобилях на сцеплении вместо демпферных пружин применяются круглые, сжимаемые при скручивании элемента. Главное отличие от демпфера – это отсутствие необходимо проводить широкую регулировку элемента. Такая пружина в процессе вращения сжимается и с помощью повышения трения передает вращающий момент на первичный вал КПП.

Видео — Теория ДВС: Коленвал часть 2, «Гаситель крутильных колебаний»

Вот так происходит снижение крутильных колебаний в двигателе и трансмиссии автомобиля при эксплуатации. Как видим, здесь нет ничего сложного или непонятного. Желаем вам удачи на дорогах!

Как не допустить крутильные колебания трансмиссии Текст научной статьи по специальности «Механика и машиностроение»

ТРАНСПОРТ

УДК 629.113-527 (07) Б.М. Тверсков

Курганский государственный университет

КАК НЕ ДОПУСТИТЬ КРУТИЛЬНЫЕ КОЛЕБАНИЯ ТРАНСМИССИИ

Аннотация

Крутильные колебания трансмиссии вызывают повышенный износ зубьев шестерен, во много раз превышающий износ, который бывает, когда колебания передаваемого крутящего момента отсутствуют. Особенно сильно изнашиваются зубья шестерен редукторов, расположенных рядом с двигателем, например, согласующего редуктора гидропередач. Существующие способы устранения отрицательного влияния крутильных колебаний направлены в основном на недопущение поломок деталей трансмиссии при ре-зонансах. В статье рассматривается способ, позволяющий исключить появление крутильных колебаний трансмиссии транспортных машин.

Ключевые слова: крутильные колебания, трансмиссия, амплитуда, жесткость, трение, резонанс, демпфер.

B.M. Tverskov Kurgan State University

DAMPENING OF TRAMSMISSION TORSIONAL VIBRATIONS

Annotation

Torsional vibrations of transmission cause the increased wear of gear teeth, which is many times as high as the wear, which occurs when there are no vibrations of transmitted torque. The gear unit teeth located near the engine is subject to especially severe wear, e.g. the matching hydrolic transmission gear unit teeth. The present methods of eliminating of the negative effect of torsional vibrations mostly target the prevention of breakage of transmission gear parts during resonance. The article examines the method, which enables to exclude the appearance of torsional vibrations of transmission in transport vehicles.

Keywords: torsional vibrations, transmission, amplitude, rigidity, friction, resonance, damper.

Крутильные колебания трансмиссии транспортных машин, особенно если появляется резонанс, нередко являются причиной разрушения валов и шестерен. Вызывающие крутильные колебания трансмиссии колебания момента двигателя зависят от угла отклонения от равномерного вращения коленчатого вала (маховика) и от жесткости соединяющего двигатель и трансмиссию демпфера. Произведение угла неравномерности на жесткость демпфера равно амплитуде колебания воздействующего на трансмиссию крутящего момента. Чем больше жесткость, тем больше амплитуда колебаний.

Неравномерность вращения коленчатого вала — величина определённая, она зависит от уравновешенности двигателя, т.е. от размеров маховика, числа цилиндров, наличия или отсутствия гасителя крутильных колебаний на носке коленчатого вала и т.д. Для каждого типа

двигателей неравномерность индивидуальна. При работе с максимальной мощностью для различных двигателей угол отклонения составляет от нескольких минут до 10. При резонансных колебаниях этот угол может быть значительно больше и достигать 5 и даже 100.

Жесткость демпфера определяется углом его закрутки под действием максимального крутящего момента двигателя, т.е. углом относительного поворота ведомой и ведущей частей демпфера, когда сжимаются установленные между ними пружины или закручивается соединяющий двигатель и трансмиссию торсион. В современных демпферах угол закрутки бывает обычно в пределах 2-50, редко больше, после чего витки тангенциально расположенных в демпфере пружин упираются один в другой и демпфер выключается или, если двигатель и трансмиссия соединены торсионом, закручивание торсиона прекращается, когда момент становится равным моменту двигателя.

Так как уменьшить угол неравномерности вращения коленчатого вала потребитель двигателей не может, для снижения амплитуды колебаний поступающего на трансмиссию крутящего момента остается увеличить угол закрутки демпфера, снизив таким образом его жесткость. Вследствие же того, что угол неравномерности вращения маховика конкретного двигателя достаточно постоянный, при снижении жесткости во столько же раз уменьшается и амплитуда колебаний поступающего на трансмиссию крутящего момента двигателя.

После снижения жесткости демпфера до определенной величины амплитуда колебаний поступающего на трансмиссию крутящего момента двигателя становится столь малой, что она не в состоянии приводить трансмиссию в колебательное движение. Для этого нужно, чтобы момент трения в первом же агрегате трансмиссии был равен или превосходил амплитуду колебания подведенного от двигателя крутящего момента. Тогда крутильные колебания трансмиссии появиться не могут.

Определить трение в агрегате можно следующим образом. Трение складывается из трения между зубьями передающих крутящий момент шестерен, трения в подшипниках, борбатажа масла. Наибольшим среди этих составляющих является трение между зубьями. Для одной пары цилиндрических шестерен в зависимости от качества обработки поверхности зубьев при изготовлении и притирке в процессе работы момент трения равен 1-1,5% от величины передаваемого крутящего момента.

В установленном сразу за двигателем 1 (рис. 1) согласующем редукторе (повышающей передаче) 2 тягачей КЗКТ крутящий момент передается через два зубчатых зацепления. Кроме того, в согласующем редукторе сделан привод вентиляторов системы охлаждения двигателя 4, от промежуточного вала приводится насос рулевого управления 7. Общие потери в согласующем редукторе составляют порядка 8-10% от передаваемого крутящего момента, что от максимального крутящего момента двигателя 2500 Н • м составляет 200-250 Н • м.

Рис. 1. Дотрансформаторная зона трансмиссии четырехосного тягача КЗКТ: 1 — двигатель; 2 — согласующий редуктор; 3 — муфта для

отключения трансмиссии; 4 — привод вентиляторов системы охлаждения двигателя; 5 — шестерня привода; 6 — демпфер; 7 — насос усилителя рулевого управления; 8 — карданный вал; 9 — насосное колесо гидротрансформатора; 10 — торсион

При отсутствии резонанса колебаний неравномерность вращения коленчатого вала тягачей находится в пределах около 10. Величина жесткости соединяющего двигатель и согласующий редуктор торсиона — 1000 НЧм/ град. Таким образом, амплитуда колебания подведенного к согласующему редуктору крутящего момента близка к 1000 Н • м, что превышает момент трения в согласующем редукторе примерно раз в 5. Такая амплитуда достаточна, чтобы приводить трансмиссию в интенсивное колебательное движение.

Исключить крутильные колебаний трансмиссии можно, если уменьшить амплитуду колебания подводимого крутящего момента на эту величину или более, для чего угол закрутки соединяющего двигатель и трансмиссию торсиона должен быть увеличен с 50, как это есть в существующей конструкции, до значения не менее 400. С учетом же различного рода неточностей угол закрутки должен быть значительно больше и составлять 90…120°. В этом случае крутильные колебания трансмиссии появиться не могут.

Такой способ означает принципиально иной подход к вопросу сохранения трансмиссии от разрушительного действия крутильных колебаний. В известном, широко используемом способе задача решается лишь частично. Крутильные колебания в этом способе не устраняются, а только снижаются, причем в основном — при резонансах. За счет работы элемента трения демпфера амплитуда колебаний при резонансах уменьшается в несколько раз. В данном же случае ставится задача исключить появление крутильных колебаний трансмиссии, а не бороться с ними, когда они уже есть.

При существующем способе трансмиссия подвержена значительным крутильным колебаниям и тогда, когда резонансы отсутствуют. Постоянно действующие на трансмиссию колебания крутящего момента маховика ведут к интенсивному износу зубьев шестерен согласующего редуктора. Ни в одном из агрегатов трансмиссии тягачей нет столь большого износа зубьев шестерен, как это имеет место в расположенном сразу за двигателем согласующем редукторе, хотя с некоторыми из использовавшихся типов двигателей значительные резонансы не отмечались. Если появляющийся резонанс колебаний опасен из-за возможных поломок трансмиссии, то безрезонансные, но постоянные колебания ведут к большим

износам зубьев, находящихся в зацеплении шестерен согласующего редуктора.

Кроме того, для определения величины момента трения в демпфере по существующей методике необходимо провести большой и сложный расчет трансмиссии на крутильные колебания. В предлагаемом способе, где крутильные колебания коленчатого вала передаваться на трансмиссию не могут, такой расчет не требуется. Ненужным становится и элемент трения в демпфере. Достаточно сделать угол закрутки демпфера таким, чтобы амплитуда подводимого к трансмиссии крутящего момента была меньше, чем момент трения в трансмиссии. Демпфер становится лишь упругим соединением двигателя и трансмиссии, а подготовленное соединение может использоваться для различных однотипных машин.

Двигатель является главным источником колебаний трансмиссии. Другим тоже достаточно сильным источником являются ведущие колеса автомобиля, когда они катятся по неровной поверхности. Но, как показали проведенные исследования, создаваемые ведущими колесами крутильные колебания трансмиссии быстро затухают по мере удаления от колес, хотя на полуосях они могут быть очень большие. Частота таких колебаний несоизмеримо меньше, чем маховика двигателя. На карданном валу между раздаточной коробкой и коробкой передач крутильные колебания от колес незначительны и влиять на колебания валов коробки передач они практически не могут, не говоря уже о колебаниях валов согласующего редуктора. Износ зубьев шестерен колесного редуктора небольшой, он не идет ни в какое сравнение с интенсивным износом зубьев шестерен согласующего редуктора.

Остальные источники крутильных колебаний (карданные шарниры, зубчатые передачи и т.п.) по сравнению с колебаниями от двигателя и от колес несущественны.

Для снижения жесткости демпфера в 40-50 раз, что необходимо для исключения крутильных колебаний трансмиссии, подходящими могут быть демпферы с центральной винтовой или спиральной пружинами. Углы закрутки этих демпферов находятся в пределах указанных выше значений или более. Конструкции таких демпферов приведены на рис. 2 и 3.

Рис. 2. Демпфер с винтовой пружиной: 1 — торсион; 2 — ступица; 3 — пружина; 4 — фланец

Показанные на этих рисунках демпферы предназначены для установки снаружи согласующего редуктора на его трубчатом входном валу — рис. 1. Торсион 10 на рис. 1 соединяет демпфер и двигатель. Через показанное на рис. 2 шлицевое соединение крутящий момент с торсиона передается на ступицу 2, далее — на закрепленную на ступице пружину 3 и на установленный на входном валу согласующего редуктора фланец 4. Аналогично

СЕРИЯ «ТЕХНИЧЕСКИЕ НАУКИ», ВЫПУСК 5

23

устроен и демпфер со спиральной пружиной.

Для изготовления винтовой пружины более подходящим является пруток прямоугольного сечения, т.к. пруток круглого сечения может не проходить по изгибным напряжениям. Наружный диаметр винтовой пружины меньше, чем спиральной, поперечные силы, которые появляются при закручивании спиральной пружины, в винтовой пружине отсутствуют, но демпфер с винтовой пружиной длиннее.

Рис. 3. Демпфер со спиральной пружиной: 1 — торсион; 2 — ступица; 3 — пружина; 4 — корпус; 5 — кольцо;

6 — гайка; 7 — фланец

Спиральная пружина (рис. 3) позволяет создать короткий демпфер, иметь большой угол закрутки и малые изгибающие напряжения в ленте. Чтобы при передаче крутящего момента не происходило боковое смещение ступицы демпфера, на корпусе сделаны соответствующие направляющие. Между витками спиральной пружины имеется зазор, поэтому графитовая смазка не требуется. Внутренний конец спиральной пружины отогнут и входит в паз на ступице 2. Гайкой 6 внутренний виток спиральной пружины, имеющий по краям скосы, плотно прижимается к цилиндрической части ступицы конусными полками на кольце 5 с одной стороны и на ступице 2 с другой. Наружный конец спиральной пружины входит в паз на корпусе 4 и болтом 8 крепится к корпусу. От бокового смещения ступица 2 удерживается за счет имеющихся на корпусе и ступице цилиндрических направляющих поверхностей, с которыми контактируют эти детали.

Итак, для того чтобы на трансмиссию транспортной машины не могли передаваться крутильные колебания коленчатого вала двигателя, жесткость соединяющего двигатель и трансмиссию демпфера необходимо снизить до величины, при которой амплитуда колебания крутящего момента двигателя будет меньше, чем момент трения в первом же агрегате трансмиссии. Для этого угол закрутки демпфера под действием максимального крутящего момента двигателя должен быть не менее четверти оборота. Тогда амплитуда подведенного к трансмиссии крутящего момента двигателя оказывается настолько малой, что она не может вызвать крутильные колебания, что исключает появление резонанса, а также большого износа зубьев шестерен согласующего редуктора, не требуется выполнять и сложнейший расчет на крутильные колебания трансмиссии, чтобы определить величину момента трения, устанавливаемого в демпфере элемента трения.

УДК 629.113 С.П. Жаров

Курганский государственный университет

ФОРМИРОВАНИЕ УСЛУГ ПО ТО И РЕМОНТУ АВТОМОБИЛЕЙ В АВТОСЕРВИСНЫХ ПРЕДПРИЯТИЯХ

Аннотация

В статье рассмотрены вопросы формирования услуг по ТО и ремонту автомобилей на СТОА, на основе разделения услуги на процессы обслуживания клиента и работы по ремонту автомобилей, с повышением уровня индивидуальной работы с каждым клиентом на всех этапах оказания услуги.

Ключевые слова: автомобиль, услуга, заказчик, обслуживание.

S.P. Zharov

Kurgan State University

FORMATION OF CAR MAINTENANCE AND REPAIRS IN THE SERVICE CENTERS

Annotation

In article question of formation of car maintenance services and car repairs in serviciу centers on the basis of division of service into processes of service of the client and work on car repairs, with increase of level of individual work with each client at all service stages rendering are considered.

Key words: car, services, client, quality.

ВВЕДЕНИЕ

Услуга — это результат взаимодействия исполнителя и заказчика и собственная деятельность исполнителя по удовлетворению потребности заказчика.

Принципиально важным для формирования систем обслуживания является фактор потребительского спроса. Ожидания заказчиков устанавливаются на уровне высоких стандартов обслуживания лучших предприятий в отрасли. Заказчики будут требовать высокого уровня качества обслуживания по более низкой цене. Заказчик должен быть уверен в том, что ему стабильно будет предоставляться обслуживание требуемого или декларируемого уровня.

При организации деятельности по обеспечению требуемого уровня обслуживания необходим системный подход к комплексу факторов. Такой подход дает возможность поддерживать требуемый уровень обслуживания на протяжении всего цикла выполнения заказов, обеспечивает увязку их по конечному результату, определяемому системой внутрифирменных стандартов, а также требованиями потребителей, сформулированными в заказе.

1. Формирование услуги в автосервисе

Понять сущность услуг автосервиса по ТО и ремонту автомобилей можно на основе анализа процесса удовлетворения потребностей автовладельцев (рис.1). Данный процесс включает в себя операции: информационные, связанные с определением способа и поиском возможностей удовлетворения потребностей; организационные, необходимость в которых возникает в связи с орга-

Королевские широты, закон Шперера и крутильные колебания на Солнце как проявление приливов от планет — статья

Королевские широты, закон Шперера и крутильные колебания на Солнце как проявление приливов от планет — статья | ИСТИНА – Интеллектуальная Система Тематического Исследования НАукометрических данных

Королевские широты, закон Шперера и крутильные колебания на Солнце как проявление приливов от планетстатья

  • Автор: Хлыстов А.И.
  • Сборник: Солнечная и солнечно-земная физика 2014
  • Год издания: 2014
  • Место издания: Главная (Пулковская) астрономическая обсерватория РАН Санкт-Петербург
  • Первая страница: 459
  • Последняя страница: 462
  • DOI: ISSN 0552-5829 ISBN 978-5-9651-0874-9
  • Аннотация: Впервые гипотеза о приливном влиянии планет на Солнце была высказана Р. Вольфом в 1859 году в связи с попыткой объяснить феномен 11-летней цикличности приливами от Юпитера, Венеры и Земли. Позже эта идея развивалась в работах многих авторов, однако, без заметного успеха. В настоящей работе впервые изложен новый подход к исследованию планетного влияния на Солнце: вместо поисков корреляций между высотами солнечных циклов и высотой прилива от планет, как это делалось до сих пор, рассмотрен вопрос о том, какие проявления динамического прилива от планет следует ожидать на Солнце. На основании численных расчетов было показано, что следствием зонального прилива от Юпитера на Солнце являются три фундаментальных наблюдательных факта: крутильные колебания, движение полярных факелов к полюсам Солнца и закон Шперера. Известно, что в современных моделях процесса генерации магнитных полей (механизм солнечного динамо) указанные процессы в той или иной степени учитываются путем введения дополнительных параметров подгонки. Это позволяет достаточно удовлетворительно описывать отдельно взятый цикл солнечной активности, однако для прогностических целей этого недостаточно в силу того, что будущее поведение вводимых параметров неизвестно. В то же время, приливные эффекты можно рассчитать на любое количество лет вперед, и потому есть надежда, что при надлежащем их учете в уравнениях солнечного динамо прогноз солнечной активности окажется более успешным. On the basis of consideration of zonal tide from the Jupiter it is established, that in the convective zone of the Sun torsional oscillations with opposite directed movements of the equatorial belt (from φ = –35°16′ up to φ =+35°16 ‘) and two subpolar areas (from φ = + 35°16′ up to North Pole and from φ = – 35°16’ up to the South Pole) can arise. Change of a direction of relative movement of these belts should occur practically instantly through each quarter of the orbital period of the Jupiter (≈ 3 years) at the moments of zero and extreme values of the heliocentric equatorial latitudes of Jupiter. On the parallels φ = ± 35°16’ (“Royal latitudes”) velocities are always equal to zero. Gradients of pressure along a latitude, induced by torsional oscillations, can create 3 types of poloidal currents: from «Royal latitudes» to equator (Schpörer’s law), from «Royal latitudes» to the latitudes φ = ± 62°.5, and from poles to the latitudes φ = ± 62°.5. It is important to note, that directions of movements in these 30° zones are kept constant at any mutual positions of the Jupiter and the Sun.
  • Добавил в систему: Хлыстов Анатолий Ильич

Крутильные колебании Формулы — Энциклопедия по машиностроению XXL

Модуль сдвига G может быть, так же как и модуль упругости Е, определён радиотехническим методом. Модуль G связан с частотой собственных крутильных колебаний формулой, аналогичной приведённой на стр. 51  [c.60]

Действительно, модуль сдвига С связан с частотой крутильных колебаний формулой  [c.245]

Однако следует считать, что если уменьшение о происходит за счет увеличения то это является чрезвычайно выгодным, так как критическая скорость (не приведенная) прямо пропорциональна собственной частоте крутильных колебаний [формула (2 1)].  [c.249]


Тогда период и частота крутильных колебаний системы, согласно формулам (20.11), в которых вместо I следует подставить выражение для а (или Ь), будут следующими  [c.537]

Основное практическое значение для валов имеют расчеты частот собственных колебаний для предотвращения резонанса колебаний, т. е. нарастания амплитуд колебаний при совпадении или кратности частоты возмущающих сил и собственной частоты колебаний. В валах наблюдаются поперечные или изгибные колебания, а также изгибно-крутильные колебания. Частоты собственных колебаний для простейших валов и осей подсчитывают по формулам, приведенным в табл. 16.10.  [c.333]

Чтобы получить формулу, не содержащую коэффициента с, надо определить путем наблюдений период крутильных колебаний эталона 7i и период крутильных колебаний испытуемой детали Гг-Тогда по формуле (82.5)  [c.220]

Второй член в правой части этого равенства выражает вынужденные крутильные колебания. Амплитуда h и начальная фаза р этих вынужденных колебаний, согласно сказанному в 3 главы И, определяются по формулам  [c.347]

При отсутствии момента сопротивления нужно в уравнениях н формулах третьей группы задач положить ц = п = 0. Тогда дифференциальное уравнение крутильных колебаний имеет вид ар = Н sin (pt), а его общее решение  [c.347]

Амплитуда вынужденных крутильных колебаний будет определяться по формуле Ь .  [c.348]

Так кяк но условию задачи при данной частоте р наблюдается резонанс, причем амплитуда вынужденных крутильных колебаний диска равна ф, то по вышеуказанной формуле  [c.348]

Для получения уравнений вынужденных крутильных колебаний дисков вычисляем амплитуды составляющих гармонических колебаний этих дисков по формуле (28.4). Тогда  [c.138]

Для облегчения понимания вопроса виброизоляции машин рассмотрим случай колебания системы только по одной оси координат с исключением крутильных колебаний. Колебательная система состоит из массы т и упругости (называемой также жесткостью) k. Такие системы носят название систем с одной степенью свободы Приведем для этой системы те исходные формулы, из которых получены зависимости, используемые далее при расчетах  [c.104]

Такое дифференциальное уравнение мы рассматривали неоднократно, последний раз — при исследовании продольных и крутильных колебании упругого стержня. Среди рассмотренных там случаев находится также случай, в котором должны быть выполнены такие же граничные условия, как и здесь определенное уже частное решение, а также все, что было сказано о возможных простых тонах и соответственных узлах, годится и здесь. Из указанных там частных решений мы составим теперь более общее для поперечных колебаний струны. Чтобы несколько сократить формулы, введем такие единицы длины и времени, чтобы / = л и продолжительность простого колебания при основном тоне была равна я. Тогда одним частным решением будет  [c.368]


Общие формулы. Пусть имеется среда, в которой могут существовать п независимых волн с постоянными распространения к[, /с2,…, кп. Примеры таких сред рассмотрены в главе 5. Продольные волны в стержне согласно теории Бернулли соответствуют случаю п = 1. Для его изгибных и крутильных колебаний п = 2. Для стержней несимметричных профилей п может равняться шести и т. д. Волновое движение такой среды описывается п обобщенными смещениями ui, U2,.. Un, являющимися функциями времени и пространственной координаты х. Ограничиваясь гармоническими процессами, в которых все величины имеют множитель ехр —iat), зависимости между ними удобно записывать в векторной форме. Обозначив через и (х) вектор-столбец, име-  [c.169]

Значение символов в формуле (IX. 5) можно найти на фиг. 117. Вся трудность решения задачи заключается в совместном решении уравнений (IX. 4) и (IX. 5). В. П. Терских дает графический метод решения этой системы уравнений. Однако он очень трудоемок и не позволяет сразу оценить влияние различных параметров нелинейного соединения на крутильные колебания при передаче им среднего крутящего момента, что и имеет место в исследуемой муфте.  [c.230]

Примеры амплитудных, фазовых, векторных диаграмм и промежуточных вычислений по компонентам числителей для некоторых случаев двухмассовых систем (с обозначениями по крутильным колебаниям) показаны на фиг. 1. 8—1. 10. Кривые фаз приведены как по компонентам числителей (е — ) и знаменателей (—Ёд) выражений амплитуд (1. 45) и (1. 46), так и для полных фаз, находимых по формулам (1. 31) и (1. 32) по разностям предыдущих.  [c.49]

Для случая г) на фиг. 1, 12 даны амплитудные и фазовые кривые свободной системы из трех масс при возбуждении на второй массе по формулам (1. 57) с обозначениями по крутильным колебаниям.  [c.61]

При действии же момента возбуждения на -й массе sin со/ амплитуды вынужденных крутильных колебаний для i-й массы Ф,-, ft определяются по формулам пропорциональности [1], [14]  [c.72]

Рис. 11.114. Поглотители крутильных колебаний. В пружинном поглотителе (рис. 11.114, а) упруго подвешенный маховичок I свободно вращается» на хвостовике вала 2. Поглотитель может быть настроен только на одну фиксированную частоту возмущения. В маятниковом поглотителе (рис. 11.114, б) центробежное силовое поле подобно гравитационному для обычного маятника. Если в формуле
Сравнивая приведенный вывод и полученные уравнения с выводом уравнений продольных колебаний (5.01, 5.49 а,Ь, с), можно увидеть полную аналогию в основных уравнениях обеих задач. Можно также увидеть, что друг другу соответствуют момент и сила, осевое перемещение и угол поворота, площадь сечения п момент инерции сечения, масса и массовый момент инерции, модуль упругости на растяжение или сжатие и модуль сдвига. Заменяя соответствующие величины, можно результаты, полученные при расчете продольных колебаний, распространить на крутильные колебания и наоборот. Уравнение (6.01 d) легко решается, если Ji x) меняется по закону. Из формулы (5.02Ь) можно сделать  [c.258]

Сравним полученные результаты со свойствами вала, у которого моменты инерции отдельных дисков распределены по всей его длине. Аналогично формуле (5. 03) для частоты собственных продольных колебаний свободного стержня, частота собственных крутильных колебаний свободного вала длиной L определяется по формуле  [c.275]

Применим полученные результаты для составления формул, необходимых для вычисления частоты собственных крутильных колебаний нескольких часто встречающихся устройств.  [c.276]

Для практических расчетов внутреннего затухания при крутильных колебаниях целесообразно преобразовать формулу (6. 61), введя в нее угол закручивания AF.  [c.300]


Перейдем к выяснению угловых колебаний фундамента под влиянием момента JJ h . Воспользуемся формулой для угловой амплитуды из теории крутильных колебаний  [c.150]

Хотя это уравнение выведено для схемы, показанной на рис. 1.1,6, но к аналогичному уравнению можно прийти при решении любой задачи о свободных колебаниях нелинейной системы с одной степенью свободы без трения. Так, для системы, совершающей крутильные колебания, в эту формулу вместо массы т нужно подставить момент инерции /, вместо перемещения X — угол поворота ф, вместо восстанавливающей силы Р х) — восстанавливающий момент М (ф).  [c.71]

Тот же принцип может быть применен и для гашения крутильных колебаний. Малый дополнительный диск может при надлежащей настройке служить динамическим гасителем крутильных колебаний двухмассовой системы (рис. IV.46). Если необходимо исключить колебания основной системы, подверженной возбуждению частоты 0), то, как следует из формулы (IV. 103), собственная частота гасителя ро, подсчитанная при неподвижности точки его крепления, должна быть равна частоте со, т. е.  [c.261]

Если кривая накопленной ошибки отличается от синусоиды, то, разлагая её в ряд Фурье, можно определить значения щ, вызываемые 2-й, 3-й, 4-й и т. д. гармониками крутильных колебаний. Для этого следует поочерёдно подставить в формулу (31д) в качестве соответствующие значения амплитуд ряда Фурье и вместо п соответственно 2т, Зи, 4/1 и т. д.  [c.284]

Часто местная накопленная ошибка или ошибка в окружном шаге имеет синусоидальный характер, например, когда ошибки в окружном шаге происходят вследствие эксцентричной посадки червяка делительной передачи зуборезного станка. В этом случае при близости системы к резонансу крутильных колебаний на зубьях может возникать значительная динамическая нагрузка, определяемая по формуле  [c.284]

В храповых стопорных механизмах двустороннего действия (храповых тормозах, рис. 98, а), характер крутильных колебаний будет отличаться от колебаний механизмов одностороннего действия, так как при колебаниях ведомой системы храповой останов двустороннего действия обладает одинаковой упругой податливостью как при вращении в одну сторону, так и в другую. Поэтому в кинематической цепи с храповым устройством двустороннего действия возможны крутильные колебания с переходом через нуль и при условиях близких к резонансу, нагрузки могут достигать довольно значительной величины, определяемой по формуле (402). Поэтому для устранения чрезмерно больших динамических нагрузок и повышения выносливости рабочих поверхностей и в этом случае необходимо подобрать жесткость так, чтобы обеспечивалось условие р ф ы или в общем виде (р ф ка,). Если учесть, что под действием демпфирования собственные колебания быстро затухают и остается только установившийся процесс вынужденных колебаний, постоянно поддерживаемый действием возмущающего момента, то второй член уравнения (401), будет равен нулю. Тогда уравнение примет вид  [c.181]

Крутильные колебания. Определение собственных частот крутильных колебаний длинного стержня или вала при различных условиях закрепления его концов и различных соотношениях моментов инерции масс, сосредоточенных на его концах, производится аналогично определению частот собственных продольных колебаний по формулам (1Г 3), (156) и (157). При этом формуле (153) соответствует формула  [c.366]

Частота собственных крутильных колебаний стержня постоянного сечения определяется по формуле  [c.400]

Умножив уравнение (176) на 0( ) и проинтегрировав в пределах от О до 1 с учетом граничных условий, получим формулу для нахождения круговых частот крутильных колебаний  [c.200]

Формула для определения частоты крутильных колебаний лопатки с защемленной вершиной имеет вид  [c.203]

Частоту свободных крутильных колебаний двухмассовой системы -определяют по формуле  [c.311]

Податливости участков различных форм, необходимые для расчета крутильных колебаний вала, можно вычислять по следующим формулам.  [c.319]

Величины 2 и з — частоты крутильных колебаний систем, представляющих собой вал с маховой массой J на одном конце и защемленным другим концом при крутильной жесткости с. Наибольшие значения сх2 и аз определяются формулами  [c.290]

По этой формуле можно найти момент инерции Ji i испытуемой детали, зная момент инерции эталона Ухсг и определив периоды крутильных колебаний Tj и Гг.  [c.220]

Собственная частота крутильных колебаний для системы с одной степенью свободы определяется по слеОующей формуле 01 = , откуда, учитывая, что с = GIJI.  [c.217]

По формулам (5.97), (5.100) для большинства рассмотренных режимов допускаемое значение критерия l7 /i] = [Л/il, имеет место резкое возбуждение крутильных колебаний вслед за зоной, в которой происходит смена знака ускорений. Физическая природа этого эффекта, связанная с резким изменением кинетической мощности ведомой части механизма, была изложена выше. Возбуждение колебаний на этих участках приобретает аварийный характер, когда нарушению отмеченного условия сопутствуют весьма низкие значения критерия Е (режим VIII).  [c.209]

Испытание на кручение может осуществляться с помощью наладок двух вариантов. Для жестких образцов, не требующих при испытании значительных динамических перемещений, используется вариант наладки с неподвижным креплением нагружаемой системы (рис. 68, б). Здесь воамущающее перемещение возбудителя 3 преобраэсюывается в крутильные колебания с помощью траверсы 9 (вид по Б). Для передачи крутящего момента на образец 6 служит жесткий вал, находящийся в корпусе 10. Конец динамометра 7 неподвижно закреплен в кронштейне 8. На концах траверсы 9 помещаются грузы k, величина которых подбирается по формуле (V. 9) так, чтобы момент инерции массы соответствовал возможно большему значению коэффициента эффективности.  [c.113]


Для испытания податливых деталей используется консервативная схема с креплением динамометра 7 (В подвижной системе, имеющей возможность совершать крутильные колебания в корпусе 11 (рис. 68, г). Моменты инерции массы 12 этой системы и траверсы ц выбираются по формуле (V. 11) таким образом, чтобы нагруженнЬсть и возмущающие перемещения возбудителя были минимальными при колебании обеих траверс в противоположных фазах. Правильно выбирая параметры колебательной системы, можно увеличить общий угол закрутки (при сравнении с предыдущим вариантом) в несколько раз и испытывать очень податливые детали, например многоопорные коленчатые валы двигателей внутреннего сгорания, полуоси задних мостов грузовых автомобилей и т. д.  [c.113]

Пренебрегая переуениостью кинетической энергии кривошипного механизма, мы допускаем некоторую ошибку. Н. Е. Кочин [24] показал, что под влиянием переменных значений кинетической энергии низшая полоса резонанса расширяется примерно на 5% [1]. Расчет крутильных колебаний с учетом переменности кинетической энергии обычно довольно сложный. Можно достичь некоторого упрощения, если предположить, что при резонансе форма колебаний вала с кривошипным механизмом будет примерно такой же, как у вала с дисками, момент инерции которых был вычислен по средней кинетической энергии. Выведем основную формулу движения, основываясь на этом предположении. Кинетическая энергия всего вала лриолиженно определяется формулой  [c.296]

Когда на винте приложены и возмущающий и демпфирующий моменты, то удобнее для подсчета работы сил трения воспользоваться формулой из книги И. А. Лурье Крутильные колебания в дизельных установках , Военмориз-дат, 1940,  [c.287]

Отсюда получаем формулу для определения собственных частот внутрипакетных крутильных колебаний лопаток переменного сечения, жестко защемленных в корневом сечении  [c.200]

Основным упрощающим предположением, вводимым ими при рассмотрении крутильных колебаний в приводе с гидромуфто11, является гипотеза статичности, заключающаяся в том, что, несмотря на существенно нестационарный характер процессов в приводе,. принимается справедливым турбинное уравнение Эйлера, записываемое в форме (1.3), и формула подобия (1.45). Рассмотрим такое рещение.  [c.286]

Крутильные колебания круглых композиционных и реологически активных стержней


Please use this identifier to cite or link to this item: https://elib.bsu.by/handle/123456789/178727

Title: Крутильные колебания круглых композиционных и реологически активных стержней
Authors: Кравчук, А. С.
Кравчук, А. И.
Тарасюк, И. А.
Keywords: ЭБ БГУ::ЕСТЕСТВЕННЫЕ И ТОЧНЫЕ НАУКИ::Физика
Issue Date: 2017
Citation: Прикладные проблемы оптики, информатики, радиофизики и физики конденсированного состояния : материалы четвертой Междунар. науч.-практ. конф., Минск, 11–12 мая 2017 г. / М-во образования Респ. Беларусь, НИУ «Ин-т приклад. физ. проблем им. А. Н. Севченко» Белорус. гос. ун-та; редкол.: В. И. Попечиц (гл. ред.), Ю. И. Дудчик, Г. А. Сенкевич. – Минск, 2017. – С. 258-260.
Abstract: Выполнено обобщение уравнения крутильных колебаний круглого стержня на случай произвольной длины стержня. Получено уравнение крутильных колебаний композиционного стержня, а также зависимость частоты собственных колебаний от характеристик его компонент. Установлено, что применение гипотезы Фойгта соответствует колебаниям волокнистого вдоль оси и коаксиально слоистого стержней, а применение гипотезы Рейсса – колебаниям поперечного слоистого стержня. Для сужения «вилки» Фойгта-Рейсса эффективных характеристик и решения задачи гомогенизации крутильных колебаний композиционного, изотропного в среднем стержня применен метод Кравчука-Тарасюка. Исследовано влияние реологического поведения материала стержня при крутильных колебаниях
Description: Секция 4. Прикладные проблемы физики конденсированного состояния
URI: http://elib.bsu.by/handle/123456789/178727
Appears in Collections:2017. Прикладные проблемы оптики, информатики, радиофизики и физики конденсированного состояния

Items in DSpace are protected by copyright, with all rights reserved, unless otherwise indicated.

Руководство для начинающих по анализу и тестированию крутильной вибрации

Какие общие приложения требуют анализа крутильных колебаний и испытаний на крутильные колебания?


Ситуации, когда могут потребоваться испытания на кручение, могут включать следующее:

[Выдержка из доклада по турбомашинному оборудованию 2009 г. «Предотвращение проблем крутильных колебаний в поршневых машинах» Т. Физа и К. Хилла]

  • Если происходит отказ какого-либо компонента, рекомендуется провести тестирование отремонтированной системы для выяснения причины (причин).
  • Если система представляет необычно высокие риски для жизни, другого оборудования или производственных процессов, необходимо провести испытания, чтобы гарантировать надежную работу. Это может быть прототип машины или существующая модель, работающая на более высоких скоростях или давлениях, чем ранее
    • .
  • Сюда могут входить системы с мягкими на кручение резиновыми муфтами и / или широким диапазоном скоростей или работой. Если на этапе анализа кручения из-за отсутствия чертежей и технической информации приходилось делать много предположений, для подтверждения результатов следует использовать испытания.
  • Новые системы, которые будут производиться серийно, должны быть испытаны в соответствии с требованиями. Гораздо проще исправить проблему с исходным устройством на заводе, чем модернизировать многие устройства, которые уже были отгружены клиентам.
  • Системы, которые были модифицированы или введены в другую службу, например, при повторном включении и / или изменении рабочих условий, должны быть повторно проанализированы или
  • Многие муниципалитеты имеют спецификации, требующие испытания новых агрегатов на крутильную вибрацию профессиональным специалистом.

В промышленных приложениях наиболее распространенным оборудованием, в котором важны испытания на крутильную вибрацию, являются двигатели с частотно-регулируемым приводом (VFD), приводящие в движение большие инерционные вентиляторы и поршневые двигатели / компрессоры.Для VFD проблемы могут возникнуть из-за настройки привода. Поршневые двигатели и компрессоры могут иметь гораздо более высокое возбуждение, чем вращающиеся механизмы. Наличие широкого диапазона рабочих скоростей увеличивает вероятность возникновения крутильного резонанса.

В морских приложениях испытания на крутильные колебания часто требуются на гребных валах для устранения проблем с движением или для количественной оценки чрезмерных вибраций, прогнозируемых компьютерной моделью крутильных колебаний. Измерения крутильных колебаний часто требуются, чтобы соответствовать определенным классификациям для новых построенных или повторно оснащенных судов.В разделе 7.9 Руководящих указаний ABS по вибрации судна подчеркивается: «Если измерения проводятся в соответствии с 4-3-2 / 7.5.8 Правил ABS для стальных сосудов, измерения крутильных колебаний должны проводиться либо на свободном конце движителя. механизмов, используя подходящий датчик крутильных колебаний, и / или на главном валу, используя тензодатчики. В качестве альтернативы, в зависимости от характеристик системы, для этой цели может использоваться механический торсиограф, приводимый в движение из подходящего положения вдоль вала или свободного конца.“

Торсионная вибрация — обзор

Непрерывная система — метод центральной конечной разности

Уравнения движения непрерывных систем представляют собой уравнения в частных производных с заданными граничными и начальными условиями. Поперечная вибрация троса (струны), продольная вибрация стержня (стержня) и крутильная вибрация вала (стержня) регулируются одним и тем же дифференциальным уравнением (Рисунок 3):

Рисунок 3. (A) Поперечная вибрация строки; (B) продольная вибрация стержня; (C) крутильные колебания вала; (D) крутильные колебания однородного вала; конечно-разностная сетка.

[33] A1∂2ϕ∂x2 + f (x, t) = B1∂2ϕ∂t2

где ϕ — поперечный прогиб (при колебании струны), осевое смещение (при продольной вибрации струны). бар) и крутильного прогиба (в случае крутильных колебаний вала), f ( x , t ) — это распределенная сила на единицу длины, A 1 — натяжение в струне (в случае поперечной вибрации струны), осевой жесткости, EA (в случае продольной вибрации стержня) и крутильной жесткости, GJ (в случае крутильной вибрации вала) и B 1 = масса на единицу длины (в случае поперечной вибрации струны), масса на единицу длины, ρA (в случае продольной вибрации стержня) и массовый полярный момент инерции на единицу длина, Дж 0 (при крутильных колебаниях вала).

Для конкретности рассмотрим крутильные колебания однородного вала с основным уравнением:

[34] GJ∂2θ (x, t) ∂x2 + f (x, t) = J0∂2θ (x, t) ∂ t2

, где GJ — жесткость на кручение, G — модуль сдвига, J — полярный момент инерции поперечного сечения, J 0 — ρJ , — полярная масса момент инерции вала на единицу длины, а ρ — плотность. Для свободной вибрации f ( x , t ) = 0 и уравнение (34) сокращается до:

[35] c2∂2θ∂x2 = ∂2θ∂t2

где:

[36] c = GJJ0 = Gρ

Решение уравнения (35) находится методом разделения переменных:

[37] θ (x, t) = U (x) T (t)

где U и T являются функциями только x и t соответственно.Использование уравнения (37) в уравнении (35) приводит к:

[38] c2Ud2Udx2 = 1Td2Tdt2 = a = constant

, которые можно переписать в виде двух отдельных уравнений:

[39] d2Udx2 − ac2U = 0

[40 ] d2Tdt2 − aT = 0

Константа α может быть доказана как отрицательная величина, так что a = — ω 2 . Решение уравнения (39) можно найти с помощью метода прямых конечных разностей следующим образом.

Разделите длину стержня l на n равных частей, как показано на рисунке 3D так, чтобы Δ x = h = l / n и x i = ih и U i = U ( x i ).Уравнение (39) можно переписать как:

[41] d2Udx2 + β2U = 0

с:

[42] β2 = ω2c2 = ρω2G

Аппроксимация центральной разности уравнения (41) в точке сетки i дает:

1h3 (Ui + 1−2Ui + Ui − 1) + β2Ui = 0

или:

[43] Ui + 1− (2 − λ) Ui + Ui − 1 = 0

где:

[44] λ = h3β2

Применение уравнения (43) в точках сетки 1, 2, 3… n −1 приводит к уравнениям:

[45] U2− (2 − λ) U1 + U0 = 0U3− (2 − λ) U2 + U1 = 0⋅⋅⋅Un − 1− (2 − λ) Un − 2 + Un − 3 = 0Un− (2 − λ) Un − 1 + Un − 2 = 0}

, который может быть выражен в матричной форме как:

[46] [- 1 (2 − λ) −100⋅⋅⋅0000−1 (2 − λ) −10⋅⋅⋅00000−1 (2 − λ) −1⋅⋅⋅000 ⋮⋮⋮⋮⋮ ⋱ ⋮⋮⋮ 00000⋅⋅⋅ (2 − λ) −1000000⋅⋅⋅ − 1 (2 − λ) −1] {U0U1U2 ⋮ Un − 1Un} = {000 ⋮ 00}

Граничные условия должны применяться к уравнению (46).Если вал зафиксирован на x = 0, мы устанавливаем U 0 = 0. Если вал свободен при x = 0, мы устанавливаем (d U / d x ) | 0 = 0. Используя формулу прямой разницы для d U / d x , это граничное условие становится эквивалентным установке U 0 = U 1 . Уравнение (46) после включения граничных условий может быть выражено как задача на собственные значения.Например, когда оба конца вала зафиксированы, мы имеем U 0 = U n = 0 и уравнение (46) сокращается до:

[47] [A − λI] U = O

, где:

A = [2−100⋅⋅⋅000−12−10⋅⋅⋅0000−12−1⋅⋅⋅000 ⋮⋮⋮⋮ ⋱ ⋮⋮⋮ 0000⋅⋅⋅ − 12−10000 ⋅⋅⋅0−12] U = {U0U1U2 ⋮ Un − 1Un}

и I = единичная матрица порядка n — 1. Уравнение (47) может быть решено для нахождения собственных частот ω и формы мод U .

Измерение и анализ вращательной и крутильной вибрации

Вибрации — это механические колебания, возникающие вокруг точки равновесия. Колебания могут быть периодическими или случайными.

Вибрации любого работающего механического устройства обычно нежелательны. Такие вибрации могут быть вызваны дисбалансом вращающихся частей, неравномерным трением, зацеплением зубьев шестерен … Мы можем минимизировать нежелательные вибрации с помощью правильной конструкции.

Мы можем разложить любую колебательную систему на элементарные части:

  • пружина — средство хранения потенциальной энергии (k)
  • масса — средство хранения кинетической энергии (м)
  • демпфирование — средство, с помощью которого энергия постепенно передается. потерян (c)

Вибрации можно классифицировать как:

  • свободные (после начального возмущения система остается вибрировать сама по себе) и принудительные (система подвергается воздействию внешней силы, часто повторяющейся сила)
  • демпфированные и незатухающие
  • линейные (все основные компоненты вибрационной системы, пружина, масса и демпфер ведут себя линейно) и нелинейные (один или несколько основных компонентов вибрационной системы не линейны)
  • детерминированная (величина возбуждения (силы или движения), действующего на колебательную систему, известна в любой момент времени) и случайная (величина возбуждения в любой момент времени не может быть предсказана — скорость ветра, неровность дороги и грунт nd движение во время землетрясения)

Когда система вибрирует со своей собственной частотой, она попадает в резонанс — она ​​колеблется с наибольшей амплитудой при той же силе возбуждения.

Величины, которые используются для описания вибраций:

  • смещение (в [м])
  • скорость (в [м / с])
  • ускорение (в [м / с2])

Все три величины напрямую связаны друг с другом: скорость является производной от смещения, а ускорение — производной скорости.

Крутильные колебания

Крутильные колебания — это угловые колебания объекта, обычно вала вдоль его оси вращения. Крутильные колебания оцениваются как изменение скорости вращения в пределах цикла вращения.Колебания числа оборотов обычно вызываются резким движущим моментом или изменяющейся нагрузкой.

Изображение 1: Торсионные колебания

Уровень крутильных колебаний зависит от ряда параметров, таких как свойства материала, условия эксплуатации (например, температура, нагрузка, частота вращения и т. Д.).

Крутильные колебания важны всякий раз, когда мощность должна передаваться с помощью вращающегося вала или муфт, например, в случае трансмиссии автомобилей, грузовиков и автобусов, транспортных средств для отдыха, морских трансмиссий или турбин для выработки электроэнергии.

Величины, которые используются для описания крутильных колебаний:

  • угловое положение (в [рад] или [°])
  • угловая скорость (в [рад / с] или [° / с] или [об / мин])
  • угловое ускорение (в [рад / с2] или [° / с2])

Все три величины напрямую связаны друг с другом и могут быть получены путем интегрирования и дифференцирования. Наиболее распространенной величиной, используемой для измерения крутильных колебаний, является угловая скорость или число оборотов в минуту.

Источник возбуждения определяется крутящим моментом.

Угловая скорость и смещение количественно определяют реакцию приложенного крутящего момента. Крутящий момент и угловая скорость связаны друг с другом:

Где T — крутящий момент в [Нм], а Jz — постоянная кручения или полярный момент инерции в [м4].

Эта формулировка аналогична формулировке закона Ньютона, который связывает силу, действующую на массу, с ускорением этой массы.

крутильные колебания | Примеры предложений

крутильной вибрации пока нет в Кембриджском словаре.Ты можешь помочь!

Торсионная Вибрация часто является проблемой в системах передачи энергии с вращающимися валами или муфтами, где она может вызвать отказы, если ее не контролировать. Из

Википедия