Напряжение в физике это: Электрическое напряжение

Содержание

Электрическое напряжение: объяснение простыми словами

Электрическим напряжением обозначается физическая величина, равная разности потенциалов между двумя точками электрического поля при перемещении единичного заряда. Для простых пользователь такое обозначение не всегда понятно. Поэтому в этой статье мы попытаемся простым, доступным языком рассказать, что собой представляет электрическое напряжение, как оно измеряется и для чего это нужно.

Что такое разность потенциалов?

Для начала проанализируем рисунок:

В первой бутылке вода находится на уровне 300 мм, а во второй – на отметке 150 мм. Разница между уровнями воды в обоих емкостях составляет 150 мм. Если рассматривать это с точки зрения науки об электричестве, это и есть разность потенциалов.

Однако, что будет, если соединить обе бутылки шлангом, а внутрь поместить обычный пластиковый шарик?

Из школьного урока физики о принципе соединяющихся сосудах знаем, что из бутылки, где уровень воды больше, жидкость постепенно перетечет в бутылку с более низким уровнем. Под воздействием потока воды шарик внутри соединяющего шланга будет перемещаться. Процесс перетекания завершится после того, как в обоих бутылках уровень жидкости уравновесится, станет одинаковым.

Иными словами, в ситуации, когда в соединенных между собой емкостях уровень жидкости станет одинаковым, результатом разности потенциалов станет ноль. Шарик останется на месте за счет электродвижущей силы, которая, по итогам эксперимента, равна нулю.

Что такое электродвижущая сила?

Аналогично напряжению, единицей измерения электродвижущей силы (ЭДС) является Вольт.

Для проведения следующего эксперимента понадобится вольтметр (прибор, измеряющий вольты) и обычная батарейка.

При исходном замере прибор покажет 1.5 В (Вольта). Однако это не является напряжением – значение указывает на величину электродвижущей силы.

На следующем этапе эксперимента к батарейке подключаются две лампочки. А напряжение измеряется в разных участках электроцепи.

Внимание следует уделить следующим показателям: напряжение для одной лампочки составляет 1 Вольт, для другой же это значение 0. 3 Вольта.

Напряжение в используемых нами осветительных устройствах напрямую зависит от их мощности, измеряемой в Ваттах.

Мощность=Напряжение*ток (Р=U*I)

Из этого следует, что чем больше будет значение мощности лампы, тем большее напряжение будет на ней.

Однако, как же получается: если мощность батарейки 1.5 Вольта, к которой подключены лампочки, разделена на 1 Вольт и 0.3 Вольта, куда направились еще 0.2 Вольта? Дело в том, что каждая батарейка наделена своим внутренним сопротивлением, поэтому недостающие 0.2 Вольта были направлены именно сюда.

Резюме

Электродвижущей силой определена физическая величина, характеризующая в источниках тока работу сторонних силовых ресурсов. Посредством электродвижущей силы мы можем определять, как переносится заряд от источника тока по всей электрической цепи. Напряжение показывает этот процесс лишь на отдельном участке этой цепи. Если проще: напряжение – это внешнее силовое воздействие, способствующее перемещению шарика в шланге, соединяющим сосуды из выше приведенного примера. В электричестве напряжение обозначено силой, которая обеспечивает перемещение электронов между атомами.

Рассмотрим еще один пример

Представьте, что вам по силам будет поднять камень, вес которого составляет 40 кг. Это означает, что вы обладаете подъемной силой, равной 40 кг – в электричестве это обозначается как электродвижущая сила. Вы следуете и на своем пути вам попадается камень весом 20 кг. Вы его также берете и переносите на расстояние 10 метров. Для осуществления этого действия вам понадобилось определенное количество энергии, что в электричестве представляется как напряжение. Далее вам попадается камень весом в 30 кг. Следовательно, для его переноса из одного места в другое вам понадобится больше энергии, чем для камня, масса которого не превышала 20 кг. Однако подъемная сила (в электричестве ЭДС), независимо от веса переносимого вами камня, остается всегда одинаковой. При этом, вес камня определяет количество энергии, которая тратится на проведение этого действия (в электричестве это обозначено напряжением). Таким образом, на каждом отрезке вашего пути вы будете испытывать разное напряжение в зависимости от веса камня, который вы намерены перенести.

Ток зависит от напряжения

Закон Ома:

Исходя из приведенной формулы следует: ток является прямо пропорциональным напряжению и обратно пропорциональным сопротивлению. Иными словами, чем больше величина электрического тока, тем больше напряжение, и наоборот.

формула и физический смысл величины, правила безопасности и единицы измерения

Физика

12.11.21

14 мин.

При проектировании различных устройств необходимо рассчитывать характеристики электричества. Для этих целей применяется законы Ома (для участка и полной цепи), позволяющие вычислять ток, сопротивление и электрическое напряжение. Формулы связывают последние параметры, а также могут быть полезны при решении задач по физике, электротехнике и микросхемотехнике.

Оглавление:

Правила безопасности

Влияние электричества на организм

Виды травм

Физический смысл

Формулы для вычислений

Тождества для переменного тока

Подготовка к обучению

Ключевым моментом перед изучением характеристик электричества являются правила безопасности, четкое выполнение которых позволит не только избежать несчастных случаев, но и спасет жизнь. Однако для понимания процесса следует подробно выяснить пагубное влияние тока на организм человека. Если начинающий физик будет владеть этой информацией, то он усвоит правила очень быстро.

Правила безопасности

Безопасность выполнения работ с монтажом и демонтажем приборов, которые работают от электричества, играет очень важную роль при сохранении жизни и здоровья. К ним относятся следующие:

Работа осуществляется только с обесточенными элементами цепи.
Запрещается работать в сырых помещениях.
Рекомендуется использовать заземление. Его сопротивление не должно превышать 4 Ом.
Соблюдать порядок на рабочем месте.
При измерении величины напряжения и тока не касаться токоведущих частей.
Под ногами должен быть прорезиненый коврик, а на руках — диэлектрические перчатки.
Работу нужно выполнять с инструментом, ручки которого изолированы.
При выполнении работ с высокими значениями напряжения запрещено работать одному.

Это только часть самых важных правил. Главное — быть внимательным и обдумывать каждое действие. Опытные электрики рекомендуют также ознакомиться с пагубным воздействием электричества на организм человека.

Влияние электричества на организм

Люди, работающие с электричеством, знают, что его опасность заключается в невидимости. Однако некоторые пробуют наличие напряжения посредством прикосновения.

Это плохая идея, которая может войти в привычку. Например, электрический прибор работает от напряжения, величина которого составляет 12 В. Однако произошел пробой изоляции и величина возросла до 220 В. Человек прикасается и становится жертвой электрического удара или травмы.

Однако величина тока и напряжения для каждого индивида являются разными. Одного может ударить 36 В, а для другого оно не опасно. Причина заключается в электрическом сопротивлении тела, которое зависит от нескольких факторов:

Внешняя среда.
Психологическое состояние.
Толщина кожи на пальцах.
Текущее состояние здоровья.
Путь прохождения.

Существуют другие факторы, играющие важную роль при увеличении вероятности поражения человека электричеством.

К ним относятся следующие:

Напряжение.
Ток.
Частота.

В первом случае среднестатистический показатель равен 36 В. Ток бывает постоянным и переменным. Первый является наиболее опасным.

Это обусловлено постоянным воздействием на организм человека. Если он является переменным, то существует вероятность освободиться, поскольку у него существует амплитуда, изменяющаяся с течением времени.

Ученые провели исследования и выяснили, что сила тока, равная 100 мА, поражает сердечную мышцу. Если показатель находится в диапазоне от 50 до 90 мА, то происходит мышечный спазм и потеря сознания. Максимальное допустимое значение тока определяется экспериментальным путем. Оно индивидуально для каждого.

К телу человека подключается электрическая установка с плавным регулированием показателя при постоянном напряжении 10 В. Увеличение длится до появления первых признаков поражения. После этого величина фиксируется, а затем из нее вычитается 5 мА.

Далее измеряется сопротивление человека. Расчет выглядит таким образом:

Максимальное допустимое значение тока (Imax): 80 мА.
Расчетная величина (во всех источниках может обозначаться «Iр»): Iр=Imax-5мА=80−5=75 мА.
Сопротивление человека (Rч): Rч=2,2 кОм.
Напряжение (U), которое является опасным для жизни: U=IpRч=0,075*2200=165 В.

Следовательно, опасным для человека с сопротивлением тела, которое равно 2,2 кОм, и током в 75 мА составляет 165 В.

Виды травм

При воздействии электричества на организм человека возникают травмы. Они классифицируются на такие виды:

Электрические ожоги — травмы, возникающие при тепловом воздействии тока на отдельный участок кожи.

Электрические знаки — изменение цвета (серый или бледно-серый) пораженной кожи при прямом контакте с токоведущей поверхностью.
Металлизация эпителия — травма, возникающая при коротком замыкании. В этом случае частицы расплавленного металла попадают вглубь кожи.
Механические — вид повреждения при сокращении мышц, после которого происходит падение.
Электроофтальмия — раздражающий эффект слизистой оболочки глаз, вызванный ярким светом (например, при сварке или образовании электрической дуги).
Электрический удар — серьезное поражение электричеством, приводящее к потере сознания, остановке сердечной мышцы, электрическому шоку, клинической и биологической смерти.

После выяснения пагубного влияния электричества на человека рекомендуется приступить к изучению определений, формул и законов, связывающих характеристики напряжения, тока и сопротивления.

Информация о напряжении

Напряжение — работа электрического тока, при которой происходит перемещение заряда из одной точки в другую. Оно имеет векторное направление. Электрическим током является движение заряженных элементарных частиц под воздействие электромагнитного поля.

Некоторые начинающие физики не знают, в чем измеряется напряжение. Знать это очень важно, поскольку элементы электрической цепи можно рассчитать неверно. Единицей измерения тока является ампер (А), а напряжения — вольт (В). В последнем случае применяется вольтметр — прибор, измеряющий величину напряжения или разности потенциалов. Он подключается параллельно в систему. Например, нужно измерить его значение на лампочке накаливания. Для этого необходимо подключиться параллельно к ней, а не последовательно.

Физический смысл

Под физическим смыслом напряжения или разности потенциалов понимают работу, необходимую для перемещения точечного заряда в 1 Кл из одного места в другое. В этом случае переносится только положительный потенциал. При этом возникает электродвижущая сила (ЭДС), которая называется напряжением или разностью потенциалов.

Для понимания физического смысла следует рассмотреть более простой пример. Пусть существует некоторая система, состоящая из насоса, труб и крана. Насос — напряженность электрического поля, трубы — провода, а кран — сопротивление системы. При включении первого происходит закачивание воды. Если немного приоткрыть кран, то она польется маленькой струйкой. При открытии его полностью жидкость будет уходить более интенсивно.

Формулы для вычислений

Все формулы для расчетов построены на законах Ома. Их всего два: для участка и для всей цепи. Формулировка первого: ток, протекающий на искомом участке, прямо пропорционален U и обратно пропорционален R. Его математическая запись имеет такой вид: I=U/R. Из последнего получаются такие соотношения:

U=IR.
R=U/I.
P=IU=(I²)R=(U²)/R, где Р — мощность.

Для полной цепи закон формулируется иначе: ток I прямо пропорционален ЭДС (E) и обратно пропорционален алгебраической сумме внешнего R и внутреннего r сопротивлений. Следует отметить, что r — проводимость источника питания. Записывается он в таком виде: I=E/(R+r). Физики вывели следующие соотношения, помогающие при расчетах:

Е=I (R+r).
R=(E/I)-r.
r=(E/I)-R.
Р=ЕI=(E²)/(R+r)=(R+r)I².

Однако ток бывает не только постоянный, но и переменный. Для него существуют другие правила и соотношения.

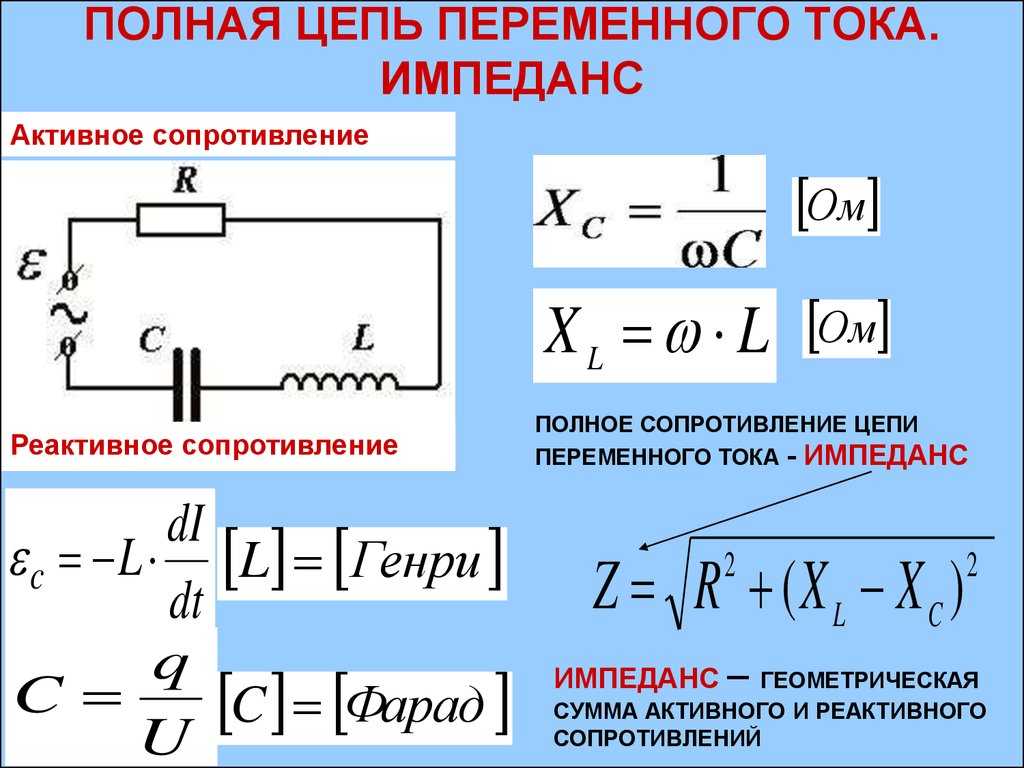
Тождества для переменного тока

Напряжение при переменном токе классифицируется на определенные виды. К ним относятся следующие:

Мгновенное или действующее — параметр, который измеряют приборы (Um).
Амплитудное — величина, характеризующее максимальную величину в определенный момент времени. Расчитывается по формуле с учетом угловой частоты (w), времени (t) и угла между фазами (f), который измеряется осциллографом: u (t)=Uмsin (wt+f).
Среднеквадратичное (Uq) — величина, вычисляемая по формуле: Uq=0,7073Uм).

Для расчета следует иметь знания об индуктивной Xl, емкостной Xc и резистивной R нагрузках. Первая — проводимость всех элементов, содержащих индуктивность (катушки, трансформаторы, электродвигатели). Во втором случае учитываются все емкостные радиодетали (варисторы и конденсаторы).

Резистивная нагрузка включает все значения резисторов.

Полный импеданс цепи (Z) равен сумме всех элементов, содержащий активную, индуктивную и емкостную. Специалисты рекомендуют использовать такие формулы, необходимые для расчетов:

Xl=wL.
Хс=1/wC.
Z=R+Xc+Xl.
I=Uм/Z.
Uм=IZ.
Z=Uм/I.

Четвертая формула является законом Ома для участка цепи, которую следует применять при переменных токах.

Таким образом, при помощи формулы напряжения можно рассчитывать не только основные параметры электричества для постоянного и переменного токов, но и его допустимые величины для человека.

Что такое сила натяжения?

Рассмотрено

Фейсал Файез Элиян, доктор философии

| Последнее обновление: 16 мая 2021 г.

Что означает сила натяжения?

Сила растяжения – это сила, возникающая при приложении нагрузки к одному или нескольким концам материала в направлении, перпендикулярном поперечному сечению материала. Силу натяжения часто называют «тянущей» силой. Нагрузка, приложенная к материалу, должна быть приложена в осевом направлении, чтобы быть силой растяжения.

Силы растяжения, которым подвергается компонент или конструкция, имеют большое значение при выборе материалов, способных выдерживать нагрузки.

Сила натяжения в физике — это сила, возникающая в веревке, струне или кабеле при растяжении под действием приложенной силы. Натяжение действует по длине каната/троса в направлении, противоположном приложенной к нему силе. Напряжение также иногда можно назвать стрессом, напряженностью или натянутостью.

Сила натяжения относится к категории контактных сил, поскольку она может проявляться только при наличии контакта между кабелем и рассматриваемым объектом. Этот тип силы всегда тянет, но никогда не толкает. Уменьшение вытягивания снижает напряжение, а увеличение вытягивания увеличивает напряжение.

Напряжение позволяет передавать силу на относительно большие расстояния.

Коррозионпедия объясняет Сила натяжения

Сила натяжения — одна из самых распространенных сил. Для этого многие материалы характеризуются так называемой прочностью на растяжение. Прочность на растяжение помогает разработчикам понять, какое усилие натяжения может выдержать материал. Из того, что известно как предел текучести при растяжении, можно рассчитать величину силы растяжения, которая может вызвать пластическую деформацию материала. По пределу прочности на растяжение можно рассчитать силу растяжения, при которой произойдет разрушение материала.

Силы натяжения встречаются во многих различных приложениях. Одним из примеров силы натяжения является зажим ремня безопасности в автомобиле при ударе. Зажим ремня безопасности должен выдерживать силу тела, толкаемого вперед во время дорожно-транспортного происшествия. Другим примером является менее острый пример силы натяжения, возникающей в подвесном мосту, который постоянно подвергается посадке и разгрузке автомобилей. Если материал кабеля не обладает достаточной прочностью на растяжение, может произойти разрушение моста.

Не существует единой формулы для расчета силы натяжения при любых обстоятельствах. Часто для расчета нормальной силы используется второй закон Ньютона:

Каждый физический объект, находящийся в контакте с другим объектом, оказывает на него некоторую силу, и наоборот. Контактные силы обозначаются разными терминами в зависимости от природы объектов. Если одна из рассматриваемых сил, которая является действующим объектом, представляет собой веревку, трос или цепь, это называется натяжением.

Поделись этим термином

Связанные термины

Кривая растяжения
Удлинение при растяжении
Модуль упругости при растяжении
Испытание на растяжение
Напряжение растяжения

Прочность на растяжение
Коэффициент нагрузки
Предел текучести
Процентное удлинение
Прочность на сдвиг

Связанное Чтение

6 способов измерения вязкости жидкости
6 испытаний для измерения прочности материала
Влияние коррозии на прочность при растяжении и пластичность материала
5 способов измерения твердости материалов
Введение в серию Galvanic: гальваническая совместимость и коррозия
Электрохимия коррозии: 6 электрохимических реакций, участвующих в коррозии

Актуальные статьи

Покрытия

8 вещей, которые нужно знать о покрытиях из полимочевины

Покрытия

5 наиболее распространенных типов металлических покрытий, о которых должен знать каждый

Научные свойства

6 способов измерения вязкости жидкости

Напряжение: значение, примеры, силы и физика

Напряжение — это не просто чувство, которое вы испытываете, когда собираетесь сдавать тест. Что касается физики, напряжение — это тип силы. Сила натяжения действует аналогично другим приложенным силам, например, если вы должны тянуть коробку по полу. Однако вместо того, чтобы тянуть коробку руками, вы будете тянуть коробку веревкой, шнуром, цепью или подобным предметом, чтобы это считалось натяжением. Поскольку напряжение похоже на приложенную силу, для него нет конкретного уравнения или формулы. Примером натяжения является ситуация, когда собака тянет поводок, пока вы берете ее на прогулку, — поводок тянет вас вперед с силой натяжения.

Определение напряжения

Напряжение убивает меня! Что такое напряжение? Натяжение — это тип контактной силы, возникающей при использовании веревки или шнура.

В физике мы определяем натяжение как силу, возникающую, когда веревка, шнур или подобный предмет натягивает объект. На противоположных сторонах веревки действуют две силы, создающие натяжение.

Натяжение представляет собой тянущую силу (поскольку вы не можете толкать веревкой) и действует в направлении веревки. Мы считаем напряжение a контактная сила , так как веревка должна коснуться объекта, чтобы оказать на него силу.

Натяжение в физике

Следует отметить, что натянутая веревка прикладывает одинаковую силу к каждому прикрепленному объекту. Например, когда мы упомянули прогулку с собакой, мы описали, как собака, дергающая за поводок, приложит к вам силу натяжения. Если бы нас интересовали только силы, действующие на вас, это все, что нас интересовало бы. Но что, если бы мы также захотели узнать силы, действующие на собаку? Мы заметим, что, когда собака тянет поводок, есть сила, которая удерживает или тянет ее обратно. Сила натяжения, тянущая вас вперед, такая же (имеет ту же величину), что и сила натяжения, удерживающая его назад. Как показано ниже, мы можем нанести на поводок две стрелки, чтобы показать эти две силы.

Силы натяжения

Натяжение в результате межатомных электрических сил. Межатомные электрические силы являются причиной всех контактных сил. Для натяжения веревка состоит из множества атомов и молекул, связанных вместе. По мере того как веревка становится натянутой под действием силы, одна из связей между атомами растягивается все дальше друг от друга на микроскопическом уровне. Атомы хотят оставаться рядом в своем естественном состоянии, поэтому электрические силы, удерживающие их вместе, возрастают. Все эти крошечные силы складываются вместе, чтобы создать одну силу натяжения. Этот принцип делает стрелки на рис. 1 более понятными: если собака и человек тянут поводок наружу, силы, удерживающие поводок вместе, направлены на поводок.

Уравнение натяжения

Для силы натяжения не существует специального уравнения, в отличие от сил трения и упругости. Вместо этого нам нужно использовать диаграмму свободного тела и второй закон движения Ньютона для решения напряженности.

Расчет натяжения с помощью диаграммы свободного тела и второго закона Ньютона

Диаграммы свободного тела помогают визуализировать силы, действующие на объект. Для ящика, тянущегося по полу веревкой, как показано на рисунке ниже,

Рис. 2 – Веревка, тянущая коробку

мы бы добавили стрелки для всех сил, действующих на коробку.

Рис. 3 — Здесь представлены все силы, действующие на коробку.

Эта цифра включает все силы, которые могут действовать в данной ситуации, включая трение $F_\text{f} $, гравитацию $F_g$, нормальное $F_\text{N} $ и напряжение $Т$.

Помните: всегда отводите стрелки силы натяжения от объекта. Напряжение — это сила притяжения, поэтому сила всегда будет направлена наружу.

Второй закон движения Ньютона утверждает, что ускорение объекта зависит от силы, действующей на объект, и массы объекта

Следующее уравнение:

$$\sum \vec F =m\vec a \mathrm{,}$$

является результатом второго закона Ньютона.

Это уравнение применимо к каждому направлению, поэтому обычно мы хотим включить одно для направления $y$ и одно для направления $x$. В нашем примере на рисунках выше нет никакого напряжения, действующего в направлении $y$, поэтому для определения напряжения мы можем сосредоточиться на направлении $x$, где у нас есть сила трения, действующая влево и напряжение, действующее вправо. Выбирая право быть положительным, наше результирующее уравнение выглядит так:

$$-F_\text{f} + T =ma\mathrm{.}$$

Затем мы можем переставить для решения натяжения:

$$T=ma+F_\text{f} \mathrm{ .}$$

Если коробка находится на поверхности без трения, сила трения равна нулю, поэтому натяжение будет равно произведению массы коробки на ускорение коробки.

Примеры натяжения

В задачах по физике вы можете увидеть множество реальных сценариев, связанных с натяжением, таких как:

Автомобили, буксирующие прицепы
Перетягивание каната
Шкивы и канаты
Тренажерный зал

Это может показаться очень разными сценариями, но для решения каждого из них вы будете использовать один и тот же метод. Ниже приведены некоторые проблемы, с которыми вы можете столкнуться, и способы их решения.

Веревка между двумя объектами

Теперь давайте все перемешаем и сделаем пример с двумя объектами, соединенными веревкой.

Рис. 4 — Веревка между двумя объектами.

На приведенном выше рисунке показана веревка между двумя ящиками и одним тянущим ящиком 2 вправо. Как мы упоминали в случае с собачьим поводком, натяжение, действующее на коробку 1, такое же, как и на коробку 2, поскольку это та же самая веревка. Поэтому на рисунке мы обозначили их одинаково $T_1 $.

В любой задаче мы можем выбрать, какой объект или группу объектов анализировать на диаграмме свободного тела. Допустим, мы хотели найти $T_1$ и $T_2$. Мы могли бы начать с просмотра поля 1, потому что это более простая сторона, и мы ищем только одно неизвестное. На следующем рисунке показана диаграмма свободного тела для ящика 1:

Рис. 5 — Диаграмма свободного тела ящика 1.

Поскольку натяжение действует только в направлении $x$, мы можем пренебречь действующими силами в $y$-направлении. Выбрав положительное значение, уравнение второго закона Ньютона будет выглядеть так:

$$-F_{\text{f}1} +T_1 = m_1 a\mathrm{.}$$

Затем мы можем переставить переменные для решения $T_1 $

$$T_1 = m_1 a + F_{\text{f}1}\mathrm{;}$$

, чтобы найти $T_2 $, мы могли посмотреть силы только на поле 2, показанном здесь:

Рис. 6 — Диаграмма свободного тела из поля 2.

Снова игнорируя $y$-направление, уравнение для $x$-направления будет следующим:

$$-T_1 — F_{\text{f}2} + T_2 = m_2 a\mathrm{.}$$

Поскольку мы знаем, что $T_1 $ одинаково для каждого блока, мы можем взять $T_1 $, который мы узнали из блока 1, и применить его к блоку 2 путем замены

$$-(m_1 a + F_{\text{f}1}) — F_{\text{f}2} +T_2 = m_2 a$$

и тогда мы можем найти $T_2 $,

$$T_2 = (m_2 + m_1 )a + F_{\text{f}1} + F_{\text{f}2}\mathrm{.}$$

Однако, если нам не нужно известно $T_1 $, мы всегда можем смотреть на оба ящика вместе, как если бы они были одним целым. Ниже мы можем увидеть, как выглядит диаграмма свободного тела, когда вы группируете два ящика:

Рис. 7. Диаграмма свободного тела обоих ящиков вместе.

Если мы напишем уравнение второго закона Ньютона для направления $x$, мы получим

$$-(F_{\text{f}1} + F_{\text{f}2})+T_2 = (m_1 +m_2 )a$$

и может переставить его, чтобы найти \(T_2 \ ),

$$T_2 = (m_1 + m_2 )a + F_{\text{f}1} + F_{\text{f}2}\mathrm{.}$$

Мы можем видеть, что это дает тот же результат, что и при рассмотрении квадратов по отдельности, а затем составлении уравнений вместе. Любой метод работает для поиска $T_2 $ (вы можете решить, какой из них проще, и использовать любой из них), но иногда переменную, которую вам нужно найти, можно найти, только сосредоточившись на одном конкретном объекте.

Тяга под углом

Теперь давайте сделаем пример со всеми любимыми: углы.

Рис. 8 — Тяга каната под углом.

На рисунке выше веревка тянется за ящик под углом, а не вдоль горизонтальной поверхности. В результате коробка скользит по поверхности горизонтально. Чтобы найти натяжение, мы использовали бы суперпозицию сил , чтобы разделить угловую силу на часть силы, которая действует в направлении $x$, и часть силы, которая действует в направлении $y$. )-направление.

Рис. 9 — Диаграмма свободного тела с разделением натяжения на компоненты $x$ и $y$.

Это показано красным на рисунке выше на диаграмме свободного тела. Тогда мы можем написать отдельное уравнение для направления $x$ и направления $y$ в соответствии с диаграммой свободного тела.

$T_x = T\cos{\theta}$ и $T_y = T\sin{\theta}$.

В этом примере теперь у нас есть некоторое напряжение, действующее в направлении $y$, поэтому мы не хотим игнорировать гравитационную и нормальную силы, как мы делали в примерах выше. Так как коробка не ускоряется в направлении $y$, сумма сил в направлении $y$ равна нулю

$$F_\text{N} + T\sin{\theta} -F_g =0\mathrm{,}$$

и перестановка для нахождения $T$ дает

$$T=\frac{ F_g — F_\text{N} }{\sin{\theta}}\\\mathrm{. }$$

Направление $x$ похоже на то, что мы сделали выше, но только с $x$ составляющая угловой силы натяжения:

$$-F_\text{f} + T\cos{\theta} = ma\mathrm{.}$$

Затем переставляем, чтобы найти $ T$:

$$T=\frac{ma+F_\text{f}}{\cos{\theta}}\\\mathrm{.}$$

Оба этих результата дадут вам одно и то же значение для $T$, поэтому в зависимости от того, какую информацию вы получили, вы можете выбрать либо сосредоточиться только на $x$-направлении, только на $y$-направлении, либо на обоих.

Свободно висящий объект

Когда объект висит на веревке, как показано ниже,

Рис. 10. Объект, висящий на веревке

Единственными силами, действующими на него, являются гравитационная сила, тянущая его вниз, и сила натяжения удерживая его.

Это показано на диаграмме свободного тела ниже.

Рис. 11. Диаграмма свободного тела объекта, подвешенного на веревке

Результирующее уравнение будет выглядеть следующим образом:

$$T-F_g =ma\mathrm{. }$$

Если мы перестроим, чтобы найти $T$ и подставим $mg$ вместо гравитационной силы, мы получим

$$T=ma +mg\mathrm{.}$$

Если объект не ускоряется , напряжение и гравитационная сила были бы равны и противоположны, поэтому $T=mg$.

Натяжение за наклонную поверхность

Когда к ящику на наклонной поверхности прикладывается натяжение, мы используем ту же стратегию, что и при натяжении веревки под углом.

Рис. 12 – Натяжение объекта на склоне

Сначала начните с диаграммы свободного тела.

Рис. 13 — Схема натяжения свободного тела на наклонной поверхности

При работе с наклонной поверхностью помните, что нормальная сила всегда действует перпендикулярно поверхности, а сила тяжести (вес) всегда действует прямо вниз .

Вместо того, чтобы разбивать силу натяжения на компоненты $x$ и $y$, мы хотим разбить гравитационную силу на компоненты. Если мы наклоним нашу систему координат, чтобы она соответствовала углу поверхности, как показано ниже, мы увидим, что натяжение действует в новом направлении $x$, а нормальная сила действует в новом направлении $y$- направление. Гравитационная сила — единственная сила под углом, так что мы разделили бы ее на компоненты, следующие новым направлениям $x$ и $y$, показанным ниже красным.

Рис. 14 — Диаграмма свободного тела с новой системой координат и гравитационной силой, разделенной на компоненты $x$ и $y$

Тогда мы применим второй закон Ньютона в каждом направлении, как и в любой другой задаче.

Подвешивание на двух веревках

Когда объект подвешен на нескольких веревках, натяжение неравномерно распределяется по веревкам, если только они не находятся под одинаковыми углами.

Рис. 15. Объект, подвешенный на двух веревках

В этом примере мы подставим действительные числа, чтобы найти $T_1 $ и $T_2 $. 92}=0\mathrm{.}$$

Мы можем решить эти два уравнения и два неизвестных алгебраически любым удобным для нас способом. В этом примере мы решим первое уравнение для $T_1 $ и заменим его вторым. Решение для $T_1 $ дает

$$\begin{align*} \frac{1}{\sqrt{2}} T_1 &= \frac{1}{2} T_2 \\ T_1 &= \frac{ \sqrt{2}}{2} T_2 \mathrm{,} \\ \end{align*}$$

и подстановка этого во второе уравнение для нахождения $T_2 $ дает

$$\begin{align *} \frac{\sqrt{2}}{2} T_2 \times \frac{1}{\sqrt{2}} + \frac{\sqrt{3}}{2} T_2 — 147,15\,\mathrm{ N} &= 0 \\ \frac{1+\sqrt{3}}{2} T_2 &= 147,15\,\mathrm{N} \\ T_2 &= 107,72\,\mathrm{N. } \\ \end {выравнивание*}$$

Затем подстановка $T_2 $ обратно в первое уравнение для решения для $T_1 $ дает нам окончательный ответ

$$\begin{align*} T_1 &= 107,72\,\mathrm{N} \ раз \frac{\sqrt{2}}{2} \\ T_1 &= 76,17\,\mathrm{N.} \\ \end{align*}$$

Шкив, наклон и подвешенный объект

Пример На изображении ниже сочетается многое из того, что мы обсуждали в каждом из приведенных выше примеров.

Рис. 17. Наклон, шкив и подвешенный объект

На следующем рисунке показано, как будут выглядеть силы, воздействующие на каждый объект, с учетом того, что сила трения может действовать в противоположном направлении в зависимости от того, как движется система. .

Рис. 18. Силы, показанные для сценария выше

Ниже приведены советы, которые мы узнали в каждой из приведенных выше задач, которые также применимы к этой задаче:

Мы можем смотреть на один объект отдельно и выполнять отдельные диаграмма тела и уравнения второго закона Ньютона.

Напряжение в физике это: Электрическое напряжение — урок. Физика, 8 класс.