2.Течение жидкости. Линейная и объемная скорости, соотношение между ними
2.Течение жидкости. Линейная и объемная скорости, соотношение между ними. Уравнение неразрывности струи. Закон Бернулли, его практическое значение.
Основной характеристикой любого движения является его скорость. Выделяют 2 разных скорости.
Скорость перемещения самих частиц жидкости (или плывущих вместе с жидкостью мелких тел — например, эритроцитов в крови) обозначают v и называют линейной скоростью. V=x/t.
Объём V жидкости, протекающей в данном потоке (в трубе, в русле реки, в кровеносном сосуде и т.п.) за единицу времени. Эту величину называют объёмной скоростью и обозначают Q.
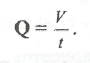
Между линейной скоростью v и объёмной скоростью Q существует простая связь. Рассмотрим трубку с площадью поперечного сечения S.
Выделим поперечный слой жидкости, который в момент времени t = 0 занимает положение 1. Через некоторое время t он переместится в положение 2, отстоящее на расстояние x= v*t. При этом через трубку пройдёт объём жидкости V = S*x . Объёмная скорость жидкости Q при этом будет равна Q =v/t=s*x/t. Но x/t=v, тогда
Q = S*V
В реальных жидкостях всегда существуют силы трения. В отличие от твёрдых тел, где силы трения действуют между двумя разными телами, в жидкостях силы трения возникают внутри жидкости (между разными её слоями). Поэтому трение в жидкостях называют внутренним трением или вязкостью.
Термин „идеальная жидкость» подразумевает, что при движении такой жидкости не происходит диссипация энергии (переход механической, энергии в тепло). Считалось, что таких жидкостей не существует, но в 1938 году академик П Л.Капица обнаружил, что при температурах, очень близких к абсолютному нулю, подобными свойствами обладает жидкий гелий (Капица назвал такое поведение гелия «сверхтекучестью».
Хотя во всех остальных случаях движение жидкости обязательно сопровождается диссипацией энергии, понятие идеальной жидкости (как, например, и понятие идеального газа) имеет большое практическое значение, потому что во многих случаях формулы, выведенные для идеальной жидкости, можно без больших ошибок применять для движения реальных жидкостей и газов. Наиболее интересным примером является теорема Бернулли, Рассмотрим горизонтальную трубку переменного сечения, по которой течёт жидкость или газ.
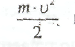 Легко
видеть, что кинетическая энергия жидкости
а правой части трубки больше, чем в
левой, потому что линейная скорость
жидкости справа больше, чем слева. Откуда
взялось это увеличение энергии ? Оно
произошло потому, что сила давления Кл
при перемещении какого-то объема жидкости
V производит некоторую работу А. По общей
формуле
Легко
видеть, что кинетическая энергия жидкости
а правой части трубки больше, чем в
левой, потому что линейная скорость
жидкости справа больше, чем слева. Откуда
взялось это увеличение энергии ? Оно
произошло потому, что сила давления Кл
при перемещении какого-то объема жидкости
V производит некоторую работу А. По общей
формуле 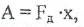
равна
самому давлению р, умноженному на площадь
S, то есть  . Отсюда
. Отсюда
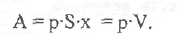
В
левой части трубки соответственно, в
правой части трубки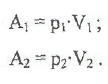 Разность работ слева и справа есть
Разность работ слева и справа есть
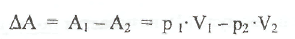
но мы уже несколько раз говорили, что через любое сечение неразветвлённой трубки проходит одинаковый объём жидкости, то 10
есть V, =V2- Обозначая объём просто V и вынося его за скобку, получим:
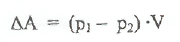
Так как мы считаем жидкость идеальной (потерь энергии нет), то разность работ равна приросту кинетической энергии;
Если
разделить это равенство на объём, то
справа вместо массы будет стоять
плотность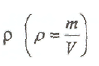 :
:
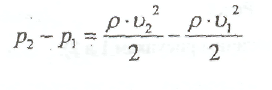
Перенося члены с индексом 1 влево, а с индексом 2 направо,
получаем:
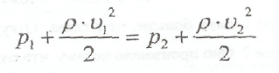
Члены
р и 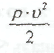
их
размерность одинакова, то есть величина 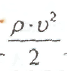 тоже
имеет
тоже
имеет
смысл давления. Её называют динамическим давлением, а член р – статическим давлением. Сумма статического и динамического давлений, стоящая в формуле называется полным давлением;
Так как при выводе мы положения сечений 1 и 2 взяли произвольно,- то из равенства (4) следует, что во всем потоке жидкости или газа полное давление (то есть сумма статического и динамического давлений) есть величина постоянная:
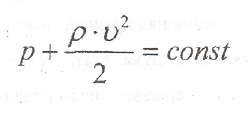
Это положение и, соответственно, формулы (4) и (5) и принято называть теоремой. Бернулли.
Статическое давление — это то давление, которое движущаяся жидкость оказывает на стенки трубки. Его можно измерить, если плоскость отверстия трубки манометра расположить параллельно линиям тока жидкости (рисунок 4-а). Если же плоскость отверстия трубки-манометра будет перпендикулярна линям тока, (рис. 4-6), то манометр покажет полное давление. При расположении манометра, как показано на рис. 4-в, мы будем измерять разность между полным и статическим давлениями, то есть динамическое давление.
Из теоремы Бернулли следует, что там, где скорость жидкости или газа больше, статическое давление меньше, и наоборот.
studfile.net
ответы на тест по биофизике
Подборка по базе: 3. Лабораторная работа №2 «Измерение объема жидкости».docx, особенности течения онкозаболеваний у гериатрических пациентов.d, меры предосторожности при заборе биологической жидкости .docx, Выбор рабочей жидкости.docx, Тема 9 Лекция Ядовитые технические жидкости.doc, Использование САПР компас-3D для автоматизации проектирования те, 5fan_ru_ОСНОВНЫЕ УРАВНЕНИЯ ОДНОМЕРНОГО УСТАНОВИВШЕГОСЯ ТЕЧЕНИЯ.d, методы исследования плевральной жидкости цель оценка результаты., Топливо, масла, охлаждающие и другие эксплуатационные жидкости.d, Топливо, масла, охлаждающие и другие эксплуатационные жидкости.d.
49.Объемной скоростью течения жидкости Q называется:
Б. Объем жидкости, протекающей в единицу времени через поперечное
сечение потока Q = V/t
50. Линейной скоростью движения жидкости v называется:
Г. Число молекул жидкости, проходящих через поперечное сечение потока в
единицу времени.
51. Связь между линейной v и объемной Q скоростями выражается формулой:
А. Q = Sv, где S – площадь поперечного сечения потока
52. Как объемная скорость установившегося течения жидкости в трубе переменного сечения зависит от площади поперечного сечения трубы?
А. Чем меньше площадь сечения, тем меньше объемная скорость.
53. Как линейная скорость движения жидкости в трубе переменного сечения при установившемся течении зависит от диаметра трубы?
Б. Чем меньше диаметр трубы, тем больше скорость.
54. Градиентом скорости течения жидкости g называют отношение:
Б. g = dv/dx
55. Сила трения между двумя слоями движущейся жидкости (основной закон вязкого течения жидкости — закон Ньютона) с вязкостью , площадью S, и градиентом скорости dv/dx имеет вид:
Б. F = — (dv/dx)S
56. Единица измерения вязкости в системе СИ:
А. Пас
57. Как изменяется вязкость жидкости при повышении температуры?
В. Вязкость уменьшается.
58. По закону Пуазейля объемная скорость Qтечения жидкости c вязкостью по трубе радиуса R, длиной l и разностью давлений на концах трубы P определяется формулой:
В. Q = (R4/8l)P
59. Какое течение жидкости называется ламинарным?
Г. Упорядоченное течение, при котором отдельные слои жидкости текут не
перемешиваясь друг с другом.
60. Закон Бернулли утверждает, что в текущей жидкости статическое давление:
А. Больше там, где скорость движения жидкости меньше.
61. Какое движение жидкости (или газа) называется турбулентным?
Г. Движение, при котором в жидкости возникают многочисленные
завихрения.
62. Какой параметр в формуле числа Рейнольдса выступает в качестве
критического размера при течении жидкости по трубе?
В. Размеры молекул жидкости.
63. Что такое поверхностно-активные вещества?
А. Вещества, способные адсорбироваться на границе раздела двух фаз,
понижая ее поверхностное натяжение.
64. Как поверхностно-активные вещества влияют на поверхностное
натяжение жидкости?
В. Уменьшают.
65. Как изменяется поверхностное натяжение жидкости с повышением температуры?
Б. С увеличением температуры коэффициент поверхностного натяжения
уменьшается.
66. Известно, что кровь является неньютоновской жидкостью, то есть ее вязкость
изменяется в зависимости от градиента скорости в потоке.
Это прежде всего объясняется тем, что:
В. Форменные элементы крови разнообразны по форме и размерам.
67. При течении жидкости по трубам гидродинамическое сопротивление определяется формулой:
Б. 8l/R4
68. Идеальной жидкостью называется:
А. Несжимаемая и не имеющая вязкости жидкость
69. Уравнение неразрывности струи имеет вид:
Б. v1S1 = v2S2
70. Закон Бернулли гласит, что:
Г. Сумма гидродинамического, статического и динамического давлений в установившемся
потоке идеальной жидкости есть величина постоянная.
71. При движении тел сферической формы в жидкости или газе сила сопротивления F равна:
В. F = — 6Rv
73. При измерении артериального давления крови по методу Короткова используют:
Г. Фиксацию появления и исчезновения шумов, связанных с турбулентным характером
течения крови.
74. Вязкость крови
В. Постоянна во всех отделах сосудистого русла.(разная)
75. Течение крови по сосудам является:
В. Преимущественно ламинарным и лишь в некоторых случаях – турбулентным.
76. В каком отделе сосудистого русла линейная скорость кровотока минимальна:
Г. В капиллярах.
77. Основной движущей силой кровотока является:
А. Кровяное давление, обусловленное превышением давления, вызванного работой сердца, над атмосферным давлением.
78. Ламинарное течение жидкости переходит в турбулентное при:
Б. При увеличении скорости течения.
79. Кинематической вязкостью жидкости называется отношение:
В. Динамической вязкости жидкости к ее плотности .
80. Дополнительное давление р под искривленной (сферической с радиусом кривизны R) поверхностью жидкости определяется по формуле Лапласа, имеющей вид:
Г. р = / 2R
81. Число Рейнольдса Re зависит от плотности жидкости , скорости ее течения v, критического размера d, вязкостижидкости и определяется формулой:
А. Re = vd /
82. Если число Рейнольдса превышает критическое значение, то:
Г. Течение жидкости имеет турбулентный характер.
83. Критической скоростью течения жидкости называется скорость,
В. При превышении которой ламинарное течение жидкости переходит в турбулентное.
106. Разность потенциалов возникает в организме человека:
Б. На мембране.
107. Какого порядка напряженность (В·м-1) электрического поля на клеточной
мембране в покое:
Б. 103.
108. Мембранным потенциалом называется:
Б. φм = φвн — φнар.
109. Выберите необходимые и достаточные условия для возникновения трансмембранной разности потенциалов: 1) Избирательная проницаемость мембраны.
2) Повышенная проницаемость мембраны. 3) Одинаковые концентрации по обе стороны от мембраны. 4) Различие концентраций ионов по обе стороны от мембраны.
Б. 1 и 4.
110. Диаметр кончика внутриклеточного электрода, используемого для измерения мембранного потенциала:
В. Много меньше размеров клетки.
111. Концентрация ионов К+:
А. Больше внутри клетки.
112. Концентрация ионов Na+:
Б. Больше вне клетки.
113. Причина мембранного потенциал покоя – диффузия:
Г. Ионов калия в клетку.
114. Какого порядка потенциал покоя:
Д. -100 мВ.
115. Потенциал покоя – это:
А. Разность потенциалов между цитоплазмой невозбужденной клетки и окружающей средой.
116. Чтобы создать равновесный нернстовский мембранный потенциал, через мембрану должно пройти по сравнению с общим количеством ионов калия в клетке:
А. 10-4 %.
Б. 2%.
В. 20%.
Г. 100%.
117. Уравнение Гольдмана учитывает диффузию через мембрану:
Г. ионов К+, Na+ и Cl—.
118. В состоянии покоя проницаемость мембраны
б. Рк >> РNa.
119. При возбуждении клетки в начальный период проницаемость мембраны:
В. РкNa.
120. В фазе деполяризации при возбуждении аксона потоки ионов Na+ направлены:
А. Внутрь клетки через потенциалзависимые каналы.
121.В фазе реполяризации аксона основной поток ионов — это:
Г. Поток калия наружу.
122. Какого порядка потенциал инверсии?
Б. –50 мВ.
123. Потенциал действия определяется по следующей формуле:
В. ПД = |ПП| + ПИ.
124. Потенциал действия развивается, если:
Б. Амплитуда деполяризующего потенциала меньше порогового.
125. Потенциал действия:
В. Зависит от интенсивности раздражителя.
126. Длительность потенциала действия аксона:
Б. 1мс.
127. Длительность потенциала действия кардиомиоцита:
В. 250 мс.
128. Каким способом можно измерить трансмембранный потенциал в эксперименте?
А. С помощью микроэлектродной техники.
129. В момент введения микроэлектрода в клетку луч на экране электронно-лучевого осциллографа:
Б. Смещается вверх.
130. В какой последовательности протекают фазы потенциала действия?
3. Фаза экзальтации.
2. Фаза деполяризации.
4. Фаза реполяризации.
1 Потенциал покоя
131. Потенциал действия возникает:
Б. На возбудимых мембранах.
132. Может ли возникать потенциал действия в фазе абсолютной рефрактерности?
Б. Нет.
133. На возбудимых мембранах располагаются:
Г. Как потенциалнезависимые, так и потенциалзависимые каналы.
134. Градуальный потенциал возникает:
Б. На возбудимых мембранах.
135. Каким состоянием является потенциал покоя с точки зрения термодинамики?
А. Равновесное
136. Если заблокировать систему активного транспорта потенциал покоя (по модулю):
А. Не изменится
Б. Уменьшится
В. Увеличится
Г. Будет равен нулю
137. При достижении критического мембранного потенциала открываются мембранные каналы:
В. Потенциалзависимые натриевые каналы
138. Если увеличить модуль потенциала покоя, величина порогового напряжения:
А. Увеличится
Б. Уменьшится
В. Не изменится
Г. Станет равной нулю
139. Если увеличить модуль потенциала покоя, возбудимость мембраны:
А. Увеличится
Б. Уменьшится
В. Не изменится
Г. Станет равной нулю
140. Если уменьшить величину порогового потенциала, возбудимость мембраны:
Г. Увеличится
141. Последовательность фаз рефрактерности при развитии возбуждения (фаза относительной рефрактерности — 1, фаза экзальтации — 2, фаза абсолютной рефрактерности — 3):
В. 3, 1, 2.
142. В сумме продолжительность АРФ и ОРФ равна длительности:
Г. Потенциала действия
143. Стабильный потенциал покоя обеспечивается:
А. Активным транспортом
144. Авторы уравнения, позволяющего рассчитать клеточный мембранный потенциал (1 – Нернст; 2 – Гольдман; 3 – Катц; 4 – Бернштейн; 5 – Ходжкин):
Б. 2, 3, 5.
145. Электронно-лучевой осциллограф измеряет:
Г. Емкость
146. Сигнал от генератора развертки электронно-лучевого осциллографа имеет форму:
А. Пилообразную
147. Для получения электронного пучка в электронно-лучевой трубке используется:
Г. Люминесценция
148. Декремент электрического потенциала в живых тканях – это:
Б. Затухание сдвига потенциала на мембране.
149. Декремент потенциала в живых тканях имеет:
Г. Экспоненциальный характер.
150. Бездекрементное распространение возбуждения – это распространение:
В. Незатухающее.
151. Потенциал действия может распространяться без затухания по нервному волокну в результате того, что:
Б. Емкость мембраны мала.
152. В каких структурах миелинизированного нервного волокна образуется потенциал действия?
А. В перехватах Ранвье.
153. По немиелинизированным (безмякотным) нервным волокнам электрический импульс распространяется:
Б. С декрементом.
154. Скорость распространения возбуждения в безмякотном (немиелинизированном) волокне выше, если оно:
Г. Толстое.
155. В каких волокнах скорость распространения выше?
А. Миелинизированных;
156. Автоволновыми процессами называют процессы распространения волн возбуждения в:
В. Активных средах.
157. Электрическая синаптическая передача возможна в синапсах:
А. При расстоянии между клетками не более 10-20 нм.
158. Какая структурная единица синапса определяет время синаптической задержки:
Г. Медиатор.
159. Возбуждающий постсинаптический потенциал (ВПСП) — это:
Г. Деполяризация постсинаптической мембраны.
160. Тормозной постсинаптический потенциал (ТПСП):
Б. Гиперполяризация постсинаптической мембраны.
161. Двухфазный потенциал возбуждения регистрируется от клетки при:
Б. Внутриклеточном отведении.
162. Сколько необходимо электродов для регистрации разности потенциалов на клеточной мембране:
Б. Два.
163. Электрокардиография позволяет оценить:
В. Распространение возбуждения по сердечной мышце.
164. Электрокардиографией называется диагностический метод, основанный на:
А. Регистрации биопотенциалов, отводимых непосредственно от сердца.
Б. Регистрации временной зависимости величины электрического момента
сердца.
В. Регистрации временной зависимости биопотенциалов, возникающих в сердце,
при отведении от окружающих тканей.
165. Кривая, отображающая изменение во времени разности потенциалов сердца, называется:
Г. Электрокардиограммой.
166. В теории Эйнтховена сердце представляется моделью единого эквивалентного генератора в виде:
А. Токового диполя.
167. Согласно теории Эйнтховена, сердце представляет собой:
В. Диполь.
168. Атипичные миокардиальные волокна участвуют:
Б. В проведении возбуждения по сердечной мышце.
169. Водителем ритма первого порядка в сердце является:
В. Сино-аурикулярный узел.
170. Скорость проведения возбуждения в разных звеньях проводящей системы:
Б. Разная.
171. Скорость проведения возбуждения выше в:
Б. Пучке Гиса.
172. Задержка проведения возбуждения происходит в:
Г. Атрио-вентрикулярном узле.
173. Источником автоматизма сердечной мышцы служат:
А. Атипичные мышечные волокна.
174. Регистрирующим устройством в электрокардиографе является:
В. Электроды.
175. Электроды, накладываемые на пациента при электрокардиографии, предназначены для регистрации:
В. Разности потенциалов между двумя точками на поверхности тела.
176. Электронный усилитель, являющийся основным узлом электрокардиографа, предназначен для:
В. Увеличения частоты переменного тока.
177. При усилении сигнала коэффициент усиления равен:
Б. Произведению амплитуд входного и выходного сигнала.
178. Электрокардиограмма — это:
В. Резонансная кривая.
179. Система стандартных электрокардиографических отведений геометрически представляет собой:
Г. Треугольник.
180. Зубец Р в ЭКГ представляет собой изменение во времени проекции интегрального вектора сердца на координатную ось при:
А. Возбуждении предсердий.
181. Комплекс QRS в ЭКГ представляет собой изменение во времени проекции интегрального вектора сердца на координатную ось при:
В. Возбуждении желудочков.
182. Зубец Т в ЭКГ представляет собой изменение во времени проекции интегрального вектора сердца на координатную ось при:
Г. Реполяризации желудочков.
183. Амплитуда зубцов ЭКГ измеряется в:
Б. мВ.
184. Расстояние между зубцами ЭКГ характеризует:
Б. Скорость распространения возбуждения.
185. Для анализа ЭКГ необходимо:
Г. Калибровать оси координат.
186. Cредняя электрическая ось сердца в треугольнике Эйнтховена представляет собой:
А. Вектор.
187. Средняя электрическая ось сердца дает представление:
Б. О положении анатомической оси сердца в грудной полости.
188. Длительность потенциала действия кардиомиоцита по сравнению с потенциалом действия аксона:
Г. Значительно больше.
189. Что является причиной изменений величины и направления интегрального электрического вектора сердца за цикл работы сердца?
Б. Последовательный охват волной возбуждения различных структур сердца.
190. Почему амплитуды одних и тех же зубцов ЭКГ в один и тот же момент времени в различных отведениях не одинаковы:
В. Для каждого отведения существует свой интегральный электрический вектор сердца.
191. Под декрементом электрического потенциала во времени понимают:
Б. Угасание потенциала со временем
192. Постоянная времени – это:
Г. Время, в течение которого Uо падает в е раз
193. Чтобы определить величину биопотенциалов сердца в различные моменты сердечного цикла, пользуясь электрокардиограммой, нужно:
В. Расстояние между двумя самыми большими зубцами умножить на цену деления
194. Чтобы определить частоту сердечных сокращений, пользуясь электрокардиограммой нужно определить:
Б. Время между зубцами PR
195. Миелиновая оболочка нервного волокна по электрическим свойствам:
Б. Диэлектрик
196. Сальтаторное проведение возбуждение это:
Г. Скачкообразное проведение возбуждения
197. Максимальная скорость распространения возбуждения по нервным волокнам равна:
Г. Скорости света
198. Фаза «плато» в кардиомиоците определяется потоком ионов:
В. Кальция
199. Самая характерная особенность биопотенциалов атипичных кардиомиоцитов:
Б. Автоматия
200. ИЭВС расшифровывается как:
А. Интегральный электрический вектор сердца
201. По интервалам ЭКГ судят о:
Б. Амплитуде зубцов
202. Средняя частота сердечных сокращений в норме:
А. 1 Гц
Б. 40 Гц
В. 60 Гц
Г. 80 Гц
203. Электрокардиография была предложена в:
Б. 1912 г.
204. Последовательность проведения возбуждения в сердце (1 — Атриовентрикулярный узел; 2 — Миокард предсердий; 3 — Синоаурикулярный узел; 4 — Волокна Пуркинье; 5 — Ножки пучка Гиса; 6 — Пучок Гиса; 7 — Миокард желудочков):
Г. 3, 2, 1, 6, 5, 4, 7.
205. Внутренняя энергия тела – это…
Г. Сумма потенциальной энергии взаимодействия и кинетической энергии хаотического движения образующих его частиц.
206. Газу сообщили 100 Дж теплоты, при этом он совершил работу в 20 Дж. Как изменилась внутренняя энергия газа?
В. Возросла на 80 Дж.
207. Газ находится в сосуде под давлением 250 кПа. При сообщении газу 550 кДж теплоты он изотермически расширился на 3 м3. На сколько изменилась внутренняя энергия газа?
А. Увеличилась на 550 кДж.
Б. Осталась неизменной.
208. Как изменилась внутренняя энергия одноатомного газа, занимающего объем 0,02 м3, при изохорном процессе, если давление возросло на 100 кПа?
В. Для ответа на вопрос нужно знать изменение температуры газа.
209. Энтропия – это:
А. Мера связанной энергии.
210. Как изменяется энтропия вещества при переходе его из жидкого состояния в газообразное:
Б. Увеличивается.
211. При переходе вещества из жидкого состояния в твердое его энтропия:
А. Уменьшается.
212. При изотермическом сжатии газ передал окружающим телам количество теплоты, равное 800 Дж. Какую работу совершили внешние силы?
А. 800 Дж.
213. Жидкость испаряется при любой температуре, потому что:
В. В жидкости всегда есть молекулы, кинетическая энергия которых больше работы по преодолению сил притяжения к другим молекулам.
214. При изотермическом сжатии газ не нагревается, хотя внешние силы совершают работу, потому что…
В. Внутреннюю энергию нельзя изменить, совершая над газом работу.
215. Повышение относительной влажности воздуха от 50% до 90% может существенно отразиться на самочувствии человека, так как это…
В. Существенно затруднит терморегуляцию организма из-за снижения испарения воды с поверхности кожи.
216. Каким способом можно изменить внутреннюю энергию тела?
В. Совершением работы и теплопередачей.
217. Какой вид теплопередачи не сопровождается переносом вещества?
Г. Излучение и теплопроводность.
218. Налитая в открытый термос вода испаряется. Как изменяется при этом температура воды в термосе?
В. Понижается.
219. Почему при испарении без подвода и отвода тепла температура жидкости уменьшается?
Б. При испарении убывает количество молекул жидкости, в результате уменьшается число их столкновений.
220. При самопроизвольно протекающих процессах в изолированной системе ее внутренняя энергия не изменяется. Изменяется ли с течением времени возможность использования этой энергии для получения полезной работы?
А. Не изменяется.
221. Какие из перечисленных ниже видов энергии тела не входят в состав внутренней энергии тела? (1 — Кинетическая энергия беспорядочного теплового движения атомов и молекул тела; 2 — Потенциальная энергия взаимодействия атомов и молекул тела между собой; 3 — Кинетическая энергия тела как целого относительно других тел; 4 — Потенциальная энергия взаимодействия тела с другими телами.)
Г. 3 и 4.
222. В металлическую кружку налита вода. Какой из перечисленных ниже способов пригоден для изменения ее внутренней энергии? (1 — Нагреть воду на горячей плите; 2 — Совершить работу над водой, приведя ее в поступательное движение вместе с кружкой; 3 — Совершить работу над водой, перемешивая ее миксером).
Б. 1 и 2.
223. Каким способом преимущественно происходит теплопередача через кожу и подкожную жировую клетчатку?
Г. Всеми перечисленными способами.
224. Изолированная термодинамическая система — это:
А. Система, которая не обменивается с окружающей средой ни веществом, ни энергией.
225. Замкнутая термодинамическая система – это:
Б. Система, которая обменивается с окружающей средой энергией, но не обменивается веществом.
226. Открытая термодинамическая система – это:
В. Система, которая обменивается с окружающей средой и веществом и энергией.
227. Внутренняя энергия термодинамической системы:
В. Определяется параметрами, характеризующими состояние системы, и зависит от процесса, в результате которого система перешла в данное состояние.
228. Работа, совершенная над системой:
Б. Зависит от пути перехода в данное состояние.
229. Количество тепла, полученного системой при переходе из одного состояния в другое:
В. Зависит от конечного состояния системы.
230. При температуре окружающей среды ниже, чем температура тела, основным видом теплообмена является:
В. Излучение.
231. При температуре окружающей среды выше, чем температура тела, основным видом теплообмена является:
Г. Испарение.
232. Химическая терморегуляция – это:
А. Изменение КПД при синтезе АТФ.
233. Идеальный газ получил 300 кДж тепла и совершил работу 200 кДж. Чему равно изменение внутренней энергии?
Б. 100 кДж.
234. Идеальный газ получил 300 кДж тепла, и над ним была совершена работа 200 кДж. Чему равно изменение внутренней энергии?
В. 500 кДж.
235. При уменьшении массы животного основной обмен:
В. Уменьшается.
236. За сутки человек средней массы тратит приблизительно:
В. 1800 ккал
237. Свободная энергия изолированной термодинамической системы, находящейся в равновесном термодинамическом состоянии:
В. Равна нулю.
238. Внутренняя энергия идеального газа является функцией
В. Температуры.
239. Изменение внутренней энергии идеального газа при переходе из одного состояния в другое пропорционально
А. Разности температур.
240. В изолированной термодинамической системе внутренняя энергия
Б. Постоянна.
241. Для идеального газа при изобарическом процессе остается постоянным
А. Отношение объема и температуры.
242. Для идеального газа при изотермическом процессе остается постоянным
Б. Произведение давления и объема.
243. Для идеального газа при изохорическом процессе остается постоянным
В. Отношение давления к температуре.
244. Первый закон термодинамики для адиабатического процесса можно сформулировать следующим образом:
Г. Работа, производимая над системой, равна изменению внутренней энергии.
245. Для организма человека изменение внутренней энергии
Г. В среднем равно нулю.
246. Организм человека – это
А. Открытая термодинамическая система.
247. Энергия потребляемой пищи равна сумме всех видов работ, совершаемых в организме и тепла, вырабатываемого в организме вследствие необратимых процессов, идущих в нем, и отводимого в окружающую среду. Приведенная формулировка первого начала термодинамики подходит для:
А. Всех открытых термодинамических систем.
248. Химический потенциал – это
Б. Удельная свободная энергия.
249. Обратимыми называются процессы, при которых
А. Изменение свободной энергии равно совершенной работе.
250. Необратимыми называются процессы, при которых
Б. Изменение свободной энергии больше совершенной работы.
251. Диссипацией свободной энергии называется процесс
Г. Перехода части свободной энергии в тепло.
252. Принципиальное отличие энергетики живых организмов от технических установок состоит в том, что промежуточным звеном между энергией топлива/пищи и совершенной работы является
В. Энергия макроэргов
253. Самопроизвольно могут протекать процессы, в ходе которых
А. Свободная энергия уменьшается.
254. Работа, производимая при химическом синтезе сложных биомолекул, пропорциональна
А. Отношению концентраций по разные стороны мембраны.
Б. Разности потенциалов на мембране.
В. Разности температур тела и окружающей среды.
Г. Изменению химического потенциала.
255. Работа по поддержанию разности концентраций на мембране пропорциональна
А. Отношению концентраций по разные стороны мембраны.
Б. Разности потенциалов на мембране.
В. Разности температур тела и окружающей среды.
Г. Изменению химического потенциала.
257. При прямой калориметрии
А. Измеряют количества тепла, выделенного за определенное время.
258. При непрямой калориметрии
Г. Определяют количества потребленного за определенное время кислорода и произведенного углекислого газа.
259. Величина, показывающая какое количество теплоты выделяется при полном окислении данного вещества до углекислого газа и воды на каждый литр поглощенного организмом кислорода, называется
Б. Калорический коэффициент.
260. Дыхательный коэффициент – это
Г. Отношение объема выделенного углекислого газа к объему поглощенного кислорода за определенное время.
261. Коэффициент теплопроводности измеряется в
А.  .
.
Б.  .
.
В.  .
.
262. Удельная теплота парообразования измеряется в
Г.  .
.
263. Человек получил за сутки 100 г белков, 120 г углеводов и 50 г жиров. Чему равна энергия, полученная с пищей? Учесть, что при полном окислении 1 г жиров выделяется 40 кДж, углеводов – 17,6 к Дж и белков – 17 кДж.
В. 5812 кДж.
264. Наружная температура -100С, температура кожи стопы 300С. Чему равен градиент температуры, если толщина подошвы утепленного ботинка составляет 7 мм?
Б. 5714 К/м.
265. При увеличении толщины теплопроводящего слоя градиент температуры
Б. Уменьшится.
266. Рассчитать величину основного обмена для человека массой 70 кг за сутки. Учесть, что за нормальную величину основного обмена принимается примерно 1 ккал/(кг ч) (1 кал = 4.18 Дж).
А. 7022,4 кДж.
267. При анализе условий труда в кузнечном цехе установлено, что температура в рабочей зоне около 300С, движение воздуха отсутствует. Какой способ теплоотдачи наиболее эффективен в данных условиях?
Г. Испарение.
268. При изотермическом расширении идеальным газом совершена работа 20 Дж. Какое количество теплоты сообщено газу?
В. 20 Дж.
269. Подведение теплоты к системе не приводит к увеличению ее внутренней энергии при
Б. Изотермическом процессе.
270. По показаниям какого прибора можно судить о внутренней энергии всего воздуха, находящегося в комнате?
Б. Психрометра.
275. В изолированной термодинамической системе, имеющей температуру 300 градусов энтропия увеличилась на 3 Дж град-1. Как изменилась свободная энергия системы?
В. Уменьшилась на 900 Дж.
276. В изолированной термодинамической системе, находящейся при температуре 300 градусов свободная энергия уменьшилась на 900 дж. Как изменилась энтропия системы?
А. Увеличилась на 3 Дж/град.
277. Энтропия изолированной термодинамической системы, находящейся в равновесном термодинамическом состоянии:
А. Максимальна.
278. Энтропия открытой термодинамической системы, находящейся в стационарном состоянии:
Б. Постоянна и отлична от нуля.
279. Свободная энергия открытой термодинамической системы, находящейся в стационарном состоянии:
Б. Постоянна.
280. Продукция энтропии открытой термодинамической системы, находящейся в стационарном состоянии:
Б. Максимальна.
283. При структурной организации (кристаллизации) энтропия вещества:
Б. Уменьшается.
284. В изолированной термодинамической системе общее изменение энтропии всегда:
Г. Постоянно и отлично от нуля.
285. Возрастание энтропии в системе свидетельствует:
Б. Об увеличении свободной энергии.
286. Полное изменение энтропии открытой термодинамической системы, находящейся в стационарном состоянии:
А. Равно нулю.
287. Энтропия открытой термодинамической системы, находящейся в стационарном состоянии, постоянна за счет:
Б. Равенства продукции и потока энтропии.
288. Изолированная термодинамическая система обменивается с окружающей средой:
Г. Ни веществом, ни энергией.
289. Открытая термодинамическая система обменивается с окружающей средой:
А. И веществом, и энергией.
290. В изолированной термодинамической системе общее изменение свободной энергии всегда:
Г. Постоянно и не равно нулю.
291. При парообразовании энтропия воды:
В. Увеличивается.
292. Энтропия – это величина … энергии на единицу температуры.
Б. Связанной.
293. В изолированной термодинамической системе, находящейся в неравновесном состоянии, происходит диссипация энергии:
А. Свободной.
Б. Полной.
В. Внутренней.
Г. Связанной.
454. Расположите в порядке возрастания длины волны электромагнитные излучения разной природы: 1) Инфракрасное излучение дровяной печи. 2) Рентгеновское излучение. 3) Видимое излучение Солнца. 4) Излучение СВЧ печей.
В. 2, 3, 1, 4.
457. Почему высокочастотный переменный ток не оказывает раздражающего действия на ткани?
В. Потому, что при этом смещение ионов становится соизмеримым с их смещением
за счет молекулярно-теплового движения.
458. В чем суть метода микроволновой терапии?
В. Прогревание тканей с помощью электромагнитных волн СВЧ диапазона.
459. Аппарат УВЧ-терапии является
В. Генератором высокочастотных электромагнитных волн.
460. Электротравма возникает под действием:
А. Низкочастотных токов.
461. Поражающий эффект электротравмы обусловлен прежде всего:
Б. Возбуждением возбудимых тканей.
462. Миллиметровые волны поглощаются почти исключительно:
А. Мышцами.
463. Электромагнитные волны отличаются от звуковых: 1) … наличием дифракции, 2) … распространением в вакууме, 3)… наличием поляризации.
А. Только 1.
Б. 2 и 3.
В. Все ответы правильные.
Г. 1 и 2.
464. В каком из приведенных ниже устройств происходит излучение электромагнитных волн?
3) В колебательном контуре с раздвинутыми обкладками конденсатора происходят электромагнитные колебания.
В. Только 3.
465. Квантовые оптические генераторы (лазеры) используются:
Д. Все ответы правильные.
466. Собственная частота колебаний контура радиопередатчика равна 106 Гц. Чему равна длина электромагнитной волны, излучаемой передатчиком?
Г. 300 м.
467. Какое явление положено в основу действия лазеров?
Б. Индуцированное излучение.
468. Собственная частота колебаний контура радиопередатчика равна v. Если c – скорость света в вакууме, то длина электромагнитной волны, излучаемой передатчиком, равна:
Б. λ = c/v.
469. Скорость распространения электромагнитных волн в среде зависит от:
А. Плотности среды.
470. Расположите в порядке увеличения частоты следующие электромагнитные излучения: 1) радиоволны; 2) гамма-излучение; 3) видимый свет; 4) ультрафиолетовое излучение.
Б. 1, 3, 4, 2.
471. При переходе электромагнитной волны из воздуха в воду длина волны:
А. Не изменяется.
473. При каком движении электрического заряда происходит излучение электромагнитных волн?
В. Только при колебательном движении по гармоническому закону.
474. Какое электромагнитное излучение из перечисленных ниже видов имеет наименьшую длину волны?
Г. Гамма-излучение.
475. Вещество, используемое в оптическом квантовом генераторе (лазере), имеет три энергетических уровня с энергиями Е3>E2>Е1. Лазерное излучение испускается при переходах между уровнями 2 и 1. Какой из уровней является метастабильным?
Б. Только 2
590. Колебания какого вектора ( или
или ) действуют на сетчатку глаза или на фотоэмульсию?
) действуют на сетчатку глаза или на фотоэмульсию?
Б. Только  .
.
616. Какое минимальное количество фоторецепторов глаза должно охватывать изображение предмета, чтобы на сетчатке глаза две крайние точки предмета не сливались в одну?
Г. Три колбочки.
619. Какова минимальная величина изображения на сетчатке глаза, чтобы две крайние точки предмета не сливались в одну?
А. 5 мм.
627. Какое изображение далеких предметов получается на сетчатке глаза?
Г. Действительное, перевернутое.
628. Палочки обеспечивают:
Б. Сумеречное, ахроматическое, периферическое зрение.
629. Колбочки обеспечивают:
А. Дневное, хроматическое, центральное зрение.
630. Острота зрения обеспечивается:
Б. Колбочками.
638. В каких единицах выражается освещенность?
В. Люкс.
639. Источник света представляет собой равномерно светящуюся сферическую поверхность. Как изменится яркость источника, если приблизиться к нему?
Б. Не изменится.
640. Найдите полный световой поток точечного источника света, у которого сила света равна 500 кд.
Б. 6280 Лм.
641. В каких единицах выражается яркость?
Г. Нит.
642. Яркость источника света увеличилась в 3 раза. Как изменился световой поток?
а. Увеличился.
643. Какая из перечисленных единиц является основной в системе световых величин?
Б. Кандела.
644. Каков характер световых волн?
А. Продольные.
Б. Поперечные.
В. В вакууме – поперечные, в среде – продольные.
645. Могут ли две световые волны с различной частотой, например красного и зеленого излучений, иметь одинаковые длины волн?
Б. Длина волны зеленого излучения всегда больше длины волны красного.
649. Фоторецепторы относятся к следующему типу рецепторов:
В. Рецепторы со специальными клетками, первичночувствующие.
650. Волосковые клетки кортиева органа относятся к следующему типу рецепторов:
Г. Рецепторы со специальными клетками вторичночувствующие.
653. Каким образом происходит кодирование частоты звука в слуховом анализаторе:
А. Максимальная амплитуда колебаний базилярной мембраны на разных частотах достигается в разных участках мембраны.
655. Ионные каналы волосковых клеток кортиева органа, ответственные за возникновение рецепторного потенциала, относятся к каналам:
Г. Механочувствительным.
656. Органы чувств относятся к части сенсорной системы:
А. Периферической.
665. Максимальная чувствительность зрительного восприятия при фотопическом зрении приходится на длину волны:
А. 555 нм.
666. Поток излучения в 1 Вт при длине волны 555 нм создает у человека ощущение светового потока в:
В. 683 Лм.
667. Световой поток выражается в:
А. Люменах.
668. Сила света выражается в:
Б. Канделах.
669. Энергия света, переносимая через поверхность в единицу времени называется:
А. Энергетическим потоком.
670. Над центром стола висит источник света. Как изменится освещенность стола, если расстояние от стола до источника увеличится в два раза:
А. Уменьшится в 2 раза.
671. Если на поверхность падает свет от нескольких источников, то общая освещенность равна:
А. Средней арифметической освещенности.
Б. Максимальной из освещенностей
Г. Средней геометрической освещенности.
672. Люксметр – это прибор для измерения:
Г. Освещенности.
673. 1 лм·м-2 =
А. 1 люкс
topuch.ru
Как объемная скорость установившегося течения жидкости в трубе переменного сечения зависит от площади поперечного сечения трубы?
Как объемная скорость установившегося течения жидкости в трубе переменного сечения зависит от площади поперечного сечения трубы?
А. Чем меньше площадь сечения, тем меньше объемная скорость.
В. Чем больше площадь сечения, тем меньше объемная скорость.
Г. Объемная скорость не зависит от площади поперечного сечения трубы.
Как линейная скорость движения жидкости в трубе переменного сечения при установившемся течении зависит от диаметра трубы?
А. Чем меньше диаметр трубы, тем меньше скорость.
Б. Чем меньше диаметр трубы, тем больше скорость.
В. Чем больше диаметр, тем больше скорость.
Г. Линейная скорость не зависит от диаметра трубы.
54. Градиентом скорости течения жидкости g называют отношение:
А. g = dv/dt
Б. g = dv/dx
В. g = dv/ds
Г. g = dx/dt
55. Сила трения между двумя слоями движущейся жидкости (основной закон вязкого течения жидкости — закон Ньютона) с вязкостью h , площадью S, и градиентом скорости dv/dx имеет вид:
А. F = — h×(dv/dx)×lБ. F = — h×(dv/dx)×S
В. F = h×(dv/dt)×S
Г. F = h×(dv/dx)×S
56. Единица измерения вязкости в системе СИ:
А. Па×с
Б. Па×с2В. Па/с Г. Па×м2
Как изменяется вязкость жидкости при повышении температуры?
А. Вязкость не меняется.
Б. Вязкость увеличивается.
В. Вязкость уменьшается.
Г. У одних жидкостей вязкость уменьшается, у других увеличивается.
Какое течение жидкости называется ламинарным?
А. Течение, при котором линейная скорость постоянна во всех точках
потока.
Б. Течение, при котором объемная скорость одинакова во всех сечениях
потока.
В. Течение, при котором скорость потока постепенно падает до нуля.
Г. Упорядоченное течение, при котором отдельные слои жидкости текут не
перемешиваясь друг с другом.
А. Движение, при котором линейная скорость частиц жидкости различна в
различных сечениях потока.
Б. Движение, при котором температура жидкости различна в различных
сечениях потока.
В. Любое движение жидкости с высокой скоростью.
Г. Движение, при котором в жидкости возникают многочисленные
завихрения.
Какой параметр в формуле числа Рейнольдса выступает в качестве
Критического размера при течении жидкости по трубе?
А. Длина трубы, по которой течет жидкость.
Б. Диаметр трубы, по которой течет жидкость.
В. Размеры молекул жидкости.
Г. Отношение длины трубы к диаметру.
Известно, что кровь является неньютоновской жидкостью, то есть ее вязкость
Изменяется в зависимости от градиента скорости в потоке.
Это прежде всего объясняется тем, что:
А. Плазма крови обладает высокой вязкостью.
Б. Форменные элементы крови образуют крупные агрегаты – «монетные столбики».
В. Форменные элементы крови разнообразны по форме и размерам.
Г. Плазма крови обладает низкой вязкостью.
68. Идеальной жидкостью называется:
А. Несжимаемая и не имеющая вязкости жидкость
Б. Жидкость, течение которой подчиняется уравнению Ньютона
В. Жидкость, молекулы которой не взаимодействуют между собой
Г. Жидкость, состоящая из однородных недеформируемых частиц.
69. Уравнение неразрывности струи имеет вид:
А. v1×Q1 = v2×Q2
Б. v1×S1 = v2×S2
В. S1×S1 = S2
Г. v1 / S1 = v2 / S2
×
При движении тел сферической формы в жидкости или газе сила сопротивления F
равна:
А. F = – 9×h×R4×v
Б. F = 3×v2×R×r
В. F = — 6×p×h×R×v
Г. F = 8×p× R2×v×r
72. Жидкости – это вещества, для которых соотношение между средней кинетической энергией частиц и их потенциальной энергией имеет вид:
А. Wпот » Wкин
Б. Wпот << Wкин
В. Wпот >> Wкин
Г. Wпот ¹ 0, Wкин » 0
Вязкость крови
А. В мелких сосудах меньше, чем в крупных.
Б. В мелких сосудах больше, чем в крупных.
В. Постоянна во всех отделах сосудистого русла.
75. Течение крови по сосудам является:
А. Всегда ламинарным.
Б. Всегда турбулентным.
В. Преимущественно ламинарным и лишь в некоторых случаях – турбулентным.
Г. Преимущественно турбулентным и лишь в некоторых случаях – ламинарным.
76. В каком отделе сосудистого русла линейная скорость кровотока минимальна:
А. В аорте.
Б. В артериях.
В. В артериолах.
Г. В капиллярах.
77. Основной движущей силой кровотока является:
А. Кровяное давление, обусловленное превышением давления, вызванного работой сердца,
над атмосферным давлением.
Б. Гидростатическое давление.
В. Сила тяжести.
Г. Статическое давление.
78. Ламинарное течение жидкости переходит в турбулентное при:
А. Повышении температуры.
Б. При увеличении скорости течения.
В. При повышении давления.
Г. При уменьшении скорости течения жидкости.
81. Число Рейнольдса Re зависит от плотности жидкости r, скорости ее течения v, критического размера d, вязкостижидкости и определяется формулой:
А. Re = r v d /h
Б. Re = r v/hd
В. Re = r /hv d
Г. Re = r h/v d
82. Если число Рейнольдса превышает критическое значение, то:
А. Течение жидкости имеет ламинарный характер.
Б. Характер течения жидкости определить нельзя.
В. Течение жидкости называется установившимся.
Г. Течение жидкости имеет турбулентный характер.
Как объемная скорость установившегося течения жидкости в трубе переменного сечения зависит от площади поперечного сечения трубы?
А. Чем меньше площадь сечения, тем меньше объемная скорость.
Б. Чем меньше площадь сечения, тем больше объемная скорость.
В. Чем больше площадь сечения, тем меньше объемная скорость.
Г. Объемная скорость не зависит от площади поперечного сечения трубы.
cyberpedia.su
§4. Течение вязкой жидкости по цилиндрическим трубам.
Формула Пуазейля. Ламинарное и турбулентное течение жидкости.
Понятие о числе Рейнольдса.

Рис.10
скорость
течения постоянна, но от слоя к слою
изменяется. Слой, прилипший к стенкам
трубы, имеет скорость равную нулю, Vmin=0.
Слой, текущий вдоль оси трубы, имеет
максимальную скорость Vmax.
Профиль скорости в этом случае является
параболой (рис.10 а). Вдоль радиуса трубы
(ось r)
скорость изменяется, и это изменение
характеризуется величиной 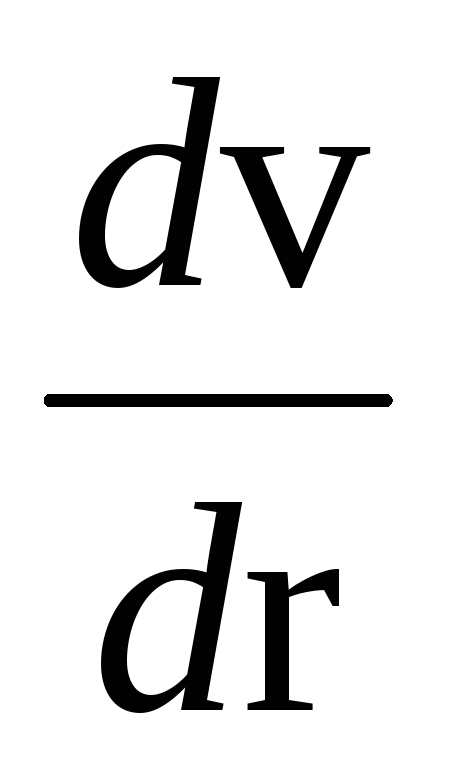 .
.
Задача о течении вязкой жидкости по цилиндрическим трубам имеет исключительно важное значение для физиологии, так как кровеносная система является системой из многократно разветвляющихся цилиндрических сосудов различных диаметров.
Важнейшей закономерностью течения вязкой жидкости по цилиндрическим трубам является формула Пуазейля, позволяющая рассчитать объем жидкости, протекающий через поперечное сечение трубы за одну секунду.
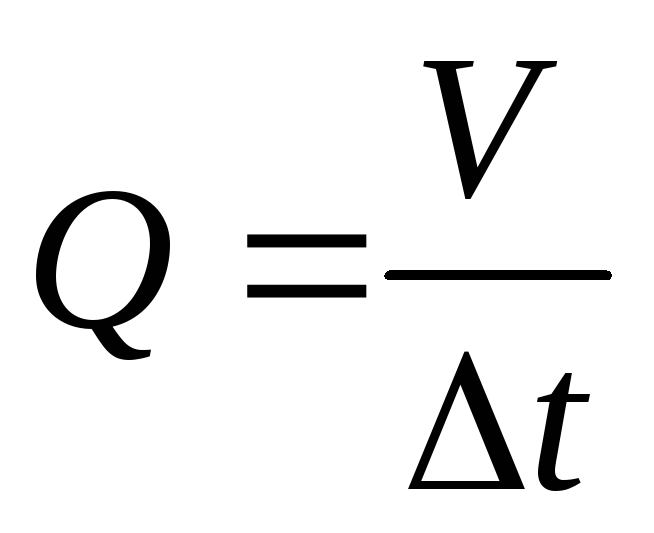 ,
,
где  —
объем жидкости, протекающей через
поперечное сечение трубы
—
объем жидкости, протекающей через
поперечное сечение трубы за время
за время .
Используя формулу (1), можно записать
.
Используя формулу (1), можно записать

где  — средняя скорость течения жидкости в
трубе. Тогда, учитывая, чтоS=
— средняя скорость течения жидкости в
трубе. Тогда, учитывая, чтоS=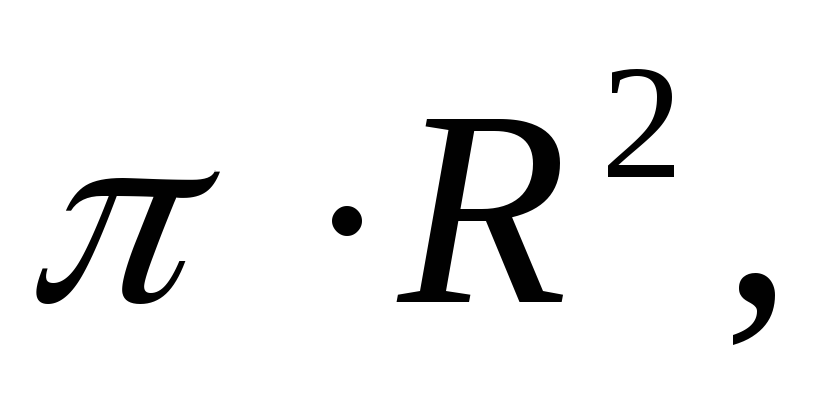 запишемQ=
запишемQ=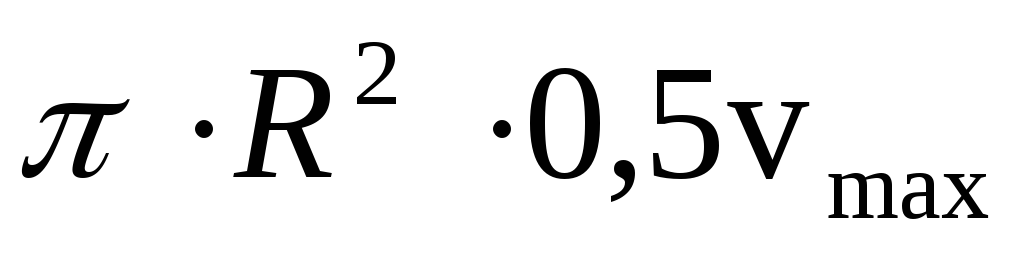
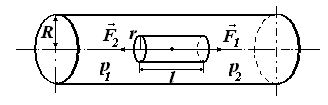
 выделим
в объеме текущей жидкости малый цилиндр
произвольного радиусаr
длиной l (рис.II).
Обозначив давление в жидкости слева от
выбранного цилиндра через Р1,
а справа через Р2.На
малый цилиндр в потоке действуют две
силы:
выделим
в объеме текущей жидкости малый цилиндр
произвольного радиусаr
длиной l (рис.II).
Обозначив давление в жидкости слева от
выбранного цилиндра через Р1,
а справа через Р2.На
малый цилиндр в потоке действуют две
силы:  1, обусловленная разностью
давлений
1, обусловленная разностью
давлений  —
Р2,
сообщающая цилиндру ускорение, и сила
—
Р2,
сообщающая цилиндру ускорение, и сила  —
сила трения (вязкости), которую испытывает
этот цилиндр, перемещаясь в потоке
жидкости.
—
сила трения (вязкости), которую испытывает
этот цилиндр, перемещаясь в потоке
жидкости.Рис.11
Для силы F1 запишем
F1= 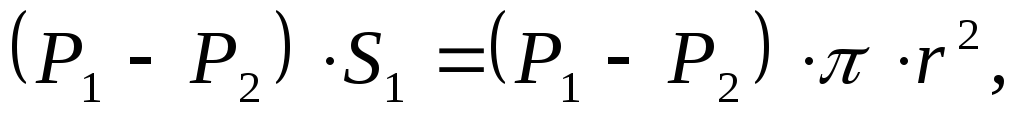
где
S1= 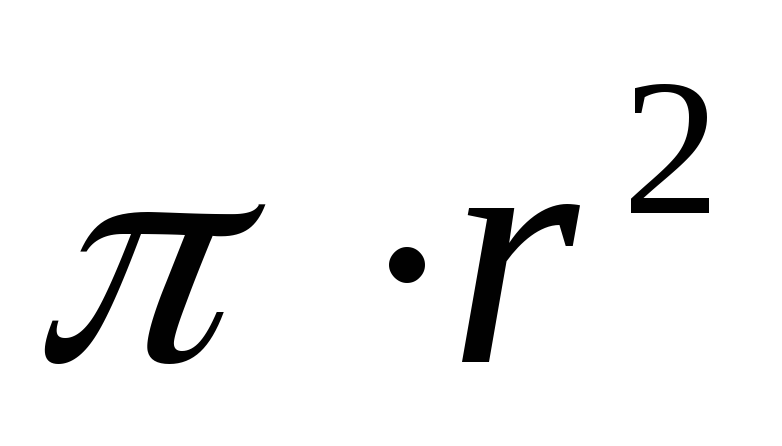 —
площадь поперечного сечения малого
цилиндра.
—
площадь поперечного сечения малого
цилиндра.
Используя формулу Ньютона, для силы F2 получим:
F2 = ,
,
где
S2 = 2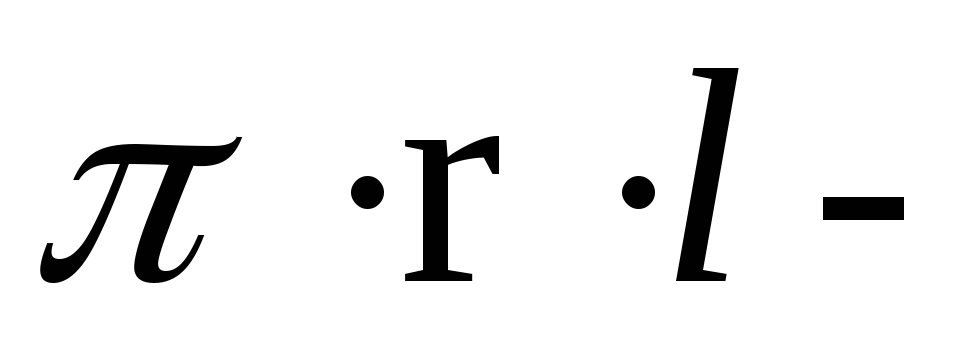 боковая поверхность малого цилиндра
/ поверхность соприкосновения этого
цилиндра с остальным объемом жидкости
/.
боковая поверхность малого цилиндра
/ поверхность соприкосновения этого
цилиндра с остальным объемом жидкости
/.
Чтобы
цилиндр двигался с постоянной скоростью,
надо, чтобы силы
и уравновешивали друг друга, т.е. должно
выполняться условие:
уравновешивали друг друга, т.е. должно
выполняться условие:
 (15)
(15)
Условие (15) через модули сил запишем в виде F1=-F2 или, подставив значение сил, получим
(Р1-Р2) =
—
=
—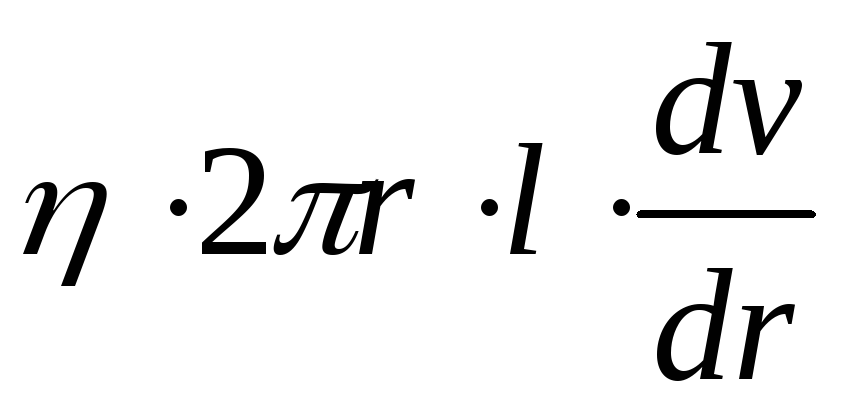 (16)
(16)
Произведем
сокращения и выразим из этого уравнения  :
:
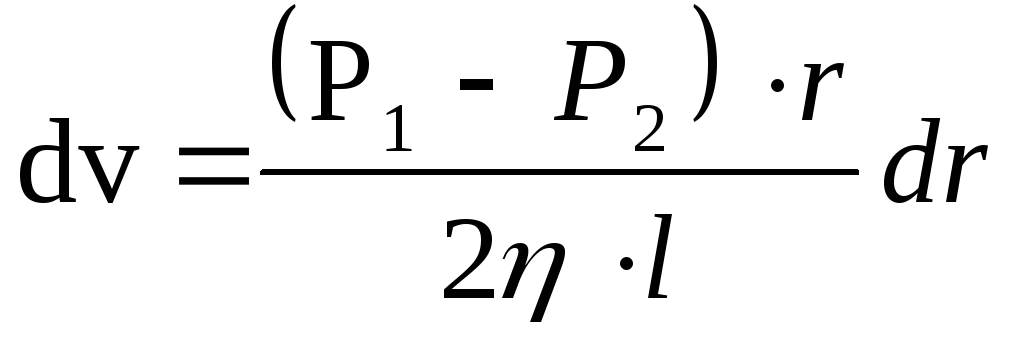
Проинтегрируем полученное уравнение, подставив предел интегрирования:
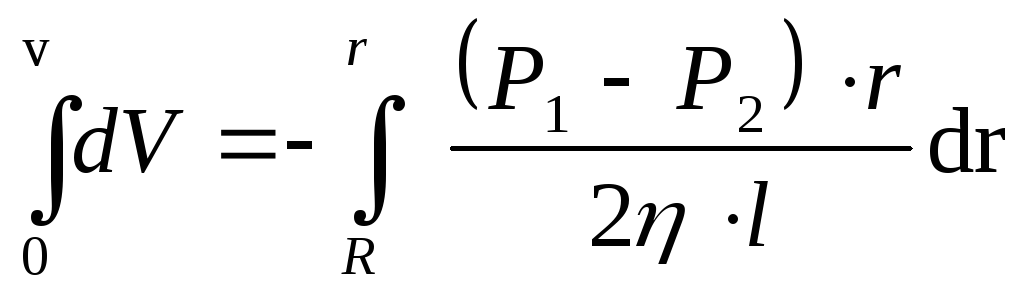
или
 . (17)
. (17)
На
осевой линии трубы r=0,
а скорость 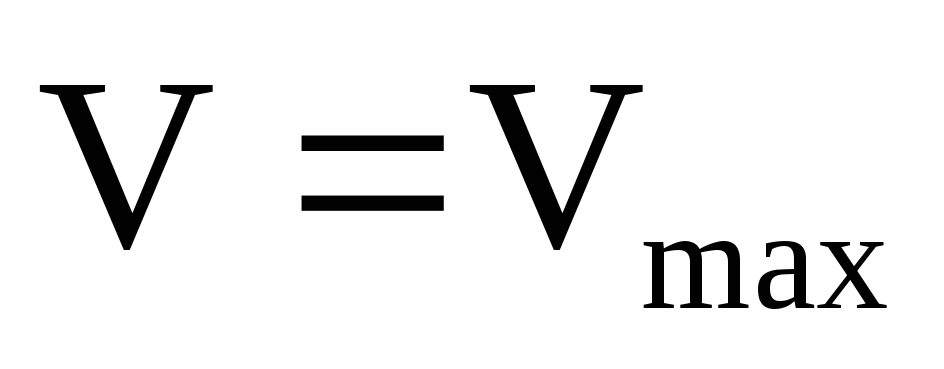 тогда
(17) можно переписать в виде
тогда
(17) можно переписать в виде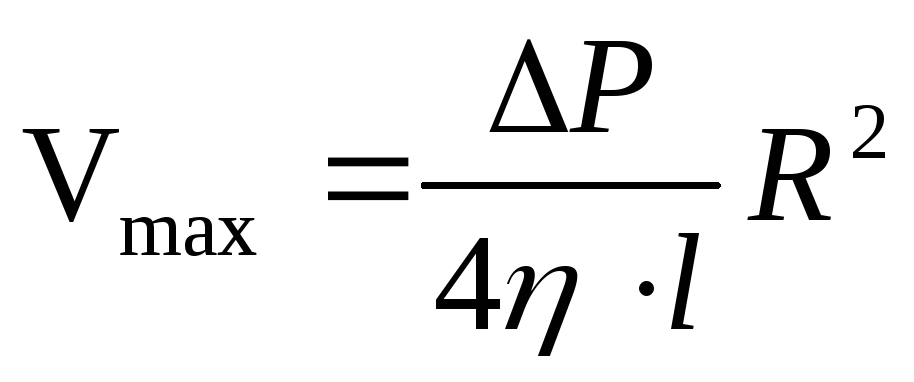 (18)
(18)
Формула
(18) была получена французским физиком
и физиологом Пуазейлем в 1841 году. Из
(18) видно, что максимальная скорость
течения жидкости по трубе прямо
пропорциональна перепаду давления 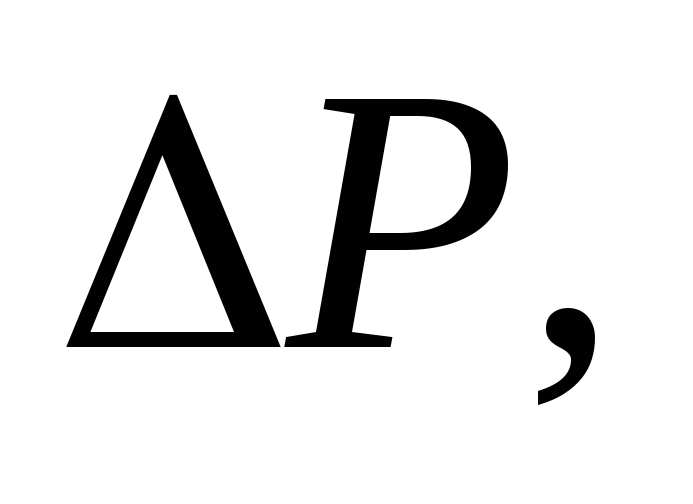 квадрату
радиуса трубыR
и обратно пропорциональна коэффициенту
вязкости
квадрату
радиуса трубыR
и обратно пропорциональна коэффициенту
вязкости  жидкости
и длине цилиндраl.Подставляя
(18) в (14),получим Q=
жидкости
и длине цилиндраl.Подставляя
(18) в (14),получим Q=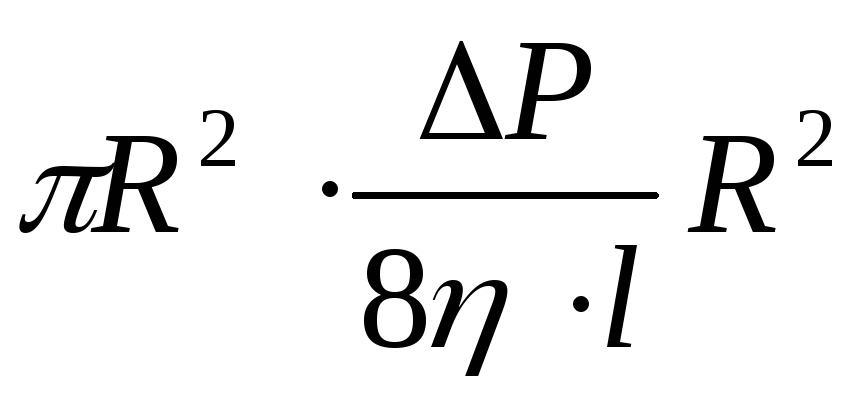 или в окончательном виде
или в окончательном виде
(19)
Q=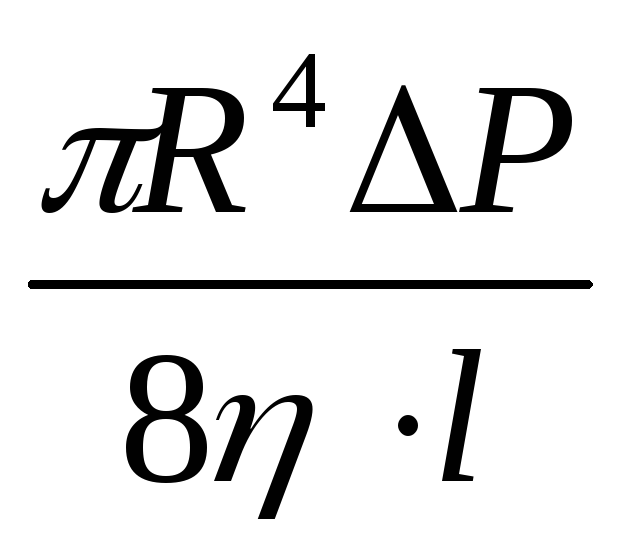
Полученное выражение носит название формулы Гагена-Пуазейля, или формулы Пуазейля.
Таким
образом, объем жидкости Q,
ежесекундно протекающей через поперечное
сечение трубы, прямо пропорционален
четвертой степени радиуса трубы R
(Q~R4),
разности давлений 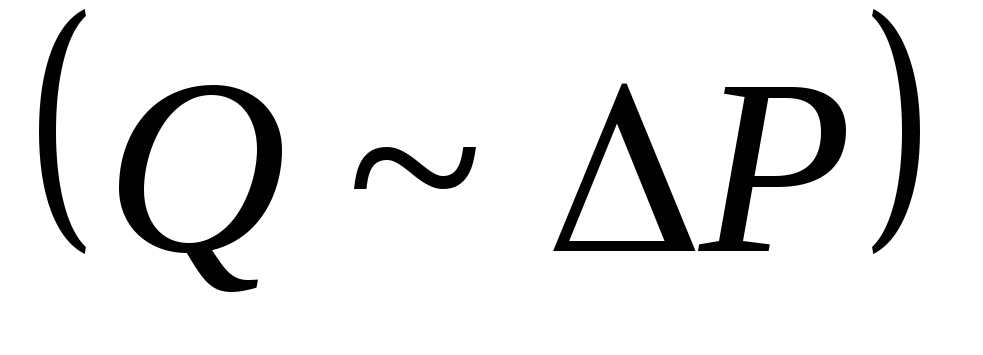 и обратно пропорционален коэффициенту
вязкости и длине трубы
и обратно пропорционален коэффициенту
вязкости и длине трубы .
.
Часто
проводят аналогию между формулой
Пуазейля и законом Ома для однородного
участка цепи 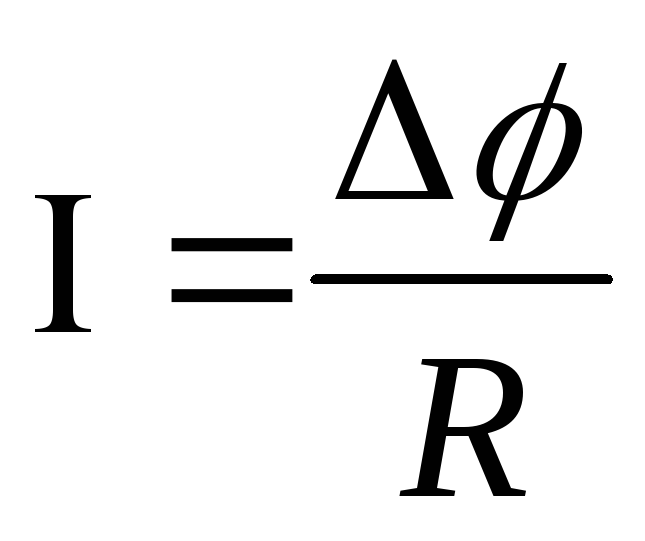 (сила
тока
(сила
тока прямо
пропорциональна разности потенциалов
прямо
пропорциональна разности потенциалов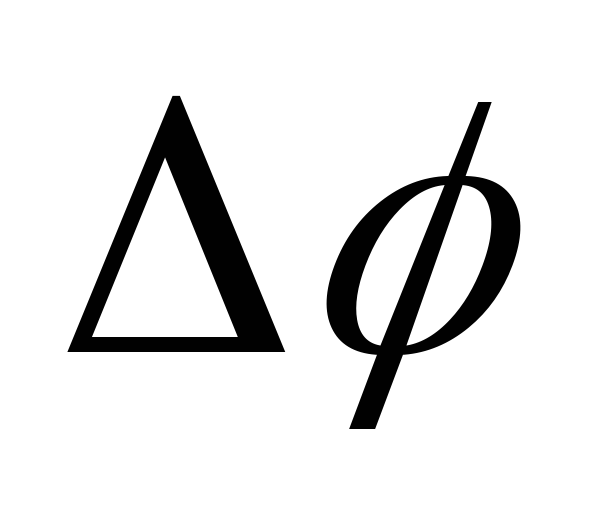 на участке цепи и обратно пропорциональна
сопротивлениюR
этого участка.) Формулу (19) представим
в виде:
на участке цепи и обратно пропорциональна
сопротивлениюR
этого участка.) Формулу (19) представим
в виде:
Q
=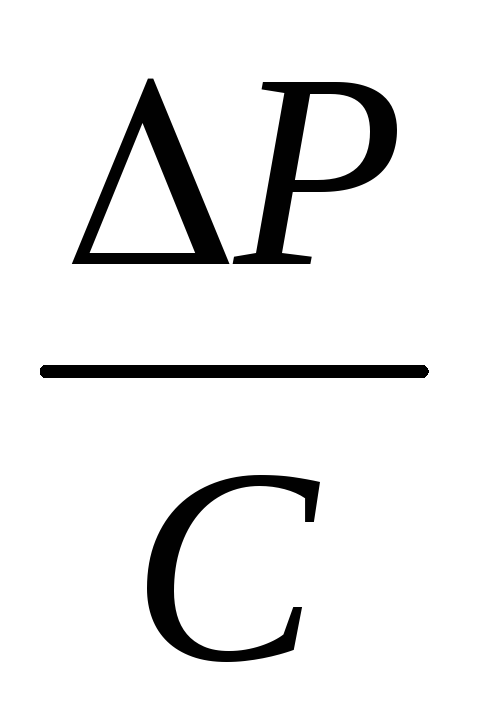 .
.
Величину
С =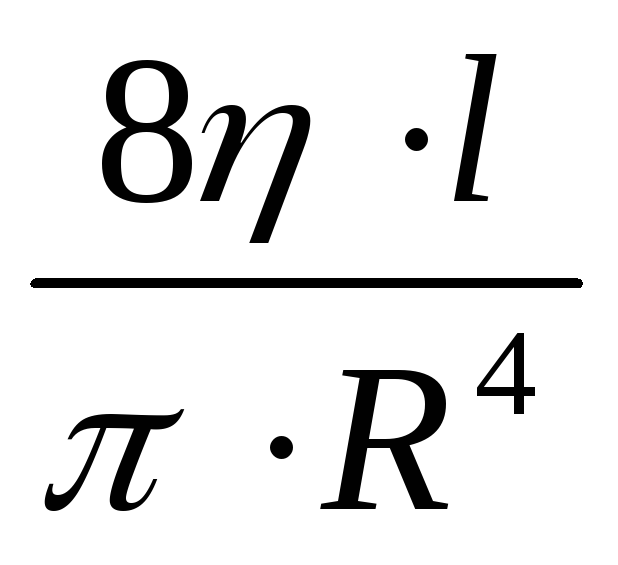 называютгидравлическим
сопротивлением.
Оно тем больше, чем больше вязкость
жидкости
называютгидравлическим
сопротивлением.
Оно тем больше, чем больше вязкость
жидкости 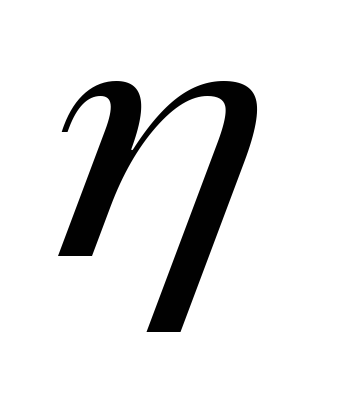 и
длина трубыl,
и зависит обратно пропорционально от
четвёртой степени радиуса трубы R.
и
длина трубыl,
и зависит обратно пропорционально от
четвёртой степени радиуса трубы R.
Таким
образом, объём жидкости, ежесекундно
протекающей через поперечное сечение
трубы, прямо пропорционален разности
давлений 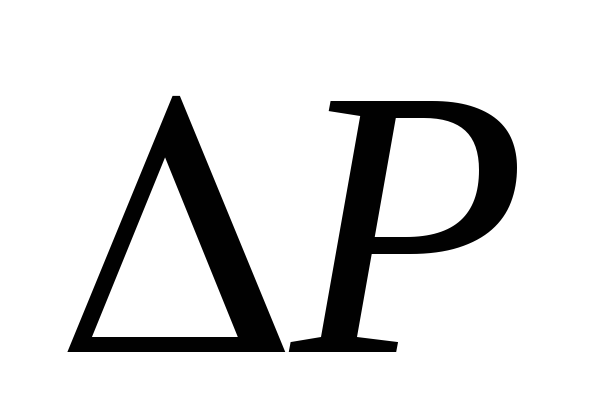 и обратно пропорционален гидравлическому
сопротивлению С.
и обратно пропорционален гидравлическому
сопротивлению С.
Аналогия между сопротивлением в электрической цепи и гидравлическим сопротивлением позволяет использовать правила для расчета сопротивления при последовательном и параллельном соединении труб с различными сопротивлениями.
Общее гидравлическое сопротивление труб, соединённых последовательно, рассчитывается по формуле:
С=С1+С2+С3+… , а соединённых параллельно, по формуле
 .
.
Формула Пуазейля справедлива не для любого течения вязкой жидкости, а только для ламинарного течения.

Турбулентным называют течение, при котором происходит интенсивное перемешивание слоёв, образуются завихрения жидкости.
Рис.12
Турбулентность увеличивает гидравлическое сопротивление. Профиль скорости такого движения в цилиндрической трубе показан на рис.12 .Вблизи стенок трубы наблюдается большой перепад скорости, скорость быстро нарастает от 0 до V – некоторого среднего значения скорости частиц, что позволяет считать такое течение в среднем однородным.
Характер течения жидкости (ламинарное или турбулентное) определяется целым рядом факторов: вязкостью жидкости, сечением трубы, скоростью течения и плотностью жидкости.
Как
уже рассматривалось выше, на любой малый
объём жидкости в потоке действуют
ускоряющая сила  и
сила вязкого трения
и
сила вязкого трения .
Характер течения будет определяться
отношением
.
Характер течения будет определяться
отношением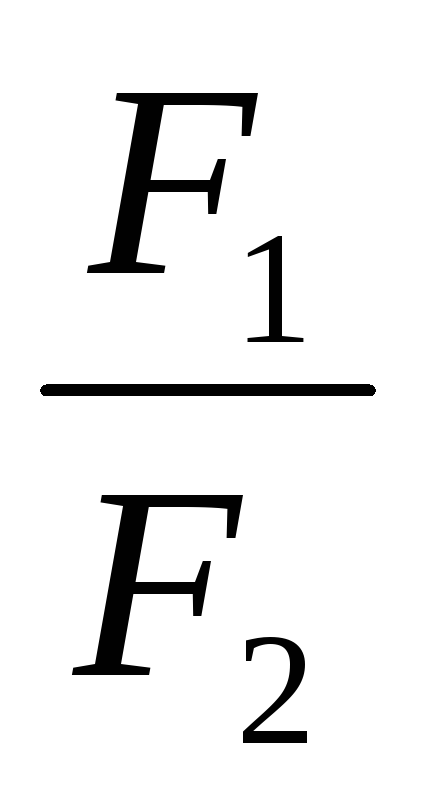 .
Чем больше это отношение, тем больше
вероятность возникновения вихрей, а
следовательно, и турбулентного течения.
Английский физик и инженер Рейнольдс
рассчитал безразмерное отношениеF1/F2.
Это отношение получило название числа
Рейнольдса Re.
Очевидно, число Re
есть величина безразмерная.
.
Чем больше это отношение, тем больше
вероятность возникновения вихрей, а
следовательно, и турбулентного течения.
Английский физик и инженер Рейнольдс
рассчитал безразмерное отношениеF1/F2.
Это отношение получило название числа
Рейнольдса Re.
Очевидно, число Re
есть величина безразмерная.
Re
=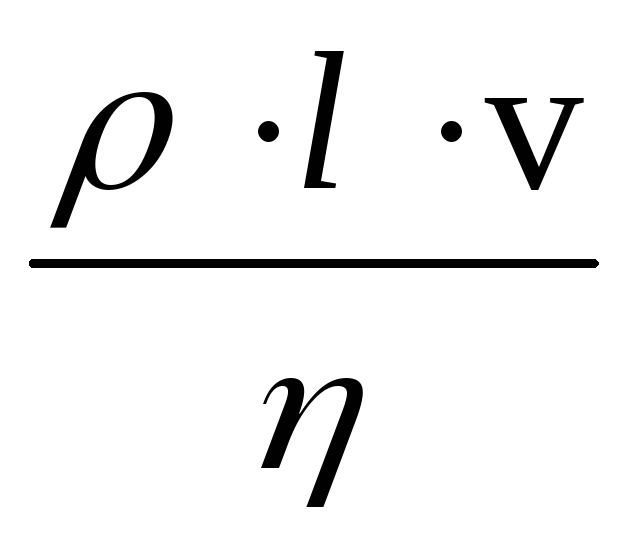
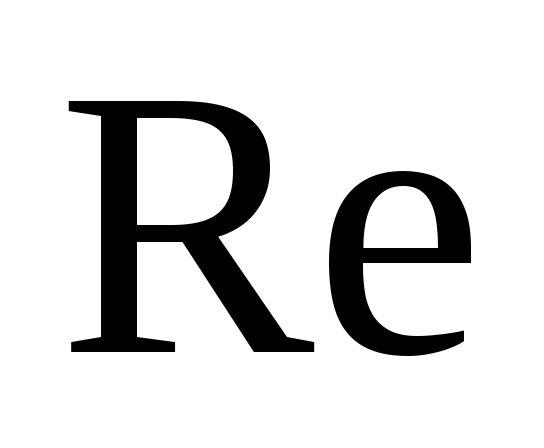 =
=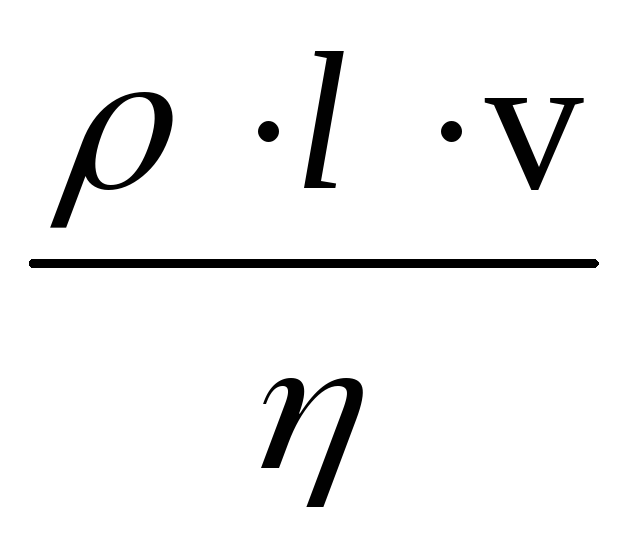
(20)
где  плотность жидкости,l –характерный линейный размер сечения
трубы (диаметр или радиус для цилиндрического
сечения трубы, высота – для треугольного,
сторона – для квадратного),
плотность жидкости,l –характерный линейный размер сечения
трубы (диаметр или радиус для цилиндрического
сечения трубы, высота – для треугольного,
сторона – для квадратного),  скорость потока,
скорость потока,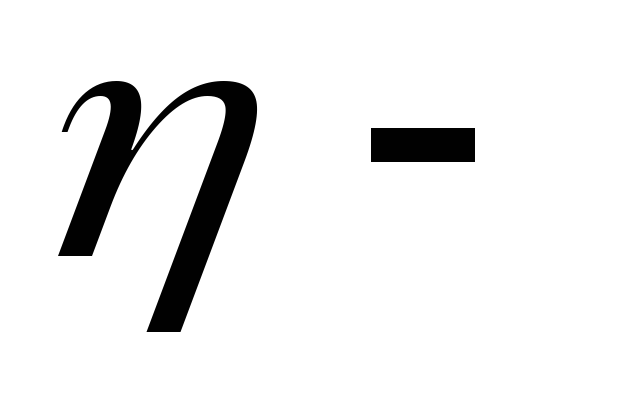 коэффициент
вязкости.
коэффициент
вязкости.
Так
как число Рейнольдса зависит от двух
характеристик жидкости – вязкости  и плотности
и плотности ,
то целесообразно ввести в это число
величину
,
то целесообразно ввести в это число
величину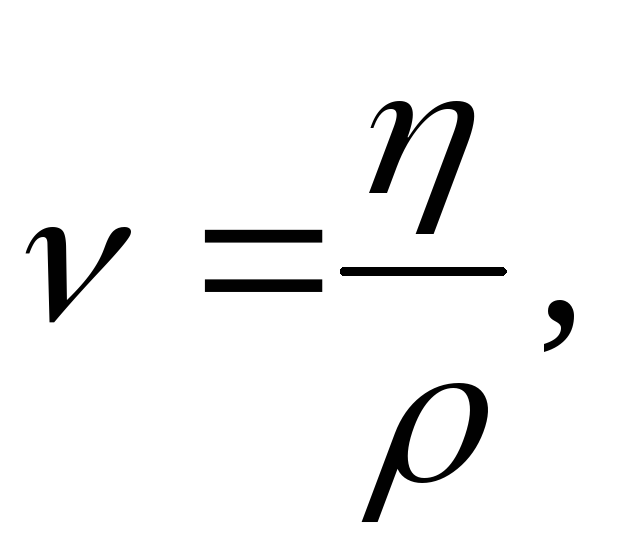 называемую кинематической вязкостью.
Тогда (20) принимает вид
называемую кинематической вязкостью.
Тогда (20) принимает вид
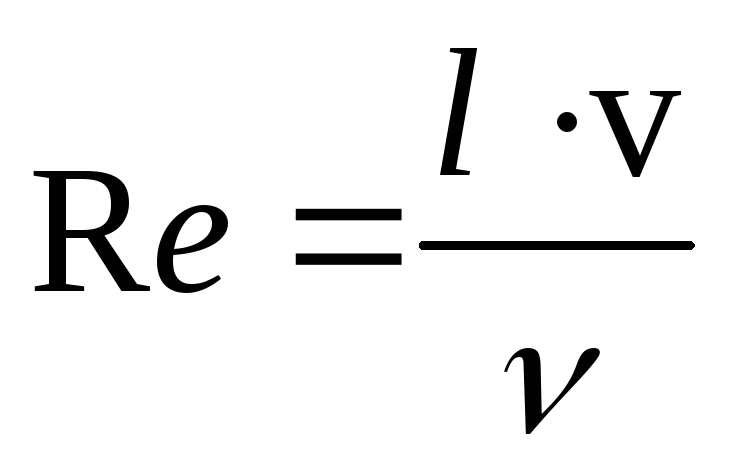
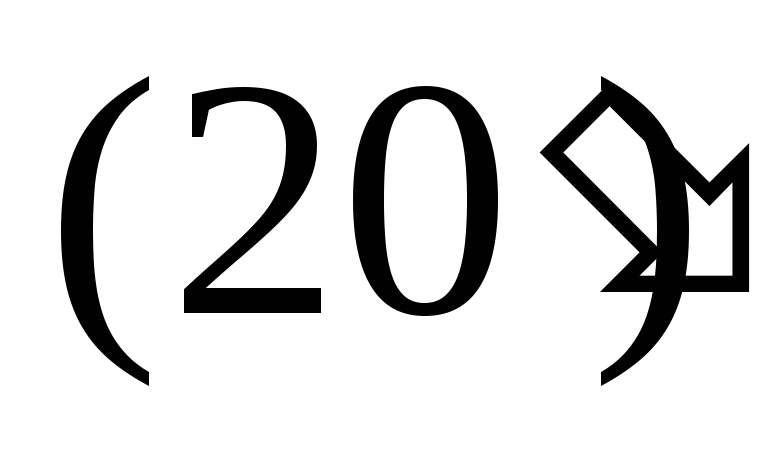
Переход от ламинарного течения к турбулентному определяется критическим числом Рейнольдса.
При
числах 

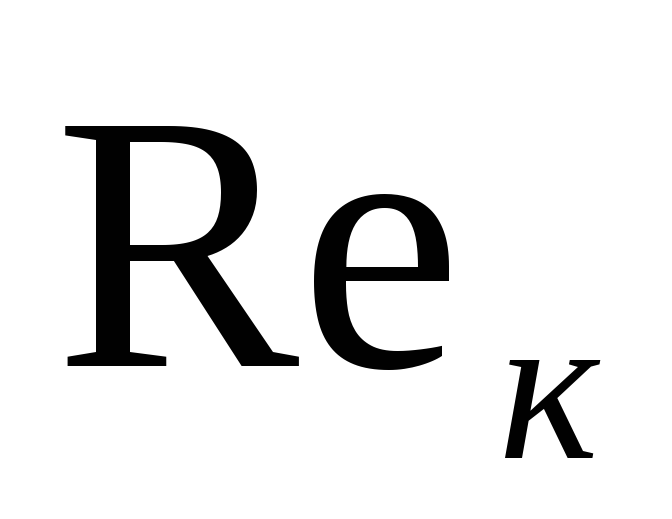 течение носит ламинарный характер, при
течение носит ламинарный характер, при >
>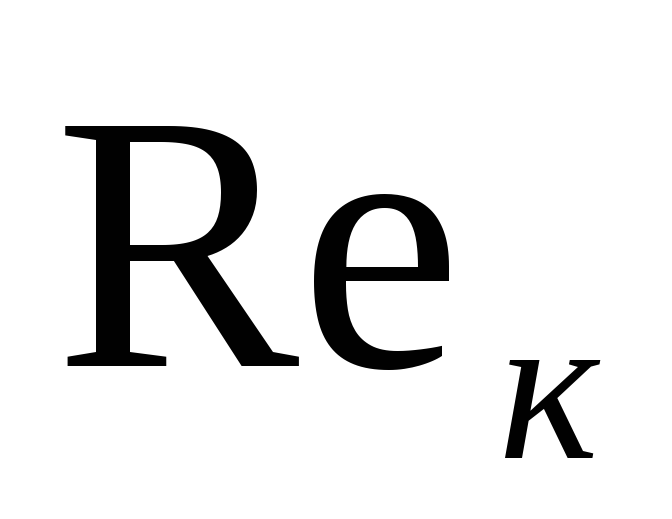 течение становится турбулентным.
Критические значения числа Рейнольдса
определяются только экспериментально.
Для гладких цилиндрических труб
течение становится турбулентным.
Критические значения числа Рейнольдса
определяются только экспериментально.
Для гладких цилиндрических труб
 1000,
если за
1000,
если за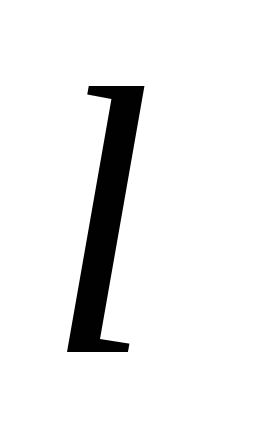 принять
радиус трубы. Число Рейнольдса играет
большую роль во многих количественных
исследованиях течения жидкости и газа.
Оно является критерием подобия при
создании моделей гидро- и аэродинамических
систем и, в частности, кровеносной
системы. Важно, чтобы модель имела то
же число Рейнольдса, что и сама система.
Это достигается соответствующим подбором
скорости, вязкости и линейного размера
сечения модели. Из (20) видно, что увеличение
размеров сечения можно скомпенсировать
уменьшением скорости течения
принять
радиус трубы. Число Рейнольдса играет
большую роль во многих количественных
исследованиях течения жидкости и газа.
Оно является критерием подобия при
создании моделей гидро- и аэродинамических
систем и, в частности, кровеносной
системы. Важно, чтобы модель имела то
же число Рейнольдса, что и сама система.
Это достигается соответствующим подбором
скорости, вязкости и линейного размера
сечения модели. Из (20) видно, что увеличение
размеров сечения можно скомпенсировать
уменьшением скорости течения или подбором жидкости с соответствующими
значениями вязкости
или подбором жидкости с соответствующими
значениями вязкости и
плотности
и
плотности .
.
Течение крови в сосудах носит в норме ламинарный характер, небольшая турбулентность наблюдается вблизи клапанов сердца. При патологии число Re может превысить критическое значение и течение станет турбулентным, что можно обнаружить по характерным шумам и использовать в диагностике заболеваний.
II. ПРАКТИЧЕСКАЯ ЧАСТЬ
А. Определение коэффициента вязкости методом Стокса
Приборы и принадлежности: стеклянный цилиндр с кольцевыми метками, исследуемая жидкость, дробинки, микрометр, секундомер, линейка, термометр.
Английским
физиком и математиком Стоксом было
установлено, что сила вязкого трения
Fс,
действующая в жидкости на движущееся
тело при небольших скоростях  прямо
пропорциональна скорости, т.е.
прямо
пропорциональна скорости, т.е.
 (21)
(21)
где
r-коэффициент
сопротивления, зависящий от размеров
и формы тела, а также от вязкости среды,
в которой оно движется. Для твёрдого
тела шарообразной формы радиуса R,
движущего в жидкости с коэффициентом
вязкости 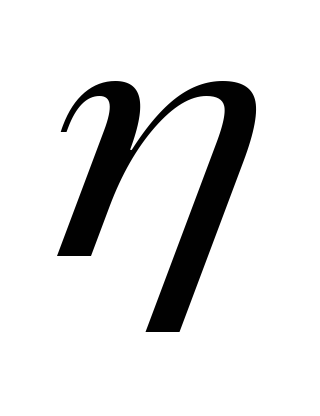 ,
коэффициент сопротивления
,
коэффициент сопротивления
r = 6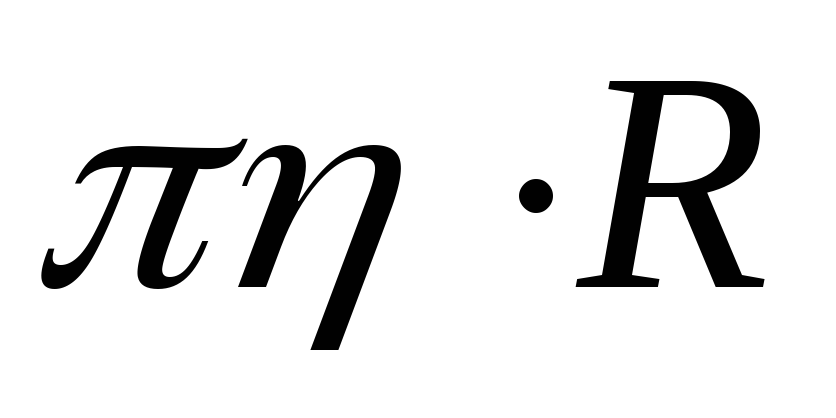
Тогда по закону Стокса для модуля силы сопротивления, действующей на шарообразное тело, можно записать выражение
Fc = 6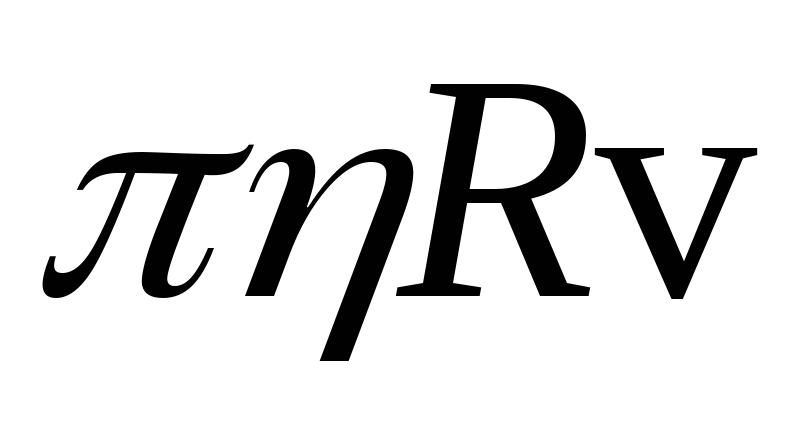 (22)
(22)
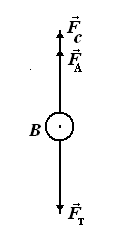
 действуют
три силы: сила тяжести
действуют
три силы: сила тяжести выталкивающая
сила
выталкивающая
сила (сила
Архимеда) и сила сопротивления
(сила
Архимеда) и сила сопротивления (рис.13).
Сила тяжести рассчитывается по формуле
(рис.13).
Сила тяжести рассчитывается по формуле Fт = mg=V 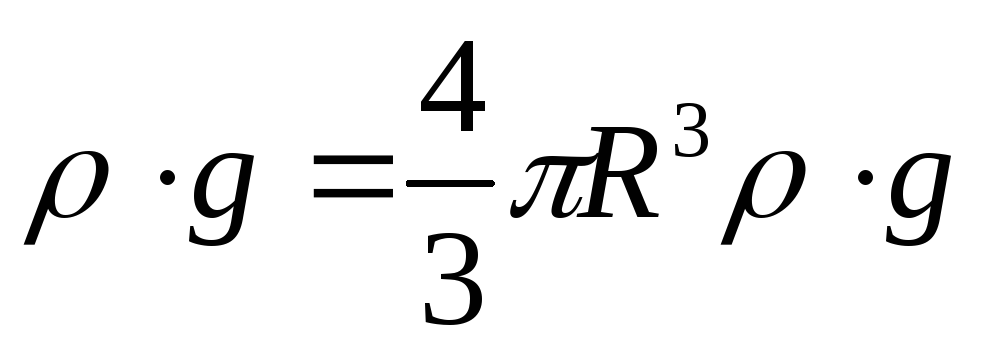 ,
где
,
где 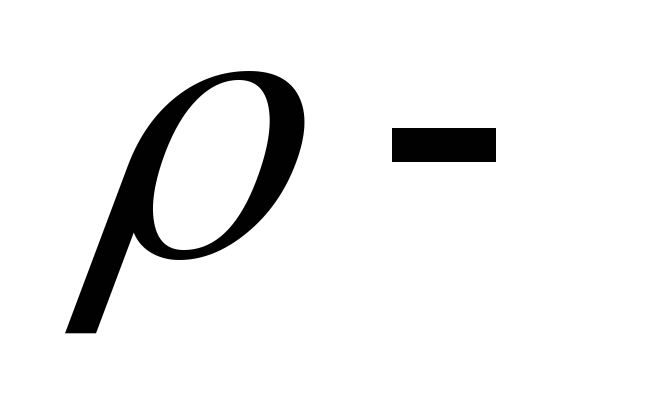 плотность
шара,g
– ускорение свободного падения. Силу
Архимеда можно рассчитать как
плотность
шара,g
– ускорение свободного падения. Силу
Архимеда можно рассчитать как
Рис.13

здесь
mж – масса
жидкости, вытесненной шаром,  плотность
этой жидкости. Сила сопротивленияFc вычисляется по формуле (22). Так как сила
плотность
этой жидкости. Сила сопротивленияFc вычисляется по формуле (22). Так как сила  ипостоянны, а сила
ипостоянны, а сила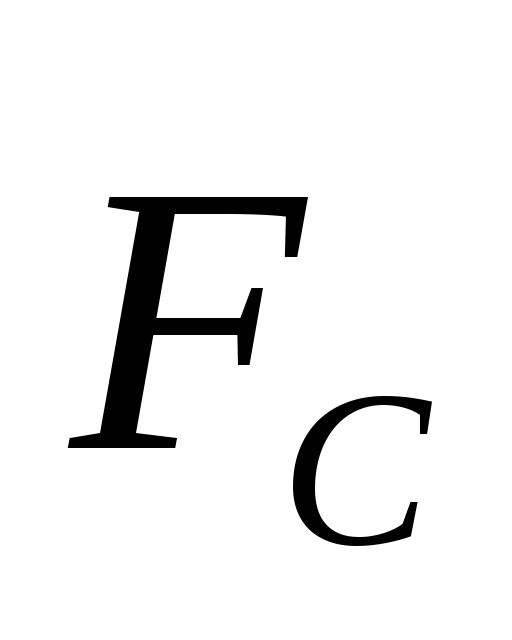 возрастает с увеличением скорости
движения шара, то с некоторого момента
времени эти три силы могут уравновесить
друг друга, и движение шара станет
равномерным. В векторной форме закон
движения шара запишется в виде
возрастает с увеличением скорости
движения шара, то с некоторого момента
времени эти три силы могут уравновесить
друг друга, и движение шара станет
равномерным. В векторной форме закон
движения шара запишется в виде
 ,
,
или через модули сил этот закон можно записать таким образом
FT= FA+ FC.
Подставим в последнее уравнение выражения для сил и получим:

откуда после соответствующих преобразований получим выражение,
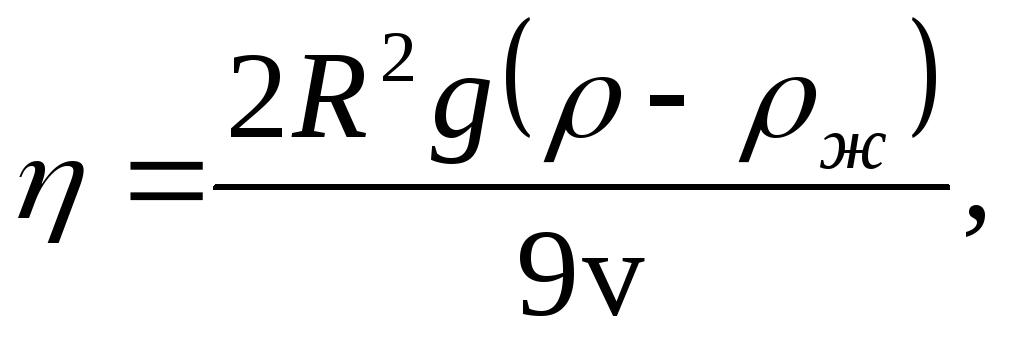
или, учитывая, что гдеD- диаметр шара, последнюю формулу запишем в виде
 (23)
(23)
studfile.net
3. Гидродинамика Поток жидкости и его параметры. Виды и режимы течения жидкости.
Гидродинамика – раздел механики, изучающий движение жидкостей и газов (в интервале дозвуковых скоростей, а также их взаимодействие с твердыми и жидкими телами, находящимися в жидкости или газе).
Движение жидкостей, называемое потоком жидкости, происходит по открытым или закрытым каналам (трубопроводам). Движение жидкости, не имеющей открытой поверхности, называется напорным движением. Напорные потоки занимают весь объём закрытого трубопровода. Движение по рекам, лоткам, каналам называется безнапорным. Движение жидкости, при котором её скорость в любой точке занятого жидкостью пространства, не меняется во времени, называется установившимся или стационарным движением. Поверхность, проведённая нормально к направлению движения жидкостей, называется поперечным или живым сечением потока. Линия, по которой ограничивается живое сечение потока жидкости, называется смоченным периметром.
Линия
тока ─
это кривая, проведенная в движущейся
жидкости в данный момент времени так,
что в каждой точке векторы скорости  совпадают с касательными к этой кривой.
совпадают с касательными к этой кривой.
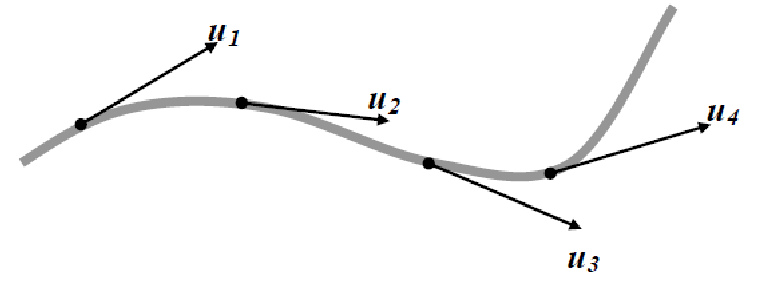
Рисунок 3.1─ Линия тока
Нужно различать траекторию и линию тока. Траектория характеризует путь, проходимый одной определенной частицей, а линия тока направление движения в данный момент времени каждой частицы жидкости, лежащей на ней.
При установившемся движении линии тока совпадают с траекториями частиц жидкости. При неустановившемся движении они не совпадают, и каждая частица жидкости лишь один момент времени находится на линии тока, которая сама существует лишь в это мгновение. В следующий момент возникают другие линии тока, на которых будут располагаться другие частицы. Еще через мгновение картина опять меняется.
Если выделить в движущейся жидкости элементарный замкнутый контур площадью dω и через все точки этого контура провести линии тока, то получится трубчатая поверхность, которую называют трубкой тока.
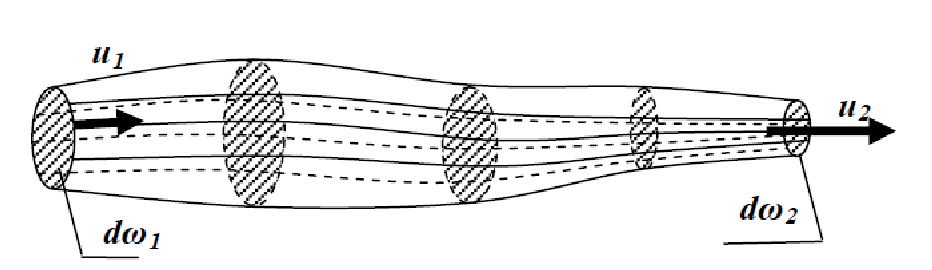
Рисунок 3.2 ─ Трубка тока
Часть потока, ограниченная поверхностью трубки тока, называется элементарной струйкой жидкости. Таким образом, элементарная струйка жидкости заполняет трубку тока и ограничена линиями тока, проходящими через точки выделенного контура с площадью dω. Если dω устремить к 0, то элементарная струйка превратится в линию тока.
Из приведённых выше определений вытекает, что в любом месте поверхности каждой элементарной струйки (трубки тока) в любой момент времени вектора скоростей направлены по касательной (и, следовательно, нормальные составляющие отсутствуют). Это означает, что ни одна частица жидкости не может проникнуть внутрь струйки или выйти наружу. При установившемся движении элементарные струйки жидкости обладают рядом свойств:
─ площадь поперечного сечения струйки и ее форма с течением времени не изменяются, так как не изменяются линии тока;
─ проникновение частиц жидкости через боковую поверхность элементарной струйки не происходит;
─ во всех точках поперечного сечения элементарной струйки скорости движения одинаковы вследствие малой площади поперечного сечения;
─ форма, площадь поперечного сечения элементарной струйки и скорости в различных поперечных сечениях струйки могут изменяться.
Трубка тока является как бы непроницаемой для частиц жидкости, а элементарная струйка представляет собой элементарный поток жидкости. При неустановившемся движении форма и местоположение элементарных струек непрерывно изменяются.
Расход потока жидкости (расход жидкости) – количество жидкости, протекающей в единицу времени через живое сечение потока. Различают объёмный, массовый и весовой расходы жидкости.
Объёмный расход жидкости это объём жидкости, протекающей в единицу времени через живое сечение потока.
Объёмный расход жидкости измеряется обычно в м3/с, дм3/с или л/с. Он вычисляется по формуле
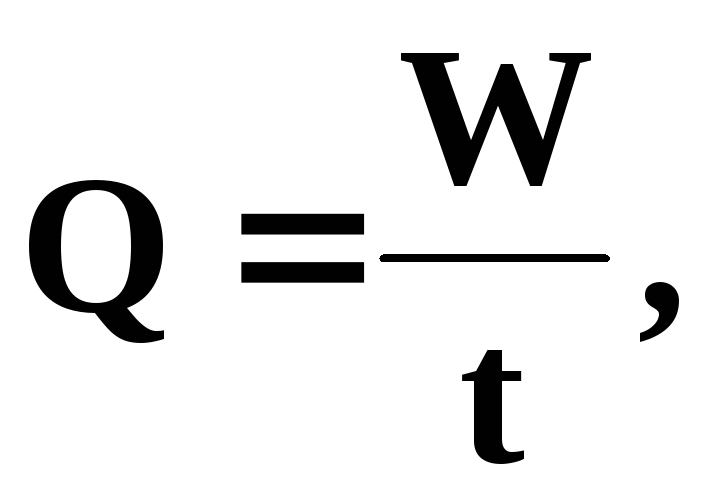 (3.1)
(3.1)
где  ─
объёмный расход жидкости;
─
объёмный расход жидкости;  ─
объём жидкости, протекающей через живое
сечение потока;
─
объём жидкости, протекающей через живое
сечение потока;  ─
время
течения жидкости.
─
время
течения жидкости.
С
учётом того, что поток складывается из
элементарных струек, то и расход потока
складывается из расходов элементарных
струек жидкости  .
.
Расход
элементарной струйки –
объем жидкости  ,
проходящей через живое сечение струйки
в единицу времени.
,
проходящей через живое сечение струйки
в единицу времени.
Таким образом,
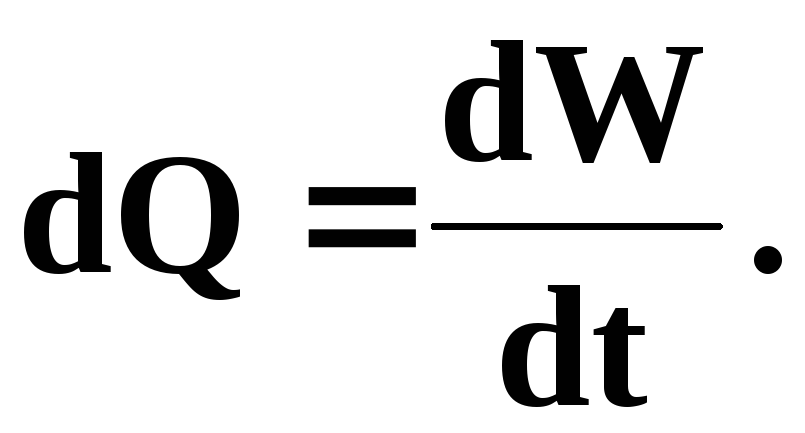 (3.2)
(3.2)
Если последнее выражение проинтегрировать по площади живого сечения потока можно получить формулу объёмного расхода жидкости, как сумму расходов элементарных струек
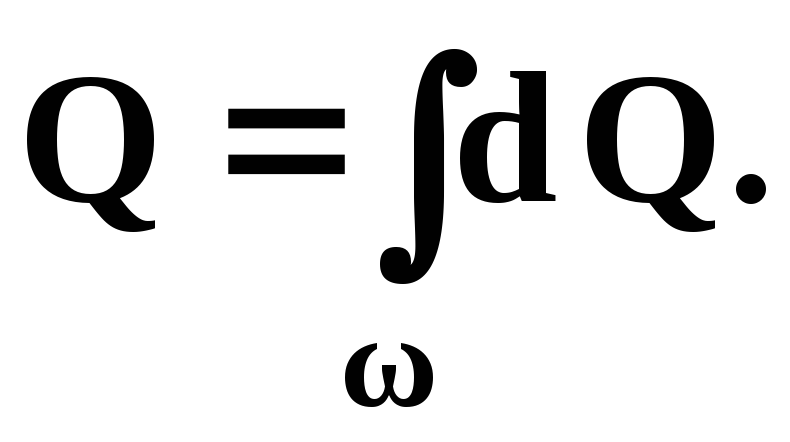
Применение этой формулы в расчетах весьма затруднительно, так как расходы элементарных струек жидкости в различных точках живого сечения потока различны. Поэтому в практике для определения расхода чаще пользуются понятием средней скорости потока.
Средняя
скорость потока жидкости  в
данном сечении это не существующая в
действительности скорость потока,
одинаковая для всех точек данного живого
сечения, с которой должна была бы
двигаться жидкость, что бы её расход
был равен фактическому.
в
данном сечении это не существующая в
действительности скорость потока,
одинаковая для всех точек данного живого
сечения, с которой должна была бы
двигаться жидкость, что бы её расход
был равен фактическому.
studfile.net
33. Ламинарный режим движения. Распределение скорости жидкости по сечению потока.
При
ламинарном движении жидкости в
цилиндрической трубе распределение
скоростей по сечению имеет вид параболы
и схематически изображается телескопическим
(рис.): у стенок трубы скорости равны
нулю, а при удалении плавно возрастают
и достигают максимального значения на
оси трубы. Определим закон распределения
скоростей в живом сечении потока при
ламинарном режиме. Для этого выделим
внутри горизонтального трубопровода
объем жидкости в виде цилиндра радиусом 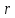 (рис.)
и длиной
(рис.)
и длиной 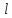 и
составим уравнение равновесия всех
действующих сил:
и
составим уравнение равновесия всех
действующих сил: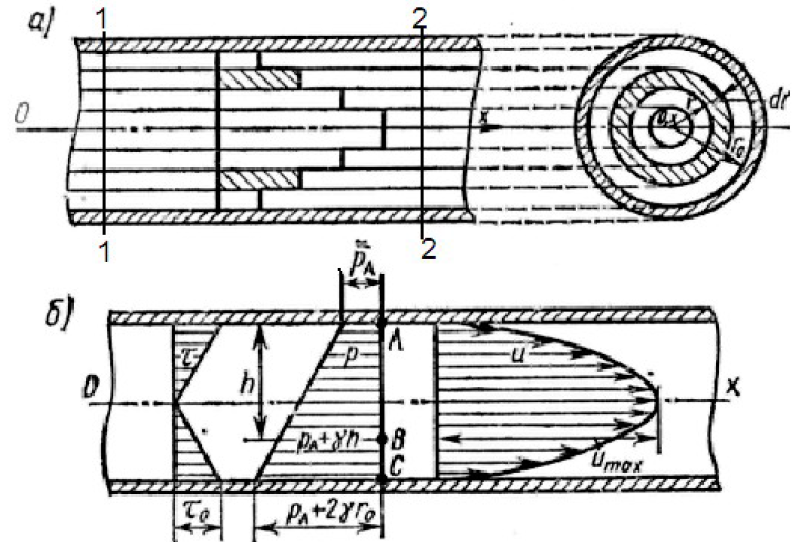
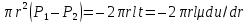 , где –
разность сил давления в сечениях 1 и 2;
, где –
разность сил давления в сечениях 1 и 2; –
сила трения на боковой поверхности
цилиндра. Знак минус в формуле Ньютона
взят потому, что градиент
–
сила трения на боковой поверхности
цилиндра. Знак минус в формуле Ньютона
взят потому, что градиент 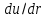 отрицателен,
поскольку с увеличением радиуса скорость
убывает. При равномерном движении
жидкости, при котором все живые сечения
по длине потока одинаковы как по форме,
так и по размерам, и скорости в
соответственных точках живых сечений
также одинаковы. Таким образом, скорость
является функцией исключительно одного
радиуса:
отрицателен,
поскольку с увеличением радиуса скорость
убывает. При равномерном движении
жидкости, при котором все живые сечения
по длине потока одинаковы как по форме,
так и по размерам, и скорости в
соответственных точках живых сечений
также одинаковы. Таким образом, скорость
является функцией исключительно одного
радиуса: 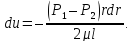 C
учетом гидравлического уклона
C
учетом гидравлического уклона 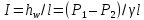 получим:
получим: 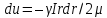 .
Интегрируя
по сечению трубы от
.
Интегрируя
по сечению трубы от 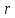 до
до 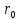 :
:
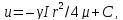 учитывая,
что при
учитывая,
что при 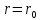 скорость
скорость 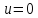 ,
тогда
,
тогда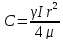 , получим
закон распределения скоростей в живом
сечении потока:
, получим
закон распределения скоростей в живом
сечении потока: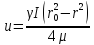
Для
центральной струйки при  :
: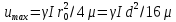 . Расход
жидкости через трубу при ламинарном
движении численно равен объему параболоида
скорости
. Расход
жидкости через трубу при ламинарном
движении численно равен объему параболоида
скорости  и
определяется из выражения
и
определяется из выражения
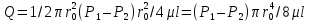 , отсюда
средняя скорость
, отсюда
средняя скорость 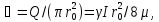 а
соотношение между максимальной и средней
скоростью
а
соотношение между максимальной и средней
скоростью 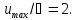 Отсюда
закон распределения скоростей может
быть записан таким образом:
Отсюда
закон распределения скоростей может
быть записан таким образом: 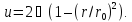
34. Определение расхода жидкости и средней скорости ламинарного потока.
Рассмотрим
движение вязкой жидкости в круглой
трубе радиусом R
при установившемся ламинарном режиме.
Выделяя в потоке цилиндрический объем
жидкости длиной 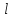 и произвольным радиусом
и произвольным радиусом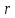 (рис.), из условия динамического равновесия
получим, что разность сил давления,
приложенных к выделенному объему в
сечениях 1-1 и 2-2, уравновешивается силами
трения, возникающими на его боковой
поверхности,
где
(рис.), из условия динамического равновесия
получим, что разность сил давления,
приложенных к выделенному объему в
сечениях 1-1 и 2-2, уравновешивается силами
трения, возникающими на его боковой
поверхности,
где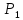 и
и  –давление
в центрах сечений 1-1 и 2-2. Из уравнения
энергетического баланса напоров для
рассматриваемого случая, следует, что
потери на трение по длине определяются
зависимостью
–давление
в центрах сечений 1-1 и 2-2. Из уравнения
энергетического баланса напоров для
рассматриваемого случая, следует, что
потери на трение по длине определяются
зависимостью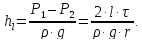 Из выражения следует, что касательные
напряжения в сечении потока распределяются
линейно
Из выражения следует, что касательные
напряжения в сечении потока распределяются
линейно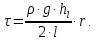 Решая
совместно (4) и (1), получаем дифференциальное
уравнение, определяющее скорость
Решая
совместно (4) и (1), получаем дифференциальное
уравнение, определяющее скорость  как функцию радиуса
как функцию радиуса  :
: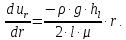 Интегрируя
уравнение с учетом граничного условия
(
Интегрируя
уравнение с учетом граничного условия
(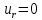 при
при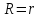 )
получаем параболический закон
распределения скоростей (рис.) по сечению
круглой трубы
)
получаем параболический закон
распределения скоростей (рис.) по сечению
круглой трубы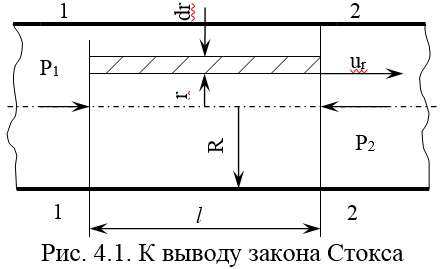
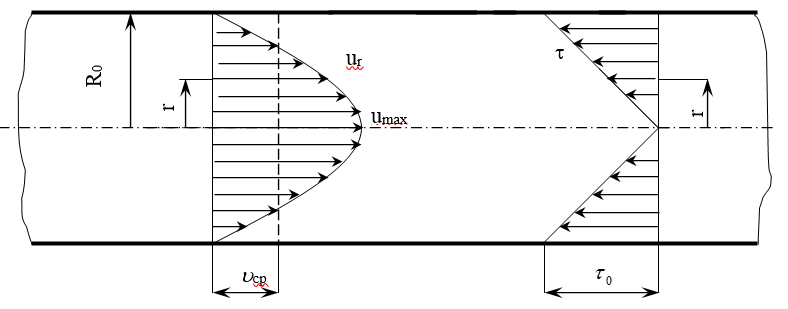
 Скорость
имеет максимальное значение на оси
трубы, когда
Скорость
имеет максимальное значение на оси
трубы, когда 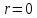 :
: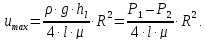 Сопоставляя
зависимости, находим закон Стокса,
выражающий параболическое распределение
скоростей в сечении трубопровода при
ламинарном движении
Сопоставляя
зависимости, находим закон Стокса,
выражающий параболическое распределение
скоростей в сечении трубопровода при
ламинарном движении
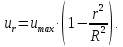 Подсчитав
расход жидкости суммированием расходов
через элементарные кольцевые площадки
толщиной
Подсчитав
расход жидкости суммированием расходов
через элементарные кольцевые площадки
толщиной 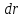 (рис.) сечения потока, находится средняя
скорость
(рис.) сечения потока, находится средняя
скорость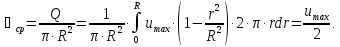 Отсюда
следует,
что средняя скорость потока при ламинарном
режиме равна половине максимальной.
Расход жидкости в круглой трубе при ее
ламинарном движении определяется
уравнением Пуазейля
Отсюда
следует,
что средняя скорость потока при ламинарном
режиме равна половине максимальной.
Расход жидкости в круглой трубе при ее
ламинарном движении определяется
уравнением Пуазейля  где
где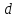 – внутренний диаметр трубы.
– внутренний диаметр трубы.
studfile.net
4.2. Основные характеристики движения жидкостей
4.2.1. Гидравлический радиус и эквивалентный диаметр
При движении жидкости через сечение любой формы, отличной от круглой, в качестве расчетного линейного размера принимают гидравлический радиус или эквивалентный диаметр.
Под гидравлическим радиусом rг (м) принимают отношение площади затопленного сечения трубопровода или канала, через которое протекает жидкость, т.е. живого сечения потока, к смоченному периметру:
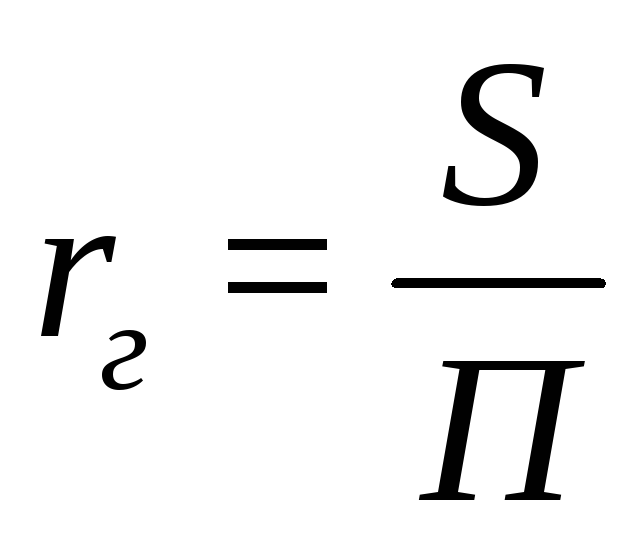 ,
,
где S – площадь сечения потока жидкости, м2;
П – смоченный периметр, м.
Смоченный периметр П — часть периметра живого сечения, ограниченное твердыми стенками (рисунок 15, выделен двойной линией).

Рисунок 15 — Смоченный периметр
Для круглой трубы
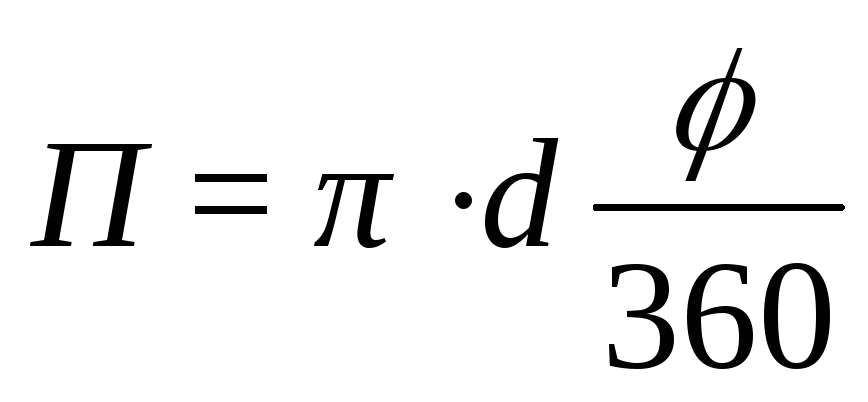 ,
,
Для круглой трубы
с внутренним диаметром d и, значит, площадью свободного сечения 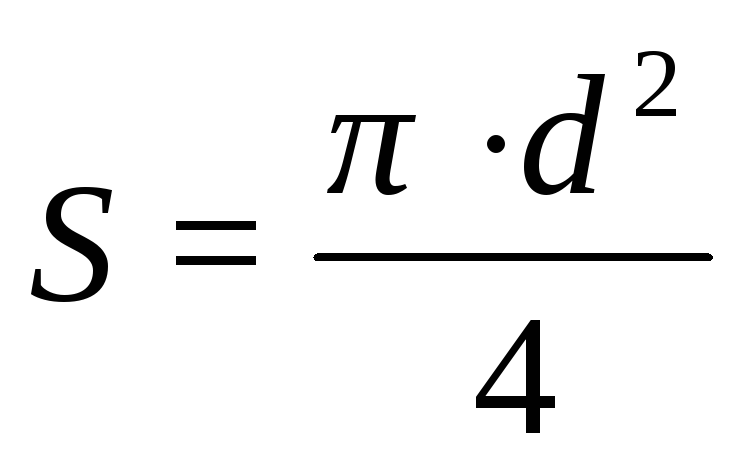 при сплошном заполнении его жидкостью
при сплошном заполнении его жидкостью  ,
откуда гидравлический радиус:
,
откуда гидравлический радиус:
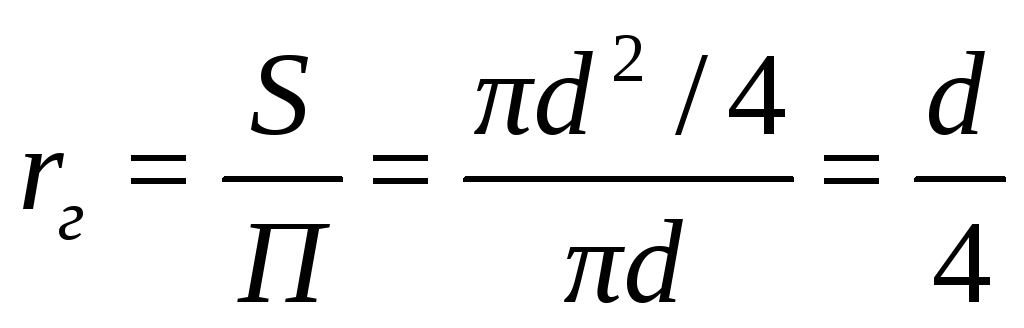 ,
,
Диаметр, выраженный через гидравлический радиус, представляет собой эквивалентный диаметр:
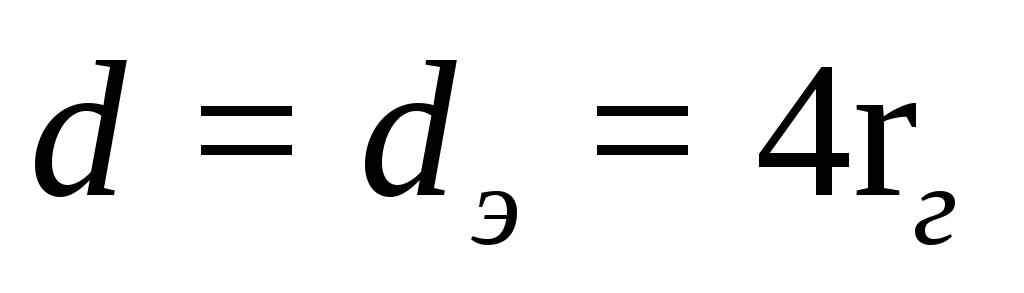 ,
,
Следовательно:
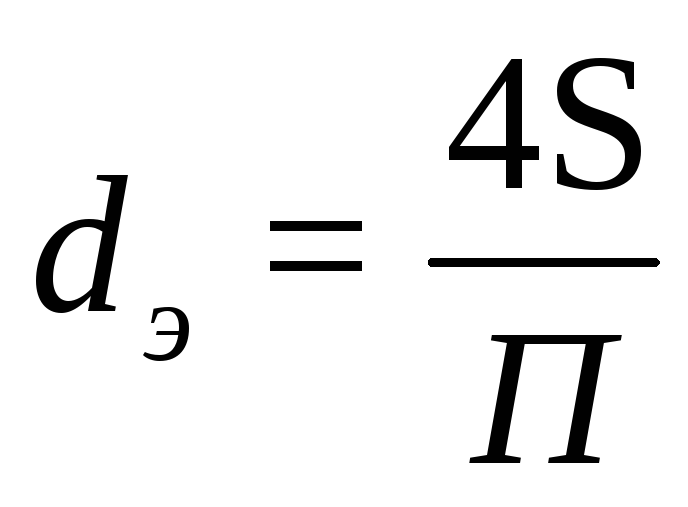 ,
,
Для канала прямоугольного сечения со сторонами a и b, полностью заполненного жидкостью, гидравлический радиус:
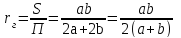 ,
,
А эквивалентный диаметр:
 ,
,
Для канала кольцевого поперечного сечения, в котором жидкость ограничена внутренней и наружной окружностями с диаметром dв и dн соответственно, эквивалентный диаметр:
 ,
,
Для круглой трубы 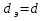 [1-5].
[1-5].
4.2.2. Скорость и расход жидкости
Рассмотрим движение жидкости по трубе постоянного сечения.
Количество жидкости, протекающей через поперечное сечение потока («живое сечение», т.е. затопленное сечение трубопровода (рисунок 16)) в единицу времени, называют расходом жидкости.
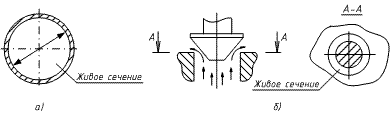
Рисунок 16 — Живые сечения: а — трубы, б — клапана
Различают Q — объемный расход [м3/с], и массовый расход М [кг/с].
В разных точках живого сечения потока скорость частиц жидкости неодинакова. Поэтому в расчетах используют не истинные (локальные) скорости, а фиктивную среднюю скорость.
Средняя скорость 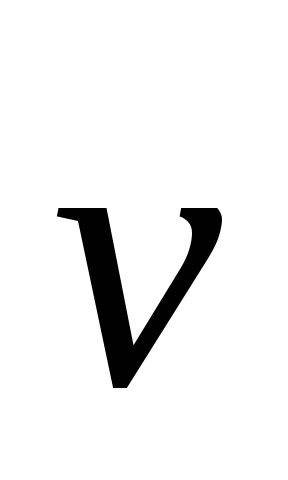 – выражается
отношением объемного расхода жидкости
к площади живого сечения потока [1,3,4].
– выражается
отношением объемного расхода жидкости
к площади живого сечения потока [1,3,4].
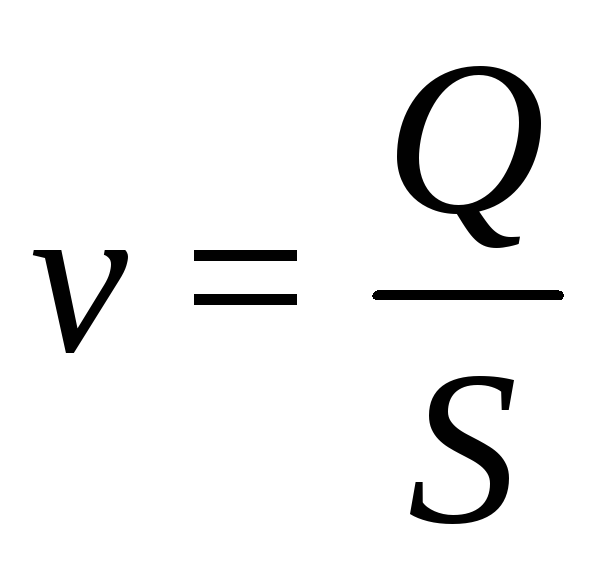 ,
,
где Q — объемный расход, м3/с;
S – площадь живого сечения, м2.
Откуда объемный расход:
 ,
,
Массовый расход М [кг/с ]:
 ,
,
где ρ – плотность жидкости кг/м3.
4.3. Виды движения жидкости
Основными видами движения жидкости являются: движение установившееся и неустановившееся, равномерное и неравномерное, напорное и безнапорное, сплошное и прерывистое.
Установившимся движением называется такое движение жидкости, при котором давление и скорость не изменяются во времени в каждой фиксированной точке пространства, через которую проходит жидкость.
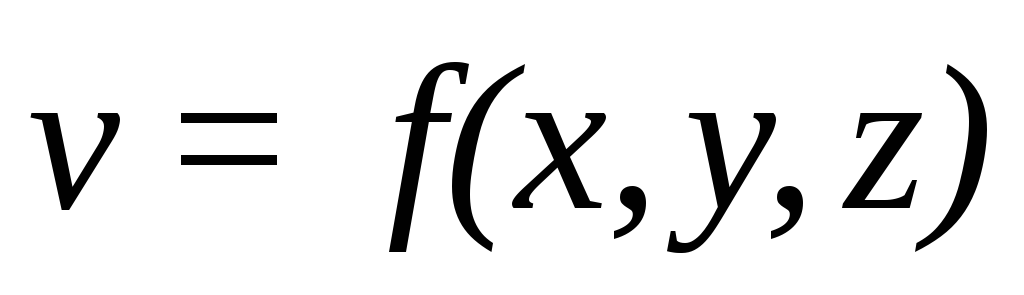 ,
,
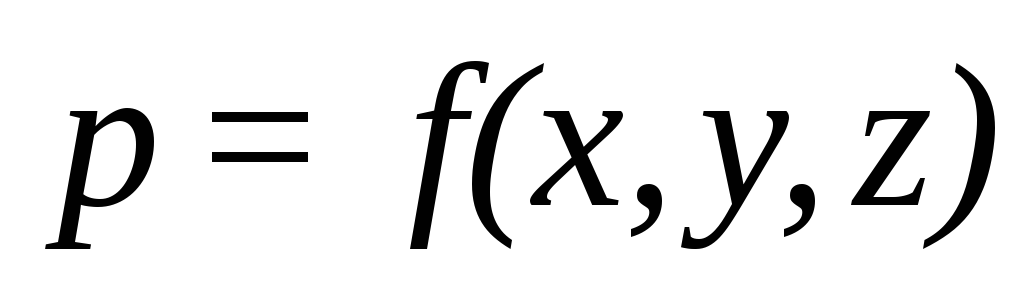
Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени, называется неустановившимся или нестационарным
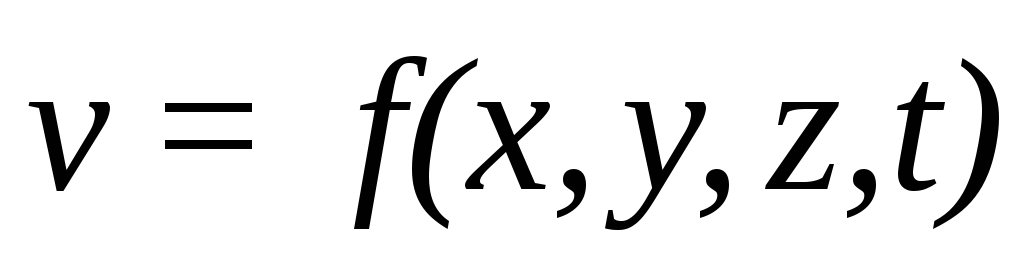 ,
,
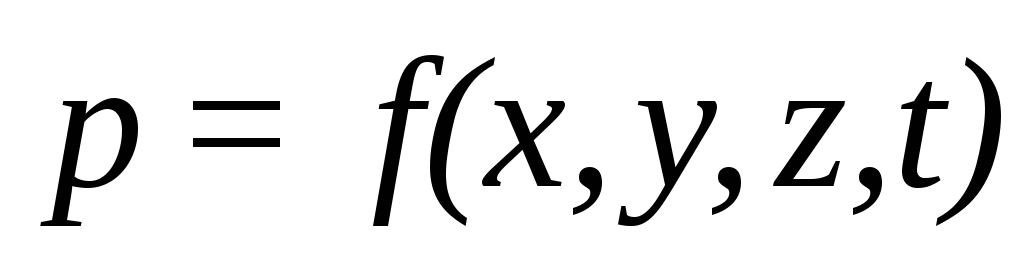 .
.
Примером неустановившегося движения может служить истечение жидкости из отверстия при переменном уровне ее в резервуаре: с понижением высоты столба жидкости скорость истечения уменьшается во времени.
Установившееся движение в свою очередь подразделяется на равномерное и неравномерное.
Равномерным называется
такое установившееся движение, при
котором живые
сечения вдоль потока не изменяются: в
этом случае  ;
средние скорости
по длине потока также не изменяются,
т.е.
;
средние скорости
по длине потока также не изменяются,
т.е. 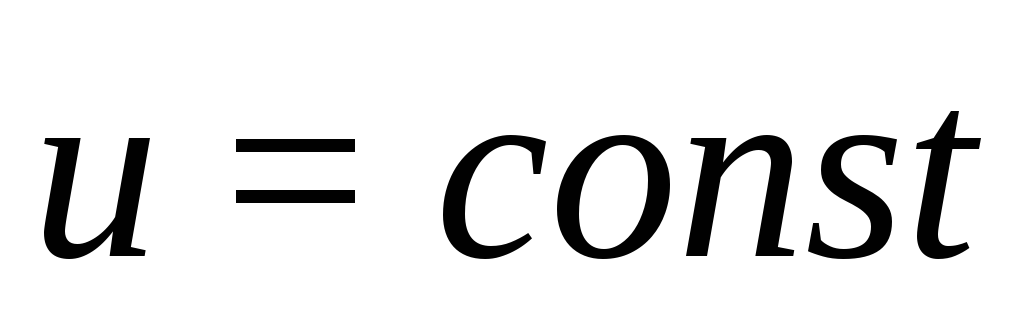 .
Примером равномерного движения является:
движение жидкости в цилиндрической
трубе,
в канале постоянного сечения при
одинаковых глубинах.
.
Примером равномерного движения является:
движение жидкости в цилиндрической
трубе,
в канале постоянного сечения при
одинаковых глубинах.
Установившееся движение называется неравномерным, когда распределение скоростей в различных поперечных сечениях неодинаково; при этом средняя скорость и площадь поперечного сечения потока могут быть и постоянными вдоль потока. Примером неравномерного движения может быть движение жидкости в конической трубе или в речном русле переменной ширины.
Напорным называется движение жидкости, при котором поток полностью заключен в твердые стенки и не имеет свободной поверхности. Напорное движение происходит вследствие разности давлений и под действием силы тяжести. Примером напорного движения является движение жидкости в замкнутых трубопроводах (например, в водопроводных трубах).
Безнапорным называется движение жидкости, при котором поток имеет свободную поверхность. Примером безнапорного движения может быть: движение жидкости в реках, каналах, канализационных и дренажных трубах. Безнапорное движение происходит под действием силы тяжести и за счет начальной скорости. Обычно на поверхности безнапорного потока давление атмосферное.
Следует отметить еще один вид движения: свободную струю. Свободной струей называется поток, не ограниченный твердыми стенками. Примером может служить движение жидкости из пожарного брандспойта, гидромонитора, водопроводного крана, из отверстия резервуара и т. п. В этом случае движение жидкости происходит по инерции (т. е. за счет начальной скорости) и под действием силы тяжести.
Для упрощения выводов, связанных с изучением потока жидкости, вводится понятие о плавно изменяющемся движении жидкости.
Плавно изменяющимся называется такое движение жидкости, при котором кривизна струек незначительна (равна нулю или близка к нулю) и угол расхождения между струйками весьма мал (равен нулю или близок к нулю), т. е. практически поток жидкости мало отличается от параллельно струйного. Это предположение вполне оправдывается при изучении многих случаев движения жидкости в каналах, трубах и других сооружениях.
Свойства потока при плавно изменяющемся движении:
1) поперечные сечения потока плоские, нормальные к оси потока;
2) распределение гидродинамических давлений по сечению потока подчиняется закону гидростатики, т.е. гидродинамические давления по высоте сечения распределяются по закону прямой. Это свойство легко можно доказать, если внутри потока выделить частицу жидкости и спроектировать все действующие на нее силы на плоскость живого сечения. Вследствие того, что скорости и ускорения в этом случае будут перпендикулярны сечению, силы инерции в уравнение не войдут; поэтому уравнение равновесия и закон распределения давления в плоскости живого сечения не будет отличаться от такового для жидкости, находящейся в покое;
3) удельная потенциальная энергия (т. е. потенциальная энергия единицы веса жидкости) по отношению к некоторой плоскости сравнения для всех точек данного сечения потока жидкости есть величина постоянная. [2-4].
studfile.net
