Определение средней скорости движения – Как найти среднюю скорость

Содержание

Как найти среднюю скорость

В данной статье рассказано о том, как найти среднюю скорость. Дано определение этого понятия, а также рассмотрено два важных частных случая нахождения средней скорости. Представлен подробный разбор задач на нахождение средней скорости тела от репетитора по математике и физике.

Определение средней скорости

Средней скоростью движения $\upsilon_{cp}$ тела называется отношение пути , пройденного телом, ко времени

, в течение которого двигалось тело:

$\upsilon_{cp} = \frac{s}{t}.$

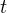
Научимся ее находить на примере следующей задачи:

Тело двигалось 3 мин. со скоростью 5 м/с, после чего 7 мин. двигалось со скоростью 3 м/с. Найти среднюю скорость движения тела.

Обратите внимание, что в данном случае это значение не совпало со средним арифметическим скоростей 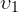$\upsilon_1$ и $\upsilon_2$

, которое равно:
$\frac{\upsilon_1+\upsilon_1}{2} = 4$

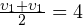м/с.

Частные случаи нахождения средней скорости

1. Два одинаковых участка пути. Пусть первую половину пути тело двигалось со скоростью 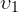$\upsilon_1$ , а вторую половину пути — со скоростью $\upsilon_2$ . Требуется найти среднюю скорость движения тела.

Пусть — общая длина пройденного пути. Тогда на первом участке пути тело двигалось в течение интервала времени $t_1 = \frac{s}{2\upsilon_1}$ . Аналогично, на втором участке пути тело двигалось в течение интервала времени $t_2 = \frac{s}{2\upsilon_2}$ .
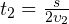Тогда средняя скорость движения равна:

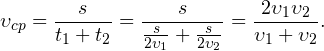
$\upsilon_{cp} = \frac{s}{t_1+t_2} = \frac{s}{\frac{s}{2\upsilon_1}+\frac{s}{2\upsilon_2}} = \frac{2\upsilon_1\upsilon_2}{\upsilon_1+\upsilon_2}.$

2. Два одинаковых интервала движения. Пусть тело двигалось со скоростью 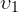$\upsilon_1$

в течение некоторого промежутка времени, а затем стало двигаться со скоростью $\upsilon_2$ в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.

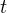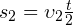Пусть — общее время пути. Тогда путь, пройденный телом в течение первой половины времени движения, равен: $s_1 = \upsilon_1\frac{t}{2}$ . Аналогично, путь, пройденный телом в течение второй половины времени движения, равен: $s_2 = \upsilon_2\frac{t}{2}$ .
Тогда средняя скорость движения равна:

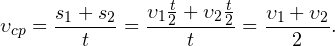
$\upsilon_{cp} = \frac{s_1+s_2}{t} = \frac{\upsilon_1\frac{t}{2}+\upsilon_2\frac{t}{2}}{t} = \frac{\upsilon_1+\upsilon_2}{2}.$

Здесь мы получили единственный случай, когда средняя скорость движения совпала со средним арифметическим скоростей 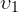$\upsilon_1$ и $\upsilon_2$

на двух участках пути.

Решим напоследок задачу из Всероссийской олимпиады школьников по физике, прошедшей в прошлом году, которая связана с темой нашего сегодняшнего занятия.

Пройденный телом путь составляет: 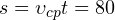$s = \upsilon_{cp}t = 80$ м. Можно найти также путь, который прошло тело за последние 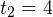с своего движения: $s_2 = \upsilon_{cp2}t_2 = 40$ м. Тогда за первые

с своего движения тело преодолело путь в

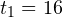
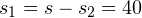м. Следовательно, средняя скорость на этом участке пути составила:
$\upsilon_{cp1} = \frac{s_1}{t_1} = 2.5$

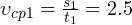м/с.

Задачи на нахождение средней скорости движения очень любят предлагать на ЕГЭ и ОГЭ по физике, вступительных экзаменах, а также олимпиадах. Научиться решать эти задачи должен каждый школьник, если он планирует продолжить свое обучение в вузе. Помочь справиться с этой задачей может знающий товарищ, школьный учитель или репетитор по математике и физике. Удачи вам в изучении физики!

Репетитор по физике на Юго-Западной
Сергей Валерьевич

yourtutor.info

Формула средней скорости движения

Рассмотрим одну из самых простейших задач, которые можно встретить в школьной программе. Итак немного теории

Средняя скорость движения — это отношение полного пути пройденного объектом на общее время затраченное на это путешествие

Естественно предположить, что если объект часть общего пути прошел за одно время, другую часть за другое время, а третью за третье время, то средняя скорость будет являтся отношением всех частей пути на все затраченное время.

А если известно например части пути и скорость объекта на каждом пути ? Не среднее арифметическое же брать от всех скоростей… хотя очень часто именно так и поступают впервые большинство учеников, да и взрослых тоже

На самом деле, при известных частях пути и скоростей на участке формула будет следующая

наверняка догадались как она получилась из предыдущей формулы.

Если в задании пути буду обозначаться как часть от общего ( например, первая половина пути, 2/3 пути и т.п.) то, учитывая что сумма таких частей будет равна всему пути ( равной единице), то средняя скорость будет определятся как

Пример:

Автомобиль проехал первую треть дороги со скоростью 60 км/ч, вторую треть дороги со скоростью 120 км/ч, третью треть дороги со скоростью 40 км/ч. найдите среднюю скорость.

Решение:

Ответ: 60 км/час

И последний вариант формулы на среднюю скорость это когда известно время и скорость на каждом из участков.

Правда есть еще четвертый вариант, но он практически никогда не встречается в задачах. Это когда встречаются комбинированные данные, например: Пешеход, преодолевает путь из точки А в точку Б. Первую половину пути пешеход прошел со скоростью 5 км/час а вторую половину пути за 1 час. Какое расстояние между А и Б, если средняя скорость пешехода, со всеми остановками и перекурами, была 3 км/час

Смотрим вот на эту формулу и думаем

Части пути нам известны, то есть общее расстояние нам известно и принимается за единицу ( половина пути+половина пути равна единице пути)

Теперь со временем

На первом участке время легко вычислить ( половину пути разделить на 5 км/ч). Получаем одну десятую пути. Не пугайтесь что получилось «время равно одной десятой пути». Оно потом понадобится..

Время на втором участке известно и равно 1 час

Напишем нашу формулу по полученным данным

Выразим расстояние от точки А до точки Б через среднюю скорость и получим

Поставим значение средней скорости получим что общее расстояние которое преодолел пешеход равно 4 километра и почти 286 метров

Сложновато? Зато интересно и увлекательно.

Из последней формулы вытекает «парадоксальный» вывод: При средней скорости приближающейся к 10 км/час расстояние между точками А и Б становится неприлично большим и уходит в бесконечность, а при 11 км/час расстояние вообще становится отрицательным.

Что хотелось бы по этому поводу сказать. не всегда надо бездумно подвергать анализу последнюю формулу, особенно когда знаменатель обращается в ноль.

Взяв предыдущую формулу — мы бы увидели что при средней скорости в 10 км/ч , расстояние просто будет неопределено. То есть при заданных условиях средняя скорость никак не может быть больше 10 км/час.

Фразеологический словарь выражения чувств и эмоций >>

abakbot.ru

Средняя скорость

При решении этих задач обязательно помним, что средняя скорость может быть найдена только делением всего пути на все время движения, даже если какое-то время объект не двигался (делал остановку). Если путь не задан, то необходимо ввести буквенное обозначение длины пути.

Задача 1. Поезд прошел путь 200 км. В течение времени ч он двигался со скоростью $\upsilon_1=100$ км/ч, затем сделал остановку на время мин. Оставшуюся часть пути он шел со скоростью $\upsilon_3=40$ км/ч. Какова средняя скорость движения поезда?

Путь в этой задаче известен. Значит, осталось определить время движения поезда. Кроме того, известно и время его движения на первом участке, значит, нам осталось определить время движения поезда на последнем кусочке, где он двигался со скоростью $\upsilon_3=40$ км/ч. Нетрудно понять, что длина этого отрезка пути равна 100 км, так как поезд уже преодолел 100 км за первый час. Поэтому

$S_3=200-\upsilon_1 \cdot t_1=200-100$

$t_3=\frac{S_3}{\upsilon_3}=\frac{100}{40}=2,5$

Таким образом,

$\upsilon_{sr}=\frac{S}{t_1+t_2+t_3}=\frac{200}{1+0,5+2,5}=50$

Ответ: 50 км/ч

Задача 2. Определить среднюю скорость поезда, если первую половину пути он шел со скоростью $\upsilon_1=50$ км/ч, а вторую половину пути – со скоростью $\upsilon_2=100$ км/ч.

В этой задаче путь неизвестен. Обозначим его . Тогда время движения поезда на первой половине пути

$t_1=\frac{\frac{S}{2}}{\upsilon_1}$

Время движения на второй половине –

$t_1=\frac{\frac{S}{2}}{\upsilon_2}$

Средняя скорость – результат деления всего пути, пройденного поездом, на все время:

$\upsilon_{sr}=\frac{S}{t_1+t_2}$

$\upsilon_{sr}=\frac{S}{\frac{S}{2\upsilon_1}+\frac{S}{2\upsilon_2}}$

$\upsilon_{sr}=\frac{2}{\frac{1}{\upsilon_1}+\frac{1}{\upsilon_2}}$

$\upsilon_{sr}=\frac{2 \upsilon_1 \upsilon_2}{\upsilon_1+\upsilon_2}$

$\upsilon_{sr}=\frac{2 \cdot50\cdot100}{150}=\frac{10000}{150}=66,7$

Ответ: $\upsilon_{sr}=66,7$ км/ч

Задача 3. Два автомобиля одновременно выехали из Москвы в Петербург. Один автомобиль первую половину пути ехал со скоростью $\upsilon_1=120$ км/ч, а вторую половину – со скоростью $\upsilon_2=80$ км/ч. Другой автомобиль первую половину времени ехал со скоростью $\upsilon_1=120$ км/ч, а вторую – со скоростью $\upsilon_2=80$ км/ч. Какой автомобиль приедет в Петербург раньше?

Если окажется, что средняя скорость одного из автомобилей больше, чем у другого, то он и должен прибыть раньше. Определим среднюю скорость каждого автомобиля. Первый:

$\upsilon_{sr1}=\frac{S}{t_1+t_2}$

$\upsilon_{sr1}=\frac{S}{\frac{S}{2\upsilon_1}+\frac{S}{2\upsilon_2}}$

$\upsilon_{sr1}=\frac{2}{\frac{1}{\upsilon_1}+\frac{1}{\upsilon_2}}$

$\upsilon_{sr1}=\frac{2 \upsilon_1 \upsilon_2}{\upsilon_1+\upsilon_2}$

$\upsilon_{sr1}=\frac{2 \cdot120\cdot80}{200}=\frac{19200}{200}=96$

Второй за первую половину времени прошел:

$S_1=\frac{t}{2}\cdot \upsilon_1$

За вторую половину времени:

$S_2=\frac{t}{2}\cdot \upsilon_2$

Тогда его средняя скорость:

$\upsilon_{sr2}=\frac{S}{t}=\frac{S_1+S_2}{t}=\frac{t\cdot \upsilon_1+t\cdot\upsilon_2}{2t}=\frac{\upsilon_1+\upsilon_2}{2}$

$\upsilon_{sr2}=\frac{120+80}{2}=100$

Таким образом, второй автомобиль прибудет раньше.

Задача 4. Найти среднюю скорость самолета, если известно, что первую треть пути он летел со скоростью $\upsilon_1=700$ км/ч, вторую треть – со скоростью $\upsilon_2=500$ км/ч, а последнюю часть пути – со скоростью, вдвое большей средней скорости на первых двух участках пути.

Найдем среднюю скорость самолета на двух первых участках пути.

$\upsilon_{sr12}=\frac{\frac{2S}{3}}{\frac{S}{3\upsilon_1}+\frac{S}{3\upsilon_2}}$

$\upsilon_{sr12}=\frac{2}{\frac{1}{\upsilon_1}+\frac{1}{\upsilon_2}}$

$\upsilon_{sr12}=\frac{2\upsilon_1 \upsilon_2}{\upsilon_1+\upsilon_2}$

$\upsilon_{sr12}=\frac{2\cdot700 \cdot500}{700+500}=583$

Тогда $\upsilon_3=1166$ .

Определяем среднюю скорость на всем участке пути:

$\upsilon_{sr123}=\frac{S}{\frac{S}{3\upsilon_1}+\frac{S}{3\upsilon_2}+\frac{S}{3\upsilon_3}}$

$\upsilon_{sr123}=\frac{3}{\frac{1}{\upsilon_1}+\frac{1}{\upsilon_2}+\frac{1}{\upsilon_3}}$

$\upsilon_{sr123}=\frac{3\upsilon_1 \upsilon_2 \upsilon_3}{\upsilon_1\upsilon_2+\upsilon_2\upsilon_3+\upsilon_1\upsilon_3}$

$\upsilon_{sr123}=\frac{500\cdot700 \cdot1166}{500\cdot700+700\cdot1166+500\cdot1166}=700$

Ответ: 700 км/ч

Задача 5. Найти среднюю скорость поезда, если известно, что на прохождение отдельных участков дистанции, длины которых относятся как , потребовались промежутки времени, находящиеся в отношении , и на последнем участке скорость поезда $\upsilon=80$ км/ч. Считать, что на каждом из участков поезд двигался равномерно.

Определим весь путь по его частям:

$S_1:S_2:S_3:S_4=1: 3: 4: 2$

Если , то , , , а весь путь

$S_1+S_2+S_3+S_4=l+3l+4l+2l=10l$

Определим время движения поезда на последнем участке, зная его скорость:

$t_4=\frac{2l}{\upsilon }$

Тогда, так как

$t_1:t_2:t_3:t_4=2:4:3:1$

Отсюда найдем :

$t_3=3t_4=\frac{6l}{\upsilon }$

$t_2=\frac{4}{3}t_3=\frac{8l}{\upsilon }$

$t_1=\frac{1}{2}t_3=\frac{4l}{\upsilon }$

Общее время движения:

$t_1+t_2+t_3+t_4=\frac{4l}{\upsilon }+\frac{8l}{\upsilon }+\frac{6l}{\upsilon }+\frac{2l}{\upsilon }=\frac{20l}{\upsilon }$

Наконец, находим среднюю скорость:

$\upsilon_{sr}=\frac{S}{t}=\frac{10l}{\frac{20l}{\upsilon }}=\frac{\upsilon }{2}$

$\upsilon_{sr}=\frac{80}{2}=40$

Ответ: средняя скорость поезда – 40 км/ч.

easy-physic.ru

Конспект «Неравномерное движение. Средняя скорость»

Неравномерное движение.
Средняя скорость

Неравномерное движение — это движение, при котором за равные промежутки времени тело проходит разные пути.

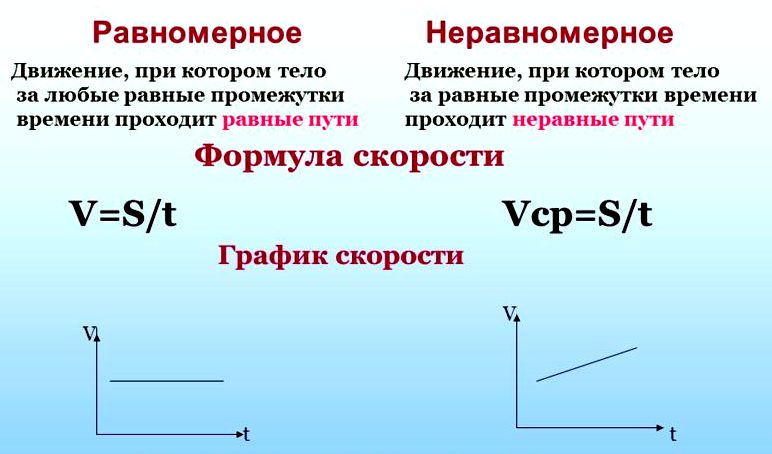
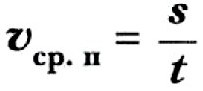Средняя путевая скорость — это физическая величина, равная отношению пути, пройденного телом за рассматриваемый промежуток времени, к длительности этого промежутка.

Средняя путевая скорость — скалярная неотрицательная величина.

Средняя скорость тела за промежуток времени t — это физическая величина, равная отношению перемещения , совершённого телом, к длительности этого промежутка времени.

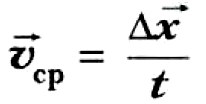
Средняя скорость — вектор. Она направлена туда, куда направлено перемещение тела за рассматриваемый промежуток времени.

Если тело всё время движется в одном направлении, то модуль средней скорости равен средней путевой скорости. Если же в процессе своего движения тело меняет направление движения, то модуль средней скорости меньше средней путевой скорости.

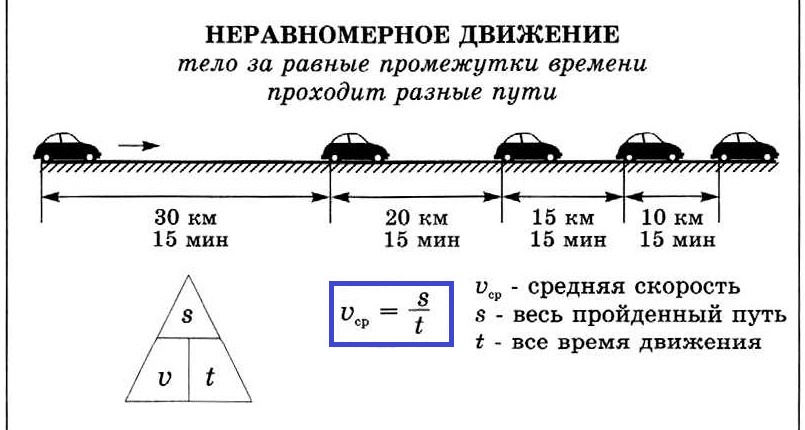
Пример решения задач на среднюю скорость при неравномерном движении

Автомобиль проехал за первый час 50 км, а за следующие два часа он проехал 160 км. Какова его средняя скорость за все время движения?

Ответ: 70 км/ч

Еще больше задач на движение (с решениями и ответами) в конспекте «Задачи на движение»

Это конспект по физике за 7 класс по теме «Неравномерное движение. Средняя скорость». Выберите дальнейшие действия:

uchitel.pro

Средняя скорость. Решение задач по физике

Задачи по физике — это просто!

Среднюю скорость движения иначе называют путевой скоростью.

где

Sобщ — общий путь, т.е. сумма всех отрезков пути

t общ — общее время, т.е. время, за которое был пройден весь путь

При решении задач очень помогает простенький чертеж, на котором надо показать все отрезки пути.
Около каждого отрезка для наглядности укажите буквенные обозначения скорости, времени, пути (с нужным индексом) и формулы для их расчета (если это необходимо).

Переходим к решению задач.
От простых к сложным!

Элементарные задачи из курса школьной физики

Задача 1

Автомобиль проехал 100 метров за 25 секунд, а следующие 300 метров за 1 минуту.
Определить среднюю скорость движения автомобиля.

Задача 2

Автомобиль ехал 2 минуты со скоростью 10 м/с, а затем проехал еще 500 метров за 30 секунд.
Определить среднюю скорость движения.

Задача 3

Автомобиль проехал 10 секунд со скоростью 10 м/с, а затем ехал еще 2 минуты со скоростью 20 м/c.
Определить среднюю скорость автомобиля.

Задача 4

Автомобиль проехал первую половину пути со скоростью 10 м/с, а вторую половину пути со скоростью 20 м/с. Определить среднюю скорость автомобиля на всем пути.

Пусть S — общий пройденный путь.

Задача 5

Автомобиль одну треть времени движения ехал со скоростью 10 м/с, а остальное время со скоростью 20 м/с. Определить среднюю скорость за все время движения.

Пусть t — общее время движения.

class-fizika.ru

Определение средней скорости движения | Теория

Средняя техническая скорость движения автомобилей и тракторов равна:

V = L/T
,где L — расстояние пробега в км
Т — время движения в часах по всему маршруту длиной L км, без учета времени на остановках

Установлено, что средняя техническая скорость движения автомобиля зависит от многих факторов и в частности от проходимости автомобиля, его максимальной конструктивной скорости Vк, от качества и состояния дороги, интенсивности движения и др. Рекомендуется определять среднюю скорость движения автомобиля с учетом неровностей на дороге. В этом случае допустимая средняя скорость принимается равной при движении по хорошему гудронированному шоссе — 70 км/час, по требующему ямочного ремонта — 55 км/час, по мостовой в хорошем состоянии — 37 км/час, по требующей ямочного ремонта — 22 км/час.

На основании практических данных можно считать, что для грузовых автомобилей с полной полезной нагрузкой средняя техническая скорость движения в составе автоэшелона составляет:

На очень хороших дорогах — около 0,8—0,9 Vк
На хороших дорогах — 0,6 Vк
На плохих дорогах — 0,2 Vк
На очень плохих дорогах — 0,1 Vк

Для тракторных поездов с тракторами сельскохозяйственного типа во время движения по большинству дорог средняя техническая скорость составляет около 0,8 — 0,9 Vк. Средняя техническая скорость движения легковых автомобилей примерно на 30% выше соответствующей скорости грузовых автомобилей.

Средняя техническая скорость движения группы автомобилей (эшелона) по сравнению со средней технической скоростью движения одиночно двигающихся автомобилей уменьшается (за исключением случаев движения по очень плохим дорогам) вследствие задержек движения на отдельных участках маршрута.

Для того чтобы увеличить среднюю скорость движения автомобилей в составе эшелона и уменьшить задержки в движении, необходимо соблюдать следующие требования:

Дистанции между автомобилями и между эшелонами должны выдерживаться пропорционально средней технической скорости движения как на легких, так и на трудных участках пути.
При значительном количестве на дороге (на маршруте) местных препятствий, на которых приходится уменьшать скорость движения, и при значительной длине участков с такими препятствиями средняя скорость движения для эшелонов будет уменьшаться и приближаться к скорости движения по участкам с препятствиями.

Для увеличения средней скорости движения эшелонов в данном случае необходимо уменьшать состав эшелона.

ustroistvo-avtomobilya.ru

Скорость. Неравномерное движение. Средняя скорость

1.	Вопросы по теме «Скорость»	1 вид — рецептивный	лёгкое	1 Б.	Предлагается ответить на вопросы по теме «Равномерное и неравномерное движение. Скорость».
2.	Перевод км/ч в м/с, м/с в км/ч	1 вид — рецептивный	лёгкое	2 Б.	Перевод км/ч в м/с, м/с в км/ч.
3.	Перевод м/с в см/с, м/мин	1 вид — рецептивный	лёгкое	2 Б.	Перевод м/с в см/с , м/мин.
4.	Скорость	1 вид — рецептивный	лёгкое	1 Б.	Определение расстояния по скорости и времени.
5.	Перевод км/ч в м/мин, см/с	1 вид — рецептивный	среднее	2 Б.	Перевод км/ч в м/мин, см/с.
6.	Вычисление скорости	2 вид — интерпретация	среднее	2 Б.	Вычисление скорости.
7.	Вычисление ускорения	2 вид — интерпретация	среднее	2 Б.	Вычисление ускорения.
8.	Сравнение скоростей	2 вид — интерпретация	среднее	3 Б.	Определяются скорости движения автомобилей в км/ч и затем сравниваются.
9.	Время движения парохода	2 вид — интерпретация	среднее	2 Б.	Определяется время движения парохода по течению.
10.	Определение скорости тела и его пути по графику	3 вид — анализ	сложное	3 Б.	Анализируется график зависимости пути от времени и определяется скорость и путь.
11.	Определение средней скорости движения	2 вид — интерпретация	сложное	3 Б.	Определяется средняя скорость транспорта при неравномерном движении.
12.	Работа с графиком движения	3 вид — анализ	сложное	6 Б.	Анализируется график зависимости пути от времени, определяется скорость и путь двух тел, сравниваются результаты.

Как найти среднюю скорость

Определение средней скорости

Частные случаи нахождения средней скорости

Формула средней скорости движения

Средняя скорость

Конспект «Неравномерное движение. Средняя скорость»

Неравномерное движение.Средняя скорость

Пример решения задач на среднюю скорость при неравномерном движении

Средняя скорость. Решение задач по физике

Средняя скорость. Решение задач по физике

Определение средней скорости движения | Теория

Скорость. Неравномерное движение. Средняя скорость

Добавить комментарий Отменить ответ

Неравномерное движение.
Средняя скорость