Погрешность измерительной линейки – —

Точность и погрешность измерений — урок. Физика, 7 класс.

Измерить какую-нибудь величину — это значит сравнить её с однородной величиной, принятой за единицу.

Всякое измерение может быть выполнено с большей или меньшей точностью.

В качестве примера рассмотрим измерение длины бруска линейкой с сантиметровыми делениями.

 

 

Вначале определим цену деления линейки. Она будет равна \(1\) см. Если левый конец бруска совместить с нулевым штрихом, то правый будет находиться между \(9\) и \(10\) штрихами, но ближе к \(10\). Какое же из этих двух значений следует принять за длину бруска? Очевидно, то, которое ближе к истинному значению, т.е. \(10\) см. Считая, что длина бруска \(10\) см, мы допустим неточность, так как брусок чуть короче \(10\) см.

В физике допускаемую при измерении неточность называют погрешностью измерений.

Погрешность измерения не может быть больше цены деления измерительного прибора. В нашем случае погрешность измерения бруска не превышает \(1\) см. Если такая точность измерений нас не устраивает, то можно произвести измерения с большей точностью. Но тогда придётся взять масштабную линейку с миллиметровыми делениями, т.е. с ценой деления \(1\) мм. В этом случае длина бруска окажется равной \(9,8\) см.

 

 

Для более точных измерений можно воспользоваться штангенциркулем с ценой деления \(0,1\) мм или \(0,05\) мм.

 

 

Из этого примера видно, что точность измерений зависит от цены деления шкалы прибора.

Чем меньше цена деления, тем больше точность измерения.

Точность измерения зависит от правильного применения измерительного прибора, расположения глаз при отсчёте по прибору.

Вследствие несовершенства измерительных приборов и несовершенства в развитии наших органов чувств, при любом измерении получаются лишь приближённые значения, несколько бóльшие или меньшие истинного значения измеряемой величины.

Во время выполнения лабораторных работ или просто измерений следует считать, что:

Погрешность измерений равна половине цены деления шкалы измерительного прибора.

При записи величин (с учётом погрешности) следует пользоваться формулой: A=a±Δa,
где \(A\) — измеряемая величина, \(a\) — результат измерений, Δa  — погрешность измерений (Δ — греческая буква «дельта»).

Источники:

Пёрышкин А.В. Физика. 7 кл. – 14-е изд., стереотип. – М.: Дрофа, 2010.

 

www.yaklass.ru

1. Измерительные металлические линейки

Теоретические сведения

Измерительная линейка представляет собой металлическую полосу, на плоскости которой нанесены деления

Очень часто измерительные линейки называют штриховыми мерами. Это название указывает, что линейка является мерой и эта мера многозначная, а размер по ней определяют между штрихами.

Номенклатура измерительных линеек в принципе включает большую разновидность — от простейших ученических деревянных линеек до высокоточных металлических линеек, на которых имеется лупа для отсчета по шкале, и далее до линеек с точностью до долей микрометра, устанавливаемых в станках.

Металлические измерительные линейки изготавливают общей длиной от 150 до 1000 мм. Обычно промежуточные размеры имеют 300 и 500 мм.

Конструкции линеек в принципе однотипны, т.е. представляют собой металлическую полосу, на широкой поверхности которой нанесены деления, в подавляющем большинстве случаев через І мм между осями штрихов (рис. І, а). Иногда линейки делают с расстоянием 0,5 мм между штрихами, но практически пользоваться линейками с отсчитыванием 0,5 мм трудно, так же как и изготавливать такие линейки.

Нулевой штрих, т.е. начало отсчета в линейках, обычно находится с левой стороны, совпадая с концом линейки. и это дает основание считать, что линейка со стороны нулевого штриха является концевой мерой.

Линейки изготавливают либо с одной, либо с двумя шкалами.

Иногда изготавливают линейки, у которых нулевые деления имеются и с левой, и с правой стороны. Ширина линейки обычно в среднем бывает 20-40 мм, а толщина — 0,5-1,0 мм. Поверхность линейки подвергают хромированию для предохранения от коррозии.

Измерение линейкой производится так называемым непосредственным методом, т.е. прикладыванием ее к измеряемому объекту и сопоставлением его длины со значением меры. Чаще всего эти измерения осуществляют совмещением нулевого штриха линейки с краем детали. Непосредственным называется метод измерения, в котором значение величины определяют непосредственно по отсчетному устройству измерительного средства.

Погрешность измерения линейкой складывается из погрешности нанесения делений, погрешности совмещения штрихов с краями измеряемой детали и погрешности отсчета значения. Если погрешность нанесения штрихов на линейках обычно находится в пределах 0.1-0.2 мм (в зависимости от длины), то погрешность отсчета доходит до 0.2-0.3 мм и более. В общем случае можно принять, что погрешность измерения находится в пределах 0.5 мм при условии острых краев измеряемой детали и тщательности измерения, но в большинстве случаев при измерении линейкой удовлетворяются погрешностью измерения в пределах 1 мм.

Поверку линеек, т.е. определение погрешности нанесения штрихов, производят по образцовым измерительным линейкам, которые называют штриховыми метрами. Штриховой метр (рис.1,б) представляет собой более жесткую конструкцию, чем обычные линейки. На скосах этого метра нанесены деления через 0.2 мм с погрешностью в пределах 0.05 мм. На специальных направляющих метра помещают две каретки с кронштейнами, на которых находятся лупы с 7-кратным увеличением. При проверке измерительной линейки штриховой метр устанавливают на проверяемую линейку и сравнивают шкалы обеих линеек. Погрешность такого сравнения не превышает 0.01 мм.

studfile.net

1. Однократные измерения размера линейкой.

Линейка является простейшим измерительным устройством. Цена деления линейки может быть различной. Для измерения с помощью линейки необходимо нулевую отметку ш

Рис. 1.1. Линейка

калы совместить с краем измеряемого отрезка.

Результат измерения считывается по шкале линейки по другому краю измеряемого отрезка.

Погрешность измерения с помощью линейки составляет не более ½ цены ее наименьшего деления. Доли наименьшего деления считываются на глаз с точностью, не превышающей погрешность измерения, то есть 0,5 цены деления.

Пример 1.По линейке с ценой деления 1 мм произведен отсчет. Результат измерения записывается так:

Пример 2.Той же линейкой измерен размер. Результат измерения записывается следующим образом:При выполнении этого задания проводятся однократные измерения размера любого предмета линейкой, например, размер грани параллелепипеда или стороны треугольника из набора принадлежностей, оцениваются погрешности измерения и результат представляется в виде:, (см. примеры 1 и 2).

2. Однократные измерения штангенциркулем.

Штангенциркуль представляет собой металлическую линейку 1, на конце которой имеется поперечный выступ 2. Другой такой же выступ имеется на обойме 3. Они движутся по линейке. Обойма имеет окно 4, позволяющее видеть основную шкалу линейки. Внутренние поверхности выступов строго перпендикулярны линейке. Когда они прилегают друг к другу, указатель «нуль» на обойме находится против нулевого деления шкалы линейки. Измеряемый предмет зажимается между выступами.

Д

Рис. 1.2. Штангенциркуль

ля измерения внутренних размеров от­верстий наружные стороны концов выступов обычно делаются строго перпендикулярными линейке и слегка закругляются. Расстояние между ними при установке обоймы на нуль шкалы (обычно 8 или 10 мм) указывается на штангенциркуле 6. Иногда для измерения внутренних размеров делаются специальные ножи на тыльной стороне выступов, концы выступов заостряются. Такое устройство позволяет измерять отверстия малых размеров, но точность измерения при этом меньше.

Достаточно высокая точность измерения штангенциркулем достигается с помощью нониуса. Нониус – это дополнительная линейка со шкалой 5, нанесенной по краю подвижной 3.

Нулевой штрих шкалы нониуса служит одновременно указателем для считывания числа целых делений по основной шкале и началом отсчета долей миллиметра по шкале нониуса. Обычно число делений нониуса n= 10 илиn=20.При 10 делениях нониуса всей длине его шкалы соответствует 19мм основной шкалы, то есть 10 делений нониуса имеют длину, на 1 мм меньшую, чем 20 делений основной шкалы. Цену деления нониуса штангенциркуля можно найти по формуле . При 10 делениях нониусаи. При 20 делениях нониуса. Погрешность градуировки штангенциркуля приn= 10 равна 0,1 мм, а приn= 20 равна 0,05 мм.

Пример 3. Нониус штангенциркуля имеет цену деления 0,1 мм. Число целых делений шкалы до нуля нониуса – 12. Штрих основной шкалы совпадает со штрихом шкалы нониуса, которому предшествует 4 деления его шкалы. Результат отсчетаРезультат измерения записывается в виде:

При выполнении этого задания проводятся однократные измерения размера любого предмета штангенциркулем, оцениваются погрешности измерения и результат представляется в виде (см. пример 3).

3. Однократные измерения размера микрометром.

Для измерения внешних размеров предметов с большой точностью, чем штангенциркулем, служит микрометр. Он состоит из скобы 1, жестко соединенной с измерительным упором 2, цилиндра 3, барабана 4, который соединен с микрометрическим винтом и подвижным измерительным упором 5. На цилиндре 3 нанесено 2 миллиметровых шкалы: нижняя – основная, верхняя – дополнительная, смещенные относительно друг друга на 0,5 мм. Левый конусный конец барабана имеет круговую шкалу 6, состоящую из 50 делений. Шаг микрометрического винта равен 0,5 мм, поэтому один оборот барабана соответствует изменению линейного размера 0,5 мм.

Рис. 1.3. Микрометр

Измеряемый предмет помещают между винтом 5 и противоположным ему упором 2 так, как показано на рисунке 1.3. Винт вращают и доводят до соприкосновения с предметом. При измерении микрометром существенно постоянство вращательного момента, приложенного к барабану при соприкосновении упоров с измеряемым предметом. Поэтому барабан 4 следует вращать, прикладывая усилие не к нему самому, а к головке 7. Она соединяется с винтом с помощью «трещотки», которая передает усилие только до тех пор, пока она не достигнет определенной величины. Когда же эта величина достигнута, дальнейшее вращение головки происходит в «холостую» и не изменяет показания микрометра.

Результат измерения получают в следующем порядке. Сначала производят отсчет размера по основной и дополнительным шкалам с точностью до 0,5 мм, после этого осуществляется отсчет сотых долей миллиметра по шкале барабана и результаты суммируются.

Погрешность градуировки микрометров составляет 0,004 мм.

Пример 4.На основной шкале видно 5 целых миллиметровых делений. Следующая справа за меткой 5 основной шкалы отметка дополнительной шкалы не видна. Отсчет по шкале барабана – 24.

Результат отсчета . Результат измерения:.

При выполнении этого задания проводятся однократные измерения размера любого предмета микрометром, оценивается погрешность и результат представляется в виде: (см. пример 4).

4. Повторное измерение размеров

Повторные измерения предметов являются прямыми наблюдениями. Процедура их осуществляется очень просто: одним и тем же измерительным инструментом – линейкой, штангенциркулем или микрометром измеряют один и тот же размер несколько раз через определенный интервал времени, и результаты заносятся в таблицу.

Обработка результатов эксперимента.

1. Погрешность величины l в каждом измерении отдельным измерительным инструментом находится по методике расчета погрешностей прямых измерений, задавая доверительную вероятностьи коэффициент Стьюдента.

, (1.17)

где

, (1.18)

. (1.19)

2. Погрешность смешанных измерений вычисляется аналогично:

(1.20)

Сравниваются погрешности 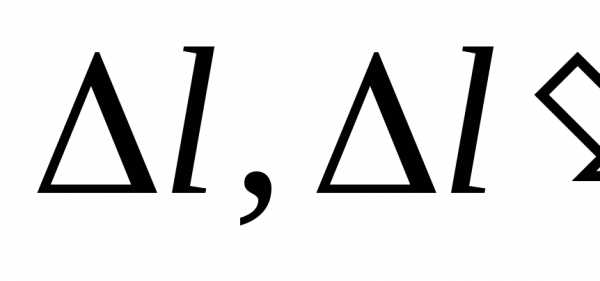и объясняются расхождения.

Задание 2. Измерение объема параллелепипеда.

Такие измерения являются косвенными и их можно осуществить двумя способами.

Способ 1. Однократные измерения

Одним из измерительных инструментов один раз определяется длина одной грани параллелепипеда и результат записывается в виде:

(1.21)

Обработка результатов эксперимента.

1. Погрешность однократных косвенных измерений различными инструментами рассчитывается по формуле (1.10). Так как объем , то

,,,

и, следовательно,

,

то есть:

,

_. (1.22)

Результат измерения представляется в виде

2. В том случае, если длина всех граней измерена одним и тем же инструментом с одинаковой погрешностью ,то

Способ 2. Повторные измерения

Осуществляются повторные измерения любым измерительным инструментом одной грани несколько раз, и результаты заносятся в таблицу.

Обработка результатов эксперимента.

Вычисляется среднее значение объема и погрешность

его определения по формуле (1.22):

, (1.23)

где ,,вычисляют по методике расчета погрешностей прямых измерений.

Любопытно провести эти измерения, используя для получения результата различные измерительные инструменты, вычислить погрешность и сравнить значения объема и погрешности, полученные при измерении линейкой, штангенциркулем и микрометром, а также при смешанных измерениях.

Задание 3. Измерение плоских углов транспортиром.

Для простейших измерений углов применяется транспортир, который представляет собой полукруг, дуга которого разделена на через. Чтобы измерить уголу,накладывают транспортир (рис. 1.4) так, чтобы вершина угла совпала с центром полукруга, а стороны – с радиусами ОА и ОВ. Тогда число градусов, содержащихся в дуге, заключенной между сторонами угла АОВ, дает числовое значение его величины. Погрешность измерения углов по транспортиру составляет половину деления шкалы – 0,5.

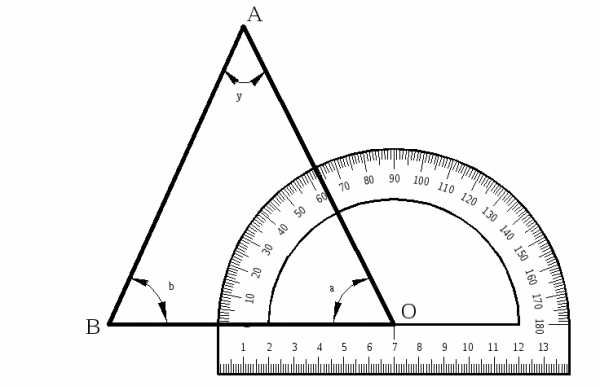
Рис. 1.4. Транспортир

Пример 5. Результат отсчета по шкале транспортира. Результат измерения

Более сложные и более точные приборы для измерения углов мы не рассматриваем.

1. Однократное измерение углов.

При выполнении этого задания проводятся однократные измерения углов треугольника из набора принадлежностей, оцениваются погрешности измерения и результат представляется в виде: , причем очевидно, что.

2. Многократные измерения углов.

Погрешности величин у, b, а находятся по формуле расчета погрешностей прямых измерений:

. (1.26)

И в первом, и во втором случае можно проверить результат, используя формулу . При этом погрешность суммы углов отличается от погрешности измерения отдельного угла и вычисляется по формуле

(1.27)

Задание 4. Измерение времени секундомером.

Для измерения времени применяются секундомеры. Механические секундомеры имеют цену деления 0,1 и 0,2 с.

Основная погрешность этих секундомеров равна цене деления, а погрешность отсчета зависит от быстроты реакции на включение и остановку секундомера. Установлено, что неточности пуска и остановки дают погрешность порядка 0,3 с. Таким образом, при работе с секундомером с ценой деления 0,2 с погрешность может достигать 0,5 с.

Применяются электронные секундомеры с ценой деления 0,01 и 0,001 с. Их целесообразно использовать вместе с устройствами, обеспечивающими совпадение пуска и остановки с началом и концом процесса, длительность которого определяется.

Пример 6.По индикатору электронного секундомера с ценой деления 0,01 с зарегистрировано некоторое время. Результат измеренияМетодика измерения интервалов времени и обработки результатов при однократных и повторных измерениях та же, что и в предыдущих заданиях по измерению линейных размеров и углов.

Задание 5. Измерение температуры термометром.

Термометр представляет собой капиллярную трубку из стекла, которая заполнена жидкостью, обычно ртутью или подкрашенным спиртом. Капиллярная трубка помещена в корпус из стекла, в котором также закреплена измерительная шкала. Погрешность измерения температуры термометрами различных типов регламентируется ГОСТ 400-80 и имеет, в большинстве случаев, величину, равную цене деления.

Методика измерения температуры и обработки результатов при однократных и многократных измерениях та же, что и в предыдущих заданиях.

Лабораторная работа 2

studfile.net

Физические величины. Точность и погрешность измерений

Физические величины. Точность и погрешность измерений

Измерять – значит, познавать

Данная тема посвящена физическим величина и их измерениям. В физике часто приходится измерять те или иные величины. Измерить можно высоту дома или длину улицы.

Можно измерить объём воды в колбе или массу воды в стакане.

Но что означают эти измерения? Измерить какую-либо величину – значит сравнить её с однородной величиной, принятой за единицу. Из приведённых выше примеров, можно заметить, что, например, единицей объёма является литр, а единицей массы является грамм. Для удобства была введена международная система единиц, которая называется СИ.

В этой системе длина измеряется в метрах, масса в килограммах, объём — в кубических метрах, время – в секундах и так далее. В процессе изучения физики будут вводиться новые величины и соответствующие им единицы измерения. Иногда физические величины можно не измерять, а вычислять по формуле. Например, для того, чтобы вычислить среднюю скорость нужно пройденное расстояние разделить на время. То есть, данная формула помогает вычислить такую физическую величину, как средняя скорость.

Известно что, иногда применяются единицы измерения, которые в десятки, сотни, тысячи и так далее раз больше принятых единиц измерения. Такие единицы измерения называются кратными.

Каждая приставка соответствует тому или иному множителю. Например, «Дека» означает в 10 раз больше, «гекто» — в сто раз больше, «кило» - в тысячу раз больше, «мега» — в миллион раз больше и так далее. Необходимо отметить, что в физике принято записывать такие множители в виде степени числа 10. Например, вместо миллиона записывается 10⁶. Также, могут быть использованы единицы, которые в десятки, сотни, тысячи и так далее раз меньше принятых единиц измерения. Такие единицы измерения называются дольными.

Каждая приставка соответствует тому или иному множителю. Например, «Деци» означает в 10 раз меньше, «санти» — в сто раз меньше, «милли» — в тысячу раз меньше, «микро» — в миллион раз меньше и так далее. Эти приставки также записываются в виде степени числа 10. Например, вместо записи числа 0,000001 записывается 10^–6.

У каждого ученика имеется линейка, длина которой измеряется в сантиметрах, то есть в единицах, которые в сто раз меньше метра. Поэтому, если длина линейки составляет 15 сантиметров, мы можем сказать, что её длина 0,15 метра.

Линейка – это прибор для измерения длины. Конечно, линейка относится к самым простым измерительным приборам. Существуют значительно более сложные приборы: например, термометр, который применяется для измерения температуры, гигрометр, который используется для измерения влажности или амперметр, который используется для измерения силы электрического тока.

Важно знать, как пользоваться измерительными приборами и насколько могут быть точны те или иные измерения. У каждого ученика есть линейка и карандаш. Можно попытаться измерить длину карандаша. В первую очередь нужно определить, какова цена деления измерительного прибора. Для этого необходимо найти два ближайших штриха шкалы, возле которых указаны значения величины (например, 1 см и 2 см). Далее нужно сосчитать число делений, заключенных между цифрами 1 и 2. При подсчёте получается, что количество этих делений равно 10. Таким образом, между отметками 1 см и 2 см заключено десять делений. Вычитаем из большего числа меньшее и делим на количество делений между ними. В результате вычислений получаем, что цена деления линейки составляет 0,1 см или 1 мм. Данный пример объясняет, как определить цену деления любого измерительного прибора.

Как видно из рисунка, длина карандаша чуть меньше десяти сантиметров. Если бы на этой линейке не было миллиметровых делений, то можно было сказать, что длина карандаша равна десяти сантиметрам. Но это было бы не совсем точное измерение. Такую неточность называют погрешностью измерения. В представленном случае, на линейке есть миллиметровые деления, поэтому можно измерить длину карандаша с более высокой точностью – 9,8 см. Это говорит о том, что чем меньше цена деления, тем больше точность измерения. Ну а большая точность измерения означает меньшую погрешность. Однако абсолютно точных измерений не существует. Если дать один и тот же карандаш каждому ученику из класса и попросить измерить длину карандаша, не у всех получится одинаковый результат. Тем не менее, погрешность измерения не может быть больше цены деления. Например, если видно, что длина карандаша не точно 9,8 см, а чуточку больше, то понятно, что длина карандаша находится в промежутке от 9,8 см до 9,9 см.

Погрешность измерений принято считать равной половине цены деления измерительного прибора. То есть, в рассмотренном случае, погрешность измерений составляет 0,5 мм. Поэтому, после того, как измерили карандаш и записали, что его длина равна 9,8 см, следует записать погрешность.

Знак «±» означает, что указанная длина может быть на полмиллиметра больше или на полмиллиметра меньше. Таким образом, истинное значение длины карандаша находится в промежутке от 9,75 см до 9,85 см.

В общем случае запись измеряемых величин с учетом погрешности имеет следующий вид:

где А – измеряемая величина;

а – результат измерения;

Da – погрешность измерений.

Необходимо отметить, что при сложении или вычитании величин с погрешностью, погрешность результата равна сумме погрешностей каждой величины. В этом легко убедиться на примере. На рисунке показаны два отрезка AB и CD, длины которых измерены с определенной погрешностью.

Рассчитаем сумму длин этих отрезков. Из рисунка видно, что отрезок AB равен 1 м ± 1 см. Истинная длина этого отрезка находится в промежутке 99 см ≤ АВ ≤ 101 см. Отрезок CD равен 12 см ± 0,5 см. Истинная длина этого отрезка находится в промежутке от 11,5 см ≤ CD ≤ 12,5 см. Поэтому, сумма длин этих отрезков будет иметь еще большую погрешность. Прежде чем производить вычисления, необходимо перевести обе длины в одинаковые единицы измерения.

Таким образом, получаем, что сумма длин отрезков AB и CD равна

Важно отметить, что этот же промежуток мы бы получили, если бы сложили наименьшие и наибольшие длины отрезков AB и CD. Следовательно, при сложении или вычитании величин, измеренных с погрешностями, погрешность результата равна сумме погрешностей каждой из величин.

Упражнения.

Упражнение 1. Заполните таблицу, указав, что из перечисленных слов является физическим телом, единицей измерения, физической величиной или физическим явлением: ветер, Луна, килограмм, дерево, длина, скорость, испарение.

Решение:

Упражнение 2. Родители измерили рост братьев Димы и Васи с помощью рулетки, цена деления которой 1 см. Подсчитайте, насколько см Дима выше, чем Вася.

Решение:

Упражнение 3. Найдите суммарную массу животных с погрешностью.

Решение:

Основные выводы:

– Для описания физических тел или физических явлений вводится физическая величина, которую можно измерить с помощью измерительных приборов или вычислить по формуле.

– Измерение величины – это сравнение её с однородной величиной, принятой за единицу.

– Кратные приставки – это приставки означающие увеличение в десятки, сотни, тысячи и так далее раз.

– Дольные приставки – это приставки, означающие уменьшение в десятки, сотни, тысячи и так далее раз.

– Погрешность измерений – неточность допускаемая при измерении. За погрешность измерений данного прибора принимают половину цены деления этого прибора.

– При сложении или вычитании величин с погрешностями, погрешность результата вычислений равна сумме погрешностей каждой величины.

videouroki.net

Измерение физических величин. Точность и погрешность измерений. 7 класс

Измерение физических величин. Точность и погрешность измерений. 7 класс

При изучений физических явлений проводят различные измерения.
Физики измеряют физические величины.

Например:

При изучении падение тела, надо измерить высоту, с которой падает тело, массу тела, его скорость и время падения.
Чтобы узнать, например, зависит ли объем воды или другой жидкости от ее температуры и как зависит, нужно, нагревая воду, измерять и объем, и температуру.
Объем и температура, время и длина, площадь, скорость, масса, сила — это физические величины.

1. Что значит измерить?

Измерить какую-либо физическую величину — это значит сравнить ее с однородной величиной, принятой за единицу этой величины.

Например:

Измерить длину стола — значит сравнить ее с другой длиной, которая принята за единицу длины, например с метром.
В результате измерения величины получаем ее числовое значение, выраженное в принятых единицах.

2. Какие бывают единицы имерения?

Для каждой физической величины приняты свои единицы измерения.

Очень удобно пользоваться одинаковыми единицами физических величин во всех странах мира.
Поэтому с 1963 г. применяется Международная система единиц — СИ (система интернациональная).

Основные единицы в системе СИ:

единица длины — 1 метр (1м),
единица времени — 1 секунда (1с),
единица массы — 1 килограмм (1 кг).

Кроме того, используются кратные единицы (кратные основной единице), которые в 10, 100, 1000 и т. д. раз больше.
Эти единицы получили наименования с приставками, взятыми из греческого языка.
«Дека» — 10, «гекто» — 100, «кило» — 1000 и др.

Используются и дольные единицы, которые в 10, 100, 1000 и т. д. раз меньше принятых единиц величин.
В них применяют приставки, также взятые из латинского языка. «Деци» — 0,1, «санти» — 0,01, «милли» — 0,001 и др.

Некоторые приставки к названиям единиц:

г — гекто (100 или 10²)
к — кило (1000 или 10³)
М — мега (1 000 000 или 10⁶)

д — деци (0,1 или 10^-1)
с — санти (0,01 или 10^-2)
м — милли (0,001 или 10^-3)

Например:

Длина столовой ложки 20 см.
Ее длина в метрах (м):
20 см = 0,20 м или 2 • 10^-1 м.

3. Что такое измерителный прибор?

Для измерения физических величин нужны измерителные приборы.

Есть измерителные приборы для простых измерений. Например, измерительная линейка, рулетка, мензурка, применяемая для измерения объема жидкости.
Есть сложные измерительные приборы: секундомеры, термометры и другие.
По мере развития физики и техники приборы усложнялись и появились, например, приборы, при помощи которых изучают строение вещества.

У измерительных приборов есть измерительная шкала, на которой штрихами нанесены деления и написаны значения величин.

Между двумя большими штрихами могут быть дополнительно нанесены несколько делений, не обозначенных числами.

Значение измеряемой величины между ближайшими штрихами называется ценой деления прибора.

Например, у обычной школьной линейки расстояние между двумя ближайшими штрихами составляет 1 мм, это цена деления линейки.

4. Как определить цену деления измерительной шкалы прибора?

Прежде чем использовать измерительный прибор, надо определить цену деления этого прибора.
Надо установить, какому значению величины соответствует каждое самое малое деление.

Для того чтобы определить цену деления, необходимо:
— найти два ближайших штриха шкалы, возле которых написаны значения величины;
— вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.

5. Примеры определения цены деления

а) Определение цены деления секундомера.
Используем любые два штриха, около которых нанесены значения измеряемой величины (времени), например штрихи с обозначениями 5 и 10 с.
Расстояние между этими штрихами разделено на 10 делений. Значит, цена каждого деления равна:

Секундомер показывает 22 с.

б) Определение цены деления термометра.
Возьмем, например, ближайшие друг к другу штрихи с обозначениями 10 °С и 20 °С. Расстояния между ними разделены на 10 делений. Следовательно,
цена каждого деления будет равна: 20 °С — 10 °С = 10 °С, далее 10 °С : 10 = 1 °С.
Термометр показывает 24 °С.

6. Что такое точность и погрешность измерений?

Любое измерение может быть выполнено с большей или меньшей точностью.
В физике допускаемую при измерении неточность называют погрешностью измерения.
Погрешность измерения не может быть больше цены деления измерительного прибора.

Из этого примера видно, что точность измерений зависит от цены деления шкалы прибора.
Чем меньше цена деления, тем больше точность измерения.
При измерении принято считать, что: погрешность измерений равна половине цены деления шкалы измерительного прибора.

При записи величин, с учетом погрешности, пользуются формулой:

где А — измеряемая величина,
а — результат измерений,
дельта а — погрешность измерений (треуголник — греч. буква «дельта»).

Например:

Если длина книги 20 см, а цена деления линейки 1 мм, то погрешность измерения будет равна 0,5 мм, или 0,05 см.
Следовательно, длину книги можно записать так:
L = (20 ±0,05) см,
где L — длина книги.
Истинное значение длины книги находится в интервале от 19,95 см до 20,05 см.

Главное:

Измерить какую-либо величину — это значит сравнить ее с однородной величиной, принятой за единицу этой величины.
Основные единицы системы СИ: метр, килограмм, секунда.
Для того чтобы определить цену деления, необходимо:
— найти два ближайших штриха шкалы, возле которых написаны значения величины;
— вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.

Следующая страница — смотреть

Назад в «Оглавление» — смотреть

class-fizika.ru

Погрешности приборов

 

В лабораторных работах метод измерений обычно задан, поэтому из систематических погрешностей учитываются только приборные.

Все приборы и инструменты, используемые для измерений физических величин: амперметр, вольтметр и т.д., характеризуются классом точности и (или) ценой деления. Класс точности L – это обобщенная характеристика прибора, показывающая относительную погрешность прибора выраженную в процентах. Класс точности обозначается числом на шкале прибора: 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4. Приборы класса точности 0,1; 0,2; 0,5; применяются для точных измерений и называются прецизионными. В технике применяют приборы классов 1,0; 1,5; 2,5; 4, которые называются техническими. Если на шкале прибора класс точности не указан, то данный прибор внеклассный, то есть имеет большую погрешность измерений.

Абсолютная систематическая погрешность прибора

, (1)

где Д – наибольшее значение физической величины, которое может быть измерено по шкале прибора.

Если класс точности прибора не известен, то его абсолютная систематическая погрешность принимается равной половине цены наименьшего деления шкалы:

(2)

При измерении линейкой, наименьшее деление которой 1мм допускается погрешность 0,5мм.

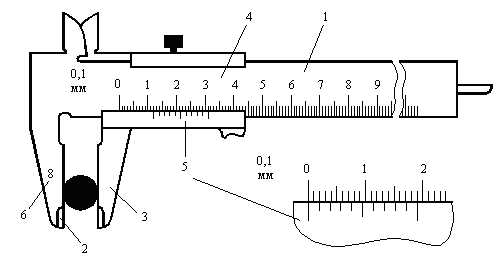
Для приборов, оснащенных нониусом, за приборную принимают погрешность, определяемую нониусом. Для штангенциркуля (рис. 1) – 0,1мм или 0,05мм; для микрометра (рис. 2) – 0,01мм.

 

Штангенциркуль – прибор для наружных и внутренних измерений. Он построен по принципу штанги 1 с основной шкалой, представляющей собой миллиметровую линейку, и подвижной рамки 2 с нониусом 3 (рис.1). Рамка может передвигаться по штанге. Закрепление рамки на штанге осуществляется с помощью винта 4. Нониус ‑ это вспомогательная шкала штангенциркуля, расположенная на рамке и служащую для отсчета долей миллиметра. В нашей стране стандартизированы штангенциркули с нониусами 0,1; 0,05; и 0,02 мм. Отсчет размеров производится по основной шкале и нониусу.

На рис. 1 представлен штангенциркуль с нониусом 0,05мм. Шкала этого нониуса получена при делении 39 мм на 20 частей. Следовательно, каждое деление нониуса равно 1,95 мм, то есть на 0,05 мм меньше делений основной шкалы. Если расположить нониус ровно так, что первый штрих нониуса совпадет с первым штрихом основной шкалы, то основное деление нониуса отойдет от основного деления шкалы на 0,05 мм. Для получения нониуса с ценой деления 0,1 мм делят 19 мм на 10 частей (19 мм : 10 = 1,9 мм), тогда каждое деление нониуса будет на 0,1 мм меньше, чем 1 мм.

 

Рис. 1

 

Измеряемый предмет располагают между ножками 5, 6 штангенциркуля и закрепляют винтом 4. Целые значения в миллиметрах отсчитывают по основной шкале от «0» основной шкалы до «0» нониуса. Затем смотрят, какое деление нониуса совпало с делением основной шкалы. Если номер совпавшего деления нониуса умножить на цену деления прибора, то получаются сотые доли миллиметра. Если с делением основной шкалы совпадает нулевое или последнее деления нониуса, то сотых долей не будет.

На рис. 2 представлены измерения штангенциркуля с нониусом 0,05 мм.

 

Рис. 2

 

Микрометр – это инструмент, применяемый для точных измерений. Принцип действия микрометра основан на работе винтовой пары, то есть преобразования вращательного движения в поступательное.

В скобе 1 микрометра при вращении барабана 2 перемещается микрометрический винт 3, между торцом которого и пяткой 4 помещают измеряемую деталь (рис. 3). Шаг микрометрического винта равен 0,5 мм, а конусная поверхность барабана разделена на 50 равных частей. Следовательно, поворот барабана на одно деление соответствует перемещению винта на 0,01мм. Вращения барабана нужно производить с помощью трещотки 5, обеспечивающей постоянное усилие на измеряемую деталь. Зажим детали производят, вращая трещотку до появления первого треска во избежание порчи инструмента.

 

Рис. 3

 

На стебле 6 микрометра расположены две шкалы. Деления нижний шкалы нанесены через 1 мм, деления верхней расположены посередине между штрихами нижней шкалы. По нижней шкале отсчитывают целые миллиметры, а по верхней ‑ половину миллиметра. При измерении встречаются два характерных случая. В первом случае (рис. 4) деления нижний шкалы расположены ближе к барабану, нежели деления верхней шкалы. При этом целые значения миллиметров отсчитываются по нижней шкале, а сотые доли ‑ по барабану. Например, показания инструмента соответствуют размеру 18,04 мм. Во втором случае деление верхней шкалы расположены ближе к барабану, чем деление нижней шкалы. При этом учитываются целые, половинка и сотые доли миллиметра. Например, показания инструмента соответствует размеру 18 целых + половинка 0,50 + 9 сотых, то есть 18,59 мм.

 

Рис. 4

 

Похожие статьи:

poznayka.org

Металлическая линейка – верная спутница мастеровых людей + видео

Измерительная металлическая линейка – это самый простой инструмент для выполнения замеров. Она хорошо знакома каждому еще со школы. Этот прибор, такой простой, привычный и знакомый, нашел свое применение не только дома, но и на производстве – столярном деле и строительстве, машиностроении и металлообработке.

Что говорит ГОСТ про измерительные металлические линейки?

Производство любых инструментов регламентируется стандартами. Не является исключением и линейка измерительная металлическая, ГОСТ 427-75 строго определяет требования к параметрам, размерам, внешнему виду этого инструмента. В соответствие со стандартами, он выпускается с различными диапазонами измерений: 150, 300, 500, 1000, 1500, 2000, 3000 мм. Инструменты с малым пределом измерений, как правило, применяются для бытовых нужд, большие можно отнести к специальным приспособлениям.

Например, метровая металлическая линейка широко применяется для построения чертежей, архитектурных и строительных планов. Основным элементом любого измерительного прибора является шкала. По ГОСТ линейка измерительная металлическая может иметь одну или две шкалы. Изделия с двумя шкалами могут иметь различную оцифровку – в одну или противоположные стороны. Изделия небольших размеров, как правило, выпускаются с одной шкалой. Для удобства работы с приспособлениями, имеющими большой диапазон измерений, используются две шкалы с разнонаправленной оцифровкой. Примером может служить простейшая строительная линейка металлическая 1000 мм.

ГОСТ определяет не только размеры и допустимые отклонения в выполняемых замерах, но и расстояния между штрихами, длины каждого штриха. На шкале наносятся миллиметровые, пятимиллиметровые, десятимиллиметровые штрихи. Они имеют разную длину с разницей не менее полутора миллиметра. Одноименные штрихи должны быть одинаковой длины с погрешностью не более 0,5 мм. То же касается и высоты оцифровки. В маркировке линеек указывается предел измерений и количество шкал:

• 500 ГОСТ 427-75 – такая маркировка означает, что перед нами линейка металлическая 500 мм с одной шкалой;
• 1500 д ГОСТ 427-75 – линейка металлическая с пределом измерений 1500 мм и двумя шкалами.

Материалом для изготовления служит холоднокатаная стальная лента. Поверхность изделия обязательно должна иметь гальваническое покрытие (хромирование). Оно играет защитную роль, предохраняя прибор от коррозии. С другой стороны, наличие покрытия минимизирует образование бликов на металлической поверхности, увеличивая тем самым точность проведения измерений мастером. Любой измерительный прибор всегда дает погрешность в измерениях. Для линеек такая погрешность не может быть более 0,1-0,2 мм.

Величина зависит от диапазона измерений: чем длиннее приспособление, тем больше будет отклонение. Максимально возможное отклонение составляет 0,2 мм на метр длины прибора.

Какие технические требования предъявляются к линейкам?

Шкала начинается с торцевой грани. К расположению этой грани ГОСТом предъявляются весьма жесткие требования – по отношению к продольной стороне она должна располагаться строго под прямым углом. За последним десятимиллиметровым штрихом с оцифровкой обязательно наносится не менее пяти дополнительных делений (цена деления 1 мм). Инструменты с закругленным концом дополняются специальным отверстием для возможности удобного подвешивания.

Диаметр отверстия составляет 5 мм при диапазоне измерений, не превышающем 500 мм, и 8 мм у изделий большей длины. При наличии на приспособлении двух шкал, добавочные миллиметровые деления не наносятся, а обе торцевые грани не должны иметь закруглений и выполняются строго перпендикулярно к продольной грани. Отклонения прямолинейности грани ГОСТ определяет как 0,04 мм. У изделий, предел замеров которых более 1000 мм, погрешность прямолинейности может составлять 0,08 мм. Торцевые грани могут иметь шероховатость, но ее показатели не должны превышать Ra £ 2,5 по ГОСТ 2789-73.

Погрешность выполняемых замеров также зависит от длины измерительного инструмента. Данные о допустимых отклонениях указаны в ГОСТ 427-75 в специальных таблицах. Цифровые обозначения обязательно наносятся рядом с каждым десятимиллиметровым штрихом. Указанная цифра обозначает расстояние от начального торца линейки до данной отметки. Инструменты с двумя шкалами могут иметь один цифровой ряд или два разнонаправленных ряда.

Где применяются изделия?

Измерительные линейки – настолько простой и привычный для каждого человека инструмент, что, казалось бы, сказать что-то новое о их применении практически невозможно. Несмотря на то, что они используются не только в бытовых нуждах, но для производственных целей, ни один мастер, работающий с металлическими деталями, для которых максимальная точность выполненных замеров критично важна, не будет использовать только линейку. С другой стороны, в строительстве или столярном деле измерения, сделанные этим простым инструментом, вполне могут стать основой для выполнения работ. 

При необходимости нанесения криволинейных линий на помощь обычному инструменту приходит лекальная линейка, но измерить с ее помощью размер не получится – шкалы лекало не имеет. Даже при условии, что инструмент для замеров выбран мастером правильно, а его погрешность соответствует ГОСТ, всегда остается вероятность совершения ошибки. Существует несколько причин, по которым снижается точность замеров:

• Применение поврежденных линеек, например, погнутых, с дефектами на шкале и т. п.
• Загрязнения на поверхности шкалы, не позволяющие проводить точные замеры.
• Неправильная установка инструмента в соответствии с нулевой отметкой относительно измеряемой заготовки.
• Нарушение температурного режима выполнения замеров, например, измерение сильно охлажденной или сильно нагретой заготовки.
• Не соответствующая условиям выполнения замеров температура воздуха (при повышении или понижении температуры металлические изделия легко изменяются в своих линейных размерах).

Простейшим способом уменьшить вероятность погрешности во время замеров является проведение нескольких измерений при соблюдении всех необходимых условий. На основе полученных в ходе нескольких измерений результатов рассчитывается среднее арифметическое значение, которое можно считать максимально точным показателем с небольшими отклонениями. При выполнении замеров нужно максимально точно совместить нулевую отметку с началом заготовки, чтобы минимизировать погрешность. Инструмент нужно располагать строго вдоль измеряемой линии, без отклонений, диагоналей.

Нельзя забывать, что даже в этом случае обычная измерительная линейка никогда не даст высокоточных результатов. Цена деления этого приспособления составляет 1 мм, а это значит, что замеры будут выполняться с точностью до миллиметра. Для слесарных работ, металлообработки такой точности недостаточно. Для того, чтобы выполнять замеры в металлообработке, машиностроении, слесарном деле требуются иные инструменты и приспособления, способные давать при выполнении замеров результаты с точностью до микрона.

remoskop.ru