Чему равна цена деления мензурки
Мензурка – измерительный прибор, позволяющий определить объём налитой в него жидкости. Для этого он изготавливается из прозрачного материала (стекла, плексигласа, полистирола или других пластиков) и оснащается градуированной шкалой на передней стороне.
Чтобы определить объём налитой в мензурку жидкости, необходимо установить сосуд на строго горизонтальную поверхность, без наклонов, и посмотреть отметку на шкале, которой достиг уровень вещества. Однако промежуточные деления обычно не имеют цифровых обозначений, что усложняет процесс.
В этой статье мы расскажем, как определить цену промежуточного деления на измерительной шкале мензурки.
Арифметический расчёт цены промежуточного деления на измерительной шкале мензурки
На измерительной шкале мензурок обычно приводятся основные деления и промежуточные. Около первых, более длинных, стоит отметка, указывающая на объём налитой в сосуде жидкости. Например, «10 мл», «20 мл» и так далее.
Промежуточные деления обычно не имеют цифровых обозначений, вследствие чего определение их цены начинающими лаборантами может быть сложным. Для этого нужно воспользоваться арифметическим расчётом:
- Определите цену двух соседних основных делений. Например, 20 и 30 мл.
- Определите разницу между ними: 30 – 20 = 10 мл.
- Посчитайте количество промежутков между промежуточными делениями внутри соседних основных. Не делений, а промежутков между ними. Например, их может быть пять (при этом промежуточных делений, соответственно, всего четыре).
- Разделите разницу между основными делениями на количество промежутков: 10 / 5 = 2 мл.
2 мл – это цена каждого промежуточного деления мензурки. Соответственно, для определения количества налитой в сосуд жидкости нужно определить, на каком промежуточном делении остановился её уровень.
Например, уровень остановился на третьем промежуточном делении после 20 мл.
Это означает, что количество жидкости – это 20 + (3 × 2) = 26 мл.
Однако важно понимать, что во многих случаях мензурки не являются точным измерительным прибором, особенно – общелабораторного назначения или предназначенные для бытового применения (либо использования в пищевой промышленности). Их погрешность составляет до половины от цены минимального промежуточного деления.
В нашем случае это – 2 / 1 = 1 мл. Как следствие, в мензурку налито 26±1 мл жидкости.
Особенности измерений с использованием мензурок
Эти лабораторные приборы крайне разнообразны. Они различаются не только ёмкостью и ценой деления шкалы, но также используемой системой измерения. Например:
- Кроме миллилитров, могут использоваться кубические сантиметры. Это также стандартная единица измерения. При этом 1 мл = 1 см3.
- В больших сосудах, рассчитанных на использование в пищевой промышленности и производственных лабораториях, в качестве системы измерения могут использоваться литры.
При этом 1 л = 1000 мл. - В сосудах, привезённых из Великобритании, США и различных западных стран, может использоваться имперская система мер для жидкостей: галлоны, кварты, пинты, джиллы, жидкие унции, жидкие драхмы и так далее. Для их перевода в метрическую систему необходимо воспользоваться таблицами или конвертерами. Жидкая унция обозначается как oz и эквивалентна 29,574 миллилитрам.
При этом 1 л = 1000 мл.Впрочем, в абсолютном большинстве представленных на российском рынке (и во всех из нашего каталога) измерительных приборах используется стандартная, метрическая система измерений, которая не требует конвертирования, перевода и использования таблиц. Достаточно помнить, что 1 см
Задание 22 ЕГЭ по физике 2023: теория и практика
Русский язык Математика (профиль) Математика (база) Обществознание История Биология Физика Химия Английский язык Информатика Литература
Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18 Задание 19 Задание 20 Задание 21 Задание 22 Задание 23 Задание 24 Задание 25 Задание 26 Задание 27 Задание 28 Задание 29 Задание 30
За это задание ты можешь получить 1 балл.
Уровень сложности: базовый.
Средний процент выполнения: 42.8%
Ответом к заданию 22 по физике может быть последовательность цифр, чисел или слов. Порядок записи имеет значение.
Разбор сложных заданий в тг-канале
Посмотреть
Задачи для практики
Задача 1
Что показывает вольтметр с учётом абсолютной погрешности? Принять абсолютную погрешность равной половине цены деления шкалы прибора.
В ответе запишите результат измерения с погрешностью без пробелов и других разделителей .
Решение
Цена деления$={3-2}/{10}={1}/{10}=0.1B; {ц.д.}/{2}={0.1}/{2}=0.05B$. Тогда имеем: $(2.40±0.05)B$. Согласно правилу записи ответа с погрешностью, результат измерения и погрешность должны иметь одинаковое количество знаков после запятой.
Ответ: 2.400.05
Показать решение
Бесплатный интенсив
Задача 2
Что показывает амперметр с учётом абсолютной погрешности? Абсолютную погрешность принять равной половине цены деления прибора.
Решение
Цена деления$={0.3-0.2}/{5}={0.1}/{5}=0.02A; {ц.д.}/{2}={0.02}/{2}=0.01A$. Тогда имеем: $(0.24±0.01)A$
Ответ: 0.240.01
Показать решение
Бесплатный интенсив
Задача 3
С помощью амперметра проводились измерения силы тока на участке электрической цепи. Чему равна сила тока с учётом погрешностей измерений, если погрешность прямого измерения составляет половину цены деления прибора, а его класс точности равен 0,5 (т.е. инструментальная погрешность составляет 0,5% от верхнего предела измерений данной шкалы амперметра)? Ответ: (_ ± _) А.
Решение
Определим погрешность прибора: если верхняя граница равна 10А, то инструментальная равна: $∆x_{пр}={10·0,5}/100=0,05$.
Погрешность измерения равна половина цены деления $∆x_{изм}=0,25$.
$∆x=∆x_{изм}+∆x_{пр}=0,05+0,25=0,3$.
$x=7.5±0.3$
Ответ: 7.50.3
Показать решение
Бесплатный интенсив
Задача 4
При определении массы воды, налитой в мензурку, ученик при помощи мензурки измерил объём воды. Запишите в ответ массу воды в граммах с учётом погрешности измерений (без пробелов). Погрешность измерения объёма равна половине цены деления мензурки. Ответ: (_ ± _) г.
Решение
Определим значение погрешности прямого измерения $∆V={V’}/{2}={5}/{2}=2.5г$. Тогда: $125±2.5г$. Количество знаков после запятой в измеренной величине должно совпадать с количеством знаков после запятой в значении погрешности. Поэтому $125.0±2.5г$
Ответ: 125.02.5
Показать решение
Бесплатный интенсивЗадача 5
Ученик собрал электрическую цепь, состоящую из батарейки, двух резисторов, амперметра и вольтметра.
После этого он провёл измерения напряжения на одном из резисторов и силы тока в цепи. Погрешности измерения силы тока в цепи и напряжения на источнике равны половине цены деления шкал приборов. Чему равно по результатам этих измерений значение напряжения на резисторе R1? Ответ: (_ ± _) В.
Решение
$U=U’+∆U; ∆U={0.2}/{2}=0.1$(половина угла деления). Запишем ответ $U’=7.2B$ как сумму, действующего измерения и погрешности: $7.2±0.1$.
Ответ: 7.20.1
Показать решение
Бесплатный интенсив
Задача 6
Найдите длину проволоки, если погрешность прямого измерения составляет половину цены деления линейки, изображённой на рисунке. Ответ: (_ ± _) см.
Решение
Погрешность измерения равна половине цены деления ${0.5}/{2}-0.25$, тогда длина проволоки $23.00±0.25$см.
Ответ: 23.000.25
Показать решение
Бесплатный интенсив
Задача 7
Запишите величину объёма с учётом погрешности, если погрешность равна половине цены деления.
Ответ: (_ ± _) мл.
Решение
$∆V={V_1}/{2}={10}/{2}=5$мл (погрешность измерения половина цены деления). Запишем ответ исходя из рисунка $V=90$мл.
Ответ: 905
Показать решение
Бесплатный интенсив
Задача 8
Запишите величину угла с учётом погрешности. С точностью до десятых. Ответ: (_ ± _)◦ .
Решение
Найдем погрешность, как половину цены деления ${5}/{2}=2.5°$. Тогда, исходя из графика получим: $55±2.5$.
Ответ: 55.02.5
Показать решение
Бесплатный интенсив
Задача 9
По рисунку определите объём жидкости с учётом погрешности измерения. Ответ: (_ ± _) мл.
Решение
По измерению проведенному измерим погрешность половины угла деления 2.5: $87.5±2.5$мл.
Ответ: 87.52.5
Показать решение
Бесплатный интенсив
Задача 10
Запишите показания спидометра с учётом его погрешности, равной половине цены деления.
Ответ: (_ ± _) км/ч. Значение величины и погрешность запишите слитно (без ±)
Решение
По рисунку видно, что стрелка ближе к 70, чем к 80 км/ч.
Погрешность измерения принимается за половину цены деления, а так как цена деления 10 км/ч, то показания спидометра (70 ± 5) км/ч.
Ответ: 705
Показать решение
Бесплатный интенсив
Задача 11
Запишите величину объёма, которая измеряется в данном эксперименте. Ответ: (_ ± _) мл.
Решение
Как известно, погрешность — это половина цены деления, где $V={V’}/{2}={1}/{2}=0.5$. Исходя из рисунка, определим объем и запишем ответ: $17.5±0.5$мл.
Ответ: 17.50.5
Показать решение
Бесплатный интенсив
Задача 12
Запишите результат измерения электрического напряжения, учитывая, что погрешность равна половине цены деления.
Укажите показание и погрешность. Ответ: (_ ± _) В.
Решение
Учитывая, что погрешность половины цены деления, определим ее: $∆U={1}/{2}=0.5B$. Запишем ответ, исходя из того, что прибор регестрирует $6В$: $6±0.5$.
Ответ: 6.00.5
Показать решение
Бесплатный интенсив
Задача 13
Для проведения опыта ученик налил воду в мензурку. Шкала мензурки проградуирована в миллилитрах (мл). Погрешность измерений объёма равна цене деления шкалы мензурки. Чему равен объём налитой учеником воды? Ответ: (__ ± __) мл.
Решение
Цена деления мензурки$={150-130}/{10}={20}/{10}=2мл$
Значит, объем налитой учеником воды равен: $V=(150±2)мл$
Ответ: 1502
Показать решение
Бесплатный интенсив
Задача 14
На рисунке показана шкала универсального прибора, измеряющего величину атмосферного давления, температуру и влажность.
Какова относительная погрешность показания шкалы барометра, проградуированной в гПа, если абсолютная погрешность равна цене деления шкалы. Ответ выразите в (%) и округлите до десятых.
Решение
Относительная погрешность $ε={∆p}/{p_{пр}}·100%$, где $∆p={ц.д.}={{(1000-950)}/{10}}={5}гПа$.
Показания прибора барометра равны: $p_{пр}=1050гПа$, тогда $ε={5·100%}/{1050}≈0.5%$
Ответ: 0.5
Показать решение
Бесплатный интенсив
Задача 15
На фотографии представлена электрическая схема для определения сопротивления резистора. По показаниям приборов определите показания вольтметра с учётом погрешности, равной цене деления прибора. Ответ: (__ ± __) В.
Решение
Цена деления$={4-3}/{5}={1}/{5}=0.2B$
Тогда показания вольтметра равны: $(3.2±0.2)В$
Ответ: 3.20.2
Показать решение
Бесплатный интенсив
Задача 16
Какую температуру показывает термометр, если погрешность прямого измерения равна половине цены деления прибора? Ответ: ( ± ) ◦ C, использовать точку, но не запятую как знак-разделитель, например 9.
90.1 .
Решение
Цена деления$={40°С-30°С}/{10}={10°С}/{10}=1°С; {ц.д.}/{2}={1°С}/{2}=0.5°С$
Тогда показания термометра равны: $(26±0.5)°С$
Ответ: 26.00.5
Показать решение
Бесплатный интенсив
Задача 17
Каковы показания амперметра, если погрешность прямого измерения равна половине цены деления прибора? Ответ выразите в(___ ± ___) А.
Решение
Цена деления$={2A-1A}/{10}=0.1A; {ц.д.}/{2}={0.1A}/{2}=0.05A$
Тогда показания алтерметра равны: $(1.80±0.05)А$
Ответ: 1,800,05
Показать решение
Бесплатный интенсив
Задача 18
Каковы показания секундомера, если погрешность прямого измерения равна половине цены деления прибора? Ответ выразите в (___ ± ___) с.
Решение
Цена деления$={50-45}/{5}=1; {ц.д.}/{2}={1}/{2}=0.5c$
Тогда показания прибора: $t=(42±0.
5)c$
Ответ: 42.00.5
Показать решение
Бесплатный интенсив
Задача 19
Каков объём воды в измерительном цилиндре, если погрешность прямого измерения равна половине цены деления прибора? Ответ выразите в (___ ± ____) мл.
Решение
Находим погрешность как половину цены деления и получаем 0.5. Соответственно записываем показание прибора с одной цифрой после запятой, чтобы это совпадало с записью погрешности.
Ответ: 21.00.5
Показать решение
Бесплатный интенсив
Показать еще
Для доступа к решениям необходимо включить уведомления от группы Турбо в вк — это займет буквально 10 секунд. Никакого спама, только самое важное и полезное для тебя. Ты всегда можешь запретить уведомления.
Включить уведомления
Бесплатный интенсив по физике
3 огненных вебинара, домашние задания, беседа курса, личный кабинет, связь с преподавателем и многое другое.
Курс стартует 4 сентября. Бесплатный интенсив
Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражения с дробями:
Дроби — используйте косую черту для деления числителя на знаменатель, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной строки и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1,45 .
Наиболее распространенные мнемоники для запоминания этого порядка операций: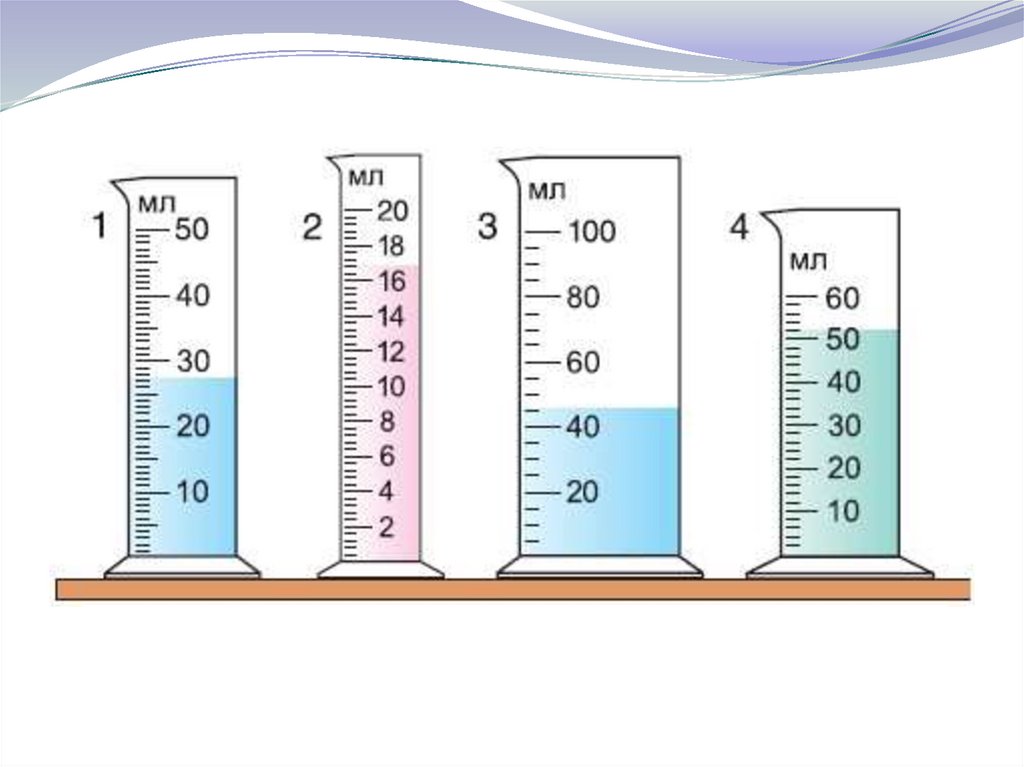 
Чему равно 3/15 в наименьшем члене?
.. все математические калькуляторы
Это то же самое, что «делить» 10 конфет между двумя детьми. У обоих детей должно получиться одинаковое количество конфет. В этом примере ответ равен 5.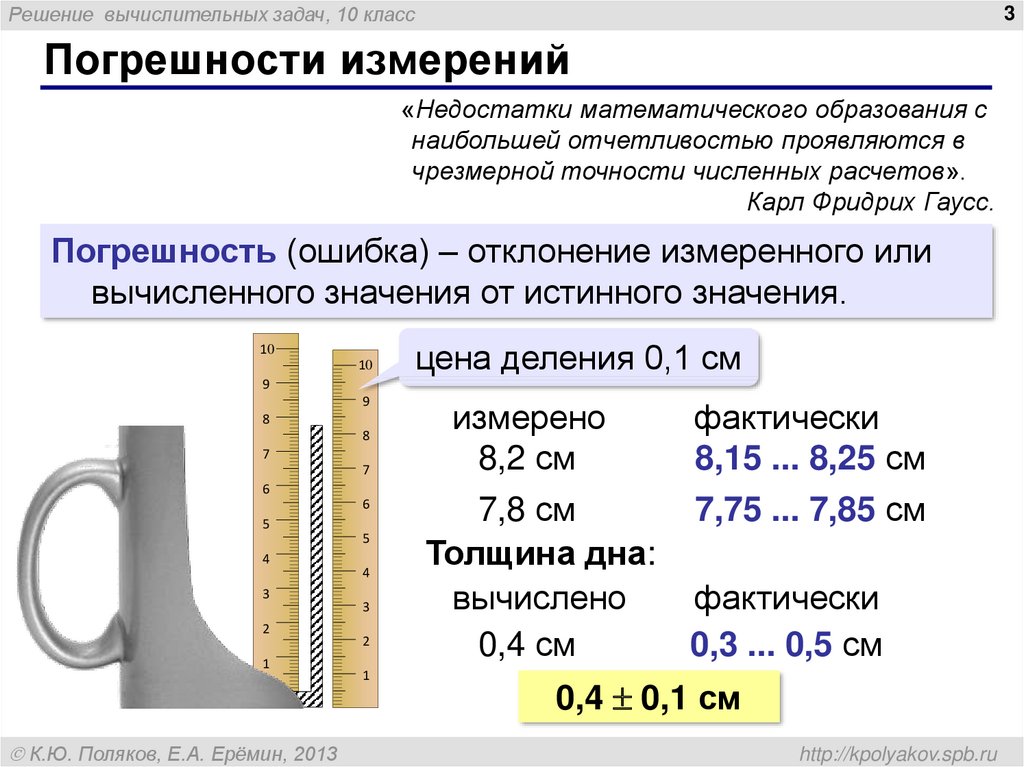
10 ÷ 2 = 5, тогда как 2 ÷ 10 = 0,2. Десять конфет, разделенных на двоих детей, сильно отличаются от 2 конфет, разделенных на 10 детей.
8 — 2 = 6 
Двигайтесь вниз по столбцу, пока не найдете нужный номер: 10 . Переместитесь по строке влево, чтобы увидеть ответ (красный затененный заголовок) 5 .
56 ÷ 8 = 7 например. Найдите 7 в верхней строке, посмотрите вниз по столбцу, пока не найдете 56 , затем найдите соответствующий номер строки, 8 .
Ему нужно заменить все четыре шины на машине плюс запаску.
Как вы увидите, это не обязательно должно быть точное целое число.
Десять раз — это слишком много.
5 × 6 = 30. Мы пишем 6 в столбце единиц нашего ответа.
Воспользуйтесь приведенной выше таблицей умножения или своей памятью. 3 × 8 = 24 — если мы разделим 24 на 8, мы получим 3. Поэтому нам нужно разделить каждый ингредиент ниже на 3, чтобы получить нужное количество смеси для приготовления 8 сказочных пирожных. 
Используя таблицу умножения, если нужно, мы можем увидеть, что 3 входит в 12 ровно 4 раза по без остатка.
(Если вам нужна помощь с единицами измерения, см. нашу страницу Системы измерения .) Если мы хотим быть более точными, мы можем попробовать разделить 5 мл на 3. 3 входит в 5 один раз (3) с 2 в остатке. 2 ÷ 3 равно ⅔, поэтому 5 мл, разделенные на 3, дают нам 1⅔ мл, что в десятичных дробях равно 1,666 мл. Мы можем использовать наши навыки оценки и сказать, что одна чайная ложка, разделенная на три, чуть больше, чем полтора мл. Если у вас на кухне есть несколько таких крошечных мерных ложек, вы можете быть очень точны!