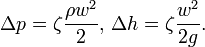Гидравлические потери или гидравлическое сопротивление — безвозвратные потери удельной энергии (переход её в теплоту) на участках гидравлических систем (систем гидропривода, трубопроводах, другом гидрооборудовании), обусловленные наличием вязкого трения[1][2]. Хотя потеря полной энергии — существенно положительная величина, разность полных энергий на концах участка течения может быть и отрицательной (например, при эжекционном эффекте).
Гидравлические потери принято разделять на два вида:
- потери на трение по длине — возникают при равномерном течении, в чистом виде — в прямых трубах постоянного сечения, они пропорциональны длине трубы;
- местные гидравлические потери — обусловлены т. н. местными гидравлическими сопротивлениями — изменениями формы и размера канала, деформирующими поток. Примером местных потерь могут служить: внезапное расширение трубы, внезапное сужение трубы, поворот, клапан и т. п.
Гидравлические потери выражают либо в потерях напора в линейных единицах столба среды, либо в единицах давления : , где — плотность среды, g — ускорение свободного падения.
Коэффициенты потерь
Основная статья: Формула Дарси — Вейсбаха
Во многих случаях приближённо можно считать, что потери энергии при протекании жидкости[3] через элемент гидравлической системы пропорциональны квадрату скорости жидкости[2]. По этой причине удобно бывает характеризовать сопротивление безразмерной величиной ζ[4], которая называется коэффициент потерь или коэффициент местного сопротивления и такова, что
То есть в предположении, что скорость w по всему сечению потока одинакова, ζ=Δp/eторм, где eторм = ρw²/2 — энергия торможения единицы объёма потока относительно канала. Реально в потоке скорость жидкости не равномерна, в справочной литературе в данных формулах принимается среднерасходная скорость w=Q/F, где Q — объёмный расход, F — площадь сечения, для которого рассчитывается скорость[1]. Таким образом, средняя энергия торможения потока обычно несколько больше ρw²/2, см. Среднее квадратическое.
Для линейных потерь обычно пользуются коэффициентом потерь на трение по длине (также коэффициент Дарси) λ, фигурирующего в формуле Дарси — Вейсбаха[2]
- ,
где L — длина элемента, d — характерный размер сечения (для круглых труб это диаметр). Иначе в единицах давления
- ;
таким образом, для линейного элемента относительной длины L/d коэффициент сопротивления трения ζтр=λL/d.
Влияние режима течения в трубах на гидравлические потери
Поскольку при турбулентном режиме течения происходит расход энергии потока на преодоление вязкости при турбулентных колебаниях, гидравлические потери при ламинарном режиме течения жидкости значительно меньше, чем при турбулентном. Так, например, если бы в системах водоснабжения и отопления при существующих скоростях движения жидкостей возможно было бы поддерживать ламинарный режим течения, то напор насосов можно было бы уменьшить в 5—10 раз
Значение в технике
На преодоление гидравлических потерь в различных технических системах затрачивается работа таких устройств, как насосы, воздуходувки.
Для уменьшения гидравлических потерь рекомендуется в конструкциях гидроборудования избегать применения деталей, способствующих резкому изменению направления потока — например, заменять внезапное расширение трубы постепенным расширением (диффузор), придавать телам, движущимся в жидкостях, обтекаемую форму и др. Даже в абсолютно гладких трубах имеются гидравлические потери
Иногда, напротив, требуется ввести гидравлическое сопротивление в поток. Для этого применяются дроссельные шайбы, редукционные установки, регулирующие клапана. По измерению давления на некотором элементе, график коэффициента гидравлического сопротивления которого известен, можно узнать скорость потока в некоторых распространённых типах расходомеров.
См. также
Ссылки
Примечания
- ↑ 1 2 Идельчик И. Е. Справочник по гидравлическим сопротивлениям/ Под ред. М. О. Штейнберга. — 3-е изд., перераб. и доп.— М.: Машиностроение, 1992. — C. 10
- ↑ 1 2 3 4 Гидравлика, гидромашины и гидроприводы: Учебник для машиностроительных вузов / Т. М. Башта, С. С. Руднев, Б. Б. Некрасов и др.. — 2-е изд., перераб.. — М.: Машиностроение, 1982. — С. 48—50, 84, 88.
- ↑ В гидродинамике жидкостью называется любая текучая среда, как капельная жидкость, так и газ.
- ↑ Также применяется обозначение ξ; буквы часто путают, иногда применяют для различения того, во входном или выходном сечении элемента измерялась скорость в формуле (для расширяющихся или сужающихся элементов).
Эта версия статьи создана: 14.07.2020. Дата первой публикации: 28.08.2019
Зачем нужен этот калькулятор?
Калькулятор умеет рассчитывать потери напора в метрах в зависимости от длины и диаметра вашего трубопровода, а также объемного расхода жидкости. Зная потери напора, вы сможете более точно подобрать нужный насос под вашу задачу.
Наш калькулятор использует формулу расчета одного немецкого института гидродинамики. Из всех протестированных нами формул эта в наибольшей степени соотносится с нашим собственным опытом.
Чтобы воспользоваться калькулятором, введите исходные данные, потом нажмите кнопку «Рассчитать».
Ниже этой кнопки будут показаны результаты расчета.
Введите исходные данные
Внутренний диаметр трубопровода
мм
Длина трубопровода
м
Расход жидкости
л/мин
м³/ч
Перекачиваемая жидкость
==Другая жидкость==
Вода
Бензин
Нефть
Керосин
Масло И-20
Масло И-50
==Другая жидкость==
Кинематическая вязкость
м²/с
Введите значение вязкости вручную
Материал внутренней стенки трубопровода
==Указать шероховатость вручную==
Сталь
Чугун
Медь
Алюминий
Резина
Бетон
Полипропилен
==Указать шероховатость вручную==
Шероховатость внутренней поверхности трубы
мм
Введите данные вручную
Ускорение свободного падения в точке измерения
м/с²
Введите корректное ускорение, оно варьируется от 9,780 м/с² на экваторе до 9,82 м/с² на полюсах.
Рассчитать
Результаты
Площадь сечения трубопровода: 0 мм²
Относительная шероховатость трубопровода: 0 мм
Скорость течения жидкости: 0 м/с
Число Рейнольдса: 0
Режим течения: 0
Коэффициент гидравлического трения: 0
Потери напора по длине: 0 м.в.ст
Подробнее о заполнении полей калькулятора
Поясним чуть подробнее как заполнить исходные данные.
-
Внутренний диаметр трубопровода
Измеряется в миллиметрах. Лучше измерять диаметр труб непосредственно штангенциркулем, а не ориентироваться на справочные данные. Также обратите внимание на то, что диаметр требуется именно внутренний. В каталогах труб часто указывают номинальный диаметр труб, который чуть больше, чем внутренний. -
Длина трубопровода
Измеряется в метрах. Длина трубопровода — это сумма длин всех прямых участков трубы, а не расстояние между начальной и конечной точкой. К примеру, если у вас труба идет 10 метров по земле, а затем поднимается на 3 метра вверх, и идет 2 метра в обратном направлении, то в калькулятор нужно занести число 15. Это важно учитывать на предприятиях, где трубы часто обходят препятствия и имеют технологические изгибы. -
Расход жидкости
В этом пункте вы самостоятельно можете выбрать единицы измерения: литры в минуту или кубометры в час. Расход жидкости — это количество жидкости, которое протекает через трубу за определенное время. Например, если 60 литровая бочка наполняется водой за 1 час, значит расход воды составляет 60 литров в час или 1
Расчет потерь напора в трубопроводах
16 ноября 2015 г.
В процессе течения нефтепродуктов имеют место потери напора на трение hτ и местные сопротивления hMC.
Потери напора на трение
Потери напора на трение при течении ньютоновских жидкостей в круглых трубах определяются по формуле Дарси—Вейсбаха
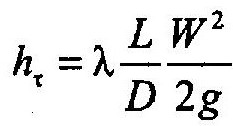
где λ — коэффициент гидравлического сопротивления; L, D — соответственно длина и внутренний диаметр трубопровода; W — средняя скорость перекачки; g — ускорение силы тяжести.
Величина коэффициента гидравлического сопротивления λ в общем случае зависит от числа Рейнольдса Re = W • D/v и относительной шероховатости труб ε = k
При ламинарном режиме перекачки (Re = ReKp) расчет λ выполняется по формуле Стокса
λ = 64/Re
В переходной зоне (ReKp < Re < Rerp) расчет λ наиболее точно может быть выполнен по формуле Гипротрубопровода
λ=(0,16·Re-13)·10-4
Эквивалентная шероховатость kэ стальных труб
Вид труб | Состояние труб | К-,, мм | |
Диапазон изменения | Среднее значение | ||
Бесшовные | Новые и чистые | 0,01-0,02 | 0,014 |
Сварные | Новые и чистые | 0,03-0,12 | 0,05 |
С незначительной коррозией после очистки | 0,1-0,2 | 0,15 | |
После нескольких лет эксплуатации | 0,15-0,3 | 0,2 | |
Умеренно заржавленные | 0,3-0,7 | 6,5 | |
Старые заржавленные | 0,8-1,5 | 1 | |
Сильно заржавленные или с большими отложениями | 2-4 | 3 | |
В зоне гидравлически гладких труб турбулентного режима (ReKp < Re < Rel) расчет λ выполняется по формуле Блазиуса
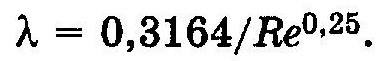
Для расчета λ в зоне смешанного трения турбулентного режима (ReI < Re = ReII) наиболее часто используется формула Альтшуля
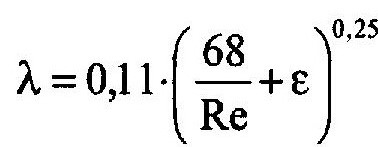
В зоне квадратичного трения турбулентного режима (Re > ReII) расчет λ обычно ведут по формуле Шифринсона
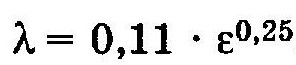
Нетрудно видеть, что формулы Стокса, Блазиуса и Шифринсона могут быть представлены зависимостью одного вида
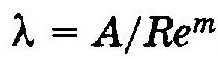
где А, т — коэффициенты, величина которых для каждой зоны трения неизменна.
Однако формула Альтшуля к этому виду не приводится. Это исключает возможность решения гидравлических задач в общем виде.
Ту же задачу можно было решить следующим образом. При Re = ReI еще справедлива формула Блазиуса, а при Re = RеI уже можно пользоваться формулой Шифринсона. Учитывая, что переходные числа Рейнольдса Альтшулем рекомендовано находить по формулам:
ReI=10/ε; ReII=500/ε.
для зоны смешанного трения получаем:
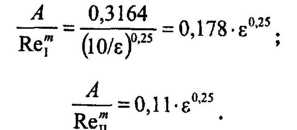
Поделив почленно получим:
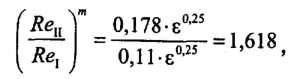
откуда
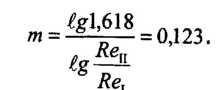
Различие в выражениях для расчета коэффициента А объясняется тем, что в первом случае не было сделано необходимое алгебраическое преобразование
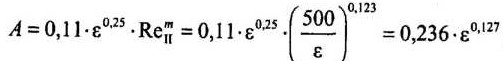
Среднеквадратичная погрешность аппроксимации В.ДБелоусова по сравнению с формулой Альтшуля составляет около 5%. Связано это, в частности, с тем, что ее автор не стремился сделать погрешность вычислений минимальной, а исходил из условия равенства коэффициентов X на границах зоны смешанного трения и соседних зон.
Автору совместно с аспиранткой Н.В. Морозовой удалось свести уравнение Альтшуля к виду со среднеквадратичной погрешностью 2,6%. Это было сделано следующим образом.
Представим формулу Альтшуля в виде
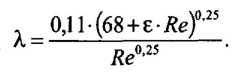
Недостатком данной записи является то, что расчетный коэффициент 0,11(68 + ε · Re) °-25 является функцией числа Рейнольдса. Вместе с тем из формул следует, что в зоне смешанного трения справедливо неравенство
10 < ε · Re < 500.
Задаваясь значениями г • Re в этом диапазоне, сначала рассчитали величины функции 0,11(68 + ε · Re)0’26, а затем, используя метод наименьших квадратов, заново описали полученные точки выражением 0,206( ε · Re)0’15.
Подставив его получили искомую зависимость
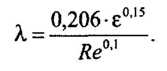
Из нее видно, что в зоне смешанного трения турбулентного режима величины коэффициентов А и т равны 0,206 • е0,15 и 0,1 соответственно. Среднеквадратичная погрешность расчетов по формуле относительно формулы Альтшуля — менее 3%, что меньше, чем по другим известным аппроксимациям.
Следует подчеркнуть, что учет наличия переходной зоны приводит к изменению критического числа Рейнольдса. Кроме того, А.Д. Альтшуль, строго говоря, для переходных чисел Рейнольдса рекомендует диапазоны
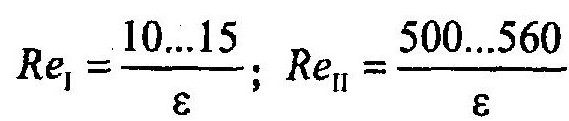
Чтобы уточнить величины Reкр, ReI ReII и найти величину Re.x,, воспользуемся следующим способом. При Re = ReKp еще справедлива формула Стокса» но в то же время уже справедлива формула Гипротрубопровода. То есть можно составить уравнение
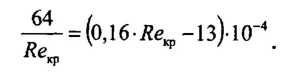
Освобождаясь от знаменателя, получаем квадратное уравнение 0,16-10-4 · Reкр-13 · 10-4 · Reкp-64 = 0, единственным положительным корнем которого является Reкp~2040.
Рассуждая аналогично, можно найти все остальные характерные числа Рейнольдса. Приравняв формулы Гипротрубопровода и Блазиуса, получаем Reкp = 2800. Из равенства правых частей формулы Блазиуса и формулы находим, что ReI = 17,5/ε. Наконец, приравняв правые части формулы и формулы Шифринсона, несложно найти, что ReII = 531/ε.
В тех случаях, когда необходимо, чтобы зависимость потерь напора на трение от расхода Q была выражена в явном виде, удобно использовать обобщенную формулу Лейбензона
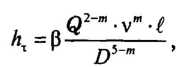
где β — расчетный коэффициент, равный
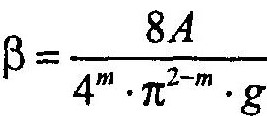
Формула получается подстановкой выражения в формулу Дарси—Вейсбаха .
Учитывая, что формулу Гипротрубопровода можно привести к виду
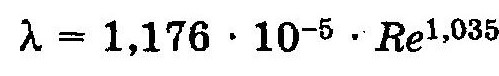
Рекомендуемые величины коэффициентов А, β и m
Режим течения | Зона трения | Область использования | A | β | m |
Лами нарный |
| Re< 2040 | 64 | 4,15 | 1 |
Переходная зона | 2040 <Re< 2800 | 1,17610-5 | 1,25-10-6 | -1,035 | |
Турбу- лентный | Г идравлически гладкие трубы | 2800 <Re< ReI | 0,3164 | 0,0246 | 0,25 |
Смешанного трения | ReI <Re< ReII | 0,206 •£ 015 | 0,0166-e0,15 | 0,1 | |
Квадра тичного трения | Re > Ren | 0J1 e0—25 | 0,0091 -e025 | 0 |
Для вычисления потерь напора на трение при течении нефтепродуктов, проявляющих вязкопластичные свойства, можно воспользоваться уравнением Букингема (в виде аппроксимации, полученной проф. В.Е. Губиным)
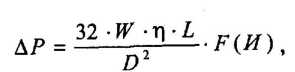
где ΔР — перепад давления при течении вязкопластичной жидкости со средней скоростью W в трубопроводе диаметром D и длиной L; η — пластическая вязкость; F(И) — расчетная функция
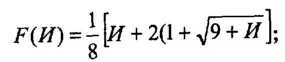
где И — число Ильюшина
Потери напора на местные сопротивления
Данный вид потерь напора определяется по формуле Вейсбаха
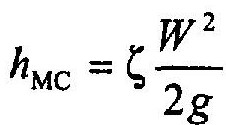
где ξ — коэффициент местного сопротивления.
Величина коэффициента ξ, зависит от вида местного сопротивления и режима течения.
При ламинарном режиме течения величину коэффициента местного сопротивления следует вычислять по формуле
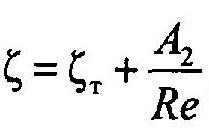
где ξг — коэффициент местного сопротивления при турбулентном режиме; А2 — постоянный коэффициент.
Коэффициенты местных сопротивлений при турбулентном режиме течения
Вид местного сопротивления | А2 | ξг |
Чялвижка открытая: | ||
— на 100% | 75 | 0,15 |
— на 75% | 350 | 0,20 |
— на 50% | 1300 | 2,00 |
— на 25% | 3000 | 20,0 |
Вентиль стандартный: | ||
— Dv = 80-100 мм | 3000 | 4,0 |
— Dy = 150-200 мм | — | 4,7 |
— Dy. = 250-300 мм | 5000 | 5,3 |
Обратный клапан: | ||
— Dy80-100 мм | — | 8,0 |
— Dy150-200 мм | — | 4,0 |
— Dy = 250-300 мм | — | 2,0 |
Компенсатор сальниковый | — | 0,2 |
Компенсатор П-образный: | ||
— Dy= 50-100 мм | 5000 | 2,2 |
— Dy = 200-300 мм | — | 2,4 |
— Dy = 400-500 мм | — | 2,8 |
Фильто для нефтепродуктов: | ||
— светлых | — | 1,70 |
— темных | — | 2,20 |
Формула Дарси — формула, определяющая потери напора или потери давления на гидравлических сопротивлениях:
где
- Δh — потери напора на гидравлическом сопротивлении;
- ξ — коэффициент потерь (коэффициент Дарси;
- V — средняя скорость течения жидкости;
- g — ускорение свободного падения;
- величина называется скоростным напором.
Формула Дарси, определяющая потери давления на гидравлических сопротивлениях, имеет вид:
где
- ΔP — потери давления на гидравлическом сопротивлении;
- ρ — плотность жидкости.
Формула Дарси-Вейсбаха
Если гидравлическое сопротивление представляет собой участок трубы длиной L и диаметром D, то коэффициент Дарси определяется следующим образом:
где λ — коэффициент потерь на трение по длине.
Тогда формула Дарси приобретает вид:
или для потери давления:
Последние две зависимости получили название формулы Дарси-Вейсбаха.
Если определяются потери на трение по длине для трубы некруглого поперечного сечения, то D представляет собой гидравлический диаметр.
Следует отметить, что потери напора на гидравлических сопротивлениях не всегда пропорциональны скоростному напору.
Определение коэффициента потерь на трение по длине
Коэффициент λ определяется по разному для разных случаев.
Для ламинарного течения в гладких трубах с жёсткими стенками, коэффициент потерь на трение по длине определяется по формуле:
где Re — число Рейнольдса.
Иногда для гибких труб в расчётах приниают
Для турбулентного течения существуют более сложные зависимости. Одна из наиболее часто используемых формул — это формула Блазиуса:
Эта формула даёт хорошие результаты при числах Рейнольдса, изменяющихся в пределах от критического числа Рейнольдса Reкр до значений Re = 105. Формула Блазиуса применяется для гидравлически гладких труб.
Для гидравлически шероховатых труб коэффициент потерь на трение по длине определяется графически по эмпирическим зависимостям. Графики для определения коэффициента потерь на трение по длине для шероховатых труб можно посмотреть здесь (k — размер шероховатости, d — диаметр трубы).
Определение коэффициента Дарси для местных сопротивлений
Рис. 1. Гидравлический конфузор: Q1 — поток жидкости в широком сечении трубы; Q2 — поток жидкости в узком сечении трубыДля каждого вида местных сопротивлений существуют свои зависимости для определения коэффициента ξ.
К числу наиболее распространённых местных сопротивлений относятся внезапное расширение трубы, внезапное сужение трубы и поворот трубы.
1. При внезапном расширении трубы:
где S1 и S2 — площади поперечного сечения трубы, соответственно перед расширением и после него.
2. При внезапном сужении трубы коэффициент Дарси определяется по формуле:
Рис. 2. Зависимость коэффициента Дарси от угла δ поворота трубыгде S1 и S2 — площади поперечного сечения трубы, соответственно, перед сужением и после него.
3. При постепенном сужении трубы (конфузор):
,
где — степень сужения; λT — коэффициент потерь на трение по длине при турбулетном режиме.
4. При резком (без закругления) повороте трубы (колено) коэффициент Дарси определяется по графическим зависимостям (рис. 2).
См. также
Литература
- Гидравлика, гидромашины и гидроприводы: Учебник для машиностроительных вузов/ Т.М. Башта, С.С. Руднев, Б.Б. Некрасов и др. — 2-е изд., перераб. – М.: Машиностроение, 1982.
- Гейер В.Г., Дулин В.С., Заря А.Н. Гидравлика и гидропривод: Учеб для вузов. — 3-е изд., перераб. и доп. — М.: Недра, 1991.
Потери напора при движении жидкости
Потери напора при движении жидкости
- Подробности
- Категория: Гидравлика
Документальные учебные фильмы. Серия «Физика».
Гидравлические потери или гидравлическое сопротивление — безвозвратные потери удельной энергии (переход её в теплоту) на участках гидравлических систем (систем гидропривода, трубопроводах, другом гидрооборудовании), обусловленные наличием вязкого трения. Хотя потеря полной энергии — существенно положительная величина, разность полных энергий на концах участка течения может быть и отрицательной (например, при эжекционном эффекте).
Гидравлические потери принято разделять на два вида:
- потери на трение по длине — возникают при равномерном течении, в чистом виде — в прямых трубах постоянного сечения, они пропорциональны длине трубы;
- местные гидравлические потери — обусловлены т. н. местными гидравлическими сопротивлениями — изменениями формы и размера канала, деформирующими поток. Примером местных потерь могут служить: внезапное расширение трубы, внезапное сужение трубы, поворот, клапан и т. п.
Гидравлические потери выражают либо в потерях напора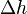 
в линейных единицах столба среды, либо в единицах давления 
: 
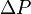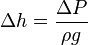, где 
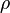— плотность среды, g — ускорение свободного падения.
Формула Дарси — Вейсбаха
Во многих случаях приближённо можно считать, что потери энергии при протекании жидкости через элемент гидравлической системы пропорциональны квадрату скорости жидкости. По этой причине удобно бывает характеризовать сопротивление безразмерной величиной ?, которая называется коэффициент потерь или коэффициент местного сопротивления и такова, что
То есть в предположении, что скорость w по всему сечению потока одинакова, ?=?p/eторм, где eторм = ?w?/2 — энергия торможения единицы объёма потока относительно канала. Реально в потоке скорость жидкости не равномерна, в справочной литературе в данных формулах принимается среднерасходная скорость w=Q/F, где Q — объёмный расход, F — площадь сечения, для которого рассчитывается скорость. Таким образом, средняя энергия торможения потока обычно несколько больше ?w?/2, см. Среднее квадратическое.
Для линейных потерь обычно пользуются коэффициентом потерь на трение по длине (также коэффициент Дарси) ?, фигурирующего в формуле Дарси — Вейсбаха
,
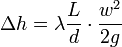,где L — длина элемента, d — характерный размер сечения (для круглых труб это диаметр). Иначе в единицах давления
- ;
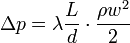;таким образом, для линейного элемента относительной длины L/d коэффициент сопротивления трения ?тр=?L/d.
По материалам Wikipedia
Гидравлические потери
Гидравлические потери или гидравлическое сопротивление — безвозвратные потери удельной энергии (переход её в теплоту) на участках гидравлических систем (систем гидропривода , трубопроводах , другом гидрооборудовании), обусловленные наличием вязкого трения . Хотя потеря полной энергии — существенно положительная величина, разность полных энергий на концах участка течения может быть и отрицательной (например, при эжекционном эффекте).
Гидравлические потери принято разделять на два вида:
- потери на трение по длине — возникают при равномерном течении, в чистом виде — в прямых трубах постоянного сечения, они пропорциональны длине трубы;
- местные гидравлические потери — обусловлены т. н. местными гидравлическими сопротивлениями — изменениями формы и размера канала, деформирующими поток. Примером местных потерь могут служить: внезапное расширение трубы, внезапное сужение трубы, поворот, клапан и т. п.
Гидравлические потери выражают либо в потерях напора в линейных единицах столба среды, либо в единицах давления : , где — плотность среды, g — ускорение свободного падения .
Коэффициенты потерь
Основная статья: Формула Дарси — Вейсбаха
Во многих случаях приближённо можно считать, что потери энергии при протекании жидкости через элемент гидравлической системы пропорциональны квадрату скорости жидкости . По этой причине удобно бывает характеризовать сопротивление безразмерной величиной ζ , которая называется коэффициент потерь или коэффициент местного сопротивления и такова, что
То есть в предположении, что скорость w по всему сечению потока одинакова, ζ=Δp /e торм, где e торм = ρw ²/2 — энергия торможения единицы объёма потока относительно канала. Реально в потоке скорость жидкости не равномерна, в справочной литературе в данных формулах принимается среднерасходная скорость w =Q /F , где Q — объёмный расход, F — площадь сечения, для которого рассчитывается скорость . Таким образом, средняя энергия торможения потока обычно несколько больше ρw ²/2, см. Среднее квадратическое .
Для линейных потерь обычно пользуются коэффициентом потерь на трение по длине (также коэффициент Дарси ) λ, фигурирующего в формуле Дарси — Вейсбаха
,где L — длина элемента, d — характерный размер сечения (для круглых труб это диаметр). Иначе в единицах давления
;таким образом, для линейного элемента относительной длины L /d коэффициент сопротивления трения ζ тр =λL /d .
Влияние режима течения в трубах на гидравлические потери
Поскольку при турбулентном режиме течения происходит расход энергии потока на преодоление вязкости при турбулентных колебаниях, гидравлические потери при ламинарном режиме течения жидкости значительно меньше, чем при турбулентном . Так, например, если бы в системах водоснабжения и отопления при существующих скоростях движения жидкостей возможно было бы поддерживать ламинарный режим течения, то напор насосов можно было бы уменьшить в 5-10 раз. Изменение режима течения с ламинарного на турбулентный вызывает скачкообразное увеличение сопротивления (при некоторых скоростях, т.е. в некотором диапазоне чисел Рейнольдса , ламинарное течение неустойчиво, но в определённых условиях может существовать). В то же время коэффициент гидравлического сопротивления при ламинарном режиме обычно получается больше, чем при турбулентном, поскольку для ламинарных режимов характерны более низкие скорости. При ламинарном режиме сопротивление примерно линейно зависит от скорости (соответственно, коэффициент примерно линейно падает, например, в круглых трубах ). При турбулентном режиме в гидравлически гладких трубах (при небольших шероховатостях и небольших Re) зависимость имеет иной характер (для круглых труб ) и во всех практически реализуемых случаях лежит выше зависимости для ламинарного режима; при бо́льших числах Рейнольдса под влиянием шероховатости график λ претерпевает сложный изгиб, и начиная с некоторого критического значения при Re>Re кр (область автомодельности) λ зависит только от шероховатости.
Лекция 6.
Потери удельной энергии (напора) , входящие в уравнение Бернулли
,
являются следствием гидравлических сопротивлений.
Гидравлически сопротивления – силытрения, появляющиеся в жидкости приее движении и вызывающие потери напора.
Определение потерь энергии потоком является одним из важнейших вопросов почти любого гидравлического расчета. Рассматривая этот вопрос, будем иметь в виду потерю энергии потоком, находящимся в неподвижном русле (труба, канал), обусловленную работой только сил трения (внешних и внутренних), возникающих в жидкости при ее движении. Именно эту потерю удельной энергии (потерю напора) учитывает уравнение Бернулли.
Различают два вида потерь напора:
Потери напора по длине, обозначаемые ;
Местные потери напора, обозначаемые .
Потеря напора по длине – та часть энергии потока, которая расходуется на преодоление трения в прямолинейных участках русел (трубе, канале), где движение жидкости равномерное или несколько нер
Потери
напора по длине иначе называют потерями
напора на трение, возникают в гладких
прямых трубах с постоянным сечением
при равномерном течении. Такие потери
обусловленны внутренним трением в
жидкости и поэтому происходит и в
шероховатых трубах, и в гладких. Основной
расчетной формулой для потерь напора
при ламинарном и турбулентном режиме
движения в круглых трубах является формула
Вейсбаха-Дарси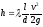 
V-средняя скорость движения
Коэффициент
трения зависит от числа Рейнольдса и
от безразмерного геометрического
фактора- относительной шероховатости 
(
—
абсолютное значение эквивалентной
шероховатости )
Коэффициент
трения при ламинарном режиме движения
жидкости 
Область турбулентного и переходного режимов разбиваются на 3 области :
1)
область гидравлически гладких труб 
2)
область доквадратического сопротивления
шероховатых труб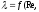 
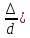
3)
область квадратичного сопротивления
шероховатых труб 
f 
При
турбулентном режиме движения жидкости
коэффициент движения определяется по
графику Мурина и по формуле Альтшуля
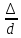относительная
шероховатость трубопровода
относительная
гладкость трубопровода
Величину абсолютной эквивалентной шероховатости при расчетах берут из справочника в зависимости от материала труб и состояния его внутренней поверхности.
12.Местные гидравлические сопротивления. Потери напора на местных сопротивлениях.
Местные сопротивления это такие участки трубопровода, на которых происходит деформация потока, т.е. происходит изменения скорости потока или по величине или по направлению.
К местным сопротивлениям относятся: вход и выход потока из трубы, внезапные сужения и расширения труб, плавные сужения и расширения труб колена, отводы, тройники, диафрагмы, регулирующие устройства (краны, вентили, задвижки и т.д)
Протекая через местное сопротивление, поток деформируется, возникают пульсации скоростей и давлений, образуются вихревые зоны с обратными токами вследствие отрыва потока от стенок трубопровода. На эти процессы смешения и вихреобразования тратится часть полной энергии потока, которая превращается в тепло и рассеивается в окружающее пространство.
Различают четыре вида местных сопротивлений
Местные сопротивления на которых происходит изменение скорости по величине (рис.25 на стр.52)
Местные сопротивления связанные с изменением направления движения жидкости (рис. 26 на стр.52)
Местные сопротивления на которых происходит смешение или разделение потока(рис.27 на стр. 53)
Трубопроводная арматура(краны, вентили, задвижки, расходомеры и т.п.)
Потери напора на местном сопротивлении рассчитываются в долях от величины скоростного напора:
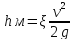
где
-коэффициент
местного сопротивления,
v-скорость движения жидкости, м/с
g-ускорение свободного падения, м/с^2
13.Виды потерь напора(давлений) в трубопроводах. Расчетные формулы.
Потери напора по длине потока. Иначе их называют потерями напора на трение, возникают в гладких прямых трубах с постоянным сечение при равномерном течении. Такие потери обусловлены внутренним трением в жидкости и поэтому происходят в шероховатых трубах, и в гладких.
где -коэффициент гидравлического трения,
l-длина трубопровода, м;
d-диаметр трубопровода, м;
v-средняя скорость движения жидкости, м/с;
g-ускорение свободного падения, м/с^2;
коэффициент
трения 
зависит от числа РейнольдсаRe(режима
движения жидкости) и от безразмерного
геометрического фактора-относительной
шероховатост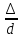и 
(или
-абсолютное
значение эквивалентной шероховатости)
коэффициент трения при ламинарном режиме движения жидкости рассчитывается по формуле:
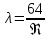
На практике при турбулентном режиме движения коэффициент трения может быть определен по графику Г.А.Мурина или рассчитан по формуле А.Д.Альтшуля:
Где Re-критерий Рейнольдса;
-коэффициент
трения;
-абсолютное
значение эквивалентной шероховатости,
м;
d- диаметр трубопровода, м;
Потери напорана местное сопротивления.
Потери напора на местном сопротивлении рассчитываются в долях от величины скоростного напора:
где
-коэффициент
местного сопротивления,
v-скорость движения жидкости, м/с
g-ускорение свободного падения, м/с^2
Принцип сложения потерь напора.
Как правило, трубопроводы имеют прямые участки и множество местных сопротивлений. Принцип сложения потерь напора заключается в том, что потери напора по длине и потери напора на местных сопротивлениях складываются, т.е общие потери напора:
т.е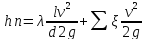 
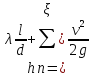
где где 
-коэффициент
гидравлического трения,
l-длина трубопровода, м;
d-диаметр трубопровода, м;
v-средняя скорость движения жидкости, м/с;
g-ускорение свободного падения, м/с^2;
-сумма
коэффициентов местных сопротивлений.
Часто
в расчетах требуется определить потерю
давления 
.
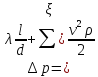
Потеря давления в трубопроводе на трение(для участка прямого трубопровода, длинного трубопровода), вычисляется по формуле
Расчет потерь на трение труб
Поток жидкости через трубу сдерживается вязкими сдвиговыми напряжениями внутри жидкости и турбулентностью, возникающей вдоль внутренней стенки трубы, которая зависит от шероховатости материала трубы.Это сопротивление называется трением в трубе и обычно измеряется в футах или метрах напора жидкости, поэтому его также называют потерей напора из-за трения в трубе.
Потеря головы в трубе
В течение многих лет было проведено большое количество исследований по созданию различных формул, которые могут рассчитывать потери напора в трубе.Большая часть этой работы была разработана на основе экспериментальных данных.
Общая потеря напора в трубе зависит от ряда факторов, которые включают вязкость жидкости, Размер внутреннего диаметра трубы, внутренняя шероховатость внутренней поверхности трубы, изменение высота между концами трубы и длиной трубы, по которой движется жидкость.
Клапаны и фитинги на трубе также вносят вклад в общую потерю напора, которая возникает, однако они должны рассчитываться отдельно от потерь на трение стенки трубы, используя метод моделирования потерь в фитингах трубы с k коэффициентами.
Дарси Вейсбах Формула
Формула Дарси или уравнение Дарси-Вейсбаха, как ее обычно называют, в настоящее время принята как наиболее точная формула потерь на трение в трубе, и, хотя с введением компьютеров, ее труднее рассчитать и использовать, чем другую формулу потерь на трение, она теперь стало стандартным уравнением для инженеров-гидравликов.
Вайсбах впервые предложил соотношение, которое мы теперь знаем как уравнение Дарси-Вейсбаха или формула Дарси-Вейсбаха, для расчета потерь на трение в трубе.2 / 2g)
где:
hf = потеря головы (м)
f = коэффициент трения
L = длина трубопровода (м)
d = внутренний диаметр трубопровода (м)
v = скорость жидкости (м / с)
г = ускорение силы тяжести (м / с²)
или:
hf = потеря напора (футы)
f = коэффициент трения
L = длина трубопровода (футы)
d = внутренний диаметр трубы (футы)
v = скорость жидкости (фут / с)
г = ускорение силы тяжести (фут / с²)
Однако установление факторов трения все еще не решено, и это действительно проблема, которая потребовалась дальнейшая работа для разработки решения, такого как решение, полученное по формуле Колебрука-Уайта, и данных, представленных в диаграмме Муди.
Диаграмма Муди
Диаграмма Муди наконец предоставила метод нахождения точного коэффициента трения, и это поощрило использование уравнения Дарси-Вейсбаха, которое быстро стало методом выбора для гидротехников.
Внедрение персонального компьютера с 1980-х годов сократило время Требуется рассчитать коэффициент трения и потери напора трубы. Это само расширило использование формулы Дарси-Вейсбаха до такой степени, что большинство других уравнений больше не используются.
Hazen-Williams Formula
До появления персональных компьютеров формула Хазена-Уильямса была чрезвычайно популярна среди инженеров по трубопроводам из-за ее относительно простых расчетных свойств.
Однако результаты Hazen-Williams основаны на значении коэффициента трения, C hw, который используется в формуле, и значение C может значительно варьироваться, от 80 до 130 и выше, в зависимости от материала трубы, размера трубы. и скорость жидкости.4,8655)
где:
hf = потеря головы в футах воды
L = длина трубы в футах
C = коэффициент трения
галлонов в минуту = галлонов в минуту (галлоны США, а не имперские галлоны)
d = внутренний диаметр трубы в дюймах
Эмпирическая природа коэффициента трения C hw означает, что формула Хазена-Вильямса не подходит для точного прогнозирования потери головы. Результаты потери на трение действительны только для жидкостей с кинематической вязкостью 1.13 сантистоков, где скорость потока составляет менее 10 футов в секунду, а диаметр трубы превышает 2 дюйма.
Примечания. Вода с температурой 60 ° F (15,5 ° C) имеет кинематическую вязкость 1,13 сСт.
Общий коэффициент трения Значения C hw, используемые для целей проектирования:
Асбестоцемент 140
Латунная труба 130
Чугунная труба 100
Бетонная труба 110
Медная труба 130
Гофрированная стальная труба 60
оцинкованная трубка 120
Стеклянная трубка 130
Свинцовый трубопровод 130
Пластиковая труба 140
Труба ПВХ 150
Общие гладкие трубы 140
Стальная труба 120
Трубы стальные клепаные 100
Чугунная труба с гудронированным покрытием 100
Жестяные трубки130
Деревянная Древесина 110
Эти значения C hw обеспечивают некоторый учет изменений шероховатости внутренней поверхности трубы из-за точечной коррозии стенки трубы при длительных периодах использования и накопления других отложений.
,потерь в трубах
На этой странице представлен краткий обзор потерь в трубопроводе, начиная с уравнения Бернулли
Основной подход ко всем системам трубопроводов состоит в том, чтобы написать уравнение Бернулли между двумя точками, соединенными линией тока, где условия известны. Например, между поверхностью резервуара и выходом трубы.
Общий напор в точке 0 должен совпадать с общим напором в точке 1, скорректированный с учетом любого увеличения напора из-за насосов, потерь из-за трения в трубе и так называемых «незначительных потерь» из-за входов, выходов, фитингов и т. Д.Развиваемый напор насоса, как правило, является функцией потока через систему, при этом подъем напора уменьшается с увеличением потока через насос.
Потери на трение в трубах
Потери на трение являются сложной функцией геометрии системы, свойств жидкости и скорости потока в системе. По наблюдениям потери напора примерно пропорциональны квадрату скорости потока в большинстве инженерных потоков (полностью развитый, турбулентный поток в трубе). Это наблюдение приводит к уравнению Дарси-Вейсбаха для потери головы из-за трения:
, который определяет коэффициент трения, ф.f нечувствителен к умеренным изменениям потока и постоянен для полностью турбулентного потока. Таким образом, часто бывает полезно оценить взаимосвязь, так как напор прямо пропорционален квадрату расхода для упрощения расчетов.
Номер Рейнольдса является основной безразмерной группой в вязком потоке. Скорость по шкале длины делится на кинематическую вязкость.
Относительная шероховатость связывает высоту типичного элемента шероховатости со шкалой потока, представленной диаметром трубы D.
Сечение трубы важно, так как отклонения от круглого сечения вызовут вторичные потоки, которые увеличат падение давления. Некруглые трубы и воздуховоды обычно обрабатывают с использованием гидравлического диаметра,
вместо диаметра и обрабатывая трубу, как будто она была круглой.
Для ламинарного потока потеря напора пропорциональна скорости, а не квадрату скорости, таким образом, коэффициент трения обратно пропорционален скорости.
Коэффициент геометрии k | |
| Площадь | 56,91 |
| Прямоугольник 2: 1 | 62,19 |
| Прямоугольник 5: 1 | 76,28 |
| параллельных пластин | 96,00 |
Число Рейнольдса должно основываться на гидравлическом диаметре.Блевинс (Руководство по прикладной гидродинамике, таблица 6-2, с. 43-48) приводит значения k для различных форм. Для турбулентного потока Colebrook (1939) нашел неявную корреляцию для коэффициента трения в круглых трубах. Эта корреляция хорошо сходится за несколько итераций. Конвергенция может быть оптимизирована путем небольшой недостаточной релаксации.
Знакомая диаграмма Муди представляет собой логарифмический график корреляции Колебрука по осям коэффициента трения и числа Рейнольдса в сочетании с f = 64 / Re результатом ламинарного потока.
Явное приближение
предоставляет значения в пределах одного процента от Colebrook в большей части полезного диапазона.
Расчет потери головы для известного расхода
Из Q и труб определяют число Рейнольдса, относительную шероховатость и, следовательно, коэффициент трения. Подставим в уравнение Дарси-Вейсбаха, чтобы получить потерю напора для данного потока. Подставьте в уравнение Бернулли, чтобы найти необходимую высоту или напор насоса.
Расчет расхода для известной головки
Получите допустимую потерю напора из уравнения Бернулли, затем начните с угадывания коэффициента трения.(0.02 — хорошее предположение, если у вас нет ничего лучше.) Рассчитайте скорость из уравнения Дарси-Вейсбаха. Исходя из этой скорости и характеристик трубопровода, рассчитайте число Рейнольдса, относительную шероховатость и, следовательно, коэффициент трения.
Повторяйте расчет с новым коэффициентом трения, пока не получите достаточную сходимость. Q = VA.
Вот видео, обсуждающее три типа проблем трубопровода:
«Малые потери»
Несмотря на то, что на них часто приходится большая часть потерь напора, особенно в технологических трубопроводах, дополнительные потери из-за входов и выходов, фитингов и клапанов традиционно называют небольшими потерями.Эти потери представляют собой дополнительное рассеяние энергии в потоке, обычно вызванное вторичными потоками, вызванными искривлением или рециркуляцией. Незначительные потери представляют собой любую потерю напора в дополнение к потере напора для такой же длины прямой трубы.
Как и в случае трения в трубе, эти потери примерно пропорциональны квадрату расхода. Определяя К, коэффициент потерь, по
позволяет легко интегрировать незначительные потери в уравнение Дарси-Вейсбаха.K является суммой всех коэффициентов потерь в длине трубы, каждый из которых вносит вклад в общую потерю напора.
Хотя K представляется постоянным коэффициентом, он изменяется в зависимости от условий потока. Факторы, влияющие на значение K, включают:
- точная геометрия рассматриваемого компонента
- поток Рейнольдса номер
- близость к другим фитингам и т. Д. (Табличные значения K относятся к изолированным компонентам — с длинными прямыми участками трубы выше и ниже по потоку.)
Некоторая очень базовая информация о значениях K для различных фитингов включена в эти примечания и в большинство вводных текстов по механике жидкости. Для более подробной информации, например, см. Блевинс, с. 55-88.
Для расчета потерь в системах трубопроводов с трением и незначительными потерями используйте
вместо уравнения Дарси-Вейсбаха. Процедуры одинаковы, за исключением того, что значения K также могут изменяться в ходе итерации.
,Некоторые таблицы потерь на трение
| Потери на трение в
Трубопроводная арматура Коэффициент сопротивления K (используйте в формуле hf = Kv 2 / 2g) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Фитинг | LD | Номинальный размер трубы | ||||||||||||
| 1/2 « | 3/4 « | 1 | 1-1 / 4 « | 1-1 / 2 « | 2 | 2-1 / 2 «-3 | 4 | 6 | 8-10 | 12-16 | 18-24 | |||
| К Значение | ||||||||||||||
| Угловой клапан | 55 | 1.48 | 1,38 | 1,27 | 1,21 | 1,16 | 1,05 | 0,99 | 0,94 | 0,83 | 0,77 | 0,72 | 0,66 | |
| Угловой клапан | 150 | 4,05 | 3,75 | 3,45 | 3,30 | 3,15 | 2,85 | 2,70 | 2,55 | 2,25 | 2,10 | 1,95 | 1,80 | |
| Шаровой кран | 3 | 0.08 | 0,08 | 0,07 | 0,07 | 0,06 | 0,06 | 0,05 | 0,05 | 0,05 | 0,04 | 0,04 | 0,04 | |
| Клапан-бабочка | 0,86 | 0,81 | 0,77 | 0,68 | 0,63 | 0,35 | 0,30 | |||||||
| Задвижка | 8 | 0.22 | 0,20 | 0,18 | 0,18 | 0,15 | 0,15 | 0,14 | 0,14 | 0,12 | 0,11 | 0,10 | 0,10 | |
| глобусный клапан | 340 | 9,2 | 8,5 | 7,8 | 7,5 | 7,1 | 6,5 | 6,1 | 5,8 | 5,1 | 4,8 | 4,4 | 4,1 | |
| Перепускной клапан Ветвь потока | 90 | 2.43 | 2,25 | 2,07 | 1,98 | 1,89 | 1,71 | 1,62 | 1,53 | 1,35 | 1,26 | 1,17 | 1,08 | |
| Заглушка клапана сразу | 18 | 0,48 | 0,45 | 0,41 | 0,40 | 0,38 | 0,34 | 0,32 | 0,31 | 0,27 | 0,25 | 0,23 | 0.22 | |
| Заглушка трехходовая сквозная | 30 | 0,81 | 0,75 | 0,69 | 0,66 | 0,63 | 0,57 | 0,54 | 0,51 | 0,45 | 0,42 | 0,39 | 0,36 | |
| Стандартный локоть | 90 ° | 30 | 0,81 | 0,75 | 0,69 | 0,66 | 0,63 | 0,57 | 0.54 | 0,51 | 0,45 | 0,42 | 0,39 | 0,36 |
| 45 ° | 16 | 0,43 | 0,40 | 0,37 | 0,35 | 0,34 | 0,30 | 0,29 | 0,27 | 0,24 | 0,22 | 0,21 | 0,19 | |
| длинный радиус 90 ° | 16 | 0,43 | 0,40 | 0,37 | 0.35 | 0,34 | 0,30 | 0,29 | 0,27 | 0,24 | 0,22 | 0,21 | 0,19 | |
| Закрыть Обратный изгиб | 50 | 1,35 | 1,25 | 1,15 | 1,10 | 1,05 | 0,95 | 0,90 | 0,85 | 0,75 | 0,70 | 0,65 | 0,60 | |
| Стандартный тройник | Thru-Flow | 20 | 0.54 | 0,50 | 0,46 | 0,44 | 0,42 | 0,38 | 0,36 | 0,34 | 0,30 | 0,28 | 0,26 | 0,24 |
| через филиал | 60 | 1,62 | 1,50 | 1,38 | 1,32 | 1,26 | 1,14 | 1,08 | 1,02 | 0,90 | 0,84 | 0,78 | 0,72 | |
| 90 изгибов, трубных отводов, фланцевых колен, сварных встык колен | р / д = 1 | 20 | 0.54 | 0,50 | 0,46 | 0,44 | 0,42 | 0,38 | 0,36 | 0,34 | 0,30 | 0,28 | 0,26 | 0,24 |
| р / д = 2 | 12 | 0,32 | 0,30 | 0,28 | 0,26 | 0,25 | 0,23 | 0,22 | 0,20 | 0,18 | 0,17 | 0,16 | 0,14 | |
| р / д = 3 | 12 | 0.32 | 0,30 | 0,28 | 0,26 | 0,25 | 0,23 | 0,22 | 0,20 | 0,18 | 0,17 | 0,16 | 0,14 | |
| р / д = 4 | 14 | 0,38 | 0,35 | 0,32 | 0,31 | 0,29 | 0,27 | 0,25 | 0,24 | 0,21 | 0,20 | 0,18 | 0,17 | |
| р / д = 6 | 17 | 0.46 | 0,43 | 0,39 | 0,37 | 0,36 | 0,32 | 0,31 | 0,29 | 0,26 | 0,24 | 0,22 | 0,20 | |
| р / д = 8 | 24 | 0,65 | 0,60 | 0,55 | 0,53 | 0,50 | 0,46 | 0,43 | 0,41 | 0,36 | 0,34 | 0,31 | 0,29 | |
| р / д = 10 | 30 | 0.81 | 0,75 | 0,69 | 0,66 | 0,63 | 0,57 | 0,54 | 0,51 | 0,45 | 0,42 | 0,39 | 0,36 | |
| р / д = 12 | 34 | 0,92 | 0,85 | 0,78 | 0,75 | 0,71 | 0,65 | 0,61 | 0,58 | 0,51 | 0,48 | 0,44 | 0,41 | |
| р / д = 14 | 38 | 1.03 | 0,95 | 0,87 | 0,84 | 0,80 | 0,72 | 0,68 | 0,65 | 0,57 | 0,53 | 0,49 | 0,46 | |
| р / д = 16 | 42 | 1,13 | 1,05 | 0,97 | 0,92 | 0,88 | 0,80 | 0,76 | 0,71 | 0,63 | 0,59 | 0,55 | 0,50 | |
| р / д = 18 | 45 | 1.24 | 1,15 | 1,06 | 1,01 | 0,97 | 0,87 | 0,83 | 0,78 | 0,69 | 0,64 | 0,60 | 0,55 | |
| р / д = 20 | 50 | 1,35 | 1,25 | 1,15 | 1,10 | 1,05 | 0,95 | 0,90 | 0,85 | 0,75 | 0,70 | 0,65 | 0,60 | |
| Mitt Bend | а = 0 ° | 2 | 0.05 | 0,05 | 0,05 | 0,04 | 0,04 | 0,04 | 0,04 | 0,03 | 0,03 | 0,03 | 0,03 | 0,02 |
| а = 15 ° | 4 | 0,11 | 0,10 | 0,09 | 0,09 | 0,08 | 0,08 | 0,07 | 0,07 | 0,06 | 0,06 | 0,05 | 0,05 | |
| а = 30 ° | 8 | 0.22 | 0,20 | 0,18 | 0,18 | 0,17 | 0,15 | 0,14 | 0,14 | 0,12 | 0,11 | 0,10 | 0,10 | |
| а = 45 ° | 15 | 0,41 | 0,38 | 0,35 | 0,33 | 0,32 | 0,29 | 0,27 | 0,26 | 0,23 | 0,21 | 0,20 | 0,18 | |
| а = 60 ° | 25 | 0.68 | 0,63 | 0,58 | 0,55 | 0,53 | 0,48 | 0,45 | 0,43 | 0,38 | 0,35 | 0,33 | 0,30 | |
| а = 75 ° | 40 | 1,09 | 1,00 | 0,92 | 0,88 | 0,84 | 0,76 | 0,72 | 0,68 | 0,60 | 0,56 | 0,52 | 0,48 | |
| а = 90 ° | 60 | 1.62 | 1,50 | 1,38 | 1,32 | 1,26 | 1,14 | 1,08 | 1,02 | 0,90 | 0,84 | 0,78 | 0,72 | |
| Примечание: Фитинги стандартные с полными отверстиями. | ||||||||||||||
| Фитинг | L / D | Минимальная скорость для полного подъема диска | Номинальный размер трубы | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1/2 « | 3/4 « | 1 | 1-1 / 4 « | 1-1 / 2 « | 2 | 2-1 / 2 «-3 | 4 | 6 | 8-10 | 12-16 | 18-24 | ||||
| Общее фут / с | Вода фут / сек | К Значение | |||||||||||||
| 100 | 35 | 4.40 | 2,70 | 2,50 | 2,30 | 2,20 | 2,10 | 1,90 | 1,80 | 1,70 | 1,50 | 1,40 | 1,30 | 1,20 | |
| 50 | 48 | 6,06 | 1,40 | 1,30 | 1,20 | 1,10 | 1,10 | 1,00 | 0,90 | 0,90 | 0,75 | 0,70 | 0.65 | 0,60 | |
| подъемный обратный клапан | 600 | 40 | 5,06 | 16,2 | 15.0 | 13,08 | 13,2 | 12,6 | 11,4 | 10,8 | 10,2 | 9,0 | 8,4 | 7,8 | 7,2 |
| 55 | 140 | 17,7 | 1,50 | 1,40 | 1,30 | 1,20 | 1.20 | 1,10 | 1,00 | 0,94 | 0,83 | 0,77 | 0,72 | 0,66 | |
| Обратный клапан наклона диска | 5 | 80 | 10,13 | 0,76 | 0,72 | 0,68 | 0,60 | 0,56 | 0,39 | 0,24 | |||||
| 15 | 30 | 3.80 | 2,30 | 2,20 | 2,00 | 1,80 | 1,70 | 1,20 | 0,72 | ||||||
| с ситом тарельчатый диск | 420 | 15 | 1,90 | 11,3 | 10,5 | 9,70 | 9,30 | 8.80 | 8,00 | 7,60 | 7,10 | 6.30 | 5,90 | 5,50 | 5,0 |
| с сетчатым фильтром Шарнирный диск | 75 | 35 | 4,43 | 2,00 | 1,90 | 1,70 | 1,70 | 1,70 | 1,40 | 1,40 | 1,30 | 1,10 | 1,10 | 1,00 | 0,90 |
| Фитинг | Описание | Все размеры труб |
|---|---|---|
| К Значение | ||
| Трубный выход | Проектирование с острыми краями Закругленный | 1.00 |
| Трубный вход | Внутреннее Проектирование | 0,78 |
| Труба входная флеш | с острыми краями | 0,50 |
| р / д = 0,02 | 0,28 | |
| р / д = 0,04 | 0,24 | |
| р / д = 0,06 | 0,15 | |
| р / д = 0,10 | 0,09 | |
| р / д <0,14 | 0,04 |
Значения K, приведенные ниже, предназначены для оценки потерь на трение в случаи, не охваченные в предыдущих таблицах.
| Тип фитинга | К Значение | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Диск или Колебания | 3,4 — 10 | ||||||||||
| Роторный Метр (Поршень Звезды или Зубчатого колеса) | 10 | ||||||||||
| поршневой поршневой метр | 15 | ||||||||||
| турбинный (двухпоточный) расходомер | 5 — 7,5 | ||||||||||
| отводов с гофрированным внутренним радиусом | 1,3 — 1,6 раза значение для плавного изгиба | ||||||||||
| Пример: Определить L
(потеря трения в фитингах в пересчете на эквивалентную длину футов прямой трубы). Предположим, что 6-дюймовый угловой клапан для трубы размера 40 соответствует. Выберите соответствующее значение K для этого и выберите D и f для трубы расписания 40 из таблицы ниже, где K — диаметр трубы в футах. | |||||||||||
| Размер трубы дюймов Sch. 40 | D футов | f | Размер трубы дюймов Sch. 40 | D футов | f | Размер трубы дюймов Sch. 40 | D футов | f | Размер трубы дюймов Sch.40 | D футов | f |
| 1/2 « 3/4″ 1 1-1 / 4 « 1-1 / 2″ 2 | 0,0518 0,0687 0,0874 0,1150 0,1342 0,1723 | 0,027 0,025 0,023 0,022 0,021 0,019 | 2-1 / 2 « 3 4 5 6 8 | 0,2058 0,2557 0,3355 0,4206 0,5054 0,6651 | 0,018 0,018 0,017 0,016 0.015 0,014 | 10 12 14 16 18 20 | 0,8350 0,9948 1,0937 1,250 1,4063 1,5678 | 0,014 0,013 0,013 0,013 0,012 0,012 | 24 30 36 42 48 | 1.8857 2.3333 2.8333 3.3333 3.8333 | 0,012 0,011 0,011 0,010 0,010 |
| Потеря трения воды в
Трубные фитинги в пересчете на эквивалент Длина — футы прямой трубы | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Номинальный размер трубы | Фактический внутри диаметр дюймов d | коэффициент трения f | Вентиль , клапан — , полный , открытый | 90 ° колено | Long радиус 90 ° или 45 ° sth колено | Sth тройник — через поток | Sth тройник — ветвь поток | Закрыть возврат изгиб | Свинг , обратный клапан , — , полностью открыт, | Угол клапан — полный открыт | Клапан Globe , — , полный клапан , | Масло- клапан с обратным клапаном | 90 ° Сварка Колено | Mit Bend | ||
| р / д = 1 | р / д = 2 | 45 ° | 90 ° | |||||||||||||
| 1/2 « 3/4″ 1 1-1 / 4 « 1-1 / 2″ | 622 .824 1,049 1,380 1,610 | .027 .025 .023 .022 .021 | ,41 .55 .70 .92 1,07 | 1,55 2,06 2,62 3,45 4,03 | ,83 1,10 1,40 1,84 2,15 | 1,04 1,37 1,75 2,30 2,68 | 3.11 4.12 5.25 6.90 8.05 | 2,59 3,43 4,37 5,75 6,71 | 5.18 6,86 8,74 11,5 13,4 | 7,78 10,3 13,1 17,3 20,1 | 17,6 23,3 29,7 39,1 45,6 | |||||
| 2 2-1 / 2 « 3 4 5 | 2,067 2,446 3,068 4,026 5,047 | .019 .018 .018 .017 .016 | 1,38 1,65 2,04 2.68 3,36 | 5,17 6,17 7,67 10,1 12,6 | 2,76 3,29 4,09 5,37 6,73 | 3,45 4,12 5,11 6,71 8,41 | 10,3 12,3 15,3 20,1 25,2 | 8,61 10,3 12,8 16,8 21,0 | 17,2 20,6 25,5 33,6 42,1 | 25,8 30,9 38,4 50,3 63,1 | 58,6 70,0 86,9 114 143 | 7.75 9,26 11,5 15,1 18,9 | 3,45 4,12 5,11 6,71 8,41 | 2,07 2,47 3,07 4,03 5,05 | 2,58 3,08 3,84 5,03 6,31 | 10,3 12,3 15,3 20,1 25,2 |
| 6 8 10 12 14 | 6,065 7,981 10,02 11,938 13,124 | .015 .014 .014 .013 .013 | 4.04 5,32 6,68 7,96 8,75 | 15,2 20,0 25,1 29,8 32,8 | 8,09 10,6 13,4 15,9 17,5 | 10,1 13,3 16,7 19,9 21,8 | 30,3 39,9 50,1 59,7 65,6 | 25,3 33,3 41,8 49,7 54,7 | 50,5 33,3 41,8 49,7 54,7 | 75,8 99,8 125 149 164 | 172 226 284 338 372 | 22.7 29,9 29,2 34,8 38,3 | 10,1 13,3 16,7 19,9 21,8 | 6,07 7,98 10,0 11,9 13,1 | 7,58 9,98 12,5 14,9 16,4 | 30,3 39,9 50,1 59,7 65,6 |
| 16 18 20 24 30 | 15,00 16,876 18,814 22,628 28 | ,013 ,012 ,012 0,12 ,011 | 10.0 16,9 12,5 15,1 18,7 | 37,5 42,2 17,0 56,6 70 | 20,0 22,5 25,1 30,2 37,3 | 25,0 28,1 31,4 37,7 46,7 | 75,0 84,4 94,1 113 140 | 62,5 70,3 78,4 94,3 117 | 62,5 70,3 78,4 94,3 | 188 210 235 283 | 425 478 533 641 | 31.3 35,2 39,2 47,2 | 25,0 28,1 31,4 37,7 46,7 | 15,0 16,9 18,8 22,6 28 | 18,8 21,1 23,5 28,3 35 | 75,0 84,4 94,1 113 140 |
| 36 42 48 | 34 40 46 | .011 .010 .010 | 22,7 26,7 30,7 | 85 100 115 | 45.3 53,3 61,3 | 56,7 66,7 76,7 | 170 200 230 | 142 167 192 | 56,7 66,7 76,7 | 34 40 46 | 43 50 58 | 170 200 230 | ||||
| L / D | 8 | 30 | 16 | 20 | 60 | 50 | 1/2 «до 6 = 100 от 24 до 48 = 50 | 150 | 340 | 20 | 12 | 15 | 60 | |||
вернуться наверх ↑
,