Путь движения: Путь движения, 10 (десять) букв

Содержание

Путь Движения 10 Букв — ответ на кроссворд и сканворд

Решение этого кроссворда состоит из 10 букв длиной и начинается с буквы Т

Ниже вы найдете правильный ответ на Путь движения 10 букв, если вам нужна дополнительная помощь в завершении кроссворда, продолжайте навигацию и воспользуйтесь нашей функцией поиска.

ответ на кроссворд и сканворд

Вторник, 5 Ноября 2019 Г.

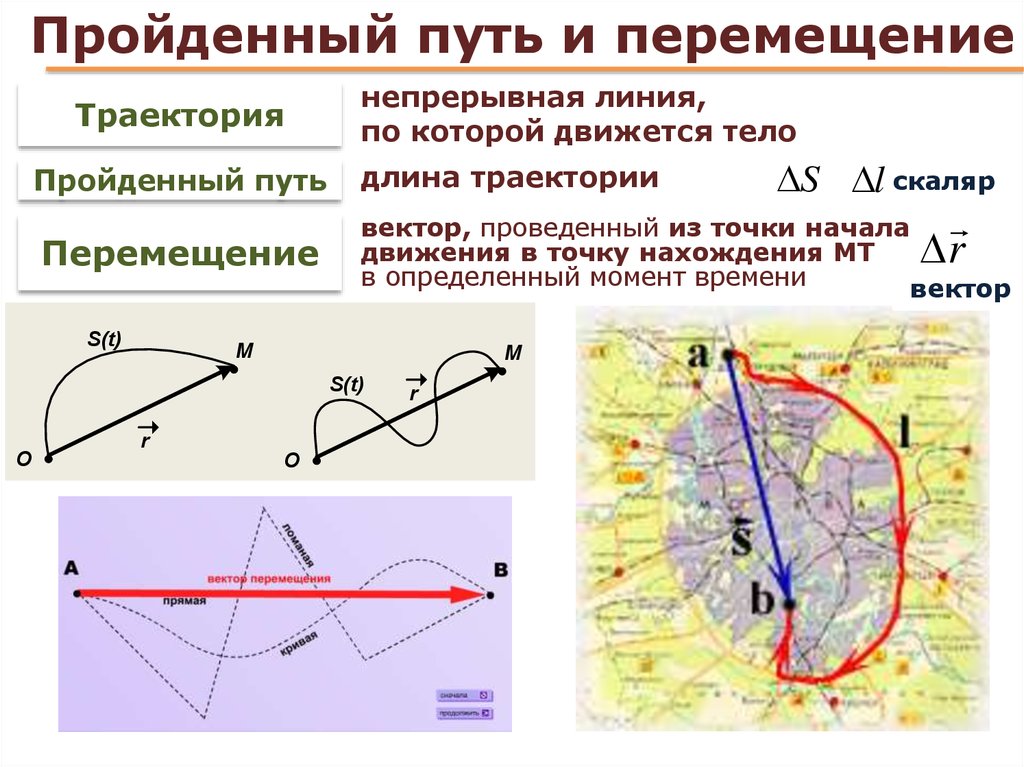
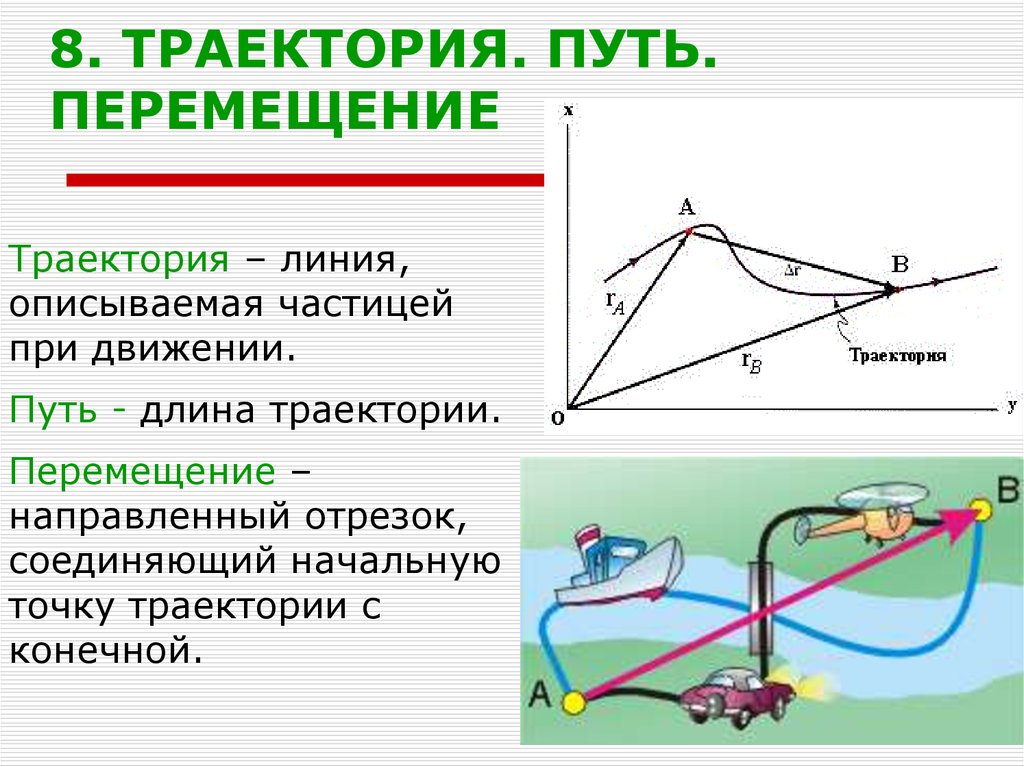
ТРАЕКТОРИЯ

предыдущий следующий

другие решения

ТРАЕКТОРИЯ

ты знаешь ответ ?

ответ:

связанные кроссворды

Траектория

Линия движения какого-нибудь тела или точки 10 букв
Линия полета пули, снаряда, ракеты 10 букв
Линия полета снаряда, пули, мины и т. п 10 букв
Линия 10 букв
Линия, являющаяся «следом» движущегося тела (точки) 10 букв
Линия движения тела или точки 10 букв

Глава 1.

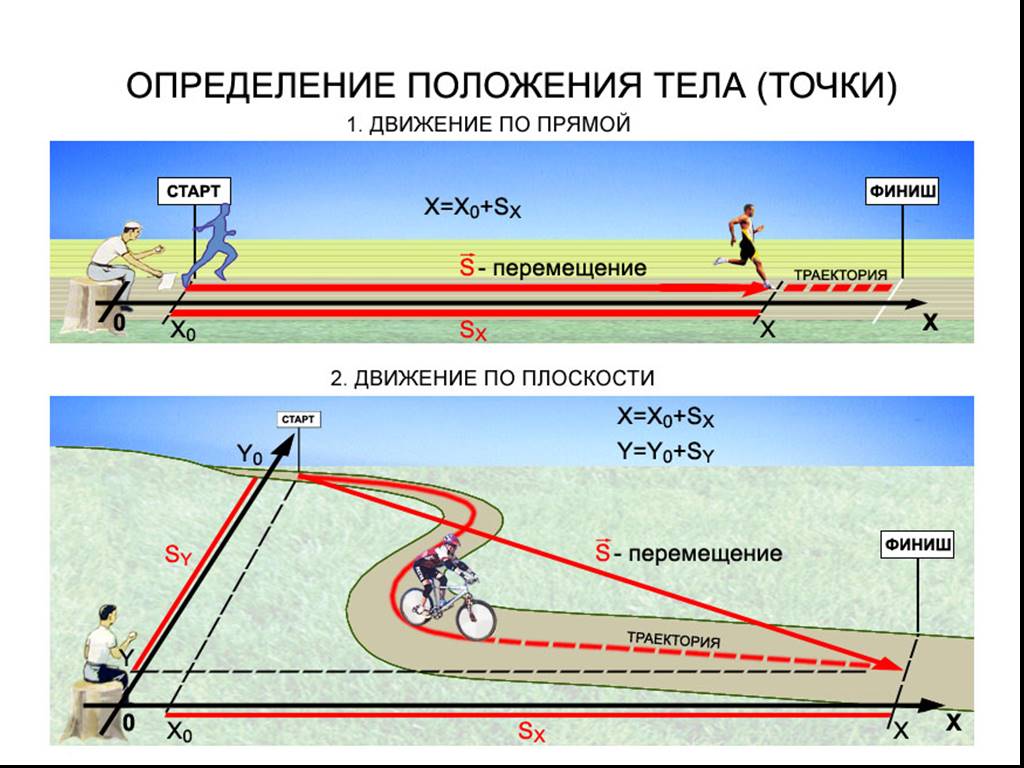Путь, перемещение, скорость. Движение с постоянной скоростью. Относительность движения

В рамках этой темы необходимо знать ряд простых определений, понимать логику определения скорости и закона сложения скоростей.

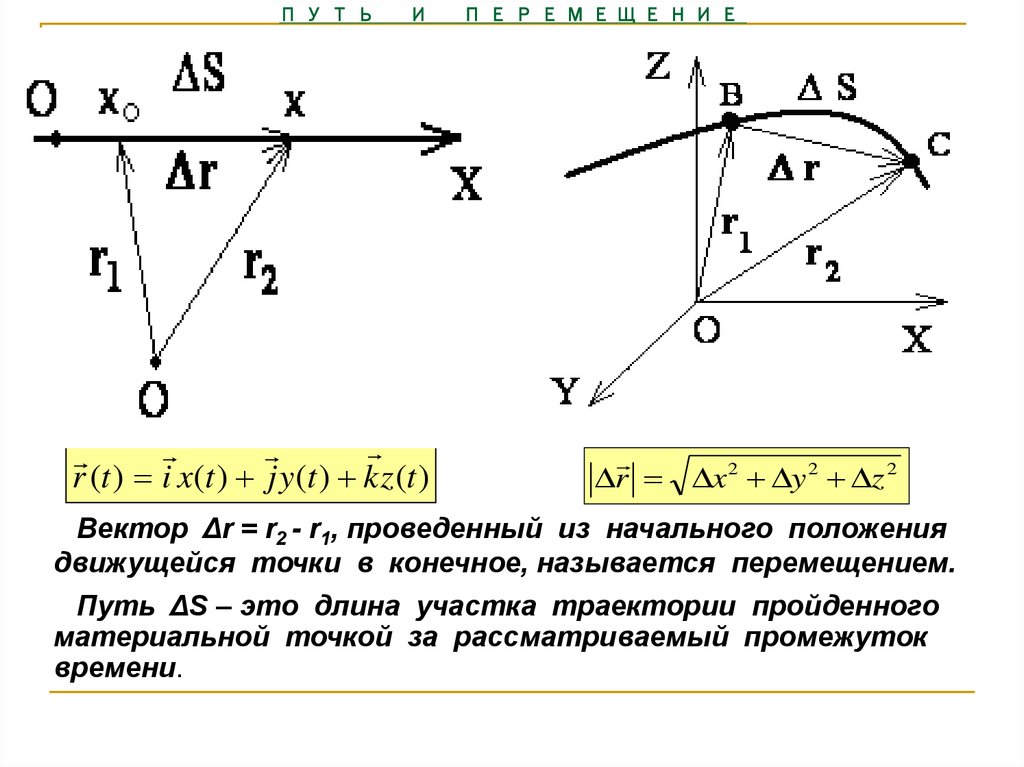
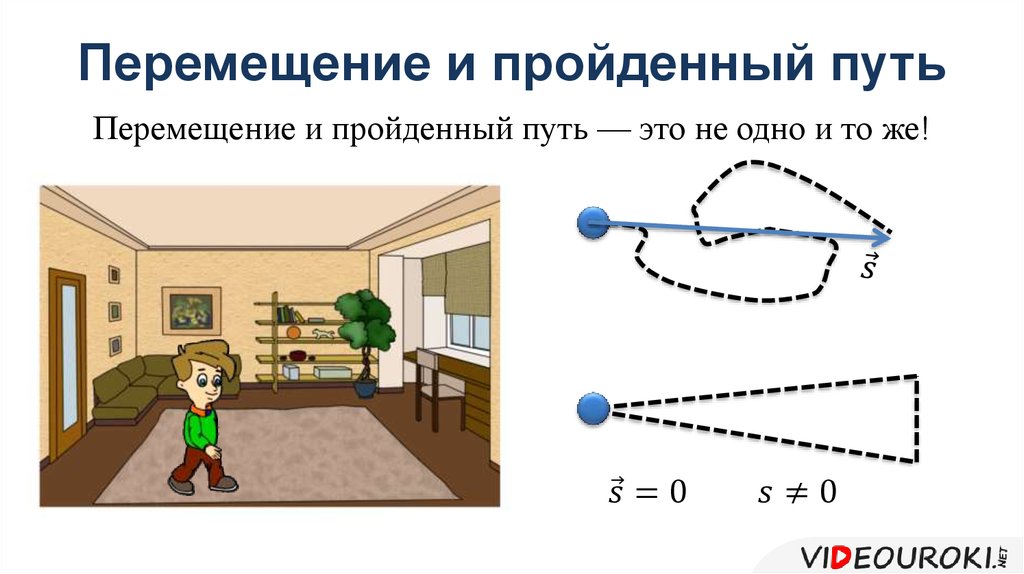
Перемещением тела называется вектор, связывающий начальное и конечное положение тела, а пройденным путем — длина траектории. Поэтому величина(или модуль) перемещения — это расстояние от конечной до начальной точки по прямой, а путь — расстояние траектории тела. В задаче 1.1.1 пройденный телом за четверть периода путь — длина четверти окружности , перемещение — (см. рисунок), правильный ответ —

Скорость тела определяется как отношение перемещения тела ко времени , затраченному на это перемещение

(1.1)

Для прямолинейного движения в одном направлении для величины вектора скорости получаем из (1.1)

(1. 2)

где — путь, пройденный за время . Если определение (1.1) приводит к одной и той же величине для любого интервала времени , то скорость тела есть величина постоянная, а такое движение называется равномерным (задача 1.1.2 — ответ 4). В этом случае согласно (1.1) и (1.2) перемещение и пройденный путь линейно зависят от времени и . По этой причине линейно зависят от времени и координаты тела в любой системе координат. Поэтому графиком зависимости координат тела от времени для равномерного движения является прямая (

задача 1.1.3 — ответ 1). Как следует из (1.1), (1.2), наклон этой прямой определяется скоростью: чем больше скорость, тем «круче» наклонен график зависимости координаты тела от времени к оси времени. Поэтому в задаче 1.1.4 на каждом из интервалов времени — от 0 до 1 с, от 1 до 2 с, от 2 до 3 с и от 3 до 4 с движение тела будет равномерным, а самой большой скорость тела будет в интервале времени от 3 до 4 с, в котором наклон графика максимален (ответ 4).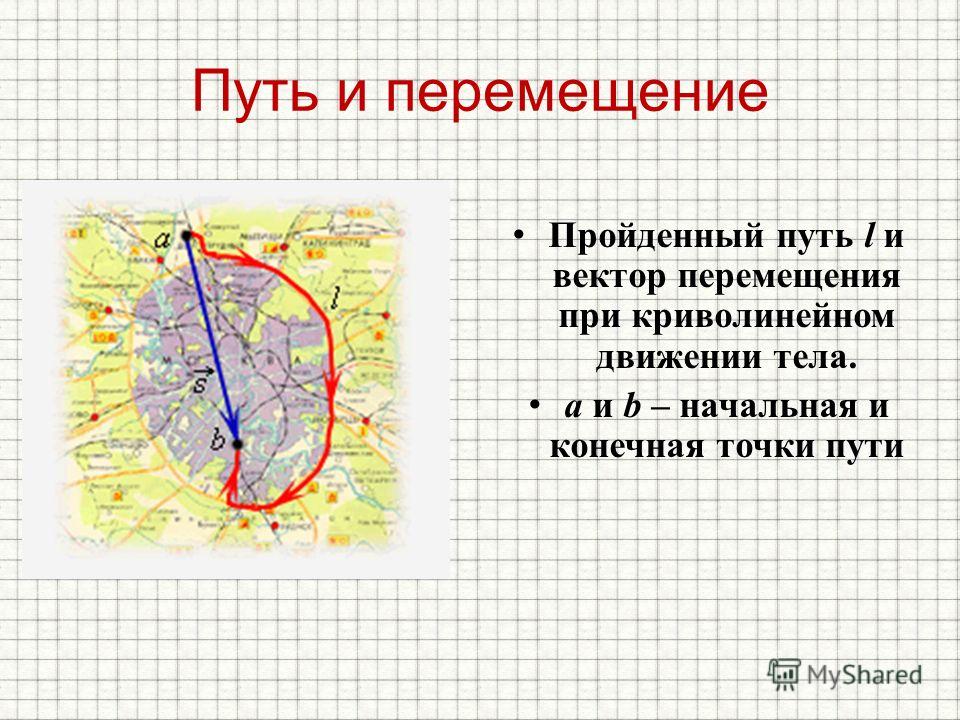

В задаче 1.1.5 нужно по графику зависимости координаты тела от времени найти его скорость. Это можно сделать так. Перемещение тела внутри каждого из интервалов времени — 0–1, 1–2 и 2–3 с — разность координат тела вначале и в конце этого интервала. Поэтому из графика находим

Таким образом, скорость тела равна 2 м/с внутри интервала времени 1–2 с (ответ 2).

Задача 1.1.6 посвящена размерности скорости. Из определения заключаем, что размерность скорости есть

И, следовательно, размерностью скорости могут быть

(или любые другие отношения единиц расстояний и времени). Для пересчета скорости из одних единиц в другие нужно выразить расстояние и время в требуемых единицах. Например, в задаче 1.1.6 имеем

(правильный ответ — 3).

При движении с постоянной скоростью определения (1.1) или (1.2) могут быть применены к любым этапам движения. Например, в задаче 1.1.7 можно из данных о движении жука вдоль периметра прямоугольника найти его скорость (=14/7=2 см/с), а затем использовать ее для описания движения жука вдоль диагонали (длина которой составляет 5 см): ₁=5/2=2,5 с (правильный ответ 2).

Аналогичные соотношения используются в задаче 1.1.8. Рассматривая движение автомобиля на одной трети пути, получаем , где — расстояние между городами. А на оставшихся двух третях (с учетом трехкратного увеличения скорости) ₁. Поэтому полное время движения равно (ответ 1).

В задаче 1.1.9 следует использовать следующее свойство графика зависимости проекции скорости тела на некоторую ось от времени: площадь под этим графиком есть проекция перемещения тела на рассматриваемую ось. Причем площадь под участками графика, лежащими выше оси времени, нужно считать положительной, ниже оси времени — отрицательной. Если же все площадь под всеми участками графика считать положительной, площадь под графиком скорости дает пройденный телом путь. Находя площадь под данным в условии графиком, получаем

(ответ — 4).

Важным физическим законом, знание которого часто проверяется на едином государственном экзамене по физике, является закон сложения скоростей.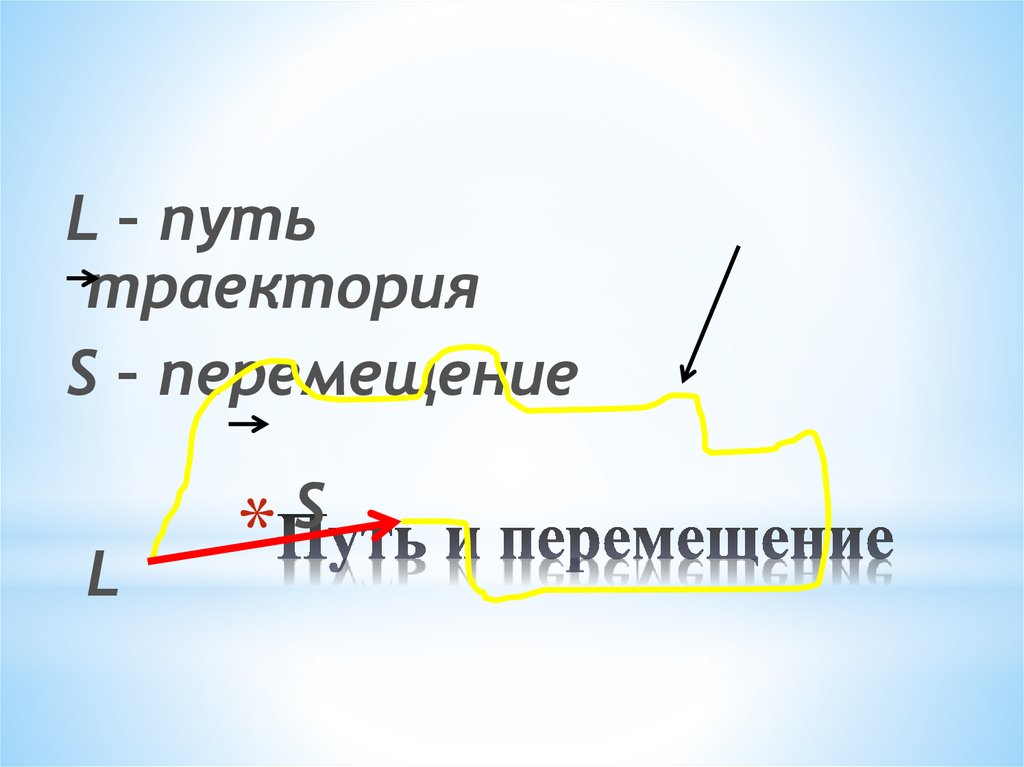

Этот закон утверждает, что скорости одного и того же тела по отношению к разным системам отсчета связаны соотношением

(1.3)

Здесь и — скорости тела относительно первой и второй системы отсчета, — скорость второй системы отсчета относительно первой. Закон сложения скоростей является векторным. Это означает, три вектора , и образуют треугольник векторного сложения, и соотношение между величинами скоростей , и — такое же, как и между длинами сторон треугольника. Углы этого треугольника равны углам между направлениями скоростей , и .

Примеры треугольников сложения скоростей приведены на рисунке, причем на среднем и правом рисунке приведены примеры «треугольников» скоростей в случаях, когда скорость тела в системе 2 и скорость системы 2 относительно системы 1 направлены одинаково (средний рисунок) и противоположно (правый рисунок). Из этих рисунков следует, что скалярное соотношение, аналогичное (1.

3) для величин скоростей , справедливо только, если векторы и направлены одинаково (средний рисунок). Если же векторы и направлены противоположно, для значений скоростей справедливо соотношение (или наоборот , если — правый рисунок. Из этих рассуждений ясно, что поскольку в задаче 1.1.10 векторы скорости пассажира относительно поезда и поезда относительно земли направлены одинаково, скорость пассажира относительно земли равна (правильный ответ — 2). В задаче 1.2.1 ситуация обратная — вектор скорости первой машины относительно земли и второй машины относительно земли направлены противоположно. Поэтому , направлен вектор на север — правильный ответ 4.

В задаче 1.2.2 эти идеи применяются к движению лодки по и против течения. Из закона сложения скоростей заключаем, что при движении лодки по течению ее скорость относительно земли равна , при движении против течения — ( — скорость лодки в стоячей воде, — скорость течения). Отсюда находим, что при движении лодки по течению, ее скорость относительно земли 15 км/ч, а при движении против течения — 5 км/ч.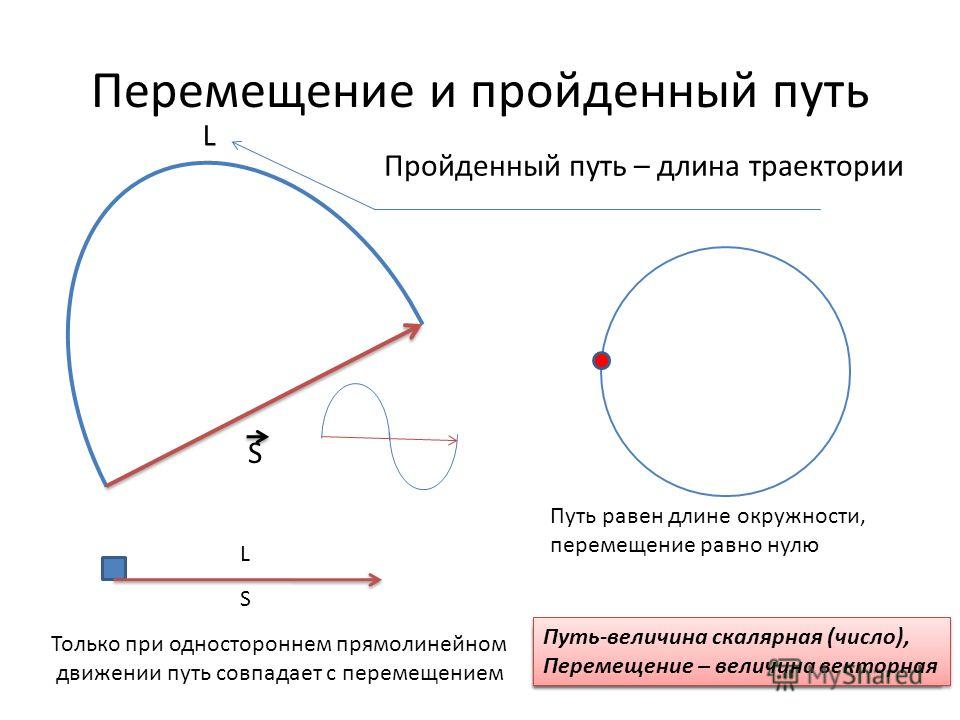 Поэтому время движения между городами и по течению втрое больше времени движения лодки между этими городами против течения (ответ — 2).

Все следующие задачи этой главы являются более сложными, поскольку в них рассматривается движение не одного, а двух тел, а закон сложения скоростей используется в случаях, когда векторы скоростей не направлены вдоль одной прямой. В задаче 1.2.3 встреча тел происходит в такой точке, что расстояния, пройденные первым и вторым телом, отличаются втрое (так как в три раза отличаются скорости тел). Поэтому при выходе из точки тела встретятся в такой точке , что длины дуг отличаются в три раза. Следовательно, угол — прямой, и длина отрезка равна . (ответ 4).

Если два тела, начав движение одновременно, движутся навстречу друг другу (задача 1.2.4), то время встречи тел можно найти следующим образом. Так как тела двигались до встречи одинаковое время, они прошли расстояния и , сумма которых равна первоначальному расстоянию между телами . Поэтому (ответ 2). Отметим, что данные в условии задачи ответы 3 и 4 имеют неправильную размерность — 1/с и потому могут быть отброшены сразу. Задача 1.2.5 решается с помощью таких соображений: время движения первого пешехода между городами , второго — , встречи пешеходов (см. предыдущую задачу). Отсюда

Сокращая в этой формуле величину , получаем

или ч (правильный ответ — 1).

В задаче 1.2.6 начальное и конечное положения вагона и человека показаны на правой и левой частях рисунка.

Отсюда заключаем, что разность перемещений вагона и человека равна длине вагона . Поэтому время, через которое провожающий окажется около конца вагона, определяется из соотношения . Из этой формулы находится время, а затем и расстояние, пройденное провожающим (ответ 1). Отметим, что ответы 3 и 4 могли быть отброшены сразу, поскольку не описывают случай одинаковых скоростей. Действительно, при одинаковых скоростях вагон никогда не обгонит провожающего, и расстояние, пройденное при «обгоне» провожающим, должно обратиться в бесконечность.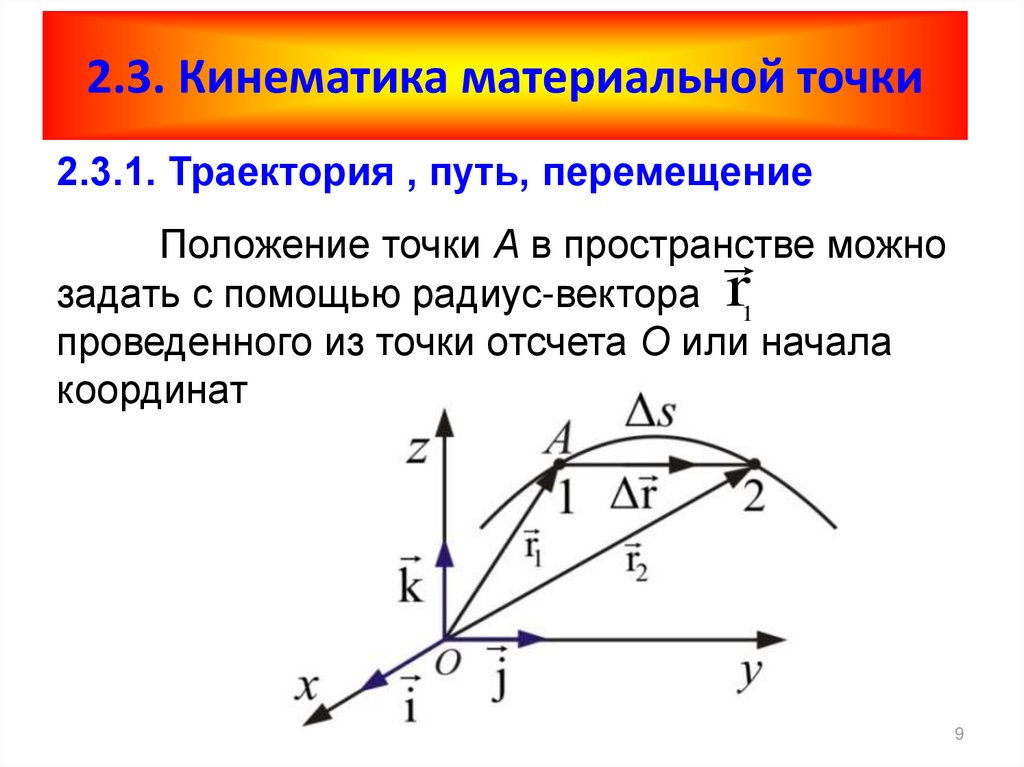 Другими словами, ответ должен содержать нуль в знаменателе при .

Задача 1.2.7 посвящена вычислению средней скорости движения на некотором пути, которая определяется как отношение этого пути к затраченному времени. Если расстояние между городами и равно , то полное время движения между городами складывается из времен, затраченных на первую и вторую половины пути

Отсюда находим км/ч (правильный ответ — 3).

В задачах 1.2.8–1.2.9 закон сложения скоростей рассматривается в ситуациях, когда векторы , и направлены не вдоль одной прямой. В этом случае необходимо использовать закон сложения скоростей в векторной форме (1.3). Когда человек в поезде идет перпендикулярно направлению его движения (задача 1.2.8), треугольник сложения скоростей (1.3) имеет вид, показанный на рисунке.

Здесь — вектор скорости поезда относительно земли, — вектор скорости человека относительно поезда, который по условию направлен перпендикулярно вектору . Поэтому согласно закону сложения скоростей вектор скорости человека относительно земли представляет собой гипотенузу прямоугольного треугольника, катетами которого являются векторы и (см. рисунок). Следовательно, величину скорости человека относительно земли можно найти по теореме Пифагора (ответ 3).

Задачи 1.2.9. и 1.2.10 удобнее решать, переходя из той системы отсчета, в которой задача поставлена (в системе отсчета, связанной с землей) в некоторую другую систему, в которой рассматриваемое явление является более простым. При переправе через реку (задача 1.2.9) скорость лодки относительно земли зависит от траектории — на траекториях, направленных под острыми углами к течению, скорость лодки больше, чем на траекториях, на которых угол между скоростью лодки и скоростью течения — тупой. Поэтому время переправы по самой короткой траектории (перпендикулярной берегам) не является минимальным. Траекторию с минимальным временем переправы легко найти в системе отсчета, связанной с водой. В этой системе отсчета вода покоится, и, следовательно, минимальное время переправы достигается на такой траектории, на которой вектор скорости лодки относительно воды перпендикулярен берегам реки. Поэтому вектор скорости лодки относительно земли на этой траектории наклонен под углом к течению (см. рисунок). Под таким углом к берегу и расположена траектория, на переправу по которой лодка затрачивает минимальное время (правильный ответ — 1).

В задаче 1.2.10 рассматривается движение трех тел. В системе отсчета, связанной с землей ответ неочевиден. Быстрый катер дольше уплывет от лодки, но будет двигаться быстрее и при обратном движении, медленный — наоборот. Однако если перейти в систему отсчета, связанную с водой, решение очень несложно. В этой системе отсчета плот покоится, каждый катер при движении от плота и к плоту движется с одинаковой скоростью. Поэтому каждый катер вернется к плоту через то же самое время после разворота, в течение которого он двигался от плота. Следовательно, катера вернутся одновременно (ответ 3).

путь определения движения | Словарь определений английского языка

n pl , пути

1 дорога или путь, особ. узкая протоптанная тропа

2 прогулка по покрытию, как по саду

3 курс или направление, в котором что-то движется
путь вихря

4 образ поведения 90 006 путь добродетели0006 (древнеанглийский pæth; родственный древневерхненемецкому, немецкому Pfad)
♦ бездорожье прил

уздечка
n путь, подходящий для верховой езды или поводка для лошадей, (также называемый (Н.З.)) bridle track

анализ критического пути
      n   метод планирования сложных проектов путем анализа альтернативных систем со ссылкой на критический путь, который представляет собой последовательность этапов, требующих наибольшего времени
   Сравнить     → Техника оценки и обзора программы

ПАТИ
N Вращаемая полоса, освещенная для использования ночью или в плохую погоду

ЛЕТА снаряд
Сравнить → подход → 10 → глиссада

ГЛИД -ПАТИ
N Путь к воздушным судам при посадке, обычно определяемый радиолокационным пучком

Средний свободный путь
N Среднее расстояние, пройденное частица, атом и т. Д. , между столкновениями

путь.
сокр. для

1 патология

2 патология

-Path
N Объединение формы

1, обозначающее человека, страдающего от указанного заболевания или расстройства
Neuropath

2, обозначающий практикующий врач конкретного метода лечения
. путь первоцвета
n часто предшествует: the приятный образ жизни

буксировочный путь
n другое имя для → тропинка

Английский словарь Коллинза — определение английского языка и тезаурус &nbsp

Смотрите также:

-траектория, траектория уздечки, траектория раструба, траектория полета

Collaborative Dictionary Определение английского языка


н.	лишать кого-либо или что-либо свободы передвижения или личной свободы.
н.	движение за права мужчин
эксп.	выражение, означающее, что у нескольких или всех членов семьи есть что-то общее (навык, черта, путь или поведение)	Например: Он тоже стал актером. Это наследственное.
в.	встретиться; пересекаются жизни друг друга; быть собраны вместе	Например: Их пути пересеклись пятнадцать лет назад, и с тех пор они лучшие друзья.
прил.	без дыхательных движений	дыхательная пауза, остановка дыхания
н.	упражнение, состоящее в контролируемом движении вниз и/или вперед, используемое для силовых тренировок
нф.	Mozette /moz-ette/ 1. Движение культа личности. 2. Женское обожание Стивена П. Моррисси. 3. Последователи харизматичного лидера с нарциссическими чертами, проявляющие необычайное количество энергии.
н.	Термин, используемый в футболе, когда игрок выполняет акробатическое движение ногами.
эксп.	Британское культурное движение, возникшее в конце 19 в.50-е и начало 1960-х в театре, романах, фильмах и т. д.	[Великобритания]; [Кино] например, «Оглянись в гневе» Джона Осборна.
н.	инновационная парадигма, предполагающая, что фирмы должны использовать внешние идеи и/или внешние пути выхода на рынок в своем инновационном процессе	[Tech.]; [Bus.] слово, введенное Генри Чесбро, который противопоставляет эту парадигму закрытой инновационной, где весь инновационный процесс происходит в границах фирмы.
в.	танцевать в одновременно чувственной и провокационной манере, включающей низкую позу на корточках с толчковыми движениями бедер и ягодиц, предполагающими половой акт	Пример: В 2013 году поп-звезда, исполняющая тверк на сцене MTV VMA, вызвала огромный резонанс в социальных сетях, что сделало термин «тверк» популярным во всем мире и, вероятно, способствовало его появлению в словаре.
в.	[subj: poiicemen] собирать [демонстрантов] в компактную группу, чтобы контролировать их движения

Вы хотите отклонить эту запись: дайте нам свои комментарии (неправильный перевод/определение, повторяющиеся записи…)

Чтобы добавлять слова в свой словарь, станьте участником сообщества Reverso или войдите в систему, если вы уже являетесь его участником. Это просто и занимает всего несколько секунд:

Или зарегистрируйтесь традиционным способом

Новый дом

Больше никаких травм.

Мы поможем вам добраться до причины вашей боли, чтобы вы могли бежать дольше, быстрее и каждый раз финишировать сильнее.

СВЯЗАТЬСЯ С НАМИ

Как работает процесс

Начать

Все в течение 14 дней, гарантировано!

Приступайте к работе

Вам сказали «Прекрати бегать» или научились «просто справляться» с болью или травмами?

Что говорят о нас другие люди:

«Результат я начал замечать на раннем этапе, и это меня очень обнадежило. У меня появились и другие проблемы (боль в спине из-за переутомления) и доктор . Райан поправился, эффективно решил эту проблему, а затем мы вернулись к исправлению моего колена. Опыт, который я имел с доктором Райаном, показал мне, что у него есть много инструментов, которые можно использовать для решения широкого круга проблем. Я бы порекомендовал его с энтузиазмом и безоговорочно. Вы будете рады, что пошли «.

Кендрик М.

«С самого начала доктор Райан смог распознать дисбаланс, который не распознал ни один другой физиотерапевт. Вначале я был настроен скептически… Как это супербазовое движение могло избавить меня от боли, которая мучила меня годами. После первых нескольких дней мое бедро и поясница перестали меня беспокоить. В последующие недели я смог улучшить свой баланс, гибкость и силу, значительно уменьшив боль. Я годами презирал скучные мельчайшие движения, которым научился в традиционная физкультура, но с движением, мои ежедневные упражнения были веселыми, и я с нетерпением ждал этого».

Kyla C.

«Я решил работать с доктором Райаном, потому что он был открытым и вдумчивым, когда я впервые связался с ним. Проработав с ним несколько месяцев, я ценю его самоотверженность и приверженность. Я не всегда уверен в себе и своих способностях бегуна, я уверен в опыте доктора Райана в качестве физиотерапевта и в его стремлении вернуть мне беговую форму».

Мэтью П.

«Как бегуну-ультра» программа «Путь к движению» помогла мне лучше понять области моего тела, которые препятствуют движению. В результате моей программы у меня увеличился диапазон движения и подвижность в некоторых областях, таких как лодыжки. , колени, бедра и верхняя часть спины. Я уверена, что с этой программой я останусь без травм и буду вести активный образ жизни еще много-много лет!!»

Кристен В.

«После работы с Райаном я заметила, что боль значительно уменьшилась, и, в качестве дополнительного бонуса, упражнения, которые он предоставил, помогли мне значительно улучшить мою силу в тренажерном зале и мой комфорт во время тренировки. бег и бег трусцой. Я НАСТОЯТЕЛЬНО рекомендую Path to Movement Health and Wellness всем, кто нуждается в тщательном, умном и исключительно сострадательном физиотерапевте, искренне заботящемся о своих пациентах и их благополучии!»

Нейт Г.

Чего ожидать от программы «Путь к движению»

Индивидуальный уход

Не существует универсального подхода.