Расход. Уравнение расхода — Основы гидравлики
Расходом называется количество жидкости, протекающее через живое сечение потока (струйки) в единицу времени. Количество жидкости можно задать объемом, массой или весом. Соответственно и расходы бывают объемный Q, массовый Qm и весовой QG.
Для элементарной струйки, имеющей бесконечно малые площади живых сечений, можно считать скорость жидкости в любой точке сечения одинаковой. Тогда
dQ = V dS; dQm=r dQ = rV dS; dQG= g dQm= grV dS,
где dS – площадь живого сечения струйки.
Для потока конечных размеров скорость в различных точках сечения будет различной, поэтому расход следует определять как сумму элементарных расходов струек
Но это чисто теоретическая формула, воспользоваться ей для определения расхода проблематично. Обычно вводят в рассмотрение среднюю по сечению скорость потока, которую можно найти по измерянному расходу
, откуда Q = VcpS.
Основываясь на законе сохранения вещества, на предположении о неразрывности (сплошности) потока и на свойстве непроницаемости трубки тока, для стационарного течения несжимаемой жидкости можно утверждать, что объемный расход во всех сечениях элементарной струйки один и тот же:
dQ = V1 dS1 = V2 dS2 = const (вдоль струйки).
Это уравнение объемного расхода для элементарной струйки.
Аналогичное уравнение можно записать и для потока конечных размеров, ограниченного непроницаемыми стенками, только скорости следует брать средние
Q = Vср1 S1 = Vсp2 S2 = const (вдоль потока).
Из последнего уравнения следует, что средние скорости в потоке несжимаемой жидкости обратно пропорциональны площадям живых сечений:
Уравнение расхода – это частный случай закона сохранения вещества для условий неразрывности потока.
students-library.com13.Расход жидкости(виды расходов) и средняя скорость. Способы их определения
Расходом называется количество жидкости, протекающей через живое сечение потока в единицу времени.
Различают:
объемный (Q) :
массовый (Qm) :
весовой (G)
расходы жидкости. Где V— объем жидкости; m — масса жидкости; ? — время.
Объемный расход потока с живым сечением F определим с использованием понятия средней скорости потока wcp:
Средняя скорость — это условная скорость потока, которая считается одинаковой для всех частиц данного сечения, но подобрана так, что расход, определенный по ее значению, равен истинному значению расхода.
14. Уравнения неразрывности для элементарной струйки и потоки жидкости.
Если несжимаемая жидкость движется без разрывов, то при установившемся движении объемный расход для всех живых сечений потока постоянен, т.е. можно записать, что вдоль потока
Это уравнение называют уравнением неразрывности потока, оно является первым основным уравнением гидродинамики. Из него следует, что средние скорости обратно пропорциональны площадям соответствующих живых сечений потока.
14(2). Уравнение неразрывности для элементарной струйки и потока жидкости при установившемся движении. В гидравлике обычно рассматривают потоки, в которых не образуются разрывы и не заполненные жидкостью пустоты, т.е. жидкость сплошь заполняет пространство.
Рассмотрим элементарную струйку несжимаемой жидкости при установившемся движении. Выделим сечение 1-1 и 2-2, расположенные на расстоянии l одно от другого (рис.1.23). Здесь Δs1 и Δs2 — площади живых сечений соответственно; u 1 и u2 — скорости; ΔQ1 и ΔQ2 — расходы элементарной струйки в сечениях.
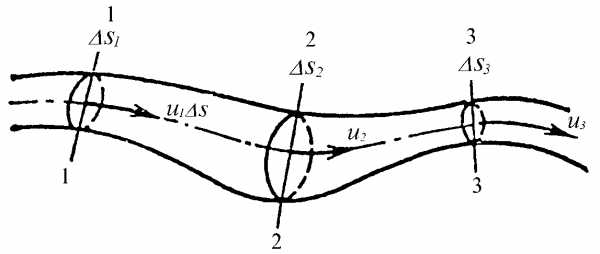
Рис. 1.23. Элементарные струйки несжимаемой жидкости при установившемся режиме движения
Очевидно, что ΔQ1 = Δs1u1 и ΔQ2 = Δs2u2, причем ΔQ1 втекает в рассматриваемый отсек, а ΔQ 2 — вытекает.
Учитывая, что форма элементарной струйки не изменяется с течением времени, поперечный приток и отток невозможен, так как скорости на боковой поверхности струйки направлены по касательным к линиям тока, из которых состоит эта боковая поверхность, получаем, что расходы ΔQ1 и ΔQ2 равны, т.е.
Δs1u 1 = Δs2u2. (1.50)
Аналогичные соотношения можно написать для любых двух сечений элементарной струйки, расположенных вдоль нее:
u1Δs1 = u2Δs2 =…= uΔs = ΔQ = const (1.51)
Это и есть уравнение неразрывности для элементарной струйки несжимаемой жидкости при установившемся движении.
Если выделить в потоке два любых сечения, отстоящих на некотором расстоянии, то, просуммировав по каждому из живых сечений обе части в уравнении (1.50)
Таким образом, в отмеченных условиях расход, проходящий через все живые сечения потока, неизменен, несмотря на то что в каждом сечении средняя скорость и площадь живого сечения могут быть различны.
Из (1.52) получим также важное соотношение
т.е. средние скорости обратно пропорциональны площадям живых сечений потока, которым соответствуют эти средние скорости.
Уравнение неразрывности (1.52) является одним из основных уравнений гидродинамики.
studfile.net
22. Гидравлические элементы потока
— Площадь живого сечения— площадь плоского поперечного сечения нормального к направлению движения.
— Площадь поперечного сечения струйки жидкости, перпендикулярного его линии тока называется площадью живого сечения струйки. Живое сечение потока представляет собой поверхность, проведенную перпендикулярно направлению движения жидкости и лежащую в пределах этого потока.
— Смоченный периметр— часть периметра, на котором поток соприкасается с твердыми стенками:
— Гидравлический радиус– отношение площади живого сечения к смоченному периметру:R = ω / χ
23. Методы определения движения жидкости (метод Лагранжа и метод Эйлера).
1. Метод Лагранжа. Этот метод не используется при описании волновых функций. Суть метода в следующем: требуется описать движение каждой частицы. Начальному моменту времени t0 соответствуют начальные координаты x0, y0, z0. Однако к моменту t они уже другие. Как видно, речь идет о движении каждой частицы. Это движение можно считать определенным, если возможно указать для каждой частицы координаты x, y, z в произвольной момент времени t как непрерывные функции от x0, y0, z0. x = x(x0, y0, z0, t) y =y (x0, y0, z0, t) z = z(x0, y0, z0, t) (1) Переменные x0, y0, z0, t, называют переменными Лагранжа.
2. Метод определения движения частиц по Эйлеру. Движение жидкости в этом случае происходит в некоторой неподвижной области потока жидкости, в котором находятся частицы. В частицах произвольно выбираются точки. Момент времени t как параметр является заданным в каждом времени рассматриваемой области, которая имеет координаты x, y, z.Рассматриваемая область, как уже известно, находится в пределах потока и неподвижна. Скорость частицы жидкости u в этой области в каждый момент времени t называется мгновенной местной скоростью.Полем скорости называется совокупность всех мгновенных скоростей. Изменение этого поля описывается следующей системой:ux = ux(x,y,z,t)uy = uy(x,y,z,t)иuz = uz(x,y,z,t)Переменные в (2) x, y, z, t называют переменными Эйлера.
24 Уравнение неразрывности (уравнение сохранения массы)
Неразрывности уравнение (далее Н) в гидродинамике, одно из уравнений гидродинамики, выражающее закон сохранения массы для любого объема движущейся жидкости (газа). В переменных Эйлера (см. Эйлера уравнения гидромеханики) Н имеет вид:где r — плотность жидкости, v — ее скорость в данной точке, a vx, vy, vz —
25. Расход жидкости (массовый, объемный, весовой).
Массовый расход — масса вещества, которая проходит через заданную площадь поперечного сечения потока за единицу времени.
Объёмный расход жидкости это объём жидкости, протекающей в единицу времени через живое сечение потока. Объёмный расход жидкости измеряется обычно в м3/с, дм3/с или л/с. Он вычисляется по формуле
,где Q — объёмный расход жидкости, V — объём жидкости, протекающий через живое сечение потока, t – время течения жидкости.
Массовый расход жидкости это масса жидкости, протекающей в единицу времени через живое сечение потока. Массовый расход измеряется обычно в кг/с, г/с или т/с и определяется по формуле
где QM — массовый расход жидкости, M -масса жидкости, протекающий через живое сечение потока, t – время течения жидкости.
Весовой расход жидкости это вес жидкости, протекающей в единицу времени через живое сечение потока. Весовой расход измеряется обычно в Н/с, КН/с. Формула для его определения выглядит так:
где QG — весовой расход жидкости, G — вес жидкости, протекающий через живое сечение потока, t – время течения жидкости.
Чаще всего используется объёмный расход потока жидкости. С учётом того, что поток складывается из элементарных струек, то и расход потока складывается из расходов элементарных струек жидкости dQ.
studfile.net
Расход жидкости- определение, формулы, единицы измерения
Жидкими телами называются физические тела, легко изменяющие свою форму под действием сил незначительной величины.
Течение жидкости характеризуется ее расходом, величина которого определяется как произведение площади поперечного сечения поршня на скорость его движения.
Расход = площадь поперечного сечения ∙ скорость перемещения
Q=S∙V
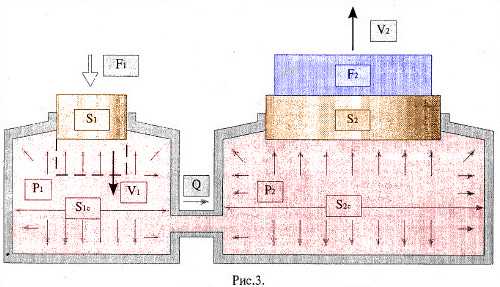
Для общего понимания, что такое расход жидкости, давайте рассмотрим на примере.
Если в поршень в первом сосуде, изображенном на рис.3, перемещать вниз с некоторой скоростью, которая обычно обозначается латинской буквой “V”, одновременно воздействуя на него усилием F1, то он будет вытеснять жидкость во второй сосуд. Поршень, которого будет подниматься со скоростью во столько раз меньшей скорости опускания поршня в первом сосуде, во сколь раз площадь его поперечного сечения больше площади поперечного первого поршня.
В Технической литературе расход жидкости обозначается латинской буквой “Q” и может быть представлен также как произведение объема жидкости перемещаемого за единицу времени:
расход = (перемещаемый объем)/время
Соответственно, выражение для расхода жидкости может быть представлено в виде:
Q=W/t;
Буквой “W” обозначена величина вытесняемого объема жидкости, а “t” – время вытеснения, или Q=S∙V. Так как V1c∙ S1с= V2∙S2с, поскольку объем жидкости, вытесненный за некоторое время из первого сосуда, поступил во второй сосуд за это же время, а значит расход жидкости вытекающей из первого сосуда, равен расходу жидкости, поступающий во второй сосуд:
V2=(V1∙S1)/S2
Жидкость во втором сосуде будет течь медленнее во столько раз, во сколько раз площадь поперечного сечения этого сосуда больше площади сечения первого сосуда (буквами S1с и S2с обозначены площади сечения сосудов),а S1 и S2 (площади сечения их горловин).
www.metalstanki.com.ua
Типы потоков жидкости
Совокупность элементарных струек жидкости представляет собой поток жидкости. Различают следующие типы потоков (или типы движений жидкости).
Напорные потоки (напорные движения) — это такие, когда поток ограничен твердыми стенками со всех сторон, при этом в любой точке потока давление отличается от атмосферного обычно в большую сторону, но может быть и меньше атмосферного. Движение в этом случае происходит за счёт напора, создаваемого, например, насосом или водонапорной башней. Давление вдоль напорного потока обычно переменное. Такое движение имеет место во всех гидроприводах технологического оборудования, водопроводах, отопительных системах и т.п.
Безнапорные потоки (безнапорные движения) отличаются тем, что поток имеет свободную поверхность, находящуюся под атмосферным давлением. Безнапорное движение происходит под действием сил тяжести самого потока жидкости. Давление в таких потоках примерно одинаково и отличается от атмосферного только за счет глубины потока. Примером такого движения может быть течение воды в реке, канале, ручье.
Свободная струяне имеет твёрдых стенок. Движение происходит под действием сил инерции и веса жидкости. Давление в таком потоке практически равно атмосферному. Пример свободной струи – вытекание жидкости из шланга, крана и т.п.
Гидравлические характеристики потока жидкости
В гидравлике различают следующие характеристики потока: живое сечение, смоченный периметр, гидравлический радиус, расход, средняя скорость.
Живым сечением потока называется поверхность (поперечное сечение), нормальная ко всем линиям тока, его пересекающим, и лежащая внутри потока жидкости. Площадь живого сечения обозначается буквой ω. Для элементарной струйки жидкости используют понятие живого сечения элементарной струйки (сечение струйки, перпендикулярное линиям тока), площадь которого обозначают через dω.
Смоченный периметр потока – линия, по которой жидкость соприкасается с поверхностями русла в данном живом сечении. Длина этой линии обозначается буквой .
В напорных потоках смоченный периметр совпадает с геометрическим периметром, так как поток жидкости соприкасается со всеми твёрдыми стенками.
Гидравлическим радиусом R потока называется часто используемая в гидравлике величина, представляющая собой отношение площади живого сечения S к смоченному периметру :
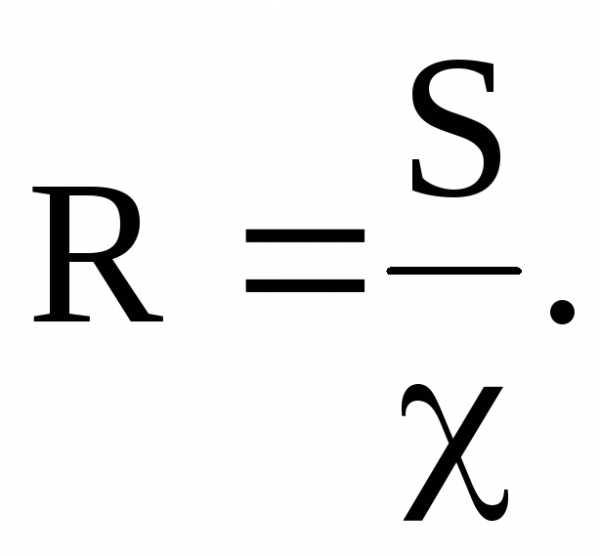
При напорном движении в трубе круглого сечения гидравлический радиус будет равен:
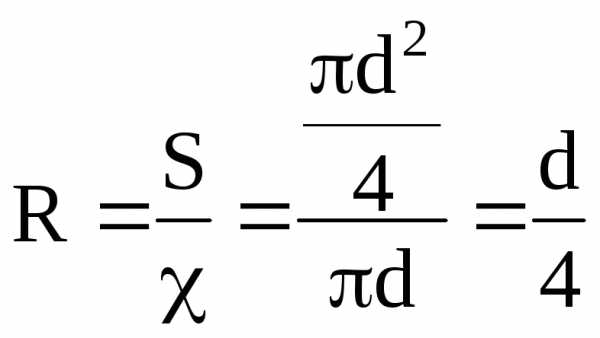 ,
,
т.е. четверти диаметра, или половине радиуса трубы.
Для безнапорного
потока прямоугольного сечения с размерами 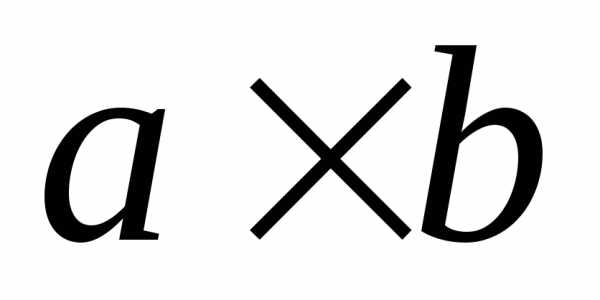 гидравлический
радиус можно вычислить по формуле
гидравлический
радиус можно вычислить по формуле
 .
.
Свободная поверхность жидкости при определении смоченного периметра не учитывается.
Расход потока жидкости (расход жидкости) – количество жидкости, протекающей в единицу времени через живое сечение потока.
Различают объёмный, массовый и весовой расходы жидкости.
Объёмный расход жидкости это объём жидкости, протекающей в единицу времени через живое сечение потока. Объёмный расход жидкости измеряется обычно в м3/с, дм3/с или л/с. Он вычисляется по формуле
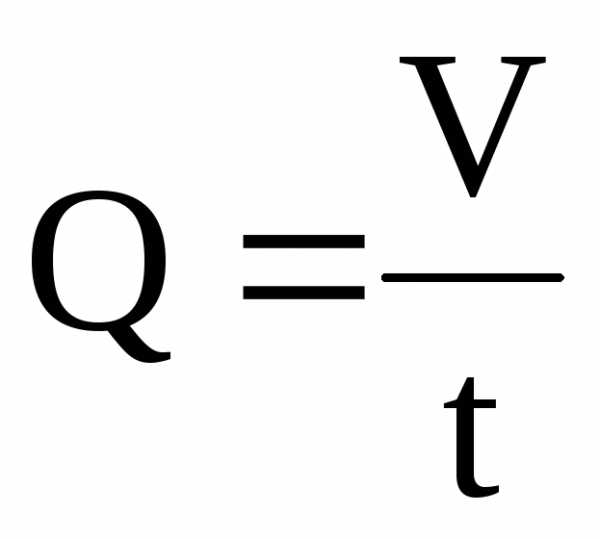 ,
,
где Q — объёмный расход жидкости,
V — объём жидкости, протекающий через живое сечение потока,
t – время течения жидкости.
Массовый расход жидкости это масса жидкости, протекающей в единицу времени через живое сечение потока. Массовый расход измеряется обычно в кг/с, г/с или т/с и определяется по формуле
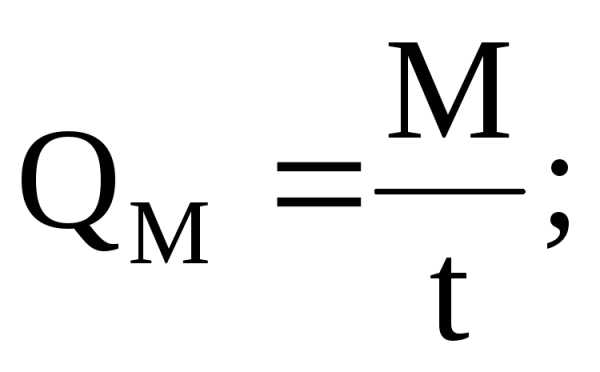
где QM — массовый расход жидкости,
M — масса жидкости, протекающий через живое сечение потока,
t – время течения жидкости.
Весовой расход жидкости это вес жидкости, протекающей в единицу времени через живое сечение потока. Весовой расход измеряется обычно в Н/с, КН/с. Формула для его определения выглядит так:
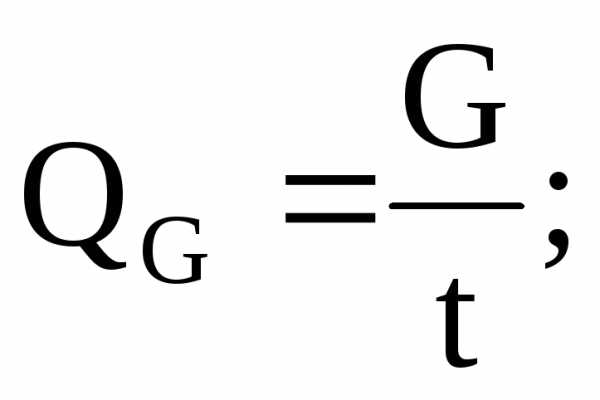
где QG — весовой расход жидкости,
G — вес жидкости, протекающий через живое сечение потока,
t – время течения жидкости.
Чаще всего используется объёмный расход потока жидкости. С учётом того, что поток складывается из элементарных струек, то и расход потока складывается из расходов элементарных струек жидкости dQ.
Расход элементарной струйки – объем жидкости dV, проходящей через живое сечение струйки в единицу времени. Таким образом:
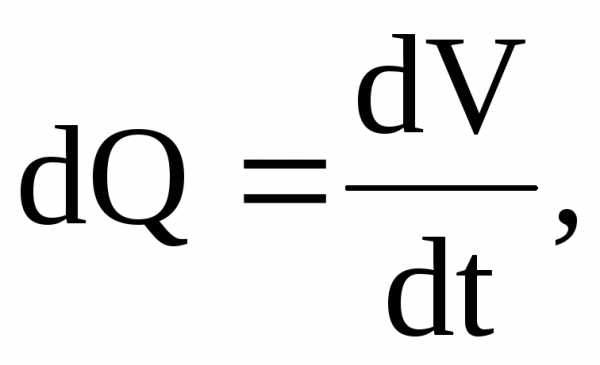
Если последнее выражение проинтегрировать по площади живого сечения потока можно получить формулу объёмного расхода жидкости, как сумму расходов элементарных струек
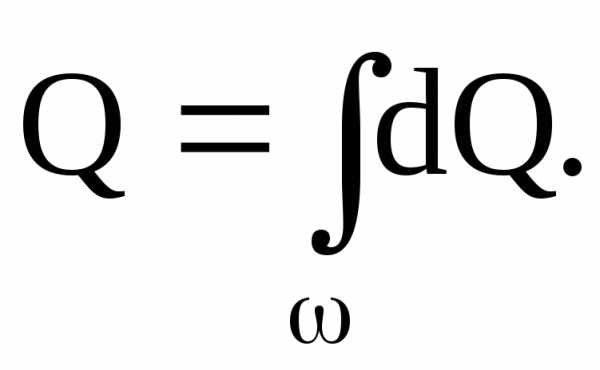
Применение этой формулы в расчетах весьма затруднительно, так как расходы элементарных струек жидкости в различных точках живого сечения потока различны. Поэтому в практике для определения расхода чаще пользуются понятием средней скорости потока.
Средняя скорость потока жидкости Vср в данном сечении это не существующая в действительности скорость потока, одинаковая для всех точек данного живого сечения, с которой должна была бы двигаться жидкость, что бы её расход был равен фактическому.
studfile.net
Расход. Уравнение расхода — Лекции-Основы гидравлики
Расход — это количество жидкости, которое протекает через данное сечение в единицу времени. Количество жидкости можно измерять в единицах объема, массы или веса. Поэтому различают объемный Q (м3/с), массовый QЬкг/с) и весовой QG (Н/с) расходы.
Для элементарной струйки, имеющей бесконечно малые площади сечений, можно считать скорость υ одинаковой во всех точках сечения. Следовательно, объемный расход для элементарной струйки dQ = υ dS.
Основываясь на законе сохранения вещества и полагая, что течение внутри элементарной струйки является сплошным и неразрывным, можно утверждать, что для установившегося течения несжимаемой жидкости
dQ = υ1 dS1 = υ2 dS2 = const. (3.1)
Это уравнение называется уравнением объемного расхода для элементарной струйки.
Для потока конечных размеров скорость в общем случае имеет различные значения в разных точках сечения, поэтому расход определяют как сумму элементарных расходов струек, составляющих поток.
(3.2)
На практике удобнее определять расход через среднюю по сечению потока скорость υср = Q / S, откуда Q = υср ·S.
Очевидно, что и для потока конечных размеров при условии его сплошности и неразрывности будет выполняться условие постоянства объемного расхода вдоль потока, то есть
Q = υср1 ·S1 = υср2 ·S2 = const. (3.3)
Из последнего уравнения следует, что средние скорости в потоке несжимаемой жидкости обратно пропорциональны площадям сечений
. (3.4)
Полученные уравнения расходов (3.1) и (3.3) являются следствием общего закона сохранения вещества.
students-library.com
23. Понятие расхода жидкости, средней скорости, живого сечения, гидравлического радиуса, смоченного периметра.
Живое сечение (w) – это поперечное сечение потока, перпендикулярное ко всем линиям тока. Например, в круглой трубке диаметром d, в которой все поперечное сечение занято жидкостью, живое сечение – это площадь круга
Смоченный периметр – та часть периметра живого сечения, которая соприкасается с твердыми стенками, образуя смоченную поверхность. Например, для русла вся боковая поверхность потока, за исключением свободной поверхности которую жидкость имеет на границе с газообразной средой; для круглой трубы, работающей полным сечением, смоченный периметр равен длине окружности, т.е.
Для круглой незаполненной трубы (рис.), если угол в радианах,
Гидравлический радиус ()– отношение площади живого сечения к смоченному периметру. Например, для круглой трубы, работающей полным сечением, гидравлический радиус четверти ее диаметра, т. е.
Гидравлический радиус характеризует удельную, т.е. приходящуюся на единицу длины смоченного периметра площадь живого сечения и позволяет оценить силу трения. Сила трения жидкости о смоченную поверхность зависит от ее площади, чем больше смоченная поверхность, тем больше при равных условиях сила трения. Расход жидкости ()– это ее объем, протекающий в единицу времени через живое сечение потока. Расход для элементарной струйки , где – истинная скорость движения частиц жидкости, – площадь сечения элементарной струйки. Средняя скорость () – отношение расхода к площади живого сеченияоткуда.
Расход – количество жидкоси, которое протекает через данное сечение в единицу времени. Различают объёмный Q(м3/с), массовый Qm(кг/с) и весовой QG (Н/с) расходы. ;

24. Дифференциальное уравнение неразрывности потока.
Выделим в движущемся потоке элементарный объем в форме прямоугольного параллелепипеда (рис.) и определим изменение массы жидкости в выделенном объеме за элементарный промежуток времени . Это изменение массы определяется разностью между втекающей и вытекающей массой жидкости через грани элементарного объема. Поскольку объем выделенного элемента остается неизменным с течением времени, то изменение массы жидкости может быть обусловлено лишь изменением ее плотности.
Определим массу жидкости, втекающую в выделенный объем за единицу времени. Жидкость втекает через грани в следующих количествах: через грань ; через грань; через грань.
Жидкость вытекает через грани в следующих количествах: через граньчерез граньчерез грань
Просуммировав количества втекающей и вытекающей жидкости по всем граням, найдем изменение массы жидкости в выделенном объеме:
Это
уравнение
называется дифференциальным
уравнением неразрывности или сплошности.
Оно также может быть записано в виде 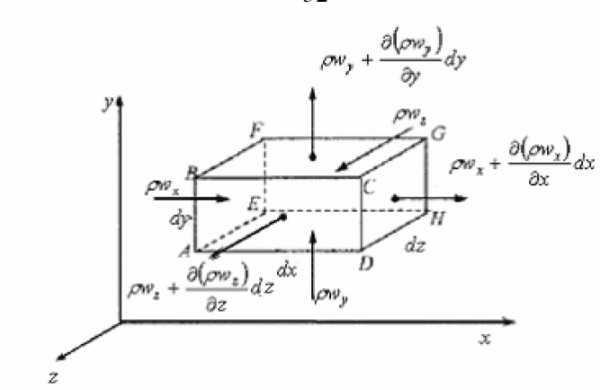
Для потоков несжимаемой жидкости (стационарных и нестационарных)
уравнение неразрывности примет вид Для стационарных потоков газа (сжимаемой жидкости) уравнение неразрывности примет видНеобходимо отметить, что существуют и другие способы вывода уравнения неразрывности.
studfile.net
