|
Острые углы в нижней части фюзеляжа На главную Степень демпфирования, создаваемого фюзеляжем и килем, зависит от их конфигурации. Значительными демпфирующими свойствами обладает киль, на котором нет горизонтального оперения и который не попадает в след от крыла. Вытяпутое по вертикали поперечное сечение фюзеляжа со скругленной нижней частью также обеспечивает эффективное демпфирование. Острые углы в нижней части фюзеляжа вызывают срыв потока на подветренной стороне, что приводит к уменьшению демпфирования или даже к антидемпфнрованию. Установка боковых наплывов (гребней) на передней верхней части фюзеляжа увеличивает демпфирование, а на нижней — уменьшает. При создании «бесштопорного» самолета необходимо прежде всего обеспечить динамическую и статическую путевую устойчивость и демпфирование по всем трем осям, В первую очередь это достигается увеличением несущих свойств крыла на больших углах атаки.  Для достижения этих целей желательно иметь также формы поперечных сечений фюзеляжа со сплющенной носовой частью или установкой наплывов на носовой части с круглым сечением. Образующиеся в этом случае боковые вихревые жгуты не только в значительной степени могут уменьшить или даже ликвидировать дестабилизирующий эффект фюзеляжа на больших углах атаки, но и привести к появлению стабилизирующего момента. Однако это может привести к созданию боковой силы и даже ускоряющего момента при вращении по рысканию, увеличивая тем самым тенденцию самолета к быстрому плоскому штопору. Улучшение обтекания крыла позволяет затягивать отрыв потока и обеспечить демпфирование крена, так же как и использование высокого киля или двух кил-ей на широкой хвостовой части фюзеляжа, а также применение системы улучшения устойчивости, использующей демпфер крена и рыскания. Все эти меры могут быть использованы, чтобы затянуть сваливание, но они не предотвратят штопор, если будет превышен максимально допустимый угол атаки.  Известно, что летчик может предупреждаться о приближении опасности посредством звуковых и световых сигналов, тряски рычагов управления и т. п. Ни одна из этих мер не обеспечивает полную безопасность в отношении штопора, особенно в условиях воздушного боя. Эффективное предотвращение штопора может быть достигнуто только системой искусственного ограничения углов атаки, обеспечивающей постепенное увеличение усилия на ручке управления. Система предотвращения штопора может быть дополнением к системе управления полетом с механической проводкой, однако наибольший эффект достигается при электродистанционной системе управления.На главную |
Теория и механизмы демпфирования в механике конструкций
Если ударить по стеклянной или металлической чаше, то она будет издавать затухающий со временем звон. В мире без демпфирования этот звон продолжался бы вечно. В реальности же, благодаря нескольким физическим процессам, кинетическая энергия и (потенциальная) энергия упругой деформации чаши переходят в другие формы энергии.
Как математически описывается демпфирование?
Есть несколько математических подходов к описанию и учету демпфирования. Давайте кратко резюмируем самые популярные из них.
Самое заметное проявления демпфирования — падение (затухание) амплитуды свободных колебаний со временем, как, например, в случае с «поющей» чашей. Скорость ослабления амплитуды зависит от того, насколько большое демпфирование в системе. Обычно амплитуда колебаний экспоненциально затухает со временем. В таком случае потери энергии за период пропорциональны амплитуде колебаний (на этом периоде).
Классическая «поющая» чаша. Изображение предоставлено Sneharamm0han — собственное произведение. Доступно по лицензии CC BY-SA 4.0 на Викискладе.
Давайте начнем с уравнения движения для системы из одной степени свободы с вязким трением в отсутствии внешних нагрузок.
\prime} = \eta
Угол потерь δ определяет фазовый сдвиг между напряжением и деформацией.
Демпфирование, заданное через коэффициент гистерезисных потерь, несколько отличается от случая вязкого демпфирования. Гистерезисные потери пропорциональны амплитуде смещений, а вязкое демпфирование пропорционально скорости. Таким образом, эти величины невозможно однозначно связать друг с другом.
На рисунке ниже сравнивается отклик системы с одной степенью свободы при использовании двух разных моделей демпфирования. Можно заметить, что модель вязкого демпфирования предсказывает более сильное затухание на частотах выше резонансной по сравнению с моделью через коэффициент гистерезисных потерь и более слабое затухание на частотах ниже резонансной.
Сравнение динамического отклика для модели вязкого демпфирования (сплошные линии) и для модели через коэффициент гистерезисных потерь (пунктирные линии).
Обычно на резонансной частоте выполняется следубщее соотношение между указанными критериями: \eta \approx 2 \zeta.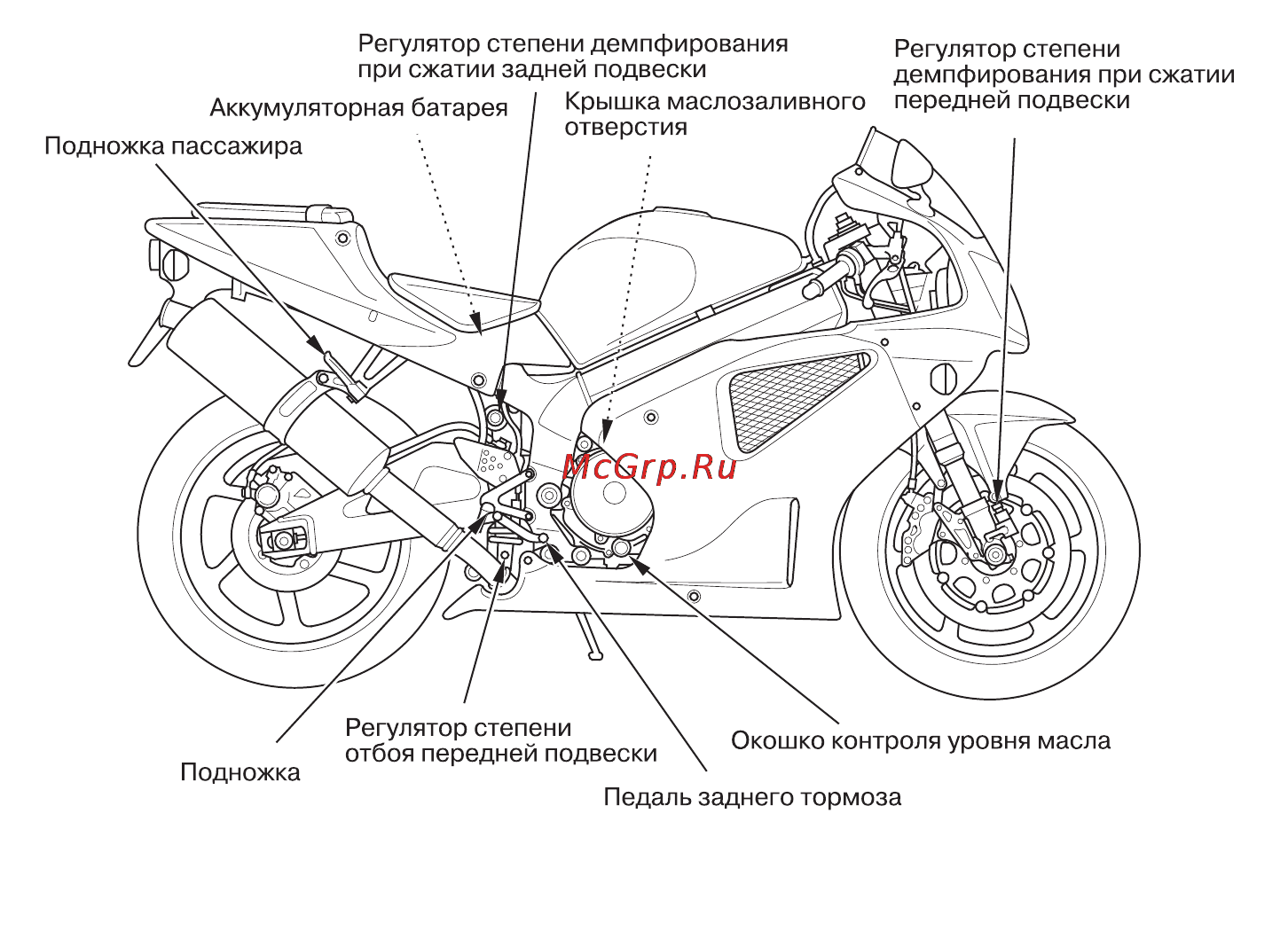
\prime} = \dfrac{D}
{2 \pi W_s}
Это определение через рассеянную энергию можно использовать, даже если петля гистерезиса не выглядит как идеальный эллипс; достаточно лишь иметь возможность определить две эти энергетических величины.
Источники демпфирования
Физических механизмов демпфирования огромное множество. Во всех естественных процессах энергия так или иначе рассеивается.
Внутренние потери в материале
Во всех реальных материалах энергия рассеивается при деформации. Можно считать это разновидностью внутреннего трения. Обратите внимание, что кривая нагружения для полного периода не укладывается на идеально прямую линию. Она больше похожа на вытянутый эллипс.
Обычно для описания демпфирования в материале применяется модель через коэффициент гистерезисных потерь, так как на опыте оказывается, что потери энергии за период слабо зависят от частоты и амплитуды. При этом математическое описание в модели коэффициента потерь основано на комплексных величинах, то есть подразумевает только случай гармонических колебаний.
Поэтому эту модель демпфирования можно использовать только для исследований в частотной области.
Коэффициенты гистерезисных потерь в материале могут сильно различаться в зависимости от точного состава материала и источников данных, которыми вы пользуетесь. В таблице ниже приведены некоторые грубые оценки.
| Материал | Коэффициент гистерезисных потерь η |
|---|---|
| Алюминий | 0.0001–0.02 |
| Бетон | 0.02–0.05 |
| Медь | 0.001–0.05 |
| Стекло | 0.0001–0.005 |
| Резина | 0.05–2 |
| Сталь | 0.0001–0.01 |
Коэффициенты потерь и схожие модели демпфирования используются, если физические механизмы затухания в материале неизвестны или не важны в контексте рассматриваемой задачи. В некоторых моделях материала, например, в вязкоупругих материалах, рассеивание энергии изначально заложено в математическую модель.
Трение в соединениях
Конструкции часто соединяются болтами или другими типами креплений. Если при колебаниях соединенные поверхности двигаются относительно друг друга, энергия рассеивается через трение. Если величина силы трения не меняется за период, потери энергии за период слабо зависят от частоты. В этом смысле трение схоже с внутренними потерями в материале.
Болтовые соединения широко распространены в задачах механики конструкций. Величина рассеиваемой в болтовых соединениях энергии может сильно зависеть от конструкции. Если важно снизить потери, болты должны плотно прилегать друг к другу и быть хорошо затянуты, чтобы уменьшить макроскопическое проскальзывание между поверхностями.
Излучение звука
Вибрирующая поверхность будет приводить в движение окружающий воздух (или другую среду) и испускать звуковые (акустические) волны. Эти волны уносят часть энергии, из-за чего конструкция теряет энергию.
Излучение звука преобразователем типа Tonpilz.
Анкерные потери
Часто небольшой компонент крепится к большой конструкции (основанию/подложке), которая не включается в расчетную модель. Когда деталь вибрирует, в несущей конструкции возникают упругие волны, также являющимися источником рассеяния энергии. В контексте микроэлектромеханических систем (МЭМС), этот эффект называют
Термоупругое демпфирование
Даже если в процессе совершенно упругой деформаций энергия не рассеивается, деформация материала слегка изменяет его температуру. Локальное растяжение приводит к снижению температуры, а сжатие — к нагреву.
Это принципиально обратимый процесс, так что при снятии напряжения температура вернется к исходному значению. Однако часто в поле напряжения есть ненулевые градиенты, которым соответствуют градиенты распределения температуры. Они вызывают тепловые потоки от теплых областей к холодным. Когда по ходу цикла нагружения напряжение «убирают», распределение температуры уже отличается от того, что было при нагрузке.
Термоупругое демпфирование (thermoelastic damping) важно при исследовании высокочастотных колебаний на малых масштабах. Например, оно может значительно снизить добротность микроэлектромеханических резонаторов.
Демпферы и гасители
Иногда в конструкцию включают специализированные выделенные гасители колебаний, например, рессоры в подвеске колес.
Рессоры. Автор изображения — Avsar Aras, собственное произведение. Доступно по лицензии CC BY-SA 3.0 на Викискладе.
Естественно, такие компоненты сильно влияют на суммарное демпфирование, по крайней мере, для некоторых мод колебаний.
Сейсмогасители
Особое внимание искуственному демпфированию колебаний уделяется при строительстве в сейсмоопасных районах. Чрезвычайно важно снизить амплитуду колебаний в зданиях при землетрясении. При этом гасители могут как изолировать здание от фундамента, так и рассеивать энергию.
Сейсмогасители в общественном здании. Изображение предоставлено Shustov — собственное произведение. Доступно по лицензии CC BY-SA 3.0 на Викискладе.
Продолжение
Во второй части данной серии вы сможете найти информацию о том, как задавать демпфирование в COMSOL Multiphysics®.
d%c3%a4mpfungsgrad — со всех языков на все языки
Все языкиАбхазскийАдыгейскийАфрикаансАйнский языкАканАлтайскийАрагонскийАрабскийАстурийскийАймараАзербайджанскийБашкирскийБагобоБелорусскийБолгарскийТибетскийБурятскийКаталанскийЧеченскийШорскийЧерокиШайенскогоКриЧешскийКрымскотатарскийЦерковнославянский (Старославянский)ЧувашскийВаллийскийДатскийНемецкийДолганскийГреческийАнглийскийЭсперантоИспанскийЭстонскийБаскскийЭвенкийскийПерсидскийФинскийФарерскийФранцузскийИрландскийГэльскийГуараниКлингонскийЭльзасскийИвритХиндиХорватскийВерхнелужицкийГаитянскийВенгерскийАрмянскийИндонезийскийИнупиакИнгушскийИсландскийИтальянскийЯпонскийГрузинскийКарачаевскийЧеркесскийКазахскийКхмерскийКорейскийКумыкскийКурдскийКомиКиргизскийЛатинскийЛюксембургскийСефардскийЛингалаЛитовскийЛатышскийМаньчжурскийМикенскийМокшанскийМаориМарийскийМакедонскийКомиМонгольскийМалайскийМайяЭрзянскийНидерландскийНорвежскийНауатльОрокскийНогайскийОсетинскийОсманскийПенджабскийПалиПольскийПапьяментоДревнерусский языкПортугальскийКечуаКвеньяРумынский, МолдавскийАрумынскийРусскийСанскритСеверносаамскийЯкутскийСловацкийСловенскийАлбанскийСербскийШведскийСуахилиШумерскийСилезскийТофаларскийТаджикскийТайскийТуркменскийТагальскийТурецкийТатарскийТувинскийТвиУдмурдскийУйгурскийУкраинскийУрдуУрумскийУзбекскийВьетнамскийВепсскийВарайскийЮпийскийИдишЙорубаКитайский
Все языкиАбхазскийАдыгейскийАфрикаансАйнский языкАлтайскийАрабскийАварскийАймараАзербайджанскийБашкирскийБелорусскийБолгарскийКаталанскийЧеченскийЧаморроШорскийЧерокиЧешскийКрымскотатарскийЦерковнославянский (Старославянский)ЧувашскийДатскийНемецкийГреческийАнглийскийЭсперантоИспанскийЭстонскийБаскскийЭвенкийскийПерсидскийФинскийФарерскийФранцузскийИрландскийГалисийскийКлингонскийЭльзасскийИвритХиндиХорватскийГаитянскийВенгерскийАрмянскийИндонезийскийИнгушскийИсландскийИтальянскийИжорскийЯпонскийЛожбанГрузинскийКарачаевскийКазахскийКхмерскийКорейскийКумыкскийКурдскийЛатинскийЛингалаЛитовскийЛатышскийМокшанскийМаориМарийскийМакедонскийМонгольскийМалайскийМальтийскийМайяЭрзянскийНидерландскийНорвежскийОсетинскийПенджабскийПалиПольскийПапьяментоДревнерусский языкПуштуПортугальскийКечуаКвеньяРумынский, МолдавскийРусскийЯкутскийСловацкийСловенскийАлбанскийСербскийШведскийСуахилиТамильскийТаджикскийТайскийТуркменскийТагальскийТурецкийТатарскийУдмурдскийУйгурскийУкраинскийУрдуУрумскийУзбекскийВодскийВьетнамскийВепсскийИдишЙорубаКитайский
раздел 8.
2 книги «МАНОМЕТРЫ» от НПО «ЮМАС»Измерение давления пульсирующих сред в большинстве случаев вызывает ускоренный износ, в первую очередь, деталей и узлов, находящихся на линии передачи от конца трубчатой пружины до трибки. Иллюстрацией пульсирующего параметра могут быть значения давления в ресиверах поршневых компрессоров, патрубках питательных насосов котельных установок. В таких режимах стрелка манометра пульсирует – дергается. При этом амплитуда пульсаций может составлять до 20…30 % шкалы прибора. Основная нагрузка в данном случае приходится на зубчатую передачу сектор – трибка. Поэтому «съедаются» зубцы этих деталей, что приводит к большим люфтам в передаточном механизме, а часто, при «разбивании» посадочных гнезд плат и износе цапф осевых держателей сектора и трибки, – к разрушению механизма.
Измерители с тензопреобразователями, как, впрочем, и с другими видами чувствительных элементов, не устойчивы к гидроударам, которые часто наблюдаются в тепловых сетях, особенно при пароводяных режимах.
В таких режимах в короткий интервал времени давление рабочего тела скачкообразно возрастает в несколько раз.
При пульсационных нагрузках мембраны измерительных преобразователей, особенно когда на их поверхностях нанесены чувствительные слои, от частых деформаций снижают свой рабочий ресурс и ухудшаются свои технические характеристики.
Чтобы уменьшить амплитуды выбросов пульсирующего давления на линии его подвода устанавливаются дополнительные устройства, например клапаны, сужающие шайбы, позволяющие увеличить гидравлическое сопротивление импульсной линии или подводящего канала. Однако такие меры должны проводиться осторожно, так как отсчет измеряемого параметра желательно производить с минимальным транспортным запаздыванием. Но это не для пульсирующего параметра. При пульсирующем давлении требуется определять оптимальные значения между скоростью измерения и усредненным за определенный отрезок времени параметром.
Для снижения пульсаций, сглаживания параметра измеряемого потока применяют различные меры.
Одним из наиболее часто используемых приемов является установка в подводящем канале дополнительных устройств, повышающих их гидравлическое сопротивление. В некоторых случаях на подводящей линии размещается вставка с пористым материалом. Причем пористость, как и длина вставки, выбирается исходя из задаваемых параметров пульсаций измеряемого давления.
К недостаткам пористых демпферов можно отнести их засоряемость и невозможность или затруднительность регенерации.
В манометрических приборах традиционно используются демпферы, монтируемые в держателе измерителя. Демпфер представляет собой вставку с малым проходным отверстием в центре (рис. 8.9). Он устанавливается в подводящем канале и ограничивает движение массы рабочего вещества между измеряемым потоком и полостью чувствительного элемента.
Рис. 8.9. Демпфер в виде сужающего устройства |
Длина канала с отверстием небольшого диаметра практически не влияет на показатели демпфирования.
Определяющим является диаметр отверстия, выбираемый в зависимости от вязкости измеряемой среды, требуемой величины усреднения и значений амплитуд пульсаций.
Основным недостатком демпферов в виде сужающего устройства является вероятность засорения малого проходного канала.
Конструкция демпферного блока с фильтром и иглой исключает возможность засорения канала и обеспечивает работоспособность устройства в комплекте с манометром при измерении сред с различными характеристиками пульсаций (рис. 8.10).
Рис. 8.10. Демпферный блок с фильтром и иглой:1 – регулирующая игла; 2 – ввод; 3 – корпус; 4 – основа; 5 – накидная гайка; 6 – фильтр |
Регулирующая игла 1, закрепленная во вводе 2, образует с корпусом 3 демпфирующий зазор. Корпус состоит из основы 4 и накидной гайки 5. Фильтр 6 устанавливается перед демпфирующим зазором и обеспечивает циркулирование через него среды без сторонних включений.
Изменение демпфирующего зазора между регулирующей иглой и корпусом обеспечивает оптимальный выбор между характеристиками сглаживания измерений и временем запаздывания измеряемого давления.
К недостаткам такой конструкции можно отнести необходимую периодическую замену фильтров.
Рис. 8.11. Демпферный блок с разделителем: 1 – основа; 2 – гнездо манометра; 3 – перегородка; 4 – эластичный колпак; 5 – манометр; 6 – подводящий штуцер; 7 – демпферное отверстие |
Демпферный блок с разделителем (рис. 8.11) представляет собой корпус, состоящий из основы 1 и гнезда манометра 2, между которыми размещается перегородка 3. К ней герметично присоединен эластичный колпак 4. В центре перегородки имеется отверстие малого диаметра, служащее демпфером. Внутренний объем эластичного колпака с внутренней полостью чувствительного элемента манометра 5 образуют единое замкнутое пространство, которое заполняется жидкостью.
Среда измеряемого давления через подводящий штуцер 6 поступает внутрь основы и воздействует на эластичный колпак. При избыточном давлении последний стремится уменьшить свои размеры – сжаться, что вызывает переток находящейся внутри него жидкости через демпферное отверстие 7 во внутреннюю полость чувствительного элемента манометра. При этом малый диаметр проходного отверстия и нежесткость формы и объема эластичного колпака позволяют отсечь основные пульсации давления измеряемой среды. чем меньше диаметр отверстия, тем больше степень сглаживания измеряемой среды, поступающей во внутреннюю полость чувствительного элемента измерителя.
Главным недостатком демпферного блока с разделителем является отсутствие возможности управления степенью демпфирования.
Более широкое распространение получило демпферное устройство, рабочая часть которого представляет набор шайб с малыми отверстиями, размещенных на определенном расстоянии друг от друга (рис. 8.12). В корпусе 1 устройства устанавливаются шайбы 2 и 3, которые имеют одинаковые габаритные размеры, но различаются расположением отверстий друг относительно друга.
Шайбы
и при установке в корпусе дистанциируются вставкой 4. Таким образом создаются малые камеры рабочей среды. Измеряемая среда пульсирующего давления через одну из шайб поступает в малую камеру и из-за смещения отверстий в шайбах друг относительно друга вынуждена изменять направление движения. Таким образом, она проходит серпантинный путь, на котором и из-за которого происходит гашение пульсаций.
Рис. 8.12. Схема (а) и вид (б) демпферного устройства с набором шайб: 1 – корпус; 2 и 3 – шайбы; 4 – вставка; 5 – фиксатор |
Диаметр отверстий в шайбах, их расположение и количество камер в значительной мере определяют степень сглаживания пульсирующего параметра.
Фиксатор 5 обеспечивает собираемость конструкции и позволяет неподвижно фиксировать шайбы.
Демпферные устройства с набором шайб используются в промышленной эксплуатации на протяжении нескольких десятков лет.
Определенную степень демпфирования могут вносить подводящие коммуникации. Так, обеспечивающие нормальные температурные условия работы манометра сифонные отводы, в особенности конструкции, в которых имеются гидравлические петли, позволяют в значительной степени уменьшить пульсации измеряемой среды.
демпфирование измеряемой среды может также производиться трехходовыми кранами и игольчатыми клапанами, установленными на импульсной линии подсоединения манометра. Степень демпфирования в этом случае во многом зависит от конструкции применяемых устройств.
Представляет интерес использование для гашения пульсаций демпферного устройства с регулировочной иглой (рис.8.13). Регулировочная игла 1 устанавливается с помощью зажимного штуцера 2 в корпусе 3 демпферного устройства. Уплотнительная прокладка 4 обеспечивает герметичность конструкции.
Таким образом, канал измеряемого потока пульсирующего давления на пути к чувствительному элементу прибора перекрывается регулировочной иглой 1.
Величина такого перекрытия определяет степень демпфирования измеряемого параметра.
Другим типом приспособлений для сглаживания пульсаций давления измеряемой среды могут служить устройства, у которых гашение скачков достигается малым размером канала (на уровне долей миллиметра) и большой его длиной (от десятков сантиметров до сотен метров). На рис. 8.14 представлено демпферное устройство с капиллярным каналом.
Измеряемая среда пульсирующего давления через подводящий штуцер 1, пористый фильтр 2 и демпферную шайбу 3 поступает в капиллярный канал, образованный конусом 4 и корпусом 5. Внутренняя наклонная плоскость корпуса 5 имеет чистую поверхность. Канал в виде спирали нарезан на внешней стороне конуса. Площадь его поперечного сечения и форма принимаются в зависимости от задаваемых параметров рабочей среды.
Выход капиллярного канала через дополнительное отверстие 6 соединен с выходом устройства.
Герметичность конструкции обеспечивается уплотнительной прокладкой 7 и резьбовой крышкой 8.
Рис. 8.14. Схема (а) и вид (б) демпферного устройство с капиллярным каналом: 1 – подводящий штуцер; 2 – пористый фильтр; 3 – демпферная шайба; 4 – конус; 5 – корпус; 6 – дополнительное отверстие; 7 – уплотнительная прокладка; 8 –резьбовая крышка |
Демпферное устройство с капиллярным каналом в комплекте, например, с показывающим манометром МП 160 реально обеспечивает время переходного процесса от 0,5 до 3 с.
Рис. 8.13. Схема (а) и вид (б) демпферного устройства с регулирующей иглой: 1 – регулировочная игла; 2 – зажимной штуцер; 3 – корпус; 4 – уплотнительная прокладка. |
Демпфирующий материал для акустических систем
Мурманск, 13 июня 2020
Андрей О. Автор 3 отзывов ХорошоДемпфирующий материал Intertechnik Pritex нет в продаже
Приобрел пять листов Intertechnik Pritex. Используя «Момент классик» приклеил их к вибропоглощающим матам STP Бимаст Бомб Premium, предварительно прикатанным ко всем стенкам изнутри АС (включая фронтальную) посредством фена и блина от гантели. Вибрации корпуса японской АС закрытого типа значительно снизились благодаря примененным материалам. Несмотря на значительный вес АС (до доработки каждая более 63 кг) ее разобранный корпус на простукивание издавал звонкий звук (особенно звенела лицевая панель). После описанной обработки звук простукивания стал глуше и ниже тоном. Однако последующее прослушивание не удовлетворило, сделал вывод, что недостаточно звукопоглощающего материала (японской минваты, которую выбросил из АС, было в три раза больше приклеенного мною Pritex-са).
Добавил по 75 грамм TWARON Angel Hear в каждую АС (обложил вокруг корзины 15-дюймового НЧ динамика). По результатам прослушивания АС дополнительно заменил японскую минвату и в СЧ отсеках (колпаки) также на TWARON Angel Hear. Использовал по 8 грамм в колпак каждого СЧ-динамика. Звук АС значительно изменился. Я перестал слышать звук фанеры, из которой изготовлена лицевая панель АС. До доработки полагал, что так звучат СЧ-динамики. Оказалось, что окраску звучанию СЧ-головок придает вибрация фанеры фронтальной панели АС. В итоге вибрации НЧ динамика стали значительно меньше влиять на звучание СЧ динамиков. Середина стала яснее и точнее. Всем удачи!
Златоуст, 4 декабря 2018
Дмитрий Г. Автор 89 отзывов ОтличноДемпфирующий материал Intertechnik Pritex нет в продаже
Материал пошёл на оклейку внутри саба Klipsch Synergy Sub12!
Ялта, 6 сентября 2018
Михаил З. Автор 22 отзывов ОтличноДемпфирующий материал Visaton Lambs Wool нет в продаже
Отлично в отдельный с.
ч. бокс.
Москва, 24 марта 2018
Алексей А. Автор 2 отзывов ОтличноДемпфирующий материал Visaton Lambs Wool нет в продаже
Преобретать другой материал не вижу смысла. За 2 года переделывали порядка 10 разных пар акустических систем (винтаж) результат всегда можно предсказать, в отличие от синтетики.
Москва, 8 марта 2018
Дмитрий М. Автор 44 отзывов ОтличноДемпфирующий материал Visaton Lambs Wool нет в продаже
Брался под замену штатного синтепона в АС в объеме один к одному. В моём случае улучшилось разрешение на нч, выровнялась середина. Но необходимо учитывать, что материал вносит заметные изменения в итоговое звучание, которые не всегда могут идти на пользу.
Брянск, 9 февраля 2018
Виктор М. Автор 5 отзывов ОтличноДемпфирующий материал Visaton Lambs Wool нет в продаже
Качественный материал, полностью заменил синтепон в колонках.
Батайск, 24 января 2018
Владимир С. ОтличноДемпфирующий материал Visaton Lambs Wool нет в продаже
Добрый день.
Заказал 1 пакет Visaton Lambs Wool, для замены акустического синтепона в напольных колонках onkyo skf-4800. Спасибо «Аудиомании» за отличный сервис и быструю доставку. Так же хочу выразить свою благодарность за предыдущие подробные развернутые отзывы. В колонках заменил такое же по размерам колличество акустического синтепона на Visaton Lambs Wool, по одному мату,разрезаному пополам в длинну, в каждую АС. Что изменилось.
СЧ и НЧ стали более открытыми натуральнее, буббнения и аггесивности стало меньше.В целом звук стал более породистый, если можно так выразится, более воздушный, более вовлекающий. Подтверждаю как было выше написано СЧ и НЧ стали на свои места. Однозначно рекомендую для замены заводского синтипона.
P.S.Применять аккуратно-возможно передемфировать. Мои АС обьемом порядка 50л, 1 пакет идет для 20литров(рекомендуется произвоителем).
Попробовал 2 мата одного пакета в одну колонку-результат отрицательный звук стал более глухой и снизилась атака. Так что в моем случае по 1 мату в каждую АС, ровно столько сколько было синтепона.
Всем мира, добра, удачи и найти свой звук.
Энгельс, 23 декабря 2017
Дмитрий П. Автор 22 отзывов ОтличноДемпфирующий материал Visaton Lambs Wool нет в продаже
Очень хорошая натуральная шерсть для акустических систем, режется очень хорошо и сильно влияет на качество звука в лучшую сторону, шерсть использую в напольных колонках и результат положителен, нареканий нету
Москва, 29 ноября 2017
Андрей К. Автор 10 отзывов ОтличноДемпфирующий материал Visaton Lambs Wool нет в продаже
Поменял старый демпферный материал в сабвуфере на новый. Звук стал намного приятнее, пропал эффект «бубнения», обычно характерный для фазоинверторных сабов.
Березники, 13 ноября 2017
Иван М. ОтличноДемпфирующий материал Visaton Lambs Wool нет в продаже
В monitor audio rs6 поменял родной поролон на Visaton. Появился нижний бас и чистые средние. Рекомендую …
Системы демпфирования — Справочник химика 21
Система демпфирования колебаний ротора может включать масляный демпфер в его нижней части и пассивный магнитный демпфер или активную электромагнитную систему в верхней части ротора [16, 17].
Вопросы оптимального демпфирования всегда сопряжены со спектром наиболее активных резонансов демпфируемой системы. Очевидно, что узлы подвески и демпфирования роторов надкритических и подкритических центрифуг сильно различаются. Некоторые варианты этих решений изложены в целом ряде патентов, которых по различным узлам конструкции газовых центрифуг имеется более ста. [c.183]
Для вибрационной защиты используют различные методы. Динамическое виброгашение позволяет снизить вибрацию присоединением к защищаемому объекту специальной системы, реакции которой уменьшают размах вибрации объекта. Демпфирование вибрации позволяет уменьшить вибрации рассеянием механической энергии с этой целью применяют специальные демпферы. [c.93]
Флюктуации бывают как внутреннего, так и внешнего происхождения. В макроскопической системе с большим числом степеней свободы всегда существуют спонтанные флюктуации.
Условие затухании флюктуаций становится условием устойчивости данного процесса. Проблема реакции системы на спонтанные флюктуации тесно связана с известным принципом Ле Шателье—Брауна (или принципом «демпфирования»). флюктуации различаются и по их масштабу. [c.173]
Эта величина мало отличается от частоты незатухающих колебаний той же системы, но лишенной демпфирования. [c.106]
Демпфирующие устройства, вводимые иногда в систему, значительно уменьшают амплитуды колебаний вала при увеличении частоты его вращения. Основная задача заключается не столько в ограничении амплитуд колебаний, сколько в изоляции несбалансированных сил корпуса. Демпфирование может увеличить степень передачи возбуждающей силы от вала корпусу, и оно целесообразно при прохождении системы через резонанс. [c.417]
Вибрации труб при поперечном обтекании. Вибрация труб не всегда сопутствует шуму, возникающему от поперечного обтекания трубных рядов [29— 311.
Наоборот, вибрация труб может не возбуждать особенно сильного шума, если движение стенок системы вызывает интенсивное демпфирование. Обычно вязкие реальные жидкости эффективно способствуют демпфированию колебания труб, тогда как вязкость газов слишком мала даже для едва заметного [c.152]
Обычно свободные колебания в результате демпфирования сравни-гельно быстро затухают. Колебания этого типа имеют большое значение, так как характеризуют динамическое свойство колебательной системы через частоты, формы, коэффициент демпфирования. Наличие информации такого рода о механической системе позволяет предсказывать ее поведение. Например, располагая достаточной информацией относительно распределения масс и жесткостей системы, можно рассчитать собственные частоты этой системы. Наибольшее влияние на погрешности обработки оказывают низкие частоты колебаний в технологической системе. Следует подчеркнуть, что при изменении состояния механической системы будет изменяться и процесс накопления энергии.
Например, если увеличить температуру системы, то изменяются собственные частоты и форма колебаний. [c.55]
Динамические характеристики механической системы (собственные частоты, форма колебаний, коэффициент демпфирования) определяют способность системы так регулировать отбор энергии от источника, чтобы в системе возникли автоколебания. Нередко автоколебания сложны и непонятны, трудно поддаются объяснению в результате отсутствия периодического возмущения. Каждое явление автоколебаний связано с тем или иным физическим процессом, природа которого не лежит на поверхности. [c.56]
Кривая, к которой приближаются ветви амплитудно-частотной характеристики при стремлении к нулю вынуждающей силы в нелинейной системе без демпфирования. [c.9]
На рис. 3.5 показаны соответственно зависимости низших пяти частот и соответствующих им коэффициентов демпфирования системы от величины Ег нри следующих значениях параметров задачи [c.
150]
Отдельные узлы и детали возбудителя конструктивно не отличаются от аналогичных узлов и деталей близких по размерам тихоходных ге-нераторов постоянного тока общепромышленного назначения. Отличие возбудителей от обычных генераторов постоянного тока определяется в основном требованиями форсировки возбуждения и быстродействия системы возбуждения. Магнитные индукции в различных участках магнитопровода в номинальном режиме должны быть выбраны с таким расчетом, чтобы при двух-трехкратной форсировке напряжения возбуждения ток возбуждения возбудителя не слишком бы возрастал из-за насыщения его магнитопровода. Напряжение между смежными коллекторными пластинами при форсировке не должно превышать 20 Ч-25 В. Эти требования приводят к увеличению главных размеров возбудителя по сравнению с машиной постоянного тока общепромышленного назначения такой же мощности и частоты вращения. Требование быстродействия системы возбуждения в ряде конструкций приводит к необходимости выполнения всего сердечника статора возбудителя, как полюсов, так и ярма (спинки), шихтованным из отдельных тонких листов, изолированных друг от друга.
При этом удается обеспечить достаточно высокую скорость нарастания магнитного потока и напряжения возбудителя, благодаря незначительному демпфированию потока при его резком изменении вихревыми токами магнитопровода. [c.73]
Наибольшее отклонение характеристика (2.123) от своих асимптот имеет в окрестности (Од. Значение этого отклонения зависит от коэффициента относительного демпфирования. Если О Точное значение резонансной частоты Шр, при котором амплитудная частотная характеристика системы второго порядка достигает максиму]у1а, можно определить из условия минимума знаменателя формулы (2.121) [c.61]
Таким образом, для системы второго порядка, у которой коэффициент относительного демпфирования лежит в пределах О частоты частота свободных колебаний Ис при переходном процессе (см. 2.78), собственная частота о> совпадающая с сопрягающей частотой, и резонансная частота сор. При = О все три частоты равны со , а амплитудная характеристика системы в этом случае имеет разрыв (штриховая линия на рис.
2.16, а). При 1,0 резонансный пик отсутствует, и ЛАХ приближается к своим асимптотам снизу (рис. 2.16, а). [c.61]
Система второго порядка при значениях I увеличение спектральной плотности выходного сигнала вблизи этой частоты, т. е. система второго порядка при слабом демпфировании может усиливать шум, поступающий на ее вход. [c.68]
Очевидно, что в зависимости от интенсивности демпфирования колебаний данная система может рассматриваться как колебательное или апериодическое звено второго порядка. Демпфирование системы изменяется прн изменении размеров дросселя в поршне и вязкости жидкости. [c.90]
Условия устойчивости гидропривода, как было выяснено в предыдущих параграфах, зависят от требований, предъявляемых к его быстродействию, степени демпфирования, создаваемого силами трения, а также от допустимого расхода жидкости из системы питания при равновесном состоянии гидропривода, т. е. от герметичности распределителя.
Если необходимо получить высокую добротность Ьг гидропривода при наличии большой приведенной к штоку массы т и малых значениях коэффициента относительного демпфирования ц, то для обеспечения устойчивости гидропривода приха с[ится применять корректирующие устройства. Известны следующие методы корректирования гидроприводов с дроссельным регулированием. [c.346]
Передаточная функция (14.56) содержит в знаменателе полином четвертой степени по 5, что указывает на возможность существования двух резонансных частот, как в механической системе с двумя степенями свободы. При слабом демпфировании резонансные частоты близки к собственным частотам недемпфированного гидропривода, которые можно найти, полагая [c.430]
На рис. 15.1 показана схема системы, в напорной линии которой давление поддерживается клапаном 1 с пружиной 2. При перемещении клапана рабочая среда протекает через дроссельное отверстие 3, в результате чего обеспечивается демпфирование клапана.
Такого типа система может быть гидравлической и пневматической. [c.440]
Проблема реакции системы на спонтанные флуктуации тесно связана с известным принципом Ле Шателье — Брауна в классической термодинамике (или принципом демпфирования ). Этот принцип гласит [143] [c.10]
Приведенная на рис. 32 диаграмма полностью подтверждает полученные в настоящем параграфе результаты. Кроме того, из нее видно, что нри таком сравнительно медленном течении колебательная система возбуждается за счет теплоподвода и потока внутренней энергии, а взаимодействие системы с потоком кинетической энергии ведет к сильному демпфированию колебаний. [c.168]
Ранее (стр. 24 — 29) упоминалось, что в спектрофотометрах с оптическим нулем (наиболее распространенном типе приборов, по данным настоящей книги) перо самописца приводится в движение электромеханической следящей системой. Она состоит из замкнутого контура, включающего гребенку или оптический ослабитель в канале сравнения, термоэлемент или другой приемник, усилитель и сервомотор (мотор отработки), который вводит или выводит оптический ослабитель из пучка сравнения.
Регулировка усиления цепи этой следящей системы оказывает определяющее влияние на работу спектрофотометра. Если усиление слишком мало, то система будет реагировать медленно и неполно, если слишком велико, то сервомотор ослабителя (и перо) будет давать очень сильные выбросы или даже переходить в режим автоколебаний. Демпфирование (успокоение) следящей системы можно регулировать временем отклика, поэтому время отклика и усиление должны быть подобраны таким образом, чтобы получить наилучший отклик следящий системы. В свою очередь с временем отклика должна согласовываться скорость сканирования. При сканировании с большей скоростью, чем может реагировать перо, ничего не приобретается, а теряется многое. [c.51]
Здесь Р — амплитуда, а — соответствующая скорость изменения амплитуды колебаний, которая реализовалась бы, если бы процесс i протекал изолированно от других процессов. Члены с положительными 8/ являются источниками усиления, а члены с отрицательными 8г — источниками потерь акустической энергии.
При 8>1 колебания нарастают и система неустойчива. Для удобства можно принять, что индекс i относится к одному из семи процессов, перечисленных выше. Относительный вклад различных факторов сильно зависит от моды колебаний, размера двигателя, типа ТРТ и т. д. Тем не менее наиболее важными факторами являются динамическая реакция (основной показатель неустойчивого горения) и демпфирование вследствие рассогласования фаз в потоке (часто — основной источник акустических потерь). [c.118]
ПОСТОЯНСТВОМ усиления и малым дрейфом нуля. На выходе усилителя включен миллиамперметр (на 10 ма) и катушка соленоида, восста-навливаюш,его балансировку при взаимодействии с магнитом. Демпфирование системы осуществляется отрицательной обратной связью по производной, осуществляемой цепочкой Вч,С . При такой системе демпфирования весы становятся нечувствительными к вибрации стола и к резкому изменению веса (падение навески с высоты [c.478]
Более универсальные, но малоэффективные системы демпфирования можно создать соответствующим взаимным расположением магнита,, связанного с подвижными деталями весов и катушкой электромагнита, уравновешивающего эти весы (Дрига [11] и Эдвардс и Белдуин [12]).
[c.76]
Наиболее совершенными являются системы демпфирования, сочетающиеся с магнитными системами уравновешивания весов, действующих по нулевому методу взвешивания (Мауер [16, 17], Эйро [18, 19] и др.). Принцип действия этих демпферов основан на том, что уравновешивающая сила при помощи соответствующих электрических схем изменяется пропорционально величине отклонения и скорости движения демпфируемых деталей весов. Более подробно некоторые такие демпферные системы рассмотрены выше в разделе магнитных систем уравновешивания. [c.77]
Если читатель не специалист по приборостроению, задача может показаться не вполне понятной. Но суть дела проста. В магнитном поле расположена легкая рамка, от малейшего сотрясения она колеблется — с этим надо бороться. Соль задачи — во множестве ограничений нельзя усложнять прибор, нельзя утяжелять рамку, нельзя применять жидкостное и магнитоиндукционное демпфирование… Дана невепольная система есть вещество (рамка) и магнитное поле, не взаимодействующие между собой.
Ответ очевиден. Надо привязать к рамке второе вещество, которое будет взаимодействовать с магнитным полем. Такое вещество — движущиеся заряды. На боковые поверхности рамки наносят электрет при колебаниях, т. е. при движении рамки в магнитном поле, позникает сила Лоренца, пропорциональная скорости перемещения зарядов и гасящая колебания (а. с. 481844). [c.114]
Наличие в системе подачи топлива полостей неза-полняе.мых топливом нежелательно. Воздух в этих полостях, растворяясь в топливе при повышении давления, может удерживаться фильтром, отчего сопротивление его будет возрастать. Если такие полости устраивать с целью демпфирования колебаний давления, они могут выполнять свою роль только как жидкостные демпферы, а не воздушные. [c.40]
Рассмотрев различные режимы работы ПМИМ при различных типах воздействий вынуждающей силы, можно выявить параметры, которые, будучи связанными с конструктивными характеристиками ПМИМ, отражали бы его динамические свойства.
Такими параметрами могут быть постоянная времени определяющая демпфирование собственных колебаний звена постоянная времени Гз, определяющая раскачивание собственных колебаний устройства отношение которое является комплексным показателем, отражающим колебательность исследуемой системы время регулирования /р, т. е. время в течение которого выходной параметр ПМИМ достигает установившегося значения после единичного скачкообразного возмущения, поданного на его вход частота собственных колебаний ПМИМ со,]. [c.276]
Зависимость р от отношения и/со при различных коэффициентах (рис. 80, а) показывают, что демпфирование значительно снижает aмпJштyды в области, близкой к резонансу, и мало влияет на амплитуду, когда частота вынуждающей силы отличается от частоты собственных колебаний системы. [c.112]
Одним из существенных факторов, порождающих вибрации, является неустойчивость равновесия деталей, обусловленная неопределенностью их базирования в ма1Ш1не.
Это объясняется тем, что часто конструктивные решения машины обусловливают возможность деталей изменять свое относительное положение по мере изменения силового поля, образованного многочисленными силами, действующими на технологические системы. Например, по мере изменения направления тех или иных сил технологической системы может наблюдаться раскрытие стыков между детгшями. Таким образом, деталь до приложения силы, лишенная шести степеней свободы, получая одну или несколько степеней свободы, приобретает консольно расположенную массу, которой достаточно малейшего толчка, чтобы возбудить ее колебания. Однако движения этих деталей ограш-чены, как правило, в обоих направлениях смежными с ними деталями. Входя в контакт с этими деталями, колеблющаяся деталь передает им колебания, а последние, вследствие наличия собственных масс, жесткостей и коэффициентов демпфирования у этих деталей, приобретают иной характер. Одновременно смежные детали оказывают влияние на колебания первой детали, ограничивая амплитуды и изменяя частоту ее колебаний.
[c.57]
Уравнения (73) — (74) определяют собственные частоты 05о системы, форму колебаний вала из(2). Демпфирование колебаний в системе ротор — подпшпники будем характеризовать коэффициентом рассеяния [c.69]
Изменение толщины кожуха выявляет слабую зависимость коэффициентов демпфирования от данного параметра, с увеличением толщины кожуха до определенного значения определяющие коэффициенты демпфирования возрастают, а затем изменяются незначительно, уменьшаясь с дальнейшим утолщением кожуха. Этот факт свидетельствует о том, что на демпфирующие характеристики структурно-неоднородной системы основное влияние оказывает не количество вязкоупругого материала, а наличие в системе близких собственных частот. Чтобы добиться максимального демпфирования колебаний, необходимо такпм образом подобрать нсесткость кожуха, чтобы его основные частоты были близки тем собственным частотам стержня 7, которые требуется задемпфировать. Скорость затухания свободных колебаний можно увеличить за счет выбора стеклопластиков с оптимальным значением модуля Ег, который зависит, в частности, от схемы армирования, вида нанолнителя, степени наполнения, материала стеклопластикового кожуха, а также путем выбора оптимального кожуха.
[c.151]
Причины нестабильности размеров могут быть различными. Основная причина появления отклонений типа а заключается в непрерывных флуктуациях температуры, давления и состава (при экструзии композиций) расплава. Отклонения в размерах типа б обычно связаны с дефектами конструкции головки. В разд. 7.13 отмечалось, что способность системы к демпфированию поступающих на вход композиционных неоднородностей определяется видом функции распределения времен пребывания (РВП). Трудно ожидать, что узкие функции РВП, типичные для существующего в головках, потока под давлением будут существенно уменьшать концентрационную или температурную неоднородность за счет смешения. Следовательно, на входе в головку необходимо обеспечить достаточно высокую стабильность температуры и давления, которая определяется конструкцией установленного перед головкой пластицирующего и транспортирующего расплав оборудования. Неправильно организованная транспортировка твердых частиц полимера, разрушение пробки, неполное плавление, малоэффективное смешение или его отсутствие вследствие чрезмерной глубины канала в зоне гомогенизации, отсутствие смесительных или фильтрующих устройств может привести к значительным колебаниям температуры и давления поступающего к головке расплава.
Примеры допустимых и недопустимых колебаний температуры и давления расплава ПЭНП на входе в головку приведены на рис. 13.3. [c.462]
Пример. Выясним, какими должны быть ЛАХ и ЛФХ разомкнутого контура рассмотренной в приме)5ах в параграфах 4.2 и 4.3 системы, чтобы она была устойчива. ЛАХ и ЛФХ разомкнутого контура получим, сложив ЛАХ и ЛФХ интегрирующего и колебательного звеньев. Предположим сначала, что Тз замкнутая система устойчива, так как имеются запасы пофазефзац и по амплитуде зап- Однако при уменьшении коэффициента относительного демпфирования 2 система может стать неустойчивой. Устойчивость системы может также нарушиться при увеличении коэффициента усиления К- Если Т > то при К > I система неустойчива (рис. 4.8, б). Приведенные выиоды об устойчивости системы полностью согласуются с результатами анализа системы, приведенного в примерах (см. параграфы 4.2 и 4.3). [c.121]
Пусть колебательная система имеет те же параметры, что были использованы в численном примере 23.
Единственное отличие будет заключаться в том, что потерями на излучение акустической энергии во внешнюю среду пренебрегать не будем. На рис. 33 приведены величины (О и V, полученные для разных гармоник без учета потерь на излучение. Если учесть эти потери, то V и со для первой гармоники вряд ли изменятся сколько-нибудь заметным образом. Вторая и третья гармоники и без учета потерь на излучение задемпфированы достаточно сильно (V 0), учет потерь на излучение лишь усилит это демпфирование. Что касается четвертой гармоники, то без учета потерь на излучение она, как и первая гармоника, почти нейтральна. Однако учет потерь резко изменит это положение, так как частота этой гармоники в 4,5 раза превосходит частоту основного тона, а потери на излучение возрастут, следовательно, в 20 раз. Это соображение позволяет считать все гармоники выше третьей задемп-фированными значительно сильнее первой. Будем поэтому в последующих расчетах учитывать лишь три первые гармоники. [c.265]
Технические основы
1. Применение вибротехнических компонентов
1.1 Общая информацияТехника виброизоляции является областью, которая приобретает все большее значение. Это обусловлено возрастающими требованиями к сроку службы механизмов и агрегатов без технического обслуживания. Технологии виброизоляции позволяют также снижать уровень шума,что повышает спрос на легкие строительные энергосберегающие конструкции. Наш опыт поставок (например, для железнодорожной промышленности) мы используем и при создании стандартных конструкционных элементов. Во всех проблемных случаях виброизоляции, которые не удается решить с помощью этих элементов, наши технические консультанты помогут найти индивидуальное решение. Все данные, описания, указания и т.д. приведены с максимальной точностью, но без гарантии. Они не освобождают потребителя от собственных испытаний. Требования возмещения убытков, вытекающие из содержания настоящего издания, независимо от их вида и правовой базы, исключаются. 1.2 Свойства эластомеров Основные свойства эластомерного материала определяются используемым базовым полимером. Однако, технические свойства конечного продукта могут изменяться в определенных пределах за счет рецептуры смесей и целенаправленно подгоняться для нужд потребителя. В результате конечные свойства являются компромиссом между различными и часто противоположными свойствами. Широкое разнообразие свойств применяемых базовых эластомеров и целый ряд специальных рецептурных добавок не оставляют сомнения, что можно получить эластомерный материал почти для любой области применения. |
Помимо приведенных здесь составов, для специальных случаев применения существует более 100 вариантов смесей. Профессиональная команда наших химиков и инженеров всегда готова дать консультацию нашим заказчикам. 1.3 Выбор материала. При проектировании эластомерных пружин и выборе материала для них необходимо принимать во внимание «динамическую жесткость». Динамическая жесткость обычно возрастает при: Для эластомерных материалов с низкими демпфирующими свойствами (напр., мягкие смеси из натурального каучука) ею можно пренебречь. Тем не менее, если используются смеси с высокими демпфирующими свойствами, динамическая составляющая может превосходить статическую в несколько раз. |
1.3.1 Свойства некоторых эластомерных смесей
| Базовый эластомер | Натуральный каучук | Акрилонитрил- бутадиен-каучук | Этилен-акрилат- каучук | Этилен-пропилен- каучук |
| Смеси, краткое обозначение по ISO | NR NR 11 | NBR NBR 68 | AEM AEM 23 | EPDM EPDM 22 |
| Значения твердости (по Шору А) | 35–80 | 45–85 | 55–85 | 40–80 |
| Прочность при растяжении | очень хор. | хорошая | хорошая | хорошая |
| Эластичность по отскоку | средн. до оч. высокой | средн. | низкая | средн. |
| Демпфирование | низкая | средн. | высокое | средн. |
| Эластичность при низк. темпер. (до °C) | –45 | –20 | –20 | –40 |
| Рабочая температура (°C) | +70 | +90 | +120 | +110 |
| Кратковременная температура (°C) | +90 | +110 | +150 | +140 |
| Устойчивость к старению и атмосферным влияниям | от средн. до хор. | хорошая | очень хор. | очень хор. |
| Устойчивость к мин. маслам | незначительное | очень хор. | средн. | незначительное |
| Устойчивость к кислотам | хорошая | хорошая | удовл. | очень хор. |
| Устойчивость к щелочам | хорошая | хорошая | удовл. | очень хор. |
1.4 Гашение и изоляция колебанийПрактически повсюду, где корпус или массы движутся равномерно или ускоряются, в системе возникают колебания. Эти колебания создают шум или вибрацию и приводят к дополнительной нагрузке на элементы конструкции.Колебания возникают только в динамических системах, т.е. в системах, имеющих массу и пружину. В то время как «массу» на практике в большинстве случаев легко определить, «пружину» с первого взгляда идентифицировать труднее. Так, роль пружины могут играть корпус, опора или рама транспортного средства. Целью процесса гашения колебаний или виброизоляции является сведение к минимуму возникающих амплитуд колебаний с помощью применения дополнительных, точно подобранных, амортизаторов или пружин. Теоретические основы гашения колебаний и виброизоляции могут быть проиллюстрированы на примере одномассовой схемы колебаний: | Исходя из уравнения движения одномассовой схемы колебаний, можно вывести |
Из передаточной функции (→Рис. 19.2) для колебаний одномассовой демпфирующей системы можно сделать следующие выводы: • Усилия на опоре достигают своих максимальных и, таким образом, критических значений, когда частота возмущения совпадает с собственной частотой (λ ≈ 1). В этом случае говорят о резонансе. • В области частот до λ ≤ всегда происходит увеличение возмущения. Это – область гашения колебаний. • В сверхкритической области, начиная с частоты λ > , реакция опоры всегда меньше, чем возмущающая сила. В этих случаях говорят о виброизоляции. Демпфирование нежелательно, так как оно увеличивает реакцию опоры. Для такого случая применения, например, для опоры стационарных механизмов, используются эластомерные пружины с низким демпфированием. • Чем меньше собственная частота по отношению к возмущающей частоте, тем лучше виброизоляция системы. Мерой снижения возмущающего усилия в опоре и, соответственно, хорошей виброизоляции является степень изоляции:
Собственная частота ne одномассовой схемы колебаний
| Из обоих вышеуказанных уравнений для одномассовой схемы колебаний следует (D = 0) →Рис. 19.2. 1.5 Пример выбора опоры Механизм, который работает с частотой вращения от 1200 об/мин. до 2500 об/мин., должен быть установлен на виброизоляционную опору. Целью является передача до 20% вибрационных усилий, возникающих в механизме в результате дисбаланса сил, на фундамент (т.е. M ≥ 80%). |
1.5.1 Решение:• Определение статической деформации, необходимой для M = 80% Передаточная функция (→Рис. 19.2) показывает, что при равномерной статической деформации степень изоляции падает при уменьшении возмущающей частоты. Таким образом, для определения необходимой статической деформации должна использоваться минимальная возмущающая частота. При n=1200 об/мин. для M ≥ 80% получается статическая деформация s ≥ 3,7 мм (→Рис. 19.3) • Расчет статических реакций опоры F1 = 3300 Н | • Выбор подходящей опоры • Обратная проверка степени изоляции Для выбранной опоры, для каждой точки закрепления, получается степень изоляции M ≥ 80%. |
2. Описание продуктов
2.1 Сайлентблоки
2.1.1 Общая информация
Сайлентблоки – это широко используемые конструкционные элементы, в которых внутренняя и внешняя прецизионные втулки прочно связаны завулканизированным слоем эластомера. Сайлентблоки гасят или изолируют радиальные и осевые колебания. Они воспринимают усилия, возникающие в результате радиальных отклонений карданного шарнира. Изготавливается около 1000 размеров, которые применяются при радиальных усилиях до 300 кН.
Особенностью сайлентблоков является то, что они изготовлены из предварительно напряженного эластомера. Это достигается с помощью пластической деформации (калибрования) внутренней втулки или обоймы после вулканизации.
Вследствие этого, при радиальной нагрузке, в допустимых пределах, резина только незначительно работает на растяжение. Таким образом, срок службы существенно увеличивается.
Благодаря прочному, за счет вулканизации, сцеплению между резиной и металлом, между ними при нагрузке не возникает «скольжения». Более того, у них надежная посадка вследствие небольшой предварительной деформации резины в обойме.
В номенклатурном перечне, кроме размеров, даны максимальные значения только статических нагрузок или эпизодических (<100).
При динамических нагрузках значения sa, sr и ϕ должны быть сокращены примерно на 50%. При максимальной карданной нагрузке исходят из того, что резина между втулками может сжиматься приблизительно на 1/6 своей толщины.
2.1.2 Применение
Сайлентблоки не требуют технического обслуживания, так как вода и грязь практически не оказывают влияния на их свойства, и, в отличие от подшипника скольжения, они не нуждаются в смазке. Они обеспечивают шумоизоляцию, благодаря эластомерному слою, и компенсируют допуски изготовления других конструкционных элементов. Типичным случаем применения являются эластичные карданные шарниры на вибрирующих храповых механизмах или эластичные опоры для валов, осей и рулевого управления. При применении сайлентблоков для связи элементов конструкции с «почти замкнутой силовой системой» используют различную жесткость сайлентблоков в различных направлениях.
2.1.3 Выбор
При выборе сайлентблоков рекомендуется следующая последовательность:
• Установить максимальную величину нагрузки (соотв., макс. угол).
Пример: Mt = 4 Нм, Fa = 250 Н, Fr = 500 Н
• Выбрать предварительно сайлентблок, максимальные значения которого в 1–3 раза выше этих значений.
Пример:
– 01 18 041 60 NR 11
– 01 18 039 60 NR 11
– 01 18 156 60 NR 11
• Выбрать:
– упругие свойства
– геометрические размеры
• Выбрано: 0118 039 60 NR 11
2.2 Сферические опоры
2.2.1 Общая информация
Сферические опоры – это конструкционные элементы, у которых внутренняя сфера и внешняя оболочка прочно связаны друг с другом завулканизированным слоем эластомера.
Как и сайлентблоки, сферические опоры производства Freudenberg отличаются тем, что они изготовлены из предварительно напряженного эластомера. От выбора калибровки, т.е. от степени этой деформации, существенно зависит срок службы. Это особенно важно для элементов, подвергающихся высоким нагрузкам, как, напр., для приводных механизмов ICE.
2.2.2 Применение
Сферические опоры применяются исключительно как карданные шарниры, подверженные нагрузке кручения в трех плоскостях.
Сферические опоры, как и сайлентблоки, не требуют технического обслуживания, так как вода и грязь практически не влияют на их свойства. Они не распространяют звук и допускают угловое движение 4°–9° по трем осям. Они применяются в подшипниках или рычагах тормозных систем автобусов и грузовых автомобилей. В железнодорожной промышленности сферические опоры тысячекратно оправдали себя в приводных механизмах (многорычажные соединения).
2.2.3 Стандартная продукция
Т.к. сферические опоры обычно изготавливаются для специальных целей, на складе имеется только небольшой запас стандартных изделий.
2.3 Приборные опоры
2.3.1 Общая информация
Эти конструкционные элементы применяются, в основном, для виброизоляции электронных устройств, измерительных приборов и аппаратов точного приборостроения. От этих опор часто требуется защита измерительной аппаратуры или приборов от вибрации и ударов, исходящих от точек крепления оборудования. Таким образом, опоры служат для защиты чувствительных приборов от внешней ударной нагрузки, в особенности, при применении в передвижных установках.
Другое назначение – это звукоизоляция, напр., в небольших электродвигателях и насосах, которые должны фиксироваться на «резонаторах» (металлических щитках).
Опоры устроены так, что они могут выдерживать нагрузки сжатия, растяжения и сдвига.
2.4 О-образные опоры
2.4.1 Общая информация
О-образные опоры из-за их относительно мягкой характеристики подрессоривания называют низкочастотными опорами.
Они состоят из кольцеобразного резинового элемента, к которому с противоположных сторон привулканизированы металлические пластины с крепежными винтами. Эта конструкция обеспечивает хорошую виброизоляцию при низких нагрузках, например, при монтаже чувствительных электронных приборов и приборов точной механики.
Для разработки каталожных изделий используется высокоэластичный натуральный каучук. Для определенных случаев применения может оказаться целесообразным применение высокодемпфирующих составов. O-образные опоры могут быть изготовлены на имеющихся оснастках с применением специальных смесей.
О-опоры имеют различные упругие характеристики подрессоривания в трех направлениях координат X, Y, и Z. Опоры мягкие по оси X, несколько жестче по оси Y и наиболее жесткие по оси Z. Таким образом, в зависимости от расположения, может быть достигнута оптимальная виброизоляция.
2.4.2 Применение
О-опоры служат для виброустойчивого крепления измерительных приборов, электрических или электронных элементов конструкций и групп элементов, а также для закрепления легких агрегатов и приборов точной механики. Они обеспечивают исключительную виброизоляцию также против ударов или колебаний, исходящих из окружающей среды.
2.5 МО-опоры
2.5.1 Общая информация
MO-опоры – это разъемные опоры, которые состоят из резино-металлической (завулканизированная стальная втулка) и резиновой частей. Они поставляются в сборе, как это показано на рисунках. Их форма такова, что жесткость в направлениях X и Y одинакова. Основная деформация происходит в направлении Z и, таким образом, достигается хороший изолирующий эффект.
МО-опоры устанавливаются так, чтобы резино-металлическая часть крепилась непосредственно к изолируемому конструкционному элементу. На →Рис. 19.5 и →Рис. 19.6 представлены варианты установки и направление сил (Z). Резиновая часть устанавливается с шайбой.
При этом нужно следить за тем, чтобы монтажные отверстия на обеих сторонах (для 3918755 только со стороны резиновой части) имели радиусы для предотвращения повреждений резины при монтаже и работе.
2.5.2 Применение
МО-опоры используются в автомобилестроении при установке основных и вспомогательных агрегатов, радиаторов, вплоть до маленьких кабин, а также в судостроении для стыковки вентиляционных каналов или трубопроводов отходящих газов.
Кроме звукоизоляции, эти опоры могут применяться для компенсации теплового расширения и технологических неточностей.
2.6 Двойные U-опоры
2.6.1 Общая информация
Двойные U-опоры служат для виброизоляции и защиты от ударов. Их форма такова, что жесткость в трех рабочих направлениях, X,Y и Z, (→ Рис.) различна. Изготавливаются опоры четырех размеров из трех резиновых смесей разной твердости по Шору.
Максимальные нагрузки на опору доходят до 2000 Н.
Двойные U-опоры должны всегда располагаться так, чтобы нагрузки от ударов и колебаний приходились на направление Z или Y, так как упругость в этих направлениях максимальная. При этом опора может подстраиваться под усилия установленного агрегата путем поворота плоскости XY по оси Z. В результате, различные жесткости по X и Y меняются местами.
Эпизодически допускаются сильные ударные нагрузки, при этом может достигаться троекратное значение статического прогиба sZ.
Применение двойных U-опор является оптимальным при одинаковых опорных усилиях (и, таким образом, при одинаковой статической деформации) в отдельных точках опоры. По возможности, должны использоваться опоры одинакового размера.
2.6.2 Применение
Двойные U-опоры используются для крепления приборов и агрегатов, а также для стыковки вентиляционных каналов. Кроме звукоизоляции, эти опоры могут применяться для компенсации теплового расширения.
2.7.1 Общая информация
При высоких динамических нагрузках, особенно при одновременном действии напряжений сжатия и сдвига, лучше всего оправдали себя круглые опоры с «втянутым» резиновым контуром. Они служат намного дольше, чем круглые опоры с цилиндрическим профилем (так как диаметр резины у этих опор такой же или больше, чем диаметр металлических частей). Круглые опоры с цилиндрическим резиновым профилем, благодаря простой геометрии оснастки для вулканизации, являются недорогим альтернативным вариантом, преимущественно для нагрузок сжатия.
2.7.2 Выбор
Для выбора круглой опоры или буфера рекомендуется:
• определить максимальную величину нагрузки для отдельной опоры
• выбрать по каталогу круглую опору, максимальное значение которой в 1–2 раза превосходит это значение
• выбрать из этих опор, принимая во внимание:
– геометрические особенности установки
– распределение нагрузки (сдвиг, сжатие или сдвиг/сжатие)
– требуемую виброизоляцию
2.8 Конические опоры
2.8.1 Общая информация
Конические опоры – это эластичные соединительные элементы с широкими коническими внутренними и внешними муфтами.
Конические опоры гасят вертикальные колебания, напр., в подвеске двигателя, и в то же время принимают на себя горизонтальные усилия, напр., при торможении. Они обеспечивают надежную опору и достаточную звукоизоляцию корпуса. Конструкционный элемент должен закрепляться горизонтально (для предотвращения перекоса). Существует большое разнообразие форм конических опор, особенно в автомобилестроении, в частности, для крепления кузова.
Конические опоры изготавливаются из высокоэластичных составов натурального каучука, не подверженных старению и воздействию озона. Благодаря специфическому контуру, напряжение сжатия-сдвига в резине при нагрузке не изменяется, это обеспечивает длительный срок службы опоры. Эластомер прочно соединен с внутренней и внешней муфтами вулканизацией, это увеличивает срок службы (относительное движение между металлом и резиной исключается) и, по сравнению с опорами, не имеющими такого соединения, существенно снижает вероятность смещения конструкции.
Конические опоры 5718065, 5718224 и 5718228 имеют различную жесткость в направлениях X и Y. Это достигается с помощью выемок (карманов) в эластомере. При установке двигателей крутящий момент можно мягко гасить, благодаря соответствующему положению опоры на шасси или раме, что способствует повышенной плавности хода и уменьшению колебаний, возникающих в точках крепления.
2.8.2 Применение
Конические опоры особенно подходят для установки двигателей, агрегатов и навесного оборудования (напр., кабин) как для стационарных случаев, так и для применения в транспортных средствах всех видов.
Конические опоры 5718 013, 5718 019, 5718 060 и 5718 226 могут поставляться с упорными и центрирующими шайбами. Для 5718 220 и 5718 224 эти упорные шайбы входят в объем поставки. Даже при экстремальных нагрузках они препятствуют перегрузке, благодаря встроенному «ограничителю хода» в направлении Z. Кроме того, упорные шайбы защищают натуральный каучук от механических повреждений и конденсатов среды (напр., масла). Характеристики демпфирования, как видно из диаграмм этого раздела, у конических опор с центрирующей шайбой остаются линейными в широком диапазоне, затем, в зависимости от конструкции, резко возрастают. Таким образом, эпизодические удары, до троекратно допустимой нагрузки, надежно гасятся.
Классическая область применения этих конических опор с упорными шайбами – установка кабин, где необходима защита от перегрузок (безопасность кузова). Они также хорошо зарекомендовали себя при установке двигателей, напр., в строительных машинах.
2.8.3 Упорные шайбы
Конические опоры 5718 013, 5718 019 и 5718 226 поставляются с соответствующими упорными шайбами 7718 007, 7718 003 или 3918 005. Упорные шайбы имеют на одной стороне привулканизированный эластомерный слой для предотвращения контакта металл-металл между внешней муфтой и упорной шайбой во время подрессоривания. Нарезной крепежный болт страхует опору при перегрузках, достигающих тройного значения допустимых пределов.
2.8.4 Центрирующие шайбы
Конические опоры 5718 013, 5718 019, 5718 060 и 5718 226 могут укомплектовываться специальными центрирующими шайбами 4018 036, 4018 035, 4018 037, 4018 038 и 4018 039. Это обеспечивает центровку крепежного болта во внешней муфте конической опоры. При перегрузке металлический контакт между центрирующей шайбой и фланцем конической опоры предотвращается, благодаря резиновому выступу на крепежном фланце.
2.9 V-опоры
2.9.1 Общая информация
V-опоры идеально подходят для изоляции активной и пассивной вибрации и звукоизоляции. Они просты при монтаже, не требуют технического обслуживания и отличаются, несмотря на низкую высоту конструкции, высокой допустимой нагрузкой в вертикальном направлении (направление Z). Это обеспечивает хорошую изоляцию также при более низких возмущающих частотах. Одинаковая жесткость в обоих горизонтальных направлениях (X и Y) предотвращает «плавание», т.е. боковое смещение изолируемого агрегата, механизма или двигателя.
Верхняя, колоколообразная, часть опоры защищает находящийся внутри, устойчивый к старению и действию озона, высокоэластичный натуральный каучук от механических повреждений и конденсата среды (напр., масла). Это обеспечивает более эффективную работу пружины при повышенных нагрузках в направлении Z. Т.е. при высоких нагрузках деформация надежно ограничивается. При экстремальной нагрузке верхняя и нижняя части опоры замыкаются. Это означает, что возрастающая деформация и тонкий резиновый слой в точке соприкосновения на нижней части предотвращают резкий удар металла о металл. V-опоры защищены от коррозии, благодаря оцинкованной или фосфатированной поверхности.
2.9.2 Применение
V-опоры применяются для установки двигателей внутреннего сгорания и электродвигателей, насосов, компрессоров и оснасток.
• V-опоры с резьбовым креплением и упором
Эти V-опоры особенно подходят для крепления навесных агрегатов и конструкций на транспортных средствах, будь то строительные машины, специальные транспортные средства или суда. Конечный упор предотвращает опасные для резины напряжения при растяжении. Он действует как ограничитель хода в направлениях X, Y или Z. При такой конструкции резиновая подушка препятствует резкому металлическому удару при перегрузке.
• Специальные конструкции
По желанию, для специальных случаев применения (напр., в пищевой или химической промышленности и судостроении), мы поставляем V-опоры из нержавеющей стали и из специальных каучуковых смесей, которые подбираются нами для каждого конкретного случая. Эти опоры можно заказать как с резьбовым креплением, так и с упором. Опоры изготавливаются по специальному заказу и не хранятся на складе стандартной продукции.
2.10 Опоры для механизмов
2.10.1 Общая информация
Опоры для механизмов служат для гашения колебаний и шумоизоляции. Их применение позволяет существенно снизить вибрацию механизмов и агрегатов, которая передается на корпус или фундамент здания. Механические опоры применяются, главным образом, при установке тяжелых механизмов и двигателей (напр., компрессоров, прокатных станов, агрегатов аварийного электроснабжения).
Благодаря своей специальной форме, они защищают встроенные плоские опоры от механических повреждений и масла. Работа встроенной плоской опоры одновременно на сжатие и сдвиг увеличивает срок службы и обеспечивает хорошую виброизоляцию, даже при малой возмущающей частоте (т.е. низких оборотах).
Если необходимо, через стандартные отверстия и резьбы опоры могут легко крепиться к фундаментам и механизмам. Анкерное крепление к фундаменту позволяет перенести нагрузки сжатия (направление Z) и нагрузки сдвига (X и Y) на опору.
2.10.2 Применение
Различная жесткость подрессоривания в трех направлениях характеризует уникальное в своем роде преимущество этой опоры для механизмов. Максимальная упругость достигается вдоль горизонтальной плоскости (направление Х) самая большая жесткость – поперек горизонтальной плоскости (направление Y). Жесткость в системе координат Z : X : Y в отдельных типах имеет следующие значения:
| Тип А | 1 : | 0,25 : | 2,0 |
| Тип B | 1 : | 0,25 : | 2,5 |
| Тип HD | 1 : | 0,25 : | 1,25 |
Эта разная жесткость может быть выгодно использована, напр., для компрессора или двигателя, где крепление установлено так, что максимальные колебания приходятся на направление Х. При небольших возмущающих частотах эффективная виброизоляция может быть достигнута за счет двойной установки (две опоры для механизмов, соединены фланцами).
2.11 М-опоры
2.11.1 Общая информация
М-опоры служат для безанкерного крепления и установки тяжелых агрегатов. Они позволяют нивелировать стоящие на них механизмы, гасят вибрацию и защищают окружающую среду, снижая уровень шума. Просто монтируемые М-опоры облегчают установку и перестановку тяжелых механизмов, так как они не крепятся жестко к фундаменту и имеют большой диапазон регулировки по высоте.
Для М-опор используются специальные маслостойкие смеси на основе нитрил-каучука (пербунан). Регулировка по высоте в широком диапазоне осуществляется посредством регулировочного винта и возможна также в установленном состоянии. Большая площадь контакта основания механизма с крышкой опоры обеспечивает стабильность.
2.11.2 Применение
Для М-опор основание механизма должно лежать на опоре, как это представлено на схеме. Регулировка по высоте производится вращением регулировочного винта, который закреплен на стойке между верхней частью и эластомером. Гайка служит для закрепления основания механизма на опоре. Таким образом, гайка в верхней части опоры не перегружается весом механизма. Основание механизма ни в коем случае не должно устанавливаться между двумя гайками, чтобы производить регулировку высоты по длине винта.
2.11.3 Специальные конструкции
Для специальных случаев применения (напр., для пищевой или химической промышленности, судостроения) мы можем поставлять М-опоры из нержавеющей стали и из специальных каучуковых смесей. Так как они изготавливаются по специальному заказу, они не хранятся на складе стандартной продукции.
2.12 Плоские опоры
2.12.1 Общая информация
Плоские опоры – это элементы для индивидуального случая применения. Они используются для установки механизмов, двигателей или узлов в машино- и автомобилестроении. Опоры, как готовые конструкционные элементы, легко устанавливаются в соответствующий узел соединительными фланцами.
Характеристики подрессоривания могут регулироваться с учетом собственной частоты остальной конструкции.
2.12.2 Применение
Плоские опоры, в зависимости от типа установки или требуемой виброизоляции, могут воспринимать нагрузки сжатия, сдвига или сжатия-сдвига одновременно (опора, расположенная под определенным углом). Оптимальное использование и при этом максимальная динамическая нагрузка опоры достигаются при напряжении сжатие-сдвиг. Допустимая нагрузка зависит от площади резиновой поверхности, формы, толщины и твердости резины. Для длительного использования плоских опор, наряду со статической нагрузкой, нужно также учитывать динамические усилия и деформацию.
Допустимые статические нагрузки сжатия в направлении Z и сдвиг в направлениях X и Y, а также деформация могут быть взяты из таблицы номенклатуры изделий.
2.13 Гидравлические опоры
2.13.1 Общая информация
Гидроопора представляет собой гидравлическую демпфирующую опору, которая позволяет решить беспокоящую инженеров проблему – как закрепить массу, которая подвергается широкому спектру возмущающих частот. Например, если возникают низкие возмущающие частоты – между 5 Гц и 25 Гц –, требуются высокие демпфирующие усилия для гашения собственной частоты системы. С другой стороны, требуются высокие изоляционные свойства выше этой собственной критической частоты (сверхкритическое крепление).
Обычные конструкционные элементы из резины и металла предназначены для использования в механизмах, агрегатах, двигателях и т.д., у которых возмущающая частота настолько высока, что необходимо сверхкритическое крепление, тогда диапазон собственных частот преодолевается относительно быстро.
Гидроопоры зарекомендовали себя преимущественно в автомобилестроении и транспортных средствах всех видов, будь то установка небольших судовых двигателей или крепление небольших дизельных моторов в строительных машинах различных размеров.
В этих случаях соответствующий узел должен устанавливаться по возможности мягко, чтобы добиться хорошей звукоизоляции.
При низкочастотных возмущениях вблизи собственных частот системы пружина-масса такая мягкая установка приводит к недопустимо высоким амплитудам. В случае резонанса, напр., при прохождении неровного дорожного полотна или при волнении моря, это возмущение может стать критическим для работы агрегата.
Следующая проблема, которая может быть решена, благодаря применению гидроопор, – это так называемая, холостая вибрация. Более низкие обороты холостого хода (для экономии топлива), в особенности в двигателях, имеющих от 1 до 4 цилиндров, приводят к ухудшению характеристик холостого хода, так как возмущающая частота двигателя приближается к собственной частоте системы. Чтобы достичь хорошей виброизоляции, собственная жесткость демпфирования определенного элемента может быть существенно сокращена, благодаря наличию гидроопоры, подрессоривающей в определенном диапазоне частот.
2.13.2 Примечания
Чтобы добиться демпфирования, зависящего от частоты, необходимо установить амортизатор последовательно с пружиной. Так как такая последовательная установка не может передавать статические усилия, то параллельно нужно подключить дополнительную пружину. На →Рис. 19.7 показана такая конструкция, где c1 упругая пружина, c2 гасящая пружина, а d – амортизатор.
Эту схему одномассового осциллятора теперь нужно «подключить» в элемент конструкции. Возможное решение представлено на →Рис. 19.8. На нем показано сечение гидроопоры. Можно видеть, что интегрированная упругая пружина и гасящая пружина, а также укрепленная на ней крышка запирают жидкость гидроопоры. При нагрузке опора подрессоривает, и жидкость гидроопоры выжимается из выходного отверстия. Таким образом, достигается желаемое демпфирование.
Из механической модели видно, что при низких возмущающих частотах почти все усилие передается через пружину c1, так как усилия, генерируемые амортизатором при этой частоте, ничтожны. В этом случае жесткость системы определяется c1, гашения колебаний еще нет. Если возмущающая частота повышается, при последовательном соединении происходит передача нагрузки от амортизатора d и гасящей пружины c2, что повышает общую жесткость системы, а также вызывает демпфирование. Начиная с определенной частоты, в амортизаторе больше не происходит относительного движения; обе пружины c1 и c2 располагаются параллельно и способствуют динамической фиксации опоры при одновременном уменьшении демпфирования.
Так как максимальное демпфирование опоры в области собственных частот может быть установлено таким образом, чтобы оно лежало в области собственной частоты закрепленного агрегата, можно существенно сократить основную и начальную жесткость c1 опоры по сравнению с таковой обычного резинового крепления.
2.13.3 Применение
Гидравлические демпфирующие резиновые опоры всегда применяются там, где возникает широкополосный спектр возмущения и собственные частоты системы находятся в пределах этого спектра, т.е. в системах, требующих хорошей изоляции при высоких частотах и высокой степени демпфирования в области резонанса.
На →Рис. 19.9 показаны значения ускорения в вертикальном и горизонтальном направлении, измеренные у основания лодочного мотора. Максимальные ускорения, возникающие при обычном резиновом креплении, при применении гидроопоры почти полностью исчезают во всем диапазоне частот вращения. Хотя опоры в этом случае устанавливаются вертикально и имеют в этом направлении свое демпфирование, они улучшают передаточные свойства также в горизонтальном направлении.
Влияние гидроопоры на уменьшение ускорения в двигателе и рельсах сиденья водителя в легковом автомобиле наглядно показывает →Рис. 19.10.
2.13.4 Стандартные гидроопоры
Благодаря своей форме и подвижному резиновому корпусу, эти конструкционные элементы имеют мягкую характеристику демпфирования в осевом направлении и, следовательно, большое статическое подрессоривание. Таким образом, обеспечивается относительно низкая частота резонанса и высокая степень изоляции в сверхкритической области. Статические осевые характеристики (направление Z) для трех стандартных гидроопор показаны на →Рис. 19.11. То, что демпфирование, т.е. угол потерь этой опоры, не зависит от возмущающей частоты, показано на →Рис. 19.12. Нужно также обратить внимание на то, что у стандартных гидроопор степень динамического подрессоривания медленно растет при повышенных частотах (→Рис. 19.13). Это приводит в сверхкритической области к незначительному уменьшению степени изоляции. Обратите внимание на то, что, как уже упоминалось, резонансная частота системы пружина-масса должна лежать в области максимального демпфирования, чтобы как можно больше сократить амплитуду.
2.14 Гидравлическая опора VL
2.14.1 Общая информация
Динамические процессы, происходящие в мощных машинах, агрегатах и установках, вызывают сотрясения, вибрацию и шумы, снижающие для обслуживающего персонала комфортность работы на них: возникают неприятная или недопустимо сильная вибрация и шум или экстремальные динамические нагрузки, что может привести к повреждению частей оборудования.
Демпфирование вибрации и акустическая изоляция механического шума в элементах опор все это эффективные меры для снижения нагрузок на людей и машины до приемлемого и невредного уровня. Встроенный в гидравлических опорах VL гидравлический демпфер ограничивает до минимума передачу вибрации. Механизм действия, известный по опорам осевого смещения, в гидравлической опоре VL значительно усовершенствован. Повышенный уровень вибрации (резонансы) значительно снижается.
2.14.2 Область применения и технические возможности
Опоры для кабин и двигателей сельскохозяйственных и строительных машин, напольных транспортных средств, машин лесного комплекса, коммунальных машин, судов, а также опоры навесных агрегатов, насосов и компрессоров. Другие сферы применения: опорные узлы машин и технологических установок/агрегатов со сложными явлениями резонанса.
В зависимости от твердости по Шору несущей пружины (45–65 Шор A) при упругих деформациях 5 мм возможна грузоподъемность в 150–420 кг.
Гидравлические опоры VL при небольших амплитудах колебания дают небольшое подрессоривание, которое достигает высокого уровня при более высоких амплитудах колебания.
2.14.3 Описание принципа действия гидравлической опоры VL
Гидравлическая опора VL состоит из конической пружины с шайбой осевого смещения или упорной шайбой, а также блока гидравлического гашения вибрации, состоящего из корпуса, мембраны и жидкости.
Укрепленная на конической пружине шайба осевого смещения разделяет заполненное жидкостью пространство и вместе с корпусом образует кольцевой зазор, через который жидкость протекает даже при малых скоростях перемещения. При больших скоростях перемещения или высоких частотах гидравлическое сопротивление сильно возрастает, так что обмен жидкости затрудняется. Деформации каркаса и мембраны обеспечивают необходимую для этого компенсацию объема и повышают жесткость гидравлической опоры VL.
Этот механизм обеспечивает характерное гашение вибрации в широком диапазоне.
2.15 Гидровтулка
2.15.1 Общая информация
Гидровтулки – это гидравлические демпфирующие конструкционные элементы для разнообразного применения в грузовых автомашинах и автобусах, строительных машинах и насосах. Они служат для крепления двигателей, кабин и навесных приборов.
Во многих технических системах конструктор часто сталкивается с проблемой крепления массы, которая возбуждается широким спектром частот. Для решения этой проблемы созданы гидровтулки и гидроопоры. Эти гидравлические демпфирующие резино-металлические элементы многократно оправдали себя, особенно как опоры для двигателей в легковых автомобилях и в транспортных средствах всех видов.
Конструкция гидровтулок объясняется далее.
2.15.2 Область применения и технические возможности
Область применения – там, где требуется высокая степень изоляции (статический прогиб до 5 мм, при высоких переменных нагрузках – около 3 мм) и одновременное подрессоривание. Если еще необходимо соединение элементов, гидровтулки являются экономически выгодным, технически современным решением.
Альтернативой могло бы быть обычное крепление системы с использованием эластомерной или стальной пружины и параллельно подсоединенного амортизатора. Если при этом еще требуется защита от отрыва, то понадобятся дополнительные и, возможно, требующие затрат технические решения.
Такой гидравлический демпфирующий элемент определенно более эффективен в сложных случаях применения, где возникают как низкие, так и высокие возмущающие частоты, напр., в двигателях внутреннего сгорания, в приводах с регулируемыми оборотами, в водительских кабинах и прессах. Проблема для этих механизмов в том, что возмущающая частота часто накладывается на собственную частоту системы.
Если механизм используется при таких условиях, т.е. с недостаточным демпфированием (без гидровтулки), наступит резонанс, который может привести к нежелательному нарушению комфорта людей и окружающей среды или даже к разрушению элементов конструкции.
Типичной областью применения гидровтулок является крепление кабин и двигателей на строительных машинах, тракторах, цеховых транспортных средствах, с/х машинах, на транспортных средствах, используемых в лесной промышленности и коммунальном хозяйстве, а также установка насосов, компрессоров и дополнительного оборудования.
2.15.3 Описание работы гидровтулок
Между двумя цилиндрическими металлическими элементами размещены две упругие пружины. Ниже и выше этих упругих пружин находятся две полости, соединенные между собой кольцеобразным каналом. С торца полости замыкаются демпфером. Полости и канал наполнены специальной жидкостью с пологой вязкостно-температурной характеристикой.
При радиальных нагрузках жидкость стремится перетечь через кольцеобразный канал из одной полости в другую, или демпфер расширяется. В зависимости от частоты, преобладает один или другой процесс, в результате достигается соответствующий угол потерь и динамическая жесткость:
• При малых частотах сопротивление потока незначительно. Угол потерь примерно соответствует таковому эластомерного материала. Динамическая жесткость определяется, в основном, упругой пружиной и примерно соответствует статическому значению.
• При увеличении частоты сопротивление потока, демпфирование и угол потерь возрастают. При возросшей массе жидкость не перекачивается, и демпфер растягивается. Таким образом, демпфер поддерживает нагрузку, и динамическая жесткость возрастает. В зависимости от состава резиновой смеси, геометрии конструкции и максимальной амплитуды угла потерь, достигается определенная частота.
• При больших частотах жидкость слишком инертна, чтобы перетечь в канал. Объем контролируется исключительно демпфером. Угол потерь уменьшается снова, и динамическая жесткость стабилизируется на определенном уровне.
Обе полости сконструированы так, что гидравлическое демпфирование в осевом направлении оказывается неэффективным. Таким образом, здесь полностью могут быть использованы хорошие изолирующие свойства именно резино-металлической пружины. За счет особенностей гидровтулки, без дополнительных конструкционных мер обеспечивается безопасная опора, напр., для вторичного подрессоривания (водительские кабины в строительных и с/х машинах).
Чтобы получить наиболее эффективные результаты при применении гидровтулки в опоре, следует убедиться, что собственная частота системы лежит в диапазоне максимального демпфирования опоры. В этом случае можно добиться высокой степени демпфирования резонансных колебаний и при этом хорошей изоляции в сверхкритической области.
: определение и формула — стенограмма видео и урока
Уравнение
Для механической системы легко понять затухающие гармонические колебания, изучив систему пружина-масса-демпфер. Как следует из названия, система с одинарной степенью свободы (SDOF) пружина-масса-амортизатор состоит из пружины, массы и амортизатора. Движение определяется одной независимой координатой, например временем.
В этой системе м обозначает подвижную массу, k обозначает жесткость пружины, а c — коэффициент демпфирования. Постоянная пружины представляет силу, прилагаемую пружиной, когда она сжимается на единицу длины. Коэффициент демпфирования — это сила, прилагаемая демпфером, когда масса движется с единичной скоростью.
Масса может свободно перемещаться вдоль одной оси, но каждый раз, когда масса перемещается, ее движению препятствуют пружина и демпфер. Теперь представьте, что на изображенном рисунке масса движется вниз на определенное расстояние. Он сжимает пружину и перемещает демпфер на такое же расстояние. Пружина накапливает и высвобождает энергию в течение одного цикла. Демпфер только поглощает энергию и не возвращает ее массе.
Уравнение системы называется обыкновенным дифференциальным уравнением второго порядка и имеет следующий вид:
Здесь
И называется собственной частотой в радианах, а
И называется коэффициентом демпфирования .
Собственная частота — это частота колебаний системы, если она нарушается (постукивает или ударяется) из состояния покоя. Представьте себе камертон: если мы постучим им по поверхности, вилка будет вибрировать с фиксированной частотой. Эта частота является собственной частотой камертона.
Недостаточное, избыточное и критическое демпфирование
Коэффициент демпфирования определяет, как колебания системы стремятся к нулю. Чтобы понять коэффициент демпфирования, воспользуемся аналогией дверей.
Во-первых, давайте рассмотрим распашные двери, подобные тем, что видели на кухнях ресторанов или в старых вестернах.Когда кто-то толкает дверь и отпускает ее, двери распахиваются назад и проходят мимо точки упора в другом направлении. Это движение вперед и назад происходит несколько раз, прежде чем двери полностью остановятся. Этот тип колебательного поведения происходит, когда в системе коэффициент демпфирования меньше 1. Такие системы называются системой с недостаточным демпфированием .
Теперь рассмотрим дверь в современном здании с приборной панелью, прикрепленной к верхнему углу. Когда эту дверь открывают и отпускают, она медленно возвращается в закрытое положение и не будет качаться вперед и назад.Эта система называется системой с избыточным демпфированием и имеет коэффициент демпфирования более 1.
В середине, когда коэффициент демпфирования равен 1, система называется с критическим демпфированием . Это было бы похоже на дверь без приборной панели, которая быстро захлопывается, не раскачиваясь.
Коэффициент демпфирования также может быть представлен отношением фактического коэффициента демпфирования к критическому коэффициенту демпфирования. Итак,
где,
Пример
Рассмотрим пример.Пружинно-массовый демпфер SDOF имеет следующие характеристики: м = 10 кг, k = 100 Н / м и c = 1 Нс / м . (Напомним, что Ns — это секунда в Ньютоне, эквивалентная килограмм-метру в секунду (кг * м / с)).
Какой у него коэффициент демпфирования?
Критический коэффициент демпфирования = 2 х квадратный корень из (kxm) = 2 х квадратный корень из (100 х 10) = 63,2 Нс / м
Поскольку фактический коэффициент демпфирования составляет 1 Нс / м , коэффициент демпфирования = (1/63.2), что намного меньше 1. Таким образом, система недостаточно демпфирована и будет колебаться вперед и назад, прежде чем остановиться.
Краткое содержание урока
Когда движение является колебательным, амплитуда колебаний со временем уменьшается из-за трения, в конечном итоге стремясь к нулю. Этот тип колебаний называется затухающими гармоническими колебаниями . Это можно понять с помощью системы с одинарной степенью свободы (SDOF). Система пружина-масса-демпфер состоит из пружины, массы и демпфера.
Определяющим уравнением для движения такой системы является обыкновенное дифференциальное уравнение второго порядка, поведение системы которого зависит от движущейся массы, жесткости пружины и коэффициента демпфирования.
Амортизированная система по-разному возвращается в состояние покоя, что определяется коэффициентом демпфирования . Коэффициент демпфирования:
- больше 1 указывает на систему с избыточным демпфированием , которая медленно возвращается в состояние покоя без колебаний. Значение
- меньше 1 указывает на систему с недостаточным демпфированием , которая возвращается в состояние покоя колебательным образом.
- , равное 1, представляет собой систему с критическим демпфированием , которая быстро возвращается в состояние покоя без колебаний.
Коэффициент демпфирования ζ — обзор
Выражения для коэффициента демпфирования и собственной частоты фугоидной моды, очевидно, очень приблизительны, поскольку они являются результатом многих упрощающих предположений. Обратите внимание, что выражение для ω p совпадает с выражением, полученным Ланчестером, уравнение (6.29), что указывает на то, что собственная частота фугоидной моды приблизительно обратно пропорциональна сбалансированной скорости. Также интересно и важно отметить, что коэффициент демпфирования фугоидной моды приблизительно обратно пропорционален отношению подъемной силы к сопротивлению самолета, уравнение (6.40). Поскольку одной из основных целей конструкции самолета является достижение высокого отношения подъемной силы к лобовому сопротивлению, легко понять, почему демпфирование фугоидной моды обычно очень низкое.
Пример 6.2Чтобы проиллюстрировать использование моделей сокращенного порядка, рассмотрим самолет A-7A Corsair II из Примера 6.1 в тех же условиях полета, что и в этом примере. Теперь уравнения движения в примере 6.1 относятся к системе осей тела, а использование описанных ранее моделей пониженного порядка требует, чтобы уравнения движения относились к системе осей ветра или устойчивости. Используя соотношения преобразования осей, приведенные в Приложениях 9 и 10 Приложения 9 Приложения 10, производные устойчивости и управления, а также параметры инерции, относящиеся к осям ветра, были рассчитаны на основе исходных значений, которые, конечно же, относятся к осям кузова.Затем уравнение продольного состояния было пересчитано с получением
(6,41) [u˙w˙q˙θ˙] = [- 0,04225−0,114210−32,2−0,20455−0,49774317.4800.00003−0,00790−0,39490] [uwqθ] + [0,00381− 24.4568−4.515760] η
Модель пониженного порядка, соответствующая короткопериодному приближению, как задано уравнением (6.15), просто берется из уравнения (6.41) и записывается как
(6.42) [w˙q˙ ] = [- 0.49774317.48−0.00790−0.39499] [wq] + [- 24.4568−4.51576] η
Решение уравнений движения (6.42) с помощью программы CC определяет следующие передаточные функции реакции пониженного порядка:
(6,43) w (s) η (s) = — 24,457 (s + 59,015) (s2 + 0,893s + 2,704) ft / s / radq ( с) η (с) = — 4,516 (с + 0,455) (с2 + 0,893 с + 2,704) рад / с / рад (град / с / град) α (с) η (с) = — 0,077 (с + 59,015) (s2 + 0.893s + 2.704) рад / рад (град / град)
Важно помнить, что эти передаточные функции приблизительно описывают краткосрочный отклик тех переменных, которые доминируют в короткопериодическом движении. Соответствующая кратковременная передаточная функция характеристики тангажа по тангажу следует из того, что для движения с малыми возмущениями
(6.44) θ (s) η (s) = 1sq (s) η (s) = — 4,516 (s + 0,455) s (s2 + 0,893s + 2,704) рад / рад (град / град)
От скорости тангажа Передаточная функция отклика в уравнениях (6.43), легко определить, что установившаяся скорость тангажа после ввода положительного единичного шага руля высоты составляет -0,76 рад / с, что означает, что летательный аппарат непрерывно движется по тангажу до тех пор, пока ввод не будет удален. Передаточная функция характеристики тангажа подтверждает это, потому что после затухания короткопериодного переходного процесса самолет ведет себя как идеальный интегратор по тангажу.На это указывает наличие члена s в знаменателе уравнения (6.44). В действительности, фугоидная динамика обычно предотвращает эту ситуацию, если только входной сигнал не очень большой и не сопровождается увеличением тяги, которое приводит к маневру с вертикальной петлей. Описанная здесь модель совершенно не подходит для анализа движения с такой большой амплитудой.
Общий знаменатель передаточных функций (6.43) представляет собой приближенный короткопериодический характеристический полином пониженного порядка, уравнение (6.19). Таким образом, приблизительные значения коэффициента демпфирования и незатухающей собственной частоты короткопериодической моды легко вычисляются:
Коэффициент демпфирования ζs = 0,27 Незатухающая собственная частота ωs = 1,64рад / с
Видно, что эти значения очень выгодно отличаются от точных значений. приведено в примере 6.1.Интерпретация модели пониженного порядка, вероятно, лучше всего проиллюстрирована наблюдением краткосрочной реакции на вход лифта. Отклики на входную ступеньку лифта 1 ° переменных, приведенных в уравнениях (6.43) показаны на рис. 6.5. На тех же графиках показаны соответствующие отклики полной модели самолета, полученные из уравнения (6.41). Ясно, что отклики со временем расходятся, как и ожидалось, поскольку в модели пониженного порядка нет динамики фугоидов. Однако в течение первых десяти секунд сравнение является благоприятным, что указывает на то, что модель пониженного порядка приемлема для большинства краткосрочных исследований реакции.
Рисунок 6.5. Продольный отклик пониженного порядка на вход руля высоты 1 °.
Теперь перейдем к приблизительным характеристикам фугоидной моды пониженного порядка. Из уравнения состояния, относящегося к осям ветра, уравнения (6.41), требуемые числовые параметры:
xu = −0,042251 / szu = −0,204551 / smu = 0,00003rad / ftsUe≡V0 = 317,48ft / s
Простая модель Ланчестера определяет, что затухание фугоида равно нулю и что собственная частота незатухания определяется уравнением (6.29). Таким образом, приблизительные характеристики фугоидной моды, рассчитанные по этой модели, составляют
Коэффициент демпфирования ζp = 0 Незатухающая собственная частота ωp = 0.143рад / с
Приблизительные характеристики фугоидной моды, определенные в соответствии с более подробной моделью пониженного порядка, даются уравнением (6.36). Поскольку выбранные условия полета действительно дозвуковые, производная m u действительно очень мала, что хорошо соответствует ограничениям модели. Приблизительные характеристики фугоидной моды, рассчитанные по этой модели, составляют
Коэффициент демпфирования ζp = 0,147 Незатухающая собственная частота ωp = 0.144рад / с
Опять же, сравнение этих приблизительных значений характеристик фугоидной моды с точными значениями в Примере 6.1 показывает хорошее совпадение, особенно для незатухающей собственной частоты. Поскольку коэффициент демпфирования фугоида всегда невелик (близок к нулю), он очень чувствителен к вычислительным ошибкам округления и к допущениям аппроксимации, что затрудняет достижение действительно хорошего приблизительного соответствия. Хорошее совпадение здесь усиливается очень дозвуковыми условиями полета, которые хорошо коррелируют с допущениями, сделанными при построении приближенных моделей.
Затухание в структурной динамике: теория и источники
Если вы ударите по чаше из стекла или металла, вы услышите звук, интенсивность которого затухает со временем. В мире без затухания тон сохранится вечно. На самом деле существует несколько физических процессов, посредством которых кинетическая и упругая энергия в чаше растворяется в других формах энергии. В этом сообщении блога мы обсудим, как может быть представлено демпфирование, и физические явления, которые вызывают демпфирование в вибрирующих конструкциях.
Как определяется демпфирование?
Существует несколько способов описания демпфирования с математической точки зрения. Некоторые из наиболее популярных описаний приведены ниже.
Одним из наиболее очевидных проявлений затухания является спад амплитуды при свободных колебаниях, как в случае поющей чаши. Скорость затухания зависит от того, насколько велико затухание. Чаще всего амплитуда колебаний экспоненциально уменьшается со временем. Это тот случай, когда энергия, теряемая во время цикла, пропорциональна амплитуде самого цикла.
Типичная «поющая чаша». Изображение Sneharamm0han — Собственная работа. 2 u = 0
Здесь \ omega_0 — собственная частота незатухания, а \ zeta — это коэффициент демпфирования .{\ frac {-2 \ pi \ zeta t} {T_0}}
, где T 0 — период незатухающей вибрации.
Затухание свободной вибрации для трех различных значений коэффициента демпфирования.
Другой используемой мерой является логарифмический декремент , δ . Это логарифм отношения амплитуд двух последующих пиков,
\ delta = \ mathrm {ln} \ left (\ dfrac {u (t_i)} {u (t_ {i + 1})} \ right) = \ mathrm {ln} \ left (\ dfrac {u (t_i) } {u (t_i + T)} \ right)
, где T — период.2}} \ приблизительно 2 \ пи \ дзета
Другой случай, в котором эффект демпфирования играет заметную роль, — это когда конструкция подвергается гармоническому возбуждению с частотой, близкой к собственной частоте. Точно в резонансе амплитуда колебаний стремится к бесконечности, если в системе нет некоторого демпфирования. Фактическая амплитуда в резонансе контролируется исключительно величиной демпфирования.
Усиление для системы с одной глубиной резкости для различных частот и коэффициентов затухания.2}} \ приблизительно \ dfrac {1} {2 \ zeta}
Другой отправной точкой для описания демпфирования является предположение, что существует определенный фазовый сдвиг между приложенной силой и результирующим смещением или между напряжением и деформацией. Говорить о фазовых сдвигах имеет смысл только для установившейся гармонической вибрации. Если вы построите график зависимости напряжения от деформации для полного периода, вы увидите эллипс, описывающий петлю гистерезиса.
История напряженно-деформированного состояния.
Вы можете рассматривать свойства материала как комплексные.{\ prime \ prime}) \ tilde \ varepsilon
Здесь действительная часть модуля Юнга называется накопительным модулем , а мнимая часть называется модулем потерь . 2}}
Различие важно только при высоких значениях коэффициента потерь.\ prime} = \ eta
Угол потерь δ — это фазовый сдвиг между напряжением и деформацией.
Демпфирование, определяемое коэффициентом потерь, ведет себя несколько иначе, чем вязкое демпфирование. Демпфирование коэффициента потерь пропорционально амплитуде смещения, тогда как вязкое демпфирование пропорционально скорости. Таким образом, невозможно напрямую преобразовать одно число в другое.
На рисунке ниже реакция системы с одной степенью свободы сравнивается для двух моделей демпфирования.Можно видеть, что вязкое демпфирование предсказывает более высокое демпфирование, чем демпфирование коэффициента потерь выше резонанса и меньшее демпфирование ниже него.
Сравнение динамического отклика на вязкое демпфирование (сплошные линии) и демпфирование коэффициента потерь (пунктирные линии).
Обычно преобразование между коэффициентом затухания и затуханием коэффициента потерь рассматривается на резонансной частоте, а затем на \ eta \ приблизительно 2 \ zeta. 2
где \ varepsilon_a — амплитуда деформации.\ prime} = \ dfrac {D} {2 \ pi W_s}
Это определение в терминах рассеянной энергии может использоваться независимо от того, является ли петля гистерезиса на самом деле идеальным эллипсом или нет — при условии, что можно определить две величины энергии.
Источники демпфирования
С физической точки зрения существует множество возможных источников демпфирования. Природа всегда находит способ рассеять энергию.
Внутренние потери в материале
Все настоящие материалы при напряжении рассеивают некоторую энергию.Вы можете рассматривать это как своего рода внутреннее трение. Если вы посмотрите на кривую «напряжение-деформация» для полного цикла нагружения, она не покажет идеальной прямой линии. Скорее вы увидите что-то похожее на тонкий эллипс.
Часто демпфирование коэффициента потерь считается подходящим представлением для демпфирования материала, поскольку опыт показывает, что потери энергии за цикл имеют довольно слабую зависимость от частоты и амплитуды. Однако, поскольку математическая основа демпфирования коэффициента потерь основана на комплексных величинах, основным предположением является гармоническая вибрация.Таким образом, эту модель демпфирования можно использовать только для анализа в частотной области.
Коэффициент потерь для материала может сильно варьироваться в зависимости от его детального состава и источников, с которыми вы обращаетесь. В таблице ниже представлены некоторые приблизительные оценки.
| Материал | Коэффициент потерь, η |
|---|---|
| Алюминий | 0,0001–0,02 |
| Конкретный | 0,02–0,05 |
| Медь | 0.001–0,05 |
| Стакан | 0,0001–0,005 |
| Резина | 0,05–2 |
| Сталь | 0,0001–0,01 |
Коэффициенты потерь и аналогичные описания демпфирования в основном используются, когда точная физика демпфирования в материале неизвестна или не важна. В некоторых моделях материалов, таких как вязкоупругость, диссипация является неотъемлемым свойством модели.
Трение в суставах
Обычно конструкции соединяются, например, с помощью болтов или заклепок.Если соединенные поверхности скользят относительно друг друга во время вибрации, энергия рассеивается за счет трения. Пока само значение силы трения не изменяется в течение цикла, потери энергии за цикл более или менее не зависят от частоты. В этом смысле трение аналогично внутренним потерям в материале.
Болтовые соединения широко используются в машиностроении. Величина рассеивания, возникающая в болтовых соединениях, может сильно варьироваться в зависимости от конструкции.Если важно низкое демпфирование, то болты должны быть расположены близко друг к другу и хорошо затянуты, чтобы избежать макроскопического скольжения между соединяемыми поверхностями.
Излучение звука
Вибрирующая поверхность вытесняет окружающий воздух (или другую окружающую среду), так что излучаются звуковые волны. Эти звуковые волны уносят некоторую энергию, что приводит к потере энергии с точки зрения конструкции.
График излучения звука в преобразователе Tonpilz.
Потери якоря
Часто небольшой компонент присоединяется к более крупной конструкции, которая не является частью моделирования. Когда компонент вибрирует, некоторые волны будут индуцироваться в опорной конструкции и уноситься. Это явление часто называют потерями в якоре , особенно в контексте MEMS.
Термоупругое демпфирование
Даже при чистой упругой деформации без рассеяния, деформация материала немного изменит его температуру.Локальное растяжение приводит к понижению температуры, а сжатие — к локальному нагреву.
По сути, это обратимый процесс, поэтому температура вернется к исходному значению, если напряжение будет снято. Однако обычно существуют градиенты в поле напряжений и связанные с ними градиенты в распределении температуры. Это вызовет поток тепла из более теплых регионов в более прохладные. Когда напряжение снимается во время более поздней части цикла нагрузки, распределение температуры больше не такое, как при перегрузке.Таким образом, локально вернуться в исходное состояние невозможно. Это становится источником рассеивания.
Эффект термоупругого демпфирования наиболее важен при работе с небольшими масштабами длины и высокочастотными колебаниями. Для резонаторов MEMS термоупругое демпфирование может привести к значительному снижению добротности.
Dashpots
Иногда конструкция содержит специально предназначенные дискретные амортизаторы, например амортизаторы подвески колеса.
Амортизаторы.Изображение Авсара Араса — Собственная работа. Под лицензией CC BY-SA 3.0 через Wikimedia Commons.
Очевидно, что такие компоненты имеют большое влияние на общее демпфирование в конструкции, по крайней мере, в отношении некоторых форм колебаний.
Сейсмические демпферы
Частным случаем, когда на демпфирование тратится много усилий, являются строительные конструкции в сейсмически активных районах. Чрезвычайно важно снизить уровень вибрации в зданиях в случае землетрясения.Назначение таких демпферов может заключаться как в изоляции конструкции от фундамента, так и в обеспечении рассеивания.
Сейсмический демпфер для муниципального здания. Изображение Шустова — Собственная работа. Под лицензией CC BY-SA 3.0 через Wikimedia Commons.
Дополнительная литература
Прочтите продолжение этого сообщения в блоге здесь: Как моделировать различные типы демпфирования в COMSOL Multiphysics®
Новый метод расчета дополнительного коэффициента демпфирования с учетом влияния частоты возбуждения
Дополнительный коэффициент демпфирования (ADR) является важным показателем для оценки демпфирующего эффекта конструкций с устройствами рассеивания энергии.Большинство существующих методов определения ADR требуют анализа динамического отклика конструкции и сложных итерационных расчетов. Предлагается инновационный упрощенный метод расчета для определения ADR конструкции, дополненной нелинейными вязкими демпферами. Этот метод не требует расчета динамического отклика конструкции, а требует только структурных характеристик, частоты возбуждения и параметров демпфера. В этом исследовании были проанализированы несколько типичных методов расчета ADR.Затем была выведена расчетная формула для ADR с учетом гармонического возбуждения при условии, что частота возбуждения равна собственной частоте конструкции, без расчета динамического отклика конструкции или итерационного процесса. Исследовано влияние частоты возбуждения на расчетное значение ADR при различных показателях затухания. Соответственно, средний период спектра реакции (RSAP) рассматривался как период возбуждения движения грунта для оценки частоты возбуждения, и был разработан упрощенный метод расчета для ADR, учитывающий влияние частоты возбуждения, характеризуемой RSAP движения грунта. .Наконец, точность и эффективность предложенного метода были проверены путем сравнения с ADR, рассчитанными другими методами.
1. Введение
За последние два десятилетия в мире произошло много сильных землетрясений, которые привели к многочисленным жертвам и значительному материальному ущербу [1–3]. Причиной потерь являются как структурные, так и неструктурные отказы, вызванные сейсмическим возбуждением. Следовательно, жизненно важно улучшить сейсмические характеристики строительных конструкций.Внедрение технологии пассивного рассеивания энергии в строительных конструкциях обеспечивает эффективное решение для увеличения структурного демпфирования и смягчения эффекта сейсмического воздействия, а важность демпфирования широко признана в области структурной динамики. Эффективное демпфирование включает три основных компонента [4]: собственное демпфирование; дополнительное демпфирование, обеспечиваемое амортизаторами; гистерезисное затухание, связанное с нелинейным поведением конструкции.
Микроскопическое внутреннее трение, локальная пластическая деформация и пластическое течение в диапазоне напряжений в пределах кажущегося предела упругости составляют основную долю рассеивания энергии из-за собственного демпфирования [5].При численном анализе важно выбрать подходящую модель внутреннего демпфирования. Несколько моделей демпфирования были предложены и широко используются в численном анализе, например, вязкое демпфирование (VD), демпфирование Рэлея (RD), массовое демпфирование (MD) и демпфирование, пропорциональное жесткости (SD). Модель RD, состоящая из MD и SD, широко используется в коммерческих конечно-элементных платформах из-за ее математической простоты. Хуанг [5] сообщил, что желаемая скорость диссипации энергии была достигнута только на двух целевых частотах и что массово-пропорциональный член применяет демпфирование к модам твердого тела, которые в действительности не могут рассеивать энергию.Для решения этой проблемы был разработан универсальный метод моделирования демпфирования, нечувствительного к частоте, который может достичь приблизительно равномерного рассеивания энергии в указанном диапазоне частот и сделать демпфирование ортогональным движению твердого тела. В нескольких исследованиях [6–8] было исследовано явление демпфирующей утечки в структурных системах, и было обнаружено, что демпфирующая утечка может привести к значительной недооценке реакции первой моды и / или реакции более высокой моды. Чтобы смягчить проблемы, связанные с неправильными моделями демпфирования в конструкции с изолированным основанием, Anajafi et al.[6] предложили подход к моделированию демпфирования, который включает удаление массового компонента демпфирования надстройки из глобальной матрицы демпфирования.
В дополнение к собственному демпфированию, дополнительный коэффициент демпфирования (ADR), который состоит из вкладов от различных устройств рассеивания энергии (EDD), использовался в различных типах конструкций для смягчения структурных откликов, вызванных сейсмическим возбуждением [9 –16]. Демпфер вязкой жидкости (VFD) — зависящий от скорости EDD — предпочитается инженерами и все чаще используется в инженерных сооружениях для уменьшения чрезмерных вибраций из-за отсутствия дополнительной жесткости и высокой скорости рассеивания энергии на различных стадиях деформации.Wu et al. [17] оценили сейсмические характеристики девятиэтажного стального каркаса с пятью типичными амортизаторами при землетрясениях, близких к разломам. Результаты показали, что частотно-регулируемый привод работает лучше, чем другие четыре типа демпферов даже при высокой амплитуде скорости импульса (PVA). Для количественной оценки демпфирующих эффектов для конструкций, дополненных частотно-регулируемыми приводами, был предложен ADR. Кроме того, в Китае ADR является ключевым структурным параметром для инженеров в процессе проектирования. Во-первых, определяется целевой ADR; затем выполняется сейсмостойкое проектирование с помощью метода анализа спектра отклика мод с учетом общего коэффициента демпфирования, суммы собственного коэффициента демпфирования и ADR.Впоследствии параметры и компоновка демпфера рассчитаны на достижение целевого показателя ADR. Процесс проектирования определяет важность оценки ADR конструкций, оборудованных EDD.
Недавно ученые предложили различные методы расчета ADR. Ли и др. [18] предложили метод оценки эквивалентного коэффициента демпфирования для систем с демпферами. В этом исследовании функция Ляпунова была впервые определена в форме модальной энергии; затем были выведены матрица Риккати и параметры коэффициента демпфирования.Наконец, формула для эквивалентного коэффициента демпфирования была получена путем аналогии вязкого модального коэффициента демпфирования. Чарни и др. [19] использовали метод модальной энергии деформации, метод логарифмического затухания свободных колебаний и метод собственных векторов для комплексных собственных значений для анализа эквивалентного отношения VD одноэтажной конструкции с одним пролетом. Результаты показали, что более высокая гибкость узлов соответствует большей разности фаз между скоростью деформации и относительной горизонтальной скоростью межслойных устройств.Однако этот вывод применим только к однослойной однопролетной конструкции. Occhiuzzi et al. В [20] предложен метод расчета модального коэффициента демпфирования с использованием уравнения для состояния динамической системы. Анализ показал, что первая мода колебаний существенно повлияла на коэффициент демпфирования, в то время как влияние мод колебаний более высокого порядка было незначительным. Вышеупомянутые методы расчета, которые включают сложные теоретические формулы и большой объем вычислений, трудны для применения инженерами.Следовательно, необходимо разработать более простой, прямой метод.
Silvestri et al. [21–23] предложили практический метод асейсмического проектирования конструкций, сконфигурированных с частотно-регулируемым приводом, в котором механические характеристики частотно-регулируемых приводов легко определяются в соответствии с целевыми характеристиками конструкции. Однако метод расчета, принятый для ADR, до сих пор не может найти широкого применения в практической инженерии. Diotallevi et al. [24] предложил метод оценки ADR по индексу демпфирования.Преимущество этого метода заключается в реализации прямой оценки ADR без итераций, но он ограничен оценкой линейно-упругих систем. Weng et al. В [25] предложен метод расчета эквивалентного ADR вязкого демпфера по спектру реакции кода. Landi et al. В [26] предложен упрощенный метод расчета ADR в соответствии со спектрами возможностей и спроса. При условии подтвержденного ускорения текучести и целевого смещения известной конструкции, соответствующий коэффициент пластичности, эквивалентный общий коэффициент демпфирования и значительный период могут быть подтверждены напрямую.Kudu et al. [27] сравнили модальные коэффициенты демпфирования, определенные с учетом времени измерения, диапазона частот и частоты дискретизации. Когда коэффициент модального демпфирования значительно изменился, собственная частота конструкции не изменилась. Ishimaru et al. [28] представили подход для расчета оптимального отношения VD и накопленной пластичности конструкции, сконфигурированной с билинейным гистерезисным демпфером и демпфером динамического качества, который имеет очень высокую точность для расчета накопленного коэффициента пластичности.Метод расчета ADR, основанный на концепции эффективного рассеивания энергии модального демпфирования, был предложен Weng et al. [29], который имеет очевидный физический смысл и полностью учитывает изменяющиеся во времени характеристики эффективного коэффициента демпфирования. К его достоинствам можно отнести простые расчеты и высокую точность. Landi et al. [30] провели вероятностную сейсмическую оценку ЖБ конструкций с демпфером и без него с использованием упрощенной программы SAC Федерального агентства по чрезвычайным ситуациям (SAC-FEMA).Результаты показали, что метод эффективен и может использоваться как упрощенная альтернатива нелинейному динамическому анализу для целей вероятностной оценки. Лав и Тейт [31] предложили простой метод предсказания эффективного демпфирования линейной структуры с нелинейными EDD. Этот метод использует свойство, состоящее в том, что средняя выходная энергия конструкции остается неизменной при ветровой нагрузке, чтобы делать прогнозы. Однако ошибка между результатами прогнозирования этого метода и результатами расчетов на основе анализа истории времени была значительной.He et al. [32] предложил эффективный метод анализа методом конечных элементов для расчета модального коэффициента демпфирования сложных материалов и доказал эффективность и точность метода посредством теоретического анализа и сравнения с экспериментальными результатами.
Большинство вышеупомянутых методов расчета ADR требуют расчета динамического отклика конструкции и повторения, что делает их громоздкими и неудобными для непосредственного использования в практической инженерии. Кроме того, решения ADR для дополнительных нелинейных частотно-регулируемых приводов, основанные на принципе энергии, редко учитывают влияние частоты возбуждения на ADR.Следовательно, необходимо установить метод расчета ADR, который отражает влияние частоты возбуждения на динамический отклик конструкции с частотно-регулируемым приводом.
Остальная часть этого документа организована следующим образом. В разделе 2 представлены два типичных метода расчета ADR: метод энергетического отношения (ERM) и метод индекса демпфирования (DIM). В разделе 3 представлен предложенный метод расчета ADR при гармоническом возбуждении с учетом влияния частоты возбуждения, которая выводится теоретически.Затем средний период спектра отклика (RSAP) используется для различения частотных характеристик различных колебаний грунта. Далее представлен упрощенный метод расчета ADR при движении по грунту. В Разделе 4 точность и эффективность предложенного метода расчета ADR подтверждены на примере конкретного случая. Выводы и направления по усовершенствованию предложенного метода представлены в разделе 5.
2. Существующие методы расчета ADR
2.1. ERM
Chopra [33] предложил классическое расчетное уравнение для ADR, основанное на принципе эквивалентности энергии гистерезиса: где представляет собой максимальную энергию деформации демпфирующей конструкции с вязким демпфером при ожидаемом смещении, представляет энергию, потребляемую вязкого демпфера за один цикл с ожидаемой деформацией, а ω, и Ω представляют собой конструктивную собственную частоту и частоту возбуждения, соответственно.
Демпфирующая сила задается следующим образом: где c α — коэффициент демпфирования, соответствующий различным значениям показателя скорости ( α ), а sgn ( x ) — знаковая функция.
Для системы с одной степенью свободы (SDOF), подверженной возбуждению гармоническим смещением с функцией u ( t ) = u 0 sin Ωt, потребление энергии нелинейной вязкой демпфер задается следующим образом:
Интегрирование уравнения (3) дает где λ — константа, связанная с α .
При = 1,, и может быть получено следующее уравнение:
Линеаризация нелинейного вязкого демпфера выполняется в соответствии с равной рассеиваемой энергией линейного вязкого демпфера и эквивалентным коэффициентом линейного демпфирования c 1 может можно определить с помощью следующего уравнения:
Разделив обе части уравнения (6) на 2 mω , ADR нелинейных вязких демпферов можно рассчитать следующим образом: где m представляет собой массу конструкции.
Этот классический метод прост для понимания. Однако для определения максимального смещения необходимо рассчитать динамический отклик конструкции, а процесс расчета является сложным, что неудобно для практического проектирования.
2.2. DIM
Чтобы преодолеть недостатки ERM, Ланди [25] предложил метод оценки ADR непосредственно по индексу демпфирования. Для системы SDOF при гармоническом возбуждении показатель демпфирования ε определяется следующим соотношением: где a 0 представляет пиковое ускорение гармонического возбуждения.
При условии резонанса, т. Е. Ω = ω , уравнения (7) и (8) можно переписать следующим образом: соответственно, где представляет собой пиковое ускорение сейсмического возбуждения.
Связь между ADR ζ sd и индексом демпфирования ε может быть выражена следующим образом: где, отражает усиление динамического отклика.
Коэффициент усиления ускорения R a может быть вычислен посредством численного анализа, а коэффициент демпфирования ε может быть определен согласно конструктивным и входным характеристикам.Затем ADR ζ sd вычисляется с использованием уравнения (11). На рисунке 1 показаны кривые отношения ADR к частотам с разными индексами демпфирования ( ε ) и α = 0,50 при гармоническом возбуждении, а на рисунке 2 показаны спектры ADR для различных показателей затухания ( ε ) и α = 0,50. под движением грунта Эль-Сентро, зарегистрированным во время землетрясения в Имперской долине 18 мая 1940 года. Согласно кривым на рисунках 1 и 2, ADR ζ sd получается напрямую, когда индекс демпфирования ε и отношение частот (Ω / ω ) или собственный период ( T ) конструкции.Похоже, что ADR можно определить напрямую, без расчета реакции конструкции. Рисунки 1 и 2 получены в результате численного анализа конструкции с дополнительными амортизаторами.
3. Новый упрощенный метод расчета для ADR
Для более удобного расчета ADR конструкции, оснащенной нелинейными вязкостными амортизаторами, на основе вышеизложенных методов предлагается упрощенный метод. В предлагаемом методе расчет отклика конструкции не требуется; скорее, следует учитывать только спектральные характеристики колебаний грунта.
3.1. ADR системы демпфирования при гармоническом возбуждении
Динамическое уравнение системы SDOF с линейным демпфером при гармоническом возбуждении: c 1 — коэффициент демпфирования линейного вязкого демпфера, когда структурное демпфирование равно 0 и a 0 представляет пиковое ускорение гармонического возбуждения.
Полное решение уравнения (12) [33] где представляет частоту конструкции с учетом демпфирования, ω представляет собственную частоту конструкции, а ζ 1 представляет коэффициент демпфирования линейного вязкого демпфера. .
Учитывая начальные условия u (0) = 0 и (0) = 0, можно получить следующее:
Согласно уравнению (13), установившийся динамический отклик u s рассчитывается следующим образом: где и.
Устойчивый отклик принимается как приблизительный отклик конструкции, т. Е.
Принимая во внимание равное энергопотребление линейных и нелинейных демпферов и идентичные пиковые динамические характеристики SDOF для линейных и нелинейных демпферов, ADR две системы демпфирования должны быть одинаковыми:
В соответствии с уравнениями (7), (16) и (17) ADR можно определить следующим образом:
ADR можно легко определить с помощью уравнения (18) без расчета реакции демпфирующей конструкции, но с итерационными расчетами.Сравнение ADR, рассчитанных с использованием уравнения (18) и ERM, представлено на рисунках 3 и 4. Как показано, когда отношение частот Ω / ω было ≤1, результаты расчета уравнения (18) хорошо согласуются с результатами. полученные с помощью ERM; когда отношение частот было> 1, результаты расчета уравнения (18) были больше, чем результаты ERM из-за влияния решения переходного состояния на отклик конструкции, что указывает на то, что отношение частот влияет на разницу между рассчитанными ADR используя уравнение (18) и ERM.
Используя уравнение (18), ADR можно определить без расчета динамического отклика, но требуются итерационные вычисления. Учитывая, что результаты, полученные с помощью двух методов расчета, аналогичны, особенно при Ω = ω , дальнейший анализ проводится для условия резонанса.
Когда Ω = ω , уравнение (15) упрощается следующим образом:
Подставив уравнение (19) в уравнение (6) и установив ζ 1 = c 1 /2 ω m дает
Затем, разделив обе части уравнения (6) на 2m ω , получим ADR в условиях резонанса:
На рисунке 5 представлены кривые зависимости ζ sd, res и a 0 для разных значений α и c α .Как показано, результаты расчетов двумя методами хорошо согласовывались, и разница между ними уменьшалась с увеличением показателя затухания. Кроме того, ADR увеличивается с коэффициентом демпфирования из-за значительного рассеяния энергии.
3.2. Упрощенный расчет ADR с учетом спектральных характеристик возбуждения
Из-за разницы между ADR, рассчитываемым с использованием уравнения (18), и ERM, зависящим от отношения частот, было важно изучить изменение ADR с различными отношениями частот.На рисунке 6 показаны кривые зависимости между ζ sd и Ω / ω , полученные с помощью ERM.
На рисунке 6 ADR слева и справа от точки резонанса демонстрируют разные тенденции, и кривая приблизительно параболическая, когда Ω / ω <1 и приблизительно линейная, когда Ω / ω > 1. Следовательно, Кривая ζ sd в зависимости от Ω / ω может быть определена как кусочная функция, содержащая точку структурного резонанса (1, ζ sd, res ) следующим образом: где a 1 и a 2 — коэффициенты, которые должны определяться путем подгонки.
На рисунках 7 и 8 представлены кривые a 1 и a 2 при различных показателях демпфирования ( α ). Численная аппроксимация показала, что где β 1 = 109,6 и γ 1 = –5,489, а где β 2 = 10,02 и γ 2 = –4,649.
Уравнение (22) использовалось для определения ADR после рассмотрения спектральной характеристики возбуждения без расчета структурной динамической характеристики.На рисунке 9 представлена кривая зависимости между ζ sd и Ω / ω при различных показателях затухания ( α ). Сравниваются результаты расчета ERM, уравнения (18) и уравнения (22). Как показано, результаты расчета уравнения (18) были самыми большими среди трех методов расчета, когда Ω / ω > 1; однако результаты расчета уравнения (22) и ERM хорошо согласуются с точностью, достаточной для практического проектирования.
3.3. Расчет ADR демпфирующей конструкции при возбуждении от движения грунта
Спектральные характеристики колебаний грунта влияют на динамический отклик конструкции, а также на ADR. Однако вышеупомянутые упрощенные методы не учитывают влияние частоты колебаний грунта на ADR. Таким образом, получен метод расчета ADR, который не требует расчета динамического отклика конструкции, но учитывает спектральные характеристики колебаний грунта.
Учитывая условие структурного резонанса при гармоническом возбуждении, u 0 аналогично a 0 /2 ω 2 ζ . Ifwhere представляет собой предполагаемое значение пикового отклика смещения, которое связано с пиковым ускорением грунта (PGA). Существует связь между и 0 и. Отношение между ними определяется как f 1 = u 0 / и отражает усиление смещения между нерезонансным и резонансным откликами структуры.
Тогда u 0 определяется следующим образом: где представляет собой пиковое ускорение сейсмического возбуждения, а ζ 1 представляет собой ADR линейного вязкого демпфера.
Для линейной структурной системы, подверженной сейсмическому воздействию, коэффициент f 1 не связан с PGA, но связан с ADR ( ζ 1 ). Следовательно, f 1 обозначается как унарный многочлен от ζ 1 : где b 1 , b 2 , b 3 и b 4 — это коэффициенты полинома, которые можно определить путем подбора.ADR структуры обычно <0,5, поэтому учет кубического полинома может обеспечить соответствующую точность.
Принимая во внимание различные частоты естественного цикла ( ω ) конструкции, ряд координатных точек ( ζ 1 , f 1 ) может быть получен посредством анализа истории во времени системы SDOF с различные ADR ( ζ 1 ). Взяв в качестве примера сейсмическую запись землетрясения в долине Империал в Эль-Сентро, с учетом различных частот естественного цикла конструкции, можно получить значения ζ 1 и соответствующие значения f 1 , как показано на рисунке 10.В таблице 1 представлены подгоночные коэффициенты для унарного полинома ζ 1 . Коэффициенты подгонки с ω = 5,39 используются в тематическом исследовании в разделе 4.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Подставив уравнение ( 26) в уравнение (9), получается ADR с Ω = ω :
Согласно уравнению (17) уравнение (28) может быть преобразовано в
Уравнение (22) используется для определения ADR, когда Ω ≠ ω : где Ω м представляет собой среднюю частоту сейсмического возбуждения.
Средний период T м сейсмической волны можно рассчитать следующим образом [29]: где C i — пиковый коэффициент Фурье, а F i представляет дискретная частота быстрого преобразования Фурье.
Тогда средняя частота Ω м ускорения движения грунта на входе сейсмических волн рассчитывается следующим образом:
На рисунках 11 и 12 представлены кривые ADR ( ζ sd ) отпериод собственных колебаний конструкции ( T ) и PGA () с разными коэффициентами демпфирования ( c a , в кН · с / м) для движения грунта El Centro, полученный с использованием ERM и уравнений (29) и (30). Здесь показатель затухания составил α = 0,50.
Как показано на рисунках, для Ω = ω результаты расчета уравнения (29) и ERM хорошо согласуются, а для Ω ≠ ω результаты расчета уравнения (30) были больше результатов расчета ERM.Результаты расчета уравнения (30) были более точными, чем результаты уравнения (29), потому что это уравнение учитывало влияние частоты колебаний грунта, а закон изменения до и после точки резонанса согласовывался с законом при гармоническом возбуждении.
4. Пример из практики
В 1997 году Такеваки [34] представил оптимальную конструкцию снижения вибрации для шестиэтажной рамы, работающей на сдвиг (рис. 13). Масса была одинаковой для всех этажей каркаса, т.е. м 1 = м 2 =… = м 6 = 0.80 × 105 кг, а поперечная жесткость распределялась равномерно, т.е. k 1 = k 2 =… = k 6 = 4,00 × 107 Н / м. Начальный коэффициент демпфирования каждого частотно-регулируемого привода был равен c 1 = 1,50 × 106 (Н · с / м), а коэффициент внутреннего структурного демпфирования был взят как ζ 0 = 0,05.
В соответствии с вышеизложенными условиями легко определить собственный период T 1 = 1,1656 с и первую моду колебаний конструкции {} T = {0.2411, 0,4681, 0,6680, 0,8290, 0,9419, 1,0000}. Согласно эквивалентному методу SDOF [33], эквивалентная масса M r , эквивалентная жесткость K r и эквивалентное демпфирование C r могут быть получены следующим образом: где M представляет матрицу масс, K представляет матрицу поперечной жесткости, C представляет матрицу демпфирования, соответствующую линейным частотно-регулируемым приводам, а {} представляет первый режим колебаний конструкции.
Согласно уравнению (33) эквивалентная масса составляет M r = 3,32 × 105 кг, эквивалентная жесткость составляет K r = 9,64 × 106 Н / м, и эквивалент демпфирование C r = 6,08 × 105 (Н · с / м). Кроме того, эквивалентный период структуры составляет T = 1,1656 с, что согласуется с периодом исходного кадра.
Информация о 10 движениях грунта, выбранных Тихоокеанским центром инженерных исследований землетрясений (PEER), а также соответствующая средняя частота Ω м представлена в таблице 2.Для анализа истории времени PGA каждого движения грунта была принята равной 500 галлонам, что аналогично интенсивности редкого землетрясения силой 8 градусов. На рисунке 14 показано межэтажное смещение сдвиговой рамы, оснащенной линейными частотно-регулируемыми приводами, подверженных сейсмическому воздействию. Ясно, что реакция смещения рамной конструкции имела тенденцию быть больше при сейсмических движениях с более низкой средней частотой Ω м .
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Когда α = 1, ADR линейных вязкостных демпферов рассчитывается по формуле (21) следующим образом: ζ 1 = C r / (2 M r ω ) = C r T /4 π M r = 17.00%. Результаты расчетов анализа временной истории представлены в таблице 2, которые близки к 17,00%, что указывает на то, что результат расчета уравнения (28) может быть использован для быстрой оценки ADR с учетом условия резонанса, несмотря на ошибку. .
Если установлено α ≠ 1, Ω = ω ; затем уравнение (6) преобразуется в
Показатель нелинейного затухания устанавливается как α = 0,5, а пиковая деформация устанавливается как u 0 = 0.05 м, что составляет примерно 1/60 высоты этажа (3 м). Это близко к пределу межъярусного смещения конструкции при редких землетрясениях, основанном на китайском сейсмическом кодексе [35]. Остальные параметры идентичны параметрам исходной конструкции. Согласно уравнению (34) эквивалентный коэффициент демпфирования составляет c a = 2,84 × 105 (Н · с / м).
Если взять в качестве примера сейсмическую запись землетрясения в Имперской долине Эль-Сентро, согласно уравнениям (31) и (32), средний период составляет T м = 0.56 с и Ом м = 11,20 рад / с. Согласно результатам подгонки в таблице 1, f 1 в уравнении (29) можно выразить следующим образом:
Решив уравнение (29), ADR ζ sd, res сдвиговой рамы под Условие структурного резонанса рассчитано как 9,74%. Подставляя это значение ζ sd, res в уравнение (30), ADR при сейсмическом возбуждении Эль-Сентро с учетом спектральных характеристик определяется как 10%.Кроме того, ADR нелинейного вязкого демпфера можно определить с помощью рисунков 11 и 12 в соответствии с коэффициентом демпфирования c a , периодом собственных колебаний конструкции T или PGA движения El Centro.
Принимая 10 входных движений грунта, перечисленных в таблице 2, как сейсмические возбуждения, ADR были рассчитаны с использованием пяти методов: ERM, двух методов нелинейного анализа динамики во времени (методы NMA [28] и Code [35]) и уравнений ( 29) и (30).Результаты представлены в Таблице 3, а сравнение ADR, рассчитанных с использованием трех методов с разными частотными соотношениями, представлено на Рисунке 15. Как показано в Таблице 3, разница между результатами, полученными с использованием ERM и уравнения (29) в условиях резонанса было очень мало. Результаты, полученные с использованием метода NMA, были больше, чем результаты, полученные с использованием метода Code, что указывает на то, что метод Code является относительно консервативным в отношении структурной безопасности.Результаты расчета уравнения (30) были больше, чем результаты расчета уравнения (29), что согласуется с законом изменения ADR при гармоническом возбуждении с отношением частот> 1 (см. Рисунок 15). Поскольку спектральные характеристики сейсмического возбуждения существенно влияют на ADR демпфирующей конструкции, результаты расчета уравнения (30), учитывающего частоту возбуждения, были более точными, чем результаты расчета уравнения (29).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ADR NMA = (энергия, рассеиваемая частотно-регулируемыми приводами / энергия, рассеиваемая за счет модального демпфирования) × собственный коэффициент структурного демпфирования. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
На рис. 16 показано сравнение временного сдвига крыши сдвиговой рамы с ADR, рассчитанными с использованием различных методов.Как показано, отклики смещения, рассчитанные с использованием ERM и уравнения (30), были аналогичными, а отклики смещения, полученные с использованием метода кода, были меньше, чем для двух других методов, что указывает на то, что предложенный метод расчета является относительно консервативным.
5. Выводы
Новый упрощенный метод расчета ADR демпфирующей конструкции, оснащенной нелинейным вязким демпфером, был разработан на основе предыдущих исследований. Правильность этого метода была проверена на анализе каркасной конструкции из шестиэтажного ЖБИ.По результатам расчетов сделаны следующие выводы: (1) Средняя частота Ω м была введена для характеристики сейсмического возбуждения, и ADR, рассчитанный с использованием предложенного метода с учетом влияния средней частоты, был больше, чем который рассчитывается с использованием ERM. Более того, по мере увеличения интенсивности землетрясения ADR уменьшался. (2) Изучение влияния частоты возбуждения на расчетное значение ADR с разными показателями скорости показало, что ADR демпфирующей конструкции было наименьшим для Ω м / ω = 1, и оно уменьшалось с увеличением отношения частот для Ω м / ω <1.Кроме того, ADR амортизирующей конструкции снижается с увеличением пикового ускорения сейсмического возбуждения. (3) Согласно тематическому исследованию сдвигового каркаса, реакция на смещение каркасной конструкции имеет тенденцию быть больше при сейсмических движениях с более низким средняя частота Ω м , что свидетельствует о значительном влиянии частотных характеристик сейсмического возбуждения на отклик конструкции. По сравнению с другими протестированными методами результаты расчетов предложенного упрощенного метода были ближе к таковым для метода Кодекса, что подтверждает эффективность предложенного метода.
Когда характеристики движения грунта, характеристики конструкции и параметры амортизатора известны, предлагаемый метод может быть использован для удобного расчета ADR амортизирующей конструкции. Однако метод расчета частоты колебаний грунта с помощью RSAP требует дальнейшего улучшения.
Доступность данных
Некоторые или все данные и модели, использованные в ходе исследования, можно получить у соответствующего автора по запросу.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Благодарности
Это исследование финансировалось Национальным фондом естественных наук Китая (гранты № 51678301 и 51678302) и Национальной ключевой программой исследований и разработок Китая (грант № 2017YFC0703600).
Оценка дополнительного эквивалентного коэффициента демпфирования демпфированной конструкции на основе рассеяния энергии
При проектировании демпфированных структур дополнительный эквивалентный коэффициент демпфирования (EDR) является важным фактором при оценке эффекта рассеивания энергии.Однако предыдущие дополнительные методы оценки МЭД сложны и их нелегко применить в практической инженерии. Поэтому в данном исследовании разработан метод, основанный на диссипации энергии, чтобы упростить оценку дополнительного МЭД. Сначала устанавливается уравнение, определяющее энергию, для расчета диссипации энергии конструкции. Посредством динамического анализа получается отношение энергии, потребляемой демпферами, к энергии, потребляемой внутренним демпфированием конструкции, при внешнем возбуждении.Поскольку способность рассеивания энергии установленных демпферов отражается дополнительным МЭД, вышеупомянутое соотношение можно использовать для оценки дополнительного МЭД демпфированной конструкции. Рассеивание энергии меняется со временем, что указывает на то, что это соотношение связано с продолжительностью движения грунта. Следовательно, рассеяние энергии в течение наиболее интенсивного периода за всю продолжительность сейсмического движения используется для расчета дополнительной МЭД. Соответственно представлена процедура предлагаемого способа.Возможность использования этого метода проверена с использованием системы с одной степенью свободы. Затем используется эталонная структура с амортизаторами, чтобы продемонстрировать полезность этого метода в практических инженерных приложениях. В заключение, предлагаемый метод не только ясен в теоретической концепции и удобен в применении, но и отражает изменяющуюся во времени характеристику дополнительного МЭД, имеющую значение в практической инженерии.
1. Введение
Технология рассеивания энергии, которая использовалась в гражданском строительстве на протяжении десятилетий, оказалась эффективным средством противодействия землетрясениям [1, 2].За счет сбалансированной установки демпферов в конструкции можно потреблять большое количество сейсмической энергии, тем самым защищая конструкцию от воздействия сильных землетрясений [3, 4]. В качестве широко используемой формы сейсмической технологии устройства рассеивания энергии широко изучались и широко разрабатывались. Различные типы демпферов, основанные на разной энергоемкой механике, были предложены и используются в инженерной практике во всем мире [4–8].
Во многих исследованиях и в инженерной практике было обнаружено, что смягчающие эффекты сейсмической реакции, возникающие в результате установки демпферов, могут быть оценены в соответствии с дополнительным эквивалентным коэффициентом демпфирования (EDR) [9, 10].Более того, исследования показывают, что диссипативная способность демпферов может быть отражена дополнительным МЭД [11, 12]. Дополнительный EDR может связать эффекты смягчения сейсмических откликов с мощностью рассеивания энергии амортизаторами, что может упростить процедуру модернизации конструкций. Таким образом, общие методы, используемые для проектирования демпфирующих конструкций, связаны с требуемым коэффициентом демпфирования [13–17]. Исходя из требуемого коэффициента демпфирования, определяются параметры демпферов.Исходя из вышеупомянутых причин, очевидно, что дополнительный МЭД, полученный от установленных демпферов, является важным фактором при проектировании демпфирующих конструкций. МЭД — это базовое понятие в структурной динамике, и существует несколько классических методов оценки МЭД конструкции, таких как метод колебаний свободного затухания и метод ширины полосы половинной мощности. Метод ширины полосы половинной мощности проверяется на неточность для оценки МЭД структуры в некоторых случаях, что требует некоторых исправлений [18, 19].Наиболее распространенным методом является метод энергии деформации, который выражается следующим образом [20]: где — EDR, — энергия, рассеиваемая системой за один цикл, и — максимальная энергия деформации за один цикл. Метод энергии деформации используется во многих расчетных нормах [21, 22]. Однако метод точен только тогда, когда система находится в резонансе. Кроме того, метод имеет некоторые недостатки в практическом применении, такие как сложность расчета рассеиваемой энергии.
Поскольку доступно большое количество демпферов, оценить дополнительный EDR непросто.Тем не менее, из-за важности дополнительного МЭД оценке этого параметра посвящено много исследований. Ли и др. [23] использовали модальную энергетическую функцию Ляпунова для получения решения в замкнутой форме для дополнительного МЭД. Двумерные сдвиговые здания с различными типами демпферов были введены для проверки точности решения. Окчиуцци [24] предложил метод, основанный на представлении динамической системы в пространстве состояний, для вычисления модального коэффициента демпфирования.Этот метод был принят для оценки дополнительной МЭД конструкций с амортизаторами, которые были настроены с помощью некоторых существующих методов проектирования. Результаты показали, что эти демпфированные структуры давали аналогичный дополнительный EDR, который составлял примерно 0,2. Diotallevi et al. [25] определили индекс демпфирования и представили метод прямой оценки EDR с использованием индекса. В методе не требовалось итераций, что было проверено с использованием системы с одной степенью свободы (SDOF). Парк [26] исследовал демпфирование неупругой системы SDOF с добавленным демпфером.Поправочные коэффициенты демпфирования и уравнения регрессии использовались для оценки дополнительной МЭД. Герреро и др. [27] предложили экспериментальный подход к измерению демпфирования конструкций с продольными скобами (BRB). Подход был подтвержден испытаниями на вибростоле, и результаты показали, что рассеяние энергии BRB необходимо учитывать при сейсмическом проектировании конструкции. Папагианнопулос и Бескос [28] разработали модель идентификации модального демпфирования для оценки модальных коэффициентов демпфирования конструкций.Этот метод был использован Katsimpini et al. [29], чтобы получить модальные коэффициенты демпфирования конструкции с системой качелей, и результаты показали, что система качелей может обеспечить значительную демпфирующую способность. Ли и др. [30] определили демпфирование в системе SDOF с демпфером Максвелла. Приняв свойства структуры в условиях свободных колебаний, они получили выводы для эквивалентного демпфирования первого и второго порядка.
Вышеупомянутые исследования показывают, что дополнительный МЭД можно точно рассчитать многими методами, но, как правило, эти методы сложны и неудобны для практического применения.Для практического применения простота метода в понимании и применении так же важна, как и точность. Следовательно, необходимо предложить простой для понимания, удобный в применении и точный подход для оценки дополнительной МЭД демпфированных конструкций.
В этом исследовании, основанном на рассеянии энергии за счет структурного демпфирования и использования демпферов, разработан простой метод оценки дополнительного МЭД, индуцированного демпферами.По сравнению с методом энергии деформации предлагаемый метод более точен, а концепция ясна и интуитивно понятна, что также удобно для практических врачей. Сначала устанавливается энергетическое уравнение системы. Согласно определению МЭД в структурной динамике [20], взаимосвязь между диссипацией энергии и МЭД устанавливается, что указывает на то, что дополнительный МЭД отражает способность демпферов к диссипации энергии. Таким образом, отношение энергии, рассеиваемой внутренним демпфированием конструкции, к энергии, рассеиваемой амортизаторами, используется для оценки дополнительного EDR.После этого обсуждается определение времени расчета диссипации энергии. Результат диссипации энергии может быть получен с помощью управляющего уравнения структурной энергии. В диапазоне значительной продолжительности движения грунта рассеяние энергии может быть рассчитано с помощью интегралов демпфирующих сил первичной конструкции и демпферов по отношению к соответствующим смещениям, соответственно, расчет которых может быть выполнен программно или с помощью программа структурного анализа.Далее представлена процедура предлагаемого метода. Кроме того, возможность использования этого метода проверена с помощью системы SDOF с добавленным вязким демпфером. Шестиэтажная эталонная модель бетона с металлическими амортизаторами текучести (MYD) представлена, чтобы проиллюстрировать полезность этого метода в практических инженерных приложениях. Наконец, точность результатов, полученных предлагаемым методом, показана путем проведения сравнительного исследования.
2. Метод, основанный на рассеивании энергии
2.1. Создание энергетического уравнения
Упрощенная модель системы SDOF с добавленным вязким демпфером показана на рисунке 1, где вязкий демпфер моделируется моделью Максвелла. Согласно структурной динамике, дифференциальное уравнение движения при горизонтальном землетрясении может быть записано следующим образом [31]: где, и — относительное смещение, скорость и ускорение массы, соответственно; ускорение грунта; масса; жесткость системы; — собственный коэффициент демпфирования системы; — упругая или неупругая сила сопротивления системы; и — демпфирующая сила демпфера.В модели Максвелла — динамическая жесткость демпфера и коэффициент демпфирования демпфера.
Путем интегрирования в уравнении (2) в диапазоне продолжительности землетрясения [0, t ] можно получить уравнение энергетического отклика:
Уравнение (3) можно переписать как уравнение (4) в терминах энергии: где — кинетическая энергия, — энергия, рассеиваемая за счет собственного демпфирования первичной структуры, и — гистерезисная энергия и энергия упругой деформации первичной структуры, соответственно.Здесь, ; когда первичная структура находится в упругом состоянии,. это энергия, рассеиваемая демпферами, и энергия, вкладываемая в движение грунта.
2.2. Расчет дополнительного EDR
В общем, способность рассеивания энергии первичной структуры указывается в терминах EDR. Точно так же мощность рассеивания энергии дополнительных устройств может быть указана в терминах дополнительного МЭД. Согласно классическому методу определения дополнительного МЭД, энергия, рассеиваемая демпферами, уравнивается с энергией, рассеиваемой эквивалентной вязкой системой за один цикл колебаний [20]: где — круговая частота возбуждения, — максимальное смещение конструкции за один цикл, — эквивалентный коэффициент демпфирования демпферов за один цикл (), — собственная круговая частота конструкции.
Это определение можно использовать для переписывания уравнения для дополнительного МЭД, обеспечиваемого демпферами во время следующего: где обозначает дополнительный МЭД, обеспечиваемый демпферами в сейсмической продолжительности, и обозначает продолжительность сейсмической записи.
Между тем, энергия, рассеиваемая за счет собственного демпфирования первичной структуры, может быть выражена следующим образом: где обозначает коэффициент собственного демпфирования первичной структуры.
Из уравнений (6) и (7) можно получить дополнительный МЭД демпферов в длительности:
Очевидно, что дополнительный МЭД может быть получен из собственного коэффициента демпфирования и отношения энергии, рассеиваемой за счет демпферы к тем, которые рассеиваются за счет собственного демпфирования во время.Следует отметить, что метод фокусируется на количестве рассеиваемой энергии, а способ рассеивания энергии не задействован, что указывает на то, что метод может быть применен к различным типам демпферов. Уравнение (8) дает выражение для расчета диссипации энергии. Когда демпфирующая сила демпферов и собственный коэффициент демпфирования известны, диссипация энергии может быть рассчитана путем получения интегралов энергии в уравнении (8).
Предполагая, что дополнительный EDR, обеспечиваемый заслонками, одинаков на всех этажах, т.е.е., где — дополнительный МЭД и -го этажа, а в вибрации конструкции преобладает мода 1-го , уравнение (8) может быть применено в мульти-степенях свободы (MDOF) система. Энергия, рассеиваемая амортизаторами на и -м этаже, где обозначает демпфирующую силу j -го амортизатора на и -м этаже, обозначает количество амортизаторов, установленных на и -м этаже, обозначает относительная скорость между i -м и ( i -1) -м этажом, и обозначает жесткость i -го этажа.А энергия, рассеиваемая собственным демпфированием на и -м этаже, равна коэффициенту демпфирования и -го этажа. Отношение энергии, рассеиваемой демпферами, и собственного демпфирования всех этажей может быть: где — это демпфер j , установленный на i -м этаже, это количество этажей, установленных с демпферами, и количество истории.
Дополнительный EDR конструкции можно получить, переписав уравнение (11) следующим образом:
Как правило, поскольку демпферы не настроены единообразно на всех этажах, это означает средний дополнительный EDR всей конструкции за период.
2.3. Определение времени расчета
В уравнении (8) дополнительный EDR демпферов является функцией продолжительности сейсмических воздействий. Землетрясение — это случайный вибрационный процесс. Сейсмический отклик меняется со временем, а дополнительный МЭД зависит от сейсмического отклика [31]. Следовательно, дополнительный МЭД меняется со временем в течение всего периода. Чтобы отразить способность рассеивания энергии установленных демпферов в течение наиболее интенсивного периода за всю продолжительность сейсмического движения, необходимо определить время расчета.Как правило, демпферы могут обеспечить максимальное использование способности рассеивания энергии при большой деформации, а большие структурные отклики могут быть вызваны интенсивным движением грунта. Следовательно, временной диапазон, охватывающий наиболее интенсивное сейсмическое движение, может быть принят в качестве времени расчета рассеяния энергии.
Значимые параметры продолжительности обычно используются для описания длительности, характерной для регистраторов движения земли [32]. Значительная продолжительность определяется как временные интервалы, в течение которых рассеивается определенное количество энергии.Интеграл от квадрата ускорения грунта называется интенсивностью арии (), где — ускорение свободного падения, хронология ускорения грунта и полная продолжительность записи о движении грунта. является одним из распространенных типов продолжительности сигнификации [33], которая представляет собой временной интервал между 5% и 75% и используется в этом исследовании.
Здесь время расчета определяется как, где — момент достижения 5% от, а — момент достижения 75% от.Дополнительный МЭД в продолжительности может быть получен следующим образом: где — дополнительный МЭД демпферов во времени расчета.
Аналогичным образом уравнение (12) может быть изменено для получения дополнительного EDR для системы MDOF в:
2.4. Процедура
Процедура метода расчета, основанного на диссипации энергии, следующая: (1) Анализ хронологии: поскольку диссипация энергии должна быть рассчитана в течение определенного периода, этот метод применим только для анализа хронологии.(2) Расчет диссипации энергии: диссипация энергии естественного демпфирования и дополнительных демпферов может быть рассчитана путем получения интегралов энергии в уравнении (8) для систем SDOF и в уравнении (12) для систем MDOF. (3) Расчет дополнительного EDR в течение всей продолжительности сейсмического движения: временная история дополнительного EDR, обеспечиваемого демпферами, может быть получена с помощью уравнения (8) для систем SDOF и уравнения (12) для систем MDOF в течение всей продолжительности сейсмического движения.(4) Определение продолжительности: должна быть определена продолжительность, охватывающая интенсивное движение грунта. — момент, достигающий 5% от, и — момент, достигающий 75% от. (5) Вычисление дополнительного МЭД в продолжительности: рассеяние энергии естественного демпфирования и дополнительных демпферов в течение продолжительности может быть вычислено путем получения интегралов в уравнении (14) для систем SDOF и уравнении (15) для систем MDOF. Затем дополнительный МЭД, индуцированный демпферами, может быть получен с использованием уравнения (14) и уравнения (15) для систем SDOF и MDOF соответственно.
3. Выполнимость предложенного метода
Для проверки осуществимости предложенного метода вводятся три системы SDOF с вязким демпфированием с разными естественными периодами. Кроме того, проводится сравнительное исследование этого метода и классического метода энергии деформации.
3.1. Системы SDOF
Естественные периоды трех систем SDOF составляют 0,5 с, 1,0 с и 2,0 с соответственно. Все их массы равны 204 т , а собственный коэффициент демпфирования равен 0.05. Жесткость трех систем составляет 32214,4 кН / м, 8048,6 кН / м и 2013,4 кН / м. К трем системам SDOF добавлен линейный вязкостный демпфер соответственно. Модель Максвелла используется для моделирования механического поведения демпфера. Коэффициент демпфирования демпфера установлен равным 250 кН / (м / с). Схема систем SDOF такая же, как и на рисунке 1. Теоретические значения дополнительных EDR, вызванных добавленным демпфером, составляют 0,049, 0,097 и 0,195 для трех систем SDOF, соответственно, которые могут быть рассчитаны с использованием дифференциала уравнение движения системы SDOF.
Три синусоидальные волны с разными периодами, искусственное движение грунта AWX и естественное движение грунта NRX выбраны для анализа временной истории. Периоды трех синусоидальных волн составляют 0,5, 1 и 2 с. И PGA всех возбуждений 0,035 г. Нормализованные спектры записей AWX и NRX показаны на рисунке 2. Информация о NRX показана в таблице 1, в которой RSN — порядковый номер записи в базе данных движения грунта PEER.
| ||||||||||||||||||||||||||||||||||||||||
3.2. Численный анализ
Из-за принятия линейного вязкого демпфера становится уравнением (8), которое указывает на то, что при определении системы SDOF изменение дополнительного EDR связано только с коэффициентом демпфирования добавленного демпфера.
Временные характеристики совокупной энергии, рассеиваемой демпфером, и собственного демпфирования могут быть получены из динамического анализа.Дополнительный МЭД можно получить с помощью уравнения (8). Временные характеристики кумулятивной энергии системы SDOF с периодом, равным 1,0 с, показаны на рисунке 3. Временные характеристики дополнительного EDR колеблются в первые несколько секунд, когда система не находится в устойчивом движении. После этого значения дополнительной МЭД становятся стабильными. Значения для всех движений земли в этой системе одинаковы и равны 0,097.
Значения дополнительных МЭД трех систем SDOF приведены в таблице 2.Частоты возбуждений не влияют на результаты расчета дополнительной МЭД. Результаты показывают реализуемость предложенного метода.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Примечание . обозначает естественный период систем SDOF и обозначает период возбуждения синусоидальных волн. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Дополнительные значения МЭД также рассчитываются методом энергии деформации для сравнения, результаты которого приведены в таблице 2.Дополнительные EDR рассчитываются с использованием уравнения (1). Учитывая, что добавленный демпфер представляет собой линейный вязкий демпфер, рассеивание энергии можно рассчитать по формуле для площади эллипса: где — максимальная выходная сила демпфера в цикле и — максимальная деформация демпфера в цикле. .
В методе энергии деформации, поскольку периоды синусоидальных волн известны, дополнительный EDR в каждом цикле колебаний может быть получен для трех случаев, связанных с синусоидальными волнами.На рис. 4 показано изменение дополнительного МЭД по результатам расчета методом энергии деформации для системы SDOF с периодом, равным 1,0 с. Кривая гистерезиса демпфера в этой системе под действием синусоиды показана на рисунке 4 (d); кривая показывает, что способность демпфера к рассеянию энергии полностью используется.
Из таблицы 2 видно, что только когда система находится в резонансе, результат дополнительного МЭД в этом случае согласуется с результатом, полученным из структурной динамики [20].В других случаях, поскольку отношение частоты возбуждения к собственной частоте конструкции вызывает ошибки в методе энергии деформации, результаты дополнительного МЭД не являются точным отражением способности демпфера рассеивать энергию.
Сравнительное исследование предложенного метода и метода энергии деформации показывает, что предложенный метод не только является более простым способом получения дополнительного МЭД, но и обеспечивает более стабильные результаты расчетов. Этот метод позволяет избежать влияния частоты возбуждения на результат расчета, что является основной проблемой метода энергии деформации.
4. Пример иллюстрации
4.1. Основная информация
Модель армированного бетона используется для демонстрации полезности этого метода в практических инженерных приложениях [34]. Согласно китайским нормам для сейсмического проектирования зданий [22], расчетный PGA для динамического анализа составляет 0,2 г, а характерный период грунта площадки составляет 0,4 с. Структурный план и отметка показаны на рисунке 5, а размеры поперечных сечений элементов указаны в таблице 3.Модель конструкции создается с помощью программного обеспечения SAP2000 [35]. Балки и колонны моделируются как упругие стержни с пластиковыми шарнирами на двух концах. Механическая модель петель представляет собой идеальную жестко-пластиковую модель, а типы пластиковых петель — это момент M3 для балок и взаимодействующие P-M2-M3 для колонн. Материал элементов — железобетон, а расчетная прочность бетона составляет 30 МПа согласно нормам проектирования бетонных конструкций [36]. Тонкий элемент оболочки используется для имитации плит перекрытия.Толщина всех этажей установлена равной 0 мм, чтобы обеспечить оптимальную передачу нагрузки. Полы подвержены распределенным нагрузкам. Распределенные статические нагрузки, включая собственный вес пола, для всех этажей. Временные нагрузки указаны для этажей 1–5 и для этажа 6. Высота этажа и нагрузки перечислены в таблице 4. Демпфирование Рэлея принято в структурной модели для динамического анализа. Коэффициент демпфирования для железобетонной конструкции установлен равным 0,05 для первого и четвертого режимов.
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||
Два MYD установлены на каждом этаже по осям X3 и X7.Параметры демпфера приведены в таблице 5. Схема установки демпфера также показана на рисунке 5.
| ||||||||||||||||||||||||||||||||||||||||
Затем выполняется нелинейный динамический анализ. Чтобы соответствовать требованиям китайского кодекса [22], выбрано семь колебаний грунта при землетрясении, из которых пять являются естественными колебаниями грунта.Естественные колебания грунта выбираются из базы данных о колебаниях грунта Тихоокеанского центра инженерных исследований землетрясений; спектры этих движений земли согласованы с расчетным спектром ускорения [37]. Искусственные колебания грунта генерируются с использованием тригонометрического метода [38] и корректируются в соответствии с расчетным спектром реакции [39, 40]. Для каждого землетрясения и определяются в соответствии с определениями в разделе 2.3. Подробная информация о колебаниях грунта приведена в таблице 6, а нормализованные спектры этих колебаний показаны на рисунке 6.PGA движений земли установлены на 0,2 g.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4.2. Дополнительный расчет МЭД
Согласно предложенному методу, дополнительный МЭД для всей продолжительности землетрясения получается с использованием уравнений (12) и (15). В этих двух уравнениях энергия, рассеиваемая собственным демпфированием и добавленными демпферами, может быть получена из результатов динамического анализа в SAP2000. В результате можно легко получить временные диаграммы и энергию, рассеиваемую естественным демпфированием и MYD, которые показаны на рисунке 7.
Для многоэтажных структур, в отличие от системы SDOF, временные истории дополнительных EDR не сохраняются. в стабильном значении, которое колеблется во времени на протяжении всей продолжительности сейсмических движений.Можно заметить, что после того, как собственное демпфирование и дополнительные демпферы начали рассеивать подводимую энергию, дополнительный МЭД резко возрастает в то же время. И рассеяние энергии амортизаторами почти прекращается, и колебания дополнительного EDR имеют тенденцию быть мягкими по прошествии определенного времени. Это указывает на то, что амортизаторы полностью используются в течение значительной продолжительности движения грунта.
Из-за разницы частотной составляющей и продолжительности колебаний грунта отклики конструкции, на которые влияют более высокие моды, будут разными.Более того, за исключением линейных вязких демпферов, дополнительная МЭД, индуцированная демпферами, тесно связана с амплитудой структурного отклика [31], что приводит к флуктуации временных диаграмм дополнительной МЭД и незначительной разнице в значениях дополнительной МЭД. полученные от разных возбуждений.
Затем используется метод энергии деформации для расчета дополнительной МЭД, вызванной MYD, с использованием уравнения (1). В уравнении рассеиваемая энергия и максимальная энергия деформации за один цикл рассчитываются следующим образом: где обозначает начальную жесткость демпфера j -го демпфера, обозначает деформацию текучести j-го демпфера , обозначает жесткость после деформации коэффициент пластичности j -го демпфера, а обозначает коэффициент пластичности j -го демпфера.Здесь, где обозначает деформацию амортизатора j -го, обозначает силу сдвига на уровне i , обозначает межэтажное смещение между уровнем i и уровнем i -1, обозначает количество амортизаторов, и обозначает количество этажей. На рисунке 8 показаны гистерезисные кривые MYD на уровнях 1, 3 и 5 при сейсмическом движении AW1. Кривые показывают, что способность MYD к рассеиванию энергии полностью используется. Значения, полученные из уравнений (12), (15) и (1), перечислены в таблице 7.
| |||||||||||||||||||||||||||||||||||||||||||||
| Примечание: — это окончательное значение, — это дополнительный МЭД, вызванный демпферами в течение продолжительности, и — это значение, полученное с помощью метода энергии деформации. | |||||||||||||||||||||||||||||||||||||||||||||
4.3. Сравнительный анализ
Отклики структур с дополнительным МЭД, полученные с помощью различных методов (ST-конец, ST-пик и ST-деформация), сравниваются с ответом исходной структуры (ST-исходный), чтобы определить, соответствуют ли результаты Дополнительного EDR может отражать способность рассеивания энергии MYD. ST-конец обозначает структуру с, ST-пик обозначает структуру с, а ST-деформация обозначает структуру с. В этих структурах способность рассеивания энергии MYD представлена дополнительным МЭД, полученным с помощью различных подходов, и в этих структурах также принято демпфирование Рэлея, значения которого относятся к первой и четвертой модам.MYD моделируются как упругие стержни с эквивалентной жесткостью, которую можно рассчитать следующим образом [21]: где обозначает эквивалентную жесткость j -го демпфера; и обозначают максимальную и минимальную демпфирующие силы демпфера j , соответственно, при определенном землетрясении; и и обозначают максимальную и минимальную деформации j -го демпфера соответственно при определенном землетрясении. Здесь — среднее значение эквивалентной жесткости при семи сейсмических колебаниях грунта.
Далее выполняется динамический анализ. Сдвиги этажей и сносы этажей трех структур сравниваются с таковыми для исходной конструкции, как показано на рисунках 9 и 10, соответственно.
Приведенное выше сравнение ясно показывает, что все ответы близки. Отклик ST-пика наиболее близок к ответу ST-оригинала. Реакция ST-конца больше, чем у ST-оригинала, тогда как реакция ST-деформации меньше, чем у ST-оригинала.Поскольку ответ ST-конца больше, чем ответ ST-оригинала, значение мало. Как правило, в течение большей части всей продолжительности землетрясения сейсмические отклики конструкций значительно меньше максимальных откликов конструкций. Следовательно, MYD не всегда используют свою максимальную мощность в течение всей продолжительности сейсмического воздействия. Способность демпферов к рассеянию энергии может быть недооценена в течение всей продолжительности землетрясения. Таким образом, дополнительный МЭД оценивается в наиболее интенсивный период за всю продолжительность сейсмического движения.
Ответы на штамм ST меньше, чем на исходный ST, что означает, что они слишком велики. В настоящее время метод энергии деформации является наиболее распространенным подходом, используемым для оценки дополнительной МЭД. Однако для практических приложений метод не только усложняется с точки зрения расчета, но и в некоторых случаях завышает дополнительный МЭД. В примере, рассмотренном в этом исследовании, ошибка может быть связана со следующими причинами: (1) Сейсмическое движение — это случайный процесс, который может быть представлен комбинацией серии синусоидальных волн с широким диапазоном частот.Как обсуждалось в разделе 3.2, частота возбуждения вызовет очевидные ошибки в результатах дополнительного МЭД, полученного методом энергии деформации. (2) Диссипация энергии получается в соответствии с максимальными деформациями демпферов на основе уравнения (18 ). Однако максимальные деформации демпферов на разных уровнях обычно не происходят одновременно во время вибрации. Сумма значений рассеивания энергии амортизаторами, основанная на максимальных деформациях во время всего землетрясения, будет переоценивать смягчающий эффект MYD.(3) Метод энергии деформации выводится с использованием упругой системы SDOF. Когда первичная структура находится в неупругом диапазоне, метод может вызвать очевидные ошибки в вычислении энергии деформации и рассеиваемой энергии; следовательно, необходимо изменить расчетные уравнения для этих энергий.
5. Заключение
В данной статье предлагается простой метод быстрой оценки дополнительной МЭД демпфированных конструкций. Метод основан на определении EDR в структурной динамике.Посредством анализа динамики во времени можно получить отношение энергопотребления собственного демпфирования к потребляемой энергии добавленных демпферов при внешнем возбуждении. Дополнительный МЭД можно оценить с помощью собственного коэффициента демпфирования и коэффициента энергопотребления. Основываясь на результатах исследования, можно сделать следующие выводы: (1) Концепция метода ясна, интуитивно понятна и проста для понимания специалистами по строительным работам. Используя коэффициент собственного демпфирования и отношение энергии, рассеиваемой демпферами, к энергии, рассеиваемой собственным демпфированием, можно точно оценить дополнительный EDR.(2) В отличие от метода энергии деформации, предлагаемый метод позволяет исключить влияние частоты возбуждения на результат дополнительного МЭД, а это означает, что дополнительный МЭД, полученный этим методом, лучше отражает способность демпферов рассеивать энергию. (3) В данном исследовании выявлена изменяющаяся во времени характеристика дополнительного МЭД. За исключением линейных вязких демпферов, дополнительный МЭД, создаваемый демпферами в конструкции, не является постоянным и колеблется в зависимости от продолжительности колебаний грунта.Для повышения точности оценку дополнительного МЭД следует рассчитывать в течение значительной продолжительности движения грунта. (4) Предлагаемый метод фокусируется на диссипации энергии собственного демпфирования и демпферов и, следовательно, не связан с состоянием конструкции. Следовательно, этот метод применим не только к упругим конструкциям, но и к конструкциям в неупругом состоянии.
Доступность данных
Данные, использованные для подтверждения выводов этого исследования, можно получить у соответствующего автора по запросу.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Благодарности
Это исследование было поддержано Шанхайской программой Пуцзян в рамках гранта No. 17PJ1409200 и Фонды фундаментальных исследований для центральных университетов в рамках гранта № 22120180064.
Динамический модуль сдвига и коэффициент демпфирования песчано-резиновых смесей при большом диапазоне деформации
Материалы (Базель). 2020 сен; 13 (18): 4017.
, 1, 2 , 1, 2 , 1, 2 , 1, 2, * и 1, 22 Гуандунский инженерный исследовательский центр по защите подземной инфраструктуры в прибрежной глинобитной зоне, Гуанчжоу 510006, Китай
Получено 20 августа 2020 г .; Принята в печать 9 сентября 2020 г.
Лицензиат MDPI, Базель, Швейцария. Эта статья представляет собой статью в открытом доступе, распространяемую в соответствии с условиями лицензии Creative Commons Attribution (CC BY) (http://creativecommons.org/licenses/by/4.0/). Эта статья цитировалась другими статьями в PMC. .Abstract
Было обнаружено, что добавление каучука в пески улучшает механические свойства песков, в том числе их динамические свойства. Однако сообщалось о неоднозначных и даже противоречивых результатах относительно динамического поведения смесей песка и каучука, особенно с точки зрения коэффициента демпфирования.Поэтому была проведена серия циклических трехосных испытаний в широком диапазоне деформаций сдвига на смесях песка и каучука с различным объемным содержанием каучука, размером частиц каучука и ограничивающим давлением. Результаты показывают, что динамический модуль сдвига уменьшается с увеличением объемного содержания каучука, уменьшением размера частиц и ограничивающего давления. Связь коэффициента демпфирования с оцениваемыми параметрами сложна и зависит от деформации; при деформации сдвига менее критического значения коэффициент демпфирования увеличивается с увеличением объемного содержания резины, тогда как при больших деформациях сдвига наблюдается противоположная тенденция.Кроме того, смеси песка и каучука с различным размером частиц резины превышают коэффициент демпфирования чистого песка при различном объемном содержании резины. Соответственно, предлагается новая эмпирическая модель для прогнозирования максимальных модулей сдвига смесей с различным объемным содержанием каучука, размером частиц каучука и ограничивающим давлением. Это исследование является справочным материалом для проектирования смесей песка и каучука в инженерных приложениях.
Ключевые слова: смесь песка и каучука, циклические трехосные испытания, динамический модуль сдвига, коэффициент демпфирования, эмпирическая модель
1.Введение
Количество изношенных резиновых шин увеличивается с каждым годом. Сообщается, что только в Соединенных Штатах ежегодно выбрасывается около 290 миллионов старых шин [1], примерно 40% из которых выбрасываются на свалки или складские помещения без эффективного использования [2,3,4]. Это чрезмерное накопление угрожает окружающей среде и здоровью человека [5,6]. Однако растущий объем выброшенных резиновых покрышек вызвал интерес к разработке новых методов повторного использования этих материалов [7,8,9] и, таким образом, побудил исследователей охарактеризовать общие геотехнические свойства смесей песка и каучука [10,11,12, 13,14,15,16,17,18,19,20].
Благодаря превосходным инженерным характеристикам резиновых / измельченных шин (низкая объемная плотность, высокая упругая деформация и высокая демпфирующая способность), в нескольких предыдущих исследованиях предлагалось использовать такой материал для смягчения последствий землетрясений, например, для демпфирования фундаментов или повышение стойкости засыпки к разжижению [21,22,23,24,25,26,27]. Однако лабораторные эксперименты, проведенные до сих пор для изучения динамического поведения смесей песка и каучука, не были исчерпывающими.В частности, только несколько предыдущих исследований изучали поведение резиносодержащих песков в широком диапазоне амплитуд сдвиговой деформации с использованием циклических трехосных испытаний, вместо этого, как правило, сосредотачиваясь на применении небольших уровней деформации с использованием устройств с резонансной колонной или изгибающих элементов.
В последние десятилетия были проведены различные исследования динамического поведения резиновых смесей. Их можно резюмировать следующим образом: Pistolas et al. [28] ясно показали, что деформация сдвига оказывает значительное влияние на коэффициент демпфирования.Сараджпур и др. [7] сообщили, что при амплитудах деформации сдвига менее примерно 0,1% увеличение объемного содержания резины приводит к более высокому коэффициенту демпфирования, тогда как при амплитудах деформации сдвига более примерно 0,1% наблюдается противоположная тенденция. Хотя Senetakis et al. [21] показали аналогичные выводы, следует отметить, что Okur et al. [29] получили противоположные результаты с помощью испытаний на резонансной колонне, показывающие, что при амплитудах деформации сдвига менее примерно 5 × 10 -2 % увеличение объемного содержания каучука приводит к более низкому коэффициенту демпфирования, причем обратное верно при более высоком сдвиге. штаммы.Мадхусудхан и др. [30] даже сообщили, что коэффициенты демпфирования смесей песка и каучука уменьшаются с увеличением диапазона деформации сдвига. Таким образом, хотя были проведены некоторые исследования динамического поведения смесей песка и каучука и получены предварительные результаты, остаются некоторые неоднозначные и даже противоречивые результаты, особенно в отношении коэффициента демпфирования. Однако эмпирические модели успешно применялись для быстрой оценки других динамических характеристик смесей песка и каучука в инженерных приложениях.Например, Nakhaei et al. [31] представили функцию для прогнозирования максимального модуля сдвига для различных ограничивающих давлений и процентного содержания гранулированного каучука, но сконцентрировались на низком объемном содержании каучука (т. Е. 8%, 10% и 14%).
Помимо объемного содержания каучука, ограничивающее давление и размер частиц оказывают значительное влияние на динамическое поведение смесей песка и каучука. Например, Youwai et al. [32] сообщили, что при соотношении размеров частиц D каучук / D песок ≤ 6, эффекты размера частиц не следует игнорировать.Lopera Perez et al. [33] выполнили серию численного моделирования методом дискретных элементов и обнаружили, что различные соотношения размеров имеют положительное или отрицательное влияние на прочность и деформируемость.
В свете вышеизложенного, в данном исследовании была проведена серия циклических трехосных испытаний с использованием динамического циклического трехосного устройства Global Digital Systems (GDS), чтобы улучшить понимание динамического поведения смесей песка и каучука, подверженных большим нагрузкам. диапазоны деформации сдвига и для уточнения ранее противоречивых наблюдений.Соответственно, влияние различных параметров, включая объемное содержание каучука, ограничивающее давление и размер резиновых частиц, на модуль сдвига и коэффициент демпфирования различных смесей песка и каучука были подробно исследованы при больших амплитудах деформации сдвига. Кроме того, была предложена и подтверждена новая эмпирическая модель для прогнозирования максимальных динамических модулей сдвига смесей песка и каучука, подверженных различным ограничивающим давлениям (например, 50 кПа, 100 кПа, 150 кПа и 200 кПа) с различным объемным содержанием каучука (т.е.е. 10%, 20%, 30%, 40% и 50%) и различные соотношения размеров частиц резины и песка.
2. Материалы и методы эксперимента
2.1. Сырье
Стандартный песок Сямыня с размером зерна от 0,075 мм до 2 мм использовался в качестве основного грунта для приготовления смеси песка и каучука в этих испытаниях. Частицы отработанной резины (RP) были предоставлены местной компанией, специализирующейся на разложении отработанных резиновых покрышек. После просеивания были отобраны частицы резины размером от 0,05 мм до 4 мм, которые были классифицированы как частицы резины в соответствии с ASTM D6270-17 [34].Чтобы изучить влияние размера зерна каучука на динамический отклик смесей песка и каучука, частицы каучука были разделены на три различных диапазона размеров зерна: RP1 с гранулометрическим составом 0,05–0,1 мм, RP2 с размером зерна. гранулометрический состав 0,1–2 мм и RP3 с гранулометрическим составом 2–4 мм. Кривые гранулометрического состава частиц песка и каучука показаны на рисунке, а их основные физические свойства представлены на рисунке.
Кривые гранулометрического состава исследуемых материалов.
Таблица 1
Основные физические свойства.
| Тип | Минимальный размер зерна D мин (мм) | Максимальный размер зерна D макс (мм) | Средний размер зерна D 50 9 мм) Соотношение размеров | |
|---|---|---|---|---|
| Песок | 0,075 | 2 | 0,66 | 0 |
| RP1 | 0,05 | 0.1 | 0,075 | 0,11 |
| RP2 | 0,1 | 2 | 0,5 | 0,75 |
| RP3 | 2 | 4 | 3 | 4,54 |
SR = (D50) каучук (D50) песок
(1)
Использовалось значение SR для количественного определения соотношения размеров частиц каучука для RP1, RP2 и RP3 с указанием средних размеров частиц каучука, соответственно, больше, чем приблизительно соответствует и меньше среднего размера частиц песка.
2.2. Подготовка образцов и конструкции смеси
Перед приготовлением образца стандартный песок помещали в печь для сушки при 100 ° C, а частицы каучука сушили на воздухе при комнатной температуре (20 ± 2 ° C) в течение 12 часов [35] . После этого частицы песка и каучука были равномерно перемешаны в течение пяти минут в соответствии с заданным объемным процентным содержанием каучука ( RV ) при комнатной температуре (20 ± 2 ° C). Значения RV , рассматриваемые в этом исследовании, составляли 0%, 10%, 20%, 30%, 40% и 50%, определенные с использованием следующего уравнения (2):
где V r — объем частиц резины, а V s — объем песка в смеси.
Относительная плотность образцов D r определялась по формуле:
Dr = ρdmax × (ρd − ρdmin) ρd × (ρdmax − ρdmin),
(3)
где ρ dmax и ρ dmin — соответственно максимальная и минимальная сухая плотность образца, а ρ d — его контролируемая сухая плотность. Максимальная плотность в сухом состоянии и минимальная плотность в сухом состоянии различных смесей были получены, соответственно, с помощью вибрационного удара и метода воронкообразного измерительного цилиндра в соответствии с ASTM D4254 [36].
В данном исследовании серия образцов диаметром 38 мм и высотой 76 мм была подготовлена с использованием сухой утрамбовки. В соответствии с сухой массой каждого образца и объемом формы каждая смесь была равномерно разделена на четыре части и последовательно уплотнена в четыре слоя снизу вверх латексной пленки формы. Затем каждый образец уплотняли, постукивая по стенке цилиндра и затем вибрируя его в течение двух минут. Относительная плотность постоянно поддерживалась на уровне 0,5. После отливки образцов их поверхности выровняли и закрыли фильтровальной бумагой и проницаемым камнем.После загрузки образца в основание ограничивающей камеры было приложено отрицательное давление, чтобы удерживать его в вертикальном положении.
2.3. Испытательное оборудование и процесс
Циклическое трехосное испытательное устройство GDS использовалось в этом исследовании для характеристики динамического поведения образцов смеси песка и каучука, которые были произведены компанией Global Digital Systems Ltd. Instrument, Хэмпшир, Соединенное Королевство. Максимальная осевая нагрузка, рабочая частота и давление аппарата составляют 10 кН, 5 Гц и 2 МПа соответственно.Циклический трехосный аппарат смог насытить и консолидировать образец под ожидаемыми боковыми и осевыми давлениями. Затем к верхней части образца прикладывалась циклическая осевая нагрузка, вызывающая периодические изменения напряжения сдвига образца.
Сначала к образцу было приложено минимальное ограничивающее давление и через него пропущен газ CO 2 в течение не менее 30 минут для облегчения процесса насыщения. Затем образец пропитывали удаленной водой и противодавлением до тех пор, пока коэффициент порового давления (значение B ) не увеличился до более чем 0.95. Затем было проведено уплотнение изотропного давления в соответствии с целевым средним эффективным ограничивающим давлением (50 кПа, 100 кПа, 150 кПа и 200 кПа) путем контроля радиального напряжения, приложенного к внутренней и внешней боковым стенкам образца, а также приложенное осевое напряжение. Следует отметить, что если объем противодавления в образце оставался стабильным в течение 5 мин после закрытия дренажного клапана, уплотнение считалось завершенным. После процесса консолидации образец был подвергнут циклическим трехосным испытаниям с контролируемым напряжением в недренированных условиях с использованием схемы нагружения синусоидальной волной, которая ступенчато увеличивалась по амплитуде для определения его динамических параметров.Согласно ASTM D3999 [37], циклические испытания проводились при различных осевых нагрузках при частоте нагружения 1 Гц до тех пор, пока осевая деформация не превысила максимальную ошибку закрытия 0,2%.
Как показано на диаграмме многоступенчатого циклического осевого нагружения в, все образцы подвергались пяти циклам нагружения на каждом уровне циклического нагружения. Для каждого синусоидального цикла было собрано всего 50 точек данных. Экспериментальная программа, использованная в данном исследовании, кратко изложена в. показаны фотографии образца схемы и экспериментальной установки.Следует отметить, что в соответствии с ASTM D3999 [37], после завершения каждого этапа нагружения и перед переходом к следующей более высокой циклической нагрузке, дренажные клапаны образца открывались для восстановления эффективного напряжения консолидации перед их повторным закрытием. снова ввести недренированные условия.
Схема применения многоступенчатого циклического осевого нагружения.
Типовая схема образца и экспериментальная установка.
Таблица 2
Экспериментальные условия циклического трехосного испытания.
| Тип | Размер частиц резины | Объемное содержание резины (%) | Соотношение размеров | Среднее эффективное удерживающее давление σ 3 (кПа) | ρ см dmax 901 г / см 80 3 ) | ρ dmin (г / см 3 ) | D r | ρ d (г / см 3 ) | Вес смеси (г) | |
|---|---|---|---|---|---|---|---|---|---|---|
| Чистый песок | — | 0 | 0 | 50, 100, 150 | 1 .97 | 1,72 | 0,5 | 1,84 | 158,6 | |
| SRP1 | RP1 | 10 | 0,11 | 50, 100, 150 | 1,86 | 1,55 | 0,5 | 1,404 | 0,5 | |
| 20 | 50, 100, 150, 200 | 1,73 | 1,44 | 1,57 | 135,3 | |||||
| 30 | 50, 100, 150 | 1,61 | 1,31 | 1.44 | 124,1 | |||||
| 40 | 50, 100, 150 | 1,48 | 1,19 | 1,32 | 113,8 | |||||
| 50 | 50, 100, 150 | 1,29 | 1,07 | 1,19 | 102,6 | |||||
| SRP2 | RP2 | 10 | 0,75 | 50, 100, 150 | 1,78 | 1,49 | 0,5 | 1,62 | 139,6 | |
| 20 | , 200 | 1.74 | 1,47 | 1,59 | 137,1 | |||||
| 30 | 50, 100, 150 | 1,67 | 1,31 | 1,47 | 126,7 | |||||
| 40 | 50, 100, 150 | 1,45 | 1,17 | 1,30 | 112,1 | |||||
| 50 | 50, 100, 150 | 1,33 | 1,07 | 1,19 | 102,6 | |||||
| SRP3 | RP3 | 4. | 50, 100, 150 | 1,91 | 1,69 | 0,5 | 1,78 | 153,4 | ||
| 20 | 50, 100, 150, 200 | 1,82 | 1,47 | 1,63 | 140,5 | |||||
| 30 | 50, 100, 150 | 1,75 | 1,43 | 1,57 | 135,3 | |||||
| 40 | 50, 100, 150 | 1,60 | 1,30 | 1,43 | 123.3 | |||||
| 50 | 50, 100, 150 | 1,47 | 1,17 | 1,30 | 112,0 |
3. Основное соотношение и параметры
Осевое напряжение и деформация в образце могут быть получены из его реакция на возрастающую динамическую нагрузку. Следует отметить, что истинные напряжения показаны в этом исследовании в зависимости от устройства циклического трехосного испытания GDS. Максимальное значение результатов в третьем цикле нагружения каждого уровня нагружения, соответственно, использовалось для определения максимального динамического напряжения сдвига τ d и динамической деформации γ d в образцах в соответствии со следующими уравнениями (4) и (5):
где σ d — максимальное динамическое напряжение в образце; ε d — максимальная динамическая деформация в образце; и ν — коэффициент Пуассона (предполагается, что он равен 0.5 в данной работе [38]).
представляет поведение деформации грунта при циклической осевой нагрузке и иллюстрирует определение динамического модуля упругости. В этом исследовании динамический модуль упругости был рассчитан следующим образом:
Ed = σdεd = (σd1 − σd2) / 2 (εd1 − εd2) / 2
(6)
где σ d 1 , σ d 2 , ε d 1 и ε d 2 — максимальные значения осевого сжатия. растягивающее напряжение, осевая деформация сжатия и осевая деформация растяжения, соответственно.Таким образом, динамический модуль сдвига образца определяется как:
Напряжение-деформация грунта при циклической осевой нагрузке и определение динамического модуля упругости.
Коэффициент демпфирования является важным динамическим параметром грунта, который выражает гистерезисные характеристики его напряженно-деформированного поведения при циклическом нагружении. Он также отражает рассеяние энергии. Как видно из, коэффициент демпфирования λ может быть определен уравнением (8) в соответствии с Хардином и Дрмевичем [39].
где W D — это площадь внутри петли гистерезиса, а W A — это площадь треугольника, выражающего каждый цикл.
Определение динамического модуля сдвига и коэффициента демпфирования смеси песка и резины.
Хардин и Дрневич [39,40] использовали гиперболическую модель для описания взаимосвязи между циклическим напряжением сдвига и циклической деформацией сдвига (т. Е. Каркасными кривыми). Модель Хардин выражается следующим образом:
где ε d — динамическое напряжение сдвига в образце; γ d — динамическая деформация сдвига в образце; и a b — параметры подгонки, где a> 0 и b > 0.Затем динамический модуль сдвига может быть получен с использованием динамического напряжения сдвига и деформации по формуле:
Затем:
С учетом уравнений (11) и (12) модель, предложенная в этом исследовании для прогнозирования значений γ dr , имеет следующий вид: выдает:
где G dmax — максимальный динамический модуль сдвига, τ dult — предельная величина динамического напряжения сдвига, а γ dr — эталонная величина деформации сдвига.Следовательно, кривую 1/ G d против γ d можно построить из экспериментальных данных для получения и подгонки параметров a и b . Затем, подставив уравнения (11) — (13) в уравнение (10):
Таким образом, из уравнений (14) и (15) можно определить, что динамический модуль сдвига смеси песка и каучука является функцией динамическая деформация сдвига.
4. Результаты динамических циклических трехосных испытаний
В этом исследовании динамическое поведение образцов смеси песка и каучука, включая их динамическое соотношение напряжения сдвига и деформации, модули сдвига и коэффициенты демпфирования при различных диапазонах деформации, определялось с помощью увеличение амплитуды касательного напряжения.Эти динамические параметры были получены для образцов с различным объемным содержанием резины, размером частиц резины и ограничивающим давлением.
4.1. Динамическое напряжение сдвига – деформация
, и представить динамическую кривую диафиза, которая может быть получена путем соединения пиков петель гистерезиса напряжения сдвига – деформации для различных этапов нагружения. Как правило, все образцы демонстрируют деформационное упрочнение при этих испытаниях с контролируемым напряжением в консолидированном недренированном трехосном режиме; то есть максимальное динамическое напряжение сдвига наблюдается при большой деформации.Общая тенденция, наблюдаемая на этих рисунках, похоже, следует хорошо известному гиперболическому закону. Также можно заметить, что при амплитудах деформации сдвига менее примерно 0,5% динамическое напряжение сдвига увеличивается, а динамическая деформация сдвига почти постоянна, демонстрируя лишь небольшое увеличение, тогда как деформация сдвига, очевидно, увеличивается при амплитудах деформации сдвига выше, чем примерно 0,5%.
Влияние содержания каучука на зависимость деформации от деформации песчано-резиновых смесей SRP2 при ограничивающем давлении 100 кПа.
Влияние размера частиц резины на соотношение напряжение-деформация смесей песка и каучука с содержанием каучука 20% при ограничивающем давлении 100 кПа.
Влияние ограничивающего давления на соотношение деформация и деформация песчано-резиновых смесей SRP2 с содержанием каучука 20%.
В случае SRP2 при ограничивающем давлении 100 кПа можно наблюдать постепенное смещение кривых динамического диафиза вниз с увеличением объемного содержания каучука, указывая на то, что при постоянной деформации сдвига образец с более высоким объемным содержанием каучука демонстрирует более низкое напряжение сдвига.Кроме того, обратите внимание, что сдвиг вниз в кривых динамического напряжения сдвига постепенно уменьшается между каждым оцененным объемным содержанием каучука. Кривая динамического диафиза сначала быстро сдвигается вниз из-за увеличения объемного содержания каучука с 0% до 10%, но это изменение замедляется или даже исчезает при увеличении между 20% и 50%, что аналогично результатам Madhusudhan et al. [30] и Mashiri et al. [41].
указывает на то, что размер частиц каучука также влияет на динамическую кривую диафиза.Если взять в качестве примера объемное содержание каучука 20% при ограничивающем давлении 100 кПа, увеличение размера частиц приводит к смещению вверх кривой динамического диафиза. Таким образом, напряжение сдвига резко возрастает с увеличением размера частиц резины при ограничивающем давлении 100 кПа.
Как показано на примере с объемным содержанием каучука SRP2 20%, увеличение ограничивающего давления также приводит к смещению вверх кривой динамического диафиза. Можно отметить, что это явление более отчетливо проявляется при низких ограничивающих давлениях (т.е.например, от 50 до 100 кПа), чем при высоких ограничивающих давлениях (т. е. от 150 до 200 кПа).
4.2. Динамический модуль сдвига
и сравните экспериментальные данные, полученные для динамического модуля сдвига в различных оцененных условиях. В общем, динамический модуль сдвига значительно уменьшается с увеличением амплитуды сдвиговых деформаций менее 0,5%, затем замедляется при деформациях сдвига более 0,5% перед установкой на низкое значение. Отмечено, что образцы, содержащие частицы каучука, демонстрируют более низкие значения динамического модуля сдвига, чем чистый песок.Более того, распределение данных динамического модуля сдвига сосредоточено при больших деформациях независимо от объемного содержания каучука, при этом значения динамического модуля сдвига образцов с различным содержанием каучука даже частично перекрываются при самых высоких деформациях. Это поведение аналогично описанному выше соотношению «напряжение-деформация».
Влияние содержания каучука на динамические модули сдвига песчано-резиновых смесей SRP2 при ограничивающем давлении 100 кПа.
Влияние размера частиц резины на динамические модули сдвига песчано-резиновых смесей с содержанием каучука 20% при ограничивающем давлении 100 кПа.
Влияние ограничивающего давления на динамические модули сдвига песчано-резиновых смесей SRP2 с содержанием каучука 20%.
В примере, где SRP2 рассматривается под ограничивающим давлением 100 кПа, можно наблюдать, что по мере увеличения объемного содержания каучука начальные динамические модули сдвига образцов при небольшой деформации постепенно уменьшаются. Очевидно, что образцы с более низким объемным содержанием каучука демонстрируют более высокие начальные динамические модули сдвига, чем образцы с более высоким объемным содержанием каучука при динамическом нагружении.Кроме того, можно наблюдать, что чистый песок демонстрирует наивысший динамический модуль сдвига примерно 46,72 МПа, динамический модуль сдвига образца с объемным содержанием каучука 10% составляет примерно 35,71 МПа (снижение на 23,57% по сравнению с песком), а динамический модуль сдвига Модуль упругости образца с объемным содержанием каучука 50% является наименьшим и составляет примерно 10,93 МПа (уменьшение на 76,61% по сравнению с песком). Кроме того, обратите внимание, что динамические модули сдвига образцов смеси немного уменьшаются при более высоком объемном содержании каучука.Feng et al. [34] и Сараджпур и др. [7] сообщили о подобных наблюдениях.
На примере образца с объемным содержанием каучука 20% под ограничивающим давлением 100 кПа ясно видно, что динамический модуль сдвига каждого образца обычно увеличивается с увеличением размера частиц каучука. Однако динамический модуль сдвига немного уменьшается с увеличением размера частиц между SRP2 и SRP1 при деформациях более 0,2%.
демонстрирует, что по мере увеличения ограничивающего давления динамические модули сдвига образцов увеличиваются.Более того, чем выше ограничивающее давление, тем больше начальное увеличение начального динамического модуля сдвига. Для SRP2 с объемным содержанием каучука 20% по сравнению с ограничивающим давлением 50 кПа начальный динамический модуль сдвига увеличивается на 94,48%, 214,92% и 280,09% при ограничивающем давлении 100 кПа, 150 кПа и 200 кПа соответственно.
4.3. Коэффициент демпфирования
Изменения коэффициента демпфирования в зависимости от деформации сдвига в зависимости от параметра образца показаны на рисунках, и.Вообще говоря, при амплитудах деформации сдвига менее примерно 1% коэффициенты демпфирования образцов увеличиваются по мере развития деформации сдвига, тогда как при амплитудах деформации сдвига более примерно 1% коэффициенты демпфирования уменьшаются.
Влияние содержания каучука на коэффициенты демпфирования песчано-резиновых смесей SRP2 при ограничивающем давлении: ( a ) 50 кПа; ( b ) 100 кПа; ( c ) 150 кПа.
Влияние размера частиц на коэффициент демпфирования смесей песка и каучука с содержанием каучука 20% при ограничивающем давлении 100 кПа.
Влияние ограничивающего давления на коэффициенты демпфирования песчано-резиновых смесей SRP2 с объемным содержанием каучука 20%.
указывает на то, что в случае SRP2 в качестве примера коэффициент демпфирования первоначально увеличивается с увеличением объемного содержания каучука. Это также можно наблюдать в результатах Ehsani et al. [42] и аналогичен результатам Sarajpoor et al. [7] и Senetakis et al. [21], как упоминалось ранее. Обратите внимание, что коэффициент демпфирования сильно зависит от размера частиц резины и показывает оптимальное значение при определенном объемном содержании резины.Для SRP2 оптимальное объемное содержание каучука, при котором коэффициент демпфирования смеси выше, чем у чистого песка, составляет примерно от 20% до 30%, в то время как в случае SRP1 (не показан) оптимальное объемное содержание каучука составляет примерно от 10% до 20%. %, но для SRP3 (также не изображенного) коэффициент демпфирования всегда ниже, чем у чистого песка. Очевидно, что влияние объемного содержания резины на коэффициент демпфирования зависит от ограничивающего давления и деформации сдвига. По мере увеличения объемного содержания резины соотношение между коэффициентом демпфирования и деформацией сдвига имеет тенденцию оставаться стабильным, что указывает на низкую чувствительность коэффициента демпфирования к изменениям амплитуды деформации сдвига.Кроме того, в b можно наблюдать, что при амплитудах деформации сдвига менее примерно 0,1% более высокое объемное содержание каучука приводит к более высокому коэффициенту демпфирования, тогда как при амплитудах деформации сдвига более 0,1% может наблюдаться противоположная тенденция. Испытания, проведенные при различных уровнях ограничивающего давления, также показали, что эти значения критической деформации увеличиваются с увеличением ограничивающего давления: критическая деформация увеличивается с 0,09% до 0,1% до 0,11% для ограничивающего давления 50 кПа, 100 кПа и 150 кПа, соответственно.
На примере образцов с объемным содержанием каучука 20% при ограничивающем давлении 100 кПа можно увидеть, что по мере увеличения размера частиц каучука коэффициент демпфирования образцов смеси уменьшается. В частности, кривая коэффициента демпфирования для SRP1 приближается к кривой для SRP2 и даже перекрывается, в то время как кривая SRP3 остается далеко от двух других.
показывает, что на примере объемного содержания каучука 10% и размера частиц SRP3 коэффициент демпфирования уменьшается с увеличением ограничивающего давления.Таким образом, влияние ограничивающего давления на ход кривой аналогично влиянию размера частиц резины.
5. Обсуждение экспериментальных результатов
Резиновые частицы имеют низкую жесткость, высокую способность к деформации и большую эластичность, и поэтому могут легко изменять форму. Напротив, частицы песка можно рассматривать как твердые частицы, особенно по сравнению с частицами каучука [38,43]. представляет схематические диаграммы внутреннего контакта и цепи передачи усилия различных типов образцов, оцениваемых в этом исследовании.Отметим, что контакт структурной поверхности ослабевает из-за добавления частиц резины в песок [44]. По мере увеличения объемного содержания каучука все больше частиц каучука вступают в контакт друг с другом, в результате чего свойства образца становятся все более похожими на каучук. Это наблюдение согласуется с результатами Liu et al. [11], которые предложили разные цепи передачи силы в образцах с разным объемным содержанием каучука. Соответственно, в механических свойствах смеси песка и резины постепенно преобладают частицы резины по мере увеличения их количества.При постоянном объемном содержании резины и относительной плотности частицы резины меньшего размера вызывают увеличение количества контактов между частицами резины и уменьшение контакта между частицами песка, потенциально увеличивая вероятность попадания песка, каучука и песка и резины в каучук. Цепи передачи силы, уменьшая при этом частоту цепей передачи силы песок-песок. Это может привести к тому, что во время динамического нагружения образцы раньше проявят каучукоподобное превращение. Кроме того, следует отметить, что частицы каучука меньшего размера могут легче перемещаться относительно друг друга, что увеличивает пластическую деформацию образца.Однако большие силы между частицами, возникающие при высоком ограничивающем давлении, препятствуют перемещению частиц при динамической нагрузке.
Принципиальная схема цепей внутреннего контакта и передачи усилия в ( a ) чистом песке; ( b ) SRP1; ( c ) SRP2; ( д ) SRP3.
Низкая жесткость и высокая упругая деформация частиц каучука, добавленных в смеси, вызывают слабый контакт между частицами образца, влияя на динамический модуль сдвига.Распространенность цепей передачи силы песок-каучук и каучук-каучук увеличивается с увеличением объемного содержания каучука и уменьшением размера частиц каучука, что потенциально увеличивает резиноподобное поведение образцов и снижает силу межкристаллитного трения. Кроме того, наблюдали, что образцы ведут себя более линейно с увеличением объемного содержания резины, таким образом, их динамические модули сдвига показывают меньшую чувствительность к уровням деформации сдвига. Ли и др. [45] и Shan et al. [46] сообщили, что контакт между жесткими частицами увеличивается, и расположение частиц затрудняется с увеличением удерживающего напряжения.Следовательно, увеличение ограничивающего давления значительно улучшает удерживающее напряжение образца, заставляя его вести себя больше как чистый песок, что приводит к более высокой сопротивляемости сдвиговым деформациям. Эти результаты можно резюмировать следующим образом: когда объемное содержание каучука увеличивается, размер частиц каучука уменьшается или ограничивающее давление уменьшается, начальный динамический модуль сдвига образца уменьшается.
Результаты демпфирования выражают собственное демпфирование, обеспечиваемое частицами каучука, а также движение частиц и межкристаллитное трение [47].Поскольку коэффициент трения для резины меньше, чем для песка [33], большая часть рассеиваемой энергии возникает в результате межкристаллитного трения между частицами песка и их скольжения при динамической нагрузке [47], поскольку чистый песок почти несжимаем [48]. Напротив, резина является высокоэластичным материалом, который в основном способствует собственному демпфированию колебаний образца [22]. Однако на механизм демпфирования также влияют уровни деформации сдвига. При небольших уровнях деформации, меньших критической, внутреннее демпфирование, обеспечиваемое частицами каучука, вносит больший вклад в рассеяние энергии, чем другие факторы, и поэтому смеси песка и каучука демонстрируют большее демпфирование, чем чистый песок.При высоких уровнях деформации, превышающей критическую, межкристаллитное трение вносит больший вклад в рассеяние энергии, чем частицы каучука [7]. Влияние объемного содержания каучука, размера частиц каучука и ограничивающего давления на коэффициент демпфирования можно резюмировать следующим образом:
Увеличение объемного содержания каучука приводит к замене некоторых частиц песка в образцах частицами каучука, что увеличивает слабые контакты между резиной и песком, что, в свою очередь, снижает межкристаллитное трение и приводит к уменьшению коэффициента демпфирования.При достаточно высоком объемном содержании каучука ожидается, что развитие более слабых точек контакта приведет к тому, что образцы будут вести себя более линейно, что приведет к коэффициенту демпфирования, который менее чувствителен к изменению амплитуды деформации сдвига. Лю и др. [11] сообщили, что частицы каучука начинают стабильно контактировать друг с другом при среднем объемном содержании каучука (20–40%). По мере увеличения количества цепей передачи силы песок-каучук и резина-резина общая жесткость образцов смеси песка и каучука еще больше снижается, а деформируемость увеличивается из-за эластичности наиболее распространенных частиц каучука.Это объясняет, почему смеси с объемным содержанием резины примерно 20–30% демонстрируют демпфирующие характеристики, превосходящие характеристики чистого песка в данном исследовании.
Хотя результаты Liu et al. [11] иллюстрируют различные цепи передачи силы в зависимости от объемного содержания резины, мы определили в этом исследовании, что количество и типы цепей передачи силы также зависят от размера частиц. Как можно видеть на фиг.4, когда объемное содержание каучука поддерживается постоянным, более мелкие частицы каучука более эффективно заполняют промежутки между частицами песка.Другими словами, количество точек контакта песка с резиной и резиной с резиной увеличивается, увеличивая количество цепей передачи силы резина-резина и песок-резина-песок и облегчая движение частиц песка во время сдвиговой нагрузки, что в конечном итоге приводит к увеличению коэффициент демпфирования. Этот вывод согласуется с результатами численного моделирования, полученными Lopera Perez et al. [33], и демонстрирует, что объемное содержание резины и размер частиц всесторонне влияют на коэффициент демпфирования смеси резина-песок.Соответственно, поскольку средний размер частиц резины SRP2 и SRP1 меньше, чем у чистого песка в этом исследовании, коэффициенты демпфирования этих образцов смеси аналогичны.
В чистом песке межкристаллитное трение увеличивается с увеличением ограничивающего давления. Этот механизм уменьшает относительное движение между частицами песка и, следовательно, уменьшает ширину петли гистерезиса, что является признанным событием в литературе по инженерно-геотехническим землетрясениям [31]. Однако гибкость добавленных частиц каучука способствует перегруппировке и относительному перемещению частиц песка, на которые влияет уровень деформации сдвига [7].Следовательно, существует критическая деформация сдвига, контролирующая демпфирующее поведение смесей песка и каучука, которое зависит от приложенного ограничивающего давления. Существование такого критического напряжения в этом исследовании согласуется с результатами Senetakis et al. [21], которые были основаны исключительно на экспериментальных данных в диапазоне деформации сдвига от 10 −3 % до 5 × 10 −2 %; поведение за пределами этого диапазона было предсказано путем аппроксимации кривой в предположении гиперболической модели. В этом исследовании испытания проводились в гораздо более широком диапазоне деформации сдвига.
Следует отметить, что, поскольку резина имеет более низкую объемную плотность, чем песок [33], распределение частиц резины будет случайным и трудно поддающимся контролю в образце, что может объяснить дисперсный характер экспериментально полученного коэффициента демпфирования. данные. Наконец, обратите внимание, что значения коэффициента демпфирования для всех типов образцов уменьшаются при больших деформациях, главным образом из-за того, что образец уплотняется по мере продолжения нагружения. В целом, способность поддерживать жесткость образца на сдвиг при одновременном увеличении его коэффициента демпфирования путем регулирования объемного содержания и размера частиц каучука в смеси составляет заметное преимущество смесей песка и каучука.
6. Эмпирическая модель
На основе экспериментальных результатов была разработана эмпирическая модель для прогнозирования влияния объемного содержания резины и ограничивающего давления на поведение смесей песка и резины. В этом разделе сначала оценивается влияние объемного содержания резины, размера частиц резины и ограничивающего давления на максимальный модуль сдвига на основе уравнения (11). Затем эмпирическая модель строится для максимального модуля сдвига, поскольку он имеет прямое влияние на расчет эталонной деформации сдвига и нормированного модуля сдвига.Наконец, эмпирическая модель используется для определения эталонной деформации сдвига и затем прогнозирования нормализованного модуля сдвига в соответствии с объемным содержанием каучука, размером частиц каучука и ограничивающим давлением с использованием уравнений (13) и (15).
6.1. Максимальный модуль сдвига
и кривые зависимости максимального динамического модуля сдвига от объемного содержания резины при различных ограничивающих давлениях, полученные с использованием уравнения (11). Можно видеть, что максимальный динамический модуль сдвига увеличивается по мере уменьшения объемного содержания каучука в соответствии с приблизительно линейной зависимостью.Как показано на фиг.1, в случае SRP1 при ограничивающем давлении 100 кПа максимальные динамические модули сдвига образцов с объемным содержанием каучука 10%, 20%, 30%, 40% и 50% составили 8,2%, 26,2%. , 41,9%, 56,0% и 67,2% соответственно меньше, чем у чистого песка. Это указывает на то, что добавление каучука в песок снижает динамический модуль сдвига смеси из-за низкой жесткости частиц каучука, что согласуется с обсуждением в разделе 5. Таким образом, изоляционные характеристики смеси песка и каучука можно улучшить, контролируя содержание каучука.Кроме того, влияние ограничивающего давления на максимальный динамический модуль сдвига для данного объемного содержания каучука, показанное на рисунке, напоминает экспоненциальную функцию. Однако с использованием данных, собранных в этом исследовании, не удалось найти никакой функции для описания влияния размера частиц резины на максимальный динамический модуль сдвига.
Влияние содержания каучука на максимальные динамические модули сдвига ( G dmax ) образцов резиновой смеси при ограничивающем давлении 100 кПа.
Влияние ограничивающего давления на максимальные динамические модули сдвига ( G dmax ) песчано-резиновых смесей с объемным содержанием каучука 20%.
6.2. Эмпирическая модель и проверка
Уравнения (13) и (15) показывают, что максимальный динамический модуль сдвига является важным параметром при вычислении эталонной деформации сдвига и нормализованного модуля сдвига, которые играют важную роль при проектировании и оценке. песчано-резиновых смесей. Таким образом, исчерпывающая функция, описывающая максимальный модуль сдвига G dmax песчано-резиновой смеси в соответствии с объемным содержанием каучука RV и ограничивающим давлением σ 3 , была получена путем рассмотрения экспериментальных данных с использованием множественной регрессии метод анализа следующим образом:
Gdmax = G0 × (αi × RV + λi) × (θi × Pa × (σ3Pa) βi)
(16)
где G 0 — параметр модели, определяемый как усредненный максимальный модуль сдвига чистого песка при трех различных оцененных ограничивающих давлениях; α i , λ i , θ i и β i — подгоночные параметры; i указывает размер частиц резины, равный 1, 2 и 3 для SRP1, SRP2 и SRP3 соответственно; и P a — эталонное напряжение, принятое равным атмосферному давлению, 101.3 кПа. Параметры подгонки были определены с использованием нелинейного поверхностного регрессионного анализа экспериментальных данных, полученных в лабораторных экспериментах, представленных в Разделе 3, Разделе 4 и Разделе 5, и результаты эмпирических функций, соответственно, нанесены на график.
Эмпирическая модель максимального динамического модуля сдвига ( G dmax ) в зависимости от содержания резины и ограничивающего давления для различных размеров частиц резины: ( a ) SRP1; ( b ) SRP2; ( c ) SRP3.
сравнивает максимальный динамический модуль сдвига, предсказанный с использованием уравнения (16), с экспериментальными данными, в которых можно заметить, что предсказанные результаты для динамического модуля сдвига представляют линейную корреляцию примерно 1: 1 с экспериментальными результатами. Это указывает на то, что уравнение (16) можно уверенно использовать для оценки и прогнозирования максимального динамического модуля сдвига смеси песка и каучука.
Проверка результатов эмпирической модели (Pre.) По сравнению с экспериментальными результатами (Exp.) для различных размеров частиц резины: ( a ) SRP1; ( b ) SRP2; ( c ) SRP3.
6.3. Справочная деформация сдвига и нормализованный модуль сдвига
Ослабление модуля сдвига является важным динамическим поведением смесей песка и каучука. Проверка уравнения (16) в разделе 6.2 показывает, что предложенную эмпирическую модель можно уверенно использовать для прогнозирования максимального динамического модуля сдвига смеси песка и каучука, но для того, чтобы четко проиллюстрировать влияние объемного содержания резины, размера частиц резины , и ограничивая давление на ослабление модуля сдвига, необходимо сначала определить эталонную деформацию сдвига, а затем нормализованный модуль сдвига.Поэтому в этом разделе предложенная эмпирическая модель используется для определения эталонной деформации сдвига и нормированного модуля сдвига с использованием ее прогнозируемого значения для максимального модуля сдвига в уравнениях (13) и (15), соответственно.
показывает, что эталонная деформация сдвига, полученная с использованием уравнений (13) и (16), почти увеличивается с увеличением объемного содержания каучука при различных ограничивающих давлениях. Можно наблюдать, что эталонная деформация сдвига значительно увеличивается при ограничивающем давлении 150 кПа, в то время как несколько противоположных тенденций можно наблюдать при ограничивающем давлении 50 и 100 кПа, особенно при низком содержании каучука.Кроме того, также наблюдается, что при объемном содержании каучука менее примерно 40% эталонная деформация сдвига почти незначительно увеличивается с увеличением объемного содержания каучука, тогда как деформация сдвига значительно увеличивается с увеличением значений объемного содержания каучука более 40 %. Эти наблюдения можно объяснить тем фактом, что большее количество частиц каучука вступает в контакт друг с другом с увеличением объемного содержания каучука и ограничивающего давления. Отношение напряжения к деформации смесей становится более похожим на отношение чистого каучука, что указывает на развитие резиноподобного поведения.Это наблюдение согласуется с результатами Liu et al. [11]. Следовательно, наклон диаграммы напряжение – деформация уменьшается, что приводит к увеличению эталонных значений деформации сдвига. Хотя при низком объемном содержании каучука и ограничивающем давлении эти контакты не были очевидны, эталонные значения деформации сдвига увеличиваются незаметно и даже, по-видимому, имеют обратную тенденцию.
Влияние объемного содержания каучука и ограничивающего давления на эталонную деформацию сдвига песчано-резиновых смесей с различным размером частиц каучука: ( a ) SRP1; ( b ) SRP2; ( c ) SRP3.
, и показывают нормированный динамический модуль сдвига, определенный как G d / G dmax , в зависимости от динамической деформации сдвига при различных значениях объемного содержания резины, размерах частиц резины и ограничивающем давлении соответственно. Значения G d / G dmax , показанные на кривых, были определены с использованием правой части уравнения (15), а прогнозируемые результаты были определены путем применения результатов уравнения (16) как G dmax слева.Можно заметить, что прогнозируемые результаты относительно хорошо согласуются с результатами расчетов, что дополнительно демонстрирует, что новую модель можно уверенно использовать для прогнозирования ослабления модуля сдвига при проектировании смесей песка и каучука. При любом постоянном ограничивающем давлении и размере частиц резины увеличение объемного содержания резины приводит к увеличению значений G d / G dmax . Это явление является результатом увеличения жесткости материала с увеличением ограничивающего давления и указывает на более эластичное и гибкое (однородное) поведение смеси с увеличением объемного содержания каучука ().Далее можно наблюдать, что значения G / G dmax увеличиваются с увеличением размера частиц резины () и ограничивающего давления ().
Нормализованный модуль сдвига в зависимости от деформации сдвига для SRP2 при ограничивающем давлении 150 кПа в соответствии с объемным содержанием каучука.
Нормализованный модуль сдвига в зависимости от деформации сдвига для 20% объемного содержания каучука при ограничивающем давлении 100 кПа в зависимости от размера частиц резины.
Нормализованный модуль сдвига в зависимости от амплитуды деформации сдвига для SRP2 с 20% -ным содержанием каучука в соответствии с приложенным ограничивающим давлением.
7. Резюме и выводы
В этом исследовании была проведена серия крупномасштабных консолидированных недренированных циклических трехосных испытаний и проведен систематический анализ результатов для исследования динамического поведения смесей песчано-резиновых частиц в широком диапазоне. амплитуд сдвиговой деформации. Было подробно рассмотрено влияние различных параметров, включая объемное содержание резины, размер частиц резины и ограничивающее давление. Эти воздействия затем были включены в предложенную эмпирическую модель для прогнозирования модулей сдвига смесей песка и каучука.На основании результатов испытаний и анализа сделаны следующие выводы:
Практически все образцы проявляли деформационное упрочнение, то есть максимальное динамическое напряжение сдвига наблюдалось при больших деформациях. Зависимость напряжения от деформации при циклическом нагружении проявляет гистерезис, нелинейность и накопление деформации. По мере увеличения объемного содержания каучука в образцах смеси кривая напряжения-деформации сдвигалась вверх, тогда как результаты были противоположными по мере увеличения ограничивающего давления.Также было замечено, что размер резиновых частиц влияет на соотношение между напряжением и деформацией.
По мере увеличения объемного содержания каучука модули сдвига всех образцов смесей сначала значительно уменьшались, но затем медленно и, наконец, имели тенденцию к стабильности с продолжающимся увеличением деформации. Однако увеличение ограничивающего давления и размера частиц резины привело к увеличению модуля сдвига. Это может быть связано с увеличением количества точек контакта песка и резины и резины с резиной с увеличением объемного содержания резины, что приводит к уменьшению модулей сдвига образцов смеси.
Было отмечено, что характеристики коэффициентов демпфирования образца смеси усложняются. При амплитудах деформации сдвига меньше критического значения деформации коэффициенты демпфирования образцов смеси увеличивались с увеличением объемного содержания резины и демонстрировали более высокий коэффициент демпфирования, чем у чистого песка. Однако при деформации сдвига, превышающей критическое значение деформации, наблюдалась обратная тенденция. Кроме того, коэффициент демпфирования немного снизился с увеличением ограничивающего давления и значительно увеличился с уменьшением размера частиц резины.
Максимальный модуль сдвига снижался с увеличением объемного содержания каучука. Было обнаружено, что зависимость между максимальным модулем сдвига и объемным содержанием каучука является линейной, а зависимость между максимальным модулем сдвига и ограничивающим давлением — экспоненциальной. Соответственно, была предложена эмпирическая модель для максимального модуля сдвига и подтверждена экспериментальными результатами. Проверенная эмпирическая модель затем использовалась для расчета эталонной деформации сдвига и нормализованного модуля сдвига в соответствии с объемным содержанием резины, размером частиц резины и ограничивающим давлением, поскольку ослабление модуля сдвига имеет решающее значение для точного представления динамического поведения песка. –Резиновые смеси.Было обнаружено, что когда ограничивающее давление и размер резиновых частиц поддерживаются постоянными, более высокое объемное содержание каучука приводит к более высоким значениям нормализованного модуля сдвига ( G d / G dmax ). Кроме того, было обнаружено, что нормированные значения модуля сдвига, рассчитанные с использованием экспериментальных результатов, совпадают со значениями, предсказанными с использованием предложенной эмпирической модели. Таким образом, предложенная эмпирическая модель может служить эталоном для оценки максимального модуля сдвига смеси песка и резины.
Смесь песка и каучука потенциально может быть недорогим и простым конструкционным изоляционным материалом, хотя ее динамические характеристики очень сложны. Таким образом, целью данного исследования было улучшить текущее понимание динамического поведения этих смесей. Результаты экспериментальных исследований показывают, что при применении смесей песка и каучука в качестве изоляционных материалов необходимо тщательно учитывать их технические свойства, поскольку положительные или отрицательные эффекты могут возникнуть в результате корректировки различных задействованных параметров.Относительная плотность может повлиять на динамическое поведение смеси песка и резины, в то время как это исследование рассматривается только для Dr = 50%. Рекомендуется провести дополнительные исследования для изучения других эффектов, включая относительную плотность, частоту и т. Д., Между смесью резины и песка.
Вклад авторов
Предпосылки для данной публикации были выполнены всеми авторами. J.L. и B.J. провели эксперименты, анализ и проверку данных; Дж.C. способствовал администрированию проекта и привлечению финансирования; Ю.С. участвовал в обработке данных и редактировании рукописи; Ю.Л. способствовал руководству исследовательской работой и редактированию рукописи; J.L. написал эту рукопись. Все авторы прочитали и согласились с опубликованной версией рукописи.
Финансирование
Это исследование финансировалось Национальной программой ключевых исследований и разработок Китая (2017YFC1500400), Национальным фондом естественных наук Китая (NSFC) (грант No.51878192, 51778159).
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Ссылки
1. Брюнет С., де ла Ллера Дж. К., Каусель Э. Нелинейное моделирование систем сейсмической изоляции, изготовленных из переработанной резины. Почва. Дин. Earthq. Англ. 2016; 85: 134–145. DOI: 10.1016 / j.soildyn.2016.03.019. [CrossRef] [Google Scholar] 2. Юн Ю.В., Хео С.Б., Ким К.С. Геотехнические характеристики отработанных шин для армирования грунта после камерных испытаний. Геотекст. Geomembr.2008. 26: 100–107. DOI: 10.1016 / j.geotexmem.2006.10.004. [CrossRef] [Google Scholar] 3. Лю Х., Ван X., Цзяо Ю., Ша Т. Экспериментальное исследование механических свойств и свойств прочности резиновой крошки из бетона. Материалы. 2016; 9: 172. DOI: 10.3390 / ma72. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar] 4. Сяо М., Ледезма М., Хартман К. Сопротивление сдвигу агрегата, полученного из шин, с использованием крупномасштабных испытаний на прямой сдвиг. J. Mater. Civ. Англ. 2015; 27: 04014110. DOI: 10.1061 / (ASCE) MT.1943-5533.0001007. [CrossRef] [Google Scholar] 5. Хеннеберт П., Ламберт С., Фуиллен Ф., Шаррас Б. Оценка воздействия измельченных шин в качестве материала насыпи на окружающую среду. Жестяная банка. Геотех. J. 2014; 51: 469–478. DOI: 10.1139 / cgj-2013-0194. [CrossRef] [Google Scholar] 6. О’Шонесси В., Гарга В.К. Земляная насыпь, армированная шинами. Часть 3: Экологическая оценка. Жестяная банка. Геотех. J. 2000; 37: 117–131. DOI: 10.1139 / t99-086. [CrossRef] [Google Scholar] 7. Сараджпур С., Каванд А., Зог П., Галандарзаде А. Динамическое поведение смесей песка и каучука на основе испытаний с полым цилиндром.Констр. Строить. Матер. 2020; 251: 118948. DOI: 10.1016 / j.conbuildmat.2020.118948. [CrossRef] [Google Scholar] 8. Xie T., Wang F., Xie C., Lei S., Yu S., Liu J., Huang D. Механические свойства натурального каучука с наполнителями из литейных отходов. Материалы. 2019; 12: 1863. DOI: 10.3390 / ma12111863. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar] 9. Петрелла А., Ди Мундо Р., Де Гизи С., Тодаро Ф., Лабианка К., Нотарникола М. Экологически безопасные цементные композиты на основе отработанной резины для шин и переработанных отходов пористого стекла.Материалы. 2019; 12: 3289. DOI: 10.3390 / ma12203289. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar] 10. Ли К., Чыонг Q.H., Ли В., Ли Дж. Характеристики смесей резино-песчаных частиц по соотношению фракций. J. Mater. Civ. Англ. 2010. 22: 323–331. DOI: 10.1061 / (ASCE) MT.1943-5533.0000027. [CrossRef] [Google Scholar] 11. Лю Л., Цай Г., Лю С. Свойства сжатия и микромеханизмы смесей частиц резины и песка с учетом измельчения зерна. Констр. Строить. Матер. 2018; 187: 1061–1072.DOI: 10.1016 / j.conbuildmat.2018.08.051. [CrossRef] [Google Scholar] 12. Ли Х., Цзян Х., Чжан В., Лю П., Ван С., Ван Ф., Чжан Дж., Яо З. Лабораторные и полевые исследования возможности применения отходов резиновой крошки для повышения гибкости противодействующих средств защиты. колейность асфальтового покрытия. Материалы. 2018; 11: 1738. DOI: 10.3390 / ma110Объяснение демпфирования
Демпфирование — это воздействие внутри или на колебательную систему, которое имеет эффект уменьшения или предотвращения ее колебаний. В физических системах затухание вызывается процессами, которые рассеивают энергию, запасенную в колебаниях. [1] Примеры включают вязкое сопротивление (вязкость жидкости может препятствовать колебательной системе, вызывая ее замедление) в механических системах, сопротивление в электронных генераторах, а также поглощение и рассеяние света в оптических генераторах. Демпфирование, не основанное на потерях энергии, может быть важным в других колебательных системах, например, в биологических системах и велосипедах [2] (например, подвеска (механика)). Не следует путать с трением, которое представляет собой диссипативную силу, действующую на систему.Трение может быть причиной или быть фактором демпфирования.
Коэффициент демпфирования — это безразмерная мера, описывающая, как колебания в системе затухают после возмущения. Многие системы демонстрируют колебательное поведение, когда они выходят из положения статического равновесия. Например, масса, подвешенная на пружине, может, если ее потянуть и отпустить, подпрыгнет вверх и вниз. При каждом отскоке система стремится вернуться в свое положение равновесия, но проскакивает его. Иногда потери (напр.грамм. трение) демпфируют систему и могут вызывать постепенное затухание амплитуды колебаний до нуля или ослабление. Коэффициент затухания — это мера, описывающая, насколько быстро колебания затухают от одного отскока к другому.
Коэффициент демпфирования — это системный параметр, обозначаемый ζ (дзета), который может варьироваться от без демпфирования , с недостаточным демпфированием до с критическим демпфированием до с избыточным демпфированием .
Поведение колебательных систем часто представляет интерес в самых разных дисциплинах, включая технику управления, химическую инженерию, машиностроение, структурную инженерию и электротехнику.Физическая величина, которая колеблется, сильно варьируется и может быть колебанием высокого здания на ветру или скоростью электродвигателя, но нормализованный или безразмерный подход может быть удобным для описания общих аспектов поведения.
Колебательные корпуса
В зависимости от степени демпфирования система демонстрирует различное колебательное поведение и скорость.
- Там, где система пружина-масса полностью без потерь, масса будет колебаться бесконечно, причем каждый отскок будет иметь одинаковую высоту с последним.Этот гипотетический случай называется незатухающий .
- Если система содержала большие потери, например, если эксперимент с пружиной и массой проводился в вязкой жидкости, масса могла бы медленно вернуться в исходное положение, не превышая. Этот случай называется overdamped .
- Обычно масса имеет тенденцию выходить за пределы своего начального положения, а затем возвращаться, снова выскакивая за пределы. При каждом выбросе некоторая энергия в системе рассеивается, и колебания затухают до нуля.Этот корпус называется underdamped.
- Между случаями с избыточным и недостаточным демпфированием существует определенный уровень демпфирования, при котором система просто не сможет перескочить и не совершит ни одного колебания. Этот случай называется с критическим демпфированием . Ключевое различие между критическим демпфированием и избыточным демпфированием заключается в том, что при критическом демпфировании система возвращается в состояние равновесия за минимальное время.
Затухающая синусоида
Демпфирование не следует путать с затухающей волной (радиопередачей).
Затухающая синусоида или затухающая синусоида — это синусоидальная функция, амплитуда которой приближается к нулю с увеличением времени, что соответствует случаю с недостаточным затуханием систем с затуханием второго порядка или дифференциальным уравнениям второго порядка с недостаточным затуханием. [3] Затухающие синусоидальные волны обычно встречаются в науке и технике, где гармонический осциллятор теряет энергию быстрее, чем подается. Истинная синусоида, начинающаяся в момент времени = 0, начинается в начале координат (амплитуда = 0).Косинусоидальная волна начинается с максимального значения из-за разницы фаз от синусоидальной волны. Данная синусоидальная форма волны может иметь промежуточную фазу, имеющую как синусоидальные, так и косинусоидальные компоненты. Термин «затухающая синусоида» описывает все такие затухающие формы волны, независимо от их начальной фазы.
Наиболее распространенная форма демпфирования, которая обычно принимается, — это форма, встречающаяся в линейных системах. Эта форма представляет собой экспоненциальное затухание, при котором внешняя огибающая последовательных пиков представляет собой кривую экспоненциального затухания.То есть, когда вы соединяете максимальную точку каждой последующей кривой, результат напоминает функцию экспоненциального затухания. Общее уравнение для экспоненциально затухающей синусоиды может быть представлено как:
y (t) = A ⋅ e -λ ⋅ \ cos (\ omega t — \ phi)
куда: — мгновенная амплитуда в момент времени t ; — начальная амплитуда огибающей; — скорость убывания, обратная единицам времени независимой переменной t ; — фазовый угол при t = 0; — угловая частота.Другие важные параметры включают:
, количество циклов в единицу времени. Выражается в обратных единицах времени. , или герц. , время уменьшения амплитуды в e раз.- Период полураспада — это время, за которое огибающая экспоненциальной амплитуды уменьшится в 2 раза. Он равен .
\ zeta = λ / \ sqrt { λ 2 + \ omega 2 } < 1
.- еще одна безразмерная характеристика величины демпфирования; высокий Q указывает на медленное затухание относительно колебаний.Определение коэффициента демпфирования
Коэффициент демпфирования — это параметр, обычно обозначаемый как ζ (греческая буква дзета), [4] , который характеризует частотную характеристику обыкновенного дифференциального уравнения второго порядка. Это особенно важно при изучении теории управления. Это также важно в гармоническом осцилляторе.В общем, системы с более высокими коэффициентами демпфирования (один или больше) будут демонстрировать больший эффект демпфирования. Системы с недостаточным демпфированием имеют значение меньше единицы. Системы с критическим демпфированием имеют коэффициент демпфирования ровно 1 или, по крайней мере, очень близок к нему.
Коэффициент демпфирования представляет собой математическое средство выражения уровня демпфирования в системе относительно критического демпфирования. Для демпфированного гармонического осциллятора с массой м , коэффициентом демпфирования c и жесткостью пружины k его можно определить как отношение коэффициента демпфирования в дифференциальном уравнении системы к критическому коэффициенту демпфирования:
\ zeta =
=
| фактическое демпфирование | |
| критическое демпфирование |
,
, где уравнение движения системы
и соответствующий критический коэффициент демпфирования
или
} = 2m \ omega_n, где } — собственная частота системы.Коэффициент демпфирования безразмерный, это отношение двух коэффициентов одинаковых единиц.
Вывод
Используя собственную частоту гармонического осциллятора \ omega_n = \ sqrt и определение коэффициента демпфирования выше, мы можем переписать это как:
Это уравнение является более общим, чем просто система масса-пружина, а также применимо к электрическим цепям и другим областям. Это можно решить с помощью подхода.
, где C и s являются комплексными константами, при этом s удовлетворяет
s = — \ omega n \ слева (\ zeta \ pm i \ sqrt { 1- \ zeta 2 } \ справа).
Два таких решения для двух значений с , удовлетворяющих уравнению, могут быть объединены для получения общих реальных решений с колебательными и затухающими свойствами в нескольких режимах:
- Незатухающий: случай, когда
- Недостаточное демпфирование: Если s представляет собой пару комплексных значений, то каждый член комплексного решения представляет собой убывающую экспоненту в сочетании с колебательной частью, которая выглядит как \ exp \ left (i \ omega_n \ sqrtt \ right). Этот случай имеет место для
- Сверхдемпфирование: Если с представляет собой пару действительных значений, то решение представляет собой просто сумму двух убывающих экспонент без колебаний. Этот случай имеет место для
- Критическое демпфирование: случай, когда
Фактор Q , коэффициент демпфирования ζ и экспоненциальная скорость затухания α связаны таким образом, что [5]
\ zeta =
= { \ alpha \ более \ omega n }.
Когда система второго порядка имеет
(то есть, когда система недостаточно демпфирована), она имеет два комплексно сопряженных полюса, каждый из которых имеет действительную часть ; то есть параметр скорости распада представляет собой скорость экспоненциального затухания колебаний.Более низкий коэффициент демпфирования подразумевает меньшую скорость затухания, и поэтому системы с очень слабым демпфированием колеблются в течение длительного времени. [6] Например, высококачественный камертон с очень низким коэффициентом демпфирования имеет длительные колебания, которые очень медленно затухают после удара молотком.Логарифмический декремент
. Коэффициент затухания может быть найден для любых двух пиков, даже если они не являются смежными. [7] Для соседних пиков: [8]\ zeta =
| \ delta | |
| \ sqrt {\ delta 2 + \ left ( 2 \ pi \ right) 2 |
, где x 0 и x 1 — амплитуды любых двух последовательных пиков.
Как показано на правом рисунке:
где
, — амплитуды двух последовательных положительных пиков и , — амплитуды двух последовательных отрицательных пиков.Процент превышения
В теории управления перерегулирование относится к выходному сигналу, превышающему его конечное установившееся значение. [9] Для ступенчатого входа процентное превышение (PO) — это максимальное значение минус значение шага, деленное на значение шага. В случае единичного шага отклонение , — это просто максимальное значение реакции на скачок минус один.
Процент превышения (PO) связан с коэффициентом демпфирования ( ζ ) следующим образом:
}} \ right)И наоборот, коэффициент демпфирования ( ζ ), который дает данный процент превышения, определяется как:
}Примеры и приложения
Вязкое сопротивление
Представьте, что вы роняете объект. Пока этот объект падает в воздухе, единственная сила, препятствующая его свободному падению, — это сопротивление воздуха. Если вы уроните объект в воду или масло, он начнет замедляться с большей скоростью, пока в конечном итоге не достигнет установившейся скорости, поскольку сила сопротивления приходит в равновесие с силой тяжести.Это концепция вязкого сопротивления. Применение этой концепции в повседневной жизни объясняет физику автоматических дверей или дверей с защитой от захлопывания. [10]
Демпфирование в электрических системах
Электрические системы, работающие с переменным током (AC), используют резисторы для гашения электрического тока, поскольку они являются периодическими. Диммерные переключатели или ручки регулировки громкости являются примерами демпфирования в электрической системе.
Магнитное демпфирование
Кинетическая энергия, вызывающая колебания, рассеивается в виде тепла электрическими вихревыми токами, которые индуцируются при прохождении через полюса магнита катушкой или алюминиевой пластиной.Другими словами, сопротивление, вызванное магнитными силами, замедляет работу системы. Примером применения этой концепции в реальном мире являются тормоза на американских горках. [11]
Список литературы
11. Британника, Энциклопедия. «Демпфирование». Британская энциклопедия , Британская энциклопедия, Inc., www.britannica.com/science/damping.
12. OpenStax, Колледж. «Физика». Люмен , course.lumenlearning.com/physics/chapter/23-4-eddy-currents-and-mintage-damping/.
Примечания и ссылки
- Книга: Введение в механические колебания. Steidel. 1971. Джон Уайли и сыновья. 37. с демпфированием — термин, используемый при изучении вибрации для обозначения рассеяния энергии.
- Труды Королевского общества, A. 463. 2084. 2007. 1955–1982. Линеаризованные уравнения динамики для баланса и управляемости велосипеда: эталон и обзор. 10.1098 / rspa.2007.1857. возмущения наклона и поворота угасают, казалось бы, приглушенным образом.Однако система не имеет истинного демпфирования и сохраняет энергию. Энергия в колебаниях наклона и поворота передается на скорость движения, а не рассеивается. 2007RSPSA.463.1955M. J. P. Meijaard. Дж. М. Пападопулос. А. Руина. А. Л. Шваб. 18309860. amp.
- Дуглас К. Джанколи (2000). [» Физика для ученых и инженеров с современной физикой (3-е издание) »]. Прентис Холл. п. 387
- Книга: Альциатор , Дэвид Г. . Введение в мехатронику и измерения.Макгроу Хилл. 2007. 3-е. 978-0-07-296305-2.
- Книга: Схемы, сигналы и системы. Уильям МакКи. Зиберт. MIT Press.
- Книга: АСУ ТП: учебник для инженеров-химиков, механиков и электриков. Мин Рао и Хаймин Цю. CRC Press. 1993 г. 978-2-88124-628-9. 96.
- https://www.brown.edu/Departments/Engineering/Courses/En4/Notes/vibrations_free_damped/vibrations_free_damped.htm
- https://pm-engr.com/damping-evaluation-2/
- Книга: Системы автоматического управления.Куо, Бенджамин С. и Голнараги М. Ф. Вили. 2003. 0-471-13476-7. Восьмой. NY. §7.3 с. 236–237.
- Веб-сайт: определение, типы и примеры демпфирования. 2021-06-09. Британская энциклопедия. en.
- Web-сайт: Физика вихревых токов и магнитного затухания. 2021-06-09. course.lumenlearning.com.