Теория погрешностей физика: теория погрешностей

теория погрешностей

В.В. Бурмистров

КРАТКАЯ

ТЕОРИЯ

ПОГРЕШНОСТЕЙ

КОЛОМНА «РИЗА»-2008

В.В. Бурмистров

КРАТКАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ

Издание третье стереотипное исправленное и дополненное

Рекомендовано кафедрой физики Коломенского института МГОУ

в качестве учебного пособия для студентов всех специальностей

.Коломна .

«РИЗА» 2008

2

УДК 535 (075)

Рецензент

канд. физ.-мат. наук, доцент кафедры общей и специальной физики Обнинского института атомной энергетики

ТихоненкоА.В.

Научный редактор: Беспалов Б.Б. Технический редактор: Тарасова Н.А. Компьютерная графика: Бурмистров В.В.

БурмистровВ.В.

Краткая теория погрешностей . / – Коломна, «Риза», 2008. – 52с.: ил.

Пособие является введением в проблемы обработки результатов эксперимента.

Приведена краткая сводка правил обработки результатов прямых и косвенных измерений. Представлены подробные рекомендации по оформлению результатов измерений.

Изложение дополнено многочисленными примерами.

Пособие предназначено для студентов технических специальностей вузов, является достаточным для работы в лабораториях общефизического практикума; полезно любому начинающему экспериментатору.

Оригинал-макет данного издания является собственностью автора, и его репродуцирование (воспроизведение) любым способом без согласия автора запрещается и преследуется по закону.

3

ПЕРЕЧЕНЬ ИСПОЛЬЗУЕМЫХ ОБОЗНАЧЕНИЙ

ОБОЗНАЧЕНИЕ ВЕЛИЧИНЫ		СМЫСЛОВОЕ ЗНАЧЕНИЕ	ВЕЛИЧИНЫ
1		2
xi	i–ое	значение прямо	измеряемой
	величины x

xабсолютная погрешность (абсолютная ошибка) измерения величины x

δx	относительная	погрешность
	(относительная ошибка) измерения
	величины x

xсреднее арифметическое значение прямо измеряемой величины, принимаемое за истинное значение x

Sx =			n				выборочное стандартное	отклонение
		1	∑(xi − x )2				для результата из n измерений прямо
		n−1	i =1				измеряемой величины x
S	x	=σ =		1	S	x	среднеквадратичная	погрешность
				n			среднего арифметического
			сл				доверительный интервал для случайной
							погрешности
		tα,n−1					коэффициент Стьюдента

αкоэффициент доверия

nобъем выборки (набор из n значений измерений)

σ = S x	стандартное	отклонение		или
	среднеквадратичная		погрешность
	среднего арифметического
σ 2	дисперсия результата из n измерений
σприб	стандартное отклонение прибора

γкласс точности прибора

пред	предельная погрешность прибора

ωцена наименьшего деления шкалы прибора

ωпредельная погрешность шкалы механического прибора

пред. подбора	предельная	погрешность	подбора
	наименьшей гири
1		2

4

пред.гирь			суммарная	предельная		погрешность
			всех гирь
пред.весов			предельная погрешность весов
пред.взвеш.			предельная погрешность взвешивания
σвзвеш.			стандартное отклонение взвешивания
σокр			стандартное	отклонение		погрешности
			округления
σсуб			стандартное	отклонение субъективной
			погрешности
σмет			стандартное	отклонение		погрешности
			метода
σсумм			стандартное	отклонение		суммарной
			погрешности
σсист			суммарная		систематическая
			погрешность
сист			доверительный		интервал		для
			систематической погрешности
сумм			доверительный		интервал		для
			суммарной погрешности
γα =		1	коэффициент Чебышева
	1−α

uкосвенно измеряемая физическая величина

uсреднее арифметическое значение косвенно измеряемой величины, принимаемое за истинное значение u

	Su	выборочное стандартное		отклонение
		для результата	из n	измерений
		косвенно измеряемой величины u
	δu	относительное стандартное отклонение
		измерения величины u
		***** ПЕРЕЧЕНЬ ОБОЗНАЧЕНИЙ *****

5

ВВЕДЕНИЕ в ТЕОРИЮ ПОГРЕШНОСТЕЙ

Физика, как известно, является экспериментальной наукой.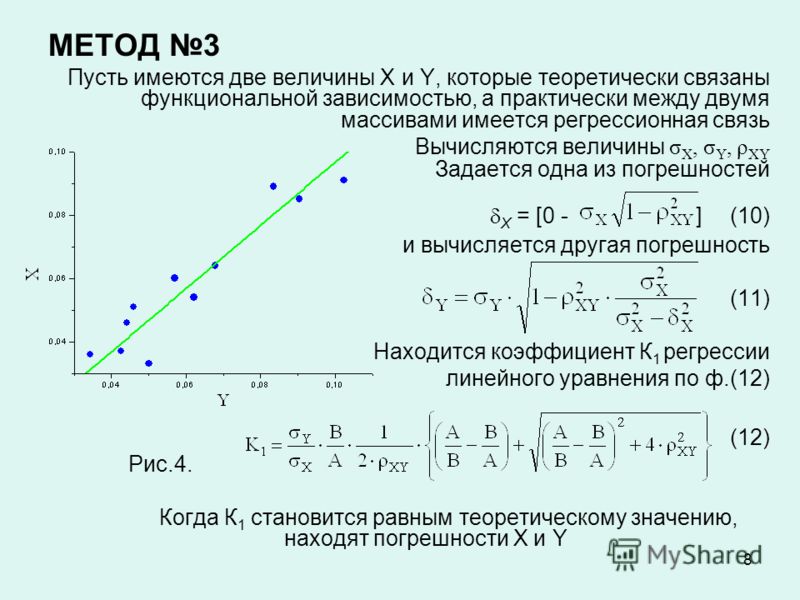 Фундаментальные законы физики, играющие значительную роль в нашей повседневной жизни, принимаются без доказательства на основе анализа огромного экспериментального материала.

При измерении физических величин экспериментатора подстерегает большое количество объективных ошибок, называемых чаще погрешностями.

Погрешности различаются, прежде всего, по характеру проявлений: то ли это случайная погрешность, обусловленная недостаточно большим объемом выборки, то ли это систематическая погрешность, которая принципиально не зависит от количества проведенных опытов, а целиком определяется погрешностями средств измерений и несовершенством методов измерений. Одним словом, систематические погрешности существуют при любом измерении. Главный вопрос – как оценить эти погрешности? Другой вопрос – как уменьшить эти погрешности?

Следует иметь в виду, что измерения могут резко отличаться по характеру последовательности осуществляемых операций. Тогда различают правила обработки, то есть правила оценки погрешностей для величин прямо и косвенно измеряемых в эксперименте. Очевидно, при использовании формул, содержащих искомую величину, значительно сложнее определить погрешность, нежели для тех величин, которые доступны измерению непосредственно каким-либо прибором.

Из вышеприведенных рассуждений напрашивается простой вывод о том, что необходимо иметь инструмент, способный оценивать пределы достоверности, или, говоря языком теории погрешностей, доверительный интервал искомых физических величин. Теория погрешностей в полной мере наделена разнообразными подходами обработки экспериментальных данных и оценки различных видов погрешностей с выдачей доверительного интервала и коэффициента доверия.

***** ВВЕДЕНИЕ в ТЕОРИЮ ПОГРЕШНОСТЕЙ *****

6

§1. Основные понятия теории погрешностей

§1.1. Физическая величина и её измерение

Физическая величина – это количественная характеристика явления, процесса или свойства материи (материальных объектов). Каждая физическая величина должна иметь определение, содержащее однозначный способ экспериментального нахождения или расчета данной физической величины в любой реальной ситуации.

Измерить физическую величину буквально означает определить, сколько раз заключается в ней однородная с ней физическая величина, принятая в качестве единицы меры (единицы измерения, меры, единицы). Физические величины называют однородными, если они характеризуют одинаковые свойства материи и отличаются друг от друга только величиной. Единицы меры устанавливаются системой единиц измерения. В нашем практикуме используется преимущественно международная система единиц СИ.

В результате измерения физической величины получается значение физической величины – именованное число, состоящее из числа и наименования той меры (единицы), которой была измерена физическая величина. Измерение – это, по существу, последовательность экспериментальных и вычислительных операций, осуществляемая с целью нахождения значения физической величины.

* * * * * * * * * * * * * * *

§1.2. Классификация измерений

Проведем классификацию измерений физической величины по характеру последовательности осуществляемых при этом операций.

Прямое измерение. Измерение называется прямым, если значение физической величины определяется либо непосредственным сравнением с мерой, либо при помощи измерительного прибора, дающего сразу значение этой величины. Такая физическая величина называется прямо измеряемой.

Косвенное измерение. Измерение называется косвенным, если искомое значение физической величины определяется путем расчета по известной зависимости измеряемой величины от прямо измеряемых величин, определяемых при неизменных условиях опыта. Такая физическая величина называется косвенно измеряемой.

Косвенно измеряемая физическая величина u связана с прямо измеряемыми величинами x, y,…, z посредством расчетной формулы

(уравнения косвенных измерений)

7

u = f (x, y,…, z) .

Вид расчетной формулы определяется модельными представлениями и связанными с ними законами физики.

Совместные измерения. В общем случае функциональная связь между прямо измеряемыми величинами x, y,…, z и величинами

u,υ,. .., w , значение которых требуется определить, может иметь произвольный вид, задаваемый уравнением

f(x, y,…, z;u,υ,…w) = 0 .

Вэтом случае для нахождения значений неизвестных величин u,υ,…, w обычно проводятся многократные измерения прямо

измеряемых величин x, y,…, z , причем эти измерения осуществляют

при изменяющихся условиях опыта. Иными словами, значения одной или нескольких прямо измеряемых величин целенаправленно изменяют от опыта к опыту, проводя, таким образом, серию из n

измерений (x1, y1,…, z1 ), (x2 , y2 ,…, z2 ),…, (xn , yn ,…, zn ). Такие измерения принято называть совместными измерениями.

Для случая двух прямо измеряемых величин x и y

функциональную взаимосвязь (уравнение совместных измерений)

часто можно представить в виде

y = f (x;u,υ,…w) ,

где u,υ,…w – искомые величины, выступающие в качестве параметров. Обычно результаты совместных измерений для наглядности и контроля правильности обработки и интерпретации изображают в виде графика зависимости величины x и y друг от

друга. Экспериментальная точка на графике изображает результат i– го совместного измерения (xi , yi ) . Отметим, что каждое измерение

(xi , yi ) не обязательно должно быть результатом одного прямого

измерения. Оно может быть как результатом обработки серии прямых измерений, так и результатом косвенных измерений.

Число совместных измерений (опытов) n в серии должно быть больше или равно числу определяемых величин m. Величина i = n −m называется числом степеней свободы при совместных измерениях.

Как видим, одна и та же физическая величина может быть прямо или косвенно измеряемой или определяться в результате обработки результатов совместных измерений.

* * * * * * *

Пример 1 (с продолжением).

8

Три студента (Иванов, Петров и Сидоров) получили задание: с помощью секундомера определить период T колебания математического маятника. Иванов решил провести прямое измерение: непосредственно измерить время одного полного колебания. Петров решил измерить время t , за которое маятник совершает N колебаний и рассчитать период по формуле T =t N .

Данная формула является уравнением косвенных измерений.

Следовательно, Петров проводит косвенные измерения. Сидоров решил последовательно измерить времена t1,t2 ,…,tk , за которые

маятник совершает N1, N2 ,…, Nk колебаний. Таким образом, Сидоров

целенаправленно изменяет значения одной из прямо измеряемых величин (в данном случае числа колебаний N ), проводя серию

совместных измерений (N1,t1 ), (N2 ,t2 ),…, (Nk ,tk ), при этом

уравнение совместных измерений имеет вид t = f (N;T ) =T N .

Продолжение следует

* * *

Далее подробно будут описаны прямые и косвенные измерения. Совместные измерения выходят за пределы рассмотрения предмета данного методического пособия.

***** §1 *****

9

§2. Погрешности измерений и их классификация

Наличие в общем случае большого числа неконтролируемых исследователем факторов приводит к тому, что в результате измерения физической величины возникают ошибки (погрешности). Иными словами, важнейшей особенностью любых измерений является несовпадение результата измерений и истинного значения измеряемой величины. Целью любой обработки результатов измерений является получение оценки истинного значения измеряемой величины с минимально возможной погрешностью.

Абсолютная погрешность (абсолютная ошибка) измерения Дx

– отклонение результата измерения x от истинного значения xист

измеряемой величины:

x = x − xист.

Относительная погрешность (относительная ошибка)

измерения δx – отношение абсолютной погрешности Дx к истинному значению измеряемой величины xист:

δx = xxист .

Как правило, истинное значение измеряемой физической величины мы не знаем и никогда не узнаем, следовательно, и погрешность измерения мы не знаем и никогда не узнаем. Однако погрешность измерения можно охарактеризовать и оценить.

* * * * * * * * * * * * * * *

§2.1. Классификация погрешностей измерения по характеру проявления

Случайная погрешность – это составляющая погрешности измерения, изменяющаяся случайным образом в данной серии измерений, проведенных при одних и тех же контролируемых условиях. Случайная погрешность возникает как результат совместного влияния различных случайных, меняющихся от измерения к измерению, не контролируемых нами факторов, влияющих на процесс измерения. Так, при измерении токов и напряжений на результаты влияет нестабильность напряжения в сети. При измерении диаметра шара микрометром разные показания возникают из-за некачественного изготовления исследуемого образца: отклонения от сферической формы, неизбежного присутствия на поверхности шара шероховатостей, микропор и т.п. При выстреле из ружья точность поражения цели зависит от«твердости» руки стрелка, знания им определенных технических тонкостей обращения с оружием и т.д.

10

Теория погрешностей — презентация онлайн

1. Лекция №2 по дисциплине : «Метрология стандартизация и сертификация»

Тема:
«Теория погрешностей»
Учебные вопросы:
Вопрос №1 Основные свойства и классификация
погрешностей измерений
Вопрос №2 Систематические и грубые погрешности,
способы их обнаружения.
Вопрос №3 Случайные погрешности и способы их
обнаружения.
1

2. В теории погрешностей существует два основных направления. Первое – погрешности средств измерения. Второе – погрешности

измерений.
2

3. Погрешность средств измерений.

Погрешность средств измерений – разность между
показаниями
средства
измерения
и
истинным
(действительным)
значением
измеряемой
физической
величины.
Для меры показанием является ее номинальное значение; а
для рабочего средства измерения настоящим (действительным)
значение измеряемой величины считается показание рабочего
эталона более низкого разряда.
Номинальное значение средства измерения – значение
физической величины, определенное в соответствии с
паспортом средства измерения.
Для сравнения оценки средств измерений используется
понятие
«точность»
средства
измерений
–
это
характеристика качества средства измерений отражающая
близость его погрешности к нулю.
3

4. Погрешность измерений.

Понятие погрешности характеризует несовершенство измерения.
Позитивной характеристикой качества измерений является точность
измерения. Точность и погрешность связаны обратной
зависимостью – измерение тем более точно, чем меньше его
погрешность.
Погрешность измерения встречается всегда при любых видах
измерений и определяется метрологами как отклонение результата
измерения от действительного размера измеряемой величины.
В числовых величинах погрешность измерения ∆Х (дельта икс)
подсчитывают как разность между результатом измерения Хизм. И
действительным размером Хдейст. измеряемой величины:
∆Х = Хдейст. — Хизм.
(1).
Процесс оценки погрешности измерений считается одним из
важнейших мероприятий в вопросе обеспечения единства
измерений.
4

5. Вопрос №1

Основные свойства и классификация
погрешностей измерений
5

6. Основные понятия теории погрешностей.

Истинное значение физической величины – значение физической
величины, которое идеальным образом отражало бы в количественном и
качественном отношениях соответствующее свойство объекта
(согл. 16263-70).
Результат любого измерения отличается от истинного значения
физической величины на некоторое значение, зависящее от точности
средств и методов измерения, квалификации оператора, условий, в
которых проводилось измерение, и т. д.
Поскольку определить истинное значение физической величины в
принципе невозможно, т. к. это потребовало бы применения идеально
точного средства измерений, то на практике вместо понятия истинного
значения физической величины применяют понятие действительного
значения измеряемой величины, которое настолько точно приближается к
истинному значению, что может быть использовано вместо него. Это
может быть, например, результат измерения физической величины
образцовым средством измерения.
6

7. Классификация погрешности измерений.

Существует огромное множество факторов, оказывающих влияние на
точность измерения, следовательно любая классификация погрешностей
измерения достаточно условна.
По способу
выражения
По источнику
возникновения
— абсолютная
— относительная
— приведенная
По условиям
возникновения
— методические
— основные
— личные
— дополнительные
(субъективные)
— инструментальные
По зависимости от
входящей величины
— аддитивные
— мультипликативные
— нелинейные
По характеру
проявления во
времени
— систематические
— случайные
— промахи
По зависимости от
инерционности
— статические
— динамические
7

8.

Описание погрешностей измерений.1. По способу выражения:
— абсолютные – это значение, вычисляемое как разность между
значением величины, полученной в процессе измерения, и настоящим
(действительным)
значением
данной
величины.
Абсолютная
погрешность вычисляется по следующей формуле:
где:
Δ= Xи – Хд
Хи — измеренная величина
(2.)
Хд — действительная величина
— относительная – погрешность измерения, выраженная отношением
абсолютной погрешности измерения к действительному или
измеренному значению измеряемой величины:
(3.)
где:
Хи — измеренная величина
Хд — действительная величина
— приведенная – это значение, вычисляемое как отношение значения
абсолютной погрешности к нормативному значению.
(4.)
8

9. Описание погрешностей измерений.

2. По источнику возникновения:
— методические – это погрешности, возникающие по следующим
причинам: неточность построения модели физического процесса,
на котором базируется средство измерения.
— личные (субъективные) – это погрешности возникающие из-за
низкой степени квалификации оператора средства измерения, а
так же из-за погрешности зрительных органов человека, т.е.
причиной возникающей субъективной погрешности является
человеческий фактор.
— инструментальные – это погрешности , возникающие из-за
допущенных в процессе изготовления функциональных частей
средств измерения ошибок.
3. По условиям возникновения
— Основные – регламентируются при нормативных условиях
производства измерений.
— Дополнительные – учитываются при изменении нормативных
9
условий измерений.

10. Описание погрешностей измерений.

4. По характеру изменения во времени:
— систематическая – это составляющая часть всей
погрешности результата измерений, не изменяющаяся
или изменяющаяся закономерно при многократных
измерениях одной и той же величины.
— случайная – вторая составляющая изменяющаяся при
повторных измерениях того же самого параметра
случайным образом.
— промахи – это случайные погрешности намного превышающие
предполагаемые в данных условиях проведения измерений
систематические и случайные погрешности. Промахи и грубые
погрешности могут появиться из-за грубых ошибок в процессе
проведения измерений, технической неисправности средства
10
измерения, неожиданного изменения внешних условий.

11. Описание погрешностей измерений.

5. По зависимости от входящих величин:
— аддитивные – это погрешности, возникающие по причине
суммирования численных значений и не независящие от значения
измеряемой величины, взятого по модулю (абсолютного).
— мультипликативные – это погрешности изменяющиеся прямо
пропорционально измеряемой величине, вместе с изменением
значения величины, подвергающейся измерениям.
— нелинейные – это погрешности имеющие не линейную
зависимость от измеряемой величины.
6. По зависимости от инерционности.
— статические — это погрешности, которые возникают в процессе
измерения постоянной (не изменяющейся во времени) величины.
— динамические — это погрешности, численное значение которых
вычисляется как разность погрешностей возникающих при
измерении непостоянной (переменной во времени) величины, и
статической погрешностью (погрешностью значения измеряемой
11
величины в определенный момент времени).
Вопрос №2
Систематические и грубые
погрешности, способы их обнаружения.
12

13. Систематические погрешности.

Систематическая погрешность – составляющая погрешности
измерения, сохраняющаяся постоянной или закономерно
изменяющаяся при многократных измерениях величины в одних
и тех же условиях.
Переменная
Постоянная
систематическая
систематическая
погрешность
погрешность
Прогрессивная
Периодическая
— Это погрешность
длительное время
сохраняющая свое
значение (например,
в течении всей
серии измерений)
Эта погрешность
встречается
наиболее часто.
систематическая
погрешность
— Это непрерывно
возрастающая
погрешность
(например, от
постоянного
устойчивого износа
измерительных
приборов.
систематическая
погрешность
— Погрешность,
значение которой
является функцией
времени или
функцией
перемещения
указателя
измерительного
13
прибора.

14. Основные причины появления систематических погрешностей.

Наличие
погрешностей в
средствах
измерения
инструментальные
погрешности.
Являются
предметом
специальной
дисциплины –
теории точности
измерительных
устройств.
Несовершенство
метода
измерений или
допущенных его
упрощений
Недостаточная
квалификация
оператора
— ее называют
личной
— проистекает от погрешностью и
ошибочности или обусловлена она
индивидуальными
недостаточной
особенностями
разработки
принятой теории наблюдателя..
метода
измерений.
Погрешности,
обусловленные
неправильной
установкой и
взаимным
расположением
средств измерения.
14

15. Способы исключения систематических погрешностей.

1. Ликвидация причин и источников погрешностей до
начала проведения измерений. Данный способ является
самым оптимальным вариантом, так как его
использование упрощает дальнейший ход измерений
(нет необходимости исключать погрешности в процессе
уже начатого измерения или вносить поправки в
полученный результат.
2. Корректировка результатов измерения посредством
внесения поправки (устранение погрешности путем
вычислений)
3. Определение пределов систематической погрешности в
случаи, если ее нельзя устранить.
15

16. Способы исключения постоянной систематических погрешностей.

4. Устранение погрешностей в процессе уже начатого
измерения.
Для
устранения
систематических
погрешностей в процессе уже начатого измерения
4.3. Способ
различают способы:
4.1 Способ
введения поправок
4.2. Способ
замещения
Базируется на
знании
систематической
погрешности и
действующих
закономерностей
ее изменения.
Состоит в том,
что измеряемая
величина
заменяется
мерой,
помещенной в те
же самые условия
в которых
находиться
объект
измерения.
компенсации
погрешности по
знаку
Состоит в том, что
измерения
выполняются два
раза таким образом,
чтобы погрешность
неизвестная по
величине ,
включалась в
результаты
измерений с
противоположным
знаком.
4.4. Способ
противопоставления
Состоит в том, что
измерения
выполняются два
раза таким образом,
чтобы источник
погрешности при
первом измерении
противоположным
образом действовал
на результат второго
измерения.
16

17. Грубые погрешности.

Грубая погрешность (или промах) – это случайная погрешность
результата отдельного измерения, входящего в ряд измерений, которая
для данных условий резко отличается от остальных результатов этого
ряда.
Источником грубых погрешностей нередко бывают резкие
изменения условий измерения и ошибки, допущенные оператором. К
ним относятся:
неправильный отсчет по шкале измерительного прибора,
происходящий из-за неверного учета цены малых делений шкалы;
неправильная запись результата наблюдений, значений отдельных
мер использованного набора, например гирь;
хаотические изменения параметров питающего СИ напряжения,
например его амплитуды или частоты.
Грубые погрешности, как правило, возникают при однократных
измерениях и устраняются обычно путем повторных измерений. Их
причинами могут быть внезапные и кратковременные изменения
условий измерения или оставшиеся незамеченными неисправности в
17
аппаратуре.

18. Критерии исключения грубых погрешностей.

Для уменьшения вероятности появления промахов измерения
проводят два-три раза и за результат принимают среднее
арифметическое полученных отсчетов.
При многократных измерениях для обнаружения промахов
используют статические критерии, предварительно определив, какому
виду распределения соответствует результат измерений.
Вопрос о том, содержит ли результат наблюдений грубую
погрешность, решается общими методами проверки статических
гипотез. Пользуясь определенными статистическими критериями,
пытаются опровергнуть выдвинутую гипотезу – результат наблюдений
х не содержит грубой погрешности, т.е. является одним из значений
измеряемой величины.
Если это удается доказать, то результат наблюдений
рассматривают как содержащий грубую погрешность и его исключают.
Для выявления грубых погрешностей задаются вероятностью q
(уровнем значимости) того, что сомнительный результат действительно
18
мог иметь место в данной совокупности результатов измерений.

19. Критерий «Трех сигм»

Критерий трех сигм применяется для результатов измерений,
распределенных по нормальному закону. По этому критерию
считается, что результат, возникающий с вероятностью Р= 0,0027,
маловероятен, и его можно считать промахом, если
где:
— среднее арифметическое результатов измерения,
S – среднее квадратическое отклонение результатов наблюдений.
Данный критерий дает достаточно надежные результаты только при
19
n>30.

20. Критерий «Шарлье»

20

21. Критерий «Шарлье» (продолжение)

для кот-го
модуль разности данного результата и среднего ариф-го превосходит Кш*Sх
21

22. Критерий Романовского для исключения грубых погрешностей и промахов

22

23. Значения критерия Романовского

Таблица 2.
n
4
6
8
10
12
15
20
Значения критерия Романосвкого
q=0,01
q=0,02
q=0,05
1,73
1,72
1,71
2,16
2,13
2,10
2,43
2,37
2,27
2,62
2,54
2,41
2,75
2,66
2,52
2,90
2,80
2,64
3,08
2,96
2,78
q=0,1
1,69
2,00
2,17
2,29
2,39
2,49
2,62
23
Вопрос №3
Случайные погрешности и способы их
обнаружения.
24

25. Случайные погрешности.

Случайная погрешность – составная часть погрешности
результата
измерения,
изменяющаяся
случайно,
незакономерно при проведении повторных измерений
одной и той же величины.
Появление
случайных
погрешностей
нельзя
предвидеть и предугадать, они неизбежны и
неустранимы и всегда присутствуют в результатах
измерений.
Каждая случайная погрешность возникает в
результате воздействия многих факторов, каждый из
которых сам по себе не оказывает значительного
влияния на результат.
25

26. Распределение случайных величин.

По своей природе
случайные величины могут
быть:
непрерывными
Дискретной (прерывной) называют случайную величину,
отдельные значения которой можно прономеровать. Пример: число
изделий, отказавших в процессе испытаний; количество
бракованных деталей в партии, и т.д.
Непрерывной называют случайную величину, возможные
значения которой непрерывно заполняют некоторый промежуток.
Пример: отклонение размера изготовленной детали от номинала,
погрешность измерения, величина отклонения формы детали.
26

27. Распределение случайных величин.

Законом распределения случайной величины
называют соотношение, устанавливающее связь
между возможными значениям случайной
величины и соответствующим им вероятностям.
Простейшей формой задания закона распределения
является таблица, в которой перечислены в порядке
возрастания все возможные значения дискретной
случайной величины и соответствующие им вероятности.
Такую таблицу называют рядом распределения.(пример
на следующем слайде)
27

28. Формы задания закона распределения.

Х1
Р1
Х2
Р2
…
…
Хn
Pn
Графическое изображение ряда распределения
полигоном распределения случайной величины.
называют
28

29. Функция распределения случайных величин.

Функцией распределения случайной величины Х называют
вероятность выполнения неравенства Х< х .
где: х — неслучайный аргумент.
Функция распределения F(x) должна
функцией своего аргумента.
быть
неубывающей
29

30. Основные законы распределения.

Использование на практике вероятностного подхода к
оценке погрешностей результатов измерений, прежде всего
предполагает знание аналитической модели закона
распределения рассматриваемой погрешности.
Множество законов распределения случайных величин
используемых
в
метрологии
целесообразно
классифицировать следующим образом:
— Трапецеидальные (плосковершинные) распределения. К
ним относятся: равномерное, собственно трапецеидальное и
треугольное (Симпсона)
— Уплощенные
(приблизительно
плосковершинные)
распределения;
— Экспонециальные распределения;
Семейство распределений Стьюдента;
Двухмодальные распределения.
30

Теория ошибок. Точность и прецизионность, ошибки измерения, анализ ошибок, распространение ошибок

ТЕОРИЯ ОШИБОК

Основой всей экспериментальной науки и техники являются измерения. результат, полученный в результате любого измерения, будет содержать некоторую неопределенность. Такой неопределенность называется ошибкой . Любой расчет, выполненный с использованием измеренных значений, также будет иметь ошибка. В эксперименте невозможно произвести точные измерения. В измерения, используются два разных термина точность и прецизионность, и их необходимо выделиться на этом этапе. Точность относится к тому, насколько мы далеки от истинного значение, а точность относится к тому, насколько хорошо мы измеряем.

 

Точность и Precision

Пусть скажем, вы знаете, что ваш истинный рост ровно 5 футов 9 дюймов. Сначала вы измеряете свой рост с помощью критерием и получите значение 5′0″. Следовательно, ваше измерение не точный. Теперь вы измеряете свой рост с помощью лазерной линейки и получаете значение 5 футов 9 дюймов. Теперь ваше измерение точно. Истинное значение также называют теоретическим значением. Уровень точность, необходимая для каждого приложения, сильно различается. Высокоточные данные могут быть очень сложным для производства и компиляции. Например, если вы постоянно измерьте свой рост как 5 футов 0 дюймов с помощью аршина, ваш измерения точны. Уровень точности, необходимый для различных приложения сильно различаются. Инженерные проекты, такие как дороги и коммунальное строительство требует очень точной информации, измеренной миллиметра или одной десятой дюйма.

Если измерение является точным, что не обязательно означает, что оно является точным. Однако, если измерение стабильно точное, оно также является точным.

Для например, если температура снаружи здания составляет 40 ^o C при измерении по метеотермометру и если реальная наружная температура составляет 40 ^o C, термометр точен. Если термометр постоянно регистрирует это точная температура подряд, термометр точен.

рассмотреть другой пример. Пусть температура холодильника многократно измеряется термометру следует дать 10,4 ^o C, 10,2 ^o C, 10,3 ^o C, 10.1 ^o С, 10.2 ^o С, 10.1 ^o С, 10.1 ^o С, 10.1 ^o C. Однако, если реальная температура внутри холодильника 9 ^o C, мы говорим, что термометр не точен (это почти один градусов от истинного значения), но так как все измеренные значения близки к 10 ^или С, следовательно, это точно.

Наглядный пример:

Цель стрельба является примером, который объясняет разницу между точностью и точность. На рис. 1.9 (а) выстрелы сфокусированы так, чтобы попасть в цель быка. глаз (средняя точка), но стрелки дошли только до этой точки. Следовательно выстрелы не точны и не точны.

В Рисунок 1.9 (б), все кадры расположены близко друг к другу, но не в центре. точка. Поэтому говорят, что выстрелы точны, но не точны. На рисунке 1.9(в) выстрелы ближе и тоже в центральную точку. Отсюда и кадры и точен, и точен.

Числовой пример

истинное значение определенной длины составляет около 5,678 см. В одном эксперименте с помощью измерительный прибор с разрешением 0,1 см, измеренное значение оказывается равным 5,5 см. В другом эксперименте с использованием измерительного прибора большей разрешение, скажем, 0,01 см, длина оказывается равной 5,38 см. Мы находим, что первое измерение является более точным, так как оно ближе к истинному значению, но оно имеет меньшую точность. Наоборот, второе измерение менее точно, но точнее.

 

Ошибки в измерении

неопределенность в измерении называется ошибкой. Случайная ошибка, систематическая ошибка и грубая ошибка — три возможные ошибки.

 

i) Систематический ошибки

Систематические Ошибки – это воспроизводимые неточности, постоянно повторяющиеся в одном и том же направление. Это часто происходит из-за проблемы, которая сохраняется на протяжении всего эксперимент. Систематические ошибки можно классифицировать следующим образом

а. Инструментальные ошибки

Когда прибор не откалиброван должным образом во время изготовления, могут возникнуть инструментальные ошибки. Если измерение производится с помощью метровой шкалы чей конец изношен, полученный результат будет иметь ошибки. Эти ошибки могут исправить путем тщательного выбора инструмента.

б. Недостатки в экспериментальный методика или процедура

Эти ошибки возникают из-за ограничений экспериментальной установки. Как например, при проведении опытов с калориметром, если нет надлежащего изоляции, будут потери на излучение. Это приводит к ошибкам и преодолеть их, необходимо применить необходимую коррекцию.

в. Личные ошибки

Эти ошибки связаны с людьми, проводящими эксперимент, могут быть связаны с неправильная первоначальная постановка эксперимента или небрежность лицо, делающее наблюдение из-за ненадлежащих мер предосторожности.

д. Ошибки по внешним причинам

изменение внешних условий во время эксперимента может вызвать ошибку в измерение. Например, изменения температуры, влажности или давления во время измерения могут повлиять на результат измерения.

эл. Наименьшая ошибка счета

Наименьшая count — наименьшее значение, которое может быть измерено измерительным прибором, и ошибка из-за этого измерения является наименьшей ошибкой счета. Инструмент разрешение, следовательно, является причиной этой ошибки. Наименьшая ошибка счета может быть уменьшена с помощью высокоточного прибора для измерения.

 

ii. Случайные ошибки

Случайные ошибки могут возникать из-за случайных и непредсказуемых изменений условий эксперимента таких как давление, температура, напряжение питания и т. д. Ошибки также могут быть вызваны личные ошибки наблюдателя, проводящего эксперимент. Случайные ошибки иногда называют «случайная ошибка». Когда разные показания получаются человек каждый раз, когда он повторяет эксперимент, происходит личная ошибка. За Например, рассмотрим случай измерения толщины проволоки с помощью винта. измерять. Снятые показания могут быть разными для разных испытаний. В таком случае, производится большое количество измерений и затем берется среднее арифметическое.

Если В эксперименте берется n пробных отсчетов, и отсчетов ₁ , а ₂ , а ₃ ,…………………. _n . Среднее арифметическое равно

Обычно это среднее арифметическое принимается за наилучшее возможное истинное значение величины.

Некоторые процедуры, которые необходимо соблюдать, чтобы свести к минимуму экспериментальные ошибки, а также примеры приведены в таблице 1.8.

 

iii. Грубая ошибка

ошибка, вызванная сдвиговой невнимательностью наблюдателя, называется грубой ошибка.

Для пример

я. Чтение инструмента без его правильной настройки.

ii. Делать наблюдения неправильно, не заботясь об источниках ошибки и меры предосторожности.

III. Запись неправильных наблюдений.

iv. Использование неправильных значений наблюдений в расчетах.

Эти ошибки могут быть сведены к минимуму только тогда, когда наблюдатель внимателен и сообразителен.

 

Ошибка Анализ

i. Абсолют Ошибка

разница между истинным значением и измеренным значением величины равна называется абсолютной ошибкой. Если ₁ , ₂ , ₃ , ………. a _n – измеренные значения любой величины ‘ a’ в проведенном эксперименте n раз, то среднее арифметическое эти значения называется истинным значением ( a _m ) количества.

абсолютная погрешность измеренных значений определяется как

 

ii. Иметь в виду Абсолютная ошибка

среднее арифметическое величины абсолютных погрешностей всех измерений равно называется средней абсолютной ошибкой.

Если a _м — истинное значение, а ∆ a _м — средняя абсолютная ошибка, тогда magnitude of the quantity may lie between a _m + ∆ a _m and a _m — ∆ a _m

 

iii . Родственник ошибка

Отношение средней абсолютной ошибки к среднему значению называется относительной ошибкой. Это также называется дробной ошибкой (или) относительной ошибкой.

Таким образом относительно error показывает, насколько велика абсолютная ошибка по сравнению с общим размером измеряемый объект. Например, спидометр водителя показывает, что его машина движется со скоростью 60 км/ч ^-1 , когда на самом деле он движется со скоростью 62 км/ч ^-1 . Тогда абсолютная погрешность спидометра 62-60 км ч ^-1 = 2 км ч ^-1 Относительная погрешность измерения 2 км ч ^-1 / 60 км ч ^-1 = 0,033.

 

iv. Процент ошибка

относительная ошибка, выраженная в процентах, называется процентной ошибкой.

А процентная ошибка очень близка к нулю означает, что единица близка к целевому значению, что хорошо и приемлемо. Всегда необходимо понимать, ошибка связана с впечатлением от используемого оборудования или ошибкой в эксперименты.

 

Распространение ошибок

А количество измеренных величин может быть задействовано в окончательном расчете эксперимент. Для взятия могли использоваться различные типы инструментов. чтения. Тогда нам, возможно, придется посмотреть на погрешности измерения различных величин, коллективно.

ошибка в конечном результате зависит от

i. Ошибки отдельных измерений

ii. О характере математических операций, выполняемых для получения конечного результата. Так мы должны знать правила объединения ошибок.

различные возможности распространения или сочетания ошибок в разных математические операции обсуждаются ниже:

 

i. Ошибка в сумме двух количества

Пусть ∆A и ∆B — абсолютные ошибки двух величин A и B соответственно. Затем

Измерено значение A = A ± ∆A

Измерено значение B = B ± ∆B

Учитывать сумма, Z = A + B

ошибка ∆Z в Z тогда определяется как

ii. Ошибка в разнице двух количества

Пусть ΔA и ΔB — абсолютные ошибки в двух величинах, A и B, соответственно. Затем

Измеренное значение A = A ± ΔA

Измеренное значение B = B ± ΔB

Рассмотрим разность Z = A – B

Ошибка ΔZ в Z определяется как Z ± ΔZ = (А ± ΔА) – (В ± ΔВ)

(iii) Ошибка в произведении двух количества

Пусть ΔA и ΔB — абсолютные ошибки в двух величинах A и B соответственно. Рассмотрим произведение Z = AB

Ошибка ΔZ в Z определяется как Z ± ΔZ = (A ± ΔA) (B ± ΔB)

Деление левой стороны на Z и правой стороны на AB, получаем,

Поскольку ΔA/A, ΔB/B равны оба небольших количества, их термин продукта ΔA/A . ΔB/B можно пренебречь. максимальная дробная ошибка в Z равна

(iv) Ошибка в делении или частное двух величин

Пусть ΔA и ΔB абсолютные ошибки в двух величинах A и B соответственно.

Поскольку термины ΔA/A и ΔB/B малы, их произведением можно пренебречь.

(v) Ошибка в степени количество

Рассмотрим n ^th мощность A, Z = A ⁿ ошибка ΔZ в Z определяется как

Получаем [(1+x) ⁿ ≈1+nx, когда x<<1] пренебрегая оставшимися членами, Деление обеих сторон на Z

: Природа физического мира и измерения

Учебный материал, Лекционные заметки, Задание, Справочник, Объяснение описания Wiki, краткая информация

11-я физика: РАЗДЕЛ 1: Природа физического мира и измерения: Теория ошибок | Точность и прецизионность, ошибки измерения, анализ ошибок, распространение ошибок

экспериментальная физика — теория строгого анализа ошибок

спросил 5 лет, 11 месяцев назад

Изменено 4 года, 9 месяцев назад

Просмотрено 1к раз

$\begingroup$

Прежде чем ответить, ознакомьтесь с нашей политикой в ​​отношении вопросов о рекомендациях ресурсов. Пожалуйста, напишите содержательные ответы, подробно описывающие стиль, содержание и требования к книге, статье или другому ресурсу. Объясните характер ресурса, чтобы читатели могли решить, какой из них лучше всего подходит для них, а не полагаться на мнение других. Ответы, содержащие только ссылку на книгу или статью, будут удалены!

Теперь, когда я закончил подготовительные лабораторные курсы, я много думал о теории ошибок, которую мы использовали для наших измерений. Я пытался найти математически строгую книгу по анализу ошибок, но это было бесполезно. Мне интересно, знает ли кто-нибудь из вас литературу на эту тему. Темы, которые я ищу, идут по линии:

1. рассмотрение результата измерения как меры вероятности;
2. , обобщающий понятие «наилучшее значение» или значение с наибольшей вероятностью для мер, которые не имеют связанной с ними плотности (производной радона-никодима), таких как мера Дирака;
3. конкретное определение неопределенности, которое совпадает со стандартным отклонением в случае гауссовского распределения, но не такое громоздкое, как 68% доверительный интервал,
4. , учитывая набор результатов измерений $\mu_1,\dots,\mu_n$ и функцию этих измерений $f$, как найти результат измерения $f$ (обратите внимание, что решение этого вопроса обобщает проблему распространения ошибки ).

Если кто-нибудь из вас, ребята, может дать краткое объяснение любой из этих тем, мы также будем очень признательны.

• экспериментальная физика
• математическая физика
• ресурсы-рекомендации
• измерения
• анализ ошибок

$\endgroup$

4

$\begingroup$

Мне пришлось обратиться к некоторым книгам и ресурсам в моем текущем исследовании, где требуется тщательный анализ ошибок. Вот два, которые я использовал много:

Введение в статистику и анализ данных для физиков (Bohm and Zech, 2010) — этот справочник полностью доступен в Интернете (всего 412 страниц!). В предисловии авторы указывают в предисловии, что ссылка написана

с акцентом на современные приложения по физике ядра и элементарных частиц

Книга предположительно предназначена для студентов магистратуры и докторантуры и составлена ​​на основе конспектов лекций Зигенского университета в Германии. Справочник имеет не столько акцент на математических основах, сколько обращение к интуиции читателя. Примеры и формулы выводятся поэтапно со значительными пояснениями.

Быстрый поиск (control-F) «Dirac» показывает пару примеров, связанных с этой темой.

Измерения и их неопределенности (Haese and Hughes, 2010) — этот справочник также полностью доступен в Интернете. Эта ссылка значительно более общая, чем первая ссылка (и короче на 153 страницы!).

В предисловии авторы заявляют, что книга представляет собой реструктуризацию практического курса физики первого года обучения в Даремском университете, но она доступна для всех уровней физического опыта, с упором на возможность использования в лаборатории и для научно-вычислительных приложений (где я это использовал) — конкретно:

Эта книга охватывает всю необходимую основу для лабораторных работ. занятия в физической лаборатории первого и второго курсов бакалавриата и содержать достаточно материала, чтобы быть полезным для проектов последнего года обучения, студенты и практикующие профессиональные ученые и инженеры.