Теплоемкость газа: 3.10. Теплоёмкость идеального газа

{T_2} C \mathrm{d}T.$$

где $Q$ — количество теплоты процесса; $T_1$ и $T_2$ — температуры начала и конца процесса.

Удельной теплоёмкостью называется теплоёмкость, отнесённая к единичному количеству вещества. Количество вещества может быть измерено в килограммах, кубических метрах и молях. В зависимости от того, к какой количественной единице относится теплоёмкость, различают массовую, объёмную и молярную теплоёмкость.

Массовая удельная теплоёмкость $c$, также называемая просто удельной теплоёмкостью — это количество теплоты, которое необходимо подвести к единице массы вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на килограмм на кельвин (Дж·кг⁻¹·К⁻¹). Массовая удельная теплоёмкость связана с теплоемкостью тела следующим соотношением:

$$C = m·c.$$

где $m$ — масса тела.

Молярная теплоёмкость $c_μ$ — это количество теплоты, которое необходимо подвести к 1 молю вещества, чтобы нагреть его на единицу температуры.

В СИ измеряется в джоулях на моль на кельвин (Дж·моль⁻¹·К⁻¹). Массовая и киломольнаятеплоемкости связаны между собой следующей зависимостью:

$$c = \frac{c_μ}{\mu}.$$

где $\mu$ — молярная масса вещества.

Объёмная теплоёмкость $c′$ — это количество теплоты, которое необходимо подвести к единице объёма вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на кубический метр на кельвин (Дж·м⁻³·К⁻¹). Киломольная и объемная теплоемкости связаны между собой следующей зависимостью:

$$c′ = \frac{c_μ}{22.4}.$$

где $22.4$ – объем киломоля любого идеального газа в нормальных физических условиях (следствие из закона Авогадро), м

3н /кмоль.

Понятие теплоёмкости определено как для веществ в различных агрегатных состояниях (твёрдых тел, жидкостей, газов), так и для ансамблей частиц и квазичастиц (в физике металлов, например, говорят о теплоёмкости электронного газа). {n} r_i·c_{μi}.$$

В этих выражениях $g_i$, $r_i$ – соответственно массовая и объемная доля $i$-го компонента газовой смеси; $c_i$, $c′_i$, $c_{μi}$ – соответственно массовая, объемная и киломольная теплоемкость $i$-го компонента; $c_{см}$, $c′_{см}$, $c_{μсм}$ – соответственно массовая, объемная и киломольная теплоемкость газовой смеси; $i$ – номер компонента смеси; $n$ – число компонентов смеси.

Переход вещества из одного агрегатного состояния в другое сопровождается скачкообразным изменением теплоёмкости в конкретной для каждого вещества температурной точке превращения — температура плавления (переход твёрдого тела в жидкость), температура кипения (переход жидкости в газ) и, соответственно, температуры обратных превращений: замерзания и конденсации.

Теплоёмкость идеального газа

В случае, если результатом теплообмена становится передача телу некоего количества теплоты Q, то его температура и внутренняя энергия претерпевают изменения.

Определение 1

Необходимое для нагревания 1 кг вещества на 1 К количество теплоты Q носит название удельной теплоемкости вещества c, а ее формула выглядит следующим образом: 

c=Qm∆T.

В большом количестве ситуаций удобной для использования является молярная теплоемкость C: 

C=M·c, где M представляет собой молярную массу вещества.

Теплоемкость, полученная таким способом, не является однозначной характеристикой вещества. Исходя из первого закона термодинамики, можно сказать, что изменение внутренней энергии тела зависимо не только от количества полученной теплоты, но и от величины совершенной телом работы. В разных условиях осуществления процесса теплопередачи тело может совершать различную работу. Таким образом, переданное телу одинаковое количество теплоты способно провоцировать изменения его внутренней энергии и, соответственно, температуры.

Подобной неоднозначностью при определении теплоемкости характеризуются только газообразные вещества. Объем в процессе нагрева практически не меняет своей величины, что сводит работу расширения к нулю. По этой причине вся полученная телом теплота уходит на изменение его внутренней энергии. Газ в процессе теплопередачи может значительно менять свой объем и совершать работу, чем отличается от твердых тел и жидкостей. Таким образом, теплоемкость газообразного вещества имеет зависимость от характера термодинамического процесса.

Изопроцессы в газах

Определение 2

Чаще всего рассматриваются два значения теплоемкости газов: 

• CV являющаяся молярной теплоемкостью в изохорном процессе (V=const);
• Cp представляющая собой молярную теплоемкость в изобарном процессе (p=const).

При условии постоянного объема газ не совершает работы: A=0. Исходя из первого закона термодинамики для 1 моля газа, можно сказать, что справедливым является следующее выражение: 

QV=CV∆T=∆U.

Изменение величины ΔU внутренней энергии газа прямо пропорционально изменению значения ΔT его температуры.

В условиях процесса при постоянном давлении первый закон термодинамики дает такую формулу: 

Qp=∆U+p(V2-V1)=CV∆T+pV.

В котором ΔV является изменением объема 1 моля идеального газа при изменении его температуры на ΔT. Таким образом, можно заявить, что: 

Cp=Qp∆T=CV+p∆V∆T.

Из уравнения состояния идеального газа, записанного для 1 моля, может выражаться отношение ΔVΔT: 

pV=R.

В котором R представляет собой универсальную газовую постоянную. При условии постоянства давления p=const, можно записать следующее:p∆V=R∆T или ∆V∆T=Rp.

Определение 3

Из этого следует, что выражающее связь между молярными теплоемкостями Cp и CV_{соотношение имеет вид (формула Майера):} 

Cp=CV+R.

В процессе с неизменным давлением молярная теплоемкость Cp газа всегда превышает молярную теплоемкость CV в процессе с не подверженным изменениям объемом, что демонстрируется на рисунке 3.10.1.

Рисунок 3.10.1. Два возможных процесса нагревания газа на ΔT=T2 –T1. При p=const газ совершает работу A=p1(V2 – V1). Поэтому Cp>CV.

Определение 4

Отношение теплоемкостей в процессах с постоянным давлением и постоянным объемом занимает важное место в термодинамике и обозначается в виде греческой буквы γ.

 

γ=CpCV.

Данное отношение включено в формулу для адиабатического процесса.

Между двумя изотермами, обладающими температурами T1 и T2 на диаграмме (p, V) реальны различные варианты перехода. Так как для всех подобных переходов изменение величины температуры ΔT=T2 –T1 является одним и тем же, выходит, что изменение значения
ΔU внутренней энергии тоже одинаково. С другой стороны, совершенные при этом работы A и количества теплоты Q, полученные в результате теплообмена, выйдут разными для различных путей перехода. Из этого следует, что газа имеет относительно приближенное к бесконечности число теплоемкостей. Cp и CV представляют собой частные, однако, очень важные для теории газов, значения теплоемкостей.

Рисунок 3.10.2. Модель теплоемкости идеального газа.

Определение 5

Термодинамические процессы, в которых теплоемкость газа не подвергается изменениям, носят название политропических.

Каждый изопроцесс являются политропическим. В изотермическом процессе ΔT=0, из-за чего CT=∞. В адиабатическом процессе ΔQ=0, выходит, что Cад=0.

Замечание 1

Стоит обратить внимание на то, что «теплоемкость» и «количество теплоты» являются крайне неудачными терминами, доставшимися современной науке в качестве наследства теории теплорода, которая господствовала в XVIII веке.

Данная теория представляла теплоту в виде содержащегося в телах особого невесомого вещества. Считалось, что оно не подвержено уничтожению и не может быть созданным. Явление нагрева объясняли повышением, а охлаждение – понижением содержания в телах теплорода. Однако теория теплорода оказалась несостоятельной, так как не смогла дать ответа на вопрос, почему одинаковое изменение внутренней энергии тела возможно получить, приводя ему разное количество теплоты в зависимости от совершаемой им работы. По этой причине утверждение, что в данном теле содержится некоторый запас теплорода лишено смысла.

Молекулярно-кинетическая теория

В молекулярно-кинетической теории устанавливается следующее соотношение между средней кинетической энергией E→ поступательного движения молекул и абсолютной температурой T: 

E→=32kT.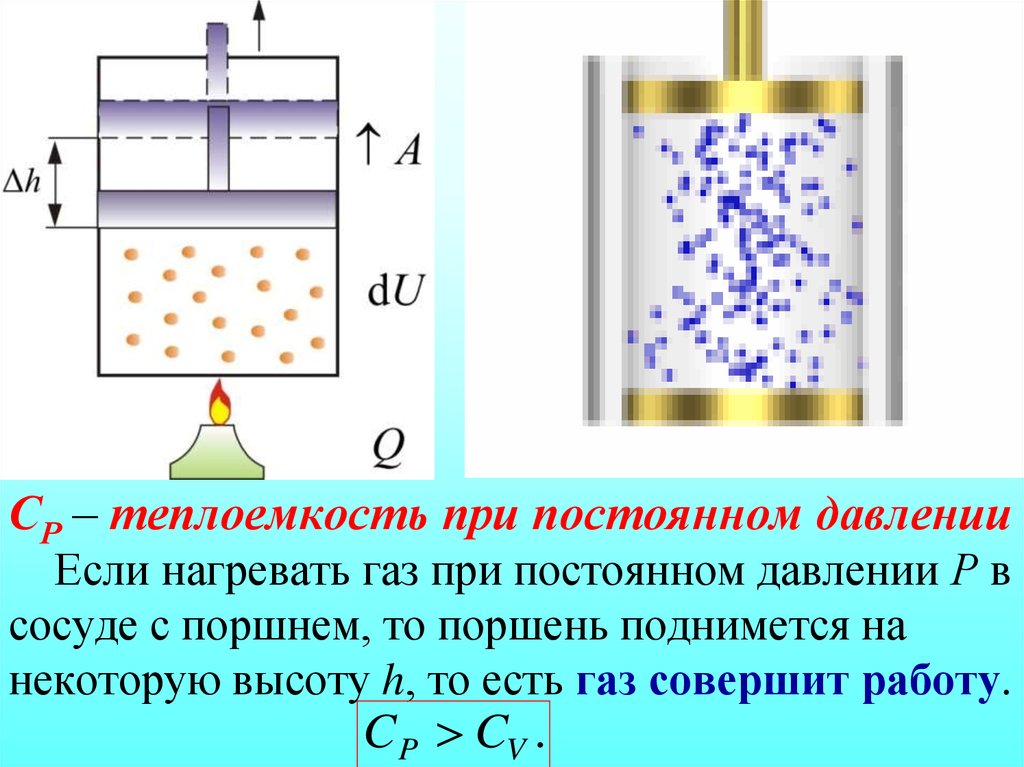

Внутренняя энергия 1 моля идеального газа эквивалентна произведению E→ на число АвогадроNА: 

U=32kNAT=32RT.

При условии изменения температуры на величину ΔT внутренняя энергия изменяется на величину:

U=32R∆T=CV∆T.

Коэффициент пропорциональности между ΔU и ΔT эквивалентен теплоемкости CV в условиях постоянного давления: 

CV=32R=12,47 ДЖ/моль·К.

Данное выражение подтверждается экспериментами с газами, которые состоят из одноатомных молекул вроде гелия, неона или аргона. При этом для двухатомных (водород, азот) и многоатомных (углекислый газ) газов такое соотношение не согласуется с полученными в результате опытов данными. Причина этого расхождения заключается в том, что для двух- и многоатомных молекул средняя кинетическая энергия должна включать энергию как поступательного, так и вращательного их движения.

 Рисунок 3.10.3. Модель двухатомной молекулы. Точка O совпадает с центром масс молекулы. 

Рисунок 3.10.3 иллюстрирует модель двухатомной молекулы. Молекула имеет возможность производить пять независимых типов движений: три поступательных движения вдоль осей X, Y, Z и два вращения относительно осей X и Y.

Опытным путем выяснено, что вращение относительно оси Z, на которой лежат центры обоих атомов, может быть возбуждено только при очень высоких значениях температуры. В условиях обычных температур вращение вокруг оси Z не происходит.

Определение 6

Каждое независимое движение в молекуле носит название степени свободы.

Выходит, что одноатомная молекула обладает 3 поступательными степенями свободы, «жесткая» двухатомная молекула 5 степенями, то есть 3 поступательными и 2 вращательными, а многоатомная молекула 6 степенями свободы, из которых 3 приходятся на поступательные и 3 на вращательные.

Теорема 1

В классической статистической физике доказывается теорема о равномерном распределении энергии по степеням свободы:

Если система молекул находится в тепловом равновесии при температуре T, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы и для каждой степени свободы молекулы она равна 12kT.

Из данной теоремы следует, что для молярных теплоемкостей газа Cp и CV и их отношения
γ справедлива запись в следующем виде: 

CV=i2R, Cp=Cv+R=i+22R, γ=CpCV=i+2i,

где i представляет собой количество степеней свободы газа.

Для газа, состоящего из одноатомных молекул (i=3)

CV=32R, Cp=Cv+R=52R, γ=CpCV=53=1,66.

Для газа, состоящего из двухатомных молекул (i=5)

CV=52R, Cp=Cv+R=72R, γ=CpCV=75=1,4.

Для газа, состоящего из многоатомных молекул (i=6)

CV=3R, Cp=Cv+R=4R, γ=CpCV=43=1,33.

В обычных условиях экспериментально измеренные теплоемкости многих газов неплохо согласуются с приведенными выражениями, но в целом классическая теория теплоемкости газов вполне удовлетворительной не является. Существует колоссальное число примеров со значительной разницей между результатами эксперимента и теорией. Данный факт объясняется тем, что классическая теория не может полностью учесть, связанную с внутренними движениями в молекуле энергию.

Теорема о равномерном распределении энергии по степеням свободы может быть применена и по отношению к тепловому движению частиц в твердом теле.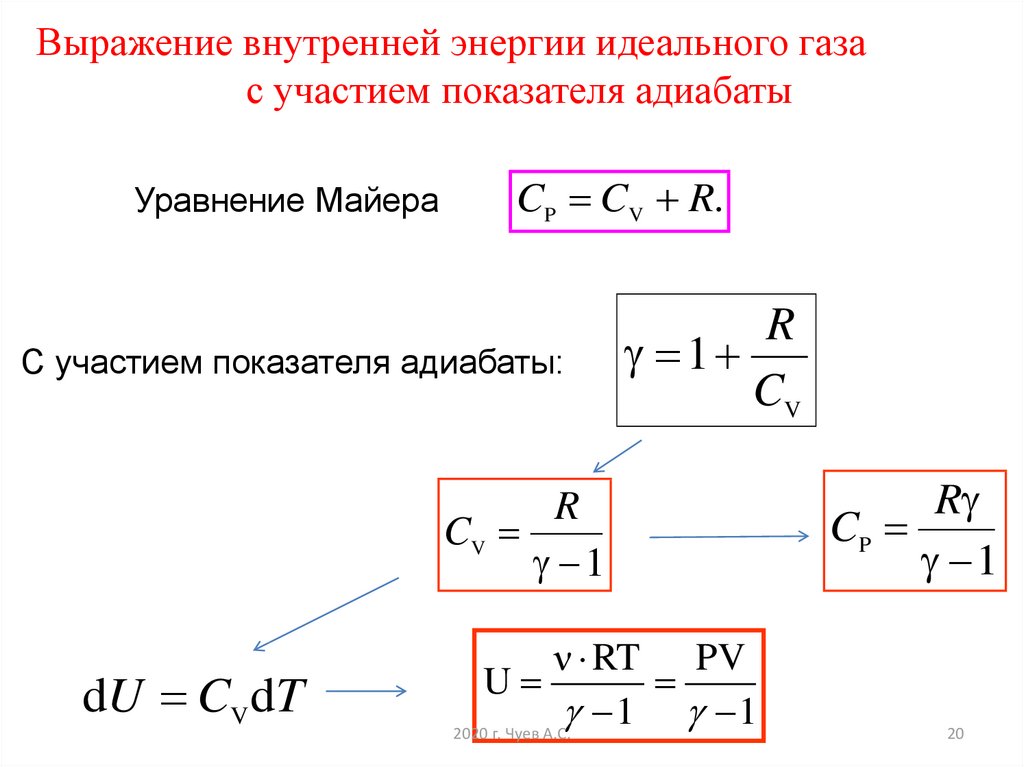 Входящие в состав кристаллической решетки атомы колеблются около положений равновесия. Энергия данных колебаний представляет собой внутреннюю энергию твердого тела. Каждый конкретный атом может колебаться в кристаллической решетке в трех взаимно перпендикулярных направлениях. Выходит, что каждый атом имеет 3 колебательные степени свободы. При условии гармонических колебаний средняя кинетическая энергия эквивалентна средней потенциальной энергии. По этой причине в соответствии с теоремой о равномерном распределении на каждую колебательную степень свободы приходится средняя энергия kT, а на один атом – 3kT. 

Определение 7

Внутренняя энергия 1 моля твердого вещества равна следующему выражению:

U=3RNAkt=3Rt.

Следовательно, молярная теплоемкость вещества в твердом состоянии равняется: 

С=3R=25,12 Дж/моль·К.

Данное выражение носит название закона Дюлонга–Пти. Для твердых тел почти нет различия между Cp и CV по причине пренебрежительно малой работы при сжатии или расширении.

Опыт показывает, что молярная теплоемкость у многих твердых тел (химических элементов) при обычных температурах на самом деле близка к 3R. При этом, в условиях низких температур заметны довольно сильные расхождения между теорией и экспериментом. Таким образом, гипотеза о равномерном распределении энергии по степеням свободы может считаться лишь приближением. Заметная в опыте зависимость теплоемкости от температуры объясняется только при условии использования квантовых представлений.

Удельная теплоемкость газов

Удельная теплоемкость газов

Удельная теплоемкость газов обычно выражается в молярной удельной нагревает. Для одноатомного идеального газа вся внутренняя энергия выражается в форме кинетической энергии, и кинетическая теория дает выражение для этой энергии, связанное с кинетической температурой. Выражение для внутренней энергии равно . Для газов определены две удельные теплоемкости, одна для постоянного объема ( С В ) и один для постоянного давления ( C P ). Для процесса постоянного объема с одноатомным идеальным газом первый закон термодинамики дает: Более общий случай Дальнейшее применение закона идеального газа и первого закона дает соотношение Показать Отношение удельных теплоемкостей γ = C P /C V является фактором адиабатических процессов двигателя и определения скорости звука в газе. Это отношение γ = 1,66 для идеального одноатомного газа и γ = 1,4 для воздуха, который является преимущественно двухатомным газом.

Индекс Концепции газового закона Концепции кинетической теории

6 Гиперфизика***** Термодинамика R Неф 3 Вернуться Молярная удельная теплоемкость при постоянном объеме определяется как Постоянный объем Используя первый закон термодинамики, это можно представить в виде . , но поскольку ΔV = 0, выражение для C V принимает вид Для одноатомного идеального газа0023 , поэтому Это значение хорошо согласуется с экспериментом для одноатомных благородных газов, таких как гелий и аргон, но не описывает двухатомные или многоатомные газы, поскольку их молекулярные вращения и колебания вносят вклад в удельную теплоемкость. Равнораспределение энергии предсказывает Индекс Концепции газового закона Концепции кинетической теории   Гиперфизика***** Термодинамика R Ступица Назад 3333333333333333333 Молярная удельная теплоемкость при постоянном давлении определяется выражением Постоянное давление Используя первый закон термодинамики для процесса с постоянным давлением, это можно представить в виде Из закона идеального газа (PV=nRT) в условиях постоянного давления видно, что Поскольку удельная теплоемкость при постоянном объеме равна , отсюда следует, что Для идеального одноатомного газа Индекс Понятия кинетической теории   Гиперфизика***** Термодинамика R Неф Назад 333333 RAVE Молярная удельная теплоёмкость идеальных одноатомных газов равна: Для двухатомных или линейных многоатомных молекул добавляются две вращательные степени свободы, соответствующие вращению вокруг двух перпендикулярных осей, проходящих через центр молекулы. Ожидается, что это даст C V = 5/2 R, что подтверждается примерами, подобными азоту и кислороду. Нелинейная многоатомная молекула сможет вращаться вокруг трех перпендикулярных осей, что, как ожидается, даст С В = 3R. Наблюдаемое отклонение от этого значения указывает на необходимость учета колебательных степеней свободы для полного описания удельных теплоемкостей газов. Примеры Таблица молярных теплоемкостей Индекс Концепции кинетической теории Sears & Salinger, Sec 9-7 Гиперфизика ***** Термодинамика R Nave Назад Модели постоянной объемной теплоемкости, основанные на равнораспределении энергии и включающие вращательные степени свободы, а также поступательные, могут объяснить теплоемкость двухатомных молекул. Отход от этой модели в случае нелинейных многоатомных молекул свидетельствует о колебательном участии. Удельная теплоемкость при постоянном давлении связана со значением постоянного объема как C P = C V + R. Отношение удельных теплоемкостей γ = C P /C V является фактором адиабатических процессов в двигателе. и при определении скорости звука в газе. Водород как пример двухатомной молекулы Index Концепции кинетической теории Sears & Salinger, Sec 9-7   Гиперфизика***** Термодинамика R Ступица Назад Поведение удельной теплоемкости водорода при изменении температуры в начале 20-го века было крайне загадочным. При низких температурах он вел себя как одноатомный газ, но при более высоких температурах его удельная теплоемкость принимала значение, подобное другим двухатомным молекулам. Потребовалось развитие квантовой теории, чтобы показать, что двухатомный водород с его крошечной инерцией вращения требует большого количества энергии для возбуждения своего первого квантового состояния возбужденного молекулярного вращения. Поскольку он не мог получить такое количество энергии при низких температурах, он вел себя как одноатомный газ. Удельная теплоемкость газов Равнораспределение энергии Индекс Понятия кинетической теории   Гиперфизика***** Термодинамика R Неф Назад 8. Коэффициенты теплоемкости для газов (Cp/Cv) Последнее обновление Сохранить как PDF Идентификатор страницы 63354 Измерение отношения теплоемкости при постоянном давлении к теплоемкости при постоянном объеме газа (Cp/Cv) Введение Теорема о равнораспределении утверждает, что любой квадратичный член энергии, такой как кинетическая энергия, дает равенство внутренней энергии системы, находящейся в тепловом равновесии. 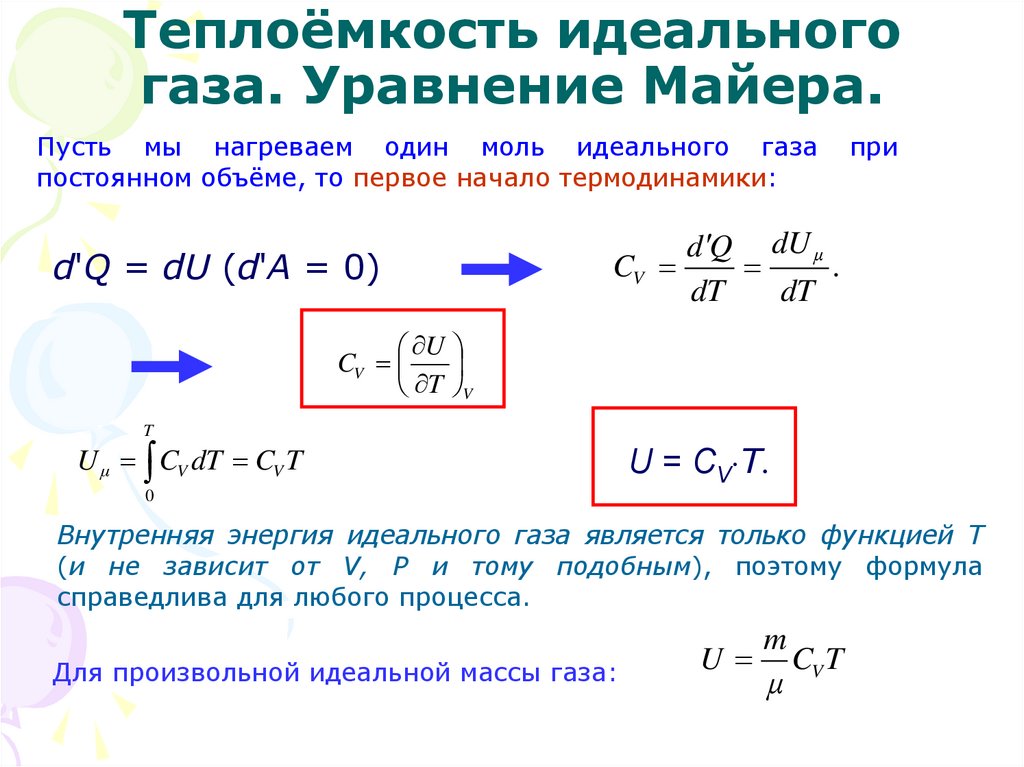Это означает, что для газа каждая степень свободы дает вклад ½ RT во внутреннюю энергию в молярном выражении (R — постоянная идеального газа) 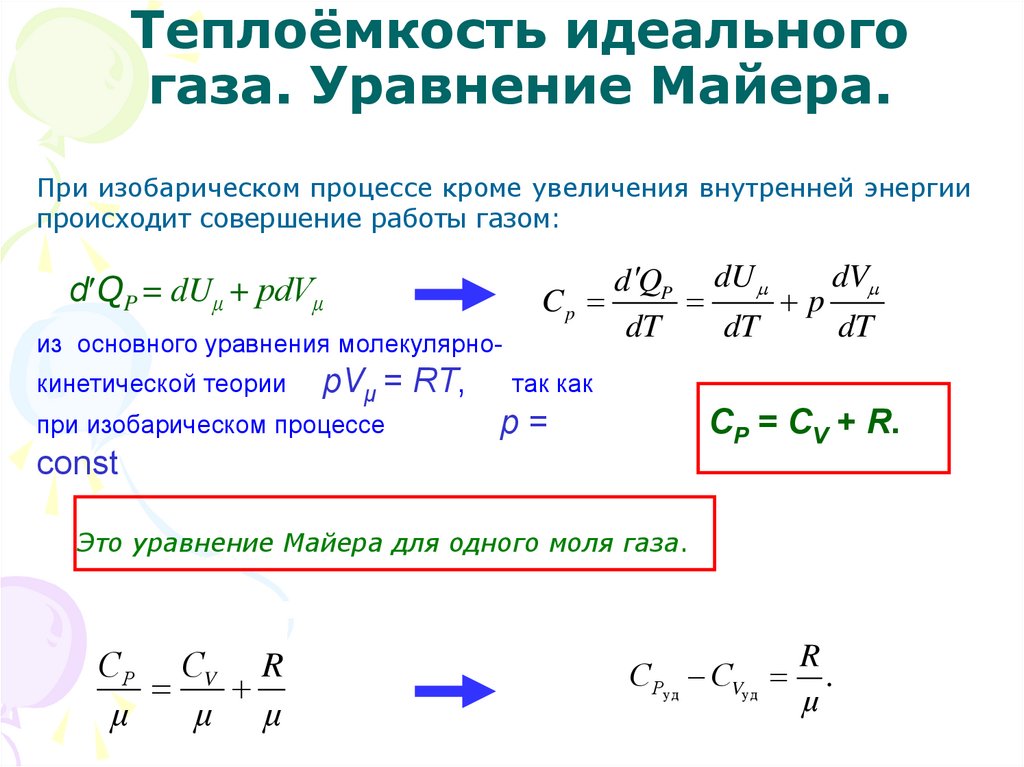Атом одноатомного газа может двигаться в трех независимых направлениях, так что благодаря поступательному движению газ имеет три степени свободы. Следовательно, его внутренняя энергия U соответствует уравнению U = 3/2 RT. Теплоемкость при постоянном объеме C v является производной внутренней энергии по температуре, поэтому для нашего одноатомного газа C v = 3/2 R. Теплоемкость при постоянном давлении может быть оценено, потому что разница между молярным C p и C v представляет собой R; C p – C v = R. Хотя это строго верно для идеального газа, это хорошее приближение для реальных газов. Вращение молекул газа добавляет дополнительные степени свободы. Линейная молекула вращается вокруг двух независимых осей. Следовательно, линейная молекула имеет две вращательные степени свободы. Общее число степеней свободы для линейной молекулы равно 5, поэтому ее внутренняя энергия U = 5/2 RT, ее молярная теплоемкость при постоянном объеме C v = 5/2 R и ее молярная теплоемкость при постоянном давлении будет C p = 7/2 R. Нелинейная молекула вращается по трем независимым осям. Следовательно, линейная молекула имеет три вращательные степени свободы. Общее число степеней свободы для линейной молекулы равно 6, поэтому ее внутренняя энергия равна U = 3 РТ, ее молярная теплоемкость при постоянном объеме C v = 3 R, а ее молярная теплоемкость при постоянном давлении будет C р = 4 р. Вибрации могут повышать теплоемкость, но только если они термически доступны. Колебательная температура \(\Theta _{vib}\) определяется уравнением: постоянная, c — скорость света, v — частота, k — постоянная Больцмана. Колебательный вклад в молярную теплоемкость от данной колебательной степени свободы частоты ν определяется выражением: \[\left ( C_{v} \right )_{vib}=N\times R\times \left ( \frac{\Theta _{vib}}{T} \right )^{2}\times \frac{\exp \left ( \Theta _{vib}/T \right )}{\left \{ \exp \ влево ( \Theta _{vib}/T \right ) -1 \right \}^{2}}\] , где N — число молей, R — постоянная идеального газа, а T — температура. Суммарный вклад в теплоемкость при постоянном объеме от всех колебательных степеней свободы равен: \[ C_{vib, Total}=\sum \left ( C_{v} \right )_{vib}\] где суммирование производится по всем колебательным степеням свободы, 3N-5 (линейные молекулы) или 3N-6 (нелинейные молекулы) Экспериментальный У вас есть большая бутыль с газовым входом и манометр, прикрепленный к пробке в горлышке бутылки, рис. 1. Рис. 1. Установка для измерения отношения Cp/Cv для газов. Теперь вы начинаете с газа при атмосферном давлении (760 торр), а затем добавляете газ, чтобы немного увеличить давление внутри бутылки, скажем, на 1,5% (11,4 торр). Теперь очень быстро вытащите пробку из узкого места и очень быстро верните ее в исходное положение, рис. 2. рис. 2. Очень быстро снимите пробку. Прежде чем читать дальше, остановитесь на мгновение и обдумайте следующие два вопроса. Что происходит с давлением и температурой в бутылке, когда вы снимаете пробку? Как изменятся давление и температура в следующие несколько минут? Обратите внимание, что бутылка не изолирована термически от окружающей среды. Сначала газ возвращается к окружающему атмосферному давлению, когда вы снимаете пробку с бутылки и газ выходит. Если вы удалите пробку и быстро вернете ее, этот процесс будет адиабатическим. Адиабатический процесс — это процесс, при котором теплота не передается (dq = 0). Когда газ расширяется, он работает против своего окружения и немного охлаждается. Секунда Через несколько минут температура газа возвращается к исходной температуре окружающей среды, поскольку баллон не изолирован термически. Что это делает с его давлением? Давление повышается из-за закона идеального газа, PV=nRT. При перестановке имеем P=nRT/V. Когда температура газа возвращается к температуре окружающей среды, давление повышается. Степень повышения давления связана с отношением теплоемкости газа при постоянном давлении к его теплоемкости при постоянном объеме. Это отношение определяется как: \[\frac{C_{p}}{C_{v}}=\frac{\ln P_{1}-\ln P_{2}}{\ln P_{1}-\ ln P_{3}}\] Где P 1 — начальное давление газа, P 2 — давление окружающей среды в помещении, а P 3 — конечное давление, достигаемое после открывания пробки. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт