Трактор сила тяги: № 139. Трактор, сила тяги которого на крюке 15 кН, сообщает прицепу ускорение 0,5 м/с2. Какое ускорение сообщит тому же прицепу трактор, развивающий тяговое усилие 60 кН?

PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2.1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2.5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3.1 МКТ
  • 3. 2 Термодинамика
• 4 Электродинамика
  • 4.1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5.2 Волновая оптика
  • 5. 3 Фотометрия
  • 5.4 Квантовая оптика
  • 5.5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике

Новые страницы

Запрос не дал результатов.

Трактор, сила тяги которого на крюке 15 кн ,сообщает прицепу ускорение… — Учеба и наука

Лучший ответ по мнению автора

10. 01.17 Лучший ответ по мнению автора

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

✔Олеся / Математика Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Физика

Похожие вопросы

Водитель настроил бортовой компьютер автомобиля так, чтобы он непрерывно показывал график зависимости средней скорости движения автомобиля от

Однажды двое мышей-хулиганов Митя и Мотя решили улучшить свои навыки в стрельбе из рогатки. Митя забрался на шкаф высотой H=1,3 м и встал у его края. Мотя остался на полу, но отошёл так, что

Решено

Решите, пожалуйста, задачи

600 p

Над поверхностью земли в неподвижном состоянии удерживают массивную плиту, на горизонтальной поверхности которой лежит небольшой шарик. Внезапно плиту начинают двигать вертикально вниз с постоянной

В герметичном сосуде объёмом V=18 л под давлением p=360 кПа находится смесь гелия и аргона. Чему равна масса гелия в сосуде, если среднеквадратичная скорость его молекул составляет u=1200м/c?

Пользуйтесь нашим приложением

Решение задач по теме «Механическая работа и мощность» 7 класс онлайн-подготовка на Ростелеком Лицей

Задача №1

 

К бруску прикрепили динамометр и переместили брусок на расстояние 30 см. Показания динамометра равны 0,8 Н. Найти работу силы тяги по перемещению бруска (рис. 1).

 

Рис. 1. К задаче №1

Прежде всего запишем краткое условие задачи и позаботимся, чтобы все данные были выражены в системе СИ (рис. 2).

Рис. 2. Краткое условие задачи №1

Для вычисления работы воспользуемся формулой

Полное решение задачи выглядит так (рис. 3).

Рис. 3. Полное решение задачи №1

 

Задача №2

 

 

Трактор перемещает платформу со скоростью 7,2 км/ч, развивая тяговое усилие в 25 кН. Какую работу совершит трактор за 10 мин (рис. 4)?

 

Рис. 4. К задаче №2

Запишем краткое условие задачи и переведем все единицы измерения в систему СИ (рис. 5).

Рис. 5. Краткое условие задачи №2

Для вычисления работы необходимо знать расстояние, пройденное телом. В условии задачи дана скорость движения трактора и время движения, поэтому воспользуемся формулой

которую подставим в выражение для работы  и получим рабочую формулу

Подстановка данных из условия задачи дает

Рис. 6. Полное решение задачи №2

 

Задача №3

 

 

Найдем работу силы тяжести при падении грузика.

 

Для решения задачи нам потребуется линейка и сам грузик. Измерим высоту, с которой будет падать грузик. Получаем 1 м. Масса грузика написана на нем самом и равна 100 г. Поднимем грузик на указанную высоту и отпустим его.

Краткое условие задачи будет выглядеть так (рис. 7):

Рис. 7. Краткое условие задачи №3

Для нахождения работы выразим силу тяжести через массу тела , и учтем, что расстояние, пройденное телом, равно высоте, с которой оно упало: .

Тогда

Подстановка чисел дает

Рис. 8. Полное решение задачи №3

Теперь у нас есть представление о том, насколько велика работа в 1 джоуль. Такая работа совершается при падении грузика массой 100 г со стола высотой 1 м.

Переходим к решению более сложных задач.

 

Задача №4

 

 

Со дна реки глубиной 4 м поднимают камень объемом 0,6 м³ на поверхность. Плотность камня 2500 кг/м³, плотность воды 1000 кг/м³. Найти работу по подъему камня.

 

Для решения задачи необходимо не только записать краткое условие задачи, но и сделать схематический рисунок и показать силы, действующие на камень. Это сила тяги F_т (работу именно этой силы мы будем находить), сила тяжести mg и сила Архимеда F_a. Кроме того, покажем высоту, на которую сила тяги перемещает камень (рис. 9).

Рис. 9. К решению задачи №4

Как видно из рисунка, искомая работа равна .

Для нахождения силы тяги воспользуемся условием равновесия тела: если оно неподвижно или движется с постоянной скоростью, то равнодействующая всех сил, приложенных к нему, равна нулю.

, откуда .

Массу камня выразим через плотность камня и его объем, а силу Архимеда – через плотность воды и объем погруженной части камня (в этом задаче он равен объему всего камня). Объем камня и ускорение выносим за скобки.

Остается подставить силу тяги в формулу для вычисления работы

Поскольку рабочая формула получилась более сложной, единицы измерения результата определим отдельно от расчета его численного значения.

Рис. 10. Полное решение задачи №4

 

Задача №5

 

 

Поршень двигателя перемещается на 20 см под давлением 800 кПа. Определите работу, совершаемую двигателем за один ход поршня, если площадь поршня 150 см² (рис. 11).

 

Рис. 11. К задаче №5

Запишем краткое условие и выразим все единицы в системе СИ (рис. 12).

Рис. 12. Краткое условие задачи №5

В данной задаче работу выполняет сила давления газа в цилиндре двигателя. Для нахождения этой силы необходимо давление в цилиндре умножить на площадь поршня. Расстояние, пройденное поршнем, мы обозначили буквой l.

Единицы измерения результата:

Численное значение результата:

Рис. 13. Полное решение задачи №5

 

Задача №6

 

 

Найти КПД (коэффициент полезного действия) наклонной плоскости (экспериментальная) (рис. 14).

 

Рис. 14. Груз поднимают вверх по наклонной плоскости

Поднимая груз по наклонной плоскости с помощью динамометра, измерим силу, которая для этого требуется. Она оказывается равной 2,2 Н. Расстояние, пройденное грузом вдоль плоскости, измеряем рулеткой. Оно составило 0,5 м. При этом груз поднялся над столом на высоту 20 см. Кроме того, известны масса бруска, равная 50 г, и общая масса трех поднимаемых грузов – 300 г.

Полученные опытные данные занесем в краткое условие задачи, выразим все величины в единицах системы СИ и сделаем схематический рисунок измерительной установки (рис. 15).

Рис. 15. Краткое условие задачи №6

Коэффициентом полезного действия механизма называется физическая величина, равная отношению полезной работы, совершенной механизмом, к работе, затраченной для приведения его в действие.

КПД также обозначают греческой буквой η (эта) и часто выражают в процентах.

В нашем случае механизмом является наклонная плоскость.

Полезная работа – эта работа, которую нужно совершить, чтобы поднять тело на высоту h.

Затраченная работа совершается силой тяги, то есть силой упругости пружины динамометра.

Тогда КПД равен

Определяем единицы измерения КПД

Такой результат означает, что КПД является безразмерной величиной (просто число без единиц измерения).

Его числовое значение

Обратите внимание, что коэффициент полезного действия не может быть больше единицы, поскольку полезная работа всегда меньше затраченной. Если у вас получилось наоборот, значит, либо при измерениях, либо в ходе вычислений допущена ошибка.

Рис. 16. Полное решение задачи №6

 

Задача №7

 

 

Трактор равномерно тянет плуг, прилагая силу в 10 кН. За 10 мин он проходит путь 1,2 км. Определить мощность, развиваемую трактором (рис. 17).

 

Рис. 17. К условию задачи №7

Запись краткого условия и перевод величин в систему СИ будет выглядеть так (рис. 18):

Рис. 18. Краткое условие задачи №7

Для нахождения мощности нужно работу, выполненную трактором, разделить на время ее выполнения. Работа вычисляется как произведение силы тяги трактора на пройденное трактором расстояние. Таким образом, получаем:

Рис. 19. Полное решение задачи №7

 

Задача №8

 

 

Поезд массой 600 тонн равномерно движется со скоростью 36 км/ч. Определить развиваемую тепловозом мощность, если сила трения составляет 0,002 веса поезда.

 

Рис. 20. К условию задачи №8

Запишем краткое условие задачи, выразим величины в единицах системы СИ, сделаем рисунок, на котором покажем силу тяги тепловоза и силу трения (рис. 21).

 

Рис. 21. Краткое условие задачи №8

Поскольку по условию задачи скорость поезда не изменяется и равна 36 км/ч, сила тяги равна силе трения  Вес в случае движения с постоянной скоростью равен силе тяжести  Тогда сила тяги равна

Для вычисления мощности воспользуемся формулой  откуда

Подстановка данных из условия дает

Рис. 22. Полное решение задачи №8

 

Список литературы

1. Перышкин А. В. Физика. 7 кл. – 14-е изд., стереотип. – М.: Дрофа, 2010.
2. Перышкин А. В. Сборник задач по физике, 7–9 кл.: 5-е изд., стереотип. – М: Издательство «Экзамен», 2010.
3. Лукашик В. И., Иванова Е. В. Сборник задач по физике для 7–9 классов общеобразовательных учреждений. – 17-е изд. – М.: Просвещение, 2004.

 

Домашнее задание

1. Лукашик В. И., Иванова Е. В. Сборник задач по физике для 7–9 классов №675–683, 706–712.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Единая коллекция Цифровых Образовательных Ресурсов (Источник)
2. Единая коллекция Цифровых Образовательных Ресурсов (Источник)

 

3.

1: Traction — Engineering LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

46845

• Николас М. Холден, Мэри Ли Вулф, Джэктон Арого Огеджо и Энда Дж. Камминс
• Университетский колледж Дублина и Технологический институт Вирджинии через Инициативу открытого образования Технических библиотек Вирджинии

Даниэль М. Кейрос

Кафедра сельскохозяйственной инженерии

Федеральный университет Викозы

Висоса, Минас-Жерайс, Бразилия

Джон К. Шуллер

Кафедра машиностроения и аэрокосмической техники

Университет Флориды

Гейнсвилл, Флорида, США

Основные термины

Механика тяги	Тяговые устройства	Тракторы
Мощность двигателя	Транспортные устройства	Прицепные орудия
Сила тяги

Переменные

Введение

Тракторы были созданы для сокращения трудозатрат человека и животных и повышения эффективности и производительности растениеводства (Schueller, 2000). В основном тракторы используются для буксировки таких орудий, как почвообрабатывающие орудия, сеялки, культиваторы и комбайны, в поле и, в некоторой степени, на дороге (Renius, 2020). Чтобы эффективно тянуть навесное оборудование, трактор должен создавать сцепление между шинами и поверхностью почвы. Тяга — это способ, которым транспортное средство использует силу для движения по поверхности.

Уже на раннем этапе разработки тракторов прямая передача мощности от тракторов к орудиям стала возможной благодаря использованию коробок отбора мощности (ВОМ), которые передают мощность вращения на орудия и машины, а также с помощью гидравлических систем для подъема и опускания навесного оборудования и перемещения части навесных машин. Тяговое орудие по-прежнему является наиболее распространенным применением мощности трактора. Полевая производительность сельскохозяйственных машин, т. е. площадь поля, которую можно обработать в единицу времени, обусловила разработку и применение более крупных орудий. Увеличенные размеры требуют большей тяги от тянущего трактора. Необходимы более эффективные системы для создания тягового усилия, чтобы обеспечить большие силы, необходимые для тяги этих орудий.

Эффективность того, как тракторы преобразуют мощность, вырабатываемую двигателем, в мощность, необходимую для тяги навесного оборудования, зависит от многих переменных, связанных с трактором и состоянием почвы. Тяга особенно важна в сельском хозяйстве, так как полевые почвы не такие твердые, как дороги, по которым ездят легковые и грузовые автомобили. В этой главе представлены основные принципы тяги, применяемые к сельскохозяйственным машинам.

Результаты

После прочтения этой главы вы сможете:

• • Объясните, как тракторы развивают тяговое усилие
• • Опишите влияние некоторых важных переменных на тяговое усилие
• • Рассчитайте, какую мощность трактор может развивать при буксировке навесного оборудования
• • Рассчитайте требуемую мощность для согласования тракторов с навесным оборудованием

Концепции

Тяговые и транспортные устройства

Согласно Американскому обществу инженеров-агрономов и биологических инженеров (стандарты ASABE, 2018 г. ), существует два типа устройств поверхностного контакта, связанных с движением транспортного средства: тяговые устройства и транспортные устройства. Тяговое устройство получает мощность от двигателя и использует реакции сил опорной поверхности для движения транспортного средства, в то время как транспортное устройство не получает мощности, но необходимо для поддержания транспортного средства на поверхности при движении транспортного средства по этой поверхности. . Колеса, шины и гусеницы могут быть тяговыми устройствами, если они подключены к двигателю или другому источнику энергии; если они не подключены, они являются транспортными устройствами. Основные узлы сельскохозяйственного трактора представлены на рис. 3.1.1. В данном примере трактор двухколесный, поэтому большие задние колеса, получающие мощность от двигателя, являются тяговыми устройствами, а малые передние колеса — транспортными. Все колеса были бы тяговыми устройствами, если бы трактор был полноприводным. Двигатель соединен с тяговым устройством трансмиссией, часто состоящей из сцепления, трансмиссии, дифференциала, осей и других компонентов. (Привод в этой главе не рассматривается.) Дышло — это точка крепления, через которую трактор может передавать тяговое усилие на навесное оборудование.

Рисунок \(\PageIndex{1}\): Схематический вид двухколесного сельскохозяйственного трактора.

Механика тяги

Самый простой способ анализа силы тяги, создаваемой тяговым устройством, таким как колесо или гусеница, заключается в рассмотрении сил трения, которые действуют при контакте тягового устройства с поверхностью, когда система находится в равновесии. Для упрощения предполагается, что машина движется с постоянной скоростью по неизменной поверхности (рис. 3.1.2). Тяговое устройство (далее упрощенное до наиболее распространенного варианта «колесо») имеет две основные функции: воспринимать нагрузку, действующую на ось колеса ( W ) и для создания чистой тяговой силы ( H ). Силу Вт обычно называют динамической нагрузкой, действующей на колесо. Динамическая нагрузка зависит от того, как вес трактора в этот момент времени распределяется на каждое колесо. Если система находится в равновесии, поверхность реагирует на W приложением к колесу вертикальной силы реакции ( R ). При контакте поверхности с колесом возникает сила трения ( F _f ) генерируется. Чтобы сохранить равновесие в горизонтальном направлении, величина чистой силы тяги H равна величине силы трения F _f . Чтобы создать результирующую силу тяги H , необходимо преодолеть силу трения. Это делается приложением крутящего момента ( T ) к оси колеса. Этот крутящий момент пропорционален крутящему моменту, создаваемому двигателем трактора в соответствии с трансмиссией, включая текущее передаточное число.

Рисунок \(\PageIndex{2}\): Упрощенная диаграмма переменных, связанных с колесом, развивающим чистую тяговую силу.

ω = угловая скорость колеса

F _F = сила трения

H = чистая тяговая сила

R = вертикальная сила реакции колеса

T = крутящий момент передается на ось колеса

v _a = фактическая скорость колеса

Вт = динамическая нагрузка на колесо

При движении колесо (рисунок 3. 1.2) вращается с постоянной угловой скоростью ( ω ), причем эта угловая скорость пропорциональна скорости вращения двигателя и зависит от передаточного числа в трансмиссии. Колесо имеет фактическую скорость v _a , которая равна угловой скорости, умноженной на радиус качения колеса, уменьшенный на проскальзывание (как обсуждается ниже). В равновесной ситуации ω и v _и являются константами. Мощность, передаваемая на ось колеса ( P _w ), может быть рассчитана как произведение крутящего момента ( T ) и угловой скорости ( ω ), как показано в уравнении 3.1.1. Тяговая мощность, развиваемая колесом ( P _t ), является произведением чистой тяговой силы ( H ) и фактической скорости ( v _a ), как показано в уравнении 3.1.2. Тяговый КПД колеса ( T _E ) можно рассчитать как отношение тяговой мощности к мощности оси колеса, как показано в уравнении 3. 1.3.

\[ P_{W}=T\omega \]

\[ P_{t}=H\nu_{a} \]

\[ T_{E}=\frac{P_{t}}{P_ {W}} \]

где P _w = мощность, передаваемая на ось колеса (Вт)

T = крутящий момент, передаваемый на ось колеса (Н·м)

ω = угловая скорость колесо (рад с ⁻¹ )

P _t = тяговая мощность, развиваемая колесом (Вт)

H = чистая тяговая сила (Н)

v _a = фактическая скорость колеса )

T _E = тяговое усилие колеса (безразмерное)

Сила трения ( F _f на рис. 3.1.2) создается за счет взаимодействия колеса с поверхностью. Силу трения можно рассчитать, умножив силу реакции ( R ) на эквивалентный коэффициент трения ( μ ). В таблице 3.1.1 представлены некоторые типичные значения. Поскольку R равно динамической нагрузке, действующей на ось колеса ( W ), а чистая тяговая сила равна силе трения, тяговую силу можно рассчитать как произведение эквивалентного коэффициента трения и динамической нагрузка, как:

Таблица \(\PageIndex{1}\): Эквивалентный коэффициент трения колеса трактора, работающего на различных поверхностях.

Тип поверхности	Эквивалентный коэффициент трения ( μ )[a]
Мягкая почва	0,26–0,31
Средний грунт	0,40–0,46
Твердая почва	0,43–0,53
Бетон	0,91–0,98

[a] Эти значения были рассчитаны на основе данных, представленных Kolator and Bialobrzewski (2011).

\[ H= \mu W \]

где μ = коэффициент трения (безразмерный).

Теоретическая скорость ( v _t ) определяется скоростью вращения колеса ( ω ), умноженной на радиус качения ( r ), как показано в уравнении 3.1.5, но фактическая скорость колеса ( v _a ) меньше из-за относительного движения на границе раздела между колесом и поверхностью. Это относительное движение представляет собой коэффициент уменьшения хода, обычно называемый проскальзыванием, и определяется как отношение потери скорости колеса к теоретической скорости, то есть скорости, которую колесо имело бы, если бы потери не было. Уравнение 3.1.6 показывает, как можно оценить коэффициент уменьшения хода:

\[ \nu_{t} = \omega r \]

\[ s= \frac{\nu_{t}-\nu_{a}}{\nu_{t}} \]

, где v _t = теоретическая скорость колеса (м с ⁻¹ )

r = радиус качения колеса (м с ⁻¹ )

с 903, 1 = коэффициент уменьшения хода Коэффициент уменьшения хода является важной переменной для анализа тягового усилия колес. Коэффициент уменьшения хода колеса может варьироваться от 0 до 1 в зависимости от состояния колеса и поверхности. Когда коэффициент уменьшения хода равен 0, относительное движение между периферией колеса и поверхностью отсутствует. Вращение колеса вызывает совершенное поступательное движение относительно поверхности. Однако опыт показал, что для того, чтобы колесо развивало тяговое усилие, должно быть относительное движение (скольжение) между колесом и поверхностью. Следовательно, колесо, создающее тяговое усилие, должно иметь передаточное отношение уменьшения хода больше нуля. Когда колесо создает большее тяговое усилие, коэффициент уменьшения хода увеличивается, а фактическая скорость колеса уменьшается. Когда коэффициент уменьшения хода равен 1, колесо не движется вперед при вращении. В моделях, используемых для расчета тяговой силы, в качестве одной из переменных обычно используется коэффициент уменьшения хода.

ω = угловая скорость колеса

F = полная тяговая сила

H = чистая тяговая сила

R = вертикальная сила реакции колеса

r = радиус качения

T = крутящий момент передается на колесо

F _r = сила сопротивления движению

v _a = фактическая скорость колеса

W = динамическая нагрузка на колесо

Еще одним важным понятием при анализе процесса тяги движущегося колеса является сила сопротивления движению ( F _r ) (рис. 3.1.3). Если колесо движется, колесо и поверхность деформируются. На эту деформацию тратится энергия. Сопротивление, создаваемое колесом, и деформации поверхности должны быть преодолены, чтобы колесо могло двигаться. Учитывая существование силы сопротивления движению, в контакте колеса с поверхностью необходимо создать силу трения большую, чем сила сопротивления движению в контакте колеса с поверхностью, чтобы создать тяговое усилие. Эта сила трения теперь называется общей силой тяги (обозначается 9).0116 Ф ). Таким образом, полная тяговая сила была бы чистой тяговой силой, создаваемой колесом, если бы не было сопротивления движению. Добавление понятий сопротивления движению и общей тяговой силы к рисунку 3.1.2 приводит к рисунку 3.1.3, который является улучшенным представлением сил, действующих на колесо.

Рисунок \(\PageIndex{3}\): Диаграмма переменных, связанных с колесом, развивающим чистую тяговую силу ( H ), включая общую тяговую силу ( F ) и силу сопротивления движению ( Ф _р ).

Если колесо, представленное на рисунке 3.1.3, не движется в вертикальном направлении (ось z), то колесо находится в статическом равновесии в этом направлении. В этом состоянии сумма сил в направлении z (вертикальном) равна нулю. Следовательно,

\[ \sum F_{z} = 0 \]

\[ R-W=0 \]

\[ R=W \]

где F _z = любая сила, приложенная к колесу в направлении z (Н)

R = вертикальная сила реакции колеса (Н)

Если фактическая скорость колеса, представленного на рис. 3.1.3, постоянна, то горизонтальные силы находятся в статическом равновесии в этом направлении и сумма горизонтальных сил равна нулю. Следовательно,

\[ \sum F_{x}=0 \]

где F _x = любая сила, приложенная к колесу в направлении x (Н)

F = полная тяговая сила (Н)

F _r = сила сопротивления движению (Н)

На основании уравнения 3.1.12 общая тяговая сила ( F ) должна быть чистой тяговой силой ( H ) плюс сила сопротивления движению ( F _r ). Если обе части уравнения 3.1.12 разделить на динамическую нагрузку ( W ), действующую на колесо, то в результате уравнения 3.1.13 получится три безразмерных числа, т. е. , и ρ , создаются, как показано в уравнениях 3.1.15, 3.1.16 и 3.1.17. Первый – чистое передаточное число (μ _n ), определяется как чистая тяговая сила, деленная на динамическую нагрузку. Второй — это общий коэффициент тяги ( μ _г ), определяемый как общая тяговая сила, деленная на динамическую нагрузку. И третье — это коэффициент сопротивления движению ( μ ), определяемый как сила сопротивления движению, деленная на динамическую нагрузку.

\[ \frac{H}{W}=\frac{F}{W}-\frac{F_{r}}{W} \]

Уравнение 3.1.14 показывает, что μ _n , мк _g и ρ не являются независимыми. С помощью метода, называемого анализом размеров, были разработаны функции для прогнозирования изменения μ _g и ρ в зависимости от переменных колес и сопротивления грунта. Этот анализ представлен Герингом и др. (2003) и выходит за рамки этой главы. Если известны μ _g , ρ и W , тяговое усилие, создаваемое колесом, можно рассчитать с помощью уравнения 3.1.18:

\[ H= (\mu_{g}-\rho)W \]

Силы R , F и F _r (рис. 3.1.3) действуют на точку, называемую центр сопротивления колеса. Эта точка не совпадает с направлением динамической нагрузки W , но немного опережает ее. Это горизонтальное расстояние называется горизонтальным смещением ( e ). Статический анализ буксируемого колеса (рис. 3.1.4) показывает, что центр сопротивления колеса не совпадает с направлением динамической нагрузки на колесо. В буксируемом колесе на его ось не действует крутящий момент. Реакция почвы ( G ) в центре сопротивления является равнодействующей сил R и F _r . Направление силы G проходит через центр колеса. Для перемещения буксируемого колеса с постоянной фактической скоростью ( v _a ) к колесу необходимо приложить чистую тяговую силу ( H ), равную силе сопротивления движению ( F _r ). Чтобы колесо сохраняло постоянную угловую скорость, сумма импульсов в центре колес должна равняться нулю. Геринг и др. (2003) показали, что горизонтальное смещение можно рассчитать с помощью уравнения 3.1.19.-3.1.21.

Рисунок \(\PageIndex{4}\): Схема сил, действующих на буксируемое колесо.

\[ Re-F_{r}r = 0 \]

, где e = смещение по горизонтали (м).

С помощью уравнения 3.1.18 можно рассчитать силу тяги. Другой важной информацией в анализе тягового усилия колес является прогнозирование того, какой крутящий момент необходимо передать на ось колеса для создания тягового усилия ( H ). В уравнении 3.1.5 радиус колеса используется для преобразования угловой скорости вращения в теоретическую скорость колеса. Радиус колеса также можно использовать для расчета крутящего момента, необходимого для создания тягового усилия колеса. Крутящий момент ( T ), необходимое для поддержания постоянной угловой скорости колеса и получения полезной тяговой силы, является произведением общей тяговой силы и радиуса крутящего момента колеса, определяемым по формуле:

ω = угловая скорость колеса колесо

e = смещение по горизонтали

G = реакция почвы в центре сопротивления

H = чистая тяговая сила

R = вертикальная сила реакции колеса

r = радиус качения

F _r = сила сопротивления движению

v _a = фактическая скорость колеса

Вт = динамическая нагрузка на колесо

\[ T=Fr_{t} \]

, где r _t = радиус крутящего момента колеса (м).

Радиус колеса, определенный в уравнении 3.1.5, отличается от радиуса крутящего момента колеса, определенного в уравнении 3.1.22, из-за взаимодействия колеса и поверхности, которое меняется на поверхности мягкого грунта. Как правило, используется радиус качения, основанный на расстоянии от центра оси колеса до твердой поверхности. Следовательно, уравнение 3.1.23 можно использовать для оценки крутящего момента, действующего на ось колеса:

\[ T=Fr \]

Мощность двигателя, необходимая для создания тягового усилия

Стандарты ASABE (2015 г.) представили диаграмму (рис. 3.1.5) примерного типичного соотношения мощности для сельскохозяйственных тракторов. Тракторы можно определить по полной номинальной мощности маховика двигателя ( P _e ). Одним из стандартов, используемых для определения полной номинальной мощности маховика двигателя, является SAE J1995 (SAE, 1995). Номинальная мощность, определяемая этим стандартом, представляет собой механическую мощность, вырабатываемую двигателем без некоторых его аксессуаров (таких как генератор переменного тока, вентилятор радиатора и водяной насос). Следовательно, полная номинальная мощность маховика двигателя больше, чем полезная мощность, вырабатываемая двигателем. Приблизительную чистую мощность двигателя на маховике можно оценить, умножив полную мощность на маховике на 0,9.2. Мощность на ВОМ трактора примерно равна полной мощности на маховике двигателя, умноженной на 0,83, или полезной мощности на маховике двигателя, умноженной на 0,90.

Мощность, которую трактор может генерировать для тяги навесного оборудования, часто называемая мощностью дышла, поскольку к дышлу трактора крепится множество навесных орудий, зависит от типа трактора, т. е. привод на 2 колеса (2WD), механический привод на передние колеса (MFWD) , полноприводная (4WD), или гусеничная. Состояние поверхности, на которой используется трактор, имеет еще большее значение. Используя эти две части информации, коэффициенты, которые показывают оценку соотношения между мощностью тягового стержня и мощностью ВОМ, приведены на рис. 3.1.5.

Мощность тяги, необходимая для тяги орудия:

\[ P_{DB} = F_{i} \nu_{i} \]

где P _DB = мощность тяги (Вт)

F _i = сила, необходимая для тяги орудия (Н)

v _i = скорость орудия (мс ⁻¹ )

Сила, необходимая для тяги орудия, зависит от орудия.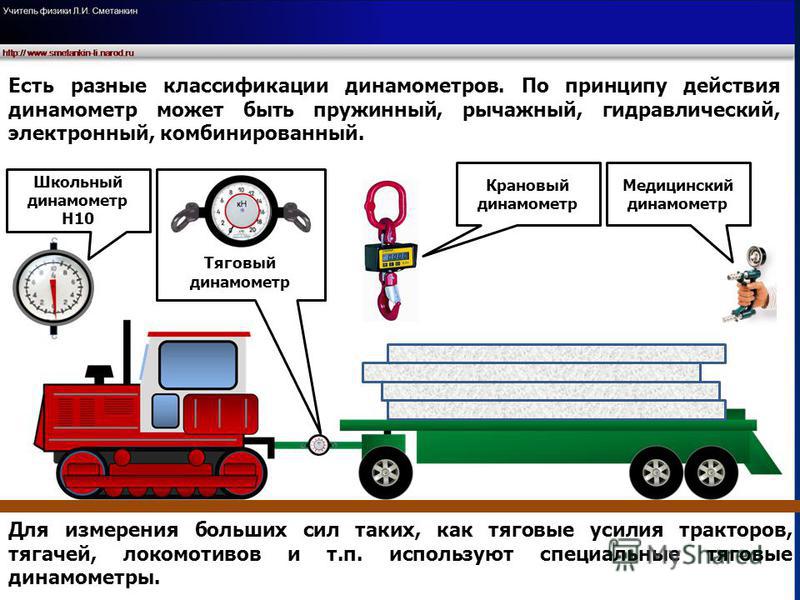 Например, сила, необходимая для вытягивания сеялки F _p — усилие, требуемое на ряд, умноженное на количество рядов:

\[ F_{p} = f_{r}n_{r} \]

, где f _r = усилие, необходимое на ряд сеялки (Н ряд ⁻¹ )

n _r = количество рядов

После определения требуемой мощности на дышле значения на рис. 3.1.5 можно использовать для расчета расчетной необходимой полной номинальной мощности на маховике трактора. тянуть орудие.

Приложения

Понятия тяги и мощности трактора необходимы для правильного согласования трактора с навесным оборудованием. Сельскохозяйственные операции нельзя выполнять, если трактор не может развить достаточную мощность или тягу для буксировки орудия. Поскольку размеры навесного оборудования с годами увеличились, необходимо, чтобы тракторы имели достаточную мощность и достаточное тяговое усилие для выполнения задач, которые они должны выполнять. Выбор слишком большого трактора отрицательно скажется на рентабельности сельского хозяйства, поскольку большие тракторы стоят дороже, чем маленькие. Негабаритный трактор также может увеличить расход топлива и выбросы выхлопных газов. Это важно, потому что даже самые эффективные тракторы получают менее 4 кВтч работы на литр дизельного топлива.

Рисунок \(\PageIndex{5}\): Схема приблизительного соотношения мощностей сельскохозяйственных тракторов (типы указаны в основном тексте) и почвенных условий (ASABE, 2015).

Тракторы сильно различаются по размеру (например, рис. 3.1.6). Например, один крупный современный производитель продает тракторы мощностью от 17 до 477 кВт. Вес трактора должен быть достаточным для создания достаточной силы тяги, как показано в уравнении 3.1.18. Однако, помимо затрат на добавление веса, дополнительный вес может увеличить уплотнение почвы и снизить урожайность. Поэтому необходимо понимать эти концепции для проектирования тракторов и навесного оборудования. Возможности двигателя трактора, элементов силовой передачи и колес необходимо соответствующим образом масштабировать. Необходимо найти компромисс между тем, чтобы сделать их большими и мощными, и сделать их компактными и недорогими. Приведенный выше анализ может быть использован для выбора и конструкции трактора.

Рисунок \(\PageIndex{6}\): Типичные современные (слева) малые и (справа) большие тракторы.

Эти концепции также применяются к другим типам сельскохозяйственной техники, например, к самоходным комбайнам и опрыскивателям. Чтобы эти машины могли выполнять свои задачи, они должны иметь возможность передвигаться по сельскохозяйственным землям. Те же расчеты можно использовать для определения достаточности мощности и для проектирования различных компонентов этих машин. Колеса, оси и компоненты силовой передачи должны выдерживать усилия, крутящие моменты и мощность во время использования машин.

Примеры

Пример \(\PageIndex{1}\)

Пример 1: Тяговое усилие

Задача:

Рассчитайте тяговое усилие, создаваемое колесом трактора, работающего на твердом грунте с динамической нагрузкой 5 кН. Скорость колеса 2 м с ⁻¹ . Если коэффициент тяги равен 0,73, какая мощность должна быть передана на ось колеса?

Раствор

Примите эквивалентный коэффициент трения равным 0,48, среднее значение для твердого грунта представлено в таблице 3. 1.1. Рассчитайте тяговую силу, используя уравнение 3.1.4:

\( H= \mu W=0,48 \times 5 = 2,4 \text{ кН} \)

Теперь рассчитайте тяговое усилие колеса трактора, используя уравнение 3.1.2:

\( P_{t} = H\nu_{a} = 2,4 \times 2 = 4,8 \text{ кВт} \)

Рассчитайте мощность, которую необходимо передать на ось колеса, используя уравнение 3.1.3 при заданном коэффициенте тяги 0,73:

\( P_{W} = \frac{P_{t}}{T_{E}} = \frac{4.8}{0.73} = 6.58 \text{ кВт} \)

Это значение необходимой мощности можно использовать для проектировать различные компоненты силовой передачи. Потребляемая мощность также может быть использована для расчета мощности, необходимой для конечного источника энергии, возможно, двигателя, для расчета расхода топлива и, следовательно, затрат на конкретную операцию в полевых условиях.

Пример \(\PageIndex{2}\)

Пример 2. Коэффициент снижения крутящего момента и хода или проскальзывание

Проблема:

Колесо другого трактора получает мощность 40 кВт от трансмиссии трактора. Колесо вращается со скоростью 25 об/мин, что соответствует угловой скорости ω, равной 2,62 рад с 90 228 -1 90 229 . (Примечание: 2π рад × 25 об/мин/60 мин с ⁻¹ = 2,62 рад с ⁻¹ .) Если радиус качения колес равен 0,81 м, а скорость трактора равна 2 м с ⁻¹ , рассчитать крутящий момент, действующий на колесо, и коэффициент уменьшения хода (обычно известный как скольжение).

Решение

Рассчитайте крутящий момент, действующий на колесо T для мощности P _w 40 кВт, используя уравнение 3.1.1:

\( T=}{\frac{P_{W} \omega} = \frac{40}{2,62} = 15,28 \text{ Нм} \)

Рассчитайте мощность, передаваемую колесу для создания тягового усилия 2,4 кН на расстоянии 2 м с ⁻¹ скорости колеса, используя Уравнение 3.1.3:

\( P_{W} = \frac{P_{t}}{T_{E}} = \frac{4,8}{0,73} =6,58 \text{кВт} \) 9{-1} \)

Поскольку фактическая скорость колеса составляет 2 м с ⁻¹ , что меньше теоретической скорости колеса, рассчитайте коэффициент уменьшения хода с , используя уравнение 3. 1.6:

\(s= \frac{\nu_{t}-\nu_{a}}{\nu_{t}} = \frac{2.12-2.00}{2.12} = 0,057, \text{or} \ 5,7\% \ )

Помимо предоставления рекомендаций по конструкции сельскохозяйственной машины и ее потребляемой мощности, расчет скольжения полезен для определения того, насколько быстро будет выполняться операция. Чрезмерное скольжение также может оказать неблагоприятное воздействие на структуру почвы и затормозить рост растений.

Пример \(\PageIndex{3}\)

Пример 3. Тяговая сила и мощность

Задача:

Рассмотрим колесо, которое работает с динамической нагрузкой 10 кН, коэффициентом сопротивления движению 0,08 и общий тяговый коэффициент 0,72. Найдите силу тяги, которую может развивать колесо. Если это колесо вращается со скоростью 40 об/мин, а радиус качения колеса равен 0,71 м, какая мощность необходима для перемещения этого колеса?

Решение

Рассчитать полную тяговую силу, развиваемую колесом F , используя уравнение 3. 1.16:

\( F= \mu_{g} W = 0,72 \times 10 = 7,2 \text{ кН} \)

Рассчитайте сопротивление движению F _r этого колеса используя уравнение 3.1.17:

\( F_{r} = \rho W = 0,08 \times 10 = 0,80 \text{ кН} \)

Тяговое усилие H , развиваемое колесом, согласно уравнению 3.1. 12, есть разница между полной тяговой силой и сопротивлением движению:

\( H = F-F_{r} = 7,2 — 0,8 = 6,4 \text{ кН} \)

Рассчитайте крутящий момент, необходимый для перемещения этого колеса, используя уравнение 3.1.23:

\( T = Fr = 7,2 \times 0,71 = 5,11 \text{ кН·м} \)

Рассчитайте мощность P _w необходимо чтобы повернуть колесо, используя уравнение 3.1.1:

\( P_{W} = T \omega = T \frac{2\pi N}{60} = 5.11 \times \frac{2 \times \pi \times 40 }{60} = 21,4 \text{ кВт} \)

Пример \(\PageIndex{4}\)

Пример 4: Полная мощность двигателя на маховике

Задача:

Рассчитайте необходимую мощность трактора MFWD для буксировки 30-рядной сеялки. Согласно стандартам ASABE (2015 г.), требуется усилие 900 Н на ряд, чтобы тянуть прицепную сеялку для пропашных культур, если она выполняет только операцию посева. Скорость трактора составит 8,1 км ч 90 228 -1 90 229 (2,25 м с 90 228 -1 90 229 ). Почва в распаханном состоянии. Учтите, что трактор должен иметь запас хода 20% для преодоления непредвиденных перегрузок.

Раствор

Рассчитайте силу тяги, необходимую для тяги сеялки, используя уравнение 3.1.25:

\( F_{p} = f_{r}n_{r} = 900 \times 30 = 27 000 \text{ N} \)

Рассчитайте мощность тягового бруса P _DB , необходимую для тяги сеялки, используя уравнение 3.1.24:

\( P_{DB} = F_{p} \nu_{p} = 27 000 \times 2,25 = 60 750 \text{ Вт } \)

Следовательно, трактор должен выдавать тяговую мощность 60,75 кВт. Из рисунка 3.1.5 найдите, что коэффициент, связывающий мощность дышла с мощностью ВОМ трактора для трактора MFWD, работающего на вспаханной почве, равен 0,72. Таким образом, мощность ВОМ трактора P _ВОМ должно быть:

\( P_{PTO} = \frac{P_{DB}}{0,72} = \frac{60,75}{0,72} = 84 \text{кВт} \)

Учитывая что коэффициент, связывающий мощность ВОМ с полной мощностью на маховике двигателя, равен 0,83 (рис. 3.1.5), полная мощность на маховике двигателя P _e равна:

\( P_{e} = \frac{P_{ ВОМ}}{0,83} = \frac{84,375}{0,83} = 102 \text{кВт} \)

Учитывая запас мощности 20% для преодоления непредвиденных перегрузок, выбранный трактор должен иметь полную мощность двигателя на маховике при как минимум на 20 % больше, чем требуется для тяги 30-рядной сеялки, или 1,2 × 102 кВт = 122 кВт.

Эти расчеты помогут управляющему фермой выбрать правильный трактор для работы.

Авторы изображений

Рис. 1. Кейрос, Д. (CC By 4.0). (2020). Схематический вид двухколесного сельскохозяйственного трактора.

Рис. 2. Queiroz, D. (CC By 4. 0). (2020). Упрощенная диаграмма переменных, связанных с колесом, развивающим чистую тяговую силу.

Рис. 3. Queiroz, D. (CC By 4.0). (2020). Диаграмма переменных, связанных с колесом, развивающим чистую тяговую силу ( H ), включая общую тяговую силу ( F ) и силу сопротивления движению ( F _r ).

Рис. 4. Queiroz, D. (CC By 4.0). (2020). Схема сил, действующих на буксируемое колесо.

Рис. 5. Стандарт ASABE ASAE D497.7 (CC By 4.0). (2020). Схема примерных соотношений мощностей сельскохозяйственных тракторов (типы указаны в основном тексте) и почвенных условий.

Рис. 6. Шуллер, Дж. (CC By 4.0). (2020). Типичные современные (а) малые и (б) большие тракторы.

Ссылки

Стандарты ASABE. (2018). ANSI/ASAE S296.5 DEC2003 (R2018): Общая терминология тяги сельскохозяйственных тягово-транспортных устройств и транспортных средств. Сент-Джозеф, Мичиган: ASABE.

Стандарты ASABE. (2015). ASAE D497.7 MAR 2011 (R2015): Данные по управлению сельскохозяйственной техникой. Сент-Джозеф, Мичиган: ASABE.

Геринг, К.Э., Стоун, М.Л., Смит, Д.В., и Тернквист, П.К. (2003). Тяговые и транспортные устройства. В Принципы проектирования внедорожных транспортных средств (стр. 351-382). Сент-Джозеф, Мичиган: ASAE.

Колатор, Б., и Бялобжевски, И. (2011). Имитационная модель производительности полноприводного трактора. Вычисл. Электрон. Агр. 76 (2): 231-239.

Рениус, К. Т. (2020). Основы конструкции трактора. Чам, Швейцария: Springer Nature.

САЕ. (1995). SAE J1995_199506: Код проверки мощности двигателя — искровое зажигание и воспламенение от сжатия — номинальная полная мощность. Трой, Мичиган: SAE.

Шуллер, Дж. К. (2000). На службе изобилия: механизация сельского хозяйства обеспечила питание для необычайного роста 20-го века. мех. англ. 122 (8):58-65.

---

Эта страница под названием 3.1: Traction распространяется под лицензией CC BY 4.0, ее авторами, ремиксами и/или кураторами являются Николас М. Холден, Мэри Ли Вулф, Джактон Арого Огеджо и Энда Дж. Камминс (Технологические библиотеки Вирджинии). Открытая образовательная инициатива) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Николас М. Холден, Мэри Ли Вулф, Джактон Арого Огеджо и Энда Дж. Камминс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Программа OER или Publisher

   Инициатива открытого образования технических библиотек Вирджинии

2. Теги

   1. мощность двигателя
   2. механика тяги
   3. навесное оборудование
   4. источник@https://vtechworks.lib.vt.edu/handle/10919/93254
   5. тяга
   6. тяговые устройства
   7. тяговое усилие
   8. тракторы
   9. транспортные устройства

Какие сельскохозяйственные шины улучшают тяговое усилие вашего трактора?

Как правило, тяговое усилие вашего трактора связано только с мощностью его двигателя.
Тем не менее, шины играют фундаментальную роль в улучшении сцепления с дорогой и часто недооцениваются или игнорируются. Именно шины передают мощность вашего трактора на землю для создания тягового усилия. Таким образом, ваши шины являются единственным связующим звеном между транспортным средством и землей.

Соблюдая особую осторожность при выборе и уходе за шинами, вы можете оптимизировать тяговое усилие вашего транспортного средства, повысить урожайность и производительность и уменьшить пробуксовку трактора.

 

Какие сельскохозяйственные шины лучше всего подходят для увеличения тягового усилия?

Сельскохозяйственные шины играют жизненно важную роль в обеспечении тягового усилия вашего трактора. Тяговое усилие зависит от нескольких переменных, связанных с внутренними качествами этих шин и их обслуживанием:

 

Конструкция протектора шин вашего трактора увеличивает тяговое усилие

ваши сельскохозяйственные шины. Они впиваются в землю и ограничивают проскальзывание, что приводит к потере сцепления шин с дорогой. Их угол относительно оси колеса влияет на тяговое усилие вашего трактора .

Чем меньше угол, тем больше сила тяги. Большинство сельскохозяйственных шин разработаны с учетом идеального угла наклона.

Но будьте осторожны! Не выбирайте сельскохозяйственную шину со скидкой со слишком малым углом наклона , так как это приводит к скоплению земли между грунтозацепами .

Слишком много земли и грязи в пятне шины может ухудшить сцепление с дорогой и увеличить проскальзывание . Но коэффициент скольжения необходимо тщательно контролировать, потому что он позволяет передавать мощность трактора на землю для создания тягового усилия. Он должен быть между 12% и 15%.

Если буксование слишком велико, трактор может застрять в грязи .

Кроме того, чем выше коэффициент проскальзывания, тем выше расход топлива .

В идеале вы должны выбрать сельскохозяйственную шину из новых моделей с многоугольной конструкцией. Выступы расположены под разными углами к центру колеса.

Обеспечивает идеальный компромисс между удалением грязи и оптимальным тяговым усилием.

Некоторые шины даже имеют рисунок выступа, который оптимизирует сцепление . Именно проникновение выступа в почву позволяет передавать крутящий момент на обод. Оптимизация профиля шины приводит к улучшению пропускной способности трансмиссии . Чем больше контакт грунта с грунтом, тем выше тяговое усилие.

 

Тяговое усилие вашего трактора зависит от давления в шинах

Меньшее давление означает большую площадь контакта между землей и шинами и, следовательно, лучшую подвижность. Поэтому давление воздуха в шинах должно быть максимально снижено.

Но недокачанная тракторная шина на дороге приведет к чрезмерному износу грунтозацепов . Его сопротивление качению слишком велико.

Кроме того, перекачанная шина вызывает чрезмерное уплотнение почвы . В зависимости от типа выполняемых работ или местности, по которой вы едете, давление в шинах может быть разным.

Поэтому необходимо проверить и отрегулировать давление в шинах, чтобы получить оптимальное тяговое усилие.

Например, при вспашке или уборке урожая требуется большее тяговое усилие, чем при разбрасывании удобрений или транспортировке. Это связано с тем, что прикрепленные инструменты и используемые машины тяжелее. Нагрузка на заднюю ось (или даже на переднюю ось) больше. В этом случае рекомендуется шина низкого давления с широким пятном контакта. Это позволяет снизить давление на почву, поскольку шина с низким давлением меньше уплотняет почву. Ваша почва будет сохранена, потому что менее уплотнена, и в результате улучшится урожайность. Технологии IF и VF позволяют увеличить вес на 20–40 % по сравнению со стандартной шиной.
Для всех различных видов работ использование широких шин с технологией VF дает значительные преимущества.
Не требуют регулировки давления в зависимости от выполняемой работы. Тяговое усилие вашего трактора оптимизировано независимо от того, находитесь ли вы на дороге или в поле.
Гарантированная экономия времени: нет необходимости регулировать давление в шинах каждое утро. Ваши шины также будут иметь более длительный срок службы. Перекачанная или недостаточно накачанная шина изнашивается быстрее.

 

Хороший коэффициент скольжения необходим для оптимизации сцепления с дорогой

Ограниченное скольжение повышает эффективность тяги. Коэффициент скольжения связан с давлением воздуха в шинах. Чтобы быть оптимальным, оно должно составлять от 12% до 15% , чтобы обеспечить достаточную тяговую силу без чрезмерного износа шин и без уплотнения почвы.

Выбор шин VF обеспечивает оптимальный коэффициент проскальзывания, поскольку шины VF обеспечивают лучшее сцепление с дорогой и маневренность благодаря низкому давлению и более широкому пятну контакта.

 

Каковы преимущества регулируемой тяговой силы?

Правильный выбор шин, адаптированных к требуемому тяговому усилию, позволяет контролировать тяговое усилие трактора. Повышение эффективности и производительности, а также экономия топлива.

Вы расходуете меньше топлива, а шины изнашиваются медленнее. Благодаря качественным сельскохозяйственным шинам вы избежите уплотнения почвы и значительно повысите урожайность.

 

---

Блог Bridgestone-agriculture.eu составляется и управляется экспертами по сельскохозяйственным шинам, которые готовы дать вам совет по поводу ваших шин. Они могут помочь вам максимизировать вашу производительность благодаря информации обо всех аспектах, связанных с шинами: Технические характеристики сельскохозяйственных шин – Характеристики сельскохозяйственных шин – Рекомендации по давлению воздуха – Решения по предотвращению уплотнения почвы – Давление в шинах опрыскивателя – 6 основных механических причин ненормального износа шин шины вашего трактора – и т. д.….

Чтобы узнать больше и увеличить прибыль вашей фермы, эксперты по тракторным шинам предлагают вам бесплатную подробную электронную книгу , в которой объясняется важная роль сельскохозяйственных шин в вашей производительности .

Большинство людей, прочитавших эту статью, также читали некоторые из следующих статей:

• 5 основных методов оптимизации сельскохозяйственных шин
• Как след сельскохозяйственных шин может помочь вам обнаружить проблему
• Управляйте давлением на землю, чтобы ваши сельскохозяйственные шины служили дольше
• Двойной монтаж лучшее решение для оптимальной производительности
• Как управлять коэффициентом скольжения шин трактора

Тяга и теория тяги, используемые в тракторах

В этой статье мы обсудим:- 1. Значение тяги 2. Теория тяги 3. Механика шасси трактора.

Значение Тяга:

Тяга — это сила в направлении движения, развиваемая средой тягового устройства (почвой) и передаваемая на транспортное средство. Мощность, развиваемая двигателем, в конечном итоге передается на колеса или гусеницы, которые перемещают трактор с прикрепленным грузом или без него. При движении колес происходит некоторая пробуксовка, что вызывает снижение скорости. Проскальзывание также происходит при увеличении нагрузки.

Сцепление можно увеличить за счет:

1. Использование резиновых шин с канавками

2. Установка цепей противоскольжения

3. Использование ребристых протекторов на звеньях гусеницы и

4. Установка грунтозацепов, шипов или грунтозацепов на колеса обод.

Тяговое устройство:

Это устройство для приведения в движение транспортного средства с использованием тяговых сил от опорной поверхности.

Коэффициент тяги:

Это отношение общей силы, выдаваемой тяговым устройством в направлении движения, к динамическому весу тягового устройства.

Тяговая эффективность:

Это отношение выходной мощности к входной мощности, обычно выражаемое в процентах.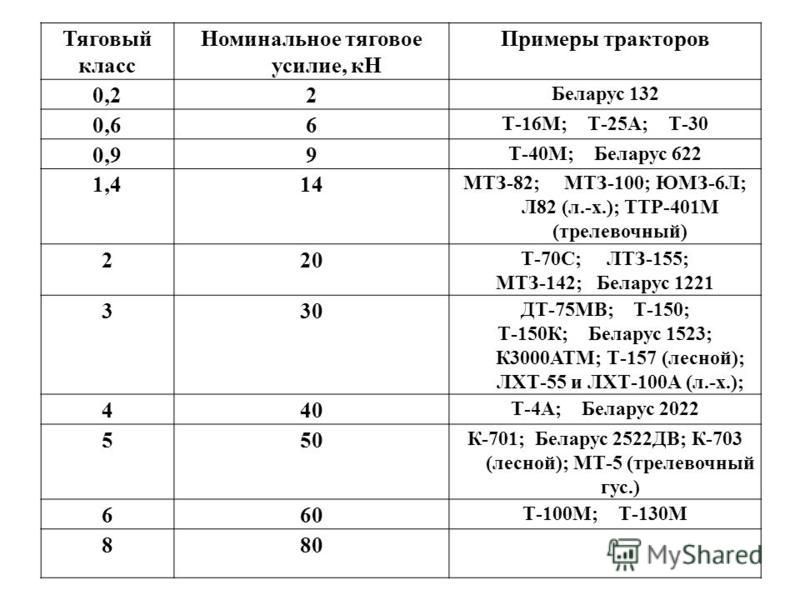

Эффективность тяги зависит от нескольких факторов, таких как:

1. Давление в шинах

2. Состояние почвы

3. Размер колес

4. Скорость движения

1

5. Уклон местности 6. Высота сцепки и

и

7. Форма и размер проушин.

Сопротивление качению:

Это сила, необходимая в направлении движения для преодоления сопротивления движению.

Коэффициент сопротивления качению:

Это соотношение между сопротивлением качению и динамическим весом.

Пробуксовка колеса или гусеницы:

Это относительное перемещение колеса или гусеницы в направлении движения на заданное расстояние под нагрузкой и без нагрузки. Его можно рассчитать по формуле:

Пробуксовка колес, % = N ₁ – N ₀ / N ₁ × 100

Где,

N ₁ = число оборотов ведущих колес или звездочек на заданное расстояние под нагрузкой и;

N ₀ = число оборотов ведущих колес или звездочек на одинаковом расстоянии без нагрузки

Тяговое усилие:

резиновые шины ведущего колеса и поверхность, по которой они движутся. Коэффициент сцепления достаточно высок, чтобы исключить проскальзывание шин. Максимальное тяговое усилие на ободе зависит от мощности двигателя и передаточного числа между двигателем и ведущими колесами.

Traction Theory :

Пневматические шины используются на обычных тракторах. При движении такого трактора по грунту он должен преодолевать сопротивление качению R, как показано на рис. (10.30).

Где,

F = сила тяги в направлении движения.

P = тяговое усилие, используемое для полезной работы, и

R = сопротивление качению.

Для расчета тягового усилия P и сопротивления качению R. Беккер предложил следующие уравнения:

F = A [C + ρ tan φ]

или, F = AC + W tan φ

Где,

A = площадь среза

ρ = давление грунта

C = сцепление грунта и

φ = угол внутреннего трения грунта

W = Aρ = вертикальная нагрузка на площадь сдвига.

Очевидно, что сила тяги обычно зависит от вертикальной силы и площади сдвига.

Для гусеничного трактора давление на грунт p определяется по формуле:

ρ ^{= W/BL}

Где B — ширина каждой гусеницы, а L — длина гусеницы в контакте с почвой.

Для колес с пневматическими шинами площадь контакта с почвой представляет собой эллипс, и для этого равномерного давления на почву ρ определяется по формуле:

= ρ W/0,78 BL

Сопротивление качению:

Сопротивление качению из-за уплотнения грунта можно аппроксимировать, приняв, что энергия, необходимая для преодоления сопротивления качению, равна работе, совершаемой при деформации грунта. Сопротивление качению R можно получить по соотношению.

Где,

n = коэффициент оседания колес

Kc = модуль сцепления деформации грунта

Kφ = модуль трения деформации грунта

B = ширина каждой гусеницы

W = вертикальная нагрузка на площадь сдвига и

L = длина контактной дорожки.

Это уравнение получено в предположении о плоской пластине, как в гусеничном тракторе. Это уравнение примерно верно и для тракторов с резиновыми колесами. После расчета сопротивления качению и силы тяги полезное тяговое усилие P можно получить по уравнению P = F – R.

Механика шасси трактора :

Механика шасси трактора включает в себя ряд сил, но для понимания основного принципа следует простой подход, рассматривая основные силы как:

1. Гравитация

2 9 , Реакция почвы

3. Тяговое усилие и

4. Тяговое усилие.

Ссылаясь на (рис. 10.31) и рассматривая трактор как свободное тело, алгебраическая сумма всех сил, действующих параллельно или перпендикулярно направлению движения, а также алгебраическая сумма моментов относительно любой точки должны быть по отдельности равны нулю.

∑H = 0, ∑V= 0, ∑ M = 0

H — горизонтальная сила, V — вертикальная сила, M — момент, a — угол между тягой (P) и горизонталью,

H = F-P cos α = 0 … (1)

Где F – сила трения

V = R ₁ + R ₂ – W-P sin α = 0 … (2)

Определение моментов относительно точки A

∑M = WX ₁ – Y ₁ P cos α – SP sin α – R ₁ X ₂ = 0 … (3)

Solving equation (3) for R ₁

The stability of the tractor in the vertical plane is determined by R ₁ and the tractive capacity by R ₂

Центр тяжести :

Это точка на корпусе трактора, в которой его вес можно считать действующим.

Точное положение центра тяжести можно определить следующими методами:

(a) Подвеска

(b) Метод балансировки и

(c) Метод взвешивания

Вышеуказанные три метода не учитывают движение масла в картере и трансмиссии, топлива в баке и вес оператора.

(a) Метод подвески:

Трактор подвешивается в любой удобной точке, достаточно прочной, чтобы выдержать его вес. Центр тяжести будет находиться в вертикальной плоскости через точку подвеса. Повторяя эту операцию с другой точкой подвеса, можно найти еще одну плоскость, и ее пересечение с предыдущей вертикальной линией определит центр тяжести.

(b) Метод балансировки:

Этот метод используется для гусеничных тракторов. Потребуется отвес и большой брус, равный по длине габаритной ширине трактора и толщиной около 15 см и более. Если трактор приводится в движение так, чтобы положения точек крепления двух гусениц совпадали, а затем медленно перемещается по бревну, чтобы его можно было сбалансировать по двум точкам крепления.