Трансверсальное ускорение: Курс теоретической механики

Курс теоретической механики

Курс теоретической механики

Березкин Е.Н. Курс теоретической механики. М.: МГУ, 1974. — 647 с. Книга предназначена служить руководством для студентов университетов при изучении курса теоретической механики, а также может быть использована в качестве дополнительной литературы студентами технических вузов. Материал книги полностью соответствует действующей программе курса теоретической механики для университетов. Книга включает теорию скользящих векторов, кинематику, геометрическую и аналитическую статику, динамику материальной точки и системы материальных точек, аналитическую динамику и элементы специальной теории относительности. Оглавление Предисловие Введение Глава I. ОСНОВЫ ТЕОРИИ ВЕКТОРОВ § 1. СВОБОДНЫЕ ВЕКТОРЫ 2. Сложение свободных векторов. 3. Проекция вектора на ось. 4. Инварианты системы свободных векторов. § 2. СКОЛЬЗЯЩИЕ ВЕКТОРЫ 2. Координаты скользящего вектора. 3. Момент скользящего вектора. Плюккеровы координаты. 4. Аналитическое определение момента скользящего вектора. 5. Проекция момента на ось. 6. Момент скользящего вектора относительно оси § 3. СИСТЕМА СКОЛЬЗЯЩИХ ВЕКТОРОВ 2. Произвольная система скользящих векторов. Элементарные операции. 3. Приведение системы скользящих векторов к простейшей эквивалентной форме. 4. Плоская система скользящих векторов. 5. Свойства системы параллельных скользящих векторов. § 4. ЗАКРЕПЛЕННЫЕ ВЕКТОРЫ § 5. ДИФФЕРЕНЦИРОВАНИЕ СВОБОДНОГО ВЕКТОРА ПО СКАЛЯРНОМУ АРГУМЕНТУ Глава II. КИНЕМАТИКА § 1. КИНЕМАТИКА ТОЧКИ 2. Ускорение точки. Проекции ускорения на прямоугольные оси координат. 3. Скорость и ускорение точки в полярных координатах. 4. Движение точки по окружности. 5. Проекции ускорения на оси естественного трехгранника. 6. Теорема о сложении скоростей в сложном движении точки. 7. Метод Роберваля построения касательных к плоским кривым. 8. Аналитическое доказательство теоремы о сложении скоростей. 9. Сложение скоростей в общем случае сложного движения точки. § 2. КИНЕМАТИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА 2. Элементарные движения твердого тела. 3. Мгновенные движения твердого тела. 4. Сложение мгновенно-поступательных и мгновенно-вращательных движений твердого тела. 5. Общий случай сложения мгновенно-поступательных и мгновенно-вращательных движений твердого тела. Непрерывное движение твердого тела. 6. Мгновенное движение твердого тела с одной неподвижной точкой. 7. Плоскопараллельное движение твердого тела. § 3. УСКОРЕНИЕ ТОЧКИ В СЛОЖНОМ ДВИЖЕНИИ 2. Замечание о дифференцировании единичного вектора. 3. Векторный вывод теоремы Кориолиса. 4. Теорема Ривальса. § 4. РАСПРЕДЕЛЕНИЕ УСКОРЕНИЙ В ПЛОСКОПАРАЛЛЕЛЬНОМ ДВИЖЕНИИ ТВЕРДОГО ТЕЛА 2. Мгновенный центр ускорений. § 5. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА Глава III. СТАТИКА I. ГЕОМЕТРИЧЕСКАЯ СТАТИКА § 1. АКСИОМЫ СТАТИКИ § 2. ПОНЯТИЕ О СИЛЕ ТРЕНИЯ § 3. РАЗЛИЧНЫЕ ЗАДАЧИ СТАТИКИ 2. Равновесие трех сил. § 4. МОМЕНТ СИЛЫ 2. Момент силы относительно оси. 3. Теорема Вариньона для системы сходящихся сил. § 5. ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО § 6. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО § 7. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО, К ДИНАМЕ. УРАВНЕНИЯ РАВНОВЕСИЯ ТВЕРДОГО ТЕЛА § 8. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ ТВЕРДЫХ ТЕЛ § 9. ПЛОСКАЯ СИСТЕМА СИЛ § 10. ЗАДАЧА О РАВНОВЕСИИ НЕСВОБОДНОГО ТВЕРДОГО ТЕЛА 2. Частные случаи равновесия твердого тела. § 11. ЗАДАЧА О РАВНОВЕСИИ ПРИ НАЛИЧИИ ТРЕНИЯ § 12. СИЛА ТЯЖЕСТИ И ЦЕНТР ТЯЖЕСТИ II. АНАЛИТИЧЕСКАЯ СТАТИКА § 1. РАБОТА СИЛЫ НА ПЕРЕМЕЩЕНИИ. СИЛОВАЯ ФУНКЦИЯ § 2. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ 2. Теорема Лагранжа о равновесии системы. 3. Принцип Торричелли. § 3. ОБЩИЕ ВОПРОСЫ АНАЛИТИЧЕСКОЙ СТАТИКИ 3. Общие теоремы о равновесии системы материальных точек. 4. Метод неопределенных множителей Лагранжа. 5. Определение реакций. § 4. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ В ОБЩЕМ СЛУЧАЕ § 5. РАВНОВЕСИЕ НИТИ 2. Естественные уравнения равновесия нити. Глава IV. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ § 1. ОСНОВНЫЕ ЗАКОНЫ ДИНАМИКИ § 2. ДВЕ ОСНОВНЫЕ ЗАДАЧИ ДИНАМИКИ. УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ В ДЕКАРТОВЫХ ОСЯХ § 3. ЕСТЕСТВЕННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ § 4. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ ДЛЯ СВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ 2. Теорема об изменении момента количества движения. 3. Следствия из теорем об изменении количества движения и момента количества движения материальной точки. 4. Теорема живых сил. 5. Интеграл живых сил. 6. Устойчивость равновесия. Теорема Лагранжа. § 5. ДВИЖЕНИЕ ТЯЖЕЛОЙ МАТЕРИАЛЬНОЙ ТОЧКИ В ПУСТОТЕ § 6. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНЫХ СИЛ 2. Формулы Бине 3. Задача о движении планет § 7. ДВИЖЕНИЕ ТОЧКИ В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ § 8. ДВИЖЕНИЕ НЕСВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ 2. Движение материальной точки по поверхности. § 9. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ 1. Теорема живых сил в относительном движении точки. 2. Уравнения относительного равновесия точки. 3. Равновесие материальной точки на поверхности Земли. Вес. 4. Задача о падении тяжелой точки в пустоте. 5. Маятник Фуко. § 10. ПРИНЦИП ДАЛАМБЕРА Глава V. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК § 1. УЧЕНИЕ О СВЯЗЯХ § 2. ПРИНЦИП ДАЛАМБЕРА – ЛАГРАНЖА § 3. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ СИСТЕМЫ 2. Теорема об изменении момента количества движения. 3. Теорема живых сил. § 4. ТЕОРЕМЫ О ДВИЖЕНИИ СИСТЕМЫ ОТНОСИТЕЛЬНО ОСЕЙ НЕИЗМЕННОГО НАПРАВЛЕНИЯ, ПРОХОДЯЩИХ ЧЕРЕЗ ЦЕНТР МАСС СИСТЕМЫ (ОСЕЙ КЕНИГА) 2. Теорема об изменении момента количества движения системы относительно осей Кёнига. 3. Теорема живых сил в движении системы относительно осей Кёнига. § 5. УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА 2. Случай существования силовой функции. 3. Замечание о лагранжевых координатах. § 6. ЭЛЕМЕНТАРНЫЕ СЛУЧАИ ИНТЕГРИРУЕМОСТИ УРАВНЕНИЙ ЛАГРАНЖА 2. Метод Рауса игнорирования циклических координат. 3. Обобщение теоремы и интеграла живых сил. § 7. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ Глава VI. ДИНАМИКА ТВЕРДОГО ТЕЛА § 1. ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ 2. Момент инерции системы относительно произвольной оси, проходящей через заданную точку. 3. Эллипсоид инерции. 4. Определение главных осей инерции для произвольной точки. § 2. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ § 3. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ 2. Уравнения движения твердого тела с одной неподвижной точкой. § 4. ДВИЖЕНИЕ ТЯЖЕЛОГО ТВЕРДОГО ТЕЛА ОКОЛО НЕПОДВИЖНОЙ ТОЧКИ 2. Интегрирование уравнений движения тяжелого твердого тела. 3. Случай Эйлера — Пуансо. Регулярная прецессия твердого тела в случае Эйлера. Геометрическая интерпретация Пуансо движения твердого тела в случае Эйлера. Устойчивость постоянных вращений твердого тела. 4. Случай Лагранжа. Особенные случаи движения твердого тела. Спящий волчок. Гироскоп. Приближенная теория. Некоторые применения гироскопов. Регулярная прецессия в случае Лагранжа. Вынужденная регулярная прецессия. 5. Случай Ковалевской. § 5. ОПРЕДЕЛЕНИЕ РЕАКЦИИ В СЛУЧАЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА С ОДНОЙ НЕПОДВИЖНОЙ ТОЧКОЙ § 6. УРАВНЕНИЯ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА § 7. ГИРОСТАТЫ Глава VII. АНАЛИТИЧЕСКАЯ ДИНАМИКА § 1. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА 1. Преобразования Лежандра. 2. Канонические уравнения Гамильтона. 3. Функция Гамильтона и ее свойства. § 2. ПРИНЦИП ГАМИЛЬТОНА – ОСТРОГРАДСКОГО 2. Вывод канонических уравнений Гамильтона из принципа Гамильтона — Остроградского. 3. Принцип Гамильтона в форме Пуанкаре. § 3. ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ УРАВНЕНИЙ ГАМИЛЬТОНА 2. Канонические преобразования. 3. Бесконечно малые канонические преобразования. 4. Теорема Лиувилля. 5. Теорема Якоби. 6. Интегрирование уравнения Гамильтона—Якоби. Метод Имшенецкого разделения переменных. 7. Скобки Пуассона. § 4. ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ 2. Принцип Лагранжа. 3. Принцип наименьшего действия в форме Якоби. Вывод уравнений Лагранжа второго рода из принципа Якоби. Сравнение принципа Якоби с принципом Гамильтона. 4. Оптико-механическая аналогия. 5. Интегральные инварианты. Линейные интегральные инварианты. Интегральный инвариант Пуанкаре — Картана. 6. Принцип наименьшего принуждения Гаусса. Уравнения Аппеля. 7. Уравнения Рауса. § 5. МАЛЫЕ КОЛЕБАНИЯ Затухающие колебания. Вынужденные колебания. Резонанс. Параметрический резонанс. Нелинейные колебания. Диссипативные системы. 2. Общий случай малых колебаний системы около положения устойчивого равновесия. Устойчивость равновесия. Теорема Лагранжа об устойчивости равновесия. Замечание об устойчивости стационарных движений. Малые колебания системы около положения устойчивого равновесия. Влияние диссипативных сил на малые колебания системы около устойчивого положения равновесия. § 6. УСТОЙЧИВОСТЬ ДВИЖЕНИЯ Прямой метод Ляпунова Теорема об асимптотической устойчивости. Теорема Четаева о неустойчивости движения. 2. Влияние новых связей на малые колебания системы около положения равновесия. 3. Влияние диссипативных сил на устойчивость равновесия. 4. Влияние гироскопических сил на устойчивость равновесия. § 7. ЭЛЕМЕНТЫ ТЕОРИИ ВОЗМУЩЕНИЙ Устойчивость консервативных систем. 2. Метод изменения произвольных постоянных. Глава VIII. ТЕОРИЯ УДАРА § 2. ТЕОРЕМЫ КАРНО § 3. ЗАДАЧА О ЦЕНТРЕ УДАРА § 4. ЗАДАЧА О БАЛЛИСТИЧЕСКОМ МАЯТНИКЕ § 5. УРАВНЕНИЯ ЛАГРАНЖА ДЛЯ УДАРА § 6. ЗАДАЧА ОБ УДАРЕ ПО ТВЕРДОМУ ТЕЛУ С ОДНОЙ НЕПОДВИЖНОЙ ТОЧКОЙ Глава IX. ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ § 2. СПЕЦИАЛЬНЫЙ ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА § 3. ГРУППА ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА § 4. ИНВАРИАНТНЫЕ ВЕЛИЧИНЫ В ТЕОРИИ ОТНОСИТЕЛЬНОСТИ. ЧЕТЫРЕХМЕРНЫЙ ВЕКТОР. МИР МИНКОВСКОГО § 5. РЕЛЯТИВИСТСКАЯ ДИНАМИКА Литература

AutumnALL

СЕМИНАРЫ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ ОСЕННЕГО СЕМЕСТРА

ПЕРВОЕ ЗАДАНИЕ.

Ф.И.О. преподавателя: Семендяев Сергей Вячеславович.

Общая информация о семинарах по теоретической механике

Сдача заданий будет происходить без отметок в зачетной книжке.

Сдача заданий – самый активный процесс обучения после посещения семинаров и лекций и домашней работы.

Если кто-то не сдает задания, ему можно в изолированных условиях (без книг) предложить на экзамене решить три задачи. Задачи не из задачника, без ответов. Задачи (все и без единой ошибки) надо защитить перед комиссией из двух человек. Даже если задачи решены, но сдающий не может объяснить решения, то получит двойку.

Когда начинается прием второго задания, у заведующего кафедрой на столе должен лежать список студентов, не приступивших к сдаче первого. Ректорат имеет право таких студентов исключить. Сообщаю об этом заранее.

Поощрительная мера нормальному студенту (посещающему занятия, хорошо и во время сдающему задания) – не дают трех задач на экзамене. Отличившиеся на семинарах и при сдаче заданий могут сдать экзамен досрочно. Это решает преподаватель, ведущий семинарские занятия.

Несколько слов о лекциях. Ходите на лекции. Лекции дают общие представления о предмете.

Несколько слов об учебниках. Список есть в сборнике программ и заданий. Рекомендую взять все учебники из списка. Также есть методические пособия на кафедре и на сайте teormech.mipt.ru.

ЗАМЕЧАНИЯ

Повторенье – мать ученья (пословица).

• Рекомендую при изучении сперва прочитать текст семинара до конца, особо не вникая в подробности формул, а стараясь уловить суть.

• При втором прочтении вникайте в подробности.

• При третьем старайтесь запомнить в общих чертах (по смыслу) и затем дословно (формулировки, формулы).

СЕМИНАР №1.

КИНЕМАТИКА ТОЧКИ.

Способы задания движения материальной точки

Движение задается радиус-вектором положения , скоростью и ускорением в каждый момент времени.

Координатный способ предусматривает введение обобщенных координат. Это любые три независимые величины, однозначно задающие положение точки в пространстве. Обознаются: .

Частный случай обобщенных координат – декартовы координаты (см. рис. 1).

Эта система ортогональных осей неподвижна. С осями связываются орты , соответственно.

Рисунок 1

Наряду с обобщенными координатами вводятся координатные линии – линии, которые описывает точка при изменении каждой из координат при фиксированных других. Выделяется произвольный момент времени . Фиксируется , т.е. . Эта даст координатную линию . Аналогично: даст координатную линию , и даст координатную линию (см. рис. 2).

Рисунок 2

Вводятся орты (локальный базис) — единичные векторы по касательным к координатным линиям . Каждому моменту времени, в общем, соответствует своя конфигурация ортов. Они могут быть неортогональны.

Еще одним частным случаем обобщенных координат являются цилиндрические координаты (см. рис. 3).

Рисунок 3

На рисунке выделены жирным координатные линии цилиндрических координат.

Каким образом можно выразить скорость через обобщенные координаты?

По правилам взятия производной сложной функции:

Орты:

Вводят величины — коэффициенты Ламе.

С их помощью выражение для скорости принимает вид:

.

Когда криволинейные координаты имеют наглядную геометрическую картину (декартовые, цилиндрические, полярные, сферические координаты и т.д.) для нахождения коэффициентов Ламе можно использовать формулу:

,

где — элемент дуги вдоль соответствующей координатной линии .

В декартовых координатах, например, все коэффициенты Ламе равны единице, и

.

Когда координатная линия является прямой, коэффициент Ламе для нее равен единице.

В цилиндрических координатах:

Оси криволинейных координат не всегда ортогональны, поэтому стараются использовать ортогональные, для которых:

.

В случае цилиндрических координат:

.

В полярных координатах () для компонент скоростей вдоль координатных линий и вводятся, соответственно, термины:

— радиальная скорость,

— трансверсальная скорость.

На рис. 4 показаны направления этих скоростей, в случае .

Рисунок 4

Каким образом задается ускорение в обобщенных координатах?

Вектор скорости задается векторным разложением по ортам координатных линий. Однако вектор ускорения задается ортогональными проекциями (см. рис 5).

Рисунок 5

Нужно помнить, что здесь и рассматриваются как независимые переменные, а не как конкретная траектория.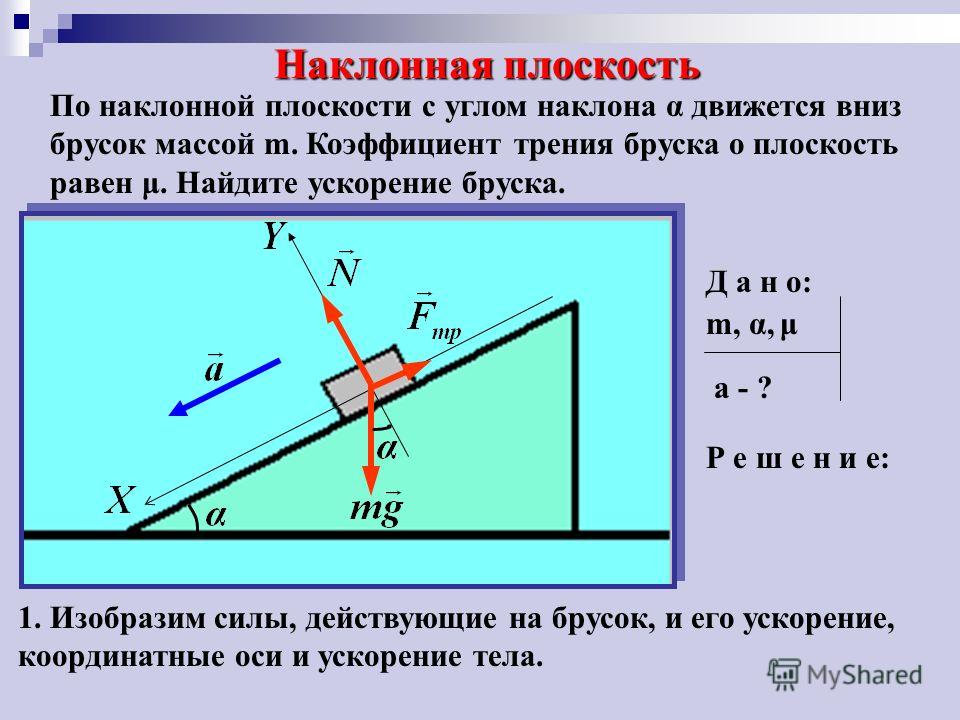

Продолжим рассмотрение случая цилиндрических координат.

Ранее мы нашли: .

Тогда

В полярных координатах () компоненты ускорений называются:

— радиальное ускорение,

— трансверсальное ускорение.

На рис. 6 показаны направления этих ускорений, в случае .

Рисунок 6

Рассмотрим еще один пример ортогональных координат – сферические (см. рис. 7).

Пользуясь формулой , находим

Если бы мы воспользовались формулой для нахождения коэффициентов Ламе, у нас бы ушло полстраницы.

Рисунок 7

Далее

и подставив в выражение для ортогональной проекции ускорения на оси криволинейных координат, получим:

Рекомендую и довести до окончательного вида самостоятельно.

Рассмотрим задачу С.1.19.

В полярных координатах , где угол отсчитывается от перигея (см. рис.8).

Закон площадей является ни чем иным, как одним из законов Кеплера.

Рисунок 8

Как было найдено ранее радиальное ускорение дается формулой

.

Постараемся уйти от дифференцирования по , и перейдем к дифференцированию по .

Здесь мы воспользовались законом площадей . Далее

Тогда, с учетом того, что , найдем

.

В центральном поле трансверсальное ускорение должно быть равно нулю. Проверим:

Действительно, продифференцируем закон площадей:

, и получим:

, что и требовалось доказать.

Теперь перейдем к следующему способу задания движения точки.

Естественный способ задания движения материальной точки

Движение рассматривается вдоль конкретной заданной траектории, а в качестве параметра выступает длина дуги траектории .

Вводится естественный трехгранник Дарбу, состоящий из ортогональных ортов касательной, нормали и бинормали к данной точке траектории (см. рис. 9).

Рисунок 9

Касательный орт направлен по касательной к траектории в данной точке, нормаль к центру кривизны траектории, а бинормаль строится как векторное произведение .

Скорость задается выражением:

Ускорение:

,

где — радиус кривизны траектории.

Заметим, что ускорение имеет две компоненты, которые для определенности называют:

— тангенциальное ускорение,

— нормальное ускорение.

Нормальное ускорение всегда направлено к центру кривизны траектории.

Поскольку базис ортогонален,

.

На данную тему предлагается рассмотреть задачу М.3.74 (или М.12.27 в зависимости от издания).

Движение точки задано в полярных координатах

.

Найти уравнение траектории, скорость, радиус кривизны.

Уравнение траектории: — логарифмическая спираль.

В полярных координатах:

радиальная скорость ,

трансверсальная скорость .

Поэтому

Радиальное ускорение .

Трансверсальное ускорение .

Так как , то .

Радиус кривизны траектории:

.

Совпадают ли по направлению нормальное ускорение с радиальным, а тангенциальное с трансверсальным? В общем случае, нет. См. рис. 10, где полное ускорение разложено на компоненты в полярных координатах и в естественных.

Рисунок 10

СЕМИНАР №2.

ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ОТНОСИТЕЛЬНО НЕПОДВИЖНОГО ПРОСТРАНСТВА.

ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ОТНОСИТЕЛЬНО НЕПОДВИЖНОГО ПРОСТРАНСТВА.

(ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СКОРОСТЕЙ И УСКОРЕНИЙ В ТВЕРДОМ ТЕЛЕ)

Материальная точка – геометрическая точка, которой поставлено в соответствие положительное число — масса.

Твердое тело – такая совокупность материальных точек, что расстояние между любыми двумя неизменно.

Рассмотрим декартову систему координат , в которой расположено твердое тело (см. рис. 11).

Рисунок 11

С твердым телом, в свою очередь, жестко связана другая система координат , с началом в точке твердого тела и движущаяся относительно неподвижного пространства.

Нас интересует скорость и ускорение точки , принадлежащей твердому телу.

Радиус-вектор точки определяется выражением:

.

Следует отметить, что постоянен по модулю: .

В греческой системе координат :

,

причем — постоянные, а — движутся относительно .

Введем вектор таким образом, что

.

Здесь и далее означает векторное произведение.

Введенный таким образом вектор называют угловой скоростью твердого тела.

Тогда скорость точки равна (эту формулу называют законом распределения скоростей в твердом теле):

,

поскольку

Аналогично можно получить ускорение точки (закон распределения ускорений в твердом теле):

где — угловое ускорение.

В случае, когда точка неподвижна,

и для определенности вводят термины:

— вращательное ускорение,

— осестремительное ускорение.

Осестремительное ускорение всегда направлено к мгновенной оси вращения, т. е. к оси проходящей через вектор (геометрическое место точек с нулевыми мгновенными скоростями).

Если рассматривается движение с неподвижной осью, то точку целесообразно брать на оси (см. рис. 12).

Рисунок 12

Тогда

направлено по касательной к окружности радиуса .

Но ,

где — вектор, задающий расстояние от оси до точки ,

, поскольку .

В итоге получаем .

— совпадает по направлению с ,

— направлено в противоположную сторону.

При раскрытии векторного произведения использовалось правило:

.

Когда мгновенная ось неподвижна (), тогда вращательное ускорение совпадает с касательным и осестремительное ускорение совпадает с нормальным . В общем случае (), данное соотношение не выполняется, и кроме того, и не ортогональны.

На рис. 13 указаны направления ускорений для случая .

Рисунок 13

— проекция точки на ось ,

— вектор от оси к точке ,

направлено по касательной к окружности радиуса ,

направлено к мгновенной оси .

Запишем , где — единичный орт вдоль .

Тогда .

Введем вектор таким образом, что .

Т.к. задает направление мгновенной оси, то является угловой скоростью поворота вектора угловой скорости .

В итоге,

Первая компонента соответствует изменению угловой скорости по модулю, вторая компонента соответствует изменению угловой скорости по направлению.

Рассмотрим подробнее плоскопараллельное движение.

Это движение твердого тела, при котором движения всех его точек лежат в плоскостях параллельных некоторой плоскости.

Формулу можно преобразовать в более простую.

Т.к. при плоскопараллельном движении , , то

Знание скоростей любых двух точек при плоскопараллельном движении позволяет найти мгновенный центр скоростей или, другими словами, мгновенную ось вращения (см. рис. 14).

Рисунок 14

Мгновенная ось восстанавливается как пересечение перпендикуляров к и , а . Распределение скоростей такое, как если бы было чистое вращение: .

Пример. Качение без проскальзывания.

В задачах данное выражение значит, что в точке касания твердого тела с поверхностью скорость тела равна скорости поверхности.

Если поверхность неподвижна, то скорость точки касания равна нулю (см. рис. 15).

Рисунок 15

Есть еще одно важное замечание, которое является свойством твердого тела (неразрывность и несжимаемость):

Проекции скоростей любых двух точек твердого тела на прямую соединяющую их равны (см. рис. 16), т.е.

Рисунок 16

Исходя из этого оценим возможные варианты распределения скоростей при плоскопараллельном движении (рис. 17).

Рисунок 17

Задача М-595 (24.17)

Рисунок 18

Найти в тот момент, когда

Посчитаем угловые скорости шестеренок.

Для первой шестеренки МЦС1 в точке .

Для второй шестеренки МЦС2 на расстоянии от точки .

(т.к. нет проскальзывания между шестеренками).

Отсюда:

, следовательно, т.к. , то

Поэтому .

(вращение полюса относительно точки )

Влияние поперечных сил тела, вызванных ускорением, на капиллярный предел тепловых труб со спиральными канавками | J. Теплопередача

Пропустить пункт назначения

Научно-исследовательские работы

С. К. Томас,

К. С. Класинг,

К. Л. Йеркс

Информация об авторе и статье

Дж. Теплопередача . May 1998, 120(2): 441-451 (11 страниц)

https://doi.org/10.1115/1.2824269

Опубликовано в Интернете: 1 мая 1998 г.

История статьи

Получено:

3 сентября 1997 г.

Пересмотрено:

18 февраля 1998 г.

Онлайн:

5 декабря 2007 г. Взгляды

• Содержание артикула
• Рисунки и таблицы
• Видео
• Аудио
• Дополнительные данные
• Экспертная оценка

Делиться

• Facebook
• Твиттер
• LinkedIn
• MailTo

Иконка Цитировать Цитировать

Разрешения

Поиск по сайту

Citation

Томас С. К., Класинг К.С. и Йеркес К.Л. (1 мая 19 г.98). «Влияние поперечных сил тела, вызванных ускорением, на капиллярный предел тепловых труб со спиральными канавками». КАК Я. Дж. Теплообмен . май 1998 г.; 120(2): 441–451. https://doi.org/10.1115/1.2824269

Скачать файл цитаты:

• Рис (Зотеро)
• Менеджер ссылок
• EasyBib
• Подставки для книг
• Менделей
• Бумаги
• КонецПримечание
• РефВоркс
• Бибтекс
• Процит
• Медларс

панель инструментов поиска

Расширенный поиск

Медная тепловая трубка со спиральными канавками и этанолом в качестве рабочей жидкости была изготовлена ​​и испытана на центрифужном столе. Тепловая трубка изгибалась по радиусу кривизны стола, чтобы можно было прикладывать однородные поперечные (перпендикулярные к оси тепловой трубки) поля объемных сил по всей длине трубки. Изменяя погонную энергию (Q _в = от 25 до 250 Вт) и скорости стола центрифуги (радиальное ускорение |a⃗ _r | = от 0 до 10g), информацию о явлениях высыхания, однородности окружной температуры, потерях тепла в окружающую среду, термическом сопротивлении и капиллярности был получен предел переноса тепла. Из-за геометрии винтовых канавок капиллярный предел увеличился в пять раз, когда радиальное ускорение увеличилось от |a⃗ _r | = от 0 до 6,0 г. Этот важный результат был подтвержден математической моделью системы тепловых трубок, в которой капиллярный предел переноса тепла каждой канавки был рассчитан с учетом угловой скорости стола центрифуги, геометрии тепловой трубы и канавок (включая шаг спирали), и зависящие от температуры свойства рабочей жидкости. Кроме того, было проведено качественное исследование медно-этанольной тепловой трубки с прямыми осевыми канавками. Это экспериментальное исследование показало, что характеристики тепловой трубы с прямыми канавками не улучшаются при увеличении радиального ускорения с |a⃗ _р | = от 0 до 10,0 г.

Раздел выдачи:

Тепловые трубы

Ключевые слова:

Экспериментальный, Теплопередача, Тепловые трубы, Жидкость, Вращение

Темы:

Тепловые трубы

1.

ASHRAE Справочник по основам , 1977, Американское общество инженеров по отоплению, охлаждению и кондиционированию воздуха, Inc., Атланта, Джорджия.

2.

Chi, S., 1976, Теория и практика тепловых труб: Справочник , Hemisphere Publ. Корп., Нью-Йорк.

3.

Faghri

A.

и

Thomas

S.

,

1989

, «

Характеристики характеристики концентрической энхро капиллярного предела

»,

ASME JOURNAL OF HEAT TRANSFER

, Vol.

111

, стр.

844

–

850

.

4.

Faghri, A., 1994, Heat Pipe Science and Technology , Taylor and Francis, Washington, DC.

5.

Gernert, N., et al., 1991, «Гибкие охлаждающие пластины с тепловыми трубками для управления температурой самолета», Proc. Конференция и выставка аэрокосмических технологий , SAE Paper No. 912105.

6.

Класинг К.С., Томас С.К. и Йеркес К.Л., 1997, «CAPLIM: программа Visual Basic для расчета капиллярного предела тепловой трубы с осевыми канавками», Proc. Межобщественная конференция инженеров по преобразованию энергии. , Том. 2, Гонолулу, Гавайи, стр. 1514–1518.

7.

Миллер, Р., 1989, Справочник по технике измерения расхода , 2-е изд., McGraw-Hill.

8.

Richter

R.

, и

Gottschlich

J. M.

,

1993 ,

0003

Термодинамические аспекты работы тепловых труб

»,

AIAA J. Теплофизика Теплопередача

, Vol.

8

, №

2

, стр.

334

–

340

.

9.

Шах Р.К. и Бхатти М.С., 1987, «Ламинарная конвективная теплопередача в воздуховодах», в: Справочник по однофазной конвективной теплопередаче , Какак С., Шах Р.К. и Аунг , W., ред., Wiley, Нью-Йорк.

10.

Shames, I., 1980, Engineering Mechanics , 3-е изд., Prentice-Hall, New Jersey.

11.

Silverstein, C., 1992, Design and Technology of Heat Pipes for Cooling and Heat Exchange , Taylor & Francis, Washington, DC.

12.

Thomas

S.

и

Yerkes

K.

,

1997

, «

0003

»,

AIAA J. Теплофизика Теплообмен

, Vol.

11

, стр.

306

–

309

.

13.

Йеркес, К., и Бим, Дж., 1992, «Работа артериальной тепловой трубы в условиях нестационарного теплового потока и силы тела», Proc. Аэрокосмическая Атлантическая конференция. , Дейтон, Огайо, SAE Paper No. 921944.

14.

Йеркес, К.Л., и Хагер, Б., 1992, «Переходная характеристика тепловых трубок для управления температурой привода», Проц. Аэрокосмическая Атлантическая конференция. , Dayton, OH, SAE Paper № 921024.

15.

Yerkes

K.

и

Hallinan

K.

,

1995

A, «

Поведение динамического поведения динамического поведения из поведения динамического поведения. ненагретый мениск, подвергнутый воздействию поля нестационарных ускорений

»,

AIAA J. Теплофизический перенос тепла

, Vol.

9

, №

2

, стр.

322

–

328

.

16.

Yerkes

K.

и

Hallinan

K.

,

1995

B, «

Поведение мениска, подлежащего преходящему аккулеруру для увеличения капиллярных номеров

,

,

,

,

,

,

,

,

,

,

,

.

AIAA J. Теплофизика Теплопередача

, Vol.

9

, №

3

, стр.

543

–

549

.

Этот контент доступен только в формате PDF.

В настоящее время у вас нет доступа к этому содержимому.

25,00 $

Покупка

Товар добавлен в корзину.

Проверить Продолжить просмотр Закрыть модальный режим

transverse%20acceleration — определение на английском языке, грамматика, произношение, синонимы и примеры

Полый профиль, разработанный как основной профиль пола (1), основной профиль крыши (2) и/или опорный профиль (3) для металлической каркасной конструкции, имеет продольную структуру (71, 72,… ) проходящей вдоль продольного направления профиля и начинающейся от внешней поверхности профиля, при этом указанная продольная конструкция выполнена в виде продольного возвышения или продольной канавки и имеет ширину в месте прикрепления к внешней поверхности профиля менее (20, 15), или (10) миллиметров в направлении поперечно к продольному направлению профиля.

патенты-wipo

поперечные усилия колеса/рельса -Y-

EurLex-2

Если челюсть или часть, поддерживающая челюсть, может поворачиваться вокруг горизонтальной поперечной оси, то соединение, обеспечивающее возможность вращения, должно быть зафиксировано в нормальное положение блокирующим моментом.

Eurlex2018q4

Согласно изобретению газовый мешок (20) содержит трубчатую удлиненную камеру (22) предварительного наполнения, которую можно надувать с помощью поперечное расширение для бокового втягивания на обшивку крыши (12) и защитную камеру (24), на которую может воздействовать топливо через боковые проточные отверстия (60) камеры предварительного наполнения (22) через выпускное отверстие (54), который открывается, когда обивка (12) крыши втягивается, и который может разворачиваться в направлении вниз, чтобы обеспечить надежное раскрытие упомянутой системы головной подушки безопасности.

патентов-ВОИС

Поперечные и продольные буферы

tmClass

В трех измерениях вибрация не ограничивается направлением распространения, а также может возникать в перпендикулярных плоскостях, подобно поперечным волнам.

WikiMatrix

Изобретение относится к переднему концевому модулю (1) для автомобиля, содержащему трубчатую поперечную опору (2) и литьевые детали из пластика, при этом упомянутые компоненты отлиты под давлением на поперечную опору (2). ).

патенты ВОИС

«Две лампы» или «четное количество ламп» означает одну светоизлучающую поверхность в форме полосы или полосы, если такая полоса или полоса расположены симметрично по отношению к срединной продольной плоскости транспортное средство, простирающееся с обеих сторон не менее чем на 0,4 м от крайней внешней кромки транспортного средства и имеющее длину не менее 0,8 м; освещение такой поверхности должно обеспечиваться не менее чем двумя источниками света, расположенными как можно ближе к ее концам; светоизлучающая поверхность может быть образована рядом расположенных рядом элементов при условии, что проекции нескольких отдельных светоизлучающих поверхностей на поперечные плоскости занимают не менее 60 процентов площади наименьшего прямоугольника, описывающего проекции указанных отдельных светоизлучающих поверхностей;

EurLex-2

Целью данной акции является поддержка сквозных мер, касающихся открытого и дистанционного обучения (ODL) и использования информационных и коммуникационных технологий (ИКТ), включая мультимедиа, в сфере образования

eurlex

Более того , внутренняя пленка с поперечной 9Волосяной покров 0427, реализованный в нем по настоящему изобретению, содержит слой для УФ-импринтинга, образованный с использованием формовочного валика, имеющего поперечный волосковый покров различной длины и шероховатости, так что внешний вид, наиболее близкий к волосяному покрову, образованному на поверхности реального металла материал может быть сформирован, что не может быть реализовано ни одной из обычных интерьерных пленок.

патенты-ВОИС

Изобретение относится к термическому станку для удаления заусенцев (10), имеющему первую и отдельную вторую часть камеры (12; 13) для приема заготовок (15), подлежащих снятию заусенцев, при этом предусмотрено закрывающее устройство (70 ), посредством которого первая часть камеры (12) может прижиматься ко второй части камеры (13) или наоборот относительно направления закрытия (73), при этом соответствующие усилия закрытия поглощаются по меньшей мере одной поддерживающей узла (30), который выполнен кольцевым по отношению к поперечная ось, ориентированная перпендикулярно направлению закрытия (73).

патенты-ВОИС

2 поперечная протяженность (измеряется внутри от борта судна под прямым углом к ​​диаметральной плоскости на уровне самой глубокой грузовой марки деления на отсеки): расстояние, равное одной пятой ширины судна; и.

ЕврЛекс-2

Если расстояние между двумя соседними основными поперечными переборками или их эквивалентными дощатыми переборками, или расстояние между поперечных плоскостей, проходящих через ближайшие уступы переборок, составляет менее 3,0 м плюс 3 % длины судна, или 11,0 м, или 10 % длины судна, в зависимости от того, что меньше , только одна из этих переборок должна рассматриваться как часть деления на отсеки судна.

ЕврЛекс-2

Мощность передается через радиальное электрическое поле и окружное магнитное поле в режиме ТЭМ00 поперечном .

WikiMatrix

Раскрыто оборудование (100) для перемещения транспортного средства, содержащее опорное устройство (1) транспортного средства и движущееся устройство (2), при этом опорное устройство (1) транспортного средства используется для поддержки транспортного средства (С), а движущееся устройство (2) используется для вертикального и в поперечном направлении перемещение опорного устройства (1) для транспортного средства на парковочном месте (C), и, таким образом, план проезда транспортного средства на парковочном месте может быть исключен, чтобы облегчить создание большего количества парковочных мест на парковке пространства одинакового размера, чтобы можно было припарковать больше транспортных средств.

патенты-WIPO

Для того, чтобы найти решение, с помощью которого в токопроводящих элементах достигается более высокая пропускная способность по току, в изобретении предлагается использовать сборную шину (8), содержащую по меньшей мере два первых проводящих элемента (18, 19), по меньшей мере два вторых проводящих элемента (20, 21) и по меньшей мере два третьих проводящих элемента (29, 30), которые расположены между первыми проводящими элементами (18, 19) и вторыми проводящими элементами (20, 21), при этом третьи проводящие элементы (29, 30) выступают за первый и второй проводящие элементы (18, 19, 20, 21) в поперечном направлении относительно продольного направления (22) сборной шины.

патенты-ВОИС

(d) Сквозные действия и мониторинг электронного обучения: около 10% от общего бюджета

ЕврЛекс-2

Листовой материал выполнен таким образом, что граница его поперечного сечения и граница его продольного сечения, хотя бы в одном из сечений, выполнены в виде элементов, различающихся по длине, различных гипербол и/или эллипсов с разными значениями эксцентриситетов и параметров фокуса, и дополнительно содержат сечение, выполненное в виде элементов, отличающихся по длине, из разных гипербол и/или эллипсов с разными значениями эксцентриситетов и параметров фокуса, при этом вышеупомянутый участок границы поперечное сечение и участок границы продольного сечения пересекаются.

патенты-ВОИС

Начало углов геометрической видимости — периметр проекции освещающей поверхности на поперечную плоскость, касательную к передней части рассеивателя фары

Действия поперечной программы

(i) « поперечная шнуровая веревка» означает любую внешнюю или внутреннюю прокладку веревки поперечно по отношению к продольной оси сети в самой задней части кулисы либо вдоль стыка двух верхней и нижней панелей, либо вдоль изгиба единственной задней панели.