Немного о турбулентности
Эта статья будет интересна новичкам, которые хотят больше узнать о турбулентном течении и подводных камнях, встречающихся при его моделировании в программных комплексах. Мы рассмотрим:
-
-
- определение турбулентности
- основные понятия
- подходы к моделированию турбулентных течений
- рекомендации по моделированию турбулентности во FlowVision
-
Введение
Начнем с определения турбулентности П. Брэдшоу:
Турбулентность – это трехмерное нестационарное движение, в котором вследствие растяжения вихрей создается непрерывное распределение хаотических пульсаций параметров потока (скорости, давления и т.д.) в интервале длин волн от минимальных, определяемых вязкими силами, до максимальных, определяемых граничными условиями течения.
Иными словами: турбулентное течение – это поток, движение которого беспорядочно во времени и пространстве.
Как изображал турбулентное течение Леонардо да Винчи
Ламинарное течение, в отличие от турбулентного, упорядочено. Среда в таком течении перемещается слоями, без перемешиваний и пульсаций. На рисунке ниже представлен ламинарно-турбулентный переход в потоке: во время перехода возникают процесы интенсивного перемешивания и вихреобразования.
Изменение характера течения с ламинарного на турбулентное
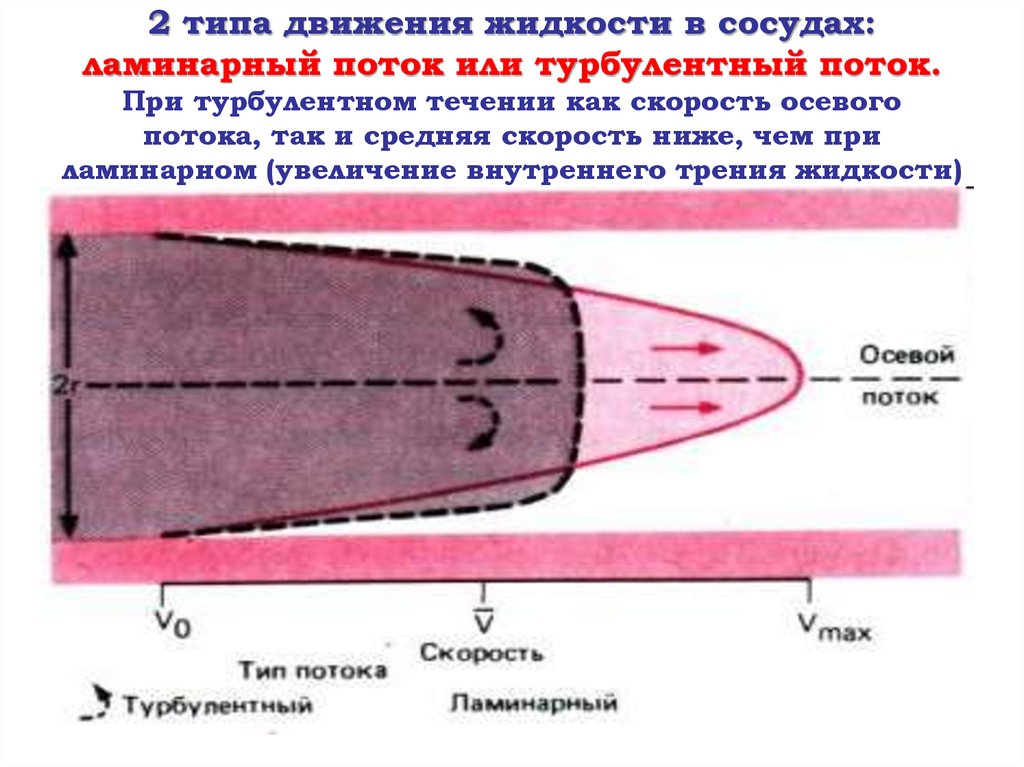
Профили скорости ламинарного и турбулентного потока
Рассмотрим течение в трубе круглого сечения и бесконечной длины.
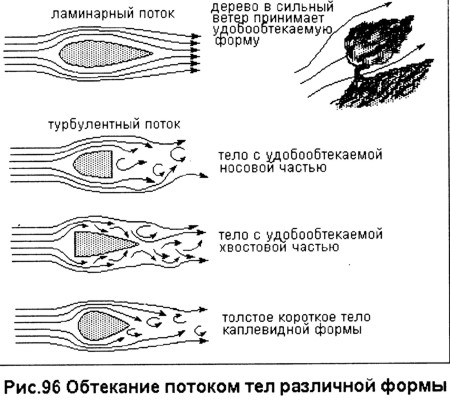
Жан Луи Пуазёйль определил, что ламинарное течение имеет a href=»https://ru.wikipedia.org/wiki/Течение_Пуазёйля&qot; target=»_blan» rel=»noopener»>параболически» профиль скорости. При переходе к турбулентному режиму течения профиль скорости изменяется до некоторого другого вида. Изменения профиля скорости вызваны инерционными силами, действующими на частицы в потоке. Другими словами, профиль скорости турбулентного потока в трубах или каналах характеризуется быстрым возрастанием скорости у стенок и меньшей кривизной в центральной части течения.
Ламинарное течение в трубе Турбулентное течение в трубе
Профили скоростей для ламинарного и турбулентного течения
За исключением тонкого слоя около стенки для турбулентного течения профиль скорости описывается логарифмическим законом (то есть скорость линейно зависит от логарифма расстояния до стенки).
Число Рейнольдса
Обычно, когда говорят о турбулентном течении, сразу вспоминают число Рейнольдса (Re). По сути, это отношение сил инерции к силам вязкого трения.
Здесь ρ — плотность, V — скорость, l — характерный геометрический размер, μ — динамическая вязкость среды (табличное значение).
Для потока, характеризующегося малым числом Рейнольдса, течение, в основном, будет зависеть от вязкостных сил. При высоких числах Рейнольдса влияние инерционных сил преобладает, вследствие чего и возникают завихрения.
Для определения границы между ламинарным и турбулентным течением вводится понятие критического числа Рейнольдса (Reкр):
- Характерное Re < Reкр – течение ламинарное
- Характерное Re > Reкр – течение турбулентное
В целом, можно сказать, что нет фиксированного значения критического числа Рейнольдса. На величину Reкр оказывают влияния такие параметры как (1) степень турбализации внешнего потока, (2) шероховатость поверхности, (3) температура стенки, (4) скорость потока (и связанный с ней градиент давления). Но если нужно оттолкнуться от конкретных численных значений, то можно использовать следующую классификацию:
На величину Reкр оказывают влияния такие параметры как (1) степень турбализации внешнего потока, (2) шероховатость поверхности, (3) температура стенки, (4) скорость потока (и связанный с ней градиент давления). Но если нужно оттолкнуться от конкретных численных значений, то можно использовать следующую классификацию:
- Внутреннее течения (опыты Рейнольдса): Reкр ∈ [2000; 4000]
- Внешнее обтекание: дозвуковым потоком Re
Где в реальной жизни возникают турбулентные течения
Как было отмечено выше, турбулентный поток отличается от ламинарного не только профилем скорости, но и наличием интенсивного вихреобразования. Поэтому явление турбулентности существенно влияет на результаты расчёта и его обязательно нужно учитывать.
Области приложения для турбулентности бесконечны: авиастроение, автомобилестроение, судостроение — моделирование движения воздуха около самолетов/автомобилей/судов, вентиляция и кондиционирование – моделирование потоков воздуха в комнатах, помещениях, вентиляционных шахтах, салонах самолетов и автомобилей; отдельную обширную область представляет биомеханика – моделирование тока крови в камерах сердца, моделирование течения крови вокруг клапанов сердца и т.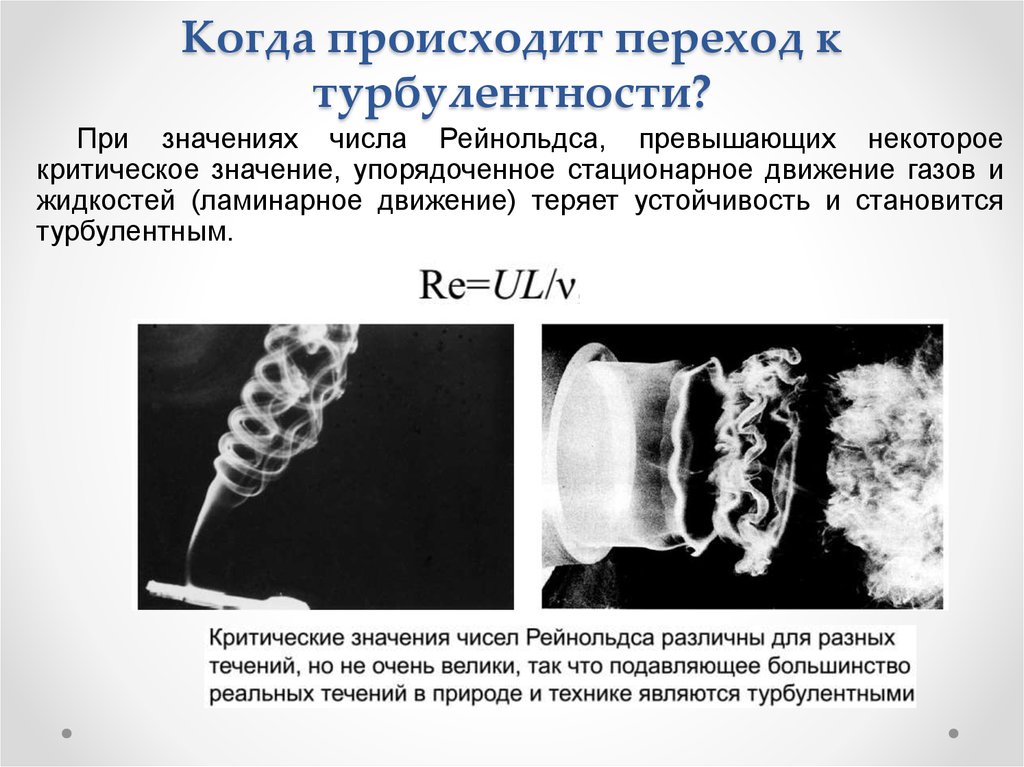 д.
д.
Моделирование турбулентности
Существует три основных подхода для математического описания турбулентного течения:
- Direct Numerical Simulation (DNS) – прямое численное моделирование;
В рамках этого подхода расчёт турбулентных течений происходит путем прямого решения a href=»https://ru.wikipedia.org/wiki/Уравнения_Навье_—_Стокса» target=»_lank» rel=»>уравнений Навье-Сток»а. Для моделирования используются трехмерные нестационарные уравнения, независимо от характера течения. Данный подход требует достаточно точного разрешения расчетной сеткой всех областей, в которых происходит вихреобразование, поэтому его применение ограничивается производительностью вычислительной техники. Шаг сетки в этом случае должен быть порядка Колмогоровского масштаба.
Понятие Колмогоровского масштаба
- Large Eddy Simulation (LES) – моделирование крупных вихрей;
Этот подход занимает промежуточное положение между DNS и RANS подходами. В нем применяется фильтрация характеристик турбулентного течения от коротковолновых неоднородностей – то есть решаются осредненные уравнения Навье-Стокса (как и в RANS), но осреднение происходит по областям с размерами порядка размера фильтра. После проведения процедуры фильтрации, формируется система осредненных уравнений Навье-Стокса, применимая к областям с размерами больше фильтра. Осредненные уравнения замыкаются при помощи «подсеточной» модели турбулентности. При расчёте турбулентного течения с помощью LES подходов вихревые структуры с размерами, превышающими размеры фильтра (расчетной сетки), разрешаются точно, а меньшие вихревые структуры моделируются.
В нем применяется фильтрация характеристик турбулентного течения от коротковолновых неоднородностей – то есть решаются осредненные уравнения Навье-Стокса (как и в RANS), но осреднение происходит по областям с размерами порядка размера фильтра. После проведения процедуры фильтрации, формируется система осредненных уравнений Навье-Стокса, применимая к областям с размерами больше фильтра. Осредненные уравнения замыкаются при помощи «подсеточной» модели турбулентности. При расчёте турбулентного течения с помощью LES подходов вихревые структуры с размерами, превышающими размеры фильтра (расчетной сетки), разрешаются точно, а меньшие вихревые структуры моделируются.
- Reynolds Averaged Navier-Stokes (RANS) – подходы, основанные на осреднении уравнений Навье-Стокса по числу Рейнольдса. Чтобы учесть потерю энергии на вихри, которые не разрешены расчетной сеткой, вводят понятие осредненной скорости (подробнее это описано ниже).
 При осреднении уравнений возникает новая неизвестная – Рейнольдсово напряжение, из-за которой нельзя решить уравнение Навье-Стокса совместно с уравнением неразрывности. Поэтому для замыкания системы уравнений (для определения Рейнольдсового напряжения) дополнительно вводятся модели турбулентности.
При осреднении уравнений возникает новая неизвестная – Рейнольдсово напряжение, из-за которой нельзя решить уравнение Навье-Стокса совместно с уравнением неразрывности. Поэтому для замыкания системы уравнений (для определения Рейнольдсового напряжения) дополнительно вводятся модели турбулентности.
Модель турбулентности — математическая модель, позволяющая описывать с той или иной точностью поведение потока. Применительно к RANS-подходам модель турбулентности — это совокупность дополнительных уравнений, призванных замкнуть систему уравнений Навье-Стокса после того, как её осреднили по Рейнольдсу.
Модели турбулентности отличаются константами, которые заложены в эти модели, а также определением турбулентной вязкости. Константы преимущественно эмпирические и их подбирают под особенности конкретной решаемой задачи. Модели турбулентности могут включать от одного до нескольких замыкающих уравнений и чем больше уравнений, тем больше требуется вычислительных ресурсов.
RANS подход позволяет получить только осредненный поток и описать его, если имеются пульсации скорости вокруг некоторого среднего значения. Такой подход позволяет получать хорошие результаты на грубой сетке. С помощью LES подхода можно разрешить вихри, влияющие на характер течения. Результаты такого расчета будут более точными, однако потребутся большее число расчетных ячеек и меньший шаг по времени. Для разрешения всех вихрей и пульсаций необходимо решать задачу напрямую (
Разница подходов на примере графика скорости потока
Основные понятия
Диссипация энергии
Перенос энергии в турбулентном потоке происходит каскадным образом: энергия поступает от осредненного потока к наиболее крупным вихрям и далее последовательно передается всё более и более мелким вихревым структурам.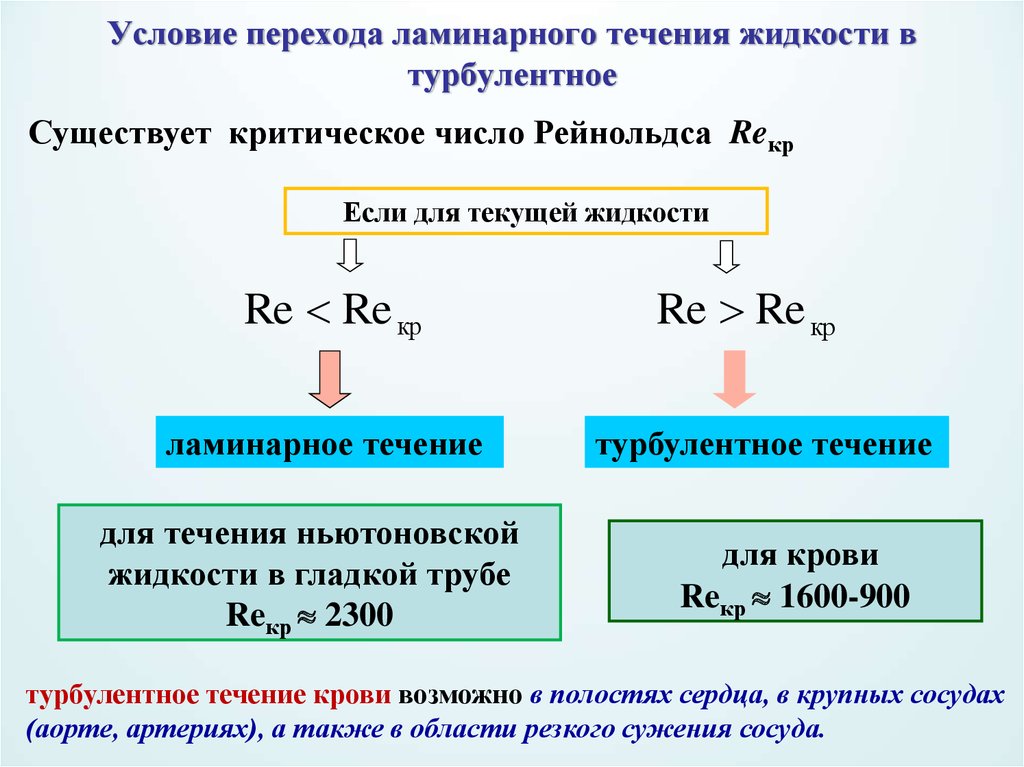 В итоге она доходит до сверхмаленьких вихрей (имеющих Колмогоровские масштабы). Они диссипируют кинетическую энергию и передают её в тепловое состояние.
В итоге она доходит до сверхмаленьких вихрей (имеющих Колмогоровские масштабы). Они диссипируют кинетическую энергию и передают её в тепловое состояние.
Каскадный перенос энергии в потоке
Пульсации
Переход от ламинарного к турбулентному течению характеризуется вихреобразованием. Результатом хаотического движения частиц, участвующих в турбулентном перемешивании, являются пульсации их скорости. Поэтому при использовании RANS-подхода к моделированию турбулентности проекции скорости можно разделить на среднюю составляющую и пульсационную добавку:
Пульсационное движение частиц, в свою очередь, является источником пульсации давления, температуры, плотности. Мерой интенсивности пульсации служит степень турбулентности потока.
Перенос импульса, идущий через вихри, учитывается за счет добавочной турбулентной вязкости. Если подставить выражения для осредненных скоростей в уравнение Навье-Стокса и преобразовать, то в итоге некоторые члены обнулятся, но останется произведение средних и произведение пульсационных составляющих.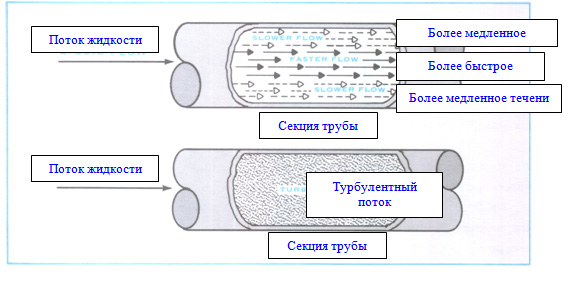 Произведение пульсационных составляющих – новая неизвестная – носит название Рейнольдсово напряжение, из-за которой нельзя решить уравнение Навье-Стокса вместе с уравнением неразрывности. Поэтому систему уравнений нужно замыкать.
Произведение пульсационных составляющих – новая неизвестная – носит название Рейнольдсово напряжение, из-за которой нельзя решить уравнение Навье-Стокса вместе с уравнением неразрывности. Поэтому систему уравнений нужно замыкать.
Для этого была введена гипотеза Бусинеска: рассматривать Рейнольдсово напряжение примерно так же, как и напряжения на трение, которые связаны с вязкостью, т.е. как некую вязкость, умноженную на деформацию потока. Поэтому появляется новая переменная — турбулентная вязкость, которая дает возможность учитывать дополнительный интегральный эффект от вихрей, хотя они и не разрешаются сеткой.
кинетическая энергия турбулентности
Понятие кинетической энергии турбулентности (k) введено Прандтлем и является, по сути, удельной кинетической энергией вихрей в турбулентном потоке или среднеквадратичной пульсацией скорости.
Прандтль заметил, что если рассмотреть пульсацию по оси у в потоке, который идет турбулентными слоями с вихрями, то она такая же, как и по оси х. Вихрь может изменять свой градиент по скоростям и пропорционален масштабу турбулентности. В качестве масштаба турбулентности было предложено рассматривать длину пути перемешивания вихря.
Вихрь может изменять свой градиент по скоростям и пропорционален масштабу турбулентности. В качестве масштаба турбулентности было предложено рассматривать длину пути перемешивания вихря.
взаимодействие потока со стенкой — Что такое Y
+Если рассмотреть картину снимков течения рядом со стенкой, то оно похоже на ламинарное — все движется слоями, далее появляются вихри, их количество увеличивается и в ядре потока наблюдается уже турбулентное течение.
Рассматривая координату удаления от стенки в координатах (x,y), можно видеть различные области пограничного слоя. В нем выделяют:
- вязкий подслой, где наблюдается абсолютно ламинарное течение.
- буферный слой — зона перемешивания, где начинает оказывать влияние число Рейнольдса и появляется турбулентный поток.
- турбулентное ядро (инерционный слой и верхний слой ПС) — развитие турбулентного слоя, где силы вязкости и влияние стенки уже незначительны.
Схема расположение слоёв в пограничном слое
Рассматривая профиль скорости в безразмерных координатах, можно определить ряд величин, описывающих течение в пограничном слое:
- безразмерная скорость, равная отношению локальной скорости к динамической, определяемой только касательным напряжением на стенке.

безразмерная скорость: динамическая скорость:
- безразмерная координата Y+ — расстояние до стенки приведенное к безразмерному значению за счёт скорости динамического трения. Параметр Y+ можно рассматривать как локальное число Рейнольдса в ячейке.
безразмерное расстояние до стенки:
Если центр первой ячейки находится в зоне, где Y+< 5, то речь идет про вязкий подслой, то течение ламинарное — профиль представляет собой параболу и в логарифмических координатах также парабола. Если 5 < Y
Два подхода к моделированию
Высокорейнольдсовый подход
Характеризуется тем, что пристеночная область плохо разрешена сеткой и центр первой ячейки не попадает ни в вязкий, ни в буферный подслой (Y+ > 5).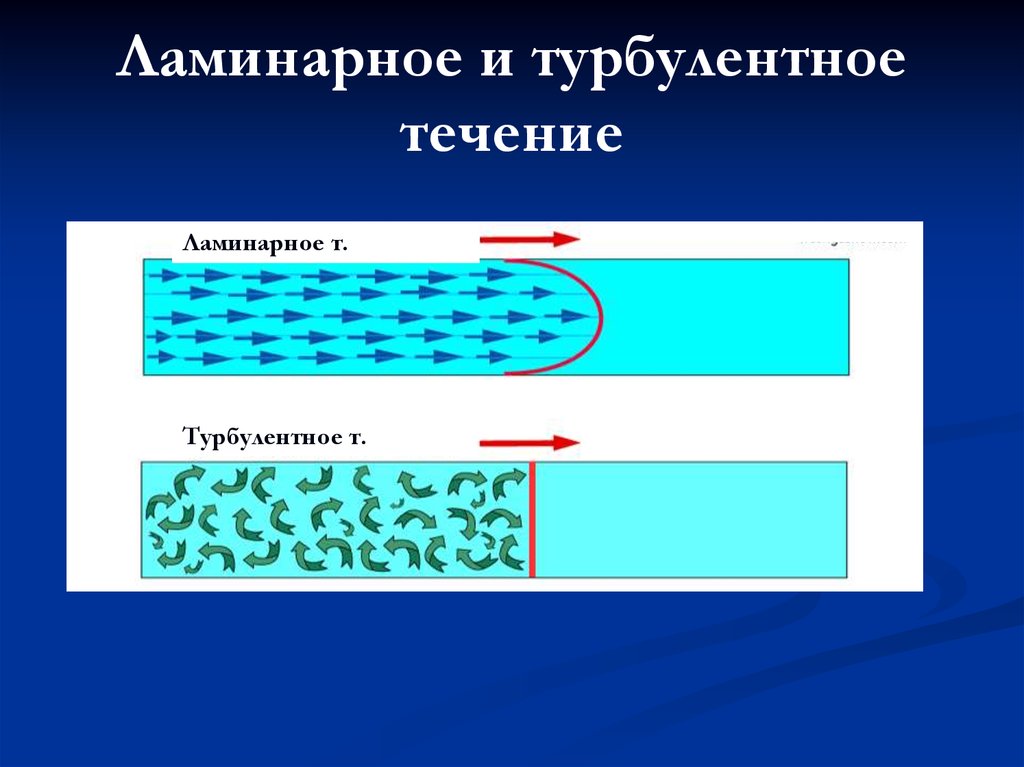 В этом случае построена относительно грубая сетка и не известно, что происходит в области пограничного слоя. Тогда для расчета пристеночного течения применяются пристеночные функции.
В этом случае построена относительно грубая сетка и не известно, что происходит в области пограничного слоя. Тогда для расчета пристеночного течения применяются пристеночные функции.
Разрешение потока крупной расчетной сеткой. Точкой показан центр первой ячейки
Пристеночные функции — это некоторые эмпирические и полу-эмпирические зависимости, призванные определить профиль скорости в пристеночном слое.
Во FlowVision реализованы 2 модели пристеночных функций: WFFV (Wall Function FlowVision) и WFS (Wall Function Standard). Подробнее о пристеночных функциях здесь.
Низкорейнольдсовый подход
Реализуется в том случае, если центр первой ячейки лежит внутри пограничного слоя. В этом случае пристеночная область разрешена сеткой (Y+ < 1), центр первой ячейки заведомо находится в ламинарной зоне. В таком случае следует отказаться от применения пристеночных функций, потому что в центре каждой ячейки профиль скорости строится за счёт численного решения.
Разрешение потока мелкой расчетной сеткой у стенки
Моделирование турбулентности во FlowVision
Модели турбулентности FlowVision
Во FlowVision реализованы 7 разных моделей турбулентности. Для своих задач Вы можете использовать одну из них:
- KES (k-ε) – стандартная модель турбулентности. Её применение возможно только в высоко-рейнольдсовых расчётах (на относительно грубой сетке с пристеночными функциями).
- KEAKN (Abe, Kondoh, Nagano) – низкорейнольдсовая модель, которую рекомендуется использовать в низко-рейнольдсовых расчётах (на сетке, разрешающей вязкий подслой около стенки, без пристеночных функций).
- KEFV – модернизированная разработчиками FlowVision k-ε модель. KEFV модель можно использовать как в низко-рейнольдсовых, так и в высоко-рейнольдсовых расчетах. В первом случае ламинарный подслой разрешается сеткой (пристеночные функции не используются), во втором случае ламинарный подслой не разрешается (используются пристеночные функции).
 Данная модель удовлетворительно предсказывает положение ламинарно-турбулентного перехода на твердой поверхности. В низко-рейнольдсовых расчетах необходимо задавать турбулентность набегающего потока.
Данная модель удовлетворительно предсказывает положение ламинарно-турбулентного перехода на твердой поверхности. В низко-рейнольдсовых расчетах необходимо задавать турбулентность набегающего потока. - KEQ (квадратичная модель) — наиболее полная, но и наиболее «капризная» из всех моделей. В ней рассматривается особый элемент — элемент тензора завихренности. Данная модель применяется для особо закрученных завихренных потоков, за обратным уступом и может использоваться только в высоко-рейнольдсовых расчетах.
- SST (модель Ментера) — известна тем, что сочетает в себе и k-ε модель и k-ω модель, которая разработана для подходов разрешения пристенной области. В этой модели появляется новое значение — ω — удельная диссипация вихрей. В пристеночной области для этой модели решаются уравнения k-ω модели, а в области, удаленной от стенки – уравнения k-ε модели.

- SA (модель Спаларта-Аллмареса) — однопараметрическая модель, которая была разработана для аэрокосмических приложений. Дает хорошие результаты для пограничных слоев, характеризующихся положительными градиентами давлений. Может быть применена как в как в низко-рейнольдсовых, так и в высоко-рейнольдсовых расчетах. Традиционно эта модель эффективно работает в низкорейнольдсовом случае.
- Sm (модель Смагоринского) — алгебраическая модель, не требующая решения конвективно-диффузионных уравнений. Sm модель можно использовать только в низко-рейнольдсовых расчетах на хорошей мелкой сетке.
Задание входной турбулентности во FlowVision
Для учёта турбулентности во FlowVision, необходимо во вкладке Фазы задать физический процесс Турбулентность, выбрав одну из предложенных моделей турбулентности.
Выбор модели турбулентности в физических процессах
В качестве начальных условий (Препроцессор > Модели > Нач. данные) по турбулентности задаются пульсации и масштаб турбулентности. Эти параметры определяют степень турболизации потока.
данные) по турбулентности задаются пульсации и масштаб турбулентности. Эти параметры определяют степень турболизации потока.
Пульсации: Масштаб турбулентности:
Формулы для вычисления входных параметров пульсаций и масштаба турбулентности
Подробнее о задании входной турбулентности читайте в этой статье блога.
На граничных условиях при турбулентном течении задаются определяющие параметры: ТурбЭнергия и ТурбДиссипация. ТурбЭнергию можно задать как пульсации: ТурбЭнергия = Пульсации. А ТурбДиссипацию, как масштаб турбулентности: ТурбДиссипация = Масштаб турбулентности.
Рекомендации для применения пристеночных функций во FV
Рекомендации по использованию пристеночных функций во FV определяется величиной Y+. Исходя из нее можно сформулировать рекомендации по применению моделей турбулентности и пристеночных функций. Однако, необходимо учитывать, что границы применимости моделей для разных задач могут изменяться.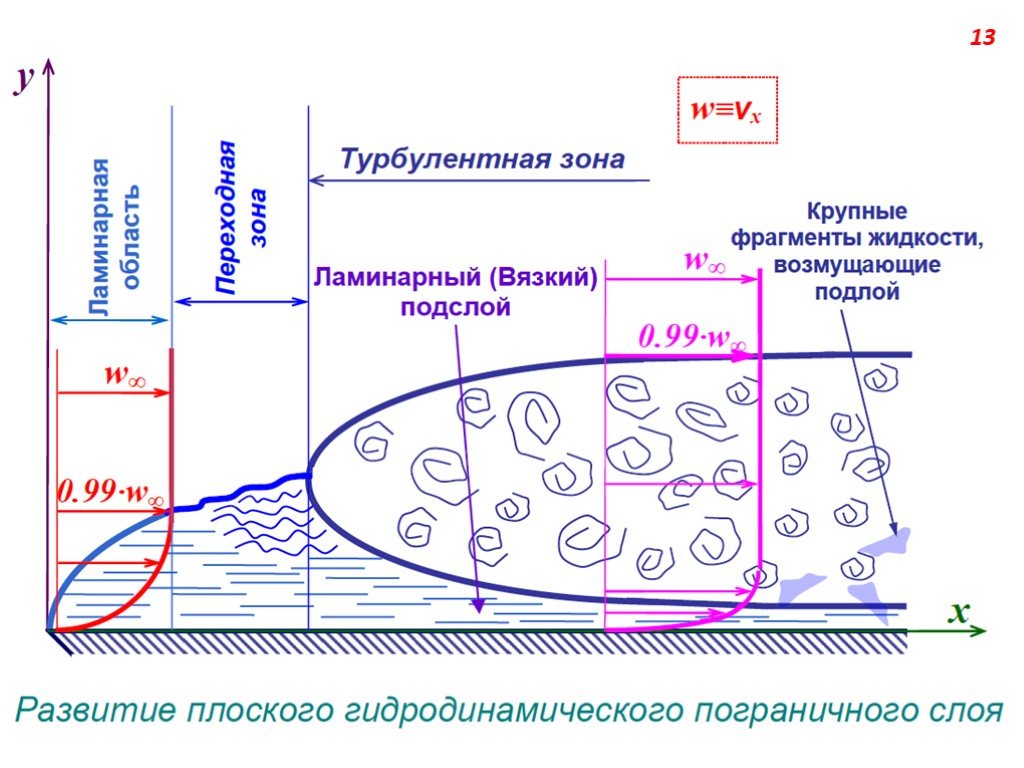
По умолчанию в интерфейсе FV задаются равновесные пристеночные функции WFFV.
Турбулентный режим движения жидкости
—
Движение жидкости, наблюдаемое при больших скоростях, называют турбулентный режим движения жидкости. В этом случае в движении жидкости нет видимой закономерности. Отдельные частицы перемешиваются между собой и движутся по самым причудливым все время меняющимся траекториям весьма сложной формы.
В этой статье подробно описывается процесс турбулентного режима, переход в турбулентный режим из ламинарного, формула и закон этого режима и многое другое.
Содержание статьи
- Турбулентный режим движения в опытах
- Переход ламинарного режима течения в турбулентный
- Формула турбулентного режима течения
- Видео режима течения
Для более конкретного представления турбулентного режима движения жидкости рассмотрим опыт Рейнольдса. Подробное описание здесь.
При добавлении краски в поток жидкости движущейся с небольшой скоростью красная краска будет двигаться ровной струйкой.
При увеличении скорости потока движение частиц так же увеличится. Струйка краски будет колебаться как на указано на рисунке.
При открытии крана и увеличении расхода через трубку, поток краски будет всё более интенсивнее перемешиваться с основным потоком жидкости, образуя всё больше вихрей.
Несмотря на кажущуюся беспорядочность движения частиц и изменения их скорости, величина средней скорости в достаточно большом промежутке времени остается постоянной.
Турбулентный режим движения жидкости всегда характеризуется пульсация скоростей. Под действием пульсации частицы жидкости, движущиеся в главном (осевом) направлении потока, получают, кроме того, так же и поперечные перемещения, вследствие чего между соседними слоями жидкости возникает обмен частицами, вызывающими непрерывное перемешивание жидкости.
Однако у стенок, ограничивающих поток, имеют место совсем иные, особые условия для движения жидкости. Наличие твердых границ делает поперечные движения частиц невозможными.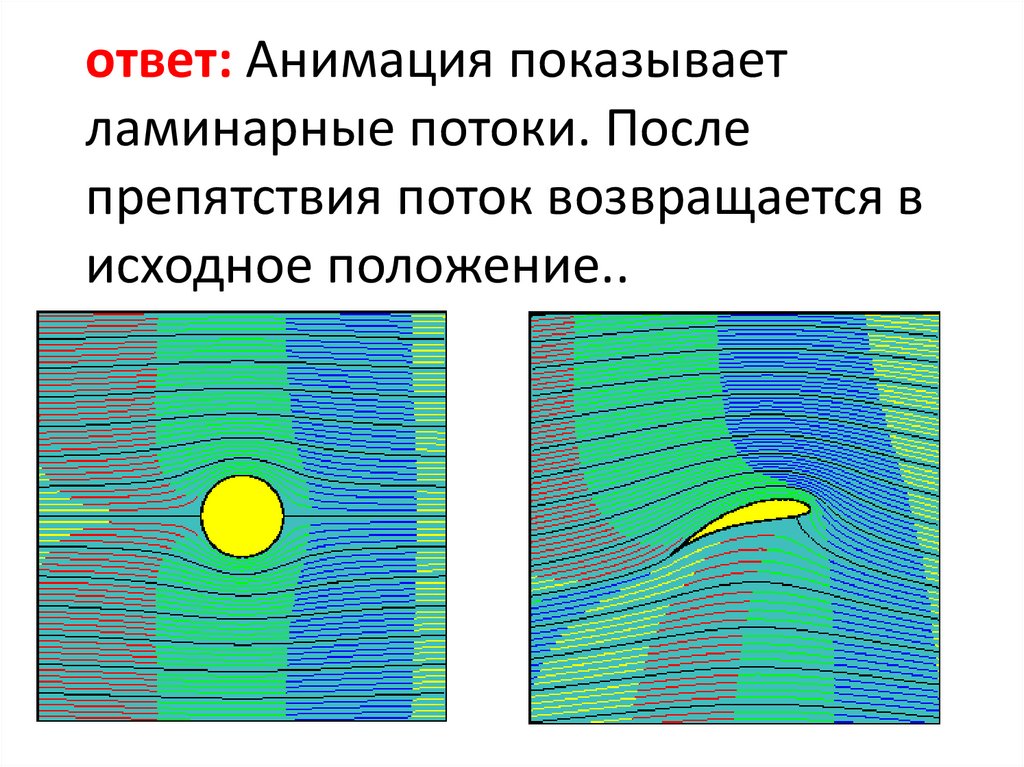 Поэтому перемешивание жидкости здесь не происходит и частицы движутся по извилистым траекториям, почти параллельно стенкам.
Поэтому перемешивание жидкости здесь не происходит и частицы движутся по извилистым траекториям, почти параллельно стенкам.
Переход ламинарного режима в турбулентный
Все выше описанное позволяет установить следующую схему движения потока жидкости, обычно и принимаемую за основную рабочую схему при исследовании турбулентного режима.
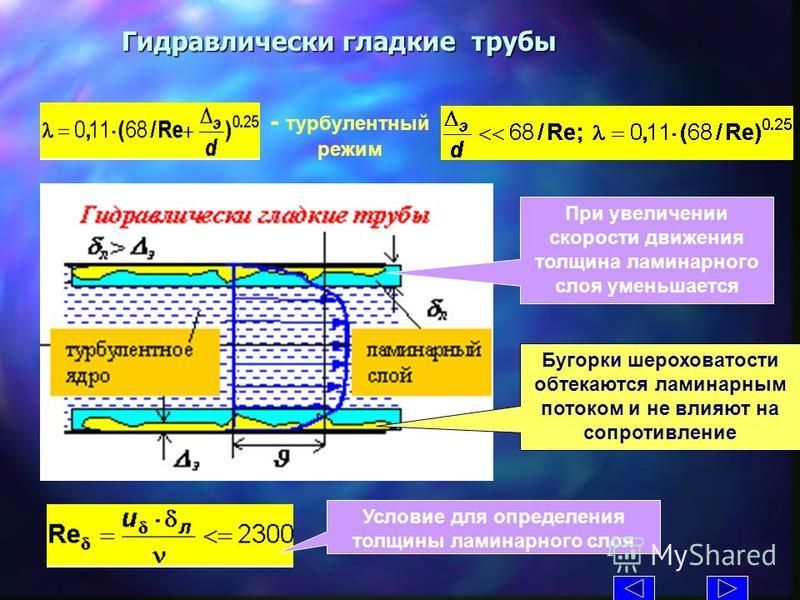
По этой схеме у стенок образуется весьма тонкий слой, в котором движение жидкости происходит по законам ламинарного режима. Основная же центральная часть потока (ядро), связанная с этим слоем, называемым вязким (или ламинарным) подслоем, короткой переходной зоной, движется турбулентно с почти одинаковой для всех частиц жидкости средней скоростью.
Наличие вязкого (ламинарного) подслоя доказано экспериментально в результате весьма тщательных и точных измерений. Толщина этого слоя очень мала и обычно определяется долями миллиметра. Она зависит от числа Рейнольдса, и тем меньше, чем больше это число, т.е. чем больше турбулентность потока.
При значениях Re < 100 000 толщину вязкого подслоя в трубе круглого сечения можно определить по следующей формуле:
δ = 62,8 * d * Re-0,875
где d – диаметр трубы.
Из чего следует, что движение жидкости при турбулентном режиме течения должно всегда происходить со значительно большей затратой энергии, чем при ламинарном.
При ламинарном режиме энергия расходуется только на преодоление сил внутреннего трения между движущимися с различной скоростью соседними слоями жидкости. При турбулентном режиме, кроме этого, значительная энергия затрачивается на процесс перемешивания, вызывающий в жидкости дополнительные касательные напряжения.
Формула турбулентного режима течения
В старых теориях о турбулентном режиме принималось, что у стенок, ограничивающих поток, образуется некоторый неподвижный слой, по которому со значительными скоростями движется вся остальная масса жидкости.
Наличие этого неподвижного слоя с неизбежностью приводило к неправдоподобным выводам о “разрыве” скоростей, т.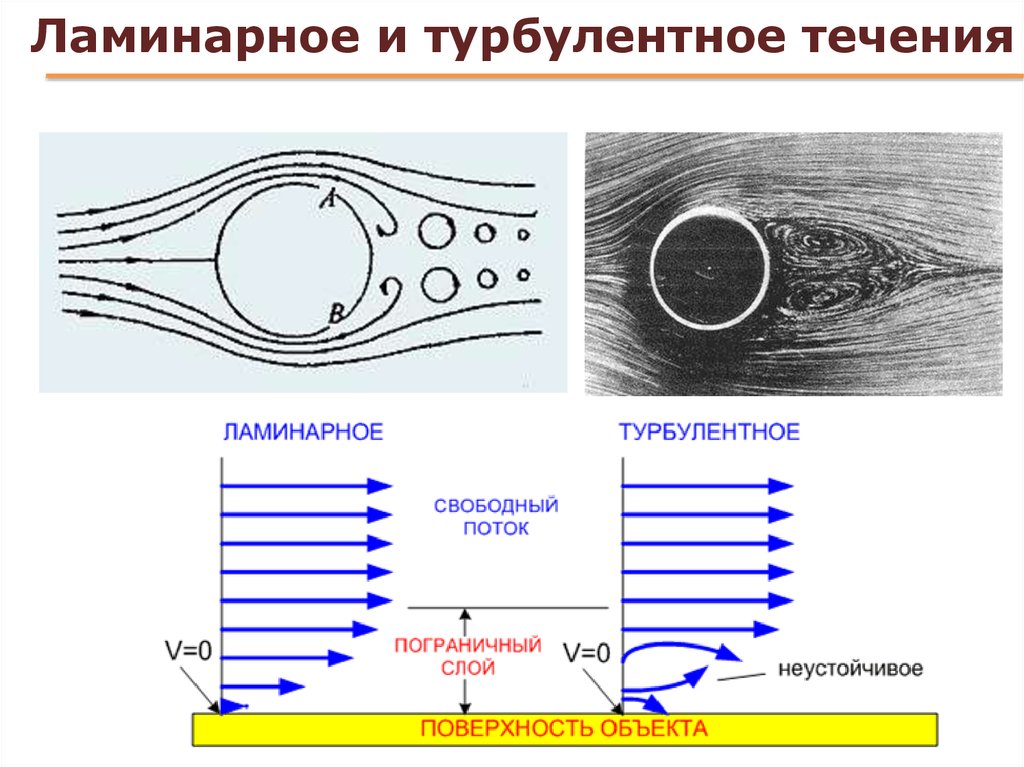 е. к такому закону распределения скоростей в поперечном сечении, при котором имеет место внезапное скачкообразное изменение скорости от нуля в неподвижном слое до конечной величины в остальной части потока.
е. к такому закону распределения скоростей в поперечном сечении, при котором имеет место внезапное скачкообразное изменение скорости от нуля в неподвижном слое до конечной величины в остальной части потока.
Современные теории турбулентного режима течения исходят из схемы Л. Прандтля, который установил теоретический закон распределения скоростей в поперечном сечении потока.
По этому закону скорость в какой-нибудь точке сечения, например цилиндрической трубы, на расстоянии y от ее оси определяется формулой.
где υ0 – осевая скорость
r – радиус трубы
χ — числовой коэффициент, определяемый опытным путем
υ* — динамическая скорость, определяется по формуле
Для практического применения применяют выведенные из указанной выше формулы.
Для гладких труб
Для шероховатых труб
Для того, чтобы в трубе установилось распределение скоростей, соответствующее турбулентному режиму, жидкость должна пройти от входного сечения трубы некоторый определенный участок, называемый начальным участком турбулентного режима.
Длина этого участка определяется по формуле
Lнач = 0,639*Re0.25 * d
Где d – диаметр трубы
Re – число Рейнольдса
Высказанные таким образом соображения о механизме движения и распределении скоростей в турбулентном потоке подтверждаются большим числом опытных данных. Из их рассмотрения следует, что при турбулентном режиме, как и нужно было ожидать, скорости распределяются по сечению более равномерно, чем при ламинарном режиме.
Для иллюстрации этого положения приведена картинка с нарисованными на ней кривыми распределения скоростей для потока жидкости в цилиндрической трубе при турбулентном режиме(сплошная линия) и при ламинарном режиме (пунктир).
При турбулентном режиме отношение средней скорости к максимальной осевой υср / υ0 изменяется от 0,75 до 0,90, в то время как при ламинарном режиме это отношении равно 0,5.
При этом следует иметь ввиду, что чем больше число Рейнольдса, т.е. чем интенсивнее происходит процесс перемешивания жидкости, тем больше будет это соотношение.
Видео по теме
Турбулентность наступает после превышения некоторого критического значения числа Рейнольдса, но в некоторых случаях она может возникнуть самопроизвольно.
Например, в случае перепада давления когда соседние области потока движутся рядом или проникают одна в другую, при воздействии силы тяжести или когда жидкая среда обтекает непроницаемую поверхность.
Вместе со статьей «Турбулентный режим движения жидкости» читают:
Что такое турбулентный поток? Вычислительная гидродинамика
В гидродинамике турбулентный режим относится к нерегулярным потокам, в которых возникают завихрения, завихрения и неустойчивость потока. Он определяется конвекцией с большим импульсом и диффузией с низким импульсом. Он отличается от ламинарного режима, когда жидкость течет параллельными слоями без разрыва между слоями. Режим турбулентности чрезвычайно част в природных явлениях и в приложениях человека; некоторые примеры — подъем сигаретного дыма, водопады, кровоток в артериях и большая часть земной атмосферной рециркуляции. С точки зрения человеческого применения, турбулентный режим возникает в аэродинамике транспортных средств, а также во многих промышленных применениях, таких как теплообменники, процессы закалки или непрерывная разливка стали. 9{й}\) век. Рейнольдс показал переход между ламинарным и турбулентным режимами с помощью ряда экспериментальных исследований. Он также предположил, что этот переход напрямую связан с соотношением между инерционными и вязкими силами. Это отношение было вычислено Джорджем Габриэлем Стоуксом в 1851 году и было названо «числом Рейнольдса» в честь Осборна Рейнольдса, который его популяризировал. Это безразмерное число определяется как:
С точки зрения человеческого применения, турбулентный режим возникает в аэродинамике транспортных средств, а также во многих промышленных применениях, таких как теплообменники, процессы закалки или непрерывная разливка стали. 9{й}\) век. Рейнольдс показал переход между ламинарным и турбулентным режимами с помощью ряда экспериментальных исследований. Он также предположил, что этот переход напрямую связан с соотношением между инерционными и вязкими силами. Это отношение было вычислено Джорджем Габриэлем Стоуксом в 1851 году и было названо «числом Рейнольдса» в честь Осборна Рейнольдса, который его популяризировал. Это безразмерное число определяется как:
$$ Re = \frac{\rho ud}{\mu}=\frac{ud}{\nu} \tag{1}$$
где:
- \(\rho\) плотность жидкости
- \(u\) — макроскопическая скорость потока
- \(d\) — характеристическая длина (или гидравлический диаметр)
- \(\mu\) — динамическая вязкость жидкости
- \(\nu\) — кинематическая вязкость жидкости.
Турбулентные потоки возникают, когда \(Re\) превышает определенный порог (зависящий от топологии приложения и физики потока), называемый «критическим числом Рейнольдса». 91\)
Этот принцип был мотивирован энергетическими соображениями; большие водовороты очень инерционны и имеют тенденцию быть неустойчивыми. Их движение питает более мелкие водовороты благодаря локальной передаче кинетической энергии. Эти меньшие вихри подвергаются тому же процессу, порождая еще меньшие вихри, которые наследуют энергию своего родительского вихря, и так далее. Этот перенос энергии обычно называют «энергетическим каскадом», и он в основном инерционный, поэтому почти не происходит рассеяния энергии до тех пор, пока не будет достигнут достаточно малый масштаб длины, так что вязкость жидкости может эффективно рассеивать кинетическую энергию. Этот последний масштаб турбулентности имеет локальный ламинарный режим и характеризуется низким значением \(Re\). Этот процесс изображен на рис.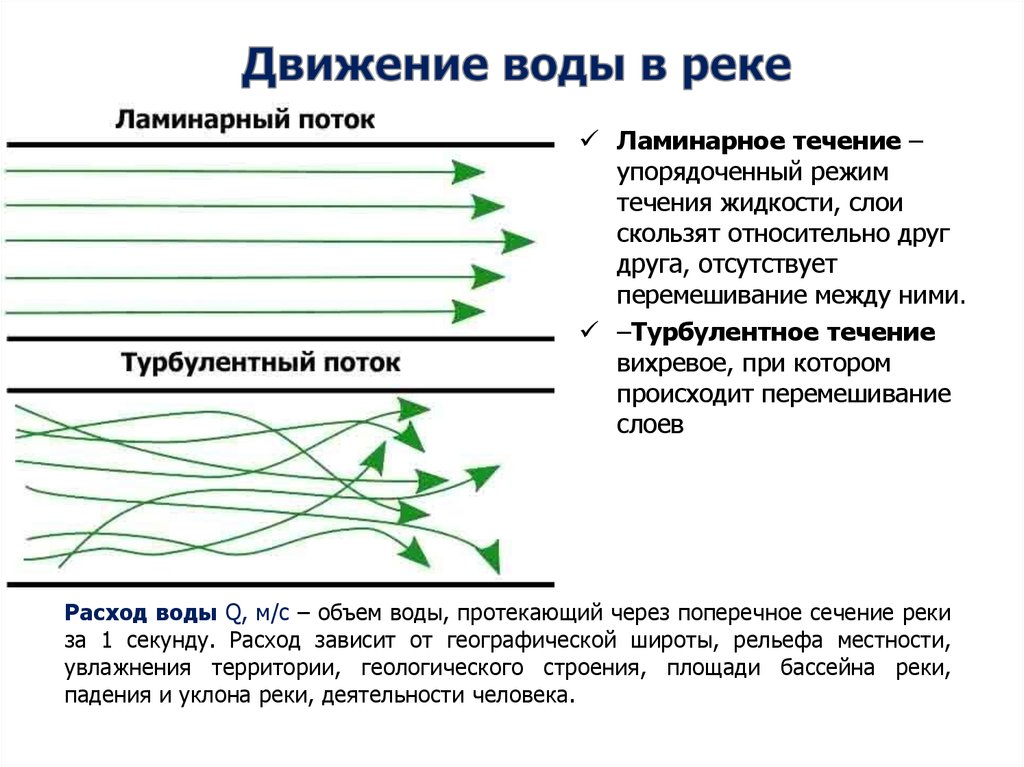 1. Исследования Ричардсона подчеркивают важную особенность турбулентных течений: они требуют много энергии. Турбулентный поток будет рассеивать энергию и превращаться в ламинарный поток, если только он не питается от внешнего источника энергии. 92\). Колмогоров постулировал, что при достаточно большом числе Рейнольдса мелкомасштабные вихри изотропны, тогда как крупные вихри могут быть анизотропными (или, во всяком случае, в зависимости от топологии конкретной области). Это допущение очень важно, поскольку оно означает, что статистический анализ малых вихрей не зависит от какой-либо конкретной геометрии и, таким образом, является универсальным для всех турбулентных течений. В соответствии с этой гипотезой Колмогоров статистически описал основные характеристики наименьшего масштаба турбулентности (известного как «микромасштабы Колмогорова») следующим образом: 9{0,25}\)
1. Исследования Ричардсона подчеркивают важную особенность турбулентных течений: они требуют много энергии. Турбулентный поток будет рассеивать энергию и превращаться в ламинарный поток, если только он не питается от внешнего источника энергии. 92\). Колмогоров постулировал, что при достаточно большом числе Рейнольдса мелкомасштабные вихри изотропны, тогда как крупные вихри могут быть анизотропными (или, во всяком случае, в зависимости от топологии конкретной области). Это допущение очень важно, поскольку оно означает, что статистический анализ малых вихрей не зависит от какой-либо конкретной геометрии и, таким образом, является универсальным для всех турбулентных течений. В соответствии с этой гипотезой Колмогоров статистически описал основные характеристики наименьшего масштаба турбулентности (известного как «микромасштабы Колмогорова») следующим образом: 9{0,25}\)
RANS
Обычно считается (но не доказано), что уравнения Навье-Стокса (НС) могут моделировать любые течения, включая турбулентные.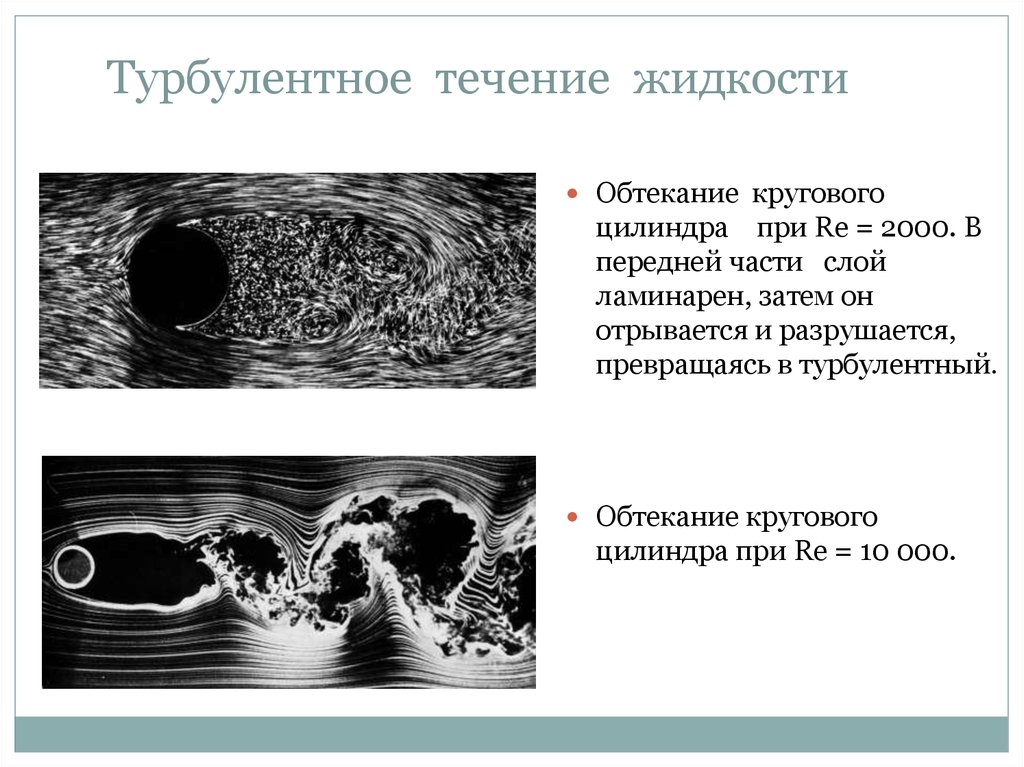 3\). Рассмотрим уравнение Навье-Стокса для несжимаемой ньютоновской жидкости: 9Tu\: dt \tag{4}$$
3\). Рассмотрим уравнение Навье-Стокса для несжимаемой ньютоновской жидкости: 9Tu\: dt \tag{4}$$
таким образом, скорость можно разложить как:
$$ u_i=U_i+u’_i \tag{5}$$
где \(U\) средняя скорость, а \(и’\) — скорость турбулентного потока (или турбулентные масштабы). \(T\) — это временной масштаб усреднения, который должен быть достаточно мал, чтобы иметь хорошее приближение к задаче, но также и достаточно большим, чем временной масштаб турбулентности, т. е. время колмогоровского оборота. Подставляя усредненные величины в уравнение Навье-Стокса, получаем уравнения RANS:
$$ \rho U_j U_{i,j} =-\rho P_{i} +\mu U_{i,jj} -\left( u_{i}’ u_{j}’\right) _j \tag {6}$$
$$ U_{i,i}=0 \tag{7}$$
, где \(\left( u_{i}’ u_{j}’\right) _j\) обычно называется «напряжением Рейнольдса» и отражает влияние мелкомасштабной турбулентности на средний поток. Уравнения RANS не имеют единственного решения, потому что они не имеют близкой формы, а неизвестных больше, чем уравнений. Таким образом, для закрытия задачи необходимы дополнительные уравнения. Наиболее распространенная стратегия, используемая в CFD, заключается в том, чтобы связать напряжение Рейнольдса со скоростью сдвига соотношением Буссинеска: 94\).
Таким образом, для закрытия задачи необходимы дополнительные уравнения. Наиболее распространенная стратегия, используемая в CFD, заключается в том, чтобы связать напряжение Рейнольдса со скоростью сдвига соотношением Буссинеска: 94\).
RANS, LES и DES
SimScale предлагает моделирование с различными моделями турбулентности на выбор из семейства RANS, LES, DES. Выберите учетную запись Community или Professional и начните моделирование.
Применения
Турбулентные потоки присутствуют во многих природных явлениях (например, речные потоки, атмосферные потоки, естественная конвекция) и человеческих приложениях (например, ветровой поток в городе, аэродинамический анализ, непрерывное литье, процесс закалки, системы охлаждения/обогрева) ).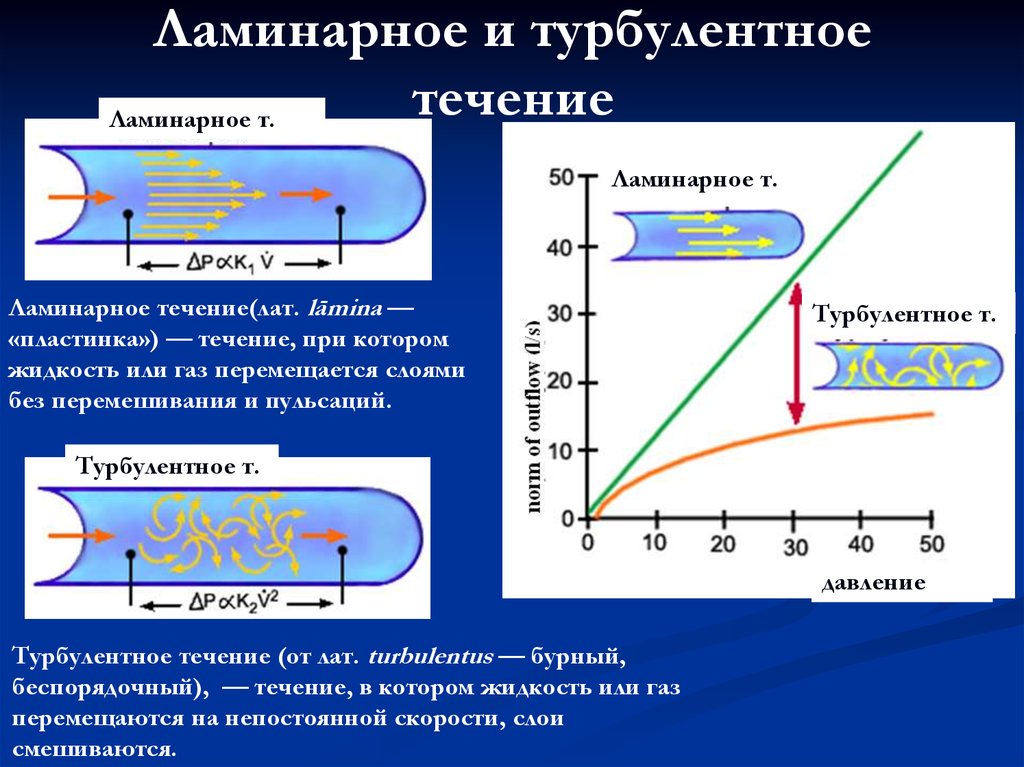 В этом разделе сообщалось о двух небольших приложениях, созданных с использованием SimScale. Первый (рис. 2) представляет собой анализ обтекания цилиндра. Случай может быть применен к течению реки вокруг колонны моста, но он также имеет большое академическое значение, поскольку является широко используемым эталоном для проверки. Кроме того, он часто используется для отображения различных режимов (связанных с наличием, размером и частотой вихрей) при различных конфигурациях задачи.
В этом разделе сообщалось о двух небольших приложениях, созданных с использованием SimScale. Первый (рис. 2) представляет собой анализ обтекания цилиндра. Случай может быть применен к течению реки вокруг колонны моста, но он также имеет большое академическое значение, поскольку является широко используемым эталоном для проверки. Кроме того, он часто используется для отображения различных режимов (связанных с наличием, размером и частотой вихрей) при различных конфигурациях задачи.
. Второй случай — аэродинамический анализ мотоцикла с водителем (рис. 3). Высокие скорости и низкая вязкость воздуха способствуют развитию турбулентного режима, даже если его максимально избегать, чтобы уменьшить сопротивление, связанное с отрывом вихрей позади транспортного средства.
Рисунок 3: Контурный график скорости воздуха вокруг мотоцикла. Такие элементы, как шлем или спицы колеса, значительно увеличивают турбулентность и, следовательно, сопротивление, если их не учитывать.
Такие элементы, как шлем или спицы колеса, значительно увеличивают турбулентность и, следовательно, сопротивление, если их не учитывать.Ссылки
- Ричардсон, Л. Ф. Прогноз погоды с помощью численного процесса (Cambridge Univ. Press, 1922)
- https://micropore.wordpress.com/2010/08/21/kolmogorov-originl-paper-on- турбулентность/
- https://web.stanford.edu/class/me469b/handouts/turbulence.pdf
- https://www.cfd-online.com/Wiki/Turbulence_modeling
Последнее обновление: 27 декабря 2022 г.
Эта статья решила вашу проблему?
Как мы можем сделать лучше?
Мы ценим и ценим ваши отзывы.
Что дальше
Что такое подъемная сила, сопротивление и тангаж?
Ламинарный поток и турбулентный поток
🕑 Время считывания: 1 минута
Жидкость, протекающая по закрытому каналу, такому как труба или между двумя плоскими пластинами, представляет собой либо ламинарный, либо турбулентный поток, в зависимости от скорости, размера трубы (или от число Рейнольдса) и вязкость жидкости.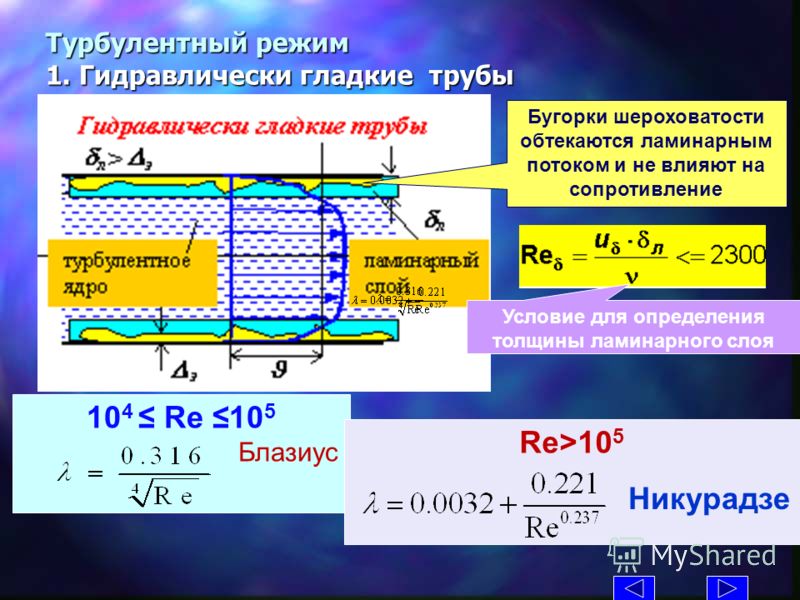
Содержание:
- Ламинарный поток
- Турбулентный поток
- Разница между ламинарным и турбулентным потоком
- Как избежать турбулентного потока?
- Часто задаваемые вопросы
Ламинарный поток
Ламинарный поток — это движение частиц жидкости по четко определенным путям или линиям тока, где все линии тока прямые и параллельные. Следовательно, частицы движутся ламинарно или слоями, плавно скользя по соседнему слою.
Ламинарный поток возникает в трубах малого диаметра, в которых жидкость течет с более низкими скоростями и высокой вязкостью. Этот тип течения также называют обтекаемым течением или вязким течением.
Ламинарный поток подразделяется на:
- Однонаправленный ламинарный поток
- Пульсирующий ламинарный поток
- Колебательный ламинарный поток
Типичными примерами ламинарного потока являются поток масла по тонкой трубке, поток крови по капиллярам прямой путь от ароматической палочки.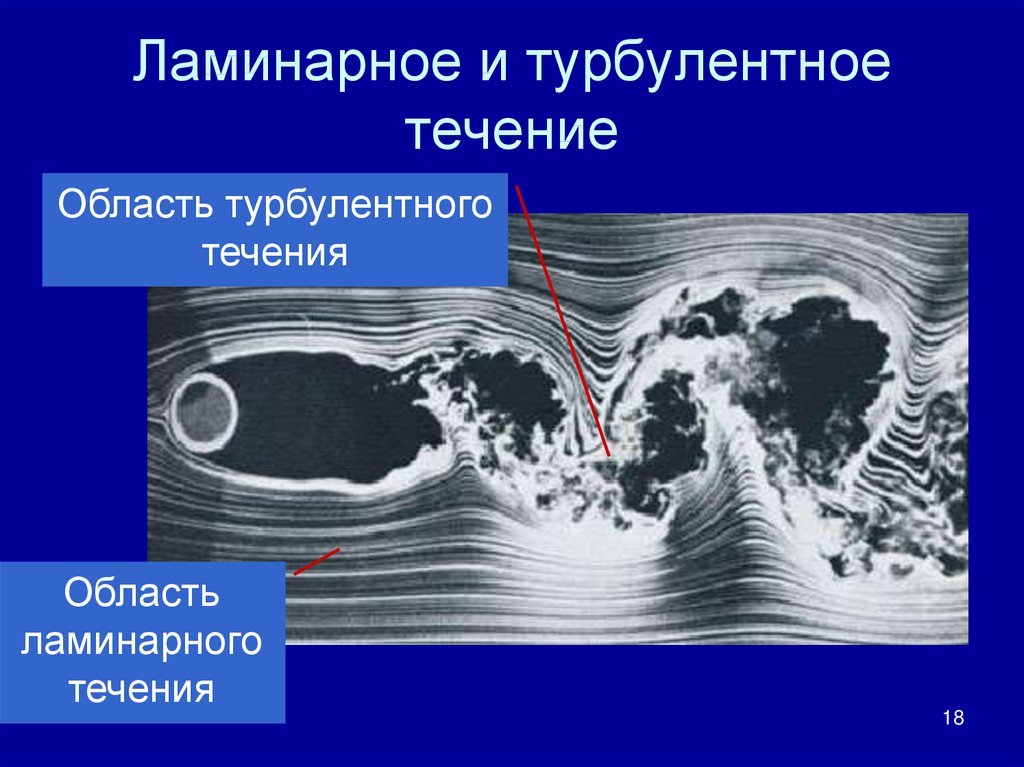 Однако дым превращается в турбулентный поток после подъема на небольшую высоту по мере того, как он отклоняется от своего обычного пути.
Однако дым превращается в турбулентный поток после подъема на небольшую высоту по мере того, как он отклоняется от своего обычного пути.
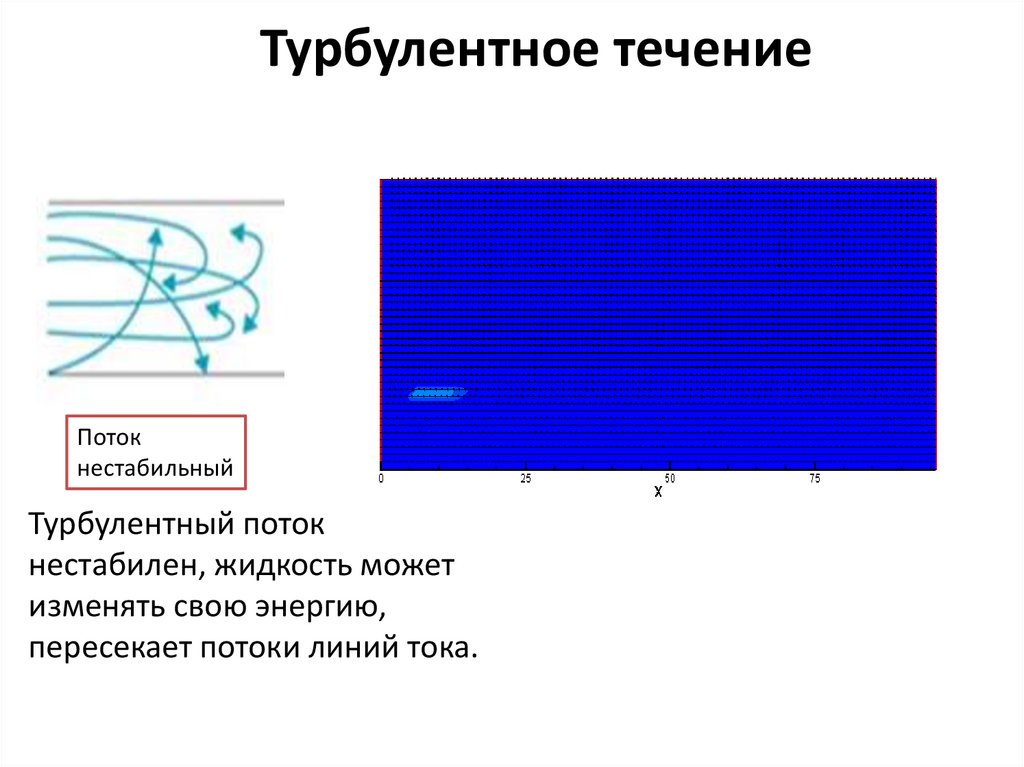
Турбулентный поток
Турбулентный поток определяется как поток, в котором частицы жидкости движутся зигзагообразно. За счет движения частиц жидкости зигзагообразным образом происходит образование вихрей, ответственных за большие потери энергии.
При турбулентном течении скорость жидкости в точке постоянно изменяется как по величине, так и по направлению. Турбулентный поток имеет тенденцию возникать в трубах большого диаметра, в которых жидкость течет с высокой скоростью.
Основным инструментом для анализа турбулентного потока является CFD-анализ. CFD — это раздел гидромеханики, использующий алгоритмы и численный анализ для анализа и решения задач, связанных с турбулентными потоками жидкости.
Широко признано, что уравнение Навье-Стокса или упрощенные уравнения Навье-Стокса, усредненные по Рейнольдсу, являются основой практически для всех кодов CFD.
Тип потока определяется безразмерным числом, называемым числом Рейнольдса для потока в трубе.
Re = (VD/v)
Где,
D = диаметр трубы
V = средняя скорость потока в трубе
v = кинематическая вязкость жидкости
Результат-
- Если число Рейнольдса меньше 2000, то течение называется ламинарным.
- Если число Рейнольдса больше 4000, то течение называется турбулентным.
- Если число Рейнольдса находится в диапазоне от 2000 до 4000, поток может быть ламинарным или турбулентным.
Типичными примерами турбулентного потока являются поток крови в артериях, транспорт нефти по трубопроводам, поток лавы, атмосферные и океанские течения, поток через насосы и турбины, поток в кильватерной струе лодки и вокруг законцовок крыла самолета.
Разница между ламинарным и турбулентным потоком
Ламинарный поток можно визуализировать с помощью эксперимента с чернилами в цилиндрической трубке. Чернила впрыскиваются в середину стеклянной трубки, по которой течет вода. Когда скорость воды еще мала, кажется, что чернила не смешиваются с водой; линии тока параллельны и называются ламинарным течением.
Чернила впрыскиваются в середину стеклянной трубки, по которой течет вода. Когда скорость воды еще мала, кажется, что чернила не смешиваются с водой; линии тока параллельны и называются ламинарным течением.
Внезапное изменение произойдет, когда скорость воды увеличится. Затем течение полностью прерывается, и вода через чернила становится однородной. Таким образом, линии тока хаотичны, а не линейны, и называются турбулентным течением.
Как избежать турбулентного потока?
- Старайтесь не допускать ограничений в процессе, таких как клапаны, адаптеры и угловые соединения.
- Не устанавливайте расходомер непосредственно за сужением, например, клапаном. Однако, если это невозможно организовать по-другому, между клапаном и расходомером используется фильтр турбулентности.
- Использование угловой муфты рядом с расходомером должно быть максимально ограничено.
- Ограничьте скорость потока, используя правильную длину трубы.
- Используйте длину трубы, в 10 раз превышающую диаметр трубы на входе прибора.

- Используйте длину трубы, в 4 раза превышающую диаметр трубы на выходе из прибора (только расходомеры).
- Используйте длину трубы для расхода газа > 100 л/мин; обычно используют трубу диаметром не менее 12 мм или ½ дюйма.
- Использование фильтра турбулентности в процессе потока отфильтрует поток до того, как он достигнет датчика, и сделает его ламинарным. В настоящее время широко используются расходомеры типа Bronkhorst low delta P.
Часто задаваемые вопросы
Что такое ламинарный и турбулентный поток?
Жидкость, протекающая по закрытому каналу, такому как труба или между двумя плоскими пластинами, представляет собой либо ламинарный, либо турбулентный поток, в зависимости от скорости, размера трубы (или числа Рейнольдса) и вязкости жидкости.
В чем разница между ламинарным и турбулентным течением?
Ламинарный поток можно визуализировать с помощью эксперимента с чернилами в цилиндрической трубке.