Рыскание — Карта знаний
- Ры́скание — угловые движения летательного аппарата, судна, автомобиля относительно вертикальной оси (см. также вертикальная ось самолёта), а также небольшие изменения курса вправо или влево, свойственные судну. Управляет этим вращением руль направления (англ. rudder). Один из трёх углов (крен, тангаж и рыскание), соответствующих трём углам Эйлера, которые задают поворотное положение летательного аппарата относительно его центра. Угол рыскания обозначается буквой ψ (пси).
В динамике полёта рыскание (вернее, угол рыскания) также означает угол поворота корпуса самолёта в горизонтальной плоскости, отсчитываемый от направления на север. Этот угол сходен с курсом, но отсчитывается строго в соответствии с выбранной системой координат.

Источник: Википедия
Связанные понятия
Танга́ж (фр. tangage — килевая качка) — угловое движение летательного аппарата или судна относительно главной (горизонтальной) поперечной оси инерции. Связанная система координат — это система координат, используемая для анализа движения воздушных судов в механике полета. Она состоит из продольной OX, поперечной OZ и вертикальной осей OY, которые проходят через центр масс движущегося объекта. Крен (от фр. carène — киль, подводная часть судна или от англ. kren-gen — класть судно на бок) — поворот объекта (судна, самолёта, фундамента) вокруг его продольной оси (см.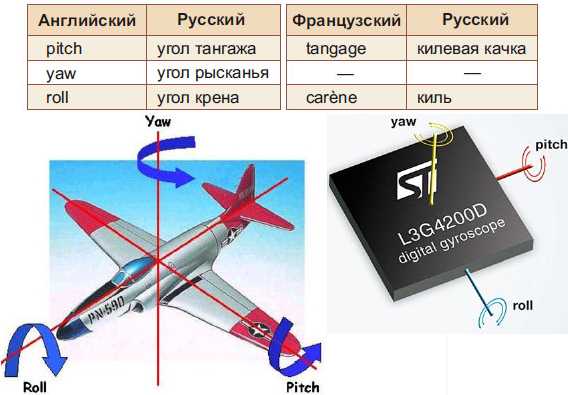 также продольная ось самолёта).
Индикатор поворота и скольжения в авиации — комбинированный пилотажный контрольно-измерительный прибор, смонтированный для удобства пользования в одном корпусе. Индикатор поворота определяет угол поворота самолёта относительно вертикальной оси, индикатор скольжения определяет угол крена самолёта и скольжения относительно продольной оси. При повороте стрелка показывает отклонение самолёта от прямой вправо – влево, при скольжении шарик передвигается в изогнутой трубке в сторону скольжения.
Руль направления — орган управления самолёта, расположенный в хвостовом оперении и предназначенный для управления самолётом относительно нормальной оси (то есть при помощи руля направления изменяется угол рыскания).
также продольная ось самолёта).
Индикатор поворота и скольжения в авиации — комбинированный пилотажный контрольно-измерительный прибор, смонтированный для удобства пользования в одном корпусе. Индикатор поворота определяет угол поворота самолёта относительно вертикальной оси, индикатор скольжения определяет угол крена самолёта и скольжения относительно продольной оси. При повороте стрелка показывает отклонение самолёта от прямой вправо – влево, при скольжении шарик передвигается в изогнутой трубке в сторону скольжения.
Руль направления — орган управления самолёта, расположенный в хвостовом оперении и предназначенный для управления самолётом относительно нормальной оси (то есть при помощи руля направления изменяется угол рыскания).Упоминания в литературе
Перекрестные связи между продольным и боковыми моментами сказываются, например, следующим образом: при изменении угла атаки α не только изменяется момент тангажа Мz, но и самопроизвольно изменяются моменты рыскания и крена (боковые моменты) и наоборот.
Связанные понятия (продолжение)
Курсовой угол — понятие навигации, обозначающее угол между диаметральной плоскостью судна и направлением на какой-либо наблюдаемый с судна объект. Курсовой угол измеряется в градусах, отсчитываемых на азимутальном круге от 0 до 180° в сторону правого или левого борта от направления в нос. Авиагоризо́нт — бортовой гироскопический прибор, используемый в авиации для определения и индикации продольного и поперечного углов наклона летательного аппарата (тангажа и крена), то есть углов ориентации относительно истинной вертикали. Прибор используется лётчиком для управления и стабилизации летательного аппарата в воздухе. Гировертикаль — гироскопический прибор, предназначенный для определения направления истинной вертикали места (направления силы земного притяжения в данной точке земной поверхности) или плоскости горизонта, а также измерения углов наклона объекта относительно этой плоскости.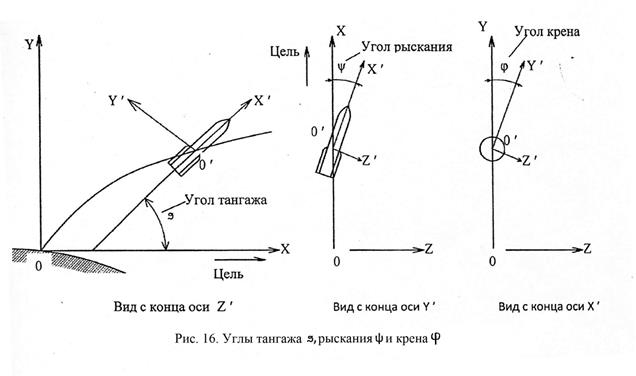 Угол пути — угол между осью OXg нормальной системы координат и направлением путевой скорости летательного аппарата.
Бо́чка — фигура пилотажа, при выполнении которой летательный аппарат (самолёт и так далее) поворачивается относительно продольной оси на 360° с сохранением общего направления полёта.
Руль высоты́ — аэродинамический орган управления самолёта, осуществляющий его вращение вокруг поперечной оси.
Аксио́метр (греч. axis ось, и metro мера) — корабельный измерительный прибор, часть рулевого устройства, с кругом делений и стрелкой-указателем, видными снаружи. Аксиометр указывает в градусах отклонение пера руля от диаметральной плоскости корабля (судна) в каждый момент времени. Аксиометр устанавливается, как правило, перед штурвалом и связывается электрической схемой с баллером руля.
Угол пути — угол между осью OXg нормальной системы координат и направлением путевой скорости летательного аппарата.
Бо́чка — фигура пилотажа, при выполнении которой летательный аппарат (самолёт и так далее) поворачивается относительно продольной оси на 360° с сохранением общего направления полёта.
Руль высоты́ — аэродинамический орган управления самолёта, осуществляющий его вращение вокруг поперечной оси.
Аксио́метр (греч. axis ось, и metro мера) — корабельный измерительный прибор, часть рулевого устройства, с кругом делений и стрелкой-указателем, видными снаружи. Аксиометр указывает в градусах отклонение пера руля от диаметральной плоскости корабля (судна) в каждый момент времени. Аксиометр устанавливается, как правило, перед штурвалом и связывается электрической схемой с баллером руля.
 Принцип действия элеронов состоит в том, что у части крыла, расположенной перед…
Элево́ны — гибрид элеронов и руля высоты. Элевоны — аэродинамические органы управления самолётом, симметрично расположенные на задней кромке консолей крыла. Элевоны выполняют роль элеронов при управлении углом крена самолёта и руля высоты при управлении нормальной перегрузкой. Элевоны применяются на самолётах без горизонтального хвостового оперения, имеющих обычно схему типа «бесхвостка» или «летающее крыло». Для управления углом крена самолёта элевоны отклоняются дифференциально, то есть, например…
Аэродинамический подхват — непроизвольный (не связанный с действиями лётчиков) рост тангажа (угла атаки) летательного аппарата (ЛА). Эффект подхвата связан с динамической разбалансировкой ЛА по отношению к среде, в которой он перемещается (воздуху).
Указатель курса — бортовой прибор, показывающий текущий курс летательного аппарата.
Принцип действия элеронов состоит в том, что у части крыла, расположенной перед…
Элево́ны — гибрид элеронов и руля высоты. Элевоны — аэродинамические органы управления самолётом, симметрично расположенные на задней кромке консолей крыла. Элевоны выполняют роль элеронов при управлении углом крена самолёта и руля высоты при управлении нормальной перегрузкой. Элевоны применяются на самолётах без горизонтального хвостового оперения, имеющих обычно схему типа «бесхвостка» или «летающее крыло». Для управления углом крена самолёта элевоны отклоняются дифференциально, то есть, например…
Аэродинамический подхват — непроизвольный (не связанный с действиями лётчиков) рост тангажа (угла атаки) летательного аппарата (ЛА). Эффект подхвата связан с динамической разбалансировкой ЛА по отношению к среде, в которой он перемещается (воздуху).
Указатель курса — бортовой прибор, показывающий текущий курс летательного аппарата.
 ..
Судово́й руль (от нидерл. roer) — элемент корабельного пассивного рулевого устройства, вертикальная пластина (перо руля), поворачивающаяся на оси (баллере) в кормовой подводной части судна. Служит для поворота корабля в ту или иную сторону при движении.
Механизм планшайба-стержни (шайбовый механизм) — это механизм, используемый в машиностроении для преобразования движения вращающегося вала в возвратно-поступательное движение стержней параллельно оси вала, или для обратного преобразования.
Да́тчик углово́й ско́рости (ДУС) — устройство, первичный прибор (датчик) для измерения угловой скорости поворота корпуса летательных аппаратов относительно невращающейся инерциальной системы координат. Используется в системах управления различных летательных аппаратов: ракет, самолётов, вертолётов и др. Выходной сигнал устройства обычно электрический, пропорциональный угловой скорости и используется в пилотажных системах летательных аппаратов, в частности, автопилоте, системах стабилизации траектории.
..
Судово́й руль (от нидерл. roer) — элемент корабельного пассивного рулевого устройства, вертикальная пластина (перо руля), поворачивающаяся на оси (баллере) в кормовой подводной части судна. Служит для поворота корабля в ту или иную сторону при движении.
Механизм планшайба-стержни (шайбовый механизм) — это механизм, используемый в машиностроении для преобразования движения вращающегося вала в возвратно-поступательное движение стержней параллельно оси вала, или для обратного преобразования.
Да́тчик углово́й ско́рости (ДУС) — устройство, первичный прибор (датчик) для измерения угловой скорости поворота корпуса летательных аппаратов относительно невращающейся инерциальной системы координат. Используется в системах управления различных летательных аппаратов: ракет, самолётов, вертолётов и др. Выходной сигнал устройства обычно электрический, пропорциональный угловой скорости и используется в пилотажных системах летательных аппаратов, в частности, автопилоте, системах стабилизации траектории.
 Де́мпфер ры́скания — электрогидравлическое устройство, предназначенное для улучшения собственных демпфирующих свойств самолёта в путевом канале рыскания. Включает в себя датчики скорости рыскания и процессор, который подаёт сигнал на исполнительный механизм, подключённый к рулю.
Шаг винта — одна из основных технических характеристик воздушного или гребного винта, зависящая от угла установки его лопастей относительно плоскости вращения при их круговом движении в газовой или жидкостной среде — это расстояние, пройденное поступательно винтом, ввинчивающимся в твёрдую среду, за один полный оборот (360°).
Гироскопический тренажёр — малогабаритный спортивный тренажёр, принцип работы которого основан на свойствах роторного гироскопа. Используется для создания нагрузки мышц и суставов кисти руки. Для достижения высоких степеней раскручивания ротора гироскопического тренажёра задействуются мышцы предплечья, плеча и плечевого пояса.
Де́мпфер ры́скания — электрогидравлическое устройство, предназначенное для улучшения собственных демпфирующих свойств самолёта в путевом канале рыскания. Включает в себя датчики скорости рыскания и процессор, который подаёт сигнал на исполнительный механизм, подключённый к рулю.
Шаг винта — одна из основных технических характеристик воздушного или гребного винта, зависящая от угла установки его лопастей относительно плоскости вращения при их круговом движении в газовой или жидкостной среде — это расстояние, пройденное поступательно винтом, ввинчивающимся в твёрдую среду, за один полный оборот (360°).
Гироскопический тренажёр — малогабаритный спортивный тренажёр, принцип работы которого основан на свойствах роторного гироскопа. Используется для создания нагрузки мышц и суставов кисти руки. Для достижения высоких степеней раскручивания ротора гироскопического тренажёра задействуются мышцы предплечья, плеча и плечевого пояса. Угол сноса — угол между продольной осью летательного аппарата (ЛА) и направлением его движения относительно земной поверхности. В горизонтальном полёте без скольжения обусловлен боковым ветром.
Осто́йчивость — способность плавучего средства противостоять внешним силам, вызывающим его крен или дифферент, и возвращаться в состояние равновесия по окончании возмущающего воздействия. Также — раздел теории корабля, изучающий остойчивость.
Гравитационный разворот — манёвр космического аппарата в гравитационном поле небесного тела, при котором направление тяги совпадает или противоположно направлению движения, изменяющемуся под действием силы тяжести.
Кастор (англ. caster angle или castor angle) — угол продольного наклона оси поворота колеса автомобиля.
Теодоли́т — измерительный прибор для определения горизонтальных и вертикальных углов при топографических съёмках, геодезических и маркшейдерских работах, в строительстве и т.
Угол сноса — угол между продольной осью летательного аппарата (ЛА) и направлением его движения относительно земной поверхности. В горизонтальном полёте без скольжения обусловлен боковым ветром.
Осто́йчивость — способность плавучего средства противостоять внешним силам, вызывающим его крен или дифферент, и возвращаться в состояние равновесия по окончании возмущающего воздействия. Также — раздел теории корабля, изучающий остойчивость.
Гравитационный разворот — манёвр космического аппарата в гравитационном поле небесного тела, при котором направление тяги совпадает или противоположно направлению движения, изменяющемуся под действием силы тяжести.
Кастор (англ. caster angle или castor angle) — угол продольного наклона оси поворота колеса автомобиля.
Теодоли́т — измерительный прибор для определения горизонтальных и вертикальных углов при топографических съёмках, геодезических и маркшейдерских работах, в строительстве и т. Дирекционный угол — горизонтальный угол, измеряемый по ходу часовой стрелки от 0° до 360°, между северным направлением осевого меридиана зоны прямоугольных координат и направлением на ориентир. Дирекционные углы направлений с точностью 1-60 угловых секунд могут определяться геодезическим, астрономическим и гироскопическим способами, а также методами космической геодезии.
Вертолёт — винтокрылый летательный аппарат вертикального взлета и посадки, у которого подъёмная и движущая (пропульсивная) силы на всех этапах полёта создаются одним или несколькими несущими винтами с приводом от одного или нескольких двигателей.
Истинный курс — угол, заключённый между северным направлением меридиана в месте измерения и направлением проекции продольной оси объекта на горизонтальную плоскость, отсчитывается по часовой стрелке от направления на географический север.
Дирекционный угол — горизонтальный угол, измеряемый по ходу часовой стрелки от 0° до 360°, между северным направлением осевого меридиана зоны прямоугольных координат и направлением на ориентир. Дирекционные углы направлений с точностью 1-60 угловых секунд могут определяться геодезическим, астрономическим и гироскопическим способами, а также методами космической геодезии.
Вертолёт — винтокрылый летательный аппарат вертикального взлета и посадки, у которого подъёмная и движущая (пропульсивная) силы на всех этапах полёта создаются одним или несколькими несущими винтами с приводом от одного или нескольких двигателей.
Истинный курс — угол, заключённый между северным направлением меридиана в месте измерения и направлением проекции продольной оси объекта на горизонтальную плоскость, отсчитывается по часовой стрелке от направления на географический север. По сути показывает направление носа самолёта (или другого объекта) относительно севера.
Инклинатор — прибор, служащий для измерения величины наклонения силы земного магнетизма.
Курсовертикаль — прибор, поставляющий данные об углах между географической системой координат (ГСК) и связанной системой координат (ССК), начальная точка которой совпадает с начальной точкой ГСК, а оси соответствуют, как правило — Y — продольной оси, Z — вертикальной, X — перпендикулярной им боковой оси транспортного средства, на котором установлена курсовертикаль.
Углова́я ско́рость — величина, характеризующая скорость вращения материальной точки вокруг центра вращения. Для вращения в двухмерном пространстве угловая скорость выражается числом, в трёхмерном пространстве представляется псевдовектором (аксиальным вектором), а в общем случае — кососимметрическим тензором.
По сути показывает направление носа самолёта (или другого объекта) относительно севера.
Инклинатор — прибор, служащий для измерения величины наклонения силы земного магнетизма.
Курсовертикаль — прибор, поставляющий данные об углах между географической системой координат (ГСК) и связанной системой координат (ССК), начальная точка которой совпадает с начальной точкой ГСК, а оси соответствуют, как правило — Y — продольной оси, Z — вертикальной, X — перпендикулярной им боковой оси транспортного средства, на котором установлена курсовертикаль.
Углова́я ско́рость — величина, характеризующая скорость вращения материальной точки вокруг центра вращения. Для вращения в двухмерном пространстве угловая скорость выражается числом, в трёхмерном пространстве представляется псевдовектором (аксиальным вектором), а в общем случае — кососимметрическим тензором. Механиза́ция крыла́ — совокупность устройств на крыле летательного аппарата, предназначенных для регулирования его несущих свойств. Механизация включает в себя закрылки, предкрылки, интерцепторы, спойлеры, флапероны, активные системы управления пограничным слоем и так далее.
Механиза́ция крыла́ — совокупность устройств на крыле летательного аппарата, предназначенных для регулирования его несущих свойств. Механизация включает в себя закрылки, предкрылки, интерцепторы, спойлеры, флапероны, активные системы управления пограничным слоем и так далее.Термин | Обозначение | Определение | Примечание |
ОБЩИЕ ПОНЯТИЯ | |||
1. Динамика летательных аппаратов в атмосфере | Раздел механики, в котором изучается движение летательных аппаратов в атмосфере | Термин «летательный аппарат» в данном стандарте относится к летательным аппаратам тяжелее воздуха, оснащенным, как правило, установкой для создания тяги (п. | |
ИНЕРЦИАЛЬНАЯ И ЗЕМНЫЕ СИСТЕМЫ КООРДИНАТ | |||
2. Инерциальная система координат | Правая прямоугольная декартова система координат, начало которой помещено в некоторой точке пространства, либо перемещается с постоянной скоростью, а направление осей относительно звезд неизменно | ||
3. Земная система координат | Правая прямоугольная декартова система координат, начало и оси которой фиксированы по отношению к Земле и выбираются в соответствии с задачей | ||
4. Нормальная земная система координат | Земная система координат, ось которой направлена вверх по местной вертикали, а направление осей и выбирается в соответствии с задачей | Под местной вертикалью понимают прямую, совпадающую с направлением силы тяжести в рассматриваемой точке | |
5. | Земная система координат, начало которой совпадает с характерной точкой летательного аппарата в начальный момент движения, ось направлена вверх по местной вертикали, а направление осей и выбирается в соответствии с задачей | ||
ПОДВИЖНЫЕ СИСТЕМЫ КООРДИНАТ | |||
6. Подвижная система координат | Правая прямоугольная декартова система координат, начало которой помещено на летательном аппарате, обычно в центре масс, а направление осей выбирается в соответствии с задачей | ||
7. Ориентированная подвижная система координат | Подвижная система координат, направление осей которой относительно звезд неизменно | ||
8. | Подвижная система координат, оси которой направлены так же, как и соответствующие оси земной системы координат | ||
9. Нормальная система координат | Подвижная система координат, ось которой направлена вверх по местной вертикали, а направление осей и выбирается в соответствии с задачей | ||
10. Связанная система координат | Подвижная система координат, осями которой являются продольная ось (п.11), нормальная ось (п.12) и поперечная ось (п.13), фиксированные относительно летательного аппарата | ||
11. | Ось связанной системы координат, расположенная в плоскости симметрии летательного аппарата или в плоскости, параллельной ей, если начало координат помещено вне плоскости симметрии, и направленная от хвостовой к носовой части летательного аппарата | 1. Направление продольной оси может быть выбрано как по базовым осям самолета, крыла или фюзеляжа, так и по главным осям инерции. Выбор продольной оси должен быть указан. 2. Для осесимметричных летательных аппаратов продольная ось располагается вдоль оси симметрии | |
12. Нормальная ось | Ось связанной системы координат, расположенная в плоскости симметрии летательного аппарата или в плоскости, параллельной ей, если начало координат помещено вне плоскости симметрии, и направленная к верхней части летательного аппарата или части, условно ей соответствующей | ||
13. | Ось связанной системы координат, перпендикулярная плоскости симметрии летательного аппарата и направленная к правой части летательного аппарата или части, условно ей соответствующей | ||
14. Полусвязанная система координат | Подвижная система координат, ось которой совпадает с проекцией скорости летательного аппарата (п.35) на плоскость связанной системы координат, ось — с осью подъемной силы (п.18), a ocь — с поперечной осью | ||
15. Связанная с пространственным углом атаки система координат | Подвижная система координат, ось которой совпадает с продольной осью, а ось лежит в плоскости, образованной продольной осью и направлением скорости летательного аппарата (п. | ||
16. Скоростная система координат | Подвижная система координат, ось которой совпадает с направлением скорости летательного аппарата (п.35), а ось лежит в плоскости симметрии летательного аппарата или в плоскости, параллельной ей, если начало координат помещено вне плоскости симметрии, и направлена к верхней части летательного аппарата или части, условно ей соответствующей | ||
17. Скоростная ось | Ось скоростной системы координат, совпадающая с направлением скорости летательного аппарата (п.35) | ||
18. Ось подъемной силы | Ось скоростной системы координат в плоскости симметрии летательного аппарата или в плоскости, параллельной ей, если начало координат помещено вне плоскости симметрии, и направленная к верхней части летательного аппарата или части, условно ей соответствующей | ||
19. | Ось, которая в совокупности со скоростной осью и осью подъемной силы составляет скоростную систему координат | ||
20. Траекторная система координат | Подвижная система координат, ось которой совпадает с направлением земной скорости (п.37), ось лежит в вертикальной плоскости, проходящей через ось , и направлена обычно вверх от поверхности Земли | ||
УГЛЫ, ОПРЕДЕЛЯЮЩИЕ НАПРАВЛЕНИЕ СКОРОСТИ ЛЕТАТЕЛЬНОГО АППАРАТА В СВЯЗАННОЙ СИСТЕМЕ КООРДИНАТ И В СИСТЕМЕ КООРДИНАТ, СВЯЗАННОЙ С ПРОСТРАНСТВЕННЫМ УГЛОМ АТАКИ(Справочное приложение 1, черт.1) | |||
21. Угол атаки | Угол между продольной осью и проекцией скорости летательного аппарата (п. | Угол атаки следует считать положительным, если проекция скорости летательного аппарата на нормальную ось отрицательна | |
22. Угол скольжения | Угол между направлением скорости летательного аппарата (п.35) и плоскостью связанной системы координат | Угол скольжения следует считать положительным, если проекция скорости летательного аппарата на поперечную ось положительна | |
23. Пространственный угол атаки | Угол между продольной осью и направлением скорости летательного аппарата (п.35) | Пространственный угол атаки всегда является положительным | |
24. | Угол между нормальной осью и осью системы координат, связанной с пространственным углом атаки | Аэродинамический угол крена следует считать положительным, когда ось совмещается с нормальной осью поворотом вокруг продольной оси по часовой стрелке, если смотреть в направлении продольной оси | |
УГЛЫ МЕЖДУ ОСЯМИ СВЯЗАННОЙ И НОРМАЛЬНОЙ СИСТЕМ КООРДИНАТ(Справочное приложение 1, черт.2) | |||
25. Угол рыскания | Угол между осью нормальной системы координат и проекцией продольной оси на горизонтальную плоскость нормальной системы координат | Угол рыскания следует считать положительным, когда ось совмещается с проекцией продольной оси на горизонтальную плоскость поворотом вокруг оси по часовой стрелке, если смотреть в направлении этой оси | |
26. | Угол между продольной осью и горизонтальной плоскостью нормальной системы координат | Угол тангажа следует считать положительным, когда продольная ось находится выше горизонтальной плоскости | |
27. Угол крена | Угол между поперечной осью и осью нормальной системы координат, смещенной в положение, при котором угол рыскания равен нулю | Угол крена следует считать положительным, когда смещенная ось совмещается с поперечной осью поворотом вокруг продольной оси по часовой стрелке, если смотреть в направлении этой оси | |
УГЛЫ МЕЖДУ ОСЯМИ СКОРОСТНОЙ И НОРМАЛЬНОЙ СИСТЕМ КООРДИНАТ(Справочное приложение 1, черт. | |||
28. Скоростной угол рыскания | Угол между осью нормальной системы координат и проекцией скоростной оси на горизонтальную плоскость нормальной системы координат | Скоростной угол рыскания следует считать положительным, когда ось совмещается с проекцией скоростной оси на горизонтальную плоскость поворотом вокруг оси по часовой стрелке, если смотреть в направлении этой оси | |
29. Скоростной угол тангажа | Угол между скоростной осью и горизонтальной плоскостью нормальной системы координат | Скоростной угол тангажа следует считать положительным, когда скоростная ось находится выше горизонтальной плоскости | |
30. | Угол между боковой осью и осью нормальной системы координат, смещенной в положение, при котором скоростной угол рыскания равен нулю | Скоростной угол крена следует считать положительным, когда смещенная ось совмещается с боковой осью поворотом вокруг скоростной оси по часовой стрелке, если смотреть в направлении этой оси | |
ТРАЕКТОРНЫЕ УГЛЫ (Справочное приложение 1, черт.4) | |||
31. Угол пути | Угол между осью нормальной системы координат и направлением путевой скорости (п.38) | Угол пути следует считать положительным, когда ось совмещается с направлением путевой скорости поворотом вокруг оси по часовой стрелке, если смотреть в направлении этой оси | |
32. | Угол между направлением земной скорости (п.37) и горизонтальной плоскостью нормальной системы координат | Угол наклона траектории следует считать положительным, когда проекция земной скорости на ось положительна | |
УГЛЫ, ОПРЕДЕЛЯЮЩИЕ НАПРАВЛЕНИЕ ВЕТРА (Справочное приложение 1, черт.5) | |||
33. Угол ветра | Угол между осью нормальной системы координат и проекцией скорости ветра (п.39) на горизонтальную плоскость нормальной системы координат | Угол ветра следует считать положительным, когда ось совмещается с проекцией скорости ветра на горизонтальную плоскость поворотом вокруг оси по часовой стрелке, если смотреть в направлении этой оси | |
34. | Угол между направлением скорости ветра (п.39) и горизонтальной плоскостью | Наклон ветра следует считать положительным, когда проекция скорости ветра на ось нормальной системы координат положительна | |
СКОРОСТИ | |||
35. Скорость летательного аппарата Скорость | Скорость начала связанной системы координат относительно среды, не возмущенной летательным аппаратом | 1. При применении термина к конкретному виду летательного аппарата следует заменять слова «летательного аппарата» на термин конкретного вида летательного аппарата, например, «скорость самолета». 2. Составляющие скоростей по осям различных систем координат следует обозначать соответственно , , , с индексом соответствующей оси, например, — составляющая земной скорости (п. | |
36. — | Модуль скорости летательного аппарата | ||
37. Земная скорость | Скорость начала связанной системы координат относительно какой-либо из земных систем координат | См. примечание 2 к п.35 | |
38. Путевая скорость | Проекция земной скорости на | То же | |
39. | Скорость среды, не возмущенной летательным аппаратом, относительно какой-либо из земных систем координат | « | |
УГЛОВЫЕ СКОРОСТИ | |||
40. Абсолютная угловая скорость летательного аппарата Абсолютная угловая скорость | Угловая скорость связанной системы координат относительно инерциальной системы координат | 1. Составляющие абсолютной угловой скорости летательного аппарата и угловой скорости летательного аппарата (п.41) по осям различных систем координат следует обозначать соответственно и с индексом соответствующей оси, например, — составляющая угловой скорости летательного аппарата по оси скоростной системы координат. 2. Составляющие абсолютной угловой скорости летательного аппарата и угловой скорости летательного аппарата следует считать положительными при вращении летательного аппарата вокруг соответствующей оси по часовой стрелке, если смотреть в направлении этой оси | |
41. Угловая скорость летательного аппарата Угловая скорость | Угловая скорость связанной системы координат относительно какой-либо из земных систем координат | См. примечания к п.40 | |
42. Скорость крена | Составляющая угловой скорости летательного аппарата по оси связанной системы координат | См. примечание 2 к п.40 | |
43. | Составляющая угловой скорости летательного аппарата по оси связанной системы координат | То же | |
44. Скорость тангажа | Составляющая угловой скорости летательного аппарата по оси связанной системы координат | « | |
МАССОВЫЕ И ИНЕРЦИОННЫЕ ХАРАКТЕРИСТИКИ ЛЕТАТЕЛЬНОГО АППАРАТА | |||
45. Масса летательного аппарата | — | Масса является одной из характеристик материального объекта и определяет его инертные и гравитационные свойства. | |
46. Момент инерции летательного аппарата относительно оси Момент инерции | — | ||
47. Центробежный момент инерции летательного аппарата Центробежный момент инерции | — | ||
48. Радиус инерции летательного аппарата относительно оси Радиус инерции | — | ||
УГЛЫ ОТКЛОНЕНИЙ ОРГАНОВ УПРАВЛЕНИЯ | |||
49. | Угол отклонения органа управления, предназначенного для создания момента тангажа (п.75), или эквивалентный угол отклонения, используемый в уравнениях движения летательного аппарата вместо углов отклонений нескольких органов управления | 1. При применении термина к конкретным видам органов управления тангажом следует заменять слова «органа управления тангажом» на термин конкретного вида органа управления, например, «угол отклонения руля высоты» (), «угол отклонения стабилизатора» (). 2. Угол отклонения органа управления тангажом осесимметричных летательных аппаратов следует обозначать . 3. Углы отклонения органов управления следует считать положительными при поворотах органов управления по часовой стрелке, если смотреть в направлении соответствующей оси связанной системы координат. При этом предполагается, что оси вращения органов управления креном и тангажом условно минимальными поворотами приведены в положение, параллельное поперечной оси, а ось вращения органа управления рысканием — в положение, параллельное нормальной оси, и знак угла отклонения органа управления креном определяется положением правого органа управления (справочное приложение 1, черт. | |
50. Угол отклонения органа управления креном | Угол отклонения органа управления, предназначенного для создания момента крена (п.73), или эквивалентный угол отклонения, используемый в уравнениях движения летательного аппарата вместо углов отклонения нескольких органов управления | 1. При применении термина к конкретным видам органов управления креном следует заменять слова «органа управления креном» на термин конкретного вида органа управления, например, «угол отклонения элеронов» () «угол отклонения дифференциального стабилизатора» (). 2. Угол отклонения органа управления креном осесимметричных летательных аппаратов следует обозначать . 3. См. примечания 3 и 4 к п.49 | |
51. | Угол отклонения органа управления, предназначенного для создания момента рыскания (п.74) или эквивалентный угол отклонения, используемый в уравнениях движения летательного аппарата вместо углов отклонения нескольких органов управления | 1. При применении термина к конкретным видам органов управления рысканием следует заменять слова «органа управления рысканием» на термин конкретного вида органа управления, например, «угол отклонения руля направления» (). 2. Угол отклонения органа управления рысканием осесимметричных летательных аппаратов следует обозначать . 3. См. примечания 3 и 4 к п.49 | |
СИЛЫ, ДЕЙСТВУЮЩИЕ НА ЛЕТАТЕЛЬНЫЙ АППАРАТ | |||
52. Результирующая сила | Главный вектор системы сил, действующих на летательный аппарат, без учета инерционных, гравитационных сил и сил, возникающих при контакте летательного аппарата с землей | Результирующая сила складывается из тяги (п. Разложение результирующей силы на эти составляющие в каждом частном случае зависит от принятых условий | |
53. Тяга | Главный вектор системы сил, действующих на летательный аппарат со стороны двигателя в результате его функционирования | Составляющие тяги по осям различных систем координат следует обозначать с индексом соответствующей оси, например, — составляющая тяги по оси связанной системы координат | |
54. Аэродинамическая сила планера Аэродинамическая сила | Главный вектор системы сил, действующих на летательный аппарат со стороны окружающей среды при его движении | В случаях, исключающих возможность различного толкования, индекс в обозначении может быть опущен | |
55. | Составляющая результирующей силы по оси связанной системы координат | ||
56. Нормальная сила | Составляющая результирующей силы по оси связанной системы координат | ||
57. Поперечная сила | Составляющая результирующей силы по оси связанной системы координат | ||
58. Тангенциальная сила | Составляющая результирующей силы по оси скоростной системы координат | ||
59. | Составляющая результирующей силы по оси скоростной системы координат | ||
60. Боковая сила | Составляющая результирующей силы по оси скоростной системы координат | ||
61. Аэродинамическая продольная сила Продольная сила | Составляющая аэродинамической силы планера по оси связанной системы координат, взятая с противоположным знаком | ||
62. Аэродинамическая нормальная сила Нормальная сила | Составляющая аэродинамической силы планера по оси связанной системы координат | ||
63. Поперечная сила | Составляющая аэродинамической силы планера по оси связанной системы координат | ||
64. Сила лобового сопротивления | Составляющая аэродинамической силы планера по оси скоростной системы координат, взятая с противоположным) знаком | ||
65. Аэродинамическая подъемная сила Подъемная сила | Составляющая аэродинамической силы планера по оси скоростной системы координат | ||
66. Аэродинамическая боковая сила Боковая сила | Составляющая аэродинамической силы планера по оси скоростной системы координат | ||
67. | Составляющая аэродинамической силы планера по оси системы координат, связанной с пространственным углом атаки, взятая с противоположным знаком | ||
68. — | Составляющая аэродинамической силы планера по оси системы координат, связанной с пространственным углом атаки | ||
69. — | Составляющая аэродинамической силы планера по оси системы координат, связанной с пространственным углом атаки | ||
МОМЕНТЫ СИЛ, ДЕЙСТВУЮЩИЕ НА ЛЕТАТЕЛЬНЫЙ АППАРАТ | |||
70. Результирующий момент | Главный момент системы сил, образующих результирующую силу, относительно характерной точки летательного аппарата | Результирующий момент обычно определяется относительно центра масс | |
71. | Главный момент сил, составляющих тягу, относительно характерной точки летательного аппарата | 1. Момент тяги обычно определяется относительно центра масс. 2. Составляющие момента тяги в различных системах координат следует обозначать с индексом соответствующей оси, например, — составляющая момента по оси связанной системы координат | |
72. Аэродинамический момент | Момент, определяемый по формуле | ||
73. Момент крена | Составляющая результирующего момента по оси связанной системы координат | 1. 2. В случаях, исключающих различное толкование, в обозначениях составляющих результирующего момента индекс может быть опущен. 3. Термины для составляющих результирующего момента в других системах координат следует образовывать добавлением к данному термину терминов соответствующих систем координат, например, «момент крена в скоростной системе координат», соответственно буквенные обозначения следует образовывать добавлением к индекса соответствующей оси, например, | |
74. Момент рыскания | Составляющая результирующего момента по оси связанной системы координат | См. примечания к п.73 | |
75. Момент тангажа | Составляющая результирующего момента по оси связанной системы координат | См. | |
76. Аэродинамический момент крена Момент крена | Составляющая аэродинамического момента по оси связанной системы координат | 1. См. примечание 1 к п.73. 2. Термины для составляющих аэродинамического момента в других системах координат следует образовывать добавлением к данному термину терминов соответствующих систем координат, например, «аэродинамический момент крена в скоростной системе координат»; соответственно буквенные обозначения следует образовывать добавлением к индекса соответствующей оси, например, | |
77. Аэродинамический момент рыскания Момент рыскания | Составляющая аэродинамического момента по оси связанной системы координат | См. | |
78. Аэродинамический момент тангажа Момент тангажа | Составляющая аэродинамического момента по оси связанной системы координат | « | |
ПЕРЕГРУЗКИ ЛЕТАТЕЛЬНОГО АППАРАТА | |||
79. Перегрузка | Отношение результирующей силы к произведению массы летательного аппарата на ускорение свободного падения | ||
Угол рыскания — это… Что такое Угол рыскания?
- Угол рыскания
Словарь военных терминов.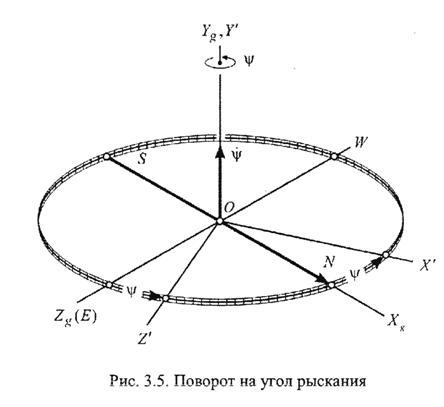 — М.: Воениздат.
Сост. А. М. Плехов, С. Г. Шапкин..
1988.
— М.: Воениздат.
Сост. А. М. Плехов, С. Г. Шапкин..
1988.
- Угол прицеливания
- Угол тангажа
Смотреть что такое «Угол рыскания» в других словарях:
Уравнения движения летательного аппарата — Обычно при анализе движения ЛА его рассматривают как абсолютно жёсткое тело. В этом случае в У. д. можно выделить две группы уравнений: У. д. центра масс (ЦМ) и У. д. относительно ЦМ. Если пренебречь вращением Земли, У. д. ЦМ ЛА можно представить … Энциклопедия техники
Рыскание — отклонение летательного аппарата от некоторого заданного направления полёта; характеризуется углом Р. и скоростью Р. Угол рыскания ( ) угол между осью OXg нормальной системы координат (СК), определяющей заданное направление движения, и проекцией… … Энциклопедия техники
рыскание — рыскание отклонение летательного аппарата от некоторого заданного направления полёта; характеризуется углом Р.
 и скоростью Р. Угол рыскания ψ угол между осью OXg нормальной системы координат (СК), определяющей заданное направление… … Энциклопедия «Авиация»
и скоростью Р. Угол рыскания ψ угол между осью OXg нормальной системы координат (СК), определяющей заданное направление… … Энциклопедия «Авиация»рыскание — рыскание отклонение летательного аппарата от некоторого заданного направления полёта; характеризуется углом Р. и скоростью Р. Угол рыскания ψ угол между осью OXg нормальной системы координат (СК), определяющей заданное направление… … Энциклопедия «Авиация»
Гироорбитант — гироорбита, гиробинормаль, гироскопическое устройство (См. Гироскопические устройства) для определения угла рыскания (отклонения от плоскости орбиты) искусственного спутника Земли. Г. представляет собой трёхстепенной астатический Гироскоп … Большая советская энциклопедия
системы координат — Рис. 1. Взаимное положение связанной, скоростной и полусвязанной систем координат. системы координат летательного аппарата правые прямоугольные системы координат, используемые при решении задач динамики полёта, а также для описания… … Энциклопедия «Авиация»
системы координат — Рис.
 1. Взаимное положение связанной, скоростной и полусвязанной систем координат. системы координат летательного аппарата правые прямоугольные системы координат, используемые при решении задач динамики полёта, а также для описания… … Энциклопедия «Авиация»
1. Взаимное положение связанной, скоростной и полусвязанной систем координат. системы координат летательного аппарата правые прямоугольные системы координат, используемые при решении задач динамики полёта, а также для описания… … Энциклопедия «Авиация»Рыскание — модели самолёта Рыскание (рысканье) угловые движения летательного аппарата, судна, автомобиля относительно вертикальной оси (см. также вертикальная ось самолё … Википедия
Рысканье — Рыскание обозначено жёлтой стрелкой. Рыскание (рысканье), угловые движения летательного аппарата, судна, автомобиля относительно вертикальной оси, а также небольшие изменения курса вправо или влево, свойственные судну. Один из трёх углов (крен,… … Википедия
рыскание — угол рыскания — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия Синонимы угол рыскания EN yaw … Справочник технического переводчика
Момент рысканья самолета в установившемся полете
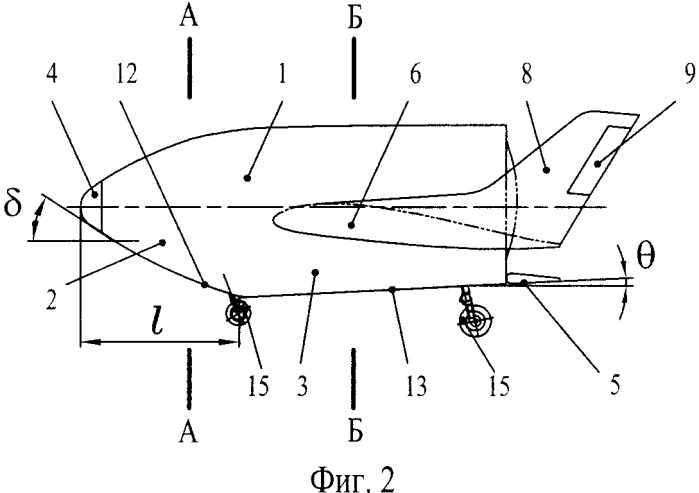
Рыскание — угловое вращение или раскачивание судна (самолёта или корабля) вокруг вертикальной оси на небольшой угол, а также небольшие изменения курса вправо или влево, свойственные судну(рис. 1). Один из трёх углов (крен, тангаж и рыскание), соответствующих трём углам Эйлера, которые задают наклон летательного средства относительно его центра.
1). Один из трёх углов (крен, тангаж и рыскание), соответствующих трём углам Эйлера, которые задают наклон летательного средства относительно его центра.
Составляющая моментов, действующих на самолет, в связанной системе координат относительно оси oy называют моментом рысканья (на риснуке My), который считается положительным, если он стремится развернуть самолет влево.
Величины аэродинамических моментов рассчитываются по формулам, аналогичным формулам для аэродинамических сил:
где my – коэффициент момента рысканья; S – площадь крыла; l – размах крыла.
Влияние вращения самолета на боковые моменты
Демпфирующий (тормозящий) момент и момент авторотации (раскручивающий) создаются как подъемными силами сечений крыла, так и силами лобового сопротивления этих сечений. При изменении углов атаки, вызванном вращением самолета, эти силы (подъемные и лобового сопротивления) изменяются не одинаково, В результате возникают моменты крена и рыскания, действующие в сторону вращения самолета. Момент рыскания появляется под действием разности сил лобового сопротивления полукрыльев. Сила лобового сопротивления у опускающегося полукрыла будет больше, чем у поднимающегося, так как у первого срыв потока развивается намного интенсивнее (у поднимающегося полукрыла углы атаки концевых сечений могут оказаться докритическими, т. е. здесь срыва пока не возникает). Возникший момент рыскания вызывает наружное скольжение (на опускающееся полукрыло)—эффективный угол стреловидности у поднимающегося полукрыла уменьшится, у опускающегося — возрастет, и, как следствие, подъемная сила у первого будет увеличиваться, у второго — уменьшаться, что приведет к усилению авторотации.
При изменении углов атаки, вызванном вращением самолета, эти силы (подъемные и лобового сопротивления) изменяются не одинаково, В результате возникают моменты крена и рыскания, действующие в сторону вращения самолета. Момент рыскания появляется под действием разности сил лобового сопротивления полукрыльев. Сила лобового сопротивления у опускающегося полукрыла будет больше, чем у поднимающегося, так как у первого срыв потока развивается намного интенсивнее (у поднимающегося полукрыла углы атаки концевых сечений могут оказаться докритическими, т. е. здесь срыва пока не возникает). Возникший момент рыскания вызывает наружное скольжение (на опускающееся полукрыло)—эффективный угол стреловидности у поднимающегося полукрыла уменьшится, у опускающегося — возрастет, и, как следствие, подъемная сила у первого будет увеличиваться, у второго — уменьшаться, что приведет к усилению авторотации.
Боковая балансировка самолета и усилия на рычагах управления
Боковая балансировкапредполагает наличие массовой, геометрической и аэродинамической симметрии самолета относительно плоскости X0Y.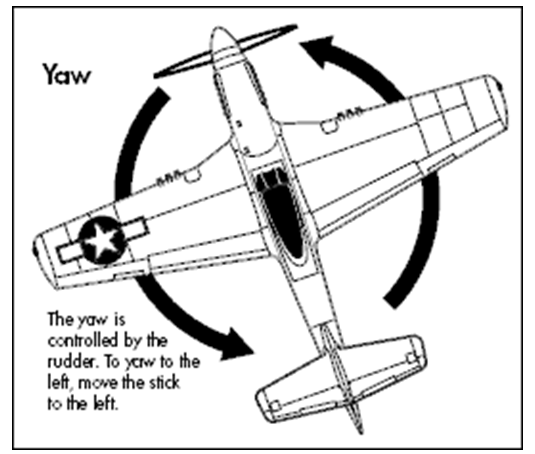 Условия боковой балансировки:
Условия боковой балансировки:
ΣMx = 0; ΣMy = 0.
В случае нарушения массовой симметрии (например, в результате отказа насосов не вырабатывается топливо из топливных баков правого крыла, рис. 7.24) под действием силы ΔG появляется момент кренаMx, самолет начинает крениться на правое крыло. Одновременно с креном появляется момент рысканияMy
Усилия управления
Усилие на командном рычаге управления может быть выражено через шарнирный момент на руле:
Pкр = Кш· mш · Sр · bр · q,
где Кш = рmax/xрmax — коэффициент передачи от командного рычага к рулю,
рmax — максимальный угол отклонения руля в радианах,
xрmax — максимальное перемещение командного рычага,
mш — коэффициент шарнирного момента руля,
Sр — площадь руля,
bр — хорда руля,
q — скоростной напор.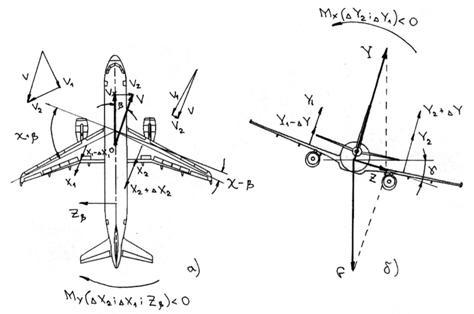
Коэффициент шарнирного момента при малых углах отклонения руля линейно зависит от величины этого угла. Отсюда следует, что в полете усилие на командном рычаге прямо пропорционально углу отклонения руля и величине скоростного напора.
Балансировочные усилия управления действуют в длительном установившемся режиме полета и обеспечивают уравновешивание (балансировку) самолета на этом режиме. Такие усилия лишь утомляют летчика и поэтому от них желательно избавиться.
Снятие балансировочных усилий с командных рычагов обеспечивается установкой на рулях триммеров — небольших поверхностей, шарнирно подвешенных в хвостовой части руля, и имеющих дополнительное, обычно электромеханическое, управление от летчика.
57.
58.
Читайте также:
АВТОМАТИЧЕСКОЕ ДЕМПФИРОВАНИЕ КОЛЕБАНИЙ ПО РЫСКАНИЮ | Авиация
6. -автоматическое отклонение руля направления от балансировочного положения демпфером рыскания; к№ — передаточный коэффициент по угловой скорости рыскания, показывающий, на какой угол должен отклониться руль направления при изменении угловой скорости рыскания на 1°/с (1 рад/с).
Другими словами, отклонение руля направления демпфером рыскания пропорционально угловой скорости рыскания.
Демпферы рыскания применяются на самолетах с бустерной или электродистанционной системой управления, если собственная путевая устой-
чивость самолета неудовлетворительна. Исполнительные устройства сервоприводов демпферов рыскания-рулевые агрегаты включаются в механическую проводку управления по последовательной схеме. Поэтому общее отклонение руля направления от балансировочного положения А6Н равно сумме ручного отклонения руля направления пилотом посредством педалей А5Е и автоматического отклонения руля направления демпфером рыскания:
А5Н = Д5Е + А5£р. (6.84)
Функциональная схема аналогового демпфера рыскания аналогична функциональным схемам демпферов тангажа и крена (рис. 6.9). Отклонение руля направления Д5Е создается пилотом путем перемещения педалей Пна величину Дхн от балансировочного положения. С помощью дифференциальной качалки осуществляется суммирование этого сигнала с управляющим сигналом демпфера рыскания А5ЕР. Рулевой привод руля направления РПЬП формирует отклонение руля направления.
6.9). Отклонение руля направления Д5Е создается пилотом путем перемещения педалей Пна величину Дхн от балансировочного положения. С помощью дифференциальной качалки осуществляется суммирование этого сигнала с управляющим сигналом демпфера рыскания А5ЕР. Рулевой привод руля направления РПЬП формирует отклонение руля направления.
Рис. 6.10. Переходные процессы в контуре угловой скорости рыскания при отклонении пилотом руля направления:
а-свободный самолет; 5-при включенном демпфере рыскания 194
При возникновении угловой скорости рыскания со датчик ДУС вырабатывает электрический сигнал иш, пропорциональный этой скорости. Вычислитель В вырабатывает управляющий сигнал ив согласно закону управления (6.83) на вход сумматора С сервопривода руля направления СПЬИ. Сервопривод преобразует этот сигнал в перемещение штока рулевого агрегата руля направления Д8£р.
Влияние демпферов рыскания на путевую устойчивость и управляемость.
Покажем, что с помощью демпфера рыскания улучшается степень путевой
статической устойчивости самолета m При отклонении руля направления демпфером появляется приращение коэффициента момента рыскания
Amy = my»A5;|p = my, k0)coy.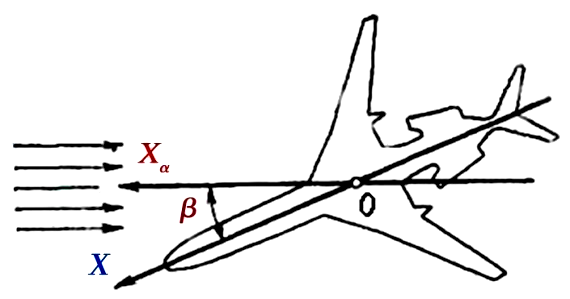 |, (6.88)
|, (6.88)
т. е. степень путевой статической устойчивости самолета с демфером рыскания выше, чем степень собственной путевой статической устойчивости самолета.
Покажем, что с помощью демпфера рыскания улучшается динамическая устойчивость бокового движения. На рис. 6.10, а представлены переходные процессы, возникающие в результате ступенчатого отклонения пилотом руля направления на угол Д5Р . Как видно из графиков рис. 6.10, б, демпфер рыскания уменьшает колебательность переходных процессов по угловой скорости и углу рыскания — уменьшаются период короткопериодических колебаний и время затухания. Так как отклонение руля направления демпфером Д6ДР вычитается из отклонения руля направления пилотом Л8Е, общее отклонение руля направления Л5Н становится меньше. Это приводит к уменьшению установившегося значения угловой скорости рыскания мурст по сравнению с управлением без демпфера, т. е. эффективность управления рулем направления от педалей уменьшается.
Особенности законов управления демпферов рыскания. р + 1) закона управления (6.90) реализуется в вычислителе блока демпфера, например, с помощью КС-цепочки.
р + 1) закона управления (6.90) реализуется в вычислителе блока демпфера, например, с помощью КС-цепочки.
Законы управления демпферов рыскания (6.89) и (6.90) позволяют уменьшить неблагоприятное влияние демпфера рыскания на путевую управляемость. Это достигается возвращением штока рулевого агрегата в нейтральное положение, когда юу = 0, т. е. А5“р = 0 при соуруст = сопзі. Поэтому противодействие демпфера пилоту прекращается и расход перемещения педалей для создания угловой скорости не изменяется. При этом, естественно, ухудшаются характеристики устойчивости.
Кроме уменьшения неблагоприятного влияния на путевую управляемость демпферы рыскания с законом управления (6.89) и (6.90) устраняют негативные последствия взаимосвязи движений по рысканию и крену. Так, в установившемся развороте с креном демпфер рыскания с законом управления (6.83) противодействует развороту отклонением руля направления при возникновении угловой скорости cov. Фильтрация постоянной
составляющей этой скорости законами управления (6. —— ray + F3ai[ Ц 1————— у+к5з—————- , (6-92)
—— ray + F3ai[ Ц 1————— у+к5з—————- , (6-92)
Тр+ 1 1 Т, р+1 TS(p+ 1 ‘
где F, aK принимает значение, равное 1 при выпуске закрылков на угол 30° и 0 при убранных закрылках.
Датчиком сигнала, пропорционального углу крена, служит гировертикаль ГВ. Датчиком сигнала, пропорционального углу отклонения элеронов, служит датчик обратной связи рулевой машины автопилота. Датчиком выпуска закрылков является концевой выключатель КВ8Ш.
Структурная схема демпфера рыскания, реализующего закон управления (6.92), представлена на рис. 6.12. Таким образом осуществляется демпфирование колебаний по рысканию с помощью системы АССУ-86.
Основной характеристикой боковой устойчивости самолета является степень путевой статической устойчивости по углу скольжения щР. Для ее увеличения и демпфирования боковых колебаний самолета в демпфере рыскания необходимо использовать сигнал, пропорциональный угловой скорости скольжения р. Однако создание датчиков такого сигнала затруднено, поэтому используют следующую упрощенную зависимость угловой скорости скольжения р от угловых скоростей рыскания и крена в горизонтальном полете с постоянным углом атаки а0 :
р = roycosa0 + caxsma0. р+1
р+1
+ ————— со* j — .
ТШР + 1 }
Передаточный коэффициент kffl корректируется по положению закрылков (принимает большее значение при выпущенных закрылках и уменьшается при убранных).
Структурная схема демпфера рыскания, реализующего закон управления (6.95), представлена на рис. 6.13. Так осуществляется демпфирование колебаний по рысканию с помощью демпфера рыскания ДР-62.
198
Значение «угол рыскания»
Лексическое значение: определение
Общий запас лексики (от греч. Lexikos) — это комплекс всех основных смысловых единиц одного языка. Лексическое значение слова раскрывает общепринятое представление о предмете, свойстве, действии, чувстве, абстрактном явлении, воздействии, событии и тому подобное. Иначе говоря, определяет, что обозначает данное понятие в массовом сознании. Как только неизвестное явление обретает ясность, конкретные признаки, либо возникает осознание объекта, люди присваивают ему название (звуко-буквенную оболочку), а точнее, лексическое значение. После этого оно попадает в словарь определений с трактовкой содержания.
После этого оно попадает в словарь определений с трактовкой содержания.
Словари онлайн бесплатно — открывать для себя новое
Словечек и узкоспециализированных терминов в каждом языке так много, что знать все их интерпретации попросту нереально. В современном мире существует масса тематических справочников, энциклопедий, тезаурусов, глоссариев. Пробежимся по их разновидностям:
- Толковые
Найти значение слова вы сможете в толковом словаре русского языка. Каждая пояснительная «статья» толкователя трактует искомое понятие на родном языке, и рассматривает его употребление в контенте. (PS: Еще больше случаев словоупотребления, но без пояснений, вы прочитаете в Национальном корпусе русского языка. Это самая объемная база письменных и устных текстов родной речи.) Под авторством Даля В.И., Ожегова С.И., Ушакова Д.Н. выпущены наиболее известные в нашей стране тезаурусы с истолкованием семантики. Единственный их недостаток — издания старые, поэтому лексический состав не пополняется.
- Энциклопедические В отличии от толковых, академические и энциклопедические онлайн-словари дают более полное, развернутое разъяснение смысла. Большие энциклопедические издания содержат информацию об исторических событиях, личностях, культурных аспектах, артефактах. Статьи энциклопедий повествуют о реалиях прошлого и расширяют кругозор. Они могут быть универсальными, либо тематичными, рассчитанными на конкретную аудиторию пользователей. К примеру, «Лексикон финансовых терминов», «Энциклопедия домоводства», «Философия. Энциклопедический глоссарий», «Энциклопедия моды и одежды», мультиязычная универсальная онлайн-энциклопедия «Википедия».
- Отраслевые
Эти глоссарии предназначены для специалистов конкретного профиля. Их цель объяснить профессиональные термины, толковое значение специфических понятий узкой сферы, отраслей науки, бизнеса, промышленности. Они издаются в формате словарика, терминологического справочника или научно-справочного пособия («Тезаурус по рекламе, маркетингу и PR», «Юридический справочник», «Терминология МЧС»).

- Этимологические и заимствований
Этимологический словарик — это лингвистическая энциклопедия. В нем вы прочитаете версии происхождения лексических значений, от чего образовалось слово (исконное, заимствованное), его морфемный состав, семасиология, время появления, исторические изменения, анализ. Лексикограф установит откуда лексика была заимствована, рассмотрит последующие семантические обогащения в группе родственных словоформ, а так же сферу функционирования. Даст варианты использования в разговоре. В качестве образца, этимологический и лексический разбор понятия «фамилия»: заимствованно из латинского (familia), где означало родовое гнездо, семью, домочадцев. С XVIII века используется в качестве второго личного имени (наследуемого). Входит в активный лексикон.
Этимологический словарик также объясняет происхождение подтекста крылатых фраз, фразеологизмов. Давайте прокомментируем устойчивое выражение «подлинная правда». Оно трактуется как сущая правда, абсолютная истина.
 Не поверите, при этимологическом анализе выяснилось, эта идиома берет начало от способа средневековых пыток. Подсудимого били кнутом с завязанными на конце узлом, который назывался «линь». Под линью человек выдавал все начистоту, под-линную правду.
Не поверите, при этимологическом анализе выяснилось, эта идиома берет начало от способа средневековых пыток. Подсудимого били кнутом с завязанными на конце узлом, который назывался «линь». Под линью человек выдавал все начистоту, под-линную правду. - Глоссарии устаревшей лексики
Чем отличаются архаизмы от историзмов?
Какие-то предметы последовательно выпадают из обихода. А следом выходят из употребления лексические определения единиц. Словечки, которые описывают исчезнувшие из жизни явления и предметы, относят к историзмам. Примеры историзмов: камзол, мушкет, царь, хан, баклуши, политрук, приказчик, мошна, кокошник, халдей, волость и прочие. Узнать какое значение имеют слова, которые больше не употребляется в устной речи, вам удастся из сборников устаревших фраз.
Архаизмамы — это словечки, которые сохранили суть, изменив терминологию: пиит — поэт, чело — лоб, целковый — рубль, заморский — иностранный, фортеция — крепость, земский — общегосударственный, цвибак — бисквитный коржик, печенье.
Иначе говоря их заместили синонимы, более актуальные в современной действительности. В эту категорию попали старославянизмы — лексика из старославянского, близкая к русскому: град (старосл.) — город (рус.), чадо — дитя, врата — ворота, персты — пальцы, уста — губы, влачиться — волочить ноги. Архаизмы встречаются в обороте писателей, поэтов, в псевдоисторических и фэнтези фильмах.
- Переводческие, иностранные Двуязычные словари для перевода текстов и слов с одного языка на другой. Англо-русский, испанский, немецкий, французский и прочие.
- Фразеологический сборник
Фразеологизмы — это лексически устойчивые обороты, с нечленимой структурой и определенным подтекстом. К ним относятся поговорки, пословицы, идиомы, крылатые выражения, афоризмы. Некоторые словосочетания перекочевали из легенд и мифов. Они придают литературному слогу художественную выразительность. Фразеологические обороты обычно употребляют в переносном смысле. Замена какого-либо компонента, перестановка или разрыв словосочетания приводят к речевой ошибке, нераспознанному подтексту фразы, искажению сути при переводе на другие языки.
 Найдите переносное значение подобных выражений в фразеологическом словарике.
Примеры фразеологизмов: «На седьмом небе», «Комар носа не подточит», «Голубая кровь», «Адвокат Дьявола», «Сжечь мосты», «Секрет Полишинеля», «Как в воду глядел», «Пыль в глаза пускать», «Работать спустя рукава», «Дамоклов меч», «Дары данайцев», «Палка о двух концах», «Яблоко раздора», «Нагреть руки», «Сизифов труд», «Лезть на стенку», «Держать ухо востро», «Метать бисер перед свиньями», «С гулькин нос», «Стреляный воробей», «Авгиевы конюшни», «Калиф на час», «Ломать голову», «Души не чаять», «Ушами хлопать», «Ахиллесова пята», «Собаку съел», «Как с гуся вода», «Ухватиться за соломинку», «Строить воздушные замки», «Быть в тренде», «Жить как сыр в масле».
Найдите переносное значение подобных выражений в фразеологическом словарике.
Примеры фразеологизмов: «На седьмом небе», «Комар носа не подточит», «Голубая кровь», «Адвокат Дьявола», «Сжечь мосты», «Секрет Полишинеля», «Как в воду глядел», «Пыль в глаза пускать», «Работать спустя рукава», «Дамоклов меч», «Дары данайцев», «Палка о двух концах», «Яблоко раздора», «Нагреть руки», «Сизифов труд», «Лезть на стенку», «Держать ухо востро», «Метать бисер перед свиньями», «С гулькин нос», «Стреляный воробей», «Авгиевы конюшни», «Калиф на час», «Ломать голову», «Души не чаять», «Ушами хлопать», «Ахиллесова пята», «Собаку съел», «Как с гуся вода», «Ухватиться за соломинку», «Строить воздушные замки», «Быть в тренде», «Жить как сыр в масле». - Определение неологизмов
Языковые изменения стимулирует динамичная жизнь. Человечество стремятся к развитию, упрощению быта, инновациям, а это способствует появлению новых вещей, техники. Неологизмы — лексические выражения незнакомых предметов, новых реалий в жизни людей, появившихся понятий, явлений.
 К примеру, что означает «бариста» — это профессия кофевара; профессионала по приготовлению кофе, который разбирается в сортах кофейных зерен, умеет красиво оформить дымящиеся чашечки с напитком перед подачей клиенту. Каждое словцо когда-то было неологизмом, пока не стало общеупотребительным, и не вошло в активный словарный состав общелитературного языка. Многие из них исчезают, даже не попав в активное употребление. Неологизмы бывают словообразовательными, то есть абсолютно новообразованными (в том числе от англицизмов), и семантическими. К семантическим неологизмам относятся уже известные лексические понятия, наделенные свежим содержанием, например «пират» — не только морской корсар, но и нарушитель авторских прав, пользователь торрент-ресурсов. Вот лишь некоторые случаи словообразовательных неологизмов: лайфхак, мем, загуглить, флэшмоб, кастинг-директор, пре-продакшн, копирайтинг, френдить, пропиарить, манимейкер, скринить, фрилансинг, хедлайнер, блогер, дауншифтинг, фейковый, брендализм.
К примеру, что означает «бариста» — это профессия кофевара; профессионала по приготовлению кофе, который разбирается в сортах кофейных зерен, умеет красиво оформить дымящиеся чашечки с напитком перед подачей клиенту. Каждое словцо когда-то было неологизмом, пока не стало общеупотребительным, и не вошло в активный словарный состав общелитературного языка. Многие из них исчезают, даже не попав в активное употребление. Неологизмы бывают словообразовательными, то есть абсолютно новообразованными (в том числе от англицизмов), и семантическими. К семантическим неологизмам относятся уже известные лексические понятия, наделенные свежим содержанием, например «пират» — не только морской корсар, но и нарушитель авторских прав, пользователь торрент-ресурсов. Вот лишь некоторые случаи словообразовательных неологизмов: лайфхак, мем, загуглить, флэшмоб, кастинг-директор, пре-продакшн, копирайтинг, френдить, пропиарить, манимейкер, скринить, фрилансинг, хедлайнер, блогер, дауншифтинг, фейковый, брендализм. Еще вариант, «копираст» — владелец контента или ярый сторонник интеллектуальных прав.
Еще вариант, «копираст» — владелец контента или ярый сторонник интеллектуальных прав. - Прочие 177+ Кроме перечисленных, есть тезаурусы: лингвистические, по различным областям языкознания; диалектные; лингвострановедческие; грамматические; лингвистических терминов; эпонимов; расшифровки сокращений; лексикон туриста; сленга. Школьникам пригодятся лексические словарники с синонимами, антонимами, омонимами, паронимами и учебные: орфографический, по пунктуации, словообразовательный, морфемный. Орфоэпический справочник для постановки ударений и правильного литературного произношения (фонетика). В топонимических словарях-справочниках содержатся географические сведения по регионам и названия. В антропонимических — данные о собственных именах, фамилиях, прозвищах.
Толкование слов онлайн: кратчайший путь к знаниям
Проще изъясняться, конкретно и более ёмко выражать мысли, оживить свою речь, — все это осуществимо с расширенным словарным запасом. С помощью ресурса How to all вы определите значение слов онлайн, подберете родственные синонимы и пополните свою лексику. Последний пункт легко восполнить чтением художественной литературы. Вы станете более эрудированным интересным собеседником и поддержите разговор на разнообразные темы. Литераторам и писателям для разогрева внутреннего генератора идей полезно будет узнать, что означают слова, предположим, эпохи Средневековья или из философского глоссария.
Последний пункт легко восполнить чтением художественной литературы. Вы станете более эрудированным интересным собеседником и поддержите разговор на разнообразные темы. Литераторам и писателям для разогрева внутреннего генератора идей полезно будет узнать, что означают слова, предположим, эпохи Средневековья или из философского глоссария.
Глобализация берет свое. Это сказывается на письменной речи. Стало модным смешанное написание кириллицей и латиницей, без транслитерации: SPA-салон, fashion-индустрия, GPS-навигатор, Hi-Fi или High End акустика, Hi-Tech электроника. Чтобы корректно интерпретировать содержание слов-гибридов, переключайтесь между языковыми раскладками клавиатуры. Пусть ваша речь ломает стереотипы. Тексты волнуют чувства, проливаются эликсиром на душу и не имеют срока давности. Удачи в творческих экспериментах!
Проект how-to-all.com развивается и пополняется современными словарями с лексикой реального времени. Следите за обновлениями. Этот сайт помогает говорить и писать по-русски правильно. Расскажите о нас всем, кто учится в универе, школе, готовится к сдаче ЕГЭ, пишет тексты, изучает русский язык.
Расскажите о нас всем, кто учится в универе, школе, готовится к сдаче ЕГЭ, пишет тексты, изучает русский язык.
Угол рыскания
Угол рыскания — угол между осевой линией автомобиля и направлением, в котором он движется при повороте… Словарь механиков
угол рыскания — Угол отклонения между продольной осью транспортного средства и его истинным направлением движения, т. Е. Разница между направлением, в которое указывает транспортное средство при повороте, и направлением, в котором оно фактически движется … Автомобильный словарь условия
Строка рыскания — Строка рыскания, также известная как струна скольжения, представляет собой простое устройство для индикации скольжения или заноса самолета в полете.Он выполняет ту же функцию, что и шарик индикатора скольжения, но более чувствителен и не требует от пилота осмотра…… Wikipedia
Рыскание — Слово рыскание может относиться к: * углу рыскания, углу относительно вертикальной оси ** оси рыскания * рысканью (бог), левантийскому богу * рысканью, компоненту ветряной турбины * YAW, Halifax / Shearwater Heliport s IATA код * Эллен Бич Яу (1869 ndash; 1947), концертная певица * Yàw… Wikipedia
индикатор рыскания — устройство, измеряющее угловое направление воздушного потока относительно продольной вертикальной плоскости самолета.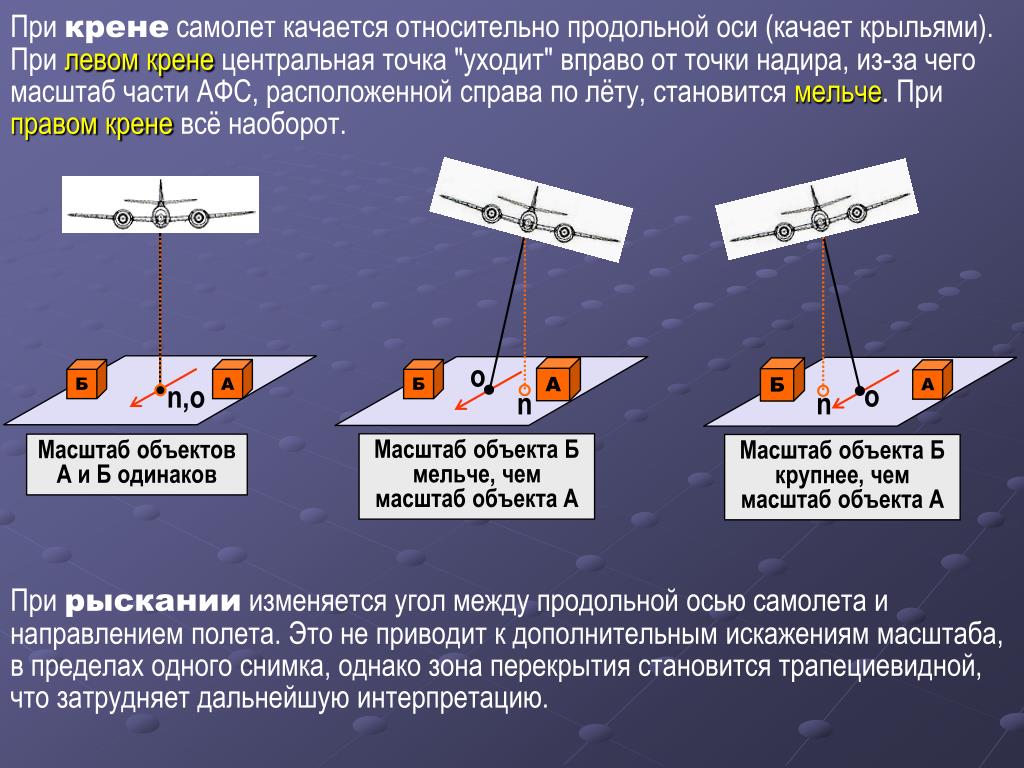 Это может быть выполнено с помощью уравновешивающей заслонки или датчика перепада давления, который выравнивает датчик по воздушному потоку и… Авиационный словарь
Это может быть выполнено с помощью уравновешивающей заслонки или датчика перепада давления, который выравнивает датчик по воздушному потоку и… Авиационный словарь
угол рыскания — Угол между линией в направлении полета и плоскостью, проходящей через продольную и вертикальную оси самолета. Он считается положительным, если нос смещен вправо, и отрицательным, если смещен влево. Также называется…… Авиационный словарь
угол — См. Угол Аккермана угол приближения угол атаки угол кулачка угол ролика угол вылета dwell dwell angle передний треугольник угол заголовка… Словарь автомобильных терминов
angle — Угол поворота по Акерману аэродинамический угол атаки угол наклона при окружающем ветре угол наклона угол развала угол поворота кастера угол курса угол курса угол наклона угол фазовый угол угол скольжения… Словарь механики
ускорение рыскания — Постоянное увеличение угла рыскания… Словарь автомобильных терминов
рысканье — [yô] vi. [ON jaga, качаться, двигаться вперед и назад & LT; или сродни Du & Ger jagen, охотиться] 1. качаться вперед и назад поперек своего курса, как корабль, толкаемый высокими волнами 2. качаться влево или вправо по вертикальной оси, так что продольный…… English World словарь
[ON jaga, качаться, двигаться вперед и назад & LT; или сродни Du & Ger jagen, охотиться] 1. качаться вперед и назад поперек своего курса, как корабль, толкаемый высокими волнами 2. качаться влево или вправо по вертикальной оси, так что продольный…… English World словарь
— это … Что такое угол рыскания?
Угол рыскания — Угол рыскания — это угол между курсом транспортного средства и исходным курсом (обычно истинным или магнитным севером).Один из углов Тейта Брайана. В аэронавтике, робототехнике и морском управлении ему обычно присваивается сокращенное обозначение psi.…… Wikipedia
угол рыскания — угол между осевой линией автомобиля и направлением, в котором он движется при повороте… Словарь механиков
угол рыскания — Угол отклонения между продольной осью транспортного средства и его истинным направлением движения, т. Е. Разница между направлением, в которое указывает транспортное средство при повороте, и направлением, в котором оно фактически движется . .. Автомобильный словарь условия
.. Автомобильный словарь условия
Строка рыскания — Строка рыскания, также известная как струна скольжения, представляет собой простое устройство для индикации скольжения или заноса самолета в полете.Он выполняет ту же функцию, что и шарик индикатора скольжения, но более чувствителен и не требует от пилота осмотра…… Wikipedia
Рыскание — Слово рыскание может относиться к: * углу рыскания, углу относительно вертикальной оси ** оси рыскания * рысканью (бог), левантийскому богу * рысканью, компоненту ветряной турбины * YAW, Halifax / Shearwater Heliport s IATA код * Эллен Бич Яу (1869 ndash; 1947), концертная певица * Yàw… Wikipedia
индикатор рыскания — устройство, измеряющее угловое направление воздушного потока относительно продольной вертикальной плоскости самолета.Это может быть выполнено с помощью уравновешивающей заслонки или датчика перепада давления, который выравнивает датчик по воздушному потоку и… Авиационный словарь
угол рыскания — Угол между линией в направлении полета и плоскостью, проходящей через продольную и вертикальную оси самолета.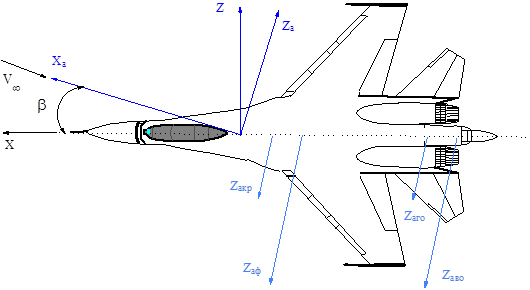 Он считается положительным, если нос смещен вправо, и отрицательным, если смещен влево. Также называется…… Авиационный словарь
Он считается положительным, если нос смещен вправо, и отрицательным, если смещен влево. Также называется…… Авиационный словарь
угол — См. Угол Аккермана угол приближения угол атаки угол кулачка угол ролика угол вылета dwell dwell angle передний треугольник угол заголовка… Словарь автомобильных терминов
angle — Угол поворота по Акерману аэродинамический угол атаки угол наклона при окружающем ветре угол наклона угол развала угол поворота кастера угол курса угол курса угол наклона угол фазовый угол угол скольжения… Словарь механики
ускорение рыскания — Постоянное увеличение угла рыскания… Словарь автомобильных терминов
рысканье — [yô] vi.[ON jaga, качаться, двигаться вперед и назад & LT; или сродни Du & Ger jagen, охотиться] 1. качаться вперед и назад поперек своего курса, как корабль, толкаемый высокими волнами 2. качаться влево или вправо по вертикальной оси, так что продольный…… English World словарь
DCM — Введение в кинематику ориентации — Starlino Electronics
Введение
Эта статья является продолжением моего руководства по IMU и охватывает дополнительные темы кинематики ориентации. Сначала я рассмотрю некоторую теорию, а затем представлю практический пример с построением кода вокруг Arduino и датчика IMU 6DOF (acc_gyro_6dof). Целью этого эксперимента является создание алгоритма объединения данных гироскопа и акселерометра с целью создания оценки ориентации устройства в пространстве. Такой алгоритм уже был представлен в части 3 моего «Руководства по IMU», а практический эксперимент Arduino с кодом был представлен в статье «Использование 5DOF IMU» и получил название «Упрощенный фильтр Калмана», представляя простую альтернативу хорошо известному Алгоритм фильтра Калмана.В этой статье мы воспользуемся другим подходом, использующим DCM (матрицу косинусов направления). Для читателя, незнакомого с датчиками MEMS, рекомендуется прочитать части 1 и 2 статьи IMU Guide. Также для проведения экспериментов, представленных в этом тексте, рекомендуется приобрести плату Arduino и датчик acc_gyro_6dof.
Сначала я рассмотрю некоторую теорию, а затем представлю практический пример с построением кода вокруг Arduino и датчика IMU 6DOF (acc_gyro_6dof). Целью этого эксперимента является создание алгоритма объединения данных гироскопа и акселерометра с целью создания оценки ориентации устройства в пространстве. Такой алгоритм уже был представлен в части 3 моего «Руководства по IMU», а практический эксперимент Arduino с кодом был представлен в статье «Использование 5DOF IMU» и получил название «Упрощенный фильтр Калмана», представляя простую альтернативу хорошо известному Алгоритм фильтра Калмана.В этой статье мы воспользуемся другим подходом, использующим DCM (матрицу косинусов направления). Для читателя, незнакомого с датчиками MEMS, рекомендуется прочитать части 1 и 2 статьи IMU Guide. Также для проведения экспериментов, представленных в этом тексте, рекомендуется приобрести плату Arduino и датчик acc_gyro_6dof.
Предпосылки
Никакой действительно сложной математики не требуется. Найдите хорошую книгу по матричным операциям, это все, что вам может понадобиться сверх школьного курса математики.Если вы хотите освежить свои знания, ниже приведены несколько быстрых статей: Декартова система координат
Найдите хорошую книгу по матричным операциям, это все, что вам может понадобиться сверх школьного курса математики.Если вы хотите освежить свои знания, ниже приведены несколько быстрых статей: Декартова система координат
— http://en.wikipedia.org/wiki/Cartesian_coordinate_system
Rotation — http://en.wikipedia.org/wiki/Rotation_%28mat Mathematics % 29
Векторное скалярное произведение — http://en.wikipedia.org/wiki/Dot_product
Векторное перекрестное произведение — http://en.wikipedia.org/wiki/Cross_product
Матричное умножение — http: //en.wikipedia. org / wiki / Matrix_multiplication
Block Matrix — http: //en.wikipedia.org / wiki / Block_matrix
Transpose Matrix — http://en.wikipedia.org/wiki/Transpose
Triple Product — http://en.wikipedia.org/wiki/Triple_product
Обозначения
Векторы выделены полужирным шрифтом – , поэтому, например, « v » — это вектор, а «v» — скаляр (если вы не можете различить два, возникает проблема с форматированием текста, где бы вы ни находились. читая это).
читая это).
Часть 1. Матрица DCM
Вообще говоря, кинематика ориентации имеет дело с вычислением относительной ориентации тела относительно глобальной системы координат.Полезно прикрепить систему координат к нашему фрейму тела и называть ее Oxyz, а другую — к нашему глобальному фрейму и назвать ее OXYZ. И глобальный, и основной фреймы имеют одно и то же фиксированное начало O (см. Fig. 1 ). Давайте также определим i, j, k как единичные векторы, сонаправленные с осями x, y и z каркаса тела — другими словами, они являются версиями Oxyz, и пусть I, J, K являются версиями глобальный фрейм OXYZ.
Рисунок 1
Таким образом, по определению, выраженный через глобальные координаты векторов I, J, K можно записать как:
I G = {1,0,0} T , J G = {0,1,0} T , K G = {0, 0,1} Т
Примечание: мы используем нотацию {…} T для обозначения вектора-столбца, другими словами, вектор-столбец — это переведенный вектор-строка. Ориентация векторов (строка / столбец) станет актуальной, как только мы начнем умножать их на матрицу позже в этом тексте.
Ориентация векторов (строка / столбец) станет актуальной, как только мы начнем умножать их на матрицу позже в этом тексте.
Аналогично, в терминах координат тела векторов i, j, k можно записать как:
i B = {1,0,0} T , j B = {0,1,0} T , k B = {0, 0,1} Т
Теперь давайте посмотрим, можем ли мы записать векторы i, j, k в глобальных координатах.Возьмем для примера вектор и и запишем его глобальные координаты:
i G = {i x G , i y G , i z G } T
Опять же, в качестве примера давайте проанализируем координату X i x G , она вычисляется как длина проекции вектора i на глобальную ось X.
i x G = | i | cos (X, i ) = cos ( I , i )
Где | i | — норма (длина) единичного вектора i , а cos ( I , i ) — косинус угла, образованного векторами I и i .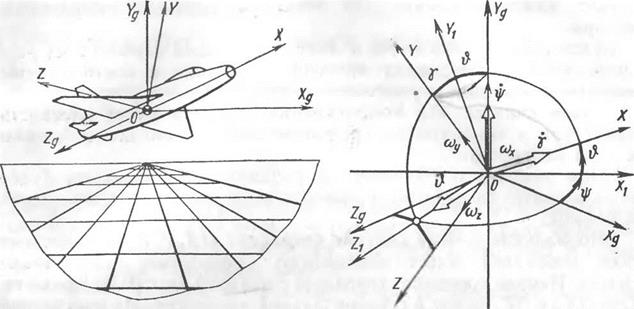 Используя тот факт, что | I | = 1 и | i | = 1 (по определению они являются единичными векторами). Мы можем написать:
Используя тот факт, что | I | = 1 и | i | = 1 (по определению они являются единичными векторами). Мы можем написать:
i x G = cos ( I , i ) = | I || i | cos ( I , i ) = I.i
Где I.i . — скалярное (точечное) произведение векторов I и i . Для целей вычисления скалярного произведения I.i не имеет значения, в какой системе координат измеряются эти векторы, если они оба выражены в одной и той же системе, поскольку поворот не изменяет угол между векторами, так что: I.i = I B .i B = I G .i G = cos ( I B .i B ) = cos () G .i G ), поэтому для простоты мы пропустим верхний индекс в скалярных произведениях Ii, Jj, Kk и косинусах cos ( I , i ), cos ( Дж , Дж ), cos ( К , К ).
Аналогичным образом мы можем показать, что:
i y G = J.i , i z G = K.i , поэтому теперь мы можем записать вектор i в глобальной системе координат как:
i G = { I.i, J.i, K.i } T
Кроме того, аналогичным образом можно показать, что j G = { I.j, J.j, K.j } T , k G = { I.k, J.k, K.k } T .
Теперь у нас есть полный набор глобальных координат для версоров нашего тела i, j, k , и мы можем организовать эти значения в удобной матричной форме:
(Ур.1.1)
Эта матрица называется Матрицей Направляющих Косинусов по очевидным причинам — она состоит из косинусов углов всех возможных комбинаций тела и глобальных версоров.
Задача выражения глобальных версоров кадров I G , J G , K G в координатах корпуса корпуса является симметричной по своей природе и может быть решена простой заменой обозначений I, J, K с i, j, k, результаты:
I B = { I. i, Ij, Ik } T , J B = { Ji, Jj, Jk } T , K B = { Ki, Kj, Kk } Т
i, Ij, Ik } T , J B = { Ji, Jj, Jk } T , K B = { Ki, Kj, Kk } Т
и организованы в матричную форму:
(уравнение 1.2)
Теперь легко заметить, что DCM B = (DCM G ) T или DCM G = (DCM B ) T , другими словами, две матрицы являются переводом друг друга, мы Позже я воспользуюсь этим важным свойством.
Также обратите внимание, что DCM B . DCM G = (DCM G ) T .DCM G = DCM B . (DCM B ) T = I 3 , где I 3 — это единичная матрица 3 × 3. Другими словами, матрицы DCM ортогональны.
Это можно доказать, просто развернув матричное умножение в виде блочной матрицы:
(уравнение 1.3)
Чтобы доказать это, мы используем такие свойства, как например: i GT . i G = | i G || i G | cos (0) = 1 и i GT . j G = 0, потому что ( i и j ортогональны) и так далее.
i G = | i G || i G | cos (0) = 1 и i GT . j G = 0, потому что ( i и j ортогональны) и так далее.
Матрица DCM (также часто называемая матрицей вращения) имеет большое значение в кинематике ориентации, поскольку она определяет поворот одного кадра относительно другого. Его также можно использовать для определения глобальных координат произвольного вектора, если мы знаем его координаты в кадре тела (и наоборот).
Рассмотрим такой вектор с координатами тела:
r B = { r x B , r y B , r z B } T и давайте попробуем определить его координаты в глобальном фрейме, с использованием известной матрицы вращения DCM G .
Начнем со следующих обозначений:
r G = {r x G , r y G , r z G } T .
Теперь займемся первой координатой r x G :
r x G = | r G | cos ( I G , r G ), потому что r x G — это проекция r G на ось X, которая сонаправлена с I G .
Далее отметим, что по определению поворот — это такое преобразование, которое не изменяет масштаб вектора и не изменяет угол между двумя векторами, которые подвергаются одинаковому вращению, поэтому, если мы выразим некоторые векторы в другой повернутой системе координат норма и угол между векторами не изменятся:
| r G | = | r B | , | I G | = | I B | = 1 и cos ( I G , r G ) = cos ( I B , r B ), поэтому мы можем использовать это свойство для записи
r x G = | r G | cos ( I G , r G ) = | I B || r B | cos ( I B , r B ) = I B .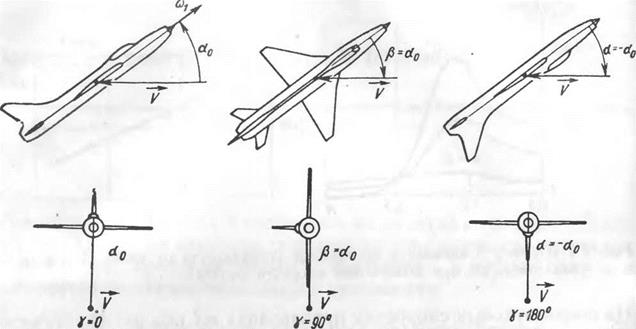 r B = I B . { r x B , r y B , r z B } T , используя одно или два определения скалярного произведения.
r B = I B . { r x B , r y B , r z B } T , используя одно или два определения скалярного произведения.
Теперь вспомним, что I B = { I.i, I.j, I.k } T и используя другое определение скалярного произведения:
r x G = I B . r B = { I.i, I.j, I.k } T . { r x B , r y B , r z B } T = r x B Ii + B Ij + r z B Ik
Таким же образом можно показать, что:
r y G = r x B J.i + r y B Jj + r z B Jk
r z G = r x B Ki4 Ki y B Kj + r z B Kk
Наконец, давайте запишем это в более компактной матричной форме:
(уравнение 1.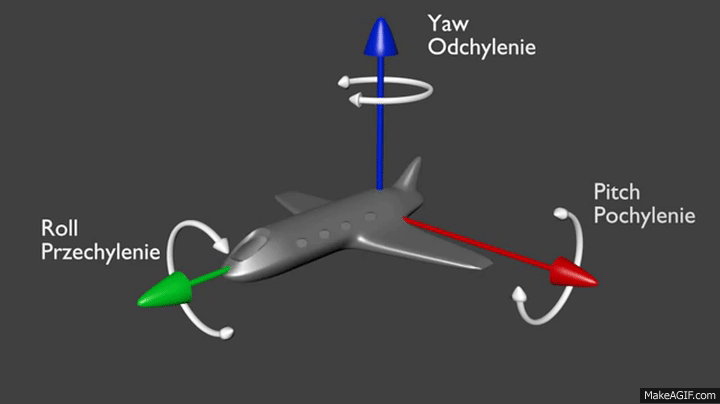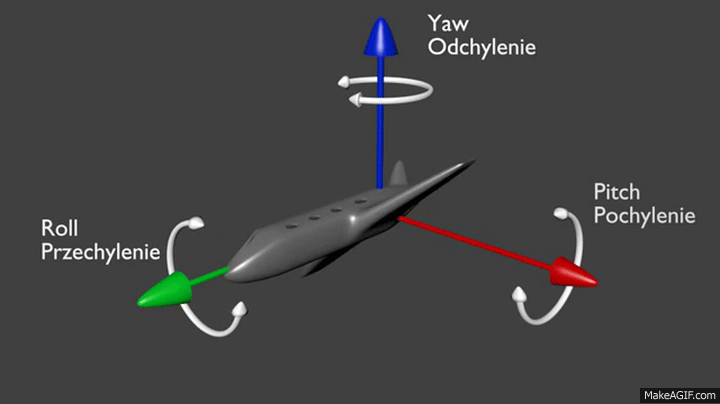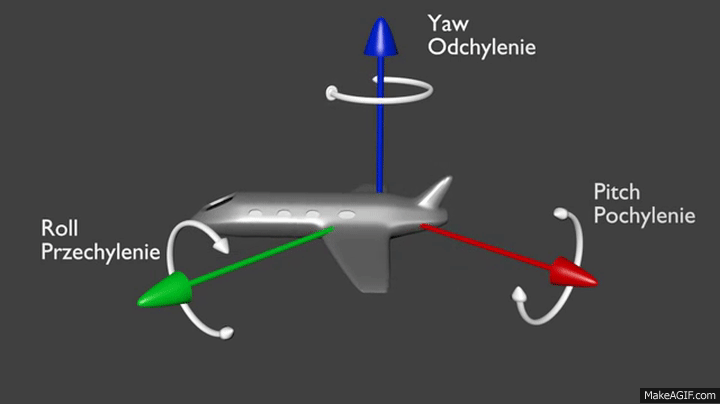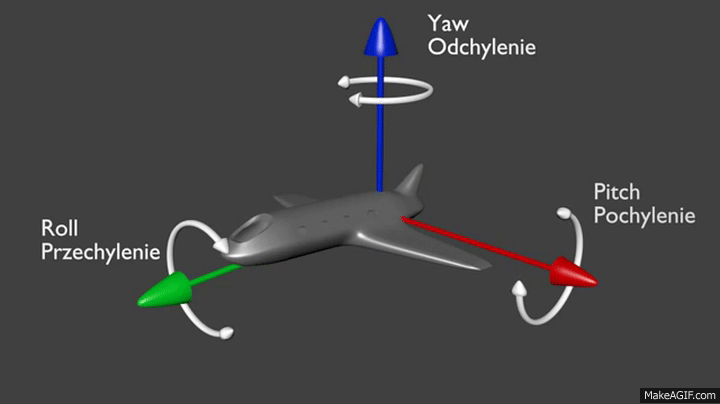 4)
4)
Таким образом, матрица DCM может использоваться для преобразования произвольного вектора r B , выраженного в одной системе координат B, в повернутую систему координат G.
Мы можем использовать аналогичную логику, чтобы доказать обратный процесс:
(уравнение 1.5)
Или мы можем прийти к такому же выводу, умножив обе части в (уравнение 1.4) на DCM B , что равно DCM GT , и используя свойство, что DCM GT .DCM G = I 3 , см. ( уравнение 1.3) :
DCM B r G = DCM B DCM G r B = DCM GT DCM G r B 26 = I 3 = r B
Часть 2.Угловая скорость
Пока у нас есть способ охарактеризовать ориентацию одного кадра относительно другого повернутого кадра, это матрица DCM, которая позволяет нам легко преобразовывать глобальные координаты и координаты тела туда и обратно с помощью (уравнение 1. 4), и ( Уравнение 1.5). В этом разделе мы проанализируем вращение как функцию времени, что поможет нам установить правила обновления матрицы DCM на основе характеристики, называемой угловой скоростью. Давайте рассмотрим произвольный вращающийся вектор r и определим его координаты в момент времени t как r (t).Теперь рассмотрим небольшой интервал времени dt и сделаем следующие обозначения: r = r (t), r ‘ = r (t + dt) и d r = r ‘ — r :
Рисунок 2
Предположим, что в течение очень небольшого временного интервала dt → 0 вектор r имеет поворот вокруг оси, сонаправленной с единичным вектором u на угол dθ, и оказался в позиции r ’.Поскольку u является нашей осью вращения, она перпендикулярна плоскости, в которой произошло вращение (плоскость, образованная r и r ‘), поэтому u ортогональна как r , так и r ‘. Есть два единичных вектора, которые ортогональны плоскости, образованной r и r ‘, они показаны на картинке как u и u’ , так как мы все еще определяем вещи, мы выберем один который сонаправлен с поперечным произведением r x r ‘, следуя правилу правой системы координат.Таким образом, поскольку и — единичный вектор | u | = 1 и является сонаправленным с r x r ’, мы можем вычесть его следующим образом:
Есть два единичных вектора, которые ортогональны плоскости, образованной r и r ‘, они показаны на картинке как u и u’ , так как мы все еще определяем вещи, мы выберем один который сонаправлен с поперечным произведением r x r ‘, следуя правилу правой системы координат.Таким образом, поскольку и — единичный вектор | u | = 1 и является сонаправленным с r x r ’, мы можем вычесть его следующим образом:
u = ( r x r ’) / | r x r ’| = ( r x r ‘) / (| r || r ‘ | sin (dθ)) = ( r x r ‘) / (| r | 2 sin (dθ)) (уравнение 2.1)
Поскольку поворот не меняет длину вектора, мы использовали свойство, что | r ’| = | р |.
Линейная скорость вектора r может быть определена как вектор :
v = d r / dt = ( r ’- r ) / dt (уравнение 2. 2)
2)
Обратите внимание, что, поскольку наша dt приближается к 0, dθ → 0, поэтому угол между векторами r и d r (назовем его α) можно найти из равнобедренного треугольника, очерченного r , r. ‘ и d r:
α = (π — dθ) / 2 и поскольку dθ → 0, то α → π / 2
Это говорит нам о том, что r перпендикулярно d r , когда dt → 0 и, следовательно, r перпендикулярно v , поскольку v и d r сонаправлены с (Ур.2.2):
v ⊥ r (уравнение 2.21)
Теперь мы готовы определить вектор угловой скорости. В идеале такой вектор должен определять скорость изменения угла θ и оси вращения, поэтому мы определяем его следующим образом:
w = (dθ / dt) u (уравнение 2.3)
Действительно норма w | w | = dθ / dt и направление w совпадает с осью вращения u .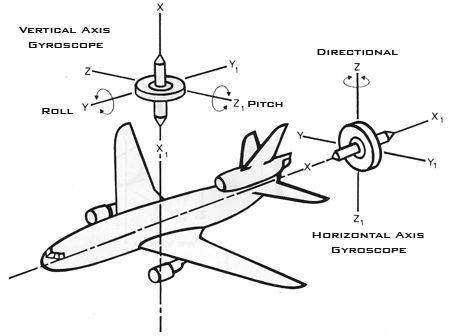 Давайте расширим (уравнение 2.3) и попытаемся установить связь с линейной скоростью v:
Давайте расширим (уравнение 2.3) и попытаемся установить связь с линейной скоростью v:
Используя (уравнение 2.3) и (уравнение 2.1) :
w = (dθ / dt) u = (dθ / dt) ( r x r ’) / (| r | 2 sin (dθ))
Теперь обратите внимание, что когда dt → 0, то же самое происходит и с dθ → 0, и, следовательно, при малых dθ, sin (dθ) ≈ dθ, мы получаем:
w = ( r x r ’) / (| r | 2 dt) (Ур.2.4)
Теперь, поскольку r ’= r + d r , d r / dt = v, r x r = 0 и с использованием распределительного свойства перекрестного произведения поверх сложения:
w = ( r x ( r + d r) ) / (| r | 2 dt) = ( r x r + r xd r) ) / (| r | 2 dt) = r x (d r / dt) / | r | 2
И наконец:
w = r x v / | r | 2 (Ур.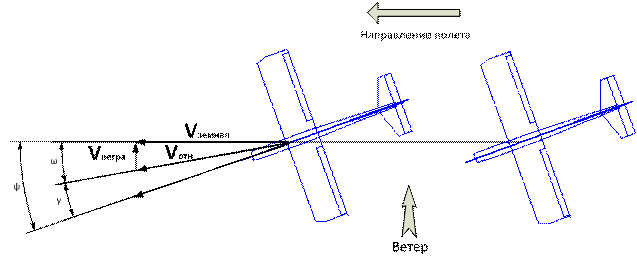 2,5)
2,5)
Это уравнение устанавливает способ вычисления угловой скорости на основе известной линейной скорости v .
Мы можем легко доказать обратное уравнение, которое позволяет вычесть линейную скорость из угловой скорости:
v = w x r (уравнение 2.6)
Это можно проверить, просто расширив w от (уравнение 2.5) и используя правило тройного произведения векторов ( a x b ) x c = ( a . c ) b — ( b . c ) a . Также мы будем использовать тот факт, что v и r перпендикулярны (уравнение 2.21) и, следовательно, v . r = 0
w x r = ( r x v / | r | 2 ) x r = ( r x v) x r / | r | 2 = (( r . r ) v + ( v . r ) r ) / | r | 2 = (| r | 2 v + 0) | r | 2 = против
Итак, мы только что доказали, что (уравнение 2.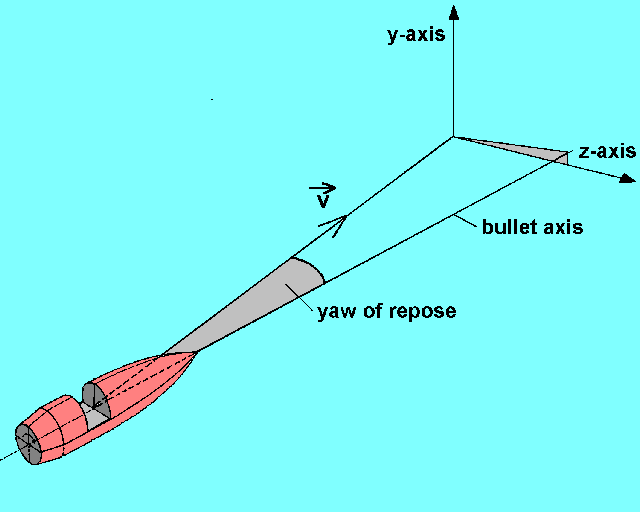 6) истинно. Просто чтобы проверить (уравнение 2.6) интуитивно — из Рисунок 2 действительно v имеет направление w x r с использованием правила правой руки и действительно v ⊥ r и v ⊥ w , потому что он находится в одной плоскости с r и r ‘.
6) истинно. Просто чтобы проверить (уравнение 2.6) интуитивно — из Рисунок 2 действительно v имеет направление w x r с использованием правила правой руки и действительно v ⊥ r и v ⊥ w , потому что он находится в одной плоскости с r и r ‘.
Часть 3. Гироскопы и вектор угловой скорости
Трехосевой гироскоп MEMS — это устройство, которое определяет вращение вокруг трех осей, прикрепленных к самому устройству (корпусу корпуса). Если мы примем систему координат устройства (рамка тела) и проанализируем некоторые векторы, привязанные к Земле (глобальная рамка), например вектор K , указывающий на зенит, или вектор I , указывающий на север, — тогда это будет казаться наблюдателю внутри устройства эти векторы вращаются вокруг центра устройства.Пусть w x , w y , w z — выходные данные гироскопа, выраженные в рад / с — измеренное вращение вокруг осей x, y, z соответственно. Преобразование необработанного вывода гироскопа в физические значения обсуждается, например, здесь: http://www.starlino.com/imu_guide.html. Если мы запрашиваем гироскоп через регулярные небольшие интервалы времени dt, , то вывод гироскопа говорит нам, что в течение этого временного интервала Земля вращалась вокруг оси гироскопа x на угол dθ x = w x dt , вокруг оси y на угол dθ y = w y dt и вокруг оси z на угол dθ z = w z dt.Эти вращения можно охарактеризовать векторами угловой скорости: w x = w x i = {w x , 0 , 0 } T , w y = w y j = {0 , w y , 0 } T , w z = w z k = {0 , 0, w z } T , где i, j, k являются версорами локальной системы координат (они сонаправлены с осями тела x, y, z соответственно).
Преобразование необработанного вывода гироскопа в физические значения обсуждается, например, здесь: http://www.starlino.com/imu_guide.html. Если мы запрашиваем гироскоп через регулярные небольшие интервалы времени dt, , то вывод гироскопа говорит нам, что в течение этого временного интервала Земля вращалась вокруг оси гироскопа x на угол dθ x = w x dt , вокруг оси y на угол dθ y = w y dt и вокруг оси z на угол dθ z = w z dt.Эти вращения можно охарактеризовать векторами угловой скорости: w x = w x i = {w x , 0 , 0 } T , w y = w y j = {0 , w y , 0 } T , w z = w z k = {0 , 0, w z } T , где i, j, k являются версорами локальной системы координат (они сонаправлены с осями тела x, y, z соответственно). Каждое из этих трех вращений вызовет линейное смещение, которое можно выразить с помощью (уравнение 2.6) :
Каждое из этих трех вращений вызовет линейное смещение, которое можно выразить с помощью (уравнение 2.6) :
d r 1 = dt v 1 = dt ( w x x r ); d r 2 = dt v 2 = dt ( w y x r ); d r 3 = dt v 3 = dt ( w z x r ) .
Комбинированный эффект этих трех смещений будет:
d r = d r 1 + d r 2 + d r 3 = dt ( w x x r + w x r + w z x r ) = dt ( w x + w y + w r (перекрестное произведение является распределительным над сложением)
Таким образом, эквивалентная линейная скорость, полученная в результате этих трех преобразований, может быть выражена как:
v = d r / dt = ( w x + w y + w z ) x r = w x где мы вводим w = w x + w y + w z = {w x , w y , w z }
Что выглядит в точности как (ур.2.6) и предполагает, что комбинация трех малых вращений вокруг осей x, y, z, характеризующихся векторами углового вращения w x , w y , w z эквивалентен одному небольшому повороту на на , характеризующемуся вектором углового поворота w = w x + w y + w z = {w x , w y , w z }.Обратите внимание, что мы подчеркиваем, что это маленьких поворота на , поскольку в целом, когда вы комбинируете большие вращения, порядок, в котором выполняются вращения, становится важным, и вы не можете просто их суммировать. Наше основное предположение, позволяющее перейти от линейного смещения к вращению с помощью (уравнение 2.6) , заключалось в том, что dt действительно мало, и, следовательно, вращения dθ , , и линейное смещение dr также малы. На практике это означает, что чем больше интервал dt между запросами гироскопа, тем больше будет наша накопленная ошибка, мы разберемся с этой ошибкой позже.Теперь, поскольку w x , w y , w z являются выходными данными гироскопа, мы приходим к выводу, что на самом деле 3-осевой гироскоп измеряет мгновенную угловую скорость мира, вращающегося вокруг центра устройства. .
Часть 4. Алгоритм дополнительного фильтра DCM с использованием датчиков IMU 6DOF или 9DOF
В контексте этого текста устройство 6DOF — это устройство IMU, состоящее из 3-х осевого гироскопа и 3-х осевого акселерометра. Устройство 9DOF представляет собой устройство IMU, состоящее из 3-х осевого гироскопа, 3-х осевого акселерометра и 3-х осевого магнитометра.Давайте прикрепим глобальную правостороннюю систему координат к земной системе отсчета так, чтобы версор I указывал на север, версор K указывал на Зенит и, таким образом, с этими двумя фиксированными версорами, версор J будет ограничен. к точке запад.
Рисунок 3
Также давайте рассмотрим систему координат тела, которая будет присоединена к нашему устройству IMU (в качестве примера используется acc_gyro),
Рисунок 4
Мы уже установили, что гироскопы могут измерять вектор угловой скорости.Давайте посмотрим, как измерения акселерометра и магнитометра попадут в нашу модель.
Акселерометры — это устройства, которые могут определять гравитацию. Вектор гравитации направлен к центру Земли и противоположен вектору, указывающему на Зенит K B . Если выходной сигнал 3-осевого акселерометра равен A = {A x , Ay, A z } и мы предполагаем, что внешних ускорений нет или мы их скорректировали, тогда мы можем оценить, что K B = — А .(См. Это руководство IMU для получения дополнительных разъяснений http://www.starlino.com/imu_guide.html).
Магнитометры — это устройства, которые действительно похожи на акселерометры, за исключением того, что вместо гравитации они могут определять магнитный север Земли. Как и акселерометры, они несовершенны и часто нуждаются в корректировке и начальной калибровке. Если скорректированный выходной сигнал 3-осевого магнитометра равен M = {M x , My, M z }, то согласно нашей модели I B указывает на север, таким образом, I B = М .
Зная I B и K B , мы можем рассчитать J B = K B x I B .
Таким образом, только акселерометр и магнитометр могут дать нам матрицу DCM, выраженную либо как DCM B , либо как DCM G
DCM G = DCM BT = [ I B , J B , K B ] T
Матрица DCM может использоваться для преобразования любого вектора из системы координат тела (устройств) в глобальную систему координат.Так, например, если мы знаем, что носовая часть самолета имеет фиксированные координаты, выраженные в системе координат тела как r B = {1,0,0}, мы можем найти, куда направляется устройство, другими словами, координаты носа в глобальных системах координат с использованием (уравнение 1.4) :
r G = DCM G r B
Пока вы спрашиваете себя, дают ли акселерометр и магнитометр нам матрицу DCM в любой момент времени, зачем нам гироскоп? Гироскоп на самом деле является более точным устройством, чем акселерометр и магнитомер, он используется для «точной настройки» матрицы DCM, возвращаемой акселерометром и магнитометром.
Гироскопы не знают абсолютной ориентации устройства, т.е. они не знают, где находится север и где находится зенит (то, что мы можем узнать с помощью акселерометра и магнитометра), вместо этого, если мы знаем ориентацию устройства в момент времени t , выраженную в виде матрицы DCM DCM (t), мы можем найти более точную ориентацию DCM (t + dt) с помощью гироскопа, а затем рассчитанную непосредственно по прямым показаниям акселерометра и магнитометра, которые подвержены сильному шуму в форме внешних (негравитационных) сил инерции (т.е. ускорение) или магнитные силы, которые не вызваны магнитным полем Земли.
Эти факты требуют алгоритма, который объединял бы показания со всех трех устройств (акселерометр, магнитометр и гироскоп), чтобы создать наше лучшее предположение или оценку относительно ориентации устройства в пространстве (или ориентации пространства в системах координат устройства), двух ориентаций связаны между собой, поскольку они просто выражаются с помощью двух матриц DCM, которые транспонируются одна в другую (DCM G = DCM BT ).
Теперь мы продолжим и представим такой алгоритм.
Мы будем работать с матрицей DCM, которая состоит из вариантов глобальной (земной) системы координат, выровненных по каждой строке:
Если мы прочитаем строки DCM G , мы получим векторы I B , J B , K B . В основном мы будем работать с векторами K B (которые можно оценить напрямую с помощью акселерометра) и вектором I B (которые можно оценить напрямую с помощью магнитометра).Вектор J B просто вычисляется как J B = K B x I B , так как он ортогонален двум другим векторам (помните, что версией являются единичные векторы с одинаковым направлением как оси координат).
Допустим, мы знаем зенитный вектор, выраженный в координатах корпуса тела в момент времени t 0 , и мы отмечаем его как K B 0. Также предположим, что мы измерили выходной сигнал нашего гироскопа и определили, что наша угловая скорость равна w = {w x , w y , w z }.Используя наш гироскоп, мы хотим узнать положение нашего вектора зенита по прошествии небольшого периода времени dt, мы отметим его как K B 1G . И мы находим это, используя (уравнение 2.6) :
K B 1G ≈ K B 0 + dt v = K B 0 + dt ( w g 9019 9015 9015 0 ) = K B 0 + (d θ g x K B 0 )
Где мы отметили d θ g = dt w g .Поскольку w g — это угловая скорость, измеренная гироскопом. Мы будем называть d θ g угловым смещением. Другими словами, он сообщает нам, на какой малый угол (заданный для всех трех осей в виде вектора) изменилась ориентация вектора K B в течение этого малого периода времени dt .
Очевидно, другой способ оценить K B — это сделать еще одно показание с акселерометра, чтобы мы могли получить показание, которое мы отмечаем как K B 1A .
На практике значения K B 1G будут отличаться от K B 1A. Один был оценен с помощью нашего гироскопа, а другой — с помощью нашего акселерометра.
Теперь оказывается, что мы можем пойти обратным путем и оценить угловую скорость w a или угловое смещение d θ a = dt w a , исходя из нового показания акселерометра K B 1A , мы будем использовать (уравнение.2.5):
w a = K B 0 x v a / | K B 0 | 2
Теперь v a = ( K B 1A — K B 0 ) / dt, и это в основном линейная скорость вектора K B 0 . И | K B 0 | 2 = 1, поскольку K B 0 — единичный вектор.Итак, мы можем рассчитать:
d θ a = dt w a = K B 0 x ( K B 1A — B )
Идея расчета новой оценки K B 1 , которая объединяет K B 1A и K B 1G , заключается в том, чтобы сначала оценить d θ как средневзвешенное из d θ a и d θ g :
d θ = (s a d θ a + s g d θ g ) / (s a + s g ), мы обсудим веса позже, но вскоре они определяются и настраиваются экспериментально для достижения желаемой скорости отклика и подавления шума.
Примечание для опытных читателей: Для улучшения алгоритма мы можем разделить d ϴ g на два компонента: один ортогонален K B 0 и один параллельный ему. Затем мы применили бы формулу усреднения только к компоненту, ортогональному к оси K B 0 , идея состоит в том, что акселерометр не может определять вращение вокруг оси K B 0 (азимут-зенит), таким образом эквивалентная параллельная составляющая d ϴ a всегда будет равна нулю .
А затем K B 1 вычисляется аналогично тому, как мы вычисляли K B 1G :
K B 1 ≈ K B 0 + (d θ x K B 0 )
Почему мы полностью рассчитали d θ и не применили формулу средневзвешенного значения непосредственно к K B 1A и K B 1G ? Поскольку d θ можно использовать для вычисления других элементов нашей матрицы DCM таким же образом:
I B 1 ≈ I B 0 + (d θ x I B 0 )
J B 1 ≈ J B 0 + (d θ x J B 0 )
Идея состоит в том, что все три версора I B , J B , K B прикреплены друг к другу и будут следовать одному и тому же угловому смещению d θ в течение нашего небольшого интервала dt.Вкратце, это алгоритм, который позволяет нам вычислить матрицу DCM 1 в момент времени t 1 из нашей предыдущей оценочной матрицы DCM 0 в момент времени t 0 . Он применяется рекурсивно через регулярные небольшие промежутки времени dt и дает нам обновленную матрицу DCM в любой момент времени. Матрица не будет слишком сильно дрейфовать, потому что она зафиксирована в абсолютном положении, определяемом акселерометром, и не будет слишком шумной из-за внешних ускорений, потому что мы также используем данные гироскопа для ее обновления.
О нашем магнитометре мы пока ни слова не упомянули. Одна из причин заключается в том, что он доступен не на всех модулях IMU (6DOF), и мы можем уйти, не используя его, но наша конечная ориентация будет иметь дрейфующий курс (т.е. он не будет отображаться, если мы идем на север, юг, запад. или восток), или мы можем ввести виртуальный магнитометр, который всегда направлен на север, чтобы придать стабильность нашей модели. Эта ситуация продемонстрирована в сопроводительном исходном коде, который использовал IMU 6DOF.
Теперь мы покажем, как интегрировать показания магнитометра в наш алгоритм. Как оказалось, это действительно просто, поскольку магнитометр действительно похож на акселерометр (они даже используют похожие алгоритмы калибровки), с той лишь разницей, что вместо оценки вектора зенита K B он оценивает вектор, указывающий на север Я В . Следуя той же логике, что и для нашего акселерометра, мы можем определить угловое смещение в соответствии с обновленными показаниями магнитометра как:
d θ м = dt w м = I B 0 x ( I B 1M — B )
Теперь давайте включим это в наше средневзвешенное значение:
d θ = (s a d θ a + s g d θ g + s m d θ m s θ м а + с г + с м )
Отсюда мы идем по тому же пути для расчета обновленного DCM 1
I B 1 ≈ I B 0 + (d θ x I B 0 ), K B 1 B 0 + (d θ x K B 0 ) и J B 1 ≈ J B 0 (d J B 0 ),
На практике мы вычислим J B 1 = K B 1 x I B 1, после корректировки K B 54 1 90 I262 и 90 I262 B 1 , чтобы снова быть перпендикулярными единичными векторами, обратите внимание, что вся наша логика аппроксимируется и зависит от малого dt, чем больше dt, тем большую ошибку мы накапливаем.
Таким образом, если векторы I B 0 , J B 0 , K B 0 образуют действительную матрицу DCM, другими словами, они ортогональны друг другу и едины векторов, то мы не можем сказать то же самое о I B 1 , J B 1 , K B 1 , формулы, используемые для их расчета, не гарантируют ортогональность или длина вектора должны быть сохранены, однако мы не получим большой ошибки, если dt мало, все, что нам нужно сделать, это исправить их после каждой итерации.
Сначала давайте посмотрим, как мы можем гарантировать, что два вектора снова ортогональны. Давайте рассмотрим два единичных вектора a и b , которые «почти ортогональны», другими словами, угол между этими двумя векторами близок к 90 °, но не точно 90 °. Мы ищем вектор b ’, который ортогонален a и находится в той же плоскости, образованной векторами a, и b. Такой вектор легко найти, как показано на рисунке 5.Сначала мы находим вектор c = a x b , который по правилам перекрестного произведения ортогонален как a , так и b и, следовательно, перпендикулярен плоскости, образованной a и b . Затем вектор b ’= c x a вычисляется как векторное произведение c и a. Из определения перекрестного произведения b ‘ ортогонален a и, поскольку он также ортогонален c , он оказывается в плоскости, ортогональной c , которая является плоскостью, образованной a и г. Таким образом, b ’ — это скорректированный вектор, который мы ищем, который ортогонален a и принадлежит плоскости, образованной a и b .
Рисунок 5
Мы можем расширить уравнение, используя правило тройного произведения и тот факт, что a.a = | a | = 1:
b ’ = c x a = ( a x b ) x a = — a ( a . b ) + b ( a . a ) = b — a ( ab ) = b + d, где d = — a (ab) ( Сценарий 1, a исправлено b исправлено)
Вы можете немного поразмышлять над результатами … Итак, мы получаем скорректированный вектор b ’ из вектора b , добавляя« корректирующий »вектор d = — a (a.b). Обратите внимание, что d параллельна a .Его направление зависит от угла между a и b , например, на Рисунке 5 a . b = cos ( a , b )> 0, потому что угол между a и b меньше 90 °, таким образом, d имеет направление, противоположное a и магнитутде cos ( a , b ) = sin ( b, b ‘).
В приведенном выше сценарии мы считали, что вектор a фиксирован, и мы нашли скорректированный вектор b ’, который ортогонален a .Можно рассмотреть симметричную задачу — фиксируем b и находим исправленный вектор a ’:
a ‘ = a — b ( b . a ) = a — b ( a . b ) = a + e , где e = — b ( ab ) (Сценарий 2, b фиксировано a исправлено)
Наконец, в третьем сценарии мы хотим, чтобы оба вектора двигались к своему исправленному состоянию, мы считаем их оба «одинаково неправильными», поэтому интуитивно мы применяем половинную коррекцию к обоим векторам из сценария 1 и 2:
a ’ = a — b ( a . b ) / 2 (Сценарий 3, оба a и b исправлены)
b ’ = b — a ( a . b ) / 2
Рисунок 6
Эту формулу относительно легко вычислить на микропроцессоре, поскольку мы можем предварительно вычислить Err = ( a . b ) / 2, а затем использовать ее для исправления обоих векторов:
a ’ = a — Err * b
b’ = b — Err * a
Обратите внимание, что мы не доказываем, что a ‘ и b’ ортогональны в Сценарии 3, но мы представили интуитивное объяснение, почему угол между a ‘ и b’ станет ближе к 90 °, если применяем указанные выше корректирующие преобразования.
Теперь, возвращаясь к нашей обновленной матрице DCM, которая состоит из трех векторов I B 1 , J B 1 , , мы применяем следующие корректирующие действия перед повторным введением матрицы DCM в следующий цикл. :
Err = ( I B 1 . J B 1 ) / 2
I B 1 ‘ = I B 1 — Err * J B 1
J B 1 B 1 — Err * I B 1
I B 1 » = Нормализовать [ I B 1 1 J B 1 » = Нормализовать [ J B 1 ‘]
K B 1 ‘ ’90 I19019 = 1 » x J B 1 »
Где нормализовать [ a ] = a / | a | , — это формула для вычисления единичного вектора, сонаправленного с a .
Итак, наконец, наша скорректированная матрица DCM 1 может быть перекомпонована из векторов I B 1 » , J B 1 » , K B 1 » , которые были ортонормированы (каждый вектор составляет строку обновленной и скорректированной матрицы DCM).
Мы повторяем цикл, чтобы найти DCM 2, , DCM 3, или вообще DCM n , в любом временном интервале n.
Каталожные номера
1. Теория прикладной робототехники: кинематика, динамика и управление (Реза Н. Джазар)
2. Линейная алгебра и ее приложения (Дэвид К. Лэй)
3. Основы матричных вычислений (Дэвид С. Уоткинс)
4. Направляющая косинусная матрица IMU: теория (В. Премерлани)
Дополнительные примечания
Для реализации алгоритма на данный момент см. Мой проект квадрокоптера, в частности, выпуски 6/7 имеют хорошую программу обработки для визуального отображения матрицы DCM и плоскости модели.


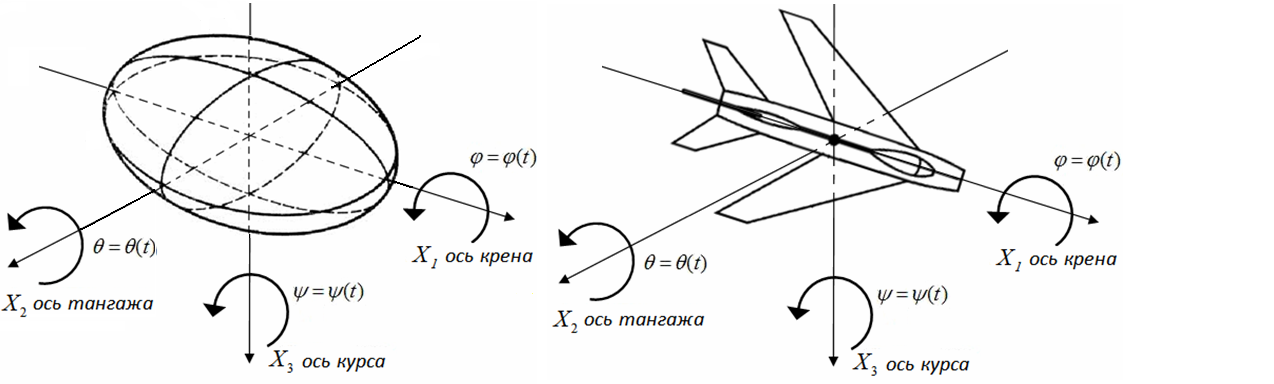
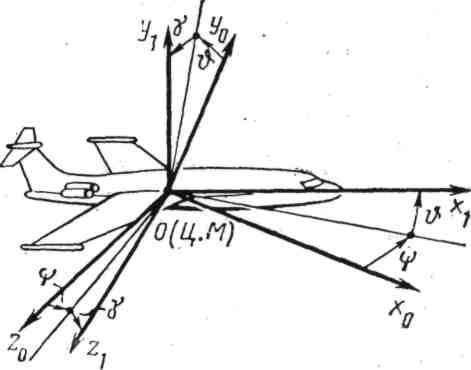 53) например, самолет, ракета, вертолет
53) например, самолет, ракета, вертолет Стартовая система координат
Стартовая система координат Земная подвижная система координат
Земная подвижная система координат Продольная ось
Продольная ось Поперечная ось
Поперечная ось 35), и направлена противоположно проекции скорости на плоскость, перпендикулярную продольной оси
35), и направлена противоположно проекции скорости на плоскость, перпендикулярную продольной оси Боковая ось
Боковая ось 35) на плоскость связанной системы координат
35) на плоскость связанной системы координат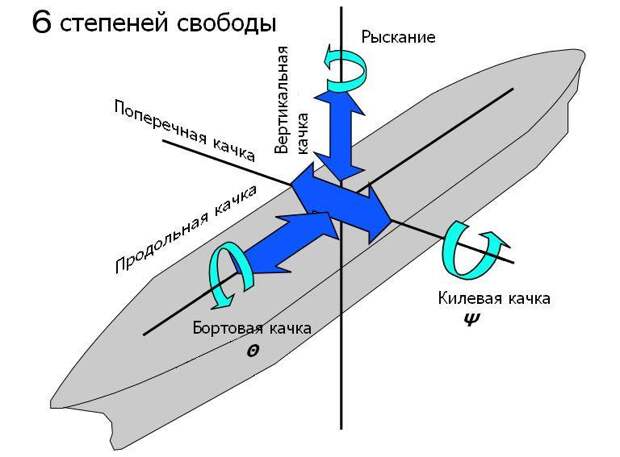 Аэродинамический угол крена
Аэродинамический угол крена Угол тангажа
Угол тангажа 3)
3) Скоростной угол крена
Скоростной угол крена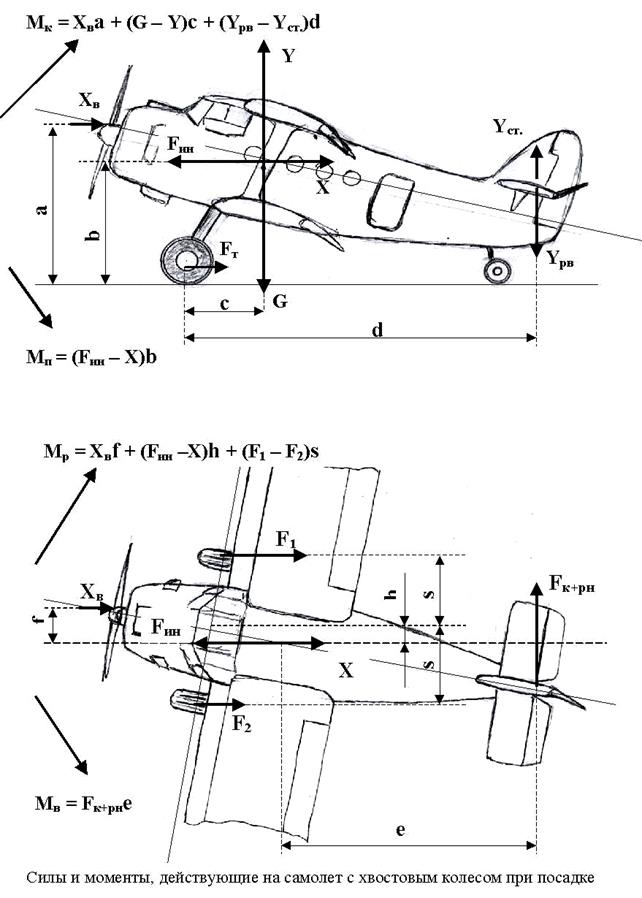 Угол наклона траектории
Угол наклона траектории Наклон ветра
Наклон ветра 37) по оси связанной системы координат; — составляющая скорости летательного аппарата по оси скоростной системы координат; при этом , а
37) по оси связанной системы координат; — составляющая скорости летательного аппарата по оси скоростной системы координат; при этом , а 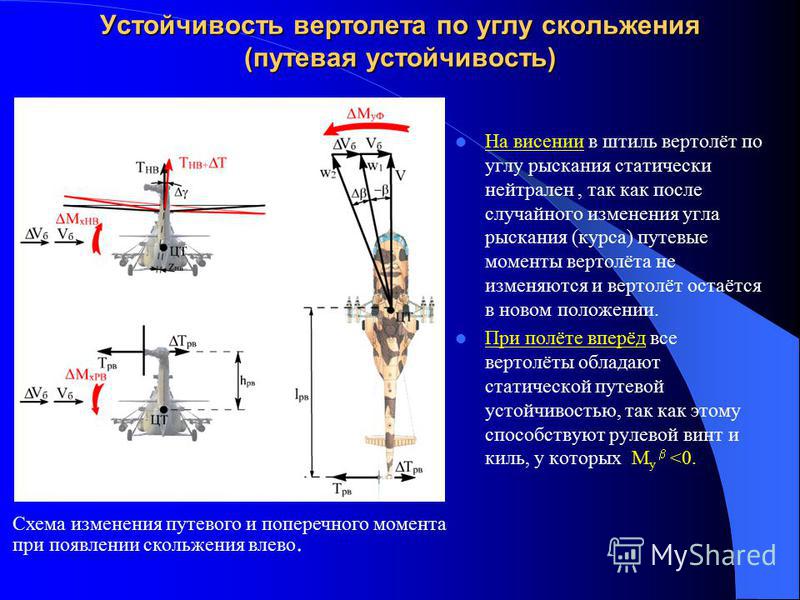 Скорость ветра
Скорость ветра
 Скорость рыскания
Скорость рыскания Масса механической системы — это сумма масс материальных точек, образующих систему
Масса механической системы — это сумма масс материальных точек, образующих систему Угол отклонения органа управления тангажом
Угол отклонения органа управления тангажом 6)
6) Угол отклонения органа управления рысканием
Угол отклонения органа управления рысканием 53) и аэродинамической силы планера (п.54).
53) и аэродинамической силы планера (п.54). Продольная сила
Продольная сила Подъемная сила
Подъемная сила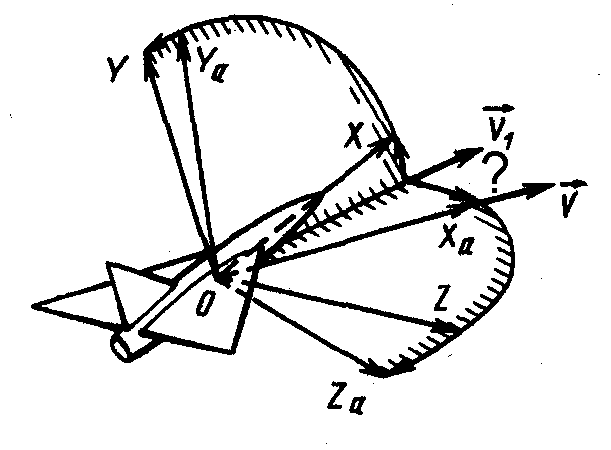 Аэродинамическая поперечная сила
Аэродинамическая поперечная сила —
—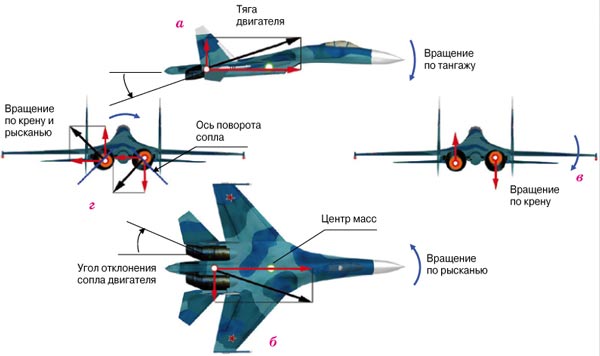 Момент тяги
Момент тяги Момент относительно рассматриваемой оси следует считать положительным, когда его вектор совпадает с направлением этой оси.
Момент относительно рассматриваемой оси следует считать положительным, когда его вектор совпадает с направлением этой оси.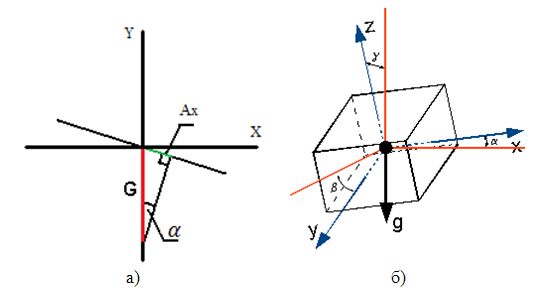 примечания к п.73
примечания к п.73 примечания к п.76
примечания к п.76