Сила упругости. Закон Гука. 7-й класс
Цель урока: выяснить природу силы упругости, сформулировать закон Гука.
Задачи:
- обучающие: сформировать знанияо деформации, силе упругости; вывести закон Гука; сформировать способности применять закон Гука при решении задач.
- развивающие: продолжить формирование у учащихся представлений о разнообразии сил в природе, развивать умение наблюдать и объяснять физические явления; проводить эксперимент, делать выводы;
- воспитательные: продолжить формирование навыков коллективной и самостоятельной работы, развивать чувства товарищеской взаимопомощи, ответственности за проделанную работу.
Оборудование: компьютер, экран, мультимедиапроектор, Презентация, 4 штатива с муфтами и лапками, набор грузов по 1Н, 2 разные пружины, 2 разные резинки, прибор для демонстрации видов деформации, резиновые и пластилиновые игрушки, губка, эспандер, гибкие металлические или пластмассовые линейки, 12 полосок бумаги шириной 6-7 см, карточки с заданиями.
Предварительная подготовка: разделить учащихся на 4 группы.
Ход урокаI. Актуализация знаний.Слайд 2
- Какая сила действует на все тела, находящиеся на Земле?
- Какая сила действует на снег, лежащий на крыше дома; на человека, лежащего в гамаке; на груз, висящий на тросе?
- Что изменяется у тела, на которое действует сила?
- Почему снег, человек, груз не падают? (на них действует сила, которая не дает упасть)
Учитель: Мы должны выяснить, что это за сила, из-за чего возникает, к какой точке приложена, куда она направлена, от чего зависит, чему равен ее модуль.
II. Изучение нового материала:Учитель: У вас на столе лежат различные резиновые и пластилиновые предметы.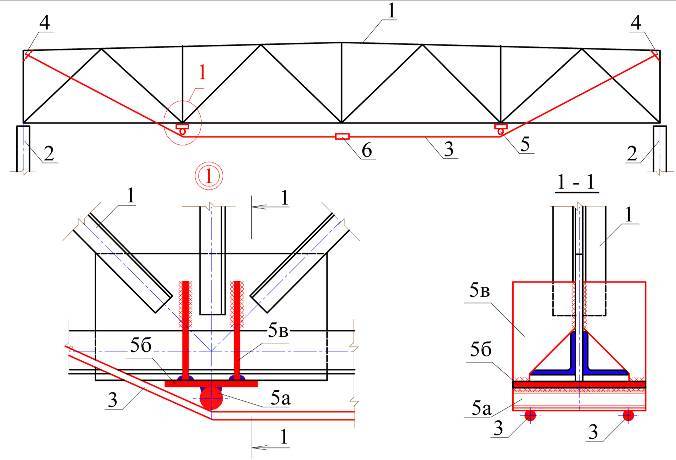
А если прекратить воздействовать на резиновые и пластилиновые предметы, что произошло?
Слайды 3-4
Показ видов деформаций на приборе для демонстрации видов деформации.
Задание группам:
Положите металлическую или пластмассовую линейку на опоры, поставьте на нее груз.
Подвесьте грузик к пружине, резинке.
Учитель: Что пронаблюдали?
Почему прогнулась (деформировалась) линейка, если положить на нее груз?
А почему через некоторое время прогибание останавливается?
Что произойдет, если снять груз?
Почему?
Почему растянулись пружина или резинка, если подвесить груз?
Почему через некоторое время растяжение останавливается?
Что произойдет, если снять груз?
Почему?
К чему приложена возникающая сила?
Куда она направлена?
Слайд 5
Выясним, в чем же причина возникновения силы упругости:
- Как называются частицы, из которых состоят вещества?
- Какие взаимодействия существуют между молекулами?
- На каком расстоянии действует сила притяжения?
- На каком расстоянии действует сила отталкивания?
Причиной возникновения сил упругости является взаимодействие молекул тела. На малых расстояниях молекулы отталкиваются, а на больших – притягиваются. В недеформированном теле молекулы находятся как раз на таком расстоянии, при котором силы притяжения, либо силы отталкивания уравновешиваются. Когда мы растягиваем или сжимаем тело, расстояния между молекулами изменяются, поэтому начинают преобладать либо силы притяжения, либо силы отталкивания. В результате и возникает сила упругости
, которая всегда направлена так, чтобы уменьшить величину деформации тела.
Слайд 6
Сила упругости – это электромагнитная сила, возникающая при деформации тела и направленная в сторону, противоположную направлению смещения частиц тела при деформации. Приложена к деформируемому телу.
Слайд 7. Начертить в тетради:
Учитель: Если тело лежит на опоре, то сила упругости обозначается N – сила реакции опоры.
Выясним, от чего зависит сила упругости (на столах у групп учащихся стоят штативы с подвешенными пружинами, резинками, грузы).
Задание группам:
- Измерить длину нерастянутой пружины (резинки) l0.
- Подвесить к пружине (резинке) один груз, отметить силу 1 Н на оси.
- Измерить длину растянутой пружины (резинки) l.
- Найти разность Δl = l — l0, отметить на оси.
- Отметить точку пересечения на графике.
- Подвесить к пружине (резинке) второй груз, отметить силу 2 Н на оси.
- Измерить длину растянутой пружины (резинки) l.
- Найти разность Δl = l — l0, отметить на оси.
- Отметить точку пересечения на графике.
- Подвесить к пружине (резинке) третий груз, отметить силу 3 Н на оси.
- Измерить длину растянутой пружины (резинки) l.
- Найти разность Δl = l — l0, отметить на оси.
- Отметить точку пересечения на графике.
- Постройте график зависимости силы упругости от удлинения и сделайте вывод.
Вывод: чем больше сила, тем больше удлиняется пружина.
Слайды 8-10
Учитель: Какая зависимость между силой упругости и удлинением?
Для упругих или пластических деформаций выполняется данная зависимость?
Учитель: В 1660 году английский ученый Роберт Гук, когда ему было 25 лет, установил закон зависимости силы упругости от упругих деформаций, названный впоследствии его именем.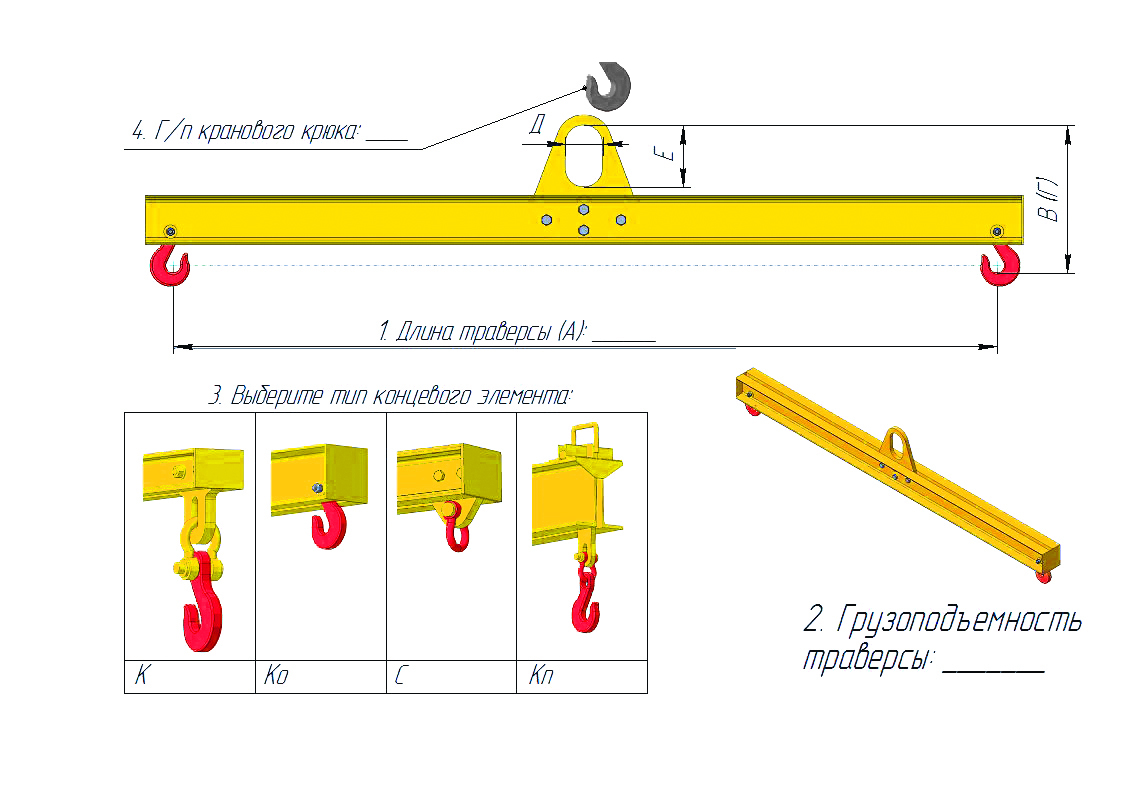
Но опубликовал он этот закон спустя 16 лет, проделав ряд экспериментов подтвердивших данный закон.
Сила упругости, возникающая при упругой деформации тела, прямо пропорциональна величине деформации) Δl и направлена в сторону противоположную перемещению частиц тела при деформации.
Fупр = k ∙ Δl
В законе Гука Δl – удлинение [м], k – коэффициент жесткости [H/м]
Учитель: всем видам деформации подвержено и человеческое тело, и при этом также возникает сила упругости.
Слайд 11 Физкультминутка:
Встали, потянулись (деформация растяжения/сжатия)
Наклоны вправо, влево, вперед, назад (деформация изгиба)
Повороты головы, кистей рук, плеч, туловища (деформация кручения)
Учитель: У каждого тела своя жесткость. От чего зависит коэффициент жесткости?
Задание группам:
- Укоротите пружину (или резинку), подвесьте грузик. Сильно растянулась пружина (резинка)? Что больше растянулось?
- Как увеличить прочность (жесткость) листочка бумаги? (на столах у групп учащихся листочки бумаги)
Учащиеся пробуют изменить форму. - Сделайте вывод.
Вывод: жесткость деформируемого тела зависит от материала, размеров и формы.
Учитель: Как же учитывают жесткость материала при строительстве? Слайды 12-17
Учитель: Людям каких профессий кроме строителей нужно учитывать силу упругости? Где применяются знания об этой силе? Слайды 18-27
Также и в природе учитывается существование деформаций и силы упругости. Кажется небольшой лес, а на самом деле …
Учитель: Как вы определяете, жесткий хлеб или мягкий?
Почему говорят стул жесткий? Кресло мягкое?
А где в животном мире используется сила упругости (домашнее задание)
III. Рефлексия.
Рефлексия.Учитель: подведем итоги:
- Какие виды деформаций мы изучили?
- Перечислить особенности действия силы упругости:
- когда возникает? (возникает при упругих деформациях)
- куда направлена? (направлена противоположно направлению смещения)
- к чему приложена? (к деформируемому телу)
- при каких деформациях выполняется закон Гука? (при упругих деформациях).
Слайд 28 Задачи по группам:
1. Под действием какой силы пружина, имеющая коэффициент жесткости 1 кН/м, сжалась на 4 см?
2. Определите удлинение пружины, если на нее действует сила 10 Н, а коэффициент жесткости пружины 500 Н/м.
3. Чему равен коэффициент жесткости стержня, если под действием груза 1000 Н он удлинился на 1 мм?
4. По своим графикам определить коэффициент жесткости пружины (или резинки).
Слайд 29
IV. Д.з.§25, задания 25.1 — 25.6 рабочей тетради; если не успели в классе, то дорешать задачи.
V. Выставление оценок.Литература, интернет-ресурсы:
- С.Е. Полянский Поурочные разработки по физике 7 класс. – Москва «Вако», 2003.
- Учебно-методический комплекс А.В. Перышкина.
- ЦОР iles.school-collection.edu.ru/dlrstore/669b2b61-e921-11dc-95ff-0800200c9a66/3_13.swf
Способы строповки, строповка грузов, графическое изображение способов строповки грузов
Схемы строповки, графическое изображение способов строповки и зацепки грузов должны быть выданы на руки стропальщикам и крановщикам или вывешены в местах производства работ. Владельцем крана или эксплуатирующей организацией также должны быть разработаны способы обвязки деталей и узлов машин, перемещаемых кранами во время их монтажа, демонтажа и ремонта, с указанием применяемых при этом приспособлений, а также способов безопасной кантовки грузов, когда такая операция производится с применением крана.
Схемы строповки и кантовки грузов и перечень применяемых грузозахватных приспособлений должны быть приведены в технологических регламентах. Перемещение груза, на который не разработаны схемы строповки, должно производиться в присутствии и под руководством лица, ответственного за безопасное производство работ кранами. Руководство морских и речных портов обязано обеспечить производство погрузочно-разгрузочных работ с применением кранов по утвержденным им технологическим картам.
Пример плакатов по технике безопасности при проведении грузоподъемных работ
Перемещение груза является одним из наиболее сложных и ответственных мероприятий в процессе производства. На производстве всех видов промышленности наиболее тяжелые грузы перемещают с помощью кранов, однако многие грузы не имеют специальных креплений для транспортировки, поэтому используются промежуточные грузоподъёмные элементы. В качестве таких промежуточных элементов чаще всего выступают канатные и ленточные стропы. На нашем предприятии мы изготавливаем большинство видов строп, с которыми вы можете ознакомиться в каталоге нашего сайта.
Для строповки предназначенного к подъему груза должны применяться грузовые стропы, соответствующие массе и характеру поднимаемого груза, с учетом числа ветвей и угла их наклона. Строп общего назначения следует подбирать так, чтобы угол между их ветвями не превышал 90°. В зависимости от вида строповки производится перерасчет грузоподъемности строп.
Листовые конструкции и мелкие стальные элементы поднимают и транспортируют к рабочему месту с применением захватов и скоб. Стальные и железобетонные элементы (прогоны, связи, плиты перекрытий, перемычки) поднимают с помощью специальных траверс, допускающих многоярусное расположение монтируемых деталей. Траверсы необходимы для равномерного распределения нагрузки и могут быть как линейными, так и пространственными, в зависимости от типа поднимаемого груза. За время работы нашего предприятия конструкторский отдел разработал большое количество готовых траверс, которые вы можете у нас заказать.
Для подъема и перемещения пакета труб, круглого проката или бревен применяется способ строповки «на удавку». Для этого продевают в петлю один конец стропа, а другой конец петли надевают на крюк крана таким образом, чтобы при подъеме петля затянулась и прочно удерживала груз на весу. Строповку пачки листового металла также производят универсальным двухпетлевым стропом на «удавку». В свободные петли вставляют крюки двухветвевого стропа и при подъеме их крюками универсальные стропы затягивают пачку металла.
Способы строповки различных материалов
В целях предупреждения падения грузов во время подъема и перемещения их кранами следует соблюдать следующие правила строповки:
- при обвязке груза стропы должны накладываться без узлов и перекруток. При перемещении грузов, имеющих острые ребра, с помощью канатных стропов между ребрами и канатами следует размещать проставки, предохраняющие последние от повреждений.
- неиспользованные для зацепки концы многоветвевого стропа должны быть укреплены так, чтобы при перемещении груза краном исключалась возможность задевания этими концами за встречающие на пути предметы.
- при обвязке грузов цепными стропами не следует допускать изгиба звеньев на ребрах груза.
- при регулярном использовании канатных стропов для обвязки грузов с закруглениями, радиусы которых составляют менее 10 диаметров каната, рекомендуется снижать допускаемую нагрузку на ветви стропа. При строповке груза с его затяжкой петлей канатного стропа рекомендуется снижать его грузоподъемность на 20%.
- перемещение грузов со свободной укладкой их на петлевые стропы допускается только при наличии на грузе элементов, надежно предотвращающих его от смещения в продольном направлении.
Плакаты «Схемы строповки грузов» (27,7Мб)
Пособие «Схемы строповки материалов» (12,9Мб)
Иллюстрированное пособие стропальщика (16,5Мб)
Прогиб рельса — Энциклопедия по машиностроению XXL
Это исследование оказалось возможным упростить рассмотрением вместо балки на отдельных упругих опорах балк на упругом основании ). При такой расчетной схеме легко определить дина-иический эффект выбоин на прогиб рельсов. Положим, например, что профиль выбоины (длиной I, глубиной 8) задан уравнением
[c.519]
При такой расчетной схеме легко определить дина-иический эффект выбоин на прогиб рельсов. Положим, например, что профиль выбоины (длиной I, глубиной 8) задан уравнением
[c.519]Можно показать, что дополнительный динамический прогиб, вызываемый выбоиной, пропорционален о и зависит от величины отношения TJT, где Т—период вертикальных колебаний колеса, возникающих под воздействием на него рельса как пружины, а Tj—время, в течение которого колесо проходит выбоину. Наибольший дополнительный прогиб, равный 1,47 S, получается при скорости, соответствующей Т 1Т=2/3. Отсюда можно заключить, что дополнительное динамическое давление, являющееся результатом выбоины, равно приблизительно нагрузке, производящей статический прогиб рельса, равный 1,5 3. Мы видим, что сравнительно малая выбоина производит при определенных скоростях весьма заметный динамический эффект. [c.519]
Приведем теперь несколько чисел, которые характеризуют изменение прогиба рельса в зависимости от расположения груза Р. При неограниченном числе опор наименьший прогиб, очевидно, будем иметь в том случае, когда груз располагается непосредственно над шпалой. Для получения приближенного значения этого прогиба нужно только значение средней опорной реакции, приведенное в последней строке таблицы П, разделить на величину D, характеризующую жесткость опоры. Действительное значение искомого прогиба будет в случае бесконечно длинного рельса несколько меньше, но этой разностью, как мы уже указывали, можно пренебречь. Таким образом, получаем [c.325]
Для разыскания наибольшего прогиба рельса неограниченной длины воспользуемся числами для балки, расположенной на шести упругих опорах. Располагая груз Р посредине пролета балки, мы при помощи известных формул для опорных реакций находим для прогиба под грузом такие значения [c.325]
Наблюдатели, изучавшие вопрос о деформациях рельс под действием катящихся колес, отмечают, что при больших скоростях движения прогибы рельс под колесами получаются часто значительно большими, чем соответствующие прогибы при статическом действии тех же колес. Такое увеличение прогибов нужно приписать действию целого ряда причин динамического характера, которые мы здесь и перечислим.
[c.334]
Такое увеличение прогибов нужно приписать действию целого ряда причин динамического характера, которые мы здесь и перечислим.
[c.334]
Представим себе идеально правильное колесо, катящееся по гладкому невесомому рельсу, опирающемуся на упругие опоры. Вследствие неодинаковости статического прогиба рельса при расположении колеса над опорой и расположении его по середине пролета между опорами траектория точки касания колеса с рельсом представится волнообразной линией. В таком случае движение колеса будет сопровождаться вертикальными перемещениями его центра тяжести и давление колеса на рельс будет зависеть не только от статической нагрузки, но также и от вертикальной силы инерции. [c.334]
Прогиб рельса в силу указанной причины будет иным, чем в случае статического действия нагрузки. [c.335]
Второй причиной, видоизменяющей прогибы рельса, являются колебания рельса и связанных с ним шпал и основания. [c.335]
Предположим, что колесо совершенно правильной формы катится по рельсу с постоянной скоростью v (рис. 6). На колесо действует какая-либо переменная сила Q. Благодаря наличию переменной силы прогиб рельса под колесом будет меняться, и движение колеса будет сопровождаться вертикальными перемещениями его центра тяжести. Напишем дифференциальное уравнение для этих перемещений. Рассматривая рельс как невесомую балку, лежащую на сплошном упругом основании, мы найдем, что вертикальная реакция R в месте соприкасания колеса с рельсом представится так (см. формулы (4), (9) и (10)) [c.337]
Величина его будет такая же, как у математического маятника, длина которого равна статическому прогибу рельса под действием [c.337]
Первый член этого выражения представляет собой не что иное, как статический прогиб рельса под действием постоянного давления колеса. Два других члена дают нам свободные колебания колеса,
[c.338]
Два других члена дают нам свободные колебания колеса,
[c.338]
Произвольные постоянные должны быть выбраны таким образом, чтобы были удовлетворены начальные условия. Если, например, в начальный момент прогиб рельса равен статическому прогибу под действием силы q (l+pm) и начальная вертикальная скорость равна нулю, то при действии постоянной силы и силы qo получим [c.339]
Если бы начальные условия были такими, как мы предполагали в двух рассмотренных частных случаях, то для вычисления наибольшего прогиба рельса, а следовательно, и наибольшего давления нужно было бы пользоваться выражениями (19 )или (19″). В действительности скорость движения поезда нарастает постепенно, и к тому времени, когда угловая скорость достигнет значения со и центробежная сила значения до, роль собственных колебаний будет ничтожна и нам придется принять в расчет лишь вынужденные колебания [c.340]
Вставляя значение ф(0 в выражение (22), найдем для прогиба рельса, вызванного наличием впадины, такое выражение [c.343]
Во всех рассматриваемых случаях мы предполагаем постоянное соприкасание колеса и рельса. Если благодаря колебаниям, вызванным впадиной, у становится отрицательным, то мы полагаем, что отрицательное значение меньше того начального прогиба рельса, который вызван статическим давлением колеса. Когда отрицательный прогиб превзойдет статический прогиб рельса, произойдет отделение колеса от рельса. [c.345]
Движение колеса по этой впадине вызывает такие же изменения прогиба рельса, как и приложение постоянной силы [c.349]
Пользуясь этими формулами, мы сможем по прогибам рельса под каждым из двух грузов найти соответствующие давления на рельс и равные им реакции, оказываемые рельсом на колеса. [c.352]
ПРОГИБЫ РЕЛЬСА ОТ ПЕРЕМЕННОЙ ВО ВРЕМЕНИ СИЛЫ 361 [c.361]
Прогибы рельса от переменной во времени поперечной силы
[c. 361]
361]
Увеличивая длину I, мы можем получить прогибы для весьма длинной балки. К сожалению, для этого случая нам не удалось подыскать какой-либо статической модели, которая позволила бы упростить результат, полученный в виде бесконечного ряда (21). То обстоятельство, что угловая скорость вращения колес мала по сравнению с частотой основного тона собственных колебаний рельса, а поступательная скорость движения поезда мала до сравнению с критической скоростью, дает основание заключить, что динамические прогибы рельса, вызванные центробежной силой противовесов, несовпадениями центров тяжести колес с осями вращения, давлением пара, а также поступательным движением колес, весьма мало отличаются от статических прогибов, вызванных теми же причинами, и потому при определении этих прогибов можно пренебрегать вибрациями рельса. [c.370]
Без особых затруднений может быть исследован также тот случай, когда осадка шпалы невелика и шпала, начиная с некоторого определенного положения колеса, уже поддерживает рельс. Пока шпала не работает, т. е. пока динамический прогиб над шпалой меньше начальной осадки б, нужно пользоваться уравнением (11). При дальнейшем движении зависимость между давлением колеса и прогибом рельса будет определяться формулой (7 ). Прогиб [c.379]
Из всего сказанного ясно, что тот прием расчета, когда рельс рассматривают как балку, лежащую на сплошном упругом основании, можно применять для изучения влияния начальной осадки шпалы на величину статических и динамических прогибов рельса. [c.380]
Если в зависимости (39) и (41) положить 2=0, то получим прогиб рельса балки под грузом Р в следующем виде [c.593]
Опорные реакции в арках 437 Осадка шпалы, влияние на прогиб рельса при динамическом нагружении 376 [c.703]
Укладка рельсовых плетей бесстыкового пути. Плети на место укладки перевозят на специальном поезде и разгружают внутри или снаружи колеи при этом обязательно применяют аппарель, которая уменьшает прогиб рельсов, исключает их кантование и удары при спуске. В новых поездах аппарель заменена наклонными лотками. Плеть выгружают так, чтобы концы ее точно совпадали с проектным положением. Выгруженные плети прикрепляют костылями к шпалам через каждые 15 м при железобетонных шпалах рельсы пришивают к кускам деревянных шпал, уложенным в шпальные ящики.
[c.369]
В новых поездах аппарель заменена наклонными лотками. Плеть выгружают так, чтобы концы ее точно совпадали с проектным положением. Выгруженные плети прикрепляют костылями к шпалам через каждые 15 м при железобетонных шпалах рельсы пришивают к кускам деревянных шпал, уложенным в шпальные ящики.
[c.369]
Сопротивление пути на прямых горизонтальных участках зависит от прогиба рельсов при прохождении вагонов по ним, сжатия бандажей и рельсов в месте их соприкосновения, ударов на стыках и неровностях пути, проскальзывания колес относительно рельсов и наличия извилистого движения вагона в пути (виляния). [c.10]
Сопротивление от качения колес по рельсам. При качении колеса по рельсу происходит сжатие материала бандажа и рельса, прогиб рельсов, трение скольжения вследствие относительного перемещения прижатых друг к другу бандажа рельса, трение соприкасающихся поверхностей рельса, шпал и балласта, износ бандажей и рельсов вследствие возникающих на их поверхности в контактных площадках пластических деформаций из-за развивающихся больших напряжений. Все эти явления вызывают расход энергии, который эквивалентен работе силы сопротивления от перекатывающегося колеса по рельсу. Если бы бандажи колес и рельсы были бы телами абсолютно жесткими, то во время движения соприкосновение их между собой осуществлялось бы в точке, причем сила реакции от рельса на колесо в точности равнялась по величине нагрузке от колеса на рельс и совпадала с ней по линии действия (по вертикали). Но бандажная и рельсовая сталь обладают свойством упругости. Вследствие этого и больших давлений, передаваемых колесом на рельс, соприкосновение их происходит не в точке, а по небольшой контактной площадке, имеющей форму эллипса. [c.72]
Величина плеча трения т отражает влияние сжатия металла, прогиба рельса, общую жесткость пути и практически не зависит от скорости. В средних условиях
[c.74]
В средних условиях
[c.74]
По исследованиям проф. Н. П. Петрова величина этого сопротивления зависит от скорости, расстояния между стыками, нагрузки от колес, величины зазора стыка, прогиба рельса и многих других случайных причин, вследствие чего определение сопротивления от ударов на стыках теоретическим путем представляет большие трудности. Имеющиеся в этой области опытные данные, весьма немногочисленные, показывают, что плохое состояние верхнего строения пути и неудовлетворительное содержание стыков являются основными причинами повышенных значений этих сопротивлений. При нормальном содержании верхнего строения пути и стыков, по исследованиям проф. [c.76]
Исключив множитель Л и координату ф (с учётом уравнения связи (10)), из уравнений (24), (25) находим уравнение для определения прогиба рельса [c.152]
Наибольший дополнительный прогиб рельса тах от дополнительных инерционных сил, возникающих при движении колеса с неровностью, зависит от отношения [c.610]
Определение расчетного положения нагрузки. Для расчета напряжений в рельсах и других элементах верхнего строения пути определенной конструкции, нагруженных заданным подвижным составом, идущим с заданной скоростью, а также для нахождения величины упругого прогиба рельса приходится устанавливать, под какой из осей эти напряжения или прогиб будут наибольшими. Эта ось и будет расчетной в любом сечении пути. [c.612]
Так как сила Яд н передается от колеса на рельс выше низа подошвы рельса, т. е. выше места передачи бокового давления шпале, упругий прогиб рельса гщ в горизонтальной плоскости, несколько уменьшенный за счет его кручения, составляет [c.626]
Обширная экспериментальная работа была проведена по измерению деформации железнодорожного пути под подвижными нагрузками. Однако на первоначальные измерения этого рода, в которых использовались измерительные приборы механического типа, положиться нельзя. А. Васютынский изобрел оптический метод, и ему удалось получить фотографические снимки деформации изгиба и прогибов рельса под колесами движущегося лoкoмoтивa ).
[c.517]
А. Васютынский изобрел оптический метод, и ему удалось получить фотографические снимки деформации изгиба и прогибов рельса под колесами движущегося лoкoмoтивa ).
[c.517]
Этим уравнением определяются свободные колебания колеса, опирающегося на рельс. Вводя обозначение aql2k=X, где X, очевидно, представляет собой статический прогиб рельса под действием веса колеса, получим для свободных колебаний колеса выражение [c.337]
При совершенно правильной форме колеса и рельса, пренебрегая местными вдавливаниями в точках касания колеса и некоторой общей деформацией колеса, мы могли считать вертикальные перемещения центра тяжести колеса равными соответствующему прогибу рельса. Если на колесе или рельсе имеются какие-либо неправильности, то указанного равенства существовать не будет и нам придется несколько видоизменить уравнение (15). Обозначим через т] глубину впадины на рельсе или на колесе, отсчитывая ее от уровня правильного рельса или окружности правильного колеса. В таком случае вертикальному прогибу рельса у будет соответствовать опускание колеса, равное у+т], где т] — ордината впадины рельса или колеса, соответствующая точке касания. Если вид впадины нам известен, то при заданной скорости движения т] представится вполне определенной функцией от времени t. Дифференциальное уравнение для вертикальных перемещений колеса напишется так [c.342]
Это перемещение представляет собой тот дополнительный прогиб рельса, который обусловлен впадиной на колесе или рельсе. Выясним значение этого прогиба в нескольких частных Q [c.343]
В настоящей заметке мы подробнее выясняем вопрос о вибрациях рельса, исследуем вынужденные колебания, возникающие в рельсе при действии переменной силы, приложенной в какой-либо точке рельса, и показываем, что амплитуда этих колебаний может значительно отличаться от статических прогибов рельса лишь в том случае, если частота переменной силы приближается к частоте собственных колебаний рельса. Далее мы выясняем, какое влияние может иметь поступательная скорость движения колеса на прогиб рельсат и показываем, что при практически достижимых скоростях этовлия, ние невелико. В заключение мы рассматриваем колебания, возникающие в рельсе при движении по рельсу переменной силы с постоянной скоростью.
[c.359]
Далее мы выясняем, какое влияние может иметь поступательная скорость движения колеса на прогиб рельсат и показываем, что при практически достижимых скоростях этовлия, ние невелико. В заключение мы рассматриваем колебания, возникающие в рельсе при движении по рельсу переменной силы с постоянной скоростью.
[c.359]
Рассмотрим теперь, как изменятся формулы (7) и (8), если начальная осадка шпалы настолько мала, что, начиная с некоторого момента, шпала уже начинает поддерживать прогибаюш,ийся рельс. Обозначим через б величину начальной осадки. Пока прогиб рельса над осевшей шпалой меньше б, мы будем иметь те же условия изгиба, что и в предыдущем случае. Когда расстояние осевшей шпалы от точки касания колеса сделается таким, что [c.374]
Следовательно, явление здесь будет происходить так же, как при пробеге колесом впадины определенного очертания. Подобную задачу мы подробно разобрали в нашей заметке ). Когда при даль-не йшем движении колеса прогиб рельса над осевшей шпалой станет меньшим, чем б и шпала перестанет поддерживать рельс, мы вновь должны будем обратиться к интегрированию уравнения (И). [c.380]
Приборы полуавтоматической блокировки связываются с поездом специальными рельсовыми контактами (педалями), которые срабатывают от прогиба рельса под тяжестью подвижного состава, или рельсовыми цепями. На сети дорог применяют в основном три сис-те.мы однопутной полуавтоматической блокировки релейную (РПБ) института Гипротранссигналсвязь и конструкторского бюро Ц111, электромеханическую с полярной линейной цепью (БПЛЦ) системы Белорусской дороги. [c.357]
Максимальное отрицательное значение ч) = —0,0432, т. е. наибольший прогиб рельса вверх, составляет примерно4% от наибольшего прогиба вниз в сечении под грузом. [c.598]
Решетки для лестниц | Ступени для винтовых лестниц
Используется
- Сварной решетчатый настил – Данный тип настила изготавливается по DIN 245371 из свариваемой стали например S235 JR, St 523N или любой другой стали согласно требованиям заказчика.
Виды лестниц из решетчатого настила, их технические особенности и основные характеристики
Настил Gratepark широко применяются для возведения лестниц. От обладает небольшим весом в сравнение с цельными изделиями, большим периодом службы, износостойкостью, высокой прочностью и устойчивостью к воздействию погодных условий. Благодаря своим эксплуатационным характеристикам он широко применяется в качестве решетчатого настила для ступеней лестниц, которые могут устанавливаться внутри или снаружи зданий.
Данные конструкции бывают двух видов винтовые и прямые.
Винтовые – отличаются высокой компактностью что позволяет применять их как на производственных, так и гражданских объектах, на которых предусмотрено небольшое пространство для размещения данных конструкций. Кроме этого, обладают высокой прочностью, надежностью, небольшим весом в сравнении с высотой, приемлемой ценой, легкостью монтажа и демонтажа. Данные изделия состоят из перил, площадки, трубы корпуса и ступеней для винтовых лестниц, угол наклона которых можно регулировать.
Прямые – производятся с перилами с обеих сторон и возможностью регулировки высотой по стандарту EN-IS0 14122. В случае необходимости, можно дополнительно заказать площадки в качестве соединительных платформ. Регулировка наклона ступеней проводится путем ослабления всех винтов, находящихся в петлях, настраивания необходимого угла и затянуть их обратно. Это позволяет всегда охранять горизонтальное положение ступеней. Данные конструкции могут выполнятся одно-, двух-, трехмаршевые и т.д. Широко применяются при обустройстве автомобильных ям, складов, подвалов, чердаков и многих других подобных зон. А также, благодаря решетчатому настилу для лестниц, отличаются легкостью сборки, универсальностью конструкции и малым весом.
Металлические ступени для лестниц могут производится с зубьями антискольжения для повышения безопасности людей во время передвижения по ним. Возможен заказ по индивидуальному проекту клиента, а также с покраской специальной краской.
Возможен заказ по индивидуальному проекту клиента, а также с покраской специальной краской.
За дополнительной информацией касательно прессованного и сварного настила для лестниц и металлических ступенях для них обращайтесь к менеджерам. Они с проведут консультацию, ответят на все интересующие Вас вопросы, и помогут с подбором продукции!
Документы
КГКУ «Информационно-технологический центр Приморского края»
КГАУ «Многофункциональный центр предоставления государственных и муниципальных услуг в Приморском крае»
КГКУ «Цифровая лаборатория Правительства Приморского края»
Ведомственный перечень
08.02.2017 16:30:10 Ведомственный перечень государственных услуг и работ оказываемых (выполняемых) краевыми государственными бюджетным и автономным учреждениями Приморского края, подведомственными департаменту, в качестве основных видов деятельности на 2017 год
Документ от 08.02.2017 16:30:10:
Загрузить
04.10.2016 09:55:07 Ведомственный перечень государственных услуг и работ оказываемых краевыми государственными бюджетным и автономным учреждениями Приморского края, подведомственными департаменту, в качестве основных видов деятельности (в ред. от 03.10.16 № пр.40-107)
Документ от 04.10.2016 09:55:07:
Загрузить
03.10.2016 16:02:03 Ведомственный перечень государственных услуг и работ оказываемых краевыми государственными бюджетным и автономным учреждениями Приморского края, подведомственными департаменту, в качестве основных видов деятельности (в ред. от 28.03.16 №пр.40-32)
Документ от 03.10.2016 16:02:03:
Загрузить
Выполнение государственных заданий на оказание услуг (выполнение работ)
9 Февраля 2021, 16:18 Аналитическая записка о выполнении государственного задания за 2020 год подведомственными учреждениями министерства цифрового развития и связи Приморского края
Документ от 09. 02.2021 16:18:58:
Загрузить
02.2021 16:18:58:
Загрузить
9 Февраля 2021, 16:16 Аналитическая записка о выполнении государственного задания за 9 месяцев 2020 года подведомственными учреждениями министерства цифрового развития и связи Приморского края
Документ от 09.02.2021 16:17:12:
Загрузить
30 Июля 2020, 10:02 Аналитическая записка о выполнении государственного задания в 1-ом полугодии 2020 года подведомственными учреждениями министерства цифрового развития и связи Приморского края
Документ от 30.07.2020 10:02:55:
Загрузить
Планы проверок
7 Апреля 2021, 16:21 Приказ Министерства цифрового развития и связи Приморского края от 24.02.2021 № пр.40-31 «О проведении проверки финансово-хозяйственной деятельности, в том числе проверки соблюдения порядка ведения бюджетного учета, составления отчетности, обеспечения тре
Документ от 07.04.2021 16:22:17:
Загрузить
7 Апреля 2021, 16:21 Приказ Министерства цифрового развития и связи Приморского края от 10.02.2021 № пр.40-26 «О внесении изменений в совместный приказ от 01.02.2021 № пр.40-22/19сп «Об утверждении плана проверок финансово-хозяйственной деятельности, в том числе проверок соб
Документ от 07.04.2021 16:21:38:
Загрузить
7 Апреля 2021, 16:19 Приказ Министерства цифрового развития и связи Приморского края от 01.02.2021 № пр.40-22 «Об утверждении плана проверок финансово-хозяйственной деятельности, в том числе проверок соблюдения порядка ведения бухгалтерского учета, составления отчетности, об
Документ от 07.04.2021 16:21:01:
Загрузить
Иные правовые акты
12 Марта 2021, 16:46 Приказ Минцифры ПК от 08. 10.2020 № пр.40-136 О внесении изменений в приказ департамента информатизации и телекоммуникаций Приморского края от 9 декабря 2019 года № пр.40-165
10.2020 № пр.40-136 О внесении изменений в приказ департамента информатизации и телекоммуникаций Приморского края от 9 декабря 2019 года № пр.40-165
Документ от 12.03.2021 16:46:53:
Загрузить
12 Марта 2021, 16:45 Приказ Минцифры ПК от 26.05.2020 № пр.40-74 О внесении изменений в приказ департамента информатизации и телекоммуникаций Приморского края от 9 декабря 2019 года № пр.40-165
Документ от 12.03.2021 16:46:07:
Загрузить
10.03.2020 15:42:34 Об утверждении Примерного положения об оплате труда работников краевых государственных учреждений Приморского края, подведомственных министерству цифрового развития и связи ПК
Документ от 10.03.2020 15:42:34:
Загрузить
Информация о среднемесячной заработной плате руководителей подведомственных учреждений министерства
Сэндвич панели инструкция: упаковка, транспортировка, складирование, хранение сэндвич-панелей
Издание №3
Изменение №0
Введено 30 августа 2012 г.
ИС 5284-014-01395087-2012
Содержание
- Упаковка, транспортирование и складирование конструкционных сэндвич-панелей Teplant(Теплант)
- Транспортирование автомобильным транспортом
- Транспортирование железнодорожным транспортом
- Транспортирование морским транспортом
- Складирование сэдвич-панелей
- Хранение сэндвич-панелей
- Приложение А. Параметры пачек сэдвич-панелей и нормы максимальной загрузки в автомобильный и железнодорожный транспорт
1. Упаковка и транспортирование сэндвич-панелей Teplant
1.1. Конструкционные сэндвич-панели укладываются в стопки, максимальный размер которых по высоте равен 1100 мм. Стопка панелей упаковывается в пакет полиэтиленовой термоусадочной и стрейч пленкой вместе с прокладками из пенополистирола на нижних панелях и пластинами гофрокартона и изолона на верхних панелях (рис. 1).
1).
1.2. Панели транспортируются в заводской упаковке любыми видами транспорта, обеспечивающими сохранность продукции и упаковки в соответствии с правилами перевозки, действующими на каждом виде транспорта.
1.3. В случае перевозки сэндвич-панелей железнодорожным или морским транспортом, упакованные в пакеты панели укладываются в специальную деревянную тару, изготовленную по чертежам предприятия, утвержденным в установленном порядке.
1.4. В случае перевозки панелей автомобильным транспортом панели могут транспортироваться в пакетах упакованных в полиэтиленовую пленку или с укладкой пакетов в специальную деревянную тару. Укладка в деревянную тару при перевозке панелей в автомобильном транспорте допускает возможность перегрузки.
1.5. Возможность при необходимости транспортирования панелей в других условиях (новый вид упаковки) устанавливается при заказе потребителя и согласовывается со специалистами конструкторского отдела.
1.6. В таблице 1 установлены виды упаковки сэндвич-панелей в зависимости от марки (стеновые или кровельные) и вида транспорта.
1.6.1. Виды упаковок (по таблице 1), представлены на рисунках Приложения Б. Рисунки не определяют конструкцию деревянной тары, она определена в чертежах, утвержденных в установленном порядке на предприятии-изготовителе.
1.7. Транспортирование автомобильным транспортом.
1.7.1. Пакеты крепятся к грузовику текстильными ремнями на максимальном расстоянии 2,5 метра. От поперечного и продольного смещения устанавливаются прокладки из пенополистирола между пакетами и с наружной стороны пакетов в местах соприкосновения со стойками автотранспорта.
Таблица 1. Виды упаковки сэнлвич-панелей.
| № п/п | Условное обозначение упаковки и номер чертежа | Назначение | Вид транспорта |
|---|---|---|---|
| 1 | УП а упаковка с линии | Упаковка пачек панелей стеновых или кровельных (ПСБ, ПСБ-2, ПКБ) в полиэтиленовую пленку для перевозки автомобильным транспортом (перегрузка на другой транспорт не рекомендуется) | автомобильный транспорт |
| 2 | УПС ТМ 1273. 01.000 01.000 | Упаковка пачек панелей стеновых (ПСБ) в полиэтиленовой пленке с укладкой в деревянную тару для перевозки железнодорожным транспортом в полувагонах (допускается перегрузка в автомобильный транспорт). | железнодорожный транспорт полувагон |
| 3 | УПС а ТМ 1273.01.000 | Упаковка пачек панелей стеновых (ПСБ) в полиэтиленовой пленке с укладкой в деревянную тару для перевозки автомобильным транспортом (допускаются перегрузки в другой транспорт). | автомобильный транспорт деревянная тара |
| 4 | УПК а ТМ 1509.00.000 СБ | Упаковка пачек панелей кровельных (ПКБ) гофра в одну сторону в полиэтиленовой пленке с укладкой в деревянную тару для перевозки автомобильным транспортом (перегрузки не допускаются) | автомобильный транспорт деревянная тара |
| 5 | УПК ТМ 1273.02.000 | Упаковка пачек панелей кровельных (ПКБ) в полиэтиленовой пленке с укладкой в деревянную тару для перевозки железнодорожным транспортом в полувагонах (допускаются перегрузка в автомобильный транспорт). | железнодорожный транспорт полувагон |
| 6 | УПК п ТМ 1524.01.000 | Упаковка пачек панелей стеновых (ПСБ) в полиэтиленовой пленке с укладкой в деревянную тару для перевозки железнодорожным транспортом на платформе (допускаются перегрузки на другой транспорт). | железнодорожный транспорт платформа |
| 7 | УПК п ТМ 1524.02.000 | Упаковка пачек панелей кровельных (ПКБ) в полиэтиленовой пленке с укладкой в деревянную тару для перевозки железнодорожным транспортом на платформе (допускаются перегрузки на другой транспорт). | железнодорожный транспорт платформа |
| 8 | УПС ам ТМ 1438.01.000 | Упаковка пачек панелей стеновых (ПСБ) в полиэтиленовой пленке с укладкой в деревянную тару для перевозки автомобильным транспортом с перегрузкой в морской транспорт (последующая перегрузка в ж/д транспорт не допускается). | морской транспорт |
| 9 | УПК ам ТМ 1438.02.000 | Упаковка пачек панелей кровельных (ПКБ) в полиэтиленовой пленке с укладкой в деревянную тару для перевозки автомобильным транспортом с перегрузкой в морской транспорт (последующая перегрузка в ж/д транспорт не допускается. | морской транспорт |
| 10 | УПС ам-2 ТМ 1530.00.000 | Упаковка пачек панелей стеновых (ПСБ-2, ширина 1190 мм) в полиэтиленовой пленке с укладкой в деревянную тару при транспортировке автомобильным транспортом с перегрузкой в морской транспорт. | морской транспорт |
| 11 | УПС м ТМ 1535.00.000 | УУпаковка пачек панелей стеновых (ПСБ) в полиэтиленовой пленке в деревянной таре при перевозке железнодорожным транспортом с перегрузкой в морской транспорт. | морской транспорт |
1.7.2. На верхний пакет устанавливается транспортировочный щит, который крепится над местом расположения пенополистирольной прокладки. При затягивании текстильных ремней проверяется стык щита с верхней панелью в пакете с целью предотвращения деформации листа верхней панели (рис.2).
1.7.3. Во время транспортировки водитель должен периодически проверять стабильность груза и плотность связки.
В случае ослабления связки — необходимо вновь затянуть текстильные ремни.
Для затягивания пакетов ЗАПРЕЩАЕТСЯ применение стального троса или проволоки.
1.8. Транспортирование автомобильным транспортом в деревянной таре.
1.8.1. Пакеты стеновых панелей укладываются в деревянную тару (контейнеры), размещаются и закрепляются в автомобильном транспорте (рис.З).
1.8.2. Пакеты кровельных панелей укладываются в деревянную тару (контейнеры), дополнительно крепятся в кузове деревянными распорками (рис. 3).
1.9. Транспортирование железнодорожным транспортом. При перевозке конструкционных сэндвич — панелей Teplant железнодорожным транспортом пакеты панелей укладываются в деревянную тару (контейнеры) (рис. 4). Контейнеры загружаются в полувагон, связываются между собой и крепятся к вагону стальным тросом на расстоянии 2,5 м друг от друга, но не менее 2 тросов на каждый контейнер (рис. 5).
Таблица 2. Максимальная вместимость конструкционных сэндвич-панелей Teplant ПКБ и ПСБ (L=6000 мм и L=12000 мм) в полувагон
| Тип панели | Толщина по утеплителю | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Марка | Ширина | 50 | 80 | 100 | 120 | 150 | 170 | 200 | 220 | 250 |
| ПКБ, м2 | 1000 | 528 | 432 | 384 | 288 | 240 | — | 192 | — | — |
| ПСБ, м2 | 1000 | 960 | 624 | 528 | 432 | 336 | 288 | 240 | 192 | 192 |
| ПСБ 2, м2 | 1190 | — | 742 | 628 | 514 | 400 | 342 | 285 | 228 | 228 |
1.10. Транспортирование морским транспортом.
1.10.1. При перевозке конструкционных сэндвич — панелей Teplant морским транспортом пакетыпанелей укладываются в деревянную тару(контейнеры) (рис. 6).
1.10.2. Размеры тары по высоте в обязательном порядке согласовывается с компанией — перевозчиком морским транспортом.
1.10.3. Дополнительные условия при перевозках панелей, предназначенных на экспорт морским транспортом, в обязательном порядке оговариваются при заказе.
1.11. Перегрузка и перенос пакетов.
1.11.1. Если упаковка имеет видимые повреждения или другие недостатки, то при приеме товара делается отметка в накладной, которая заверяется подписями перевозчика и приемщика груза.
1.11.2. Перенос, перегрузка или разгрузка пакетов с панелями Teplant осуществляется с помощью любых типов кранов с использованием специальных металлических траверс различных длин.
Перенос, перегрузка или разгрузка пакетов панелей в полиэтиленовой пленке производится в соответствии с требованиями «Правил по переносу и хранению панелей» (оранжевая этикетка, которая наклеена на каждый пакет (упаковку) панелей).
При переносе пакетов ЗАПРЕЩАЕТСЯ использование стального троса или проволоки.
Для переноса пакетов применять только мягкие стропы соответствующего размера и типа(см. таблицу 3) и Схему строповки пакетов (рис. 7). При поднятии пакета необходимо обращать внимание на центр тяжести.
ВСЕГДА ПОДНИМАТЬ И ПЕРЕНОСИТЬ ТОЛЬКО ОДИН ПАКЕТ.
Разгрузка пакетов с панелями из автомобиля осуществляется через боковой борт. Упаковки выгружаются на ровную, заранее подготовленную поверхность.
Пакеты с панелями нельзя толкать или тащить.
Таблица 3.
| Длина упаковки (L), м | Максимальная масса груза, т. | Тип стропы | Высота (H), мм | Угол (β) | Длина распорки (L) |
|---|---|---|---|---|---|
| 0.5-4.5 | 2.04 | СТП 2.0-8.0 | 3000+3350 | 31°3’h3°4″ | 1240 |
| 4.5-7.5 | 2.23 | СТП 2.0-8.0 | 2850 | 38° | 1240 |
| 7.5-10 | 3.43 | СТП 4.0-11.0 | 3910+4560 | 39°3′ | 1240 |
| 10-14 | 3.94 | СТП 4.0-11.0 | 4050 | 44°3″ | 1240 |
2. Складирование сэндвич — панелей
2.1. Упакованные пакеты с сэндвич — панелями Teplant следует складировать на стройплощадке на заранее подготовленную ровную поверхность, имеющую уклон для отвода дождевых и талых вод.
2.2. Пачки укладываются на широкие и прочные подставки, обеспечивающие равномерное распределение веса пакета на нижнюю панель и защищающие панель от прогибания или повреждения.
2.3. Упаковки с панелями ЗАПРЕЩАЕТСЯ толкать или тащить, так как в этом случае скольжение панелей в пакете может повредить их поверхность.На пакеты с панелями или на незащищенные панели ЗАПРЕЩАЕТСЯ укладывать тяжелые предметы во избежание повреждения поверхности панели.
2.4. Пакеты с панелями Teplant нельзя складывать друг на друга.
2.5. Расстояние между упаковками должно быть не менее 100 м.
2.6. Рекомендуется не нарушать заводскую упаковку пакета, которая обеспечивает водонепроницаемость пакета. Если же упаковка нарушена, то необходимо пакет с оставшимися панелями защитить от влаги полиэтиленовой пленкой.
2.7. При складировании упакованных пакетов с панелями Teplant на открытом воздухе (не под навесом) следует защищать верхнюю панель в пакете от воздействия прямых солнечных лучей. В противном случае устранение защитной монтажной пленки будет затруднительно.
Срок хранения панелей с не удаленной защитной пленкой не более трех месяцев.
ВНИМАНИЕ: ЗАЩИТНУЮ МОНТАЖНУЮ ПЛЕНКУ НЕОБХОДИМО УДАЛЯТЬ НЕМЕДЛЕННО ПОСЛЕ МОНТАЖА ПАНЕЛЕЙ.
3. Хранение сэндвич — панелей Teplant
3.1. Панели в стопках и комплектующие изделия следует хранить в заводской упаковке, обеспечивающей водонепроницаемость в складах закрытого или полузакрытого типа с соблюдением установленных мер противопожарной безопасности.
3.2. Допускается кратковременное, не более месяца, хранение на открытых площадках при условии сохранности заводской упаковки и защиты от осадков и воздействия солнечных лучей водонепроницаемым материалом таким образом, чтобы была возможность проветривания.
3.3. При изготовлении обшивок панелей из оцинкованного (без полимерного покрытия) проката рекомендуемый срок хранения не должен превышать 30 дней с даты изготовления при условии хранения в складах закрытого типа.
При попадании внутрь упаковки влаги, упаковку следует распаковать, обшивки панелей просушить.
Приложение А (справочное)
Параметры пачек сэндвич-панелей и нормы максимальной загрузки в автомобильный, железнодорожный и морской транспорт (при длине панелей 6 м. или 12 м.)
| Марка панели | Максимальное количество панелей в пачке, шт. | Высота пачки, мм. | Высота пачки, мм | Максимальная высота трех пачек панелей | Максимальная норма загрузки в автотранспорт при длине панелей 6 или 12 и, м2 | Максимальная норма загрузки в ж/д транспорт при длине панелей 6 или 12 и, м2 |
|---|---|---|---|---|---|---|
| Стеновые сэндвич-панели | ||||||
| ПСБ-50 | 13 | 650 | 750 | 2250 | 936 | 960 |
| ПСБ-80 | 8 | 664 | 764 | 2292 | 576 | 576 |
| ПСБ-100 | 6 | 590 | 690 | 2070 | 432 | 480 |
| ПСБ-120 | 5 | 590 | 690 | 2070 | 360 | 384 |
| ПСБ-150 | 4 | 592 | 692 | 2076 | 288 | 288 |
| ПСБ-200 | 3 | 597 | 697 | 2091 | 216 | 240 |
| Кровельные сэндвич-панели | ||||||
| ПКБ-50 | 9 | 650 | 750 | 2250 | 648 | 528 |
| ПКБ-80 | 6 | 609 | 709 | 2127 | 432 | 432 |
| ПКБ-100 | 5(*) | 600 | 700 | 2100 | 360 | 384 |
| ПКБ-120 | 4 | 546 | 646 | 1938 | 288 | 288 |
| ПКБ-150 | 4 | 666 | 766 | 2298 | 288 | 240 |
| ПКБ-200 | 2 | 472 | 572 | 2288(*) | 192 | 192 |
На ОП ППС-2
| Марка панели | Максимальное количество панелей в пачке, шт. | Высота пачки, мм. | Высота пачки, мм | Максимальная высота трех пачек панелей | Максимальная норма загрузки в автотранспорт при длине панелей 6 или 12 и, м2 | Максимальная норма загрузки в ж/д транспорт при длине панелей 6 или 12 и, м2 |
|---|---|---|---|---|---|---|
| Стеновые сэндвич-панели | ||||||
| ПCБ-80 | 12 | 1020 | 1120 | 2240 | 576 | 624 |
| ПCБ-2-80 | 685 | 742 | ||||
| ПCБ-100 | 10 | 100 | 1100 | 2200 | 480 | 528 |
| ПCБ-2-100 | 471 | 628 | ||||
| ПCБ-120 | 9 | 1080 | 1180 | 2360 | 432 | 432 |
| ПCБ-2-120 | 514 | 514 | ||||
| ПCБ-150 | 7 | 1050 | 1150 | 2300 | 336 | 336 |
| ПCБ-2-150 | 400 | 400 | ||||
| ПCБ-170 | 6 | 1038 | 1138 | 2276 | 288 | 288 |
| ПCБ-2-170 | 342 | 342 | ||||
| ПCБ-200 | 5 | 1005 | 1105 | 2210 | 240 | 240 |
| ПCБ-2-200 | 285 | 285 | ||||
| ПCБ-220 | 3 | 669 | 769 | 2307(*) | 216 | 192 |
| ПCБ-2-220 | 257 | 228 | ||||
| ПCБ-250 | 4 | 1004 | 1104 | 2208 | 192 | 192 |
| ПCБ-2-250 | 228 | 228 | ||||
Приложение Б (справочное)
Рисунки видов упаковки в соответствии с таблицей 1.
1. УП а упаковка с линии
(автомобильный транспорт)
Упаковка пачек панелей стеновых или кровельных (ПСБ, ПСБ-2, ПКБ) в полиэтиленовую пленку для перевозки автомобильным транспортом (перегрузка на другой транспорт не рекомендуется).
2. УПС ТМ 1273.01.000
(железнодорожный транспорт полувагон)
Упаковка пачек панелей стеновых (ПСБ) в полиэтиленовой пленке с укладкой в деревянную тару для перевозки железнодорожным транспортом в полувагонах (допускается перегрузка в автомобильный транспорт).
3. УПС а ТМ 1273.01.000
(автомобильный транспорт деревянная тара)
Упаковка пачек панелей стеновых (ПСБ) в полиэтиленовой пленке с укладкой в деревянную тару для перевозки автомобильным транспортом (допускаются перегрузки в другой транспорт)
4. УПК а ТМ 1509.00.000 СБ
(автомобильный транспорт деревянная тара)
Упаковка пачек панелей кровельных (ПКБ) гофра в одну сторону в полиэтиленовой пленке с укладкой в деревянную тару для перевозки автомобильным транспортом, (перегрузки не допускаются)
5. УПК ТМ 1273.02.000т
(железнодорожный транспорт полувагон)
Упаковка пачек панелей кровельных (ПКБ) в полиэтиленовой пленке с укладкой в деревянную тару для перевозки железнодорожным транспортом в полувагонах (допускаются перегрузка в автомобильный транспорт).
6. УПС п ТМ 1524.01.000
(железнодорожный транспорт платформа)
Упаковка пачек панелей стеновых (ПСБ) в полиэтиленовой пленке с укладкой в деревянную тару для перевозки железнодорожным транспортом на платформе (допускается перегрузки на другой транспорт).
7. УПК п ТМ 1524.02.000
(железнодорожный транспорт платформа)
Упаковка пачек панелей кровельных (ПКБ) в полиэтиленовой пленке с укладкой в деревянную тару для перевозки железнодорожным транспортом на платформе (допускаются перегрузки на другой транспорт).
8. УПС ам ТМ 1438.01.000
(морской транспорт)
Упаковка пачек панелей стеновых (ПСБ) в полиэтиленовой пленке с укладкой в деревянную тару для перевозки автомобильным транспортом с перегрузкой в морской транспорт, (последующая перегрузка в ж/д транспорт не допускается)
9. УПК ам ТМ 1438.02.000
(морской транспорт)
Упаковка пачек панелей кровельных (ПКБ) в полиэтиленовой пленке с укладкой в деревянную тару для перевозки автомобильным транспортом с перегрузкой в морской транспорт, (последующая перегрузка в ж/д транспорт не допускается)
10. УПС ам-2 ТМ 1530.00.000
(морской транспорт)
Упаковка пачек панелей стеновых (ПСБ-2, ширина 1190 мм) в полиэтиленовой пленке с укладкой в деревянную тару при транспортировке автомобильным транспортом с перегрузкой в морской транспорт.
11. УПС мТЛЛ 1535.00.000
(морской транспорт)
Упаковка пачек панелей стеновых (ПСБ) в полиэтиленовой пленке в деревянной таре при перевозке железнодорожным транспортом с перегрузкой в морской транспорт.
Экспериментальное производство ATLANT. Технологии быстрого прототипирования. 3D принтеры, ЧПУ-станки
ЗАО «АТЛАНТ» изготавливает опытные образцы изделия с использованием технологий быстрого прототипирования (RapidPrototyping). Быстрое прототипирование широко используется в производстве бытовой техники «АТЛАНТ», помогая значительно сократить время, необходимое для обновления модельного ряда продукции.
3D принтеры
Описание FDM
Созданные CAD-данные деталей материализуются на технологическом оборудовании FDM Vantage SE фирмы «Stratasys».
Модель, образно говоря, «выращивается» в данных установках, реализующих принцип послойного синтеза. «Выращивание» моделей открывает неограниченные возможности в технологии литья металлов, позволяет реализовать конструкции, ранее не доступные вследствие технологических ограничений.
Технологии быстрого прототипирования позволяют получить литейные модели в течение нескольких часов или дней (для сложных габаритных отливок) без создания специальной технологической литейной оснастки.
Получение моделей деталей методами быстрого прототипирования минимизируют риск ошибочных конструкторских и технологических решений, так как разработчик, имея реальную физическую модель будущего изделия, может выявить и устранить конструктивные ошибки, скорректировать пути продолжения процесса проектирования.
Изготовление моделей-прототипов, с толщиной слоя от 0,127 до 0,254 мм на установке FDM Vantage SE, осуществляется с точностью пластмассовых деталей, изготовленных в обычных инжекционных пресс-формах.
Оборудование позволяет создавать прототипы деталей с максимальными размерами 355х406х406 мм.
Описание SLA
Созданные CAD-данные деталей материализуются также на технологическом оборудовании SLA-250 фирмы «3D-Systems».
По технологии стереолитографии, одной из наиболее распространенных технологий быстрого прототипирования, изготавливаются детали с максимальными размерами 250х250х250 мм на установке SLA-250. Процесс стереолитографии позволяет добиться линейной точности ±100 мкм при толщине слоя 0,1 мм.
Для тиражирования широко применяется метод получения деталей с помощью вакуумного литья в гибкие формы. Модель-прототип используется для изготовления оснастки из силикона, с помощью которой в дальнейшем идет отливка деталей.
Эта технология получила широкое распространение при изготовлении мелких партий изделий из пластмассы, которая заливается непосредственно в силиконовую форму.
ЧПУ-станки
Координатно-пробивной пресс Bosсhert Multipunch с ЧПУ предназначен для раскроя тонколистового метала с выполнением различных контурных элементов (круглые, овальные, прямоугольные, пуклевка) с высокой производительностью и точностью. Точность вырубки по заданным координатам, быстрая смена инструмента (max 5 сек), а так же рабочая зона с системой фиксации листа с 2-мя пневматическими захватами являются залогом качества и высоких скоростей обработки. Наличие 8-ми независимых индексных инструментальных головок, которым оборудован координатно-пробивной пресс, наличие специального инструмента позволяет достигнуть высокой производительности обрабатываемых изделий.
ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ:
- Max толщина листа, мм – 0,5;
- Max размер обрабатываемой заготовки, мм, — 1250х2500;
- Точность по осям в процессе пробивки, мм — ±0,1.
При работе оборудования используется метод холодной гибки рабочего металла, без его предварительного нагрева. Наличие ЧПУ значительно увеличивает производительность оборудования и существенно повышает точность изгиба. Гидравлическая система работает бесшумно и точно. Также пресс оснащен системой анти-прогибания, системой механического зажима с возможностью быстрой смены инструментов.
ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ:
- Толщина обрабатываемого металла, мм – 0,4-4;
- Max рабочая длина металла, мм – 2000;
- Мах угол гибки, º — 120.
Отклик на большой прогиб стальных стальных балок при пожаре и взрыве
Здесь представлены несколько числовых примеров. На основе численных результатов анализируются некоторые особенности реакции и предельная температура балки, а также обсуждаются эффекты взаимодействия поведения конструкции при двух типах нагрузок.
Например, обсуждается реакция стальной балки с Н-образным поперечным сечением, показанной на рис. 2. Ниже приведены некоторые параметры конструкции, материалов и нагрузок.
Рис.2Геометрическая конфигурация балки с Н-образным сечением
Геометрические размеры балки Н-образного сечения:
Пролет балки: L = 1,14 м
Высота поперечного сечения: H = 0,08 м
Ширина фланца: B = 0.046 м
Толщина фланца: т f = 0,0052 м
Толщина стенки: т Вт = 0,0038 м
Константы материала стали при нормальной температуре:
Плотность и коэффициент теплового расширения: \ (\ rho = 7850 \) кг / м 3 , \ (\ alpha = 1.{\ circ} {\ text {C}} \)
Модуль Юнга, предел текучести и коэффициент Пуассона: \ (E = 205 \) ГПа, \ (\ sigma_ {s} = 399 \) МПа, \ (\ nu = 0,3 \)
Константы скорости деформации: D = 40,4 с −1 , q = 5
Коэффициент нагрузки определяется как \ (\ eta = \) P / P c , в котором P c = 4M -п. / L , M -п. — предельный изгибающий момент пластика.
Стальная балка при повышенных температурах
На деформационное поведение балки при пожаре может серьезно повлиять сдерживающее действие окружающих конструкций из-за теплового расширения. В качестве модели с уменьшенной балкой на практике шарнирно-шарнирная балка продемонстрировала лучшую огнестойкость (Liu et al. 2002).
Два традиционных пластмассовых шарнира и две концепции предельной температуры
Как известно, эффекты теплового расширения и торцевых осевых ограничений на шарнирно-шарнирную балку при повышенных температурах приведут к цепной реакции.Соответственно, следует учитывать большие эффекты отклонения, и можно улучшить огнестойкость балки. Однако в случае большого отклонения осевая сила также включается в сечение вместе с изгибающим моментом. Необходимо учитывать влияние взаимодействия этих факторов на выход материала. Таким образом, определение предельных температур в таких случаях — это вопрос, который будет обсуждаться на этом этапе.
Кривые зависимости прогиба в середине пролета от температуры, соответствующие нескольким ситуациям с соотношением нагрузок, представлены на рис.3. Что касается повышения температуры, прогибы не изменяются быстро, а постепенно увеличиваются. Таким образом, определение предельной температуры разрушения представляется трудным, поскольку осевые ограничения на концах балки не только ограничивают осевые смещения на концах, но также заставляют балку создавать осевое усилие на сечение. Более того, сила раннего осевого сжатия может быть изменена на силу растяжения при повышении температуры. Затем осевая сила растяжения и изгибающий момент совместно противостоят нагрузкам и замедляют увеличение прогибов балки.Вышеупомянутый феномен называется эффектом цепного действия (Yin and Wang 2005).
Рис. 3Кривые зависимости прогиба середины пролета от температуры при различных соотношениях нагрузок
Для полностью закрепленной стальной балки, находящейся под огнем, два критерия для определения предельной температуры предложены Си и Луан (2012) следующим образом:
Критерий 1: Первая предельная температура, T 1 лим , может быть определен, когда безразмерная контактная сила равна нулю или безразмерный изгибающий момент равен единице, что соответствует традиционному изгибающемуся пластиковому шарниру.
Критерий 2: Вторая предельная температура, T 2 лим , может быть определено, когда безразмерная контактная сила равна единице или безразмерный момент равен нулю, что соответствует традиционному растягивающемуся пластиковому шарниру.
Затем проверяется применимость вышеупомянутых критериев к шарнирно-шарнирной балке.
Кривые безразмерного изгибающего момента M T x / M т пол и осевое усилие Н T x / N т пол от температуры представлены на рис.4, где M T x и N T x — изгибающий момент и осевое усилие средней секции при температуре T соответственно, тогда как M т пол и N т пол — это полный изгибающий момент и полная осевая сила соответствующей температуры, соответственно.Изгибающий момент увеличивается при повышении температуры с 20 ° C до момента, когда будет достигнуто максимальное значение, равное единице. Однако при повышении температуры осевая сила сначала увеличивается, а затем уменьшается из-за комбинированного воздействия теплового расширения и большого отклонения. Безразмерная осевая сила также равна нулю при увеличении изгибающего момента до единицы. Таким образом, в средней части балки формируется традиционный изгибающийся пластиковый шарнир. Соответствующая температура, которую следует определить как предельную температуру разрушения, называется первой предельной температурой T . 1 лим .Однако, поскольку температура продолжает расти, этот пластиковый шарнир не прослужит долго. Более того, повышенное отклонение приводит к осевым силам растяжения или цепным воздействиям, которые заставляют стальную балку сохранять свою несущую способность. Очевидно, что при температуре выше Т 1 лим , момент уменьшается, а осевая сила увеличивается с ростом температуры. Это явление демонстрирует, что режим деформации стальной балки изменяется от в основном изгибного изгиба до цепного состояния, в котором преобладает растягивающая сила, после того, как изгибающийся пластичный шарнир исчезает.Вместе с повышением температуры увеличивается и безразмерная осевая сила, достигая максимального значения единицы, а момент равен нулю. Таким образом, на секции формируется традиционный растягивающийся пластиковый шарнир, а стальная балка демонстрирует статус полностью пластичного пояса. Этот растягивающийся пластиковый шарнир выдерживает постоянное повышение температуры, пока стальная балка не сломается и полностью не потеряет свою несущую способность. Таким образом, в начале этой фазы можно определить другую предельную температуру отказа и назвать ее второй предельной температурой T 2 лим . {2} \).{1} \), используя критерий, согласно которому максимальный прогиб равен размаху / 20. Этот вывод соответствует случаю фиксированного фиксированного пучка, обсуждаемому в работе Xi and Luan (2012).
Следует подчеркнуть, что некоторые результаты, полученные здесь, уже хорошо известны в пожарном сообществе, это указывает на то, что принцип минимального ускорения может быть использован для эффективного анализа статического поведения конструкций при большом прогибе, подверженных пожарной нагрузке. По сравнению с методом Ньютона – Рафсона, обычно используемым при анализе реакции конструкций при огневом воздействии, предлагаемый метод более прямолинеен и прост и не требует итерационных вычислений.
Стальная балка, подвергшаяся взрыву с последующим возгоранием
Балка, описанная ранее, затем последовательно подвергается следующим нагрузкам.
- ①
Сначала к середине пролета прикладывается поперечная статическая нагрузка P \ (P = \ eta P_ {c} \).
- ②
Далее, взрывная нагрузка, представляющая собой прямоугольный импульс с интенсивностью \ (P_ {d} \) и длительностью t 0 = 0.25 с, применяется в середине пролета. Коэффициент взрывной нагрузки (сокращенно ELR) равен \ (\ eta_ {e} = P_ {d} / P_ {c} \).
- ③
Огонь применяется. Предполагается, что температура равномерно распределена по каждому направлению луча.
Несомненно, реакция стальной балки на эти комбинированные нагрузки сложна.В настоящее время, в частности, исследуется влияние взрывных нагрузок на предельную температуру разрушения.
Для четырех случаев отношения нагрузок (\ (\ eta = 0,2,0,5,0,7,0,85 \)) кривые остаточного прогиба в середине пролета в зависимости от температуры представлены на рис. 6a – d. Четыре кривые на каждом рисунке соответствуют четырем случаям ELR \ (\ eta_ {e} = 0,1,2,3 \), соответственно, в котором \ (\ eta_ {e} = 0 \) обозначает отсутствие взрывная нагрузка. Наблюдая за каждой кривой этих фигур, можно увеличить прогиб балки за счет взрывной нагрузки.Более того, если увеличение отклонения настолько велико, как увеличение ELR, то это повлияет на предельную температуру луча.
Фиг.6a Кривые отклонения середины пролета от температуры для коэффициента нагрузки \ (\ eta = 0,2 \). b Кривые отклонения середины пролета от температуры для коэффициента нагрузки \ (\ eta = 0,5 \). c Кривые отклонения среднего пролета от температуры для \ (\ eta = 0.7 \). d Кривые отклонения середины пролета от температуры для \ (\ eta = 0,85 \)
Для анализа изменений критической температуры на рисунке также изображены горизонтальные линии L / 20 и L / 10. Максимальные остаточные прогибы превышают горизонтальную линию L / 20 для двух случаев ELR (\ (\ eta_ {e} = 2,3 \)). Следовательно, только горизонтальную линию L / 10 можно использовать для определения критической температуры корпусов с относительно высоким ELR.{1} = 473 — \) \ (225 = 248 \) ° C соответственно.
Четыре кривые на каждом рисунке имеют тенденцию накладываться друг на друга при повышении температуры, что указывает на то, что влияние взрывной нагрузки было превышено из-за серьезного ухудшения прочности и жесткости материала, вызванного повышенной температурой. Таким образом, деформация балки, вызванная взрывной нагрузкой, больше не играет ведущей роли. Этот эффект заметен, когда взрывная нагрузка мала, например, когда \ (\ eta_ {e} = 0 \) и \ (\ eta_ {e} = 1 \), что соответствует ситуации, когда вторые критические температуры \ ( T_ {cr} ^ {2} \) такие же.{2} = 656 — 206 = 450 \) ° С соответственно. Таким образом, разница в критических температурах также увеличивается с увеличением отношения нагрузки.
Стальная балка, подвергшаяся возгоранию с последующим взрывом
Шарнирно-шарнирная балка последовательно подвергается следующим нагрузкам:
- ①
Сначала к середине пролета прикладывается поперечная статическая нагрузка P \ (P = \ eta P_ {c} \).
- ②
Затем прикладывается пожарная нагрузка до тех пор, пока не будет достигнута заданная температура.
- ③
Затем прикладывают взрывную нагрузку с прямоугольным импульсом. ELR и длительность равны \ (\ eta_ {e} = P_ {d} / P_ {c} \) и \ (t_ {0} = 0,05 \) с соответственно.
Очевидно, что реакция стальной балки на эти комбинированные нагрузки сложна, особенно потому, что взрывная или ударная нагрузка прикладывается к стальной балке, которая подвергается пожарной нагрузке.Чувствительность скорости деформации материалов отличается от чувствительности при нормальной температуре. Таким образом, оба параметра D и q уравнения Каупера – Симондса связаны с температурой. Однако таких тестовых данных нет. В недавнем исследовании поведения стальной балки, подвергшейся воздействию огня и последующего импульсного нагружения (Xi et al. 2014), было предложено предположение о взаимосвязи между параметрами скорости деформации и температуры. В настоящем исследовании мы по-прежнему используем это предположение.Хотя это предположение не обязательно соответствует действительности, разница не должна быть значительной, и основное внимание в настоящем исследовании уделяется описанию метода. В любом случае реальное поведение конструкции может быть эффективно смоделировано с использованием предложенной вычислительной модели, если испытание точно обеспечивает параметры скорости деформации, зависящие от температуры.
Для случая нагрузки \ (\ eta = 0,2 \), заданных температур 20, 400, 600 и 700 ° C и ELR \ (\ eta_ {e} = 3 \), кривые изменения во времени среднего Прогиб пролета представлен на рис.7, где 20 ° C соответствует случаю, когда пожарная нагрузка отсутствует. Очевидное увеличение прогибов происходит, когда заданная температура превышает 400 ° C. Однако разница между прогибами, соответствующими 20 и 400 ° C, минимальна. Когда заданная температура <400 ° C, жесткость материала снижается и возникает деформация теплового расширения, тогда как прочность материала ухудшается только при температурах выше 400 ° C. Следовательно, для балки, подверженной этим нагрузкам, основным фактором, вызывающим быстрое увеличение смещения, является снижение прочности, вызванное повышенными температурами, тогда как влияние деформации теплового расширения и ухудшения жесткости, вызванного изменениями температуры, минимально.
Рис.7Кривые отклонения в середине пролета от времени
На основе кривых зависимости прогиба от времени, показанных на рис. 7, кривые остаточного прогиба в середине пролета (рассматриваемого как равномерный прогиб остаточной упругой вибрации) в зависимости от температуры при нескольких случаях отношения нагрузок \ (\ eta = 0,2 , 0.5,0.7 \) и ELR \ (\ eta_ {e} = 3 \) представлены на рис. 8. Для сравнения также изображена кривая, соответствующая случаю, когда \ (\ eta_ {e} = 0 \) на этом рисунке.Видно, что форма кривых изменилась, а деформация балки увеличилась в результате взрывной нагрузки. Таким образом, критическая температура снижается. Однако прогиб не всегда явно увеличивается при повышении температуры, например, когда T <400 ° C. Это явление можно объяснить увеличением деформации осевого теплового расширения балки при повышении температуры до 400 ° C, что указывает на то, что в механизме деформации преобладает осевое тепловое расширение.Когда температура превышает 400 ° C, прочность материала начинает ухудшаться, и механизм деформации принимает на себя ведущую роль в прогибе при изгибе. Затем прогиб быстро увеличивается по мере того, как температура продолжает расти. Очевидно, что для такого режима деформирования можно легко определить предельную температуру разрушения.
Рис.8Кривые зависимости прогиба в середине пролета от температуры
По сравнению с тремя кривыми, которые соответствуют случаю без взрывной нагрузки, три кривые \ (\ eta_ {e} = 3 \) значительно ближе друг к другу, что означает, что влияние первой статической нагрузки с разными Коэффициенты нагрузки на деформацию балки минимальны.
Для \ (\ eta = 0,5 \) и \ (\ eta_ {e} = 0,1,2,3,4 \) кривые температуры постоянного прогиба в середине пролета представлены на рис. 9. Прогибы увеличиваются по мере увеличения взрывных нагрузок, и каждая кривая демонстрирует характеристики, которые показывают, что прогиб резко увеличивается с повышением температуры. Таким образом, для каждого варианта нагружения существует температура разрушения.
Рис. 9Кривые зависимости остаточных прогибов средних пролетов от температуры
Горизонтальные линии L / 20 и L / 10 также изображены на рис.9, так что соответствующую критическую температуру можно легко определить. Результаты представлены в таблице 2. Для сравнения также приведены критические температуры, полученные на этапе 3.2. Таблица 2 показывает, что эти два результата различаются. Критическая температура стальной балки, которая подвергается возгоранию с последующим взрывом, ниже, чем у балки, которая подвергается взрыву с последующим возгоранием. Эти результаты показывают, что разные последовательности нагружения могут приводить к различным реакциям, влияя, таким образом, на критическую температуру конструкции.
Таблица 2 Сравнение критических температурНа рис. 10 показаны кривые остаточного прогиба в середине пролета в зависимости от ELR для случаев \ (\ eta = 0,5 \) и различных температур. Очевидно, что смещение не увеличивается резко по мере увеличения ELR, что может быть связано со скоростью деформации и инерцией, препятствующими возникновению явления, аналогичного статическому случаю. Таким образом, соответствующие динамические предельные нагрузки не определены.Следовательно, взрывобезопасная нагрузка также не будет существовать в этом случае, если не рассматривать разрушение материалов.
Рис.10Кривые остаточного прогиба относительно ELR
Чтобы оценить влияние температуры на диаграмму давление-импульс, на рис. 11a представлены несколько кривых ELR-импульс в трех температурных условиях и двух статических соотношениях нагрузки. Площадь зоны безопасности в нижнем левом углу кривой уменьшается с повышением температуры.В частности, площади зон с температурами 300 и 600 ° C существенно различаются, и, таким образом, зона безопасности серьезно сокращается из-за высоких температур. Напротив, влияние коэффициента статической нагрузки незначительно. Для η = 0,5 поверхность изоповреждений в трехмерном параметрическом пространстве температуры, ELR и импульса представлена на рис. 11b, эта трехмерная поверхность делит пространство на две области. Область под поверхностью является безопасной пространственной зоной, а область над ней — небезопасной пространственной зоной.При проектировании конструкции на огнестойкость и взрывобезопасность необходимо обеспечить, чтобы температура, ELR и импульс находились в безопасной зоне.
Фиг.11a Диаграмма давление-импульс при трех температурных условиях. b График давление – температура – импульс для η = 0,5
Когда это проблема?
Размещено 9 июн, 2020
Таблицы балок производителя обычно основаны на равномерно распределенных нагрузках.И грузоподъемность, и прогиб балки будут изменяться, если нагрузка на балки грузовой полки распределяется неравномерно. Хотя некоторая степень отклонения является нормальным явлением для нагруженной стеллажной системы, как определить, когда величина отклонения указывает на уменьшение грузоподъемности балки?
Полезный совет: Любую балку с видимой деформацией или растрескиванием концевых соединителей или сварных швов балки следует разгрузить и заменить. При установке убедитесь, что балки полностью вошли в зацепление, а предохранители установлены правильно.
Как определить, не перегружены ли балки
1. Обратите внимание на прогиб балки
Максимально допустимый прогиб равен длине балки, деленной на 180. Отклонение больше указанного — это перегруженная балка. Максимальный прогиб находится в средней точке балки для равномерно распределенной нагрузки. *
Некоторые AS / RS или автоматизированные системы обычно определяют более жесткий предел прогиба для нагрузочных балок, такой как длина балок, деленная на 240 (или 0.42%). Это требование более жесткого отклонения сводит к минимуму риск контакта автоматики (или нагрузки) с балками во время установки или снятия.
Есть ли постоянный прогиб при разгруженной балке?
Если «да», балка перегружена и ее необходимо заменить.
2. Проверить соединение на раме
Осмотрите область, где балка соединяется с рамой. При наличии любого из следующих условий балку следует заменить.
- Имеется какая-либо визуальная деформация стойки и / или зажима, указывающая на то, что балка была повреждена в результате удара или перегрузки
- В сварных швах есть трещины.
- Предохранительный зажим не может быть правильно подсоединен и полностью зафиксирован.
Хотя сам по себе прогиб балки не влияет на грузоподъемность или безопасность вашей стойки, он может повлиять на нагрузку стойки и тех, кто взаимодействует с системой. Когда балки отклоняются, нагрузки могут наклоняться друг к другу, увеличивая вероятность контакта.Это может вызвать повреждение продукта или создать опасность во время погрузки и разгрузки.
Для получения дополнительной информации см. Раздел «Нагрузочная балка RMI» в списке часто задаваемых вопросов.
* в блоге по безопасности RMI Отклонение балки поддона: насколько приемлемо? Статья от 30 апреля 2018 года: «Однако этот предел прогиба не соответствует требованиям для обеспечения структурной целостности балки или стойки. Напротив, это необходимо для того, чтобы персонал, взаимодействующий со стеллажом и работающий вокруг него, чувствовал себя в безопасности, когда видит нормальный прогиб балки поддона.В 1960-х годах RMI определила, что расчетная длина, деленная на 180, дает количественную оценку точки, в которой люди считают ситуацию небезопасной, когда наблюдается отклонение стеллажа для поддонов ».
Использованные источники и дополнительная информация доступна по адресу:
www.mhi.org
www.rmiracksafety.org
ANSI Mh26.1: 2012; Спецификация для проектирования, испытаний и использования промышленных стальных стеллажей
Рекомендации RMI для планирования и использования промышленных стальных стеллажей 3-21-2018
Руководство RMI по оценке и ремонту или замене поврежденных стеллажей
RMI Safety Blog Паллетная балка Отклонение: насколько приемлемо? От 30 апреля 2018 г.
Опубликовано в Безопасность объекта | Tagged осмотр стойки, безопасность стойки | Оставить комментарий
Введение
ВведениеГибка балки
Джон Джонстон, Ph.Д., П.Е. и Эдвард Даммель, доктор философии.
Департамент гражданского строительства
Калифорнийский государственный университет Сакраменто
октябрь 1999
Введение
В этом упражнении мы нагружаем балку с простой опорой и измеряем результирующий прогиб в центре. Построив график прогибов в зависимости от нагрузки, мы сможем вычислить модуль упругости материала балки, что является важным показателем прочности материала.Хотя это измерение само по себе имеет некоторое практическое значение, более широкая полезность этого упражнения заключается в том, что оно служит трамплином для нескольких важных тем в инженерной практике. К ним относятся эластичность, факторы безопасности, выбор материалов, важность формы в сопротивлении нагрузкам, а также учет нескольких видов нагрузки и видов отказов. По мере продвижения будут предлагаться несколько домашних заданий — как математических, так и физических.
Фон
Чтобы понять, как балка будет реагировать на нагрузку, полезно сначала узнать кое-что о поведении инженерных материалов.Многие инженерные материалы, особенно металлы, обладают так называемым эластичным поведением . Если, например, вы потянете за концы стального стержня, он растянется. (См. Рис. 1.) Затем, когда вы ослабите усилие (также известное как нагрузка ), штанга вернется к своей исходной форме. Так работает пружина или резинка, за исключением того, что изменение длины будет составлять лишь доли дюйма или миллиметра. В большинстве эластичных материалов это явление одинаково, как при вытягивании (, , растяжение, сил), так и при толкании ( сжатие сил) образец.
Когда материал действует упруго, изменение длины из-за силы прямо пропорционально силе. Обычно мы выражаем изменение длины как деформация (e ) — изменение длины на единицу длины.
e = D L / L (уравнение 1)
где
e = деформация (длина / длина или без единицы измерения)
D L = изменение длины из-за нагрузки
L = исходная (без патронов) длина
Мы также измеряем силу как напряжение — силу, приходящуюся на площадь поперечного сечения.
с = F / A (уравнение 2)
где
с = напряжение (фунт / дюйм 2 или Н / мм 2 или аналогичные единицы)
F = приложенная сила (фунты или Н)
A = площадь поперечного сечения образца (дюймы 2 или м 2 или аналогичные единицы)
Сказать, что изменение длины пропорционально силе, — это то же самое, что сказать, что деформация пропорциональна напряжению.Константа пропорциональности называется модулем упругости (E).
с = E e (уравнение 3)
где
с = напряжение (сила / площадь)
e = деформация (длина / длина)
E = модуль упругости (единицы силы / площади)
Как это относится к изгибу? Когда балка изгибается, верхняя часть балки сдвигается, а нижняя — раздвигается. (См. Рисунок 2.Другими словами, верхняя часть балки испытывает сжатие, а нижняя — растяжение. Степень деформации балки под действием этих сил зависит от модуля упругости. Таким образом, было бы логично, что E появится в любом уравнении, которое мы могли бы придумать для прогнозирования прогиба из-за нагрузки. На самом деле так и происходит.
Когда балка длиной L просто поддерживается на концах (т. Е. Опирается на опоры, которые не ограничивают ее и не препятствуют ее перемещению) и нагружена посередине с силой P, отклонение балки в средняя точка равна
(уравнение 4)
где
y = прогиб посередине (знак «-» означает, что балка отклоняется вниз)
L = длина балки
P = нагрузка (сила)
E = модуль упругости
I = момент инерции
Момент инерции (I) является функцией формы поперечного сечения балки.Это все, что нам нужно знать для проведения эксперимента. Мы вернемся к этой теме позже.
Мини-эксперимент № 1
Раскройте скрепку так, чтобы она превратилась в плоский провод. Прижмите один конец проволоки к краю стола, чтобы другой конец выходил в воздух. Пальцем немного потяните свободный конец вниз и отпустите. Он возвращается к своей первоначальной форме, не так ли? это эластичное поведение. Теперь, если вы нажмете слишком сильно, вы превысите так называемый предел текучести проволоки, и она будет изгибаться безвозвратно.Это поведение пластика . Поскольку мы не хотим, чтобы балки в зданиях или мостах прогибались, инженеры обычно используют в своих расчетах коэффициент запаса прочности , чтобы конструкция никогда не была нагружена настолько, чтобы вызвать остаточную деформацию. Исключением из этого правила является расчет на сейсмостойкость. Здесь конструкции позволяют прогибаться, пока она не упадет.
Экспериментальные процедуры
Если переставить уравнение 4, получится
Вы можете узнать это как уравнение линии:
г = м P
, где m = наклон = L 3 / (48IE).
В этом эксперименте мы произведем ряд парных измерений нагрузки (P) и прогиба (y) на трех круглых балках — одной из стали, одной из алюминия и одной из латуни. После сбора данных нанесите на график нагрузку по оси x и отклонение по оси y. Данные должны попадать на прямую линию. Резкий «перегиб» на линии означал бы, что мы превысили предел упругости и заставили балку деформироваться. (Посмотрите на балку. Вернулась ли она к своей первоначальной форме?) В этом случае используйте только линейную часть кривой (т.е.е., меньшие нагрузки). Измерьте наклон на графике и вычислите E, учитывая длину балки и момент инерции. Уравнение для момента инерции твердого круглого сечения:
I x = p г 4 /4 = р г 4 /64
Экспериментальная установка будет продемонстрирована во время семинара. Фотографии будут сделаны и размещены на домашней странице доктора Джонстона:
(https://www.csus.edu/indiv/j/johnstonj)
Также будет размещен полный список материалов и предложения по материалам для тестирования.Обратите внимание, что в аппарате нет ничего волшебного. То, что мы продемонстрируем на семинаре, было построено из того, что у нас было под рукой в нашей лаборатории. Любая установка , которую вы придумаете, которая позволяет вам измерять нагрузку и прогиб, подойдет. Если вы хотите поделиться своим дизайном с другими, отправьте нам фотографии или заметки по электронной почте для публикации. Или, если вы разместите их на сайте своей школы, пришлите нам адрес, чтобы мы могли предоставить ссылку на ваш сайт.
Инженерные приложения
1. Выбор материала
Инженеры всегда выбирают, какой материал использовать в конструкции. Доступен ряд материалов — сталь, бетон, дерево, железо, алюминий и, в последнее время, пластик. Каждый из этих материалов имеет свой набор характеристик, которые необходимо учитывать при разработке. Модуль упругости (E) является одним из примеров. Таблица 1 содержит информацию по ряду других материалов.
Некоторые материалы, например сталь, действуют одинаково как при растяжении, так и при сжатии.Другие, например бетон, действуют по-разному, в зависимости от того, как они загружены. Бетон, например, очень силен на сжатие, но очень слаб на растяжение. Другими словами, его сложно раздавить, но относительно легко разобрать. Если изогнуть бетонную балку, в растянутом участке быстро образуются трещины, и балка выходит из строя. Чтобы противодействовать этому, в бетон закладывают арматурные стержни из стали (прочной на растяжение) (см. Рисунок 3). Когда железобетон изгибается, сталь обеспечивает прочность на разрыв, поэтому балка не трескается.
Несмотря на то, что прочностные характеристики очень важны, их следует учитывать при выборе материала для конкретного применения. Еще о чем следует подумать инженерам:
- вес (в конструкции вес самой конструкции является частью нагрузки)
- Стоимость самих материалов
- простота строительства (иногда стоит использовать более дорогой материал, если вы сэкономите достаточно денег на строительстве), а Наличие
- (стальные балки должны изготавливаться на металлургическом заводе).
Возможная домашняя задача № 1
Учитывая набор параметров — нагрузку, форму, длину и максимально допустимый прогиб, выберите подходящий материал из таблицы 2. Учащиеся будут использовать полученную информацию для определения требуемого E с помощью уравнения 4. Затем они могут выбрать материал с значение E, равное или превышающее требуемое значение E.
Расширение: укажите учащимся, что редко бывает только один технически правильный ответ.Попросите их выбрать несколько материалов, которые подойдут, и написать небольшую памятку с описанием плюсов и минусов каждого из них.
2. Выбор формы
До сих пор мы отмечали, что отклонение зависит от момента инерции, который, в свою очередь, зависит от формы. Момент инерции — это второй момент относительно некоторой оси. По математике это:
где
I x = момент инерции относительно оси x
y = расстояние от оси x до дифференциальной области dA
Без математических расчетов и дополнительных знаний в области механики трудно объяснить слишком много подробностей об I.К счастью, доступны уравнения для вычисления I для ряда фигур (см. Таблицу 2). Выбор оси важен. При вертикальных нагрузках и изгибе в вертикальной плоскости следует использовать I x .
Мини-эксперимент № 2
Выберите значение нагрузки, обеспечивающее умеренный прогиб круглых балок. Теперь примените эту нагрузку к нескольким другим формам. Например, попробуйте положить плоский приклад «плашмя», а затем такой же брус уложить «набок».Прогибы очень разные. Это отражено в уравнении 4 как изменение I. Вычислите I x для двух случаев, используя уравнения в таблице 2. Попробуйте другие формы, чтобы увидеть эффект не только формы, но и поворота той же формы и нагрузки. это с другой стороны.
Возможная домашняя задача № 2
Дайте ученикам набор параметров — нагрузку, максимально допустимый прогиб, материал и длину — и попросите их выбрать форму и размеры.Они могут сделать это, сначала вычислив требуемый I x из уравнения 4, а затем выбрав методом проб и ошибок форму из таблицы 2.
Расширение: укажите размеры пространства (например, 3 дюйма в ширину, 5 дюймов в высоту и длину L), в которое должны входить их балки.
Удлинитель: запросите наиболее экономичную форму. Это будет форма, в которой используется наименьшее количество материала, что можно рассчитать, умножив площадь поперечного сечения на длину.
3. Рассмотрение нескольких дел
Вы, наверное, заметили, что чем выше балка, тем меньше она отклоняется от вертикальной нагрузки. Что, если бы мы довели это до крайности и использовали очень высокий и очень тонкий срез, как кусок алюминиевой фольги. Если бы мы нагружали его, он не прогибался бы, но не выдержал бы изгиба. Чрезмерный прогиб в вертикальной плоскости — это только одна из причин отказа. Другое дело — коробление. (Устойчивость к устойчивости — довольно сложный предмет, и мы не будем пытаться его здесь предсказать.) Другой вид отказа — чрезмерный прогиб в горизонтальной плоскости из-за горизонтальных нагрузок, таких как ветер.
Дело в том, что инженер должен думать обо всех различных вещах, которые могут произойти с его или ее структурой — о различных вещах, которые могут быть загружены в конструкцию (люди, машины, шкафы для документов, станки), о влиянии лед, снег или лужа воды на крыше, ветровые нагрузки и землетрясения (которые являются горизонтальными, а не вертикальными) — и попытайтесь предсказать, как конструкция будет реагировать (вертикальные прогибы, горизонтальные прогибы, изгиб, скручивание) для каждого из них.Необходимо рассмотреть очень много случаев. Раньше у инженерных фирм были комнаты, заполненные людьми, выполняющими эти расчеты, и они не охватывали все возможные случаи. Сегодня компьютерные модели помогают нам гораздо быстрее анализировать гораздо больше случаев.
Возможная домашняя задача № 3
Выполните домашнюю задачу №2, за исключением того, что укажите горизонтальную нагрузку и максимально допустимый горизонтальный прогиб. Горизонтальные нагрузки обычно намного меньше вертикальных (скажем, 5-10%).Уравнение 4 можно использовать для расчета прогиба, за исключением того, что следует использовать I y вместо I x .
Таблица 1
(выдержки из: Beer and Johnston, Mechanics of Materials , McGraw-Hill, 1981)| Материал | Модуль упругости (10 6 psi) |
СТАЛЬ | |
Структурный (ASTM-A36) | 29 |
Высокопрочный низколегированный ASTM-A514 | 29 |
Закаленный и отпущенный сплав ASTM-A514 | 29 |
Нержавеющая сталь (302) — холоднокатаная | 28 |
Нержавеющая сталь (302) — отожженная | 28 |
ЧУГУН | |
Серый, 4.5% C, ASTM A-48 | 10 |
Гибкий, ASTM A-47 | 24 |
АЛЮМИНИЙ | |
Сплав 1100-h24 (99% Al) | 10,1 |
Сплав 2014-T6 (4,4% Cu) | 10,6 |
Сплав 6061-T6 (1% Mg) | 10 |
ЖЕЛТАЯ ЛАТУНЬ (65% Cu, 35% Zn) | |
Холоднокатаный | 15 |
Отожженный | 15 |
ФОСФОР БРОНЗА | |
Холоднокатаный | 15.9 |
Пружина | 16 |
ДЕРЕВО, воздушная сушка | |
Пихта Дугласа | 1,8 |
Ель восточная | 1,3 |
Сосна южная | 1.6 |
БЕТОН | |
Средняя прочность | 3,6 |
Высокая прочность | 4,5 |
НЕЙЛОН формованный | 0,3 |
ПОЛИСТИРОЛ | 0.45 |
ГРАНИТ | 10 |
СТЕКЛО, 98% кремнезема | 9,6 |
Таблица 2
(ссылка: Lindeburg, M., Справочное руководство по гражданскому строительству , Professional Publications, Inc, 1992)Балки — поддерживаются с обеих сторон
Напряжение в изгибаемой балке можно выразить как
σ = y M / I (1)
где
σ = напряжение (Па (Н / м 2 ), Н / мм 2 , psi)
y = расстояние до точки от нейтральной оси (м, мм, дюйм)
M = изгибающий момент (Нм, фунт-дюйм)
I = момент инерции (м 4 , мм 4 , дюйм 4 )
Калькулятор ниже можно использовать для расчета максимального напряжения и прогиба балок с одной одиночной или равномерно распределенной нагрузкой.
Балка, поддерживаемая на обоих концах — равномерная непрерывная распределенная нагрузка
Момент в балке с равномерной нагрузкой, поддерживаемой на обоих концах в положении x, может быть выражен как
M x = qx (L — x) / 2 (2)
где
M x = момент в положении x (Нм, фунт дюйм)
x = расстояние от конца (м, мм, дюйм)
Максимум момент находится в центре балки на расстоянии L / 2 и может быть выражен как
M max = q L 2 /8 (2a)
где
M макс = максимальный момент ( Нм, фунт-дюйм)
q = равномерная нагрузка на единицу длины балки (Н / м, Н / мм, фунт / дюйм)
9039 6 L = длина балки (м, мм, дюйм)
Максимальное напряжение
Уравнения 1 и 2a могут быть объединены для выражения максимального напряжения в балке с равномерной нагрузкой, поддерживаемой на обоих концах на расстоянии L / 2 как
σ max = y max q L 2 / (8 I) (2b)
где
σ max = максимальное напряжение (Па (Н / м 2 ), Н / мм 2 , psi)
y max = расстояние до крайней точки от нейтральной оси (м, мм, дюйм)
- 1 Н / м 2 = 1×10 -6 Н / мм 2 = 1 Па = 1.4504×10 -4 фунт / кв. Дюйм
- 1 фунт / дюйм (фунт / дюйм 2 ) = 144 фунт / кв. Дюйм (фунт фут / фут 2 ) = 6 894,8 Па (Н / м 2 ) = 6,895×10 — 3 Н / мм 2
Максимальный прогиб :
δ max = 5 q L 4 / (384 EI) (2c)
где
δ макс = максимальный прогиб (м, мм, дюйм)
E = Модуль упругости (Па (Н / м 2 ), Н / мм 2 , psi)
Прогиб в положении x:
δ x = qx ( L 3 — 2 L x 2 + x 3 ) / (24 EI) (2d)
Примечание! — прогиб часто является ограничивающим фактором при проектировании балки.Для некоторых применений балки должны быть прочнее, чем требуется при максимальных нагрузках, чтобы избежать недопустимого прогиба.
Силы, действующие на концы:
R 1 = R 2
= q L / 2 (2e)
где
R = сила реакции (Н, фунт)
Пример — балка с равномерной нагрузкой, метрические единицы
Балка UB 305 x 127 x 42 длиной 5000 мм несет равномерную нагрузку 6 Н / мм .Момент инерции балки составляет 8196 см 4 (81960000 мм 4 ) , а модуль упругости стали, используемой в балке, составляет 200 ГПа (200000 Н / мм 2 ) . Высота балки 300 мм (расстояние от крайней точки до нейтральной оси 150 мм ).
Максимальное напряжение в балке можно рассчитать
σ max = (150 мм) (6 Н / мм) (5000 мм) 2 / (8 (81960000 мм 4 ))
= 34.3 Н / мм 2
= 34,3 10 6 Н / м 2 (Па)
= 34,3 МПа
Максимальный прогиб балки можно рассчитать
δ макс = 5 (6 Н / мм) (5000 мм) 4 / (( 200000 Н / мм 2 ) ( 81960000 мм 4 ) 384)
= 2,98 мм
Расчет балок с равномерной нагрузкой — метрические единицы
- 1 мм 4 = 10 -4 см 4 = 10 -12 м 4
- 1 см 4 = 10 -8 м = 10 4 мм
- 1 дюйм 4 = 4.16×10 5 мм 4 = 41,6 см 4
- 1 Н / мм 2 = 10 6 Н / м 2 (Па)
Расчет балки с равномерной нагрузкой — Британские единицы
Пример — балка с равномерной нагрузкой, британские единицы
Максимальное напряжение в стальной широкополкой балке W 12 x 35 дюймов, 100 дюймов длиной , момент инерции 285 дюймов 4 , модуль упругости 200 psi
, при равномерной нагрузке 100 фунтов / дюйм можно рассчитать как
σ max = y max q L 2 / (8 I)
= (6.25 дюймов (100 фунтов / дюйм) (100 дюймов) 2 / (8 (285 дюймов 4 ))
= 2741 (фунт / дюйм 2 , psi)
Максимальное отклонение может рассчитывается как
δ max = 5 q L 4 / (EI 384)
= 5 (100 фунтов / дюйм) (100 дюймов) 4 / ((2
00 фунтов / дюйм
2 ) (285 дюймов 4 ) 384)= 0,016 дюйма
Балка, поддерживаемая на обоих концах — нагрузка в центре
Максимальный момент в балке с центральной нагрузкой, поддерживаемой с обоих концов :
M max = FL / 4 (3a)
Максимальное напряжение
Максимальное напряжение в балке с одноцентровой нагрузкой, поддерживаемой на обоих концах:
σ max = y max FL / (4 I) (3b) 900 16
, где
F = нагрузка (Н, фунт)
Максимальное отклонение может быть выражено как
δ max = FL 3 / (48 EI) (3c)
Силы, действующие на концы:
R 1 = R 2
= F / 2 (3d)
Калькулятор балки с одним центром нагрузки — метрические единицы
Калькулятор балки с одним центром нагрузки — британская система мер Единицы
Пример — балка с одной центральной нагрузкой
Максимальное напряжение в стальной широкополочной балке «W 12 x 35», 100 дюймов длиной , момент инерции 285 дюймов 4 , модуль упругости 200 psi
, с центральной нагрузкой 10000 фунтов можно рассчитать как
σ max = y max FL / (4 I)
= (6.25 дюймов) (10000 фунтов) (100 дюймов) / (4 (285 дюймов 4 ))
= 5482 (фунт / дюйм 2 , фунт / кв. Дюйм)
Максимальный прогиб можно рассчитать как
δ макс = FL 3 / EI 48
= (10000 фунтов / дюйм) (100 дюймов) 3 / ((200 фунтов / дюйм
2 ) (285 дюймов 4 ) 48 )
= 0,025 дюйма
Некоторые типичные пределы отклонения по вертикали
- Полное отклонение: пролет / 250
- Отклонение при динамической нагрузке: пролет / 360
- консольных балок: пролет / 180
- Балки деревянных перекрытий в домашних условиях: пролет 330 (макс. 14 мм)
- хрупкие элементы: пролет / 500
- подкрановые балки: пролет / 600
Балка, поддерживаемая на обоих концах — эксцентричная нагрузка
Максимальный момент в балке с одиночной эксцентрической нагрузкой в точке нагрузки:
M макс = F ab / L (4a)
Максимальное напряжение
Максимальное напряжение в балке с одноцентровой нагрузкой, поддерживаемой с обоих концов:
σ max = y max F ab / (LI) (4b)
Максимальный прогиб в точке нагрузки может быть выражен как
δ F = F a 2 b 2 / (3 EIL) (4c)
Силы, действующие на концы:
R 1 = F b / L (4d)
R 2 = F a / L (4e)
Балка, поддерживаемая на обоих концах — две эксцентриковые нагрузки
Максимальный момент (между нагрузками) в балке с двумя эксцентрическими нагрузками:
M max = F a (5a)
Максимальное напряжение
Максимальное напряжение в балке с двумя эксцентрическими нагрузками, поддерживаемыми на обоих концах:
σ max = y max F a / I (5b)
Максимум прогиб в точке нагрузки можно выразить как
δ F = F a (3L 2 — 4 a 2 ) / (24 EI) (5c)
Силы, действующие на концы:
R 1 = R 2
= F (5d)
Вставьте балки в свою модель Sketchup с помощью Engineering ToolBox Sketchup Extension
Балка, поддерживаемая на обоих концах — трехточечная нагрузка
Максимальный момент (между нагрузками) в балке с тремя точечными нагрузками:
M max 90 038 = FL / 2 (6a)
Максимальное напряжение
Максимальное напряжение в балке с тремя точечными нагрузками, поддерживаемыми с обоих концов:
σ max = y max FL / (2 I) ( 6b)
Максимальный прогиб в центре балки можно выразить как
δ F = FL 3 / (20.22 E I) (6c)
Силы, действующие на концы:
R 1 = R 2
= 1,5 F (6d)
Прочность материалов | Механика материалов
ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.
Сопротивление материалов , также известное как Механика материалов , ориентировано на анализ напряжений и прогибов в материалах под нагрузкой.Знание напряжений и прогибов позволяет безопасно проектировать конструкции, способные выдерживать предполагаемые нагрузки.
Напряжение и деформация
Когда к конструктивному элементу прикладывается сила, в этом элементе в результате силы возникают как напряжение, так и деформация. Напряжение — это сила, переносимая элементом на единицу площади, и типичными единицами измерения являются фунт-сила / дюйм 2 (фунт / кв. Дюйм) для стандартных единиц США и Н / м 2 (Па) для единиц СИ:
где F — приложенная сила, а A — площадь поперечного сечения, на которую действует сила.Приложенная сила вызовет деформацию конструктивного элемента на некоторую длину, пропорциональную его жесткости. Деформация — это отношение деформации к исходной длине детали:
где L — деформированная длина, L 0 — исходная недеформированная длина, а δ — деформация (разница между ними).
Существуют различные типы нагрузки, которые приводят к различным типам напряжений, как показано в таблице ниже:
| Тип нагрузки | Тип напряжения | Иллюстрация |
|---|---|---|
| Осевая сила |
| |
| Усилие сдвига | Напряжение поперечного сдвига | |
| Изгибающий момент | Напряжение изгиба | |
| Торсион | Напряжение кручения |
Осевое напряжение и изгибающее напряжение являются формами нормального напряжения , σ, поскольку направление силы перпендикулярно области, противодействующей силе.Поперечное напряжение сдвига и напряжение скручивания являются формами напряжения сдвига , τ, поскольку направление силы параллельно области, противодействующей силе.
| Нормальное напряжение | |
|---|---|
| Осевое напряжение: | |
| Напряжение изгиба: | |
| Напряжение сдвига | |
|---|---|
| Поперечное напряжение: | |
| Торсионное напряжение: | |
В уравнениях для осевого напряжения и поперечного напряжения сдвига F — это сила, а A — площадь поперечного сечения элемента.В уравнении для изгибающего напряжения M — изгибающий момент, y — расстояние между центральной осью и внешней поверхностью, а I c — центроидный момент инерции поперечного сечения относительно соответствующей оси. В уравнении для напряжения скручивания T — это кручение, r — радиус и J — полярный момент инерции поперечного сечения.
В случае осевого напряжения на прямом участке напряжение распределяется равномерно по всей площади.В случае напряжения сдвига распределение максимально в центре поперечного сечения; однако среднее напряжение определяется как τ = F / A, и это среднее напряжение сдвига обычно используется при расчетах напряжений. Более подробное обсуждение можно найти в разделе о касательных напряжениях в балках. В случае напряжения изгиба и напряжения кручения максимальное напряжение возникает на внешней поверхности. Более подробное обсуждение можно найти в разделе о напряжениях изгиба в балках.
Так же, как основными типами напряжения являются нормальное напряжение и напряжение сдвига, основными типами деформации являются нормальная деформация и деформация сдвига .В случае нормальной деформации деформация перпендикулярна области, на которую действует сила:
В случае деформации поперечного сдвига деформация параллельна области, на которую действует сила:
где γ — деформация сдвига (безразмерная) и & phiv; — деформированный угол в радианах.
В случае деформации кручения элемент поворачивается на угол & phiv; вокруг своей оси.Максимальная деформация сдвига возникает на внешней поверхности. В случае круглого стержня максимальная деформация сдвига определяется как:
где & phiv; — угол закручивания, r — радиус стержня, а L — длина.
Деформации сдвига пропорциональны внутренней части стержня и связаны с максимальной деформацией сдвига на поверхности следующим образом:
где ρ — радиальное расстояние от оси стержня.
Закон Гука
Напряжение пропорционально деформации в упругой области кривой напряжения-деформации материала (ниже предела пропорциональности, когда кривая является линейной).
Нормальное напряжение и деформация связаны между собой:
σ = E & varepsilon;
где E — модуль упругости материала, σ — нормальное напряжение, а & varepsilon; это нормальный штамм.
Напряжение сдвига и деформация связаны между собой:
τ = G γ
где G — модуль сдвига материала, τ — напряжение сдвига, а γ — деформация сдвига.Модуль упругости и модуль сдвига связаны соотношением:
где ν — коэффициент Пуассона.
Закон Гука аналогичен уравнению силы пружины F = k δ. По сути, все можно рассматривать как пружину. Закон Гука можно перестроить, чтобы получить деформацию (удлинение) в материале:
| Осевое удлинение (от нормального напряжения) | ||
| Угол кручения (от напряжения сдвига / скручивания) |
Энергия деформации
Когда к конструктивному элементу прикладывается сила, этот элемент деформируется и накапливает потенциальную энергию, как пружина.Энергия деформации (то есть количество потенциальной энергии, накопленной из-за деформации) равна работе, затраченной на деформацию элемента. Полная энергия деформации соответствует площади под кривой отклонения нагрузки и имеет единицы дюйм-фунт-сила в обычных единицах США и Н-м в единицах СИ. Энергия упругой деформации может быть восстановлена, поэтому, если деформация остается в пределах упругого предела, то вся энергия деформации может быть восстановлена.
Энергия деформации рассчитывается как:
| Общая форма: | U = Работа = ∫ F dL | (площадь под кривой нагрузки-прогиб) |
| В пределах эластичности: | (площадь под кривой нагрузки-прогиб) | |
| (потенциальная энергия пружины) |
Обратите внимание, что есть два уравнения для энергии деформации в пределах упругости.Первое уравнение основано на площади под кривой прогиба нагрузки. Второе уравнение основано на уравнении для потенциальной энергии, запасенной в пружине. Оба уравнения дают один и тот же результат, просто они выводятся несколько по-разному.
Более подробную информацию об энергии деформации можно найти здесь.
Жесткость
Жесткость, обычно называемая жесткостью пружины, — это сила, необходимая для деформации элемента конструкции на единицу длины.Все конструкции можно рассматривать как совокупность пружин, а силы и деформации в конструкции связаны уравнением пружины:
F = k δ макс
где k — жесткость, F — приложенная сила, а δ max — максимальное отклонение при прогибе в элементе.
Если прогиб известен, то жесткость элемента можно найти, решив k = F / δ max . Однако максимальный прогиб обычно неизвестен, поэтому жесткость необходимо рассчитывать другими способами.Таблицы прогиба балки можно использовать в общих случаях. Два наиболее полезных уравнения жесткости, которые необходимо знать, — это уравнения для балки с приложенной осевой нагрузкой и для консольной балки с концевой нагрузкой. Обратите внимание, что жесткость зависит от модуля упругости материала E, геометрии детали и конфигурации нагрузки.
Торсионный эквивалент уравнения пружины:
Т = к & phiv;
Особый интерес представляет жесткость вала при скручивающей нагрузке:
| Жесткость [дюйм * фунт-сила / рад] | Максимальный прогиб [рад] | Иллюстрация | |
|---|---|---|---|
| Вал с крутильной нагрузкой: |
Конструкция с несколькими путями нагружения
Если в конструкции есть несколько путей загрузки (т.е. в конструкции есть несколько элементов, которые разделяют нагрузку), нагрузка будет выше в более жестких элементах. Чтобы определить нагрузку, которую несет какой-либо отдельный элемент, сначала вычислите эквивалентную жесткость элементов на пути нагружения, рассматривая их как пружины. В зависимости от их конфигурации они будут рассматриваться как некоторая комбинация пружин, включенных последовательно, и пружин, включенных параллельно.
Если элементы на пути нагружения нельзя рассматривать исключительно как пружины, включенные последовательно или как пружины, включенные параллельно, а скорее представляют собой комбинацию пружин, включенных последовательно и параллельно, тогда проблему необходимо будет решать итеративно.Определите подгруппу элементов, которые находятся либо последовательно, либо параллельно, и используйте приведенные уравнения для расчета эквивалентной жесткости, силы и прогиба в подгруппе. Затем подгруппу можно рассматривать как одиночную пружину с рассчитанными жесткостью, силой и прогибом, а затем эту пружину можно рассматривать как часть другой подгруппы пружин. Продолжайте группировать участников и решать, пока не будет достигнут желаемый результат.
Концентрации напряжений
Можно подумать, что силы и напряжения протекают через материал, как показано на рисунке ниже.Когда геометрия материала изменяется, линии потока перемещаются ближе друг к другу или дальше друг от друга, чтобы приспособиться. Если в материале имеется разрыв, такой как отверстие или выемка, напряжение должно течь вокруг неоднородности, и линии потока будут уплотняться вместе вблизи этого разрыва. Это внезапное уплотнение потоковых линий приводит к резкому скачку напряжения — это пиковое напряжение называется концентрацией напряжений . Элемент, вызывающий концентрацию напряжений, называется подъемником напряжений .
Концентрации напряжений учитываются с помощью коэффициента концентрации напряжений . Чтобы найти фактическое напряжение в вязкости несплошности, рассчитайте номинальное напряжение в этой области и затем увеличьте его с помощью соответствующего коэффициента концентрации напряжений:
σ макс = K σ ном
где σ max — фактическое (масштабированное) напряжение, σ nom — номинальное напряжение, а K — коэффициент концентрации напряжений.При расчете номинального напряжения используйте максимальное значение напряжения в этой области. Например, на рисунке выше должна использоваться наименьшая площадь у основания галтеля.
Многие справочники содержат таблицы и кривые коэффициентов концентрации напряжений для различных геометрических форм. Двумя наиболее полными наборами факторов концентрации напряжения являются факторы концентрации напряжения Петерсона и формулы Рорка для напряжения и деформации. MechaniCalc также предоставляет набор интерактивных графиков для общих факторов концентрации стресса.
По мере того, как мы удаляемся от источника стресса, концентрация стресса рассеивается. Принцип Сен-Венана — это общее практическое правило, гласящее, что расстояние, на котором рассеивается концентрация напряжений, равно наибольшему размеру поперечного сечения, несущего нагрузку.
Расчет концентрации напряжений особенно важен, когда материалы очень хрупкие или когда существует только один путь нагрузки. В пластичных материалах местная податливость позволит перераспределить напряжения и снизит напряжение вокруг стояка.По этой причине коэффициенты концентрации напряжений обычно не применяются к элементам конструкции из пластичных материалов. Коэффициенты концентрации напряжений также обычно не применяются при наличии избыточного пути нагружения, и в этом случае податливость одного элемента позволит перераспределить силы на элементы на других путях нагружения. Примером этого является набор болтов. Если один болт начинает прогибаться, другие болты в шаблоне принимают на себя большую нагрузку.
Комбинированные напряжения
В любой точке нагруженного материала общее состояние напряжения можно описать тремя нормальными напряжениями (по одному в каждом направлении) и шестью напряжениями сдвига (по два в каждом направлении):
Индексы нормальных напряжений σ указывают направление нормальных напряжений.Индексы касательных напряжений τ состоят из двух компонент. Первый указывает направление нормали к поверхности, а второй указывает направление самого напряжения сдвига.
Обычно напряжения в одном направлении равны нулю, так что полное напряжение возникает в одной плоскости, как показано на рисунке ниже. Это называется напряжением в плоскости . Плоское напряжение возникает в тонких пластинах, но оно также возникает на поверхности любой нагруженной конструкции. Напряжения на поверхности обычно являются наиболее критическими напряжениями, поскольку напряжение изгиба и скручивания максимизируется на поверхности.
На рисунке выше σ x и σ y — нормальные напряжения, а τ — напряжение сдвига. Напряжения уравновешиваются, так что точка находится в статическом равновесии. Поскольку все касательные напряжения равны по величине, для простоты индексы опущены. (Обратите внимание, однако, что знак напряжений на грани x будет противоположен знаку напряжений на грани y ).
Правильные условные обозначения показаны на рисунке.Для нормального напряжения растягивающее напряжение положительное, а сжимающее — отрицательное. Для напряжения сдвига, по часовой стрелке положительно, а против часовой стрелки — отрицательно.
Если напряжения из рисунка выше известны, можно найти нормальное напряжение и напряжение сдвига в плоскости, повернутой на некоторый угол θ относительно горизонтали, как показано на рисунке ниже. Уравнения преобразования , приведенные ниже, дают значения нормального напряжения и напряжения сдвига на этой повернутой плоскости.
| Нормальное напряжение: | |
| Напряжение сдвига: |
Обратите внимание, что на рисунке выше θ отсчитывается от оси x, а положительное значение θ — против часовой стрелки.
В любой точке материала можно найти углы плоскости, при которых нормальные напряжения и напряжения сдвига максимизируются и минимизируются.Максимальное и минимальное нормальные напряжения называются главными напряжениями . Максимальные и минимальные касательные напряжения называются экстремальными касательными напряжениями . Углы главных напряжений и крайних касательных напряжений находятся путем взятия производной каждого уравнения преобразования по θ и нахождения значения θ, при котором производная равна нулю.
| Углы главного напряжения: | |
| Предельные углы напряжения сдвига: |
Указанные выше углы можно подставить обратно в уравнения преобразования, чтобы найти значения главных напряжений и экстремальных касательных напряжений:
| Основные напряжения: | |
| Экстремальные напряжения сдвига: |
Углы, при которых возникают основные напряжения, составляют 90 ° друг от друга.Главные напряжения всегда сопровождаются нулевым напряжением сдвига. Углы возникновения экстремальных касательных напряжений составляют 45 ° от углов главных напряжений. Экстремальные напряжения сдвига сопровождаются двумя равными нормальными напряжениями (σ x & plus; σ y ) / 2.
Вот пара полезных отношений:
| σ 1 и плюс; σ 2 = σ x и плюс; σ y | Сумма нормальных напряжений постоянна. |
| Максимальное напряжение сдвига составляет половину разницы главных напряжений. |
Круг Мора
Круг Мора — это способ визуализировать состояние напряжения в точке нагруженного материала. Это дает интуитивное представление о уравнениях преобразования напряжений и показывает, как напряжения на элементе изменяются в зависимости от угла поворота θ. Из круга Мора также становится ясно, каковы основные напряжения, экстремальные напряжения сдвига и углы, под которыми возникают эти напряжения.Пример круга Мора показан на рисунке ниже:
Чтобы построить круг Мора, сначала найдите центр круга, взяв среднее значение нормальных напряжений:
Поместите точки на окружности, представляющие напряжения на гранях x и y элемента напряжения. Напряжения на грани x будут иметь координаты (σ x , −τ), а напряжения на грани y будут иметь координаты (σ y , τ).Поместите точки на окружности для главных напряжений. Максимальное главное напряжение будет иметь координаты (σ 1 , 0), а минимальное главное напряжение будет иметь координаты (σ 2 , 0). Поместите точки на окружности для экстремальных касательных напряжений. Максимальное экстремальное напряжение сдвига будет иметь координаты (σ c , τ 1 ), а минимальное экстремальное напряжение сдвига будет иметь координаты (σ c , τ 2 ).
Все точки будут лежать по периметру круга.Круг имеет радиус, равный величине предельных касательных напряжений:
Напряженное состояние на гранях x и y элемента напряжения представлено черной линией в круге Мора, соединяющим точки (σ x , −τ) и (σ y , τ). Эта линия в круге Мора соответствует невращающемуся элементу на рисунке ниже. Если эту линию повернуть на некоторый угол, то значения точек на конце повернутой линии дадут значения напряжения на гранях x и y повернутого элемента.Важно отметить, что 360 градусов круга Мора эквивалентны 180 градусам элемента напряжения. Например, точки для грани x и грани y расположены на 180 градусов друг от друга на круге Мора, но они всего на 90 градусов на элементе напряжения.
Чтобы получить более интуитивное представление о том, как круг Мора связывает напряжения в элементе напряжения и как состояние напряжения изменяется в зависимости от угла поворота, см. Прилагаемый калькулятор круга Мора.
Приложения
Есть много структурных компонентов, которые обычно подвергаются анализу напряжений. Подробности анализа этих компонентов приведены в других разделах:
Расчет допустимого напряжения
Знание напряжений и прогибов позволяет безопасно проектировать конструкции, способные выдерживать предполагаемые нагрузки. Всегда желательно, чтобы напряжения в конструкции оставались в пределах прочности конструкции.Предел текучести материала обычно выбирается как предел прочности, с которым сравниваются расчетные напряжения.
Коэффициент запаса прочности , FS, рассчитывается как:
где σ фактическое — это расчетное напряжение в конструкции, а предел — это максимальный предел напряжения, обычно прочность материала, например предел текучести (S ty ). Коэффициент запаса прочности показывает, насколько фактическое напряжение ниже предельного напряжения.Значение FS должно быть больше или равно 1, чтобы конструкция не вышла из строя, но инженеры почти всегда проектируют с некоторым требуемым коэффициентом безопасности, превышающим 1. Требуемый коэффициент безопасности будет варьироваться в зависимости от критичности конструкции (т. Е. последствия разрушения конструкции), а также условия нагружения (т. е. какие типы нагрузок применяются, насколько они предсказуемы и т. д.). Высокое значение FS приведет к очень безопасной конструкции, но если значение FS слишком велико, конструкция может стать настолько большой и тяжелой, что больше не сможет успешно выполнять свою функцию.Поэтому при выборе подходящего запаса прочности приходится идти на компромиссы. Типичные значения FS варьируются от 1,15 до 10.
Запас прочности рассчитывается как:
В приведенном выше уравнении любое значение выше нуля указывает на то, что фактическое напряжение ниже предельного напряжения. Хотя запасы прочности обычно указываются в виде десятичных значений, гораздо более интуитивно понятно думать о запасах в процентах. Например, если предельное напряжение конструкции равно 1.В 5 раз превышающее фактическое напряжение, запас прочности составляет 50% (MS = 0,5).
Когда сообщается о факторах безопасности и запасах прочности, иногда требуемый коэффициент безопасности будет «вплетаться» в сообщаемые факторы. Например, инженеры могут потребовать, чтобы конструкция поддерживала коэффициент безопасности не менее 2, так что FS req = 2. Чтобы обеспечить требуемый коэффициент безопасности, сообщаемые FS и MS рассчитываются как:
Обратите внимание, что при включении необходимого коэффициента безопасности, FS req , сообщаемые FS и MS фактически являются запасами по отношению к FS req , а не по напряжению.
Список литературы
- Будинас-Нисбетт, «Машиностроительный проект Шигли», 8-е издание
- Доулинг, Норман Э., «Механическое поведение материалов: инженерные методы для деформации, разрушения и усталости», 3-е издание
- Гир, Джеймс М., «Механика материалов», 6-е издание
- Линдебург, Майкл Р., «Справочное руководство по машиностроению для экзамена на физическую форму», 13-е издание
- Пилки, Уолтер Д.и Пилки, Дебора Ф., «Факторы концентрации стресса Петерсона», 3-е издание.
- «Формулы Рорка для стресса и деформации», 8-е издание
| Калькуляторы прогиба балки — сплошные прямоугольные балки, полые прямоугольные балки, сплошные круглые балки Введите значение и нажмите «Рассчитать». Будет отображен результат | |||||||||||||||||||||||||||
| Расчет прогиба для сплошных прямоугольных балок Расчет прогиба для полых прямоугольных балок Расчет прогиба для сплошных круглых балок Расчет прогиба для круглых трубчатых балок | |||||||||||||||||||||||||||
Расчет прогиба сплошных прямоугольных балок
| |||||||||||||||||||||||||||
Расчет прогиба для полых прямоугольных балок
| |||||||||||||||||||||||||||
Расчет прогиба сплошных круглых балок
| |||||||||||||||||||||||||||
Расчет прогиба для круглых трубных балок
| |||||||||||||||||||||||||||
Длительный прогиб | Ассоциация строительных компонентов
Вопрос:
Проводились ли какие-либо исследования или исследования долговременного прогиба деревянных ферм, соединенных металлическими пластинами? Насколько допускается прогиб?
Ответ:
Для соответствия нормам допустимая величина отклонения составляет l /360, где l — в дюймах.Для более жесткого пола обычно используют л /480. Вы также можете использовать отношение длины к глубине, которое обычно равно 18 для хорошей производительности. Чем меньше число, тем жестче пол.
Учитывается ли временная нагрузка или полная нагрузка при определении прогиба, зависит от типа фермы.
В 1973 году Лаборатория лесных товаров Министерства сельского хозяйства США (FPL) начала исследование по определению долговечности деревянных ферм. Фермы с семью различными системами соединения наблюдались под нагрузкой в течение 5, 10 и 15 лет.В конце каждого периода образцы выгружали и оценивали на прочность и жесткость в лабораторных условиях. Фермы были спроектированы в соответствии с преобладающими техническими условиями того времени (TPI-65), которые для всех практических целей предполагали соединения с шарнирным соединением без трения. Изгибающие моменты были проанализированы в предположении непрерывности верхних поясов фермы. При расчете моментных напряжений в поясах днища фермы не учитывалась непрерывность. Предполагаемые для передачи только осевых нагрузок, нижние пояса были спроектированы как балки с простой опорой и наложенными моментами.Забитые и приклеенные гвозди фермы подверглись оценке производительности вместе с деревянными фермами, соединенными металлическими пластинами, для сравнения результатов испытаний. В качестве контрольной группы в лаборатории была максимально загружена одна ферма каждого типа соединительной системы. Еще по три каждого типа были загружены и подвергнуты воздействию навесов или на открытом воздухе. После каждого пятилетнего перерыва в лаборатории максимально загружалась одна ферма каждой конструкции. Каждая ферма поддерживалась и нагружалась независимо. Нагрузка 20 фунтов / фут.(расчетная статическая нагрузка 10 фунтов на квадратный фут для расстояния 24 дюйма) была приложена к нижним поясам, и нагрузка 36 фунтов / фут. (расчетная статическая нагрузка плюс половина расчетной временной нагрузки) была приложена к верхним поясам. Эта нагрузка представляет собой ту нагрузку, которую ферма будет испытывать в течение срока службы. Размах размаха (общая нижняя хорда) составлял 28 футов
Со временем прогиб под нагрузкой (ползучесть) произошел для всех ферм. Общая величина прогиба, по-видимому, связана с жесткостью суставов. По прошествии десяти лет, гвоздями фанерные фермы с косынками имели общий прогиб в три раза превышающий первоначальный прогиб, деревянные фермы, соединенные металлическими пластинами, имели общий прогиб в два с половиной раза выше первоначального прогиба, а гвоздь-склеенные фанерные фермы имели общий прогиб немного меньше. чем в два раза больше первоначального прогиба.Большая часть ползучести произошла на ранних стадиях воздействия. За исключением ферм с гвоздями из фанеры, значения прогиба через 10 лет были на приемлемом уровне, исходя из критерия пролета, деленного на 360. После 10 лет воздействия, по-видимому, не было заметного влияния на прочность и жесткость, как было определено в результате лабораторной оценки. за исключением гвоздей фанерных ферм с косынками, жесткость которых снизилась на 30%. Все фермы соответствовали приемлемым критериям краткосрочной эффективности. Забивные пластинчатые фермы соответствовали критериям прогиба для пролета, деленного на 360.
Перед этим исследованием производители соединителей для анкерных пластин провели испытания под нагрузкой на сотнях ферм, в некоторых ситуациях при обстоятельствах, гораздо более жестких, чем в FPL. Однако большая часть отраслевых исследований была закрытой и служила в первую очередь для того, чтобы заверить производителя и разработчика в том, что проектные предположения подтверждаются тестированием. Типы металлических соединительных пластин, используемых на фермах, изготовленных в 1973 году, больше не продаются на рынке. Хотя используемые сегодня конструкции разъемов отличаются от тех, что использовались в 1973 году, ожидается, что их производительность будет аналогична, если не лучше, результатам, полученным при тестировании FPL.
