Неньютоновская жидкость. Учебно-исследовательская работа по физике
li{counter-increment:lst-ctn-kix_list_3-8}#doc6840845 .lst-kix_list_2-6>li{counter-increment:lst-ctn-kix_list_2-6}#doc6840845 .lst-kix_list_1-1>li:before{content:»\0025cf «}#doc6840845 ol.lst-kix_list_2-0.start{counter-reset:lst-ctn-kix_list_2-0 0}#doc6840845 .lst-kix_list_3-2>li:before{content:»» counter(lst-ctn-kix_list_3-2,lower-roman) «. «}#doc6840845 ol.lst-kix_list_4-0.start{counter-reset:lst-ctn-kix_list_4-0 5}#doc6840845 ol.lst-kix_list_4-8.start{counter-reset:lst-ctn-kix_list_4-8 0}#doc6840845 .lst-kix_list_1-2>li:before{content:»\0025cf «}#doc6840845 .lst-kix_list_2-8>li{counter-increment:lst-ctn-kix_list_2-8}#doc6840845 .lst-kix_list_1-5>li:before{content:»\0025cf «}#doc6840845 .lst-kix_list_2-3>li{counter-increment:lst-ctn-kix_list_2-3}#doc6840845 .lst-kix_list_2-3>li:before{content:»» counter(lst-ctn-kix_list_2-3,decimal) «. «}#doc6840845 .lst-kix_list_1-4>li:before{content:»\0025cf «}#doc6840845 . lst-kix_list_3-3>li{counter-increment:lst-ctn-kix_list_3-3}#doc6840845 ol.lst-kix_list_4-2.start{counter-reset:lst-ctn-kix_list_4-2 0}#doc6840845 .lst-kix_list_2-0>li{counter-increment:lst-ctn-kix_list_2-0}#doc6840845 ol.lst-kix_list_3-7.start{counter-reset:lst-ctn-kix_list_3-7 0}#doc6840845 ol.lst-kix_list_2-3.start{counter-reset:lst-ctn-kix_list_2-3 0}#doc6840845 .lst-kix_list_4-3>li:before{content:»» counter(lst-ctn-kix_list_4-3,decimal) «. «}#doc6840845 .lst-kix_list_2-7>li:before{content:»» counter(lst-ctn-kix_list_2-7,lower-latin) «. «}#doc6840845 .lst-kix_list_3-7>li{counter-increment:lst-ctn-kix_list_3-7}#doc6840845 .lst-kix_list_1-8>li:before{content:»\0025cf «}#doc6840845 ol.lst-kix_list_3-6.start{counter-reset:lst-ctn-kix_list_3-6 0}#doc6840845 ol.lst-kix_list_3-0.start{counter-reset:lst-ctn-kix_list_3-0 5}#doc6840845 .lst-kix_list_2-5>li{counter-increment:lst-ctn-kix_list_2-5}#doc6840845 .lst-kix_list_3-3>li:before{content:»» counter(lst-ctn-kix_list_3-3,decimal) «. «}#doc6840845 .
lst-kix_list_3-3>li{counter-increment:lst-ctn-kix_list_3-3}#doc6840845 ol.lst-kix_list_4-2.start{counter-reset:lst-ctn-kix_list_4-2 0}#doc6840845 .lst-kix_list_2-0>li{counter-increment:lst-ctn-kix_list_2-0}#doc6840845 ol.lst-kix_list_3-7.start{counter-reset:lst-ctn-kix_list_3-7 0}#doc6840845 ol.lst-kix_list_2-3.start{counter-reset:lst-ctn-kix_list_2-3 0}#doc6840845 .lst-kix_list_4-3>li:before{content:»» counter(lst-ctn-kix_list_4-3,decimal) «. «}#doc6840845 .lst-kix_list_2-7>li:before{content:»» counter(lst-ctn-kix_list_2-7,lower-latin) «. «}#doc6840845 .lst-kix_list_3-7>li{counter-increment:lst-ctn-kix_list_3-7}#doc6840845 .lst-kix_list_1-8>li:before{content:»\0025cf «}#doc6840845 ol.lst-kix_list_3-6.start{counter-reset:lst-ctn-kix_list_3-6 0}#doc6840845 ol.lst-kix_list_3-0.start{counter-reset:lst-ctn-kix_list_3-0 5}#doc6840845 .lst-kix_list_2-5>li{counter-increment:lst-ctn-kix_list_2-5}#doc6840845 .lst-kix_list_3-3>li:before{content:»» counter(lst-ctn-kix_list_3-3,decimal) «. «}#doc6840845 . lst-kix_list_4-4>li{counter-increment:lst-ctn-kix_list_4-4}#doc6840845 ol.lst-kix_list_2-1.start{counter-reset:lst-ctn-kix_list_2-1 0}#doc6840845 .lst-kix_list_3-6>li:before{content:»» counter(lst-ctn-kix_list_3-6,decimal) «. «}#doc6840845 .lst-kix_list_4-7>li{counter-increment:lst-ctn-kix_list_4-7}#doc6840845 .lst-kix_list_4-5>li{counter-increment:lst-ctn-kix_list_4-5}#doc6840845 ol.lst-kix_list_3-2.start{counter-reset:lst-ctn-kix_list_3-2 0}#doc6840845 .lst-kix_list_2-7>li{counter-increment:lst-ctn-kix_list_2-7}#doc6840845 ol.lst-kix_list_2-6.start{counter-reset:lst-ctn-kix_list_2-6 0}#doc6840845 .lst-kix_list_3-2>li{counter-increment:lst-ctn-kix_list_3-2}#doc6840845 .lst-kix_list_4-7>li:before{content:»» counter(lst-ctn-kix_list_4-7,lower-latin) «. «}#doc6840845 ol.lst-kix_list_2-5.start{counter-reset:lst-ctn-kix_list_2-5 0}#doc6840845 .lst-kix_list_1-6>li:before{content:»\0025cf «}#doc6840845 .lst-kix_list_2-6>li:before{content:»» counter(lst-ctn-kix_list_2-6,decimal) «. «}#doc6840845 .
lst-kix_list_4-4>li{counter-increment:lst-ctn-kix_list_4-4}#doc6840845 ol.lst-kix_list_2-1.start{counter-reset:lst-ctn-kix_list_2-1 0}#doc6840845 .lst-kix_list_3-6>li:before{content:»» counter(lst-ctn-kix_list_3-6,decimal) «. «}#doc6840845 .lst-kix_list_4-7>li{counter-increment:lst-ctn-kix_list_4-7}#doc6840845 .lst-kix_list_4-5>li{counter-increment:lst-ctn-kix_list_4-5}#doc6840845 ol.lst-kix_list_3-2.start{counter-reset:lst-ctn-kix_list_3-2 0}#doc6840845 .lst-kix_list_2-7>li{counter-increment:lst-ctn-kix_list_2-7}#doc6840845 ol.lst-kix_list_2-6.start{counter-reset:lst-ctn-kix_list_2-6 0}#doc6840845 .lst-kix_list_3-2>li{counter-increment:lst-ctn-kix_list_3-2}#doc6840845 .lst-kix_list_4-7>li:before{content:»» counter(lst-ctn-kix_list_4-7,lower-latin) «. «}#doc6840845 ol.lst-kix_list_2-5.start{counter-reset:lst-ctn-kix_list_2-5 0}#doc6840845 .lst-kix_list_1-6>li:before{content:»\0025cf «}#doc6840845 .lst-kix_list_2-6>li:before{content:»» counter(lst-ctn-kix_list_2-6,decimal) «. «}#doc6840845 . lst-kix_list_4-2>li{counter-increment:lst-ctn-kix_list_4-2}#doc6840845 .lst-kix_list_3-6>li{counter-increment:lst-ctn-kix_list_3-6}#doc6840845 ul.lst-kix_list_1-0{list-style-type:none}#doc6840845 ul.lst-kix_list_1-2{list-style-type:none}#doc6840845 .lst-kix_list_2-2>li:before{content:»» counter(lst-ctn-kix_list_2-2,lower-roman) «. «}#doc6840845 ul.lst-kix_list_1-1{list-style-type:none}#doc6840845 ol.lst-kix_list_3-3.start{counter-reset:lst-ctn-kix_list_3-3 0}#doc6840845 .lst-kix_list_4-1>li{counter-increment:lst-ctn-kix_list_4-1}#doc6840845 ul.lst-kix_list_1-4{list-style-type:none}#doc6840845 ul.lst-kix_list_1-3{list-style-type:none}#doc6840845 ul.lst-kix_list_1-6{list-style-type:none}#doc6840845 ul.lst-kix_list_1-5{list-style-type:none}#doc6840845 ul.lst-kix_list_1-8{list-style-type:none}#doc6840845 ol.lst-kix_list_4-3.start{counter-reset:lst-ctn-kix_list_4-3 0}#doc6840845 ul.lst-kix_list_1-7{list-style-type:none}#doc6840845 ol.lst-kix_list_4-5.start{counter-reset:lst-ctn-kix_list_4-5 0}#doc6840845 .
lst-kix_list_4-2>li{counter-increment:lst-ctn-kix_list_4-2}#doc6840845 .lst-kix_list_3-6>li{counter-increment:lst-ctn-kix_list_3-6}#doc6840845 ul.lst-kix_list_1-0{list-style-type:none}#doc6840845 ul.lst-kix_list_1-2{list-style-type:none}#doc6840845 .lst-kix_list_2-2>li:before{content:»» counter(lst-ctn-kix_list_2-2,lower-roman) «. «}#doc6840845 ul.lst-kix_list_1-1{list-style-type:none}#doc6840845 ol.lst-kix_list_3-3.start{counter-reset:lst-ctn-kix_list_3-3 0}#doc6840845 .lst-kix_list_4-1>li{counter-increment:lst-ctn-kix_list_4-1}#doc6840845 ul.lst-kix_list_1-4{list-style-type:none}#doc6840845 ul.lst-kix_list_1-3{list-style-type:none}#doc6840845 ul.lst-kix_list_1-6{list-style-type:none}#doc6840845 ul.lst-kix_list_1-5{list-style-type:none}#doc6840845 ul.lst-kix_list_1-8{list-style-type:none}#doc6840845 ol.lst-kix_list_4-3.start{counter-reset:lst-ctn-kix_list_4-3 0}#doc6840845 ul.lst-kix_list_1-7{list-style-type:none}#doc6840845 ol.lst-kix_list_4-5.start{counter-reset:lst-ctn-kix_list_4-5 0}#doc6840845 . lst-kix_list_2-1>li:before{content:»» counter(lst-ctn-kix_list_2-1,lower-latin) «. «}#doc6840845 .lst-kix_list_4-8>li:before{content:»» counter(lst-ctn-kix_list_4-8,lower-roman) «. «}#doc6840845 .lst-kix_list_3-0>li{counter-increment:lst-ctn-kix_list_3-0}#doc6840845 ol.lst-kix_list_2-8.start{counter-reset:lst-ctn-kix_list_2-8 0}#doc6840845 ol.lst-kix_list_2-0{list-style-type:none}#doc6840845 .lst-kix_list_2-8>li:before{content:»» counter(lst-ctn-kix_list_2-8,lower-roman) «. «}#doc6840845 ol.lst-kix_list_2-1{list-style-type:none}#doc6840845 ol.lst-kix_list_2-2{list-style-type:none}#doc6840845 .lst-kix_list_3-7>li:before{content:»» counter(lst-ctn-kix_list_3-7,lower-latin) «. «}#doc6840845 ol.lst-kix_list_2-3{list-style-type:none}#doc6840845 ol.lst-kix_list_2-4{list-style-type:none}#doc6840845 .lst-kix_list_3-4>li{counter-increment:lst-ctn-kix_list_3-4}#doc6840845 ol.lst-kix_list_2-5{list-style-type:none}#doc6840845 .lst-kix_list_2-0>li:before{content:»» counter(lst-ctn-kix_list_2-0,decimal) «.
lst-kix_list_2-1>li:before{content:»» counter(lst-ctn-kix_list_2-1,lower-latin) «. «}#doc6840845 .lst-kix_list_4-8>li:before{content:»» counter(lst-ctn-kix_list_4-8,lower-roman) «. «}#doc6840845 .lst-kix_list_3-0>li{counter-increment:lst-ctn-kix_list_3-0}#doc6840845 ol.lst-kix_list_2-8.start{counter-reset:lst-ctn-kix_list_2-8 0}#doc6840845 ol.lst-kix_list_2-0{list-style-type:none}#doc6840845 .lst-kix_list_2-8>li:before{content:»» counter(lst-ctn-kix_list_2-8,lower-roman) «. «}#doc6840845 ol.lst-kix_list_2-1{list-style-type:none}#doc6840845 ol.lst-kix_list_2-2{list-style-type:none}#doc6840845 .lst-kix_list_3-7>li:before{content:»» counter(lst-ctn-kix_list_3-7,lower-latin) «. «}#doc6840845 ol.lst-kix_list_2-3{list-style-type:none}#doc6840845 ol.lst-kix_list_2-4{list-style-type:none}#doc6840845 .lst-kix_list_3-4>li{counter-increment:lst-ctn-kix_list_3-4}#doc6840845 ol.lst-kix_list_2-5{list-style-type:none}#doc6840845 .lst-kix_list_2-0>li:before{content:»» counter(lst-ctn-kix_list_2-0,decimal) «. «}#doc6840845 ol.lst-kix_list_3-1{list-style-type:none}#doc6840845 ol.lst-kix_list_3-2{list-style-type:none}#doc6840845 ol.lst-kix_list_3-3{list-style-type:none}#doc6840845 ol.lst-kix_list_3-4{list-style-type:none}#doc6840845 ol.lst-kix_list_3-0{list-style-type:none}#doc6840845 ol.lst-kix_list_3-6{list-style-type:none}#doc6840845 ol.lst-kix_list_3-5{list-style-type:none}#doc6840845 ol.lst-kix_list_3-8{list-style-type:none}#doc6840845 ol.lst-kix_list_3-7{list-style-type:none}#doc6840845 ol.lst-kix_list_2-7{list-style-type:none}#doc6840845 .lst-kix_list_4-6>li{counter-increment:lst-ctn-kix_list_4-6}#doc6840845 ol.lst-kix_list_2-6{list-style-type:none}#doc6840845 .lst-kix_list_2-4>li:before{content:»» counter(lst-ctn-kix_list_2-4,lower-latin) «. «}#doc6840845 .lst-kix_list_3-5>li:before{content:»» counter(lst-ctn-kix_list_3-5,lower-roman) «. «}#doc6840845 ol.lst-kix_list_2-8{list-style-type:none}#doc6840845 .lst-kix_list_3-5>li{counter-increment:lst-ctn-kix_list_3-5}#doc6840845 ol.lst-kix_list_4-5{list-style-type:none}#doc6840845 ol.
«}#doc6840845 ol.lst-kix_list_3-1{list-style-type:none}#doc6840845 ol.lst-kix_list_3-2{list-style-type:none}#doc6840845 ol.lst-kix_list_3-3{list-style-type:none}#doc6840845 ol.lst-kix_list_3-4{list-style-type:none}#doc6840845 ol.lst-kix_list_3-0{list-style-type:none}#doc6840845 ol.lst-kix_list_3-6{list-style-type:none}#doc6840845 ol.lst-kix_list_3-5{list-style-type:none}#doc6840845 ol.lst-kix_list_3-8{list-style-type:none}#doc6840845 ol.lst-kix_list_3-7{list-style-type:none}#doc6840845 ol.lst-kix_list_2-7{list-style-type:none}#doc6840845 .lst-kix_list_4-6>li{counter-increment:lst-ctn-kix_list_4-6}#doc6840845 ol.lst-kix_list_2-6{list-style-type:none}#doc6840845 .lst-kix_list_2-4>li:before{content:»» counter(lst-ctn-kix_list_2-4,lower-latin) «. «}#doc6840845 .lst-kix_list_3-5>li:before{content:»» counter(lst-ctn-kix_list_3-5,lower-roman) «. «}#doc6840845 ol.lst-kix_list_2-8{list-style-type:none}#doc6840845 .lst-kix_list_3-5>li{counter-increment:lst-ctn-kix_list_3-5}#doc6840845 ol.lst-kix_list_4-5{list-style-type:none}#doc6840845 ol. lst-kix_list_4-4{list-style-type:none}#doc6840845 ol.lst-kix_list_4-7{list-style-type:none}#doc6840845 .lst-kix_list_4-2>li:before{content:»» counter(lst-ctn-kix_list_4-2,lower-roman) «. «}#doc6840845 ol.lst-kix_list_4-6{list-style-type:none}#doc6840845 ol.lst-kix_list_4-8{list-style-type:none}#doc6840845 ol.lst-kix_list_2-4.start{counter-reset:lst-ctn-kix_list_2-4 0}#doc6840845 .lst-kix_list_4-6>li:before{content:»» counter(lst-ctn-kix_list_4-6,decimal) «. «}#doc6840845 .lst-kix_list_4-5>li:before{content:»» counter(lst-ctn-kix_list_4-5,lower-roman) «. «}#doc6840845 .lst-kix_list_2-1>li{counter-increment:lst-ctn-kix_list_2-1}#doc6840845 .lst-kix_list_4-1>li:before{content:»» counter(lst-ctn-kix_list_4-1,lower-latin) «. «}#doc6840845 .lst-kix_list_3-0>li:before{content:»» counter(lst-ctn-kix_list_3-0,decimal) «. «}#doc6840845 .lst-kix_list_2-5>li:before{content:»» counter(lst-ctn-kix_list_2-5,lower-roman) «. «}#doc6840845 .lst-kix_list_1-0>li:before{content:»\0025cf «}#doc6840845 .lst-kix_list_2-4>li{counter-increment:lst-ctn-kix_list_2-4}#doc6840845 ol.
lst-kix_list_4-4{list-style-type:none}#doc6840845 ol.lst-kix_list_4-7{list-style-type:none}#doc6840845 .lst-kix_list_4-2>li:before{content:»» counter(lst-ctn-kix_list_4-2,lower-roman) «. «}#doc6840845 ol.lst-kix_list_4-6{list-style-type:none}#doc6840845 ol.lst-kix_list_4-8{list-style-type:none}#doc6840845 ol.lst-kix_list_2-4.start{counter-reset:lst-ctn-kix_list_2-4 0}#doc6840845 .lst-kix_list_4-6>li:before{content:»» counter(lst-ctn-kix_list_4-6,decimal) «. «}#doc6840845 .lst-kix_list_4-5>li:before{content:»» counter(lst-ctn-kix_list_4-5,lower-roman) «. «}#doc6840845 .lst-kix_list_2-1>li{counter-increment:lst-ctn-kix_list_2-1}#doc6840845 .lst-kix_list_4-1>li:before{content:»» counter(lst-ctn-kix_list_4-1,lower-latin) «. «}#doc6840845 .lst-kix_list_3-0>li:before{content:»» counter(lst-ctn-kix_list_3-0,decimal) «. «}#doc6840845 .lst-kix_list_2-5>li:before{content:»» counter(lst-ctn-kix_list_2-5,lower-roman) «. «}#doc6840845 .lst-kix_list_1-0>li:before{content:»\0025cf «}#doc6840845 .lst-kix_list_2-4>li{counter-increment:lst-ctn-kix_list_2-4}#doc6840845 ol. lst-kix_list_4-0{list-style-type:none}#doc6840845 ol.lst-kix_list_2-2.start{counter-reset:lst-ctn-kix_list_2-2 0}#doc6840845 ol.lst-kix_list_4-1{list-style-type:none}#doc6840845 ol.lst-kix_list_4-2{list-style-type:none}#doc6840845 .lst-kix_list_4-4>li:before{content:»» counter(lst-ctn-kix_list_4-4,lower-latin) «. «}#doc6840845 ol.lst-kix_list_4-3{list-style-type:none}#doc6840845 ol.lst-kix_list_4-7.start{counter-reset:lst-ctn-kix_list_4-7 0}#doc6840845 .lst-kix_list_3-4>li:before{content:»» counter(lst-ctn-kix_list_3-4,lower-latin) «. «}#doc6840845 .lst-kix_list_1-3>li:before{content:»\0025cf «}#doc6840845 ol.lst-kix_list_4-4.start{counter-reset:lst-ctn-kix_list_4-4 0}#doc6840845 ol.lst-kix_list_2-7.start{counter-reset:lst-ctn-kix_list_2-7 0}#doc6840845 .lst-kix_list_4-3>li{counter-increment:lst-ctn-kix_list_4-3}#doc6840845 ol.lst-kix_list_4-1.start{counter-reset:lst-ctn-kix_list_4-1 0}#doc6840845 .lst-kix_list_4-0>li{counter-increment:lst-ctn-kix_list_4-0}#doc6840845 ol.lst-kix_list_3-5.
lst-kix_list_4-0{list-style-type:none}#doc6840845 ol.lst-kix_list_2-2.start{counter-reset:lst-ctn-kix_list_2-2 0}#doc6840845 ol.lst-kix_list_4-1{list-style-type:none}#doc6840845 ol.lst-kix_list_4-2{list-style-type:none}#doc6840845 .lst-kix_list_4-4>li:before{content:»» counter(lst-ctn-kix_list_4-4,lower-latin) «. «}#doc6840845 ol.lst-kix_list_4-3{list-style-type:none}#doc6840845 ol.lst-kix_list_4-7.start{counter-reset:lst-ctn-kix_list_4-7 0}#doc6840845 .lst-kix_list_3-4>li:before{content:»» counter(lst-ctn-kix_list_3-4,lower-latin) «. «}#doc6840845 .lst-kix_list_1-3>li:before{content:»\0025cf «}#doc6840845 ol.lst-kix_list_4-4.start{counter-reset:lst-ctn-kix_list_4-4 0}#doc6840845 ol.lst-kix_list_2-7.start{counter-reset:lst-ctn-kix_list_2-7 0}#doc6840845 .lst-kix_list_4-3>li{counter-increment:lst-ctn-kix_list_4-3}#doc6840845 ol.lst-kix_list_4-1.start{counter-reset:lst-ctn-kix_list_4-1 0}#doc6840845 .lst-kix_list_4-0>li{counter-increment:lst-ctn-kix_list_4-0}#doc6840845 ol.lst-kix_list_3-5. start{counter-reset:lst-ctn-kix_list_3-5 0}#doc6840845 .lst-kix_list_3-8>li:before{content:»» counter(lst-ctn-kix_list_3-8,lower-roman) «. «}#doc6840845 .lst-kix_list_4-0>li:before{content:»» counter(lst-ctn-kix_list_4-0,decimal) «. «}#doc6840845 ol.lst-kix_list_3-4.start{counter-reset:lst-ctn-kix_list_3-4 0}#doc6840845 .lst-kix_list_4-8>li{counter-increment:lst-ctn-kix_list_4-8}#doc6840845 ol.lst-kix_list_4-6.start{counter-reset:lst-ctn-kix_list_4-6 0}#doc6840845 .lst-kix_list_3-1>li:before{content:»» counter(lst-ctn-kix_list_3-1,lower-latin) «. «}#doc6840845 ol.lst-kix_list_3-8.start{counter-reset:lst-ctn-kix_list_3-8 0}#doc6840845 .lst-kix_list_1-7>li:before{content:»\0025cf «}#doc6840845 ol.lst-kix_list_3-1.start{counter-reset:lst-ctn-kix_list_3-1 0}#doc6840845 .lst-kix_list_3-1>li{counter-increment:lst-ctn-kix_list_3-1}#doc6840845 .lst-kix_list_2-2>li{counter-increment:lst-ctn-kix_list_2-2}#doc6840845 ol{margin:0;padding:0}#doc6840845 .c9{padding-left:3pt;line-height:1.5;padding-top:0pt;widows:2;orphans:2;text-align:justify;direction:ltr;margin-left:36pt;padding-bottom:0pt}#doc6840845 .
start{counter-reset:lst-ctn-kix_list_3-5 0}#doc6840845 .lst-kix_list_3-8>li:before{content:»» counter(lst-ctn-kix_list_3-8,lower-roman) «. «}#doc6840845 .lst-kix_list_4-0>li:before{content:»» counter(lst-ctn-kix_list_4-0,decimal) «. «}#doc6840845 ol.lst-kix_list_3-4.start{counter-reset:lst-ctn-kix_list_3-4 0}#doc6840845 .lst-kix_list_4-8>li{counter-increment:lst-ctn-kix_list_4-8}#doc6840845 ol.lst-kix_list_4-6.start{counter-reset:lst-ctn-kix_list_4-6 0}#doc6840845 .lst-kix_list_3-1>li:before{content:»» counter(lst-ctn-kix_list_3-1,lower-latin) «. «}#doc6840845 ol.lst-kix_list_3-8.start{counter-reset:lst-ctn-kix_list_3-8 0}#doc6840845 .lst-kix_list_1-7>li:before{content:»\0025cf «}#doc6840845 ol.lst-kix_list_3-1.start{counter-reset:lst-ctn-kix_list_3-1 0}#doc6840845 .lst-kix_list_3-1>li{counter-increment:lst-ctn-kix_list_3-1}#doc6840845 .lst-kix_list_2-2>li{counter-increment:lst-ctn-kix_list_2-2}#doc6840845 ol{margin:0;padding:0}#doc6840845 .c9{padding-left:3pt;line-height:1.5;padding-top:0pt;widows:2;orphans:2;text-align:justify;direction:ltr;margin-left:36pt;padding-bottom:0pt}#doc6840845 . c12{line-height:1.0;padding-top:0pt;widows:2;orphans:2;height:11pt;text-align:justify;direction:ltr;padding-bottom:0pt}#doc6840845 .c15{line-height:1.0;padding-top:0pt;widows:2;orphans:2;height:11pt;text-align:right;direction:ltr;padding-bottom:10pt}#doc6840845 .c1{line-height:1.0;padding-top:0pt;widows:2;orphans:2;height:11pt;text-align:justify;direction:ltr;padding-bottom:10pt}#doc6840845 .c5{line-height:1.0;padding-top:8.4pt;widows:2;orphans:2;text-indent:18pt;text-align:justify;direction:ltr;padding-bottom:0pt}#doc6840845 .c0{line-height:1.0;padding-top:8.4pt;widows:2;orphans:2;height:11pt;text-align:justify;direction:ltr;padding-bottom:0pt}#doc6840845 .c10{line-height:1.5;padding-top:0pt;widows:2;orphans:2;height:11pt;text-align:justify;direction:ltr;padding-bottom:10pt}#doc6840845 .c18{line-height:1.0;padding-top:0pt;widows:2;orphans:2;height:11pt;text-align:justify;direction:ltr;padding-bottom:7.8pt}#doc6840845 .c16{line-height:1.0;padding-top:0pt;widows:2;orphans:2;text-align:center;direction:ltr;padding-bottom:10pt}#doc6840845 .
c12{line-height:1.0;padding-top:0pt;widows:2;orphans:2;height:11pt;text-align:justify;direction:ltr;padding-bottom:0pt}#doc6840845 .c15{line-height:1.0;padding-top:0pt;widows:2;orphans:2;height:11pt;text-align:right;direction:ltr;padding-bottom:10pt}#doc6840845 .c1{line-height:1.0;padding-top:0pt;widows:2;orphans:2;height:11pt;text-align:justify;direction:ltr;padding-bottom:10pt}#doc6840845 .c5{line-height:1.0;padding-top:8.4pt;widows:2;orphans:2;text-indent:18pt;text-align:justify;direction:ltr;padding-bottom:0pt}#doc6840845 .c0{line-height:1.0;padding-top:8.4pt;widows:2;orphans:2;height:11pt;text-align:justify;direction:ltr;padding-bottom:0pt}#doc6840845 .c10{line-height:1.5;padding-top:0pt;widows:2;orphans:2;height:11pt;text-align:justify;direction:ltr;padding-bottom:10pt}#doc6840845 .c18{line-height:1.0;padding-top:0pt;widows:2;orphans:2;height:11pt;text-align:justify;direction:ltr;padding-bottom:7.8pt}#doc6840845 .c16{line-height:1.0;padding-top:0pt;widows:2;orphans:2;text-align:center;direction:ltr;padding-bottom:10pt}#doc6840845 . c14{line-height:1.0;padding-top:8.4pt;widows:2;orphans:2;text-align:justify;direction:ltr;padding-bottom:0pt}#doc6840845 .c26{line-height:1.0;padding-top:0pt;widows:2;orphans:2;text-align:right;direction:ltr;padding-bottom:10pt}#doc6840845 .c22{line-height:1.5;padding-top:0pt;widows:2;orphans:2;height:11pt;direction:ltr;padding-bottom:10pt}#doc6840845 .c6{line-height:1.0;padding-top:0pt;widows:2;orphans:2;text-align:center;direction:ltr;padding-bottom:0pt}#doc6840845 .c8{line-height:1.0;padding-top:0pt;widows:2;orphans:2;text-align:justify;direction:ltr;padding-bottom:10pt}#doc6840845 .c41{line-height:1.5;padding-top:0pt;widows:2;orphans:2;text-align:center;direction:ltr;padding-bottom:10pt}#doc6840845 .c39{vertical-align:baseline;color:#0000ff;font-size:14pt;background-color:#ffffff;font-family:»Arial»;text-decoration:underline;font-weight:normal}#doc6840845 .c4{line-height:1.0;padding-top:8.4pt;widows:2;orphans:2;height:11pt;direction:ltr;padding-bottom:0pt}#doc6840845 .c29{line-height:1.
c14{line-height:1.0;padding-top:8.4pt;widows:2;orphans:2;text-align:justify;direction:ltr;padding-bottom:0pt}#doc6840845 .c26{line-height:1.0;padding-top:0pt;widows:2;orphans:2;text-align:right;direction:ltr;padding-bottom:10pt}#doc6840845 .c22{line-height:1.5;padding-top:0pt;widows:2;orphans:2;height:11pt;direction:ltr;padding-bottom:10pt}#doc6840845 .c6{line-height:1.0;padding-top:0pt;widows:2;orphans:2;text-align:center;direction:ltr;padding-bottom:0pt}#doc6840845 .c8{line-height:1.0;padding-top:0pt;widows:2;orphans:2;text-align:justify;direction:ltr;padding-bottom:10pt}#doc6840845 .c41{line-height:1.5;padding-top:0pt;widows:2;orphans:2;text-align:center;direction:ltr;padding-bottom:10pt}#doc6840845 .c39{vertical-align:baseline;color:#0000ff;font-size:14pt;background-color:#ffffff;font-family:»Arial»;text-decoration:underline;font-weight:normal}#doc6840845 .c4{line-height:1.0;padding-top:8.4pt;widows:2;orphans:2;height:11pt;direction:ltr;padding-bottom:0pt}#doc6840845 .c29{line-height:1. 0;padding-top:8.4pt;widows:2;orphans:2;direction:ltr;padding-bottom:5pt}#doc6840845 .c31{line-height:1.0;padding-top:0pt;widows:2;orphans:2;direction:ltr;padding-bottom:7.8pt}#doc6840845 .c33{line-height:1.0;padding-top:0pt;widows:2;orphans:2;direction:ltr;padding-bottom:10pt}#doc6840845 .c35{line-height:1.0;padding-top:0pt;widows:2;orphans:2;direction:ltr;padding-bottom:0pt}#doc6840845 .c17{vertical-align:baseline;color:#0000ff;font-size:14pt;font-family:»Times New Roman»;text-decoration:underline;font-weight:normal}#doc6840845 .c30{line-height:1.0;padding-top:5pt;widows:2;orphans:2;direction:ltr;padding-bottom:7.8pt}#doc6840845 .c13{line-height:1.0;padding-top:5pt;widows:2;orphans:2;direction:ltr;padding-bottom:5pt}#doc6840845 .c24{vertical-align:super;color:#000000;font-size:14pt;font-family:»Georgia»;font-weight:normal}#doc6840845 .c11{vertical-align:baseline;color:#000000;font-size:14pt;font-family:»Times New Roman»;font-weight:bold}#doc6840845 .c36{vertical-align:baseline;color:#64280e;font-size:14pt;font-family:»Georgia»;font-weight:normal}#doc6840845 .
0;padding-top:8.4pt;widows:2;orphans:2;direction:ltr;padding-bottom:5pt}#doc6840845 .c31{line-height:1.0;padding-top:0pt;widows:2;orphans:2;direction:ltr;padding-bottom:7.8pt}#doc6840845 .c33{line-height:1.0;padding-top:0pt;widows:2;orphans:2;direction:ltr;padding-bottom:10pt}#doc6840845 .c35{line-height:1.0;padding-top:0pt;widows:2;orphans:2;direction:ltr;padding-bottom:0pt}#doc6840845 .c17{vertical-align:baseline;color:#0000ff;font-size:14pt;font-family:»Times New Roman»;text-decoration:underline;font-weight:normal}#doc6840845 .c30{line-height:1.0;padding-top:5pt;widows:2;orphans:2;direction:ltr;padding-bottom:7.8pt}#doc6840845 .c13{line-height:1.0;padding-top:5pt;widows:2;orphans:2;direction:ltr;padding-bottom:5pt}#doc6840845 .c24{vertical-align:super;color:#000000;font-size:14pt;font-family:»Georgia»;font-weight:normal}#doc6840845 .c11{vertical-align:baseline;color:#000000;font-size:14pt;font-family:»Times New Roman»;font-weight:bold}#doc6840845 .c36{vertical-align:baseline;color:#64280e;font-size:14pt;font-family:»Georgia»;font-weight:normal}#doc6840845 .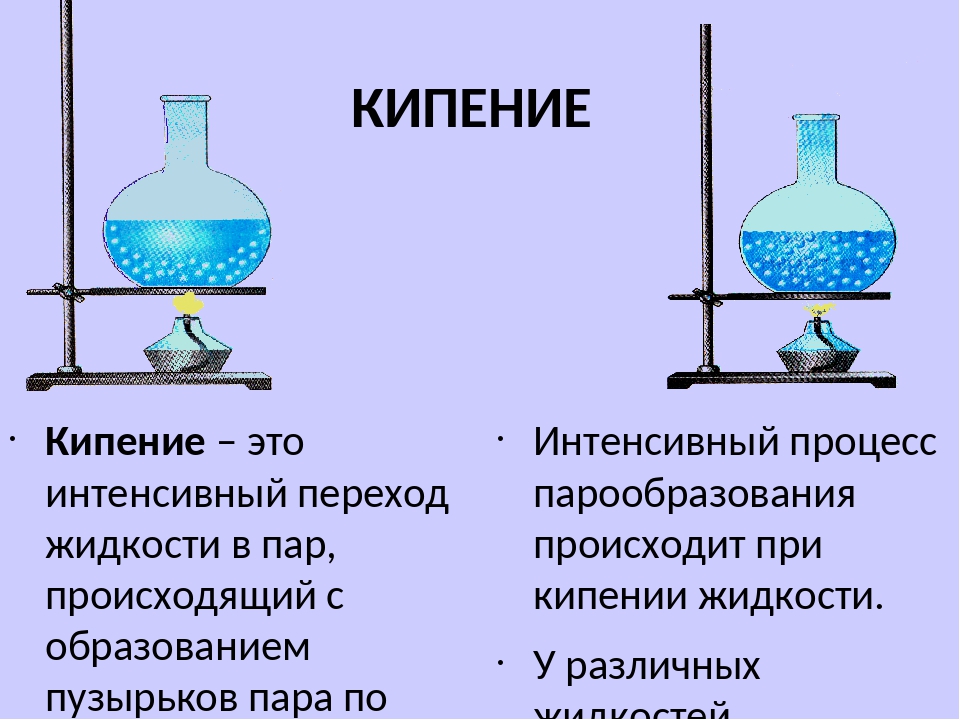 c3{vertical-align:baseline;color:#000000;font-size:14pt;font-family:»Times New Roman»;font-weight:normal}#doc6840845 .c27{vertical-align:baseline;color:#0000ff;font-size:14pt;font-family:»Times New Roman»;font-weight:normal}#doc6840845 .c2{vertical-align:baseline;color:#000000;font-size:14pt;font-family:»Georgia»;font-weight:normal}#doc6840845 .c42{vertical-align:baseline;color:#000000;font-size:6pt;font-family:»Trebuchet MS»;font-weight:normal}#doc6840845 .c21{vertical-align:baseline;color:#000000;font-size:14pt;font-family:»Trebuchet MS»;font-weight:bold}#doc6840845 .c7{vertical-align:baseline;color:#000000;font-size:14pt;font-family:»Georgia»;font-weight:bold}#doc6840845 .c37{max-width:484.5pt;background-color:#ffffff;padding:56.7pt 42.5pt 56.7pt 85pt}#doc6840845 .c40{margin:0;padding:0}#doc6840845 .c25{color:inherit;text-decoration:inherit}#doc6840845 .c34{padding-left:0pt;margin-left:36pt}#doc6840845 .c19{text-indent:35.4pt}#doc6840845 .c20{text-align:justify}#doc6840845 .c23{margin-left:18pt}#doc6840845 .
c3{vertical-align:baseline;color:#000000;font-size:14pt;font-family:»Times New Roman»;font-weight:normal}#doc6840845 .c27{vertical-align:baseline;color:#0000ff;font-size:14pt;font-family:»Times New Roman»;font-weight:normal}#doc6840845 .c2{vertical-align:baseline;color:#000000;font-size:14pt;font-family:»Georgia»;font-weight:normal}#doc6840845 .c42{vertical-align:baseline;color:#000000;font-size:6pt;font-family:»Trebuchet MS»;font-weight:normal}#doc6840845 .c21{vertical-align:baseline;color:#000000;font-size:14pt;font-family:»Trebuchet MS»;font-weight:bold}#doc6840845 .c7{vertical-align:baseline;color:#000000;font-size:14pt;font-family:»Georgia»;font-weight:bold}#doc6840845 .c37{max-width:484.5pt;background-color:#ffffff;padding:56.7pt 42.5pt 56.7pt 85pt}#doc6840845 .c40{margin:0;padding:0}#doc6840845 .c25{color:inherit;text-decoration:inherit}#doc6840845 .c34{padding-left:0pt;margin-left:36pt}#doc6840845 .c19{text-indent:35.4pt}#doc6840845 .c20{text-align:justify}#doc6840845 .c23{margin-left:18pt}#doc6840845 . c28{font-style:italic}#doc6840845 .c32{height:11pt}#doc6840845 .c38{text-indent:18pt}#doc6840845 .title{widows:2;padding-top:0pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:11pt;font-family:»Arial»;padding-bottom:0pt}#doc6840845 .subtitle{widows:2;padding-top:0pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:11pt;font-family:»Arial»;padding-bottom:0pt}#doc6840845 li{color:#000000;font-size:11pt;font-family:»Arial»}#doc6840845 p{color:#000000;font-size:11pt;margin:0;font-family:»Arial»}#doc6840845 h2{widows:2;padding-top:0pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:11pt;font-family:»Arial»;padding-bottom:0pt}#doc6840845 h3{widows:2;padding-top:0pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:11pt;font-family:»Arial»;padding-bottom:0pt}#doc6840845 h4{widows:2;padding-top:0pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:11pt;font-family:»Arial»;padding-bottom:0pt}#doc6840845 h5{widows:2;padding-top:0pt;line-height:1.
c28{font-style:italic}#doc6840845 .c32{height:11pt}#doc6840845 .c38{text-indent:18pt}#doc6840845 .title{widows:2;padding-top:0pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:11pt;font-family:»Arial»;padding-bottom:0pt}#doc6840845 .subtitle{widows:2;padding-top:0pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:11pt;font-family:»Arial»;padding-bottom:0pt}#doc6840845 li{color:#000000;font-size:11pt;font-family:»Arial»}#doc6840845 p{color:#000000;font-size:11pt;margin:0;font-family:»Arial»}#doc6840845 h2{widows:2;padding-top:0pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:11pt;font-family:»Arial»;padding-bottom:0pt}#doc6840845 h3{widows:2;padding-top:0pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:11pt;font-family:»Arial»;padding-bottom:0pt}#doc6840845 h4{widows:2;padding-top:0pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:11pt;font-family:»Arial»;padding-bottom:0pt}#doc6840845 h5{widows:2;padding-top:0pt;line-height:1.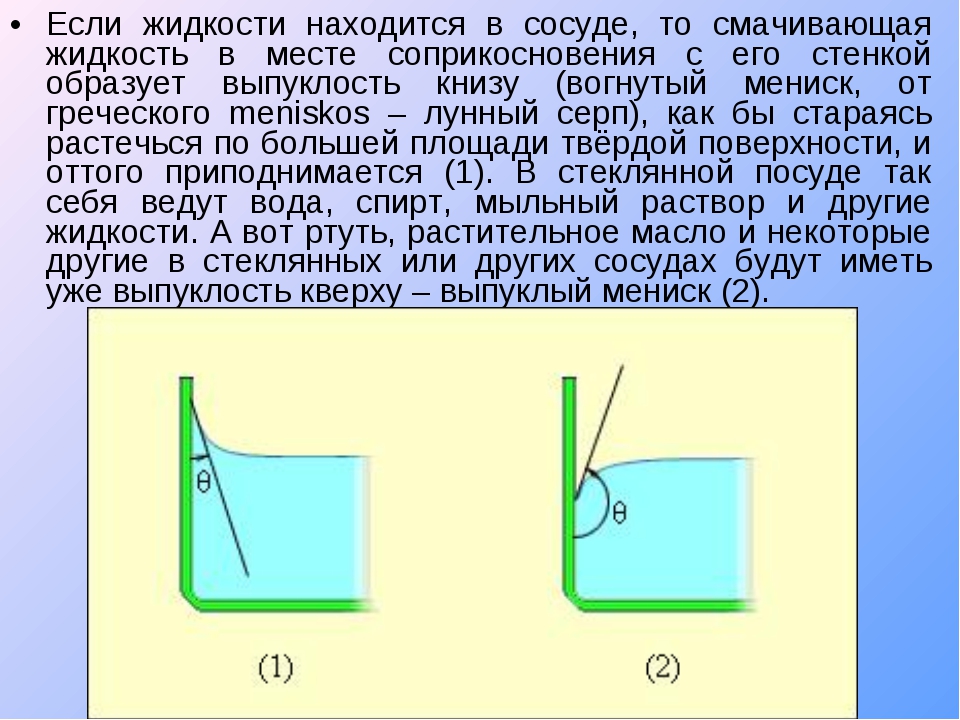 15;orphans:2;text-align:left;color:#000000;font-size:11pt;font-family:»Arial»;padding-bottom:0pt}#doc6840845 h5{widows:2;padding-top:0pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:11pt;font-family:»Arial»;padding-bottom:0pt}#doc6840845 h6{widows:2;padding-top:0pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:11pt;font-family:»Arial»;padding-bottom:0pt}#doc6840845 ]]>
15;orphans:2;text-align:left;color:#000000;font-size:11pt;font-family:»Arial»;padding-bottom:0pt}#doc6840845 h5{widows:2;padding-top:0pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:11pt;font-family:»Arial»;padding-bottom:0pt}#doc6840845 h6{widows:2;padding-top:0pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:11pt;font-family:»Arial»;padding-bottom:0pt}#doc6840845 ]]>Муниципальное автономное общеобразовательное учреждение
Средняя общеобразовательная школа №3
Неньютоновская жидкость
Учебно-исследовательская работа по физике
Исполнители:
Маслов Александр, уч. 10А кл.
Терёшин Владислав, 10В кл.
Носарев Сергей, 10А кл.
Руководители:
Игумнова И.О.
Учитель физики.
Кировград
2013 г.
Оглавление
1. Введение
2. Характеристика жидкого состояния
3. Ньютоновские и Неньютоновские жидкости
4. Свойства жидкости
a. Вязкость
b. Плотность
c. Кипение
5. Методика определения свойств жидкости
6. Образование свободной поверхности и поверхностное натяжение
7. Эксперименты
8. Применение Неньютоновских жидкостей
Литература
1. Введение
Цель: изучить современные проблемы использования неньютоновской жидкости в современном мире
Задачи: — изучить разновидности жидкостей;
-изучить свойства неньютоновской жидкости;
— экспериментально показать свойства неньютоновской жидкости
Методы исследования: изучение научной литературы по проблеме (Интернет-ресурсы), экспериментальные исследования.
Необходимо уметь: пользоваться ресурсами сети Интернет, уметь видеть проблемы, проводить эксперименты.
Актуальность выбранной темы: В курсе физики 9-10 класса мы изучали вопросы, которые когда-то были проблемами в науке, но были решены на определенном этапе. Нас заинтересовал тот вопрос, что при открытии новых физических явлений постоянно происходит переосмысление физической картины мира. Каждое новое открытие является революционным и продвигает науку на новый виток развития. Очень интересно, что сегодня еще может человечество узнать о природе. Может ли полезное применение неньютоновской жидкости упростить жизнь человека и помочь в освоении науки?
Каждое новое открытие является революционным и продвигает науку на новый виток развития. Очень интересно, что сегодня еще может человечество узнать о природе. Может ли полезное применение неньютоновской жидкости упростить жизнь человека и помочь в освоении науки?
Последовательность выполнения исследования
- Найти проблему.
- Определить современные пути решения проблемы.
- Изучить виды жидкостей.
- Изучить свойства неньютоновской жидкости.
- Изучение образования свободной поверхности и поверхностного натяжения.
- Экспериментально показать свойства неньютоновской жидкости.
- Предложить свои идеи полезного применения неньютоновской жидкости.
Жидкость окружает везде и всегда. Сами люди состоят из жидкости, вода дает нам жизнь, из воды мы вышли и к воде всегда возвращаемся. Но что же такое жидкость, с научной точки зрения жидкость это — одно из агрегатных состояний вещества. Основным свойством жидкости является, то, что она способна менять свою форму под действием механического воздействия. Жидкости бывают идеальные и реальные. Идеальные — невязкие жидкости, обладающие абсолютной подвижностью, т.е. отсутствием сил трения и касательных напряжений и абсолютной неизменностью, а объёме под воздействием внешних сил. Реальные — вязкие жидкости, обладающие сжимаемостью, сопротивлением, растягивающим и сдвигающим усилиям и достаточной подвижностью, т.е. наличием сил трения и касательных напряжений.
Жидкости бывают идеальные и реальные. Идеальные — невязкие жидкости, обладающие абсолютной подвижностью, т.е. отсутствием сил трения и касательных напряжений и абсолютной неизменностью, а объёме под воздействием внешних сил. Реальные — вязкие жидкости, обладающие сжимаемостью, сопротивлением, растягивающим и сдвигающим усилиям и достаточной подвижностью, т.е. наличием сил трения и касательных напряжений.
2. Характеристика жидкого состояния: Жидкое состояние обычно считают промежуточным между твёрдым телом и газом: газ не сохраняет ни объём, ни форму, а твёрдое тело сохраняет и то, и другое. Жидкости бывают идеальные и реальные. Идеальные — невязкие жидкости, обладающие абсолютной подвижностью, т.е. отсутствием сил трения и касательных напряжений и абсолютной неизменностью, а объёме под воздействием внешних сил. Реальные — вязкие жидкости, обладающие сжимаемостью, сопротивлением, растягивающим и сдвигающим усилиям и достаточной подвижностью, т.е. наличием сил трения и касательных напряжений. Реальные жидкости могут быть ньютоновскими и неньютоновскими (бингамовскими).
Реальные жидкости могут быть ньютоновскими и неньютоновскими (бингамовскими).
3. Ньютоновские и Неньютоновские жидкости: Если в движущейся жидкости её вязкость зависит только от её природы и температуры и не зависит от градиента скорости, то такие жидкости называют ньютоновскими. К ним относятся однородные жидкости. Когда жидкость неоднородна, например, состоит из крупных молекул, образующих сложные пространственные структуры, то при её течении вязкость зависит от градиента скорости. Такие жидкости называют неньютоновскими. Неньютоновские жидкости не поддаются законам обычных жидкостей, эти жидкости меняют свою плотность и вязкость при воздействии на них физической силой, причем не только механическим воздействие, но и даже звуковыми волнами. Если воздействовать механически на обычную жидкость то чем большее будет воздействие на нее, тем больше будет сдвиг между плоскостями жидкости, иными словами чем сильнее воздействовать на жидкость, тем быстрее она будет течь и менять свою форму. Если воздействовать на Неньютоновскую жидкость механическими усилиями, мы получим совершенно другой эффект, жидкость начнет принимать свойства твердых тел и вести себя как твердое тело, связь между молекулами жидкости будет усиливаться с увеличением силы воздействия на нее, в следствии мы столкнемся с физическим затруднением сдвинуть слои таких жидкостей. Вязкость неньютоновских жидкостей возрастает при уменьшение скорости тока жидкости
Если воздействовать на Неньютоновскую жидкость механическими усилиями, мы получим совершенно другой эффект, жидкость начнет принимать свойства твердых тел и вести себя как твердое тело, связь между молекулами жидкости будет усиливаться с увеличением силы воздействия на нее, в следствии мы столкнемся с физическим затруднением сдвинуть слои таких жидкостей. Вязкость неньютоновских жидкостей возрастает при уменьшение скорости тока жидкости
ПУЗЫРЬ, ПОДНИМАЮЩИЙСЯ В НЬЮТОНОВСКОЙ И НЕНЬЮТОНОВСКОЙ ЖИДКОСТЯХ
4. Свойства жидкости: Как у всего сущего на земле, у жидкости есть свои свойства, такие как вязкость, плотность, текучесть, температура кипения и замерзания и многие другие. Данная работа больше основана на изучении вязкости жидкости, но стоит упомянуть и о других ее свойствах
a. Вязкость (внутреннее трение) — одно из трёх явлений переноса, свойство текучих тел оказывать сопротивление перемещению одной их части относительно другой. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.
Различают динамическую вязкость(первая) [единицы измерения: пуаз, Па*с], вторая, вязкость жидкостей, вязкость полимера, разряжённых газов, и кинематическую вязкость [единицы измерения: стокс, м²/с, внесистемная единица — градус Энглера].Вторая вязкость (коэффициент второй вязкости) ζ, подобно динамической (первой) вязкости η, является положительной величиной и зависит от химической природы вещества, давления и температуры. Вязкость в жидкостях подчиняется тем же дифференциальным уравнениям, что и соответствующие явления в газах. Кинематическая вязкость может быть получена как отношение динамической вязкости к плотности вещества и своим происхождением обязана классическим методам измерения вязкости, таким как измерение времени вытекания заданного объема через калиброванное отверстие под действием силы тяжести. Вязкость полимерных растворах характеризуется следующими величинами: относительной вязкостью, или вязкостным отношением. Внутреннее трение разряжённых газовотсутствует и существует лишь внешнее трние движущегося газа. Прибор для измерения вязкости называется вискозиметром.
Прибор для измерения вязкости называется вискозиметром.
b. Плотность — физическая величина, определяемая для однородного вещества массой его единичного объёма. Плотность воды при температуре 4оС равна 1г/см3.
c. Кипение — процесс парообразования внутри жидкости. При достаточно высокой температуре давление пара становится выше давления внутри жидкости, и там начинают образовываться пузырьки пара, которые (в условиях земного притяжения) всплывают наверх.
5. Методика определения свойств жидкости
a. определение вязкости: Капиллярные вискозиметры измеряют расход фиксированного объема жидкости через малое отверстие при контролируемой температуре. Скорость сдвига можно измерить примерно от нуля до 106 с-1, заменяя капиллярный диаметр и приложенное давление. Типы капиллярных вискозиметров и их режимы работы: Стеклянный капиллярный вискозиметр (ASTM D 445) — Жидкость проходит через отверстие устанавливаемого — диаметра под влиянием силы тяжести. Скорость сдвига — меньше чем 10 с-1. Кинематическая вязкость всех автомобильных масел измеряется капиллярными вискозиметрами. Капиллярный вискозиметр высокого давления (ASTM D 4624 и D 5481) — Фиксированный объем жидкости выдавливается через стеклянный капилляр диаметра под действием приложенного давления газа. Скорость сдвига может быть изменена до 106 с-1. Эта методика обычно используется, чтобы моделировать вязкость моторных масел в рабочих коренных подшипниках. Эта вязкость называется, вязкостью при высокой температуре и высоком сдвиге (HTHS) и измеряется при 150°C и 106 с-1. HTHS вязкость измеряется также имитатором конического подшипника, ASTM D 4683
Кинематическая вязкость всех автомобильных масел измеряется капиллярными вискозиметрами. Капиллярный вискозиметр высокого давления (ASTM D 4624 и D 5481) — Фиксированный объем жидкости выдавливается через стеклянный капилляр диаметра под действием приложенного давления газа. Скорость сдвига может быть изменена до 106 с-1. Эта методика обычно используется, чтобы моделировать вязкость моторных масел в рабочих коренных подшипниках. Эта вязкость называется, вязкостью при высокой температуре и высоком сдвиге (HTHS) и измеряется при 150°C и 106 с-1. HTHS вязкость измеряется также имитатором конического подшипника, ASTM D 4683
6. Образование свободной поверхности и поверхностное натяжение. Из-за сохранения объёма жидкость способна образовывать свободную поверхность. Такая поверхность является поверхностью раздела фаз данного вещества: по одну сторону находится жидкая фаза, по другую — газообразная (пар), и, возможно, другие газы, например, воздух. Если жидкая и газообразная фазы одного и того же вещества соприкасаются, возникают силы, которые стремятся уменьшить площадь поверхности раздела — силы поверхностного натяжения. Поверхность раздела ведёт себя как упругая мембрана, которая стремится стянуться. Поверхностное натяжение может быть объяснено притяжением между молекулами жидкости. Каждая молекула притягивает другие молекулы, стремится «окружить» себя ими, а значит, уйти с поверхности. Соответственно, поверхность стремится уменьшиться. Поэтому мыльные пузыри и пузыри при кипении стремятся принять сферическую форму: при данном объёме минимальной поверхностью обладает шар. Если на жидкость действуют только силы поверхностного натяжения, она обязательно примет сферическую форму — например, капли воды в невесомости. Маленькие объекты с плотностью, большей плотности жидкости, способны «плавать» на поверхности жидкости, так как сила тяготения меньше силы, препятствующей увеличению площади поверхности.
Поверхность раздела ведёт себя как упругая мембрана, которая стремится стянуться. Поверхностное натяжение может быть объяснено притяжением между молекулами жидкости. Каждая молекула притягивает другие молекулы, стремится «окружить» себя ими, а значит, уйти с поверхности. Соответственно, поверхность стремится уменьшиться. Поэтому мыльные пузыри и пузыри при кипении стремятся принять сферическую форму: при данном объёме минимальной поверхностью обладает шар. Если на жидкость действуют только силы поверхностного натяжения, она обязательно примет сферическую форму — например, капли воды в невесомости. Маленькие объекты с плотностью, большей плотности жидкости, способны «плавать» на поверхности жидкости, так как сила тяготения меньше силы, препятствующей увеличению площади поверхности.
Эксперимент №1
Цель: изучение некоторых свойств неньютоновских жидкостей
Реактивы: крахмал картофельный, вода
Посуда: глубокая чашка, металлическая палочка
Ход работы:
1. Взять крахмал
2. Налить небольшое количество воды и размешать с помощью металлической палочки (не использовать стеклянные палочки, из-за их хрупкости)
Налить небольшое количество воды и размешать с помощью металлической палочки (не использовать стеклянные палочки, из-за их хрупкости)
3. Постепенно подливать воды и мешать, пока не получится однородная масса
Получившуюся жидкость можно налить в руку и попробовать скатать шарик, при воздействии на жидкость, пока мы будем катать шарик, в руках будет твердый шар из жидкости, причем, чем быстрее и сильнее мы будем на него воздействовать, тем плотнее и тверже будет наш шарик. Как только мы разожмем руки, твердый до этого времени шар тут же растечется по руке. Связанно это будет с тем, что, после прекращения воздействия на него, жидкость снова примет свойства жидкой фазы.
Если налить получившейся жидкости в высокий резервуар, и положить
сверху бросок дерева, в него свободно можно будет забить гвоздь. Так же можно просто свободно без усилий погрузить палец в данный раствор, но если попробовать быстро ткнуть в него, палец остановится именно на поверхности раствора, не проникнув внутрь, и чем быстрее и сильнее пробовать пробить верхнюю мембрану, тем большее сопротивление мы будем получать в замен.
Применение Неньютоновских жидкостей: Так же Неньютоновские жидкости используются в автопроме, моторные масла синтетического производства на основе неньютоновских жидкостей уменьшают свою вязкость в несколько десятков раз, пи повышении оборотов двигателя, позволяя при этом уменьшить трение в двигатели.
Данный эксперимент позволяет нам не только познакомится с неньютоновскими жидкостями, но и изучить некоторые свойства данных жидкостей, а так позволяют наглядно продемонстрировать свойства жидкости, наглядные примеры помогают лучше запомнить данную преподавателем теорию.
«Эффект Кайе»
Введение: В 1963 году ученый химик и физик Артур Кайе проводил опыты на основе неньютоновских жидкостей и наблюдал интересные изменения. Ученый заметил, что если жидкость вливать с небольшой высоты в такую же жидкость или в жидкость с одинаковой плотностью и вязкостью, то струйка не растворяется в жидкости, а как бы отскакивает от самой себя. Связанно данное явление с тем, что струя жидкости, падающая вниз не может пробить поверхностное натяжение верхнего слоя и отскакивает в сторону. Это явление назвали «Эффект Кайе».
Это явление назвали «Эффект Кайе».
Цель: изучение образования слоя поверхностного натяжения
Реактивы: жидкое мыло (шампунь)
Посуда: глубокая, широкая чашка, бюретка, штатив, металлическая пластина
Ход работы:
1. установить штатив на ровную поверхность и закрепить на ней бюретку на высоте 20-25 см от поверхности стола
2. под бюретку установить кристаллизатор
3. налить в кристаллизатор исследуемую жидкость слоем в 3-5 см
4. аккуратно заполнить бюретку исследуемой жидкостью, ровным слоем, без образования воздушных пузырьков
После того как жидкость через бюретку падает с высоты 20 см вниз в себе подобную жидкость, мы можем наблюдать интересное явление связанное с поверхностным натяжением. Струйка жидкости, падающая вниз, начинает отскакивать от поверхности жидкости находящейся внизу. Объяснить это можно тем что, проникая внутрь жидкости, находящейся в кристаллизаторе, струйка несет в себе запас кинетической энергии, а поскольку жидкость имеет высокую плотность и вязкость, и по закону сохранения энергии, кинетическая энергия, внесенная в уравновешенную систему, должна, куда-то перейти, и выстреливает такой же струйкой из жидкости. Если поставить под струйку металлическую пластину под углом примерно 450 и смочить ее тем же жидким мылом, то струйка падающая вниз будет по наклонной траектории падать отскакивая пару раз от пластины.
Если поставить под струйку металлическую пластину под углом примерно 450 и смочить ее тем же жидким мылом, то струйка падающая вниз будет по наклонной траектории падать отскакивая пару раз от пластины.
Данный опыт дает представление о кинетической энергии и уравновешенных системах, так же данный опыт очень эффектно выглядит и запоминается надолго, что позволяет лучше воспринять пройденный теоретический материал.
Литература
Интернет-ресурсы:
Физика жидкостей — Википедия (с комментариями)
Материал из Википедии — свободной энциклопедии
Физика жидкостей (физика жидкого состояния вещества) — раздел физики, в котором изучаются механические и физические свойства жидкостей. Статистическая теория жидкостей является разделом статистической физики. Важнейшим результатом является вывод уравнений гидродинамики из уравнений Лиувилля, реализованный Н. Н. Боголюбовым в 1948 году. В физике квантовых жидкостей изучается явление сверхтекучести, нашедшее объяснение в работах Н. Н. Боголюбова 1947—1949 годов.
Н. Боголюбова 1947—1949 годов.
Успехи теории фазовых переходов между газообразным и жидким состоянием вещества, созданной Ван-дер-Ваальсом, укрепили представления о структурной близости этих состояний, как неупорядоченных и различающихся лишь плотностью частиц. После первых ренгеноструктурных исследований распределения частиц в жидкости выяснилось, что жидкости не являются бесструктурными. В теории рассеяния света в жидкости, разработанной Цернике и Пирсом в 1927 году, возникает функция распределения. Я. И. Френкель ввел представление о колебательно-поступательном движении молекул в жидкостях и развил кинетические модели в физике жидкостей. Строгая статистическая теория жидкостей была построена в работах Н. Н. Боголюбовым в 1947—1949 годах.
И. З. Фишер использовал цепочку уравнений Боголюбова во втором порядке  А. Крокстон писал в 1976 году: «Последние два или три десятилетия физика жидкого состояния … достигла значительных успехов, в основном благодаря пионерским работам советских авторов — главным образом Н. Н. Боголюбова, Я. И. Френкеля и И. З. Фишера».[1]
А. Крокстон писал в 1976 году: «Последние два или три десятилетия физика жидкого состояния … достигла значительных успехов, в основном благодаря пионерским работам советских авторов — главным образом Н. Н. Боголюбова, Я. И. Френкеля и И. З. Фишера».[1]
Напишите отзыв о статье «Физика жидкостей»
Литература
- Боголюбов Н. Н. «Уравнения гидродинамики в статистической механике» (1948) в Боголюбов Н. Н. Избранные труды в трех томах. Том 2. Киев: Наукова думка, 1970. стр.258-276.
- Боголюбов Н. Н. «К теории сверхтекучести» Изв. АН СССР, Сер физ. 1947. Том 11. N.1. 77-90; Боголюбов Н. Н. Избранные труды в трех томах. Том 2. Киев: Наукова думка, 1970. стр.210-224.
- Крокстон К. Физика жидкого состояния. Статистическое введение. пер с англ. М.: Мир, 1978. — 400с.
- Оно С., Кондо С. Молекулярная теория поверхностного натяжения в жидкостях. М.: ИИЛ, 1963. — 292с.
- Фишер И. З. Статистическая теория жидкостей. М.: Наука, 1961.
 — 280с.
— 280с. - Френкель Я. И. Кинетическая теория жидкостей. Изд-во АН СССР, 1945. и Л.: Наука, 1975.
- Пайнс Д., Нозьер Ф., Теория квантовых жидкостей, пер. с англ., М., 1967.
- Резибуа П., Де Ленер М. Классическая кинетическая теория жидкостей и газов. М.: Мир, 1980. — 424с.
- Данилов В. И. Строение и кристаллизация жидкости.Избранные статьи. Под.ред. Курдюмова Г. В. Киев. Изд-во АН УССР, 1956. — 568 с.
- Юльметьев Р. М. Введение в статистическую физику жидкостей. Казань: Изд-во КГПИ, 1972. — 218с.
- Физика простых жидкостей. 1. Статистическая теория. Перевод с англ. под ред. Д. Н. Зубарева и Н. М. Плакиды. М.: Мир, 1971. — 308 с.
- Физика простых жидкостей. 2. Экспериментальные исследования. Перевод с англ. под ред. А. 3. Голика и Ю. И. Шиманского. М.: Мир, 1973. — 400 с.
- Скрипов В. П. Метастабильная жидкость. М.: Наука, 1972. — 312 с
См. также
Примечания
- ↑ 1 2 Крокстон К.
 Физика жидкого состояния. Статистическое введение. пер с англ. М.: Мир, 1978. — 400с.
Физика жидкого состояния. Статистическое введение. пер с англ. М.: Мир, 1978. — 400с.
Отрывок, характеризующий Физика жидкостей
– Боком, закройтесь пистолетом, – проговорил Несвицкий.– 3ак’ойтесь! – не выдержав, крикнул даже Денисов своему противнику.
Пьер с кроткой улыбкой сожаления и раскаяния, беспомощно расставив ноги и руки, прямо своей широкой грудью стоял перед Долоховым и грустно смотрел на него. Денисов, Ростов и Несвицкий зажмурились. В одно и то же время они услыхали выстрел и злой крик Долохова.
– Мимо! – крикнул Долохов и бессильно лег на снег лицом книзу. Пьер схватился за голову и, повернувшись назад, пошел в лес, шагая целиком по снегу и вслух приговаривая непонятные слова:
– Глупо… глупо! Смерть… ложь… – твердил он морщась. Несвицкий остановил его и повез домой.
Ростов с Денисовым повезли раненого Долохова.
Долохов, молча, с закрытыми глазами, лежал в санях и ни слова не отвечал на вопросы, которые ему делали; но, въехав в Москву, он вдруг очнулся и, с трудом приподняв голову, взял за руку сидевшего подле себя Ростова.
 Ростова поразило совершенно изменившееся и неожиданно восторженно нежное выражение лица Долохова.
Ростова поразило совершенно изменившееся и неожиданно восторженно нежное выражение лица Долохова.– Скверно! но не в том дело. Друг мой, – сказал Долохов прерывающимся голосом, – где мы? Мы в Москве, я знаю. Я ничего, но я убил ее, убил… Она не перенесет этого. Она не перенесет…
– Кто? – спросил Ростов.
– Мать моя. Моя мать, мой ангел, мой обожаемый ангел, мать, – и Долохов заплакал, сжимая руку Ростова. Когда он несколько успокоился, он объяснил Ростову, что живет с матерью, что ежели мать увидит его умирающим, она не перенесет этого. Он умолял Ростова ехать к ней и приготовить ее.
Ростов поехал вперед исполнять поручение, и к великому удивлению своему узнал, что Долохов, этот буян, бретёр Долохов жил в Москве с старушкой матерью и горбатой сестрой, и был самый нежный сын и брат.
Пьер в последнее время редко виделся с женою с глазу на глаз. И в Петербурге, и в Москве дом их постоянно бывал полон гостями. В следующую ночь после дуэли, он, как и часто делал, не пошел в спальню, а остался в своем огромном, отцовском кабинете, в том самом, в котором умер граф Безухий.
Он прилег на диван и хотел заснуть, для того чтобы забыть всё, что было с ним, но он не мог этого сделать. Такая буря чувств, мыслей, воспоминаний вдруг поднялась в его душе, что он не только не мог спать, но не мог сидеть на месте и должен был вскочить с дивана и быстрыми шагами ходить по комнате. То ему представлялась она в первое время после женитьбы, с открытыми плечами и усталым, страстным взглядом, и тотчас же рядом с нею представлялось красивое, наглое и твердо насмешливое лицо Долохова, каким оно было на обеде, и то же лицо Долохова, бледное, дрожащее и страдающее, каким оно было, когда он повернулся и упал на снег.
«Что ж было? – спрашивал он сам себя. – Я убил любовника , да, убил любовника своей жены. Да, это было. Отчего? Как я дошел до этого? – Оттого, что ты женился на ней, – отвечал внутренний голос.
 [Я вас люблю.] Всё от этого! Я и тогда чувствовал, думал он, я чувствовал тогда, что это было не то, что я не имел на это права. Так и вышло». Он вспомнил медовый месяц, и покраснел при этом воспоминании. Особенно живо, оскорбительно и постыдно было для него воспоминание о том, как однажды, вскоре после своей женитьбы, он в 12 м часу дня, в шелковом халате пришел из спальни в кабинет, и в кабинете застал главного управляющего, который почтительно поклонился, поглядел на лицо Пьера, на его халат и слегка улыбнулся, как бы выражая этой улыбкой почтительное сочувствие счастию своего принципала.
[Я вас люблю.] Всё от этого! Я и тогда чувствовал, думал он, я чувствовал тогда, что это было не то, что я не имел на это права. Так и вышло». Он вспомнил медовый месяц, и покраснел при этом воспоминании. Особенно живо, оскорбительно и постыдно было для него воспоминание о том, как однажды, вскоре после своей женитьбы, он в 12 м часу дня, в шелковом халате пришел из спальни в кабинет, и в кабинете застал главного управляющего, который почтительно поклонился, поглядел на лицо Пьера, на его халат и слегка улыбнулся, как бы выражая этой улыбкой почтительное сочувствие счастию своего принципала.Презентация на тему «Свойства жидкости» по физике
pptcloud Добавить презентацию Войти- Главная
- Физика
- Свойства жидкости
Категории
- Астрономия
- Биология
- География
- Изобразительное искусство
- Иностранные языки
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Обществознание
- ОБЖ
- Окружающий мир
- Педагогика
- Правоведение
- Праздники
- Психология
- Русский язык
- Социология
- Технология
- Физика
- Термодинамика
- Оптика
- Квантовая
- Теория относительности
- Атомная
- Электродинамика
- Механика
- Ученые
- Физкультура
- Философия
- Химия
- Черчение
- Экономика
- Другое
Физика
- Скачать презентацию (3.
 86 Мб)
86 Мб) - 85 загрузок
- 5.0 оценка
Характеристика жидкого состояние вещества.
Коллоидная химия
Характеристика жидкого состояние вещества.
Жидкость – промежуточное состояние между твёрдым телом и газом.
Жидкое состояние является промежуточным между газообразным и кристаллическим. По одним свойствам жидкости близки к газам, по другим – к твёрдым телам.С газами жидкости сближает, прежде всего, их изотропность и текучесть. Последняя обуславливает способность жидкости легко изменять свою форму.
Однако высокая плотность и малая сжимаемость жидкостей приближает их к твёрдым телам.
Жидкость может обнаруживать механические свойства, присущие твёрдому телу. Если время действия силы на жидкость мало, то жидкость проявляет упругие свойства. Например, при резком ударе палкой о поверхность воды палка может вылететь из руки или сломаться.
Камень можно бросить так, что он при ударе о поверхность воды отскакивает от неё, и лишь совершив несколько скачков, тонет в воде.
Если же время воздействия на жидкость велико, то вместо упругости проявляется текучесть жидкости. Например, рука легко проникает внутрь воды.
Способность жидкостей легко изменять свою форму говорит об отсутствии в них жёстких сил межмолекулярного взаимодействия.
В то же время низкая сжимаемость жидкостей, обусловливающая способность сохранять постоянный при данной температуре объём, указывает на присутствие хотя и не жёстких, но всё же значительных сил взаимодействия между частицами.
Соотношение потенциальной и кинетической энергии
Для каждого агрегатного состояния характерно своё соотношение между потенциальной и кинетической энергиями частиц вещества.
У твёрдых тел средняя потенциальная энергия частиц больше их средней кинетической энергии. Поэтому в твёрдых телах частицы занимают определённые положения друг относительно друга и лишь колеблются относительно этих положений.
Для газов соотношение энергий обратное, вследствии чего молекулы газов всегда находятся в состоянии хаотического движения и силы сцепления между молекулами практически отсутствуют, так что газ всегда занимает весь предоставленный ему объём.
В случае жидкостей кинетическая и потенциальная энергия частиц приблизительно одинаковы, т.е. частицы связаны друг с другом, но не жёстко. Поэтому жидкости текучи, но имеют постоянный при данной температуре объём.
Взаимодействие частиц, образующих жидкость
Расстояния между молекулами жидкости меньше радиуса молекулярного действия.
Если вокруг молекулы жидкости описать сферу молекулярного действия, то внутри этой сферы окажутся центры многих других молекул, которые будут взаимодействовать с нашей молекулой. Эти силы взаимодействия удерживают молекулу жидкости около её временного положения равновесия примерно в течение 10-12 – 10-10 с, после чего она перескакивает в новое временное положение равновесия приблизительно на расстояние своего диаметра.
Молекулы жидкости между перескоками совершают колебательное движение около временного положения равновесия.
Время между двумя перескоками молекулы из одного положения в другое называется временем оседлой жизни. Это время зависит от вида жидкости и температуры. При нагревании жидкости среднее время оседлой жизни молекул уменьшается.
В течение времени оседлой жизни (порядка 10-11 с) большинство молекул жидкости удерживается в своих положениях равновесия, и лишь небольшая часть их успевает за это время перейти в новое положение равновесия.
За более длительное время уже большинство молекул жидкости успеет переменить своё местоположение.
Так как молекулы жидкости расположены почти вплотную друг к другу, то получив достаточно большую кинетическую энергию, они хотя и могут преодолеть притяжение своих ближайших соседей и выйти из сферы их действия, но попадут в сферу действия других молекул и окажутся в новом временном положении равновесия.
Лишь находящиеся на свободной поверхности жидкости молекулы могут вылететь за пределы жидкости, чем и объясняется процесс её испарения.
Если в жидкости выделить очень малый объём, то в течение времени оседлой жизни в нём существует упорядоченное расположение молекул, подобное их расположению в кристаллической решётке твёрдого тела. Затем оно распадается, но возникает в другом месте. Таким образом, всё пространство, занятое жидкостью, как бы состоит из множества зародышей кристаллов, которые, однако, не устойчивы, т.е. распадаются в одних местах, но снова возникают в других.
Стуктуры жидкостей и аморфных тел схожи
В результате применения к жидкостям методов структурного анализа установлено, что по структуре жидкости подобны аморфным телам. В большинстве жидкостей наблюдается ближний порядок – число ближайших соседей у каждой молекулы и их взаимное расположение приблизительно одинаковы во всём объёме жидкости.
Степень упорядоченности частиц у различных жидкостей различна. Кроме того, она изменяется при изменении температуры.
При низких температурах, незначительно превышающих температуру плавления данного вещества, степень упорядоченности расположения частиц данной жидкости велика.
С ростом температуры она падает и по мере нагревания свойства жидкости всё больше и больше приближаются к свойствам газа. При достижении критической температуры различие между жидкостью и газом исчезает.
Вследствии сходства во внутренней структуре жидкостей и аморфных тел последние часто рассматриваются как жидкости с очень высокой вязкостью, а к твёрдым телам относят только вещества в кристаллическом состоянии.
Уподобляя аморфные тела жидкостям, следует, однако, помнить, что в аморфных телах в отличие от обычных жидкостей частицы имеют незначительную подвижность – такую же как в кристалах.
Физика (7 класс)/Давление — Викиверситет
Давление. Единицы давления.
Человек на лыжах, и без них.По рыхлому снегу человек идёт с большим трудом, глубоко проваливаясь при каждом шаге. Но, надев лыжи, он может идти, почти не проваливаясь в него. Почему? На лыжах или без лыж человек действует на снег с одной и той же силой, равной своему весу. Однако действие этой силы в обоих случаях различно, потому что различна площадь поверхности, на которую давит человек, с лыжами и без лыж. Площадь поверхности лыж почти в 20 раз больше площади подошвы. Поэтому, стоя на лыжах, человек действует на каждый квадратный сантиметр площади поверхности снега с силой, в 20 раз меньшей, чем стоя на снегу без лыж.
Ученик, прикалывая кнопками газету к доске, действует на каждую кнопку с одинаковой силой. Однако кнопка, имеющая более острый конец, легче входит в дерево.
Значит, результат действия силы зависит не только от её модуля, направления и точки приложения, но и от площади той поверхности, к которой она приложена (перпендикулярно которой она действует).
Этот вывод подтверждают физические опыты.
Опыт.Результат действия данной силы зависит от того, какая сила действует на единицу площади поверхности.По углам небольшой доски надо вбить гвозди. Сначала гвозди, вбитые в доску, установим на песке остриями вверх и положим на доску гирю. В этом случае шляпки гвоздей лишь незначительно вдавливаются в песок. Затем доску перевернем и поставим гвозди на острие. В этом случае площадь опоры меньше, и под действием той же силы гвозди значительно углубляются в песок.
Опыт. Вторая иллюстрация.От того, какая сила действует на каждую единицу площади поверхности, зависит результат действия этой силы.
В рассмотренных примерах силы действовали перпендикулярно поверхности тела. Вес человека был перпендикулярен поверхности снега; сила, действовавшая на кнопку, перпендикулярна поверхности доски.
Величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности, называется давлением.
Чтобы определить давление, надо силу, действующую перпендикулярно поверхности, разделить на площадь поверхности:
давление = сила / площадь.
Обозначим величины, входящие в это выражение: давление — p, сила, действующая на поверхность, — F и площадь поверхности — S.
Тогда получим формулу:
p = F/S
Понятно, что бóльшая по значению сила, действующую на ту же площадь, будет производить большее давление.
За единицу давления принимается такое давление, которое производит сила в 1 Н, действующая на поверхность площадью 1 м2 перпендикулярно этой поверхности.
Единица давления — ньютон на квадратный метр ( 1 Н / м2 ). В честь французского ученого Блеза Паскаля она называется паскалем (Па). Таким образом,
1 Па = 1 Н / м2.
Используется также другие единицы давления: гектопаскаль (гПа) и килопаскаль (кПа).
1 кПа = 1000 Па;
1 гПа = 100 Па;
1 Па = 0,001 кПа;
1 Па = 0,01 гПа.
Пример. Рассчитать давление, производимое на пол мальчиком, масса которого 45 кг, а площадь подошв его ботинок, соприкасающихся с полом, равна 300 см2.
Запишем условие задачи и решим её.
Дано: m = 45 кг, S = 300 см2; p = ?
В единицах СИ: S = 0,03 м2
Решение:
p = F/S,
F = P,
P = g·m,
P = 9,8 Н · 45 кг ≈ 450 Н,
p = 450/0,03 Н / м2 = 15000 Па = 15 кПа
‘Ответ’: p = 15000 Па = 15 кПа
Способы уменьшения и увеличения давления.
Тяжелый гусеничный трактор производит на почву давление равное 40 — 50 кПа, т. е. всего в 2 — 3 раза больше, чем давление мальчика массой 45 кг. Это объясняется тем, что вес трактора распределяется на бóльшую площадь за счёт гусеничной передачи. А мы установили, что чем больше площадь опоры, тем меньше давление, производимое одной и той же силой на эту опору.
В зависимости от того, нужно ли получить малое или большое давление, площадь опоры увеличивается или уменьшается. Например, для того, чтобы грунт мог выдержать давление возводимого здания, увеличивают площадь нижней части фундамента.
Шины грузовых автомобилей и шасси самолетов делают значительно шире, чем легковых. Особенно широкими делают шины у автомобилей, предназначенных для передвижения в пустынях.
Тяжелые машины, как трактор, танк или болотоход, имея большую опорную площадь гусениц, проходят по болотистой местности, по которой не пройдет человек.
С другой стороны, при малой площади поверхности можно небольшой силой произвести большое давление. Например, вдавливая кнопку в доску, мы действуем на нее с силой около 50 Н. Так как площадь острия кнопки примерно 1 мм2, то давление, производимое ею, равно:
p = 50 Н/ 0, 000 001 м2 = 50 000 000 Па = 50 000 кПа.
Для сравнения, это давление в 1000 раз больше давления, производимого гусеничным трактором на почву. Можно найти еще много таких примеров.
Лезвие режущих и острие колющих инструментов (ножей, ножниц, резцов, пил, игл и др.) специально остро оттачивается. Заточенный край острого лезвия имеет маленькую площадь, поэтому при помощи даже малой силы создается большое давление, и таким инструментом легко работать.
Режущие и колющие приспособления встречаются и в живой природе: это зубы, когти, клювы, шипы и др. — все они из твердого материала, гладкие и очень острые.
Давление
Известно, что молекулы газа беспорядочно движутся. Опыт. Здесь мы узнаем, что газ давит на стенки сосуда по всем направлениям одинаково.Мы уже знаем, что газы, в отличие от твердых тел и жидкостей, заполняют весь сосуд, в котором находятся. Например, стальной баллон для хранения газов, камера автомобильной шины или волейбольный мяч. При этом газ оказывает давление на стенки, дно и крышку баллона, камеры или любого другого тела, в котором он находится. Давление газа обусловлено иными причинами, чем давление твердого тела на опору.
Известно, что молекулы газа беспорядочно движутся. При своем движении они сталкиваются друг с другом, а также со стенками сосуда, в котором находится газ. Молекул в газе много, поэтому и число их ударов очень велико. Например, число ударов молекул воздуха, находящегося в комнате, о поверхность площадью 1 см2 за 1 с выражается двадцатитрехзначным числом. Хотя сила удара отдельной молекулы мала, но действие всех молекул на стенки сосуда значительно, — оно и создает давление газа.
Итак, давление газа на стенки сосуда (и на помещенное в газ тело) вызывается ударами молекул газа.
Рассмотрим следующий опыт. Под колокол воздушного насоса поместим резиновый шарик. Он содержит небольшое количество воздуха и имеет неправильную форму. Затем насосом откачиваем воздух из-под колокола. Оболочка шарика, вокруг которой воздух становится все более разреженным, постепенно раздувается и принимает форму правильного шара.
Как объяснить этот опыт?
Для хранения и перевозки сжатого газа используются специальные прочные стальные баллоны.В нашем опыте движущиеся молекулы газа непрерывно ударяют о стенки шарика внутри и снаружи. При откачивании воздуха число молекул в колоколе вокруг оболочки шарика уменьшается. Но внутри шарика их число не изменяется. Поэтому число ударов молекул о внешние стенки оболочки становится меньше, чем число ударов о внутренние стенки. Шарик раздувается до тех пор, пока сила упругости его резиновой оболочки не станет равной силе давления газа. Оболочка шарика принимает форму шара. Это показывает, что газ давит на ее стенки по всем направлениям одинаково. Иначе говоря, число ударов молекул, приходящихся на каждый квадратный сантиметр площади поверхности, по всем направлениям одинаково. Одинаковое давление по всем направлениям характерно для газа и является следствием беспорядочного движения огромного числа молекул.
Попытаемся уменьшить объем газа, но так, чтобы масса его осталась неизменной. Это значит, что в каждом кубическом сантиметре газа молекул станет больше, плотность газа увеличится. Тогда число ударов молекул о стенки увеличится, т. е. возрастет давление газа. Это можно подтвердить опытом.
На рисунке а изображена стеклянная трубка, один конец которой закрыт тонкой резиновой пленкой. В трубку вставлен поршень. При вдвигании поршня объем воздуха в трубке уменьшается, т. е. газ сжимается. Резиновая пленка при этом выгибается наружу, указывая на то, что давление воздуха в трубке увеличилось.
Наоборот, при увеличении объема этой же массы газа, число молекул в каждом кубическом сантиметре уменьшается. От этого уменьшится число ударов о стенки сосуда — давление газа станет меньше. Действительно, при вытягивании поршня из трубки объем воздуха увеличивается, пленка прогибается внутрь сосуда. Это указывает на уменьшение давления воздуха в трубке. Такие же явления наблюдались бы, если бы вместо воздуха в трубке находился бы любой другой газ.
Итак, при уменьшении объема газа его давление увеличивается, а при увеличении объема давление уменьшается при условии, что масса и температура газа остаются неизменными.
А как изменится давление газа, если нагреть его при постоянном объеме? Известно, что скорость движения молекул газа при нагревании увеличивается. Двигаясь быстрее, молекулы будут ударять о стенки сосуда чаще. Кроме того, каждый удар молекулы о стенку будет сильнее. Вследствие этого, стенки сосуда будут испытывать большее давление.
Следовательно, давление газа в закрытом сосуде тем больше, чем выше температура газа, при условии, что масса газа и объем не изменяются.
Из этих опытов можно сделать общий вывод, что давление газа тем больше, чем чаще и сильнее молекулы ударяют о стенки сосуда.
Для хранения и перевозки газов их сильно сжимают. При этом давление их возрастает, газы необходимо заключать в специальные, очень прочные баллоны. В таких баллонах, например, содержат сжатый воздух в подводных лодках, кислород, используемый при сварке металлов. Конечно же, мы должны навсегда запомнить, что газовые баллоны нельзя нагревать, тем более, когда они заполнены газом. Потому что, как мы уже понимаем, может произойти взрыв с очень неприятными последствиями.
Закон Паскаля.
Давление передается в каждую точку жидкости или газа. Давление поршня передается в каждую точку жидкости, заполняющей шар.В отличие от твердых тел отдельные слои и мелкие частицы жидкости и газа могут свободно перемещаться относительно друг друга по всем направлениям. Достаточно, например, слегка подуть на поверхность воды в стакане, чтобы вызвать движение воды. На реке или озере при малейшем ветерке появляется рябь.
Подвижностью частиц газа и жидкости объясняется, что давление, производимое на них, передается не только в направлении действия силы, а в каждую точку. Рассмотрим это явление подробнее.
На рисунке, а изображен сосуд, в котором содержится газ (или жидкость). Частицы равномерно распределены по всему сосуду. Сосуд закрыт поршнем, который может перемещаться вверх и вниз.
Прилагая некоторую силу, заставим поршень немного переместиться внутрь и сжать газ (жидкость), находящийся непосредственно под ним. Тогда частицы (молекулы) расположатся в этом месте более плотно, чем прежде(рис, б). Благодаря подвижности частицы газа будут перемещаться по всем направлениям. Вследствие этого их расположение опять станет равномерным, но более плотным, чем раньше (рис, в). Поэтому давление газа всюду возрастет. Значит, добавочное давление передается всем частицам газа или жидкости. Так, если давление на газ (жидкость) около самого поршня увеличится на 1 Па, то во всех точках внутри газа или жидкости давление станет больше прежнего на столько же. На 1 Па увеличится давление и на стенки сосуда, и на дно, и на поршень.
Давление, производимое на жидкость или газ, передается на любую точку одинаково во всех направлениях.
Это утверждение называется законом Паскаля.
На основе закона Паскаля легко объяснить следующие опыты.
На рисунке изображен полый шар, имеющий в различных местах небольшие отверстия. К шару присоединена трубка, в которую вставлен поршень. Если набрать воды в шар и вдвинуть в трубку поршень, то вода польется из всех отверстий шара. В этом опыте поршень давит на поверхность воды в трубке. Частицы воды, находящиеся под поршнем, уплотняясь, передают его давление другим слоям, лежащим глубже. Таким образом, давление поршня передается в каждую точку жидкости, заполняющей шар. В результате часть воды выталкивается из шара в виде одинаковых струек, вытекающих из всех отверстий.
Если шар заполнить дымом, то при вдвигании поршня в трубку из всех отверстий шара начнут выходить одинаковые струйки дыма. Это подтверждает, что и газы передают производимое на них давление во все стороны одинаково.
Давление в жидкости и газе.
Под действием веса жидкости резиновое дно в трубке прогнется.На жидкости, как и на все тела на Земле, действует сила тяжести. Поэтому, каждый слой жидкости, налитой в сосуд, своим весом создает давление, которое по закону Паскаля передается по всем направлениям. Следовательно, внутри жидкости существует давление. В этом можно убедиться на опыте.
В стеклянную трубку, нижнее отверстие которой закрыто тонкой резиновой пленкой, нальем воду. Под действием веса жидкости дно трубки прогнется.
Опыт показывает, что, чем выше столб воды над резиновой пленкой, тем больше она прогибается. Но всякий раз после того, как резиновое дно прогнулось, вода в трубке приходит в равновесие (останавливается), так как, кроме силы тяжести, на воду действует сила упругости растянутой резиновой пленки.
| По мере опускания трубки | резиновая пленка постепенно выпрямляется. | Силы, действующие на резиновую пленку, | одинаковы с обеих сторон. |
Опустим трубку с резиновым дном, в которую налита вода, в другой, более широкий сосуд с водой. Мы увидим, что по мере опускания трубки резиновая пленка постепенно выпрямляется. Полное выпрямление пленки показывает, что силы, действующие на нее сверху и снизу, равны. Наступает полное выпрямление пленки тогда, когда уровни воды в трубке и сосуде совпадают.
Такой же опыт можно провести с трубкой, в которой резиновая пленка закрывает боковое отверстие, как это показано на рисунке, а. Погрузим эту трубку с водой в другой сосуд с водой, как это изображено на рисунке, б. Мы заметим, что пленка снова выпрямится, как только уровни воды в трубке и сосуде сравняются. Это означает, что силы, действующие на резиновую пленку, одинаковы со всех сторон.
Возьмем сосуд, дно которого может отпадать. Опустим его в банку с водой. Дно при этом окажется плотно прижатым к краю сосуда и не отпадет. Его прижимает сила давления воды, направленная снизу вверх.
Будем осторожно наливать воду в сосуд и следить за его дном. Как только уровень воды в сосуде совпадет с уровнем воды в банке, оно отпадет от сосуда.
В момент отрыва на дно давит сверху вниз столб жидкости в сосуде, а снизу вверх на дно передается давление такого же по высоте столба жидкости, но находящейся в банке. Оба эти давления одинаковы, дно же отходит от цилиндра вследствие действия на него собственной силы тяжести.
Выше были описаны опыты с водой, но если взять вместо воды любую другую жидкость, результаты опыта будут те же.
Итак, опыты показывают, что внутри жидкости существует давление, и на одном и том же уровне оно одинаково по всем направлениям. С глубиной давление увеличивается.
Газы в этом отношении не отличаются от жидкостей, ведь они тоже имеют вес. Но надо помнить, что плотность газа в сотни раз меньше плотности жидкости. Вес газа, находящегося в сосуде, мал, и его «весовое» давление во многих случаях можно не учитывать.
Расчет давления жидкости на дно и стенки сосуда.
Расчет давления жидкости на дно и стенки сосуда.Рассмотрим, как можно рассчитывать давление жидкости на дно и стенки сосуда. Решим сначала задачу для сосуда, имеющего форму прямоугольного параллелепипеда.
Сила F, с которой жидкость, налитая в этот сосуд, давит на его дно, равна весу P жидкости, находящейся в сосуде. Вес жидкости можно определить, зная ее массу m. Массу, как известно, можно вычислить по формуле: m = ρ·V. Объем жидкости, налитой в выбранный нами сосуд, легко рассчитать. Если высоту столба жидкости, находящейся в сосуде, обозначить буквой h, а площадь дна сосуда S, то V = S·h.
Масса жидкости m = ρ·V, или m = ρ·S·h .
Вес этой жидкости P = g·m, или P = g·ρ·S·h.
Так как вес столба жидкости равен силе, с которой жидкость давит на дно сосуда, то, разделив вес P на площадь S, получим давление жидкости p:
p = P/S , или p = g·ρ·S·h/S,
то есть
p = g·ρ·h.
Мы получили формулу для расчета давления жидкости на дно сосуда. Из этой формулы видно, что давление жидкости на дно сосуда зависит только от плотности и высоты столба жидкости.
Следовательно, по выведенной формуле можно рассчитывать давление жидкости, налитой в сосуд любой формы (строго говоря, наш расчет годится только для сосудов, имеющих форму прямой призмы и цилиндра. В курсах физики для института доказано, что формула верна и для сосуда произвольной формы). Кроме того, по ней можно вычислить и давление на стенки сосуда. Давление внутри жидкости, в том числе давление снизу вверх, также рассчитывается по этой формуле, так как давление на одной и той же глубине одинаково по всем направлениям.
При расчете давления по формуле p = gρh надо плотность ρ выражать в килограммах на кубический метр (кг/м3), а высоту столба жидкости h — в метрах (м), g = 9,8 Н/кг, тогда давление будет выражено в паскалях (Па).
Пример. Определите давление нефти на дно цистерны, если высота столба нефти 10 м, а плотность ее 800 кг/м3 .
Запишем условие задачи и запишем ее.
Дано:
h = 10 м
ρ = 800 кг/м3
P = ?
Решение:
p = gρh,
p = 9.8 Н/кг · 800 кг/м3 · 10 м ≈ 80 000 Па ≈ 80 кПа.
Ответ: p ≈ 80 кПа.
Сообщающиеся сосуды.
Сообщающиеся сосуды.На рисунке изображены два сосуда, соединённые между собой резиновой трубкой. Такие сосуды называются сообщающимися. Лейка, чайник, кофейник — примеры сообщающихся сосудов. Из опыта мы знаем, что вода, налитая, например, в лейку, стоит всегда на одном уровне в носике и внутри.
| Сообщающиеся сосуды встречаются нам часто. Например, им может быть чайник, лейка или кофейник. | Поверхности однородной жидкости устанавливаются на одном уровне в сообщающихся сосудах любой формы. | Разные по плотности жидкости. |
С сообщающимися сосудами можно проделать следующий простой опыт. В начале опыта резиновую трубку зажимаем в середине, и в одну из трубок наливаем воду. Затем зажим открываем, и вода вмиг перетекает в другую трубку, пока поверхности воды в обеих трубках не установятся на одном уровне. Можно закрепить одну из трубок в штативе, а другую поднимать, опускать или наклонять в разные стороны. И в этом случае, как только жидкость успокоится, ее уровни в обеих трубках уравняются.
В сообщающихся сосудах любой формы и сечения поверхности однородной жидкости устанавливаются на одном уровне (при условии, что давление воздуха над жидкостью одинаково) (рис. 109).
Это можно обосновать следующим образом. Жидкость покоится, не перемещаясь из одного сосуда в другой. Значит, давления в обоих сосудах на любом уровне одинаковы. Жидкость в обоих сосудах одна и та же, т. е. имеет одинаковую плотность. Следовательно, должны быть одинаковы и ее высоты. Когда мы поднимаем один сосуд или доливаем в него жидкость, давление в нем увеличивается и жидкость перемещается в другой сосуд до тех пор, пока давления не уравновесятся.
Если в один из сообщающихся сосудов налить жидкость одной плотности, а во второй — другой плотности, то при равновесии уровни этих жидкостей не будут одинаковыми. И это понятно. Мы ведь знаем, что давление жидкости на дно сосуда прямо пропорционально высоте столба и плотности жидкости. А в этом случае плотности жидкостей будут различны.
При равенстве давлений высота столба жидкости с большей плотностью будет меньше высоты столба жидкости с меньшей плотностью (рис.).
Опыт. Как определить массу воздуха.Вес воздуха. Атмосферное давление.
Существование атмосферного давления. Атмосферное давление больше, чем давление разреженного воздуха в сосуде.На воздух, как и на всякое тело, находящееся на Земле, действует сила тяжести, и, значит, воздух обладает весом. Вес воздуха легко вычислить, зная его массу.
На опыте покажем, как вычислить массу воздуха. Для этого нужно взять прочный стеклянный шар с пробкой и резиновой трубкой с зажимом. Выкачаем из него насосом воздух, зажмем трубку зажимом и уравновесим на весах. Затем, открыв зажим на резиновой трубке, впустим в него воздух. Равновесие весов при этом нарушится. Для его восстановления на другую чашку весов придется положить гири, масса которых будет равна массе воздуха в объеме шара.
Опытами установлено, что при температуре 0 °С и нормальном атмосферном давлении масса воздуха объемом 1 м3 равна 1,29 кг. Вес этого воздуха легко вычислить:
P = g·m, P = 9,8 Н/кг · 1,29 кг ≈ 13 Н.
Воздушная оболочка, окружающая Землю, называется атмосфера (от греч. атмос — пар, воздух, и сфера — шар)
Давление жидкости, Рон Куртус
SfC На главную> Физика> Материя> Жидкости>
, Рон Куртус (редакция 8 мая 2017 г.)
Давление жидкости — это измерение силы на единицу площади объекта в жидкости или на поверхности закрытого контейнера. Это давление может быть вызвано силой тяжести, ускорением или силами вне закрытого контейнера.
Поскольку жидкость не имеет определенной формы, ее давление распространяется во всех направлениях.Давление жидкости также может быть увеличено за счет гидравлических механизмов и изменений скорости жидкости.
Вопросы, которые могут у вас возникнуть:
- Как гравитация вызывает давление жидкости?
- Как давление воздуха и воды распространяется во всех направлениях?
- Какие еще области применения давления жидкости?
Этот урок ответит на эти вопросы. Полезный инструмент: Конвертация единиц
Давление жидкости под действием силы тяжести или ускорения
Вес жидкости может оказывать давление на все, что находится под ней.Кроме того, относительное движение жидкости или газа может оказывать давление.
Давление
Давление определяется как сила, деленная на площадь, на которую действует сила. ( Подробности см. В уроке «Давление». ) Вы можете записать это в виде уравнения, если хотите произвести некоторые вычисления:
P = F / A
где
- P = давление
- F = сила
- A = площадь
- F / A = F разделить на A
Давление под действием силы тяжести
Поскольку вес предмета или материала равен силе, которую они испытывают под действием силы тяжести,
Объект может оказывать давление вниз из-за своего веса и силы тяжести.Давление, которое вы оказываете на пол, — это ваш вес, разделенный на площадь подошвы вашей обуви. Если сила обусловлена весом ( W ) объекта, тогда уравнение будет следующим: P = W / A
Давление воды
Давление воды на дне озера равно весу водяного столба над ним, деленному на площадь этого столба.
Давление на глубине Вес / Площадь
Колонна верхняя
Если бы вы стояли на дне бассейна (при условии, что вы не начали плавать), то на вас был бы столб воды диаметром с вашу голову, поднимающийся до поверхности воды.Если вы возьмете этот столб воды и взвесите его, а затем разделите этот вес на площадь макушки, вы получите значение давления воды на вашу голову.
Причина, по которой это не влияет на вас, заключается в том, что ваше внутреннее давление тела увеличивается, чтобы нейтрализовать большую часть давления воды. Но на большей глубине давление воды может стать настолько большим, что может навредить дайверу.
Демонстрация с банкой
Демонстрация того, как давление воды увеличивается с увеличением глубины воды, может быть проведена с помощью большой консервной банки.Проделайте отверстия для гвоздей по вертикальной линии вверх по стенке банки через каждые дюймы или несколько сантиметров. Затем наполните банку водой. Вода может просто капать через верхние отверстия, но повышенное давление с глубиной заставляет воду брызгать с большим давлением в нижние отверстия.
Давление воздуха
Точно так же давление воздуха на макушку вашей головы — это вес столба воздуха (высотой несколько миль), деленный на площадь макушки вашей головы. Среднее давление воздуха на вашу голову — 14.7 фунтов на квадратный дюйм! Это большой вес, который вы держите.
Атмосферное давление при погодных условиях
Когда в сводке погоды указывается высокое давление, это означает, что столб воздуха поднимается выше, чем для считывателя низкого давления. Барометр измеряет давление воздуха или вес столба воздуха.
Давление воздуха возникает из-за веса всего воздуха, поднимающегося над вами на несколько миль. Это примерно 16 фунтов на квадратный дюйм во всех направлениях вашего тела.К счастью, в наших телах есть внутреннее давление, которое уравнивает давление воздуха.
Воздушные шары
Давление воздуха внутри воздушного шара толкает наружу во всех направлениях. Когда давление увеличивается, размер воздушного шара увеличивается, пока он наконец не лопнет. Внутреннее давление воздуха намного больше, чем внешнее давление.
Различная высота
Нормальное давление воздуха в Денвере, штат Колорадо, ниже, чем в городе. Это связано с тем, что большая высота Денвера означает, что его столб воздуха не такой высокий, как в Милуоки.
Поскольку многие закуски запечатаны в пакеты под давлением, пакет, запечатанный в Милуоки, требует более высокого внутреннего давления, чем пакет, сделанный в Денвере. Таким образом, пакет с закусками Milwaukee расширяется при более низком давлении воздуха, чем в Денвере, и может даже взорваться.
Направление давления жидкости
Что же касается давления, создаваемого жидкостью или газом, то это не только давление, которое толкает вниз в данной точке, но также такое же давление, толкающее вверх и в стороны.
Все направления
Давление в жидкости одинаково во всех направлениях в данной точке. Это верно, поскольку жидкости и газы имеют свойство принимать форму своего сосуда.
Давление воды одинаково во всех направлениях
Это также означает, что любой полый контейнер, погруженный в жидкость, оказывает давление на каждый квадратный дюйм своей поверхности, сверху и снизу.
Плавание под водой
Когда вы плаваете под водой, давление воды на ваше тело тем выше, чем глубже вы погружаетесь.Теперь вопрос: «Почему ты не раздавлен всем этим весом?»
Причина в том, что ваше тело компенсирует это, создавая внутреннее давление, равное давлению воздуха или воды. Вы чем-то похожи на воздушный шар, наполненный жидкостью под давлением. Теперь, когда вы погружаетесь очень глубоко под воду, давление воды может стать больше, чем ваше тело может компенсировать, и вы почувствуете дискомфорт.
Прочие воздействия давления
Другими эффектами давления жидкости являются движение, нагрев и химические эффекты, а также приложения в области гидравлики и в самолетах.
( Подробнее см. «Применение принципов жидкости». )
Ветер и течение
Движение жидкости, такое как ветер или течение реки, может оказывать на объект давление, пропорциональное площади поверхности, перпендикулярной направлению движения.
Обтекаемость объекта снижает это давление.
Нагревание и химическое воздействие
Когда вы нагреваете жидкость, она обычно расширяется.Если вы нагреете жидкость, которая находится в закрытом контейнере, расширение приведет к увеличению внутреннего давления. Например, при нагревании воздушного шара он расширяется.
Подобным образом химические реакции с выделением газов увеличивают давление внутри контейнера. Например, встряхивание бутылки с газированным напитком выделяет больше газа и приводит к увеличению внутреннего давления. Это может произойти, когда вы открываете бутылку, и напиток весь брызжет.
Гидравлика
Когда жидкость — особенно жидкость — находится в частично закрытом контейнере, сила, приложенная в одной области, может привести к большей силе в другой области.Этот эффект используется в гидравлике для создания механического преимущества за счет приложения силы к маленькому поршню, в результате чего большее усилие применяется к большому поршню.
Самолет
Ученый Бернулли обнаружил, что давление воздуха в трубке падает, когда скорость воздуха в трубке увеличивается. Это открытие стало известно как Принцип Бернулли .
Наибольшее применение этот принцип используется в самолетах. Крыло самолета обычно изогнутое вверху и плоское внизу.Когда воздух движется над изогнутой верхней частью крыла, он ускоряется из-за формы. Это снижает давление по отношению к нижней части крыла. Более низкое давление на верхнюю часть приводит к подъемной силе, необходимой для удержания самолета в воздухе.
Сводка
Давление жидкости под действием силы тяжести — это вес жидкости выше, деленный на площадь, на которую она воздействует. Давление жидкости действует во всех направлениях. Внутреннее давление объекта равно внешнему давлению жидкости, иначе объект может быть раздавлен.Ветер и отопление также могут создавать давление.
Уметь работать под давлением
Ресурсы и ссылки
Полномочия Рона Куртуса
Сайты
Материальные ресурсы
Физические ресурсы
Книги
Книги с самым высоким рейтингом по вопросам
Книги по физике с самым высоким рейтингом
Книги по физике жидкостей с самым высоким рейтингом
Механика жидкости Иры М.Коэн и Пижуш К. Кунду, Academic Press (2004) $ 74,95
Векторы, тензоры и основные уравнения механики жидкости Резерфорд Арис, Dover Publications (1990) $ 14,95
Основы механики жидкости Брюс Р. Мансон, Дональд Ф. Янг, Теодор Х. Окииси; Wiley (2001) $ 37,95
Вопросы и комментарии
Есть ли у вас какие-либо вопросы, комментарии или мнения по этой теме? Если это так, отправьте свой отзыв по электронной почте.Я постараюсь вернуться к вам как можно скорее.
Поделиться страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/science/
fluid_pressure.htm
Пожалуйста, включите это как ссылку на свой веб-сайт или как ссылку в своем отчете, документе или диссертации.
Авторские права © Ограничения
Где ты сейчас?
Школа чемпионов
Физические темы
Давление жидкости
Medical Xpress — Физика жидкостей
Physics of Fluids — ежемесячный рецензируемый научный журнал по гидродинамике, который издается Американским институтом физики в сотрудничестве с Отделом гидродинамики Американского физического общества с 1958 года.Основное внимание в журнале уделяется динамике флюидов — газов, жидкостей и многофазных потоков — и журнал содержит оригинальные исследования, полученные в результате теоретических, расчетных и экспериментальных исследований. До 1988 года журнал освещал физику жидкости и плазмы. С 1989 по 1993 год журнал был разделен на два отдельных журнала: Physics of Fluids A охватывала гидродинамику, а Physics of Fluids B — физику плазмы. В 1994 году журнал Physics of Plasmas был отделен, а журнал гидродинамики продолжил свое существование под своим первоначальным названием Physics of Fluids.С 1985 года Physics of Fluids представляет Галерею движения жидкости, содержащую отмеченные наградами фотографии, изображения и визуальные потоковые медиа потока жидкости, полученные в результате экспериментов и вычислений. Ежегодная премия Франсуа Нафтали Френкиля была учреждена Американским физическим обществом в 1984 году и награждает молодого ученого, опубликовавшего статью, содержащую значительный вклад в гидродинамику, в этом номере
.- Издатель
- Американский институт физики
- Страна
- США
- История
- 1958-настоящее время
- Сайт
- http: // pof.aip.org/
- Импакт-фактор
- 1,722 (2010)
Некоторый контент из Википедии, под лицензией CC BY-SA
физика жидкостей Wikipedia
Раздел физики, связанный с механикой жидкостей (жидкостей, газов и плазмы) и действующих на них сил; раздел механики сплошных сред
Механика жидкостей — это раздел физики, связанный с механикой жидкостей (жидкостей, газов и плазмы) и действующих на них сил. [1] : 3 Он имеет приложения в широком спектре дисциплин, включая механическую, гражданскую, химическую и биомедицинскую инженерию, геофизику, океанографию, метеорологию, астрофизику и биологию.
Его можно разделить на статику жидкости, исследование жидкости в состоянии покоя; и гидродинамика, изучение влияния сил на движение жидкости. [1] : 3 Это раздел механики сплошной среды, предмет, который моделирует материю без использования информации о том, что она состоит из атомов; то есть он моделирует материю с точки зрения макроскопического , а не с микроскопического .Гидромеханика, особенно гидродинамика, является активной областью исследований, как правило, математически сложной. Многие проблемы частично или полностью не решены, и их лучше всего решать численными методами, обычно с использованием компьютеров. Этому подходу посвящена современная дисциплина, называемая вычислительной гидродинамикой (CFD). [2] Велосиметрия изображения частиц, экспериментальный метод для визуализации и анализа потока жидкости, также использует преимущества очень визуальной природы потока жидкости.
Краткая история []
Изучение механики жидкостей восходит, по крайней мере, к временам Древней Греции, когда Архимед исследовал статику жидкости и плавучесть и сформулировал свой знаменитый закон, известный теперь как принцип Архимеда, который был опубликован в его работе О плавающих телах — в целом. считается первой крупной работой по механике жидкости.Быстрый прогресс в механике жидкостей начался с Леонардо да Винчи (наблюдения и эксперименты), Евангелисты Торричелли (изобрел барометр), Исаака Ньютона (исследовал вязкость) и Блеза Паскаля (исследовал гидростатику, сформулировал закон Паскаля), и был продолжен Даниэлем Бернулли с введение математической гидродинамики в Hydrodynamica (1739).
Невязкий поток был дополнительно проанализирован различными математиками (Жан ле Ронд д’Аламбер, Жозеф Луи Лагранж, Пьер-Симон Лаплас, Симеон Дени Пуассон), а вязкое течение было исследовано множеством инженеров, включая Жана Леонара Мари Пуазейля и Готхильфа Хагена.Дальнейшее математическое обоснование было предоставлено Клодом-Луи Навье и Джорджем Габриэлем Стоксом в уравнениях Навье-Стокса, и были исследованы пограничные слои (Людвиг Прандтль, Теодор фон Карман), в то время как различные ученые, такие как Осборн Рейнольдс, Андрей Колмогоров и Джеффри Ингрэм Тейлор. продвинул понимание вязкости жидкости и турбулентности.
Основные филиалы []
Статика жидкости []
Статика жидкости или гидростатика — это раздел механики жидкости, изучающий жидкости в состоянии покоя.Он включает изучение условий, при которых жидкости находятся в состоянии покоя в устойчивом равновесии; и противопоставляется гидродинамике, изучению движущихся жидкостей. Гидростатика предлагает физические объяснения многих явлений повседневной жизни, например, почему атмосферное давление меняется с высотой, почему дерево и нефть плавают на воде и почему поверхность воды всегда ровная, независимо от формы емкости. Гидростатика лежит в основе гидравлики, проектирования оборудования для хранения, транспортировки и использования жидкостей.Это также актуально для некоторых аспектов геофизики и астрофизики (например, для понимания тектоники плит и аномалий в гравитационном поле Земли), для метеорологии, медицины (в контексте кровяного давления) и многих других областей.
Гидродинамика []
Гидродинамика — это раздел механики жидкости, который имеет дело с потоками жидкости. — наука о движении жидкостей и газов. [3] Гидродинамика предлагает систематическую структуру, лежащую в основе этих практических дисциплин, которая охватывает эмпирические и полуэмпирические законы, полученные из измерения расхода и используемые для решения практических задач.Решение проблемы гидродинамики обычно включает в себя вычисление различных свойств жидкости, таких как скорость, давление, плотность и температура, как функции пространства и времени. В нем есть несколько дисциплин, в том числе аэродинамика [4] [5] [6] [7] (исследование воздуха и других газов в движении) и гидродинамика [8] [9] (исследование движущихся жидкостей). Гидродинамика имеет широкий спектр приложений, включая расчет сил и движений в самолетах, определение массового расхода нефти по трубопроводам, прогнозирование меняющихся погодных условий, понимание туманностей в межзвездном пространстве и моделирование взрывов.Некоторые гидродинамические принципы используются в управлении движением и динамике толпы.
Связь с механикой сплошных сред []
Механика жидкости — это подраздел механики сплошных сред, как показано в следующей таблице.
| Механика сплошной среды Изучение физики сплошных материалов | Механика твердого тела Изучение физики сплошных материалов с заданной формой покоя. | Эластичность Описывает материалы, которые возвращаются в исходную форму после снятия приложенных напряжений. | |
| Пластичность Описывает материалы, которые необратимо деформируются после значительного приложенного напряжения. | Реология Исследование материалов с твердыми и жидкими характеристиками. | ||
| Механика жидкости Изучение физики сплошных материалов, которые деформируются под действием силы. | Неньютоновские жидкости не подвергаются деформации со скоростью, пропорциональной приложенному напряжению сдвига. | ||
| Ньютоновские жидкости претерпевают деформации, пропорциональные приложенному напряжению сдвига. | |||
С механической точки зрения жидкость — это вещество, которое не поддерживает напряжение сдвига; поэтому покоящаяся жидкость имеет форму сосуда, в котором она находится. Жидкость в состоянии покоя не имеет напряжения сдвига.
Допущения []
Допущения, присущие механической обработке физической системы жидкостью, могут быть выражены в терминах математических уравнений.По сути, предполагается, что каждая жидкостная механическая система подчиняется:
Например, предположение, что масса сохраняется, означает, что для любого фиксированного контрольного объема (например, сферического объема), ограниченного контрольной поверхностью, скорость изменения массы, содержащейся в этом объеме, равна скорости, с которой масса проходит через поверхность от снаружи до внутри , за вычетом скорости, с которой масса проходит от внутри к снаружи .Это можно выразить в виде интегрального уравнения по контрольному объему. [10] : 74
Предположение о континууме — это идеализация механики сплошной среды, согласно которой жидкости можно рассматривать как непрерывные, даже если в микроскопическом масштабе они состоят из молекул. В предположении континуума макроскопические (наблюдаемые / измеряемые) свойства, такие как плотность, давление, температура и объемная скорость, считаются хорошо определенными для «бесконечно малых» элементов объема — малых по сравнению с характерным масштабом длины системы, но большой по сравнению с масштабом молекулярной длины.Свойства жидкости могут непрерывно изменяться от одного элемента объема к другому и представляют собой средние значения молекулярных свойств. Гипотеза континуума может привести к неточным результатам в таких приложениях, как сверхзвуковые скоростные потоки или молекулярные потоки в наномасштабе. [11] Проблемы, для которых гипотеза континуума не работает, могут быть решены с помощью статистической механики. Чтобы определить, применима или нет гипотеза континуума, оценивается число Кнудсена, определяемое как отношение длины свободного пробега молекулы к характерному масштабу длины.Проблемы с числами Кнудсена ниже 0,1 можно оценить с помощью гипотезы континуума, но можно применить молекулярный подход (статистическая механика), чтобы найти движение жидкости для больших чисел Кнудсена.
Уравнения Навье – Стокса []
Уравнения Навье – Стокса (названные в честь Клода-Луи Навье и Джорджа Габриэля Стокса) представляют собой дифференциальные уравнения, описывающие баланс сил в данной точке жидкости. Для несжимаемой жидкости с векторным полем скоростей u {\ displaystyle \ mathbf {u}} уравнения Навье – Стокса: [12] [13] [14] [15]
- ∂u∂t + (u⋅∇) u = −1ρ∇P + ν∇2u {\ displaystyle {\ frac {\ partial \ mathbf {u}} {\ partial t}} + (\ mathbf {u} \ cdot \ nabla) \ mathbf {u} = — {\ frac {1} {\ rho}} \ nabla P + \ nu \ nabla ^ {2} \ mathbf {u}}.
Эти дифференциальные уравнения для деформируемых материалов являются аналогами уравнений движения Ньютона для частиц — уравнения Навье – Стокса описывают изменение количества движения (силы) в ответ на давление P {\ displaystyle P} и вязкость, параметризованные кинематической вязкостью. ν {\ displaystyle \ nu} здесь. Иногда к уравнениям добавляются объемные силы, такие как гравитационная сила или сила Лоренца.
Решения уравнений Навье – Стокса для данной физической задачи необходимо искать с помощью математического анализа.На практике точно таким образом можно решить только самые простые случаи. Эти случаи обычно связаны с нетурбулентным устойчивым потоком, в котором число Рейнольдса мало. Для более сложных случаев, особенно связанных с турбулентностью, таких как глобальные погодные системы, аэродинамика, гидродинамика и многие другие, решения уравнений Навье – Стокса в настоящее время можно найти только с помощью компьютеров. Эта область науки называется вычислительной гидродинамикой. [16] [17] [18] [19] [20]
Невязкие и вязкие жидкости []
Невязкая жидкость не имеет вязкости, ν = 0 {\ displaystyle \ nu = 0}.На практике невязкий поток — это идеализация, облегчающая математическое рассмотрение. Фактически известно, что чисто невязкие течения реализуются только в случае сверхтекучести. В противном случае жидкости обычно имеют вязкость , свойство, которое часто является наиболее важным в пограничном слое около твердой поверхности, [21] , где поток должен соответствовать условию отсутствия проскальзывания в твердом теле. В некоторых случаях математику жидкостной механической системы можно рассматривать, предполагая, что жидкость за пределами пограничных слоев является невязкой, а затем согласовывать свое решение с решением для тонкого ламинарного пограничного слоя.
Для потока жидкости через пористую границу скорость жидкости может быть разной между свободной жидкостью и жидкостью в пористой среде (это связано с условием Бивера и Джозефа). Кроме того, при низких дозвуковых скоростях полезно предположить, что газ несжимаем, то есть плотность газа не изменяется даже при изменении скорости и статического давления.
Ньютоновская и неньютоновская жидкости []
Ньютоновская жидкость (названная в честь Исаака Ньютона) определяется как жидкость, напряжение сдвига которой линейно пропорционально градиенту скорости в направлении, перпендикулярном плоскости сдвига.Это определение означает, что независимо от сил, действующих на жидкость, она продолжает течь . Например, вода — это ньютоновская жидкость, потому что она продолжает проявлять свойства жидкости независимо от того, сколько ее перемешивают или перемешивают. Чуть менее строгое определение состоит в том, что сопротивление небольшого объекта, медленно перемещающегося через жидкость, пропорционально силе, приложенной к объекту. (Сравните трение). Важные жидкости, такие как вода, а также большинство газов, ведут себя — с хорошим приближением — как ньютоновские жидкости при нормальных условиях на Земле. [10] : 145
Напротив, перемешивание неньютоновской жидкости может оставить после себя «дыру». Со временем он будет постепенно заполняться — такое поведение наблюдается в таких материалах, как пудинг, облек или песок (хотя песок строго не является жидкостью). В качестве альтернативы, перемешивание неньютоновской жидкости может привести к снижению вязкости, поэтому жидкость будет казаться «тоньше» (это наблюдается в красках без капель). Существует много типов неньютоновских жидкостей, поскольку они определяются как нечто, что не подчиняется определенному свойству — например, большинство жидкостей с длинными молекулярными цепями могут реагировать неньютоновским образом. [10] : 145
Уравнения ньютоновской жидкости []
Константа пропорциональности между тензором вязких напряжений и градиентом скорости известна как вязкость. Простое уравнение для описания поведения несжимаемой ньютоновской жидкости:
- τ = −μdvdy {\ displaystyle \ tau = — \ mu {\ frac {dv} {dy}}}
где
- τ {\ displaystyle \ tau} — напряжение сдвига, оказываемое жидкостью («сопротивление»)
- μ {\ displaystyle \ mu} — вязкость жидкости — коэффициент пропорциональности
- dvdy {\ displaystyle {\ frac {dv} {dy}}} — градиент скорости, перпендикулярный направлению сдвига. {th}} направления.
Если жидкость несжимаема, общая форма вязкого напряжения в ньютоновской жидкости
- τij = μ (∂vi∂xj + ∂vj∂xi − 23δij∇⋅v) + κδij∇⋅v {\ displaystyle \ tau _ {ij} = \ mu \ left ({\ frac {\ partial v_ {i}) } {\ partial x_ {j}}} + {\ frac {\ partial v_ {j}} {\ partial x_ {i}}} — {\ frac {2} {3}} \ delta _ {ij} \ nabla \ cdot \ mathbf {v} \ right) + \ kappa \ delta _ {ij} \ nabla \ cdot \ mathbf {v}}
где κ {\ displaystyle \ kappa} — второй коэффициент вязкости (или объемная вязкость) .Если жидкость не подчиняется этому соотношению, ее называют неньютоновской жидкостью, которая бывает нескольких типов. Неньютоновские жидкости могут быть пластичными, пластическими по Бингэму, псевдопластическими, дилатантными, тиксотропными, реопектическими, вязкоупругими.
В некоторых приложениях делается еще одно грубое разделение на жидкости: идеальные и неидеальные жидкости. Идеальная жидкость не является вязкой и не оказывает никакого сопротивления силе сдвига. Идеальной жидкости действительно не существует, но в некоторых расчетах это предположение оправдано.Одним из примеров этого является течение вдали от твердых поверхностей. Во многих случаях вязкие эффекты сосредоточены вблизи твердых границ (например, в пограничных слоях), в то время как в областях поля течения, удаленных от границ, вязкими эффектами можно пренебречь, и жидкость там рассматривается как невязкая (идеальная течь). Если вязкостью пренебречь, член, содержащий тензор вязких напряжений τ {\ displaystyle \ mathbf {\ tau}} в уравнении Навье – Стокса, обращается в нуль. Приведенное в таком виде уравнение называется уравнением Эйлера. Кунду, Пижуш К .; Коэн, Ира М .; Доулинг, Дэвид Р. «10». Гидравлическая механика (6-е изд.). Академическая пресса. ISBN 978-0124059351 .
Дополнительная литература []
- Фалькович, Грегори (2011), Механика жидкости (краткий курс для физиков) , Cambridge University Press, DOI: 10.1017 / CBO9780511794353, ISBN 978-1-107-00575-4
- Kundu, Pijush K .; Коэн, Ира М. (2008), Fluid Mechanics (4-е пересмотренное изд.), Academic Press, ISBN 978-0-12-373735-9
- Карри, И. Г. (1974), Фундаментальная механика жидкостей , McGraw-Hill, Inc., ISBN 0-07-015000-1
- Massey, B .; Уорд-Смит, Дж. (2005), Механика жидкостей (8-е изд.), Тейлор и Фрэнсис, ISBN 978-0-415-36206-1
- Назаренко, Сергей (2014), Гидродинамика через примеры и решения , CRC Press (группа Тейлора и Фрэнсиса), ISBN 978-1-43-988882-7
Внешние ссылки []
В поисках фундаментальной теории физики
Зимняя школа Wolfram Physics 4-15 января 2021 г. | Применить сейчас Следите за проектом в Twitter Последние новости, обновления и анонсы Теперь доступно Книга проекта Ближайшие прямые трансляции Увидеть все 26.01.21, 14:30 EST Рабочая сессия: подлежит уточнению Объявление о проекте Последние бюллетени Предыстория проекта Визуальное резюме Техническое введение Материалы иТехнические документы Программные инструменты Прямые трансляции и
Видеоархив Вопросы и ответы по проекту люди Реестр выдающихся Модели Вселенной Визуальная галерея Архив рабочих материалов Глоссарий Возможности образования и сотрудничества Дискуссионный форум Членство: Поддержите проект Как ты можешь помочь Связаться с нами хранить Подписка на дайджест новостей .
