11. Потери напора по длине. Порядок определения коэффициента трения.
Потери напора по длине иначе называют потерями напора на трение, возникают в гладких прямых трубах с постоянным сечением при равномерном течении. Такие потери обусловленны внутренним трением в жидкости и поэтому происходит и в шероховатых трубах, и в гладких. Основной расчетной формулой для потерь напора при ламинарном и турбулентном режиме движения в круглых трубах является формула Вейсбаха-Дарси
V-средняя скорость движения
Коэффициент трения зависит от числа Рейнольдса и от безразмерного геометрического фактора- относительной шероховатости (- абсолютное значение эквивалентной шероховатости )
Коэффициент трения при ламинарном режиме движения жидкости
Область турбулентного и переходного режимов разбиваются на 3 области :
1) область гидравлически гладких труб
2) область доквадратического сопротивления шероховатых труб
3) область квадратичного сопротивления шероховатых труб f
При турбулентном режиме движения жидкости коэффициент движения определяется по графику Мурина и по формуле Альтшуля
относительная шероховатость трубопровода
относительная гладкость трубопровода
Величину абсолютной эквивалентной шероховатости при расчетах берут из справочника в зависимости от материала труб и состояния его внутренней поверхности.
12.Местные гидравлические сопротивления. Потери напора на местных сопротивлениях.
Местные сопротивления это такие участки трубопровода, на которых происходит деформация потока, т.е. происходит изменения скорости потока или по величине или по направлению.
К местным сопротивлениям относятся: вход и выход потока из трубы, внезапные сужения и расширения труб, плавные сужения и расширения труб колена, отводы, тройники, диафрагмы, регулирующие устройства (краны, вентили, задвижки и т.д)
Протекая через местное сопротивление, поток деформируется, возникают пульсации скоростей и давлений, образуются вихревые зоны с обратными токами вследствие отрыва потока от стенок трубопровода. На эти процессы смешения и вихреобразования тратится часть полной энергии потока, которая превращается в тепло и рассеивается в окружающее пространство.
Различают четыре вида местных сопротивлений
Местные сопротивления на которых происходит изменение скорости по величине (рис.25 на стр.52)
Местные сопротивления связанные с изменением направления движения жидкости (рис. 26 на стр.52)
Местные сопротивления на которых происходит смешение или разделение потока(рис.27 на стр. 53)
Трубопроводная арматура(краны, вентили, задвижки, расходомеры и т.п.)
Потери напора на местном сопротивлении рассчитываются в долях от величины скоростного напора:
где-коэффициент местного сопротивления,
v-скорость движения жидкости, м/с
g-ускорение свободного падения, м/с^2
13.Виды потерь напора(давлений) в трубопроводах. Расчетные формулы.
Потери напора по длине потока. Иначе их называют потерями напора на трение, возникают в гладких прямых трубах с постоянным сечение при равномерном течении. Такие потери обусловлены внутренним трением в жидкости и поэтому происходят в шероховатых трубах, и в гладких.
где -коэффициент гидравлического трения,
l-длина трубопровода, м;
d-диаметр трубопровода, м;
v-средняя скорость движения жидкости, м/с;
g-ускорение свободного падения, м/с^2;
коэффициент трения зависит от числа РейнольдсаRe(режима движения жидкости) и от безразмерного геометрического фактора-относительной шероховатости (или-абсолютное значение эквивалентной шероховатости)
коэффициент трения при ламинарном режиме движения жидкости рассчитывается по формуле:
На практике при турбулентном режиме движения коэффициент трения может быть определен по графику Г.А.Мурина или рассчитан по формуле А.Д.Альтшуля:
Где Re-критерий Рейнольдса;
-коэффициент трения;
-абсолютное значение эквивалентной шероховатости, м;
d- диаметр трубопровода, м;
Потери напорана местное сопротивления.
Потери напора на местном сопротивлении рассчитываются в долях от величины скоростного напора:
где-коэффициент местного сопротивления,
v-скорость движения жидкости, м/с
g-ускорение свободного падения, м/с^2
Принцип сложения потерь напора.
Как правило, трубопроводы имеют прямые участки и множество местных сопротивлений. Принцип сложения потерь напора заключается в том, что потери напора по длине и потери напора на местных сопротивлениях складываются, т.е общие потери напора:
т.е
где где -коэффициент гидравлического трения,
l-длина трубопровода, м;
d-диаметр трубопровода, м;
v-средняя скорость движения жидкости, м/с;
g-ускорение свободного падения, м/с^2;
-сумма коэффициентов местных сопротивлений.
Часто в расчетах требуется определить потерю давления .
Потеря давления в трубопроводе на трение(для участка прямого трубопровода, длинного трубопровода), вычисляется по формуле
studfiles.net
Гидравлические потери по длине
Потери напора по
длине, иначе их называют потерями напора
на трение  ,
в чистом виде, т.е. так, что нет никаких
других потерь, возникают в гладких
прямых трубах с постоянным сечением
при равномерном течении. Такие потери
обусловлены внутренним трением в
жидкости и поэтому происходят и в
шероховатых трубах, и в гладких. Величина
этих потерь выражается зависимостью
,
в чистом виде, т.е. так, что нет никаких
других потерь, возникают в гладких
прямых трубах с постоянным сечением
при равномерном течении. Такие потери
обусловлены внутренним трением в
жидкости и поэтому происходят и в
шероховатых трубах, и в гладких. Величина
этих потерь выражается зависимостью
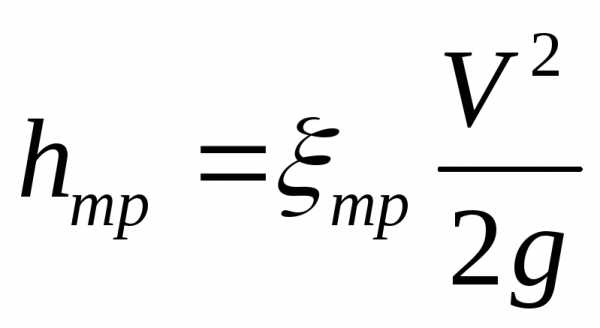 ,
,
где 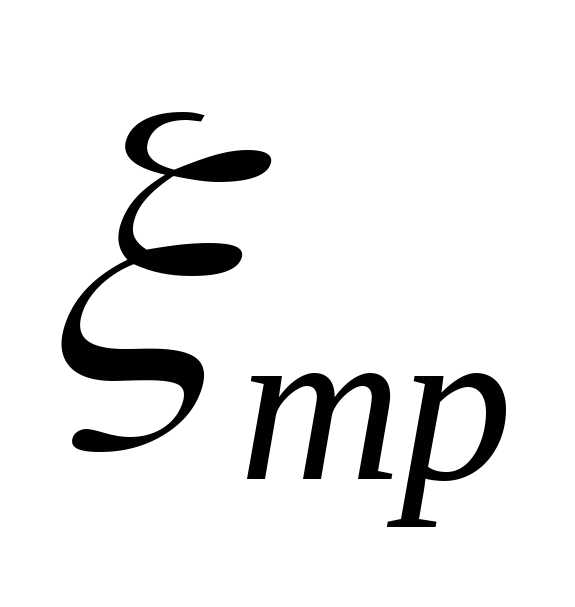 — коэффициент сопротивления, обусловленный
трением по длине.
— коэффициент сопротивления, обусловленный
трением по длине.
При равномерном движении жидкости на участке трубопровода постоянного диаметра d длиной l этот коэффициент сопротивления прямо пропорционален длине и обратно пропорционален диаметру трубы
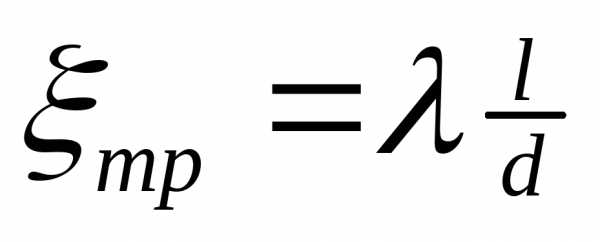 ,
,
где – коэффициент гидравлического трения (иначе его называют коэффициент потерь на трение или коэффициент сопротивления трения).
Из этого выражения нетрудно видеть, что значение — коэффициент трения участка круглой трубы, длина которого равна её диаметру.
С учетом последнего выражения для коэффициента сопротивления потери напора по длине выражаются формулой Дарси
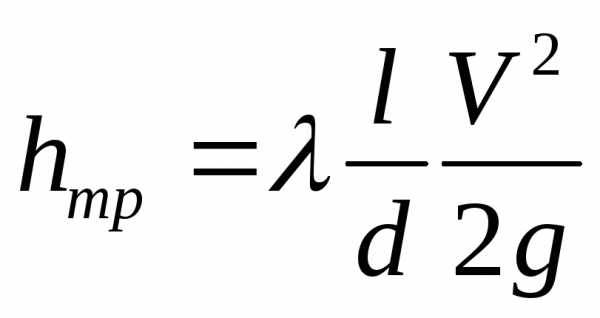 .
.
Эту формулу можно
применять не только для цилиндрических
трубопроводов, но тогда надо выразить
диаметр трубопровода d через гидравлический
радиус потока 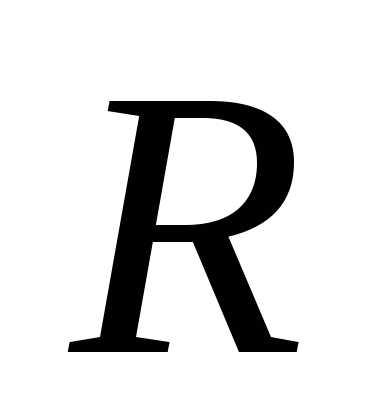
 или
или 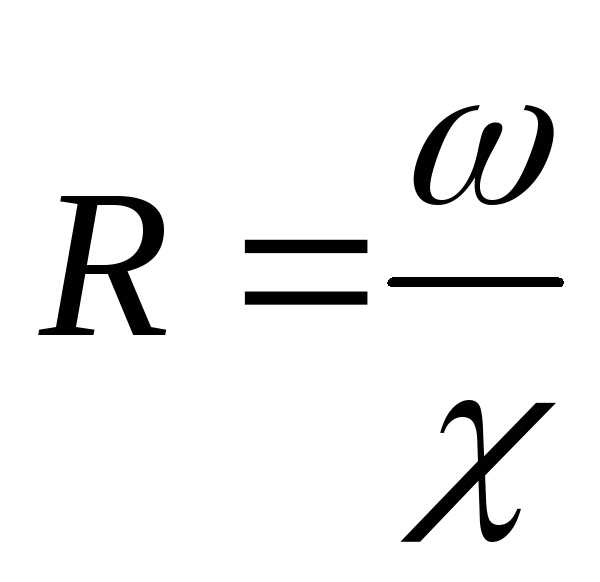
где, напомним, ω – площадь живого сечения потока,
χ — смоченный периметр.
Гидравлический радиус можно вычислить для потока с любой формой сечения, и тогда формула Дарси принимает вид
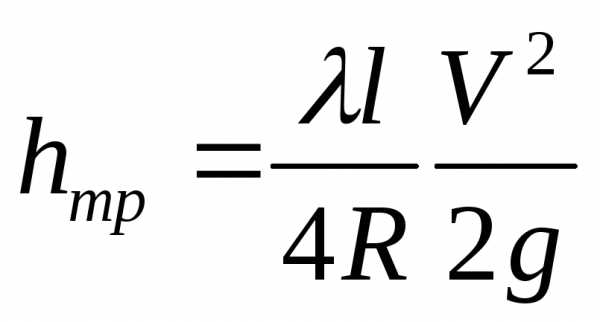 .
.
Эта формула справедлива как для ламинарного, так и для турбулентного режимов движения жидкости, однако коэффициент трения по длине λ не является величиной постоянной.
Для определения физического смысла коэффициентаλ рассмотрим объём жидкости длиной l, который равномерно движется в трубе диаметром d со скоростью V. На этот объём действуют силы давления P1и P2, причём P1 > P2, и силы трения рассматриваемого объёма о стенки трубы, которые определяются напряжением трения на стенке трубы τ0. Условием равномерного движения под действием сказанных сил будет следующее равенство:
.
Если учесть, что
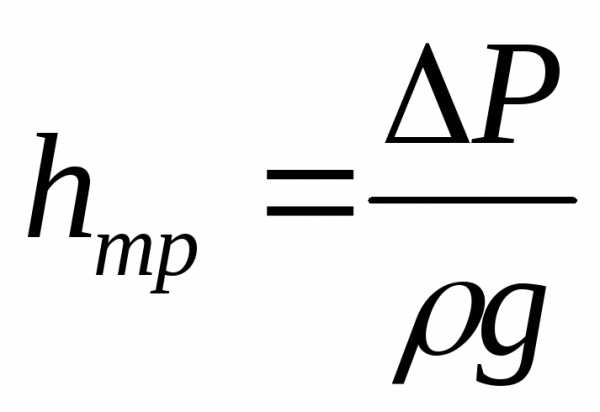 , то
, то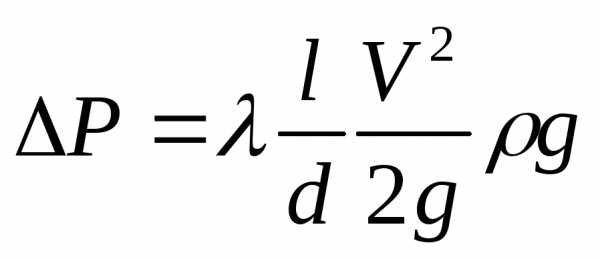
и подставить эту величину в уравнение сил, действующих на рассматриваемый объём, получим:
.
Сократив последнее
выражение, получим  . Выразив из негоλ,
окончательно будем иметь
. Выразив из негоλ,
окончательно будем иметь
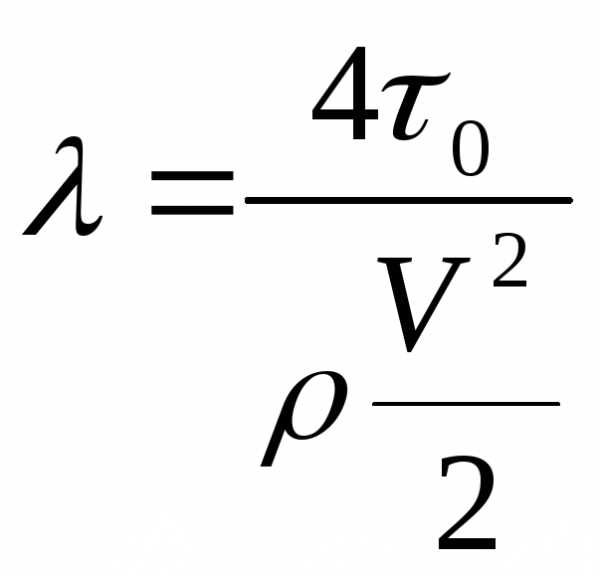 .
.
Из полученного выражения следует, что коэффициент гидравлического трения есть величина, пропорциональная отношению напряжения трения на стенке трубы к гидродинамическому давлению, посчитанному по средней скорости потока. Приведённые выше рассуждения и полученные в результате них формулы справедливы как для ламинарного, так и для турбулентного потоков. Однако коэффициент λ не является величиной постоянной и зависит от многих факторов. Для выяснения его величины, и связанных с ним потерь энергии необходимо подробно проанализировать режимы движения жидкости.
Ламинарное течение жидкости
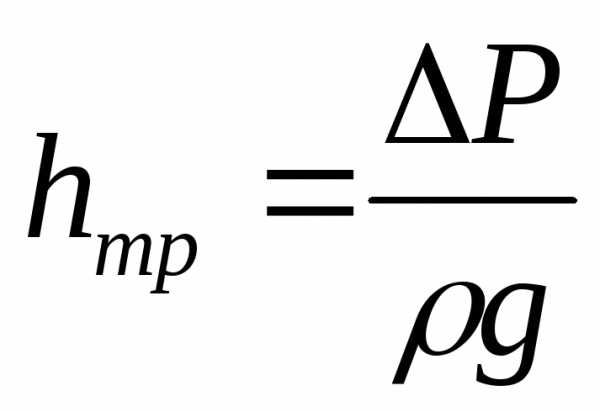
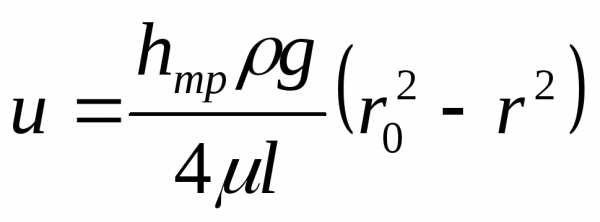
Используя значение скорости u, определим величину расхода через кольцевую площадь dωc шириной dr, находящуюся на расстоянии r от центра трубы. Выше было отмечено, что скорость в любой точке этого кольца одинакова, и тогда
 .
.
Проинтегрировав dQ по всей площади трубы (т.е. от r = 0 до r = r0), получим
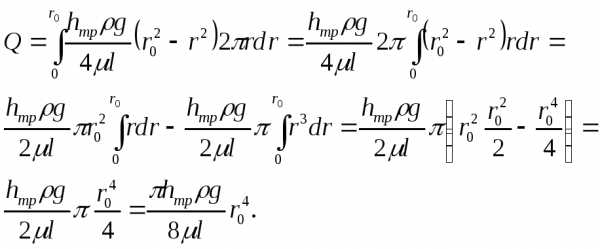
Средняя скорость в таком потоке будет
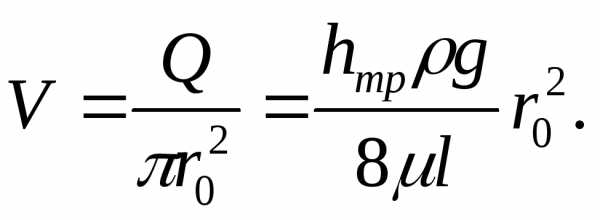
Заметим, что средняя скорость потока с параболическим распределением скоростей вдвое меньше максимальной.
Из последнего выражения легко получить закон сопротивления потоку, т.е. зависимость потерь энергии от размеров и параметров движения жидкости:
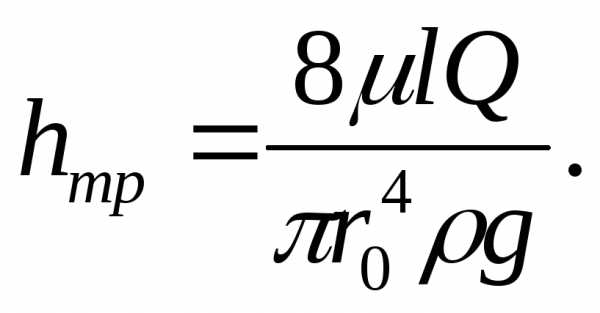
Заменив в этом
выражении динамический коэффициент
вязкости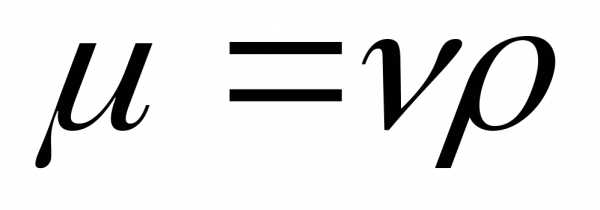 кинематическим и выразив радиус трубыr0 через диаметр d, получим
кинематическим и выразив радиус трубыr0 через диаметр d, получим

Полученное выражение носит название закона Пуазейля и применяется для расчета потерь энергии с ламинарным течением.
Эту же величину потерь на трение ранее мы выразили формулой Дарси. Если приравнять правые части формулы Дарси и закона Пуазейля, получится:
Заменим расход
произведением  и подставим в последнее равенство
и подставим в последнее равенство
.
Искусственно умножим и разделим числитель и знаменатель на V:
Очевидно, что в этом случае
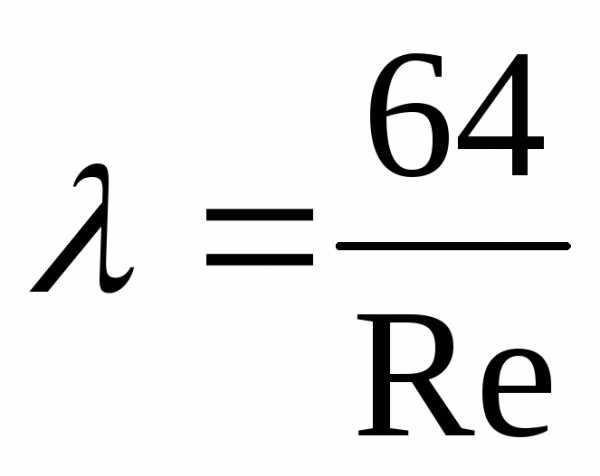 .
.
Это выражение для
коэффициента гидравлического трения
при ламинарном движении жидкости хорошо
подтверждается экспериментом и
используется на практике для определения
потерь энергии в потоке при ламинарном
течении. Иногда этот коэффициент
обозначается 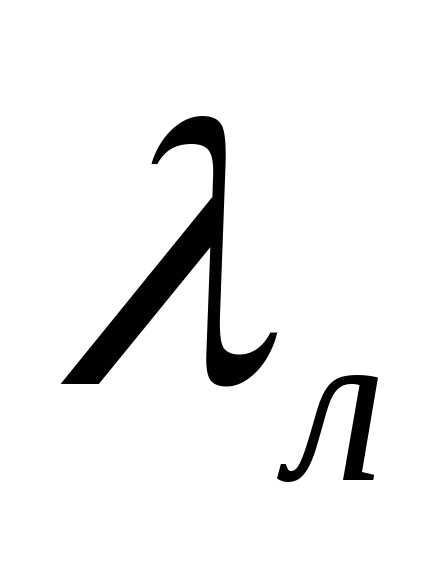 .
.
studfiles.net
5.1. Потери на трение (потери по длине)
с = Gv/S = сonst. | (5.2) |
Расчёт гидравлических сопротивлений (потерь) различных устройств пневмо-гидравлических систем является одним из основных вопросов гидравлики.
Вчистом виде потери на трение можно наблюдать в прямом горизонтальном трубопроводе постоянного сечения (см. рис. 5.1). Эти потери обусловлены внутренним трением в жидкости, возрастают пропорционально длине трубопровода. Структура формулы для определения потерь на трение аналогична (5.1) и в метрах столба соответствующей жидкости имеет вид:
h | = ξ |
| c2 | , | (5.3) | |
ò ð 2g | ||||||
ò ð |
|
|
| |||
где ξтр – коэффициент гидравлических потерь на трение, с – сред-
нерасходное значение скорости, которое можно определить по формуле (5.2).
Коэффициент гидравлических потерь на трение удобнее представить в следующем виде:
ξò ð = λò ð | l |
| (5.4) | |
d , | ||||
| ||||
где λтр – коэффициент сопротивления трению трубы длиной в один калибр, то есть трубы с l/d = 1.
Физический смысл коэффициента трения λтр найдём из ра-
венства нулю суммы двух сил, действующих на выделенный объём жидкости между сечениями 1 и 2:
pò ð | π d | 2 | −π dlτ =0, | (5.5.) |
4 |
| |||
|
|
|
|
где τ – напряжение трения на стенке трубы.
74
После подстановки в (5.5) |
|
| l |
| ρc | 2 | и сокращений | |
|
|
|
|
|
| |||
ðò ð = λò ð d | 2 |
| ||||||
|
|
|
| |||||
λò ð = | 4τ ò ð | , |
|
|
|
|
| |
|
| ρc2 |
|
|
|
|
|
|
2
то есть λтр – величина, пропорциональная отношению напряжения
трения на стенке трубы к динамическому (скоростному) напору. Значение λтр сложным образом зависит от режима течения
(ламинарный, турбулентный), критерия Рейнольдса, относительной шероховатости стенки канала. Подробнее этот вопрос изложен в лабораторной работе № 4 (см. приложение А).
5.2. Местные гидравлические сопротивления
Этот вид потерь возникает за счёт местного изменения скорости, вихреобразования, связанного с местным отрывом потока от стенки канала или преграды на пути потока. Примеры наиболее распространённых местных гидравлических сопротивлений представлены на рис. 5.2-5.4. Структура формулы для расчёта местных гидравлических сопротивлений аналогична (5.1), в которой индекс г – «гидравлические» заменен на индекс м – «местные»:
pм = ξ м ρс22
Для большинства встречающихся в технике местных гидравлических сопротивлений значения ξ м определены теоретически
либо экспериментально и представлены в справочной литературе. Характерные сечения 1 и 2 до и после местного гидравлического сопротивления необходимо выбирать там, где параметры потока жидкости выровнялись. Важно отметить, что если площади характерных сечений у одного местного гидравлического сопротивления различны (см. канал с внезапным расширением на рис. 5.2), то в
75
расчёте гидравлических потерь участвует меньшая площадь (диаметр), то есть в гидравлический расчет закладывается большее значение скорости.
Рис. 5.2. Расширение канала
Рис. 5.3. Сужение канала
Рис. 5.4. Поворот канала
76
5.3. Истечение жидкости из отверстий и насадков
Этот процесс реализуется при подаче топлива через форсунки
вкамерах сгорания авиационных, ракетных, автомобильных двигателей и других топливосжигающих установок; при подаче воды через сопла на лопасти гидротурбин, для получения реактивной тяги водомётных судов; при перетекании жидкости через жиклёры
всистемах регулирования двигателей.
Впроцессе истечения потенциальная энергия жидкости частично превращается в кинетическую энергию струи, а частично затрачивается на преодоление гидравлических сопротивлений.
Вобщем случае решение поставленной задачи состоит в определении скорости истечения жидкости; её расхода; гидравлических потерь при заданных условиях как в прямой, так и в обратной постановке.
5.3.1.Истечение жидкости через малое отверстие
втонкой стенке при постоянном напоре
На рис. 5.5 показана расчётная схема, применительно к которой сформулированы следующие основные и дополнительные условия.
Основные условия:
1.Сосуд неограниченной ёмкости (размеров).
2.Заданы свойства жидкости (плотность ρ, вязкость ν).
3.Истечение жидкости происходит в газообразную среду.
4.Отверстие находится под постоянным перепадом давления
(p1 + ρgz1 – p2 = сonst).
Дополнительные условия:
1. do | < 0,1 | — отверстие мало, следовательно, можно принять | |
|
|
| |
ρpg1 + z1
напор постоянным для любой его точки по высоте;
77
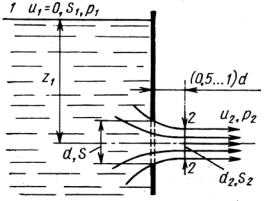
Рис. 5.5. Истечение жидкости
2.Стенка тонкая либо имеет острую кромку. В результате потери на трение по длине отверстия отсутствуют (ξтр = 0), несмотря на наличие местного гидравлического сопротивления (ξм > 0).
3.Отверстие достаточно удалено от свободной поверхности 1–1 и боковых стенок сосуда. В результате струйки жидкости подтекают к отверстию свободно, криволинейно и симметрично со всех сторон.
Требуется определить скорость истечения, расход жидкости и местное гидравлическое сопротивление отверстия в тонкой стенке.
Коэффициент сужения струи (ε). Траектории частиц жидко-
сти перед отверстием криволинейны. В результате возникают центробежные силы, направленные к оси отверстия, что приводит к сужению струи до своего минимального значения (d2 min) в характерном сечении 2–2, расположенном на расстоянии (0,5…1,0)d0 от отверстия. В сечении 2 давление в струе жидкости равно давлению газовой среды, в которую происходит истечение. Этот процесс оценивается коэффициентом сужения струи, представляющим собой отношение минимальной площади струи жидкости к площади отверстия через которое происходит истечение:
78

|
| S2 |
|
|
| 2 | |||
ε = |
|
| d2 |
| |||||
|
|
| |||||||
S0 | = |
|
|
| |||||
| d0 |
| |||||||
|
| S |
|
|
| 2 | |||
|
| 2 | d | 2 |
| ||||
ε = |
|
| = |
| . | ||||
| S |
|
|
| |||||
|
| 0 | d | 0 |
| ||||
|
|
|
|
| |||||
Коэффициент скорости (ϕ). Запишем уравнение Бернулли для участка 1–2. Исходя из основных и дополнительных условий: с1 = 0; с2 = const по сечению 2; нивелирная плоскость проходит через ось струи; Lмех = Lтр = 0. В результате
|
|
|
|
|
|
|
|
|
| p |
| p |
|
| c2 |
| c2 | |||||
|
|
|
|
|
|
| z | + | 1 |
| = | 2 | + | 2 | + ξ |
| 2 | . | ||||
|
|
|
|
|
| ρ g | ρ g |
| ì |
| ||||||||||||
|
|
|
|
|
| 1 |
|
|
|
|
| 2g | 2g | |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
После преобразований |
|
|
|
|
|
|
|
|
|
| ||||||||||||
| c | 2 | = | 1 |
|
|
|
| 2g(z + | p1 − p2 | ) = ϕ 2gH , | |||||||||||
|
|
|
|
|
|
| ||||||||||||||||
|
|
|
|
|
| 1 + ξ ì |
|
|
|
| 1 |
|
| ρ g |
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
где ϕ = | c2 | = |
|
| 1 |
|
| – коэффициент скорости, представляющий | ||||||||||||||
| c2 ò |
|
|
| 1 + ξ ì |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
собой отношение реальной скорости истечения жидкости из отверстия к теоритическй.
Отличие коэффициента скорости от единицы связано с вязкостью жидкости и другими причинами, вызывающими неравномерность профиля скорости по высоте отверстия.
Коэффициент расхода (ψ). Расход жидкости через отверстие определяется по параметрам в сечении 2: G2 = ρ S2 c2.
Используя коэффициенты сужения струи (ε) и скорости (ϕ) этот расход записывается через площадь отверстия и идеальную скорость истечения: G2 = ρ ε S0 ϕ w2m.
Обозначим через коэффициент расхода ψ ψ = G2 — отноше-
G2 ò
ние фактического расхода к теоретическому. Учтем, что ψ = ε ϕ.
79
studfiles.net
Тема 4 Гидравлические сопротивления и потери напора. Виды гидравлических сопротивлений. Потери напора на трение по длине потока
Цель: Изучить виды сопротивления. Местные потери и потери по длине потока.
План:
1. Потери напора по длине. Формула Дарси-Вейсбаха. Местные потери.
2. Коэффициент гидравлического трения при различных режимах движения жидкости. График Никурадзе.
3. Скорость при равномерном движении жидкости.
Как отмечалось выше при движении потока реальной жидкости, ограниченного твердыми стенками, возникают потери напора, вызванные сопротивлениями двух видов: сопротивлениями по длине, обусловленными силами трения; местными сопротивлениями, обусловленными изменениями скорости потока по величине и направлению в связи с различными препятствиями, встречающимися на пути потока.
При проведении расчетов по определению потерь напора используют принцип наложения потерь, когда общие потери напора с определенными допущенными рассматривают как сумму потерь напора вызываемых каждым видом сопротивлений отдельности:
Чему же равен каждый из видов потерь напора, входящих в уравнение и как их можно определить?
Р ассмотрим
потери напора на трение. Возьмем участок
горизонтальной трубы, по которому
движется жидкость.
ассмотрим
потери напора на трение. Возьмем участок
горизонтальной трубы, по которому
движется жидкость.
Рисунок 20 — К определению потерь напора на трение.
Выделим два сечения и напишем для них уравнение Бернулли с учетом, что движение в трубе равномерное, а местные сопротивления отсутствуют, т. е.hw = hl:
Следующее уравнение
называется формулой Пуазейля и служит для определения потерь напора на трение при ламинарном течении жидкости в круглой трубе. Умножив
числитель и знаменатель уравнения на 2ν, получим новое выражение потерь на трение:
Введя обозначение
получим уравнение Дарси-Вейсбаха для определения потерь напора на трение в круглых трубах:
где к — безразмерная величина, называемая коэффициентом гидравлического сопротивления. Коэффициент показывает, какая часть напора расходуется на преодоление гидравлического трения.
Заменив в уравнении диаметр на гидравлический радиус (d=4R), получим уравнение Дарси-Вейсбаха для определения потерь на трение в некруглых трубах и открытых руслах:
Формулы Дарси-Вейсбаха применимы и для турбулентного движения. В этом случае коэффициент гидравлического трения будет иметь иное значение, определяемое по другим зависимостям.
Преобразуя уравнение относительно скорости потока, получим:
где
Коэффициент С введен Шези и назван его именем. Уравнение легко преобразуется в формулу Шези:
Зависимость коэффициента гидравлического сопротивления от различных факторов.
При турбулентном режиме коэффициент находят по эмпирическим формулам или с помощью графиков, построенных на основе экспериментальных данных. Выяснению влияния различных факторов на значение коэффициента λ посвящено большое количество экспериментальных и теоретических работ. Рассмотрим опыты Никурадзе, выполненные еще в 1932 г. и не утратившие своего значения до настоящего времени.
Содержание опытов заключалось в следующем. На внутреннюю поверхность труб разного диаметра наклеивали зерна песка, создавая искусственную однородную шероховатость. В трубах с полученной таким образом шероховатостью при разных расходах измеряли потери напора и по формуле рассчитывали коэффициент λ. Затем строили графики зависимости коэффициента λ от числа Рейнольдса Re и от шероховатости D. Такой график показан на рисунке.
На графике на оси абсцисс отложены значения lg Re, а на оси ординат — значения lg (100 λ).
Кривые построены по точкам, представляющим усредненные значения относительной шероховатости труб: ε =D / d. Анализируя график, можно выделить характерные области.
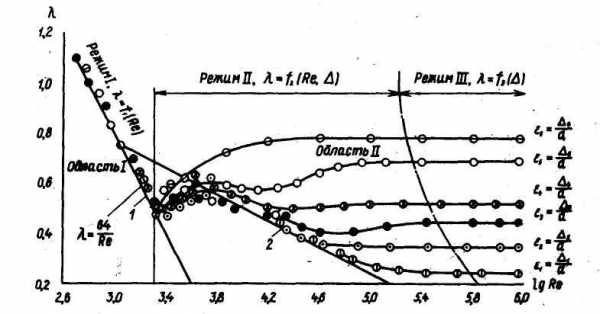
Рисунок 21 — Зависимость коэффициента гидравлического сопротивления λ от числа RE и от шероховатости.
Необходимо подчеркнуть, что опытные зависимости Никурадзе, полученные для цилиндрических труб, были подтверждены другими исследователями для напорных и безнапорных потоков с расчетов нет необходимости различать жидкости разного рода, а нужно рассматривать жидкость, всеобъемлющей характеристикой которой является число Рейнольдса.
Местные сопротивления и потери напора на их преодоление.
Движение жидкости по трубам и другим руслам связано с преодолением различных препятствий. Так, простые трубопроводы представляют собой последовательное соединение труб одного или различных диаметров. В местах соединения труб различных диаметров имеются переходные муфты. В трубопроводах могут быть повороты, внезапные и постепенные сужения, запорная арматура в виде кранов, вентилей, задвижек и др. Все эти местные включения оказывают сопротивление потоку жидкости, протекающему по трубопроводу. препятствия, встречающиеся на пути движения потока жидкости, которые вызывают изменение скорости потока либо по величине, либо направлению, либо одновременно и по величине, и по направлению.
Потери напора от местных сопротивлений особенно ощутимы, если трубопроводы составлены из коротких участков, часто изменяющих направление, имеющих изгибы, насыщенных различными местными включениями. Такие трубопроводы особенно распространены в маслопроводах гидросистем автомобилей, тракторов, самолетов, а также в водопроводных системах жилых зданий, промышленных цехов.
В учебной и справочной литературе приводятся эмпирические формулы определения коэффициента x для различных местных сопротивлений, имеются таблицы значений коэффициентов x в зависимости от вида местного сопротивления.
Литература: 1, с.87-103, 3, с.95-106.
Контрольные вопросы:
1. Что такое переходная область сопротивления, гидравлически гладкие и гидравлическая шероховатые стенки? В чем условность этих понятий?
2.
Объясните, от чего зависит коэффициент  при
ламинарном и турбулентном движении
жидкости.
при
ламинарном и турбулентном движении
жидкости.
3. Какие существуют формулы для определения коэффициента Шези?
studfiles.net
§ 8. Потери на трение. Конструирование передач
Потери на трение в цепных передачах складываются из потерь: а) на трение в шарнирах; б) на трение между пластинами; в) на трение между звездочкой и звеньями цепи, а в роликовых цепях также между роликом и втулкой, при входе звеньев в зацепление и выходе из зацепления; г) на трение в опорах; д) потерь на разбрызгивание масла.
Основными являются потери на трение в шарнирах и опорах.
Потери на разбрызгивание масла существенны только при смазывании цепи оку-нанием на предельной для этого вида смазки скорости v=10…15 м/с.
Средние значения КПД при передаче полной расчетной .мощности достаточно точно изготовленных и хорошо смазываемых передач составляют 0,96…0,98.
Цепные передачи располагают так, чтобы цепь двигалась в вертикальной плоскости, причем взаимное положение по высоте ведущей и ведомой звездочек может быть произвольным. Оптимальными расположениями цепной передачи являются горизонтальное и наклонное под углом до 45° к горизонту. Вертикально расположенные передачи требуют более тщательной регулировки натяжения цепи, так как ее провисание не обеспечивает самонатяжения; поэтому целесообразно хотя бы небольшое взаимное смещение звездочек в горизонтальном направлении.
Ведущей в цепных передачах может быть как верхняя, так и нижняя ветви. Ведущая ветвь должна быть верхней в следующих случаях:
а) в передачах с малым межосевым расстоянием (а<30P при и> 2) и в передачах, близких к вертикальным, во избежание захвата провисающей верхней ведомой ветвью дополнительных зубьев;
б) в горизонтальных передачах с большим межосевым расстоянием (а> 60Р) и малыми числами зубьев звездочек во избежание соприкосновения ветвей.
Натяжение цепей. Цепные передачи в связи с неизбежным удлинением цепи в результате износа и контактных обмятий в шарнирах, как правило, должны иметь возможность регулирования ее натяжения. Предварительное натяжение существенно в вертикальных передачах. В горизонтальных и наклонных передачах зацепление цепи со звездочками обеспечивается натяжением от собственной силы тяжести цепи, но стрела провисания цепи должна быть оптимальной в указанных выше пределах.
Для передач с углом наклона до 45° к горизонту стрелу провисания f выбирают приближенно равной 0,02а. Для передач, близких к вертикальным, f=(0,01… 0,015)а.
Натяжение цепи регулируют:
а) перемещением оси одной из звездочек;
б) регулирующими звездочками или роликами.
Желательна возможность компенсировать удлинение цепи в пределах двух звеньев, после чего два звена цепи удаляют.
Регулирующие звездочки и ролики следует по возможности устанавливать на ведомой ветви цепи в местах ее наибольшего провисания. При невозможности установки на ведомой ветви их ставят на ведущей, но для уменьшения вибраций — с внутренней стороны, где они работают как оттяжные. В передачах с зубчатой цепью ПЗ-1 регулирующие звездочки могут работать только как оттяжные, а ро лики как натяжные. Число зубьев регулирующих звездочек выбирают равным числу малой рабочей звездочки или большим. При этом в зацеплении с регулирующей звездочкой должно быть не меньше трех звеньев цепи. Перемещение регулирующих звездочек и роликов в цепных передачах аналогично таковому в ременных передачах и осуществляется грузом, пружиной или винтом. Наибольшее распространение имеет конструкция звездочки с эксцентрической осью, поджимаемой спиральной пружиной.
Известно успешное применение цепных передач роликовыми цепями повышенного качества в закрытых картерах при хорошем смазывании с неподвижными осями звездочек без специальных натяжных устройств.
Картеры. Для обеспечения возможности непрерывного обильного смазывания цепи, защиты от загрязнений, бесшумности работы и для обеспечения безопасности эксплуатации цепные передачи заключают в картеры (рис. 12.7).
Внутренние размеры картера должны обеспечивать возможность провисания цепи, а также возможность удобного обслуживания передачи. Для наблюдения за состоянием цепи и уровнем масла картер снабжают окном и указателем уровня масла.
studfiles.net
Гидравлические потери по длине
Потери напора по длине, иначе их называют потерями напора на трение , в чистом виде, т.е. так, что нет никаких других потерь, возникают в гладких прямых трубах с постоянным сечением при равномерном течении. Такие потери обусловлены внутренним трением в жидкости и поэтому происходят и в шероховатых трубах, и в гладких. Величина этих потерь выражается зависимостью
,
где — коэффициент сопротивления, обусловленный трением по длине.
При равномерном движении жидкости на участке трубопровода постоянного диаметра d длиной l этот коэффициент сопротивления прямо пропорционален длине и обратно пропорционален диаметру трубы
,
где – коэффициент гидравлического трения (иначе его называют коэффициент потерь на трение или коэффициент сопротивления).
Из этого выражения нетрудно видеть, что значение l — коэффициент трения участка круглой трубы, длина которого равна её диаметру.
С учетом последнего выражения для коэффициента сопротивления потери напора по длине выражаются формулой Дарси
.
Рисунок 3.16 – Схема к определению коэффициента гидравлического трения
Для определения физического смысла коэффициента λ рассмотрим объём жидкости длиной l, который равномерно движется в трубе диаметром d со скоростью (рисунок 3.16). На этот объём действуют силы давления P1 и P2, причём P1 > P2, и силы трения рассматриваемого объёма о стенки трубы, которые определяются напряжением трения на стенке трубы τ0. Условием равномерного движения под действием сказанных сил будет следующее равенство
Если учесть, что
, то ,
и подставить эту величину в уравнение сил, действующих на рассматриваемый объём, получим
.
Преобразовав это выражение и выразив из него λ, окончательно будем иметь
.
Из полученного выражения следует, что коэффициент гидравлического трения есть величина, пропорциональная отношению напряжения трения на стенке трубы к гидродинамическому давлению, посчитанному по средней скорости потока. Приведённые выше рассуждения и полученные в результате них формулы справедливы как для ламинарного, так и для турбулентного потоков.
3.13.3 Течение жидкости в шероховатых трубопроводах
Исследование течения жидкости в шероховатых трубах практически полностью основываются на экспериментальных исследованиях. На их результатах основаны зависимости и расчётные формулы, применяющиеся для определения потерь энергии в подобных условиях. Основная формула для определения потерь напора – формула Дарси. Отличие заключается только в коэффициенте потерь на трение. В отличие от турбулентных потоков в гладких трубах, где коэффициент на трение полностью определяется числом Рейнольдса Re, для потоков в трубах имеющих шероховатые внутренние поверхности зависит ещё и от размеров этой шероховатости.
Установлено, что решающее значение имеет не абсолютная высота неровностей (абсолютная шероховатость) k (рисунок 3.17) а отношение высоты этих неровностей к радиусу трубы r0. Эта величина обозначается и называется относительной шероховатостью. Одна и та же абсолютная шероховатость может практически не влиять на коэффициент трения в трубах большого диаметра, и существенно увеличивать сопротивление в трубах малого диаметра. Кроме того, на сопротивление потоку жидкости влияет характер шероховатости.
Рисунок 3.17 – Естественная шероховатость трубопровода
По характеру шероховатость разделяют на естественную(рисунок 3.17), при которой величина неровностей k по длине трубы различна, и регулярную(рисунок 3.18), при которой размеры неровностей по всей трубе одинаковы.
Рисунок 3.18 – Искусственная шероховатость трубопровода
Регулярная шероховатость создаётся искусственно и характеризуется тем, что имеет одинаковую высоту и форму неровностей по всей длине трубы. Шероховатость такого вида называют равномерно распределённой зернистой шероховатостью. Регулярная шероховатость является следствием особенностей технологии изготовления труб, создаётся искусственно и характеризуется тем, что имеет одинаковую высоту и форму неровностей по всей длине трубы. Шероховатость такого вида называют равномерно распределённой зернистой шероховатостью. Средняя шероховатость стальных новых труб равна 0,05 мм.
Коэффициент потерь на трение в этом случае описывается функцией
.
Эта зависимость проявляется в соотношении величины абсолютной шероховатости и величины ламинарного подслоя в потоке жидкости (рисунок 3.19).
Рисунок 3.19 – Схемы течения жидкости
Экспериментальным изучением влияния числа Рейнольдса и относительной шероховатости занимался Никурадзе И. И., который проводил опыты для диапазонов и =1/500…1/15.
Результаты этих исследований сведены к графику в логарифмических координатах.
На графике (рисунок 3.20) цифрами обозначены:
1 – зона ламинарного течения, т.е. при Re < 2320, коэффициент гидравлического трения l зависит только от числа Рейнольдса и не зависит от относительной шероховатости. Т.к. величина ламинарного подслоя δ (рисунок 3.19) значительно больше величины шероховатости стенки. Поток жидкости плавно обтекает выступы, не давая образовываться вихревым зонам. Коэффициент гидравлического трения l определяется по формуле Пуазейля
.
2 – зона турбулентного гладко стенного течения (область гидравлически гладких труб), 2320 < < . Здесь выступы шероховатости k меньше толщины ламинарного подслоя d (рисунок 3.19) и коэффициент l зависит только от числа Рейнольдса. Коэффициент l может быть определен по формуле Конакова или Блазиуса:
или .
3 – зона, так называемого, доквадратичного течения
<Re< .

Рисунок 3.20 – Экспериментальный график Никурадзе
В этой области коэффициент l зависит как от числа Рейнольдса, так и от величины шероховатости . Здесь выступы шероховатости k соизмеримы с толщиной ламинарного подслоя dл и начинают оказывать влияние на коэффициент гидравлического трения l. Коэффициент l может быть определен по формуле Альтшуля
.
4 – зона квадратичного сопротивления <Re. Здесь ламинарный подслой почти полностью разрушается, обнажая выступы шероховатости (рисунок 3.19). В этой области коэффициент сопротивления l является функцией только относительной шероховатости k/d и не зависит от числа Re. Коэффициент l определяется по формуле Никурадзе или Шифринсона
или
На практике для определения потерь напора в реальных шероховатых трубах чаще всего используют формулу Альдшуля.
Похожие статьи:
poznayka.org
Потери напора на трение по длине потока. — КиберПедия
Рассмотрим кольцевой слой жидкости толщины dr на расстоянии r от оси трубы, площадь сечения кольца равна dω=2πrdr, а расход жидкости через это сечение равен:
dQ=udr= u2πrdr
Подставляя сюда выражение скорости и интегрируя, получим:
, т.е. .
Это есть выражение расхода через осевую скорость в трубе.
С другой стороны , где v-средняя скорость в живом сечении потока.
=> .Т.о., средняя скорость потока при лам.режиме равна половине осевой.
С учетом этого результата из выражения для потерь напора на трение
можно получить выражение для потерь напора по длине l в виде:
или, введя вместо радиуса диаметр трубы и выражая абсолютную вязкость η через кинематическую (η=v∙ρ), в виде .
Из этой формулы видно, что потери напора при ламинарном движении пропорциональны первой степени средней скорости или расхода жидкости.
Эту формулу можно представить в другом виде, если учесть, что .
Делая соответствующую подстановку, получим
Или, введя обозначение , окончательно получим
Это универсальная формула Вейсбаха-Дарси,
где λ — коэффициент гидравлического трения или коэф. гидравлического сопротивления.
Формула Дарси-Вейсбаха используется для определения потерь на трение как для ламинарного, так и для турбулентного течения, однако, если для ламинарного движения коэффициент гидравлического сопротивления λ вычисляется по формуле λ=64/Re, то для турбулентного движения формулы будут иметь другой вид.
Формула Пуазейля.
Течение Пуазейля— ламинарное течение жидкости через тонкие цилиндрические трубки. Описывается законом Пуазейля.
Окончательно потери напора при ламинарном движении жидкости в трубе:
Несколько преобразовав формулу для определения потерь напора, получим формулу Пуазейля:
Закон установившегося течения в вязкой несжимаемой жидкости в тонкой цилиндрической трубке круглого сечения. Сформулирован впервые ГоттфильхомХагеном в 1839 и вскоре повторно выведен Ж.Л. Пуазейлем в 1840. Согласно закону, секундный объемный расход жидкости пропорционален перепаду давления на единицу длины трубки. Закон Пуазейля применим только при ламинарном течении и при условии, что длина трубки превышает так называемую длину начального участка необходимую для развития ламинарного течения в трубке.
Свойства течения Пуазейля:
-Течение Пуазейля характеризуется параболическим распределением скорости по радиусу трубки.
-В каждом поперечном сечении трубки средняя скорость вдвое меньше максимальной скорости в этом сечении.
Из формулы Пуазейля видно, что потери напора при ламинарном движении пропорциональны первой степени скорости или расхода жидкости.
Формулой Пуазейля пользуются при расчетах показателей транспортировки жидкостей и газов в трубопроводах различного назначения. Ламинарный режим работы нефте- и газопроводов является наиболее выгодным в энергетическом отношении. Так, в частности, коэффициент трения при ламинарном режиме практически не зависит от шероховатости внутренней поверхности трубы (гладкие трубы).
cyberpedia.su
