Абсолют температура: Недопустимое название | Наука

Содержание

Самые низкие температуры на Земле и во Вселенной

Самая низкая в принципе

ГДЕ Нигде. В природе такое не встречается

СКОЛЬКО –273,15 °С, или 0 К (градусов Кельвина) [pullquote align=»right»][note note_color=»#dcdcdc» text_color=»#000000″ radius=»0″]

Уильям Томсон, лорд Кельвин Британский физик, специалист в области термодинамики, электродинамики и механики. В его честь названа одна из семи единиц измерения Международной системы — единица термодинамической температуры Кельвин.[/note][/pullquote]

Однажды лорд Кельвин обозвал нерасторопного дворецкого абсолютным нулём. Так появился термин. Шутка. Более того, совсем не этот учёный первым определил самую низкую температуру.

Ещё в начале XVIII века об «абсолютном холоде» задумался французский физик Гийом Амонтон. Он обнаружил, что воздух при нагреве от 0 °С (точка замерзания воды) до 100 (кипение) увеличивает давление примерно на треть. Учёный задумался: насколько нужно охладить воздух, чтобы давление исчезло, то есть воздух превратился в твёрдое вещество? И получил –293 °С. Спустя полтора столетия британский физик Уильям Томпсон (тогда ещё не удостоенный титула лорда Кельвина), исходя из похожих соображений, рассчитал почти точное значение абсолютного нуля. Впоследствии Кельвин построил свою шкалу, отталкиваясь от этой точки.

В реальности абсолютный ноль не существует. Почему? Температуру тела создаёт движение атомов, а значит, при –273,15 °С все они должны находиться в полном покое. Но это невозможно из-за квантовых эффектов, так называемых нулевых колебаний, которые есть даже у вакуума.

Самая низкая в природе

ГДЕ Туманность Бумеранг, которая находится на расстоянии 5 тысяч световых лет от Земли

СКОЛЬКО 1 К (–272 °С)

Где же попытаться найти наименьшую температуру? Наверное, там, где нет никаких источников тепла — например, в открытом космосе вдали от галактик? Увы, мы потерпим неудачу, ибо даже космическое захолустье нагрето на несколько градусов, а именно до 2,725 К, за счёт реликтового излучения, оставшегося после Большого взрыва.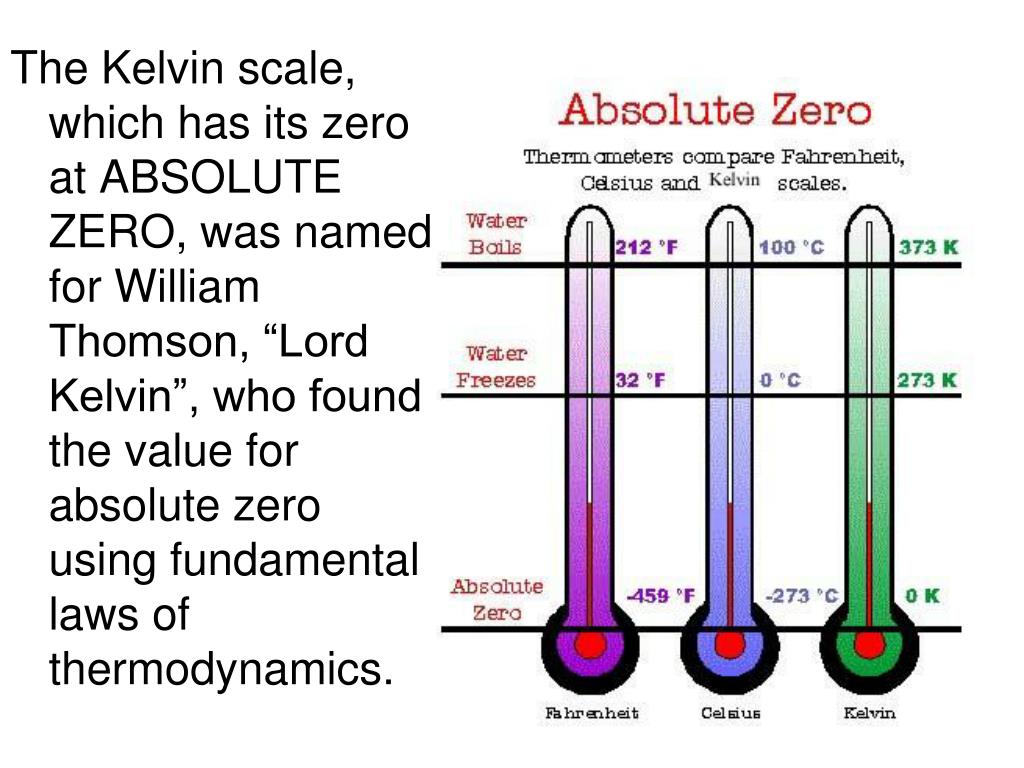

Но, оказывается, в космосе может быть что-то холоднее пустоты. В 1995 году астрономы Европейской южной обсерватории, расположенной в Чили, рассчитали, что звёздный газ в туманности Бумеранг извергается со скоростью в 600 тыс. км/ч. Такой «быстрый» газ охлаждается до 1К за счёт адиабатического процесса, суть которого в том, что если газ очень быстро расширяется, то он одновременно и охлаждается, потому что его внутренняя тепловая энергия расходуется — например, как в случае с туманностью, на увеличение газовой оболочки. Этот принцип лежит в основе работы большинства холодильников.

Самая низкая в Солнечной системе

ГДЕ Луна

СКОЛЬКО –240 °С

Казалось бы, чем дальше от Солнца, тем холоднее, и в некоторой степени это верно. В тройку самых холодных мест входят спутник Нептуна Тритон (не выше –237,6 °С), Плутон (–230 °С) и, неожиданно, — Луна.

Почему так холодно на Тритоне, понятно: как-никак 4,5 миллиарда километров от Солнца. Плутон холоднее, чем должен быть, из-за того, что азотный лёд на его поверхности тает при приближении планеты к Солнцу и вновь образуется при удалении.

В результате поверхность охлаждается подобно телу потеющего человека. Луна же стала рекордсменкой за счёт глубоких кратеров, дна которых не достигает солнечный свет. Притом что её поверхность может разогреваться более чем до 100 °С.

Надо заметить, в Солнечной системе ещё много, очень много неисследованных тел, и, вполне возможно, какие-то объекты из Облака Оорта или пояса Койпера могут подвинуть Луну с пьедестала.

Самая низкая из созданных человеком

ГДЕ Лаборатория низких температур, Хельсинкский технологический университет

СКОЛЬКО 50 пикокельвин (0,000 000 000 05 К)

Многие материалы проявляют удивительные свойства при сверхнизких температурах. Например, металлы становятся сверхпроводящими, жидкости и сконденсированные газы — сверхтекучими. При температуре около абсолютного нуля существует конденсат Бозе — Эйнштейна, состояние вещества, при котором все атомы приобретают один и тот же энергетический уровень и становятся неотличимы друг от друга.

Весной этого года физик Марк Касевич и его коллеги из Стэнфордского университета смогли охладить конденсат из 100 тысяч атомов рубидия до температуры около 50 пикокельвин, говорится в статье, опубликованной в Physical Review Letters. Таких показателей удалось достигнуть с помощью специального лазера, подавлявшего движение атомов.

Самая низкая на Земле

ГДЕ Станция «Восток», Антарктида

СКОЛЬКО –89,2 °С

Восток — дело не только тонкое, но и очень холодное, если речь идёт об антарктической станции. Температурный рекорд –89,2 °С, зафиксированный советскими метеорологами в 1983 году, сейчас пытаются оспорить. Например, недавно сообщалось, что рядом с японской полярной станцией «Купол Фудзи» было на два градуса холоднее. Однако измерение проводилось с помощью спутника, а он считывает только температуру поверхности, а не воздуха.

За право считаться полюсом холода в Северном полушарии борются два населённых пункта в Якутии: город Верхоянск и село Оймякон (на самом деле правильнее говорить о местности Оймякон, ибо наблюдения ведутся в 40 километрах от села).

Похоже, что в Верхоянске рекордная температура всё же немного ниже и составляет –67,8 °С.

Впрочем, защитники Оймякона не сдаются и не только пытаются подвинуть соседей-соперников, но и посягают на общемировой рекорд. Станция «Восток», справедливо замечают они, находится на высоте более трёх километров над уровнем моря, а Оймякон — 700 метров, и если привести их к одному уровню, Оймякон будет самым холодным местом на планете. В этих рассуждениях, правда, забывается Верхоянск, находящийся чуть более чем в сотне метрах над уровнем моря.

Опубликовано в журнале «Кот Шрёдингера»

Климат и одежда по погоде / Туристский портал Томска и Томской области

Travel Tomsk » Климат и одежда по погоде

Тип климата — континентально-циклонический (переходный от европейского умеренно континентального к сибирскому резко континентальному). Среднегодовая температура: 0,9 °C. Безморозный период составляет 110—120 дней. Зима суровая и продолжительная, минимальная зарегистрированная температура −55 °C (январь 1931 года).

Максимальная зарегистрированная температура +37,7 °C (июль 2004). Средняя температура января: −17,1 °C, средняя температура июля: +18,7 °C. В конце января и февраля бывают кратковременные оттепели до +3 °C, которые приносятся с циклонами из северной Атлантики. Смена сезонов происходит достаточно быстро, но наблюдаются возвраты к холодам и оттепелям. Годовое количество осадков — 568 мм.
Таблица температуры Томска за год.

Месяц	Абсолют. минимум	Средний минимум	Средняя	Средний максимум	Абсолют. максимум
январь	-55. 0 (1931)	-20.9	-17.1	-13.0	3.7 (1948)
февраль	-51.3 (1951)	-18.9	-14.7	-9.6	7.1 (1983)
март	-42.4 (1892)	-12.0	-7.0	-1.1	17.7 (2009)
апрель	-31.1 (1964)	-3. 3	1.3	7.0	26.5 (1972)
май	-17.5 (1898)	4.7	10.4	17.5	34.4 (2004)
июнь	-3.5 (1961)	10.5	15.9	22.3	34.7 (1931)
июль	1.5 (1945)	13.7	18. 7	24.8	35.1 (1975)
август	-1.6 (1902)	11.0	15.7	21.7	33.8 (1998)
сентябрь	-8.1 (1955)	5.1	9.0	14.4	31.7 (2010)
октябрь	-29.1 (1940)	-1.4	1.7	6. 0	25.1 (1928)
ноябрь	-48.3 (1952)	-11.4	-8.3	-4.7	11.6 (2006)
декабрь	-50.0 (1938)	-18.9	-15.1	-11.1	6.5 (1975)
год	-55.0 (1931)	-3.5	0.9	6.2	35. 1 (1975)

Климатические особенности Томска определяются его географическим положением на крайнем юго-востоке Западно-Сибирской равнины, которая с востока и запада ограничена горными поднятиями, влияющими на перемещение воздушных масс в широтном направлении.

Наклон к северу и равнинность территории благоприятствуют вторжению глубоко на юг холодных арктических масс воздуха. Огибая Уральские горы, с запада в Западную Сибирь проникают умеренные воздушные массы, несущие влагу. На погоду в Томске оказывают влияние в первую очередь преобладающий в умеренных широтах северного полушария западный перенос воздушных масс, а также периферийные части циклонов и антициклонов. Резкие изменения погоды в Томске, как правило, происходят при перемещении циклонов с меридиональной составляющей.

Чаще всего циклоны приходят с Баренцева и Карского морей. Они вызывают резкие понижения температуры воздуха, усиление ветра до 15 м/сек и более, увеличение облачности, выпадение осадков. Большая часть южных и юго-западных циклонов приходит летом и в межсезонья. С ними связано увеличение облачности до 100%, выпадение осадков с грозами. После прохождения теплого фронта наступает жаркая погода с повышением температуры до 36°С.

Зимой при выходах южных циклонов ясная морозная погода может смениться пасмурной с сильным снегопадом и метелями. Зимой прослеживается влияние отрога азиатского антициклона. Антициклональные условия усиливаются из-за вторжения арктического воздуха в тылу серий циклонов, проходящих по северу области. При этом устанавливается погода с низкими температурами и значительными скоростями ветра. Это усиливает суровость зимы в Томске. Сильные морозы иногда удерживаются в районе города 10-15 дней подряд.

Летом высокое давление возникает под действием азорского антициклона, формирующего малооблачную и жаркую погоду. Летние процессы протекают медленнее зимних. Циклоны летом менее глубоки, а антициклоны менее мощны, поэтому ветры не так сильны, как зимой. С циклонами и антициклонами в Томск и его окрестности.

Совет для любого путешественника, который собрался посетить Томск, — теплые вещи с собой брать обязательно. Даже если Вы едите летом, так как по ночам бывает прохладно и дождливые дни летом – явление достаточно частотное. Так же, если Вы едите весной, летом или осенью – обязательно возьмите зонтик. Если Вам довелось ехать в Томск зимой – обязательно в вашем гардеробе должны быть: шапка, варежки или зимние перчатки, а также зимний пуховик или шуба.

3.4: Абсолютная температура и энтропия

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 32021

В. Парамешваран Наир
City College of New York

Другим следствием второго закона является существование абсолютной температуры. Хотя мы использовали понятие абсолютной температуры, оно не было доказано. Теперь мы можем показать это только из законов термодинамики.

Мы уже видели, что эффективность цикла Карно определяется выражением

\[η = 1 − \frac{Q_2}{Q_3}\]

, где \(Q_3\) — количество тепла, отбираемого из более горячего резервуара, а \(Q_2\) — количество тепла, отдаваемого более холодному резервуару. Эффективность не зависит от материала и зависит только от нижней и верхней температуры. Можно считать, что рассматриваемая система находится в тепловом контакте с резервуарами, которые можно считать очень большими. Между резервуарами и системой нет обмена частицами или какой-либо другой физической величиной, поэтому никакой другой параметр, кроме температуры, не может играть в этом роли. Пусть \(θ\) обозначает эмпирически определенную температуру, где \(\theta_3\) и \(θ_2\) соответствуют резервуарам, между которыми работает двигатель. Таким образом, мы можем написать

\[\frac{Q_2}{Q_3} = f(θ_2, θ_3)\]

для некоторой функции \(f\) температур. Теперь рассмотрим другую машину Карно, работающую между \(θ_2\) и \(θ_1\), с соответствующими Q, так что мы имеем

\[\frac{Q_1}{Q_2} = f(θ_1, θ_2)\]

Теперь мы можем соединить два двигателя и запустить их вместе как один двигатель, работающий между \(θ_3\) и \(θ_1\), с

\[\frac{Q_1}{Q_3} = f(θ_1, θ_3)\]

Очевидно

\[\frac{Q_2}{Q_3} \;\frac{Q_1}{Q_2} = \frac{Q_1}{Q_3}\]

, чтобы мы получили отношение

\[f(θ_1, θ_2)\; f(θ_2, θ_3) = f(θ_1, θ_3)\]

Для этого требуется, чтобы функция \(f\) имела вид

\[f(θ_1, θ_2) = \frac{f(θ_1)}{f(θ_2)}\]

для некоторой функции \(f(θ)\). Таким образом, должна существовать некоторая функция эмпирической температуры, которую можно определить независимо от материала. Эта температура называется абсолютной температурой. Обратите внимание, что, поскольку \(Q_1 < Q_2\), мы имеем \(|f(θ_1)| < |f(θ_2)|\), если \(θ_1 < θ_2\). Таким образом, \(|f|\) должна быть возрастающей функцией эмпирической температуры. Далее, мы не можем иметь \(f(θ_1) = 0\) для некоторой температуры \(θ_1\). Для этого потребуется \(Q_1 = 0\). Соответствующий двигатель будет брать некоторое количество тепла \(Q_2\) из более горячего резервуара и полностью преобразовывать его в работу, что противоречит утверждению Кельвина. Это означает, что мы должны считать f либо всегда положительным, либо всегда отрицательным для всех \(0\). Обычно мы принимаем это как положительное. Конкретный вид функции определяет шкалу температуры. Самый простой — взять линейную функцию эмпирических температур (как это определено обычными термометрами). Сегодня мы принимаем это за

\[f(θ) ≡ T = \text{Температура в градусах Цельсия} + 273,16\]

Единицей абсолютной температуры является кельвин.

После определения понятия абсолютной температуры мы можем упростить формулу для КПД двигателя Карно как

\[η = 1 − \frac{T_L}{T_H}\]

Рисунок \(\PageIndex{1}\): Иллюстрация теоремы Клаузиуса

. Кроме того, мы имеем \(\frac{Q1}{Q2} = \frac{T1}{T2}\), который можно переписать как {Q1}{T1} = \frac{Q2}{T2}\). Поскольку Q2 — это поглощенное тепло, а Q1 — это тепло, отданное в резервуар, мы можем присвоить знаки ± знакам Q, + для поступления и — для выделения тепла, и записать это уравнение как

\[\frac{Q_1}{T_1} + \frac{Q_2}{T_2} = 0\]

Другими словами, если мы суммируем по различным шагам (обозначаемым индексом i) цикла с соответствующими алгебраическими знаками,

\[\sum_{цикл} \frac{Q_i}{T_i} = 0 \label{3.4.11} \]

Если мы рассмотрим любой замкнутый и обратимый цикл, как показано на рис. 3.4.1, мы можем разделить его на маленькие циклы, каждый из которых является циклом Карно. Некоторые из этих меньших циклов показаны пунктирными линиями, например, длинные пунктирные линии обозначают адиабатические циклы, а короткие пунктирные линии — изотермические. Если делать такие деления все тоньше и тоньше, ошибка аппроксимации цикла серией замкнутых циклов Карно будет стремиться к нулю по мере того, как число циклов Карно стремится к бесконечности. Поскольку вдоль адиабатики изменение \(Q\) равно нулю, мы можем использовать результат из уравнения \ref{3.4.11} выше, чтобы написать

\[\oint_{цикл} \frac{dQ}{T}= 0 \label{3.4.12}\]

где мы обозначаем тепло, поглощаемое или отдаваемое на каждом бесконечно малом шаге, как \(dQ\). Утверждение в уравнении \ref{3.4.12} принадлежит Клаузиусу. Важно то, что это относится к любой замкнутой кривой в пространстве термодинамических переменных при условии, что процесс обратим.

Это уравнение имеет еще одно очень важное следствие. Если интеграл дифференциала вокруг любой замкнутой кривой равен нулю, то мы можем записать дифференциал как производную некоторой функции. Таким образом, должна существовать функция \(S(p, V )\) такая, что

\[\frac{dQ}{T} = dS,\;\;\; или\; dQ = TdS\]

Эта функция \(S\) называется энтропией. Это функция состояния, заданная в терминах термодинамических переменных.

Неравенство Клаузиуса

Открытие Клаузиусом энтропии — одно из важнейших достижений в физике материальных систем. Для обратимого процесса у нас есть результат

\[\oint_{цикл} \frac{dQ}{T}= \oint_{цикл} dS = 0\]

, как мы уже видели. Мы можем сделать еще одно уточнение, рассматривая необратимые процессы. Есть много процессов, таких как диффузия, которые необратимы. Для такого процесса мы не можем написать \(dQ = T dS\). Тем не менее, поскольку энтропия является функцией состояния системы, мы все же можем определить энтропию для каждого состояния. Для необратимого процесса тепло, переданное системе, меньше, чем \(T dS\), где \(dS\) — изменение энтропии, вызванное необратимым процессом. Это легко увидеть из второго закона. В самом деле, пусть некоторое количество теплоты \(dQ_{irr}\) поглощается системой в необратимом процессе. Рассмотрим комбинированный процесс, в котором система переходит из состояния А в состояние В необратимым образом, а затем мы восстанавливаем состояние А посредством обратимого процесса. Для последнего шага \(dQ_{rev} = T dS\). Таким образом, комбинация поглощает количество тепла, равное \(dQ_{irr} -T dS\) без изменения состояния. Если это положительно, это должно быть полностью преобразовано в работу. Однако это нарушило бы второй закон. Следовательно, у нас должно быть

\[dQ_{irr} −T dS < 0\]

Если у нас есть циклический процесс, \(\oint dS = 0\), так как \(S\) является функцией состояния, и, следовательно,

\[ \oint \frac{dQ}{T} ≤ 0\]

с равенством для обратимого процесса. Это известно как неравенство Клаузиуса.

Для системы в термической изоляции \(dQ = 0\), и условие \(dQ_{irr} < T dS\) становится

\[dS > 0\]

Другими словами, энтропия система, предоставленная самой себе, может только возрастать, причем равновесие достигается, когда энтропия (при заданных значениях внутренней энергии, числа частиц и т. д.) максимальна.

Второй закон используется для определения энтропии. Но как только мы ввели понятие энтропии, второй закон эквивалентен утверждению, что энтропия имеет тенденцию к увеличению. Для любого процесса мы можем сказать, что

\[\frac{dS}{T} ≥ 0\]

На самом деле мы можем видеть, что это эквивалентно следующему утверждению Кельвина второго закона.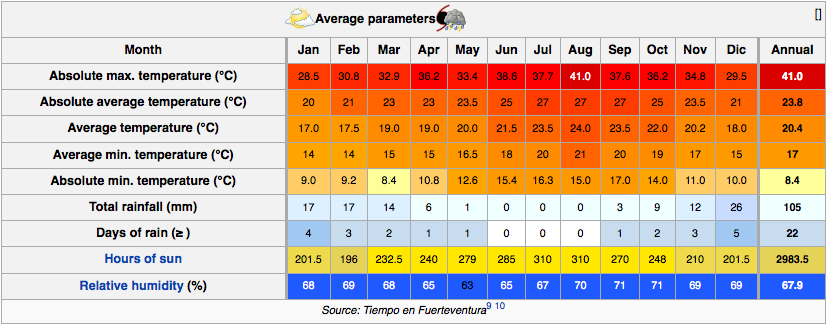 Рассмотрим систему, поглощающую тепло \(∆Q\) при температуре \(T\). Для системы (обозначенной цифрой 1) вместе с источником тепла (обозначенной цифрой 2) имеем \(∆S_1 + ∆S_2 ≥ 0\). Но источник теряет тепло при температуре \(T\), и если это обратимо, то \(∆S_2 = −\frac{∆Q}{T}\). Далее, если в системе нет других изменений, \(∆S_1 = 0\) и \(∆U_1 = 0\). Таким образом

\[∆S_1 + ∆S_2 ≥ 0 \Стрелка вправо — \frac{∆Q}{T} ≥ 0 \Стрелка вправо ∆Q ≤ 0\]

Так как \(∆U_1 = 0, ∆Q = ∆W\) и из этого уравнения следует, что работа, совершаемая системой, не может быть положительной, если мы имеем \(\frac{dS}{dt} ≥ 0\). Таким образом, мы пришли к утверждению Кельвина о том, что система не может поглощать тепло от источника и полностью преобразовывать его в работу без каких-либо других изменений. Таким образом, мы можем переформулировать второй закон в следующем виде:

Предложение 4

Второй закон термодинамики: энтропия системы, предоставленной самой себе, будет стремиться к увеличению до максимального значения, совместимого с указанными значениями внутренней энергии, числа частиц, и т. д.

Природа теплового потока

Легко видеть, что тепло само по себе перетекает от более горячего тела к более холодному. Это может показаться очевидным, но это ключевой результат второго закона. В некотором роде второй закон является формализацией таких утверждений, которые «очевидны» из нашего опыта.

Рассмотрим два тела при температурах \(T_1\) и \(T_2\), термически изолированные от остальной Вселенной, но во взаимном тепловом контакте. Второй закон говорит нам, что \(dS ≥ 0\). Это означает, что

\[\frac{dQ_1}{T1} + \frac{dQ_2}{T2}≥ 0\]

Поскольку тела изолированы от остального мира, \(dQ_1 + dQ_2 = 0\), поэтому что мы можем записать приведенное выше условие как

\[(\frac{1}{T_1} − \frac{1}{T_2}) dQ_1 ≥ 0\]

Если \(T_1 > T_2\), мы должны иметь \(dQ_1 < 0\) и если \(T_1 < T_2, dQ_1 > 0\). В любом случае тепло передается от более горячего тела к более холодному.

Рисунок \(\PageIndex{2}\): Цикл Отто для автомобильного двигателя.

Эта страница под названием 3.4: Абсолютная температура и энтропия распространяется в соответствии с лицензией CC BY-NC-SA и была создана, переработана и/или курирована В. Парамесвараном Наиром.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или Страница
Автор
В. Парамешваран Наир
Лицензия
CC BY-NC-SA
Показать оглавление
нет
Теги

GISTEMP — Неуловимая абсолютная температура приземного воздуха

Неуловимая абсолютная приземная температура воздуха (SAT)

(обновлено 18 марта 2022 г.)

Анализ GISTEMP основан на расчете температурных аномалий, а не абсолютной температуры. Температурные аномалии рассчитаны относительно нашего базового периода 1951-1980 гг. Причина, по которой мы работаем с аномалиями, а не с абсолютной температурой, заключается в том, что абсолютная температура сильно варьируется на коротких расстояниях, в то время как месячные или годовые температурные аномалии характерны для гораздо большей области. Действительно, мы показали (Hansen and Lebedeff, 1987), что температурные аномалии сильно коррелируют на расстояниях порядка 1000 км. Это значительно повышает точность оценки аномалий между станциями и в районах с разбросанным данными.

Q. Что именно мы подразумеваем под SAT?
A. В метеорологии SAT обычно относится к температуре воздуха на 2-метровом экране.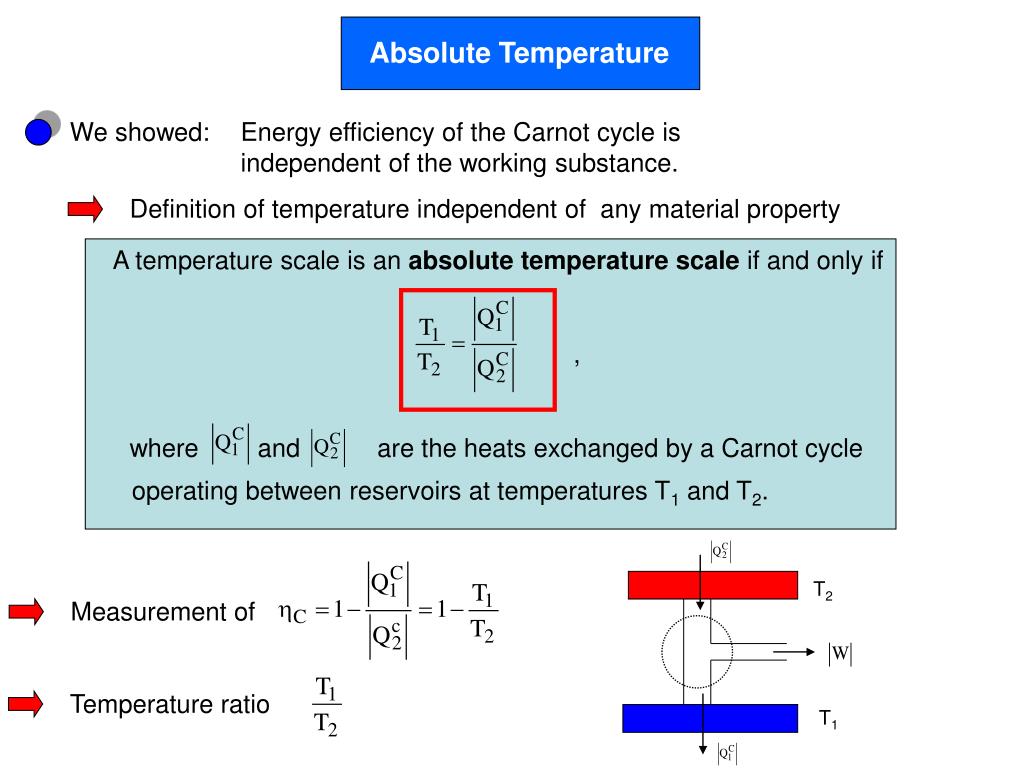 Это температура воздуха, которая будет измерена на высоте 2 метра (около шести футов) над землей на станции мониторинга погоды с экраном Стивенсона. Это то, что сообщается для большинства метеостанций с 1890-х годов. Тем не менее, SAT варьируется весьма существенно, и поэтому это число не обязательно отражает более широкое среднее значение по региону.

Q. Что мы подразумеваем под среднесуточной SAT?
A. С точки зрения эксплуатации среднесуточный SAT менялся по определению по мере развития технологий. Когда использовались максимальные/минимальные термометры, среднесуточное значение давалось как среднее двух крайних значений. С более современным оборудованием можно рассчитать среднее значение почасовых или даже поминутных данных. Различные подходы могут систематически давать разные ответы в зависимости от особенностей погоды в этот день. Однако аномалии, как правило, более устойчивы, независимо от методологии. Однако, если методология меняется на конкретной станции, это может привести к неклиматическому смещению долгосрочного тренда, который необходимо скорректировать, например, как это обсуждалось в отношении температурных рекордов США в Hansen et al. (2001).

Q. Какой SAT сообщают местные синоптики?
A. Синоптики часто сообщают о показаниях определенных термометров на ближайшей станции, часто в аэропорту или центре города. Это точечное измерение, которое может не отражать более широкое среднее значение. В прогнозах используются данные моделей погоды, иногда статистически уменьшенные до конкретных станций, но которые не отражают мелкомасштабную неоднородность SAT в реальном мире.

В. Если заявленные SAT не являются истинными SAT, почему они все еще полезны?
A. Сообщаемая температура действительна для метеостанции на момент измерения сообщаемой температуры. Однако в дополнение к SAT в отчетах обычно также упоминается, является ли текущая температура необычно высокой или необычно низкой, то есть насколько она отличается от нормальной температуры в этом месте и в это время года, и эта информация (аномалия) имеет смысл. для более широкой области.

В. Если невозможно измерить SAT, как создаются карты SAT?
A. Карты SAT могут быть созданы только с использованием какой-либо модели. Это может быть статистический подход, использующий входные данные из карт наземного покрова, местности и высоты, или, что чаще, компьютерная модель, например, используемая для составления прогнозов погоды. Из-за различий в том, как разрабатываются разные модели погоды и какие данные они принимают, разные модели будут давать несколько разные оценки SAT. В среднем по миру эта вариация составляет около 0,5 °C и может быть значительно больше в региональном масштабе. Статистические подходы (например, используемые Джонсом и др. (1999)) имеют аналогичную неопределенность.

В. Что делать, если мне нужны абсолютные SAT, а не аномалии?
A. В большинстве случаев вы обнаружите, что вам нужны именно аномалии, а не абсолютные температуры. В остальных случаях вам, вероятно, будет лучше использовать данные ближайших станций или результаты повторного анализа. Хотя изменения будут совместимы с данными GISTEMP для региона, абсолютные значения могут значительно различаться в разных источниках.

Q. Я нашел старые статьи и сообщения в СМИ, в которых среднегодовая абсолютная температура указывается с точностью до двух знаков после запятой, почему вы не можете сделать это сейчас?
A. Действительно, существует много исторических отчетов, в которых обсуждаются результаты среднегодовой температуры в терминах абсолютной температуры. До 2000 года в этих отчетах обычно учитывались аномалии и добавлялись к базовой температуре 15 ° C, которая была обычно используемым средним значением. После 2000 г. они часто использовали исходную температуру около 14 °C (вслед за Джонсом и др., 1999 г.). Однако эти исходные данные были лишь приблизительными, о чем свидетельствует тот факт, что после дальнейших исследований они были изменены на градус Цельсия! Сравнение отчетов об абсолютной температуре до 2000 г. и после 2000 г. может создать ложное впечатление, что температура резко понизилась, в отличие от явных доказательств того, что она потеплела. Этой ситуации можно было бы избежать, если бы люди уделяли больше внимания тому, как они комбинируют числа с разными оценками ошибок.

Абсолют температура: Недопустимое название | Наука | Fandom