Абсолютная температура газа формула: Абсолютную температуру идеального газа увеличили в 2 раза. Как надо изменить его массу, чтобы при…

Абсолютная температура и средняя кинетическая энергия молекул

1. Основное уравнение молекулярно-кинетической теории

Идеальный газ. Если потенциальной энергией взаимодействия молекул в газе можно пренебречь по сравнению с кинетической энергией их хаотического движения, то можно считать, что вся внутренняя энергия газа – это сумма кинетических энергий его молекул. Такую упрощенную модель реального газа называют идеальным газом.

Молекулярно-кинетическая теория идеального газа объясняет свойства газов, рассмотренные в предыдущем параграфе.

Согласно этой теории давление газа обусловлено частыми ударами молекул.

Поставим опыт
Будем сыпать на лист тонкого картона песок (рис. 41.1).

Мы увидим, что лист картона согнется, будто на него действует постоянная сила, хотя его деформация обусловлена ударами отдельных песчинок. Таким образом, частые удары мелких частиц создают постоянную силу.

Исходя из того, что давление газа создается ударами молекул, немецкий физик Рудольф Клаузиус вывел соотношение

где p – давление газа, n – концентрация его молекул, m₀ – масса молекулы, – среднее значение квадрата скорости молекул, которое определяется формулой

Здесь N – число молекул в газе.

Уравнение (1) называют основным уравнением молекулярно-кинетической теории идеального газа.

Запишем это уравнение с учетом того, что средняя кинетическая энергия поступательного движения молекулы связана со средним квадратом ее скорости соотношением

(Если молекула состоит более чем из одного атома, у нее есть также кинетическая энергия вращательного движения. Расчет, выходящий за рамки нашего курса, показывает, что при нахождении давления газа ее учитывать не нужно.)

Отсюда следует, что m₀ = 2. Подставляя это выражение в формулу (1), получаем другую форму записи основного уравнения молекулярно-кинетической теории идеального газа:

Значение основного уравнения молекулярно-кинетической теории идеального газа состоит в том, что оно выражает макроскопический параметр (давление газа) через микроскопические параметры – концентрацию молекул, массу молекулы и средний квадрат скорости или среднюю кинетическую энергию молекул.

Вывод основного уравнения

План наших действий таков.

• Найдем число ударов молекул о стенку сосуда за короткий промежуток времени ∆t.
• Найдем импульс, передаваемый стенке одной молекулой при ударе.
• Найдем импульс, передаваемый стенке молекулами за промежуток времени ∆t.
• Найдем силу давления, используя второй закон Ньютона в импульсной форме.
• Найдем давление.

Направим ось x перпендикулярно стенке сосуда, давление на которую мы рассматриваем. Ее площадь обозначим S. Предположим сначала для простоты, что у всех молекул одинаковое по модулю значение проекции скорости на ось x.

Сколько молекул ударятся о стенку за коротким промежуток времени ∆t? За этот промежуток времени молекулы пролетают по направлению к стенке или от нее расстояние, равное v_x∆t (рис. 41.2). Следовательно, успеет долететь до стенки и удариться о нее половина молекул, находящихся у стенки в слое толщиной v

x∆t (см. рис. 41.2).

Почему только половина? Потому, что со стенкой столкнутся только молекулы, у которых проекция скорости vx положительна – они движутся к стенке.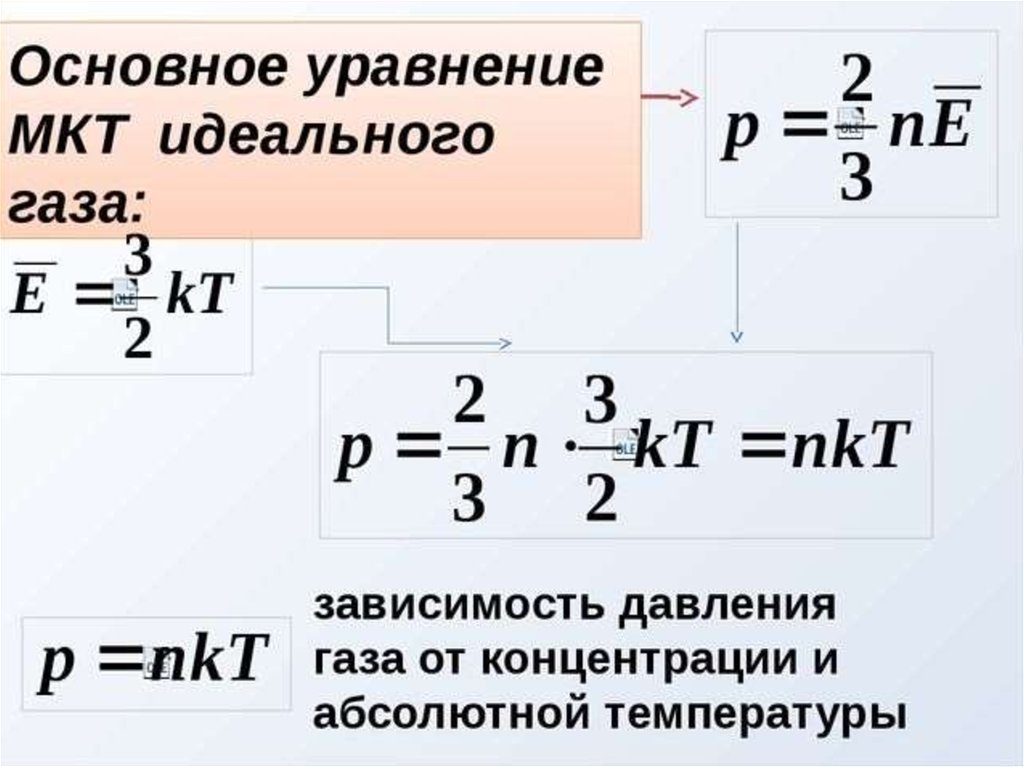 А к стенке и от стенки летит примерно равное число молекул.

? 1. Докажите, что в объеме слоя толщиной v_x∆t и площадью S находится nSv_x∆t молекул, а число Z ударов молекул о стенку за время ∆t выражается формулой

Какой импульс передает стенке при ударе одна молекула? Перед ударом проекция скорости молекулы равна v_x, а после дара она равна –v_x (молекула летит от стенки). Поэтому для одуля импульса, переданного стенке одной молекулой, получаем:

2m₀v_x.

Чему равен импульс, переданный стенке молекулами за время ∆t? Для ответа на этот вопрос надо просто умножить число Z ударов молекул на импульс, передаваемый одной молекулой. Мы получим:

В этой формуле мы учли, что на самом деле молекулы движутся с различными скоростями, поэтому в ней стоит среднее значение квадрата проекции скорости.

С какой силой газ давит на стенку? Согласно второму закону Ньютона, записанному в виде (см. § 25), сила давления газа равна отношению импульса, переданного стене за время ∆t, к этому промежутку времени. Следовательно,

Чему равно давление газа на стенку? По определению, давление p равно силе давления F, деленной на площадь поверхности S, на которую действует эта сила. Следовательно,

По теореме Пифагора (в трехмерном пространстве) квадрат модуля скорости равен сумме квадратов проекций скорости:

v² = v_x² + v_y² + v_z

².

Учтем, что все направления скоростей молекул равновероятны. Поскольку молекул очень много и их движение хаотично, то средние значения квадратов проекций скорости молекул на оси координат x, y и z равны:

Выполнив усреднение (см. формулу (2)), получим:

Из формул (6) и (7) следует, что

Подставляя это выражение в формулу (5), получаем:

Это и есть основное уравнение молекулярно-кинетической теории идеального газа.

2. Связь между температурой и средней кинетической энергией молекул

Напишем теперь рядом основное уравнение молекулярно-кинетической теории и уравнение состояния идеального газа в удобной для сравнения форме

Левые части этих уравнений совпадают. Значит, их правые части равны. Приравнивая их, получаем:

Эта формула раскрывает физический смысл абсолютной температуры:
абсолютная температура является мерой средней кинетической энергии движения молекул.

Таким образом, температура является энергетической характеристикой газа.

Обратите внимание: средняя кинетическая энергия поступательного движения молекул газа зависит только от абсолютной температуры. Она не зависит ни от массы молекул, ни от давления газа. Например, молекулы кислорода и водорода при одинаковой температуре имеют одинаковые средние кинетические энергии поступательного движения (независимо от того, равны ли давления этих газов).

? 2. В воздухе содержится небольшое количество аргона (молярная масса 40 * 10^-3 кг/моль) и неона (молярная масса 20 * 10^-3 кг/моль). Чему равна средняя кинетическая энергия молекул каждого из этих газов при нормальных условиях? Есть ли в условии задания лишние данные? (Это одноатомные молекулы)

3.

Скорости молекул

Среднеквадратичной скоростью молекул называют корень квадратный из среднего квадрата скорости молекул:

Ее можно использовать для оценки среднего значения модуля скорости молекул. (Расчет, выходящий за рамки нашего курса, показывает, что среднее значение модуля скорости примерно равно среднеквадратичной скорости.)

Среднеквадратичную скорость молекул газа можно выразить через микроскопические параметры газа: абсолютную температуру T и молярную массу M, а также через давление p и плотность ρ.

? 3. Объясните, почему справедлива формула

? 4. Чему равны среднеквадратичные скорости молекул водорода, кислорода и радона при комнатной температуре?

Обратите внимание: при одной и той же температуре среднеквадратичные скорости молекул разных газов не равны это следствие того, что у них одинаковая средняя кинетическая энергия. Чем меньше масса молекулы, тем больше ее среднеквадратичная скорость при той же температуре.

? 5. Объясните, почему справедлива формула

? 6. В сосуде объемом 10 л находится 14 г азота. Давление в сосуде 2 * 10⁵ Па. Чему равна среднеквадратичная скорость молекул газа? Есть ли в условии лишние данные?

Выполнив это задание, вы убедитесь, что молекулы действительно движутся со скоростями артиллерийских снарядов!

Измерение скоростей молекул

Значения скоростей молекул, предсказываемые молекулярно-кинетической теорией, казались некоторым ученым слишком большими, что было одним из возражений против этой теории.

В начале 20-го века немецкий физик Отто Штерн поставил опыт, в котором скорости молекул были измерены непосредственно. Вдоль общей оси двух жестко соединенных цилиндров А и В расположена покрытая серебром проволока (рис. 41.3). Воздух из пространства между цилиндрами откачан. Проволоку нагревают электрическим током, вследствие чего атомы серебра начинают испаряться. Из цилиндра А они могут вылететь только через узкую щель. В результате через некоторое время на внутренней поверхности цилиндра В появлялась узкая серебряная полоса 1 точно напротив щели.

Затем ток выключали, раскручивали соединенные цилиндры вокруг их общей оси и снова включали ток. На этот раз вместо узкой полосы напротив щели возникала довольно широкая и к тому же смещенная полоса 2.

Чем же обусловлены смещение полосы и ее расширение?

Смещение полосы было обусловлено тем, что за то время, пока атомы серебра пролетали от щели в цилиндре А до поверхности цилиндра В, сами цилиндры успевали повернуться на заметный угол.

Расширение же полосы было обусловлено тем, что скорости атомов при одной и той же температуре различны. Поэтому можно говорить только о средних значениях модуля скорости или о среднеквадратичной скорости.

Результаты опыта Штерна полностью подтвердили предсказания молекулярно-кинетической теории.

Дополнительные вопросы и задания

7. Температура воздуха повысилась от 0 ºС до 20 ºС. На сколько процентов увеличилась при этом:
а) средняя кинетическая энергия молекул в воздухе?
б) среднеквадратичная скорость молекул?

8. При нагревании водорода от 300 К до 1350 К все его молекулы распались на атомы.
а) Во сколько раз увеличилась средняя кинетическая энергия частиц?
б) Во сколько раз увеличилась среднеквадратичная скорость частиц?

9. При повышении температуры газа на 900 К среднеквадратичная скорость молекул газа увеличилась в 2 раза. Чему равна начальная температура газа?

10. На Луне есть атмосфера, хотя и очень разреженная. Когда поверхность Луны не освещена Солнцем, концентрация газа вблизи поверхности Луны составляет 2 * 10⁵ м^-3. Температура газа при этом равна -150 ºС.
а) Чему равно давление газа?
б) Во сколько раз это давление меньше земного атмосферного давления?
в) Во сколько раз средняя кинетическая энергия молекул этого газа меньше средней кинетической энергии молекул при нормальных условиях?
г) Во сколько раз среднеквадратичная скорость молекул газа на поверхности Луны меньше среднеквадратичной скорости молекул того же газа при нормальных условиях?

11.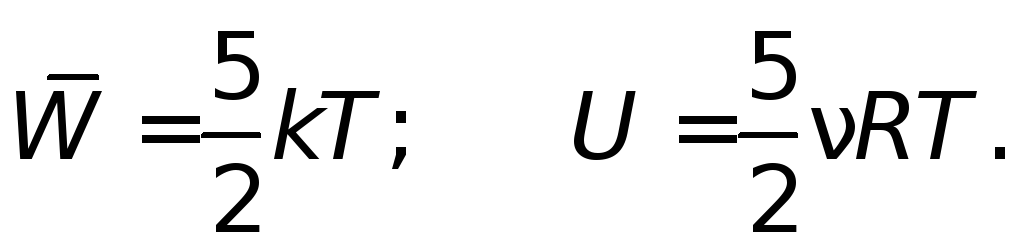 В первом сосуде содержится гелий, а во втором – кислород. Температура гелия равна –100 ºС. При какой абсолютной температуре кислорода:
а) средняя кинетическая энергия молекул кислорода равна средней кинетической энергии молекул гелия?
б) среднеквадратичная скорость молекул кислорода равна среднеквадратичной скорости атомов гелия?

Абсолютная температура идеального газа. Формулы. Пример задачи

От Masterweb

16.01.2019 21:00

Температура — термодинамическая макроскопическая характеристика, которая играет важную роль практически во всех физических процессах. В данной статье сосредоточим свое внимание на освещении вопросов, что такое абсолютная температура газа идеального и как ее можно вычислить.

Абсолютная шкала температур

Для начала познакомимся со шкалой, которая используется в физике для описания температуры. Она называется абсолютной или шкалой Кельвина. Впервые ее ввел в использование английский физик лорд Кельвин в 1848 году. При этом ученый основывался на завоевавшей популярность шкале Цельсия.

Абсолютная температура так называется потому, что она имеет нижний предел — 0 кельвин, при котором считается «замороженным» любой вид движения (на самом деле при 0 К существуют так называемые нулевые колебания). Верхнего предела у этой шкалы нет.

С градусами Цельсия C абсолютная шкала T связана следующим простым равенством:

T = C + 273,15.

В отличие от других температурных шкал, например, от шкалы Фаренгейта, кельвин имеет точно такой же масштаб, что и градус Цельсия. Последнее означает, что для перевода в абсолютную любой температуры по Цельсию достаточно добавить к ней число 273,15. Так, по шкале Кельвина вода замерзает при 273,15 К, а кипит при 373,15 К.

Краткое понятие о газе идеальном

Поскольку далее будет рассмотрена формула для определения абсолютной температуры газа идеального, то будет полезным познакомиться с этим понятием поближе. Под идеальным понимают такой газ, молекулы которого практически не взаимодействуют друг с другом, обладают большой кинетической энергией по сравнению с потенциальной, и расстояния между которыми значительно превышают их собственные размеры.

Все реальные газы проявляют поведение идеальных при небольших давлениях и высоких температурах. Примерами могут служить благородные газы, воздух, метан и другие. В то же время пар h3O даже при низких давлениях сильно отличается от идеального газа, поскольку в нем всегда присутствуют значительные водородные связи между полярными молекулами воды.

Температура абсолютная идеального газа

Существует два подхода к определению температуры в газах. Рассмотрим каждый из них.

Первый подход заключается в привлечении положений молекулярно-кинетической теории (МКТ) и физического смысла самой температуры T. Последний заключается в кинетической энергии частиц газа. Чем больше эта энергия, тем выше температура, причем зависимость является прямо пропорциональной. Используя формулу из механики для энергии кинетической и постоянную Больцмана kB можно записать следующее равенство МКТ:

m*v2/2 = 3/2*kB*T.

Где m — масса движущейся поступательно частицы. Выражая из этого равенства величину T, получаем формулу:

T = m*v2/(3*kB).

Чем меньше масса частицы и чем больше ее скорость, тем выше абсолютная температура.

Второй подход в определении величины T заключается в использовании универсального уравнения Клапейрона-Менделеева. Это уравнение было записано в XIX веке Эмилем Клапейроном (впоследствии модифицировано Д. И. Менделеевым) как результат обобщения открытых экспериментально в XVII-XIX веках газовых законов (Шарля, Гей-Люссака, Бойля-Мариотта, Авогадро). Математически универсальное уравнение записывается так:

P*V = n*R*T.

Как видно, оно связывает три основных термодинамических величины системы: давление P, объем V и температуру абсолютную T. Две другие величины, присутствующие в уравнении, — это n — количество вещества и R — газовая постоянная.

Не представляет особого труда получить формулу для температуры из Клапейрона-Менделеева закона:

T = P*V/(n*R).

В закрытой системе (n = const) температура газа прямо пропорциональна произведению объема на давление.

Пример задачи

Воздух, которым мы дышим, является смесью газов идеальных. Известно, что молярная масса воздуха составляет 29 г/моль. Необходимо определить температуру воздуха, если средняя скорость его молекул составляет 530 м/с.

Очевидно, что решение этой задачи можно получить, если воспользоваться следующим выражением:

T = m*v2/(3*kB).

Массу одной молекулы m воздуха можно получить, если поделить величину M на число Авогадро NA. Произведение же числа NA на константу Больцмана kB — это не что иное, как газовая постоянная R, которая равна 8,314 Дж/(К*моль). Учитывая эти рассуждения, получаем рабочую формулу:

T = M*v2/(3*R ) = 0,029*6002/(3*8,314) = 326,60 К.

В градусах Цельсия найденной температуре соответствует значение 53,45 oC. На нашей планете такие температуры характерны для жарких песчаных пустынь в полдень.

Уравнение идеального газа — GeeksforGeeks

Термометр с заполненной жидкостью колбой на одном конце, наиболее часто используемыми жидкостями являются ртуть, толуол, спирт, пентан, креозот, показывает разные показания для температур, отличных от фиксированных, из-за их различного расширения. характеристики. С другой стороны, термометр, использующий газ, показывает те же показания для температуры. Неважно, какой тип газа используется. Эксперименты показывают, что все газы расширяются одинаково при малых плотностях.

Давление (P), объем (V) и температура (T), где T = t + 273,15, а t — температура в °C, являются переменными, которые объясняют поведение данного количества (массы) газа. Закон идеального газа, также известный как универсальное газовое уравнение, представляет собой состояние уравнения для гипотетического идеального газа. Несмотря на свои недостатки, закон идеального газа дает хорошее приближение к поведению многих газов в различных ситуациях. Бенуа Поль Эмиль Клапейрон предложил закон идеального газа в 1834 году как смесь эмпирического закона Шарля, закона Бойля, закона Авогадро и закона Гей. Люссака.

Уравнение идеального газа

Законы идеального газа представляют собой комбинацию наблюдений Бойля в семнадцатом веке и Чарльза в восемнадцатом веке.

Закон Бойля: Давление газа обратно пропорционально объему газа для данного количества газа при фиксированной температуре, т.е. при постоянной температуре отношение между давлением и объемом количества газа можно записать как

П ∝ 1 / В

или

PV = константа

, где P — давление, а V — объем.

Закон Шарля: Объем газа прямо пропорционален температуре газа для данного фиксированного количества газа, поддерживаемого при постоянном давлении, т.е. при постоянной температуре соотношение между объемом и температурой количества газа может быть записано как, 

В ∝  T

или  

В / T = константа

, где T — температура.

Эти два закона применимы к газам с низкой плотностью и могут быть объединены в одну взаимосвязь. Стоит отметить, что

PV = константа  

и

V/T = константа

Для определенного количества газа тогда

PV/T также должно быть константой.

Это можно сформулировать в более общей форме, которая применяется к любому количеству любого газа с низкой плотностью, а не просто к определенному количеству этого газа. Это соотношение описывает закон идеального газа и известно как уравнение идеального газа .

Это может быть выражено как

PV / T = nR

или

PV = nRT

где n

где n газа. газовая постоянная.

Примечание: Универсальная газовая постоянная (R) имеет значение 8,314 кДж/моль в системе СИ.

Его также можно сформулировать в более общей форме, которая применяется к любому количеству любого газа с низкой плотностью, а не просто к определенному количеству этого газа.

Вывод уравнения идеального газа

Пусть P — давление газа, V — объем газа, T — температура.

в соответствии с законом Бойла,

P ∝ 1/V

или

V ∝ 1/P …… (1)

в соответствии с законом Чарльза,

V ∝ T …… .. (2)

в соответствии с законом Авогадро,

Когда P и T постоянны, объем газа пропорционален количеству моль газа, т.е.

V ∝ N ……. (3)

Сравните уравнения (1), (2) и (3) как значение 8,314 Дж/моль-К

Абсолютная температура

Термодинамическая температура — другое название абсолютная температура . При этой температуре термодинамическая энергия системы минимальна. Абсолютная температура равна нулю по Кельвину или -273 °C, широко известная как 9.0011 абсолютный ноль . Скорость частиц газа останавливается при температуре абсолютного нуля. Это означает, что частицы газа на самом деле не движутся. При абсолютном нуле объем газа равен нулю. В результате объем газа измеряется его абсолютным нулем.

Температура имеет прямую зависимость от давления и объема, т. е.

PV ∝ T  

Это соотношение позволяет использовать газ для определения температуры в газовом термометре с постоянным объемом.

Таким образом, при постоянном объеме соотношение может быть записано как  

P ∝ T , а температура считывается в терминах давления с помощью газового термометра постоянного объема.

Прямая линия выходит из графика зависимости давления от температуры.

При постоянном объеме график Давление в зависимости от температуры газа с низкой плотностью  

Наблюдения за реальными газами отличаются от значений, ожидаемых законом идеального газа при низких температурах. Однако зависимость является линейной в широком диапазоне температур, и кажется, что если бы газ оставался газом, давление падало бы до нуля при понижении температуры. Экстраполяция прямой на ось дает абсолютный минимум температуры идеального газа. Абсолютный ноль определяется как температура – ​​273,15 градуса по Цельсию. Температурная шкала Кельвина, часто известная как абсолютная шкала температуры, основана на абсолютном нуле.

Та же абсолютная нулевая температура на графике зависимости давления от температуры и экстраполяции линий для газов с низкой плотностью.

В температурной шкале Кельвина за нуль точек принимается –273,15 °C, то есть 0 K. В температурных системах Кельвина и Цельсия размер единицы одинаков. Таким образом, отношение между ними может быть выражено как

T = t + 273,15

, где t — температура в °C

Примеры задач  

Задача 1: Какой объем занимают 2,34 грамма углекислого газа при STP?

Решение:

Дано,

Вес (м) углекислого газа 2,34 грамма.

При СТП температура 273,0 К.

Давление 1,00 атм.

Универсальная газовая постоянная (R) имеет значение 0,08206 л атм моль¯ ¹ K¯ ¹ .

Выражение для количества молей:

n = m/M

где n — количество молей, m — вес, а M — молярная масса вещества.

Молярная масса диоксида углерода 44,0 г моль¯ ¹ .

Таким образом, значение n может быть рассчитано как

n = 2,34 г / 44,0 г MOL¯ ¹

= 0,0532 моль

Согласно уравнению идеального газа,

PV = NRT

Заднее значение уравнение, 

V = nRT / P

Подстановка всех значений,

В = [0,0532 моль) (0,08206 л атм моль¯1 К¯1) (273,0 К)] / 1,00 атм . Определить количество молей аргона и массу аргона в образце.

Решение:

Дано,

Объем (V) газообразного аргона составляет 56,2 литра.

При СТП температура 273,0 К.

Давление 1,00 атм.

Молярная масса газообразного аргона 390,948 г/моль.

Согласно уравнению идеального газа,

PV = nRT

Преобразуя уравнение,

n = PV / RT

Подставив все значения в приведенное выше уравнение,

n = [(1,00 л) (56,00 л) (56,00 л) ) ] / [ (0,08206 л атм моль¯1 K¯1) (273,0 K)]

  = 2,50866 моль

m = нМ

Подставляя все значения в приведенное выше уравнение,

м = (2,50866 моль) × (39,948 г/моль)

   = 100 г

Решение:

Дано,

Объем (V) газа неона составляет 12,30 литров.

Давление 1,95 атм.

Количество молей 0,654 моля.

Согласно уравнению идеального газа

PV = nRT

Преобразование уравнения,

T = PV / nR

Подстановка всех значений в приведенном выше уравнении,

T = [(1,95 атм) × (12,30 л)] / [(0,654 моль) × (0,08206 л атм моль¯ ¹ K¯ ¹ )]

   = 447 K

Задача 4. Вывести уравнение идеального газа?

Решение:

Пусть P — давление газа, V — объем газа, T — температура.

в соответствии с законом Бойла,

P ∝ 1/V

или

V ∝ 1/P …… (1)

Согласно закону Чарльза,

V ∝ T . ……..(2) 

Согласно закону Авогадро,

Когда P и T постоянны, объем газа пропорционален количеству молей газа, т.е.

V ∝ N ……. (3)

Сравнение уравнения (1), (2) и (3) как,

V ∝ NT/P

или 

PV = nRT

, где R – универсальная газовая постоянная, значение которой равно 8,314 Дж/моль-K

л контейнера при температуре 300 К. Когда весь твердый СО2 станет газом, какое будет давление в контейнере?

Решение:

Дано,

Вес (m) углекислого газа составляет 5,600 г.

Объем (V) диоксида углерода составляет 4,00 л.

Температура 300 К.

Молярная масса диоксида углерода 44,0 г моль¯1

Выражение для количества молей

n = m/M

Подставляя все значения в приведенное выше уравнение,

n = (5,600 г)/(44,009 г/моль)

= 0,1272467 моль

в соответствии с уравнением идеального газа,

PV = NRT

. все значения в приведенном выше уравнении,

P = (0,1272467 моль) × (0,08206 л ATM MOL¯ ¹ K¯ ¹ ) × (300 К)/ (4,00 л)

= 0,7831 Атм

111.

Создано Steven Wooding

Отзыв от Krishna Nelaturu

Последнее обновление: 11 октября 2022 г.

Содержание:

• Что такое идеальный газ?
• Как рассчитать температуру с помощью закона идеального газа
• Как пользоваться калькулятором температуры идеального газа
• Другие калькуляторы закона идеального газа
• Часто задаваемые вопросы

Используя этот калькулятор температуры идеального газа, вы можете найти температуру идеального газа на основе количества газа и его объема. В этой статье мы объясним:

• Определение идеального газа;
• Формула для расчета его температуры по закону идеального газа;
• Рассчитайте температуру идеального газа, если не заданы моли; и
• Какая единица измерения температуры используется в расчетах газового закона?

Что такое идеальный газ?

Идеальный газ состоит из молекул, которые мы моделируем как точечных частиц без взаимодействия между ними . Такой теоретический газ точно подчиняется газовым законам, что делает математику намного более управляемой.

К счастью, некоторые газы ведут себя как идеальные газы при нормальных температурах и давлениях без особых ошибок. Среди этих газов воздух, водород, кислород, азот, благородные газы и углекислый газ. Реальный газ очень похож на идеальный газ при более высоких температурах и более низких давлениях.

Как рассчитать температуру с помощью закона идеального газа

Какова температура идеального газа? Чтобы ответить на этот вопрос, нам нужно использовать закон идеального газа, который дается следующей формулой:

PV=nRT\small PV = nRTPV=nRT

где:

• PPP – Давление;
• ВВВ – Объем;
• nnn – количество частиц газа в молях;
• ТТТ – Температура; и
• RRR – Газовая постоянная, равная 8,3145 Дж·К ^-1 ·моль ^-1 .

Чтобы найти уравнение для температуры идеального газа, разделим обе части уравнения идеального газа на nRnRnR:

T=PVnR\small T = \frac{PV}{nR}T=nRPV​

Как пользоваться калькулятором температуры идеального газа

Вот как пользоваться нашим калькулятором температуры идеального газа:

1. Введите давление газа (сначала выберите предпочтительные единицы измерения).

2. Введите объем газа.

3. На последнем шаге введите количество молей газа.

4. Калькулятор немедленно отобразит полученный

   объем идеального газа.

Чтобы рассчитать температуру идеального газа, если не заданы моли, вы можете использовать расширенный режим калькулятора для расчета количества молей. Вас просят указать общую массу газа и его молярную массу (массу одного моля).

Другие калькуляторы закона идеального газа

Вот некоторые другие калькуляторы закона идеального газа, которые могут вас заинтересовать:

• Калькулятор закона идеального газа;
• Давление идеального газа; и
• Объем идеального газа.

Часто задаваемые вопросы

Какая единица измерения температуры используется в расчетах газового закона?

Кельвин. Шкала температуры Кельвина начинается с абсолютного нуля и составляет 273,15 точки замерзания воды. Он используется в расчетах закона идеального газа, поскольку стандартная газовая постоянная имеет единицы измерения Дж·К⁻¹·моль⁻¹, включая температуру в градусах Кельвина.

Какова температура 0,2 моля воздуха в 5-литровой бутыли?

31,5 °C при стандартном атмосферном давлении воздуха (101 325 Па). Этот результат рассчитывается следующим образом:

1. Умножьте давление и объем воздуха в единицах СИ. Таким образом, 0,005 м³ × 101325 Па = 506,625 м³·Па .

2. Разделите результат шага 1 на количество молей и газовую постоянную, чтобы получить температуру в кельвинах:

   506,625 / (0,2 × 8,3145) = 304,7 К

3. Преобразовать в градусы Цельсия путем вычитания 273,15 : 304,7 — 273,15 = 31,5 °C

Steven Wooding

Давление (P)

Количество вещества (n)

моль

Том (V)

Результат

Температура (T)

Проверьте 37 Расчеты с аналогичными термодинамиками 🌡

BioT numberboltzmann -фактор.