| Service Manual Мануалы, руководства, контрольные данные, datasheet для ремонта и обслуживания автомобилей |
| Диагностика и всё по OBD II Компьютерная диагностика и всё по протоколу OBD II. Коды ошибок и расшифровки по различным маркам авто. |
| Жидкости автомобиля Масла, антифриз и тосол, тормозные жидкости, омывайки и незамерзайки. Категории, лучшие, допуски, подделки. |
| Схемы электрооборудования Cхемы электрооборудования для авто. Электросхемы и мануалы автомобилей. Распиновки. OBD 2. Генератор и АКБ. Зарядные устройства и приборы проверки. |
| Программы для СТО Программы для СТО. Диагностика, чип-тюнинг, проверка, измерение, замеры, учёт, контроль, замена, удаление. |
| Электрооборудование Электрооборудование автомобилей. Стартеры, генераторы, блоки управления, ЭБУ, ЕГР, предохранители, реле, щитки приборов. |
| Acura Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Alfa Romeo Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Audi Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| BMW Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Chery Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Chevrolet Компьютерная диагностика и ремонт автомобилей на автосервисе. |
| Chrysler Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Citroen Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Dacia Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Daewoo Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Daihatsu Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Dodge |
| Fiat Компьютерная диагностика и ремонт автомобилей на автосервисе. |
| Ford Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| GMC Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Geely Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Great Wall Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Honda Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Infiniti Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Isuzu Компьютерная диагностика и ремонт автомобилей на автосервисе. |
| Iveco Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Jeep Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Lancia Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Land Rover Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Lexus Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Mazda Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Mecedes Компьютерная диагностика и ремонт автомобилей на автосервисе. |
| Mitsubishi Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Nissan Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Opel Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Peugeot Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Renault Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Saab Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Seat Компьютерная диагностика и ремонт автомобилей на автосервисе. |
| Skoda Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| SsangYong Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Subaru Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Suzuki Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Toyota Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| VW Компьютерная диагностика и ремонт автомобилей на автосервисе. СТО в Рогачеве. |
| Volvo Компьютерная диагностика и ремонт автомобилей на автосервисе. |
| Другие Автосервис и автозапчасти в одном месте, Рогачев. СТО ИП Кечик В.А. |
Геометрические размеры кузова RENAULT | Новый Logan
НАИМЕНОВАНИЕ | РАЗМЕР X | РАЗМЕР Y | РАЗМЕР Z | ДИАМЕТР | НАКЛОН % | |
А | Заднее крепления переднего подрамника | 205 | 402,5 | 71 | 18,5 | |
В | Переднее крепление заднего моста | 1999,3 | 657 | 71,3 | 20 х 20 | X: 8°20 |
С | Переднее крепление левого переднего подрамника | -418 | 447 | 130 | 10 х 10 (квадрат) | |
Переднее крепления правого переднего подрамника | -418 | 465 | 130 | 10 х 10 (квадрат) | ||
Е | Верхнее крепление амортизаторной стойки задней подвески | 2333,13 | 545,75 | 184 | 12,5 | |
F | Верхнее крепления амортизаторной стойки передней подвески | 18,5 | 545,50 | 657 | 48 | X: 3°02 У: 1° |
G1 | Задняя часть левого переднего лонжерона | 600 | -375 | 20 х 20 (квадрат) | ||
Задняя часть правого переднего лонжерона | 600 | 351,6 | 20 х 20 (квадрат) | |||
J | Задняя контрольная точка заднего лонжерона | 2918 | 497,5 | 151 | 12,2 х 16,2 | X: 3° |
К | Передняя поперечина кузова | 575 | 315 | 280 | 14,25 | X: 4°30 Z: 5° |
L | Задняя поперечина кузова (панель задка) | 3121 | -497,5 | 151 | М8 | |
Р | Переднее крепления двигателя | -247 | 483,5 | 514 | М10 | |
Заднее крепления двигателя | -113 | 483,5 | 514 | М10 |
I — ОСНОВНЫЕ ОПОРНЫЕ ТОЧКИ ДЛЯ ПРОВЕРКИ ГЕОМЕТРИИ КУЗОВА
А — ЗАДНЕЕ КРЕПЛЕНИЕ ПЕРЕДНЕГО ПОДРАМНИКА
Данная точка является главной передней опорной точкой.
Правая сторона
Левая сторона
1 — Со снятием агрегатов передней части шасси
Калибр устанавливается с упором под заднюю часть лонжерона и центрируется в отверстии под болт крепления подрамника.
ПРИМЕЧАНИЕ:
— с левой стороны отверстие круглое;
— с правой стороны отверстие овальное.
I — ОСНОВНЫЕ ОПОРНЫЕ точки для ПРОВЕРКИ ГЕОМЕТРИИ КУЗОВА (продолжение)
2 — Без снятия агрегатов передней части шасси
Калибр надевается на болт крепления подрамника и упирается в шайбу болта крепления.
ПРИМЕЧАНИЕ: крепления елевой и правой сторон несимметричны: с правой стороны крепление смонтировано на сайлент-блоке.
В случае восстановления целостности конструкции задней части кузова данных двух точек достаточно для выверки положения и поддержки передней части автомобиля.
I — ОСНОВНЫЕ ОПОРНЫЕ ТОЧКИ ДЛЯ ПРОВЕРКИ ГЕОМЕТРИИ КУЗОВА (продолжение)
В — ПЕРЕДНЯЯ КОНТРОЛЬНАЯ ТОЧКА ЗАДНЕГО МОСТА
Данная точка является главной задней опорной точкой.
Со снятием агрегатов шасси
Без снятия агрегатов шасси
Без снятия или со снятием агрегатов шасси
Калибр устанавливается с упором под лонжерон и центрируется в отверстии (квадратном).
При восстановлении целостности конструкции передней части кузова этих двух точек достаточно для выверки положения и поддержки задней части автомобиля.
II — ДОПОЛНИТЕЛЬНЫЕ ОПОРНЫЕ ТОЧКИ ДЛЯ ПРОВЕРКИ ГЕОМЕТРИИ КУЗОВА
Данные точки используются в качестве временных точек вместо основных в случаях, когда последние смещаются в результате полученного повреждения кузова.
G — ЗАДНЯЯ ЧАСТЬ ПЕРЕДНЕГО ЛОНЖЕРОНА
Данная точка используется также в качестве опорной для определения положения задней части переднего лонжерона при ее замене.
Со стороны удара данная точка обеспечивает поддержку кузова в дополнение к главной опорной точке, расположенной с противоположной стороны.
ПРИМЕЧАНИЕ: эти точки используются только в выше указанных случаях. При правильном положении основных точек (точек А и В) в их использовании нет надобности.
При правильном положении основных точек (точек А и В) в их использовании нет надобности.
В качестве дополнительных опорных точек можно также использовать контрольные точки концов лонжеронов при ударе сзади, и наоборот.
1 — ОПОРНЫЕ ТОЧКИ ДЛЯ ОПРЕДЕЛЕНИЯ ПОЛОЖЕНИЯ ЗАМЕНЯЕМЫХ ДЕТАЛЕЙ
3 — ПЕРЕДНЕЕ КРЕПЛЕНИЕ ПЕРЕДНЕГО ПОДРАМНИКА
1 — Со снятием агрегатов шасси
Калибр устанавливается с упором под кронштейн крепления переднего подрамника и центрируется в отверстии вместе с болтом крепления.
Калибр используется при замене-.
— передней поперечины кузова;
— части лонжерона;
— колесной арки в сборе с лонжероном.
2 — Без снятия агрегатов шасси
Калибр устанавливается на шайбу и болт
крепления подрамника.
Калибр используется:
— при незначительном повреждении от удара спереди;
— при диагностике состояния кузова для проверки его передней части методом проверки линейных размеров.
III — ОПОРНЫЕ ТОЧКИ ДЛЯ ОПРЕДЕЛЕНИЯ ПОЛОЖЕНИЯ ЗАМЕНЯЕМЫХ ДЕТАЛЕЙ (продолжение)
Е — ВЕРХНЕЕ КРЕПЛЕНИЕ ЗАДНЕЙ АМОРТИЗАТОРНОЙ СТОЙКИ
Калибр устанавливается в месте крепления вилки амортизатора и служит для определения положения данного крепления при замене:
— заднего лонжерона;
— заднего пола в сборе.
Он должен использоваться также при рихтовке деталей.
F — ВЕРХНЕЕ КРЕПЛЕНИЕ ПЕРЕДНЕЙ АМОРТИЗАТОРНОЙ СТОЙКИ
Калибр устанавливается с упором под чашку верхнего крепления амортизаторной стойки и центрируется в отверстии под болт крепления амортизаторной стойки.
Он используется при замене:
— колесной арки;
— колесной арки в сборе с лонжероном.
Он должен также использоваться при рихтовке деталей.
III — ОПОРНЫЕ ТОЧКИ ДЛЯ ОПРЕДЕЛЕНИЯ ПОЛОЖЕНИЯ ЗАМЕНЯЕМЫХ ДЕТАЛЕЙ (продолжение)
Р — ПЕРЕДНЕЕ И ЗАДНЕЕ КРЕПЛЕНИЯ ДВИГАТЕЛЯ
Калибр устанавливается поверх опоры подвески двигателя и центрируется в отверстиях под болты крепления кронштейна подвески двигателя.
Калибр используется при замене передней колесной арки в сборе с лонжероном при снятых агрегатах шасси.
J — ЗАДНИЙ КОНЕЦ ЗАДНЕГО ЛОНЖЕРОНА
Калибр устанавливается с упором под лонжерон и центрируется в направляющем отверстии (овальном).
Он может использоваться при устранении повреждений от легкого удара сзади без снятия заднего моста. Однако при этом требуется снятие крепления выпускной системы.
Однако при этом требуется снятие крепления выпускной системы.
III — ОПОРНЫЕ ТОЧКИ ДЛЯ ОПРЕДЕЛЕНИЯ ПОЛОЖЕНИЯ ЗАМЕНЯЕМЫХ ДЕТАЛЕЙ (продолжение)
L — КРАЙНЯЯ ЗАДНЯЯ ПОПЕРЕЧИНА (ПАНЕЛЬ ЗАДКА)
Калибр служит для установки задней поперечины и устанавливается вертикально с упором в поперечину панели задка, после чего центрируется в отверстии под болт крепления кронштейна ударопоглощающего элемента.
Калибр используется при замене панели задка в сборе со снятием или без снятия агрегатов шасси.
К — ПЕРЕДНЯЯ ПОПЕРЕЧИНА КУЗОВА
Калибр используется при установке поперечины и устанавливается вертикально с упором в переднюю поперечину, затем центрируется центровочным болтом в точке (К).
1 — Со снятием агрегатов шасси
Калибр используется при замене передней поперечины со снятием или без снятия агрегатов шасси.
ПРИМЕЧАНИЕ: операция замены передней поперечины выполняется без снятия силового агрегата, но при снятом радиаторе.
2 — Без снятия агрегатов шасси
Калибр используется при диагностике состояния передней поперечины.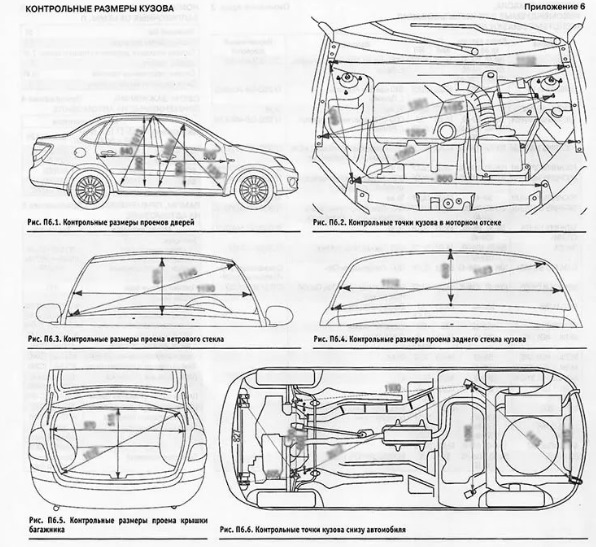
СТАПЕЛЬ CELETTE
IV — СВЕДЕНИЯ О СПЕЦИАЛЬНЫХ ПРИСПОСОБЛЕНИЯХ
BLACKHAWK
Специальные головки для системы MS
Адрес для заказа: BLACKHAWK S.A.
Centre Eurofret Rue de Rheinfeld 67100 STRASBOURG
Каталожный номер поставщика: REN 88200
CELETTE
Специальные головки для системы MS
Адрес для заказа: CELETTE S.A.
В.Р.9
38026 VIENNE Каталожный номер поставщика: 760 300
Специальный инструмент и приспособления
Точки (А) и (В) являются опорными для установки приспособления на кузов.
Перед установкой приспособления следует при диагностике состояния убедиться в правильности положения данных точек.
Точки (Е), (F), (G) и симметричные им точки служат прежде всего для крепления и выверки положения заменяемых деталей.
Однако при невозможности использования одной из точек (А) или (В) в качестве опорной (выявленной при диагностике), опорными точками для выверки положения деталей служат точки, расположенные со стороны, противоположной месту удара.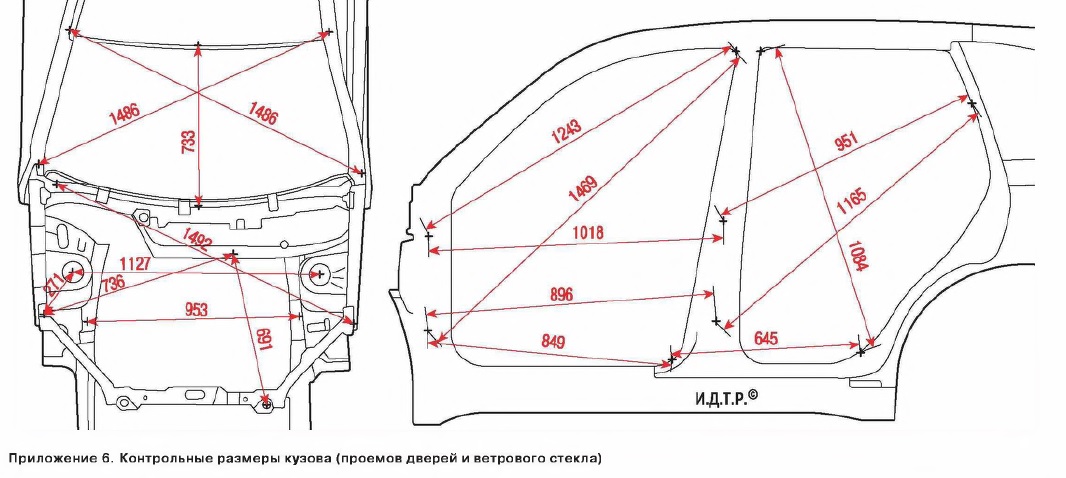
Обозначение и каталожный номер приспособления
Рисунок | Обозначение | Каталожный номер, указываемый при заказе | Наименование | |
Саг. 1439 | 00 00143 900 | Приспособление для передней панели кузова | ||
Контрольные геометрические размеры и точки кузова Nissan Juke / Ниссан Жук (джук)
Все приведенные на иллюстрациях размеры являются реальными (не проекционными).
При использовании приспособления для обмеров кузова, отрегулировать оба указателя на одинаковую длину. Убедиться в отсутствии посторонних люфтов в приспособлении.
• При использовании рулетки убедиться в отсутствии её растяжений, скручиваний или перегибов.
• Измерения должны проводиться от центра монтажных отверстий.
• Значения, отмеченные «*», указывают на то, что они соответствуют измерениям, проведенным с другой стороны автомобиля по симметричным меткам.
• Координаты мерных меток приведены в стандартной системе измерения по осям «X», «V» и «Z».
• Ось «Z» — воображаемая базовая линия (200 мм ниже базисной линии («0Z» на чертеже)).
1. Центр автомобиля. 2. Центр передней оси. 3. Воображаемая основная линия.
Центральные контрольные точки кузова
Центральные метки расположены на каждой части кузова для определения центра автомобиля. При восстановлении деталей, поврежденных в результате столкновения, способного нарушить геометрию автомобиля (элементы, стойки и т.п.), проведение более точного и эффективного ремонта возможно только при использовании данных меток со спецификацией кузовных размеров.
| Точка | Участок | Метка |
| А | Передняя часть крыши | Насечка |
| В | Верхняя часть капота | Насечка |
| С | Верхняя часть перегородки | Насечка |
| D | Усиливающий элемент рычага переключения коробки передач | Отверстие Ø 16 мм |
| Е | Усиливающий элемент стояночного тормоза | Отверстие Ø 12 мм |
| F | Задняя панель | Выступ |
| G | Задняя часть крыши | Насечка |
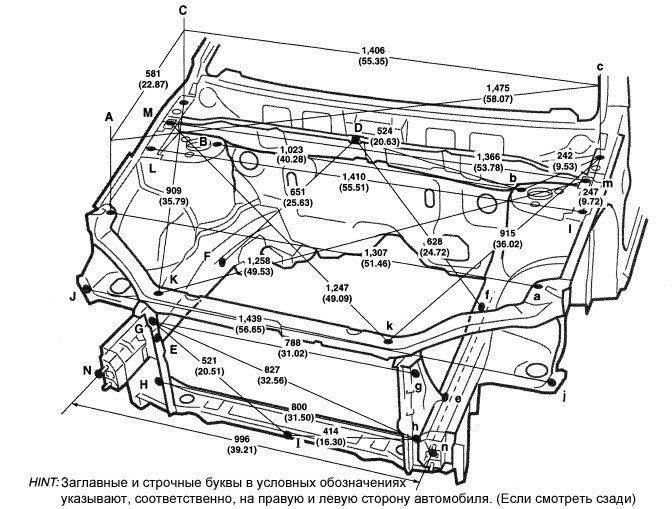
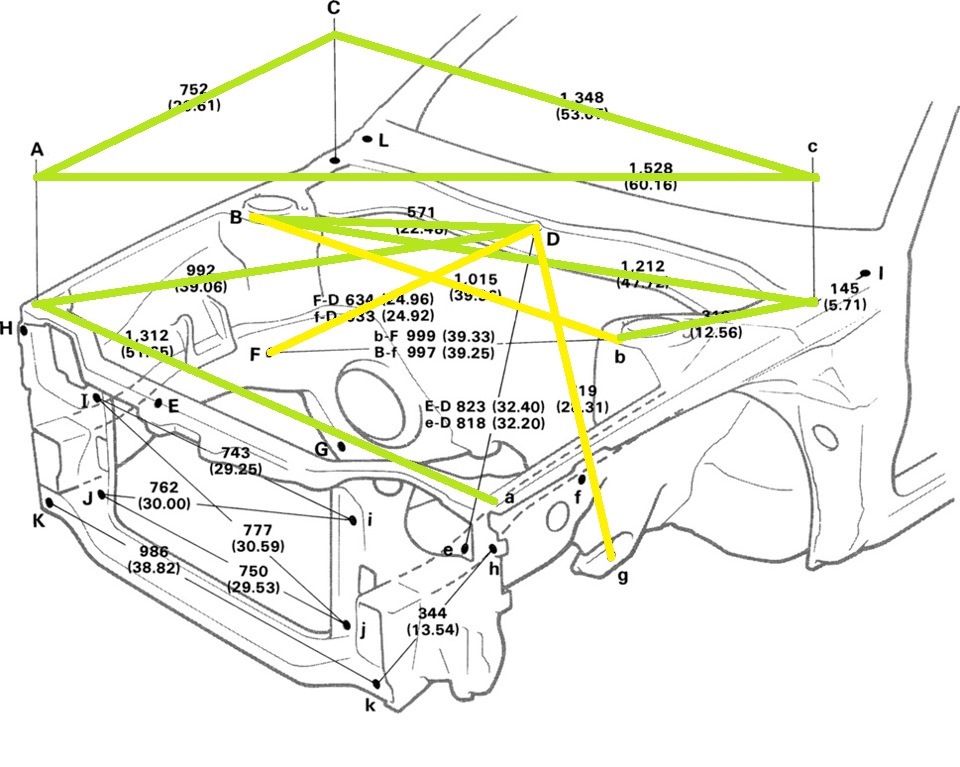
Размеры передней части кузова, моторный отсек
Неуказанные размеры
(Версии с передним приводом)
| Точки измерения | Размер | Точки измерения | Размер | Точки измерения | Размер | Точки измерения | Размер |
| А-С | 729 (28. 70)* 70)* | A-J | 673 (26.50) | 1441 (56.73) | F-f | 1366 (53.78) | |
| A-D | 729 (28.70)* | В-Е | 298 (11.73)* | D-d | 1429 (56.26) | G-h | 1192 (46.93)* |
| A-F | 798 (31.42)* | В-е | 1233 (48.54)* | Е-е | 1037 (40.83) | J-j | 965 (37.99) |
(Версии с полным приводом)
| Точки измерения | Размер | Точки измерения | Размер | Точки измерения | Размер | Точки измерения | Размер |
| А-С | 729 (28. 70)* 70)* | В-Е | 298 (11.73)* | D-d | 1429 (56.26) | G-h | 1192 (46.93)* |
| A-D | 729 (28.70)* | В-е | 1233 (48.54)* | Е-е | 1037 (40.83) | J-j | 958 (37.72) |
| A-F | 798 (31.42)* | С-с | 1441 (56.73) | F-f | 1366 (53.78) |
| Точка | Описание |
| А | Центральная метка кузова — насечка верхней части перегородки |
| В, b | Центр установочного отверстия навеса капота (14×10 мм) |
| С, с, F, f | Центр установочного отверстия переднего крыла (Ø 7 мм) |
| D,d | Центр установочного отверстия передней комбинированной фары головного освещения (Ø 7 мм) |
| Е, е | Центр установочного отверстия передней стойки 16×10 мм |
| G, g, Н, h | Центр установочного отверстия верхней опоры радиатора: G. g: Ø 12 мм H, h: 14×12 мм g: Ø 12 мм H, h: 14×12 мм |
| J | Центр отверстия передней боковой балки (Ø 7 мм) |
| j | Центр отверстия монтажного кронштейна двигателя (Ø 11 мм) |
| К, k, М, m | Центр установочного отверстия стойки переднего бампера (Ø 15 мм) |
Размеры днища кузова
Версии с передним приводом (2WD)
| Точка | Координаты | Описание | ||
| X | Y | Z | ||
| А | 473.5(18.642) | -557.0 (-21.929) | 293.0 (11.535) | Отверстие Ø 11 мм |
| а | -491. 0 (-19.331) 0 (-19.331) | -557.0 (-21.929) | 301.9(11.886) | Отверстие Ø 11 мм |
| в | 472.4(18.598) | -455.0 (-17.913) | 328.9 (12.949) | Отверстие Ø 16 мм |
| b | -489.7 (-19.279) | -455.0 (-17.913) | 328.9 (12.949) | Отверстие Ø 18 мм |
| С, С | ±410.0 (±16.142) | 547.0 (21.535) | 190.2 (7.488) | Отверстие Ø 16 мм |
| D, d | ±410.0 (±16.142) | 815.0 (32.087) | 184.0 (7.244) | Отверстие Ø 14 мм |
| Ее | ±410.0 (±16.142) | 1173.0 (46.181) | 170.1 (6.697) | Отверстие 14×2 мм |
| F, f | ±633.0 (±24.921) | 2032.3 (80.012) | 318.0(12.520) | Отверстие Ø 16 мм |
| G,g | ±350.0 (±13.780) | 2253. 0 (88.701) 0 (88.701) | 390.4(15.370) | Отверстие Ø 11 мм |
| Н, h | ±482.3 (±18.988) | 2374.2 (93.472) | 348.3 (13.713) | Отверстие Ø 12 мм |
| J | 499.5 (19.665) | 2448.0 (96.378) | 378.0 (14.882) | Отверстие Ø 21 мм |
| i | -487.5 (-19.193) | 2448.0 (96.378) | 378.0 (14.882) | Отверстие Ø 21 мм |
| К | 498.0 (19.606) | 2743.0 (107.992) | 378.0 (14.882) | Отверстие 17×16 мм |
| k | -487.5 (-19.193) | 2743.0 (107.992) | 378.0 (14.882) | Отверстие 17×16 мм |
| M | 498.0 (19.606) | 2970.0(116.929) | 375.4(14.779) | Отверстие Ø 16 мм |
| m | -485.1 (-19.098) | 2965.8(116.764) | 375. 4 (14 779) 4 (14 779) | Отверстие Ø 16 мм |
| N, n | ±583.6 (±22.976) | 6.6 (0.261) | 868.2(34.181) | Отверстие Ø 98 мм |
| O,o | ±575.4 (±22.653) | 2569.2(101 149) | 734.4 (28.913) | Отверстие Ø 20 мм |
Версии с полным приводом (4WD)
| Точка | Координаты | Описание | ||
| X | Y | Z | ||
| А | 473.5 (18.642) | -557.0 (-21.929) | 293.0(11.535) | Отверстие Ø 11 мм |
| а | -491. 0 (-19.331) 0 (-19.331) | -557.0 (-21.929) | 301.9(11.886) | Отверстие Ø 11 мм |
| в | 472.4 (18.598) | -455.0 (-17.913) | 328.9 (12.949) | Отверстие Ø 18 мм |
| b | -489.7 (-19.279) | -455.0 (-17.913) | 328.9 (12.949) | Отверстие Ø 18 мм |
| С, с | ±410.0 (+16.142) | 547.0 (21.535) | 190.2 (7.488) | Отверстие Ø 16 мм |
| D, d | ±410.0 (±16.142) | 815.0 (32.037) | 184.0 (7.244) | Отверстие Ø 12 мм |
| Е е | ±410.0 (±16.142) | 1173.0 (46.181) | 170.1 (6.697) | Отверстие 14×2 мм |
| F, f | ±601.8 (±23.693) | 2016.4(79.386) | 315.0(12.402) | Отверстие Ø 15 мм |
| G,g | ±515.1 (±20.279) | 2318. 6 (91.283) 6 (91.283) | 357.2 (14.063) | Отверстие Ø 12 мм |
| Н, h | ± 330.0 (±12.992) | 2339.7 (92.114) | 419.0 (16.496) | Отверстие 33×30 мм |
| J, i | ±482.0 (±18.976) | 2648.0 (104.252) | 422.2 (16.622) | Отверстие 20×6 мм |
| К, k | ±300.0 (±11.811) | 2815.0(110.827) | 417.2(16.425) | Отверстие 18×6 мм |
| М, m | ±482.7 (±19.004) | 2910.5(114.586) | 421.4(16.591) | Отверстие Ø 23 мм |
| N, n | ±583.6 (±22.976) | 6.6 (0.261) | 868.2(34.181) | Отверстие Ø 98 мм |
| O, о | ±558.6 (±22.000) | 2568.4(101.118) | 734.4(28.913) | Отверстие Ø 20 мм |
Размеры проёмов дверей и лобового стекла
Неуказанные размеры
| Точки измерения | Размер | Точки измерения | Размер | Точки измерения | Размер | Точки измерения | Размер |
| А-Е | 724(28.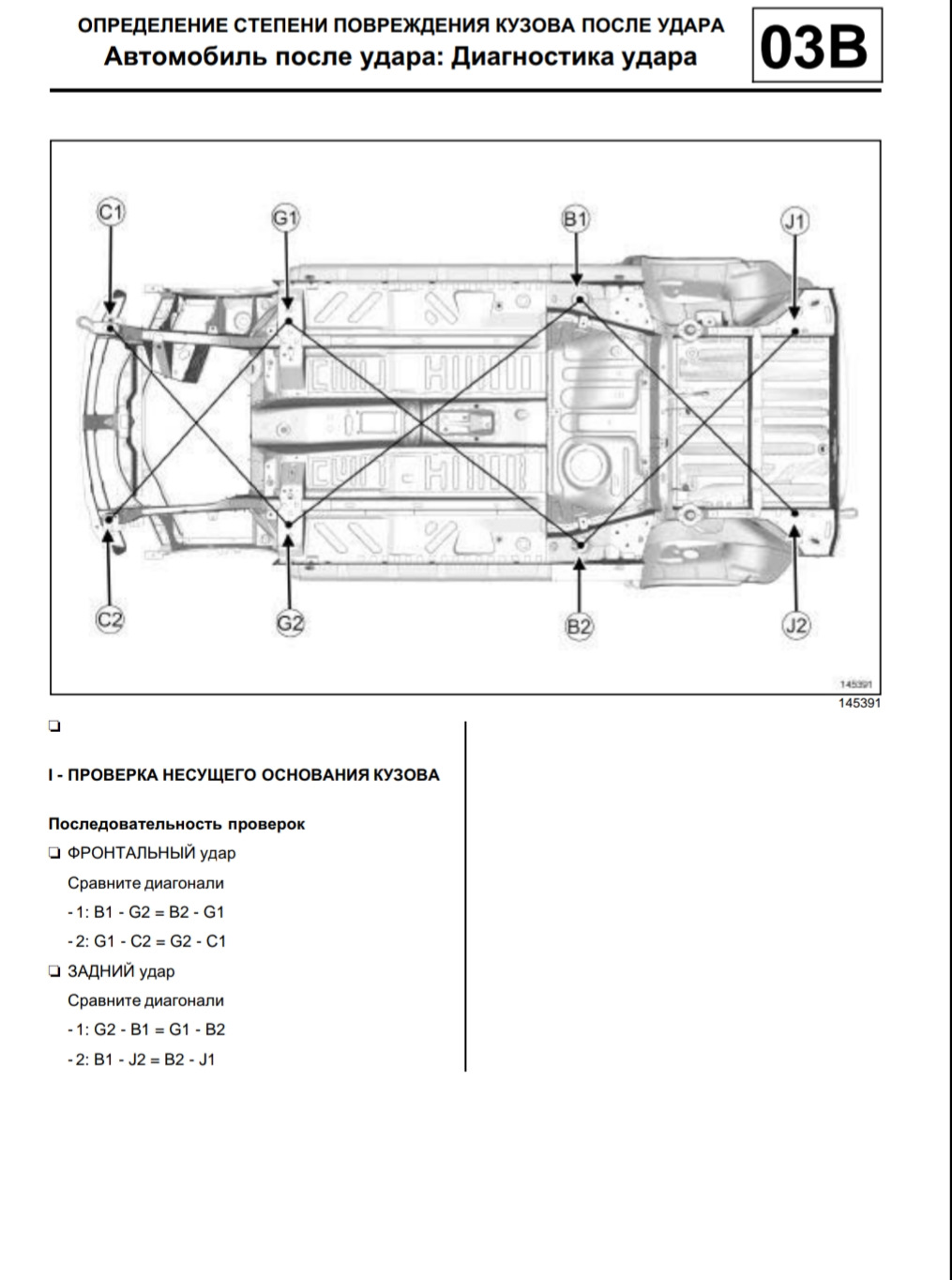 50)* 50)* | H-h | 1406 (55.35) | N-n | 1423 (56.02) | R-J | 1394 (54.88)* |
| В-Е | 1028 (40.47)* | H-j | 1829 (72.01)* | N-o | 1585 (62.40)* | R-K | 1072 (42.20)* |
| C-d | 1290 (50.79)* | H-k | 1663 (65.47)* | N-p | 1554(61 18)* | S-M | 1094 (43.07)* |
| С-е | 1423 (55.02)* | J-J | 1257 (49.49) | N-q | 1506 (59.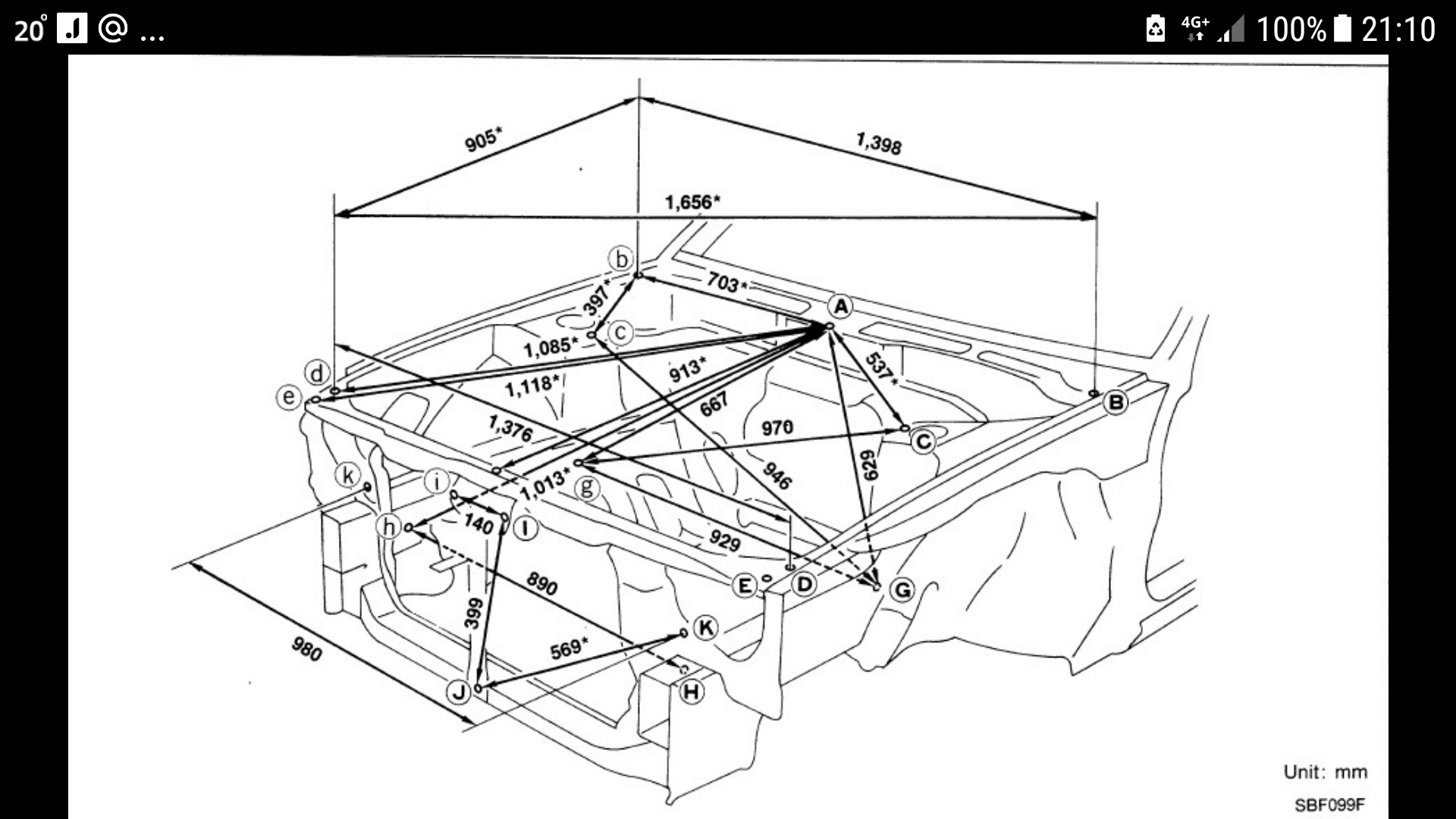 29)* 29)* | S-N | 786 (30.94)* |
| F-f | 1222 (48.11) | J-k | .1463 (57.60)* | O-o | 1326 (52.20) | S-0 | 1248 (49.13)* |
| F-h | 1569 (61 77)* | K-k | 1425 (56.10) | Oq | 1518 (59.76)* | S-P | 1126(44.33)* |
| F-j | 1386 (54.57)* | M-m | 1248 (49.13) | P-p | 1397 (55.00) | S-0 | 905 (35.63)* |
| F-k | 1519 (59.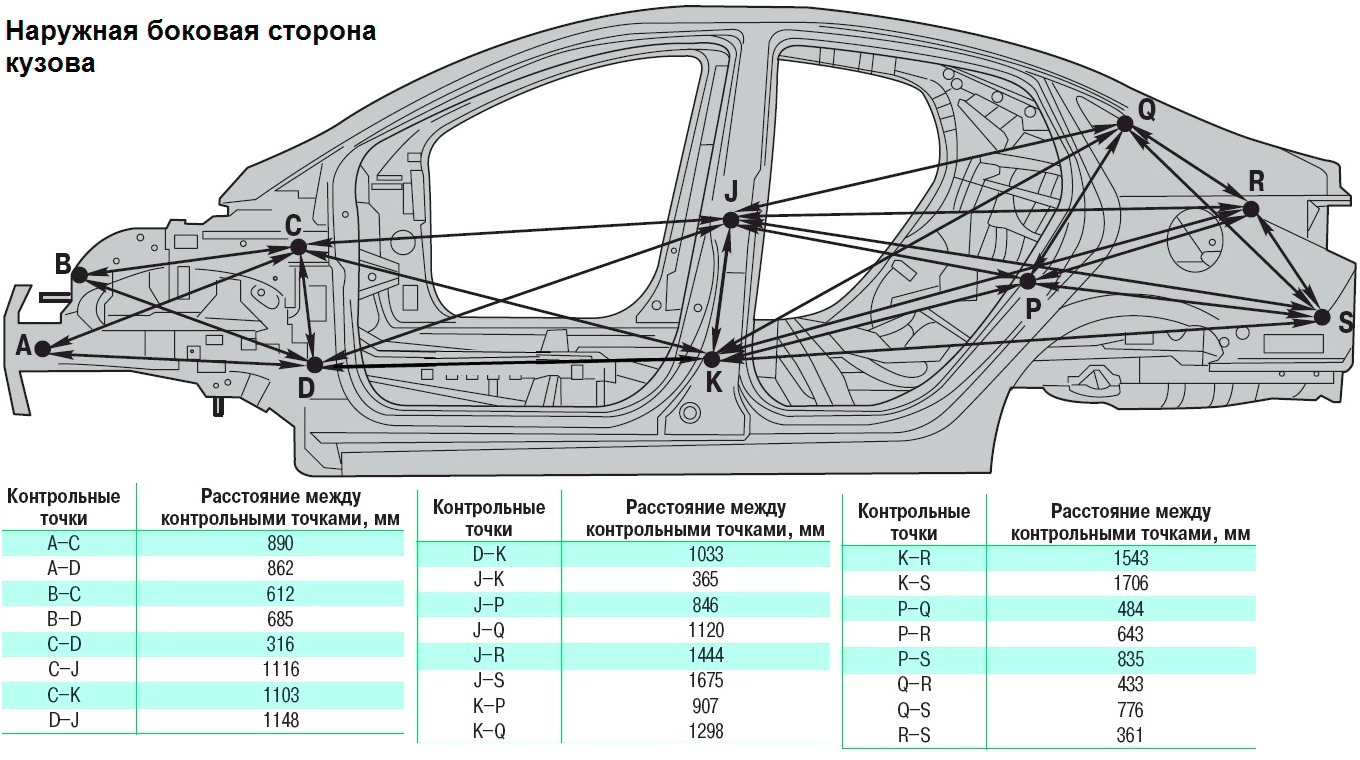 80)* 80)* | M-n | 1451 (5713)* | G-q | 1444 (56.85) | T-V | 1128 (44.41)* |
| G-g | 1359 (53.50) | M-o | 1441 (56.73)* | R-F | 1104 (43.46)* | T-W | 1105(43.50)* |
| G-j | 1630 (64.17)* | M-p | 1486 (58.50)* | R-G | 885 (34.84)* | U-V | 1204 (47.40)* |
| G-k | 1616 (63.62)* | M-q | 1578 (62.13)* | R-H | 720 (28.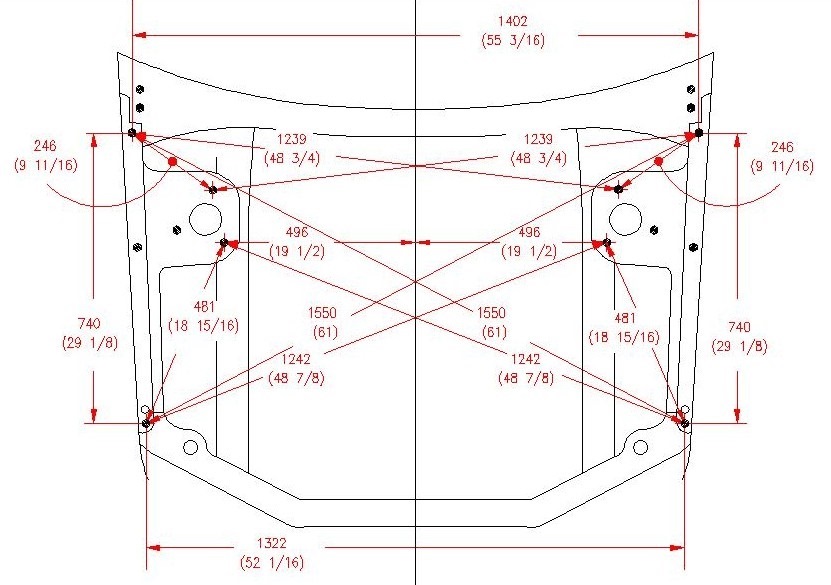 35)* 35)* | U-W | 1091 (42.95)* |
| Точка | Описание |
| А | Центральная метка кузова — насечка верхней части перегородки |
| В | Центральная метка кузова — выпуклость на краю крыши |
| С, с | Соединительный шип снаружи боковины кузова |
| D, d, G, g | Соединительный шип внутри передней стойки |
| Е, е | Центр установочного отверстия навеса капота (Ø 12 мм) |
| F, f, Н, h | Выпуклость передней стойки |
| J, j, К, k, М, т, N, n | Выпуклость центральной стойки |
| О, о,Q, q | Выпуклость заднего крыла |
| Р, p | Соединительный шип снаружи задней колесной арки |
| R | Центральная метка кузова — центр отверстия усиливающего элемента рычага переключения коробки передач (Ø 16 мм) |
| S | Центральная метка кузова — центр отверстия усиливающего элемента рычага стояночного тормоза (Ø 12 мм) |
| Т, t, U, u V, V, W, w | Центр установочного отверстия дверного навеса: T,t, U, u, W, w: Ø 12 мм V, v: Ø 9 мм |
Размеры проёма багажного отделения, задняя часть кузова
| Точка | Описание |
| А | Центральная метка кузова — выпуклость на краю крыши |
| В, b | Соединительный шип продолжения заднего крыла |
| С, с D, d | Соединительный шип основания заднего комбинированного фонаря |
| Е | Центральная метка кузова — выпуклость задней поперечины |
Габаритные и геометрические размеры кузова ВАЗ 2110
Сходящие с конвейера автомобили имеют строго выверенные кузовные размеры.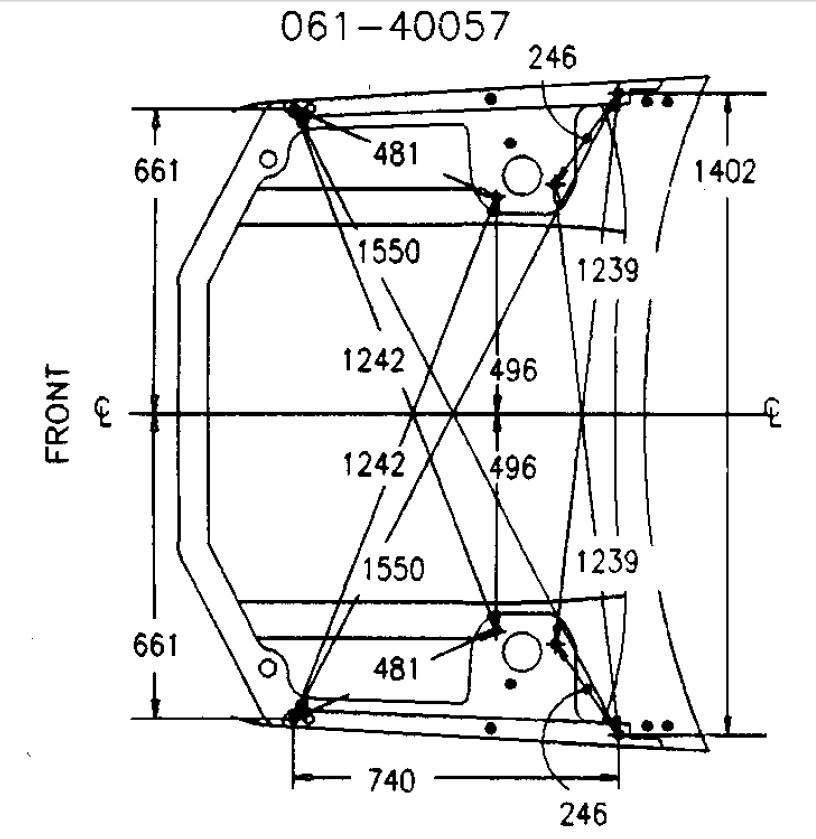 Как правило, при покупке нового автомобиля на это особого внимания никто не обращает.
Как правило, при покупке нового автомобиля на это особого внимания никто не обращает.
Однако потребность измерять и сверять с руководством по эксплуатации геометрические размеры кузова у ВАЗ 2110 может возникнуть в таких случаях:
- вы покупаете автомобиль с рук, и не уверены в том, что он не побывал в аварии. Именно из-за этого, как правило, чаще всего нарушается геометрия ВАЗ 2110;
- вы сами попали в аварию, даже налетели на камень, бордюр и т.п., от чего машина получила серьезный удар.
Основные справочные размеры точек крепления узлов и агрегатов
Заводские габариты
Все линейные размеры кузова ВАЗ 2110 можно найти, полистав книжку по эксплуатации или «порывшись» в интернете.
Но главные габариты таковы:
Длина:
- если взять конечные точки переднего и заднего бамперов, то здесь имеем 4265 мм;
- длина между центрами передних и задних колес, т.
 н. колесная база, составляет 2492 мм;
н. колесная база, составляет 2492 мм; - от центра переднего колеса до крайней точки переднего бампера – 829 мм;
- от центра заднего колеса до конечной точки заднего бампера – 944 мм.
С подробностями демонтажа бампера на ВАЗ 2110-2112 можно ознакомиться в данном материале: https://vazweb.ru/desyatka/kuzov/kak-snyat-bamper-na-vaz-2110.html
Высота ВАЗ 2110 – 1420 мм.
Заводские габариты по длине и ширине
Ширина:
- спереди по крайним точкам «заводских» зеркал – 1875;
- спереди без учета зеркал (чисто «железо») – 1680 мм;
- расстояние между центрами передних колес – 1400 мм;
- задняя часть автомобиля имеет ширину между центрами колес 1370 мм.
Визуальная проверка
Как проверить, что у ВАЗ 2110 все в порядке с геометрией кузова? Для визуального определения есть два метода, которые желательно применять оба:
- Визуальный осмотр стоящего автомобиля со всех сторон. Особое внимание следует уделить зазорам.
 У ВАЗовских машин они довольно заметные. Но главное – они должны быть одинаковыми с обеих сторон машины;
У ВАЗовских машин они довольно заметные. Но главное – они должны быть одинаковыми с обеих сторон машины;Размеры проемов и зазоры сопрягаемых деталей
- Проверка во время езды. Причем, находиться нужно не за рулем, а в машине, едущей вслед за «десяткой». Битая и «топорно» исправленная геометрия кузова выдаст себя тем, что машина на прямом участке дороги будет двигаться как бы немного боком.
Кузова у ВАЗ 2110 довольно надёжны и устойчивы перед коррозией, так как обрабатываются заводской антикоррозийной обработкой. Подробнее о преимуществах кузова данного автомобиля можно прочитать здесь: https://vazweb.ru/desyatka/kuzov/dlina-kuzova.html
Инструментальная проверка по контрольным точкам
И все же, далеко не всегда все так просто. И даже опытный глаз не всегда заметит маленькие «несоответствия». При грамотном ремонте кузова геометрические размеры можно проверить, только произведя замеры. Профессионалы для этого используют специальные измерители.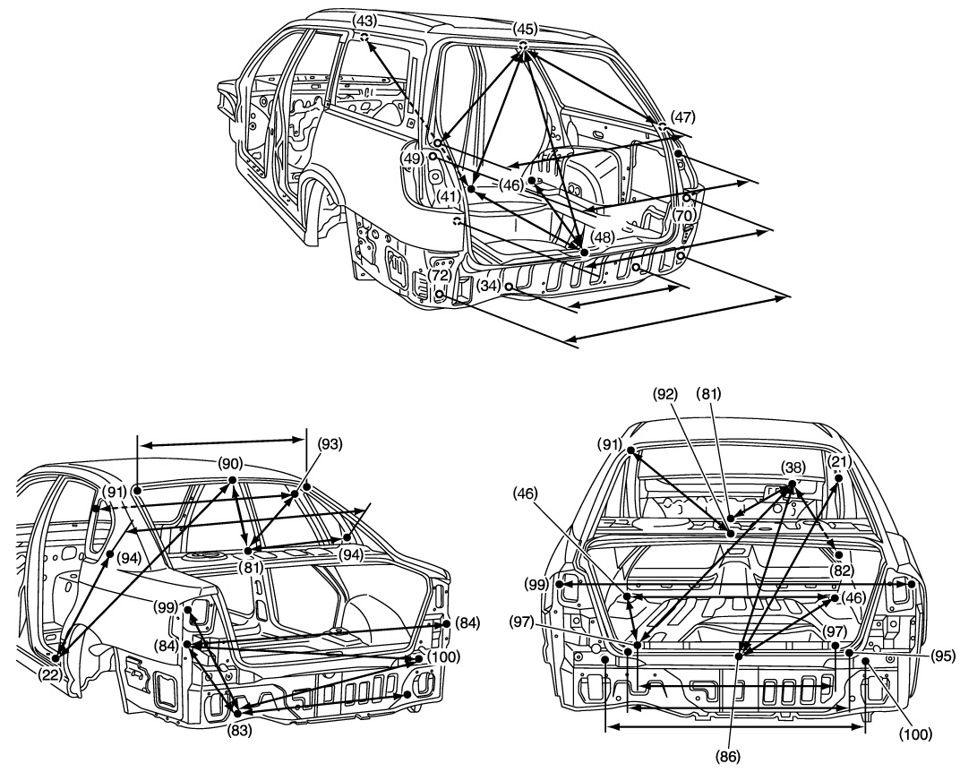
Но для проведения данной процедуры в домашних условиях достаточно обычной рулетки. Нужно найти специальные контрольные отметки, которые находятся на днище ВАЗовского кузова. Именно от них следует производить замеры. Как и в какой последовательности – можно узнать из эксплуатационной инструкции к ВАЗ 2110.
Если же, скажем, вам нужно убедиться, что линейные размеры именно вашей машины (например, вы меняли крылья, дверь и т.п.) совпадают, то не всегда следует доверять даже инструкции по эксплуатации, там тоже иногда можно найти ошибки.
Как контрольные габариты кузова используйте самолично снятые размеры с той стороны автомобиля, где никаких замен и рихтовок не проводилось.
Контрольные точки на кузове и днище
Снимать размеры необходимо по следующим точкам:
- Диагональ. Прежде, чем, используя контрольные точки, измерять кузовные размеры, можно сделать всего два замера, которые помогут прояснить картину.
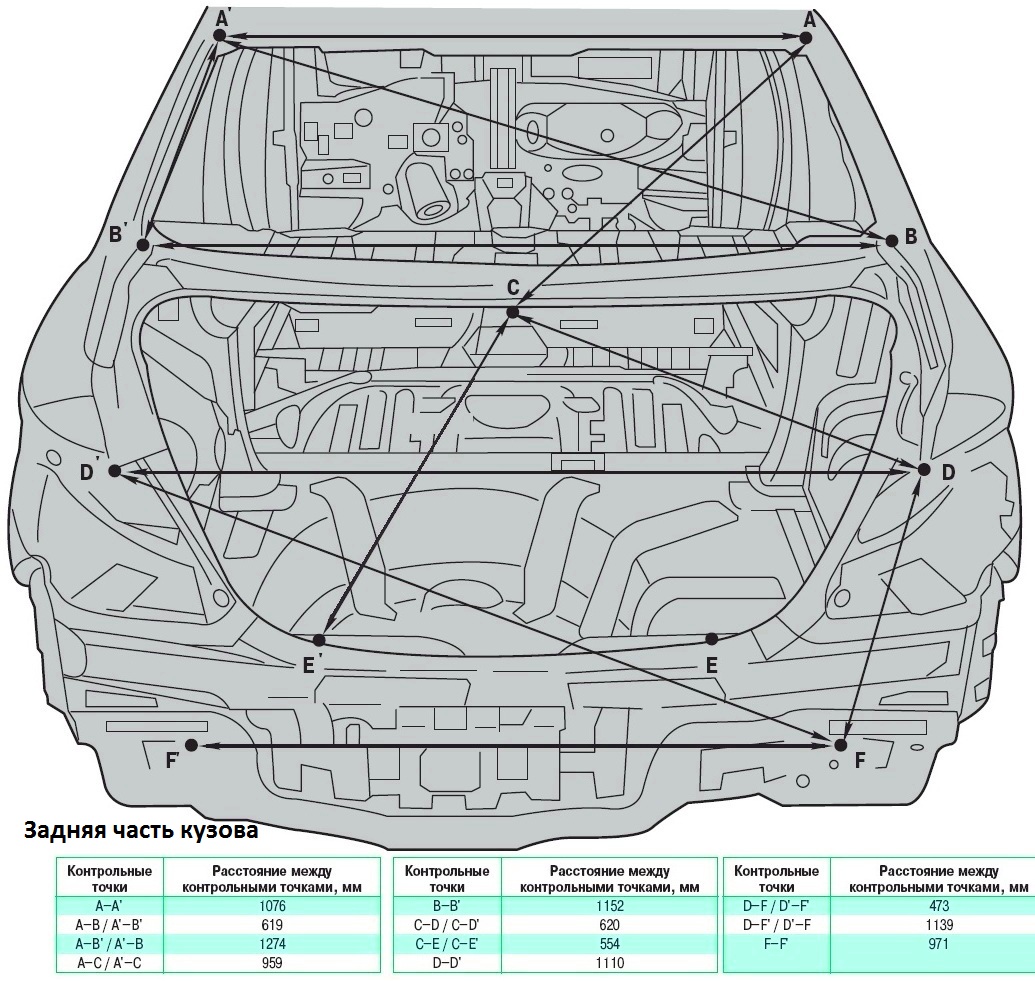 Загоните машину на эстакаду или яму и рулеткой снизу промерьте размеры по диагонали. Они должны совпадать, что называется, тютелька в тютельку. Совпадают? Отлично, но на этом останавливаться не стоит;
Загоните машину на эстакаду или яму и рулеткой снизу промерьте размеры по диагонали. Они должны совпадать, что называется, тютелька в тютельку. Совпадают? Отлично, но на этом останавливаться не стоит; - Стойки. Обязательно нужно проверить стойки. Вначале – с не битой стороны (если такая известна), затем – с битой. В принципе, кузовные точки в данном случае можно выбрать любые (главное – одни и те же с обеих сторон). К примеру, от стойки до края загиба на задних дверях. Также – на передних. Размеры совпадают – великолепно. Перемещаемся дальше;
- Крыша. Чтобы убедиться, что у ВАЗ 2110 не «повело» крышу, необходимо замерить размеры дверных диагоналей – от нижнего заднего угла по диагонали до верхнего переднего угла. Естественно, размеры с обеих сторон должны быть одинаковыми. Дополнительно к этому желательно померить и диагонали самой крыши;
- Переднее стекло. Почему-то многие считают, что если лобовое стекло «сидит» нормально, то контрольные замеры не нужны, мол, геометрические размеры кузова в порядке.
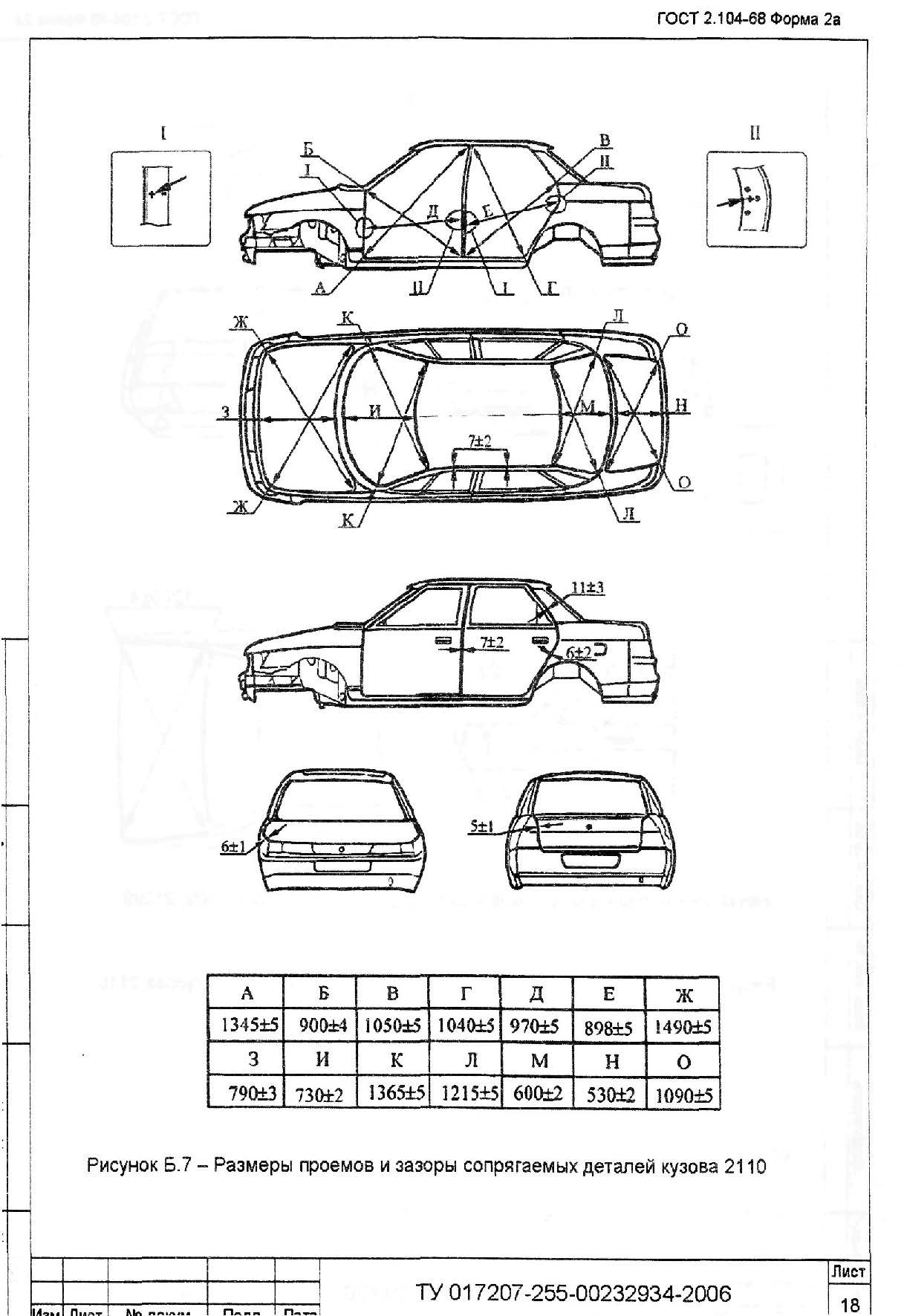 Это ошибка. Замерять нужно – причем, по диагонали, и выбрав точки на одинаковом расстоянии с обеих сторон.
Это ошибка. Замерять нужно – причем, по диагонали, и выбрав точки на одинаковом расстоянии с обеих сторон.
Тонкости кузовного ремонта
Ремонт кузова чаще всего проводится именно после ДТП, но также и в том случае, если какие-то детали проржавели. Но все же нужно стараться избегать сварочных и других работ, подразумевающих термическое нагревание металла.
Мелкие царапины и сколы в будущем могут стать очагом коррозии. Для того чтобы этого избежать, небольшие дефекты лучше всего подкрашивать. Подробности: https://vazweb.ru/desyatka/obschee/kak-podkrasit-skolyi-na-mashine-samomu.html
По возможности старайтесь не снимать лицевых панелей. Это также может привести к изменению кузовной геометрии. И после любых ремонтных работ, связанных с кузовом, обязательно проверяйте его линейные размеры.
Оцените статью: Поделитесь с друзьями!Геометрия кузова ВАЗ 2112 и его ремонт
Для самостоятельного решения проблемы восстановления деталей автомобиля ВАЗ 2112 требуется наличие геометрических размеров его кузова. В профессиональных мастерских обязательно учитываются эти параметры, и для каждой модели машины они индивидуальны. Нарушение кузовной геометрии подлежит устранению, поскольку оно значительно снижает безопасность езды на таком авто. Из этой статьи можно узнать важную информацию о показателях, от которых зависит качественный ремонт кузова ВАЗ 2112.
В профессиональных мастерских обязательно учитываются эти параметры, и для каждой модели машины они индивидуальны. Нарушение кузовной геометрии подлежит устранению, поскольку оно значительно снижает безопасность езды на таком авто. Из этой статьи можно узнать важную информацию о показателях, от которых зависит качественный ремонт кузова ВАЗ 2112.
Влияние геометрии кузова на управление
В процессе эксплуатации автомобиля ВАЗ 2112 рано или поздно происходит деформация кузовных деталей. От уровня их изношенности зависитбезопасность в дороге и легкость в управлении.
ВАЗ 2112 производится с 1999 года. Автокузов данной модели схож с модификацией 2110, разница в том, что первый немного короче второго.
Длина кузова 2112 составляет 4170 мм, объем багажного отсека составляет 400 литров. Благодаря данным изменениям агрегат проще поддается управлению в сравнении с десятой моделью.
Рулевое колесо позволяет легче и быстрее выполнять повороты.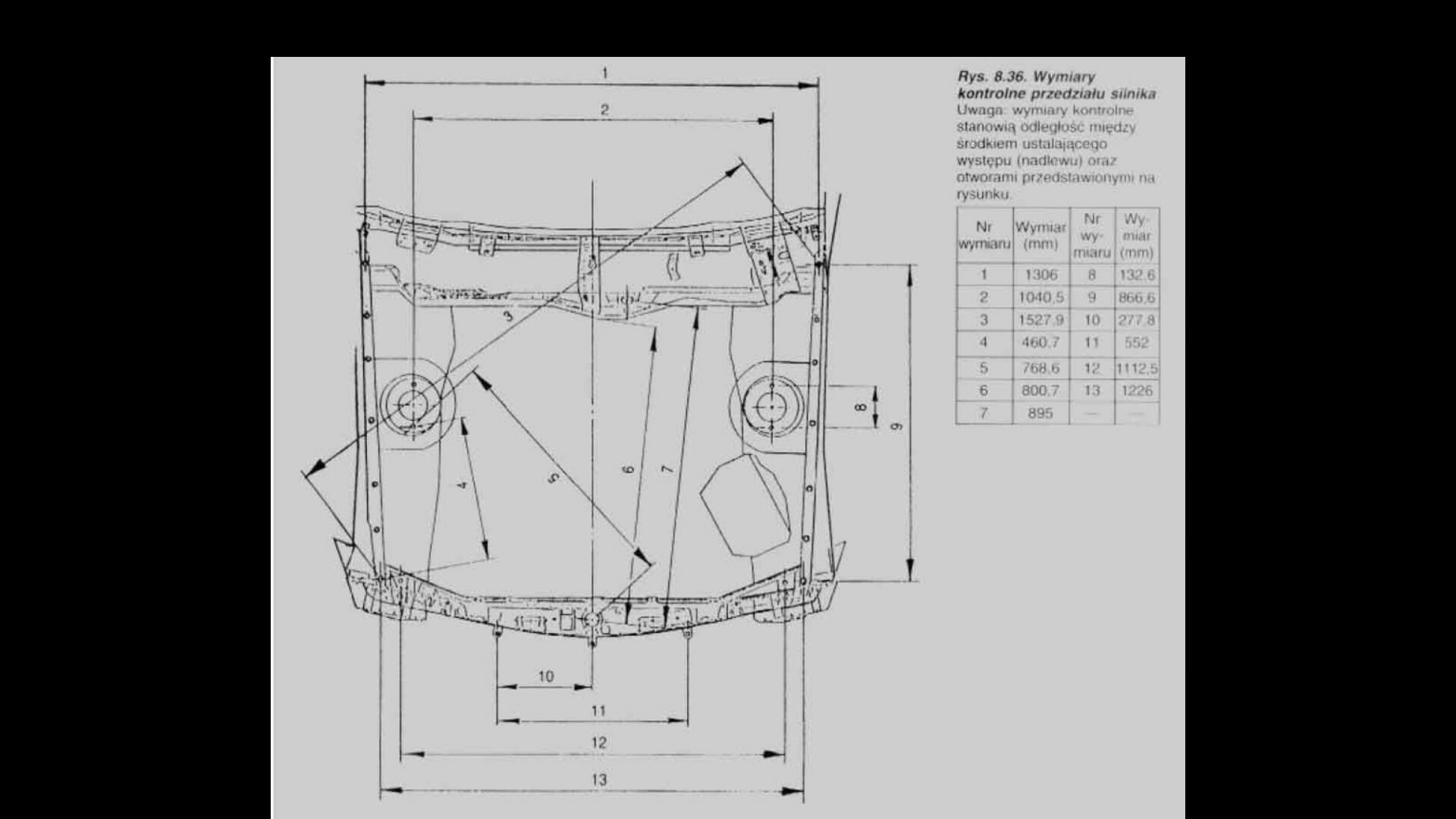
Модель 2112 характеризуется спортивным характером. В ней сочетаются выигрышные части, характерные для «десятки», а также заднее сиденье универсала от модели 2111, что сделало автомобиль намного вместительнее и маневреннее. Возможность трансформировать заднее сиденье позволяет при необходимости значительно увеличить объем салона. Усовершенствованные показатели управляемости упростили процесс входа в поворот, что существенно увеличило уровень безопасности участников движения на автодорогах.
ВАЗ 2112 имеет несколько модификаций, например, модель 21123 характеризуется оригинальным выполнением капота и бампера, что позволило кузову автомобиля стать популярным среди многих автолюбителей. Спустя некоторое время у ВАЗ 2112 появилась новая модель решетки, а капот принял стандартный вид.
Геометрические габариты «двенашки»
ВАЗ 2112 является одной из самых популярных моделей среди машин, которые выпускает отечественная автомобильная промышленность. Она сравнительно недорогая, обладает хорошим дизайном и разными исполнениями кузова.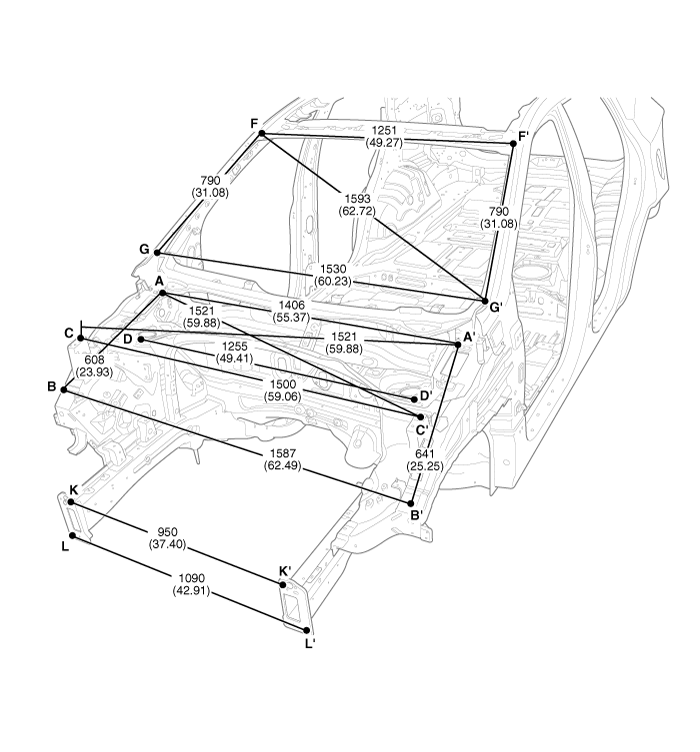
Основные геометрические размеры кузова этого авто таковы (в мм):
- длина – 4170;
- ширина без зеркал – 1680;
- высота – 1435;
- ширина с зеркалами – 1875;
- диагональ проема задней двери – 1320;
- короткая диагональ рамы бокового заднего окна – 230;
- расстояние между центром верхней балки проема задней двери до середины его нижней балки – 1050;
- длинная диагональ рамы бокового заднего окна – 710.
Самым редким типом кузова 2112 является купе, или трехдверный хэтчбек. Это спортивная модель, она выделяется на фоне других, которые однообразны в плане геометрических размеров кузова. Именно конструктивные особенности ВАЗ 2112 купе позволили модели стать в свое время востребованной. Однако после выпуска десяти тысяч экземпляров 2112 купе производство прекратилось, поэтому она считается редкой моделью.
Несколько модификаций ВАЗ 2112 оборудовались люками, что на порядок увеличило комфорт водителя и пассажиров в дороге.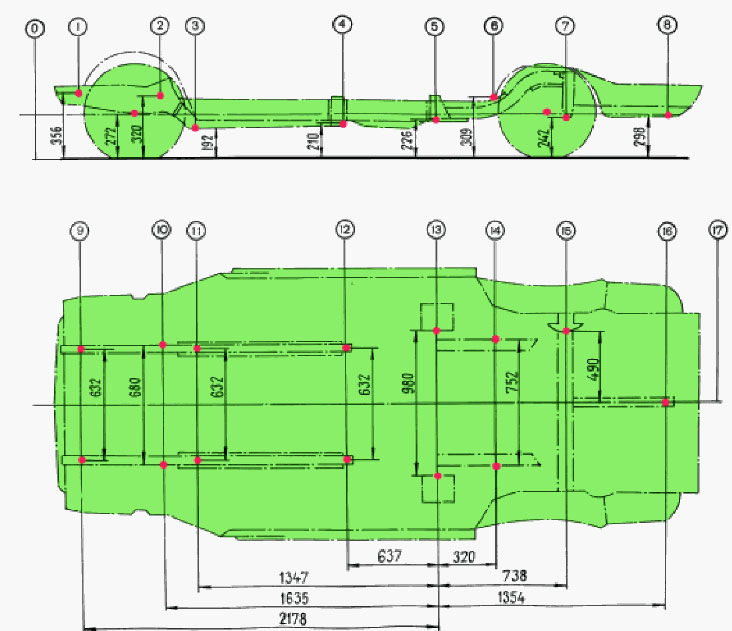 Показатели геометрических размеров 2112 позволили оборудовать автомобиль множеством дополнительных функциональных способностей.
Показатели геометрических размеров 2112 позволили оборудовать автомобиль множеством дополнительных функциональных способностей.
Части кузова, наиболее подверженные деформации
Резкое торможение или несвоевременный старт провоцируют, прежде всего, повреждение бампера. Если оно незначительное, то при ремонте можно достигнуть показателей стандартной геометрии. При наличии сложных деформаций сделать это невозможно, поэтому проще заменить поврежденную деталь кузова новой.
Если хозяин автомобиля недостаточным образом заботится о состоянии кузова, то те части, которые имеют близкий контакт с дорожным покрытием, быстро съедает коррозия. А произвести ремонт капота, дверей и скрытых деталей кузова вместо своевременной профилактики уже сложнее и дороже.
Интересное по теме:
Геометрические размеры кузова Daewoo.
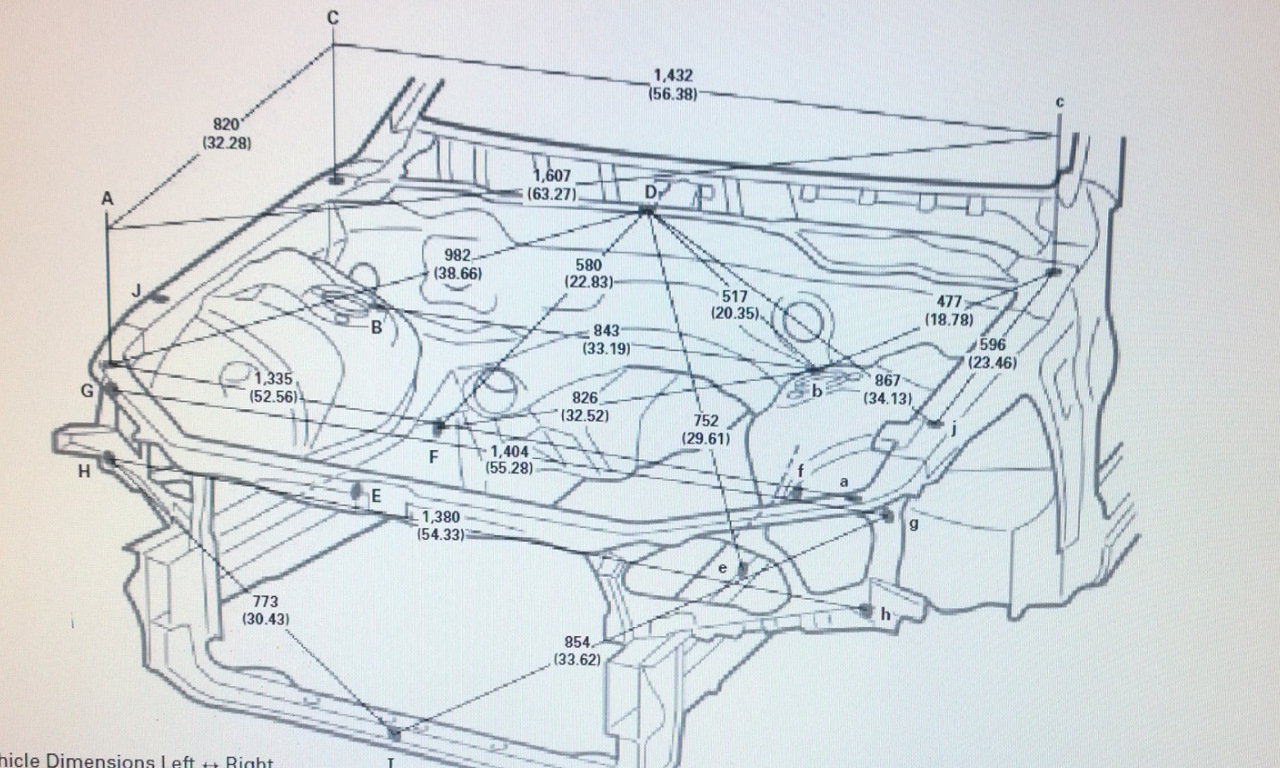 Информация о геометрических размерах и параметрах кузова, с фотографиями контрольных точек кузовов продукции компании DAEWOO.
Информация о геометрических размерах и параметрах кузова, с фотографиями контрольных точек кузовов продукции компании DAEWOO. Геометрические размеры кузова 2000г. Daewoo Lanos.
СкачатьГеометрические размеры кузова 2000г. Daewoo Leganza.
СкачатьГеометрические размеры кузова 2000г. Daewoo Nubira.
СкачатьГеометрические размеры кузова Daewoo.
Контрольные точки геометрии кузова.
Геометрические размеры DAEWOO ARCADIA SEDAN модель WA19 (1994—г.)
СкачатьГеометрические размеры DAEWOO ESPERO NOTCHBACK TYPE JF19 (1990-1995г.)
СкачатьГеометрические размеры DAEWOO ESPERO 4-DOOR SEDAN (1995-2001г.)
СкачатьГеометрические размеры DAEWOO NEXIA, CIELO, RACER 3-дверный HATCHBACK (1995—г.)
СкачатьГеометрические размеры DAEWOO NEXIA, CIELO, RACER 4-дверный SEDAN (1995—г.)
СкачатьГеометрические размеры DAEWOO NEXIA, CIELO, RACER 5-дверный HATCHBACK (1995—г.)
СкачатьГеометрические размеры DAEWOO ESPERO 4 -дверный SEDAN (1995—г. )
)
Геометрические размеры DAEWOO ESPERO NOTCHBACK модель JF19 (1990—г.)
СкачатьГеометрические размеры DAEWOO EVANDA 4-дверный SEDAN (2003-2004г.)
СкачатьГеометрические размеры DAEWOO LANOS 3-дверный HATCHBACK (1997—г.)
СкачатьГеометрические размеры DAEWOO LANOS 4-дверный SEDAN (1997—г.)
СкачатьГеометрические размеры DAEWOO LANOS 5-дверный HATCHBACK (1997—г.)
СкачатьГеометрические размеры DAEWOO LACETTI 5-дверный HATCHBACK (2004—г.)
СкачатьГеометрические размеры DAEWOO LEMANS 4-дверный SEDAN модель TF19 (1986—г. )
СкачатьГеометрические размеры DAEWOO LEGANZA 4-дверный SEDAN (1997—г.)
СкачатьГеометрические размеры DAEWOO LUBLIN II TRUCK (1998—г.)
СкачатьГеометрические размеры DAEWOO LUBLIN II VAN (1998—г.)
СкачатьГеометрические размеры DAEWOO KALOS 4-дверный SEDAN (2003-2004г.)
СкачатьГеометрические размеры DAEWOO KALOS 5-дверный HATCHBACK (2003-2004г.)
СкачатьГеометрические размеры DAEWOO KORANDO 4WD WAGON (1997-2002г. )
)
Геометрические размеры DAEWOO MATIZ 5-дверный (1998—г.)
СкачатьГеометрические размеры DAEWOO NUBIRA 4-дверный SEDAN (1997—г.)
СкачатьГеометрические размеры DAEWOO NUBIRA 5-дверный HATCHBACK (1997—г.)
СкачатьГеометрические размеры DAEWOO NUBIRA 5-дверный WAGON (1997—г. )
СкачатьГеометрические размеры DAEWOO NUBIRA 4-дверный SEDAN. (1999-2003г.)
СкачатьГеометрические размеры DAEWOO NUBIRA 5-дверный WAGON. (2000-2004г.)
СкачатьГеометрические размеры DAEWOO NUBIRA 5-дверный WAGON.. (2004—г.)
СкачатьГеометрические размеры DAEWOO NUBIRA LACETTI 4-дверный SEDAN (2003-2004г.)
СкачатьГеометрические размеры DAEWOO TICO 5-дверный HATCHBACK (1992—г.)
СкачатьГеометрические размеры DAEWOO TACUMA, REZZO 5-дверный WAGON, MPV (2000-2004г.)
СкачатьИздательство: Третий Рим
Автор: Погребной С.Н.
Страниц: 384 Год: 2009
Размер: 40Мб.
Для работников СТО и автосервисов. Поддерживать машину в надлежащем рабочем состоянии, экономить время и деньги.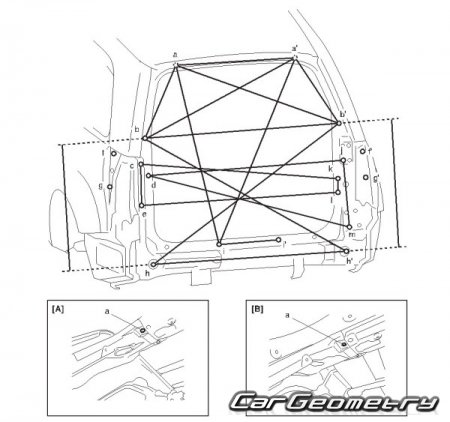 Мануал содержит более 2000 цветных снимков, досконально отображающих процесс пошагового ремонта Дэу Нексия, в том числе ремонта двигателя, технические характеристики автомобиля, перечни возможных неисправностей и рекомендации по их устранению.
Скачать
Мануал содержит более 2000 цветных снимков, досконально отображающих процесс пошагового ремонта Дэу Нексия, в том числе ремонта двигателя, технические характеристики автомобиля, перечни возможных неисправностей и рекомендации по их устранению.
Скачать
Геометрические размеры кузова ваз 2115
Lada 2115, 2114
Подборка размеры кузова, данные по геометрии кузова ВАЗ 2115 и контрольным точкам ВАЗ 2115, ВАЗ — 2114 из заводской документации.
Значительная часть ремонтных работ по автомобилям, тем более поступающим после дорожно-транспортных происшествий, приходится на ремонт кузовов. В большинстве случаев при ремонте требуется проверка геометрии точек крепления узлов и агрегатов шасси автомобиля.
Размеры кузова ВАЗ 2115: 0 – базовые линии; 1 – оси передних болтов крепления растяжек передней подвески; 2 – центр опоры передней подвески силового агрегата; 3 – центр опоры левой подвески силового агрегата; 4 – центры верхних шарниров передних телескопических стоек передней подвески; 5 – центры шарниров рычагов передней подвески; 6 – точки пересечения осей приварных болтов крепления рулевого механизма с поверхностями кронштейнов; 7 – точки крепления задней опоры подвески силового агрегата; 8 – точки пересечения осей задних приварных болтов крепления рычагов задней подвески с поверхностями задних лонжеронов; 9 – центры верхних опор амортизаторов задней подвески
Повреждения кузова автомобилей могут быть самыми различными.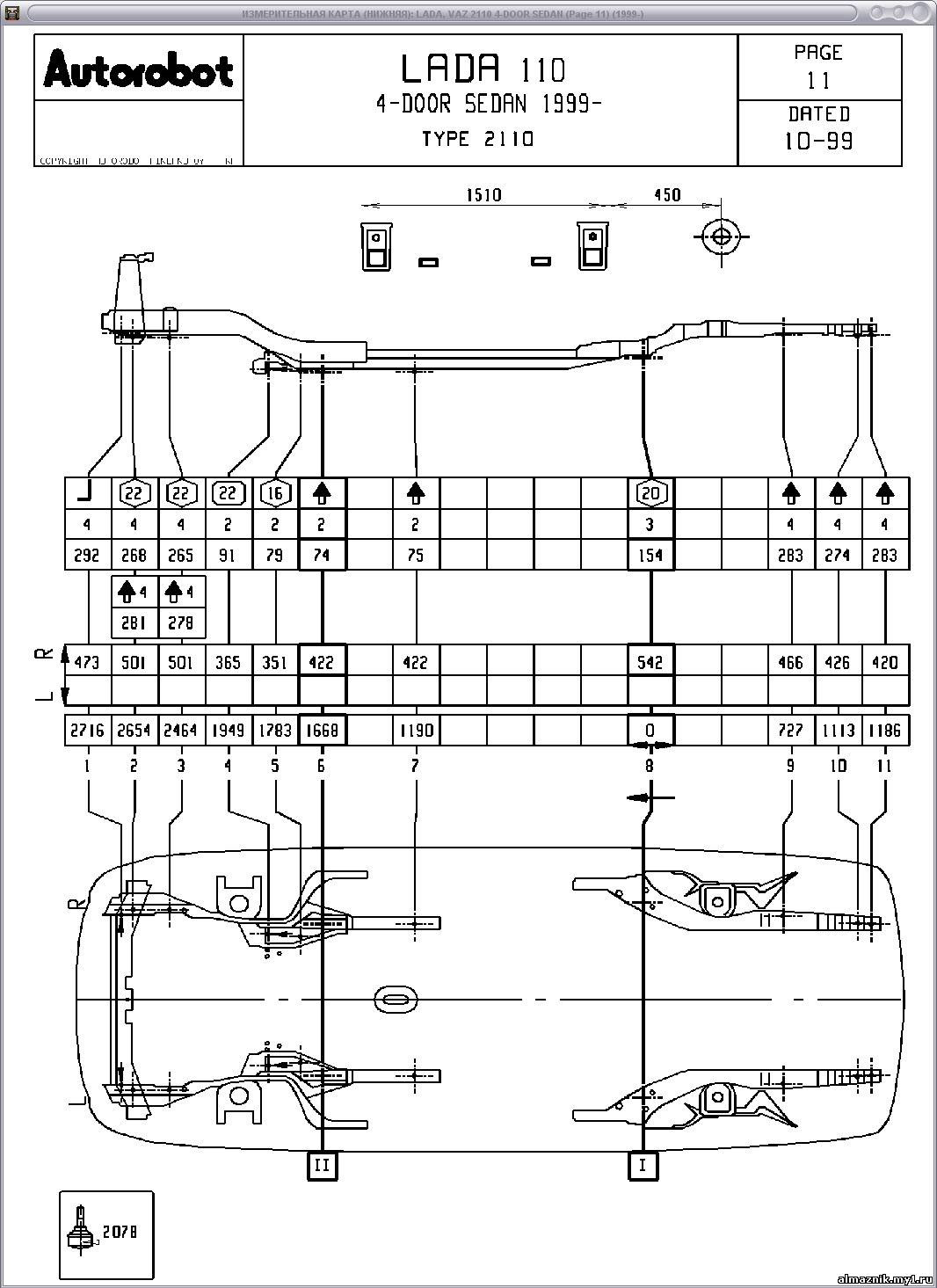 Поэтому правила ремонта в каждом отдельном случае должны быть свои, наиболее подходящие для этих повреждений, при этом необходимо максимально использовать возможности рихтовки поврежденных панелей. По возможности необходимо избегать термического воздействия на металл, чтобы не нарушать заводскую сварку и антикоррозионную защиту кузова. Лицевые панели кузова снимать только в крайних случаях, чтобы определить места повреждений, выправить или выверить кузов.
Поэтому правила ремонта в каждом отдельном случае должны быть свои, наиболее подходящие для этих повреждений, при этом необходимо максимально использовать возможности рихтовки поврежденных панелей. По возможности необходимо избегать термического воздействия на металл, чтобы не нарушать заводскую сварку и антикоррозионную защиту кузова. Лицевые панели кузова снимать только в крайних случаях, чтобы определить места повреждений, выправить или выверить кузов.
В случаях значительных повреждений кузова рекомендуется снимать все внутренние обивочные детали, чтобы облегчить измерение, контроль и установку гидравлических и винтовых домкратов для устранения перекосов и повреждений кузова.
Правкой необходимо восстановить первоначальные линейные размеры и местоположения силовых агрегатов, размеры проемов ветрового окна, капота, дверей. Выступание лицевых поверхностей и съемных деталей относительно соседних панелей устраняется их подгонкой и регулировкой.
Контрольные размеры кузова, данные по геометрии Lada 2115 и контрольным точкам Ваз 2115 из различных ремонтных баз.
Стоимость скачивания файла: 10.00 usd Ссылка будет доступна в течении 16 ч. после оплаты
После оплаты на указанный емейл будет выслана ссылка на скачивание файла, либо вы можете
повторно нажать кнопку ‘Купить’ и загрузка файла начнется автоматически.
Какие размеры кузова ВАЗ-2115
Кузов ВАЗ-2115 пришел на смену достаточно популярному у российских потребителей, но серьезно устаревшему корпусу 21099. Обще черты предшественницы без труда можно разглядеть у более новой модели.В то же время 2115 получил немало и уникальных отличительных особенностей. К таковым следует отнести:
В этом материале будет рассказано, каковы размеры кузова ВАЗ-2115 и другие особенности его внешнего вида.
Изменения
В целом, невзирая на определенную схожесть, 2115 имеет значительно более современный дизайн. Во многом это произошло благодаря наличию бамперов и других внешних элементов, изготовленных из пластика. Все они позволяют защитить кузов от мелких повреждений и негативного действия коррозии.
Наиболее заметные нововведения в этой модели следующие:
- добавочный тормозной сигнал, установленный непосредственно на спойлере;
- новые задние огни;
- высоконадежная система безопасности;
- порожек багажной двери, разрешивший снизить высоту погрузки;
- более обтекаемая геометрия кузова;
- молдинги на дверях;
- современное электрическое оборудование.
На момент завершения проектирования ВАЗ-2115 был современной и достаточно красивой машиной. При этом салон намного у нее оказался более комфортный, чем у старых моделей Волжского автозавода. Водитель получил возможность регулировать:
- высоту руля;
- положение сиденья и пр.
Между передними креслами конструкторы установили консоль. Более совершенной также оказалась и система обогрева, и ЭБУ. Причем багажник у рассматриваемой модели намного вместительней, чем у предшественниц.
Проектировщики немало элементов позаимствовали от 2114, при этом многие приборы и узлы перешли по наследству от «восьмерки». К примеру, неизменной перекочевала в новый седан ходовая часть.
К примеру, неизменной перекочевала в новый седан ходовая часть.
Основные понятия
Геометрией кузова именуют точные размеры транспортного средства, установленные конструкторами завода-производителя. Основные параметры, имеющие первостепенное значение таковы:- ширина – как передней, так и задней колей;
- протяженность колесной базы;
- расстояние между лонжеронами и их длина.
Как показывает практика, нарушение одного или сразу нескольких упомянутых выше параметров, приводит к заметному ухудшению в плане управляемости машины.
Второстепенные габариты следующие:
- проемы дверей;
- окон;
- объем отсека двигателя;
- вместительность багажника;
- размер салона машины.
Если происходит нарушение указанных нормативов, то это приводит только к ухудшению внешнего вида средства передвижения.
Колеей именуют расстояние, пролегающее между соосными колесами. Причем эта дистанция измеряется от точки до точки, которые расположены по центру протектора.
В свою очередь, колесной базой называют расстояние между осями автомобиля. Контрольные точки здесь – середина ступиц.
Составляющие части кузова и их размеры у ВАЗ-2115
Кузов в автомашине ВАЗ-2115 является несущим элементом всей конструкции. По типу данная модель считается 5-дверным седаном, приводимым в движение полуторалитровой силовой установкой.Каркас кузова машины состоит из таких элементов:
- крыша;
- боковины;
- основание;
- неразборные части;
- навесные узлы;
- части интерьера.
В число навесных входят:
- капот;
- двери;
- крылья;
- бамперы;
- радиаторная декоративная решетка;
- крышка багажного отделения.
- длина автомобиля составляет в миллиметрах – 4330;
- от середины переднего колеса до передка – 860;
- от центра переднего до середины заднего колес – 2460;
- до задка от последней упомянутой точки – 1010;
- общая высота транспортного средства – 1420;
- дистанция между боковыми зеркалами – 1979;
- расстояние между колесами, расположенными спереди – 1400;
- габарит бампера, установленного сзади – 1650;
- задние колеса расположены друг от друга на 1370 миллиметров.
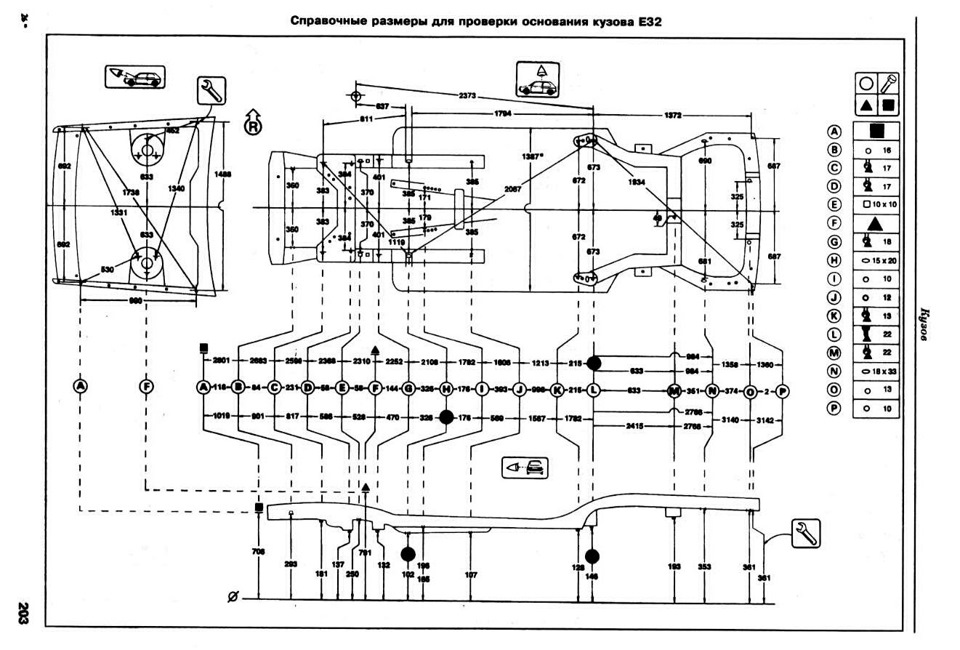
Геометрия кузова ВАЗ 2114: размеры и особенности
Геометрия кузова ваз 2114 определяется, как и в любых других моделях, по уникальным контрольным точкам, которые предусмотрел автопроизводитель. Подобный параметр может быть нарушен не только в результате ДТП, но даже и при попадании колеса движущегося автомобиля в открытый люк либо глубокую яму.
Геометрия кузова ваз 2114 и ее значение
Нарушения геометрии кузова имеют определенные последствия, которые отражаются на общем состоянии автомобиля такими проявлениями:
- Ухудшение управляемости и вибрации в момент набора скорости (проявляется при 80км/ч и выше).
- Увеличение износа резины.
- Шум элементов подвески.
- Рост расхода топлива и пр.
ВАЗ 2114 имеет тип кузова хэтчбек, для которого, впрочем, как и для других типов (универсал, седан и пр.), нарушение геометрии влияет на различные параметры.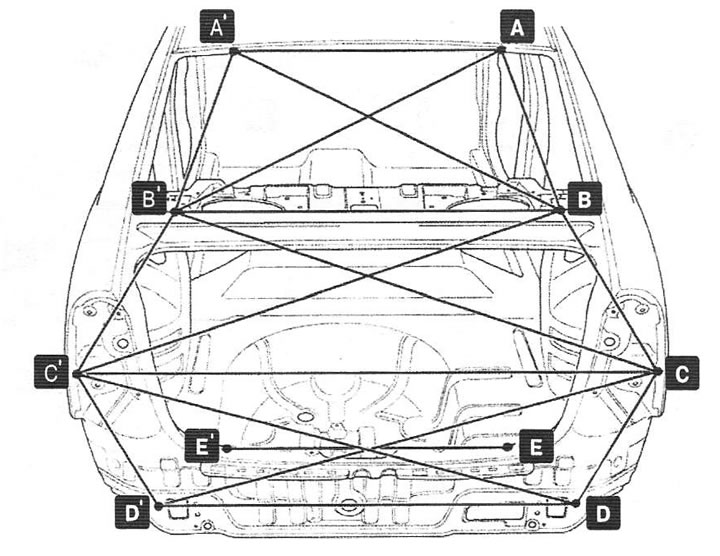
Симметрия колес нарушается, о чем можно судить по:
- снижению устойчивости машины на трассе;
- неравномерному износу шин.
У кузова нарушаются диагонали, что заметно по рамкам передних/задних стекол и по дверным проемам авто.
На днище или раме могут образоваться специфические складки.
Для автомобилей, которые подолгу эксплуатируются на дорогах плохого качества, рекомендуется периодическое проведение проверки геометрии кузова (не реже 1-2 раза в год).
Кузов четырнадцатой модели и его особенности
Четырнадцатой модели можно сказать, что она относится к российским автомобилям нового класса, имея максимальное приближение к иномаркам. При этом ВАЗ 2114 все же остается автомобилем народным. Однако, при желании автовладелец может тюнинговать авто, с легкостью превратив его в стильный спорткар, который имеет стремительные кузовные линии и современный обвес.
Кузов этой марки авто стоит рассмотреть отдельно, поскольку он имеет очень удачное конструкторское решение.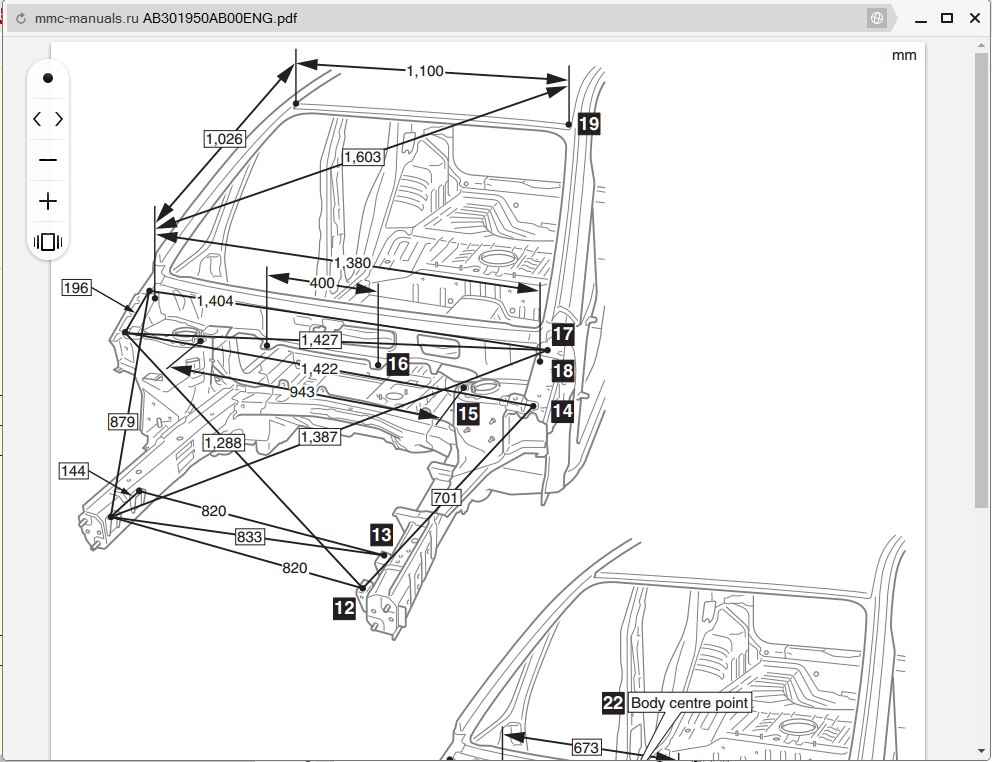 По аналогии с другими моделями ВАЗа, для соединения кузовных частей используют надежные болтовые либо сварные соединения. Весь кузов, включая самые труднодоступные места, тщательно обработан антикором.
По аналогии с другими моделями ВАЗа, для соединения кузовных частей используют надежные болтовые либо сварные соединения. Весь кузов, включая самые труднодоступные места, тщательно обработан антикором.
Этот факт не исключает необходимости дополнительной обработки, которая гарантированно обеспечит кузовным элементам дополнительные стойкость и долговечность.
Основным отличием кузова ваз 2114 является его граненая форма. Именно она придает модели привлекательный внешний вид. Но имеется и недостаток – процессы коррозии чаще затрагивают полые места в каркасе. В этом отношении можно выделить передние стойки, которые в машинах четырнадцатой модели страдают довольно часто.
Передние крылья автомобиля можно с легкостью снять. Бамперы выполнены из пластмассы, но имеют дополнительное усиление в виде алюминиевых балок.
Габаритные размеры кузова ваз 2114
Габаритные размеры кузова 2114 (в мм) имеют такие значения:
- Длина – 4122.
- Ширина – 1650.
- Высота – 1402.
Если учитывать факт, что данная ВАЗовская модель имеет тип кузова хэтчбек, то не лишним будет отметить, что багажный отсек довольно вместительный (объем 330л), а при складывании задних сидений общий объем достигает 600 литров.
Геометрия кузова ваз 2114 размеры – это важный показатель состояния авто. На этот момент следует обращать внимание тем автоводителям, которые решили приобрести подержанную машину.
Правка поврежденного кузова
Очень большой процент работ по ремонту автомобилей ваз 2114 после ДТП приходится именно на кузовные работы. В ходе ремонта обязательно следует контролировать геометрию кузова по контрольным точкам.
Поскольку повреждения автомобилей могут быть совершенно разными, то и единых правил восстановления не существует. В каждом случае понадобиться свой подход, однако важно по максимуму использовать те возможности, которые дает рихтовки поврежденных поверхностей. При этом термическое воздействие на металл следует минимизировать, сохраняя целостность заводской сварки и защиты кузова от коррозии.
Касательно лицевых панелей: снимать их нужно лишь в крайнем случае.
Основные задачи, которые при этом решаются:
- Выявление мест повреждений.
- Выправление кузова.
- Выверение кузова.
Если кузов автомобиля поврежден значительно, то следует снимать все обивочные детали внутри. Эта мера позволит существенно упростить измерения и контроль, а также облегчить установку винтовых и гидравлических домкратов (для устранения имеющихся на кузове повреждений и перекосов).
Для полного анализа нарушений геометрии кузова на СТО используют современные стенды. На них в полуразобранном состоянии машина закрепляется, а дальнейшая диагностика проводится при помощи высокоточных электронных датчиков. Эти датчики предоставляют на головной компьютер полную картину состояния кузова.
Конечно, можно самостоятельно проверить соответствие кузова авто тем стандартам, которые предусмотрел производитель. Для этого опытному водителю достаточно измерить диагонали при помощи обычной рулетки. Однако подобные измерения не будут отличаться точностью. Гораздо целесообразнее обратиться на специализированное СТО.
Однако подобные измерения не будут отличаться точностью. Гораздо целесообразнее обратиться на специализированное СТО.
Не стоит пренебрегать систематической процедурой контроля геометрии кузова ваз 2114, поскольку, даже наличие небольших отклонений может со временем привести к серьезным последствиям, а их устранение – к большим денежным тратам.
Геометрические размеры кузова ваз 2115
Геометрия отремонтированного кузова определяется:
— величинами зазоров по дверям, капоту и крышке багажника;
— углами установки управляемых колес;
— взаимным расположением подвесок, мостов.
Размеры проемов и зазоры сопрягаемых деталей кузова ВАЗ-1111
Размерыпроемов и сопрягаемых деталей кузова VAZ-2101-2107
Размеры проемов и сопрягаемых деталей кузова VAZ-2108,2113
Размеры проемов и сопрягаемых деталей кузова VAZ- 2108
Размеры проемов и сопрягаемых деталей кузова VAZ-2109
Размеры проемов и сопрягаемых деталей кузова VAZ-2115
Размеры проемов и сопрягаемых деталей кузова VAZ-2110
Размеры проемов и сопрягаемых деталей кузова VAZ-2111,2112.21123
Размеры проемов и сопрягаемых деталей кузова VAZ-2121,21213,2131
Размеры проемов и сопрягаемых деталей кузова VAZ-2123
Размеры проемов и сопрягаемых деталей кузова VAZ-2120
Размеры проемов и сопрягаемых деталей кузова VAZ-1118
Размеры проемов и сопрягаемых деталей кузова VAZ-1117
Размеры проемов и сопрягаемых деталей кузова VAZ-1119
Размеры проемов и сопрягаемых деталей кузова VAZ-2170
Размеры проемов и сопрягаемых деталей кузова VAZ-2172
Размеры проемов и сопрягаемых деталей кузова VAZ-2170
Точки крепления двигателя и подвесок на кузове VAZ-1111
Точки крепления двигателя и подвесок на кузове VAZ-2101,2107
Точки крепления двигателя и подвесок на кузове VAZ-2108, 2109, 21099, 2113, 2114, 2115
Точки крепления двигателя и подвесок на кузове VAZ-2110, 2111, 2112, 2170
Точки крепления двигателя и подвесок на кузове VAZ- 21213
Точки крепления двигателя и подвесок на кузове VAZ-2123
Точки крепления двигателя и подвесок на кузове VAZ-2131
Точки крепления двигателя и подвесок на кузове VAZ-2120
Точки крепления двигателя и подвесок на кузове VAZ-1118, 1117, 1119
Схема замера межосевых размеров
Линейные размеры Лада Гранта
Размеры разъемов дверей Лада Гранта
Размеры моторного отсека автомобиля Лада Гранта
Размеры рамки ветрового стекла автомобиля Лада Гранта
Размеры рамки заднего стекла автомобиля Лада Гранта
Размеры проема двери багажного отделения автомобиля Лада Гранта
Размеры днища кузова автомобиля Лада Гранта
0 0 голос
Рейтинг статьи
Что такое твердые геометрические формы или тела?
Вы наверняка знаете о плоских геометрических фигурах, поэтому сегодня мы поговорим о твердых геометрических фигурах , которые также известны как геометрических фигур или тел .
Эти фигуры имеют три измерения — длину, глубину и высоту. Другими словами, эти цифры имеют объем и можно сказать, что они занимают место в космосе.
Основные типы твердых геометрических фигур
Многогранники
Слово многогранник происходит от греческого слова «поли», что означает много и от «эдрон», что означает основание или сиденье .Мы говорим о геометрических формах, которые имеют несколько граней и являются плоскими. Среди них у нас:
- Правильные многогранники: они известны как платоновы тела и характеризуются наличием равных граней. Их пять: тетраэдр, шестигранник (куб), октаэдр, додекаэдр и икосаэдр.
- Призмы: состоят из двух многоугольных оснований одинакового размера и формы, а их боковые грани представляют собой параллелограммы.
- Пирамиды: состоят из многоугольной грани, которая является его основанием, и боковых граней в форме треугольников.
В реальной жизни мы можем найти очень много объектов в форме многогранников, таких как кубик льда, пирамида или пакет молока.
Характеристики многогранников:- Грань : грани многогранника — это плоские поверхности на внешней стороне многогранника.
- Ребро: ребра многогранников состоят из сторон, образующих каждую грань.
- Вершины: вершины многогранника — это точки пересечения его ребер. Три грани встречаются в одной вершине.
Круглые тела
Есть несколько твердых геометрических фигур, полностью состоящих из изогнутых и плоских поверхностей. Среди них наиболее часто встречаются круглые тела:
- Конус: круглый корпус, состоящий из круглого основания и изогнутой поверхности.
- Сфера: полностью искривленное геометрическое тело, состоящее из искривленной поверхности.
- Цилиндр: геометрическое тело, состоящее из изогнутой поверхности и двух плоских круглых оснований.
Мы можем найти множество круглых тел в реальных объектах, таких как вулкан (конус), бильярдный шар (сфера) или ведро с краской (цилиндр). Если вы хотите продолжать изучать геометрические фигуры и другие темы первичной математики, зарегистрируйтесь в Smartick и попробуйте бесплатно!
Подробнее:
Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.
Геометрия энергии в человеческом теле
Обладая необходимым выравниванием, вы сможете упражнять свое воображение таким образом, чтобы вы могли проявлять то, что вы хотите, вне себя. Чтобы усилить свое воображение, вам нужно поднять направленный вверх треугольник, который с точки зрения геометрии тела является фундаментом, до такой степени, что он включает в себя вишуддхи , который является основой вашего воображения. .Есть садхана, чтобы поднять его и удерживать там все время. Если у вас нет такой садханы, простой способ достичь этого — не есть какое-то время. Обычно, когда желудок пуст, треугольник, направленный вверх, имеет тенденцию подниматься сам по себе. Как только вы едите, он снова спускается.
Важность сохранения подвижности чакр
В теле сто четырнадцать чакр . Семьдесят две тысячи нади , или энергетические пути в системе, имеют сто четырнадцать важных точек соединения, где нади встречаются в значительном количестве и перераспределяются.Эти точки обычно называются чакрами, что буквально означает «колесо» или «круг», хотя на самом деле они являются треугольниками. Мы называем их «чакрами», потому что это предполагает движение — движение вперед. Из этих ста четырнадцати двое находятся за пределами физического царства. Для большинства людей эти двое очень слабы, если не совершат необходимую садхану. Из оставшихся ста двенадцати чакр несколько обычно расположены в определенных частях тела на физиологическом уровне. Остальные чакры могут до некоторой степени двигаться.
Выполнение необходимой работы для поддержания подвижности чакр важно, потому что подвижность чакр определяет, насколько вы гибки и эффективны в различных типах ситуаций, чтобы соответствовать различным типам требований.
Способ движения чакр зависит от того, что вы делаете с собой. Если вы хотите дать себе силы выполнять различные виды деятельности и приспосабливаться к различным типам ситуаций, физиология праны или физиология чакр тела должна иметь возможность соответствующим образом адаптироваться.Выполнение необходимой работы по поддержанию подвижности чакр важно, потому что подвижность чакр определяет, насколько вы гибки и эффективны в различных типах ситуаций, чтобы соответствовать различным типам требований. Проблема большинства людей в одной ситуации: они хорошо функционируют. В другой ситуации они в полном беспорядке. Это потому, что они могут думать, чувствовать и действовать только определенным образом.
Вы должны уметь все делать хорошо, немного попрактиковавшись.Но это не сработает, если ваша энергетическая система жесткая. Итак, поддерживать мобильность вашей системы важно не только потому, что мы хотим заниматься разными видами деятельности в мире. Это также дает вам определенную гибкость опыта, позволяющую вам чувствовать себя комфортно в любой ситуации. Чтобы чувствовать себя непринужденно, ваша энергия должна быть гибкой. Эти сто двенадцать чакр можно использовать как сто двенадцать дверей к вашей высшей природе. Вот почему Адийоги дал сто двенадцать способов достичь высшего.
Чтобы иметь возможность перемещать эту сложную треугольную структуру вашей физиологии так, как вы этого хотите, требуется другой уровень садханы. Но самое главное — эти два треугольника должны пересекаться. Обычно треугольник, указывающий вверх, находится внизу, а треугольник, направленный вниз, вверху. Если вы поднесете два равносторонних треугольника к точке, где они пересекаются таким образом, что они образуют звезду с шестью равносторонними треугольниками, система находится в равновесии и становится очень восприимчивой.Моя работа — это присутствие и передача чего-то, для чего вам нужна восприимчивость. Мои слова не просветят вас. Я говорю только то, что сбивает вас с толку, потому что вы не можете никого просветить, говоря. Именно присутствие способно трансформировать.
От выводов к заблуждению к сознанию
Разговор — хороший инструмент только для того, чтобы разрушить идиотские выводы, которые делают люди. Когда выводы разрушаются, возникает путаница. Радостно запутаться во вселенной — хорошее состояние.Это значит, что вы постоянно на все обращаете внимание. Как только вы понимаете, что ничего не знаете, вы становитесь восприимчивыми. Если у вас есть выводы обо всем, нет возможности, нет восприимчивости. Если есть выводы, не надо быть внимательным — по жизни можно идти как мертвый. Чем больше вы сделаете выводов, тем больше окоченения будет в вашем сознании и в вашем теле.
Когда выводы разрушаются, возникает путаница. Радостно запутаться во вселенной — хорошее состояние.Это значит, что вы постоянно на все обращаете внимание.
Если вы занимаетесь хатха-йогой каждый день, вы заметите, что в день, когда ваше отношение к чему-то жесткое, ваше тело не сгибается. В другой день, когда вы будете счастливы и умственно гибкими, ваше тело будет сгибаться намного лучше. Природа вашего сознания проявляется в каждой клетке вашего тела, в каждый момент вашей жизни. Вот почему сегодня в мире существует много видов болезней, вызываемых самим собой. Никогда раньше у людей не было такого количества вариантов еды, как сегодня.Раньше люди ели то, что было доступно на месте. Сегодня, несмотря на такое разнообразие, очень много болезней. На самом деле, чем больше у людей выбора, тем хуже они становятся.
Подписаться
Получайте еженедельные обновления последних блогов с помощью информационных бюллетеней прямо в свой почтовый ящик.
Соединенные Штаты, вероятно, являются одной из стран с наибольшим разнообразием выбора продуктов питания, но они также тратят огромные деньги на здравоохранение — три триллиона долларов в год.Это преступление против человечности. Если болеют те, кто не получает достаточного питания, это понятно. Но если те, кто хорошо ест, болеют, значит, что-то фундаментальное идет не так. Мы не поняли, что каждая клетка вашего тела была создана природой вашего сознания. Если вы не знаете, как сохранить природу своего сознания в хорошем состоянии, вы не будете знать, как сохранить в хорошем состоянии свою систему. Тогда вы будете действовать случайно, чего не должно быть.
Мы, люди, делаем то же, что и другие существа — едим, спим, размножаемся и умираем.Одна вещь, которая отличает нас, это то, что мы поднимаем много шума из-за всего этого, просто в стороне. Самая важная разница в человеческих существах заключается в том, что мы можем делать все это полностью осознанно. Например, вы можете полностью осознанно есть. Допустим, вы голодны. Если бы вы были каким-то другим существом, вы бы просто подобрали все, что вам подходит, и сожрали бы это. Но как человеческое существо вы можете ждать до еды, сидеть за столом, повторять заклинание и вместо того, чтобы набивать лицо обеими руками, есть правой рукой.Это осознанно. Если вы идете по телу в одиночку, вам сразу захочется поесть. Но поскольку у вас есть необходимый интеллект и осознание, чтобы сдерживать навязчивые действия тела, вы можете сознательно реагировать на ситуацию. Если кто-то ведет себя очень компульсивно, говорят, что он как животное. Итак, это путь от компульсивности к сознанию.
Сознание дает вам возможность освободиться от своих наклонностей. Даже если до этого момента вами управляли всевозможные тенденции, если вы откликаетесь сейчас полностью осознанно, между вами и накопленными у вас склонностями будет дистанция.Если вы сделаете каждый аспект жизни осознанным — не только в действии, но также в мыслях, эмоциях и энергии, — вы будете на вершине мира.
Примечание редактора: Найдите больше идей Садхгуру в электронной книге «О мистиках и ошибках», в которой Садхгуру напоминает нам, что каждый из нас может пройти путь от заблуждения к ясности, от ошибки к просветлению, от себя. обман к самопознанию — если только мы выберем.
Версия этой статьи была первоначально опубликована в Isha Forest Flower.Загрузите в формате PDF «назовите свою цену, без минимума» или подпишитесь на версию для печати.
Размер, форма и форма: концепции аллометрии в геометрической морфометрии
Адамс Д.К., Нистри A (2010) Онтогенетическая конвергенция и эволюция морфологии стопы у европейских пещерных саламандр (семейство: Plethodontidae). BMC Evol Biol 10: 216
PubMed PubMed Central Статья Google Scholar
Adams DC, Rohlf FJ, Slice DE (2013) Поле достигает зрелости: геометрическая морфометрия в 21 веке.Hystrix 24: 7–14
Google Scholar
Airoldi J-P, Flury B (1988) Применение анализа общих главных компонентов к морфометрии черепа у Microtus californicus и M. orchogaster (Mammalia, Rodentia). J Zool (Lond) 216: 21–36
Статья Google Scholar
Барбейто-Андрес Дж., Вентрис Ф., Анзельмо М., Пуччарелли Х.М., Сарди М.Л. (2015) Ковариация развития свода и основания человека на протяжении всего постнатального онтогенеза.Анн Анат 197: 59–66
PubMed Статья Google Scholar
Бастир М., О’Хиггинс П., Росас А. (2007) Онтогенез лица у неандертальцев и современных людей. Proc R Soc Lond B Biol Sci 274: 1125–1132
Статья Google Scholar
Бастир М. и др. (2015) Актуальность первых ребер из местонахождения Эль-Сидрон (Астурия, Испания) для понимания грудной клетки неандертальцев.J Hum Evol 80: 64–73
PubMed Статья Google Scholar
Baur H, Leuenberger C (2011) Анализ соотношений в многомерной морфометрии. Syst Biol 60: 813–825
PubMed PubMed Central Статья Google Scholar
Bensmihen S, Hanna AI, Langlade NB, Micol JL, Bangham A, Coen E (2008) Мутационные пространства для формы и размера листа. HFSP J 2: 110–120
PubMed PubMed Central Статья Google Scholar
Berge C, Kazmierczak J-B (1986) Влияние размера и двигательной адаптации на таз гоминида: оценка двуногости австралопитеков с помощью нового многомерного метода.Folia Primatol 46: 185–204
CAS PubMed Статья Google Scholar
Birch JM (1999) Аллометрия черепа морской жабы, Bufo marinus . J Morphol 241: 115–126
CAS PubMed Статья Google Scholar
Boitard M, Lefebvre J, Solignac M (1982) Анализируйте основные составные части вариабельности хвоста, круассанов и конформации сложных форм Jaera albifrons (Crustacés Isopodes).Cah Biol 23 марта: 115–142
Google Scholar
Bolzan DP, Pessôa LM, Peracchi AL, Strauss RE (2015) Аллометрические закономерности и эволюция у неотропических летучих мышей, питающихся нектаром (Chiroptera, Phyllostomidae). Acta Chiropt 17: 59–73
Статья Google Scholar
Bookstein FL (1986) Размер и форма пространства для данных ориентиров в двух измерениях (с комментариями и репликой).Stat Sci 1: 181–242
Статья Google Scholar
Bookstein FL (1989) «Размер и форма»: комментарий к семантике. Syst Zool 38: 173–180
Статья Google Scholar
Bookstein FL (1991) Морфометрические инструменты для ориентировочных данных: геометрия и биология. Издательство Кембриджского университета, Кембридж
Google Scholar
Bookstein FL, Chernoff B, Elder RL, Humphries JM, Jr., Смит Г.Р., Штраус Р.Э. (1985) Морфометрия в эволюционной биологии: геометрия изменения размера и формы, с примерами из рыб, специальная публикация 15. Академия естественных наук Филадельфии, Филадельфия
Брейкер К.Дж., Паттерсон Дж.С., Klingenberg CP (2006) Единая основа для буферизации развития формы крыла Drosophila . PLoS ONE 1, e7
PubMed PubMed Central Статья Google Scholar
Булыгина Е., Миттерокер П., Айелло Л. (2006) Онтогенез лицевого диморфизма и паттерны индивидуального развития в пределах одной человеческой популяции.Am J Phys Anthropol 131: 432–443
CAS PubMed Статья Google Scholar
Барнаби Т.П. (1966) Рост-инвариантные дискриминантные функции и обобщенные расстояния. Биометрия 22: 96–110
Статья Google Scholar
Cadima JFCL, Jolliffe IT (1996) Анализ главных компонентов, связанных с размером и формой. Биометрия 52: 710–716
Статья Google Scholar
Calder WA III (1984) Размер, функции и жизненный цикл.Издательство Гарвардского университета, Кембридж
Google Scholar
Чапова М., Златницка И., Ковач В., Катина С. (2008) Онтогенетическая изменчивость внешней морфологии бычка-обезьяны, Neogobius fluviatilis (Pallas, 1814) и ее отношение к потенциалу инвазии. Hydrobiologia 607: 17–26
Статья CAS Google Scholar
Cardini A, Polly PD (2013) Более крупные млекопитающие имеют более длинные лица из-за ограничений, связанных с размером черепа.Nat Commun 4: 2458
PubMed Статья CAS Google Scholar
Chatzigianni A, Halazonetis DJ (2009) Геометрическая морфометрическая оценка формы шейных позвонков и ее связь с созреванием скелета. Am J Orthod Dentofacial Orthop 136: 481.e481–481.e489
Google Scholar
Cheverud JM (1982) Взаимосвязь онтогенетической, статической и эволюционной аллометрии.Am J Phys Anthropol 59: 139–149
CAS PubMed Статья Google Scholar
Кобб С.Н., О’Хиггинс П. (2007) Онтогенез полового диморфизма лицевого скелета африканских обезьян. J Hum Evol 53: 176–190
PubMed Статья Google Scholar
Cock AG (1966) Генетические аспекты метрического роста и формы животных. Q Rev Biol 41: 131–190
CAS PubMed Статья Google Scholar
Крейтон Г.К., Штраус Р.Э. (1986) Сравнительные модели роста и развития грызунов-крикетинов и эволюция онтогенеза.Evolution 40: 94–106
Статья Google Scholar
Дарроч Дж. Н., Мосиман Дж. Э. (1985) Канонические и основные компоненты формы. Биометрика 72: 241–252
Артикул Google Scholar
Дэвис Р.Г., Браун В. (1972) Многофакторный анализ постэмбрионального роста двух видов Ectobius (Dictyoptera: Blattidae). J Zool 168: 51–79
Статья Google Scholar
Drake AG, Klingenberg CP (2008) Темпы морфологических изменений: историческая трансформация формы черепа в Св.Собаки Бернарда. Proc R Soc Lond B Biol Sci 275: 71–76
Статья Google Scholar
Drake AG, Coquerelle M, Colombeau G (2015) Трехмерный морфометрический анализ ископаемых черепов собак противоречит предполагаемому одомашниванию собак в период позднего палеолита. Научный представитель 5: 8299
CAS PubMed Статья Google Scholar
Драйден, Иллинойс, Мардиа К.В. (1992) Анализ размеров и формы ориентиров.Биометрика 79: 57–68
Статья. Google Scholar
Драйден Иллинойс, Мардиа К.В. (1998) Статистический анализ формы. Wiley, Чичестер
Google Scholar
Fadda C, Leirs H (2009) Роль остановки роста как морфогенетического фактора в Mastomys natalensis (Rodentia: Muridae). Biol J Linn Soc 97: 791–800
Статья Google Scholar
Feng X et al (2009) Эволюция аллометрии у Antirrhinum .Растительная ячейка 21: 2999–3007
CAS PubMed PubMed Central Статья Google Scholar
Flury B (1988) Общие главные компоненты и связанные многомерные модели. Уайли, Нью-Йорк
Google Scholar
Frédérich B, Vandewalle P (2011) Двучастный жизненный цикл рыб коралловых рифов способствует увеличению несоответствия формы скелета головы в онтогенезе: пример из стрекоз (Pomacentridae).BMC Evol Biol 11:82
PubMed PubMed Central Статья Google Scholar
Frédérich B, Adriaens D, Vandewalle P (2008) Онтогенетические изменения формы у Pomacentridae (Teleostei, Perciformes) и их взаимосвязь со стратегиями питания: геометрический морфометрический подход. Biol J Linn Soc 95: 92–105
Статья Google Scholar
Freidline SE, Gunz P, Harvati K, Hublin J-J (2012) Морфология лица человека среднего плейстоцена в контексте эволюции и развития.J Hum Evol 63: 723–740
PubMed Статья Google Scholar
Freidline SE, Gunz P, Hublin J-J (2015) Онтогенетическая и статическая аллометрия в человеческом лице: контрастирование койсанского и инуитского языков. Am J Phys Anthropol 158: 116–131
PubMed Статья Google Scholar
Frost SR, Marcus LF, Bookstein FL, Reddy DP, Delson E (2003) Черепная аллометрия, филогеография и систематика крупнотелых папионинов (Primates: Cercopithecinae), выведенные из геометрического морфометрического анализа данных ориентиров.Anat Rec 275A: 1048–1072
Статья Google Scholar
Gerber S, Eble GJ, Neige P (2008) Аллометрическое пространство и аллометрическое неравенство: перспективы развития в макроэволюционном анализе морфологического несоответствия. Evolution 62: 1450–1457
PubMed Статья Google Scholar
Гибсон А. Р., Бейкер А. Дж., Моид А. (1984) Морфометрическая изменчивость интродуцированных популяций майны обыкновенной ( Acridotheres tristis ): применение складного ножа для анализа главных компонентов.Syst Zool 33: 408–421
Статья Google Scholar
Гидашевский Н.А., Байлак М., Клингенберг С.П. (2009) Эволюция полового диморфизма формы крыла в подгруппе Drosophila melanogaster . BMC Evol Biol 9: 110
PubMed PubMed Central Статья Google Scholar
Голубович А., Томович Л., Иванович А. (2015) Геометрия самовосстановления — случай черепах Германа.Zool Anz 254: 99–105
Статья Google Scholar
Гонсалес П.Н., Перес С.И., Бернал В. (2010) Онтогенез устойчивости черепно-лицевых черт у современных людей: исследование популяций Южной Америки. Am J Phys Anthropol 142: 367–379
PubMed Статья Google Scholar
Гонсалес П.Н., Перес С.И., Бернал В. (2011) Онтогенетическая аллометрия и диверсификация формы черепа среди человеческих популяций из Южной Америки.Anat Rec 294: 1864–1874
Статья Google Scholar
Good P (2000) Перестановочные тесты: практическое руководство по методам повторной выборки для проверки гипотез, 2-е изд. Спрингер, Нью-Йорк
Бронировать Google Scholar
Goodall CR (1991) Методы Прокруста в статистическом анализе формы. J R Statist Soc B 53: 285–339
Google Scholar
Goodall CR, Mardia KV (1991) Геометрический вывод плотности формы.Adv Appl Prob 23: 496–514
Статья Google Scholar
Goodall CR, Mardia KV (1993) Многомерные аспекты теории формы. Ann Stat 21: 848–866
Статья Google Scholar
Госвами A (2006a) Изменения модульности черепа в ходе эволюции млекопитающих. Am Nat 168: 270–280
PubMed Статья Google Scholar
Goswami A (2006b) Морфологическая интеграция в черепе хищника.Эволюция 60: 169–183
PubMed Статья Google Scholar
Госвами А. (2007) Филогения, диета и черепная интеграция австралодельфийских сумчатых. PLoS ONE 2, e995
PubMed PubMed Central Статья Google Scholar
Gould SJ (1966) Аллометрия и размер в онтогенезе и филогении. Biol Rev 41: 587–640
CAS PubMed Статья Google Scholar
Хаксли Дж. С. (1924) Постоянные дифференциальные коэффициенты роста и их значение.Nature 114: 895–896
Статья Google Scholar
Хаксли Дж. С. (1932) Проблемы относительного роста. Переиздано изд. 1993 г. Johns Hopkins University Press, Baltimore
Huxley JS, Teissier G (1936) Терминология относительного роста. Nature 137: 780–781
Статья Google Scholar
Иванович А., Калезич М.Л. (2010) Проверка гипотезы морфологической интеграции на черепе позвоночного животного с двухфазным жизненным циклом: тематическое исследование альпийского тритона.J Exp Zool B Mol Dev Evol 314: 527–538
PubMed Статья Google Scholar
Johnson RA, Wichern DW (1988) Прикладной многомерный статистический анализ, 2-е изд. Прентис-Холл, Энглвудские скалы
Google Scholar
Jojić V, Blagojević J, Vujošević M (2012) Двухмодульная организация нижней челюсти у желтошейной мыши: сравнение двух различных морфометрических подходов.J Evol Biol 25: 2489–2500
PubMed Статья Google Scholar
Jolicoeur P (1963) Многомерное обобщение уравнения аллометрии. Биометрия 19: 497–499
Статья Google Scholar
Jolicoeur P, Mosimann JE (1960) Изменение размера и формы нарисованной черепахи: анализ главных компонентов. Рост 24: 339–354
CAS PubMed Google Scholar
Jolliffe IT (2002) Анализ главных компонентов, 2-е изд.Спрингер, Нью-Йорк
Google Scholar
Jones CS (1992) Сравнительный онтогенез дикого тыквенного и производного от него сорта. Evolution 46: 1827–1847
Статья Google Scholar
Jungers WL, Falsetti AB, Wall CE (1995) Форма, относительный размер и корректировки размеров в морфометрии. Yearb Phys Anthropol 38: 137–161
Статья Google Scholar
Kazmierczak JB (1985) Анализировать логарифмический анализ: два примера приложения.Rev Stat Appl 33: 13–24
Google Scholar
Кендалл Д.Г. (1984) Формы многообразий, прокрустовы метрики и комплексные проективные пространства. Bull Lond Math Soc 16: 81–121
Статья Google Scholar
Кендалл Д.Г. (1989) Обзор статистической теории формы. Stat Sci 4: 87–120
Статья Google Scholar
Кендалл Д.Г., Барден Д., Карне Т.К., Ле Х. (1999) Форма и теория формы.Уайли, Чичестер
Забронировать Google Scholar
Klingenberg CP (1996a) Индивидуальные вариации онтогенеза: продольное исследование роста и времени. Evolution 50: 2412–2428
Статья Google Scholar
Klingenberg CP (1996b) Многомерная аллометрия. В: Marcus LF, Corti M, Loy A, Naylor GJP, Slice DE (eds) Advances in morphometrics, vol 284. Plenum, New York, pp 23–49
Google Scholar
Klingenberg CP (1998) Гетерохрония и аллометрия: анализ эволюционных изменений в онтогенезе.Biol Rev 73: 79–123
CAS PubMed Статья Google Scholar
Klingenberg CP (2009) Морфометрическая интеграция и модульность в конфигурациях ориентиров: инструменты для оценки априорных гипотез. Evol Dev 11: 405–421
PubMed PubMed Central Статья Google Scholar
Klingenberg CP (2010) Эволюция и развитие формы: интеграция количественных подходов.Nat Rev Genet 11: 623–635
CAS PubMed Google Scholar
Klingenberg CP (2013a) Черепная интеграция и модульность: понимание эволюции и развития на основе морфометрических данных. Hystrix 24: 43–58
Google Scholar
Klingenberg CP (2013b) Визуализации в геометрической морфометрии: как читать и как создавать графики, показывающие изменения формы. Hystrix 24: 15–24
Google Scholar
Klingenberg CP (2014) Изучение морфологической интеграции и модульности на нескольких уровнях: концепции и анализ.Philos Trans R Soc Lond B Biol Sci 369: 20130249
PubMed PubMed Central Статья Google Scholar
Klingenberg CP (2015) Анализ флуктуирующей асимметрии с помощью геометрической морфометрии: концепции, методы и приложения. Симметрия 7: 843–934
Статья Google Scholar
Klingenberg CP, Ekau W (1996) Комбинированный морфометрический и филогенетический анализ экоморфологической тенденции: пелагизация антарктических рыб (Perciformes: Nototheniidae).Biol J Linn Soc 59: 143–177
Статья Google Scholar
Klingenberg CP, Froese R (1991) Многомерное сравнение аллометрических моделей роста. Syst Zool 40: 410–419
Статья Google Scholar
Klingenberg CP, Marugán-Lobón J (2013) Эволюционная ковариация в геометрических морфометрических данных: анализ интеграции, модульности и аллометрии в филогенетическом контексте.Syst Biol 62: 591–610
PubMed Статья Google Scholar
Klingenberg CP, Spence JR (1993) Гетерохрония и аллометрия: уроки от рода водомеров Limnoporus . Evolution 47: 1834–1853
Статья Google Scholar
Klingenberg CP, Zimmermann M (1992a) Статическая, онтогенетическая и эволюционная аллометрия: многомерное сравнение девяти видов водомеров.Am Nat 140: 601–620
Статья Google Scholar
Клингенберг К.П., Циммерманн М. (1992b) Правило Дьяра и многомерный аллометрический рост девяти видов водно-болотных странников (Heteroptera, Gerridae). J Zool 227: 453–464
Статья Google Scholar
Клингенберг С.П., Бадяев А.В., Соври С.М., Беквит Н.Дж. (2001) Вывод модульности развития из морфологической интеграции: анализ индивидуальных вариаций и асимметрии крыльев шмелей.Am Nat 157: 11–23
CAS PubMed Статья Google Scholar
Klingenberg CP, Mebus K, Auffray J-C (2003) Интеграция развития в сложную морфологическую структуру: насколько различны модули в нижней челюсти мыши? Evol Dev 5: 522–531
PubMed Статья Google Scholar
Klingenberg CP, Duttke S, Whelan S, Kim M (2012) Пластичность развития, морфологическая изменчивость и эволюционируемость: многоуровневый анализ морфометрической интеграции в форме сложных листьев.J Evol Biol 25: 115–129
CAS PubMed Статья Google Scholar
Kölliker-Ott UM, Blows MW, Hoffmann AA (2003) Связаны ли размер, форма и асимметрия крыльев с полевой пригодностью паразитоидов яиц Trichoramma ? Oikos 100: 563–573
Статья Google Scholar
Langlade NB et al (2005) Эволюция через генетически контролируемое пространство аллометрии.Proc Natl Acad Sci U S A 102: 10221–10226
CAS PubMed PubMed Central Статья Google Scholar
Larson PM (2004) Хондрокраниальная морфология и онтогенетическая аллометрия у личинок Bufo americanus (Anura, Bufonidae). Зооморфол (Берл) 123: 95–106
Статья. Google Scholar
Lazić M, Carretero MA, Crnobrnja-Isailović J, Kaliontzopoulou A (2015) Влияние нарушения окружающей среды на фенотипические вариации: комплексная оценка канализации, стабильности развития, модульности и аллометрии формы головы ящерицы.Am Nat 185: 44–58
PubMed Статья Google Scholar
Le H (1994) Броуновские движения по форме и пространству размера и формы. J Appl Prob 31: 101–113
Статья Google Scholar
Le H (1995) Средние размеры и формы и средние формы: геометрическая точка зрения. Adv Appl Prob 27: 44–55
Статья Google Scholar
Leamy L, Bradley D (1982) Статическая аллометрия и ростовая аллометрия морфометрических признаков у хаотичных домовых мышей.Evolution 36: 1200–1212
Статья Google Scholar
Leamy L, Thorpe RS (1984) Морфометрические исследования у инбредных и гибридных домашних мышей. Гетерозис, гомеостаз и наследственность размера и формы. Biol J Linn Soc 22: 233–241
Статья Google Scholar
Lele S, Richtsmeier JT (1991) Матричный анализ евклидова расстояния: бескординатный подход для сравнения биологических форм с использованием данных ориентиров.Am J Phys Anthropol 86: 415–427
CAS PubMed Статья Google Scholar
Lessa EP, Patton JL (1989) Структурные ограничения, повторяющиеся формы и аллометрия у карманных сусликов (род Thomomys ). Biol J Linn Soc 36: 349–363
Статья Google Scholar
Ljubisavljević K, Urošević A, Aleksić I, Ivanović A (2010) Половой диморфизм формы черепа у видов ящериц-лацертидов ( Podarcis spp., Dalmatolacerta sp., Dinarolacerta sp.), Выявленных методом геометрической морфометрии. Зоология (Йена) 113: 168–174
Статья Google Scholar
Loy A, Cataudella S, Corti M (1996) Изменения формы во время роста морского окуня, Dicentrarchus labrax (Teleostea: Perciformes), в зависимости от различных условий выращивания. В: Marcus LF, Corti M, Loy A, Naylor GJP, Slice DE (eds) Достижения в морфометрии.Пленум, Нью-Йорк, стр. 399–405
Google Scholar
Loy A, Mariani L, Bertelletti M, Tunesi L (1998) Визуализация аллометрии: геометрическая морфометрия при изучении изменений формы на ранних стадиях двулепестного морского леща, Diplodus vulgaris (Perciformes, Sparidae) . J Morphol 237: 137–146
Статья Google Scholar
Ludoški J, Djurakic M, Pastor B, Martínez-Sánchez AI, Rojo S, Milankov V (2014) Фенотипическая изменчивость комнатной мухи, Musca domestica : количество и характер асимметрии формы крыльев в диких популяциях и лабораторных колониях .Bull Entomol Res 104: 35–47
PubMed Статья Google Scholar
Malhotra A, Thorpe RS (1997) Изменение размера и формы анола Малых Антильских островов, Anolis oculatus (Sauria: Iguanidae) в зависимости от среды обитания. Биол Дж. Линн Соц 60: 53–72
Google Scholar
Marcus LF, Bello E, García-Valdecasas A (eds) (1993) Вклад в морфометрию.Museo Nacional de Ciencias Naturales, Мадрид
Google Scholar
Маркус LF, Corti M, Loy A, Naylor GJP, Slice DE (eds) (1996) Достижения в морфометрии. Пленум, Нью-Йорк
Google Scholar
Маркус Л.Ф., Хингст-Захер Э., Захер Х. (2000) Применение ориентировочной морфометрии к черепам, представляющим отряды живых млекопитающих. Гистрикс 11: 27–47
Google Scholar
Мардиа К.В., Кент Дж. Т., Бибби Дж. М. (1979) Многомерный анализ.Академик, Лондон
Google Scholar
Мардиа К.В., Кумбс А., Киркбрайд Дж., Линни А., Боуи Дж. Л. (1996) О статистических проблемах с идентификацией лиц по фотографиям. J Appl Stat 23: 655–675
Статья Google Scholar
Martínez-Abadías N, Heuzé Y, Wang Y, Jabs EW, Aldridge K, Richtsmeier JT (2011) Передача сигналов FGF / FGFR координирует развитие черепа путем модуляции величины морфологической интеграции: данные на моделях мышей с синдромом Аперта.PLoS ONE 6, e26425
PubMed PubMed Central Статья CAS Google Scholar
Мартинес-Варгас Дж., Муньос-Муньос Ф., Медарде Н., Лопес-Фустер М.Дж., Вентура Дж. (2014) Влияние хромосомных реорганизаций на морфологическую ковариацию нижней челюсти мыши: выводы из Робертсоновской системы Mus musculus domesticus . Front Zool 11:51
Статья Google Scholar
Мартин-Серра А., Фигейридо Б., Палмквист П. (2014) Трехмерный анализ морфологической эволюции и двигательных функций передней конечности карнивора.PLoS ONE 9, e85574
PubMed PubMed Central Статья CAS Google Scholar
McCoy MW, Bolker BM, Osenberg CW, Miner BG, Vonesh JR (2006) Коррекция размера: сравнение морфологических признаков среди популяций и сред. Oecolog (Berl) 148: 547–554
Статья Google Scholar
Milne N, O’Higgins P (2012) Масштабирование формы и функции ксенартрановой бедренной кости: 100-кратное увеличение массы тела смягчается перемещением третьего вертела.Proc R Soc Lond B Biol Sci 279: 3449–3456
Статья Google Scholar
Milne N, Toledo N, Vizcaíno SF (2012) Аллометрические и групповые различия в ксенартране бедренной кости. J Mamm Evol 19: 199–208
Статья Google Scholar
Mitteroecker P, Bookstein FL (2007) Концептуальная и статистическая взаимосвязь между модульностью и морфологической интеграцией.Syst Biol 56: 818–836
PubMed Статья Google Scholar
Mitteroecker P, Gunz P (2009) Успехи в геометрической морфометрии. Evol Biol 36: 235–247
Статья Google Scholar
Mitteroecker P, Gunz P, Bernhard M, Schaefer K, Bookstein FL (2004) Сравнение краниальных онтогенетических траекторий у человекообразных обезьян и людей. J Hum Evol 46: 679–698
PubMed Статья Google Scholar
Mitteroecker P, Gunz P, Bookstein FL (2005) Гетерохрония и геометрическая морфометрия: сравнение роста черепа у Pan paniscus и Pan troglodytes .Evol Dev 7: 244–258
PubMed Статья Google Scholar
Mitteroecker P, Gunz P, Windhager S, Schaefer K (2013) Краткий обзор формы, формы и аллометрии в геометрической морфометрии с приложениями к морфологии лица человека. Hystrix 24: 59–66
Google Scholar
Монтейро Л. Р. (1999) Модели многомерной регрессии и геометрическая морфометрия: поиск причинных факторов в анализе формы.Syst Biol 48: 192–199
CAS PubMed Статья Google Scholar
Монтейро Л.Р., дос Рейс С.Ф. (1999) Princípios de morfometria geométrica. Holos, Ribeirão Preto
Google Scholar
Моримото Н., Огихара Н., Катаяма К., Шиота К. (2008) Трехмерные онтогенетические изменения формы черепа человека во время эмбрионального периода. J Anat 212: 627–635
PubMed PubMed Central Статья Google Scholar
Mosimann JE (1970) Аллометрия размера: переменные размера и формы с характеристиками логнормального и обобщенного гамма-распределений.J Am Stat Assoc 65: 930–945
Статья Google Scholar
Mosimann JE, James FC (1979) Новые статистические методы аллометрии применительно к краснокрылым черным дроздам Флориды. Evolution 33: 444–459
Статья Google Scholar
Мурта-Фонсека Р.А., Фернандес Д.С. (2016) Череп Hydrodynastes gigas (Duméril, Bibron & Duméril, 1854) (Serpentes: Dipsadidae) как модель онтогенетической аллометрии змей, полученный с помощью геометрической морфометрии.Зооморфол (Берл). DOI: 10.1007 / s00435-015-0297-0
Google Scholar
Mydlová M, Dupej J, Koudelová J, Velemínská J (2015) Половой диморфизм лица у стареющих взрослых людей: поперечное исследование. Forensic Sci Int 257: 519.e1–519.e9
О’Хиггинс П., Джонс Н. (1998) Рост лица у Cercocebus torquatus : применение методов трехмерной геометрической морфометрии для изучения морфологических изменений.J Anat 193: 251–272
PubMed PubMed Central Статья Google Scholar
О’Хиггинс П., Милн Н. (2013) Применение геометрической морфометрии для сравнения изменений размера и формы, возникающих в результате анализа методом конечных элементов. Hystrix 24: 126–132
Google Scholar
Openshaw GH, Keogh JS (2014) Эволюция формы головы у варанов ( Varanus ): взаимодействие между крайним несоответствием размеров, филогенезом и экологией.J Evol Biol 27: 363–373
CAS PubMed Статья Google Scholar
Oxnard CE (1974) Функциональные выводы из морфометрии: проблемы, связанные с уникальностью и разнообразием среди приматов. Syst Zool 22: 409–424
Статья Google Scholar
Patterson JS, Schofield CJ, Dujardin J-P, Miles MA (2001) Морфометрический анализ популяции тропикополитического жука Triatoma rubrofasciata и связи с видами Старого Света Triatoma : свидетельство происхождения Нового Света.Med Vet Entomol 15: 443–451
CAS PubMed Статья Google Scholar
Пирсон К. (1901) О линиях и плоскостях, наиболее приближенных к системам точек в пространстве. Philos Mag J Sci 2: 559–572
Статья Google Scholar
Pélabon C, Bolstad GH, Egset CK, Cheverud JM, Pavlicev M, Rosenqvist G (2013) О взаимосвязи между онтигенетической и статической аллометрией.Am Nat 181: 195–212
PubMed Статья Google Scholar
Пиментель Р.А. (1979) Морфометрия: многомерный анализ биологических данных. Кендалл / Хант, Дубьюк
Google Scholar
Pitman EJG (1937) Тесты значимости, которые могут применяться к образцам из любых популяций. II. Тест коэффициента корреляции. J R Statist Soc B 4: 225–232
Google Scholar
Ponssa ML, Candioti MFV (2012) Паттерны развития черепа бесхвостых животных: соотношение размера и формы во время постметаморфического черепного онтогенеза у пяти видов группы Leptodactylus fuscus (Anura: Leptodactylidae).Зооморфол (Берл) 131: 349–362
Статья Google Scholar
Reyment RA, Blackith RE, Campbell NA (1984) Многомерная морфометрия, 2-е изд. Академик, Лондон
Google Scholar
Richtsmeier JT, Lele S (1993) Бескординатный подход к анализу моделей роста: модели и теоретические соображения. Biol Rev 68: 381–411
CAS PubMed Статья Google Scholar
Rodríguez-Mendoza R, Muñoz M, Saborido-Rey F (2011) Онтогенетическая аллометрия синезуба, Helicolenus dactylopterus dactylopterus (Teleostei: Scorpametidae), в северо-восточной части Атлантического океана и Средиземноморья.Hydrobiologia 670: 5–22
Статья Google Scholar
Rohlf FJ (1990) Морфометрия. Annu Rev Ecol Syst 21: 299–316
Статья Google Scholar
Rohlf FJ (1996) Морфометрические пространства, компоненты формы и эффекты линейных преобразований. В: Marcus LF, Corti M, Loy A, Naylor GJP, Slice DE (eds) Достижения в морфометрии. Пленум, Нью-Йорк, стр. 117–129
Google Scholar
Rohlf FJ (1999) Статистика формы: прокрастные наложения и касательные пространства.J Classif 16: 197–223
Статья Google Scholar
Rohlf FJ (2000) Об использовании пространств форм для сравнения морфометрических методов. Гистрикс 11: 9–25
Google Scholar
Rohlf FJ, Bookstein FL (1987) Комментарий к стрижке как методу «коррекции размера». Syst Zool 36: 356–367
Статья Google Scholar
Rohlf FJ, Bookstein FL (ред.) (1990) Труды Мичиганского семинара по морфометрии.Специальная публикация № 2. Музей зоологии Мичиганского университета, Анн-Арбор, Мичиган
Rohlf FJ, Marcus LF (1993) Революция в морфометрии. Trends Ecol Evol 8: 129–132
Статья Google Scholar
Rosas A, Bastir M (2002) Тонкопластинчатый сплайн-анализ аллометрии и полового диморфизма в черепно-лицевом комплексе человека. Am J Phys Anthropol 117: 236–245
PubMed Статья Google Scholar
Rosas U, Zhou RW, Castillo G, Collazo-Ortega M (2012) Нормы реакции развития для проростков суккулентных кактусов, испытывающих водный стресс.PLoS ONE 7, e33936
CAS PubMed PubMed Central Статья Google Scholar
Sallan LC, Friedman M (2012) Орел или решка: ступенчатая диверсификация в эволюционной радиации позвоночных. Proc Roy Soc Lond Biol Sci 279: 2025–2032
Статья Google Scholar
Сарди М.Л., Рамирес Роззи Ф.В. (2012) Различный черепной онтогенез у европейцев и южноафриканцев.PLoS ONE 7, e35917
CAS PubMed PubMed Central Статья Google Scholar
Сарди М.Л., Вентрис Ф., Рамирес Роцци Ф. (2007) Аллометрия в позднем пренатальном и раннем постнатальном черепно-лицевом онтогенезе человека. Anat Rec 290: 1112–1120
Статья Google Scholar
Schmidt-Nielsen K (1984) Масштабирование: почему так важен размер животного? Издательство Кембриджского университета, Кембридж
Книга Google Scholar
Shea BT (1985) Двумерная и многомерная аллометрия роста: статистические и биологические соображения.J Zool 206: 367–390
Статья Google Scholar
Sherratt E, Gower DJ, Klingenberg CP, Wilkinson M (2014) Эволюция формы черепа у слепых слепых (Amphibia: Gymnophiona). Evol Biol 41: 528–545
Статья Google Scholar
Сидлаускас Б.Л., Мол Дж. Х., Вари Р.П. (2011) Работа с аллометрией в линейной и геометрической морфометрии: таксономическое исследование группы Leporinus cylindriformis (Characiformes: Anostomidae) с описанием нового вида из Суринама.Zool J Linn Soc 162: 103–130
Статья Google Scholar
Singleton M (2002) Паттерны изменения формы черепа у Papionini (приматы: Cercopithecinae). J Hum Evol 42: 547–578
PubMed Статья Google Scholar
Синглтон М., Розенбергер А.Л., Робинсон С., О’Нил Р. (2011) Аллометрические и метамерные вариации формы моляров нижней челюсти Pan : цифровой морфометрический анализ.Anat Rec 294: 322–334
Статья Google Scholar
Small CG (1996) Статистическая теория формы. Спрингер, Нью-Йорк
Бронировать Google Scholar
Смит М.Ф., Паттон Дж.Л. (1988) Подвиды карманных сусликов: причинные основы географической дифференциации Thomomys botae . Syst Zool 37: 163–178
Статья Google Scholar
Sneath PHA, Sokal RR (1973) Числовая таксономия: принципы и практика числовой классификации.В. Х. Фриман, Сан-Франциско
Google Scholar
Solignac M, Cariou M-L, Wimitzky M (1990) Изменчивость, специфичность и эволюция градиентов роста в комплексе видов Jaera albifrons (Isopoda, Asellota). Ракообразные (Лейден) 59: 121–145
Статья Google Scholar
Somers KM (1986) Многомерная аллометрия и удаление размера с анализом главных компонентов.Syst Zool 35: 359–368
Статья Google Scholar
Strelin MM, Benitez-Vieyra SM, Fornoni J, Klingenberg CP, Cocucci AA (2016) Изучение гипотезы онтогенетического масштабирования во время диверсификации синдромов опыления у Caiophora (Loasaceae, subfam. Loasoideae). Энн Бот DOI: 10.1093 / aob / mcw1035
Thorpe RS (1983) Обзор численных методов распознавания и анализа расовой дифференциации.В: Felsenstein J (ed) Числовая таксономия. Springer, Berlin, pp. 404–423
Google Scholar
Тимм Н.Х. (2002) Прикладной многомерный анализ. Спрингер, Нью-Йорк
Google Scholar
Урошевич А., Любисавлевич К., Иванович А. (2013) Паттерны краниального онтогенеза у ящериц-ящериц: морфологические и аллометрические различия. J Evol Biol 26: 399–415
PubMed Статья Google Scholar
Viscosi V (2015) Геометрическая морфометрия и фенотипическая пластичность листьев: оценка флуктуирующей асимметрии и аллометрии у европейских белых дубов ( Quercus ).Bot J Linn Soc 179: 335–348
Статья Google Scholar
Viscosi V, Cardini A (2011) Морфология листа, таксономия и геометрическая морфометрия: упрощенный протокол для начинающих. PLoS ONE 6, e25630
CAS PubMed PubMed Central Статья Google Scholar
Walker JA (1993) Онтогенетическая аллометрия формы тела трехиглой колюшки с использованием морфометрии на основе ориентиров.В: Marcus LF, Bello E, García-Valdecasas A (eds) Вклад в морфометрию. Museo Nacional de Ciencias Naturales, Мадрид, стр. 193–214
Google Scholar
Watanabe A, Slice DE (2014) Полезность краниального онтогенеза для филогенетических выводов: тематическое исследование крокодилов с использованием геометрической морфометрии. J Evol Biol 27: 1078–1092
CAS PubMed Статья Google Scholar
Weber GW, Bookstein FL (2011) Виртуальная антропология: руководство в новой междисциплинарной области.Springer, Вена
Забронировать Google Scholar
Weisbecker V (2012) Искажение в фиксированном формалином мозге: использование геометрической морфометрии для количественной оценки наихудшего сценария у мышей. Функция Brain Struct Funct 217: 677–685
PubMed Статья Google Scholar
Weisensee KE, Jantz RL (2011) Вековые изменения черепно-лицевой морфологии португальцев с использованием геометрической морфометрии.Am J Phys Anthropol 145: 548–559
PubMed Статья Google Scholar
White J (2009) Геометрическое морфометрическое исследование разнообразия формы моляров у современных лемуров и лорисов. Anat Rec 292: 701–719
Статья Google Scholar
Wilson LAB (2013) Аллометрические различия в эволюции грызунов. Ecol Evol 3: 971–984
PubMed PubMed Central Статья Google Scholar
Wilson LAB, Sánchez-Villagra MR (2010) Тенденции разнообразия и их онтогенетическая основа: исследование аллометрических различий у грызунов.Proc R Soc Lond B Biol Sci 277: 1227–1234
Статья Google Scholar
Zelditch ML, Sheets HD, Fink WL (2000) Пространственно-временная реорганизация темпов роста в эволюции онтогенеза. Evolution 54: 1363–1371
CAS PubMed Статья Google Scholar
Zelditch ML, Sheets HD, Fink WL (2003) Онтогенетическая динамика неравенства форм. Палеобиол 29: 139–156
Статья Google Scholar
Зельдич М.Л., Свидерски Д.Л., Sheets HD (2012) Геометрическая морфометрия для биологов: учебник, 2-е изд.Эльзевир, Амстердам
Google Scholar
Ziezold H (1977) Об ожидаемых числах и усиленном законе больших чисел для случайных элементов в квазиметрических пространствах. В: Труды седьмой Пражской конференции по теории информации, функциям статистических решений и случайным процессам, том A. Reidel, Dordrecht, Holland, pp 591–602
Ziezold H (1994) Средние числа и средние формы применительно к биологическим фигурам. и распределения формы в плоскости.Biom J 36: 491–510
Статья Google Scholar
Zollikofer CPE, Понсе де Леон М.С. (2002) Визуализация паттернов изменения черепно-лицевой формы у Homo sapiens . Proc R Soc Lond B Biol Sci 269: 801–807
Статья Google Scholar
Введение в геометрию | SkillsYouNeed
Когда вы начинаете изучать геометрию, важно знать и понимать некоторые основные концепции.
Эта страница поможет вам понять концепцию размеров в геометрии и понять, работаете ли вы в одном, двух или трех измерениях.
Он также объясняет некоторые основные термины и указывает на другие страницы для получения дополнительной информации.
На этой странице представлены точки, линии и плоскости.
На других страницах этой серии рассказывается об углах и формах, включая многоугольники, круги и другие изогнутые формы, а также трехмерные формы.
Что такое геометрия?
Геометрия , н.та часть математики, которая рассматривает свойства точек, линий, поверхностей и твердых тел…
Словарь английского языка Chambers, издание 1989 года
Геометрия происходит от греческого слова «измерение земли» и представляет собой визуальное изучение форм, размеров и узоров, а также того, как они сочетаются друг с другом в пространстве. Вы обнаружите, что наши страницы геометрии содержат множество диаграмм, которые помогут вам понять предмет.
Когда вы сталкиваетесь с проблемой, связанной с геометрией, может быть очень полезно нарисовать диаграмму самостоятельно.
Работа в разных размерах
Нет, не континуум пространства-времени! Мы говорим о формах в одном, двух и трех измерениях.
То есть объекты, которые имеют длину (одно измерение), длину и ширину (два измерения) и длину, ширину и глубину или высоту (три измерения).
очков: особый случай: без размеров
A точка — это отдельная точка в пространстве. Он часто представлен точкой на странице, но на самом деле не имеет реального размера или формы.
Вы не можете описать точку с точки зрения длины, ширины или высоты, поэтому она является безразмерной . Однако точку можно описать координатами. Координаты ничего не определяют о точке, кроме ее положения в пространстве по отношению к контрольной точке с известными координатами. Вы встретите координаты точек во многих приложениях, например, когда вы рисуете графики или читаете карты.
Практически все в геометрии начинается с точки, будь то линия или сложная трехмерная форма.
линий: одно измерение
Линия — кратчайшее расстояние между двумя точками. Он имеет длину, но не ширину, что делает его одномерным.
Везде, где встречаются или пересекаются две или более прямых, есть точка, и говорят, что эти две линии имеют общую точку:
Отрезки и лучи
Есть два типа линий: те, которые имеют определенную начальную и конечную точки, и те, которые продолжаются вечно.
Линии, которые перемещаются между двумя точками, называются сегментами .Они начинаются с определенной точки и переходят к другой, конечной точке. Как и следовало ожидать, они нарисованы как линия между двумя точками.
Второй тип линий называется луч , и они продолжаются вечно. Их часто проводят в виде линии, начинающейся от точки со стрелкой на другом конце:
Параллельные и перпендикулярные линии
Есть два типа линий, которые особенно интересны и / или полезны в математике. Параллельные линии никогда не пересекаются и не пересекаются.Они просто идут вечно бок о бок, как железнодорожные пути. Условием показа параллельности линий на диаграмме является добавление «перьев», которые выглядят как наконечники стрелок.
Перпендикулярные линии пересекаются под прямым углом, 90 °:
Плоскости и двумерные формы
Теперь, когда мы разобрались с одним измерением, пора перейти к двум.
Плоскость — это плоская поверхность, также известная как двумерная. Технически он неограничен, что означает, что он продолжается вечно в любом заданном направлении, и поэтому его невозможно нарисовать на странице.
Одним из ключевых элементов геометрии является количество измерений, с которыми вы работаете в любой момент времени. Если вы работаете в одной плоскости, то это либо одна (длина), либо две (длина и ширина). При наличии более чем одной плоскости он должен быть трехмерным, потому что высота / глубина также учитываются.
Двумерные формы включают многоугольники, такие как квадраты, прямоугольники и треугольники, у которых есть прямые линии и точки в каждом углу.
Более подробная информация о полигонах представлена на нашей странице Полигоны .Другие двумерные формы включают круги и любую другую форму, которая включает кривую. Вы можете узнать больше об этом на нашей странице Curved Shapes .
Три измерения: многогранники и изогнутые формы
Наконец, есть также трехмерных фигур , таких как кубы, сферы, пирамиды и цилиндры.
Чтобы узнать больше об этом, посетите нашу страницу Трехмерные фигуры .
Знаки, символы и терминология
Показанная здесь форма представляет собой неправильный пятиугольник, пятисторонний многоугольник с разными внутренними углами и длинами линий (подробнее об этих формах см. Нашу страницу о Многоугольники ).
Градусы ° являются мерой поворота и определяют величину угла между двумя сторонами.
Углы обычно обозначаются в геометрии с использованием сегмента окружности (дуги), если только они не являются прямым углом, когда они «возведены в квадрат». В данном примере угловые метки обозначены зеленым цветом. См. Нашу страницу о Angles для получения дополнительной информации.
Отметки (показаны оранжевым цветом) обозначают стороны фигуры одинаковой длины (стороны фигуры совпадают с или совпадают).Одиночные линии показывают, что две вертикальные линии имеют одинаковую длину, а двойные линии показывают, что две диагональные линии имеют одинаковую длину. Нижняя горизонтальная линия в этом примере отличается по длине от остальных 4 линий и поэтому не отмечена. Отметки также могут называться « штриховки ».
Вершина — это точка пересечения линий (линии также называются лучами или ребрами). Множественное число вершин — это вершины. В этом примере пять вершин помечены как A, B, C, D и E.Называть вершины буквами — обычное дело в геометрии.
В замкнутой форме, такой как в нашем примере, математическое соглашение гласит, что буквы всегда должны располагаться в порядке по часовой стрелке или против часовой стрелки. Нашу форму можно описать как «ABCDE», но было бы неправильно обозначать вершины так, чтобы форма была, например, «ADBEC». Это может показаться несущественным, но в некоторых сложных ситуациях важно избегать путаницы.
Символ угла ‘’ используется как сокращенный символ в геометрии при описании угла.Выражение ∠ABC является сокращением для описания угла между точками A и C в точке B. Средняя буква в таких выражениях всегда является вершиной угла, который вы описываете — порядок сторон не важен. ABC совпадает с ∠CBA, , и оба описывают вершину B в этом примере.
Если вы хотите записать измеренный угол в точке B в сокращенном виде, вы должны использовать:
m∠ABC = 128 ° (m просто означает «мера»)
или
м∠CBA = 128 °
В нашем примере мы также можем сказать:
м∠EAB = 90 °
м∠BCD = 104 °
Почему эти концепции имеют значение?
Точки, линии и плоскости лежат в основе почти всех концепций геометрии.Углы образуются между двумя линиями, начинающимися от общей точки. Фигуры, двухмерные или трехмерные, состоят из линий, соединяющих точки. Плоскости важны, потому что двумерные формы имеют только одну плоскость; трехмерные их два и более.
Другими словами, вам действительно нужно понять идеи на этой странице, прежде чем вы сможете перейти к любой другой области геометрии.
Дополнительная литература по навыкам, которые вам нужны
Руководство по навыкам, которые вам нужны
Это руководство из четырех частей познакомит вас с основами математики от арифметики до алгебры с остановками на дробях, десятичных дробях, геометрии и статистике.
Если вы хотите освежить в памяти основы или помочь детям в учебе, эта книга для вас.
Что такое трехмерные формы?
Трехмерные игры
Объем с использованием юнит-кубовЕдиничный куб — это куб, имеющий объем или емкость 1 юнит. Вы можете подсчитать количество единичных кубиков, которые могут поместиться в твердое тело, чтобы определить его объем.
охватывает Common Core Curriculum 5.MD.5.aИграть сейчасПосмотреть все игры по геометрии >>Учитесь с полной программой обучения математике K-5
Что такое трехмерные формы? В геометрии трехмерную фигуру можно определить как твердую фигуру или объект или форму, имеющую три измерения — длину, ширину и высоту.В отличие от двухмерных форм, трехмерные формы имеют толщину или глубину.

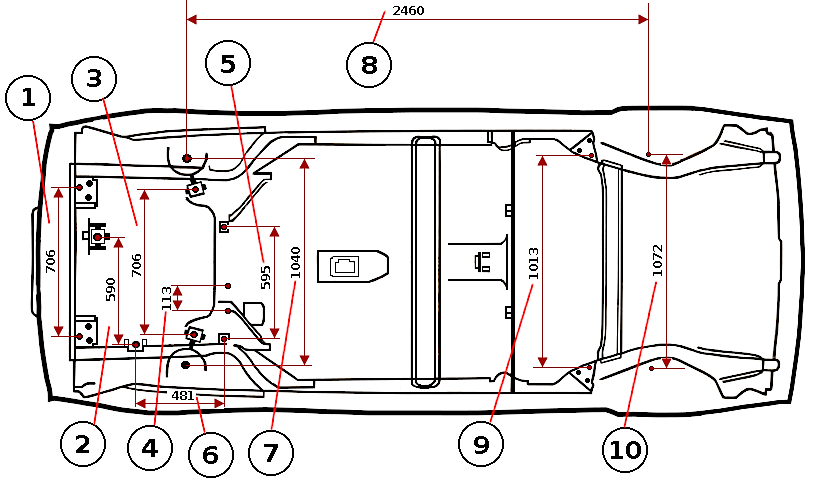
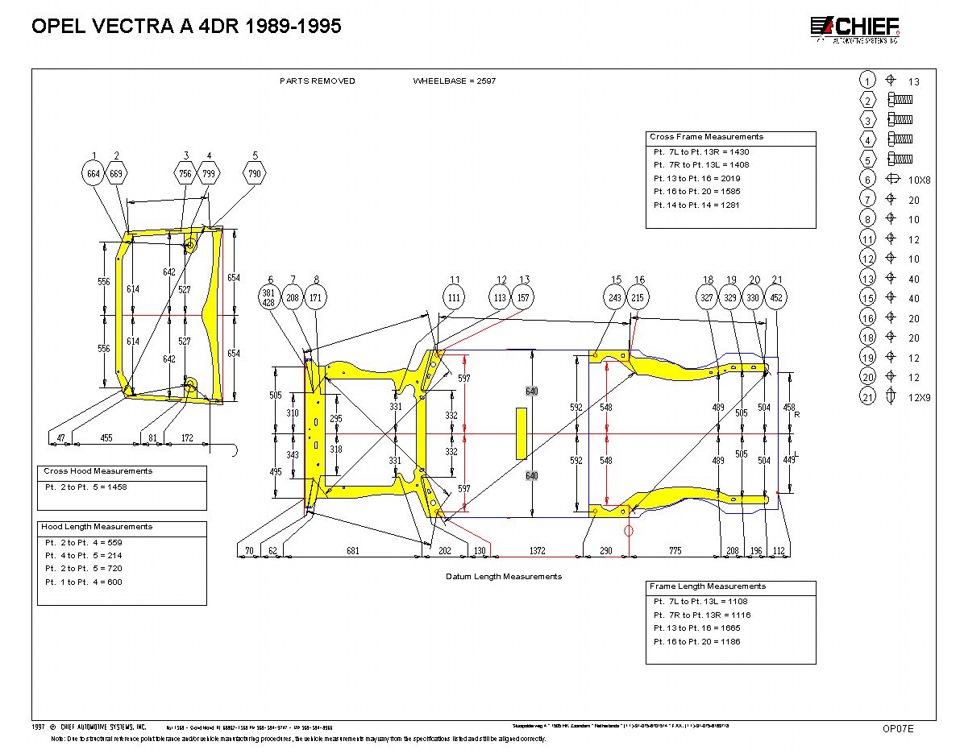 СТО в Рогачеве.
СТО в Рогачеве. СТО в Рогачеве.
СТО в Рогачеве.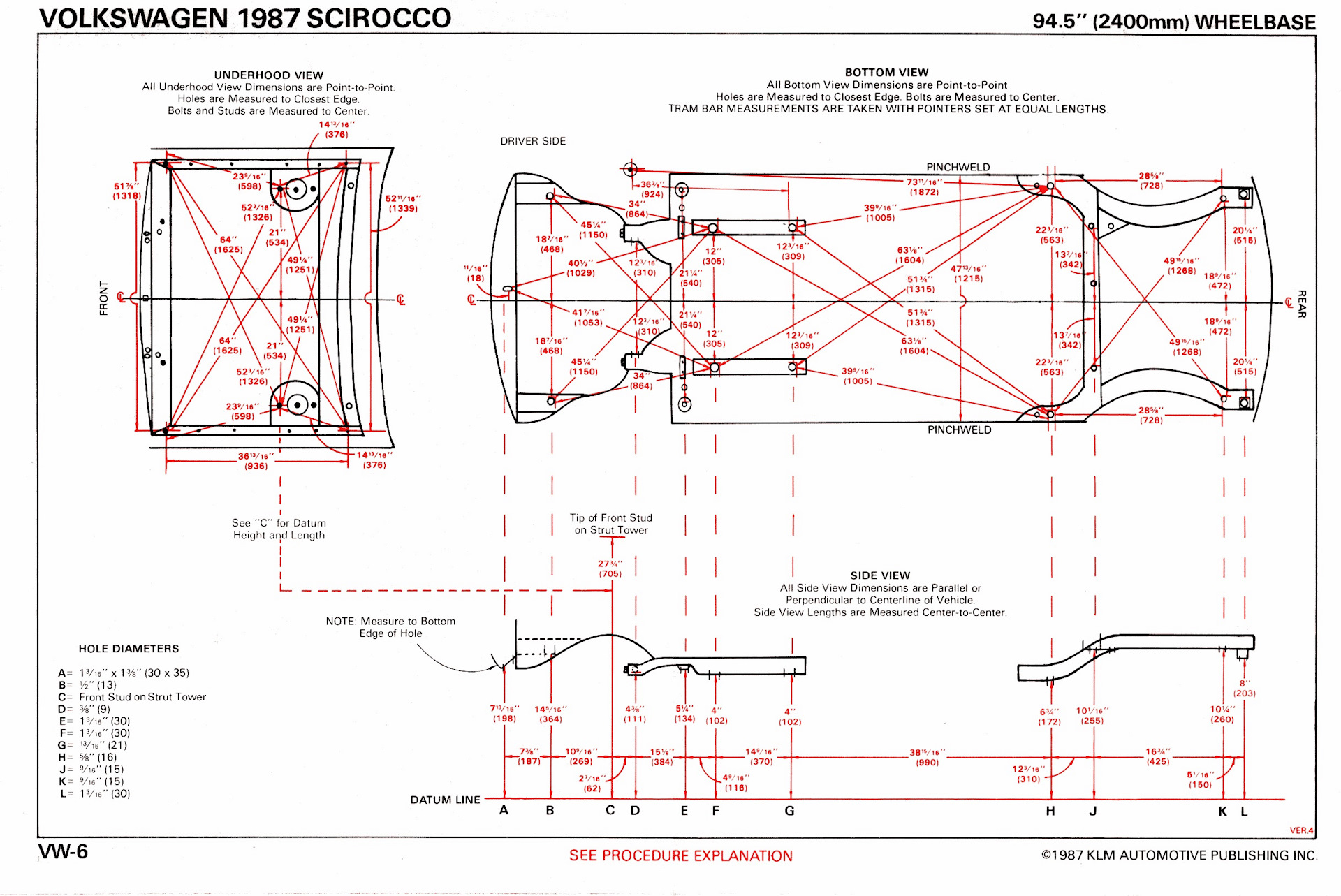 СТО в Рогачеве.
СТО в Рогачеве.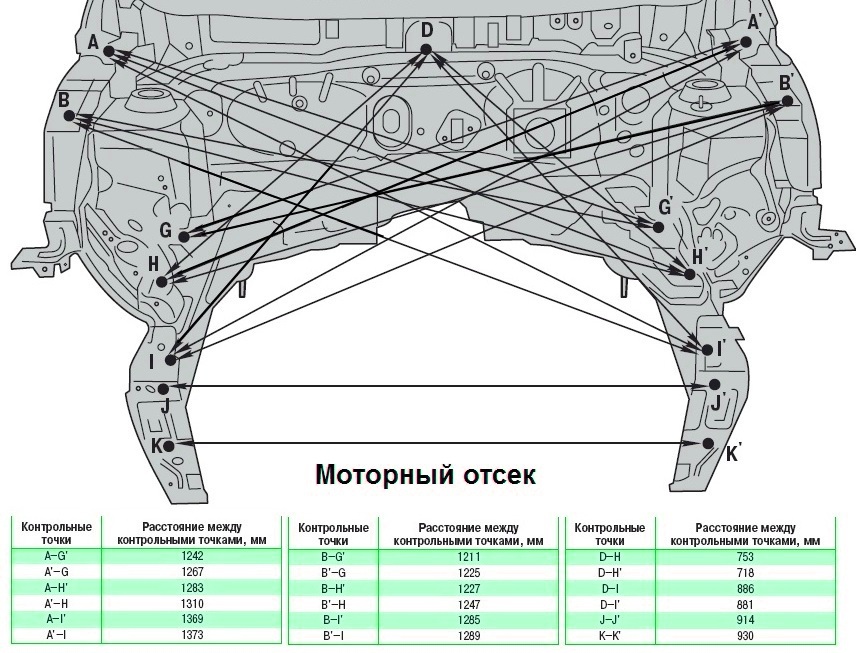 СТО в Рогачеве.
СТО в Рогачеве.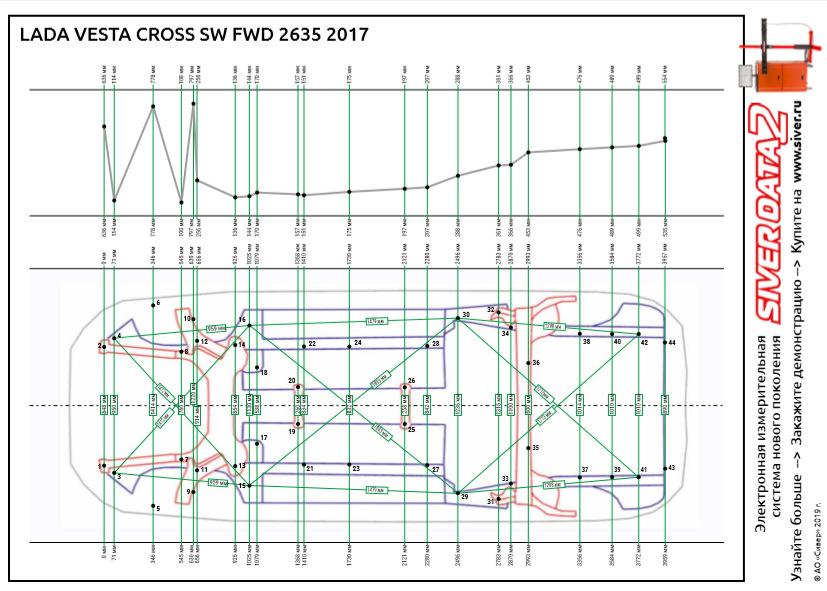 СТО в Рогачеве.
СТО в Рогачеве. СТО в Рогачеве.
СТО в Рогачеве.