Автомобиль трогается с места куда направлен вектор: Автомобиль трогается с места. Куда направлен вектор изменения импульса?

Физика. 8 класс

Физика. 8 класс

Кикоин И.К., Кикоин А.К. Физика. 8 класс. Учебное пособие. — 4-е изд., перераб. — М.: Просвещение, 1973. — 256 с. Советская фундаментальная наука, и физика в частности, была одной из сильнейших в мире. А по каким учебникам учились в школе и готовились к экзаменам будущие лучшие в мире ученые? Вашему вниманию предлагается учебник по физике для советских восьмиклассников. Охватывает разделы «Кинематика», «Динамика, «Равновесие тел» и «Законы сохранения в механике». Оглавление Глава 1. Общие сведения о движении § 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ § 3. ПЕРЕМЕЩЕНИЕ § 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ТЕЛА § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ) § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ Глава 2. Прямолинейное неравномерное движение § 13. СРЕДНЯЯ СКОРОСТЬ § 14. МГНОВЕННАЯ СКОРОСТЬ § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ § 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ Глава 3. Криволинейное движение § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ § 23. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ § 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА Динамика Глава 4. Законы движения § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ § 31. ИНЕРТНОСТЬ ТЕЛ § 32. МАССА ТЕЛ § 33. МАССА ЛУНЫ § 34. СИЛА § 35. ВТОРОЙ ЗАКОН НЬЮТОНА § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение) § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА Глава 5. Силы природы § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ § 41. СИЛА УПРУГОСТИ § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ § 44. СИЛА ТЯЖЕСТИ § 45. ВЕС ТЕЛ § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ § 47. МАССА ЗЕМЛИ § 48. СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ Глава 6. Применение законов движения § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ § 54. НЕВЕСОМОСТЬ § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ § 58. ДВИЖЕНИЕ ПЛАНЕТ § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА Равновесие тел Глава 7. Элементы статики § 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ § 67. ПРАВИЛО МОМЕНТОВ § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ Законы сохранения в механике Глава 8. Закон сохранения импульса § 70. СИЛА И ИМПУЛЬС § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ Глава 9. Механическая работа и мощность § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ § 77. РАБОТА СИЛЫ ТЯЖЕСТИ § 78. РАБОТА СИЛЫ УПРУГОСТИ § 79. РАБОТА СИЛЫ ТРЕНИЯ § 80. МОЩНОСТЬ Глава 10. Закон сохранения энергии § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ § 36. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ § 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ § 91. СТОЛКНОВЕНИЕ ТЕЛ § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ Заключение Лабораторные работы 1. Определение ускорения тела при равноускоренном движении 2. Определение коэффициента трения скольжения 3. Изучение движения тела по параболе 4. Выяснение условия равновесия рычага 5. Определение центра тяжести плоской пластины Ответы к упражнениям

Направление ускорения | Образовательный портал. Решение задач по физике, математике, химии. Справочник физико-химических величин. Онлайн-учебники.

При прямолинейном движении векторы $\vec{v}_{0}$ и $\vec{v}$ направлены вдоль одной прямой, которая является в то же время и траекторией движения. Вдоль этой же прямой в направлении движения тела мы условились направлять и координатную ось (ось $X$). В таком случае вектор разности $\vec{v} — \vec{v}_{0}$, а значит и вектор ускорения $\vec{a}$, лежит на той же прямой (см. § 6). Но куда он направлен — в сторону движения (так же как ось $X$) или против него?

В § б мы видели, что проекция разности двух векторов на какую-нибудь ось равна разности их проекций на ту же ось. Следовательно, для проекций векторов $\vec{v}_{0}, \vec{v}$ и $\vec{a}$ она на ось $X$ можно написать

$a = \frac{v -v_{0} }{t}$. (1)

Здесь $a$ — проекция вектора $\vec{a}$ на ось $X$; $v$ и $v_{0}$ — проекции векторов $\vec{v}$ и $\vec{v}_{0}$ на ту же ось.

Так как все три вектора лежат па одной прямой (оси $X$), то абсолютные значения их проекций равны абсолютным значениям самих векторов.

Рассмотрим 2 случая ускоренного движения тела.

Первый случай. Скорость тела по абсолютному значению растет (тело «разгоняется»). Это значит, что $v > v_{0}$. Тогда из формулы (1) видно, что проекция ускорения а положительна и равна $| \vec{a} |$ . Вектор $\vec{a}$, следовательно, направлен так же, как ось $X$, т. е. в сторону движения. Когда, например, бронебойный снаряд движется при выстреле в стволе орудия, его скорость растет и ускорение направлено так же, как и скорость (рис.).

Второй случай. Тело тормозится, т. е. абсолютное значение его скорости уменьшается ($v

Из формулы (1) можно получить выражение для скорости $v$:

$v = v_{0} + at$. (2)

В этой формуле, повторяем, $v, v_{0}$ и $a$ — проекции векторов $\vec{v}, \vec{v}_{0}$ и $\vec{a}$ на ось $X$, которые могут быть как положительными, так и отрицательными.

При решении задач выражение для скорости (2) удобно записывать так, чтобы из него сразу было видно, как направлен вектор ускорения.

Если скорость тела растет (разгон), то $a = | \vec{a} |$ и

$v = v_{0} + | \vec{a} | t$. (2а)

Когда же скорость тела уменьшается (торможение), $a = — | \vec{a} |$ и

$v = v_{0} — | \vec{a} |t$. (2б)

Понятно, что тело, которое тормозится, должно когда-то остановиться. Это произойдет, как это видно нз формулы (2б), тогда, когда $v_{0}$ станет равным $| \vec{a} |t$, т. е. в момент времени $t = \frac{v_{0} }{| \vec{a} |}$. Но если ускорение остается постоянным (по модулю и направлению) и после этого момента, то тело, остановившись, начнет двигаться в противоположную сторону. Это видно из того, что при $t > \frac{v_{0} }{ | \vec{a} | } | \vec{a}|t $ станет больше, чем $v_{0}$; скорость $v$ изменит свой знак на обратный. Так движется, например, тело, брошенное вертикально вверх: долетев до высшей точки траектории, тело начинает движение вниз.

Если $v_{0} = 0$ и вектор ускорения направлен так же, как и ось координат, то из формулы (2а) следует, что

$v = + | \vec{a} | t$.

Если же ось координат выбрана так, что направление вектора ускорения противоположно направлению оси координат, то из формулы (26) следует, что

$v = — | \vec{a}| t$.

Знак «-» в этой формуле означает, что вектор скорости, так же как и вектор ускорения, направлен противоположно направлению оси координат. Модуль скорости, конечно, и в этом случае увеличивается со временем.

Обычно мы называем движение с возрастающей по абсолютной величине скоростью ускоренным движением, а движение с убывающей скоростью — замедленным движением. Но в механике любое неравномерное движение является ускоренным движением. Трогается ли автомобиль с места или тормозит, в обоих случаях он движется с ускорением. Ускоренное прямолинейное движение отличается от замедленного только знаком проекции вектора ускорения.

Мы знаем, что и перемещение, и скорость, и траектория движения различны относительно разных тел отсчета, движущихся друг относительно друга.

А ускорение? Относительно ли оно?

Ускорение тела, как мы теперь знаем, определяется векторной разностью двух значений его скорости в различные моменты времени. При переходе от одной системы координат к другой, движущейся относительно первой равномерно и прямолинейно, изменятся оба значения скорости.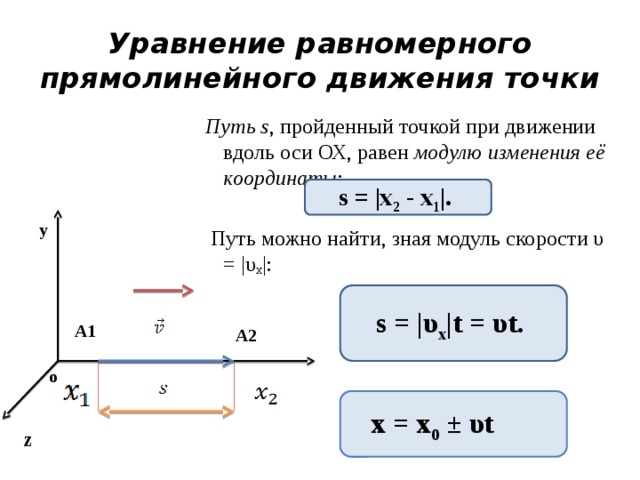

{2} } } = 10 сек$.

Результат получился тот же. Да он и не может зависеть от того, как выбрано направление оси координат!

Положение и смещение

Положение и смещение

Многие предметы, с которыми мы сталкиваемся в повседневной жизни, находятся в движении или состоят из частей. которые находятся в движении. Движение – это правило, а не исключение. Физические законы, управляющие движением этих объектов универсальны, т.е. все объекты движутся по одним и тем же правилам, и одна из целей этого класса состоит в том, чтобы понять эти правила.

Когда объект движется, его позиция изменяется как функция времени.

Положение объекта дано относительно некоторой согласованной точки отсчета. Недостаточно просто укажите расстояние от ориентир. Мы также должны указать направление . Расстояние скаляр количество, это число, данное в каких-то единицах . Позиция — это вектор количество. Он также имеет величину как направление. Величина векторной величины представляет собой число (с единицами) сообщая вам, сколько есть количества, и направление говорит вам, какое как он указывает. Единичный вектор — это направление индикатор. Это безразмерный вектор с величиной 1, используемый для указания направление. В тексте векторные величины обычно выделяются жирным шрифтом. введите или со стрелкой над символом. Таким образом, хотя d = расстояние, д = смещение.

Ссылки:
Скаляры и векторы (Пожалуйста, изучите!)
Направление вектора

---

Позиция

Удобный способ указать позицию объекта с помощью системы координат . Мы выбираем фиксированную точку, называемую началом координат . и три направленные линии, которые проходят через начало координат и перпендикулярны друг другу. Эти линии называются оси координат трехмерной прямоугольной (декартовой) системы координат и помечены оси x, y и z. Три числа с единицами определяют положение точка P. Эти числа представляют собой координаты x, y и z точки P. Координаты точки P на на диаграмме справа (а, б, в).

Координаты точки P являются компонентами вектора положения. Единичный вектор указание в направлении x имеет x-компоненту 1 и y- и z-компоненты нуль. Обозначается цифрой и . Точно так же единичный вектор , указывающий в направлении y, обозначается j , а единичный вектор направление в направлении z обозначается как k . Единичные векторы являются указателями поворота.

Компоненты любого вектора в сумме образуют сам вектор.
Вектор положения точки P с координатами (a, b, c) может быть записано с точки зрения его компонентов как
р = а и + б к + с к .
Величина вектора положения равна его длине r. Это зависит от выбора начала системы координат. Это — прямолинейное расстояние P от начала координат.

Ниже приведено трехмерное представление вектора положения. r = a i + b j + c k . Пожалуйста, нажмите на изображении!
(Используйте современный браузер. 3D-приложения не работают в Internet Explorer. или более старые браузеры.)
Чтобы получить наилучший вид, измените окно просмотра, перетащив мышь и увеличить или уменьшить масштаб по мере необходимости.
Нажмите кнопки, чтобы выбрать другой вектор или другая схема добавления векторов компонентов.

Пример:

Вектор положения здания Nielsen Physics Building на небольшой карте с левым нижним углом в качестве начала координат.

---

Рабочий объем

Изменение положения называется смещением . На приведенной ниже диаграмме показано позиции P ₁ и P ₂ игрока в два разных момента времени.

Стрелка, указывающая от P ₁ к P ₂ , является вектор смещения .
Его величина — прямая линия расстояние между P ₁ и P ₂ .
Компоненты смещения вектор из P ₁ по P ₂ (x ₂ — x ₁ ) вдоль оси x, (y ₂ — y ₁ ) по оси Y.
Вектор смещения d   от P ₁ до P ₂ может можно записать как d = (x ₂ — x ₁ ) i + (y ₂ -у ₁ ) у .
Водоизмещение d составляет (x ₂ — x ₁ ) единиц в направление x плюс (y ₂ — y ₁ ) единицы измерения в направлении y.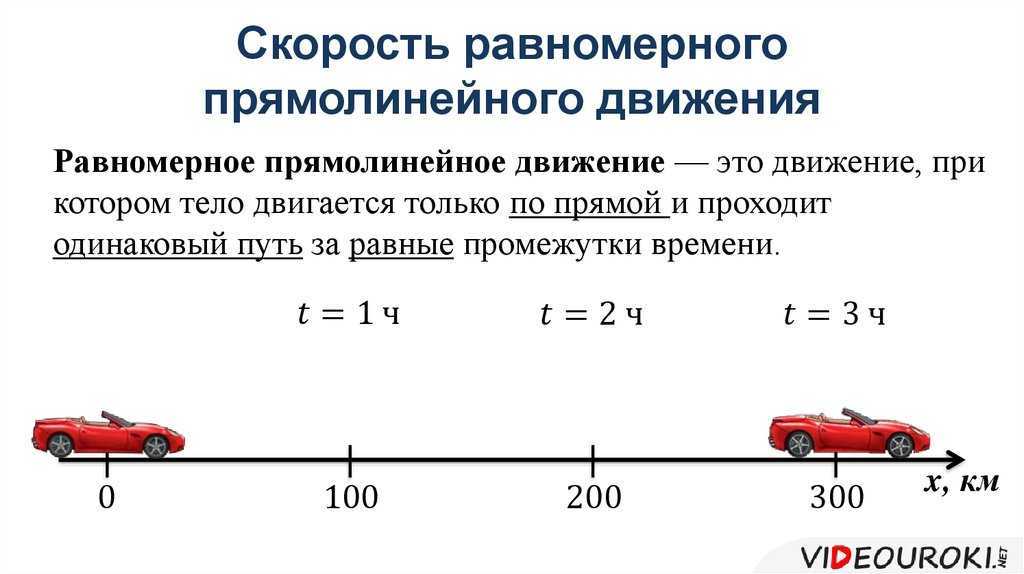
Величина смещения d = ((x ₂ — х ₁ ) ² + (у ₂ — у ₁ ) ² ) ^½ . Этот следует из пифагорейский теорема.

Расстояние между двумя точками P ₁ с координатами (х ₁ , у ₁ , z ₁ ) и P ₂ с координатами (x ₂ , y ₂ , z ₂ ) равно
d = ((х ₂ — х ₁ ) ² + (у ₂ — у ₁ ) ² + (z ₂ — z1) ^{2 )½} .

• Расстояние d является величиной вектора смещения д .
• Направление вектора смещения d – направленный отрезок прямой от P ₁ к Р ₂ .
• Мы называем этот направленный отрезок геометрической или графической представление вектора d .
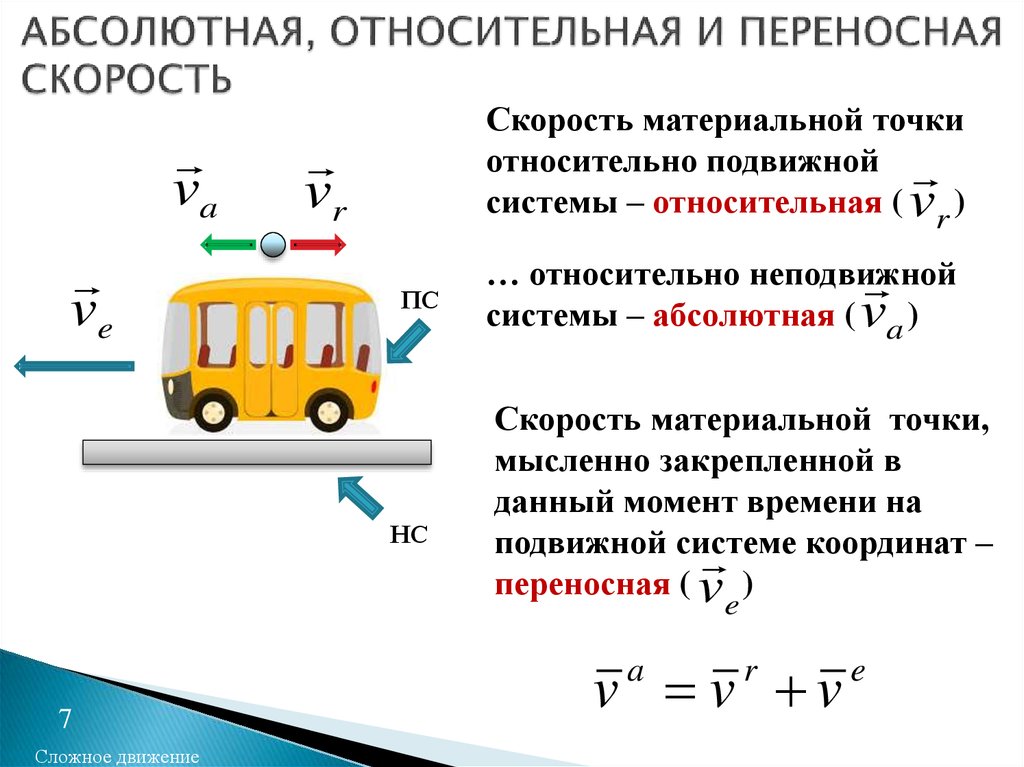
• Мы рисуем стрелку на P ₂ , чтобы указать что сегмент линии начинается с P ₁ и заканчивается на P ₂ .

Тройка действительных чисел d _x = (x ₂ — x ₁ ), d _y = (y ₂ — y ₁ ), d _z = (z ₂ — z ₁ ) называются декартовыми компонентами d .

Ссылка: Расстояние и смещение  (Пожалуйста, изучите!)

Проблема:

Футбольный защитник пробегает 15,0 м. прямо на игровом поле (в положительное направление x) за 2,50 с. Затем его ударили и толкнули на 3,00 м. прямо назад за 1,75 с. Он ломает снасти и бежит прямо вперед еще 21,0 м за 5,20 с. Вычислите его вектор смещения и общее пройденное расстояние.

Решение:

Проблема:

Во время движения по прямому межгосударственному шоссе вы обратите внимание, что на отметке 260 миль. отметку, а затем вернитесь к отметке 175 миль. Что величина вашего результирующего смещения от 260-мильной отметки?

Решение:

• Обоснование:
  Результирующее смещение представляет собой вектор d , сумму двух векторов д ₁ и d ₂ , которые указывают в противоположных направлениях.
• Детали расчета:
  Сумма двух векторов смещения равна d = d ₁ + д ₁ = (-110 м) + 25 м = -85 м.
  Также можно рассуждать следующим образом.
  Для полного водоизмещения важно только то, где вы начинаете и где вы останавливаться.
  d = позиция 2 — позиция 1 = 175 м — 260 м = -85 м.

Проблема:

Кончик лопасти вертолета 5,00 м от центра вращения. За один оборот лезвия вычислить вектор смещения и общее расстояние, пройденное наконечником лезвия.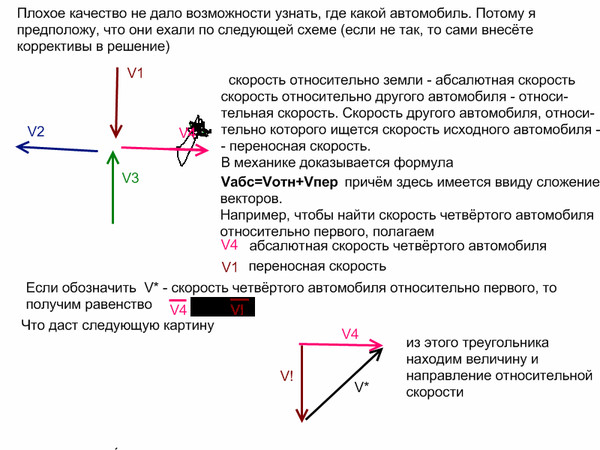

Решение:

• Обоснование:
  После одного оборота наконечник возвращается в исходное положение. Вектор его смещения d = 0.
• Детали расчета:
  Общее пройденное расстояние кончик равен окружности окружности радиусом r = 5 м.
  Окружность = 2πr = 31,42 м.
  Общее расстояние, пройденное вершина 31,42 м.

---

Вектор смещения имеет одинаковую величину и направление независимо от выбор начала координат системы координат. Величина и направление вектор смещения, однако, зависит от системы отсчета , в которой система координат закреплена и находится в состоянии покоя.

Пример:

Автомобиль двинулся вперед расстояние 6 м, пока ребенок переместился с заднего сиденья на переднее сидеть на расстоянии 1 м.

• Использование автомобиля в качестве системы отсчета и привязка системы координат в машине водоизмещение ребенка d (автомобиль) = (1 м) i .
• Использование дороги в качестве системы отсчета и привязка системы координат на дороге перемещение ребенка d (дорога) = (6 м) i + (1 м) i = (7 м) i .

6.2 Равномерное движение по окружности — физика

Раздел Цели обучения

К концу этого раздела вы сможете делать следующее:

• Описывать центростремительное ускорение и связывать его с линейным ускорением
• Описать центростремительную силу и связать ее с линейной силой
• Решение задач на центростремительное ускорение и центростремительную силу

Поддержка учителей

Поддержка учителей

Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:

• (4) Научные концепции. Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
  • (C) анализировать и описывать ускоренное движение в двух измерениях, используя уравнения, включая примеры снарядов и окружностей.
  • (D) рассчитать действие сил на объекты, включая закон инерции, связь между силой и ускорением и природу пар сил между объектами.

Кроме того, руководство по физике для старших классов рассматривает содержание этого раздела лабораторной работы под названием «Круговое и вращательное движение», а также следующие стандарты:

• (4) Научные концепции. Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
  • (C) анализировать и описывать ускоренное движение в двух измерениях, используя уравнения, включая примеры снарядов и окружностей.

Основные термины раздела

центробежная сила

центростремительное ускорение

центростремительная сила

равномерное круговое движение

Центростремительное ускорение

Поддержка учителей

Поддержка учителей

[BL][OL] Проверьте равномерное круговое движение. Попросите учащихся привести примеры кругового движения. Просмотрите линейное ускорение.

В предыдущем разделе мы определили круговое движение. Простейшим случаем кругового движения является равномерное круговое движение, когда объект движется по круговой траектории на постоянной скорости . Обратите внимание, что, в отличие от скорости, линейная скорость объекта в круговом движении постоянно меняется, потому что он всегда меняет направление. Из кинематики мы знаем, что ускорение есть изменение скорости либо по величине, либо по направлению, либо по тому и другому. Следовательно, объект, совершающий равномерное круговое движение, всегда ускоряется, даже если величина его скорости постоянна.

Вы сами испытываете это ускорение каждый раз, когда едете в машине, когда она поворачивает за угол. Если вы держите руль неподвижно во время поворота и двигаетесь с постоянной скоростью, вы выполняете равномерное круговое движение. Что вы заметите, так это ощущение скольжения (или отбрасывания, в зависимости от скорости) от центра поворота.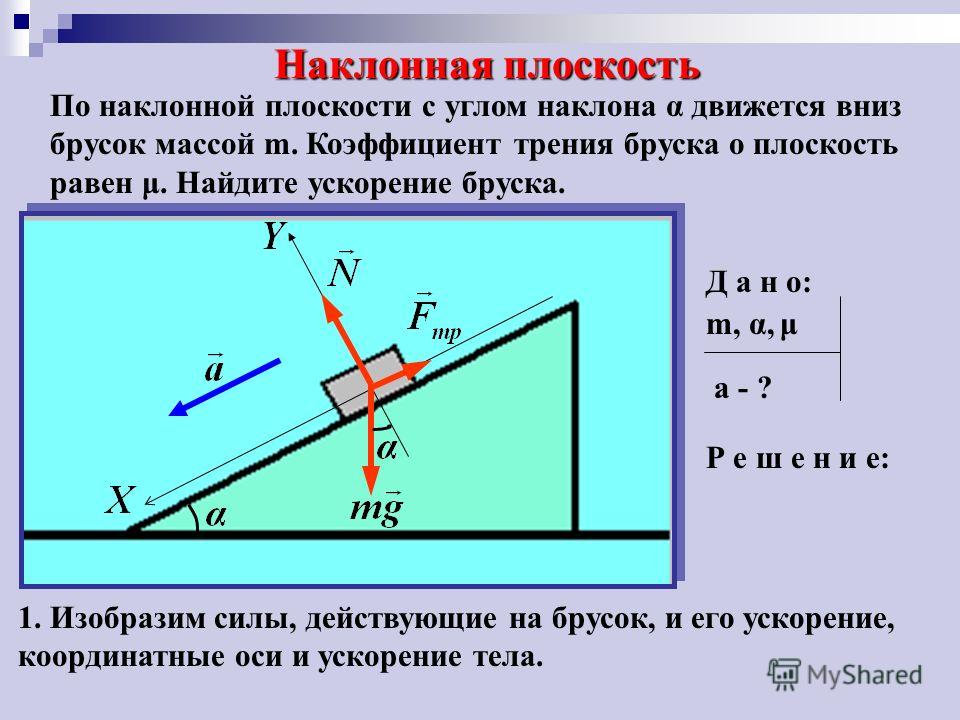 Это не реальная сила, действующая на вас — это происходит только потому, что ваше тело хочет продолжать движение по прямой линии (согласно первому закону Ньютона), в то время как автомобиль сворачивает с этой прямолинейной траектории. Внутри машины создается впечатление, что вас выталкивает из центра поворота. Эта фиктивная сила известна как центробежная сила. Чем круче кривая и чем больше ваша скорость, тем заметнее становится этот эффект.

Поддержка учителей

Поддержка учителей

[BL][OL][AL] Продемонстрируйте круговое движение, привязав груз к веревке и вращая его. Спросите учащихся, что произойдет, если вы внезапно перережете веревку? В каком направлении будет двигаться объект? Почему? Что это говорит о направлении ускорения? Попросите учащихся привести примеры случаев, когда они столкнулись с центростремительным ускорением.

На рис. 6.7 показан объект, движущийся по круговой траектории с постоянной скоростью.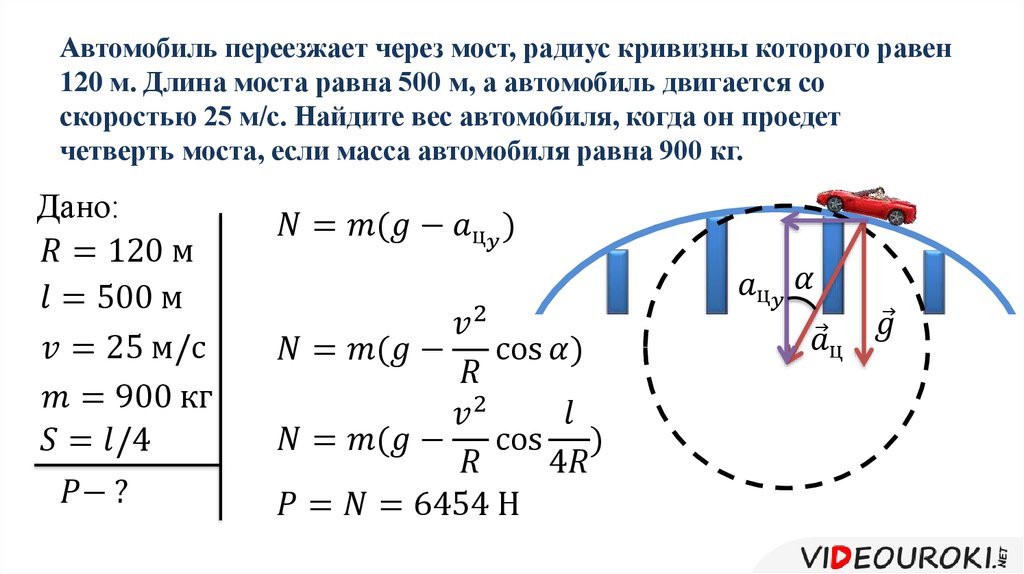 Направление мгновенной тангенциальной скорости показано в двух точках вдоль траектории. Ускорение направлено в сторону изменения скорости; в этом случае он указывает примерно на центр вращения. (Центр вращения находится в центре кругового пути). Если представить, что ΔsΔs становится все меньше и меньше, то ускорение будет равно точно к центру вращения, но этот случай сложно нарисовать. Мы называем ускорение объекта, движущегося в равномерном круговом движении, центростремительным ускорением a _c , потому что центростремительное означает поиск центра .

Рисунок 6.7 Показаны направления скорости объекта в двух разных точках, и видно, что изменение скорости ΔvΔv указывает примерно на центр кривизны (см. маленькую вставку). Для чрезвычайно малого значения ΔsΔs ΔvΔv указывает точно на центр круга (но это трудно нарисовать). Поскольку ac=Δv/Δtac=Δv/Δt, ускорение также направлено к центру, поэтому a _c называется центростремительным ускорением.

Поддержка учителей

Поддержка учителей

См. рис. 6.7. На рисунке изображен объект, движущийся по круговой траектории с постоянной скоростью и направлением мгновенной скорости двух точек по траектории. Ускорение направлено в сторону изменения скорости и указывает на центр вращения. Это строго верно только тогда, когда ΔsΔs стремится к нулю.

Теперь, когда мы знаем, что направление центростремительного ускорения направлено к центру вращения, давайте обсудим величину центростремительного ускорения. Для объекта, движущегося со скоростью v по круговой траектории с радиусом r , модуль центростремительного ускорения равен

ac=v2r.ac=v2r.

Центростремительное ускорение больше на высоких скоростях и в крутых поворотах (меньший радиус), как вы могли заметить, управляя автомобилем, потому что автомобиль фактически толкает вас к центру поворота. Но немного удивительно, что a _c пропорционально квадрату скорости. Это означает, например, что ускорение в четыре раза больше при движении по кривой на скорости 100 км/ч, чем на скорости 50 км/ч.

Мы также можем выразить a _c через величину угловой скорости. Подставляя v=rωv=rω в приведенное выше уравнение, мы получаем ac=(rω)2r=rω2ac=(rω)2r=rω2 . Следовательно, величина центростремительного ускорения через величину угловой скорости равна

ac=rω2.ac=rω2.

6,9

Советы для успеха

Уравнение, выраженное в форме a _c = rω ² , полезно для решения задач, где вы знаете угловую скорость, а не тангенциальную скорость.

Виртуальная физика

Божья коровка в 2D

В этой симуляции вы экспериментируете с положением, скоростью и ускорением божьей коровки в круговом и эллиптическом движении. Переключите тип движения с линейного на круговой и наблюдайте за векторами скорости и ускорения. Затем попробуйте эллиптическое движение и обратите внимание, как векторы скорости и ускорения отличаются от векторов кругового движения.

Проверка захвата

Каков угол между ускорением и скоростью при равномерном круговом движении? Какое ускорение испытывает тело при равномерном движении по окружности?

1. Угол между ускорением и скоростью равен 0°, и тело испытывает линейное ускорение.
2. Угол между ускорением и скоростью равен 0°, и тело испытывает центростремительное ускорение.
3. Угол между ускорением и скоростью равен 90°, и тело испытывает линейное ускорение.
4. Угол между ускорением и скоростью равен 90°, и тело испытывает центростремительное ускорение.

Центростремительная сила

Поддержка учителей

Поддержка учителей

[BL][OL][AL] Используя ту же демонстрацию, что и раньше, попросите учащихся предсказать отношения между величинами угловой скорости, центростремительного ускорения, массы и центростремительной силы. Предложите учащимся поэкспериментировать, используя веревки разной длины и разного веса.

Поскольку объект в равномерном круговом движении претерпевает ускорение (за счет изменения направления движения, но не скорости), мы знаем из второго закона Ньютона, что на объект должна действовать результирующая внешняя сила. Поскольку величина ускорения постоянна, постоянна и величина результирующей силы, а поскольку ускорение направлено к центру вращения, то же самое и результирующая сила.

Любая сила или комбинация сил может вызвать центростремительное ускорение. Всего несколько примеров: натяжение веревки на шаре, сила земного притяжения на Луне, трение между дорогой и шинами автомобиля при движении по кривой или нормальная сила американских горок. след на тележке во время петли.

Компонент любой результирующей силы, вызывающей круговое движение, называется центростремительной силой. Когда результирующая сила равна центростремительной силе, а ее величина постоянна, возникает равномерное круговое движение. Центростремительная сила направлена ​​к центру вращения, как и центростремительное ускорение. Согласно второму закону движения Ньютона, результирующая сила вызывает ускорение массы в соответствии с F _нетто = м a . Для равномерного кругового движения ускорение равно центростремительному ускорению: a = a _c . Следовательно, величина центростремительной силы F _c равна Fc=macFc=mac .

Используя две разные формы уравнения для величины центростремительного ускорения, ac=v2/rac=v2/r и ac=rω2ac=rω2, мы получаем два выражения, включающие величину центростремительной силы FcFc. Первое выражение в терминах тангенциальной скорости, второе в терминах угловой скорости: Fc=mv2rFc=mv2r и Fc=mrω2Fc=mrω2.

Обе формы уравнения зависят от массы, скорости и радиуса кругового пути. Вы можете использовать любое более удобное выражение для центростремительной силы. Второй закон Ньютона также гласит, что объект будет ускоряться в том же направлении, что и результирующая сила. По определению центростремительная сила направлена ​​к центру вращения, поэтому объект также будет ускоряться по направлению к центру. Прямая линия, проведенная от кругового пути к центру круга, всегда будет перпендикулярна тангенциальной скорости. Обратите внимание, что если вы решите первое выражение для р , получится

r=mv2Fc.r=mv2Fc.

Из этого выражения мы видим, что при данной массе и скорости большая центростремительная сила вызывает малый радиус кривизны, то есть крутую кривую.

Рисунок 6,8 На этом рисунке сила трения f служит центростремительной силой F _c . Центростремительная сила перпендикулярна тангенциальной скорости и вызывает равномерное круговое движение. Чем больше центростремительная сила F _c , тем меньше радиус кривизны r и тем острее кривая.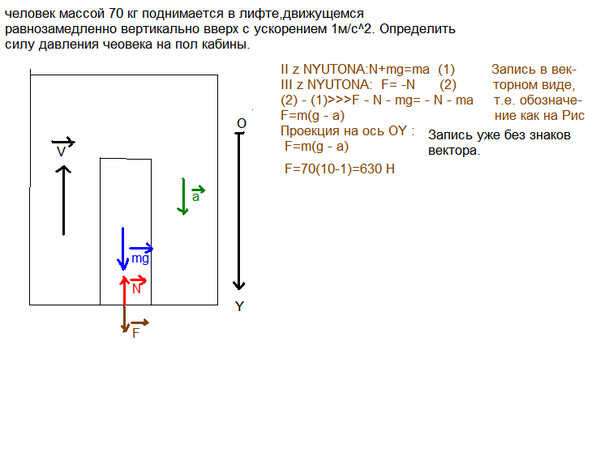 Нижняя кривая имеет ту же скорость v , но большая центростремительная сила F _c дает меньший радиус r′r′ .

Смотреть физику

Центростремительная сила и интуиция ускорения

Это видео объясняет, почему центростремительная сила, когда она равна чистой силе и имеет постоянную величину, создает центростремительное ускорение и равномерное круговое движение.

Поддержка учителей

Поддержка учителей

Предупреждение о заблуждении

Некоторые студенты могут путать центростремительную силу и центробежную силу. Центробежная сила — это не реальная сила, а результат ускоряющейся системы отсчета, такой как вращающаяся машина или вращающаяся Земля. Центробежная сила относится к вымышленному центру , убегающему от силы .

Представьте, что вы раскачиваете йойо по вертикали по часовой стрелке перед собой, перпендикулярно направлению взгляда. Если струна порвется, как только йо-йо достигнет крайнего нижнего положения, ближайшего к полу. Что будет с йойо после того, как порвется струна?

1. Йо-йо полетит внутрь в направлении действия центростремительной силы.

2. Йо-йо будет лететь наружу в направлении действия центростремительной силы.

3. Йо-йо полетит влево в направлении тангенциальной скорости.

4. Йо-йо полетит вправо в направлении тангенциальной скорости.

Решение задач центростремительного ускорения и центростремительной силы

Чтобы получить представление о типичных величинах центростремительного ускорения, мы проведем лабораторную работу, оценив центростремительное ускорение теннисной ракетки, а затем в нашем первом рабочем примере сравним центростремительное ускорение автомобиля, совершающего поворот, с гравитационным ускорением. Для второго рабочего примера мы рассчитаем силу, необходимую для поворота автомобиля по кривой.

Снап Лаборатория

Оценка центростремительного ускорения

В этом упражнении вы измерите замах клюшки для гольфа или теннисной ракетки, чтобы оценить центростремительное ускорение конца клюшки или ракетки. Вы можете сделать это в замедленном темпе. Напомним, что уравнение для центростремительного ускорения имеет вид ac=v2rac=v2r или ac=rω2ac=rω2.

• Одна теннисная ракетка или клюшка для гольфа
• Один таймер
• Одна линейка или рулетка

Процедура

1. Работа с партнером. Стойте на безопасном расстоянии от партнера, когда он или она размахивает клюшкой для гольфа или теннисной ракеткой.
2. Опишите движение качелей — это равномерное круговое движение? Почему или почему нет?
3. Постарайтесь, чтобы качание было как можно ближе к равномерному круговому движению. Какие коррективы должен был внести ваш партнер?
4. Измерьте радиус кривизны. Что вы измеряли физически?
5. Используя таймер, найдите либо линейную, либо угловую скорость, в зависимости от того, какое уравнение вы решите использовать.
6. Каково приблизительное центростремительное ускорение на основе этих измерений? Как вы думаете, насколько они точны? Почему? Как вы и ваш партнер можете сделать эти измерения более точными?

Поддержка учителей

Поддержка учителей

Замах клюшки для гольфа или ракетки можно сделать очень близким к равномерному круговому движению. Для этого человек должен был бы перемещать его с постоянной скоростью, не сгибая руки. Длина руки плюс длина клюшки или ракетки – это радиус кривизны. Точность измерений угловой скорости и углового ускорения будет зависеть от разрешающей способности используемого таймера и ошибки человеческого наблюдения. Замах клюшки для гольфа или ракетки можно сделать очень близким к равномерному круговому движению. Для этого человек должен был бы перемещать его с постоянной скоростью, не сгибая руки. Длина руки плюс длина клюшки или ракетки – это радиус кривизны. Точность измерений угловой скорости и углового ускорения будет зависеть от разрешающей способности используемого таймера и ошибки человеческого наблюдения.

Проверка захвата

Было ли полезнее использовать уравнение ac=v2rac=v2r или ac=rω2ac=rω2 в этом упражнении? Почему?

1. Должно быть проще использовать ac=rω2ac=rω2, потому что измерение угловой скорости путем наблюдения было бы проще.
2. Должно быть проще использовать ac=v2rac=v2r, поскольку было бы проще измерить тангенциальную скорость посредством наблюдения.
3. Должно быть проще использовать ac=rω2ac=rω2, потому что измерение угловой скорости путем наблюдения будет затруднено.
4. Должно быть проще использовать ac=v2rac=v2r, потому что измерение тангенциальной скорости путем наблюдения будет затруднено.

Рабочий пример

Сравнение центростремительного ускорения автомобиля, огибающего кривую, с ускорением под действием силы тяжести

Автомобиль следует по кривой радиусом 500 м со скоростью 25,0 м/с (около 90 км/ч). Чему равно центростремительное ускорение автомобиля? Сравните центростремительное ускорение для этой довольно плавной кривой, снятой на скорости шоссе, с ускорением под действием силы тяжести ( г ).

Стратегия

Поскольку дана линейная, а не угловая скорость, наиболее удобно использовать выражение ac=v2rac=v2r для нахождения величины центростремительного ускорения.

Решение

Ввод данных значений v = 25,0 м/с и r = 500 м в выражение для a _c дает

ac=v2r=(25,20 м/с) м/с2.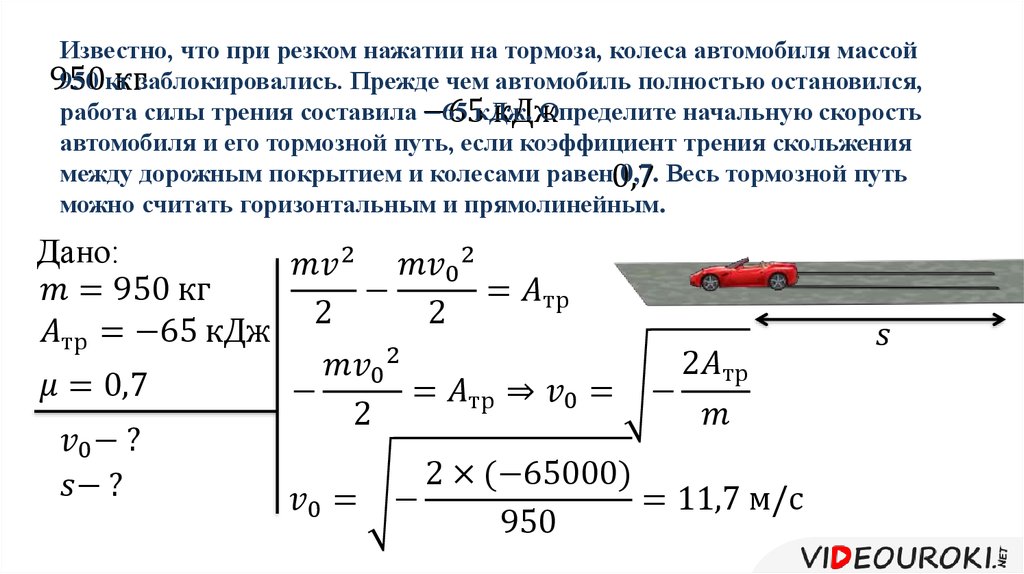 ac=v2r=(25,0 м/с)2500 м=1,25 м/с2.

Обсуждение

Чтобы сравнить это с ускорением свободного падения ( г = 9,80 м/с ² ), возьмем отношение ac/g=(1,25 м/с2)/(9,80 м/с2)=0,128ac/ g=(1,25 м/с2)/(9,80 м/с2)=0,128 . Следовательно, ac=0,128gac=0,128g, что означает, что центростремительное ускорение составляет примерно одну десятую ускорения свободного падения.

Рабочий пример

Сила трения на автомобильных шинах, огибающих кривую

1. Рассчитайте центростремительную силу, действующую на автомобиль массой 900 кг, который движется по кривой радиусом 600 м на горизонтальной поверхности со скоростью 25,0 м/с.
2. Статическое трение предотвращает скольжение автомобиля. Найдите величину силы трения между шинами и дорогой, которая позволяет автомобилю пройти поворот без соскальзывания по прямой.
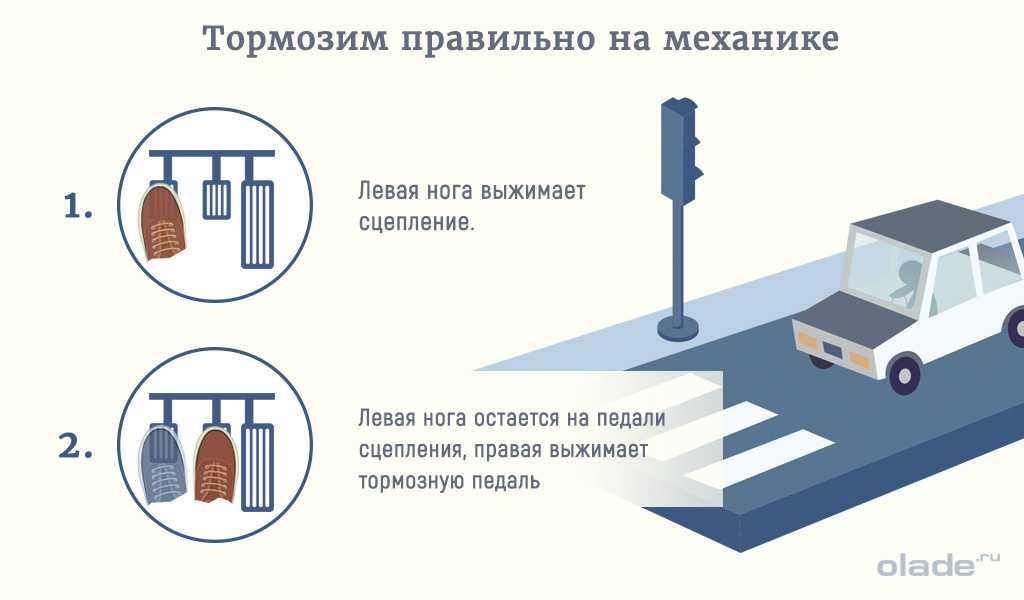
3. Если бы автомобиль скользил, если бы он двигался немного быстрее, каков коэффициент статического трения между шинами и дорогой? Могли бы мы сделать какие-либо выводы о коэффициенте трения покоя, если бы не знали, может ли автомобиль двигаться быстрее по кривой без проскальзывания?

Стратегия и решение для (а)

Мы знаем, что Fc=mv2rFc=mv2r . Следовательно,

Fc=mv2r=(900кг)(25,0м/с)2600м=938Н.Fc=mv2r=(900кг)(25,0м/с)2600м=938Н.

Стратегия и решение для (б)

На изображении выше показаны силы, действующие на автомобиль при движении по кривой. На этой диаграмме автомобиль въезжает на страницу, как показано, и поворачивает налево. Трение действует влево, ускоряя автомобиль к центру кривой. Поскольку трение является единственной горизонтальной силой, действующей на автомобиль, в данном случае оно обеспечивает всю центростремительную силу. Следовательно, сила трения является центростремительной силой в этой ситуации и направлена ​​к центру кривой.

f=Fc=938Nf=Fc=938N

Стратегия и решение для (c)

Если автомобиль вот-вот начнет скользить, трение покоя достигнет максимального значения и f=µsN=µsmgf=µsN=µsmg. Решая для мксмкс, получаем мкс=938900×9,8=0,11 мкс=938900×9,8=0,11. Независимо от того, знаем ли мы максимально допустимую скорость для скругления кривой, мы можем сделать вывод, что это минимальное значение коэффициента.

Обсуждение

Поскольку мы нашли силу трения в части (b), мы могли также найти коэффициент трения, поскольку f=µsN=µsmgf=µsN=µsmg. Трение покоя равно только µsNµsN, когда оно имеет максимально возможное значение. Если бы автомобиль мог двигаться быстрее, трение при заданной скорости было бы таким же, как мы рассчитали, но коэффициент статического трения был бы больше.

Практические задачи

9.

Какое центростремительное ускорение испытывают пассажиры автомобиля, движущегося со скоростью 12 м/с по кривой радиусом 2,0 м?

1. 3 м/с ²

2. 6 м/с ²

3. 36 м/с ²

4. 72 м/с ²

10.

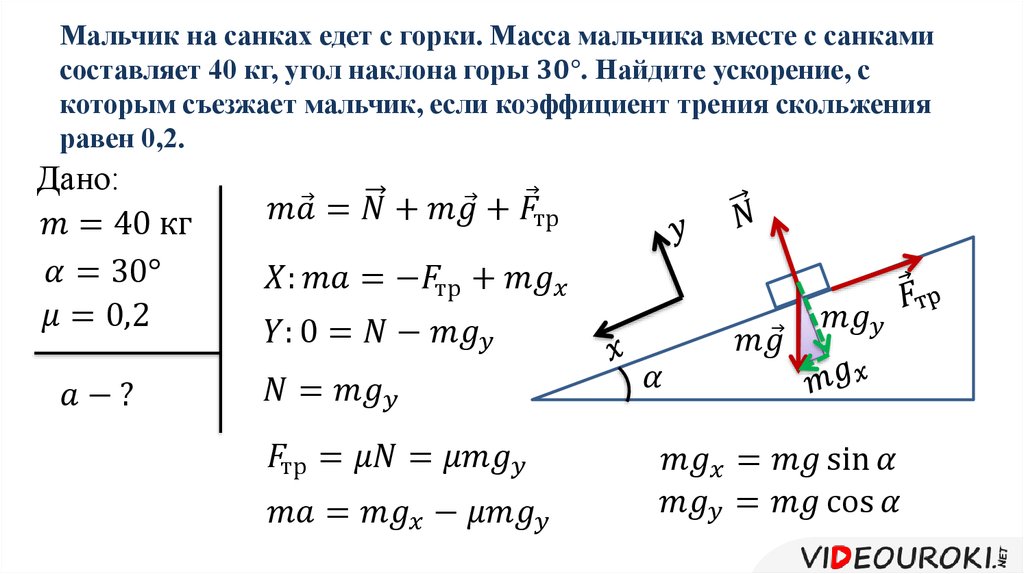
Рассчитайте центростремительное ускорение объекта, следующего по пути с радиусом кривизны 0,2 м и с угловой скоростью 5 рад/с.

1. 1 м/с
2. 5 м/с
3. 1 м/с ²
4. 5 м/с ²

Проверьте свое понимание

11.

Что такое равномерное круговое движение?

1. Равномерное круговое движение — это когда объект ускоряется по круговой траектории с постоянно увеличивающейся скоростью.

2. Равномерное круговое движение — это когда объект движется по круговой траектории с переменным ускорением.

3. Равномерное круговое движение — это когда объект движется по круговой траектории с постоянной скоростью.

4. Равномерное круговое движение — это когда объект движется по круговой траектории с переменной скоростью.

12.

Что из следующего является центростремительным ускорением?

1. Ускорение объекта, движущегося по круговой траектории и направленного радиально к центру круговой орбиты
2. Ускорение объекта, движущегося по круговой траектории и направленного по касательной по круговой траектории
3. Ускорение объекта, движущегося по прямолинейному пути и направленного в направлении движения объекта
4. Ускорение объекта, движущегося по прямолинейному пути и направленного в сторону, противоположную движению объекта

13.

Существует ли результирующая сила, действующая на объект, совершающий равномерное круговое движение?

1. Да, объект ускоряется, поэтому на него должна действовать результирующая сила.

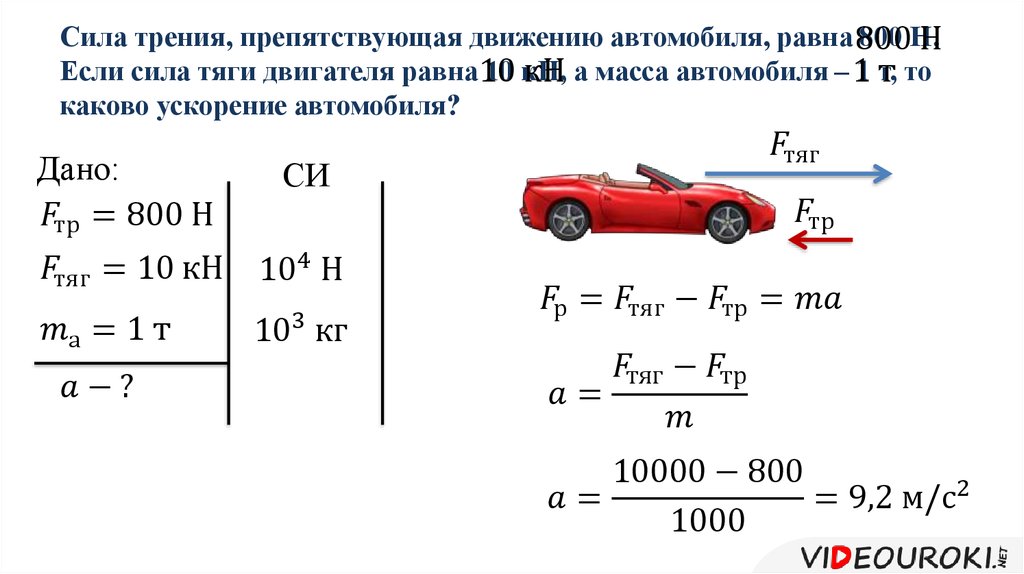
2. Да потому что разгона нет.

3. Нет, потому что есть ускорение.

4. Нет, потому что нет ускорения.

14.

Приведите два примера сил, которые могут вызвать центростремительное ускорение.

1. Сила земного притяжения на Луне и нормальная сила
2. Сила земного притяжения на Луне и натяжение веревки на орбитальном шаре
3. Нормальная сила и сила трения, действующие на движущийся автомобиль
4. Нормальная сила и натяжение веревки на шаре

Поддержка учителей

Поддержка учителей

Используйте вопросы «Проверьте свое понимание», чтобы оценить, справляются ли учащиеся с целями обучения этого раздела.