Чему равна сила сопротивления воздуха: 422. Парашютист, масса которого 70 кг, равномерно опускается. Чему равна сила сопротивления воздуха, действующая на парашютиста?

№ 422 Сборник задач по физике 7-9 класс Лукашик. Чему равна сила сопротивления воздуха, действующая на парашютиста? – Рамблер/класс

№ 422 Сборник задач по физике 7-9 класс Лукашик. Чему равна сила сопротивления воздуха, действующая на парашютиста? – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Парашютист, масса которого 70 кг, равномерно опускается.

Чему равна сила сопротивления воздуха, действующая на парашютиста?
 

ответы

Вот так решается:

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г.Я.

Психология

Химия

похожие вопросы 5

№ 179 Сборник задач по физике 7-9 класс Лукашик. Почему патрон продолжает вращаться?

У кого есть ответ?
Почему после выключения двигателя сверлильного станка патрон продолжает вращаться?
 

ГДЗФизика7 класс8 класс9 классЛукашик В.И.

Приготовление раствора сахара и расчёт его массовой доли в растворе. Химия. 8 класс. Габриелян. ГДЗ. Хим. практикум № 1. Практ. работа № 5.

Попробуйте провести следующий опыт. Приготовление раствора
сахара и расчёт его массовой доли в растворе.
Отмерьте мерным (Подробнее…)

ГДЗШкола8 классХимияГабриелян О.С.

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №475 В обоих случаях поплавок плавает. В какую жидкость он погружается глубже?

Привет. Выручайте с ответом по физике…
Поплавок со свинцовым грузилом внизу опускают
сначала в воду, потом в масло. В обоих (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.

Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

Ребята нужны ответы на пересдачу по математике 9 класс 11 регион. Срочно!

ГИА9 класс

Чему равна работа силы сопротивления воздуха формула.

Движение тела в поле тяжести с учётом сопротивления воздуха. Сопротивлением воздуха заинтересовались артиллеристы

Решение.

Для решения задачи рассмотрим физическую систему «тело – гравитационное поле Земли». Тело будем считать материальной точкой, а гравитационное поле Земли — однородным. Выделенная физическая система является незамкнутой, т.к. во время движения тела взаимодействует с воздухом.
Если не учитывать выталкивающую силу, действующую на тело со стороны воздуха, то изменение полной механической энергии системы равняется работе силы сопротивления воздуха, т.е. ∆ E = A c .

Нулевой уровень потенциальной энергии выберем на поверхности Земли. Единственной внешней силой в отношении системы «тело – Земля» является сила сопротивления воздуха, направленная вертикально вверх. Начальная энергия системы E 1 , конечная E 2 .

Работа силы сопротивления A.

Т.к. угол между силой сопротивления и перемещением равен 180° , то косинус равен -1, поэтому A = — F c h .

Приравняем A.

Рассматриваемую незамкнутую физическую систему можно также описать теоремой от изменении кинетической энергии системы взаимодействующих между собой объектов, согласно которой изменение кинетической энергии системы равно работе, совершенной внешними и внутренними силами при ее переходе из начального состояния в конечное. Если не учитывать выталкивающую силу, действующую на тело со стороны воздуха, а внутренней – сила тяжести. Следовательно ∆ E к = A 1 + A 2 , где A 1 = mgh – работа силы тяжести, A 2 = F c hcos 180° = — F c h – работа силы сопротивления; ∆ E = E 2 – E 1 .

Это творческое задание для мастер-класса по информатике для школьников при ДВФУ.
Цель задания — выяснить, как изменится траектория тела, если учитывать сопротивление воздуха. Также необходимо ответить на вопрос, будет ли дальность полёта по-прежнему достигать максимального значения при угле бросания в 45°, если учитывать сопротивление воздуха.

В разделе «Аналитическое исследование» изложена теория. Этот раздел можно пропустить, но он должен быть, в основном, понятным для вас, потому что бо льшую часть из этого вы проходили в школе.
В разделе «Численное исследование» содержится описание алгоритма, который необходимо реализовать на компьютере. Алгоритм простой и краткий, поэтому все должны справиться.

Аналитическое исследование

Введём прямоугольную систему координат так, как показано на рисунке. В начальный момент времени тело массой m находится в начале координат. Вектор ускорения свободного падения направлен вертикально вниз и имеет координаты (0, —g ).
— вектор начальной скорости. Разложим этот вектор по базису: . Здесь , где — модуль вектора скорости, — угол бросания.

Запишем второй закон Ньютона: .
Ускорение в каждый момент времени есть (мгновенная) скорость изменения скорости, то есть производная от скорости по времени: .

Следовательно, 2-й закон Ньютона можно переписать в следующем виде:
, где — это равнодействующая всех сил, действующая на тело.
Так как на тело действуют сила тяжести и сила сопротивления воздуха, то
.

Мы будем рассматривать три случая:
1) Сила сопротивления воздуха равна 0: .
2) Сила сопротивления воздуха противоположно направлена с вектором скорости, и её величина пропорциональна скорости: .
3) Сила сопротивления воздуха противоположно направлена с вектором скорости, и её величина пропорциональна квадрату скорости: .

Вначале рассмотрим 1-й случай.
В этом случае , или .

Из следует, что (равноускоренное движение).

Так как (r — радиус-вектор), то .
Отсюда .
Эта формула есть не что иное, как знакомая вам формула закона движения тела при равноускоренном движении.
Так как , то .
Учитывая, что и , получаем из последнего векторного равенства скалярные равенства:

Проанализируем полученные формулы.
Найдём время полёта тела. Приравняв y к нулю, получим

Дальность полёта равна значению координаты x в момент времени t 0:

Из этой формулы следует, что максимальная дальность полёта достигается при .
Теперь найдём уравнение трактории тела . Для этого выразим t через x

И подставим полученное выражение для t в равенство для y .

Полученная функция y

(x ) — квадратичная функция, её графиком является парабола, ветви которой направлены вниз.
Про движение тела, брошенного под углом к горизонту (без учёта сопротивления воздуха), рассказывается в этом видеоролике.

Теперь рассмотрим второй случай: .

Второй закон приобретает вид ,
отсюда .
Запишем это равенство в скалярном виде:

Мы получили два линейных дифференциальных уравнения .
Первое уравнение имеет решение

В чём можно убедиться, подставив данную функцию в уравнение для v x и в начальное условие .
Здесь e = 2,718281828459… — число Эйлера .
Второе уравнение имеет решение

Так как , , то при наличии сопротивления воздуха движение тела стремится к равномерному, в отличие от случая 1, когда скорость неограниченно увеличивается.
В следующем видеоролике говорится, что парашютист сначала движется ускоренно, а потом начинает двигаться равномерно (даже до раскрытия парашюта).

Найдём выражения для x и y .
Так как x (0) = 0, y (0) = 0, то

Нам осталось рассмотреть случай 3, когда .
Второй закон Ньютона имеет вид
, или .
В скалярном виде это уравнение имеет вид:

Это система нелинейных дифференциальных уравнений . Данную систему не удаётся решить в явном виде, поэтому необходимо применять численное моделирование.

Численное исследование

В предыдущем разделе мы увидели, что в первых двух случаях закон движения тела можно получить в явном виде. Однако в третьем случае необходимо решать задачу численно. При помощи численных методов мы получим лишь приближённое решение, но нас вполне устроит и небольшая точность. (Число π или квадратный корень из 2, кстати, нельзя записать абсолютно точно, поэтому при расчётах берут какое-то конечное число цифр, и этого вполне хватает.

)

Будем рассматривать второй случай, когда сила сопротивления воздуха определяется формулой. Отметим, что при k = 0 получаем первый случай.

Скорость тела подчиняется следующим уравнениям:

В левых частях этих уравнений записаны компоненты ускорения .
Напомним, что ускорение есть (мгновенная) скорость изменения скорости, то есть производная от скорости по времени.
В правых частях уравнений записаны компоненты скорости. Таким образом, данные уравнения показывают, как скорость изменения скорости связана со скоростью.

Попробуем найти решения этих уравнений при помощи численных методов. Для этого введём на временной оси сетку : выберем число и будем рассматривать моменты времени вида : .

Наша задача — приближённо вычислить значения в узлах сетки.

Заменим в уравнениях ускорение (мгновенную скорость изменения скорости) на среднюю скорость изменения скорости, рассматривая движение тела на промежутке времени :

Теперь подставим полученные аппроксимации в наши уравнения.

Полученные формулы позволяют нам вычислить значения функций в следующем узле сетки, если известны значения этих функций в предыдущем узле сетки.

При помощи описанного метода мы можем получить таблицу приближённых значений компонент скорости.

Как найти закон движения тела, т.е. таблицу приближённых значений координат x (t ), y (t )? Аналогично!
Имеем

Значение vx[j] равняется значению функции , для других массивов аналогично.
Теперь остаётся написать цикл, внутри которого мы будем вычислять vx через уже вычисленное значение vx[j], и с остальными массивами то же самое. Цикл будет по j от 1 до N .
Не забудьте инициализировать начальные значения vx, vy, x, y по формулам , x 0 = 0, y 0 = 0.

В Паскале и Си для вычисления синуса и косинуса имеются функции sin(x) , cos(x) . Обратите внимание, что эти функции принимают аргумент в радианах.

Вам необходимо построить график движения тела при k = 0 и k > 0 и сравнить полученные графики. Графики можно построить в Excel.
Отметим, что расчётные формулы настолько просты, что для вычислений можно использовать один только Excel и даже не использовать язык программирования.
Однако в дальнейшем вам нужно будет решить задачу в CATS, в которой нужно вычислить время и дальность полёта тела, где без языка программирования не обойтись.

Обратите внимание, что вы можете протестировать вашу программу и проверить ваши графики, сравнив результаты вычислений при k = 0 с точными формулами, приведёнными в разделе «Аналитическое исследование».

Поэкспериментируйте со своей программой. Убедитесь в том, что при отсутствии сопротивления воздуха (k = 0) максимальная дальность полёта при фиксированной начальной скорости достигается при угле в 45°.
А с учётом сопротивления воздуха? При каком угле достигается максимальная дальность полёта?

На рисунке представлены траектории тела при v 0 = 10 м/с, α = 45°, g = 9,8 м/с 2 , m = 1 кг, k = 0 и 1, полученные при помощи численного моделирования при Δt = 0,01.

Вы можете ознакомиться с замечательной работой 10-классников из г. Троицка, представленной на конференции «Старт в науку» в 2011 г. Работа посвящена моделированию движения теннисного шарика, брошенного под углом к горизонту (с учетом сопротивления воздуха). Применяется как численное моделирование, так и натурный эксперимент.

Таким образом, данное творческое задание позволяет познакомиться с методами математического и численного моделирования, которые активно используются на практике, но мало изучаются в школе. К примеру, данные методы использовались при реализации атомного и космического проектов в СССР в середине XX века.

Силами сопротивления называются силы, препятствующие движению автомобиля. Эти силы направлены против его движе­ния.

При движении на подъеме, характеризуемом высотой H п, длиной проекции В п на гори­зонтальную плоскость и углом подъема дороги α, на автомобиль действуют следующие силы со­противления (рис. 3.12): сила со­противления качению Р к , равная сумме сил сопротивления каче­нию передних (Р К|) и задних (Р К2) колес, сила сопротивления подъе­му Р п , сила сопротивления воз­духа Д и сила сопротивления раз­гону Р И . Силы сопротивления ка­чению и подъему связаны с особенностями дороги. Сумма этих сил называется силой сопротивления дороги Р Д .

Рис. 3.13. Потери энергии на внутреннее трение в шине:

а — точка, соответствующая мак­симальным значениям нагрузки и прогиба шины

Сила сопротивления качению

Возникновение силы сопротивления качению при движении обусловлено потерями энергии на внутреннее трение в шинах, поверхностное трение шин о дорогу и образование колеи (на деформируемых дорогах).О потерях энергии на внутреннее трение в шине можно судить по рис. 3.13, на котором приведена зависимость между вертикаль­ной нагрузкой на колесо и деформацией шины — ее прогибом f ш .

При движении колеса по неровной поверхности шина, испы­тывая действие переменной нагрузки, деформируется. Линия αО, которая соответствует возрастанию нагрузки, деформирующей шину, не совпадает с линией аО, отвечающей снятию нагрузки. Площадь области, заключенной между указанными кривыми, ха­рактеризует потери энергии на внутреннее трение между отдель­ными частями шины (протектор, каркас, слои корда и др.).

Потери энергии на трение в шине называются гистерезисом, а линия ОαО — петлей гистерезиса.

Потери на трение в шине необратимы, так как при деформа­ции она нагревается и из нее выделяется теплота, которая рассе­ивается в окружающую среду. Энергия, затрачиваемая на дефор­мацию шины, не возвращается полностью при последующем вос­становлении ее формы.

Сила сопротивления качению Р к достигает наибольшего зна­чения при движении по горизонтальной дороге. В этом случае

где G — вес автомобиля, Н; f — коэффициент сопротивления качению.

При движении на подъеме и спуске сила сопротивления каче­нию уменьшается по сравнению с Р к на горизонтальной дороге, и тем значительнее, чем они круче. Для этого случая движения сила сопротивления качению

где α — угол подъема, °.

Зная силу сопротивления качению, можно определить мощ­ность, кВт,

затрачиваемую на преодоление этого сопротивления:

где v -скорости автомобиля,м/c 2

Для горизонтальной дороги соs0°=1 и

З
ависимости силы сопротивления качениюР к и мощности N К от скорости автомобиля v показаны на рис. 3.14

Коэффициент сопротивления качению

Коэффициент сопротивления качению существенно влияет на потери энергии при движении автомобиля. Он зависит от многих конструктивных и эксплуатационных

Рис 3.15. Зависимости коэффициента сопротивления качению от

Скорости движения (а), давления воздуха в шине (б) и момента, передаваемого через колесо (в)

факторов и определяется экспериментально. Его средние значения для различных дорог при нормальном давлении воздуха в шине составляют 0,01 …0,1.Рассмотрим влияние различных факторов на коэффициент сопротивления качению.

Скорость движения . При изменении скорости движения в ин­тервале 0…50 км/ч коэффициент сопротивления качению изме­няется незначительно и его можно считать постоянным в указан­ном диапазоне скоростей.

При повышении скорости движения за пределами указанного интервала коэффициент сопротивления качению существенно уве­личивается (рис. 3.15, а) вследствие возрастания потерь энергии в шине на трение.

Коэффициент сопротивления качению в зависимости от ско­рости движения можно приближенно рассчитать по формуле

где — скорость автомобиля, км/ч.

Тип и состояние покрытия дороги. На дорогах с твердым по­крытием сопротивление качению обусловлено главным образом деформациями шины.

При увеличении числа дорожных неровностей коэффициент сопротивления качению возрастает.

На деформируемых дорогах коэффициент сопротивления ка­чению определяется деформациями шины и дороги. В этом случае он зависит не только от типа шины, но и от глубины образую­щейся колеи и состояния грунта.

Значения коэффициента сопротивления качению при рекомен­дуемых уровнях давления воздуха и нагрузки на шину и средней скорости движения на различных дорогах приведены ниже:

Асфальто- и цементобетонное шоссе:

в хорошем состоянии………………………………. 0,007…0,015

в удовлетворительном состоянии…………… 0,015…0,02

Гравийная дорога в хорошем состоянии…. 0,02…0,025

Булыжная дорога в хорошем состоянии…… 0,025…0,03

Грунтовая дорога сухая, укатанная………….. 0,025…0,03

Песок………………………………………………………….. 0,1…0,3

Обледенелая дорога, лед…………………………. 0,015…0,03

Укатанная снежная дорога……………………….. 0,03…0,05

Тип шины. Коэффициент сопротивления качению во многом зависит от рисунка протектора, его износа, конструкции каркаса и качества материала шины. Изношенность протектора, уменьше­ние числа слоев корда и улучшение качества материала приводят к падению коэффициента сопротивления качению вследствие снижения потерь энергии в шине.

Давление воздуха в шине . На дорогах с твердым покрытием при уменьшении давления воздуха в шине коэффициент сопро­тивления качению повышается (рис. 3.15, б). На деформируемых дорогах при снижении давления воздуха в шине уменьшается глу­бина колеи, но возрастают потери на внутреннее трение в шине. Поэтому для каждого типа дороги рекомендуется определенное давление воздуха в шине, при котором коэффициент сопротивле­ния качению имеет минимальное значение.

. При увеличении вертикальной нагрузки на колесо коэффициент сопротивления качению существенно возрастает на деформируемых дорогах и незначительно — на до­рогах с твердым покрытием.

Момент, передаваемый через колесо . При передаче момента через колесо коэффициент сопротивления качению возрастает (рис. 3.15, в) вследствие потерь на проскальзывание шины в месте ее контакта с дорогой. Для ведущих колес значение коэффициента сопротивления качению на 10… 15 % больше, чем для ведомых.

Коэффициент сопротивления качению оказывает существен­ное влияние на расход топлива и, следовательно, на топливную экономичность автомобиля. Исследования показали, что даже не­большое уменьшение этого коэффициента обеспечивает ощути­мую экономию топлива. Поэтому неслучайно стремление конст­рукторов и исследователей создать такие шины, при использова­нии которых коэффициент сопротивления качению будет незна­чительным, но это весьма сложная проблема.

При движении любого предмета по поверхности или в воздухе возникают силы, препятствующие этому. Их называют силами сопротивления или трения. В этой статье мы расскажем, как найти силу сопротивления, и рассмотрим факторы, влияющие на нее.

Для определения силы сопротивления необходимо воспользоваться третьим законом Ньютона. Эта величина численно равна силе, которую нужно приложить, чтобы заставить равномерно двигаться предмет по ровной горизонтальной поверхности. Это можно сделать при помощи динамометра. Сила сопротивления вычисляется по формуле F=μ*m*g. Согласно этой формуле, искомая величина прямо пропорциональна массе тела. Стоит учесть, что для правильного подсчета необходимо выбрать μ – коэффициент, зависящий от материала, из которого изготовлена опора. Принимают во внимание и материал предмета. Этот коэффициент выбирается по таблице. Для расчета используется постоянная g, которая равна 9,8 м/с2. Как рассчитать сопротивление, если тело движется не прямолинейно, а по наклонной плоскости? Для этого в первоначальную формулу нужно ввести cos угла. Именно от угла наклона зависит трение и сопротивление поверхности тел к движению. Формула для определения трения по наклонной плоскости будет иметь такой вид: F=μ*m*g*cos(α). Если тело движется на высоте, то на него действует сила трения воздуха, которая зависит от скорости движения предмета. Искомую величину можно рассчитать по формуле F=v*α. Где v – скорость движения предмета, а α – коэффициент сопротивления среды. Эта формула подходит исключительно для тел, которые передвигаются с небольшой скоростью.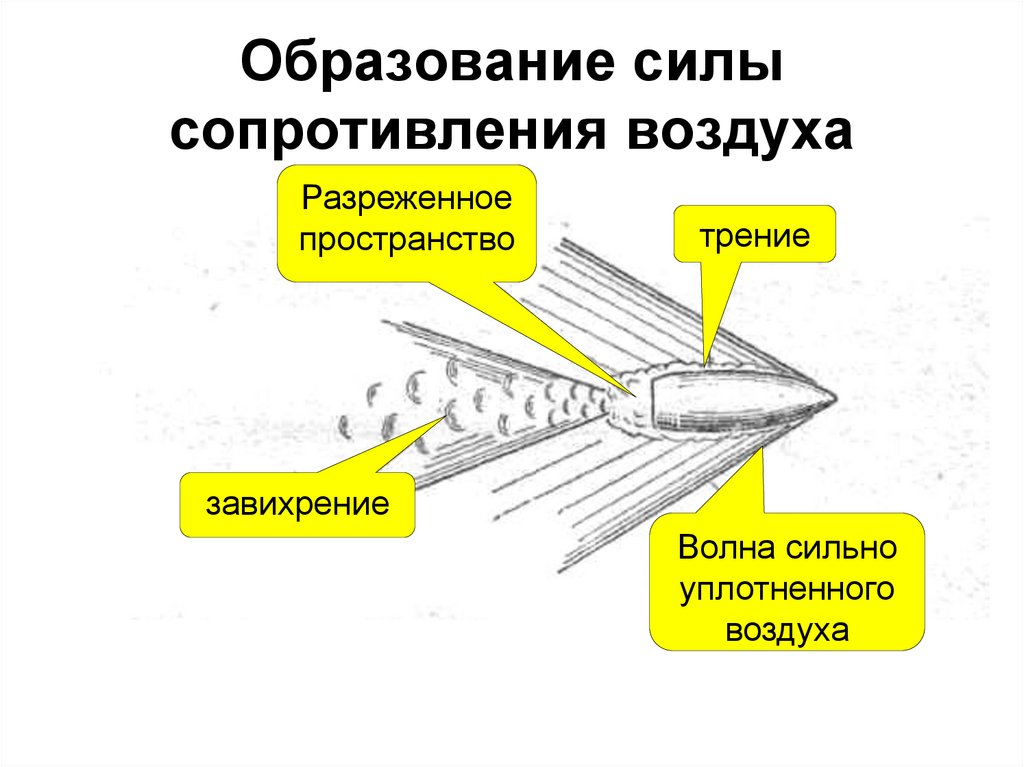 Для определения силы сопротивления реактивных самолетов и других высокоскоростных агрегатов применяют другую – F=v2*β. Для расчета силы трения высокоскоростных тел используют квадрат скорости и коэффициент β, который рассчитывается для каждого предмета отдельно. При движении предмета в газе или жидкости при расчете силы трения необходимо учитывать плотность среды, а также массу и объем тела. Сопротивление движению существенно снижает скорость поездов и автомобилей. Причем на движущие предметы действует два вида сил – постоянные и временные. Общая сила трения представлена суммой двух величин. Для снижения сопротивления и повышения скорости машины конструкторы и инженеры изобретают разнообразные материалы со скользящей поверхностью, от которой воздух отталкивается. Именно поэтому передняя часть скоростных поездов имеет обтекаемую форму. Рыбы очень быстро движутся в воде благодаря обтекаемому телу, покрытому слизью, которая снижает трение. Не всегда сила сопротивления отрицательно сказывается на движении машин. Чтобы вытащить автомобиль из грязи, необходимо под колеса насыпать песок или щебень. Благодаря увеличению трения авто отлично справляется с болотистой почвой и грязью.

Сопротивление движения в воздухе используется во время прыжков с парашютом. В результате возникающего трения между куполом и воздухом скорость движения парашютиста снижается, что позволяет без ущерба для жизни заниматься парашютным спортом.

Веб-сайт кабинета физики

Предположим, что слон и перо падают с очень высокого здания с одинаковой высоты в одно и то же время. Предположим реалистичную ситуацию, когда и перо, и слон сталкиваются с сопротивлением воздуха. Какой предмет — слон или перо — первым упадет на землю? Анимация справа точно изображает эту ситуацию. Показано движение слона и пера при наличии сопротивления воздуха. Кроме того, ускорение каждого объекта представлено векторной стрелкой.

Большинство людей не удивляется тому факту, что слон ударяется о землю раньше, чем перо. Но почему слон падает быстрее? Этот вопрос является источником большой путаницы (а также различных заблуждений).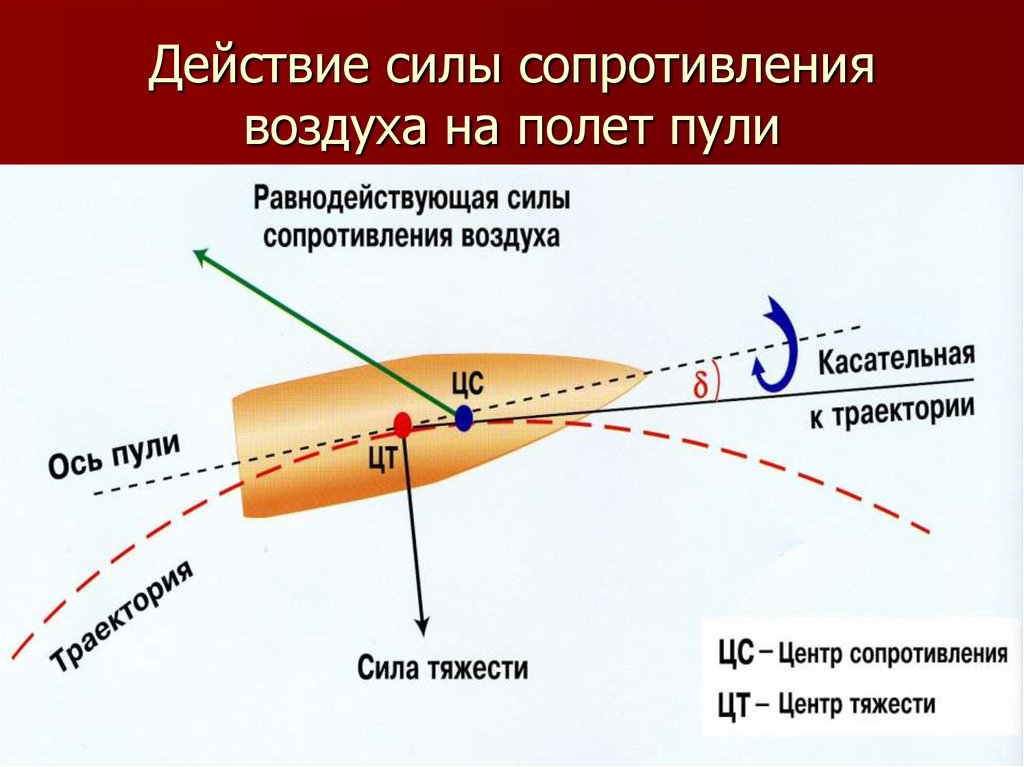 Проверьте свое понимание, постаравшись определить следующие утверждения как истинные или ложные.

ИСТИНА или ЛОЖЬ:

1. Слон сталкивается с меньшей силой сопротивления воздуха, чем перо, и поэтому падает быстрее.
2. У слона большее ускорение свободного падения, чем у пера, и поэтому он падает быстрее.
3. И слон, и перо имеют одинаковую силу тяжести, но ускорение силы тяжести у слона наибольшее.
4. И слон, и перо имеют одинаковую силу тяжести, но перо испытывает большее сопротивление воздуха.
5. Каждый объект испытывает одинаковое сопротивление воздуха, но слон испытывает наибольшую силу гравитации.
6. Каждый объект испытывает одинаковое сопротивление воздуха, но на перо действует наибольшая сила тяжести.
7. Перо весит больше, чем слон, и поэтому не будет ускоряться так же быстро, как слон.
8. И слон, и перо весят одинаково, но большая масса пера приводит к меньшему ускорению.
9. Слон испытывает меньшее сопротивление воздуха и, чем перо, и, таким образом, достигает большей конечной скорости.
10. Перо испытывает большее сопротивление воздуха, чем слон, и поэтому достигает меньшей конечной скорости.
11. Слон и перо сталкиваются с одинаковым сопротивлением воздуха, но конечная скорость слона выше.

Если вы ответили ВЕРНО на любой из приведенных выше вопросов, то, возможно, у вас есть некоторая путаница в отношении понятий веса, силы тяжести, ускорения свободного падения, сопротивления воздуха и конечной скорости. Слон и перо тянутся вниз под действием силы тяжести. При первоначальном падении эта сила тяжести представляет собой неуравновешенную силу. Таким образом, и слон, и перо начинают разгоняться (т. е. набирать скорость). Когда слон и перо начинают набирать скорость, они сталкиваются с восходящей силой сопротивления воздуха. Сопротивление воздуха является результатом объекта пробивает через слой воздуха и сталкивается с молекулами воздуха. Чем больше молекул воздуха сталкивается с объектом, тем больше сила сопротивления воздуха. Следовательно, величина сопротивления воздуха зависит от скорости падающего объекта и площади поверхности падающего объекта. Основываясь только на площади поверхности, можно с уверенностью предположить, что (при той же скорости) слон столкнется с большим сопротивлением воздуха, чем перо.

Но почему же тогда слон, встречающий большее сопротивление воздуха, чем перо, падает быстрее? В конце концов, разве сопротивление воздуха не замедляет объект? Не будет ли объект с большим сопротивлением воздуха падать медленнее?

Ответы на эти вопросы требуют понимания первого и второго законов Ньютона и концепции конечной скорости. Согласно законам Ньютона, объект будет ускоряться, если силы, действующие на него, неуравновешены; и, кроме того, величина ускорения прямо пропорциональна величине чистой силы (неуравновешенной силы), действующей на него. Падающие объекты сначала ускоряются (набирают скорость), потому что нет достаточно большой силы, чтобы уравновесить направленную вниз силу тяжести. Однако по мере того, как объект набирает скорость, он сталкивается с возрастающей силой восходящего сопротивления воздуха. На самом деле объекты будут продолжать ускоряться (набирать скорость) до тех пор, пока сила сопротивления воздуха не увеличится до достаточно большого значения, чтобы уравновесить направленную вниз силу тяжести. Поскольку слон имеет большую массу, он весит больше и испытывает большую нисходящую силу тяжести. Слону придется ускоряться (набирать скорость) в течение более длительного периода времени, прежде чем возникнет достаточное восходящее сопротивление воздуха, чтобы уравновесить большую нисходящую силу тяжести.

Как только восходящая сила сопротивления воздуха на объект становится достаточно большой, чтобы уравновесить направленную вниз силу тяжести, говорят, что объект достиг конечной скорости. Конечная скорость — это конечная скорость объекта; объект будет продолжать падать на землю с этой конечной скоростью. В случае слона и пера слон имеет гораздо большую конечную скорость, чем перо. Как упоминалось выше, слон должен был бы ускоряться в течение более длительного периода времени. Слону требуется большая скорость, чтобы накопить достаточную восходящую силу сопротивления воздуха, чтобы уравновесить нисходящую силу тяжести. На самом деле слон никогда не достигает конечной скорости; анимация выше показывает, что слон все еще имеет ускорение за момент до удара о землю. Если бы мы изобразили относительную величину двух сил, действующих на слона и перо в разное время их падения, возможно, она выглядела бы так, как показано ниже. (ПРИМЕЧАНИЕ. Величина вектора силы указана относительным размером стрелки.)

Обратите внимание на приведенные выше диаграммы и приведенную выше анимацию, что перо быстро достигает баланса сил и, следовательно, нулевого ускорения (т. Е. Конечной скорости). С другой стороны, слон никогда не достигает предельной скорости во время падения; силы никогда не становятся полностью уравновешенными, поэтому ускорение все же есть. Если бы у него было достаточно времени, слон, возможно, наконец разогнался бы до достаточно высоких скоростей, чтобы столкнуться с достаточно большой восходящей силой сопротивления воздуха, чтобы достичь конечной скорости. Если бы оно действительно достигло конечной скорости, то эта скорость была бы чрезвычайно большой — намного больше, чем конечная скорость пера.

Итак, в заключение слон падает быстрее пера, потому что никогда не достигает предельной скорости; он продолжает ускоряться по мере падения (аккумулируя все большее и большее сопротивление воздуха), приближаясь к конечной скорости, но никогда не достигая ее. С другой стороны, перо быстро достигает предельной скорости. Не требуя большого сопротивления воздуха, прежде чем оно прекратит свое ускорение, перо достигает состояния предельной скорости на ранней стадии своего падения. Малая конечная скорость пера означает, что оставшаяся часть его падения будет происходить с малой конечной скоростью.

А если бы сопротивления воздуха не было? Если бы можно было каким-то образом устранить сопротивление воздуха (проведя эксперимент в вакууме), то какой предмет — слон или перо — ударился бы о землю первым? Изучите эти вопросы, перейдя по соответствующим ссылкам на «Слон и перо (свободное падение)» в студии Multimedia Physics Studios.

---

Для получения дополнительной информации о физических описаниях движения посетите Учебное пособие по физике. Подробная информация доступна там по следующим темам:

Ускорение гравитации

Первый закон движения Ньютона

Сила тяжести и вес

Второй закон движения Ньютона

Диаграммы свободного тела

Свободное падение против сопротивления воздуха

Сопротивление воздуха: определение, формула и пример

У вас когда-нибудь возникало ощущение, что что-то пытается замедлить вас, когда вы едете на велосипеде? Когда вы движетесь вперед, сила трения воздуха снижает вашу скорость. Сила трения действует на ваше лицо и тело в направлении, противоположном движению велосипеда. Сила сопротивления воздуха увеличивается пропорционально скорости. Приседание на велосипеде позволяет уменьшить влияние силы сопротивления воздуха и двигаться быстрее.

Сейчас вы можете думать о силе сопротивления воздуха как о чем-то негативном и препятствующем движению, но на самом деле она оказывается весьма полезной в нашей повседневной жизни. Например, когда парашютист выпрыгивает из самолета и раскрывает парашют, воздух замедляет падение. Скорость парашютиста уменьшается по мере приближения к земле из-за сопротивления воздуха. В результате человек благополучно и плавно достигает земли — все из-за силы сопротивления. В этой статье мы более подробно обсудим науку о сопротивлении воздуха.

Определение сопротивления воздуха

До сих пор в большинстве физических задач, связанных с движением, прямо указывалось, что сопротивлением воздуха можно пренебречь. В реальной жизни это не так, поскольку все объекты испытывают определенный уровень сопротивления при прохождении через воздух.

Сопротивление воздуха или Сопротивление Сила Тип трения, возникающего между объектом и окружающим его воздухом.

Эти силы сопротивления заставляют объект двигаться медленнее, действуя в направлении входящего потока и пропорциональны скорости. Это тип неконсервативных сил, поскольку он заставляет энергию рассеиваться. 2\). Подробнее об этом читайте в глубоком погружении! 92\). К сожалению, такой глубокий анализ сопротивления воздуха выходит за рамки уровня AP Physics, поэтому мы будем рассматривать сопротивление воздуха, линейное по скорости воздуха.

Коэффициент сопротивления воздуха

Как обсуждалось ранее, \(k\) является константой пропорциональности. Его значение определяется свойствами среды и уникальными характеристиками объекта. Основными факторами, влияющими на это, являются плотность среды, площадь поверхности объекта и безразмерная величина, известная как коэффициент сопротивления. В реальном примере с парашютистом средой будет воздух, а площадь поверхности будет относиться либо к парашютисту, либо к парашюту. 92$$

где \(D\) — коэффициент сопротивления, \(\rho\) — плотность среды, \(A\) — площадь поверхности объекта, \(\vec{v} \) — скорость.

Давайте посмотрим на диаграмму свободного тела, чтобы лучше понять его движение.

Схема свободного тела сопротивления воздуха

Что происходит с объектом, когда он падает и падает? На него действует нисходящая сила в виде веса и сила сопротивления в направлении, противоположном движению, из-за сопротивления воздуха, оба из которых визуализируются на диаграмме свободного тела, видимой ниже.

Рис. 1 — Когда объект падает, сила сопротивления действует на него вверх, в то время как вес тянет его вниз.

Согласно второму закону Ньютона, результирующая сила, действующая на объект \(\vec{F}_{\mathrm{net}}\), равна массе \(m\) объекта, умноженной на его ускорение \( \vec{а}\). Итак, зная все это, мы можем получить следующее выражение

$$ m\vec{g} — k\vec{v} = m\vec{a}.$$

0\), его начальная скорость равна \(\vec{v}_0=0\), следовательно, начальная сила сопротивления воздуха также равна нулю. По прошествии времени, когда объект начинает двигаться, в конце концов он достигает постоянной скорости, которая называется конечной скоростью \(\vec{v}_\mathrm{T}\). Поскольку скорость постоянна, ускорение будет равно нулю. Правая часть выражения становится равной нулю, и мы можем переставить оставшиеся члены

$$ m\vec{g} = k\vec{v}_\mathrm{T} $$

найти уравнение для конечной скорости

$$ \vec{v}_\mathrm{T}= \frac{m\vec{g}}{k}. $$

Конечная скорость – это максимальная скорость, достигаемая объектом, движущимся под действием постоянной силы и силы сопротивления, действующих на объект в противоположных направлениях.

Конечная скорость достигается, когда к объекту не прилагается результирующая сила, что означает, что ускорение равно нулю. Давайте рассмотрим пример задачи, связанной с предельной скоростью.

Формула сопротивления воздуха

Теперь найдем скорость как функцию времени. Для этого нам нужно преобразовать второй закон Ньютона в дифференциальное уравнение. Ускорение является первой производной скорости, поэтому \(\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}\). Тогда мы можем написать

$$ m\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=m\vec{g}-k\vec{v}. $$

Разделим наши переменные:

$$ \frac{\mathrm{d}v}{mg- kv}=\frac{\mathrm{d}t}{m}.$$

Чтобы выполнить все необходимые математические операции, мы пока рассмотрим только одно измерение и будем рассматривать векторные величины как скаляры.

Здесь важно установить пределы интегрирования. Время идет от нуля до времени \(t_{\mathrm{f}}\). Когда время равно нулю, наша начальная скорость также равна нулю, а по мере того, как время приближается к \(t_{\mathrm{f}}\), наша скорость становится скоростью \(v_{\mathrm{f}}\).

Причина, по которой мы не устанавливаем верхний предел конечной скорости, заключается в том, что мы пытаемся найти скорость как функцию времени! 9{-\frac{t_{\mathrm{f}}}{T}}) $$

, где \(T\) — постоянная времени и равна \(\frac{m}{k}\) .

Вот как мы получаем выражение скорости как функцию времени! Окончательное уравнение подтверждает наши предыдущие выводы о конечной скорости. Если значение \(t_{\mathrm{f}}\) установлено равным нулю, \(\vec{v_{\mathrm{f}}}\) также будет равно нулю, между тем, если \(t_{\mathrm {f}}\) установлен на что-то огромное, скажем, бесконечность, у нас останется \(\vec{v_{\mathrm{f}}} = \vec{v_\mathrm{T}}\).

Что же произошло бы, если бы начальная скорость была не нулевой?

Допустим, у нас есть автомобиль с начальной скоростью \(\vec{v}_0\) против некоторой силы сопротивления \(\vec{F}_\mathrm{r}\), которая снова равна \(-k \vec{v}\). Когда мы рисуем диаграмму свободного тела автомобиля, вес направлен вниз, нормальная сила направлена ​​вверх, а сила сопротивления воздуха направлена ​​в направлении, противоположном движению.

В этом случае конечная скорость будет равна нулю, и машина остановится. Единственная сила, действующая на объект в направлении движения, — это сила сопротивления, поэтому это будет наша результирующая сила. Тогда мы можем написать

$$ m\vec{a} = -k\vec{v}.$$

Мы собираемся повторить ту же процедуру, что и ранее, поскольку это становится дифференциальным уравнением, когда мы записываем ускорение как \(\vec{a }=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}\) и получить

$$ \begin{align} m \frac{\mathrm{d}\vec{v }}{\mathrm{d}t} & = — k\vec{v} \\ \frac{\mathrm{d}v}{v} & =\frac{-k}{m} \mathrm{d} т. \end{align}$$

Еще раз для расчетов рассмотрим скалярную версию уравнения. Здесь мы должны взять интегралы от обеих сторон, но сначала нам нужно определиться с пределами. Время снова идет от нуля до \(t\). Однако теперь у нас есть начальная скорость, поэтому наш предел скорости от \(v_0\) до \(v\) 9{\frac{-kt_{\mathrm{f}}}{m}}.$$

Пример сопротивления воздуха

Давайте рассмотрим пример задачи с тем же парашютистом, о котором упоминалось ранее, чтобы проверить наши знания!

Парашютист падает с начальной скоростью \(\vec{v}_0\) по воздуху. В этот момент (\(t = 0\)) они раскрывают парашют и испытывают силу сопротивления воздуха, величина которой определяется уравнением \(\vec{F} = -k\vec{v}\), где переменные такие же, как определены ранее. Суммарная масса парашютиста и снаряжения равна \(m\).

Определите выражение для ускорения парашютиста, конечной скорости и постройте график зависимости скорости от времени.

Решение

Мы знаем, что

$$ \vec{F}_{\mathrm{net}} = \vec{F}_\mathrm{g} — \vec{F}_\mathrm{r } $$

поэтому, рассматривая диаграмму свободного тела, описанную ранее, мы можем найти выражение для ускорения

$$ \begin{align} m\vec{a} & = m\vec{g} — k\vec{ v}, \\ \vec{a} & = \frac{m\vec{g} — k\vec{v}}{m}.\end{align}$$

Основываясь на предыдущем определении, парашютист достигнет своей конечной скорости, когда скорость постоянна (\(\vec{v} = \vec{v}_\mathrm{T}\)). Это означает, что ускорение становится равным нулю. \vec{v}_\mathrm{T} = \frac{m\vec{g}}{k}. $$

Теперь воспользуемся этим выражением для построения графика зависимости скорости от времени.

Рис. 3. Изменения скорости от начального спуска парашютиста до момента, когда они приближаются к конечной скорости с течением времени. Градиент этого графика представляет собой ускорение парашютиста.

Первоначально парашютист спускается со скоростью \(\vec{v}_0\) и ускоряется примерно с ускорением свободного падения \(\vec{g}\). При раскрытии парашюта на парашютиста действует значительная сила сопротивления — сопротивление воздуха. Ускорение от силы сопротивления приводит к восходящему ускорению, поэтому нисходящая скорость уменьшается. Градиент нашего графика зависимости скорости от времени представляет собой ускорение. Основываясь на предыдущих наблюдениях, она не будет постоянной, а скорее будет приближаться к нулю, когда скорость достигает конечной скорости \(\vec{v}_\mathrm{T}\). В результате сюжет нелинейный.

Некоторые другие примеры сопротивления воздуха в нашей повседневной жизни:

1. Ходьба во время шторма довольно часто затрудняет ходьбу. Человек, идущий против ветра, испытывает значительное сопротивление, что затрудняет продвижение вперед. По той же причине сложно держать зонт в руке при сильном ветре.

2. Перо, падающее на землю , имеет тенденцию плавать и двигаться медленно, а не падать в течение нескольких секунд, как другие объекты, немного большей массы. Сила гравитации притягивает перо к земле; однако сила сопротивления воздуха предотвращает падение или движение пера во время движения.

3. Бумажные самолетики, , если правильно построить, летают в воздухе без особых усилий. Для этого переднюю поверхность бумажного самолета затачивают. В результате бумажный самолет рассекает воздух и избегает силы сопротивления воздуха ровно настолько, чтобы дольше оставаться в воздухе.

4. Двигатель настоящего самолета , крылья и пропеллеры созданы для обеспечения достаточной тяги, чтобы помочь самолету преодолеть силу сопротивления воздуха. Турбулентность также вызвана трением, которое создает воздух. Однако космические корабли должны беспокоиться только о сопротивлении воздуха при запуске и посадке, поскольку в космосе воздуха нет.

Сопротивление воздуха — основные выводы

• Силы, препятствующие относительному движению объекта при его движении в воздухе, называются сопротивлением воздуха.
• Эти силы сопротивления заставляют объект двигаться медленнее, действуя в направлении входящего потока и пропорциональны скорости.
• Математическое выражение для сопротивления воздуха: \( \vec{F}_\mathrm{r} = — k \vec{v}\), где отрицательный знак указывает на противоположное направление движения.
• Конечная скорость определяется как максимальная скорость, достигаемая объектом, движущимся под действием постоянной силы и силы сопротивления, действующих на объект в противоположных направлениях.
• Когда к объекту не прилагается результирующая сила, что означает, что ускорение равно нулю, достигается конечное состояние.