что это в геометрии, виды и элементы, ось, образующая
Содержание:
- Что такое цилиндр в геометрии
- Виды цилиндров
- Как найти высоту цилиндра
-
Развертка
- Развертка боковой поверхности
- Развертка полной поверхности
Содержание
- Что такое цилиндр в геометрии
- Виды цилиндров
- Как найти высоту цилиндра
-
Развертка
- Развертка боковой поверхности
- Развертка полной поверхности
Разбираемся в особенностях трехмерного геометрического тела под названием цилиндр. Смотрим виды цилиндров, его свойства, какие бывают развертки, а также даем определения составным частям этой фигуры.
Смотрим виды цилиндров, его свойства, какие бывают развертки, а также даем определения составным частям этой фигуры.
Что такое цилиндр в геометрии
Источник: simple-math.ruОпределения
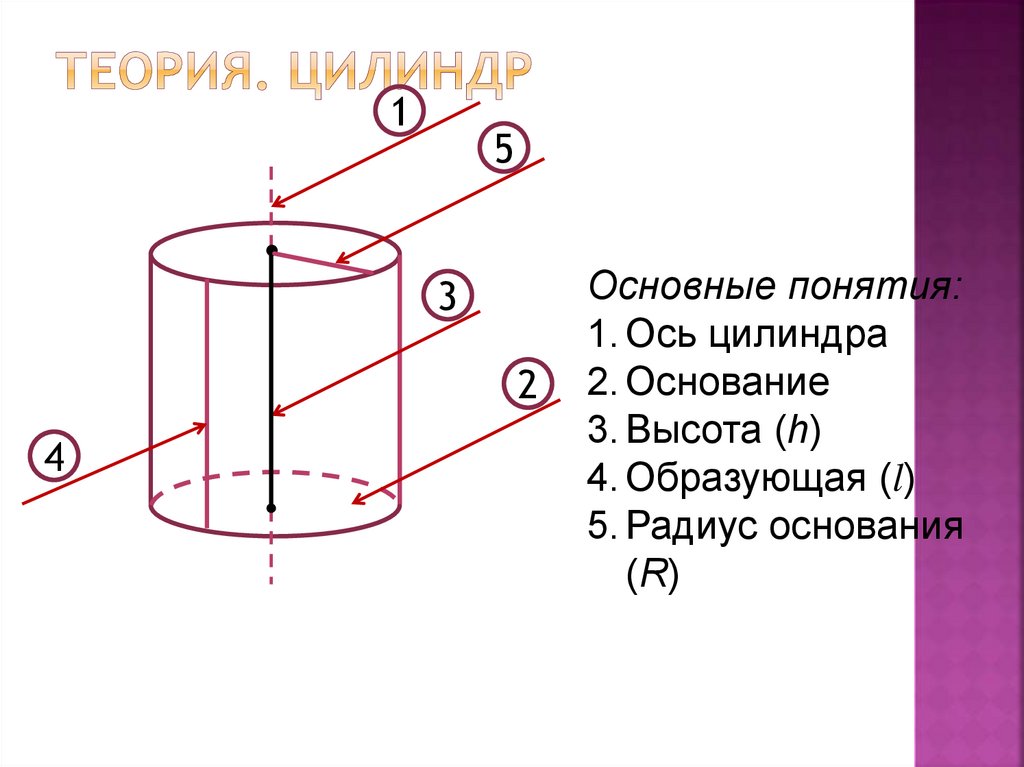
Цилиндр — это трехмерное геометрическое тело, которое ограничено цилиндрической поверхностью и двумя параллельными плоскостями.
Цилиндрическая поверхность — это поверхность, которая образуется за счет движения в пространстве прямой (образующей) параллельно самой себе, пересекающей данную линию (направляющую).
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Основания — это одинаковые круги, которые ограничивают цилиндр и находятся параллельно друг другу.
Образующая — отрезок, который соединяет точки окружностей оснований цилиндра и перпендикулярный плоскостям этих оснований.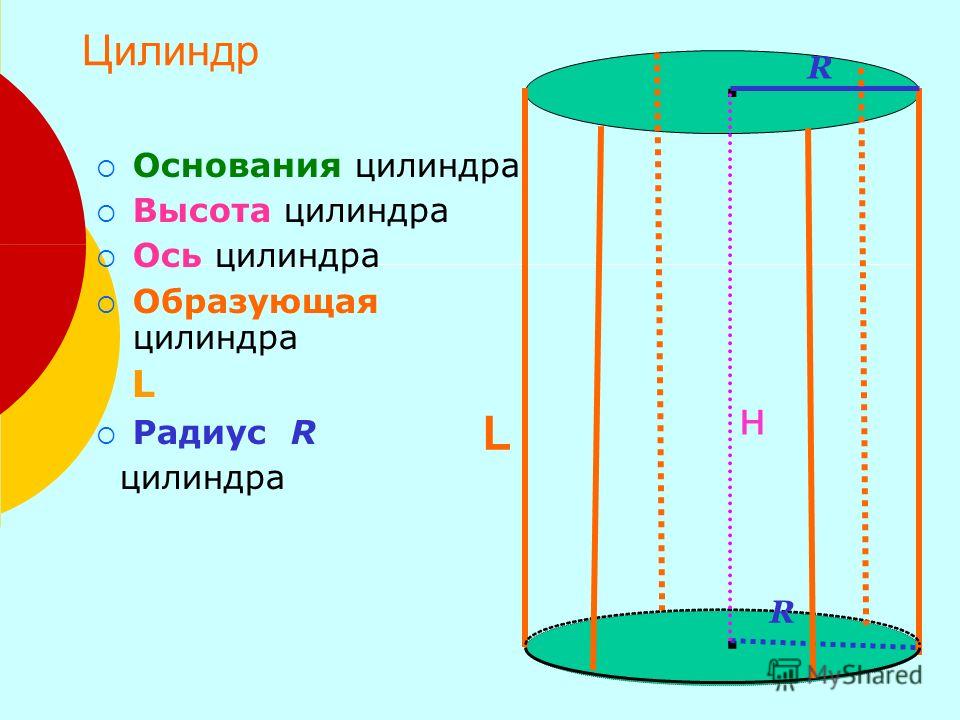 2}\)
2}\)
Развертка
Как уже было упомянуто выше, всего существует две площади поверхности цилиндра: боковой поверхности и полной поверхности. У каждой из них также есть и своя развертка. Разберемся, как они выглядят.
Развертка боковой поверхности
Источник: studopedia.ruЛегче всего представить себе развертку боковой поверхности цилиндра, посмотрев на этикетку пластиковой бутылки. Когда вы ее отклеиваете, то видите прямоугольник. То же самое и с цилиндрическим геометрическим телом: развёрткой его боковой поверхности является прямоугольник. Его длина соответствует длине окружности, лежащей в основании, а ширина — высоте самой трехмерной фигуры.
Развертка полной поверхности
Если развернуть полную поверхность цилиндра, получится примерно то же самое, только с двумя дополнительными элементами в виде окружностей оснований. Выглядит это так:
Источник: tepka.ruНасколько полезной была для вас статья?
Рейтинг: 5.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Геометрия Понятие цилиндра
Материалы к уроку
Конспект урока
Понятие цилиндра
|
Введем понятие цилиндра – геометрического тела.
Ну конечно, все вы видели много предметов в быту, похожих на данное тело.
|
|
|
|
Рассмотрим окружность Р с центром О и радиусом r в плоскости α .Через каждую точку окружности проведем прямые, перпендикулярные к плоскости α. Они параллельны друг другу. Все прямые образуют поверхность, которая называется цилиндрической. Каждая из этих прямых называется образующей цилиндрическую поверхность, а прямая, проходящая через центр окружности, – осью цилиндрической поверхности. |
|
|
|
Далее проведем плоскость сигма, параллельную плоскости альфа, таким образом, что они отделят отрезки образующих, которые равны и параллельны между собой. В плоскости сигма получим окружность Р1 . Ось цилиндрической поверхности пройдет через центр О1 окружности Р1, радиус окружностей будет равный r. Таким образом, мы получили цилиндр. Цилиндром называется тело, ограниченное цилиндрической поверхностью и двумя кругами, лежащими в параллельных плоскостях. Ось ОО1 – называют осью цилиндра, отрезок образующей цилиндрической поверхности ТТ1– образующая цилиндра.
|
Текст: Тело ограниченное цилиндрической поверхностью и двумя кругами, называется цилиндром.
Текст:
ОО1–ось цилиндра ТТ1– образующая цилиндра r– радиус цилиндра |
|
Цилиндрическая поверхность, т.е. поверхность, составленная из образующих, называется боковой поверхностью цилиндра, а круги – основаниями цилиндра. |
Картинка:
|
|
Длина образующей называется высотой цилиндра, а радиус основания — радиусом цилиндра.
|
Картинка: Текст: радиус основания — радиусом цилиндра длина образующей – высотой цилиндра
|
|
|
Цилиндр может быть получен вращением прямоугольника вокруг одной из его сторон. |
Картинка: Показать вращение прямоугольника
|
|
Рассмотрим сечение цилиндра.1) Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра. Такое сечение называется осевым.2) Если секущая плоскость перпендикулярна оси цилиндра, то сечение является кругом.
|
Картинка: Текст: Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник. Картинка:
Текст: Если секущая плоскость перпендикулярна оси цилиндра, то сечение – круг Картинка: Й28 Текст: Если секущая плоскость под углом с оси, то сечение – эллипс. |
|
Теперь давайте посмотрим, какие бывают цилиндры.1) Прямые и наклонные, в зависимости от того, перпендикулярны или наклонны плоскости оснований к образующим.2) Сложные цилиндры.На первом рисункеизображён цилиндр, каждое основание которого представляет собой фигуру, ограниченную частью параболы и отрезком.На втором рисунке изображен цилиндр, основаниями которого являются круги, но образующие цилиндра не перпендикулярны к плоскости оснований (наклонный цилиндр). |
Картинка (схема):
Картинка: Сложные цилиндры
|
|
ЗадачаДокажите, что осевое сечение цилиндра является прямоугольником, две противоположные стороны которого – образующие, а две другие – диаметры оснований цилиндра. Найти диагональ осевого сечения, если радиус цилиндра равен 1,5 м, а высота равна 4 м. Найти диагональ осевого сечения, если радиус цилиндра равен 1,5 м, а высота равна 4 м.
Решение1) так как АВ и CD – образующие то они равны и параллельны, и по определению образующих цилиндра АВ и CD перпендикулярны основанию.AD и BC равны как диаметры оснований,следовательно, четырехугольник ABCD по признаку параллелограмма и определению является прямоугольником.2) Диагональ АС делит прямоугольник на два равных прямоугольных треугольника, тогда,из прямоугольного треугольника АВС находим АС: по теореме Пифагора АС равна корню квадратному из суммы квадратов сторон АВ и АС, где АВ равна высоте цилиндра, а ВС диаметру основания то есть двум радиусам.Получаем АС равно 5 м. |
Текст:Дано: цилиндр, АВСD –осевое сечение цилиндра, АВ иCD – образующие, BC и AD– диаметры, r=1,5м, h=4м. 1) Доказать, что АВСD– прямоугольник. 2) Найти: АС. Картинка:
Текст: Решение: 1) АB=CD, АВ||CD (образующие) AB AD, СD AD (образующая и диагональ основания), AD=BC (диаметры) АВСD– прямоугольник
2) ΔАВС –прямоугольный, АС–диагональ прямоугольника (гипотенуза), BC= d =2r=3м. АВ=h=4м АС= = =5 м
Ответ: АС=5м.
|
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
Цилиндр – формула, определение, примеры
Цилиндр – это трехмерная твердая фигура, имеющая два одинаковых круглых основания, соединенных криволинейной поверхностью на определенном расстоянии от центра, которое является высотой цилиндра. Рулоны туалетной бумаги, банки из-под прохладительных напитков — это реальные примеры цилиндров. А знаете ли вы, что Пизанская башня имеет цилиндрическую форму? Давайте узнаем больше о форме цилиндра в этой статье.
Рулоны туалетной бумаги, банки из-под прохладительных напитков — это реальные примеры цилиндров. А знаете ли вы, что Пизанская башня имеет цилиндрическую форму? Давайте узнаем больше о форме цилиндра в этой статье.
| 1. | Определение цилиндра |
| 2. | Типы цилиндров |
| 3. | Свойства цилиндра |
| 4. | Формулы цилиндра |
| 5. | Часто задаваемые вопросы о цилиндре |
Определение цилиндра
Цилиндр представляет собой трехмерное тело, состоящее из двух одинаковых и параллельных оснований, соединенных изогнутой поверхностью. Эти основания подобны круглым дискам. Линия, проходящая из центра или соединяющая центры двух круговых оснований, называется осью формы цилиндра. Расстояние между двумя основаниями называется перпендикулярным расстоянием и обозначается высотой «h».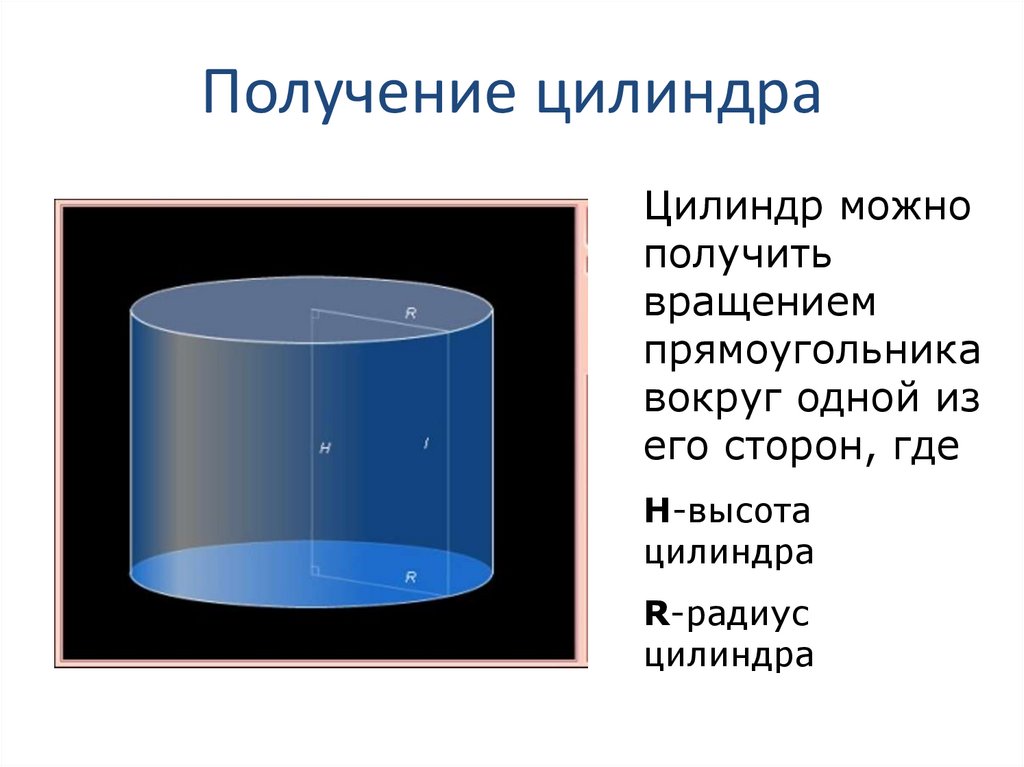 Два круглых основания имеют расстояние от центра до внешней границы, которое известно как радиус цилиндра, обозначенный буквой «r». Цилиндр представляет собой комбинацию 2 кругов + 1 прямоугольник. Посмотрите на данное изображение, показывающее формирование формы цилиндра.
Два круглых основания имеют расстояние от центра до внешней границы, которое известно как радиус цилиндра, обозначенный буквой «r». Цилиндр представляет собой комбинацию 2 кругов + 1 прямоугольник. Посмотрите на данное изображение, показывающее формирование формы цилиндра.
Некоторыми реальными примерами формы цилиндра являются трубы, огнетушители, резервуары для воды, банки из-под прохладительных напитков и т. д.
Типы цилиндров
Мы только что прочитали о некоторых реальных примерах цилиндра, которые показывают, что он может быть разных типов. В геометрии есть четыре различных типа цилиндров. Они следующие:
- Прямой круговой цилиндр: Если оси двух параллельных оснований перпендикулярны центру основания, он называется правильным круговым цилиндром.
- Наклонный цилиндр: Наклонный цилиндр — это цилиндр, стороны которого опираются на основание. При этом стороны не перпендикулярны центру основания.
 Пизанская башня — реальный пример наклонного цилиндра.
Пизанская башня — реальный пример наклонного цилиндра. - Эллиптический цилиндр: Цилиндр, основание которого имеет форму эллипса, называется эллиптическим цилиндром.
- Правый круговой полый цилиндр или цилиндрическая оболочка: Состоит из двух правильных круговых цилиндров, заключенных один внутри другого. Точка оси общая и перпендикулярна центральному основанию. Он отличается от правильного круглого цилиндра тем, что он полый по своей природе, то есть внутри есть некоторое пространство или пустота.
Посмотрите на изображение ниже, чтобы получить обзор всех четырех типов цилиндров, описанных выше.
Свойства цилиндра
Каждая геометрическая фигура имеет свои характеристики или некоторые свойства, отличные от других фигур. Точно так же давайте изучим некоторые свойства формы цилиндра, перечисленные ниже:
- Цилиндр имеет одну изогнутую поверхность и две одинаковые плоские грани.
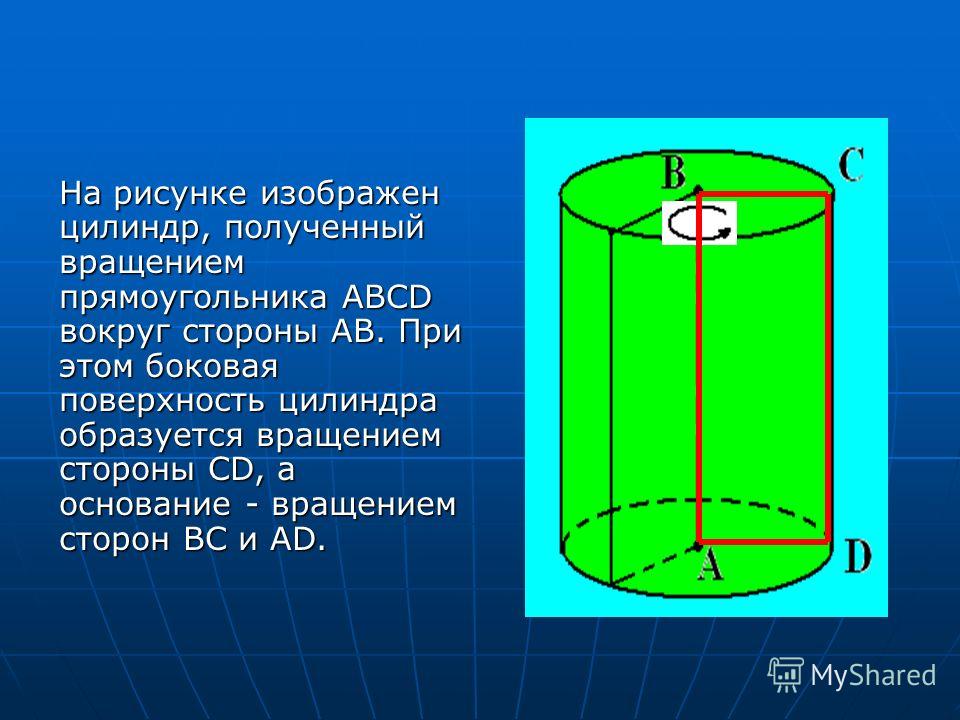
- Два круговых основания конгруэнтны друг другу.
- Его размер зависит от радиуса основания и высоты криволинейной поверхности.
- В отличие от конуса, куба или прямоугольного параллелепипеда, цилиндр не имеет вершины. Это означает, что в цилиндре нет определенного угла.
- Основание и вершина цилиндра идентичны, т.е. у него одно и то же основание — либо круглое, либо эллиптическое.
Формулы цилиндра
Каждая трехмерная геометрическая фигура имеет две основные формулы: площадь поверхности и объем. Точно так же цилиндр имеет три основные формулы, связанные с его площадью поверхности и объемом.
- Площадь боковой поверхности или площадь изогнутой поверхности
- Общая площадь поверхности
- Том
Давайте подробно узнаем о приведенных выше формулах цилиндров.
Изогнутая поверхность цилиндра:
Изогнутая поверхность также называется боковой поверхностью. Площадь, образованная криволинейной поверхностью цилиндра, т. е. пространство, занимаемое между двумя параллельными круглыми основаниями, известна как его ППС. Формула для площади криволинейной поверхности цилиндра имеет следующий вид:
Площадь, образованная криволинейной поверхностью цилиндра, т. е. пространство, занимаемое между двумя параллельными круглыми основаниями, известна как его ППС. Формула для площади криволинейной поверхности цилиндра имеет следующий вид:
Площадь криволинейной поверхности (CSA) = 2πrh квадратных единиц
(Примечание: «h» — высота, «r» — радиус, а значение π равно 22/7 или приблизительно 3,14).
Общая площадь поверхности цилиндра:
Общая площадь поверхности определяет общую площадь, которую он занимает, включая основания. Цилиндр состоит из двух кругов и одного изогнутого листа. Итак, чтобы узнать общую площадь поверхности цилиндра, мы вычисляем площадь криволинейной поверхности и площадь двух кругов.
Площадь криволинейной поверхности (CSA) = окружность × высота 90 121
CSA= 2πr × h
Площадь круга = πr 2
Общая площадь поверхности (TSA) = площадь криволинейной поверхности + 2 (площадь круга)
Общая площадь поверхности (TSA) = 2πrh + 2πr 2 = 2πr(h+r) квадратных единиц
(Примечание: «h» — это высота, а «r» — радиус. Есть две окружности, поэтому мы умножаем площадь основной окружности на 2)
Есть две окружности, поэтому мы умножаем площадь основной окружности на 2)
Объем цилиндра:
Объем цилиндра определяет плотность или занимаемое им пространство. Если мы хотим, чтобы цилиндр наполнился водой, то необходимое количество воды можно рассчитать, найдя его объем.
Объем цилиндра = Площадь круга × высота
Объем = πr 2 × ч
Объем цилиндра, V = πr 2 h кубических единиц
где «h» — высота, а «r» — радиус.
Цилиндрическая сетка
Цилиндрическая сетка представляет собой двумерную структуру, созданную путем ее развертывания. Это помогает нам визуализировать форму цилиндра и площадь его поверхности. Когда мы разворачиваем цилиндр, мы получаем прямоугольник, соединенный двумя одинаковыми окружностями, которые образуют верхнее и нижнее основания цилиндрической формы. Посмотрите на изображение сетки цилиндра, показанное ниже.
☛ Статьи по теме
Ознакомьтесь со следующими темами, связанными с формой цилиндра.
- Калькулятор высоты цилиндра
- Сфера
- Полусфера
Примеры цилиндров
Пример 1: Бритт хочет купить канистру, вмещающую 1 галлон масла. Радиус банки 5 дюймов. Помогите Бритт найти высоту банки, которую она должна купить. Подсказка: банка имеет форму цилиндра.
Решение:
Объем, V = 1 галлон
1 галлон = 231 кубический дюйм
Радиус, r = 5 дюймов (дан)
Объем цилиндра, V = πr 2 hПодставляя значения в формулу объема, получаем
231 = 22/7 × (5) 2 × ч
(231 × 7)/(22 × 25) = ч
ч = 2,94 дюйма
Следовательно, высота банки должна быть 2,94 дюйма.Пример 2. У Эммы дома есть старый цилиндрический резервуар для воды. Радиус 40 дюймов, высота 150 дюймов. Она хочет заменить его на новый с такими же размерами. Помогите Эмме определить площадь резервуара для воды.
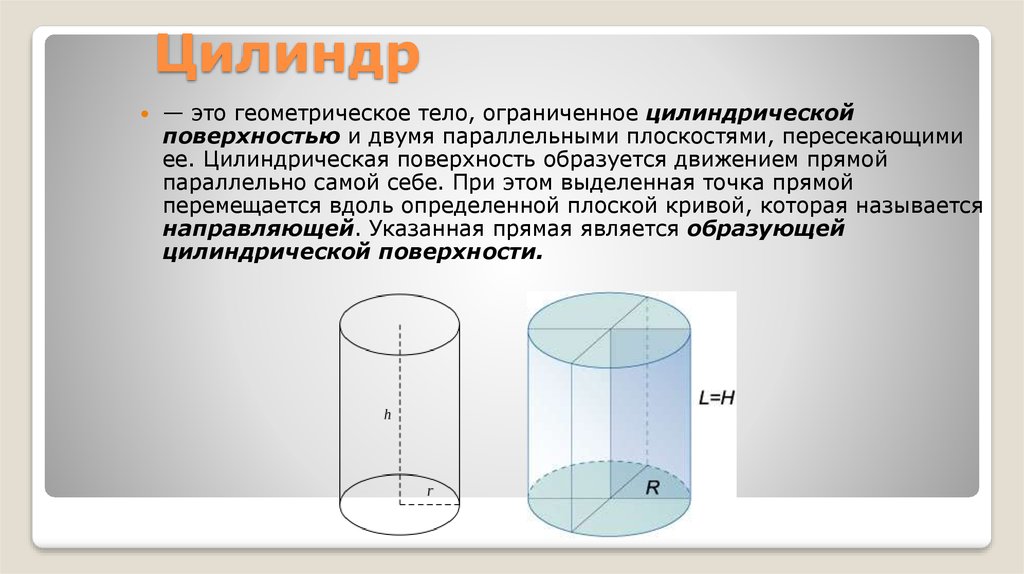
Решение:
Резервуар для воды имеет форму цилиндра.
Общая площадь поверхности цилиндра = 2πr(h+r)Подставляя значения, указанные в вопросе, в эту формулу, мы получаем,
ВСП = 2 × 22/7 × 40 (150 + 40)
ВСП = 2 × 22/7 × 7600
TSA = 47 771,42 кв. дюйма
Следовательно, площадь резервуара для воды = 47 771,42 кв. дюйма.Пример 3. Каков объем цилиндра радиусом 5 единиц и высотой 8 единиц?
Решение:
Радиус, r = 5 единиц
Высота, h=8 шт.
Объем цилиндра, V = πr 2 ч куб.ед.
V = (22/7) × 5 2 × 8
V = 22/7 × 25 × 8
V= 628,57 куб.ед.
Следовательно, необходимый объем составляет 628,57 куб.
перейти к слайдуперейти к слайдуперейти к слайду
Хотите создать прочную основу в математике?
Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.
Испытайте Cuemath и приступайте к работе.
Записаться на бесплатный пробный урок
Практические вопросы по цилиндру
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о цилиндрической форме
Что такое цилиндр в геометрии?
Цилиндр представляет собой трехмерную объемную фигуру, состоящую из двух круглых оснований, соединенных с криволинейной поверхностью, образованной путем складывания прямоугольника. Верхняя и нижняя грани цилиндра конгруэнтны. Всего у него 3 грани, 2 ребра и нет вершин.
Каков объем цилиндра?
Объем цилиндра – это занимаемое им пространство. Его можно рассчитать по формуле: V = πr 2 ч кубических единиц.
Что такое площадь поверхности цилиндра?
Цилиндр имеет два основания и изогнутую поверхность. Существует два типа формул площади для формы цилиндра: площадь криволинейной поверхности и общая площадь поверхности. Формулы площади поверхности цилиндра приведены ниже:
- Общая площадь поверхности = 2πr(r+h) квадратных единиц
- Площадь криволинейной поверхности = 2πrh квадратных единиц
Каковы реальные примеры цилиндров?
Реальные примеры цилиндра: рулоны туалетной бумаги, банки, трубы, мензурки и т. д.
д.
Что такое формулы цилиндра?
Три основные формулы цилиндра:
- Общая площадь поверхности = 2πr(r+h) квадратных единиц
- Площадь изогнутой поверхности = 2πrh квадратных единиц
- Объем = πr 2 ч кубических единиц
Сколько ребер у цилиндра?
Цилиндр имеет 2 грани. Край — это место, где встречаются 2 грани. Край может быть прямым или изогнутым. Например, у куба 12 прямых граней, а у цилиндра 2 изогнутых. Мы знаем, что цилиндр представляет собой комбинацию двух кругов и одного прямоугольника. Два прямых края прямоугольника сгибаются, образуя изогнутые края цилиндра.
Что такое общая площадь поверхности цилиндра?
Общая площадь поверхности цилиндра равна сумме площади криволинейной поверхности и площади двух круглых оснований. Это дается как:
Общая площадь поверхности = площадь криволинейной поверхности + две круглые площади основания
Общая площадь поверхности (TSA) = 2πrh + πr 2 = 2πr(h+r) квадратных единиц
Что такое площадь основания цилиндра?
Площадь, занимаемая в пределах границы круглого основания цилиндра, называется площадью его основания. Единицы площади основания цилиндра всегда выражаются в квадратных сантиметрах, квадратных дюймах, квадратных футах и т. д. В геометрии у нас есть специальная формула для нахождения площади основания цилиндра, равная πr 2 где r — радиус основания.
Единицы площади основания цилиндра всегда выражаются в квадратных сантиметрах, квадратных дюймах, квадратных футах и т. д. В геометрии у нас есть специальная формула для нахождения площади основания цилиндра, равная πr 2 где r — радиус основания.
Каковы свойства цилиндра?
Ниже перечислены некоторые свойства цилиндра:
- Он имеет одну криволинейную поверхность, две изогнутые кромки и две плоские круглые грани.
- Два плоских круглых основания конгруэнтны друг другу.
- Не имеет вершин.
- Размер цилиндра зависит от радиуса круглого основания и его высоты.
Сколько граней у цилиндра?
В цилиндре имеются две плоские круглые поверхности и одна криволинейная поверхность. Таким образом, у него всего 3 лица.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочие листы по форме цилиндра
Определение и значение цилиндра — Merriam-Webster
цилиндр · внутренний · дер ˈsi-lən-dər
1
а
: поверхность, очерченная прямой линией, движущейся параллельно фиксированной прямой линии и пересекающей фиксированную плоскую замкнутую кривую
б
: твердое тело или поверхность, ограниченная цилиндром и двумя параллельными плоскостями, пересекающими все его элементы
особенно : правильный круглый цилиндр
см. таблицу формул объема
таблицу формул объема
2
: цилиндрическое тело или пространство: например,
а
: поворотный патронник револьвера
б(1)
: камера поршня в двигателе
(2)
: камера в насосе, из которой поршень вытесняет жидкость
с
: любой из различных вращающихся элементов в прессе (например, в печатном станке)
особенно : тот, который отпечатывает бумагу на чернильном бланке
г
: цилиндрический глиняный предмет с клинописными надписями
цилиндрический
ˈsi-lən-dərd
имя прилагательное
Фразы
на всех цилиндрах
: с максимальным усилием или интенсивностью : с полной мощностью или скоростью
экономика работает на всех цилиндрах
Примеры предложений
цилиндр револьвера
Недавние примеры в Интернете
Вид внутри стали цилиндр специального клапана производства Clarke Valve, препятствующего утечке газа метана из газопроводов. Алекса Гагош, BostonGlobe.com , 31 октября 2022 г.
Его тяжелый бетон цилиндр стал его визитной карточкой.
Келси Эйблс, Washington Post , 31 октября 2022 г.
Основное отличие — то, что касается Central Arkansas Water — состоит в том, что двухтактные подвесные моторы работают на топливно-масляной смеси 50:1, которая смазывает поршни, кольца и 9 поршней.0428 цилиндр стенки.
Брайан Хендрикс, Arkansas Online , 30 октября 2022 г.
Кроме того, коробка цилиндров достаточно интересна, чтобы выставить ее на обозрение.
Сара Янг, Sunset Magazine , 28 октября 2022 г.
Это отчетливо современный диван с квадратными подлокотниками, квадратными подушками спинки и цилиндром 9.
Алекса Гагош, BostonGlobe.com , 31 октября 2022 г.
Его тяжелый бетон цилиндр стал его визитной карточкой.
Келси Эйблс, Washington Post , 31 октября 2022 г.
Основное отличие — то, что касается Central Arkansas Water — состоит в том, что двухтактные подвесные моторы работают на топливно-масляной смеси 50:1, которая смазывает поршни, кольца и 9 поршней.0428 цилиндр стенки.
Брайан Хендрикс, Arkansas Online , 30 октября 2022 г.
Кроме того, коробка цилиндров достаточно интересна, чтобы выставить ее на обозрение.
Сара Янг, Sunset Magazine , 28 октября 2022 г.
Это отчетливо современный диван с квадратными подлокотниками, квадратными подушками спинки и цилиндром 9. 0429 боковые подушки.
Хит Оуэнс, Good Housekeeping , 26 октября 2022 г.
Картер видит свою роль педагога в том, чтобы задействовать другой цилиндр в двигателе, который ведет его по пути величия.
Деметриус Паттерсон, Variety , 22 октября 2022 г.
Чтобы собрать, загните нижний угол на начинку; переверните один раз и сложите стороны, и продолжайте сворачивать в цилиндр .
People Staff, Peoplemag , 27 сентября 2022 г.
Kichler Lighting, которая в начале этого года перенесла свою штаб-квартиру из Индепенденса в Солон, пожертвует дорожные светильники на столбах, цилиндрических настенных светильников , двухсветные прожекторы и несколько наружных настенных фонарей, согласно постановлению.
Эд Виттенберг, , Кливленд, , 19 сентября 2022 г.
0429 боковые подушки.
Хит Оуэнс, Good Housekeeping , 26 октября 2022 г.
Картер видит свою роль педагога в том, чтобы задействовать другой цилиндр в двигателе, который ведет его по пути величия.
Деметриус Паттерсон, Variety , 22 октября 2022 г.
Чтобы собрать, загните нижний угол на начинку; переверните один раз и сложите стороны, и продолжайте сворачивать в цилиндр .
People Staff, Peoplemag , 27 сентября 2022 г.
Kichler Lighting, которая в начале этого года перенесла свою штаб-квартиру из Индепенденса в Солон, пожертвует дорожные светильники на столбах, цилиндрических настенных светильников , двухсветные прожекторы и несколько наружных настенных фонарей, согласно постановлению.
Эд Виттенберг, , Кливленд, , 19 сентября 2022 г. Узнать больше
Узнать больше
Эти примеры предложений автоматически выбираются из различных онлайн-источников новостей, чтобы отразить текущее использование слова «цилиндр». Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв.
История слов
Этимология
среднефранцузский или латынь; Среднефранцузский cylindre , от латинского cylindrus , от греческого kylindros , от kylindein катиться; возможно родственно греческому kyklos колесо — больше за колесом
Первое известное употребление
1570, в значении, определенном в смысле 1а
Путешественник во времени
Первое известное использование цилиндра было
в 1570 г.
Посмотреть другие слова того же года
Словарные статьи рядом с
цилиндромкруглоротый
цилиндр
цилиндрический блок
Посмотреть другие записи поблизости
Процитировать эту запись «Цилиндр».
Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/cylinder. По состоянию на 10 ноября 2022 г.Copy Citation
Kids Definition
цилиндр
цилиндр · внутренний · дер ˈsil-ən-dər
1
: геометрическая форма, состоящая из двух параллельных граней одинакового размера и формы (в виде кругов) и изогнутой поверхности, полностью соединяющей их границы
2
: двигатель, ствол помпы или часть револьвера, которая удерживает патроны) в форме цилиндра
цилиндрический
сə-лин-дри-кəл
имя прилагательное
цилиндрически
-dri-k(ə-)lē
наречие
Еще от Merriam-Webster на
цилиндрАнглийский: Перевод цилиндр для говорящих на испанском языке
Британский английский: Перевод цилиндр для говорящих на арабском языке
Britannica.

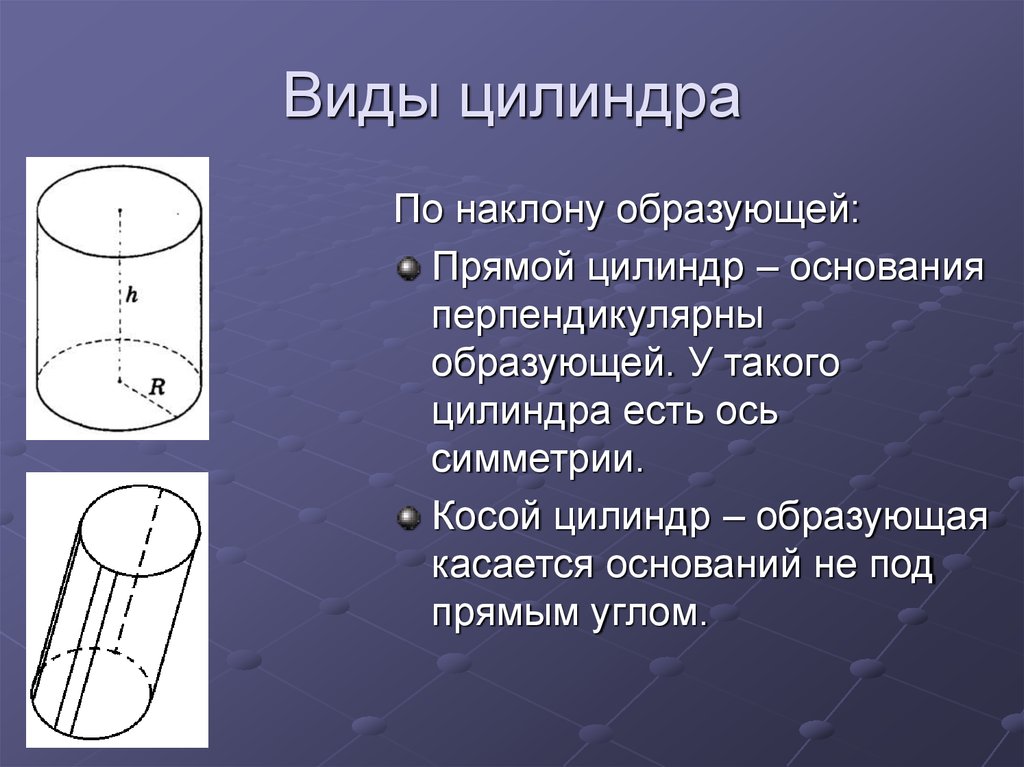
 На рисунке изображен цилиндр, полученный вращением прямоугольника вокруг стороны ОО1.
На рисунке изображен цилиндр, полученный вращением прямоугольника вокруг стороны ОО1.