Что такое средняя скорость: Средняя скорость | это... Что такое Средняя скорость?

Содержание

Средняя скорость на протяжении всего пути. Как вычислить среднюю скорость.

Альфашкола
Статьи
Вычисление средней скорости

Давайте разберем как вычислить среднюю скорость
Для этого надо сделать три шага:

вычислить весь путь;
вычислить время, за которое прошел объект весь путь;
путь разделить на время;

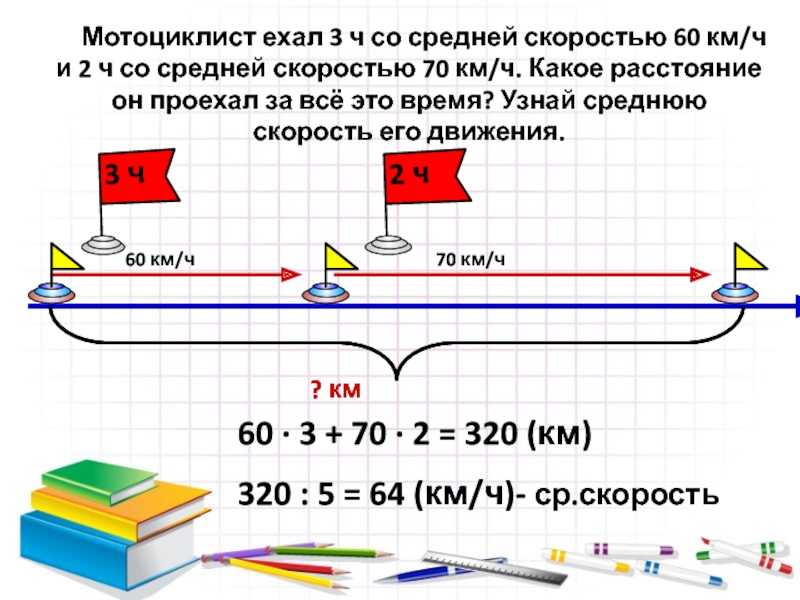
Пример 1. Саша прошел за 3 часа 9 км, а Сергей за 2 часа 6 км. Найдите их среднюю скорость.

Решение:

\(v_{ср}=\frac{9+6}{3+2}=\frac{15}{5}=3\) км/час

Ответ: 3 км/час.

Пример 2. Пешеход прошел за 4 часа 10 км, а велосипедист за 3 часа 11 км.

Найдите их среднюю скорость.

Решение:

\(v_{ср}=\frac{10+11}{4+3}=\frac{21}{7}=3\) км/час

Ответ: 3 км/час.

Пример 3. Пароход проплыл за 2 часа со скоростью 20 км/ч и 3 часа со скоростью 30 км/ч. Вычислите среднюю скорость парохода.

Решение:

\(2*20 + 3*30 = 40 +90 =130 \) (км) — весь путь .
\(2+3=5 \) (час) — все время.
\(130:5 =26 \) (км/час) — средняя скорость .

Ответ : 26 км/час.

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Ольга Анатольевна Лизогуб

Репетитор по математике

Стаж (лет)

Образование:

Мозырский государственный педагогический университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по математике и русскому языку 1-5 классов. На своих уроках я использую разные формы и методы работы, наглядный и дидактический материал, учитываю индивидуальные особенности учащихся. Прежде всего, стремлюсь научить ученика получать информацию и уметь её применять. Считаю важным создавать на своих уроках среду, которая благоприятна для развития личности и реализации человеческого потенциала каждого учащегося, не ущемляя его прав и свобод. Стараюсь всегда достигать поставленных целей и задач.

Татьяна Михайловна Столят

Репетитор по математике

Стаж (лет)

Образование:

Белорусский государственный педагогический университет им. М. Танка

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Я — учитель начальных классов и учитель-дефектолог.

Мой стаж работы – 22 года. Работа с детьми — это то, что я действительно люблю. В своей работе использую индивидуальный подход к каждому ребёнку. Кто-то быстро «схватывает» и надолго сохраняет в памяти информацию и алгоритмы действий, а другому нужно больше времени и другие способы подачи материала. Я пытаюсь найти эти способы и помочь ребенку в устранении пробелов в знаниях, понимании сложных тем. Я работаю с разными категориями детей по разным программам. В занятия включаю упражнения на развитие памяти, внимания, мышления. Стремлюсь, чтобы каждый мой ученик был успешен. Я надеюсь, что наше сотрудничество поможет вам решить проблемы в освоении математики.

Юлия Геннадьевна Газданова

Репетитор по математике

Стаж (лет)

Образование:

Актюбинский педагогический техникум

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 1-5 классов. Люблю работать с детьми и умею находить с ними общий язык. Математику люблю за точность и преподаю её так, как хотела бы, чтобы учили моего ребенка. При обучении настраиваю на позитивное восприятие всего нового и непонятного. Весело и интересно объясняю сложный материал. Со мной вашим детям будет легко, занимательно и познавательно. До встречи на уроках!

Что такое личная «средняя скорость» и как она влияет на нашу жизнь

10 июляПродуктивность

Чтобы добиться успеха, прилагать максимум усилий и устраивать гонки на выживание совсем не обязательно.

Джеймс Клир

Бизнесмен, автор книги «Атомные привычки. Как приобрести хорошие привычки и избавиться от плохих».

Что такое «средняя скорость»

У меня есть друг по имени Нейтан Барри. Недавно он написал три книги всего за девять месяцев. Как? С помощью одной нехитрой стратегии — писать 1 000 слов в день, а это около 2–3 страниц. Он делал так 253 дня подряд.

А теперь сравните его стратегию с типичным образом писателя, который запирается в домике в лесу на несколько недель и как сумасшедший строчит книгу. Такой автор‑маньяк работает на «максимальной скорости» — 20, может, 30 страниц в день. Но после нескольких недель такого безумного «марафона» есть два варианта развития событий — закончится либо работа над книгой, либо моральные силы автора.

Для сравнения: «максимальная скорость» Нейтана ни разу не достигла уровня сумасшедшего писателя из домика в лесу. Однако за год или два «средняя скорость» моего друга была гораздо выше.

Этот принцип можно применить не только к писательству. Например, кто угодно может почувствовать прилив вдохновения, отправиться в тренажёрный зал и позаниматься там один раз. Это «максимальная скорость». Мы придаём ей слишком большое значение и буквально зацикливаемся на ней. Насколько тяжёлой была тренировка? Что там с мотивацией? Как быстро выполнялись упражнения?

Но что, если вы попытаетесь вычислить средние показатели за последний месяц? Сколько дней вы тренировались? А если взять последние три месяца? Или год? Какой была ваша «средняя скорость»?

Стоит только посмотреть на ситуацию под таким углом, и сразу оказывается, что сначала вы неделю болели, потом пропустили тренировки из‑за усталости, а затем вообще уехали в командировку. В результате вы понимаете, что ваша «максимальная скорость» иногда бывает высокой, а вот «средняя» гораздо ниже, чем кажется.

По моим наблюдениям, этот принцип правдив для любой сферы жизни, в том числе и для привычек, связанных с работой, питанием или отношениями.

Удивительный факт о «средней скорости»: она позволяет довольно быстро добиться успеха.

Мы очень часто тратим время и энергию на мысли о том, что необходимо приложить гигантские усилия, чтобы добиться чего‑то значительного. Мы говорим себе, что нам нужно запастись мотивацией и желанием. Мы думаем, что важно работать больше, чем остальные.

Но посмотрите на людей, которые двигаются вперёд и достигают прогресса, и вы увидите другую тенденцию. Нейтан каждый день писал по 1 000 слов. И что произошло через девять месяцев? Он написал три книги. При этом он ни разу не старался работать больше других. В конце концов, написать 2–3 страницы в день — это далеко не шокирующий показатель эффективности. Мой друг просто был более последователен, чем остальные, а его «средняя скорость» за эти 253 дня была гораздо выше, чем у большинства.

Как повысить «среднюю скорость»

Недавно мне рассказали об идее «выпускного вечера для привычек». Она заключается в том, чтобы закончить какую‑то одну нынешнюю привычку и подняться на уровень выше. В целом эта тактика и нужна для улучшения «средней скорости».

Вот несколько примеров:

Если ваша «средняя скорость» — три здоровых блюда в неделю, вы можете «выпуститься» из неё с новой привычкой есть одно здоровое блюдо каждый день.
Если ваша «средняя скорость» — две тренировки в месяц, доведите их количество до одной в неделю.
Если у вас сумасшедшая работа и вы общаетесь со старыми друзьями только раз в три месяца, пора включить звонки в свой календарь и увеличить «среднюю скорость» до разговоров каждый месяц.

Уверен, вы уловили смысл идеи. «Выпускной вечер для привычек» заключается в том, чтобы оценить свои цели и «среднюю скорость» и придумать, как можно улучшить результат с помощью повторяющихся действий и привычек.

Я думал, как применить этот метод в своей жизни. Последние восемь месяцев я публиковал новые статьи каждые понедельник и четверг. Как «выпуститься» из этой привычки? Можно воспользоваться стратегией Нейтана и писать по 1 000 слов в день. Это позволит мне не только продолжать выдавать по две статьи в неделю, но и трудиться над другими вещами, скажем, начать работу над книгой.

Когда дело касается привычек, у каждого из нас своя «средняя скорость». И если говорить честно, обычно она гораздо ниже, чем нам хотелось бы. Правда в том, что нам несложно мотивировать себя и подтолкнуть к действию на один день. А вот удержать эту мотивацию и прилагать последовательные усилия каждую неделю под силу немногим.

Но не стоит осуждать или винить себя за низкую «среднюю скорость». Главное — понять, что происходит, и осознать, что вы способны это контролировать. А затем смириться с тем, что только маленькие, но последовательные изменения в ежедневных привычках могут скорректировать вашу «среднюю скорость». Огромные усилия не нужны — важна только последовательность.

Средняя скорость по перемещению определение.

Средняя скорость перемещения. Средняя путевая скорость

Все задачи, в которых присутствует движение объектов, их перемещение или вращение, так или иначе связаны со скоростью.

Данный термин характеризует перемещение объекта в пространстве за определенный отрезок времени – число единиц расстояния за единицу времени. Он является частым «гостем» как разделов математики, так и физики. Исходное тело может менять свое расположение как равномерно, так и с ускорением. В первом случае величина скорости статична и в ходе движения не меняется, во втором наоборот – увеличивается или уменьшается.

Как найти скорость – равномерное движение

Если скорость движения тела оставалась неизменной от начала перемещения и до окончания пути, то речь идет о перемещении с постоянным ускорением – равномерном движении. Оно может быть прямолинейным или же криволинейным. В первом случае траекторией перемещения тела является прямая.

Тогда V=S/t, где:

V – искомая скорость,
S – пройденное расстояние (общий путь),
t – общее время движения.

Как найти скорость – ускорение постоянно

Если объект двигался с ускорением, то его скорость по мере движения менялась. В таком случае найти искомую величину поможет выражение:

V=V (нач) + at, где:

V (нач) – первоначальная скорость движения объекта,
a – ускорение тела,
t – общее время пути.

Как найти скорость – неравномерное движение

В данном случае имеет место ситуация, когда разные участки пути тело проходило за разное время.
S(1) – за t(1),
S(2) – за t(2) и т.д.

На первом участке движение происходило в “темпе” V(1), на втором – V(2) и т.д.

Чтобы узнать скорость перемещения объекта на всем пути (ее среднее значение) воспользуйтесь выражением:

Как найти скорость – вращение объекта

В случае вращения речь идет об угловой скорости, определяющей угол, на который поворачивается элемент за единицу времени. Обозначается искомая величина символом ω (рад/с).

ω = Δφ/Δt, где:

Δφ – пройденный угол (приращение угла),
Δt – прошедшее время (время движения – приращение времени).

В случае, если вращение равномерное, искомая величина (ω) связана с таким понятием как период вращения – за какое время наш объект совершит 1 полный оборот. В таком случае:

ω = 2π/T, где:
π – константа ≈3,14,
T – период.

Или ω = 2πn, где:
π – константа ≈3,14,
n – частота обращения.

При известной линейной скорости объекта для каждой точки на пути движения и радиусе окружности, по которой она перемещается, для нахождения скорости ω потребуется следующее выражение:

ω = V/R, где:
V – численное значение векторной величины (линейной скорости),

R – радиус траектории следования тела.

Как найти скорость – сближение и отдаление точек

В подобного рода задачах уместным будет использование терминов скорость сближения и скорость отдаления.

Если объекты направляются друг к другу, то скорость сближения (отдаления) будет следующей:
V (сближ) = V(1) + V(2), где V(1) и V(2) – скорости соответствующих объектов.

Если одно из тел догоняет другое, то V (сближ) = V(1) – V(2), V(1) больше V(2).

Как найти скорость – движение по водоему

Если события разворачиваются на воде, то к собственной скорости объекта (движение тела относительно воды) добавляется еще и скорость течения (т.е. движение воды относительно неподвижного берега). Как взаимосвязаны эти понятия?

В случае перемещения по течению V=V(собст) + V(теч).
Если против течения – V=V(собств) – V(теч.).

Средней скоростью называется скорость, которая получается, если весь путь поделить на время, за которое объект преодолел этот путь. Формула средней скорости:

V ср = S/t.

S = S1 + S2 + S3 = v1*t1 + v2*t2 + v3*t3
V ср = S/t = (v1*t1 + v2*t2 + v3*t3) / (t1 + t2 + t3)

Чтобы не путаться с часами и минутами, переводим все минуты в часы: 15 мин. = 0,4 час, 36 мин. = 0,6 час. Подставляем числовые значения в последнюю формулу:

V ср = (20*0,4 + 0,5*6 + 0,6*15) / (0,4 + 0,5 + 0,6) = (8 + 3 + 9) / (0,4 + 0,5 + 0,6) = 20 / 1,5 = 13,3 км/час

Ответ: средняя скорость V ср = 13,3 км/час.

Как найти среднюю скорость движения с ускорением

Если скорость в начале движения отличается от скорости в его конце, такое движение называют ускоренным. Причём далеко не всегда тело действительно двигается всё быстрее и быстрее. Если движение замедляется, всё равно говорят, что оно движется с ускорением, только ускорение будет уже отрицательным.

Иными словами, если автомобиль, трогаясь с места, через секунду разогнался до скорости 10 м/сек, то его ускорение а равно 10 м в секунду за секунду а = 10 м/сек². Если в следующую секунду автомобиль остановился, то его ускорение тоже равно 10 м/сек², только уже со знаком минус: а = -10 м/сек².

Скорость движения с ускорением в конце временного отрезка вычисляется по формуле:

V = V0 ± at,

где V0 — начальная скорость движения, a — ускорение, t — время, за которое наблюдалось данное ускорение. Плюс или минус в формуле ставится в зависимости от того, увеличивалась скорость или уменьшалась.

Средняя скорость за отрезок времени t вычисляется как среднее арифметическое начальной и конечной скорости:

V ср = (V0 + V) / 2.

Находим среднюю скорость: задача

Шарик толкнули по ровной плоскости с начальной скоростью V0 = 5 м/сек. Через 5 сек. шарик остановился. Чему равны ускорение и средняя скорость?

Конечная скорость шарика V = 0 м/сек. Ускорение из первой формулы равно

а = (V — V0)/ t = (0 — 5)/ 5 = — 1 м/сек².

Средняя скорость V ср = (V0 + V) / 2= 5 /2 = 2,5 м/сек.

Механическим движением тела называется изменение его положения в пространстве относительно других тел с течением времени. При этом тела взаимодействуют по законам механики.

Раздел механики, описывающий геометрические свойства движения без учета причин, его вызывающих, называется кинематикой.

В более общем значении движением называется любое пространственное или временное изменение состояния физической системы. Например, можно говорить о движении волны в среде.

Относительность движения

Относительность — зависимость механического движения тела от системы отсчёта Не указав систему отсчёта, не имеет смысла говорить о движении.

Траектория материальной точки — линия в трёхмерном пространстве, представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве. Существенно, что понятие о траектории имеет физический смысл даже при отсутствии какого-либо по ней движения. Кроме того, и при наличии движущегося по ней объекта, траектория сама по себе не может ничего дать в отношении причин движения, то есть о действующих силах.

Путь — длина участка траектории материальной точки, пройденного ею за определённое время.

Скорость (часто обозначается , от англ. velocity или фр. vitesse) — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта (например, угловая скорость). Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.

В науке используется также скорость в широком смысле, как быстрота изменения какой-либо величины (не обязательно радиус-вектора) в зависимости от другой (чаще изменения во времени, но также в пространстве или любой другой). Так, например, говорят о скорости изменения температуры, скорости химической реакции, групповой скорости, скорости соединения, угловой скорости и т. д. Математически характеризуется производной функции.

Единицы измерения скорости

Метр в секунду, (м/с), производная единица системы СИ

Километр в час, (км/ч)

узел (морская миля в час)

Число Маха, 1 Мах равен скорости звука в данной среде; Max n в n раз быстрее.

Как единица, зависящая от конкретных условий среды, должна дополнительно определяться.

Скорость света в вакууме (обозначается c )

В современной механике движение тела подразделяется на виды, и существует следующая классификация видов движения тела :

Поступательное движение, при котором любая прямая линия, связанная с телом, остаётся при движении параллельной самой себе

Вращательное движение или вращение тела вокруг своей оси, считающейся неподвижной.

Сложное движение тела, состоящее из поступательного и вращательного движений.

Каждое из этих видов может быть неравномерным и равномерным (с не постоянной и постоянной скоростью соответственно).

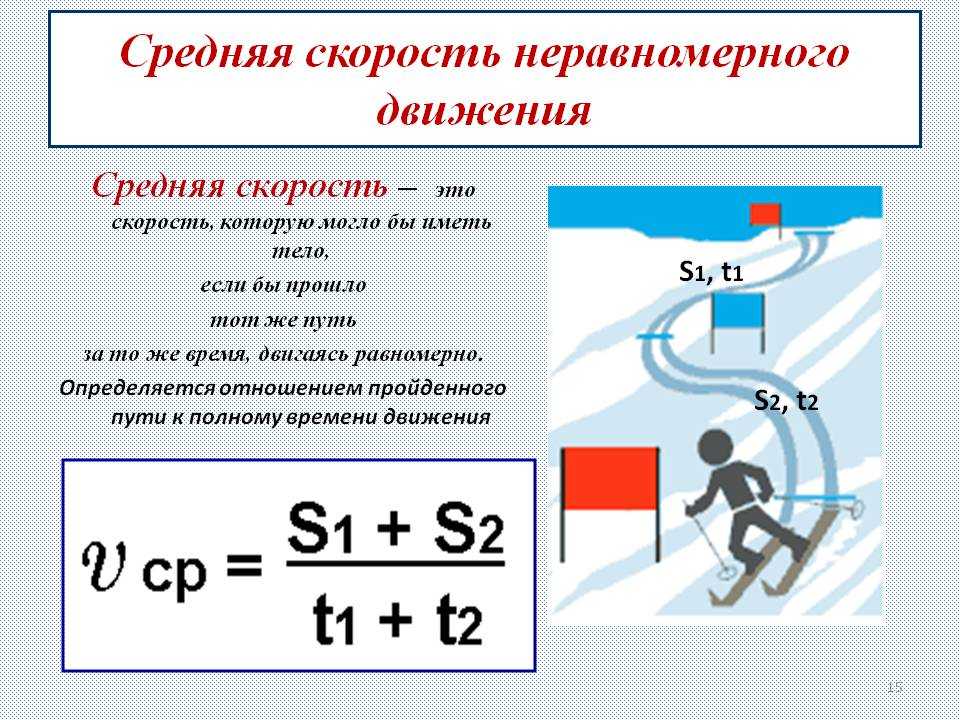
Средняя скорость неравномерного движения

Средняя путевая скорость — это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден:

Средняя путевая скорость, в отличие от мгновенной скорости не является векторной величиной.

Средняя скорость равна среднему арифметическому от скоростей тела во время движения только в том случае, когда тело двигалось с этими скоростями одинаковые промежутки времени.

В то же время если, например, половину пути автомобиль двигался со скоростью 180 км/ч, а вторую половину со скоростью 20 км/ч, то средняя скорость будет 36 км/ч. В примерах, подобных этому, средняя скорость равна среднему гармоническому всех скоростей на отдельных, равных между собой, участках пути.

Средняя скорость по перемещению

Можно также ввести среднюю скорость по перемещению, которая будет вектором, равным отношению перемещения ко времени, за которое оно совершено:

Средняя скорость, определённая таким образом, может равняться нулю даже в том случае, если точка (тело) реально двигалась (но в конце промежутка времени вернулась в исходное положение).

Если перемещение происходило по прямой (причём в одном направлении), то средняя путевая скорость равна модулю средней скорости по перемещению.

Прямолинейное равномерное движение – это движение, при котором тело (точка) за любые равные промежутки времени совершает одинаковые перемещения. Вектор скорости точки остаётся неизменным, а её перемещение есть произведение вектора скорости на время:

Если направить координатную ось вдоль прямой, по которой движется точка, то зависимость координаты точки от времени является линейной: , где — начальная координата точки, — проекция вектора скорости на координатную ось x.

Точка, рассматриваемая в инерциальной системе отсчёта, находится в состоянии равномерного прямолинейного движения, если равнодействующая всех сил, приложенных к точке, равна нулю.

Вращательное движение — вид механического движения. При вращательном движении абсолютно твердого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землей, ось вращения ротора генератора на электростанции неподвижна.

Характеристики вращения тела

При равномерном вращении (N оборотов в секунду),

Частота вращения — число оборотов тела в единицу времени,

Период вращения — время одного полного оборота. Период вращения T и его частота v связаны соотношением T = 1 / v.

Линейная скорость точки, находящейся на расстоянии R от оси вращения

,
Угловая скорость вращения тела.

Кинетическая энергия вращательного движения

Где I z — момент инерции тела относительно оси вращения. w — угловая скорость.

Гармонический осциллятор (в классической механике) — это система, которая при смещении из положения равновесия испытывает действие возвращающей силы, пропорциональной смещению.

Если возвращающая сила — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.

Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором. Если трение не слишком велико, то система совершает почти периодическое движение — синусоидальные колебания с постоянной частотой и экспоненциально убывающей амплитудой. Частота свободных колебаний затухающего осциллятора оказывается несколько ниже, чем у аналогичного осциллятора без трения.

Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.

Механическими примерами гармонического осциллятора являются математический маятник (с малыми углами смещения), груз на пружине, торсионный маятник и акустические системы. Среди других аналогов гармонического осциллятора стоит выделить электрический гармонический осциллятор (см. LC-цепь).

Звук , в широком смысле — упругие волны, продольно распространяющиеся в среде и создающие в ней механические колебания; в узком смысле — субъективное восприятие этих колебаний специальными органами чувств животных или человека.

Как и любая волна, звук характеризуется амплитудой и спектром частот. Обычно человек слышит звуки, передаваемые по воздуху, в диапазоне частот от 16 Гц до 20 кГц. Звук ниже диапазона слышимости человека называют инфразвуком; выше: до 1 ГГц, — ультразвуком, более 1 ГГц — гиперзвуком. Среди слышимых звуков следует также особо выделить фонетические, речевые звуки и фонемы (из которых состоит устная речь) и музыкальные звуки (из которых состоит музыка).

Физические параметры звука

Колебательная скорость — величина, равная произведению амплитуды колебаний А частиц среды, через которую проходит периодическая звуковая волна, на угловую частоту w :

где В — адиабатическая сжимаемость среды; р — плотность.

Как и световые волны, звуковые тоже могут отражаться, преломляться и т.д.

Если Вам понравилась эта страница, и Вам захотелось, чтобы Ваши друзья тоже её увидели, то выберите внизу значок социальной сети, где вы имеете свою страницу, и выразите своё мнение о содержании.

Ваши друзья и случайные посетители благодаря этому добавят Вам и моему сайту рейтинг

Понятие скорости − одно из главных понятий в кинематике.
Многим наверняка известно, что скорость − это физическая величина, показывающая насколько быстро (или насколько медленно) перемещается в пространстве движущееся тело. Разумеется, речь идет о перемещении в выбранной системе отсчета. Известно ли, однако, Вам, что используются не одно, а три понятия скорости? Есть скорость в данный момент времени, называемая мгновенной скоростью, и есть два понятия средней скорости за данный промежуток времени − средняя путевая скорость (по английски speed) и средняя скорость по перемещению (по-английски velocity).
Будем рассматривать материальную точку в системе координат x , y , z (рис. а).

Положение A точки в момент времени t характеризуем координатами x(t) , y(t) , z(t) , представляющими три составляющих радиуса-вектора (t ). Точка движется, ее положение в выбранной системе координат с течением времени изменяется − конец радиуса-вектора (t ) описывает кривую, называемую траекторией движущейся точки.
Траектория, описанная за промежуток времени от t до t + Δt , показана на рисунке б.

Через B обозначено положение точки в момент t + Δt (его фиксирует радиус-вектор (t + Δt )). Пусть Δs − длина рассматриваемой криволинейной траектории, т. е. путь, пройденный точкой за время от t до t + Δt .
Среднюю путевую скорость точки за данный промежуток времени определяют соотношением

Очевидно, что v п − скалярная величина; она характеризуется только числовым значением.
Показанный на рисунке б вектор

называют перемещением материальной точки за время от t до t + Δt .
Среднюю скорость по перемещению за данный промежуток времени определяют соотношением

Очевидно, что v ср − векторная величина. Направление вектора v ср совпадает с направлением перемещения Δr .
Заметим, что в случае прямолинейного движения средняя путевая скорость движущейся точки совпадает с модулем средней скорости по перемещению.
Движение точки по прямолинейной либо криволинейной траектории называют равномерным, если в соотношении (1) величина vп не зависит от Δt . Если, например, уменьшить Δt в 2 раза, то и длина пройденного точкой пути Δs уменьшится в 2 раза. При равномерном движении точка проходит за равные промежутки времени пути равной длины.
Вопрос :
Можно ли считать, что при равномерном движении точки от Δt не зависит также вектор ср средней скорости по перемещению?

Ответ :
Так можно считать только в случае прямолинейного движения (при этом, напомним, модуль средней скорости по перемещению равен средней путевой скорости). Если же равномерное движение совершается по криволинейной траектории, то с изменением промежутка усреднения Δt будут изменяться как модуль, так и направление вектора средней скорости по перемещению. При равномерном криволинейном движении равным промежуткам времени Δt будут соответствовать разные векторы перемещения Δr (а значит, и разные векторы v ср ).
Правда, в случае равномерного движения по окружности равным промежуткам времени будут соответствовать равные значения модуля перемещения |r| (а значит, и равные |v ср | ). Но направления перемещений (а значит, и векторов v ср ) и в данном случае будут различными для одинаковых Δt . Это видно на рисунке,

Где равномерно движущаяся по окружности точка описывает за равные промежутки времени равные дуги AB , BC , CD . Хотя векторы перемещений 1 , 2 , 3 имеют одинаковые модули, однако направления у них различны, так что о равенстве этих векторов говорить не приходится.
Примечание
Из двух средних скоростей в задачах обычно рассматривают среднюю путевую скорость, а среднюю скорость по перемещению используют довольно редко. Однако она заслуживает внимания, так как позволяет ввести понятие мгновенной скорости.

1. Материальная точка прошла половину окружности. Найти отношение средней путевой скорости к модулю средней векторной скорости.

Решение . Из определения средних значений путевой и векторной скоростей с учетом того, что путь, пройденный материальной точкой за время движенияt , равенR , а величина перемещения 2R , гдеR — радиус окружности, получим:

2. Автомобиль проехал первую треть пути со скоростью v 1 = 30 км/ч, а оставшуюся часть пути — со скоростью v 2 = 40 км/ч. Найти среднюю скорость на всем пройденном пути.

Решение . По определению =гдеS — путь, пройденный за времяt . Очевидно, что
Поэтому искомая средняя скорость равна

3. Студент проехал половину пути на велосипеде со скоростьюv 1 = 12 км/ч. Далее половину оставшегося времени он ехал со скоростьюv 2 = 10 км/ч, а оставшуюся часть пути шел пешком со скоростьюv 3 = 6 км/ч. Определить среднюю скорость движения студента на всем пути.

Решение . По определению
гдеS – путь, аt — время движения. Ясно, чтоt =t 1 +t 2 +t 3 . Здесь
— время движения на первой половине пути,t 2 – время движения на втором участке пути иt 3 — на третьем. По условию задачиt 2 =t 3 . Кроме того,S /2 =v 2 t 2 + v 3 t 3 = (v 2 +v 3)t 2 . Отсюда следует:

Подставив t 1 и t 2 +t 3 = 2t 2 в выражение для средней скорости, получим:

4. Расстояние между двумя станциями поезд прошел за времяt 1 = 30 мин. Разгон и торможение длилисьt 2 = 8 мин, а остальное время поезд двигался равномерно со скоростью v = 90 км/ч. Определить среднюю скорость поезда , считая, что при разгоне скорость увеличивалась с течением времени по линейному закону, а при торможении уменьшалась тоже по линейному закону.

ешение . Построим график зависимости скорости поезда от времени (см. рис.). Этот график описывает трапецию с длинами оснований, равнымиt 1 иt 1 –t 2 и высотой, равной v. Площадь этой трапеции численно равна пути, пройденному поездом от начала движения до остановки. Поэтому средняя скорость равна:

Задачи и упражнения

1.1. Мяч упал с высотыh 1 = 4 м, отскочил от пола и был пойман на высотеh 2 = 1 м. Чему равен путьS и величина перемещения
?

1.2. Материальная точка переместилась на плоскости из точки с координатамиx 1 = 1 см иy 1 = 4cм в точку с координатамиx 2 = 5 см иy 2 = 1 см. Построить вектор перемещения и с помощью линейки определить модуль вектора перемещения и проекции вектора перемещения на осиx иy . Найти эти же величины аналитически и сравнить результаты.

1.3. Первую половину пути поезд шел со скоростью вn = 1,5 раза большей, чем вторую половину пути. Средняя скорость поезда на всем пути = 43,2 км/ч. Каковы скорости поезда на первой и второй половинах пути?

1.4. Первую половину времени своего движения велосипедист проехал со скоростью v 1 = 18 км/ч, а вторую половину времени — со скоростью v 2 = 12 км/ч. Определить среднюю скорость движения велосипедиста.

1.5. Движение двух автомобилей описывается уравнениями
и
, где все величины измеряются в системе СИ. Запишите закон изменения расстояния
между автомобилями от времени и найдите
через время
с. после начала движения.

Совместимость Водолей (женщина) — Весы (мужчина)

К чему снится шуба во сне?

Средняя скорость Определение и значение

Лучшие определения
Викторина
Подробнее о средней скорости
Примеры

Показывает уровень оценки в зависимости от сложности слова.

Сохрани это слово!

Показывает уровень сложности слова.

Определение средней скорости

существительное

общее пройденное расстояние, деленное на общее прошедшее время.

ВИКТОРИНА

Сыграем ли мы в «ДОЛЖЕН» ПРОТИВ. «ДОЛЖЕН» ВЫЗОВ?

Следует ли вам пройти этот тест на «должен» или «должен»? Это должно оказаться быстрым вызовом!

Вопрос 1 из 6

Какая форма обычно используется с другими глаголами для выражения намерения?

Слова рядом со средней скоростью

средний регулятор, среднее отклонение, средний Джо, средняя жизнь, средний доход, средняя скорость, усредняющий экспонометр, Ave Regina Coelorum, Averil, averment, Averno

ПОДРОБНЕЕ О СРЕДНЕЙ СКОРОСТИ

Что такое

средняя скорость ?

Средняя скорость рассчитывается путем деления общего расстояния, пройденного объектом, на общее количество времени, которое потребовалось для прохождения этого расстояния.

Скорость — это скорость, с которой что-то движется в определенный момент. Средняя скорость измеряет среднюю скорость на протяжении поездки. Средняя скорость обычно применяется к транспортным средствам, таким как автомобили, поезда и самолеты. Она часто измеряется в милях в час (миль в час) или километрах в час (км/ч).

Средняя скорость используется во всех областях, включая физику, астрономию и транспорт.

Как найти

среднюю скорость

Давайте замедлимся и начнем с примера. Если бы вы проехали 200 миль за два часа, вы могли бы рассчитать свою среднюю скорость , разделив общее расстояние (200 миль) на общее количество времени, затраченного на это (два часа), что дало бы среднюю скорость 100 миль. в час. (Это означает, что следующее, что вам нужно будет рассчитать, это как оплатить штраф за превышение скорости.)

Средняя скорость может показаться простой и очевидной концепцией, но на протяжении большей части истории у людей не было особой практической необходимости в таком расчете (плюс на лошадях не было спидометров). В 1600-х годах физик и астроном Галилео Галилей попытался рассчитать скорость света, измерив, сколько времени потребуется человеку, чтобы увидеть свет через поле. Это не сработало (свет слишком быстр, чтобы его можно было измерить таким образом), но Галилей вывел формулу расстояние/время = средняя скорость 9.0048 . (Другие, вероятно, обсуждали эту концепцию до этого, но Галилей обычно получает признание.)

Средняя скорость не следует путать с мгновенной скоростью , которая измеряет скорость объекта в определенный момент времени. Мгновенная скорость — это физический термин. В повседневной жизни мы просто называем это скоростью , что говорит вам спидометр в вашей машине — как быстро вы едете в данный момент. Скорость иногда путают с скорость , но это не одно и то же. В физике скорость измеряет скорость чего-либо относительно направления его движения.

В практических ситуациях средняя скорость обычно используется в контексте транспорта, например, средняя скорость поезда или самолета во время поездки.

Знаете ли вы…?

Свет имеет среднюю скорость приблизительно 186 000 миль (около 300 000 километров) в секунду.

Каковы реальные примеры

средней скорости ?
Средняя скорость используется в физике и других областях науки, но также используется во всех практических приложениях, особенно в транспорте. Программное обеспечение, которое запускает ваше приложение GPS (Global Positioning System), использует среднюю скорость для расчета продолжительности поездки.

Только что проехав 30 миль со скоростью 50 миль в час ночью, как это работает на практике? Сомневаюсь, что ночью камеры смогут снять все номерные знаки и т.д.
Мысли?
— Стив Литчфилд (@stevelitchfield) 16 февраля 2020 г.
Поезд, преодолевающий 900 км за 20 часов со средней скоростью 45 км/ч, в Индии называют сверхбыстрым.
Просто для сравнения, в Японии такое же расстояние занимает 5 часов.
— पंक्चर वाला (@pun_cture_wala) 21 февраля 2020 г.
Проверьте себя!
Правда или ложь?
Средняя скорость и средняя скорость являются разными измерениями.
Как использовать среднюю скорость в предложении
Итак, это виды вещей, которые связаны с движением, уровнем заторов, средней скоростью, которые зависят от времени суток, дня недели .
Использование машинного обучения для создания карт, которые дают более разумные советы по вождению|MIT Technology Review Insights|23 июня 2021 г.|MIT Technology Review
Его печатание вольным стилем — ответы на вопросы — в целом соответствовали производительности и соответствовали средней скорости набора текста большим пальцем для его возрастной группы.
Новый имплантат мозга превращает мысли в текст с точностью 90%|Shelly Fan|18 мая 2021 г.|Центр Singularity поворот, но ему все же удалось сохранить среднюю скорость, которая была второй по скорости в 19-й гонке.-лошадь Дерби Филд.
Две лошади, которые могут победить победителя Кентукки Дерби Медина Спирит на кольях Прикнесс|Нил Гринберг|13 мая 2021 г.|Washington Post
Средняя скорость частиц соответствует температуре газа — чем быстрее, тем горячее.
Как демон Максвелла продолжает пугать ученых — такие романтичные факты|Джонатан О’Каллаган|29 апреля 2021|Наутилус
Средняя скорость частиц соответствует температуре газа — чем быстрее, тем горячее.
Как демон Максвелла продолжает пугать ученых|Джонатан О’Каллаган|22 апреля 2021 г.|Журнал Quanta
Ограничение сроков полномочий может быть предписанием для ускорения перемен.
Невыносимая белизна Конгресса|Дин Обейдаллах|8 января 2015|DAILY BEAST
Он почувствовал, как его тело обмякло (как в высокоскоростных фильмах о увядающем цветке).
Влиятельный конгрессмен пишет о «мясистых грудях»|Асавин Суебсенг|7 января 2015 г.|DAILY BEAST
Реактивный двигатель мгновенно принес два преимущества по сравнению с пропеллерами: он удвоил скорость и стал намного надежнее.
Flight 8501 Poses Вопрос: современные самолеты слишком автоматизированы, чтобы летать?|Клайв Ирвинг|4 января 2015 г.|DAILY BEAST
Более тысячи отверстий, в среднем я делаю менее четырех ударов на отверстие.
Потерянный на тысячи ударов: «Гольф в пустыне» — это «Angry Birds» как современное искусство|Алек Кубас-Мейер|2 января 2015 г.|DAILY BEAST
Эффективность вакцины в среднем составляет около 60 процентов.
Когда вы заболеете гриппом этой зимой, вы можете винить антипрививочников|Кент Сепковиц|1 января 2015 г.|DAILY BEAST
Действительно, он развил поразительную скорость для того, кто проложил себе путь под туннелем.
Сказка о дедушке Кроте|Артур Скотт Бейли
Я не думаю, что среднее количество пассажиров на соответствующем маршруте в нашей стране может быть меньше двадцати.
Взгляд на Европу|Гораций Грили
Затем последовал длинный участок гладкого льда, по которому он скользил с постоянно увеличивающейся скоростью.
Великан Севера|Р.М. Ballantyne
Никогда больше он не сядет за руль, радуясь дерзости скорости.
Веселые приключения Аристида Пухоля|Уильям Дж. Локк
Хотя средний говорящий обычно ограничивается одним типом голоса, который он несколько варьирует, он не часто маскируется.
Культура выразительного голоса|Джесси Элдридж Саутвик
Формула средней скорости — Как найти среднюю скорость?
Средняя скорость является решающим фактором для определения времени, необходимого для прохождения пути. Средняя скорость — это, по сути, механизм, который помогает нам рассчитать скорость движения и расстояние. Очевидно, что скорость продолжает меняться в пути, что делает определение средней скорости более важным. Существует несколько способов определения средней скорости объекта или транспортного средства. Наиболее часто используемый определитель средней скорости упоминается ниже.
Это наиболее часто используемый и один из самых простых методов определения средней скорости. Это наиболее желательно в тех случаях, когда скорость, с которой движется объект, одинакова на протяжении всего пути, то есть она не увеличивается и не уменьшается. Процедура нахождения средней скорости заключается в использовании деления. Разделите расстояние, пройденное транспортным средством, на время, за которое оно проедет, и вы получите ответ.
Приведенная выше формула S = D/T, если «S» считается «скоростью», «D» принимается за «расстояние», а «T» интерпретируется как «время». Другими словами, общее расстояние / общее время = средняя скорость.
Что такое средняя скорость?
Среднюю скорость объекта можно определить как общее расстояние, пройденное им за определенный интервал времени. Его можно рассчитать, разделив общее пройденное расстояние на общее затраченное время.
Если объект проходит разные расстояния с разными скоростями, то средняя скорость объекта является единственным значением скорости, при котором, если объект движется равномерно, он пройдет одно и то же расстояние за один и тот же интервал времени.
Математически средняя скорость (Savg) = \[\frac{\text{Общее пройденное расстояние}}{\text{Общее затраченное время}}\]
Если объект проходит x ₁ , x ₂ , x ₃ ,……,x _n расстояния в t ₁ , t ₂ , t ₃ ,…..,t _n секунд соответственно, затем
\ [S_{среднее} = \frac{x_{1} + x_{2} + . . . . + x_{n}}{t_{1} + t_{2} + . . . . + t_{n}}\]
Единицей средней скорости в СИ является м/с, и это скалярная величина, что означает, что она имеет только величину.
Решенные примеры на средней скорости
1. Поезд движется со скоростью 300 км/ч в течение 2 часов, а затем замедляется до 220 км/ч в течение следующих 2 часов. Какова средняя скорость поезда?
Решение: Расстояние, пройденное за первые 2 часа, D1 = 300 * 2 = 600 миль
Расстояние, пройденное за следующие 2 часа, D2 = 220 * 2 = 440 миль
Общее пройденное расстояние, D = D1 + D2
D = 600 + 440 = 1040 миль
Общее время = 4 часа
Таким образом, средняя скорость поезда = \[\frac{\text{Общее пройденное расстояние (D)}}{\text{Общее затраченное время (T)}}\]
= 1040/4 = 260 м /с
2. Частица движется со скоростью 4 м/с в течение 20 с. Он снова движется со скоростью 6 м/с в течение следующих 20 с и, наконец, движется со скоростью 8 м/с в течение следующих 20 с. Вычислить среднюю скорость частицы? (в м/с)
Решение: Расстояние = скорость x время
Расстояние, пройденное за первые 20 с, D1 = 20 с × 4 м
= 80 м
Расстояние, пройденное за следующие 20 с, D2 = 20 × 6 м
= 120 м
Расстояние, пройденное за последние 20 с, D3 = 20 × 8 м
= 100 м
Общее расстояние, пройденное частицей, D = 80 + 120 + 160 м
= 360 мс
Общее затраченное время, T = 20×3 = 60 с
Следовательно, средняя скорость, S = D/T
= 360/60 м/с
= 60 м /s
3. Человек идет из пункта А в пункт Б за 10 с и возвращается обратно за 8 с. Найдите среднюю скорость человека, если расстояние между А и В равно 36 м.
Решение: Здесь общее пройденное расстояние = 72 м
Общее затраченное время = 18 с
Следовательно, средняя скорость = \[\frac{\text{Общее пройденное расстояние}}{\text{Общее затраченное время}} = \frac{ 72}{18}\] = 4 м/с.
Практические вопросы
Мальчик едет на велосипеде со скоростью 12 км/ч в течение 2 часов, а затем со скоростью 15 км/ч в течение 1 часа. Найдите среднюю скорость мальчика.
Автомобиль движется со средней скоростью 35 миль в час. За какое время автомобиль проедет 14,5 км?
Мальчик прошел полный цикл по кругу радиусом 35 м за 22 с. Найдите среднюю скорость мальчика.
Другие примеры средней скорости
1. Рахул пробегает 4 мили от своего дома до детской площадки за 2 часа каждый день. Какова его средняя скорость?
Ответ: Средняя скорость = общее расстояние ÷ общее время
Средняя скорость = 4 мили ÷ 2 часа
Средняя скорость = 2 мили в час
2. Анитья идет от А до Б, преодолевая 8 миль за 2 часы. Какова средняя скорость?
Ответ: Средняя скорость = общее расстояние ÷ общее время
Средняя скорость = 8 миль ÷ 2 часа
Средняя скорость = 4 мили в час
Другая формула используется, когда скорость во время поездки изменяется. Если объект проходит часть пути с одной скоростью и меняет скорость, чтобы пройти другую часть пути, применяется эта формула. Давайте учиться на примере.
3. Самолет летит из США в Малайзию на расстояние 9000 миль, за 18 часов и путешествие из Малайзии в Индию, расстояние 3000 миль за 5 часов.
Ответ: Чтобы найти среднюю скорость локомотива, вам нужно будет сделать следующую формулу.
пройденное расстояние = 9000 миль + 3000 миль
Проверленное.
Кинематика — Средняя скорость
Кинематика — Средняя скорость
[Глава 2 цели]
БХС -> Мистер Стэнбро -> Физика -> Механика -> Кинематика -> эта страница
Средняя скорость
Средняя скорость объекта говорит вам о (средней) скорости в которое он покрывает расстояние. Если средняя скорость автомобиля 65 км/ч. час, это означает, что положение автомобиля изменится (в среднем) на 65 миль каждый час.
Средняя скорость равна скорости . В кинематике, ставка — это всегда количество, деленное на время, затраченное на получение этого количество (прошедшее время ). Так как средний скорость — это скорость изменения положения, средняя скорость = расстояние пройдено/затраченное время.
Пример:
Автомобиль проезжает между двумя городами, расстояние между которыми 60 миль, за 2 часа. Что такое его средняя скорость?
Ответ:
средняя скорость = расстояние/время Следовательно, средняя скорость автомобиль 60 миль/2 часа = 30 миль/час.
Пример:
Если человек может идти со средней скоростью 2 метра в секунду, как далеко они пройдут за 4 минуты?
Ответ:
В 1 минуте 60 секунд, поэтому их 4 (60 секунд) = 240 секунд за 4 минуты. Кроме того, если средняя скорость = расстояние/время, тогда расстояние = (средняя скорость) (время). Следовательно, расстояние, человек проходит (2 м/с)(240 с) = 480 метров.
Единицы скорости
Так как средняя скорость всегда рассчитывается как расстояние (длина), деленное на время, единицами средней скорости являются всегда единица расстояния, деленная на единицу времени. Общие единицы скорости метры в секунду (сокращенно м/с), сантиметры в секунду (см/с), километры в час (km/hr), мили в час (mi/hr — старайтесь избегать общих аббревиатура mph) и многие другие.
Пример:
Что из следующего может быть измерением скорости?
2,5 метра
2,5 секунды/метр
2,5 метра в секунду
2,5 метра в секунду в секунду
Ответ:
Измерением скорости может быть только 2,5 метра в секунду. Скорость всегда имеет единицы измерения расстояния (длины), деленные на единицу времени.
Какое расстояние?
Фермер Джонс проехал 6 миль по прямой дороге. Она разворачивается и едет 4 мили назад. Каков был ее средний скорость этой поездки, если она заняла 1 час?
Ваш ответ на эту задачу зависит от вашей интерпретации «пройденный путь». Можно сказать:
общее расстояние , пройденное фермером Джонсом составляет 10 миль. Следовательно, ее средняя скорость равна 10 км/ч.
Чистое расстояние , пройденное Фермером Джонсом, равно 2 мили. Следовательно, ее средняя скорость равна 2 км/ч.
Есть веские причины использовать любую интерпретацию — в основном это вопрос предпочтений. Мы будем интерпретировать «пройденное расстояние» как чистое расстояние ( также называется смещением). 901:57 Средняя скорость фермера Джонса составляла 2 мили в час.
ПРИМЕЧАНИЕ: Могут использоваться различные тексты. другие условности! На самом деле, в нашем учебнике по физике AP используется общее количество расстояние для расчета скорости, но чистое расстояние для расчета скорость. Здесь будьте осторожны!
Опасности усреднения средних значений 90 020
Вот интересная задачка:
Сюзи запланировала поездку в город в 60 милях от нее. Она желает иметь среднюю скорость 60 миль/час для поездки. В связи до пробки, правда, у нее только средняя скорость 30 миль/час за первые 30 миль. Как быстро ей нужно идти на оставшиеся 30 миль так, чтобы ее средняя скорость была 60 миль/час за всю поездку?
Скорее всего, вы подумали: «О, 90 миль в час — ведь средняя 30 и 90 это 60! Мальчик, это легко!»
Однако, к сожалению, ответ , а не 90 миль/час. И вот почему: вы знаете, что средняя скорость = расстояние/время (v = d/t). Чтобы иметь среднюю скорость 60 миль/час на расстояние 60 миль, вы должны совершить поездку за 1 час:

Но Сюзи уже потратила час (1 час уходит на 30 миль со средней скоростью 30 миль/час) — а она всего наполовину путь! это невозможно для нее завершить поездку со средней скоростью 60 миль в час! Ей придется уйти бесконечно быстро!
Обратите внимание, что для прохождения последних 30 минут потребуется 1/3 часа.