Административная работа за 1 четверть
Административная работа по физике
8 класс 1 четверть
Вариант 1
1. Внутренняя энергия тела зависит…
А. От скорости движения тела.
Б. От энергии движения частиц, из которых состоит тело.
В. От энергии взаимодействия частиц, из которых состоит тело.
Г. От энергии движения частиц и от энергии их взаимодействия.
2. После того как распилили бревно, пила нагрелась. Каким способом изменили внутреннюю энергию пилы?
А. При совершении работы. Б. При теплопередаче.
3. Чтобы увеличить внутреннюю энергию автомобильной шины, нужно…
А. Выпустить из шины воздух.
Б. Накачать в шину воздух.
4. Два одинаковых пакета с молоком вынули из холодильника. Один пакет оставили на столе, а второй перелили в кастрюлю и вскипятили.
В каком случае внутренняя энергия молока изменилась меньше?
А. В обоих случаях не изменилась.
Б. В обоих случаях изменилась одинаково.
В. В первом случае.
Г. Во втором случае.
5. Конвекцией называют вид теплопередачи, при котором энергия…
A. Передается от нагретого тела с помощью лучей.
Б. От нагретого конца тела передается к холодному, но само вещество при этом не перемещается.
В. Переносится самими частицами вещества.
6. Каков способ теплопередачи от костра?
А. Излучение.
Б. Теплопроводность.
В. Конвекция.
7. Ложка, опущенная в стакан с горячей водой, нагревается. Каким способом происходит теплопередача?
А. Излучение.
Б. Теплопроводность.
В. Конвекция.
8.
Что такое количество теплоты?
А. Количество внутренней энергии, которое необходимо для нагревания вещества на 1 °С.
Б. Часть внутренней энергии, которую тело получает или теряет при теплопередаче.
В. Количество внутренней энергии, необходимое для нагревания вещества массой 1 кг на 1 °С.
Г. Часть внутренней энергии, которую получает тело при совершении над ним работы.
9. В каких единицах измеряют удельную теплоемкость?
А. Дж. Б. Вт. В. Дж/кг*С. Г. Н
10. Какое количество теплоты потребуется для нагревания 10 г меди на 15 °С?
А. 600 Дж. Б. 3,75 Дж. В. 60 Дж. Г. 266,7 Дж. Д. 60 000 Дж.
11. При охлаждении медного прута на 25 °С выделилось 200 Дж энергии. Какова масса медного прута?
А. 50 кг. Б. 0,02 кг. В. 2 кг. Г. 0,5 кг. Д. 2 000 000 кг.
12. Что означает выражение: «удельная теплота сгорания каменного угля q = 27 ∙106 »? Это означает, что при полном сгорании.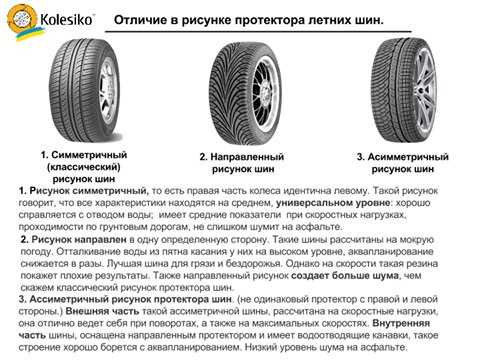
..
A. Угля массой 1 кг выделяется 27 ∙106 Дж энергии.
Б. Угля массой 27 кг выделяется 106 Дж энергии.
B. Угля массой 27 ∙106 кг выделяется 1 Дж энергии.
Г. Угля объемом 1 м3 выделяется 27 ∙106 Дж энергии.
13. Какое количество теплоты выделяется при полном сгорании 50 г спирта? Удельная теплота сгорания спирта q = 30 ∙106 .
А. 0,6∙106 Дж. Г. 1,5∙106 Дж.
Б. 600 ∙106 Дж. Д. 1,67∙106 Дж.
В. 1500∙106 Дж.
14. Переход вещества из жидкого состояния в твердое называют…
А. Плавлением.
Б. Диффузией.
В. Отвердеванием.
Г. Нагреванием.
Д. Охлаждением.
15. Чугун плавится при температуре 1200 °С. Что можно сказать о температуре отвердевания чугуна?
А. Может быть любой.
Б. Равна 1200 °С.
В. Выше температуры плавления.
Г. Ниже температуры плавления.
Административная работа по физике
8 класс 1 четверть
Вариант 2
1. Каким способом можно изменить внутреннюю энергию тела?
А. Только совершением работы.
Б. Совершением работы и теплопередачей.
В. Только теплопередачей.
Г. Внутреннюю энергию тела изменить нельзя.
2. Сок поставили в холодильник и охладили. Каким способом изменили внутреннюю энергию сока?
А. При совершении работы. Б. При теплопередаче.
3. Резиновую нить слегка растянули.
Чтобы внутренняя энергия нити увеличилась ее надо…
А. Растянуть сильнее. Б. Отпустить.
4. Два алюминиевых бруска массами 100 и 300 г, взятых при комнатной температуре, нагрели до одинаковой температуры. У какого бруска внутренняя энергия изменилась больше?
A. У обоих не изменилась.
Б. У обоих одинаково.
B. У первого бруска.
Г. У второго бруска.
5. Вид теплопередачи, при котором энергия от нагретого тела передается холодному с помощью лучей, называется…
А. Излучением.
Б. Конвекцией.
В. Теплопроводностью.
6. Каков способ теплопередачи водяного отопления?
А. Излучение.
Б. Теплопроводность.
В. Конвекция.
7. Количество теплоты, затраченное на нагревание тела, зависит от…
А. Массы, объема и рода вещества.
Б. Изменения его температуры, плотности и рода вещества.
В. Массы тела, его плотности и изменения температуры.
Г. Рода вещества, его массы и изменения температуры.
8. Удельная теплоемкость свинца 140 . Это значит, что для нагревания…
А. Свинца массой 140 кг на 1 °С требуется 1 Дж энергии.
Б. Свинца массой 1 кг на 140 °С требуется 1 Дж энергии.
B. Свинца массой 1 кг на 1 °С требуется 140 Дж энергии.
Г. Свинца массой 1 кг на 140 °С требуется 140 Дж энергии.
9 Какое количество теплоты выделите и при охлаждении 20 г спирта на 6 °С?
А. 300 Дж.
Б. 8 333,3 Дж.
В. 0,048 Дж.
Г. 400 000 Дж.
Д. 750 Дж.
10. При нагревании 4 г спирта передано 200 Дж количества теплоты. На сколько градусов изменилась температура спир-та?
А. 2 000 000 °С.
Б. 50 °С. В. 2000 °С. Г. 0,05 °С. Д. 20 °С.
11. Что означает выражение: «удельная теплота сгорания бензина q = 45 ∙106 »? Это означает, что при полном сгорании…
A. Бензина объемом 1 м3 бензина выделяется 45 ∙106 Дж энергии.
Б. Бензина массой 45 ∙106 кг выделяется 1 Дж энергии.
B. Бензина массой 45 кг выделяется 106 Дж энергии.
Г. Бензина массой 1 кг выделяется 45 ∙106 Дж энергии.
12. Какое количество теплоты выделяется при полном сгорании 200 г березовых дров? Удельная теплота сгорания березовых дров qбер.дров = 15∙106 .
А. 3∙109 Дж.
Г. 75∙103 Дж.
Б. 3∙106 Дж. Д. 75∙106 Дж.
В. 0,0133∙10-6 Дж.
13. Какую массу березовых дров нужно сжечь, чтобы получить такое же количество теплоты, как при сжигании бензина массой 5 кг?
А. 0,067 кг. Б. 1,67 кг. В. 15 кг. Г. 135 кг. Д. 3375 кг.
14. В процессе плавления тело…
A. Получает энергию.
Б. Отдает энергию.
B. Не получает и не отдает энергию.
15. Олово отвердевает при температуре 232 °С. Что можно сказать о температуре его плавления?
A. Выше температуры отвердевания.
Б. Может быть любой.
B. Ниже температуры отвердевания.
Г. Равна 232 °С.
Административная работа по физике
8 класс 1 четверть
Вариант 3
1.
Внутренней энергией тела называют…
A. Энергию движения и взаимодействия частиц, из которых состоит тело.
Б. Энергию движущегося тела.
B. Энергию взаимодействия молекул.
Г. Энергию тела, поднятого над Землей.
Д. Энергию движения молекул.
2. Чайник с водой поставили на огонь и вскипятили воду. Каким способом изменилась внутренняя энергии воды?
А. При теплопередаче. Б. При совершении работы.
3. В сосуде находится газ. Чтобы внутренняя энергия газа уменьшилась, нужно…
A. Сжать газ. Б. Увеличить объем газа.
4. В две одинаковые кастрюли налили одинаковое количество воды. В первой кастрюле воду довели до кипения, а во второй слегка подогрели. В каком случае внутренняя энергия воды изменилась меньше?
А. В обоих случаях не изменилась.
Б.
В первой кастрюле.
B. Во второй кастрюле.
Г. В обоих случаях одинаково.
5. Теплопроводностью называют вид теплопередачи,
при котором энергия…
А. Переносится самими частицами вещества.
Б. Передается от нагретого конца тела холодному, но само вещество при этом не перемещается.
В. Передается с помощью лучей.
6. На чем основано нагревание нижних слоев атмосферы?
А. Конвекция.
Б. Излучение.
В. Теплопроводность.
7. Каков способ теплопередачи энергии стенкам стакана, в который налит горячий чай?
А. Излучение.
Б. Теплопроводность.
В. Конвекция.
8. Что называют удельной теплоемкостью?
A. Количество теплоты, необходимое для нагревания вещества массой 1 кг на 1 °С.
Б. Количество внутренней энергии, которую получает тело при совершении работы.
B. Количество теплоты, которое необходимо для нагревания вещества на 1 °С.
Г. Количество внутренней энергии, которое отдает или получает тело при теплопередаче.
9. В каких единицах измеряют количество теплоты?
А.Н . Б. .Па В.кг Г. Дж. Д. Вт.
10. Какое количество теплоты потребуется для нагревания цинка массой 50 г на 25 °С?
А. 200 Дж.
Б. 500 Дж.
В. 800 Дж.
Г. 3,125 Дж.
Д. 500 000 Дж.
11. На сколько градусов изменилась температура цинка массой 20 г, если при его охлаждении выделилось 200 Дж энергии?
А. 16 000 °С. Б. 0,04 °С. В. 25 °С. Г. 1 600 000 °С. Д. 40 °С.
12. Количество теплоты, выделившееся при полном сгорании топлива равно…
A. Отношению массы сгоревшего топлива к удельной теплоте сгорания топлива.
Б. Отношению удельной теплоты сгорания топлива к массе сгоревшего топлива.
B. Произведению удельной теплоты сгорания топлива на массу сгоревшего топлива.
13. Что означает выражение: «удельная теплота сгорания бурового угля q = 20 ∙106 »? Это означает, что при полном сгорании…
A. Бурого угля массой 20 кг выделяется 106 Дж энергии.
Б. Бурого угля массой 1 кг выделяется 20 ∙106 Дж энергии.
B. Бурого угля объемом 1 м3 выделяется 20 ∙106 Дж энергии.
Г. Бурого угля массой 20 ∙106 кг выделяется 1 Дж энергии.
14. Какое количество теплоты выделяется при полном сгорании мазута массой 500 г? Удельная теплота сгорания мазута qмазута = 15∙106 .
А. 20∙106 Дж.
Г. 80∙103 Дж.
Б. 80 ∙106 Дж. Д. 12,5∙10-3 Дж.
В. 20∙109 Дж.
15. Кристаллическое вещество отвердевает при температуре…
А. Меньше температуры плавления.
Б. При любой температуре.
В. Больше температуры плавления.
Г. Равной температуре плавления.
Административная работа по физике
8 класс 1 четверть
Вариант 4
1. От чего зависит внутренняя энергия тела?
А. От энергии взаимодействия частиц, из которых состоит тело.
Б. От энергии движения этих частиц.
В. От энергии движения частиц и от энергии их взаимодействия.
Г. От скорости движения тела.
2. При затачивании топор нагревается. Каков способ изменения внутренней энергии топора?
А.
При теплопередаче. Б. При совершении работы.
3. Изменится ли температура тела, если оно испускает энергии больше, чем поглощает?
A. Тело нагреется.
Б. Температура тела не изменится.
B. Тело охладится.
4. Два медных бруска массами 400 и 200 г, взятых при комнатной температуре, охладили до одной и той же температуры. У какого бруска внутренняя энергия изменилась больше?
А. У первого бруска.
Б. У второго бруска.
В. У обоих одинаково.
Г. У обоих не изменилась.
5. Вид теплопередачи, при котором энергия переносится самими частицами вещества, называется…
А. Конвекцией.
Б. Излучением.
В. Теплопроводностью.
6. Какой способ теплопередачи используется при поджа-
ривании яичницы?
А. Излучение.
Б.
Теплопроводность.
В. Конвекция.
7. Какой способ теплопередачи участвует в нагревании
воды солнечными лучами в открытых водоемах?
А. Теплопроводность.
Б. Конвекция.
В. Излучение.
8. Количеством теплоты называют ту часть внутренней энергии, которую…
А. Имеет тело.
Б. Получает тело при совершении над ним работы.
В. Тело получает от другого тела при теплопередаче.
Г. Тело отдает другому телу при теплопередаче.
Д. Тело получает или теряет при теплопередаче.
9. В каких единицах измеряют удельную теплоемкость?
А. Дж Б. Н В..Дж/кг*С Г. Вт.
10. Какое количество теплоты выделится при охлаждении 10 г стали на 8 °С?
А. 40 000 Дж.
Б. 0,16 Дж.
В. 625 Дж.
Г. 40 Дж.
Д. 400 Дж.
11.
Какую массу стали нагрели до температуры 20 °С, если ей сообщили 200 Дж количества теплоты?
А. 0,02 кг.
Б. 50 кг.
В. 2 кг.
Г. 0,5 кг.
Д. 2 000 000 кг.
12. Что означает выражение: «удельная теплота сгорания сосновых дров q = 10 ∙106 »? Это означает, что при полном сгорании…
А. Сосновых дров массой 10 ∙106 кг выделяется 1 Дж энергии.
Б. Сосновых дров массой 10 кг выделяется 106 Дж энергии.
В. Сосновых дров массой 1 кг выделяется 10 ∙106 Дж энергии.
Г. Сосновых дров объемом 1 м3 выделяется 10 ∙106 Дж энергии.
13. Какое количество теплоты выделяется при полном
сгорании 80 г пороха? q пороха = 4∙106 .
А. 0,02 ∙ 10-6 Дж. Г. 320∙106 Дж.
Б. 0,05∙106 Дж. Д. 0,32∙106 Дж.
В. 50∙106 Дж.
14. Какую массу пороха надо сжечь, чтобы получить такое же количество теплоты, как при сжигании 2 кг сосновых дров?
А. 0,2 кг. Б. 5 кг. В. 0,8 кг. Г. 20 кг. Д. 80 кг.
15. Сталь отвердевает при температуре 1500 °С. Что можно сказать о температуре ее плавления?
А. Ниже температуры отвердевания.
Б. Выше температуры отвердевания.
В. Равна 1500 °С.
Г. Может быть любой
Административная работа по физике
8 класс 1 четверть
Вариант 5
1. Каким способом можно изменить внутреннюю энергию тела?
А. Совершением работы и теплопередачей.
Б. Внутреннюю энергию тела изменить нельзя.
В. Только совершением работы.
Г. Только теплопередачей.
2. Кувшин с молоком отнесли в погреб, где оно охладилось. Каким способом изменилась внутренняя энергия молока?
А. При совершении работы. Б. При теплопередаче.
3. Пружину слегка сжали. Что нужно сделать, чтобы увеличить внутреннюю энергию пружины?
А. Сжать пружину сильнее. Б. Отпустить пружину.
4. Одну из двух одинаковых серебряных ложек опустили в стакан с кипятком, а другую в стакан с тёплой водой. В каком случае внутренняя энергия ложки изменится меньше?
А. В обоих случаях не изменится.
Б. И обоим случаях одинаково.
В. В первом случае.
Г. Во втором случае.
5. Излучением называют вид теплопередачи, при котором энергия…
А. Передается от нагретого конца тела холодному, но само вещество при этом не перемещается.
Б. Переносится самими частицами вещества.
В. Передается от нагретого тела с помощью лучей.
6. Какой способ теплопередачи осуществляется при
хранении продуктов в погребе?
А. Конвекция.
Б. Излучение.
В. Теплопроводность.
7. Благодаря какому способу теплопередачи можно
греться у камина?
А. Конвекция.
Б. Излучение.
В. Теплопроводность.
8. Количество теплоты, выделенное при охлаждении
тела, зависит от…
А. Массы тела, его плотности и изменения температуры.
Б. Массы, объема и рода вещества.
В. Рода вещества, его массы и изменения температуры.
Г. Изменения его температуры, плотности и рода вещества.
9. В каких единицах измеряют внутреннюю энергию?
А. Дж Б. А В.Н Г. кг Д. Вт.
10. Удельная теплоемкость графита — 750. Это значит, что для нагревания…
A. Графита массой 750 кг на 1 °С требуется 1 Дж энергии.
Б. Графита массой 1 кг на 750 °С требуется 750 Дж энергии.
B. Графита массой 1 кг на 750 °С требуется 1 Дж энергии.
Г. Графита массой 1 кг на 1 °С требуется 750 Дж энергии.
11. Какое количество теплоты потребуется для нагревания 20 г латуни на 5 °С?
А. 100 Дж.
Б. 40 Дж.
В. 40 000 Дж.
Г. 1600 Дж.
Д. 0,25 Дж.
12. При охлаждении латуни на 50 °С выделилось 200 Дж энергии. Какова масса латуни?
А. 4000 кг. Б. 1 кг. В. 4 000 000 кг. Г. 0,01 кг. Д. 100 кг.
13. Что означает выражение: «удельная теплота сгорания антрацита q = 30 ∙106 »? Это означает, что при полном сгорании.
..
A. Антрацита массой 1 кг выделяется 30 ∙106 Дж энергии.
Б. Антрацита объемом 1 м3 выделяется 30 ∙106 Дж энергии.
B. Антрацита массой 30 ∙106 кг выделяется 1 Дж энергии.
Г. Антрацита массой 30 кг выделяется 106 Дж энергии.
14. Какое количество теплоты выделяется при полном сгорании 180 г нефти? q нефти = 45∙106
А. 4 ∙ 10-6 Дж. Г. 0,25∙109 Дж.
Б. 0,004∙10-6 Дж. Д. 8,1∙109 Дж.
В. 8,1∙106 Дж.
15. В процессе отвердевания тело…
A. Не получает и не отдает энергию.
Б. Получает энергию.
B. Отдает энергию.
Тест на тему «Внутренняя энергия тела»
Вариант 1.
1.Внутренняя энергия тела зависит…
А) От скорости движения тела.
Б) От энергии движения частиц, из которых состоит тело.
В) От энергии взаимодействия частиц, из которых состоит тело.
Г) От энергии движения частиц и от энергии их взаимодействия.
2.Чтобы увеличить внутреннюю энергию автомобильной шины, нужно…
А) Выпустить из шины воздух.
Б) Накачать в шину воздух.
3.В две одинаковые кастрюли налили одинаковое количество воды. В первой кастрюле воду довели до кипения, а во второй слегка подогрели. В каком случае внутренняя энергия воды изменилась меньше?
А) В обоих случаях не изменилась.
Б) В первой кастрюле.
В) Во второй кастрюле.
Г) В обоих случаях одинаково.
4.В каком из перечисленных случаев внутренняя энергия воды не меняется: 1) воду несут в ведре; 2) воду переливают из ведра в чайник; 3) воду нагревают до кипения.
А) 1. Д) 1 и 3.
Б) 2. Е) 2иЗ.
В) 3. Ж) 1, 2, 3.
Г) 1и2.
5.Энергию движения и взаимодействия частиц, из которых состоит тело, называют…
А) Механической энергией.
Б) Кинетической энергией.
В) Потенциальной энергией.
Г) Внутренней энергией.
6. Чем отличаются молекулы горячего чая от молекул этого же чая, когда он остыл?
А)Размером.
Б)Скоростью движения.
В)Числом атомов в них.
Г) Цветом.
7. К тепловым явлениям относится
А) нагревание воды
Б) течение воды
В) равновесие рычага
Г) давление жидкости
Вариант 2.
1.Внутренней энергией тела называют…
А) Энергию движения и взаимодействия частиц, из которых состоит тело.
Б) Энергию движущегося тела.
В) Энергию взаимодействия молекул.
Г) Энергию тела, поднятого над Землей.
Д) Энергию движения молекул.
2. В сосуде находится газ.
Чтобы внутренняя энергия газа уменьшилась, нужно…
А) Сжать газ.
Б) Увеличить объем газа.
3. Одну из двух одинаковых серебряных ложек опустили в стакан с кипятком, а другую в стакан с теплой водой. В каком случае внутренняя энергия ложки изменится меньше?
А) В обоих случаях не изменится.
Б) В обоих случаях одинаково.
В) В первом случае.
Г) Во втором случае.
4. Резиновую нить слегка растянули. Чтобы внутренняя энергия нити увеличилась ее надо…
А) Растянуть сильнее.
Б) Отпустить.
5. В каком из перечисленных случаев внутренняя энергия чашки не изменилась: 1) чашку переставили из шкафа на стол; 2) чашку передвинули по столу; 3) в чашку налили горячий чай.
А) 1,2, 3. Г) 3. Ж) 2 и 3.
Б) 1. Д) 1 и 2.
В) 2. Е) 1 и 3.
6.Внутренняя энергия — это энергия частиц тела. Она состоит из…
А) …кинетической энергии всех молекул.
Б) …потенциальной энергии взаимодействия молекул.
В) …кинетической и потенциальной энергий всех молекул.
7. К тепловым явлениям относится
А) движение по инерции
Б) таяние льда
В) падение камня
Г) давление жидкости
13.3 Закон идеального газа
Цели обученияКроты и число АвогадроЗакон идеального газа с использованием молейГрафическое представление закона идеального газаЗакон идеального газа и энергия
Цели обучения
К концу этого раздела вы сможете делать следующее:
- Изложите закон идеального газа в терминах молекул и молей
- Используйте закон идеального газа для расчета изменения давления, изменения температуры, изменения объема или количества молекул или молей в заданном объеме
- Используйте число Авогадро для преобразования количества молекул в количество молей
Рис. 13.16 Воздух внутри этого воздушного шара, пролетающего над Путраджайей, Малайзия, горячее окружающего воздуха.
В результате воздушный шар испытывает выталкивающую силу, толкающую его вверх. (кредит: Кевин Пох, Flickr)
В этом разделе мы продолжаем исследовать тепловое поведение газов. В частности, мы исследуем характеристики атомов и молекул, из которых состоят газы. Большинство газов, например азот, N2N2, размер 12{N rSub {размер 8{2} } } {}, и кислород, O2O2 размер 12{O rSub {размер 8{2} } } {}, состоят из двух или более атомы. В основном мы будем использовать термин молекула при обсуждении газа, потому что этот термин также может применяться к одноатомным газам, таким как гелий.
Газы легко сжимаются. Доказательства этого можно увидеть в таблице 13.2, где вы заметите, что газы имеют наибольших коэффициентов объемного расширения. Большие коэффициенты означают, что газы очень быстро расширяются и сжимаются при изменении температуры. Кроме того, вы заметите, что большинство газов расширяются с той же скоростью, что и , или имеют одинаковый размер ββ 12{β} {}.
Ответ заключается в большом расстоянии друг от друга атомов и молекул в газах по сравнению с их размерами, как показано на рис. 13.17. Поскольку атомы и молекулы имеют большие расстояния, силами между ними можно пренебречь, за исключением случаев, когда они сталкиваются друг с другом во время столкновений. Движение атомов и молекул — при температурах значительно выше температуры кипения — происходит быстро, так что газ занимает весь доступный объем, а расширение газов происходит быстро. Напротив, в жидкостях и твердых телах атомы и молекулы расположены ближе друг к другу и весьма чувствительны к силам между ними.
Рис. 13.17 Как показано на рисунке, атомы и молекулы в газе обычно находятся далеко друг от друга. Так как силы между ними на этих расстояниях довольно слабы, свойства газа больше зависят от числа атомов в единице объема и от температуры, чем от типа атома.
Чтобы получить некоторое представление о том, как связаны друг с другом давление, температура и объем газа, представьте, что происходит, когда вы накачиваете воздух в изначально спущенную шину. Объем шины сначала увеличивается прямо пропорционально количеству впрыскиваемого воздуха без значительного увеличения давления в шине. Как только шина расширяется почти до своего полного размера, стенки ограничивают объемное расширение. Если мы продолжаем накачивать в него воздух, давление возрастает. Давление будет увеличиваться, когда автомобиль движется и шины двигаются. Большинство производителей указывают оптимальное давление в холодных шинах (см. рис. 13.18).
Рисунок 13.18 (a) Когда воздух нагнетается в спущенную шину, ее объем сначала увеличивается без значительного увеличения давления. (b) Когда шина заполнена до определенной точки, стенки шины сопротивляются дальнейшему расширению, и давление увеличивается с увеличением количества воздуха. (c) Когда шина накачана, ее давление увеличивается с температурой.
При комнатной температуре столкновениями между атомами и молекулами можно пренебречь. В этом случае газ называется идеальным газом, и в этом случае связь между давлением, объемом и температурой определяется уравнением состояния, называемым законом идеального газа.
Закон об идеальном газе
Закон об идеальном газе гласит, что
13.18 PV=NkT,PV=NkT, размер 12{ ital «PV»= ital «NkT»} {}
, где PP размер 12{P} {} — абсолютное давление газа, размер VV 12{V} {} — объем, который он занимает, размер NN 12{N} {} — число атомов и молекул в газе, размер TT 12{T} {} это его абсолютная температура. Константа kk размером 12{k} {} называется постоянной Больцмана в честь австрийского физика Людвига Больцмана (1844–1906) и имеет значение
13,19 k=1,38×10-23 Дж/К.k=1,38×10-23 Дж/К. размер 12{k=1 «.» «38» умножить на «10» rSup { size 8{ — «23»} } » J»/K} {}
Закон идеального газа можно вывести из основных принципов, но первоначально он был выведен из экспериментальных измерений закона Шарля — объем, занимаемый газом, пропорционален температуре при фиксированном давлении — и из закона Бойля — что при фиксированной температуре произведение PVPV size 12{ ital «PV»} {} является константой.
В модели идеального газа объем, занимаемый его атомами и молекулами, составляет пренебрежимо малую долю размера VV 12{V} {}. Закон идеального газа описывает поведение реальных газов в большинстве условий. Обратите внимание, например, что размер NN 12{N} {} представляет собой общее количество атомов и молекул, не зависящее от типа газа.
Давайте посмотрим, как закон идеального газа согласуется с поведением заполнения шины при медленном накачивании и постоянной температуре. Сначала давление ПП размером 12{P} {} практически равно атмосферному давлению, а объем ВВ размером 12{V} {} увеличивается прямо пропорционально количеству атомов и молекул NN размера 12{N} {} положить в шину. Поскольку объем шины постоянен, уравнение PV=NkTPV=NkT size 12{ ital «PV»= ital «NkT»} {} предсказывает, что давление должно увеличиваться пропорционально число N атомов и молекул .
Пример 13.6 Расчет изменений давления в связи с изменениями температуры: Давление в шинах
Предположим, шина вашего велосипеда полностью накачана, а абсолютное давление составляет 7 × 105 Па7 × 105 Па.
— манометрическое давление чуть менее 90 фунтов/дюйм290 фунтов/дюйм2
— при температуре 18 ºC.18 ºC.
Каково давление после того, как его температура поднялась до 35ºC35ºC размера 12{«35» «.» 0°C} {}? Предположим, что нет заметных утечек или изменений объема.
Стратегия
Давление в шине меняется только из-за изменения температуры. Во-первых, нам нужно определить, что мы знаем и что мы хотим узнать, а затем определить уравнение, которое нужно решить для неизвестного.
Известно начальное давление P0=7×105 Па P0=7×105 Па, начальная температура
T0=18 ºCT0=18 ºC, а конечная температура
Tf=35 ºCTf=35 ºC. Мы должны найти конечное давление
ПфПф. Как мы можем использовать уравнение
PV=NkTPV=NkT? Поначалу может показаться, что дано недостаточно информации, ведь объем
VV и число атомов
NN не указаны. Что мы можем сделать, так это использовать уравнение дважды:
P0V0=NkT0P0V0=NkT0 и
PfVf=NkTfPfVf=NkTf. Если мы разделим
PfVfPfVf от
P0V0P0V0, мы можем составить уравнение, которое позволит нам найти
ПфПф.
13.20 PfVfP0V0=NfkTfN0kT0PfVfP0V0=NfkTfN0kT0
Поскольку громкость постоянна, VfVf size 12{V rSub { size 8{f} } } } {} and V0V0 size 12{V rSub { size 8{0} } } {} являются то же самое, и они отменяются. То же самое верно для NfNf размера 12{N rSub { size 8{f} } } {} и N0N0 размера 12{N rSub { size 8{0} } } {} и kk размера 12{k} {}, которые является константой. Следовательно,
13,21 PfP0=TfT0.PfP0=TfT0. размер 12{ { {P rSub { размер 8{f} } } над {P rSub { размер 8{0} } } } = {{T rSub { размер 8{f} } } над {T rSub { размер 8{0 } } } } «.» } {}
Затем мы можем изменить это, чтобы найти PfPf size 12{P rSub { size 8{f} } } {}
13.22 Pf=P0TfT0,Pf=P0TfT0, размер 12{P rSub { размер 8{f} } =P rSub { размер 8{0} } { {T rSub { размер 8{f} } } над {T rSub { размер 8{ 0} } } } ,} {}
, где температура должна быть выражена в кельвинах, поскольку размер T0T0 12{T rSub { размер 8{0} } } {} и размер TfTf 12{T rSub { размер 8{f } } } {} — абсолютные температуры.
Решение
1. Преобразование температуры из градусов Цельсия в градусы Кельвина.
13.23 T0=18,0+273 K=291 KTf=35,0+273 K=308 KT0=18,0+273 K=291 KTf=35,0+273 K=308 Kalignl { stack { size 12{T rSub { size 8{0} } = left («18» «.» 0+»273″ right )» K»=»291 K»} {} # T rSub {размер 8{f}} = левый («35» «.» 0+»273″ правый)» K»=»308 K» {} } } {}
2. Подставьте известные значения в уравнение.
13,24 Pf=P0TfT0=7,00×105 Па308 K291 K=7,41×105PaPf=P0TfT0=7,00×105 Па308 K291 K=7,41×105 Па размер 12{P rSub { размер 8{f} } =P rSub { размер 8{ 0 } } {{T rSub { размер 8{f} } } над {T rSub { размер 8{0} } } } =7 «.» «00» умножить на «10» rSup { размер 8{5} } «Pa» осталось ( { {«308 K»} более {«291 K»} } right )=7 «.» «41» умножить на «10» rSup {размер 8{5} } `»Pa»} {}
Обсуждение
Конечная температура примерно на 6 процентов выше исходной температуры, поэтому конечное давление также примерно на 6 процентов выше.
Обратите внимание, что в законе идеального газа должны использоваться абсолютное давление и абсолютная температура.
Установление связей: домашний эксперимент — охлаждение воздушного шара
Надуть воздушный шар при комнатной температуре. Оставьте надутый шарик в холодильнике на ночь. Что происходит с воздушным шаром и почему?
Пример 13.7 Расчет количества молекул в кубическом метре газа
Сколько молекул содержится в обычном объекте, таком как газ в шине или вода в напитке? Мы можем использовать закон идеального газа, чтобы дать нам представление о том, насколько велик обычно размер NN 12{N} {}.
Рассчитайте количество молекул в кубическом метре газа при стандартной температуре и давлении (STP), которое определяется как 0ºC0ºC, размер 12{0°C} {} и атмосферное давление.
Стратегия
Поскольку давление, объем и температура заданы, мы можем использовать закон идеального газа PV=NkTPV=NkT size 12{ ital «PV»= ital «NkT»} {}, чтобы найти NN size 12{N} { }.
Решение
1. Определите известные.
13,25 T=0ºC=273 KP=1,01×105 ПаВ=1,00 м3k=1,38×10−23 Дж/KT=0°C=273 KP=1,01×105 ПаВ=1,00 м3k=1,38×10−23 Дж/K
2. Определите неизвестное: количество молекул, размер NN 12{N} {}.
3. Измените закон идеального газа, чтобы найти решение для размера NN 12{N} {}.
13.26 PV=NkTN=PVkTPV=NkTN=PVkTalignl {стек { размер 12{ ital «PV»= ital «NkT»} {} # размер 12{N= {{ ital «PV»} over { ital «kT»} } } {} } } {}
4. Подставьте известные значения в уравнение и найдите размер NN 12{N} {}.
13,27 N=PVkT=1,01×105 Па1,00 м31,38×10−23 Дж/K273 K=2,68×1025 молекул N=PVkT=1,01×105 Па1,00 м31,38×10−23 Дж/K273 K=2,68 ×1025молекул размером 12{N= {{ ital «PV»} over { ital «kT»} } = {{ left (1 «.» «01» times «10» rSup { size 8{5} } «Pa» right ) слева (1 «.» «00 м» rSup { размер 8 {3} } справа )} над { слева (1 «.» «38» умножить на «10» rSup { размер 8 { — «23»} } » J /K» вправо ) влево («273 K» вправо )} } =2 «.
» «68» умножить на «10» rSup { size 8{«25″} } `»молекулы»} {}
Обсуждение
Это число, несомненно, велико, учитывая, что газ в основном представляет собой пустое пространство. Размер NN 12{N}{} огромен даже в небольших объемах. Например, 1 см31 см3 размером 12{1″ см» rSup {размер 8{3} } } {} газа при СТП имеет размер 2,68×10192,68×1019 размер 12{2 «.» «68»´»10″ rSup {размер 8{«19»} } } {} молекул в нем. Еще раз отметим, что размер NN 12{N} {} одинаков для всех типов или смесей газов.
Моль и число Авогадро
Иногда при измерении количества вещества удобно работать с единицей, отличной от молекулы. Моль (моль) определяется как количество вещества, которое содержит столько атомов или молекул, сколько атомов содержится ровно в 12 граммах (0,012 кг) углерода-12. Фактическое число атомов или молекул в одном моле называется числом Авогадро (NA) (NA) size 12 { \( N rSub { size 8 {A} } \) } {}, по признанию итальянского ученого Амедео Авогадро (1776–1776 гг.
). 1856 г.). Он разработал концепцию моля, основанную на гипотезе о том, что равные объемы газа при одинаковых давлении и температуре содержат одинаковое количество молекул. То есть число не зависит от типа газа. Эта гипотеза подтвердилась, и значение числа Авогадро равно 9.0003
13,28 NA=6,02×1023моль-1.NA=6,02×1023моль-1. размер 12 {N rSub { размер 8 {A}} = 6 «.» «02» умножить на «10» rSup {размер 8{«23″} } `»mol» rSup {размер 8{- 1} } «.» } {}
Число Авогадро
Один моль всегда содержит 6,02×10236,02×1023 размера 12{6 «.» «02»´»10″ rSup { размер 8{«23»} } } {} частицы — атомы или молекулы — независимо от элемента или вещества. Моль любого вещества имеет массу в граммах, равную его молекулярной массе, которую можно рассчитать по атомным массам, приведенным в периодической таблице элементов.
13,29 NA=6,02×1023моль-1NA=6,02×1023моль-1 размер 12{N rSub { размер 8{A}} =6 «.» «02» умножить на «10» rSup {размер 8{«23″} } `»mol» rSup {размер 8{- 1} } } {}
Рис.
13.19 Насколько велика родинка? На макроскопическом уровне один моль шариков для настольного тенниса покроет Землю на глубину около 40 км.
Проверьте свое понимание
Активным ингредиентом в таблетке тайленола является 325 мг ацетаминофена (C8H9NO2)(C8H9NO2) размер 12{ \( C rSub { размер 8{8} } H rSub { размер 8{9} } «НЕТ » rSub { размер 8 {2} } \) } {}. Найдите количество активных молекул ацетаминофена в одной таблетке.
Решение
Сначала нам нужно рассчитать молярную массу — массу одного моля — ацетаминофена. Для этого нам нужно умножить количество атомов каждого элемента на атомную массу элемента.
13,30 (8 моль углерода)(12 грамм/моль)+(9 моль водорода)(1 грамм/моль)+(1 моль азота)(14 грамм/моль)+(2 моль кислорода)(16 грамм/моль) )= 151 г (8 моль углерода) (12 грамм/моль) + (9 моль водорода) (1 грамм/моль) + (1 моль азота) (14 грамм/моль) + (2 моль кислорода) (16 грамм/моль) моль) = 151 г
Затем нам нужно рассчитать количество молей в 325 мг.
13,31 325 мг151 грамм/моль1 грамм1000 мг=2,15×10-3 моля325 мг151 грамм/моль1 грамм1000 мг=2,15×10-3моля
Затем используйте число Авогадро для расчета количества молекул.
13,32 N=2,15×10-3моль6,02×1023молекул/моль=1,30×1021молекулN=2,15×10-3моль6,02×1023молекул/моль=1,30×1021молекул размер 12{N= слева (2 «.» «15» умножить на «10» rSup { размер 8{ — 3} } `»моли» справа ) слева (6 «.» «02» умножить на «10» rSup { размер 8{«23″} } `»молекул/моль» справа ) =1 «.» «30» умножить на «10» rSup { size 8{«21″} } `»молекулы»} {}
Пример 13.8 Расчет молей на кубический метр и литров на моль
Рассчитайте: (a) количество молей в 1,00 м31,00 м3 размером 12{1 «.» «00»» m» rSup {размер 8{3} } } {} газа при нормальных условиях и (b) количество литров газа на моль.
Стратегия и решение
(а) Нас просят найти число молей на кубический метр, и мы знаем из примера 13.7, что число молекул на кубический метр при СТП равно 2,68×10252,68×1025 размера 12{2″».
«68»´»10″ rSup {размер 8{«25»} } } {}. Количество молей можно найти, разделив количество молекул на число Авогадро. Пусть nn size 12{n} {} обозначает количество родинок:
13,33 нмоль/м3=Nмолекул/м36,02×1023молекул/моль=2,68×1025молекул/м36,02×1023молекул/моль=44,5моль/м3.нмоль/м3=Nмолекул/м36,02×1023молекул/моль=2,68× 1025 молекул/м36,02×1023 молекул/моль=44,5моль/м3. размер 12{n`»моль/м» rSup { размер 8{3} } = {{N`»молекул/м» rSup { размер 8{3} } } свыше {6 «.» «02» умножить на «10» rSup {размер 8{«23″} } `»молекул/моль»} } = {{2 «.» «68» умножить на «10» rSup {размер 8{«25″} } `»молекул/м» rSup {размер 8{3} } } более {6 «.» «02» умножить на «10» rSup {размер 8{«23″} } `»молекул/моль»} } =»44″ «.» 5`»моль/м» rSup { размер 8{3} } «.» } {}
(б) Используя полученное значение числа молей в кубическом метре и переведя кубические метры в литры, мы получим
13,34 103л/м344,5моль/м3=22,5л/моль.103л/м344,5моль/ m3=22,5 л/моль. размер 12{ { { левый («10″ rSup { размер 8{3} } `»L/m» rSup { размер 8{3} } правый )} более {44 «.
» 5`»моль/м» rSup {размер 8{3} } } } =»22″ «.» 5`»л/моль» «.» } {}
Обсуждение
Это значение очень близко к принятому значению 22,4 л/моль. Небольшая разница возникает из-за ошибок округления, вызванных использованием трехзначного ввода. Опять же, это число одинаково для всех газов. Другими словами, он не зависит от газа.
Средняя молярная масса воздуха — примерно 80% N2N2 размер 12{N rSub { размер 8{2} } } {} и 20% O2O2 размер 12{O rSub { размер 8{2} } } {} — это M =28,8 г.М=28,8 г. размер 12{М=»28″ «.» 8″ г» «.» } {} Таким образом, масса одного кубического метра воздуха равна 1,28 кг. Если жилое помещение имеет размеры 5 м × 5 м × 3 м, 5 м × 5 м × 3 м, размер 12{5″ м» умножить на «5 м» умножить на «3 м»} {} масса воздуха внутри комната 96 кг, что является типичной массой человека.
Проверьте свои знания
Плотность воздуха при стандартных условиях (P=1 атм(P=1атм размер 12{ \( P=1″ атм»} {} и T=20ºC)T=20ºC) размер 12{T=» 20″°C \) } {} составляет 1,28 кг/м31,28 кг/м3 размер 12{1 «.
» «28» «кг/м» rSup {размер 8{3} } } {}. При каком давлении плотность 0,64 кг/м30,64 кг/м3 размер 12{0 «.» «64 кг/м» rSup {размер 8{3} } } {}, если температура и число молекул остаются постоянными?
Решение
Лучший способ ответить на этот вопрос — подумать о том, что происходит. Если плотность падает вдвое по сравнению с исходным значением и ни одна молекула не теряется, то объем должен удвоиться. Если мы посмотрим на уравнение PV=NkTPV=NkT size 12{ ital «PV»= ital «NkT»} {}, мы увидим, что при постоянной температуре давление обратно пропорционально объему. Следовательно, если объем удвоится, давление должно упасть вдвое по сравнению с первоначальным значением, и Pf=0,50 атм. Pf=0,50 атм. размер 12{P rSub { размер 8{f}} =0 «.» «50» «атм» «.» } {}
Закон об идеальном газе, переформулированный с использованием молей
В очень распространенном выражении закона об идеальном газе используется число молей, размер nn 12{n} {}, а не число атомов и молекул, размер NN 12{N} {}.
Начнем с закона идеального газа
13,35 PV=NkT,PV=NkT, размер 12{ итал. «PV»= итал. «NkT»} {}
, умножьте и разделите уравнение на число Авогадро NANA size 12{N rSub { size 8{A} } } {}. Это дает
13,36 PV=NNANAkT.PV=NNANAkT. size 12{ ital «PV»= { {N} over {N rSub { size 8{A} } } } N rSub { size 8{A} } ital «kT» «.» } {}
Обратите внимание, что n=N/NAn=N/NA size 12{n=N/N rSub { size 8{A} } } {} – это число молей. Определим универсальную газовую постоянную R=NAkR=NAk size 12{R=N rSub {size 8{A} } k} {} и получим закон идеального газа в терминах молей.
Закон идеального газа в молях
Закон идеального газа в молях:
13,37 PV=nRT.PV=nRT. размер 12{ ital «PV»= ital «nRT»} {}
Числовое значение RR размера 12{R} {} в единицах СИ составляет
13,38 R=NAk=6,02×1023моль−11,38×10−23Дж/ K=8,31 Дж/моль⋅K.R=NAk=6,02×1023моль−11,38×10−23 Дж/K=8,31 Дж/моль⋅K. размер 12{R=N rSub { размер 8{A} } k= левый (6 «.
» «02» умножить на «10» rSup { размер 8 {«23″} } `»моль» rSup { размер 8{- 1 } } справа ) слева (1 «.» «38» умножить на «10» rSup { size 8{ — «23»} } `»J/K» справа )=8 «.» «31» Дж/»моль» cdot K} {}
В других единицах
13,39 R=1,99 кал/моль⋅KR=0,0821 л⋅атм/моль⋅K.R=1,99 кал/моль⋅KR=0,0821 л⋅атм/моль⋅K.alignl { stack { размер 12{R=1 «.» «99»» кал/моль» cdot K} {} # размер 12{R»=0″ «.» «0821 л» cdot «атм/моль» cdot K «.» } {} } } {}
Вы можете использовать любое значение размера RR 12{R} {}, наиболее удобное для конкретной задачи.
Пример 13.9 Расчет количества молей: газ в велосипедной шине
Сколько молей газа содержится в велосипедной шине объемом 2×10–3 м3 (2,00 л), 2×10–3 м3 (2,00 л), размер 12{2 «.» «00»´»10″ rSup { размер 8{ +- 3} } «m» rSup { размер 8{3} } \( 2 «.» «00 L» \) ,} {} давление 7×105 Па7 ×105Па размер 12{7 «.» «00»´»10″ rSup {размер 8{5} } «Па»} {} — манометрическое давление чуть меньше 90 фунтов/дюйм290 фунтов/дюйм2 размер 12{«90» «.
» 0″ фунт/дюйм» rSup { размер 8{2} } } {} — и при температуре 18ºC18ºC размер 12{«18» «.» 0°C} {}?
Стратегия
Определите известные и неизвестные и выберите уравнение для решения неизвестного. В этом случае мы решаем закон идеального газа, PV=nRTPV=nRT size 12{ ital «PV»= ital «nRT»} {}, для числа молей nn size 12{n} {}.
Решение
1. Определите известные.
13,40 P=7×105ПаВ=2×10−3м3T=18,0ºC=291 KR=8,31Дж/моль⋅KP=7×105ПаВ=2×10−3м3T=18,0ºC=291 KR=8,31Дж/моль⋅Kalignl { куча { размер 12{P=7 «.» «00» умножить на «10» rSup {размер 8{5} } «Pa»} {} # V=2 «.» «00» умножить на «10» rSup { размер 8{ — 3} } «m» rSup { размер 8{3} } {} # Т=»18″ «.» 0°C=»291 К» {} # R=8 «.» «31» «Дж/моль» cdot K {} } } {}
2. Измените уравнение, чтобы решить его для размера nn 12{n} {}, и подставьте известные значения.
13,41 n=PVRT=7×105Па2×10-3м38,31Дж/моль⋅K291 K= 0,579мольн=PVRT=7×105Па2×10-3м38,31Дж/моль⋅K291 K = 0,579molalignl {стек {
size 12{n= {{ ital «PV»} over { ital «RT»} } = { {left (7 «.
» «00» умножить на «10» rSup { size 8{5} } `»Pa» right ) слева (2 «.» 00 раз «10» rSup { размер 8 { — 3} } `m rSup { размер 8 {3} } справа )} над { слева (8 «.» «31»`»Дж/моль» cdot K справа ) слева («291″» K» справа )} } } {} #
» «=» 0″ «.» «579»`»моль» {}
} } {}
Обсуждение
Наиболее удобный выбор для RR размера 12{R} {} в данном случае 8,31 Дж/моль⋅K, 8,31 Дж/моль⋅K, размер 12{8 «.» «31»» Дж/моль» cdot «K,»} {} потому что наши известные величины указаны в единицах СИ. Давление и температура получены из начальных условий в примере 13.6, но мы получили бы тот же ответ, если бы использовали окончательные значения.
Закон идеального газа можно рассматривать как еще одно проявление закона сохранения энергии [см. Закон сохранения энергии]. Работа, совершаемая над газом, приводит к увеличению его энергии, увеличению давления и/или температуры или уменьшению объема. Это увеличение энергии также можно рассматривать как увеличение внутренней кинетической энергии, учитывая атомы и молекулы газа.
Графическое представление закона идеального газа
Закон идеального газа может быть выражен как PV=NkTPV=NkT, где N — число атомов или молекул, а k — постоянная Больцмана, или как PV=nRTPV=nRT, где n — число молей, а R — универсальная газовая постоянная. Считая количество газа постоянным, можно зафиксировать один из трех оставшихся параметров ( P, V, T ), а между двумя другими установить связь:
Константа P : V=(const.)TV=(const.)T, где константа равна NkP=nRPNkP=nRP
Константа V : P=(const.)TP=(const.)T, где константа равна NkV=nRVNkV=nRV
Константа T : P=(const.)VP=(const.)V, где константа равна NkT=nRTNkT=nRT
Можно разработать эксперименты, чтобы проверить справедливость этих соотношений для реальных газов.
Например, для проверки первого соотношения можно использовать контейнер с поршнем, который позволяет давлению оставаться постоянным, в то время как объем изменяется в ответ на изменения температуры. Если график зависимости объема от температуры линейный, газ ведет себя как идеальный газ. Количество газа можно либо определить по наклону, либо, если количество газа известно, можно использовать как вторичное подтверждение поведения идеального газа. На рис. 13.20 давление одного моля газа зафиксировано на уровне 10 5 Па при изменении температуры и измерении давления. Очевиден небольшой экспериментальный разброс, поэтому выполняется линейная подгонка. Линия регрессии имеет наклон 8,36×10-58,36×10-5, что очень близко к ожидаемому значению nRP=(1)(8,31)(105)=8,31×10-5nRP=(1)(8,31)(105). )=8,31×10−5. Можно было бы заключить, что этот газ ведет себя очень похоже на идеальный газ.
Рис. 13.20 График температура-давление газа, который ведет себя как идеальный газ.
Аналогичным образом можно проводить испытания при постоянном объеме или давлении.
График зависимости давления от температуры показывает линейную зависимость при постоянном объеме. График зависимости давления от объема показывает обратную зависимость, когда температура поддерживается постоянной.
Закон идеального газа и энергия
Теперь рассмотрим роль энергии в поведении газов. Когда вы накачиваете велосипедную шину вручную, вы постоянно прилагаете усилие на расстоянии. Эта энергия идет на повышение давления воздуха внутри шины и повышение температуры насоса и воздуха.
Закон об идеальном газе тесно связан с энергией: единицы измерения с обеих сторон — джоули. Правая часть закона идеального газа в PV=NkTPV=NkT size 12{ ital «PV»= ital «NkT»} {} равна NkTNkT size 12{ ital «NkT»} {}. Этот член приблизительно представляет собой количество поступательной кинетической энергии атомов или молекул NN размером 12{N} {} при абсолютной температуре TT размером 12{T} {}, как мы формально увидим в кинетической теории: атомное и молекулярное объяснение давления.
и температура. Левая часть закона идеального газа представляет собой размер PVPV 12 { ital «PV»} {}, который также имеет единицы измерения в джоулях. Из нашего исследования жидкостей мы знаем, что давление — это один из видов потенциальной энергии на единицу объема, поэтому давление, умноженное на объем, — это энергия. Важным моментом является то, что в газе есть энергия, связанная как с его давлением, так и с его объемом. Энергия может изменяться, когда газ совершает работу по мере расширения — это мы исследуем в разделе «Методы теплопередачи» — аналогично тому, что происходит в бензиновых или паровых двигателях и турбинах.
Стратегия решения проблем: Закон об идеальном газе
Шаг 1 Изучите ситуацию, чтобы определить, что речь идет об идеальном газе. Большинство газов почти идеальны.
Шаг 2 Составьте список величин, которые даны или могут быть выведены из поставленной задачи — определите известные величины. Преобразуйте известные значения в правильные единицы СИ: K для температуры, Па для давления, м3м3 размера 12{m rSup {размер 8{3} } } {} для объема, молекулы для размера NN 12{N} {} и моли для nn размер 12 {n} {}.
Шаг 3 Точно определите, что нужно определить в задаче — определите неизвестные величины. Письменный список полезен.
Шаг 4 Определите, известно ли количество молекул или число молей, чтобы решить, какую форму закона идеального газа использовать. Первая форма PV=NkTPV=NkT size 12{ ital «PV»= ital «NkT»} {} и включает NN size 12{N} {}, количество атомов или молекул. Вторая форма — PV=nRTPV=nRT size 12{ ital «PV»= ital «nRT»} {} и включает nn size 12{n} {}, количество молей.
Шаг 5 Решите закон идеального газа для определяемой величины (неизвестной величины). Возможно, вам придется взять отношение конечных состояний к начальным состояниям, чтобы исключить неизвестные величины, которые остаются фиксированными.
Шаг 6 Подставьте известные величины вместе с их единицами измерения в соответствующее уравнение и получите численное решение с единицами измерения. Обязательно используйте абсолютную температуру и абсолютное давление.
Шаг 7 Проверьте ответ, чтобы убедиться, что он разумен: Имеет ли он смысл?
Проверьте свое понимание
Плотность жидкостей и твердых тел примерно в 1000 раз больше плотности газов. Объясните, как это означает, что расстояния между атомами и молекулами в газах примерно в 10 раз больше, чем размер их атомов и молекул.
Решение
Атомы и молекулы находятся близко друг к другу в твердых и жидких телах. В газах они разделены пустым пространством. Таким образом, газы имеют более низкую плотность, чем жидкости и твердые тела. Плотность — это масса на единицу объема, а объем связан с размером тела, такого как сфера, в кубе. Так, если расстояние между атомами и молекулами увеличивается в 10 раз, то занимаемый объем увеличивается в 1000 раз, а плотность уменьшается в 1000 раз.
- Печать
- Поделиться
Ч.
12 Концептуальных элементов — ФизикаЭлементы концепции
12.1 Нулевой закон термодинамики: тепловое равновесие
1.
Когда два тела находятся в тепловом равновесии?
- Когда они находятся в тепловом контакте и находятся под разным давлением
- Когда они не находятся в тепловом контакте, но находятся под одинаковым давлением
- Когда они не находятся в тепловом контакте, но имеют разные температуры
- Когда они находятся в тепловом контакте и имеют одинаковую температуру
2.
Что такое термоконтакт?
- Говорят, что два объекта находятся в тепловом контакте, когда они соприкасаются друг с другом таким образом, что между ними может происходить передача энергии посредством тепла.
- Говорят, что два объекта находятся в тепловом контакте, когда они соприкасаются друг с другом таким образом, что между ними может происходить передача энергии массой.
- Говорят, что два объекта находятся в тепловом контакте, если они не теряют и не приобретают энергию за счет тепла. Между ними нет передачи энергии.
- Говорят, что два объекта находятся в тепловом контакте, если они получают энергию только за счет тепла. Между ними происходит передача энергии.
3.
Какому математическому свойству подобен нулевой закон термодинамики?
- Ассоциативное имущество
- Коммунальное имущество
- Распределительное имущество
- Переходное свойство
12.2 Первый закон термодинамики: тепловая энергия и работа
4.
Почему происходит тепловое расширение?
Повышение температуры вызывает увеличение межмолекулярных расстояний.
Повышение температуры вызывает уменьшение межмолекулярных расстояний.
Повышение температуры вызывает увеличение работы системы.
Повышение температуры вызывает увеличение работы, совершаемой системой.
5.
Как работа давления-объема связана с теплотой и внутренней энергией системы?
- Энергия, сообщаемая системе за счет тепла, за вычетом изменения внутренней энергии этой системы равна работе давление-объем, совершаемой система.
- Сумма энергии, выделяемой системой за счет тепла, и изменения внутренней энергии этой системы равна работе давление-объем, совершаемой
система.
- Произведение энергии, сообщенной системе теплом, и изменение внутренней энергии этой системы равно произведенной работе давление-объем. системой.
- Если энергию, присоединенную к системе за счет тепла, разделить на изменение внутренней энергии этой системы, то частное равно отношению давления к объему. работу, совершаемую системой.
6.
От чего зависит внутренняя энергия?
- Путь изменения энергии в системе
- Состояние системы
- Размер системы
- Форма системы
7.
Первый закон термодинамики помогает нам понять отношения между какими тремя величинами?
- Теплота, работа и внутренняя энергия
- Теплота, работа и внешняя энергия
- Теплота, работа и энтальпия
- Теплота, работа и энтропия
12.3 Второй закон термодинамики: энтропия
8.
Освежитель воздуха распыляется из бутылки. Молекулы распространяются по комнате и не могут вернуться в бутылку. Почему это так?
- Энтропия молекул увеличивается.
- Энтропия молекул уменьшается.
- Содержание тепла ( энтальпия , или полная энергия, доступная для нагревания) молекул увеличивается.
- Содержание тепла ( энтальпия , или полная энергия, доступная для нагревания) молекул уменьшается.
9.
Приведите пример энтропии в повседневной жизни.
- вращение Земли
- формирование солнечного затмения
- наполнение автомобильной шины воздухом
- движение маятника
12,4 Приложения термодинамики: тепловые двигатели, тепловые насосы и холодильники.
10.
По какому качеству оцениваются кондиционеры?
- Количество энергии, генерируемой за счет тепла из горячей среды, по сравнению с требуемой подводимой работой
- Количество энергии, переданной теплом из холодной среды, по сравнению с требуемой работой
- Количество энергии, переданной теплом от горячей среды, по сравнению с требуемой мощностью работы
- Количество энергии, переданной теплом из холодной среды, по сравнению с требуемой мощностью работы
11.