Формула эдс аккумулятора
В электрической или электронной схеме есть два типа элементов: пассивные и активные. Активный элемент способен непрерывно подавать энергию в цепь — аккумулятор, генератор. Пассивные элементы — резисторы, конденсаторы, катушки индуктивности, только потребляют энергию. Источник тока — это устройство, непрерывно питающее цепь электроэнергией.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Формула ЭДС
- Методические указания по решению задач, модуль 5
- Внутреннее сопротивление
- Формула ЭДС
- Электродвижущая сила аккумулятора — ЭДС.
Эдс батареи
- Электрический аккумулятор
- ЭДС аккумулятора
- Закон Ома для полной цепи
- Аккумуляторные батареи — Электрические характеристики аккумуляторных батарей
- КПД источника тока
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: ФИЗИКА закон Ома для полной цепи и ЭДС
Формула ЭДС
Для поддержания электрического тока в проводнике длительное время, необходимо чтобы от конца проводника, имеющего меньший потенциал учтем, что носители тока предполагаются положительными зарядами постоянно убирались доставляемые током заряды, при этом к концу с большим потенциалом заряды постоянно подводились.
Такие силы именуются сторонними. Получается, что для поддержания тока нужны сторонние силы, которые действуют на всем протяжении цепи или на отдельных участках цепи.
Скалярная физическая величина, которая равна работе сторонних сил по перемещению единичного положительного заряда, называется электродвижущей силой ЭДС , действующей в цепи или на участке цепи. ЭДС обозначается. Математически определение ЭДС запишем как:.
Электродвижущая сила источника численно равна разности потенциалов на концах элемента, если он разомкнут, что дает возможность измерить ЭДС по напряжению. ЭДС, которая действует в замкнутой цепи, может бытьопределена как циркуляция вектора напряжённости сторонних сил:. Если напряженность поля сторонних сил не равна нулю только в части цепи, например, на отрезке , тогда интегрирование в выражении 2 можно вести только по данному участку.
Соответственно, ЭДС, действующая на участке цепи определяется как:. Участок цепи, на котором действуют сторонние силы, называют неоднородным. Для него выполняется равенство:. Следует учитывать, что ЭДС может быть положительной и отрицательной. ЭДС называют положительной, если она увеличивает потенциал в направлении тока ток течет от минуса к плюсу источника.
Размерность ЭДС совпадает с размерностью потенциала. Электродвижущая сила элемента равна 10 В. Он создает в цепи силу тока равную 0,4 А. Какова работа, которую совершают сторонние силы за 1 мин? В качество основы для решения задачи используем формулу для вычисления ЭДС:. Металлический диск, имеющий радиус a, вращается с угловой скоростью , включен в электрическую цепь при помощи скользящих контактов, которые касаются оси диска и его окружности рис.
Какой будет ЭДС, которая появится между осью диска и его наружным краем? В условиях, которые описаны в задаче, на каждый электрон проводника действует центробежная сила F которая является сторонней. Вследствие ее действия, в диске возникает ЭДС и между осью диска и его наружным краем появляется напряжение.
Вследствие ее действия, в диске возникает ЭДС и между осью диска и его наружным краем появляется напряжение.
Формулу для вычисления центробежной силы запишем как:. Fдействует на заряженную частицу электрон , следовательноучитывая 2. Читать дальше: Формулы по физике. Копирование материалов с сайта возможно только с разрешения администрации портала и при наличие активной ссылки на источник.
Образовательные онлайн-сервисы Меню. Решение задач онлайн. Отправить задания. Главная Справочник Формулы по физике Формула ЭДС Для поддержания электрического тока в проводнике длительное время, необходимо чтобы от конца проводника, имеющего меньший потенциал учтем, что носители тока предполагаются положительными зарядами постоянно убирались доставляемые током заряды, при этом к концу с большим потенциалом заряды постоянно подводились.
Определение и формула ЭДС Определение Скалярная физическая величина, которая равна работе сторонних сил по перемещению единичного положительного заряда, называется электродвижущей силой ЭДС , действующей в цепи или на участке цепи.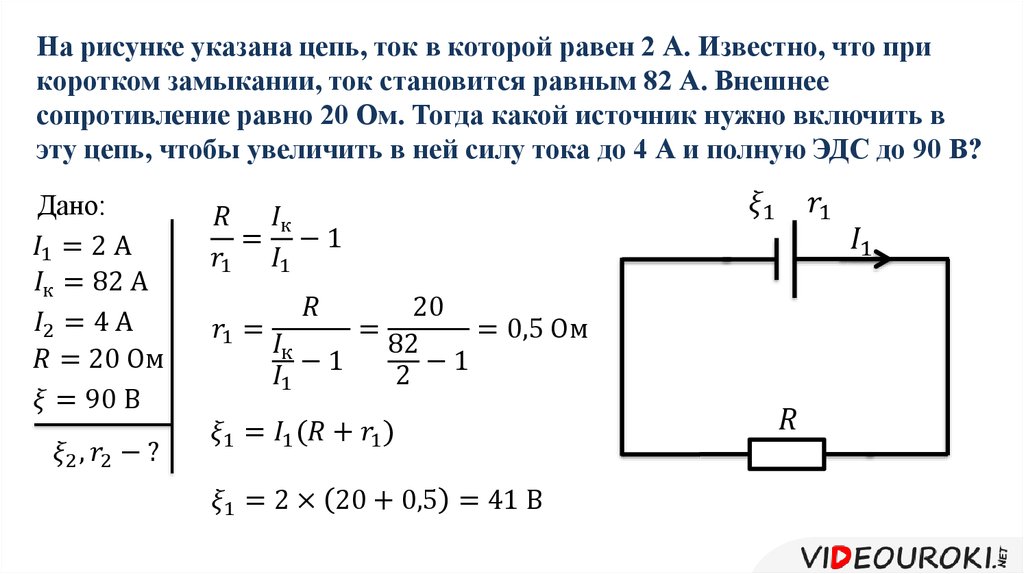 Математически определение ЭДС запишем как: где A — работа сторонних сил, q — заряд, над которым производится работа.
Математически определение ЭДС запишем как: где A — работа сторонних сил, q — заряд, над которым производится работа.
Пример Задание. В качество основы для решения задачи используем формулу для вычисления ЭДС: Заряд, который проходит в рассматриваемой цепи за 1 мин. Формулу для вычисления центробежной силы запишем как: где m — масса электрона, r — расстояние от оси диска. В соответствии с формулой, определяющей ЭДС участка цепи, получаем: Ответ. Вы поняли, как решать? Помощь с решением. Рассчитайте цену решения ваших задач. Узнать точную цену.
Сервисы Онлайн калькуляторы Справочник Примеры решений Образовательный форум. Услуги Контрольные на заказ Курсовые на заказ Дипломы на заказ Рефераты на заказ. Webmath О проекте Новости Контакты Политика конфиденциальности.
Методические указания по решению задач, модуль 5
Основные характеристики аккумуляторов и аккумуляторных батарей. ЭДС аккумулятора представляет собой разность электродных потенциалов, измеренную при разомкнутой внешней цепи.
ЭДС аккумулятора это разность электродных потенциалов при Эта формула истинна при рабочей плотности электролита в.
Внутреннее сопротивление
Для поддержания электрического тока в проводнике длительное время, необходимо чтобы от конца проводника, имеющего меньший потенциал учтем, что носители тока предполагаются положительными зарядами постоянно убирались доставляемые током заряды, при этом к концу с большим потенциалом заряды постоянно подводились. То есть следует обеспечить круговорот зарядов. В этом круговороте заряды должны перемещаться по замкнутому пути. Движение носителей тока при этом реализуется при помощи сил неэлектростатического происхождения. Такие силы именуются сторонними. Получается, что для поддержания тока нужны сторонние силы, которые действуют на всем протяжении цепи или на отдельных участках цепи.
Формула ЭДС
До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи , то есть в проводниках, подсоединённых к клеммам источника тока. Как мы знаем, положительный заряд :. Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется!
Источник — это устройство, которое преобразует механическую, химическую, термическую и некоторые другие формы энергии в электрическую. Другими словами, источник является активным сетевым элементом, предназначенным для генерации электроэнергии.
Электродвижущая сила аккумулятора — ЭДС.
 Эдс батареи
Эдс батареиЗагрузить всю книгу. Определить внутреннее сопротивление батареи. Сопротивлением амперметра пренебречь. В помещении, удаленном от генератора на расстояние м включены параллельно 44 лампочки накаливания сопротивлением Ом каждая. Напряжение на лампочках равно В.
Электрический аккумулятор
Инженерам «от сохи» и прапорам Советской Армии посвящается Прежде всего, считаю долгом отметить, что не смотря на мои старания нижеприведенные соображения основаны на фундаментальных науках, а потому требуют все же некоторых усилий для осмысления. Не желающим прилагать эти усилия, а также тем, кто путает напряжение и емкость, читать не рекомендуется — берегите себя! Для ясности изложения, и не желая перегружать текст слишком сложными понятиями термодинамики и химической кинетики, далеко выходящими за рамки общих курсов физики и химии технических вузов, я позволю себе некоторые упрощения во всех случаях корректные , которые ни в коем случае не будут противоречить истине — заранее приношу свои извинения перфекционистам.
на полюсах аккумулятора равна U = 2 В, ЭДС аккумулятора – ЕА = 1,3 теплоты выделяемое в аккумуляторе определим по формуле.
ЭДС аккумулятора
Электродвижущая сила и напряжение. Электродвижущей силой ЭДС называется разность потенциалов положительного и отрицательного электродов аккумулятора при разомкнутой внешней цепи. Величина ЭДС зависит, главным образом, от электродных потенциалов, т. ЭДС кислотного аккумулятора зависит также от плотности электролита.
Закон Ома для полной цепи
ВИДЕО ПО ТЕМЕ: all-audio.pro определить плотность электролита АКБ математическим способом, по напряжению на клеммах.
На нашем сайте собрано более бесплатных онлайн калькуляторов по математике, геометрии и физике. Не можете решить контрольную?! Мы поможем! Более 20 авторов выполнят вашу работу от руб! Здесь — ЭДС, — работа сторонних сил, — величина заряда.
Но, разговорной речи на бытовом уровне может также применяться в отношении нескольких отдельных элементов, соединённых последовательно для увеличения напряжения или параллельно для увеличения силы тока друг с другом, то есть для обозначения аккумуляторной батареи.
Аккумуляторные батареи — Электрические характеристики аккумуляторных батарей
Оказывается, все до боли просто! Имеем источник ЭДС. Давайте вспомним, что такое ЭДС. ЭДС — это что-то такое, что создает электрический ток. Если к такому источнику напряжения подцепить любую нагрузку хоть миллиард галогенных ламп, включенных параллельно , то он все равно будет выдавать такое же напряжение, какое-бы он выдавал, если бы мы вообще не цепляли никакую нагрузку.
ЭДС — это что-то такое, что создает электрический ток. Если к такому источнику напряжения подцепить любую нагрузку хоть миллиард галогенных ламп, включенных параллельно , то он все равно будет выдавать такое же напряжение, какое-бы он выдавал, если бы мы вообще не цепляли никакую нагрузку.
КПД источника тока
Проверка должна производиться измерением плотности электролита, а так же замером напряжения на выводных клеммах аккумуляторной батарей. У полностью заряженной батареи, напряжение должно быть не ниже 12 В, и плотность соответствовать норме. Работоспособность аккумуляторной батареи определят проверкой ее под нагрузкой.
ЭДС. Закон Ома для полной цепи
Оглавление:
- Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.

- Сторонняя сила
- Закон Ома для полной цепи
- КПД электрической цепи
- Закон Ома для неоднородного участка
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.
Как мы знаем, положительный заряд :
• уходит во внешнюю цепь с положительной клеммы источника;
• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;
• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.
Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила , направленная против движения заряда (т.е. против направления тока).
к оглавлению ▴
Сторонняя сила
Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).
1).
Рис. 1. Сторонняя сила
Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.
Обозначим через работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы называется также работой источника тока.
Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, — это также работа сторонней силы по перемещению заряда по всей цепи.
Таким образом, — это также работа сторонней силы по перемещению заряда по всей цепи.
Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.
Опыт показывает, что работа прямо пропорциональна перемещаемому заряду . Поэтому отношение уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается :
(1)
Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.
Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.
к оглавлению ▴
Закон Ома для полной цепи
Любой источник тока обладает своим сопротивлением , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.
Пусть источник тока с ЭДС, равной , и внутренним сопротивлением подключён к резистору (который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).
Рис. 2. Полная цепь
Наша задача — найти силу тока в цепи и напряжение на резисторе .
За время по цепи проходит заряд . Согласно формуле (1) источник тока совершает при этом работу:
(2)
Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях и . Данное количество теплоты определяется законом Джоуля–Ленца:
(3)
Итак, , и мы приравниваем правые части формул (2) и (3):
После сокращения на получаем:
Вот мы и нашли ток в цепи:
(4)
Формула (4) называется законом Ома для полной цепи.
Если соединить клеммы источника проводом пренебрежимо малого сопротивления , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:
Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.
Зная силу тока (формула (4)), мы можем найти напряжение на резисторе с помощью закона Ома для участка цепи:
(5)
Это напряжение является разностью потенциалов между точками и (рис. 2). Потенциал точки равен потенциалу положительной клеммы источника; потенциал точки равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.
Мы видим из формулы (5), что в реальной цепи будет — ведь умножается на дробь, меньшую единицы. Но есть два случая, когда .
1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При формула (5) даёт .
Так называется источник с нулевым внутренним сопротивлением. При формула (5) даёт .
2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: . Тогда величина неотличима от , и формула (5) снова даёт нам .
Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.
к оглавлению ▴
КПД электрической цепи
Нетрудно понять, почему резистор называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.
Количество теплоты, выделяющееся на полезной нагрузке за время , обозначим .
Если сила тока в цепи равна , то
Некоторое количество теплоты выделяется также на источнике тока:
Полное количество теплоты, которое выделяется в цепи, равно:
КПД электрической цепи — это отношение полезного тепла к полному:
КПД цепи равен единице лишь в том случае, если источник тока идеальный .
к оглавлению ▴
Закон Ома для неоднородного участка
Простой закон Ома справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.
Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.
На рис. 3 показан неоднородный участок, содержащий резистор и источник тока. ЭДС источника равна , его внутреннее сопротивление считаем равным нулю (если внутреннее сопротивление источника равно , можно просто заменить резистор на резистор ).
Рис. 3. ЭДС «помогает» току:
Сила тока на участке равна , ток течёт от точки к точке . Этот ток не обязательно вызван одним лишь источником . Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток является результатом совокупного действия всех источников, имеющихся в цепи.
Поэтому ток является результатом совокупного действия всех источников, имеющихся в цепи.
Пусть потенциалы точек и равны соответственно и . Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.
Напряжение на нашем участке равно: . За время через участок проходит заряд , при этом стационарное электрическое поле совершает работу:
Кроме того, положительную работу совершает источник тока (ведь заряд прошёл сквозь него!):
Сила тока постоянна, поэтому суммарная работа по продвижению заряда , совершаемая на участке стационарным электрическим полем и сторонними силами источника, целиком превращается в тепло: .
Подставляем сюда выражения для , и закон Джоуля–Ленца:
Сокращая на , получаем закон Ома для неоднородного участка цепи:
(6)
или, что то же самое:
(7)
Обратите внимание: перед стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки к точке .
Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки к точке .
Отметим два следствия выведенных формул (6) и (7).
1. Если участок однородный, то . Тогда из формулы (6) получаем — закон Ома для однородного участка цепи.
2. Предположим, что источник тока обладает внутренним сопротивлением . Это, как мы уже упоминали, равносильно замене на :
Теперь замкнём наш участок, соединив точки и . Получим рассмотренную выше полную цепь. При этом окажется, что и предыдущая формула превратится в закон Ома для полной цепи:
Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.
Может быть и другой случай подключения, когда источник «мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от к , направлен против действия сторонних сил источника.
4. Здесь ток, идущий от к , направлен против действия сторонних сил источника.
Рис. 4. ЭДС «мешает» току:
Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!
Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:
Тогда закон Ома для неоднородного участка примет вид:
(8)
или:
где по-прежнему — напряжение на участке.
Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:
Ток при этом течёт от точки к точке . Если направление тока совпадает с направлением сторонних сил, то перед ставится «плюс»; если же эти направления противоположны, то ставится «минус».
Повторим основные понятия и определения по теме «Закон Ома».
Напомним, что напряжение измеряется в вольтах.
Сила тока измеряется в амперах.
Сопротивление измеряется в омах. Эта единица измерения названа в честь Георга Симона Ома, открывшего взаимосвязь между напряжением, сопротивлением цепи и силой тока в этой цепи.
Основные определения, которые мы используем в решении задач:
Источник тока – это устройство, способное создавать необходимую для существования тока разность потенциалов.
Можно сказать, что источник тока действует, как насос. Он «качает» электроны по проводникам, как водяной насос воду по трубам. Эту аналогию можно продолжить. При этом источник тока совершает работу, за счёт химических реакций, происходящих внутри него.
Если эту работу разделить на переносимый источником заряд q (суммарный заряд всех проходящих через источник электронов), то мы получим величину, которую называют электродвижущей силой или сокращённо ЭДС.
Измеряется эта ЭДС, как и разность потенциалов, в вольтах и имеет примерно тот же смысл.
По определению, сила тока равна отношению суммарного заряда электронов, проходящих через сечение проводника, ко времени прохождения. Измеряется сила тока в амперах (А).
Свойство проводника препятствовать прохождению по нему тока характеризуется величиной, которую назвали электрическим сопротивлением – R. Проходя через проводник, электрический ток нагревает его.
Сопротивление измеряют в омах (Ом).
Сам источник тока тоже обладает сопротивлением. Такое сопротивление принято называть внутренним сопротивлением источника r (Ом).
Именно немецкому учёному Георгу Ому удалось установить, от чего может зависеть электрическое сопротивление проводника. Проведя многочисленные эксперименты, Ом сделал следующие выводы:
- Сопротивление проводника тем больше, чем больше его длина.
- Сопротивление проводника тем больше, чем меньше его толщина или площадь поперечного сечения.

Кроме того, Ом выяснил, что каждый материал обладает своим электрическим сопротивлением. Величина, которая показывает, каким сопротивлением будет обладать проводник единичной длины и единичной площади сечения из данного материала, называется удельным электрическим сопротивлением: (Ом*мм2/м). Эта величина справочная. Таким образом, получается, что электрическое сопротивление проводника равно:
Рассмотрим задачи ЕГЭ по теме «Закон Ома» для полной цепи.
Задача 1. На рисунке приведён график зависимости напряжения на концах железного провода площадью поперечного сечения 0,05 мм2 от силы тока в нём. Чему равна длина провода? Ответ дайте в метрах. Удельное сопротивление железа 0,1 Ом*мм2/м.
Решение:
Из закона Ома для проводника или участка цепи без источника следует:
По графику: при
Из формулы сопротивления выражаем и находим длину проводника:
Ответ: 10.
Задача 2. Через поперечное сечение проводников за 8 с прошло 1020 электронов. Какова сила тока в проводнике? Ответ дайте в амперах.
Решение:
По определению силы тока:
Заряд всех электронов: где е — модуль заряда электрона, Кл.
Тогда
Ответ: 2.
Задача 3. Идеальный амперметр и три резистора общим сопротивлением 66 Ом включены последовательно в электрическую цепь, содержащую источник с ЭДС равной 5 В, и внутренним сопротивлением r=4 Ом. Каковы показания амперметра? (Ответ дайте в амперах, округлив до сотых.)
Решение:
По закону Ома для полной цепи:
Тогда
Ответ: 0,07.
Задача 4. ЭДС источника тока равна 1,5 В. Определите сопротивление внешней цепи, при котором сила тока будет равна 0,6 А, если сила тока при коротком замыкании равна 2,5 А. Ответ дайте в Ом, округлив до десятых.
Решение:
Сила тока короткого замыкания определяется следующим образом:
Отсюда выражаем и находим внутреннее сопротивление источника:
При внешнем сопротивлении, не равном нулю, сила тока в цепи определяется законом Ома для полной цепи:
Отсюда выражаем сопротивление резистора и находим его:
Ответ: 1,9.
Задача 5. На рисунке изображена схема электрической цепи, состоящей из источника постоянного напряжения с ЭДС 5 В и пренебрежимо малым внутренним сопротивлением, ключа, резистора с сопротивлением 2 Ом и соединительных проводов. Ключ замыкают. Какой заряд протечет через резистор за 10 минут? Ответ дайте в кулонах.
Решение:
Выражаем время в секундах: t = 10 минут = 600 с.
Определяем силу тока по закону Ома для полной цепи:
Внутреннее сопротивление пренебрежимо мало, поэтому r = 0.
По определению силы тока:
Отсюда Кл.
Ответ: 1500.
Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «ЭДС. Закон Ома для полной цепи» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена: 02.01.2023
Как рассчитать ЭДС | Наука
Обновлено 2 ноября 2020 г.
Автор Lee Johnson
Электродвижущая сила (ЭДС) — незнакомое большинству людей понятие, но оно тесно связано с более знакомым понятием напряжения. Понимание разницы между ними и того, что означает ЭДС, дает вам инструменты, необходимые для решения многих задач в физике и электронике, и вводит понятие внутреннего сопротивления батареи. ЭДС говорит вам о напряжении батареи без уменьшения внутреннего сопротивления, как это происходит при обычном измерении разности потенциалов. Вы можете рассчитать его несколькими способами, в зависимости от того, какая информация у вас есть.
TL;DR (слишком длинный; не читал)
Рассчитайте ЭДС по формуле:
ε = V + Ir
ток в цепи и (r) означает внутреннее сопротивление элемента.
Что такое ЭДС?
Электродвижущая сила представляет собой разность потенциалов (т. е. напряжение) на клеммах батареи при отсутствии тока. Может показаться, что это не имеет значения, но каждая батарея имеет «внутреннее сопротивление». Это похоже на обычное сопротивление, уменьшающее ток в цепи, но оно существует внутри самой батареи. Это связано с тем, что материалы, используемые для изготовления элементов батареи, имеют собственное сопротивление (поскольку практически все материалы имеют его).
Когда через ячейку не протекает ток, это внутреннее сопротивление ничего не меняет, потому что нет тока, который мог бы его замедлить. В некотором смысле, ЭДС можно рассматривать как максимальную разность потенциалов на клеммах в идеализированной ситуации, и на практике она всегда больше, чем напряжение батареи.
Уравнения для расчета ЭДС
Существуют два основных уравнения для расчета ЭДС. Наиболее фундаментальное определение — это количество джоулей энергии (E), которое получает каждый кулон заряда (Q), проходя через ячейку:
Наиболее фундаментальное определение — это количество джоулей энергии (E), которое получает каждый кулон заряда (Q), проходя через ячейку:
Где (ε) — символ электродвижущей силы, (E) — энергия в цепи, а (Q) — заряд цепи. Если вы знаете результирующую энергию и количество заряда, прошедшего через ячейку, это самый простой способ рассчитать ЭДС, но в большинстве случаев у вас не будет этой информации.
Вместо этого вы можете использовать определение, больше похожее на закон Ома (V = IR). Это можно выразить следующим образом:
\epsilon = I(R+r)
Где (I) означает ток, (R) — сопротивление рассматриваемой цепи, а (r) — внутреннее сопротивление ячейки. Расширение этого показывает тесную связь с законом Ома:
\epsilon =IR+Ir=V+Ir
Это показывает, что вы можете рассчитать ЭДС, если знаете напряжение на клеммах (напряжение, используемое в реальных ситуациях), протекающий ток и внутреннее сопротивление клетка.
Как рассчитать ЭДС: пример
В качестве примера представьте, что у вас есть цепь с разностью потенциалов 3,2 В, с текущим током 0,6 А и внутренним сопротивлением батареи 0,5 Ом. Используя приведенную выше формулу:
Используя приведенную выше формулу:
\epsilon =V+Ir = 3,2\text{ V}+(0,6\text{A})(0,5\text{ }\Omega)=3,5\text{V}
Таким образом, ЭДС этой цепи равно 3,5 V.
10.2: Электродвижущая сила — Физика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4407
- OpenStax
- OpenStax
Цели обучения
К концу раздела вы сможете:
- Описывать электродвижущую силу (ЭДС) и внутреннее сопротивление батареи
- Объясните основные принципы работы батареи
Если вы забудете выключить автомобильные фары, они постепенно притухнут по мере разрядки аккумулятора. Почему они не мигают внезапно, когда энергия батареи заканчивается? Их постепенное затемнение означает, что выходное напряжение батареи уменьшается по мере разрядки батареи. Причина снижения выходного напряжения у разряженных аккумуляторов заключается в том, что все источники напряжения имеют две основные части — источник электрической энергии и внутреннее сопротивление. В этом разделе мы исследуем источник энергии и внутреннее сопротивление.
Почему они не мигают внезапно, когда энергия батареи заканчивается? Их постепенное затемнение означает, что выходное напряжение батареи уменьшается по мере разрядки батареи. Причина снижения выходного напряжения у разряженных аккумуляторов заключается в том, что все источники напряжения имеют две основные части — источник электрической энергии и внутреннее сопротивление. В этом разделе мы исследуем источник энергии и внутреннее сопротивление.
Введение в электродвижущую силу
Напряжение имеет множество источников, некоторые из которых показаны на рисунке \(\PageIndex{2}\). Все такие устройства создают разность потенциалов и могут подавать ток, если они подключены к цепи. Особый тип разности потенциалов известен как электродвижущая сила (ЭДС) . ЭДС вообще не является силой, но термин «электродвижущая сила» используется по историческим причинам. Он был придуман Алессандро Вольта в 1800-х годах, когда он изобрел первую батарею, также известную как 9. 0013 вольтова столб . Поскольку электродвижущая сила не является силой, эти источники принято называть просто источниками ЭДС (произносится буквами «э-э-э-э»), а не источниками электродвижущей силы.
0013 вольтова столб . Поскольку электродвижущая сила не является силой, эти источники принято называть просто источниками ЭДС (произносится буквами «э-э-э-э»), а не источниками электродвижущей силы.
Если электродвижущая сила вовсе не сила, то что такое ЭДС и что является источником ЭДС? Чтобы ответить на эти вопросы, рассмотрим простую схему 12-вольтовой лампы, подключенной к 12-вольтовой батарее, как показано на рисунке \(\PageIndex{2}\). Батарея может быть смоделирована как устройство с двумя выводами, в котором один вывод имеет более высокий электрический потенциал, чем второй вывод. Более высокий электрический потенциал иногда называют положительной клеммой и обозначают знаком плюс. Клемму с более низким потенциалом иногда называют отрицательной клеммой и обозначают знаком минус. Это источник ЭДС.
Батарея может быть смоделирована как устройство с двумя выводами, в котором один вывод имеет более высокий электрический потенциал, чем второй вывод. Более высокий электрический потенциал иногда называют положительной клеммой и обозначают знаком плюс. Клемму с более низким потенциалом иногда называют отрицательной клеммой и обозначают знаком минус. Это источник ЭДС.
Когда источник ЭДС не подключен к лампе, в источнике ЭДС нет чистого потока заряда. Как только батарея подключена к лампе, заряды текут от одной клеммы батареи, через лампу (заставляя лампу загораться) и обратно к другой клемме батареи. Если мы рассмотрим положительный (обычный) ток, положительные заряды покидают положительную клемму, проходят через лампу и входят в отрицательную клемму.
Положительный ток полезен для большинства анализов цепей в этой главе, но в металлических проводах и резисторах наибольший вклад в ток вносят электроны, протекающие в направлении, противоположном положительному току. Поэтому более реалистично рассматривать движение электронов для анализа схемы на рисунке \(\PageIndex{2}\). Электроны покидают отрицательную клемму, проходят через лампу и возвращаются к положительной клемме. Чтобы источник ЭДС поддерживал разность потенциалов между двумя клеммами, отрицательные заряды (электроны) должны перемещаться от положительной клеммы к отрицательной. Источник ЭДС действует как зарядовый насос, перемещая отрицательные заряды от положительного вывода к отрицательному для поддержания разности потенциалов. Это увеличивает потенциальную энергию зарядов и, следовательно, электрический потенциал зарядов.
Поэтому более реалистично рассматривать движение электронов для анализа схемы на рисунке \(\PageIndex{2}\). Электроны покидают отрицательную клемму, проходят через лампу и возвращаются к положительной клемме. Чтобы источник ЭДС поддерживал разность потенциалов между двумя клеммами, отрицательные заряды (электроны) должны перемещаться от положительной клеммы к отрицательной. Источник ЭДС действует как зарядовый насос, перемещая отрицательные заряды от положительного вывода к отрицательному для поддержания разности потенциалов. Это увеличивает потенциальную энергию зарядов и, следовательно, электрический потенциал зарядов.
Сила электрического поля, действующая на отрицательный заряд, действует в направлении, противоположном электрическому полю, как показано на рисунке \(\PageIndex{2}\). Чтобы отрицательные заряды переместились на отрицательный полюс, над отрицательными зарядами должна быть совершена работа. Для этого требуется энергия, которая возникает в результате химических реакций в аккумуляторе. Потенциал поддерживается высоким на положительной клемме и низким на отрицательной клемме, чтобы поддерживать разность потенциалов между двумя клеммами. ЭДС равна работе, совершаемой над зарядом на единицу заряда \(\left(\epsilon = \frac{dW}{dq}\right)\) при отсутствии тока. Поскольку единицей работы является джоуль, а единицей заряда — кулон, единицей ЭДС является вольт \((1 \, V = 1 \, J/C)\).
Потенциал поддерживается высоким на положительной клемме и низким на отрицательной клемме, чтобы поддерживать разность потенциалов между двумя клеммами. ЭДС равна работе, совершаемой над зарядом на единицу заряда \(\left(\epsilon = \frac{dW}{dq}\right)\) при отсутствии тока. Поскольку единицей работы является джоуль, а единицей заряда — кулон, единицей ЭДС является вольт \((1 \, V = 1 \, J/C)\).
Напряжение на клеммах \(V_{клемма}\) батареи — это напряжение, измеренное на клеммах батареи, когда к клемме не подключена нагрузка. Идеальная батарея представляет собой источник ЭДС, который поддерживает постоянное напряжение на клеммах, независимо от тока между двумя клеммами. Идеальная батарея не имеет внутреннего сопротивления, а напряжение на клеммах равно ЭДС батареи. В следующем разделе мы покажем, что реальная батарея имеет внутреннее сопротивление и напряжение на клеммах всегда меньше, чем ЭДС батареи.
Происхождение потенциала батареи
Комбинация химических веществ и состав клемм в батарее определяют ее ЭДС. Свинцово-кислотный аккумулятор , используемый в автомобилях и других транспортных средствах, представляет собой одну из наиболее распространенных комбинаций химических веществ. На рисунке \(\PageIndex{3}\) показан один элемент (один из шести) этой батареи. Катодная (положительная) клемма элемента соединена с пластиной из оксида свинца, тогда как анодная (отрицательная) клемма подключена к свинцовой пластине. Обе пластины погружены в серную кислоту, электролит для системы.
Свинцово-кислотный аккумулятор , используемый в автомобилях и других транспортных средствах, представляет собой одну из наиболее распространенных комбинаций химических веществ. На рисунке \(\PageIndex{3}\) показан один элемент (один из шести) этой батареи. Катодная (положительная) клемма элемента соединена с пластиной из оксида свинца, тогда как анодная (отрицательная) клемма подключена к свинцовой пластине. Обе пластины погружены в серную кислоту, электролит для системы.
Знание того, как взаимодействуют химические вещества в свинцово-кислотном аккумуляторе, помогает понять потенциал, создаваемый аккумулятором. На рисунке \(\PageIndex{4}\) показан результат одной химической реакции. Два электрона размещены на анод , что делает его отрицательным, при условии, что катод поставляет два электрона. Это оставляет катод положительно заряженным, потому что он потерял два электрона. Короче говоря, разделение заряда было вызвано химической реакцией.
Два электрона размещены на анод , что делает его отрицательным, при условии, что катод поставляет два электрона. Это оставляет катод положительно заряженным, потому что он потерял два электрона. Короче говоря, разделение заряда было вызвано химической реакцией.
Обратите внимание, что реакция не происходит, если нет полной цепи, позволяющей подавать два электрона на катод. Во многих случаях эти электроны исходят от анода, проходят через сопротивление и возвращаются к катоду. Заметим также, что, поскольку в химических реакциях участвуют вещества, обладающие сопротивлением, невозможно создать ЭДС без внутреннего сопротивления.
Рисунок \(\PageIndex{4}\): В свинцово-кислотном аккумуляторе два электрона направляются на анод элемента, а два электрона удаляются с катода элемента. Химическая реакция в свинцово-кислотном аккумуляторе помещает два электрона на анод и удаляет два электрона с катода. Для продолжения требуется замкнутая цепь, поскольку два электрона должны быть подведены к катоду.
Внутреннее сопротивление и напряжение на клеммах
Величина сопротивления протеканию тока внутри источника напряжения называется внутреннее сопротивление . Внутреннее сопротивление r батареи может вести себя сложным образом. Обычно он увеличивается по мере разрядки аккумулятора из-за окисления пластин или снижения кислотности электролита. Однако внутреннее сопротивление может также зависеть от величины и направления тока через источник напряжения, его температуры и даже его истории. Внутреннее сопротивление перезаряжаемых никель-кадмиевых элементов, например, зависит от того, сколько раз и насколько глубоко они разряжались. Простая модель батареи состоит из идеализированного источника ЭДС \(\эпсилон\) и внутреннего сопротивления r (Рисунок \(\PageIndex{5}\)).
Рисунок \(\PageIndex{5}\): Батарея может быть смоделирована как идеализированная ЭДС \((\эпсилон)\) с внутренним сопротивлением ( r ). Напряжение на клеммах батареи равно \(V_{terminal} = \epsilon — Ir\).
Предположим, внешний резистор, известный как сопротивление нагрузки R , подключен к источнику напряжения, например к батарее, как показано на рисунке \(\PageIndex{6}\). На рисунке представлена модель батареи с ЭДС ε, внутренним сопротивлением Ом и нагрузочный резистор R , подключенный к его клеммам. Используя обычный ток, положительные заряды покидают положительную клемму батареи, проходят через резистор и возвращаются к отрицательной клемме батареи. Напряжение на выводах батареи зависит от ЭДС, внутреннего сопротивления и тока и равно
Примечание
\[V_{клемма} = \эпсилон — Ir\]
При заданных ЭДС и внутреннем сопротивлении , напряжение на клеммах уменьшается по мере увеличения тока из-за падения потенциала Ir внутреннего сопротивления.
Рисунок \(\PageIndex{6}\): Схема источника напряжения и его нагрузочного резистора R . Поскольку внутреннее сопротивление r включено последовательно с нагрузкой, оно может существенно повлиять на напряжение на клеммах и ток, подаваемый на нагрузку.
График разности потенциалов на каждом элементе цепи показан на рисунке \(\PageIndex{7}\). По цепи протекает ток I , а падение потенциала на внутреннем резисторе равно Ир . Напряжение на клеммах равно \(\эпсилон — Ir\), что равно падению потенциала на нагрузочном резисторе \(IR = \эпсилон — Ir\). Как и в случае с потенциальной энергией, важно изменение напряжения. Когда используется термин «напряжение», мы предполагаем, что на самом деле это изменение потенциала или \(\Delta V\). Однако \(\Delta\) часто опускается для удобства.
Рисунок \(\PageIndex{7}\): График зависимости напряжения в цепи аккумулятора и сопротивления нагрузки. Электрический потенциал увеличивает ЭДС батареи из-за химических реакций, совершающих работу над зарядами. В аккумуляторе происходит уменьшение электрического потенциала из-за внутреннего сопротивления. Потенциал уменьшается из-за внутреннего сопротивления \(-Ir\), делая напряжение на клеммах батареи равным \((\эпсилон — Ir)\). Затем напряжение уменьшается на ( ИР ). Ток равен \(I = \frac{\epsilon}{r + R}\).
Затем напряжение уменьшается на ( ИР ). Ток равен \(I = \frac{\epsilon}{r + R}\).Ток через нагрузочный резистор равен \(I = \frac{\epsilon}{r + R}\). Из этого выражения мы видим, что чем меньше внутреннее сопротивление r , тем больший ток источник напряжения отдает на свою нагрузку R . По мере разрядки батарей r увеличивается. Если r становится значительной долей сопротивления нагрузки, то ток значительно снижается, как показано в следующем примере.
Пример \(\PageIndex{1}\): Анализ цепи с батареей и нагрузкой
Данная батарея имеет ЭДС 12,00 В и внутреннее сопротивление \(0,100 \, \Омега\). (a) Рассчитайте напряжение на его клеммах при подключении к \(10,00 \, \Омега\) нагрузке. (b) Каково напряжение на клеммах при подключении к нагрузке \(0,500 \, \Омега\)? в) Какую мощность рассеивает нагрузка \(0,500 \, \Омега\)? г) Если внутреннее сопротивление возрастает до \(0,500 Ом, \Омега\), найти ток, напряжение на клеммах и мощность, рассеиваемую нагрузкой \(0,500 Ом, \Омега\).
Стратегия
Приведенный выше анализ дал выражение для тока с учетом внутреннего сопротивления. Как только ток найден, напряжение на клеммах можно рассчитать, используя уравнение \(V_{клемма} = \эпсилон — Ir\). Как только ток найден, мы также можем найти мощность, рассеиваемую резистором.
Решение
- Ввод заданных значений ЭДС, сопротивления нагрузки и внутреннего сопротивления в приведенное выше выражение дает \[I = \frac{\epsilon}{R + r} = \frac{12,00 \, V }{10,10 \, \Omega} = 1,188 \, A.\] Введите известные значения в уравнение \(V_{терминал} = \epsilon — Ir\), чтобы получить напряжение на клеммах: \[V_{терминал} = \ эпсилон — Ir = 12,00 \, V — (1,188 \, А)(0,100 \, \Омега) = 11,90 \, В. \] Напряжение на клеммах здесь лишь немного ниже, чем ЭДС, что означает, что ток, потребляемый этой легкой нагрузкой, незначителен.
- Аналогично, при \(R_{нагрузка} = 0,500 \, \Omega\), ток равен \[I = \frac{\epsilon}{R + r} = \frac{12,00 \, V}{0,600 \, \Omega} = 20,00 \, A.
 2(0,500 Ом, \Омега) = 72,00 Ом, Вт.\] Мы видим, что увеличение внутреннего сопротивления значительно уменьшило напряжение на клеммах, ток и мощность, подаваемая на нагрузку.
2(0,500 Ом, \Омега) = 72,00 Ом, Вт.\] Мы видим, что увеличение внутреннего сопротивления значительно уменьшило напряжение на клеммах, ток и мощность, подаваемая на нагрузку.
Значение
Внутреннее сопротивление батареи может увеличиться по многим причинам. Например, внутреннее сопротивление перезаряжаемой батареи увеличивается по мере увеличения количества перезарядок батареи. Повышенное внутреннее сопротивление может иметь два последствия для батареи. Во-первых, напряжение на клеммах уменьшится. Во-вторых, батарея может перегреться из-за увеличения мощности, рассеиваемой внутренним сопротивлением.
Упражнение \(\PageIndex{1}\)
Если вы поместите провод прямо через две клеммы батареи, эффективно закоротив клеммы, батарея начнет нагреваться. Как вы думаете, почему это происходит?
- Раствор
Если к клеммам подсоединен провод, сопротивление нагрузки близко к нулю или, по крайней мере, значительно меньше внутреннего сопротивления батареи.
 2r)\). Мощность рассеивается в виде тепла.
2r)\). Мощность рассеивается в виде тепла.
Тестеры аккумуляторов
Тестеры аккумуляторов, подобные показанным на рисунке \(\PageIndex{8}\), используют небольшие нагрузочные резисторы для преднамеренного отбора тока, чтобы определить, падает ли потенциал на клеммах ниже допустимого уровня. Хотя измерить внутреннее сопротивление батареи сложно, тестеры батарей могут обеспечить измерение внутреннего сопротивления батареи. Если внутреннее сопротивление высокое, батарея слабая, о чем свидетельствует низкое напряжение на клеммах.
Рисунок \(\PageIndex{8}\): Тестер батарей измеряет напряжение на клеммах под нагрузкой, чтобы определить состояние батареи. (a) Техник по электронике ВМС США использует тестер батарей для проверки больших батарей на борту авианосца USS Nimitz . Тестер батареи, который она использует, имеет небольшое сопротивление, которое может рассеивать большое количество энергии. (b) Показанное небольшое устройство используется на небольших батареях и имеет цифровой дисплей для индикации допустимого напряжения на клеммах. (кредит a: модификация работы Джейсона А. Джонстона; кредит b: модификация работы Кейта Уильямсона)
(кредит a: модификация работы Джейсона А. Джонстона; кредит b: модификация работы Кейта Уильямсона)Некоторые аккумуляторы можно заряжать, пропуская через них ток в направлении, противоположном току, который они подают в электроприбор. Это обычно делается в автомобилях и в батареях для небольших электроприборов и электронных устройств (рис. \(\PageIndex{9}\)). Выходное напряжение зарядного устройства должно быть больше, чем ЭДС аккумулятора, чтобы ток через него изменил направление. Это приводит к тому, что напряжение на клеммах батареи больше, чем ЭДС, поскольку \(V = \эпсилон — Ir\) и I теперь отрицательный.
Рисунок \(\PageIndex{9}\): Зарядное устройство автомобильного аккумулятора меняет нормальное направление тока через аккумулятор, обращая его химическую реакцию и восстанавливая его химический потенциал. Важно понимать последствия внутреннего сопротивления источников ЭДС, таких как батареи и солнечные элементы, но часто анализ цепей выполняется с напряжением на клеммах батареи, как мы делали в предыдущих разделах.

 Эдс батареи
Эдс батареи