Физика жидкости: Свойства жидкости

Содержание

Физика жидкостей | это… Что такое Физика жидкостей?

Физика жидкостей (физика жидкого состояния вещества) — раздел физики, в котором изучаются механические и физические свойства жидкостей. Статистическая теория жидкостей является разделом статистической физики. Важнейшим результатом является вывод уравнений гидродинамики из уравнений Лиувилля, реализованный Н. Н. Боголюбовым в 1948 году. В физике квантовых жидкостей изучается явление сверхтекучести, нашедшее объяснение в работах Н. Н. Боголюбова 1947—1949 годов.

Успехи теории фазовых переходов между газообразным и жидким состоянием вещества, созданной Ван-дер-Ваальсом, укрепили представления о структурной близости этих состояний, как неупорядоченных и различающихся лишь плотностью частиц. После первых ренгеноструктурных исследований распределения частиц в жидкости выяснилось, что жидкости не являются бесструктурными. В теории рассеяния света в жидкости, разработанной Цернике и Пирсом в 1927 году, возникает функция распределения. Я. И. Френкель ввел представление о колебательно-поступательном движении молекул в жидкостях и развил кинетические модели в физике жидкостей. Строгая статистическая теория жидкостей была построена в работах Н. Н. Боголюбовым в 1947—1949 годах. И. З. Фишер использовал цепочку уравнений Боголюбова во втором порядке ^[1] для описания жидкости. Также, И. З. Фишер создал лагранжеву теорию тепловых гидродинамических флуктуаций. В предисловии автора к русскому изданию своей книги К. А. Крокстон писал в 1976 году: «Последние два или три десятилетия физика жидкого состояния … достигла значительных успехов, в основном благодаря пионерским работам советских авторов — главным образом Н. Н. Боголюбова, Я. И. Френкеля и И. З. Фишера».^[1]

Литература

Боголюбов Н. Н. «Уравнения гидродинамики в статистической механике» (1948) в Боголюбов Н. Н. Избранные труды в трех томах. Том 2. Киев: Наукова думка, 1970. стр.258-276.
Боголюбов Н. Н. «К теории сверхтекучести» Изв. АН СССР, Сер физ. 1947. Том 11. N.1. 77-90; Боголюбов Н. Н. Избранные труды в трех томах. Том 2. Киев: Наукова думка, 1970. стр.210-224.
Крокстон К. Физика жидкого состояния. Статистическое введение. пер с англ. М.: Мир, 1978. — 400с.
Оно С., Кондо С. Молекулярная теория поверхностного натяжения в жидкостях. М.: ИИЛ, 1963. — 292с.
Фишер И. З. Статистическая теория жидкостей. М.: Наука, 1961. — 280с.
Френкель Я. И. Кинетическая теория жидкостей. Изд-во АН СССР, 1945. и Л.: Наука, 1975.
Пайнс Д., Нозьер Ф., Теория квантовых жидкостей, пер. с англ., М., 1967.
Резибуа П., Де Ленер М. Классическая кинетическая теория жидкостей и газов. М.: Мир, 1980. — 424с.

Данилов В. И. Строение и кристаллизация жидкости.Избранные статьи. Под.ред. Курдюмова Г. В. Киев. Изд-во АН УССР, 1956. — 568 с.
Юльметьев Р. М. Введение в статистическую физику жидкостей. Казань: Изд-во КГПИ, 1972. — 218с.
Физика простых жидкостей. 1. Статистическая теория. Перевод с англ. под ред. Д. Н. Зубарева и Н. М. Плакиды. М.: Мир, 1971. — 308 с.
Физика простых жидкостей. 2. Экспериментальные исследования. Перевод с англ. под ред. А. 3. Голика и Ю. И. Шиманского. М.: Мир, 1973. — 400 с.
Скрипов В. П. Метастабильная жидкость. М.: Наука, 1972. — 312 с

См. также

Цепочка уравнений Боголюбова
Гидродинамика

Примечания

↑ ¹ ² Крокстон К. Физика жидкого состояния. Статистическое введение. пер с англ. М.: Мир, 1978. — 400с.

ФИЗИКА ЖИДКОСТЕЙ — NovaUm.Ru

ФИЗИКА ЖИДКОСТЕЙ

№10, 14.12.2017

Физико-математические науки

Быстров Дмитрий Сергеевич

Научный руководитель: Шабаев Р.Б., кандидат педагогических наук, доцент.

Ключевые слова: ФИЗИКА ЖИДКИХ ТЕЛ; ЖИДКОСТЬ; ТИПЫ ЖИДКОСТЕЙ; PHYSICS OF FLUIDS; LIQUID; LIQUIDS.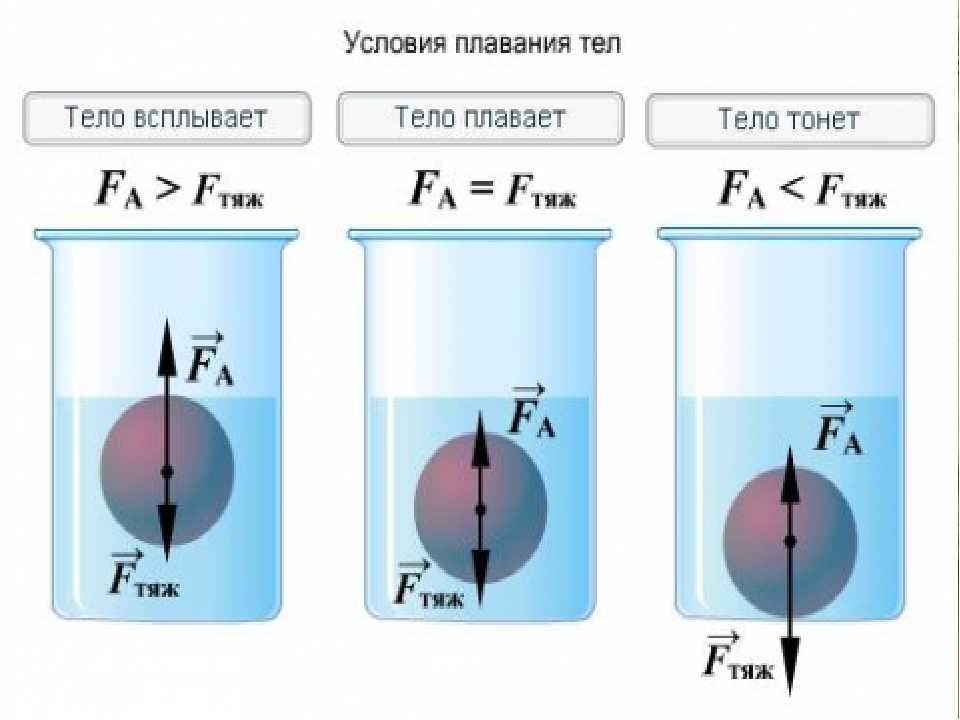

Аннотация: В статье рассматриваются основные принципы физики жидких тел. Раскрыты основы поведения различных типов жидкостей и их характеристика. Жидкости постоянно окружают нас в повседневной жизни, не говоря уж о профессиональной. По этой причине понимание основ физики жидкостей чрезвычайно важно.

Все вещества можно разделить на три агрегатных состояния: твердое, жидкое и газообразное. Это три очень большие группы, нашедшие свое применение во всех областях человеческой деятельности. Жидкости мы используем, как и для поддержания основных жизненных функций не только человека, но и всего живого на планете, так и для создания благ, что направлены на удовлетворения потребностей всего живого. Все вещества очень важны ведь не известно, как пошла бы эволюция на нашей планете, если бы не было какого-либо элемента или вещества, особенно если бы отсутствовала такая важная субстанция как вода.

Жидкие тела отличаются от твердых тел. По этой причине и физика жидких тел кардинально отличается от физики твердых тел.

Например, рассмотрим самую распространенную жидкость на нашей планете – воду. Вода встречается в трех агрегатных состояниях: твердое – лед, жидкое – вода и газообразное – водяной пар. При переходе из одного состояния в другое происходит не только изменение агрегатного состояния вещества, но также происходит изменение физических свойств. При переходе из твердого состояния в жидкое: объем вещества уменьшается, так как молекулы больше не расположены в жесткой кристаллической решетке, температура увеличивается, так как процесс перехода воды из твердого состояния в жидкое называется плавлением и происходит при достижении температуры плавления. У воды при обычном атмосферном давлении она равно нулю градусов Цельсия. Так же в зависимости от изменения давления может изменятся температура плавления, парообразования.

Процесс парообразования — это процесс перехода из жидкого агрегатного состояния в парообразное. Когда вода переходит в пар, то происходит увеличение объема вещества, из-за еще большего ослабления межмолекулярных связей и отдаления молекул, так же для парообразования нужна высокая температура, для воды она достигает ста градусов Цельсия.

Жидкость – это агрегатное состояние тела, промежуточное состояние между твердой и газообразной формой. Сила межмолекулярного взаимодействия меньше чем у твердых тел, что позволяет ей изменять свою форму, но сильнее чем у газообразных тел, что не дает ей перейти в газообразное состояние. Из-за этого свойства жидкость обладает свойствами как твердых тел, так и газообразных тел.

Свойства твердых тел, наблюдаемые у жидкостей:
1. Сохраняют собственный объем;
2. Образуют поверхность;
3. Обладают прочностью на разрыв.

Свойства газов, наблюдаемые у жидкостей:
1. Принимают форму сосуда.

Молекулы располагаются близко друг к другу и взаимодействуют между собой силой межмолекулярной притяжения, она является достаточной для того, чтобы молекулы не могли свободно передвигаться и уходить с места. Молекулы жидкостей колеблются возле положения равновесия. Но если приложить достаточную силу, то молекулы могут преодолеть силу взаимодействия и перейти на другое место. Это объясняется текучестью жидкостей.

Главной характеристикой жидких тел является текучесть. Текучесть – это способность тела вязко или пластично деформироваться под действием даже незначительной внешней силой или суммы сил. Из-за этого способности жидкие тела могут течь струйками или ручьями, или же принимать форму любого сосуда, в котором она находится. Текучестью обладают абсолютно все жидкости на Земле. Текучесть в основном определяется тремя параметрами жидкости: плотностью жидкости, давлением и скоростью движения жидкости.

Когда речь заходит за изучение жидкостей, то все жидкости принято разделять на идеальные и реальные. Различие их заключается в том, что у идеальных жидкостей отсутствует сила внутреннего трения между молекулами. Из-за этого идеальные жидкости не сопротивляются касательным силам сдвига и силам растяжения. Идеальные жидкости нельзя сжать, так как они оказывают несоизмеримо большое сопротивление всем силам сжатия. К сожалению таких жидкостей не существует другими словами это научная абстракция, созданная специально для упрощенного применения физических законов для жидкостей. Теперь рассмотрим другой тип жидкостей. Реальные жидкости в отличии от идеальных имеют силу внутреннего трения между молекулами, так же они в какой-то степени сопротивляются касательным силам сдвига и силам растяжения. В связи с чем работать с реальными жидкостями при изучении физики жидкостей куда сложнее чем с идеальными жидкостями. По этой причине и были созданы идеальные жидкости.

Так же описывая физику жидкостей нельзя не уделить внимание физическим свойствам жидкости таким как:
1. Плотность жидкости. При уменьшении температуры плотность жидкости возрастает, но в природе встречаются жидкости, чья плотность ведет себе совершенно по-другому.
2. Вязкость – это способность газов и жидкостей создавать сопротивление между двигающимися взаимно соприкасающимися поверхностями. Таким образом эта величина равна силе внутреннего трения газов или жидкостей.
3. Поверхностное натяжение жидкости. Данная величина характеризует удельную энергию взаимодействия молекул. Это означает, что, меняя энергию взаимодействия мы изменяем и коэффициент поверхностное натяжение.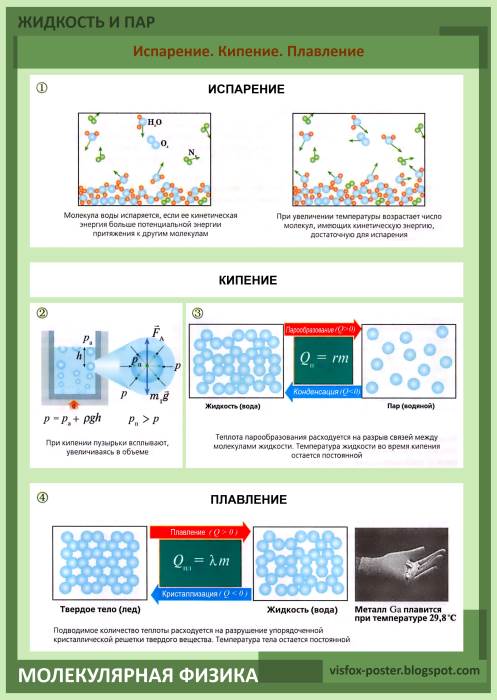 Таким образом коэффициент поверхностное натяжения зависит от: природы вещества, свойств жидкости, температуры, наличия поверхностно-активных веществ.
4. Теплопроводность – это явления переноса энергии от более нагретых участком тела к менее нагретым участкам тела, осуществляемые за счет хаотического движения молекул.
5. Теплоемкость – это количество теплоты необходимое сообщить жидкости для нагревания одного килограмма жидкости на один градус.

Так же рассматривая жидкости стоит отметить, что их подразделяют на две большие группы: ньютоновские и неньютоновские жидкости

Ньютоновские жидкости полностью подчиняются законам Ньютона. Неньютоновские жидкости – это жидкости, не подчиняющиеся законам Ньютона, то есть при изменении давления или скорости жидкости так же изменяется вязкость.

Таким образом можно подвести итог. Жидкости существуют разные, и квалифицировать их можно по разным признакам. Так же они имеют целый ряд свойств, что похожи на свойства как твердых тел, так и газов, что говорит о том, что жидкости находятся в переходном состоянии между твердым и газообразным агрегатным состоянием. Жидкости очень интересны и сложны, ведь изменив один даже малозначительный параметр, могут измениться все остальные, причем очень значительно.

Список литературы

Боголюбов Н. Н. «К теории сверхтекучести» Изв. АН СССР, Сер физ. 1947. Том 11. N.1. С. 77-90
Боголюбов Н. Н. Избранные труды в трех томах. Том 2. Киев: Наукова думка, 1970. С. 210-224
Трофимова, Т. И. Курс физики [Текст] : учеб. пособие для инженерно-техн. спец. высш. учеб. заведений / Т. И. Трофимова. – 6-е изд., стер. – М.: Высш. шк., 2000. – 542 с.

Гидродинамическое моделирование

Дэн Шредер, Физический факультет, Государственный университет Вебера

60 х 2475 х 30100 х 40120 х 48150 х 60200 х 80300 х 120600 х 240

Скорость потока = 0,100 Вязкость = 0,020

Нарисуйте барьерыСтирайте барьерыПеретащите жидкостьФормы барьеров

Плотность графикаГрафик х скоростьГрафик у скоростиГрафика скоростьИзгиб графика Контраст:

Скорость анимации: Шагов в секунду: 0 Быстрее?

Показывать: Трейсеры Выкидные линии Сила на барьерах Датчик Данные

Это имитация двухмерной жидкости.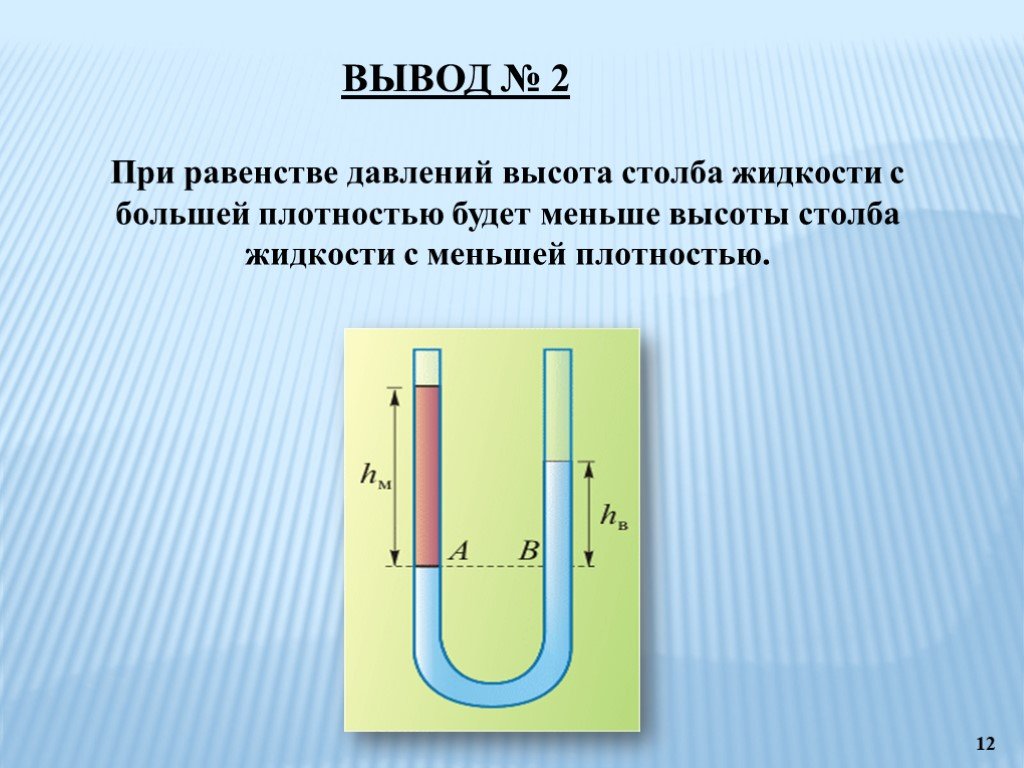 Первоначально жидкость течет слева направо, а линейный барьер (показан черным) отклоняет жидкость и создает вихри. Цвета обозначают завиток или локальное вращательное движение жидкости. Используйте элементы управления для регулировки скорости потока и вязкости, рисуйте различные барьеры, перетаскивайте жидкости вокруг, изобразите другие величины, кроме завихрения, покажите силу, действующую на жидкость на барьерах и измерять плотность и скорость жидкости в любой точке. Наслаждаться!

Это моделирование предназначено для качественных и полуколичественных образовательных демонстрации — не для серьезного инженерного использования. Одним очевидным ограничением является то, что он имитирует жидкость только в двух измерениях, а не в трех. Он также ограничен моделированием жидкостей при при постоянной температуре и со скоростями потока, по крайней мере в несколько раз меньшими скорости звука. Однако, пожалуй, самое важное ограничение касается продолжительности и масштаба времени.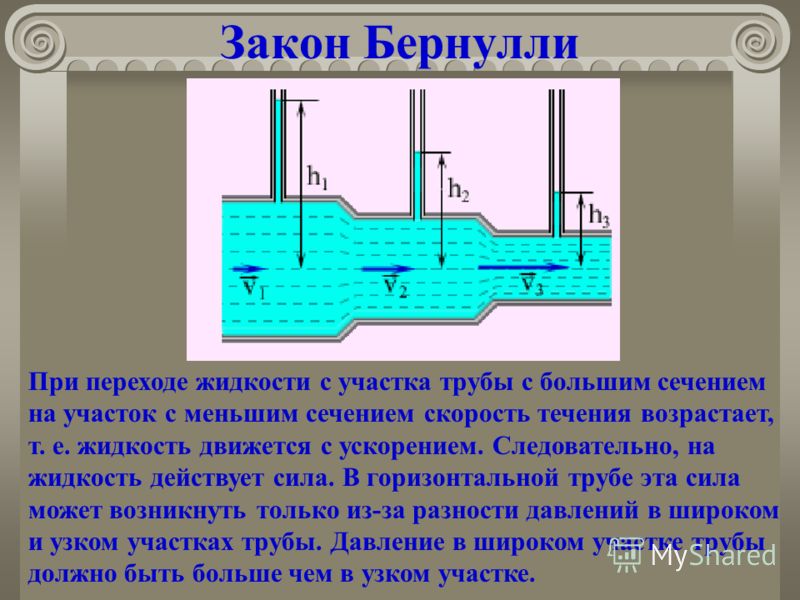

Моделирование использует произвольную систему единиц, поэтому единственный способ сравнить с реальным миром — это безразмерное число Рейнольдса, определяемое как (длина) (скорость)/(вязкость), где «длина» — это характерный размер всего, вокруг или через что течет жидкость. Практический предел число Рейнольдса в этом моделировании составляет несколько сотен, тогда как типичное число Рейнольдса для воздух, обтекающий велосипедиста, составляет примерно 100 000. Более высокие числа Рейнольдса приводят к большему количеству уровней Структура и турбулентность жидкости. Это моделирование просто не может справиться со многими высокими числами Рейнольдса. ситуации, которые так важны в повседневной жизни.

Симуляция использует довольно простой алгоритм решетки-Больцмана, который вы можете увидеть, просмотрев исходный код JavaScript (используйте в своем браузере View Source или Page Source команду меню). По состоянию на 2019 год он работает с приятной скоростью на большинстве персональных компьютеров в Chrome, Firefox, и браузеры Opera. Другие браузеры, не говоря уже о мобильных устройствах, могут давать меньшую производительность. Некоторые очень старые браузеры могут даже не отображать ползунки.

Связанные материалы:

Аналогичная симуляция на Java
Аналогичная симуляция в Python
Постерная презентация на летнем собрании AAPT, 2013 г. (pdf, 2,6 МБ)
Инструкции для проекта решетки-Больцмана в курсе вычислительной физики
Более подробное объяснение алгоритма решетки-Больцмана (скоро)

Жидкости

А 9Жидкость 0038 — это вещество, которое не может сохранять свою форму, но принимает форму своего сосуда. Жидкостные законы предполагают идеализированные жидкости, которые нельзя сжать.

Плотность и давление

Плотность (ρ) вещества однородного состава равна его массе в единице объема: ρ = m / V . В системе СИ плотность измеряется в килограммах на кубический метр.

Представьте себе вертикальный цилиндрический стакан, наполненный жидкостью. Жидкость оказывает давление на дно сосуда из-за своего веса. Давление определяется как сила на единицу площади: P = F / А, или по величине P = мг/А , где мг — вес жидкости. Единицей давления в СИ является Н/м

2 , называемая паскалем. Давление на дне жидкости можно выразить через плотность (ρ) и высоту (h) жидкости:

или P = ρ hg . Давление в любой точке жидкости действует одинаково во всех направлениях. Эту концепцию иногда называют Основной закон давления жидкости.

Принцип Паскаля

Принцип Паскаля можно сформулировать так: Давление, приложенное в одной точке в замкнутой жидкости в условиях равновесия, передается в равной степени всем частям жидкости. Это правило используется в гидравлических системах. На рисунке 1 нажатие на цилиндрический поршень в точке a поднимает объект в точке b.

Рисунок 1

Принцип Паскаля используется, чтобы легко поднять автомобиль.

Пусть нижние индексы a и b обозначают количества на каждом поршне. Давления равны; следовательно, P _a = P _b . Подставим выражение для давления через силу и площадь, чтобы получить f _a / A _a = ( F _б / А _б ). Substitute π r ² for the area of a circle, simplify, and solve for F _b : F _b =( F _a )( r _b ² / r _a ² ). Поскольку сила, действующая в точке a умножается на квадрат отношения радиусов и

r _b > r _a , небольшое усилие на маленьком поршне a 9004 может поднять относительно больший вес 9046. б .

Закон Архимеда

Вода обычно частично поддерживает любой объект, помещенный в нее. Восходящая сила, действующая на объект, помещенный в жидкость, называется выталкивающей силой . По Принцип Архимеда, величина выталкивающей силы, действующей на полностью или частично погруженный в воду объект, всегда равна весу жидкости, вытесненной этим объектом.

Принцип Архимеда можно проверить нематематическим аргументом. Рассмотрим кубический объем воды в сосуде с водой, показанном на рис. 2. Этот объем находится в равновесии с действующими на него силами — весом и выталкивающей силой; следовательно, направленная вниз сила груза ( W ) должна быть уравновешена выталкивающей силой вверх ( B ), которая обеспечивается остальной водой в контейнере.

Рисунок 2

Вес уравновешивается выталкивающей силой в объеме воды.

Если твердое тело плавает, частично погруженное в жидкость, объем вытесненной жидкости меньше объема твердого тела. Сравнение плотности твердого тела и жидкости, в которой оно плавает, приводит к интересному результату. Формулы для плотности D _s = m _s / V _s and D _l = m _l / V _l , где D — плотность, V — объем, m — масса, а нижние индексы s и l относятся к количествам, связанным с твердым телом и жидкостью соответственно. Решение для масс приводит к

m _s = D _s V _s and m l = D _l V _l .

По закону Архимеда массы твердого тела и вытесненной жидкости равны. Поскольку веса — это просто масса, умноженная на константу (g) , массы также должны быть равны; поэтому D _s V _s = D _l V _l or D _s / D _l = V _л В _л . Теперь В = Ач, где А — площадь поперечного сечения, а ч — высота. Для твердого вещества, плавающего в жидкости, A _L = A _S и H _L — высота твердого вещества, который подтолкнут, H _Sub. С этими заменами приведенное выше соотношение становится следующим: D _s / D _l = h _sub / h 900; поэтому доля погруженного твердого тела равна отношению плотности твердого тела к плотности окружающей его жидкости, в которой оно плавает.

Физика жидкости: Свойства жидкости — урок. Физика, 7 класс.