Формула средней скорости в физике
Содержание:
- Определение и формула средней скорости
- Вектор средней скорости
- Единицы измерения
- Примеры решения задач
Определение и формула средней скорости
Определение
Средней путевой скоростью материальной точки на отрезке времени $\Delta t$называется скалярная физическая величина, равная отношению длины пути, пройденного точкой к промежутку времени, в течение которого данный путь пройден. Среднюю скорость обозначают:
$$\langle v\rangle, \bar{v}, v_{s r}$$
Математически определение средней скорости можно записать в следующем виде:
$$\langle v\rangle(t+\Delta t)=\frac{\Delta s}{\Delta t}=\frac{s(t+\Delta t)-s(t)}{\Delta t}(1)$$
где $\Delta s=s(t+\Delta t)-s(t)$ — длина пути, которую прошла точка за время $\Delta t$.
Если перейти к пределу при $\Delta t \rightarrow 0$ , получим:
$$\lim _{\Delta t \rightarrow 0}\langle v\rangle=\lim _{\Delta t \rightarrow 0} \frac{\Delta s}{\Delta t}=\frac{d s}{d t}=v(t)(2)$$
средняя путевая скорость в пределе совпадает с величиной (модулем) мгновенной скорости точки в момент времени t.
При равномерном движении:
$$\langle v\rangle=v(3)$$
Вектор средней скорости
Определение
Вектором средней скорости $\langle\vec{v}\rangle$ материальной точки на отрезке времени $\Delta t$называют величину, равную приращению радиус-вектора, который определяет положение данной точки к промежутку времени $\Delta t$:
$$\langle\bar{v}\rangle(t+\Delta t)=\frac{\Delta \bar{r}}{\Delta t}=\frac{\bar{r}(t+\Delta t)-\bar{r}(t)}{\Delta t}(4)$$
где $\Delta \bar{r}$ – приращение радиус-вектора материальной точки.
Вектор средней скорости в пределе при $\Delta t \rightarrow 0$ совпадает с вектором скорости в момент времени t:
$$\lim _{\Delta t \rightarrow 0}\langle\bar{v}\rangle=\lim _{\Delta t \rightarrow 0} \frac{\Delta \bar{r}}{\Delta t}=\frac{d \bar{r}}{d t}=\bar{v}(t)(5)$$где $\bar{v}(t)$ – вектор мгновенной скорости токи.
Если точка совершает равномерное и прямолинейное движение, то выполняется равенство:
$$\langle\bar{v}\rangle=\bar{v}(6)$$
Средняя путевая скорость и модуль вектора средней скорости равны
$(\langle v\rangle=|\langle\bar{v}\rangle|)$ только при прямолинейном движении. При всех остальных видах движения выполняется неравенство:
При всех остальных видах движения выполняется неравенство:
$$\langle v\rangle>|\langle\bar{v}\rangle|(7)$$
Единицы измерения
Основной единицей измерения средней скорости в системе СИ является: м/с
В СГС: см/с
Примеры решения задач
Пример
Задание. Какова средняя скорость материальной точки за время ее движения, если точка прошла первую половину
пути имея скорость v
Решение. В качестве основы для решения задачи формулу:
$$\langle v\rangle=\frac{s}{\Delta t}(1.1)$$
где время потраченное на путь ($\Delta t$) делится на три части:
$$\Delta t=t_{1}+t_{2}+t_{3}(1.2)$$
При этом имеют место следующие соотношения между отрезками пути, скоростью их преодоления и временем:
$$\left\{\begin{array}{c}\frac{1}{2} s=v_{1} t_{1} \rightarrow t_{1}=\frac{s}{2 v_{1}} \\ \frac{1}{2} s=v_{2} t_{2}+v_{3} t_{3} \rightarrow t_{3}=\frac{s}{2\left(v_{2}+v_{3}\right)}(1. 3) \\ t_{2}=t_{3}=\frac{1}{2} t\end{array}\right.$$
$$\langle v\rangle=\frac{2 v_{1}\left(v_{2}+v_{3}\right)}{v_{2}+v_{3}+2 v_{1}}$$
3) \\ t_{2}=t_{3}=\frac{1}{2} t\end{array}\right.$$
$$\langle v\rangle=\frac{2 v_{1}\left(v_{2}+v_{3}\right)}{v_{2}+v_{3}+2 v_{1}}$$
Ответ. $\langle v\rangle=\frac{2 v_{1}\left(v_{2}+v_{3}\right)}{v_{2}+v_{3}+2 v_{1}}$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Какова средняя скорость частицы, движущейся по оси Xза время в течение которого, она пройдет первые s метров пути, если функция скорости задана уравнением: $v=A \sqrt{x}$, где A=const>0. Считать, что x=0 при t=0.
Решение. Сделаем рисунок.
В качестве основы для решения задачи используем формулу для средней путевой скорости, так как движение прямолинейное, то средняя путевая скорость равна модулю вектора средней скорости. По условию задачи точка движется по оси X, тогда:
 {2}}{4}$ . Выразим время, которое точка затратила на путьs :
{2}}{4}$ . Выразим время, которое точка затратила на путьs :$$t=\frac{2 \sqrt{s}}{A}(2.5)$$
Подставим время из (2.4) в формулу (2.2):
$$\langle v\rangle=\frac{A}{2} \sqrt{s}$$
Ответ. $\langle v\rangle=\frac{A}{2} \sqrt{s}$
Читать дальше: Формула угловой скорости.
расчёты и формулы / Справочник :: Бингоскул
Вычисление средней скорости движения в физике: расчёты и формулыдобавить в закладки удалить из закладок
Содержание:
Под средней скоростью движения какого-либо тела понимают отношение пройденного расстояния к временному промежутку, который был затрачен на его преодоление. Определение средней скорости может понадобиться в случае, когда в процессе перемещения тела на разных участках его скорость изменялась. Неважно в каком направлении совершалось движение и изменялось ли оно с течением времени. Характер движения может быть сложным или простым. Средняя скорость является скалярной величиной, поэтому алгоритм вычисления всегда будет примерно одинаковым.
Характер движения может быть сложным или простым. Средняя скорость является скалярной величиной, поэтому алгоритм вычисления всегда будет примерно одинаковым.
Как найти среднюю скорость тела?
Для случая, когда движение происходило с изменением скорости, но на протяжении равных отрезков времени наблюдалась разная скорость, применяют формулу среднего арифметического значения.
Пример. Автомобиль всего проехал 1 километр и 200 метров. После каждых 400 м он изменял скорость движения. Первые 400 метров он двигался со скоростью 20 км/ч, потом со скоростью 40 км/ч, 50 км/ч и последний участок проехал на скорости 35 км/ч. Определение средней скорости движения производим так:
\frac {20+40+50+35} {4} = 36,25 км/ч
В любом другом случае вычисление средней скорости в физике производят более сложным путем по формуле:
- Si – отрезок пути, км;
- ti – время прохождения отрезка пути, ч.
Пример задачи на вычисление средней скорости в физике
Человек прошел 1 час со скоростью 7 км/ч, а затем на протяжении 2-х часов шел со скоростью 4 км/ч. Определить среднюю скорость движения.
Определить среднюю скорость движения.
Сначала найдем путь, который был пройден за каждый из промежутков времени:
S1 = 1 х 7 = 7 км
S2 = 2 х 4 = 8 км
Далее пишется вышеприведенная формула в более привычном виде, как обычно, подставляются необходимые данные и определяется средняя скорость:
vcp. = \frac { S_1 + S_2 } { t_1 + t_2 } = \frac { 7 + 8 } { 1 + 2 } = 5 км/ч
Средняя скорость при равноускоренном движении
На практике очень часто встречаются задачи, когда вычисление средней скорости необходимо производить для случая, когда тело, двигаясь с какой-то начальной скоростью, с течением времени начало ускоряться и в конце пути достигло какой-то новой скорости. Тогда следует использовать формулу, которая выражает среднюю скорость через величину ускорения:
vcp. = v0 + \frac { at } { 2 } , где:
- v0 – начальная скорость,
- а – ускорение,
- t – время движения тела.
Пример. Двигаясь с начальной скоростью 160 м/с, самолет в течение двух минут ускорял свое движение на 1,5 м/с2. Какова его средняя скорость за этот промежуток времени?
Какова его средняя скорость за этот промежуток времени?
vcp. = 160 + \frac { 1,5 * 120 } { 2 } = 250 м/с
Поделитесь в социальных сетях:
20 ноября 2021, 14:40
Геометрия
Could not load xLike class!
Средняя скорость и средняя скорость
Прежде чем понять среднюю скорость и среднюю скорость, мы должны сначала понять разницу между расстоянием и перемещением. Скалярная величина «расстояние» представляет собой расстояние, пройденное объектом. Кратчайшее расстояние между двумя точками представлено смещением, которое является векторной величиной. Например, если частица движется по кругу, расстояние, пройденное за один оборот, равно длине окружности, а смещение равно нулю.
Давайте посмотрим на определения скорости и скорости.
Различие между средней скоростью и средней скоростью
Чтобы узнать о средней скорости и средней скорости, во-первых, мы должны знать некоторые термины и их значения.
Пройденное расстояние – Пройденное расстояние, как понятно из названия, представляет собой общее расстояние, пройденное объектом.
Затраченное время – Время, затраченное объектом на перемещение на заданное расстояние.
Смещение. Смещение — это кратчайшее расстояние между начальной точкой, в которой находился объект, и конечной точкой, в которой он оказался.
Скорость. Скорость — это расстояние, пройденное объектом в единицу времени. Скорость является скалярной величиной. Это означает, что у него нет определенного направления. Скорость относится к тому, насколько быстро движется объект, или, по сути, к скорости, с которой преодолевается расстояние.
Скорость — Скорость — это полное перемещение объекта в заданном направлении в единицу времени. Скорость является векторной величиной. Это означает, что он имеет определенное направление. Скорость относится к скорости перемещения объекта во времени. Представьте себе человека, который проходит некоторое расстояние, прежде чем вернуться в исходное положение. Поскольку скорость — это скорость смещения, это движение приводит к нулевой скорости. Если человек хочет максимизировать свою скорость, он должен максимизировать смещение от своего исходного положения. Поскольку скорость является векторной величиной, при ее оценке мы должны следить за направлением.
Поскольку скорость — это скорость смещения, это движение приводит к нулевой скорости. Если человек хочет максимизировать свою скорость, он должен максимизировать смещение от своего исходного положения. Поскольку скорость является векторной величиной, при ее оценке мы должны следить за направлением.
Основное различие между скоростью и скоростью состоит в том, что скорость не учитывает направление, так как это скалярная величина, а скорость зависит от пройденного пути, тогда как скорость является векторной величиной, учитывающей направление, а скорость зависит от смещение.
Средняя скорость — это отношение общего расстояния, пройденного объектом, к общему затраченному времени. Однако средняя скорость представляет собой изменение положения или смещения (∆x), деленное на интервалы времени (∆t), в течение которых происходит смещение.
Итак, какая разница в определении средней скорости и средней скорости? Являются ли они одинаковыми с точки зрения параметров, используемых в соответствующих формулах? Предположим, что оба термина передают одно и то же значение; тем не менее, имеют ли они одни и те же единицы и обладают ли количествами одной и той же природы?
Хорошо! Ответы на все вопросы есть на этой странице. Кроме того, мы поймем разницу в средней скорости и формуле средней скорости, а также проиллюстрируем примеры из реальной жизни.
Кроме того, мы поймем разницу в средней скорости и формуле средней скорости, а также проиллюстрируем примеры из реальной жизни.
Средняя скорость
Средняя скорость любого объекта равна общему расстоянию, пройденному этим объектом, деленному на общее время, затраченное на преодоление указанного расстояния. Средняя скорость объекта говорит вам о средней скорости, с которой он будет преодолевать расстояние; то есть объект имеет скорость 30 км/час, его положение будет изменяться в среднем на 30 км каждый час. Средняя скорость — это показатель, который представляет собой количество, деленное на время, затраченное на получение этого количества. Единицей скорости в СИ является метр в секунду.
Средняя скорость рассчитывается по формуле S = d/t, где S — средняя скорость, d — общее расстояние, t — общее время.
Средняя скорость
Средняя скорость объекта может быть определена как смещение относительно исходного положения, деленное на время. Другими словами, это скорость, с которой объект перемещается со временем. Как и средняя скорость, единицей СИ является метр в секунду. Можно также сказать, что средняя скорость представляет собой отношение полного смещения объекта к общему времени, в течение которого это действие должно произойти.
Другими словами, это скорость, с которой объект перемещается со временем. Как и средняя скорость, единицей СИ является метр в секунду. Можно также сказать, что средняя скорость представляет собой отношение полного смещения объекта к общему времени, в течение которого это действие должно произойти.
Направление средней скорости является направлением смещения. Даже если скорость объекта колеблется и его величина меняется, его направление все равно будет таким же, как и направление смещения. Величина средней скорости всегда либо меньше, либо равна средней скорости, потому что перемещение всегда меньше или равно пройденному расстоянию.
Средняя скорость рассчитывается по формуле V = D/t, где V — средняя скорость, D — полное перемещение, t — общее время.
Формула для средней скорости и средней скорости
vср = Δx/Δt
Вы заметили, что формулы для средней скорости и средней скорости одинаковы.
Единственная разница заключается в типе физической величины, т.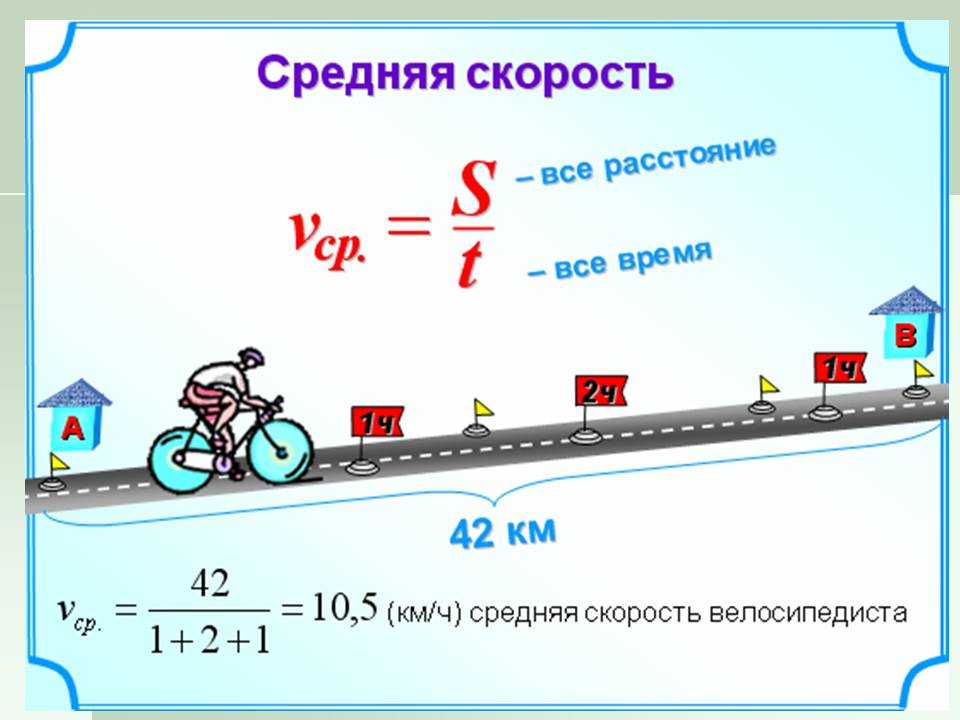 е. скорости и скорости. Скорость — это скалярная величина, которая имеет только величину. Однако скорость является векторной величиной, которая имеет как величину, так и направление.
е. скорости и скорости. Скорость — это скалярная величина, которая имеет только величину. Однако скорость является векторной величиной, которая имеет как величину, так и направление.
Теперь рассмотрим некоторые задачи на среднюю скорость:
Задачи:
1. Автомобиль проезжает расстояние 70 км за 2 часа. Какова средняя скорость?
Ответ: средняя скорость = расстояние/время
Следовательно, средняя скорость автомобиля 70 км/2 часа = 35 км/час.
2. Человек может ходить со скоростью 1,5 метра в секунду. Какое расстояние он пройдет за 4 минуты?
Ответ: средняя скорость = расстояние/время
Расстояние = средняя скорость (время)
= 1,5(4) (60) = 360 метров
3. Поезд движется по прямой с постоянной скоростью 60 км/ч на определенное расстояние d, а затем проходит еще одно расстояние, равное 2d в том же направлении. с постоянной скоростью 80 км/ч в том же направлении, что и раньше. а) Какова средняя скорость поезда на всем пути?
а) Какова средняя скорость поезда на всем пути?
Решение: а) Время t1 для преодоления расстояния d со скоростью 60 км/ч определяется как t1 = d / 60
Время t2 для преодоления расстояния 2d со скоростью 80 км/ч определяется как t2 = 2d / 80
Средняя скорость = расстояние/время = (d + 2d) / (d/60) + (2d/80)
= 3d / (80d + 2d × 60)/(60 × 80)
= 3 d/ (200d/4800) = 3d (4800)/200d = 72 км/ч
4. Вычислить среднюю скорость человека за определенный промежуток времени, если он проходит 7 м за 4 с и 18 м за 6 с по оси x -ось?
Решение: Начальное расстояние, пройденное человеком, xi = 7 м,
Конечное пройденное расстояние, xf = 18 м,
Начальный интервал времени ti = 4 с,
Конечный временной интервал tf = 6 с,
Средняя скорость v = xi − xf / ti − tf = 18 − 7 / 6 − 4 = 11 / 2 = 5,5 м/с.
Из приведенного выше текста мы понимаем, что средняя скорость любого объекта равна общему расстоянию, пройденному этим объектом, деленному на общее время, затраченное на преодоление указанного расстояния.
Средняя скорость объекта говорит вам о средней скорости, с которой он будет преодолевать расстояние; то есть объект имеет скорость 30 км/час, его положение будет изменяться в среднем на 30 км каждый час. Средняя скорость — это показатель, который представляет собой количество, деленное на время, затраченное на получение этого количества. Единицей скорости в СИ является метр в секунду.
Средняя скорость рассчитывается по формуле S = d/t, где S — средняя скорость, d — общее расстояние, t — общее время.
Средняя скорость
Из приведенного выше текста мы понимаем, что среднюю скорость объекта можно определить как смещение относительно исходного положения, деленное на время.
Другими словами, это скорость, с которой объект перемещается со временем.
Например, средняя скорость в системе СИ равна метрам в секунду. Можно также сказать, что средняя скорость представляет собой отношение полного смещения объекта к общему времени, в течение которого это действие должно произойти.
Средняя скорость объекта может быть определена как смещение относительно исходного положения, деленное на время. Другими словами, это скорость, с которой объект перемещается со временем. Как и средняя скорость, единицей СИ является метр в секунду. Можно также сказать, что средняя скорость представляет собой отношение полного смещения объекта к общему времени, в течение которого это действие должно произойти.
Направление средней скорости является направлением смещения. Даже если скорость объекта колеблется и его величина меняется, его направление все равно будет таким же, как и направление смещения. Величина средней скорости всегда меньше или равна средней скорости, потому что перемещение всегда меньше или равно пройденному расстоянию.
Средняя скорость рассчитывается по формуле V = D/t, где V равно средней скорости, D равно полному перемещению и t равно общему времени.
Теперь давайте рассмотрим некоторые задачи на среднюю скорость.
Задачи:
1. Водитель грузовика проезжает 20 км по дороге за 5 минут. Затем он дает задний ход и проезжает 12 км по дороге за 3 минуты. Какова его средняя скорость?
Решение: v = D/t
v = (20 — 12)/(5 + 3)
= 8/8 = 1 км/мин
2. Человек проходит 10 км на восток за 2 часа, а затем 2,5 км на запад за 1 час. Вычислите полную среднюю скорость человека?
Решение: vср = D/t
= (10 — 2,5)/2 + 1
= 7,5/3
vср = 2,5 км/ч
человека, если он пройдет 7 м за 4 с и 18 м за 6 с по оси абсцисс?
Решение: Начальное расстояние, пройденное человеком, xi = 7 м,
Конечное пройденное расстояние, xf = 18 м,
Начальный интервал времени ti = 4 с,
Конечный интервал времени tf = 6 с,
Средняя скорость vav = xi − xf / ti − tf
= 18 /(6 − 4) = 11/2 = 5,5 м /s
Различия и сходства между средней скоростью и средней скоростью
Сходства – Оба этих термина являются средними некоторой длины по времени. Единица СИ и другие стандартные единицы измерения как средней скорости, так и средней скорости одинаковы. Формула, используемая для расчета средней скорости и средней скорости, практически одинакова, v = D/t, s = d/t, с той лишь небольшой разницей, что в первом случае нужно указать направление.
Единица СИ и другие стандартные единицы измерения как средней скорости, так и средней скорости одинаковы. Формула, используемая для расчета средней скорости и средней скорости, практически одинакова, v = D/t, s = d/t, с той лишь небольшой разницей, что в первом случае нужно указать направление.
Различия — Средняя скорость является скаляром и не зависит от наличия или отсутствия направления, в то время как средняя скорость, являющаяся вектором, нуждается в направлении. Средняя скорость зависит от расстояния, то есть общей длины, пройденной при измерении, в то время как средняя скорость зависит от смещения, то есть прямого расстояния от исходного положения до конечного положения.
Задачи, относящиеся как к средней скорости, так и к средней скорости
1. Автомобиль проезжает по прямой дороге 120 метров на восток за 5 секунд, затем 60 метров на запад за 1 секунду. Определить среднюю скорость и среднюю скорость.
Решение:
Расстояние = 120 метров + 60 метров = 180 метров
Перемещение = 120 метров – 60 метров = 60 метров на восток.
Прошедшее время = 5 секунд + 1 секунда = 6 секунд.
Средняя скорость = расстояние / прошедшее время = 180 метров / 6 секунд = 30 метров в секунду.
Средняя скорость = перемещение / прошедшее время = 60 метров / 6 секунд = 10 метров в секунду.
2. Бегун бежит по прямоугольной дорожке длиной = 50 метров и шириной = 20 метров. Он дважды проходит по прямоугольной дорожке и, наконец, возвращается к исходной точке. Если общее время, затрачиваемое им на бег по дорожке, равно 100 секундам, определите среднюю скорость и среднюю скорость.
Решение:
Окружность прямоугольника, равная расстоянию, пройденному за один круг = 2(50 метров) + 2(20 метров) = 100 метров + 40 метров = 140 метров.
Когда бегун пробегает прямоугольник дважды = 2(140 метров) = 280 метров.
Расстояние = 280 метров
Перемещение = 0 метров. (Поскольку бегун вернулся в исходную точку)
Средняя скорость равна расстоянию/прошедшему времени = 280 метров/100 секунд = 2,8 метра/секунду.
Средняя скорость равна перемещению/прошедшему времени = 0/100 секунд = 0
3. Человек начинает идти из точки на круглом поле радиусом 0,5 км и через 1 час оказывается в той же точке, где он изначально начал.
а) Какова средняя скорость на всем пути, который он проехал? Какова средняя скорость этого человека для того же?
Решение: а) Если этот человек обходит круглое поле и возвращается в ту же точку, то он прошел расстояние, равное длине окружности.
Таким образом, средняя скорость, которую он проехал = Расстояние/время = время прохождения окружности = π (0,5) (2)/1 час = 3,14 км/час (приблизительно).
б) Если он ходит по кругу и возвращается в ту же точку, с которой начал движение по кругу, то изменение его положения равно нулю. Поскольку изменение его положения равно нулю, перемещение также равно нулю. Это означает, что средняя скорость также равна нулю.
Перемещение, время и средняя скорость: значения и формулы
«Мы уже там?» Если вы когда-либо были пассажиром в ужасно долгом путешествии на летние каникулы или каникулы, вы знаете, насколько важны каждые миль. Возможно, вы попросили своего водителя немного ускориться, зная, что можете прибыть в пункт назначения немного раньше. И когда ответ на этот вопрос был « N о!» , возможно, вы изучали свой запланированный маршрут, ища более короткий путь, чтобы получить несколько дополнительных минут удовольствия.
Возможно, вы попросили своего водителя немного ускориться, зная, что можете прибыть в пункт назначения немного раньше. И когда ответ на этот вопрос был « N о!» , возможно, вы изучали свой запланированный маршрут, ища более короткий путь, чтобы получить несколько дополнительных минут удовольствия.
Даже самые, казалось бы, простые сценарии движения, такие как скучная поездка в гораздо менее скучный тематический парк, сводятся к набору фундаментальных величин кинематики. Ваше путешествие к пониманию того, как устроен мир, начинается с изучения того, как движутся самые основные системы: почему физическое положение в пространстве, направление движения, скорость движения и время имеют значение. В этой статье мы рассмотрим определения, а также соответствующие формулы и примеры смещения, расстояния, времени и средней скорости. Прежде чем вы это узнаете, вы гораздо лучше поймете все причины ответа, «Мы доберемся, когда доберемся!»
Определение смещения в физике
Возможно, наиболее легко наблюдаемым аспектом движения является изменение положения во времени. Всякий раз, когда вы встаете со стула и идете на кухню, едете на автобусе из дома в школу или идете от входной двери к почтовому ящику, вы меняете физическое положение своего тела в пространстве. Мы понимаем эту концепцию позиционного изменения как смещение.
Всякий раз, когда вы встаете со стула и идете на кухню, едете на автобусе из дома в школу или идете от входной двери к почтовому ящику, вы меняете физическое положение своего тела в пространстве. Мы понимаем эту концепцию позиционного изменения как смещение.
Смещение — общее изменение положения объекта.
Смещение является векторной величиной: оно имеет направление и величину.
Есть несколько способов измерения перемещения. Мы можем использовать стандартную декартову координатную плоскость и вычислить разницу между различными точками. В качестве альтернативы мы можем рассчитать изменения положения различных зданий, городов, штатов или стран относительно друг друга на карте. Мы даже можем использовать координаты GPS. Независимо от того, как вы решите измерять, вам нужно помнить, чтобы сначала определить начало координат, положительное и отрицательное направления — не зная этих деталей, вы можете получить неправильный расчет!
Расстояние по сравнению с перемещением
Вы должны быть хорошо знакомы с понятием расстояния от путешествий в повседневной жизни. Вы, наверное, знаете, сколько миль нужно, чтобы добраться до продуктового магазина от вашего дома, дома друга или члена большой семьи или другого места, которое вы часто посещаете. Теперь давайте определим, что мы подразумеваем под расстоянием в контексте физики.
Вы, наверное, знаете, сколько миль нужно, чтобы добраться до продуктового магазина от вашего дома, дома друга или члена большой семьи или другого места, которое вы часто посещаете. Теперь давайте определим, что мы подразумеваем под расстоянием в контексте физики.
Расстояние равно величине смещения.
Расстояние является скалярной величиной: оно имеет величину, но не имеет направления.
Теперь расстояние иногда путают с термином пройденного расстояния.
Пройденное расстояние — это длина пути от начала до конца.
Итак, в чем разница между всеми этими терминами? В отличие от смещения, которое может иметь отрицательное, положительное или нулевое значение, измерения расстояния всегда неотрицательны . Если это звучит немного запутанно, давайте проведем быстрый мысленный эксперимент. Представьте, что вы бегун, участвующий в гонке \(400\,\mathrm{m}\). Звучит пушка, и вы начинаете пробираться по трассе к финишу. Теперь длина вашего пути от начала до конца равна \(400\,\mathrm{m}, \), однако смещение от начала до конца равно \(0\,\mathrm{m} \) в каждом направлении.
Теперь длина вашего пути от начала до конца равна \(400\,\mathrm{m}, \), однако смещение от начала до конца равно \(0\,\mathrm{m} \) в каждом направлении.
Почему? Ну, ваша общая позиция не изменилась, так как вы закончили в той же позиции, что и начали. В результате расстояние между началом и концом также равно \(0\,\mathrm{m} \), поскольку расстояние является величиной смещения, а величина нуля равна нулю.
Рис. 1. Гонка на треке как пример зависимости пройденного расстояния от расстояния.
Формулы расстояния и смещения
Теперь, когда мы познакомились с различиями между расстоянием и перемещением, давайте посмотрим на формулы, которые нам нужно знать. Запишем формулу смещения математически как
\begin{align*} \text{смещение} &=\text{конечная позиция} — \text{начальная позиция} \\ \Delta x&=x_\text{f}-x_\text{i}, \ end{align*}
, где \(x_\text{i}\) — начальная позиция, а \(x_\text{f}\) — конечная позиция. Греческая буква \(\Дельта\), произносимая как «Дельта», указывает на изменение некоторой переменной . Таким образом, под \(\Delta x\) мы подразумеваем изменение положения или перемещение.
Таким образом, под \(\Delta x\) мы подразумеваем изменение положения или перемещение.
Если вы знаете длину каждого отрезка пути по прямой между несколькими парами точек, вы можете вычислить расстояние, просто найдя сумму всех отдельных длин. Мы также можем вычислить расстояние \(d\) между двумя точками на двумерной плоскости, используя формулу: 92.}} \end{align*}
Проще говоря, мы вычисляем величину вектора смещения , что приводит к скалярной величине. И расстояние, и перемещение измеряются в единицах длины с соответствующей базовой единицей СИ в метрах, представленной символом \(\mathrm{m}\).
Давайте рассмотрим пример сравнения формул смещения и расстояния, чтобы увидеть, как эти расчеты могут сильно отличаться на практике.
Допустим, вам нужно пойти в местный зоомагазин за припасами, расположенный в пяти милях от вашего дома. Вы начинаете свое путешествие дома, едете на машине в магазин и возвращаетесь домой. Какой у вас пройденный путь и перемещение в конце пути?
Какой у вас пройденный путь и перемещение в конце пути?
Рис. 2: График, демонстрирующий расчеты расстояния, пройденного расстояния и перемещения для одной поездки.
Начнем с расчета пройденного расстояния. В этом случае вы проехали пять миль дважды, поэтому пройденное расстояние равно просто
\begin{align*} s &=\mathrm{5\, mi+5\, mi=10\, mi}. \end{align*}
Расстояние, которое вы преодолели от начала до конца поездки, составляет десять миль. Далее посчитаем смещение,
\begin{align*} \Delta x &= x_\text{f} — x_\text{i}=0\,\mathrm{mi} \end{align*}
Итак, несмотря на то, что вы проехали десять миль, ваше перемещение и расстояние равно нулю миль, потому что вы оказались в том же положении, что и начали.
В предыдущем примере ваше перемещение равно нулю миль, потому что ваше начальное и конечное положения не изменились. Другими словами, ваше положение не изменилось с тех пор, как вы начали и закончили дома. Давайте рассмотрим другой пример, на этот раз с поездкой, заканчивающейся в позиции, отличной от исходной.
Давайте рассмотрим другой пример, на этот раз с поездкой, заканчивающейся в позиции, отличной от исходной.
Вместо этого скажем, что после посещения того же зоомагазина, что и раньше, вы решили пойти в обход. На этот раз вы начинаете из дома, едете в зоомагазин, посещаете пекарню, а затем едете в школу. Пекарня находится в трех милях от зоомагазина, а школа — в десяти милях от пекарни. Найдите пройденное расстояние и свое перемещение в конце пути. Также рассчитайте расстояние до начальной точки.
Рис. 3: График, демонстрирующий расчеты расстояния, пройденного расстояния и перемещения для многоэтапной поездки.
Опять же, давайте просуммируем длину между каждой позицией для трех этапов пути, чтобы узнать пройденное расстояние:
\begin{align*} s&=\mathrm{5\, mi+3\, mi+ 10\, ми=18\, ми}. \end{align*}
Наконец, давайте найдем разницу в расположении между школой и домом, чтобы получить общее смещение:
\begin{align*} \Delta x &=\mathrm{-2\, mi-0\ , mi=-2\, mi}. \end{выравнивание*}
\end{выравнивание*}
У нас отрицательное значение смещения после этой поездки, потому что школа расположена слева от нашего дома, а мы выбрали положительное направление вправо. Теперь, чтобы вычислить расстояние, мы должны взять величину нашего смещения следующим образом:
$$\begin{align}\mathrm{distance}&=|-2\,\mathrm{mi}| =2\,\mathrm{mi}\end{align}.$$
Наше расстояние в конце этой поездки до исходной позиции равно \( 2\,\mathrm{mi} \).
Смещение в предыдущем примере равно \(\mathrm{-2\, mi}\), поскольку и зоомагазин, и пекарня расположены на положительной оси \(x\) справа от \(x=0 \,\mathrm{mi}\), а школа расположена на отрицательной оси \(x\). Школа находится в двух милях от вашего дома, но в противоположном направлении от зоомагазина и пекарни. Давайте рассмотрим еще один пример сравнения вычислений расстояния и смещения.
В предыдущих примерах исходной позицией был ваш дом. Если ваше начальное положение — школа, найдите расстояние и чистое перемещение для поездки, начинающейся в школе, посещающей пекарню и заканчивающейся в зоомагазине.
Опять же, начиная с расчета расстояния:
\begin{align*} d&=\mathrm{10\, mi+3\, mi=13\, mi}.\end{align*}
И, наконец, расчет смещения:
\begin{align*} \Delta x &=8\, \mathrm{mi}-(-2\,\mathrm{mi})=10\, \mathrm{mi}. \end{выравнивание*}
На этот раз наше смещение от начала координат положительное.
Давайте вспомним, что мы уже узнали о расстоянии и смещении.
- Расстояние представляет собой величину смещения и всегда неотрицательно.
- Пройденное расстояние — это длина пути от начала до конца.
- Расстояние не учитывает направление и является скалярной величиной.
- Смещение — это изменение положения между двумя точками, которое может быть нулевым, положительным или отрицательным.
- Перемещение зависит от направления и является векторной величиной.
Формула времени в физике
Понятие времени уже стало очень привычной частью повседневной жизни. У вас есть школьное расписание для смены занятий в определенные часы дня, будильник, установленный на определенный час, чтобы вставать по утрам, и представление о том, какую часть дня будут занимать определенные задачи. В физике время является важной переменной для понимания всех видов физических систем, и, в частности, его можно наблюдать по изменению некоторой величины.
У вас есть школьное расписание для смены занятий в определенные часы дня, будильник, установленный на определенный час, чтобы вставать по утрам, и представление о том, какую часть дня будут занимать определенные задачи. В физике время является важной переменной для понимания всех видов физических систем, и, в частности, его можно наблюдать по изменению некоторой величины.
Время — это измерение того, сколько времени требуется для возникновения события или наблюдаемого изменения.
Мы измеряем время в секундах, \(\mathrm{s}\), так как это основная единица времени в системе СИ. В практическом смысле, например, во время лаборатории, мы измеряем течение времени секундомером или обычными часами. Мы также можем определить время, прошедшее для движущегося объекта, используя формулу
\begin{align} \mathrm{time} &=\frac{\text{пройденное расстояние}}{\text{скорость}}, \\t& =\фрак{с} {v}. \end{выравнивание}
Конечно, время является скалярной величиной, математически определяемой с использованием других скалярных величин и измеряемой относительно предыдущей отметки времени, выбранной на часах. Мы понимаем, что время постоянно движется вперед, без отрицательного направления или эквивалента, и нет возможности отменить то, что уже было сделано в прошлом. Мы используем время как меру того, как долго длилось событие.
Мы понимаем, что время постоянно движется вперед, без отрицательного направления или эквивалента, и нет возможности отменить то, что уже было сделано в прошлом. Мы используем время как меру того, как долго длилось событие.
Определение средней скорости
Объект, положение которого изменяется, имеет измеримую скорость изменения, известную как скорость.
Скорость — скорость изменения положения.
Скорость — это еще один способ сказать: «Объект перемещается на это большое расстояние за каждую единицу прошедшего времени». Средняя скорость — это просто средняя скорость изменения положения за весь период времени, в отличие от i мгновенной скорости , которая измеряется в определенный момент времени с использованием заданной функции скорости.
Скорость против скорости
Точно так же, как существует ключевое различие между расстоянием и перемещением, такое же различие существует для скорости и скорости.
Скорость — величина скорости.
Скорость описывает, насколько быстро объект перемещается в пространстве относительно времени или какое расстояние преодолевает объект за определенный период времени. В повседневном языке мы могли бы использовать термины «скорость» и «скорость» взаимозаменяемо, но в физике мы делаем важное различие между ними. Скорость — скалярная величина, числовое значение без направления, а скорость — векторная величина, имеющая как величину, так и направление.
Формулы скорости и средней скорости
В зависимости от имеющейся системы и заданных начальных условий существует несколько формул, которые мы можем использовать в физике для определения средней скорости и скорости. Простейшая формула для средней скорости:
\begin{align*} \text{средняя скорость} &= \frac{\text{смещение}}{\text{прошедшее время}}, \\ v_{\mathrm{avg }}&=\frac{\Delta x}{\Delta t}, \\ v_{\mathrm{avg}}&=\frac{x_\text{f} — x_\text{i}}{t_\text {f} — t_\text{i}}. \end{выравнивание*}
\end{выравнивание*}
Мы можем рассчитать среднюю скорость движущегося объекта, используя аналогичную формулу:
\begin{align*}\text{средняя скорость}&= \frac{\text{пройденное расстояние}}{\text{истекшее время} } =\frac{s}{t}.\end{align*}
И скорость, и скорость измеряются в единицах \(\mathrm{\frac{длина}{время}}\), наиболее распространенная единица измерения будучи \ (\ mathrm {\ frac {m} {s}} \). Давайте рассмотрим краткий пример расчета скорости движущегося автомобиля.
Обратите внимание, что пройденное расстояние обозначается \( с. \)
Допустим, вы едете на машине и проехали \( 10,2 \) миль за \( 25 \) минут. Какая у вас средняя скорость в милях в час?
Во-первых, мы хотим преобразовать \(\mathrm{25\, min}\) в \(\mathrm{h}\):
\begin{align*} \mathrm{\frac{1\, h} {60\, мин}\умножить на 25\, мин=0,42\, ч}. \end{align*}
Далее, мы хотим использовать формулу для средней скорости и решить:
\begin{align*} \text{средняя скорость}&=\frac{s}{t}, \\ & = \ mathrm {\ frac {10,2 \, mi} {0,42 \, h}}, \\ & = 24 \, \ mathrm {\ frac {mi} {h}}. \end{выравнивание*}
\end{выравнивание*}
Таким образом, ваша средняя скорость равна \(24\, \mathrm{ми}/ч\). Поскольку скорость является скалярной величиной, мы ожидали, что этот ответ будет неотрицательным, так что это хорошо.
Давайте рассмотрим пример расчета средней скорости с использованием уравнения для средней скорости.
Вы бежите \( 100.1\,\mathrm{m} \) к автобусной остановке, но роняете блокнот на \( 72\,\mathrm{m}. \) Затем бежите обратно, чтобы забрать его в \ ( 23\,\mathrm{s}. \) Найдите свою среднюю скорость за 23-секундный интервал времени.
Рассчитаем скорость, используя \(x_\text{i}=0\, \mathrm{m}\) и \(x_\text{f}=72\, \mathrm{m}\):
\ begin{align*} v_\mathrm{avg}&=\frac{\Delta x}{\Delta t}, \\ v_\mathrm{avg}&=\mathrm{\frac{72\, m-0\, m}{23\, s}}, \\ v_\mathrm{avg}&=\mathrm{3.1\, \frac{m}{s}}. \end{align*}
Теперь, какой будет ваша средняя скорость, если вы также бросите перо в исходное положение и побежите за ним обратно? Скажем, вам потребуется дополнительно \( 18\,\mathrm{s} \), чтобы вернуться в исходное положение. Давайте рассчитаем среднюю скорость вашего бега до автобусной остановки и обратно, чтобы забрать свой блокнот и ручку.
Давайте рассчитаем среднюю скорость вашего бега до автобусной остановки и обратно, чтобы забрать свой блокнот и ручку.
На этот раз общее истекшее время равно \(\mathrm{23\, s+18\, s=41\, s}\). Теперь найдем вашу среднюю скорость:
\begin{align*} v_\mathrm{avg}&=\mathrm{\frac{0\, m-0\, m}{41\, s}} \\ v_ \mathrm{avg}&=\mathrm{0\, \frac{m}{s}}. \end{align*}
Поскольку для этого расчета мы использовали только конечные точки, обе из которых равны нулю, средняя скорость также равна нулю. Какова средняя скорость? Используя формулу для средней скорости, при общем пройденном расстоянии \(\mathrm{200,2\, м}\) от бега туда и обратно между автобусной остановкой, мы получаем
\begin{align*} \text{средняя скорость}=\mathrm{\frac{200,2\, м}{41\, с}} =4,9\, \mathrm{\frac{м}{с}}. \end{align*}
Чтобы закончить наше обсуждение средней скорости, давайте кратко рассмотрим нахождение скоростей на графике.
График средней скорости
В дополнение к численному решению средней скорости, также полезно графически отображать различные переменные движения, чтобы визуализировать проблему. Мы можем использовать позицию — временной график в качестве инструмента для изучения скорости объекта с учетом функции положения. Давайте используем следующий график, чтобы попрактиковаться в нахождении скорости между несколькими разными точками кривой.
Мы можем использовать позицию — временной график в качестве инструмента для изучения скорости объекта с учетом функции положения. Давайте используем следующий график, чтобы попрактиковаться в нахождении скорости между несколькими разными точками кривой.
Рис. 4: График положения в зависимости от времени, где наклон между любыми двумя точками равен средней скорости.
Мы можем найти среднюю скорость, рассчитав наклон между двумя точками на кривой. Рассчитаем среднюю скорость для трех разных отрезков графика по двум точкам с графика. Мы будем использовать нашу формулу \(v_{\mathrm{avg}}=\frac{\Delta x}{\Delta t}\) для каждого расчета.
Сначала найдем среднюю скорость между второй точкой \((4,8)\) и четвертой точкой \((12,2)\):
\begin{align*} v_{\mathrm{avg }} = \ mathrm {\ frac {2 \, m-8 \, m} {12 \, s-4 \, s} = -0,8 \, \ frac {m} {s}}. \end{align*}
Здесь средняя скорость отрицательна, и на графике мы видим нисходящий тренд. Далее найдем среднюю скорость между третьей точкой \((8,6)\) и пятой точкой \((18, 6)\):
Далее найдем среднюю скорость между третьей точкой \((8,6)\) и пятой точкой \((18, 6)\):
\begin{align*} v_{\mathrm{avg}} = \mathrm{\frac{6\, m-6\, m}{18\, s-8\, s}=0\, \frac{m}{s}}. \end{выравнивание*}
Средняя скорость равна нулю, поскольку положение не изменяется. Наконец, вычислим среднюю скорость между точками один \((1, 3)\) и два \((4,8)\):
\begin{align*} v_{\mathrm{avg}}= \mathrm {\ гидроразрыва {8 \, м-3 \, м} {4 \, с-1 \, с} = 2 \, \ гидроразрыва {м} {с}}. \end{align*}
Между точками один и два наблюдается восходящий тренд, поэтому средняя скорость положительна.
Смещение, время и средняя скорость — основные выводы
Смещение — это общее изменение положения объекта.
Расстояние — это величина смещения.
Пройденное расстояние — это длина пути от начала до конца.
Время — это мера того, сколько времени занимает событие или наблюдаемое изменение.

