Силы сопротивления движению подвижного состава
- Подробности
- Категория: Подвижной состав
- тяга
- движение поезда
Содержание материала
- Силы сопротивления движению подвижного состава
- Основное сопротивление движению
- Сопротивление от трения качения колес по рельсам
- Сопротивление от трения скольжения колес по рельсам
- Диссипация энергии при взаимодействии колес с рельсами
- Сопротивление воздушной среды
- Диссипация энергии в окружающую среду
- Расчет основного сопротивления
- Добавочное сопротивление при трогании поезда с места
- Пути снижения сопротивления движению поездов
Страница 1 из 10
Классификация сил сопротивления
Работа касательной силы тяги, создаваемой при взаимодействии движущихся колес локомотива с рельсами, преимущественно затрачивается на преодоление внешних сип, препятствующих движению поезда. Природа и причины возникновения, а также величина этих внешних сил различны. Многие внешние силы случайны, многие взаимосвязаны по физике явления. Неуправляемые внешние силы, направленные в сторону противоположную направлению движения поезда и, следовательно, препятствующие его движению, называются действительными силами сопротивления движению.
Природа и причины возникновения, а также величина этих внешних сил различны. Многие внешние силы случайны, многие взаимосвязаны по физике явления. Неуправляемые внешние силы, направленные в сторону противоположную направлению движения поезда и, следовательно, препятствующие его движению, называются действительными силами сопротивления движению.
Силы сопротивления движению подвижного состава принято обозначать буквой W (от немецкого слова der Wiederstand — сопротивление, противодействие).
Классификация сил сопротивления основана на их разделении по следующим признакам с соответствующими обозначениями.

Классификация сил сопротивления по отношению к весу подвижного состава:
- полное сопротивление — W, Н;
- удельное сопротивление — w, Н/кН.
Полное сопротивление W представляет собой сопротивление движению поезда или единицы подвижного состава в целом.
Удельное сопротивление w — сила сопротивления, в Н, движению каждой единицы веса поезда, в кН. Удельные силы сопротивления движению широко используются при выполнении тяговых расчетов.
Полное Wв Н, и удельное w в Н/кН, сопротивления взаимосвязаны:
или
где Р + Q — вес поезда, кН.
Классификация сил сопротивления по условиям эксплуатации:
- основное сопротивление — Wo, wo;
-дополнительные сопротивления — Wдоп, wдоп;
-добавочное сопротивление при трогании с места — Wтр;
- общее сопротивление — WK,wK.
За основное сопротивление принимают те силы, которые препятствуют движению подвижного состава по прямому горизонтальному пути на открытой местности при нормальных метеоусловиях с любой допустимой по безопасности движения скоростью.
Необходимо отметить, что в теории локомотивной тяги движение всех единиц подвижного состава, в том числе локомотивов, описывается одним и тем же уравнением движения повозки. Наличие на локомотивах тяговых электродвигателей и зубчатых тяговых передач, а также механических трансмиссий на тепловозах с гидропередачами делает основное сопротивление движению локомотивов отличным от вагонов. На величину основного сопротивления движению также существенное влияние оказывает режим работы локомотива в эксплуатации.
В этой связи дополнительно различают силы основного сопротивления в зависимости от режима работы локомотива (тягового режима или холостого хода):
- основное сопротивление движению поезда с локомотивом, работающим в режиме тяги, — Wо,wо;
- основное сопротивление движению поезда с локомотивом, работающим в режиме холостого хода, — Wox, wοχ.
Основная физическая природа основного сопротивления — силы механического трения.
Основное сопротивление всегда сопутствует движению подвижного состава; при любых условиях его эксплуатации величина Wo не может быть равна нулю.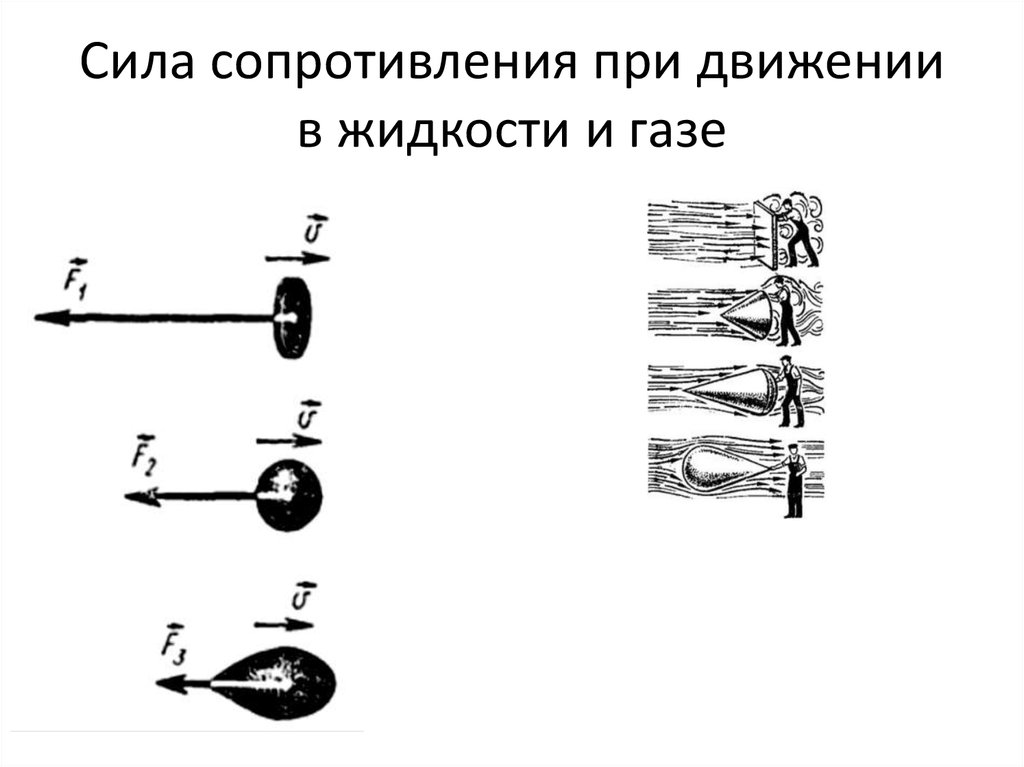
Дополнительные сопротивления — временно действующие силы, возникающие в конкретных условиях эксплуатации подвижного состава, например при движении по уклону профиля пути, в кривой, в тоннелях и прочее.
Добавочное сопротивление возникает при трогании с места единиц подвижного состава. Это сопротивление ограничено по времени действия, его физическая природа и причины возникновения заметно отличаются от сил основного сопротивления. По этим и раду других причин добавочное сопротивление при выполнение тяговых расчетов учитывается отдельно.
Классификация сил сопротивления по типу подвижного состава:
- сопротивление движению локомотива — вводится один штрих вверху — W’,w’;
- сопротивление движению состава (вагонов) — вводятся два штриха вверху — W», w»;
- сопротивление движению поезда — штрихи не применяются — W,w.

- Вперёд
- Назад
- Вперёд
Близкие публикации:
- Системы управления ЭПС
- Тормозные силы и торможение поездов
- Подтягивание вагонов
- Использование присадок к маслам на тепловозах
- Надежность механической части подвижного состава
© 2009-2022 — lokomo.ru, железные дороги.
СИЛЫ СОПРОТИВЛЕНИЯ ДВИЖЕНИЮ ПОЕЗДА
6.1. Силы основного сопротивления движению поезда
Общие сведения. К силам сопротивления движению поезда относят внешние неуправляемые силы, направленные, как правило, против движения поезда. Как и силы тяги, они приводятся к точкам касания колес с рельсами.
Силы сопротивления движению делят на Основные, действующие при движении поезда всегда, и Дополнительные, возникающие только при движении по отдельным участкам пути или в отдельные периоды времени. Сумму сил основного и дополнительного сопротивлений называют Общим сопротивлением движению поезда №к.
Силы сопротивления движению поезда складываются из сил сопротивления движению локомотива W’ и состава W». В свою очередь силы сопротивления движению состава являются суммой сил сопротивления движению вагонов.
В расчетах используют удельные силы сопротивления движению, т. е. силы, выраженные в ньютонах, отнесенные к 1 кН веса поезда.
Силы основного сопротивления движению W0, действующие при движении по прямолинейному горизонтальному пути, обусловлены в основном трением в подшипниках подвижного состава, взаимодействием колесных пар с рельсами и сопротивлением воздушной среды при отсутствии ветра.
Сила трения в подшипниках подвижного состава. На рис. 6.1 Показан подшипник трения скольжения.
Под воздействием нагрузки на
Шейку оси подвижного состава Qol и вращении колесной пары по часовой стрелке возникает сила трения, равная произведению силы Qoi на коэффициент трения (р. Очевидно, сила <701ф, умноженная на радиус шейки оси D/2, дает момент сопротивления вращению:
Заменим этот момент сопротивления равным ему моментом М2 с приложением силы А в точке касания колеса и рельса:
Момент М2 действует также против направления вращения колеса. тр всего поезда. Если пренебречь разницей между нагрузкой от колес на рельсы и нагрузкой на шейку оси (определяемую весом колесной пары), то удельная сила сопротивления движению, Н/кН:
тр всего поезда. Если пренебречь разницей между нагрузкой от колес на рельсы и нагрузкой на шейку оси (определяемую весом колесной пары), то удельная сила сопротивления движению, Н/кН:
Поскольку отношение D/D колеблется для вагонных колесных пар в небольших пределах, удельная сила сопротивления движению от трения в буксовых подшипниках зависит от коэффициента трения ф. Он изменяется в зависимости от вязкости смазки, ее физико-химических свойств, силы нажатия на единицу площади подшипника, частоты вращения шейки и температуры наружного воздуха. С понижением температуры возрастает вязкость смазки и увеличивается коэффициент трения.
На рис. 6.2 приведены зависимости коэффициентов трения ф буксовых подшипников от скорости движения V, из которых видно, что роликовые подшипники имеют значительно меньшие значения ф по сравнению с подшипниками скольжения. Большой разброс точек объясняется разными нагрузками на колесные пары и отклонениями в вязкости смазки. Зона больших коэффициентов трения соответствует малым нагрузкам на ось и большей вязкости смазки. С увеличением этой нагрузки и уменьшением вязкости смазки коэффициент ф снижается.
С увеличением этой нагрузки и уменьшением вязкости смазки коэффициент ф снижается.
При трогании с места ф имеет большую величину из-за выжимания смазки с контактной поверхности подшипника и отсутствия масляной пленки. Это особенно заметно у подшипников скольжения. По мере вращения оси в зоне контакта появляется смазка, и коэффициент трения снижается. В дальнейшем при наличии смазки и увеличения скорости движения коэффициент трения возрастает.
Можно считать, что удельное сопротивление движению за счет трения в подшипниках скольжения составляет в среднем 0,5…
1 Н/кН, а при роликовых подшипниках — 0,1…0,2 Н/кН. Поэтому на отечественных дорогах занимались переводом буксовых подшипников скольжения на роликовые. В настоящее время подавляющее большинство подвижного состава работает на роликовых подшипниках. Кроме уменьшения сопротивления движению роликовые подшипники позволили упростить уход за ними в эксплуатации и уменьшить расход смазки.
В случае движения локомотивов на выбеге или при механическом торможении (на холостом ходу без тока) в силы сопротивления движению от трения й^р х входят также силы трения в элементах передачи, моторно-осевых подшипниках (опорно-осевое подвешивание) или подшипниках редуктора (опорно-рамное подвешивание). тр в режиме тяги или электрического торможения их не включают. Таким образом получается, что W >W’
тр в режиме тяги или электрического торможения их не включают. Таким образом получается, что W >W’
№трх №тр-
Сила трения качения колес по рельсам. Эта сила возникает вследствие деформации опорных поверхностей колес, рельсов и просадки пути. На рис. 6.3, А показано колесо в состоянии покоя. Под действием его нагрузки на рельс Q0 деформируются и колесо, и рельс. В результате они соприкасаются по площадке, имеющей форму эллипса с длинной осью, равной АВ. На силу Q0 со стороны рельса по всей площадке возникают симметричные относительно вертикальной оси силы реакции. Равнодействующая этих сил R направлена вертикально и уравновешивает силу Q0.
В случае качения колеса по рельсу (рис. 6.3, Б) силы реакции со стороны рельса перераспределяются: в набегающей части колеса они больше, а в сбегающей части — меньше, как показано стрелками на длине CD. Равнодействующая этих сил R, приложенная в точке Е и направленная перпендикулярно поверхности колеса и рельса, оказы-
Вается наклоненной в сторону, противоположную направлению движения. тр к всех колес. Удельная сила сопротивления от трения качения колес по рельсам, Н/кН:
тр к всех колес. Удельная сила сопротивления от трения качения колес по рельсам, Н/кН:
С увеличением твердости материала колеса и рельса отрезок 8 уменьшается. На величину №трк аналогично влияет и жесткость пути. Таким образом, сопротивление движению от трения качения снижается с уменьшением нагрузки от колесных пар на рельсы, увеличением диаметра колес, твердости материала колес, рельсов и жесткости пути. Удельная сила сопротивления движению от трения качения колес в среднем составляет 0,2…0,4 Н/кН.
Сила трения скольжения колес по рельсам. Качение колес по рельсам сопровождается их проскальзыванием, вызывающим силу трения скольжения между колесами и рельсами. Проскальзывание вызвано конусностью рабочих поверхностей бандажей колесных пар и отклонением их диаметров (см. рис. 1.3), отклонениями колесных пар от перпендикулярного к оси пути положения из-за нарушения размеров при сборке тележек вагонов и локомотива, а также вследствие виляния кузовов, тележек и колесных пар, создающих колебания в горизонтальной плоскости при их движении по прямолинейному пути. нер, направленная против движения, явится силой сопротивления движению от стыка.
нер, направленная против движения, явится силой сопротивления движению от стыка.
Аналогичная картина возникает и при прохождении других неровностей пути. Эта сила зависит от скорости движения, нагрузки от колес на рельсы, расстояния между стыками, зазора в стыке. Сила сопротивления движению от стыков уменьшается при длинных и более тяжелых рельсах и щебеночном балласте. Наибольший эффект дает применение бесстыкового пути. В среднем сила сопротивления движению поезда от ударов на неровностях пути составляет 0,05…0,5 Н/кН.
Силы сопротивления воздушной среды. При движении поезда перед его лобовой частью образуется зона сжатого воздуха, который оказывает встречное давление на лобовую стенку локомотива. Боковые поверхности и крыши подвижного состава соприкасаются со струями скользящего по ним воздуха, увлекают часть его за собой, создавая поток воздуха и трение части воздуха о стенки подвижного состава. В междувагонном пространстве и у выступающих частей образуются завихрения.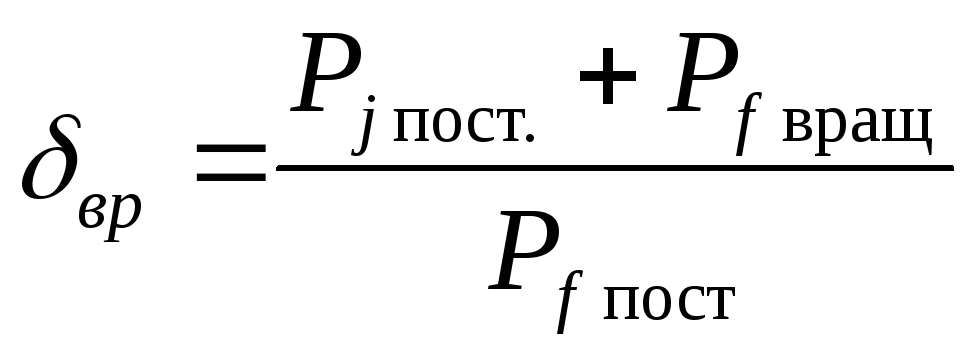
Под подвижным составом часть воздуха увлекается поездом, создаются завихрения и поток, соприкасающийся с верхним строением пути. За последним вагоном поезда образуется разрежение. Эти явления вызывают внешние силы, действующие на поезд, направленные против движения. Их называют силами сопротивления воздушной среды. Данные силы зависят от площади поперечного сечения поезда, его длины, взаимного расположения разных типов вагонов в составе, формы лобовой части локомотива и задней стенки хвостового вагона, наличия выступающих частей у подвижного состава и от скорости движения.
Сила сопротивления воздушной среды примерно пропорциональна квадрату скорости и имеет важное значение при скоростном движении. Наименьшим сопротивлением обладает поезд, имеющий обтекаемую «сигарообразную» форму с выпуклой лобовой и хвостовой стенками без выступов и неровностей на подвижном составе.
Требованиям обтекаемости в большей мере удовлетворяют высокоскоростные электропоезда. Так, высокоскоростной электропоезд ЭР200, рассчитанный на движение со скоростью до 200 км/ч, имеет закруг
Ленную в плане и скошенную верхнюю часть головного и хвостового вагонов, убранные внутрь вагонов поручни и другие выступающие части.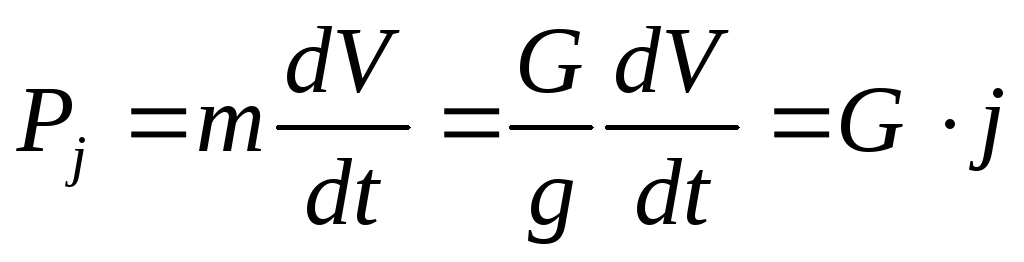
Сила сопротивления: определение, формула и примеры
Насколько был уверен первый парашютист в том, что использование парашюта спасет его от верной смерти? Наверное, вполне уверенно, если бы знали свою физику! Их безопасность основывалась на их знании той же концепции, которая заставляет нас чувствовать ветер на наших лицах сильнее, когда мы ездим быстрее. Все дело в силах сопротивления. Силы сопротивления — это, как следует из названия, силы, препятствующие движению. На примере с парашютом мы видим, что они могут быть как полезными, так и ограничивающими. В этой статье мы обсудим, что они из себя представляют и как действуют.
Сила сопротивления Определение
Сила сопротивления \(\vec{F}_r\) на движущийся объект — это сила, противодействующая движению этого объекта, или сила, препятствующая движению неподвижного объекта. Силы сопротивления всегда действуют в направлении, противоположном его движению.
В физике мы склонны сосредотачивать внимание на движущих силах, заставляющих объекты двигаться, а не на противодействующих силах. Сила может перемещать объект через среду или через контактную поверхность, и эта среда / поверхность часто может сопротивляться движению, применяя силу в направлении, противоположном движению тела, это сила трения, и она будет в центре внимания. сил сопротивления в этой статье. Однако есть и другие силы, которые можно считать силами сопротивления, и они будут кратко рассмотрены в следующем разделе.
Сила может перемещать объект через среду или через контактную поверхность, и эта среда / поверхность часто может сопротивляться движению, применяя силу в направлении, противоположном движению тела, это сила трения, и она будет в центре внимания. сил сопротивления в этой статье. Однако есть и другие силы, которые можно считать силами сопротивления, и они будут кратко рассмотрены в следующем разделе.
Типы сил сопротивления
Трение скольжения является примером силы сопротивления и возникает, когда два тела пытаются скользить друг по другу. Из-за этого трения возникает противодействие направлению движения тел. Сопротивление воздуха (или лобовое сопротивление) — еще один пример силы сопротивления, когда объект замедляется при движении через воздух, который является средой. Сопротивление воздуха классифицируется как тип жидкостного трения. Сила сопротивления всегда противоположна направлению движения объекта относительно среды.
Силу гравитации также можно считать силой сопротивления, если она, например, препятствует вертикальному взлету ракеты. Кроме того, нормальная сила также является силой сопротивления. Представьте себе объект, покоящийся на горизонтальной поверхности. Сила гравитации (веса) притягивает объект к центру Земли. Однако нормальная сила сопротивляется этому с равной и противоположной силой, в результате чего объект остается неподвижным на поверхности.
Кроме того, нормальная сила также является силой сопротивления. Представьте себе объект, покоящийся на горизонтальной поверхности. Сила гравитации (веса) притягивает объект к центру Земли. Однако нормальная сила сопротивляется этому с равной и противоположной силой, в результате чего объект остается неподвижным на поверхности.
Сила сопротивления трения
Мы определили силу сопротивления как силу, противодействующую движению объекта из-за свойств среды, через которую он движется. Одной из наиболее известных из этих сил сопротивления является трение. Мы сосредоточимся на статическом трении и кинетическом трении.
Сила трения
Сила трения возникает между двумя твердыми объектами, которые скользят друг по другу. Относительное движение между поверхностями двух объектов воздействует на каждый объект силой, параллельной обеим поверхностям и противодействующей каждому из их движений. Сила трения зависит от материала каждого предмета и от того, насколько сильно они прижаты друг к другу.
В качестве примера представьте, что ламинированная книга скользит по относительно гладкой поверхности стола. Книга будет довольно легко скользить по столу, прежде чем остановиться; сила трения существует, но невелика. Затем, если вы добавите тяжелый груз поверх книги и снова толкнете ее по столу, она остановится раньше, поскольку сила трения между ее поверхностью и поверхностью стола увеличится.
Мы обсудим типы сил трения позже, но общее уравнение для силы трения \(F_\mathrm{friction}\) таково:
\[F_{\mathrm{friction}}=\mu N,\]
где \(\mu\) — коэффициент трения поверхности, по которой движется объект, а \(N\) — нормальная контактная сила между поверхностью и объектом.
Статическая сила трения
Статическая сила трения возникает, когда объект и поверхность покоятся друг относительно друга. Нет движения одного относительно другого. Объект будет оставаться в состоянии покоя до тех пор, пока не будет приложена сила, которая больше по величине, чем максимальная статическая сила трения \(f_s\), которая определяется выражением \[f_{s}^{max}=\mu_{s} N,\ ] где \(\mu_s\) известен как коэффициент статического трения поверхности, а \(N\) — нормальная контактная сила между объектом и поверхностью.
Кинетическая сила трения
Кинетическая сила трения \(f\) для движущегося объекта массой \(m\) определяется следующим уравнением, \[f_k=\mu_{k}N,\], где \( \mu_{k}\) известен как коэффициент кинетического трения, а \(N\) представляет собой величину нормальной силы реакции, которую поверхность прикладывает к объекту. Обратите внимание, что кинетическая сила трения может быть силой трения качения или скольжения.
Сила вязкости
Силы вязкости возникают, когда твердые тела движутся в жидкости. Твердый объект перемещает слои жидкости, проходя через него. Относительное движение между двумя слоями жидкости создает силу сопротивления движению объекта. Вязкая сила зависит от свойства жидкости, называемого вязкостью. Чем больше вязкость жидкости, тем большая сила вязкости будет действовать на движущийся сквозь нее объект. Величина вязкой силы \ (F _ {\ mathrm {вязко}} \) определяется уравнением
\[F_\mathrm{viscous}=\alpha v,\]
где \(\alpha\) — константа, зависящая от вязкости и других физических свойств жидкости, а \(v\) — скорость предмета, движущегося в жидкости. 2,\], где \(\beta\) равно коэффициент сопротивления жидкости.
2,\], где \(\beta\) равно коэффициент сопротивления жидкости.
Сила вязкости зависит от вязкости жидкости, через которую движется объект, из-за сопротивления жидкости деформации. Сила вязкости удерживает неподвижный объект неподвижным. В то время как сила сопротивления зависит от относительного движения между объектом и средой, через которую он проходит.
Формула силы сопротивления
Мы собираемся рассмотреть случай объекта, движущегося с малой скоростью через среду. Мы будем думать о сценарии, в котором объект движется со скоростью \(\vec{v}\) относительно некоторой среды, в которой он чувствует силу сопротивления \(\vec{F}_r.\). В этом случае сопротивление сила прямо пропорциональна скорости тела и в обратном направлении, то есть
\[\vec{F}_r \propto \vec{v}.\]
Нам нужно включить константу в это выражение, чтобы превратить его в уравнение. Уравнение для силы сопротивления в терминах скорости принимает вид физические свойства объекта и среды, в которой он движется. 2.\)
2.\)
Конечная скорость
Рассмотрим пример медленно движущегося объекта; перо, медленно падающее с дерева на землю. Перо в какой-то момент достигнет постоянной скорости при падении на Землю. Если сила сопротивления прямо пропорциональна скорости пера, она равна нулю, когда скорость пера равна нулю; в начале своего спуска. В этот момент единственной силой, действующей на перо, является его вес \(m\vec{g}\), а величина его ускорения равна \(g.\). Когда его скорость увеличивается от нуля, оно начинает испытывать сопротивление. сила \(\vec{F}_r\) в противоположном направлении из-за сопротивления воздуха, когда он движется через эту среду. Чистая сила, действующая на перо, может быть представлена как \[\begin{align}\vec{F}_{\text{net}}&=m\vec{g}+\vec{F}_r,\\|\ vec{F}_{\text{net}} |&=mg-kv,\end{align}\]
, который можно использовать для определения чистого ускорения \(a\) пера в любое время с использованием второго закона Ньютона,
\[\begin{align}ma&=mg-kv,\\a&=g-\frac {k}{m}v.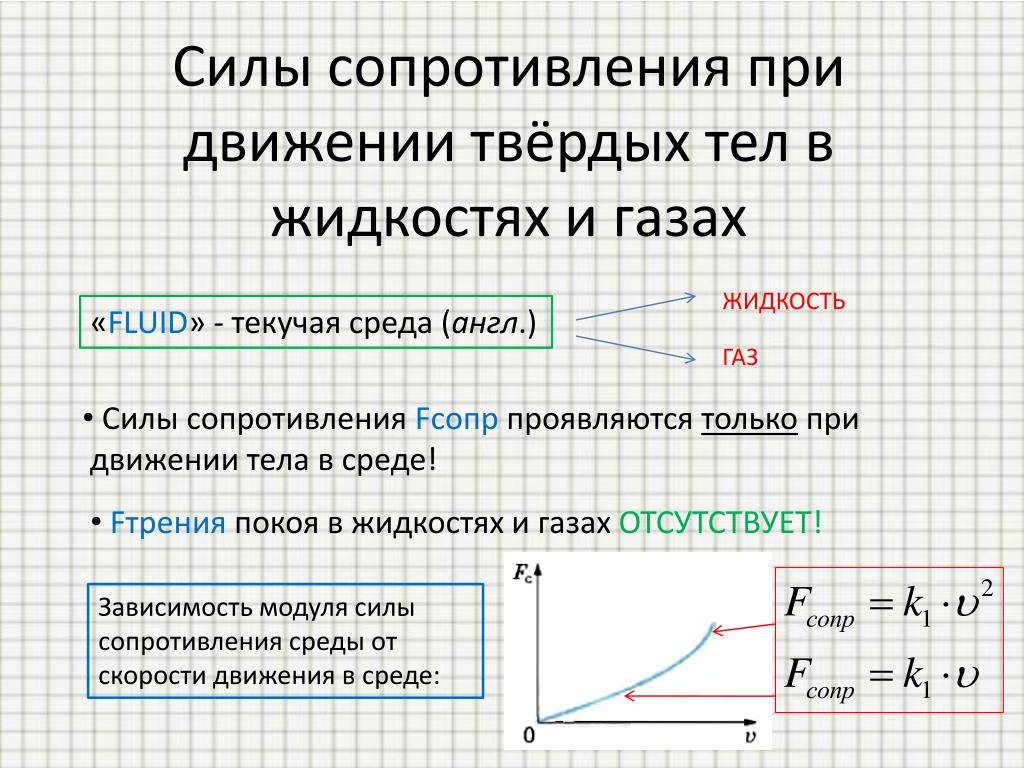 \end{align}\]
\end{align}\]
Помните, что сила сопротивления увеличивается со скоростью, следовательно, результирующая сила постоянно уменьшается, и, согласно приведенному выше уравнению, то же самое имеет результирующее ускорение. Когда перо достигает точки, в которой его скорость постоянна, мы говорим, что оно достигло конечной скорости \(v_T\) . Перо больше не ускоряется, и мы можем найти конечную скорость из приведенного выше уравнения, установив \(a=0\), \[\begin{align}0&=g-\frac{k}{m}v_T,\\v_T& =\frac{mg}{k}.\end{align}\] Мы можем визуализировать этот сценарий с помощью изображения ниже.
График зависимости скорости от времени для объекта, испытывающего сопротивление воздуха при падении, показан на Рис. 2. ниже.
Рис. 2. График зависимости скорости от времени для падающего объекта, испытывающего сопротивление воздуха, демонстрирующий конечную скорость
Скорость изменения скорости (ускорения) максимальна в начале падения и постепенно снижается по мере увеличения величины силы сопротивления и противодействия весу. {-kt/m} \right).\] Здесь мы предполагаем, что скорость объекта \(v=0\) в момент времени \(t=0\), что верно для пера, падающего из состояния покоя. Обратите внимание, что для жидкости вязкость жидкости обеспечивает силу сопротивления на объекте. Давайте проверим наши новые знания, рассмотрев следующий пример. 9{-1}}.\)
{-kt/m} \right).\] Здесь мы предполагаем, что скорость объекта \(v=0\) в момент времени \(t=0\), что верно для пера, падающего из состояния покоя. Обратите внимание, что для жидкости вязкость жидкости обеспечивает силу сопротивления на объекте. Давайте проверим наши новые знания, рассмотрев следующий пример. 9{-1}}.\)
Работа, выполненная против сил сопротивления
Напомним, что при воздействии сил обычно происходят преобразования энергии, что, в свою очередь, означает, что над объектом будет совершена работа. Работа, совершаемая над объектом \(W\) приложенной силой \(F\), представляет собой сумму прироста кинетической энергии \(\Delta E_K \) объекта и работы, совершаемой объектом против силы сопротивления \(W_r\). То есть
\[\begin{align}W&=\Delta E_K+W_r,\\W_r&=W-\Delta E_K.\end{align}\] Работа, совершаемая над объектом приложенной силой, увеличивает его кинетическую энергия. Работа, совершаемая объектом против силы сопротивления, отнимает энергию у объекта, уменьшая его кинетическую энергию.
Сила сопротивления — ключевые выводы
- Сила сопротивления \(\vec{F}_r\) на объект, движущийся относительно некоторой среды, — это сила, противодействующая движению этого объекта, которая возникает из-за физических свойств среды и объект.
- На низких скоростях сила сопротивления прямо пропорциональна скорости объекта и направлена в противоположную сторону, то есть \[\vec{F}_r = -k\vec{v}.\]
- Конечная скорость \(v_T\) на объект, испытывающий силу сопротивления при движении через среду, равен \[v_T=\frac{mg}{k}.\] 9{-kt/m}\right).\]
- Трение является примером силы сопротивления, не зависящей от скорости объекта.
- Работа, совершаемая над объектом \(W\) приложенной силой \(F\), равна сумме прироста кинетической энергии \( \Delta E_K \) объекта и работы, совершаемой объектом против сила сопротивления \(W_r.\)
Ссылки
- Рис. 2 — Оригиналы StudySmarter
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 8886
- Джереми Татум
- Университет Виктории
Трудно представить себе реальную ситуацию, в которой единственной силой является сила сопротивления, пропорциональная скорости. Тело, падающее по воздуху, не годится, потому что помимо силы сопротивления есть ускорение за счет силы тяжести. Возможно, мы могли бы представить себе шайбу, скользящую по льду. Лед должен был бы считаться полностью лишенным трения, и единственной силой, действующей на шайбу, было бы сопротивление воздуха. Это немного искусственная ситуация, потому что мы хотим, чтобы шайба двигалась так быстро, чтобы сила трения была пренебрежимо мала по сравнению с сопротивлением воздуха, но не настолько быстро, чтобы воздушный поток был турбулентным — но нам нужно с чего-то начинать. Сила трения, по крайней мере в очень хорошем приближении, не зависит от скорости, а постоянна, и мы начнем с предположения, что ею можно пренебречь и что единственной горизонтальной силой, действующей на шайбу, является сопротивление воздуха, а сопротивление воздуха пропорциональна скорости. 9{-\гамма т}. \tag{6.3.3}\label{eq:6.3.3} \]
Тело, падающее по воздуху, не годится, потому что помимо силы сопротивления есть ускорение за счет силы тяжести. Возможно, мы могли бы представить себе шайбу, скользящую по льду. Лед должен был бы считаться полностью лишенным трения, и единственной силой, действующей на шайбу, было бы сопротивление воздуха. Это немного искусственная ситуация, потому что мы хотим, чтобы шайба двигалась так быстро, чтобы сила трения была пренебрежимо мала по сравнению с сопротивлением воздуха, но не настолько быстро, чтобы воздушный поток был турбулентным — но нам нужно с чего-то начинать. Сила трения, по крайней мере в очень хорошем приближении, не зависит от скорости, а постоянна, и мы начнем с предположения, что ею можно пренебречь и что единственной горизонтальной силой, действующей на шайбу, является сопротивление воздуха, а сопротивление воздуха пропорциональна скорости. 9{-\гамма т}. \tag{6.3.3}\label{eq:6.3.3} \]
Здесь \(v_{0}\) — начальная скорость. Это показано на рисунке VI.2
Скорость снижается до половины начальной скорости за время
\[ t_{\frac{1}{2}} = \frac{\ln2}{\gamma} = \frac{0,693}{\gamma}. \tag{6.3.4}\label{eq:6.3.4} \]
\tag{6.3.4}\label{eq:6.3.4} \]
Второй временной интеграл можно найти, записав \( v\) в уравнении \( \ref{eq:6.3.3}\) как \( \frac{dx}{dt}\). Интегрирование с начальным условием \(x = 0\), когда \(t = 0\), дает 9{-\gamma t}), \tag{6.3.5}\label{eq:6.3.5} \]
, где \(x_{\infty}=\frac{v_{0}}{\gamma}\). Это показано на рисунке VI.3. Видно, что шайба проходит возможное расстояние \(x_{\infty}\), но только через бесконечное время.
Мы можем получить пространственный интеграл , либо исключив \(t\) между двумя временными интегралами, либо записав уравнение движения как
\[ v\frac{dv}{dx} = — \gamma v.\tag{6.3.6}\label{eq:6.3.6} \]
С начальным условием \(v = v_{0}\), когда \(x = 0\), это становится
\[ v = v_{0} — \gamma x, \tag{6.3.7}\label{eq:6.3.7} \]
, который показан на рисунке VI.4. Скорость падает линейно с расстоянием (но экспоненциально со временем), достигая нуля после прохождения конечного расстояния \( x_{\infty}=\frac{v_{0}}{\gamma}\) за бесконечное время.
