Технические характеристики Лада Х Рей Кросс 2022
Двигатель
106 л.с
122 л.с
113 л.с
Привод
Передний
Цвет:
Огненно-красный, металлик
Ледниковый
Серый базальт, металлик
Янтарь, металлик
Кашемир, металлик
Черная жемчужина, металлик
Платина, металлик
Специальная цена
на
от 899 910 ₽
* спецпредложение до
Телефон *
Основные размеры Лада Х Рей Кросс
- Длина
- 4171 см
- Клиренс
- 215 см
- Ширина
- 1810 см
- Масса
- 1295 кг
- Высота
- 1645 см
- Объём багажника
- 361 л.
Комплектации и цены Lada XRAY Cross
Модификации Лада Х Рей Кросс: Двигатель, КПП, привод
Выберите модификацию для сравнения характеристик:
1. 8 5MT (122 л.с.)
8 5MT (122 л.с.)
1.6 AT (113 л.с.)
1.6 MT (106 л.с.)
Характеристики
1.8 5MT (122 л.с.) | 1.6 AT (113 л.с.) | 1.6 MT (106 л.с.) | |
|---|---|---|---|
| Двигатель и трансмиссия | |||
| Тип двигателя: | Бензиновый | Бензиновый | Бензиновый |
| Рабочий объём: | 1774 см³ | 1598 см³ | 1596 см³ |
| Рекомендуемое топливо: | АИ-95 | АИ-95 | АИ-95 |
| Количество цилиндров: | 4 | 4 | 4 |
| КПП: | Механическая | Автоматическая | Автоматическая |
| Топливный бак: | 50 л | 50 л | 50 л |
| Динамика | |||
| Мощность двигателя | 122 л. при 6050 об/мин | 113 л.с при 5500 об/мин | 106 л.с при 5500 об/мин |
| Крутящий момент: | 170 Н∙м при 3700 об/мин | 152 Н∙м при 4000 об/мин | 152 Н∙м при 4000 об/мин |
| Разгон до 100 км/ч: | 10.9 сек | 12.8 сек | 13.5 сек |
| Максимальная скорость: | 180 км/ч | 180 км/ч | 165 км/ч |
| Расход топлива | |||
| Расход в городском цикле: | 9. | ||
| Расход в загородном цикле: | 5.9 л на 100 км | ||
| Расход в смешанном цикле: | 7.5 л на 100 км | 7.4 л на 100 км | |
| Подвеска и тормозная система | |||
| Передняя подвеска: | Независимая, типа Макферсон, пружинная, с гидравлическими или газонаполненными телескопическими амортизаторами, со стабилизатором поперечной устойчивости | Независимая, типа Макферсон, пружинная, с гидравлическими или газонаполненными телескопическими амортизаторами, со стабилизатором поперечной устойчивости | Независимая, типа Макферсон, пружинная, с гидравлическими или газонаполненными телескопическими амортизаторами, со стабилизатором поперечной устойчивости |
| Задняя подвеска: | Полузависимая, рычажная, пружинная, с гидравлическими или газонаполненными телескопическими амортизаторами | Полузависимая, рычажная, пружинная, с гидравлическими или газонаполненными телескопическими амортизаторами | Полузависимая, рычажная, пружинная, с гидравлическими или газонаполненными телескопическими амортизаторами |
| Передние тормоза: | Дисковые | Дисковые | Дисковые |
| Задние тормоза: | Барабанные | Барабанные | Барабанные |
| Габариты и масса | |||
| Длина: | 4171 мм | 4171 мм | 4171 мм |
| Ширина: | 1810 мм | 1810 мм | 1810 мм |
| Высота: | 1645 мм | 1645 мм | 1645 мм |
| Колесная база: | 2592 мм | 2592 мм | 2592 мм |
| Клиренс: | 215 мм | 215 мм | |
| Объем багажника: | 361 л | 361 л | 361 л |
| Снаряженная масса: | 1295 кг | 1295 кг | 1295 кг |
| Грузоподъемность: | — | — | — |
Другие автомобили
Lada
Largus
от 887 310 ₽Lada
Niva Legend 5dv
от 602 010 ₽
Lada
Niva Legend 3dv
от 562 010 ₽
Lada
Niva Travel
от 735 210 ₽
Lada
Granta Drive Active
от 621 810 ₽
Lada
Vesta Sport
от 1 213 110 ₽
Lada
Vesta CNG
от 960 210 ₽
Lada
Largus Фургон
от 888 210 ₽
Lada
Largus Cross
от 1 015 110 ₽
Lada
Granta
от 430 110 ₽
Lada
Granta Cross
от 544 410 ₽
Lada
Granta Хэтчбек
от 475 650 ₽
Lada
Granta Лифтбек
от 449 910 ₽
Lada
Granta Универсал
от 453 510 ₽
XRAY
от 771 210 ₽
Lada
Vesta
от 784 710 ₽
Lada
Vesta SW
от 867 510 ₽
Lada
Vesta Cross
от 917 910 ₽
Lada
Vesta SW Cross
от 971 010 ₽
Lada
XRAY Cross
от 899 910 ₽
объем багажника.
 Размеры и сколько литров.
Размеры и сколько литров.Перед покупкой автомобиля одним из самых насущных вопросов, от ответа на который зависит выбор большинства автомобилистов, является вместимость багажника. И это предсказуемо, поскольку задачей автотранспорта является перемещение не только пассажиров, но и грузов. В наших же условиях личный автотранспорт является рабочей лошадкой и помощником по хозяйству в большей мере, чем средством проведения досуга. Поэтому большой багажник является крайне желательной, а еще чаще – необходимой характеристикой машины.
Частота запросов вроде «Багажник для Лада Хray», «Х рей багажник фото» или «Лада Х Рей фото салона и багажника» постоянно растет, и связано это с тем, что новые автомобили семейства Лада пока еще мало известны нашим автолюбителям. Решиться на покупку этих тольятинских новинок трудно, даже если позволяют средства, но нет представления о фактических размерах багажника Х Рей, и, как следствие – о хозяйственной ценности автомобиля, пусть даже трижды красивого, качественного и современного.
Сегодня мы прольем свет на то, что так заботит покупателей, а именно на размер багажника Лада Х Рей.
Багажник на Х Рей: характеристики и описание
Поскольку новый автомобиль очень отличается от привычных моделей Жигулей семейства Лада, то и багажник у него абсолютно новый. Габариты Лада Х Рей следующие:
- 1,77 м. по ширине;
- 1,57 м. по высоте;
- 4,16 м. в длину.
При этом линейные размеры багажника х рей таковы:
- Ширина – 0,9 м. Это минимальный размер, поскольку в самом широком месте (у пола багажника) ширина будет составлять примерно 0,99 м.;
- Высота – 0,8 м. Со снятой крышкой фальшпола к высоте добавляется еще 10 см. При закрытой багажной полке показатель высоты ограничивается размером 0,4 м.;
- Длина – 0,79 м. При откинутой вперед спинке заднего дивана длина увеличивается до 1,5 м., хотя это уже геометрическая характеристика не багажника, а автомобиля в целом. К сожалению, спинка не откидывается до образования ровной поверхности, так полезной при габаритной загрузке.
 Для того, чтобы использовать эту возможность полностью, придется снимать заднее сиденье, иначе спинка не откинется на 180о.
Для того, чтобы использовать эту возможность полностью, придется снимать заднее сиденье, иначе спинка не откинется на 180о.
Ниже вы можете увидеть, как выглядит Лада Хray багажник на фото.
Если же измерять объем багажника лада х рей в литрах, что актуально в случае транспортировки мелкого или мягкого груза, то показатель вместимости останавливается на 361 литре. Сложив спинку заднего дивана, удается увеличить грузовую вместимость автомобиля до 1207 л., а при сложенном переднем кресле – объем багажника х рей увеличивается до 1514 л.
Как и в случае с любым другим автомобилем, у Xray размеры багажника не являются абсолютной величиной, и всегда хочется больше, если возникает нужда. Однако есть и абсолютные характеристики, и не сказать что привычные для продукции отечественного автопрома. Например:
• Разрезная спинка заднего дивана позволяет варьировать грузовместимость в случае перевозки длинномерных грузов: лыж, удилищ, профиля, досок и т.д. Просто откинув фрагмент спинки заднего сиденья, остальную ее часть можно не трогать, и использовать по назначению – для перевозки пассажиров;
• Идеально ровный пол багажника. Фальшпол (верхняя поверхность пола) снабжена петлями, за которые можно застропить груз во избежание его перемещения при движении;
Фальшпол (верхняя поверхность пола) снабжена петлями, за которые можно застропить груз во избежание его перемещения при движении;
• Двойной пол. Приподняв верхнюю крышку пола, мы видим внизу еще одно полезное пространство, которое можно загрузить, к примеру, постоянным грузом (аптечкой, ящиком с инструментами, автомобильными аксессуарами), или деликатным грузом, требующим отдельного грузового места;
• Скрытые колесные крылья, не отбирающие полезной площади и не образующие неудобных углов;
Убедиться во всем этом вы можете, просто набрав запрос «Лада Х Рей багажник фото».
Lada Xray багажник: много или мало?
Итак, мы не знаем, можно ли для Lada xray объем багажника в 361 литр считать достаточным, большим или маленьким. Это число не является предельным показателем для автомобилей, поэтому придется провести сравнение с другой техникой того же класса. Например, Х Рей объем багажника всего на 9 литров меньше, чем у Hyundai Solaris и на 28 литров меньше, чем KIА Rio. При этом он обладает значительно большей вместимостью, чем багажники Renault Sandero и Ford Fiesta. В этом отношении для Лада Х рей багажник такой емкости выглядит вполне приемлемым и даже хорошим решением, и уже по этому функционалу автомобиль может составить конкуренцию иностранным аналогам. Возможно, приведенное сравнение не совсем корректно, но такие высокие хэтчбеки в данном ценовом диапазоне, доступные отечественному потребителю – редкое явление, и остается сравнивать с самыми знакомыми нашему обывателю иномарками.
В этом отношении для Лада Х рей багажник такой емкости выглядит вполне приемлемым и даже хорошим решением, и уже по этому функционалу автомобиль может составить конкуренцию иностранным аналогам. Возможно, приведенное сравнение не совсем корректно, но такие высокие хэтчбеки в данном ценовом диапазоне, доступные отечественному потребителю – редкое явление, и остается сравнивать с самыми знакомыми нашему обывателю иномарками.
Вообще, современные легковые автомобили оснащаются багажниками, объемом от 300 до 500 литров, если не принимать во внимание чисто спортивные модели или полугрузовые машины с универсальным кузовом, которые редко продаются и ограничено выпускаются. Поэтому можно заключить, что для автомобиля Лада Xray объем багажника в 361 л. можно считать средним для всех легковых авто, независимо от класса. Существенное увеличение размера Х рей багажника может привести либо к увеличению габаритов автомобиля, либо к уменьшению полезного пространства салона, что в первую очередь ощутят на себе пассажиры.
Если все же мало?
Несмотря на все сказанное, такой багажник кому-то может показаться недостаточно вместительным, тем более, что существуют ситуации, когда нужно по-максимуму использовать грузоподъемность, в то время как задача по перевозке пассажиров не актуальна. Для таких случаев стоит демонтировать заднее сиденье, благо сделать это достаточно просто.
Также проблему можно решить, купить красивый и аэродинамичный автобокс, который станет прекрасным эстетическим дополнением внешнего вида автомобиля. Если такой вариант не подходит – можно обзавестись легкими рейлингами или универсальным багажником на крышу.
В остальных случаях придется понимать, что автомобиль имеет ограничение по грузоподъемности, и слишком большой груз иногда лучше тянуть, чем везти на себе. Для этих целей приобретается или берется напрокат автоприцеп.
Кроме того, существуют предметы, которые не поместятся в багажник со свободным салоном даже самого большого легкового автомобиля, хотя перевозить их все-таки можно: например, доска для серфинга или лодка.

Вообще, выбирать среди всех моделей Лада Х Рей по объему багажника в литрах самую подходящую комплектацию бесполезно, т.к. все они имеют одну и ту же вместимость. И если автомобиль вам понравился всем остальным, то лучше попробовать увеличить его грузовые характеристики одним из указанных способов.
объем, габариты, вместимость, плюсы и минусы (на основе отзывов владельцев) || AutBar.Ru
В сегодняшней статье мы рассмотрим багажный отсек Лада Х—Рей/Лада Х—Рей Кросс (Lada Xray/Lada Xray Cross) и узнаем, каким реальным объемом, габаритными размерами, практичностью, вместимостью, функциональностью, отличительными особенностями, плюсами/минусами может похвастать багажник отечественной модели компании ОАО “АвтоВАЗ” (на основе отзывов автовладельцев).
РЕКОМЕНДУЕМ К ПРОЧТЕНИЮ: ЧЕСТНЫЙ ОБЗОР KIA SPORTAGE SL D4HA 2.0 CRDI 136/184 Л. С
С
По многочисленным отзывам автовладельцев, багажник Лада Х—Рей/Х—Рей Кросс отличается вместительностью и удобством пользования. А при сложенном заднем диване позволяет перевозить в салоне длинномерные и крупногабаритные грузы. Багажник для многих автомобилистов считается едва ли не важнейшим критерием, по которому оценивается уровень практичности машины. Ведь от его вместительности в значительной мере зависит комфортабельность путешествия, успех выезда на природу или простой перевозки вещей. Не зря же покупатели Lada Xray/Xray Cross тщательно осматривают багажный отсек хэтчбека/кросс-хэтчбека перед покупкой, оценивая его удобство, интересуясь у менеджера объемом и другими параметрами.
С моторной гаммой новой Лада Веста и Лада Х—Рей 2022/2023, вы можете ознакомиться здесь.
Насколько удобен багажник Лада Х—Рей/Х—Рей Кросс? Каковы его размеры? И есть ли у багажного отсека слабые стороны?
Сперва давайте рассмотрим габаритные размеры Лада Х—Рей/Х—Рей Кросс, чтобы представлять примерную долю багажного отсека в общем объеме салона автомобиля.
Итак, кузов модели обладает следующими габаритными размерами:
— длина: 4164 миллиметра;
— высота: 1570 миллиметров;
— ширина: 1764 миллиметра;
— колесная база: 2592 миллиметра.
Характеристики на бумаге, откровенно, не самые внушительные. В частности, своему ближайшему конкуренту в лице французского Рено Сандеро Степвей он уступает в длине на 84 миллиметра и в ширине на 7 миллиметров. Да и колесная база на 3 миллиметра меньше. Зато по высоте победа за Лада Х—Рей/Х—Рей Кросс с преимуществом в 48 миллиметров. Именно с оглядкой на небольшие габариты, объем багажника Lada Xray/Xray Cross приобретает новое значение.
С плюсами двс ВАЗ 11182 1.6 новой Лада Гранта/Лада Ларгус, вы можете ознакомиться здесь.
Официальный показатель объема багажного отсека Лада Х—Рей/Х—Рей Кросс составляет 361 литр. Немного, но при сложенном заднем диване он возрастает уже до 1207 литров. Если же вдобавок разложить и переднее пассажирское кресло, можно добиться объема в 1515 литров, а еще свободно разместить внутри длинномеры типа лыж, строительных профилей и прочего. Этому способствует и разрезная спинка заднего дивана, раскладывающаяся в пропорции 60 на 40.
Немного, но при сложенном заднем диване он возрастает уже до 1207 литров. Если же вдобавок разложить и переднее пассажирское кресло, можно добиться объема в 1515 литров, а еще свободно разместить внутри длинномеры типа лыж, строительных профилей и прочего. Этому способствует и разрезная спинка заднего дивана, раскладывающаяся в пропорции 60 на 40.
Однако объем багажника — это далеко не самое главное. Не менее важен показатель удобства использования имеющегося пространства. И здесь инженеры компании АвтоВАЗ оказались на высоте! Внутренняя часть багажного отсека обладает идеально ровным полом, да и колесные арки не выступают внутрь. Это значит, что весь объем будет использован по назначению и внутри не останется пустых углов. Верх ограничивается пластиковой полкой, но при необходимости ее можно демонтировать и уложить скарб под самое стекло, хотя в данном случае требуется быть осторожным, дабы не разбить его.
В Лада Х—Рей/Лада Х—Рей Кросс предусмотрена функция двойного пола, причем верхняя его часть оборудована специальными фиксаторами, посредством которых можно, используя ремни, надежно закрепить груз, чтобы в пути он не искал пятый угол. Жаль только, что при сложенном заднем диване внутри автомобиля не образуется ровной погрузочной площадки – спинка складывается с небольшим углом. Так что с этим придется либо мириться, либо убирать из автомобиля подушку заднего дивана, что отнюдь не всегда удобно и приемлемо.
Жаль только, что при сложенном заднем диване внутри автомобиля не образуется ровной погрузочной площадки – спинка складывается с небольшим углом. Так что с этим придется либо мириться, либо убирать из автомобиля подушку заднего дивана, что отнюдь не всегда удобно и приемлемо.
Кроме того, немаловажна и удобная погрузочная высота, а также короткий задний свес. Это значит, что задний бампер не выдается далеко назад и не мешает в процессе погрузки. Ровной погрузочной площадки при сложенном заднем диване в Лада Х—Рей/Х—Рей Кросс не образуется.
СРАВНЕНИЕ БАГАЖНОГО ОТСЕКА ЛАДА Х—РЕЙ/Х—РЕЙ КРОСС С КОНКУРЕНТАМИ СЕГМЕНТА
Как показывает практика, объем багажного отделения Лада Х—Рей/Х—Рей Кросс вполне приличен и полностью соответствует своему классу. Кстати, задний диван в отечественной модели всегда можно сложить, увеличив полезный объем багажника. Однако, какие результаты показывает отечественный хэтчбек в сравнении с ближайшими соперниками своего сегмента? Это можно наглядно оценить в сравнительной таблице, представленной ниже:
Однако, какие результаты показывает отечественный хэтчбек в сравнении с ближайшими соперниками своего сегмента? Это можно наглядно оценить в сравнительной таблице, представленной ниже:
Как видно из таблицы, бесспорно, лучшим в состязании предсказуемо стал лифтбек Шкода Рапид. Тем не менее Лада Х—Рей/Х—Рей Кросс также занимает лидирующие позиции, превосходя ближайшего соперника Рено Сандеро/Сандеро Степвей по объему багажника (в штатном положении) на 41 литр, при этом уступая ему при сложенном диване на 193 литра.
Конечно, отображенные в сравнительной таблице модели подобраны не совсем корректно, правда нужно учитывать и тот факт, что рынок высоких бюджетных хэтчбеков по умеренной цене на российском рынке крайне ограничен, поэтому данное отступление можно считать вполне оправданным. И на фоне конкурентов, параметры багажного отсека отечественной модели смотрятся довольно привлекательно.
В завершении пару слов добавим и о конструктивно продуманном багажном проеме Лада Х—Рей/Х—Рей Кросс. Продуманность заключается в том, что в багажник можно без труда поместить груз размером 80 сантиметров (по высоте) на 90 сантиметров (по ширине), при этом у самого проема еще останется немного места по ширине (в самом широком месте проем имеет около 99,5 сантиметров). Что касается высоты проема (от пола до крыши), то данный показатель составляет 80 сантиметров (с фальшполом) и 90 сантиметров (без фальшпола). Также заметим, что при складывании спинки заднего ряда сидений, в багажный отсек войдет груз длиной 148-150 сантиметров, а если предельно сдвинуть водительское и пассажирское кресла вперед, то поместиться “крупногабарит” длиной 175-180 сантиметров. Таким образом, в отечественный пятидверный хэтчбек/кросс-хэтчбек, при желании, можно загрузить ящик габаритным размером 150х80х90 сантиметров.
Таким образом, в отечественный пятидверный хэтчбек/кросс-хэтчбек, при желании, можно загрузить ящик габаритным размером 150х80х90 сантиметров.
ИСТОЧНИК МАТЕРИАЛА — НАШ КАНАЛ НА ЯНДЕКС ДЗЕН
БЛАГОДАРИМ ВАС ЗА ВНИМАНИЕ! ПРОЯВЛЯЙТЕ ВЗАИМОУВАЖЕНИЕ НА ДОРОГАХ!
Габаритные размеры Лада X-RAY (размеры салона, багажинка и клиренс)
Автомобиль Лада Х-RAY, изготовлен на одной платформе с Рено Сандеро, но имеет несколько другие габариты. Поскольку данная модель, выпущенная АвтоВАЗом – первый отечественный кроссовер, то она должна иметь довольно просторный и вместительный салон, высокую грузоподъемность и проходимость, большой клиренс, и относительно небольшие размеры кузова. Соответствует ли Lada Xray данным критериям, можно узнать, прочитав статью.
Кузов
По своим размерам, Лада Х-Рей полностью подходит под категорию европейских и других зарубежных кроссоверов. Для поездок в городе, среди большого потока автомобилей, у нее достаточно небольшие размеры кузова.
В длину, от передней крайней точки (переднего бампера), до задней крайней точки (заднего бампера), автомобиль Lada Xray достигает 4315 мм. Если сравнивать его с Renault Sandero, с которым, как было сказано ранее, Лада Х-Рей делит одну базу, то можно убедится в том, что длина у обоих кроссоверов абсолютно одинаковая.
Ширина отечественного внедорожника, от крайней левой точки (от левого бокового зеркала заднего вида), до правой крайней точки (до правого бокового зеркала заднего вида), составляет 1980 мм. При сложенных зеркалах, ширина будет меряться по колесным аркам, и уменьшиться до 1820 мм. Вернемся к Рено Сандеро. Его ширина имеет такие самые размеры: с сложенными зеркалами – 1822 мм, а с выдвинутыми – 2000 мм.
Высота автомобиля Lada Xray измеряется также в двух положениях: с дополнительными рейлингами, и без них. В первом положении, высота машины будет составлять 1685 см, что примерно на 200 мм выше, чем высота среднестатистического седана. Без рейлингов, высота кузова уменьшиться до 1625 мм. Учитывая то, что дорожный просвет у Сандеро и Лада Х-Рей практически одинаковый, то высота у них так же полностью идентична.
Учитывая то, что дорожный просвет у Сандеро и Лада Х-Рей практически одинаковый, то высота у них так же полностью идентична.
Подвеска
Размеры подвески модели Lada Xray, несколько меньше, чем у его аналога – Рено Сандреро. Конечно, такая разница особых различий в проходимости не играет, также, как и в управлении, но визуально является заметным отличием, особенно если смотреть по колесным аркам.
Ширина между передними колесами отечественного кроссовера немного меньше, чем ширина между задними колесами. Такое расположение колес сделано специально для того, чтоб улучшить проходимость внедорожника на грязи и заболоченной местности. Размер передней колеи автомобиля, равен 1482 мм, а задней – 1513 мм. Если сравнить данные размеры с кроссовером Рено, то его передняя колея имеет размер 1560 мм, а задняя – 1567 мм.
Расстояние между передней и задней осью (колесная база), у модели Лада Х-Рей, также несколько меньше, чем у аналога, и равняется 2592 мм. На сандеро, колесная база имеет размеры несколько больше – 2673 мм.
Что касается клиренса, то тут Lada Xray также незначительно уступает Рено. Дорожный просвет у отечественного внедорожника, равен 195 мм. Такой клиренс вполне достаточный для хорошей проходимости по бездорожью, а также очень сильно влияет на внешний вид автомобиля, максимально приближая его к городскому типу. А вот у Сандеро, клиренс немного больше – 210 мм, и в городе данная машина смотрится немного неуместно.
Размер салона и грузоподъемность
Учитывая довольно небольшие габариты кузова Лада Х-Рей, размеры салона также не особо просторные. Для водителя и переднего пассажира, места вполне достаточно, а вот на счет заднего сидения – вопрос спорный.
Что касается высоты сидений, то она полностью одинаковая, как для заднего, так и для двух передних, и равна – 935 мм. Само сидение, имеет несколько разную величину. Заднее сидение достигает длины в 460 мм, а переднее немного больше – 480 мм.
Для ног водителя и переднего пассажира, в автомобиле Lada Xray, просто предостаточно.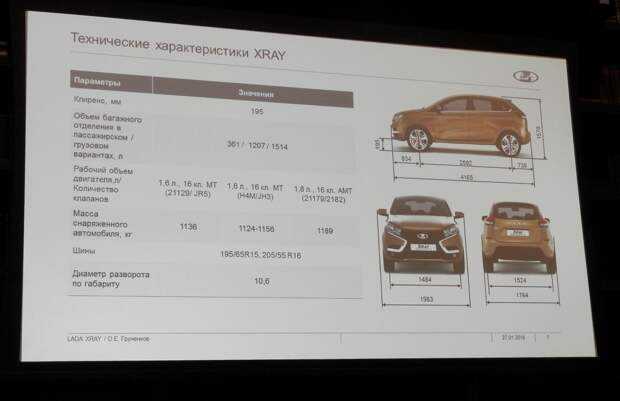 Если сменить положение сидения, опустив спинку, то на нем можно будет расположиться лежа, практически во всю длину. А вот для пассажиров сзади, ноги постоянно будут упираться в спинку передних сидений. Это является одним из немногочисленных минусов модели Лада Х-Рей.
Если сменить положение сидения, опустив спинку, то на нем можно будет расположиться лежа, практически во всю длину. А вот для пассажиров сзади, ноги постоянно будут упираться в спинку передних сидений. Это является одним из немногочисленных минусов модели Лада Х-Рей.
При увеличении объема багажного отделения, и соответственно веса дополнительного груза, стоит учитывать, что дорожный просвет, также будет уменьшаться. Поэтому, по бездорожью ездить не рекомендуется, при нагруженном автомобиле.
Также, хочется обратить особое внимание на размеры проема багажного отделения. Разработчики Lada Xray, максимально постарались улучшить его вместительные качества, и сделали довольно просторный проем. Ширина проема багажника, составляет 975 мм, а высота – 740 мм. Немного подкачала высота порога – 770 мм. Это слишком много для погрузочной платформы, и тяжелый груз поместить в багажное отделение будет очень непросто.
Багажник новой Лада
Вывод
В целом, новый отечественный кроссовер Лада Х-Рей довольно хороший, и с легкостью сможет конкурировать с зарубежными аналогами. Ее габариты довольно невелики, что позволяет запросто маневрировать даже в плотном городском потоке. Салон также достаточно вместительный.
По подвеске, данная модель очень хорошо подойдет, как для городских условий, так и для условий полного бездорожья. Клиренс достаточно большой, для преодоления препятствий любого рода, и вовсе не портит внешний вид машины. Большой плюс данного внедорожника – доступная цена. Благодаря всем этим плюсам, модель Х-Рей станет довольно популярной, как на территории России, так и в зарубежных странах.
Загрузка …
Двумерная структура из изображений случайного многочастичного рентгеновского рассеяния с использованием кросс-корреляций
Введение
Большинство макромолекулярных структур, доступных в настоящее время с атомарным разрешением, являются результатом рентгеновской криокристаллографии на синхротронах, для которой требуются кристаллы размером более несколько микрометров во избежание чрезмерного радиационного повреждения 1 . Трехмерные (3D) молекулярные формы также могут быть извлечены из раствора методом малоуглового рассеяния рентгеновских лучей (SAXS) 2,3 , при этом предел в несколько нанометров в разрешении 4,5 обусловлен тем, что доступна только изотропная составляющая интенсивности одночастичного рассеяния.
Трехмерные (3D) молекулярные формы также могут быть извлечены из раствора методом малоуглового рассеяния рентгеновских лучей (SAXS) 2,3 , при этом предел в несколько нанометров в разрешении 4,5 обусловлен тем, что доступна только изотропная составляющая интенсивности одночастичного рассеяния.
Появление рентгеновских лазеров на свободных электронах (XFEL) 6 стимулирует появление новых методов визуализации 7,8 . Среди них серийная кристаллография на субмикронных кристаллах, которые проще выращивать, в режиме «дифрагировать и уничтожить», который, как недавно было продемонстрировано, обеспечивает разрешение, близкое к атомному 9 . Однако доступ к структурной информации о некристаллических и неориентированных образцах за пределами возможностей SAXS остается сложной задачей. Мгновенная дифракция от одиночных частиц рассматривалась несколькими группами 10,11,12 , мотивированными высокой интенсивностью импульсов XFEL длительностью фс. Но, несмотря на огромное увеличение пиковой яркости, прогнозируется, что типичное однократное дифракционное изображение изолированной биомолекулы, полученное XFEL, дает гораздо меньше одного фотона на когерентный пиксель при соответствующем разрешении, что требует сложных статистических и вычислительных методов для создания модели Интенсивность трехмерной дифракции, которая лучше всего согласуется с зашумленными экспериментальными данными 10,11 .
Но, несмотря на огромное увеличение пиковой яркости, прогнозируется, что типичное однократное дифракционное изображение изолированной биомолекулы, полученное XFEL, дает гораздо меньше одного фотона на когерентный пиксель при соответствующем разрешении, что требует сложных статистических и вычислительных методов для создания модели Интенсивность трехмерной дифракции, которая лучше всего согласуется с зашумленными экспериментальными данными 10,11 .
Замечательной альтернативой, использующей те же свойства излучения XFEL, является метод, предложенный еще в 1977 г. Камом 13 , предложившим оценивать взаимные корреляции (ВК) интенсивности рассеяния от идентичных частиц в растворе. Эти корреляции чувствительны к угловым флуктуациям, которые усредняются в традиционном анализе SAXS. Недостаток метода CC, заключающийся в том, что одночастичная дифракционная картина должна быть получена косвенно, в значительной степени компенсируется тем фактом, что множественное рассеяние допускается неявно, что легко объяснить экспериментальные осложнения, такие как фоновое рассеяние и неоднородный профиль пучка. и, самое главное, что работа с большим количеством изображений рассеяния, необходимых для противодействия низкой скорости счета фотонов, абсолютно проста.
и, самое главное, что работа с большим количеством изображений рассеяния, необходимых для противодействия низкой скорости счета фотонов, абсолютно проста.
В нашем демонстрационном эксперименте на синхротронном источнике уменьшенная плотность потока рентгеновского излучения была компенсирована за счет использования сильно рассеивающих наноструктур и их иммобилизации для обеспечения сколь угодно долгого сбора данных. Поведение в жидком состоянии имитировали путем освещения различных случайных конфигураций частиц. Уменьшение числа эффективных размерностей в задаче с трех до двух упростило как пробоподготовку, так и анализ данных КЦ. Недавно такой эксперимент был предложен 14,15 и с наноцилиндрами 16 . Однако реконструированная структура затемнена заметным элементом в форме шара, а заявленное разрешение соответствует размеру небольшого цилиндра, что ограничивает качество изображения. Мы сообщаем здесь о двухмерных структурных определениях наночастиц золота, демонстрирующих тройную симметрию, с использованием строгого протокола на основе CC. Несколько нововведений впервые позволяют полностью и независимо от модели рассчитать рентгенограммы отдельных частиц, а полученные реконструкции очень хорошо соответствуют изображениям частиц, полученным с помощью сканирующей электронной микроскопии (СЭМ). Мы также экспериментально подтверждаем ключевой прогноз о том, что отношение сигнал/шум КК практически не зависит от среднего числа рассеивателей 17 .
Несколько нововведений впервые позволяют полностью и независимо от модели рассчитать рентгенограммы отдельных частиц, а полученные реконструкции очень хорошо соответствуют изображениям частиц, полученным с помощью сканирующей электронной микроскопии (СЭМ). Мы также экспериментально подтверждаем ключевой прогноз о том, что отношение сигнал/шум КК практически не зависит от среднего числа рассеивателей 17 .
Результаты
Метод CC в 2D
Рабочий процесс метода CC схематически показан на рис. 1. Входные данные состоят из большого набора изображений рассеяния с интенсивностью I , полученных на 2D-жидкости, что означает, что каждое воздействие берется случайный ансамбль из нескольких одинаковых частиц. Важнейшим шагом является косвенное определение дифракционной картины одиночной частицы в обратном пространстве
Рис. 1: Обзор метода, основанного на взаимной корреляции, применяемого для определения двумерной структуры.
Течение протокола соответствует пурпурным стрелкам: ( a ) мембрана, несущая золотые наноструктуры, сканируется рентгеновским лучом, и в разных положениях получается ряд изображений рассеяния с интенсивностью I . . КК ( C (1) , C (2) и C (3) ) рассчитываются как средние значения по всем изображениям, а ( b ) картина дифракции одной частицы S вычисляется. Красная полоса представляет передачу обратного пространственного импульса 0,1 нм −1 . ( c ) Двумерная плотность электронов ρ окончательно реконструируется с использованием алгоритма фазирования. Красная полоса соответствует 100 нм. ( d ) СЭМ-изображение небольшой части мембраны образца, показывающее частицы в случайной ориентации. Увеличение представляет собой косой вид одиночной наноструктуры. Оранжевый пунктирный прямоугольник покрывает площадь 14 × 6 мкм 2 , что примерно соответствует площади освещения рентгеновским лучом (предел интенсивности луча по полуширине в двух направлениях). ( e ) СЭМ-вид сверху одной частицы, на который наложен пунктирный оранжевый контур реконструированной формы. Красная полоса снова соответствует 100 нм.
( e ) СЭМ-вид сверху одной частицы, на который наложен пунктирный оранжевый контур реконструированной формы. Красная полоса снова соответствует 100 нм.
Полноразмерное изображение
, по которому восстанавливается двухмерная электронная плотность частицы посредством восстановления фазы, как в стандартной когерентной дифракционной визуализации 18,19 . Полярная система координат ( q , φ ) с центром в начале координат обратного пространства является естественным выбором для анализа CC. являются азимутальными компонентами Фурье, которые обращаются в нуль при нечетных n в силу закона Фриделя, а для которого , так как S является действительной величиной.
Мы определяем SAXS или порошковый узор как 1-точечный CC,
, который зависит только от абсолютного значения переданного импульса q . Знаком ‹…› обозначено среднее по изображениям, а вращательным – среднее по азимутальному углу (рис. 2а). 1-точечный CC связан с интенсивностью рассеяния одной частицы как
Рис. 2: Изображения рассеяния и определение взаимной корреляции.
2: Изображения рассеяния и определение взаимной корреляции. Три примера из 3751 различных изображений рассеяния золотых наноструктур на рис. 1d в логарифмической цветовой шкале. Накладываются параметры, относящиеся ( a ) к определению 1-точечного CC (уравнение (2)), ( b ) к 2-точечному CC (уравнение (4)) и ( c ) к определению 3-точечный CC (уравнение (6)). Красные пунктирные кружки обозначают азимутальные средние значения. На вставке a показан экспериментальный C (1) ( q ), где зеленая пунктирная кривая представляет собой вычтенный фоновый сигнал. Красные полосы соответствуют q = 0,1 нм -1 .
Полноразмерное изображение
где N — эффективное среднее число частиц в рентгеновском луче, и в данном случае это просто коэффициент масштабирования.
Дополнительная структурная информация может быть извлечена из корреляций более высокого порядка. Двухточечный CC получается из среднего произведения двух интенсивностей рассеяния. Он зависит только от абсолютных значений двух переданных импульсов и угла между ними (рис. 2б). Определение 14,15,16
Он зависит только от абсолютных значений двух переданных импульсов и угла между ними (рис. 2б). Определение 14,15,16
where δI ( q , φ )= I ( q , φ )− C (1) ( q ) is отличие измеренной интенсивности от ее среднего значения. Компоненты Фурье связаны с интенсивностью одночастичного рассеяния соотношением
κ (2) ≤1 — коэффициент, который зависит только от формы рентгеновского пучка (см. Методы). Уравнение (5) составляет основу метода СС. При условии, что экспериментальные данные в левой части не возмущены, можно найти решения s n ( q ), которые уникальны с точностью до коэффициента масштабирования и векторов exp(− iχ n ) (см. Методы). В отличие от предыдущих работ 15,20 , для разрешения этих неясностей мы используем 3-точечный СС, который определяется аналогично 2-точечному СС и представляет собой обобщение предыдущих предложений 21,22 ,
.
и компоненты Фурье которого дают
κ (3) — аналог κ (2). Эти уравнения используются для фиксации значений N и х n . Таким образом, оставшаяся двусмысленность в коэффициентах Фурье S 0 ( Q ) и { S N ( Q )} N c Q )} N c 0
Экспериментальное определение 2D-структуры
Образцы для демонстрационного эксперимента 2D CC состояли из большого количества номинально идентичных 2D золотых наноструктур, прикрепленных к мембране, со случайными положениями и ориентациями (рис. 1d). Мембрану сканировали с помощью сфокусированного рентгеновского луча с длиной волны 2 Å, и картины рассеяния регистрировали с помощью малошумящего пиксельного детектора 23 , расположенного на расстоянии 7,2 м от образца. Мы измерили образцы с частицами, имеющими тройную симметрию, размером 350 (рис. 1e) или 200 нм и тремя различными плотностями: 1,25, 10 или 40 частиц на 100 мкм9.0005 2 район. Для каждого образца было получено 3751 изображение рассеяния в разных местах на мембране, имитирующее мгновенное воздействие двумерной жидкости. Такой набор изображений был проанализирован в соответствии с протоколом CC, и пример окончательной 2D-структуры наночастиц показан в конце схемы рабочего процесса на рис. 1c для наноструктур 350 нм и реконструирован из набора данных, взятых на образце с средняя плотность 10 частиц на 100 мкм 2 . Панель ( е ) фигуры демонстрирует превосходное соответствие восстановленной 2D-формы с формой отдельной наноструктуры, полученной на СЭМ-микрофотографии.
Мы измерили образцы с частицами, имеющими тройную симметрию, размером 350 (рис. 1e) или 200 нм и тремя различными плотностями: 1,25, 10 или 40 частиц на 100 мкм9.0005 2 район. Для каждого образца было получено 3751 изображение рассеяния в разных местах на мембране, имитирующее мгновенное воздействие двумерной жидкости. Такой набор изображений был проанализирован в соответствии с протоколом CC, и пример окончательной 2D-структуры наночастиц показан в конце схемы рабочего процесса на рис. 1c для наноструктур 350 нм и реконструирован из набора данных, взятых на образце с средняя плотность 10 частиц на 100 мкм 2 . Панель ( е ) фигуры демонстрирует превосходное соответствие восстановленной 2D-формы с формой отдельной наноструктуры, полученной на СЭМ-микрофотографии.
Далее мы проходим этапы, описанные в предыдущем разделе, которые ведут к окончательной реконструкции, более подробно представляя промежуточные результаты. На рис. 2 показаны три примера изображений рассеяния. Вставка в ( a ) показывает 1-точечный CC после вычитания фонового сигнала, полученного при экспозиции пустой мембраны. На всех трех изображениях видны тонкие азимутальные флуктуации интенсивности. Они отфильтровываются C (1) — азимутальные осреднения, но они дают именно ту дополнительную информацию, которая способствует корреляциям более высокого порядка. Рис. 3 посвящен 2-точечным КС. Панели ( C ) и ( D ) Показывают примеры C (2) ( Q 1 , Q 2 , ψ ), а PANEL PANELS ). и ( b ) отображают коэффициенты и , соответственно, где 2D-представление как функция q 1 и q 2 служат для того, чтобы подчеркнуть важность недиагональных ( q 1 ≠ q 2 ) CC в нашем протоколе. Закодированная информация затем использовалась в сочетании с информацией из 3-точечного CC для извлечения компонентов Фурье интенсивность дифракции.
Вставка в ( a ) показывает 1-точечный CC после вычитания фонового сигнала, полученного при экспозиции пустой мембраны. На всех трех изображениях видны тонкие азимутальные флуктуации интенсивности. Они отфильтровываются C (1) — азимутальные осреднения, но они дают именно ту дополнительную информацию, которая способствует корреляциям более высокого порядка. Рис. 3 посвящен 2-точечным КС. Панели ( C ) и ( D ) Показывают примеры C (2) ( Q 1 , Q 2 , ψ ), а PANEL PANELS ). и ( b ) отображают коэффициенты и , соответственно, где 2D-представление как функция q 1 и q 2 служат для того, чтобы подчеркнуть важность недиагональных ( q 1 ≠ q 2 ) CC в нашем протоколе. Закодированная информация затем использовалась в сочетании с информацией из 3-точечного CC для извлечения компонентов Фурье интенсивность дифракции. В анализируемом диапазоне переданного импульса (0,009≤ q ≤0,24 nm −1 ), только коэффициенты с n = 6, 12, 18, 24, 30, показанные на рис. 4а, могут быть последовательно рассчитаны и подтверждены. На рис. 4b показаны отношения трехточечных компонентов CC к одночастичным коэффициентам s n в виде точек на комплексной плоскости (см. уравнение (13) в Методах для точной формулировки), а достоверность определяется выражением тот факт, что почти все такие точки попадают в одно и то же действительно-положительное значение, которое пропорционально . Это определяет эффективное среднее число рассеивающих частиц равным 9.0041 Н ≈20. Другие коэффициенты далее не рассматривались, потому что их нельзя было ни определить самосогласованно, ни подтвердить (см. дополнительные рисунки S1 и S2b – e). Их вклад в любом случае незначителен (дополнительный рис. S2a), за исключением n = 2, а мотивы рассмотрения s 2 ( q ) в качестве артефакта подробно описаны в дополнительном Методы.
В анализируемом диапазоне переданного импульса (0,009≤ q ≤0,24 nm −1 ), только коэффициенты с n = 6, 12, 18, 24, 30, показанные на рис. 4а, могут быть последовательно рассчитаны и подтверждены. На рис. 4b показаны отношения трехточечных компонентов CC к одночастичным коэффициентам s n в виде точек на комплексной плоскости (см. уравнение (13) в Методах для точной формулировки), а достоверность определяется выражением тот факт, что почти все такие точки попадают в одно и то же действительно-положительное значение, которое пропорционально . Это определяет эффективное среднее число рассеивающих частиц равным 9.0041 Н ≈20. Другие коэффициенты далее не рассматривались, потому что их нельзя было ни определить самосогласованно, ни подтвердить (см. дополнительные рисунки S1 и S2b – e). Их вклад в любом случае незначителен (дополнительный рис. S2a), за исключением n = 2, а мотивы рассмотрения s 2 ( q ) в качестве артефакта подробно описаны в дополнительном Методы.
( a , b ) Двумерные представления экспериментально полученных 2-точечных компонент CC Фурье в зависимости от q 1 и q 2 . Данные нормализованы с S 0 ( Q 1 ) S 0 ( Q 2 ) и показаны для N = 6 и 6 и 6. 6. и 6. 6. и 6 и 6. 6. и 6. 6. и 6 и 6. 60041 и . ( c ) Двухточечные CC C (2) ( q 1 , q 2 , ψ ) в зависимости от ψ . Значения (фиксированные) q 1 и (переменные) q 2 следуют путям пурпурных стрелок в a , b для графиков в левом столбце и черных стрелок в a , b для тех, кто в правой колонке. Пики, наблюдаемые для q 1 = q 2 при ψ =0, обусловленные шумом и межчастичной интерференцией, а при ψ = π , обусловленные только межчастичной интерференцией, отмечены оранжевыми и красными точками соответственно. ( D ) Диагональный 2-точечный CC C (2) ( Q 1 , Q 2, ψ ), как функция ψ , , для разнообразных , 40041. значения, соответствующие по-разному обозначенным черным точкам на диагонали в a , b . Шипы помечены, как описано в c .
( D ) Диагональный 2-точечный CC C (2) ( Q 1 , Q 2, ψ ), как функция ψ , , для разнообразных , 40041. значения, соответствующие по-разному обозначенным черным точкам на диагонали в a , b . Шипы помечены, как описано в c .
Изображение в полный размер
Рис. 4: Дифрактограмма одиночных частиц. ( a ) Коэффициент Фурье s n ( q ) одночастичной дифрактограммы, извлеченной из экспериментальных КК, как функция q . Данные показаны для n =6, 12, 18, 24, 30 и перемасштабированы с s 0 ( q ). Сплошная и штриховая кривые соответствуют действительной и мнимой частям соответственно. ( B ) Комплексная плоскость презентации соотношений R нм ( Q A , Q B 6, Q B 6, Q B 6, Q B , Q 5 B 6, Q 5 B 6, Q 5 . Изображение в полный размер Интенсивность одночастичной дифракции S ( q , φ ), показанная на рис. ( a ) Усредненная двумерная электронная плотность ρ по 50 реконструкциям. р нормализуется, чтобы быть в среднем единицей в ядре структуры. Один пиксель реального пространства соответствует 13,0 нм, а красная полоса соответствует 100 нм. Заштрихованный белый прямоугольник ограничивает область компактной поддержки, введенной во время итеративной процедуры восстановления фазы. Две пунктирные пурпурные линии представляют собой контурные уровни ρ =0,9 и ρ =0,1, а их среднее расстояние дает оценку достигнутого разрешения в 17,5 нм. ( b ) Передаточная функция восстановления фазы PRTF( q ) в результате 50 реконструкций в зависимости от q . Красной пунктирной вертикальной линией отмечено значение q , соответствующее разрешению, оцененному в a . ( c ) Горизонтальный разрез (h–h′) и вертикальный разрез (v–v′) двумерной плотности электронов ρ в позициях, отмеченных голубым цветом в a . Изображение в натуральную величину Для более мелких частиц размером 200 нм мы получили аналогичные результаты, проиллюстрированные на рис. 6. В этом случае разрешение оценивается в ~13,5 нм (соответствует q = 0,23 нм -1 ). Для размеров частиц 350 и 200 нм экспериментальные данные, измеренные при трех различных поверхностных плотностях, подразумевают среднее число рассеивающих частиц N ≈2,5/20/80, что согласуется с известными значениями плотности образца, размера луча и формы луча. (см. Методы). Более того, как видно на рис. 7а, данные, полученные на разных выборках, демонстрируют, что 2-точечные КК правильно масштабируются с N , как того требует уравнение (5), с некоторыми отклонениями при больших к . Эквивалентно рис. 7b показывает, что извлеченные s 0 ( q ) и s n ( q ) в общем случае независимы1 от 9004 N 9004 . Только при больших q наблюдается заметное подавление s n с уменьшением N , наблюдение, которое мы пока не можем объяснить. ( a ) Дифрактограмма одиночных частиц S ( q , φ ). Представление такое же, как на рис. 4c, с максимальной частотой обратного пространства q max =0,37 нм -1 . Красная полоса соответствует q = 0,1 нм -1 . ( b ) Усредненная двумерная электронная плотность ρ по 50 реконструкциям. Представление такое же, как на рис. 5а, с одним пикселем, соответствующим 8,4 нм, и красной полосой 100 нм. Разрешение, определяемое расстоянием между двумя пурпурными контурами, составляет 13,5 нм. ( c ) Передаточная функция восстановления фазы PRTF( q ), полученная в результате 50 реконструкций, как функция q . Красной пунктирной вертикальной линией отмечено значение q , соответствующее разрешению, оцененному в b . Изображение в полный размер Данные для наночастиц размером 350 нм (левый столбец) и частиц размером 200 нм (правый столбец), а также для трех различных поверхностных плотностей частиц, соответствующих N =2,5 (красный), N =20 (синий) и N =80 (черный). ( a ) Примеры диагональных 2-точечных CCS C (2) ( Q 1 , Q 2, ψ ), как функция ψ , двух. разные значения q для каждого размера частиц. Данные масштабируются с помощью N . ( b ) Коэффициенты Фурье нулевого порядка s 0 ( q ) одночастичной дифракционной картины в зависимости от к . Фоновый сигнал представлен пунктирной зеленой кривой. ( c ) Амплитуда коэффициентов Фурье s n ( q ) одночастичной дифракционной картины в зависимости от q . Значения показаны для n =6 и n =12 и перемасштабированы с помощью s 0 ( q ), рассчитанных из набора данных N =20. Полноразмерное изображение Полученные результаты в рамках рентгеновской дифракции представляют собой первое независимое от модели экспериментальное подтверждение принципа применения метода CC для определения двумерной структуры. Из низкого отношения сигнала одной частицы к фону, выделенного на рис. 7b, очевидно, что стандартное определение 2D-структуры путем восстановления фазы из уникального изображения дифракции одной частицы будет безуспешным. Разница между реконструированной формой и реальной формой одной репрезентативной частицы намного меньше достигнутого разрешения ~15 нм, что не является внутренним ограничением метода, а скорее отражает сложность изготовления идентичных, но случайно ориентированных наноструктур. Характерными особенностями протокола, подробно описанными в Методах, являются процедура «диагонализации» для последовательного решения 2-точечного уравнения (5) и использование 3-точечного уравнения (7) для проверки одночастичных дифракционные компоненты Фурье. ), для разных N и M , для 60041 Q A = 0,066 нм –1 и Q B = 0.115 — B = 0.115 — B = 0.115 — B 9015 = 0,115 — B 9015. и для большого числа q c . Центральная точка, выделенная оранжевым цветом, является медианой всех точек, а оранжевый круг охватывает область, содержащую ближайшие 80% всех точек. Мнимая часть точки центроида пренебрежимо мала, а ее действительная часть соответствует , при . ( c ) Дифрактограмма одиночной частицы S ( q , φ ) в логарифмической цветовой шкале, определенная по дискообразной области с максимальной частотой в обратном пространстве q макс =0,24 нм −1 . Темные области в углах не содержат данных. Красная полоса соответствует q = 0,1 нм -1 .
), для разных N и M , для 60041 Q A = 0,066 нм –1 и Q B = 0.115 — B = 0.115 — B = 0.115 — B 9015 = 0,115 — B 9015. и для большого числа q c . Центральная точка, выделенная оранжевым цветом, является медианой всех точек, а оранжевый круг охватывает область, содержащую ближайшие 80% всех точек. Мнимая часть точки центроида пренебрежимо мала, а ее действительная часть соответствует , при . ( c ) Дифрактограмма одиночной частицы S ( q , φ ) в логарифмической цветовой шкале, определенная по дискообразной области с максимальной частотой в обратном пространстве q макс =0,24 нм −1 . Темные области в углах не содержат данных. Красная полоса соответствует q = 0,1 нм -1 . )} n = 6,12,18,24,30 вместе с s 0 ( q ) и, очевидно, демонстрирует шестикратную симметрию. Результаты моделирования показывают, что небольшие области с отрицательной интенсивностью возникают из-за не совсем идентичных рассеивателей (см. Дополнительный рисунок S3). S впоследствии использовался в качестве входных данных для алгоритма восстановления фазы для восстановления двумерной плотности электронов ρ , показанной на рис. 5а, нормализованной к среднему значению единицы внутри структуры. Мы оцениваем пространственное разрешение в ~17,5 нм по средней резкости края структуры, определяемой как среднее расстояние между 0,1 и 0,9уровни контура. Высокая надежность реконструкции восстановления фазы оценивалась по передаточной функции восстановления фазы (PRTF) 24 , показанной как функция передачи импульса q на рис. 5b, значение которой значительно выше 0,5 в соответствующем диапазоне в обратное пространство ( q <0,18 нм -1 ).
)} n = 6,12,18,24,30 вместе с s 0 ( q ) и, очевидно, демонстрирует шестикратную симметрию. Результаты моделирования показывают, что небольшие области с отрицательной интенсивностью возникают из-за не совсем идентичных рассеивателей (см. Дополнительный рисунок S3). S впоследствии использовался в качестве входных данных для алгоритма восстановления фазы для восстановления двумерной плотности электронов ρ , показанной на рис. 5а, нормализованной к среднему значению единицы внутри структуры. Мы оцениваем пространственное разрешение в ~17,5 нм по средней резкости края структуры, определяемой как среднее расстояние между 0,1 и 0,9уровни контура. Высокая надежность реконструкции восстановления фазы оценивалась по передаточной функции восстановления фазы (PRTF) 24 , показанной как функция передачи импульса q на рис. 5b, значение которой значительно выше 0,5 в соответствующем диапазоне в обратное пространство ( q <0,18 нм -1 ).


 7: Зависимость от размера частиц и поверхностной плотности.
7: Зависимость от размера частиц и поверхностной плотности. 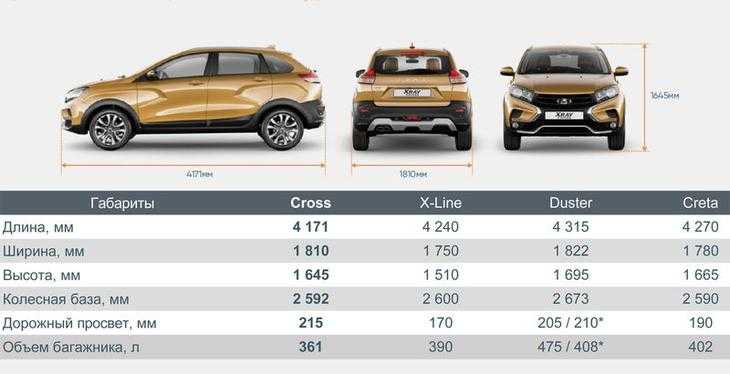 ( d ) Средние отклонения Δ с 6 ( q ) коэффициентов Фурье s 6 ( q ), как функция q (Методы).
( d ) Средние отклонения Δ с 6 ( q ) коэффициентов Фурье s 6 ( q ), как функция q (Методы). Обсуждение
 Таким образом, одночастичная дифракционная картина определяется однозначно и независимо от модели. Это отличает наш протокол от предыдущей работы. Салдин и др. . 16 вывел фазы таких компонентов Фурье на основе предыдущих знаний об удлиненной форме исследуемых частиц и не обсуждал в явной форме общее соотношение между n >0
Таким образом, одночастичная дифракционная картина определяется однозначно и независимо от модели. Это отличает наш протокол от предыдущей работы. Салдин и др. . 16 вывел фазы таких компонентов Фурье на основе предыдущих знаний об удлиненной форме исследуемых частиц и не обсуждал в явной форме общее соотношение между n >0  16.
16.
Основные уравнения (5) и (7) строго справедливы в пределе бесконечного числа образов рассеяния N im , что необходимо для усреднения вкладов в КЦ от пар частиц в то же изображение (дополнительное примечание 1). На практике это означает, что должно быть получено «достаточное» количество изображений, что приводит к рассмотрению флуктуаций, или отношения сигнал-шум, CC в целом N im и как функции количество рассеивателей Н . Отношение сигнал/шум двухточечной CC было оценено аналитически для трехмерного случая 17 и оказалось, что оно не зависит от N , если только фоновое рассеяние не сравнимо с рассеянием от отдельной частицы, и в этом случае увеличение N становится выгоднее. Эти выводы подтверждаются соответствующим анализом наших данных. Мы берем коэффициенты { s n ( q )} n >0 в качестве сигнала, который равен N -независимый, поэтому оценка отношения сигнал/шум Δ s n ( q ) становится эквивалентной оценке шума. На рис. 7г показаны Δ s n ( q ), полученные из экспериментальных данных для N im =100 (Методы) и для трех различных N =2. для частиц с длиной волны 350 нм Δ с n ( q ) не зависит от N , а для более мелких структур размером 200 нм, имеющих менее благоприятное отношение рассеяния сигнала к фону (рис. 7б), наблюдается уменьшение q ) при большом q становится очевидным при увеличении N с 2,5 до 20. ближе друг к другу, чем поперечная длина когерентности. Поскольку этот член модулируется по фазе расстоянием между частицами, случайные положения частиц вызывают его вклад в C (2) ( q 1 , q 2 , ψ ) to average out in the limit of an infinite number of images, with the exception at q 1 = q 2 и ψ = 0 или ψ = π (см.
На рис. 7г показаны Δ s n ( q ), полученные из экспериментальных данных для N im =100 (Методы) и для трех различных N =2. для частиц с длиной волны 350 нм Δ с n ( q ) не зависит от N , а для более мелких структур размером 200 нм, имеющих менее благоприятное отношение рассеяния сигнала к фону (рис. 7б), наблюдается уменьшение q ) при большом q становится очевидным при увеличении N с 2,5 до 20. ближе друг к другу, чем поперечная длина когерентности. Поскольку этот член модулируется по фазе расстоянием между частицами, случайные положения частиц вызывают его вклад в C (2) ( q 1 , q 2 , ψ ) to average out in the limit of an infinite number of images, with the exception at q 1 = q 2 и ψ = 0 или ψ = π (см. дополнительное примечание 2). Этим объясняются два пика одинаковой высоты, присутствующие в диагональных КС, которые пропорциональны квадрату среднего числа частиц в области когерентности и отмечены оранжевыми и красными точками на рис. 3г и 7а. Таким образом, оптимальный размер области когерентности в два раза превышает размер одной частицы, чтобы обеспечить выборку Найквиста и в то же время минимизировать количество мешающих частиц.
дополнительное примечание 2). Этим объясняются два пика одинаковой высоты, присутствующие в диагональных КС, которые пропорциональны квадрату среднего числа частиц в области когерентности и отмечены оранжевыми и красными точками на рис. 3г и 7а. Таким образом, оптимальный размер области когерентности в два раза превышает размер одной частицы, чтобы обеспечить выборку Найквиста и в то же время минимизировать количество мешающих частиц.
Стоит упомянуть и другие факторы, влияющие на идентификацию CC. Пуассонский шум и (некоррелированное) фоновое рассеяние приводят к всплеску при ψ = 0 в C (2) ( Q 1 , Q 2 , ψ Q 2 , ψ Q . 1 = q 2 (дополнительный рисунок S4 и дополнительное примечание 3), отмечены оранжевыми точками на рисунках 3d и 7a. Поскольку возмущения от шумовых и интерференционных эффектов проявляются как локальные всплески, оценить их значимость несложно, а в нашем случае мы могли также легко убедиться, что они были отфильтрованы в ходе процедуры для получения коэффициентов с n (Методы). Предпочтительная ориентация одинаковых частиц также требует корректировок (5) и (7) (дополнительное примечание 1). Наконец, следует кратко остановиться на общем случае неидентичных рассеивающих частиц. Если ситуацию можно свести к конечному числу видов двумерных частиц с некоррелированной ориентацией, справедливость уравнения (5) восстанавливается заменой правой части суммой по видам , и аналогичная модификация необходима в (3 ) и (7). Это открывает двери для изучения систем различных видов 2D-частиц, находящихся в «химическом равновесии», или идентичных 3D-частиц, представляющих конечное число различных 2D-проекций по отношению к входящему лучу. Для простейшего случая двухкомпонентной системы частица/растворитель можно вычесть отдельно измеренный вклад в КК только растворителя. В наших экспериментах растворитель представлен мембраной, на которой были закреплены наночастицы, и, таким образом, мы определили вклад растворителя, используя данные рассеяния от пустой мембраны. Явный вклад в 1-балльную СС, который мы приписываем флуктуациям толщины мембраны, учитывался путем вычитания фона (вставка к рис.
Предпочтительная ориентация одинаковых частиц также требует корректировок (5) и (7) (дополнительное примечание 1). Наконец, следует кратко остановиться на общем случае неидентичных рассеивающих частиц. Если ситуацию можно свести к конечному числу видов двумерных частиц с некоррелированной ориентацией, справедливость уравнения (5) восстанавливается заменой правой части суммой по видам , и аналогичная модификация необходима в (3 ) и (7). Это открывает двери для изучения систем различных видов 2D-частиц, находящихся в «химическом равновесии», или идентичных 3D-частиц, представляющих конечное число различных 2D-проекций по отношению к входящему лучу. Для простейшего случая двухкомпонентной системы частица/растворитель можно вычесть отдельно измеренный вклад в КК только растворителя. В наших экспериментах растворитель представлен мембраной, на которой были закреплены наночастицы, и, таким образом, мы определили вклад растворителя, используя данные рассеяния от пустой мембраны. Явный вклад в 1-балльную СС, который мы приписываем флуктуациям толщины мембраны, учитывался путем вычитания фона (вставка к рис. 2а). Однако для 2- и 3-точечных СС мы получаем эффективно исчезающий вклад.
2а). Однако для 2- и 3-точечных СС мы получаем эффективно исчезающий вклад.
Существует ряд двумерных статических систем, которые строго не включены в рамки, описанные выше, и которые изучаются или характеризуются измерениями МУРР на синхротронных источниках. Оценка СС более высокого порядка рассеянных изображений тривиальна и уже в настоящее время может дать дополнительную информацию 25,26 , например, среднюю анизотропию доменов в магнитных запоминающих устройствах или пор в мембранах топливных элементов. Анализ CC также может быть полезен для доступа к структурным свойствам ближнего действия в неупорядоченных, медленно меняющихся системах. Вокнер и др. . 27 использовали диагональную 2-точечную CC, полученную из данных синхротронной когерентной рентгеновской дифракции высококонцентрированных суспензий наносфер ПММА, для определения предпочтительной симметрии трехмерных кластеров 25 , которые временно формируются в образце. Что касается возможных будущих исследований трехмерных структурных особенностей макромолекул или других частиц в растворе, которые используют великолепие источников излучения XFEL, представляется, что применение метода CC в духе его первоначальной формулировки 13 подходит; к динамической информации можно получить доступ путем прямого обобщения анализа CC на изображения рассеяния лазерной накачки/рентгеновского зонда или даже на данные рассеяния, полученные с помощью данных разделения и задержки рентгеновского излучения 28,29 . Настоящий двухмерный демонстрационный эксперимент и его обсуждение имеют прямое отношение к трехмерному случаю в отношении эффектов межчастичной интерференции и неизбежно неоднородного профиля интенсивности пучка, а также независимости отношения сигнал/шум от среднего числа рассеивающие частицы. Однако увеличение размерности с 2D на 3D требует некоторых дополнительных соображений. Трехмерную дифракционную картину одной частицы можно разложить на сферические гармоники
Настоящий двухмерный демонстрационный эксперимент и его обсуждение имеют прямое отношение к трехмерному случаю в отношении эффектов межчастичной интерференции и неизбежно неоднородного профиля интенсивности пучка, а также независимости отношения сигнал/шум от среднего числа рассеивающие частицы. Однако увеличение размерности с 2D на 3D требует некоторых дополнительных соображений. Трехмерную дифракционную картину одной частицы можно разложить на сферические гармоники
и компонентов явно больше, чем для 2D случая. Напротив, количество двухточечных тождеств CC 13,30 в 3D такое же, как и в 2D:
q 2, ψ ) относительно полиномов Лежандра n -го порядка от cos ψ . Elser 31 недавно показал, что без дополнительных предположений эти уравнения не могут быть решены для коэффициентов s нм ( q ) в той же степени, что и в 2D (т.е. в пределах параметров N и χ n ). для моделирования трехмерной электронной плотности частиц с более высоким разрешением, чем это возможно с помощью уравнения (10) один. Что касается использования 3-точечной СС, то определение (6) применимо и в 3D-случае. Он представляет собой обобщение того, что выдвинуто в исх. При больших углах рассеяния необходимы прямые поправки на анизотропное рассеяние из-за линейной поляризации 33 падающего луча и на кривизну сферы Эвальда. Однако узким местом в достижении субнанометрового разрешения является то, что ключевым параметром, определяющим точность метода CC, является количество рассеянных фотонов на когерентный пиксель и на частицу 17 , что особенно для макромолекул может быть значительно ниже единицы. Нет никаких сомнений в том, что этот метод, как и любой другой подход, основанный на использовании одной частицы, значительно выиграет от увеличения плотности потока рентгеновского излучения. Образцы были приготовлены на мембране 2 × 2 мм 2 Si 3 N 4 толщиной 200 нм, удерживаемой пластиной Si/Au (5Cr/Au). 20 нм) затравочный слой. Наночастицы золота были изготовлены путем гальванопокрытия в форме резиста из ПММА толщиной 500 нм с нанесением рисунка с помощью электронно-лучевой литографии. Более подробную информацию о процедурах нанопроизводства можно найти в другом месте 34 . Частицы с разработанной тройной симметрией были случайным образом ориентированы вокруг оси, перпендикулярной мембране, и размещены в случайных положениях в пределах 800 × 800 мкм 2 , с ограничением минимального расстояния между частицами 500 нм. Рентгеновские измерения проводились на линии луча cSAXS (X12SA) синхротрона Swiss Light Source в Институте Пауля Шеррера. На линии луча была установлена энергия фотонов 6,2 кэВ с относительной шириной полосы ~10 −4 , полученное с помощью двухкристального монохроматора Si(111) и с потоком ~2·10 11 фотонов в секунду. Луч фокусировался на образец; горизонтальная и вертикальная фокусировка достигались за счет соответствующего изгиба второго кристалла монохроматора и зеркала подавления высших гармоник, расположенных на расстоянии 5,5 и 4,5 м выше по потоку от образца соответственно. Размер пучка составлял 14 × 6 мкм 2 FWHM (см. ниже), а поперечная длина когерентности не менее чем в два раза превышала размер наноструктуры, то есть не менее 700 нм. Поправочные параметры κ (2) и κ (3) и связь между эффективным параметром N и плотностью частиц определяются двумерной функцией интенсивности освещения на образце, Ω( x , y ), according to κ ( j ) =(∬d x d y Ω j )/(∬d x d y Ом) (дополнительное примечание 4). Эти предположения могут включать априорные знания о симметрии частиц, которые уменьшают количество независимых параметров в S ( q , θ , φ ). Для осесимметричных частиц отличны от нуля только коэффициенты s n 0 13 . Точно так же, если частицы обладают икосаэдрической симметрией, как это часто бывает у вирусов 21 , для каждого n имеется не более одной компоненты, пропорциональной икосаэдрической гармонике 32 . В обоих случаях задача становится эквивалентной двумерному случаю. В общем, уравнение (9) можно интерпретировать как ограничение на S , которое следует использовать в дополнение к трехмерному эквиваленту (3):
Эти предположения могут включать априорные знания о симметрии частиц, которые уменьшают количество независимых параметров в S ( q , θ , φ ). Для осесимметричных частиц отличны от нуля только коэффициенты s n 0 13 . Точно так же, если частицы обладают икосаэдрической симметрией, как это часто бывает у вирусов 21 , для каждого n имеется не более одной компоненты, пропорциональной икосаэдрической гармонике 32 . В обоих случаях задача становится эквивалентной двумерному случаю. В общем, уравнение (9) можно интерпретировать как ограничение на S , которое следует использовать в дополнение к трехмерному эквиваленту (3): 21, поскольку подразумевает доступ к трем, а не к двум векторам обратного пространства. Хотя экспериментальная геометрия в экспериментах по дифракции рентгеновских лучей ограничивает эти тройки компланарностью, новое определение накладывает дополнительные ограничения, которые можно использовать для фиксации s нм ( q ) коэффициенты аналогично тому, как это описано в ссылке. 21.
21, поскольку подразумевает доступ к трем, а не к двум векторам обратного пространства. Хотя экспериментальная геометрия в экспериментах по дифракции рентгеновских лучей ограничивает эти тройки компланарностью, новое определение накладывает дополнительные ограничения, которые можно использовать для фиксации s нм ( q ) коэффициенты аналогично тому, как это описано в ссылке. 21. Преимущество использования СС заключается в том, что низкую рассеивающую способность можно компенсировать, просто резко увеличив количество получаемых изображений, хотя даже слабое рассеяние растворителя может стать существенной дополнительной проблемой. По этой причине следующий этап экспериментов, в ходе которого будет предпринята попытка идентифицировать нанометровые характеристики трехмерных молекул в жидкостных или аэрозольных струях, считается решающим для развития метода CC.
Преимущество использования СС заключается в том, что низкую рассеивающую способность можно компенсировать, просто резко увеличив количество получаемых изображений, хотя даже слабое рассеяние растворителя может стать существенной дополнительной проблемой. По этой причине следующий этап экспериментов, в ходе которого будет предпринята попытка идентифицировать нанометровые характеристики трехмерных молекул в жидкостных или аэрозольных струях, считается решающим для развития метода CC. Методы
Образцы
 Измерения проводились на нескольких образцах, отличающихся диаметром/толщиной наноструктур (350/350 нм, соответственно 200/250 нм), и средней поверхностной плотностью частиц (1,25/10/40 частиц на 100 мкм 2 район).
Измерения проводились на нескольких образцах, отличающихся диаметром/толщиной наноструктур (350/350 нм, соответственно 200/250 нм), и средней поверхностной плотностью частиц (1,25/10/40 частиц на 100 мкм 2 район). Установка линии луча и сбор данных
 Рассеянное рентгеновское излучение транспортировалось через вакуумированную пролетную трубу к детектору, который располагался на расстоянии 7,2 м за образцом. Детектор 23 представлял собой Pilatus 2M с 1675 × 1475 квадратных пикселей размером 172 мкм и был защищен от прямого луча центральным светоотражателем. Диаметр рентгеновского луча в месте расположения детектора, измеренный с ослабленным пучком и без введенного образца, соответствовал 3–4 пикселям детектора. Для каждого образца было получено 3751 изображение рассеяния с временем сбора данных 1 с, при сканировании мембраны по прямоугольной сетке 121 × 31 точка, которая покрывала площадь 600 × 600 мкм 2 .
Рассеянное рентгеновское излучение транспортировалось через вакуумированную пролетную трубу к детектору, который располагался на расстоянии 7,2 м за образцом. Детектор 23 представлял собой Pilatus 2M с 1675 × 1475 квадратных пикселей размером 172 мкм и был защищен от прямого луча центральным светоотражателем. Диаметр рентгеновского луча в месте расположения детектора, измеренный с ослабленным пучком и без введенного образца, соответствовал 3–4 пикселям детектора. Для каждого образца было получено 3751 изображение рассеяния с временем сбора данных 1 с, при сканировании мембраны по прямоугольной сетке 121 × 31 точка, которая покрывала площадь 600 × 600 мкм 2 . Параметры формы рентгеновского луча и оценка формы луча
 Ом ( х , y ) был определен экспериментально, как описано на дополнительном рисунке S5 и в дополнительных методах, и дал κ (2) ≈0,26, κ (3) 9042
Ом ( х , y ) был определен экспериментально, как описано на дополнительном рисунке S5 и в дополнительных методах, и дал κ (2) ≈0,26, κ (3) 9042
Дискретизация дифрагированной интенсивности
Положение центра рассеяния на пиксельном детекторе было установлено путем усреднения ряда точек центра тяжести пар противоположных брэгговских отражений, созданных двумерным гексагональным периодическим массивом (дополнительный рис. S5c ). Вокруг этого центра была определена полярная сетка «паутина» ( q a, φ k ), with a {1,…, N q } and φ k = k 2 π k/N φ , for k {0,…, N φ −1}, что также задает бинирование пикселей детектора. Интенсивности рассеяния в полярных координатах I ( q a , φ k ) затем рассчитывались как среднее значение по пикселям, принадлежащим одному и тому же полярному бину. Для структур размером 350 нм q a были определены как разнесенные на эквивалент двух пикселей детектора (0,0015, нм -1 ) и трех различных q a . рассматривались диапазоны: 0,009–0,006 нм −1 ( N q =35), 0,015–0,12 нм −1 ( N q =71) and 0.03–0.24 nm −1 ( N q =141), with N φ =32, 64 and 128 azimuthal sectors, respectively. Для 200-нм структур q a были определены как разнесенные на расстояние, эквивалентное четырем пикселям детектора (0,003 нм -1 ), и рассматривались четыре различных диапазона q a 9004: 0,009–0,06 нм −1 ( N Q = 18), 0,015–0,12 нм −1 ( N Q = 36), 0,03–0,24 НМ –19006 (41414419292929292929292929292929292929292929156.
Интенсивности рассеяния в полярных координатах I ( q a , φ k ) затем рассчитывались как среднее значение по пикселям, принадлежащим одному и тому же полярному бину. Для структур размером 350 нм q a были определены как разнесенные на эквивалент двух пикселей детектора (0,0015, нм -1 ) и трех различных q a . рассматривались диапазоны: 0,009–0,006 нм −1 ( N q =35), 0,015–0,12 нм −1 ( N q =71) and 0.03–0.24 nm −1 ( N q =141), with N φ =32, 64 and 128 azimuthal sectors, respectively. Для 200-нм структур q a были определены как разнесенные на расстояние, эквивалентное четырем пикселям детектора (0,003 нм -1 ), и рассматривались четыре различных диапазона q a 9004: 0,009–0,06 нм −1 ( N Q = 18), 0,015–0,12 нм −1 ( N Q = 36), 0,03–0,24 НМ –19006 (41414419292929292929292929292929292929292929156. 929292929156.
929292929156.
Расчет одночастичной дифракционной картины: теория
Основная часть представленной работы касается расчета одночастичной дифракционной картины S ( q , φ ) из КК, то есть решение уравнений (3), (5) и (7) для s n ( q ). Пусть q a будет конечным дискретным набором q значений. Вдохновленные Камом и его коллегами 22 , а также Салдином и коллегами 30 , для n ≠0 мы используем двухточечные коэффициенты CC для определения эрмитовой матрицы , которую можно диагонализовать для получения реальных собственных значений λ n,i ( i {1,…, N q }). Обозначим λ n, 1 как наибольшее положительное собственное значение и запишем разложение собственного вектора как
Обозначим λ n, 1 как наибольшее положительное собственное значение и запишем разложение собственного вектора как
с и ( i {2,…, N
}). Обратите внимание, что вектор s n определен с точностью до общей фазы х n . Согласно (5) ожидается единственное ненулевое положительное собственное значение λ n ,1 . Таким образом, сигнатура различных возмущений, таких как конечное число изображений, дробовой шум, некоррелированный фоновый шум, интерференция между частицами, предпочтительная ориентация частиц и неэквивалентные частицы, мала, это
, что эквивалентно требованию второго члена справа -сторона (11) пренебрежимо мала. В этом случае используются собственные векторы s n для вычисления отношений
Последнее равенство получается из 3-точечного уравнения CC (7) в сочетании с уравнением (15) ниже и позволяет зафиксировать χ n и эффективное число частиц N . Эти параметры фактически переопределены, что позволяет провести дополнительную проверку. Наконец, требуемые компоненты одночастичной дифракции устанавливаются равными
Эти параметры фактически переопределены, что позволяет провести дополнительную проверку. Наконец, требуемые компоненты одночастичной дифракции устанавливаются равными
и
Расчет одночастичной дифракционной картины: практика
Описанная выше двумерная дискретизация в обратном пространстве использовалась для всех расчетов, при этом каждое соответствующее уравнение преобразуется в простой путь к дискретной форме. Перед вычислением CC из каждого отдельного дифракционного изображения вычиталась средняя интенсивность, чтобы устранить возможные артефакты линии луча, которые приводят к независимым от конфигурации вкладам в интенсивность рассеяния. Диагонализация по линиям уравнения (11) выполнялась даже для n в трех или четырех диапазонах q и для структур 350 или 200 нм соответственно (дополнительные методы). Требование (12) переводилось в , а при невыполнении поднималась нижняя граница диапазона q a (из-за высокой чувствительности к возмущениям C n,ab , когда s n ≈0 при низких q a ). с 9Затем 0045 n из диапазонов q и были объединены путем сопоставления их фаз на перекрывающихся интервалах q и . The phase relations of equation (13), for the relevant n and m and for a number of different q a , q b and q c , представляют собой сверхсвязанную систему уравнений первого порядка в общих фазах коррекции χ n , которое решается напрямую, следуя процедуре, описанной в дополнительных методах. Из-за зеркальной симметрии наноструктур, рассматриваемых в экспериментах, s n могут быть выбраны реальными, так что фазовая неоднозначность фактически является только неоднозначностью знака. Однако метод фиксации общих фаз s n является абсолютно общим, как показано на дополнительном рис.
с 9Затем 0045 n из диапазонов q и были объединены путем сопоставления их фаз на перекрывающихся интервалах q и . The phase relations of equation (13), for the relevant n and m and for a number of different q a , q b and q c , представляют собой сверхсвязанную систему уравнений первого порядка в общих фазах коррекции χ n , которое решается напрямую, следуя процедуре, описанной в дополнительных методах. Из-за зеркальной симметрии наноструктур, рассматриваемых в экспериментах, s n могут быть выбраны реальными, так что фазовая неоднозначность фактически является только неоднозначностью знака. Однако метод фиксации общих фаз s n является абсолютно общим, как показано на дополнительном рис. 6. Наконец, параметр N был выбран для наилучшего выполнения амплитудного соотношения (13) для различных n , m . Окончательные значения S 0 ( Q A ) и S N ( Q A ( Q 9 A ( Q A ( Q A ( Q A ( Q A). , а коэффициенты с n 6 N использовались для расчета одночастичной дифрактограммы S ( q , φ ) с уравнением (1) на полярной сетке с N φ = 128 азимутальных точек для структур 350 нм (| N | ≤30) и N φ
6. Наконец, параметр N был выбран для наилучшего выполнения амплитудного соотношения (13) для различных n , m . Окончательные значения S 0 ( Q A ) и S N ( Q A ( Q 9 A ( Q A ( Q A ( Q A ( Q A). , а коэффициенты с n 6 N использовались для расчета одночастичной дифрактограммы S ( q , φ ) с уравнением (1) на полярной сетке с N φ = 128 азимутальных точек для структур 350 нм (| N | ≤30) и N φ
Восстановление фаз
Для реконструкции структур полярные выражения для одночастичных дифракционных интенсивностей S ( q , φ ) были интерполированы на декартову сетку ( q x , q y ), подходит для алгоритмов быстрого преобразования Фурье. Для частиц размером 350 нм сетка состояла из 512 × 512 точек с q max = 0,24 нм −1 , что соответствует размеру пикселя в реальном пространстве 13,0 нм. Для структур 200 нм сетка составляла 500 × 500 точек с q max = 0,37 нм -1 , что давало размер пикселя в реальном пространстве 8,4 нм. Вариант высокочастотной автокорреляции структуры 35 , заданное обратным преобразованием Фурье S ( q x , q y ), использовалось для определения размера автокорреляции поддержки. Затем опорная область двумерной электронной плотности была определена как прямоугольник вдвое меньшего размера, увеличенный на один пиксель в каждом направлении, чтобы избежать искусственного повышения резкости краев реконструкции. Реконструкция двумерных структур была выполнена с помощью алгоритма итеративного преобразования с использованием вышеупомянутой опоры в качестве ограничения реального пространства и в качестве ограничения модуля обратного пространства.
Для частиц размером 350 нм сетка состояла из 512 × 512 точек с q max = 0,24 нм −1 , что соответствует размеру пикселя в реальном пространстве 13,0 нм. Для структур 200 нм сетка составляла 500 × 500 точек с q max = 0,37 нм -1 , что давало размер пикселя в реальном пространстве 8,4 нм. Вариант высокочастотной автокорреляции структуры 35 , заданное обратным преобразованием Фурье S ( q x , q y ), использовалось для определения размера автокорреляции поддержки. Затем опорная область двумерной электронной плотности была определена как прямоугольник вдвое меньшего размера, увеличенный на один пиксель в каждом направлении, чтобы избежать искусственного повышения резкости краев реконструкции. Реконструкция двумерных структур была выполнена с помощью алгоритма итеративного преобразования с использованием вышеупомянутой опоры в качестве ограничения реального пространства и в качестве ограничения модуля обратного пространства. Процедура 36 состоял из серии из 45 гибридных итераций ввода-вывода 37 , за которыми следовали пять шагов по уменьшению ошибок, которые повторялись до тех пор, пока не было достигнуто в общей сложности 1000 итераций. На шагах проекции обратного пространства алгоритму разрешалось заполнять области, закрытые светофильтром ( q <0,009 нм −1 ) и области с отрицательным значением y ) значений. Как полярная реконструкция S ( q , φ ) ограничен областью в форме диска, декартово представление имеет большие области отсутствующих данных в углах. Чтобы избежать артефактов от резкого прерывания данных на границе этого диска, мы использовали фурье-взвешенные проекции 36 с небинарной маской, позволяющей алгоритму слегка экстраполировать измеренные данные на несколько пикселей без введения большое количество свободных параметров в реконструкции. Начиная с разных случайных наборов фаз, было выполнено 50 реконструкций, которые затем были зарегистрированы в пределах небольшой доли пикселя 38 и усреднены для получения окончательной двумерной структуры, показанной на рис.
Процедура 36 состоял из серии из 45 гибридных итераций ввода-вывода 37 , за которыми следовали пять шагов по уменьшению ошибок, которые повторялись до тех пор, пока не было достигнуто в общей сложности 1000 итераций. На шагах проекции обратного пространства алгоритму разрешалось заполнять области, закрытые светофильтром ( q <0,009 нм −1 ) и области с отрицательным значением y ) значений. Как полярная реконструкция S ( q , φ ) ограничен областью в форме диска, декартово представление имеет большие области отсутствующих данных в углах. Чтобы избежать артефактов от резкого прерывания данных на границе этого диска, мы использовали фурье-взвешенные проекции 36 с небинарной маской, позволяющей алгоритму слегка экстраполировать измеренные данные на несколько пикселей без введения большое количество свободных параметров в реконструкции. Начиная с разных случайных наборов фаз, было выполнено 50 реконструкций, которые затем были зарегистрированы в пределах небольшой доли пикселя 38 и усреднены для получения окончательной двумерной структуры, показанной на рис. 5а. Надежность реконструкции оценивалась по среднему азимуту PRTF 24 , рассчитанному по 50 реконструкциям.
5а. Надежность реконструкции оценивалась по среднему азимуту PRTF 24 , рассчитанному по 50 реконструкциям.
Оценки отношения сигнал/шум
Для заданного числа изображений рассеяния, N im , мы оцениваем шум Δ s n ( q 90 ) одиночного коэффициента Фурье — картина дифракции частиц следующая:
Здесь N наборов — количество наборов изображений рассеяния, использованных для оценки, каждый из которых состоит из N im случайно выбранных изображений из полного набора из 3751. s σ,n — коэффициент, рассчитанный по изображениям в наборе σ , а s ref, n — эталонное значение, рассчитанное по всем 3751 изображению.
Дополнительная информация
Как цитировать эту статью: Педрини, Б. и др. . Двумерная структура из случайных изображений многочастичного рентгеновского рассеяния с использованием кросс-корреляций. Нац. коммун. 4:1647 doi: 10.1038/ncomms2622 (2012).
Нац. коммун. 4:1647 doi: 10.1038/ncomms2622 (2012).
Ссылки
Хендерсон, Р. Потенциал и ограничения нейтронов, электронов и рентгеновских лучей для микроскопии с атомным разрешением неокрашенных биологических молекул. Q. Rev. Biophys. 28 , 171–193 (1995).
КАС Статья Google ученый
Свергун Д.И. Восстановление структуры биологических макромолекул с низким разрешением из рассеяния в растворе с использованием имитации отжига. Биофиз. J. 76 , 2879–2886 (1999).
КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Чакон, П., Моран, Ф., Диас, Дж. Ф. и Андреу, Дж. М. Структуры белков в растворе с низким разрешением, извлеченные из рассеяния рентгеновских лучей с помощью генетического алгоритма. Биофиз.
 J. 74 , 2760–2775 (1998).
J. 74 , 2760–2775 (1998).ОБЪЯВЛЕНИЕ Статья Google ученый
Липферт Дж. и Дониач С. Малоугловое рассеяние рентгеновских лучей на РНК, белках и белковых комплексах. Энн. Преподобный Биофиз. биомол. Структура 36 , 307–327 (2007).
КАС Статья Google ученый
Мертенс, Х.Д.Т. и Свергун, Д.И. Структурная характеристика белков и комплексов с использованием малоуглового рассеяния рентгеновских лучей в растворе. Дж. Структура. биол. 172 , 128–141 (2010).
КАС Статья Google ученый
Эмма, П. и др. Первая генерация и работа ангстремного лазера на свободных электронах. Нац. Фотон. 4 , 641–647 (2010).
КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Чепмен Х.
 и др. Фемтосекундная дифракционная визуализация с помощью мягкого рентгеновского лазера. Нац. физ. 2 , 839–843 (2006).
и др. Фемтосекундная дифракционная визуализация с помощью мягкого рентгеновского лазера. Нац. физ. 2 , 839–843 (2006).КАС Статья Google ученый
Seibert, M.M. et al. Отдельные частицы мимивируса перехватываются и визуализируются с помощью рентгеновского лазера. Природа 470 , 78–82 (2011).
КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Чепмен Х. и др. Фемтосекундная рентгеновская кристаллография белков. Природа 470 , 73–77 (2011).
КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Фунг Р., Шнеерсон В., Салдин Д. К. и Урмазд А. Структура мимолетного освещения слабых вращающихся объектов в полете. Нац. физ. 5 , 61–64 (2009).
Артикул Google ученый
Лох, Н.
 -Т. Д. и Эльзер, В. Алгоритм реконструкции для экспериментов по дифракционной визуализации отдельных частиц. Физ. Ред. E 80 , 026705 (2009 г.).
-Т. Д. и Эльзер, В. Алгоритм реконструкции для экспериментов по дифракционной визуализации отдельных частиц. Физ. Ред. E 80 , 026705 (2009 г.).ОБЪЯВЛЕНИЕ Статья Google ученый
Лох, Н.-Т. Д. и др. Криптотомография: восстановление трехмерных интенсивностей Фурье по случайно ориентированным однократным дифракционным картинам. Физ. Преподобный Летт. 104 , 225501 (2010 г.).
КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Кам З. Определение структуры макромолекул в растворе по пространственным корреляциям флуктуаций рассеяния. Макромолекулы 10 , 927–934 (1977).
КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Салдин Д.К. и др. Структура отдельной частицы от рассеяния многими частицами, случайно ориентированными вокруг оси: к растворению структуры без кристаллизации? Нью-Джерси Phys.
 12 , 035014 (2010 г.).
12 , 035014 (2010 г.).Артикул Google ученый
Салдин Д.К. и др. Помимо малоуглового рассеяния рентгеновских лучей: использование угловых корреляций. Физ. Ред. B 81 , 411705 (2010 г.).
Артикул Google ученый
Салдин Д.К. и др. Новый взгляд на неупорядоченные ансамбли: ab initio определение структуры одной частицы по рассеивающим флуктуациям многих копий. Физ. Преподобный Летт. 106 , 115501 (2011).
КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Кириан, Р. А., Шмидт, К. Э., Ван, X., Доак, Р. Б. и Спенс, Дж. С. Х. Сигнал, шум и разрешение в коррелированных флуктуациях при малоугловом рентгеновском рассеянии. Физ. Ред. E 84 , 011921 (2011 г.).
ОБЪЯВЛЕНИЕ Статья Google ученый
Чепмен, Х.
 Н. и Ньюджент, К. А. Когерентное безлинзовое рентгеновское изображение. Нац. Фотон. 4 , 833–839 (2010).
Н. и Ньюджент, К. А. Когерентное безлинзовое рентгеновское изображение. Нац. Фотон. 4 , 833–839 (2010).КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Ньюджент К. А. Когерентные методы в рентгенологии. Доп. физ. 59 , 1–99 (2010).
ОБЪЯВЛЕНИЕ Статья Google ученый
Эльзер, В. Трехмерная структура из корреляций интенсивности. Нью-Джерси Phys. 13 , 123014 (2011).
Артикул Google ученый
Кам З. и Гафни И. Трехмерная реконструкция формы вируса бородавок человека с использованием пространственных корреляций. Ультрамикроскопия 17 , 251–262 (1985).
КАС Статья Google ученый
Кам, З.
 , Гафни, И. и Кессель, М. Улучшение двумерных проекций изображений, полученных с помощью электронного микроскопа, с использованием пространственных корреляций. Ультрамикроскопия 7 , 311–320 (1982).
, Гафни, И. и Кессель, М. Улучшение двумерных проекций изображений, полученных с помощью электронного микроскопа, с использованием пространственных корреляций. Ультрамикроскопия 7 , 311–320 (1982).Артикул Google ученый
Хенрих Б. и др. Pilatus: пиксельный детектор со счетом одиночных фотонов для рентгеновских исследований. Нукл. Инструм. Мет. физ. Рез. А 607 , 247–249 (2009).
КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Шапиро, Д. и др. Биологическая визуализация с помощью мягкой рентгеновской дифракционной микроскопии. Проц. Натл акад. науч. США 102 , 15343–15346 (2005 г.).
КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Альтарелли М., Курта Р. П., Вартанянц И. А. Рентгеновско-корреляционный анализ и локальные симметрии неупорядоченных систем: общая теория.
 Физ. Ред. B 82 , 104207 (2010 г.).
Физ. Ред. B 82 , 104207 (2010 г.).ОБЪЯВЛЕНИЕ Статья Google ученый
Курта Р.П., Альтарелли М., Веккерт Э., Вартанянц И.А. Применение рентгеновского кросс-корреляционного анализа для неупорядоченных двумерных систем. Физ. B 85 , 184204 (2012).
ОБЪЯВЛЕНИЕ Статья Google ученый
Wochner, P. et al. Рентгеновский кросс-корреляционный анализ выявляет скрытые локальные симметрии в неупорядоченном веществе. Проц. Натл акад. науч. США 106 , 11511–11514 (2009 г.).
КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Gutt, C. et al. Измерение временных спекл-корреляций в источниках сверхбыстрого рентгеновского излучения. Опц. Эксп. 17 , 55–61 (2009).
КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Кам, З.
 и Риглер, Р. Кросс-корреляционное рассеяние света. Биофиз. Дж. 39 , 7–13 (1982).
и Риглер, Р. Кросс-корреляционное рассеяние света. Биофиз. Дж. 39 , 7–13 (1982).КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Салдин Д.К., Шнеерсон В.Л., Фунг Р. и Урмазд А. Структура изолированных биомолекул, полученных с помощью ультракоротких рентгеновских импульсов: исследование симметрии случайных ориентаций. J. Phys.: Cond. Материя 21 , 134014 (2009).
КАС ОБЪЯВЛЕНИЯ Google ученый
Эльзер, В. Стратегии обработки данных дифракции от случайно ориентированных частиц. Ультрамикроскопия 111 , 788–792 (2011).
КАС Статья Google ученый
Салдин Д.К., Пун Х.К., Швандер П., Уддин М. и Шмидт М. Реконструкция икосаэдрического вируса из экспериментов по дифракции отдельных частиц.
 Опц. Эксп. 19 , 17318–17335 (2011).
Опц. Эксп. 19 , 17318–17335 (2011).КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Нильсен, Дж. А. и МакМорроу, Д. Элементы современной физики рентгеновских лучей Wiley (2001).
Горелик С., Гузенко В., Вила-Комамала Дж. и Дэвид С. Прямая запись электронным лучом плотных наноструктур с высоким соотношением сторон в толстых слоях ПММА для гальваники. Нанотехнологии 21 , 295303 (2010).
Артикул Google ученый
Тибо, П., Эльзер, В., Якобсен, К., Шапиро, Д. и Сейр, Д. Реконструкция дрожжевой клетки по данным рентгеновской дифракции. Акта Кристалл. А 62 , 248–261 (2006).
Артикул Google ученый
Guizar-Sicairos, M. & Fienup, J.R. Поиск фазы с проекциями, взвешенными по Фурье.
 J. Опт. соц. Являюсь. 25 , 701–709 (2008).
J. Опт. соц. Являюсь. 25 , 701–709 (2008).ОБЪЯВЛЕНИЕ Статья Google ученый
Финуп, Дж. Р. Алгоритмы поиска фаз: сравнение. Заяв. Опц. 21 , 2758–2769 (1982).
КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Гизар-Сикайрос М., Турман С. Т. и Финуп Дж. Р. Эффективные алгоритмы регистрации субпиксельных изображений. Опц. лат. 33 , 156–158 (2008).
ОБЪЯВЛЕНИЕ Статья Google ученый
Ссылки на скачивание
Угловой рентгеновский кросс-корреляционный анализ (AXCCA): основные концепции и последние приложения к мягкому веществу и наноматериалам
1. Чайкин П., Лубенский Т. Основы физики конденсированного состояния. Издательство Кембриджского университета; Кембридж, Великобритания: 1995. [Google Scholar]
[Google Scholar]
2. Селинджер Дж. В. Введение в теорию мягкой материи. Международное издательство Спрингер; Cham, Switzerland: 2016. [Google Scholar]
3. De Gennes P.G. Мягкая материя. Преподобный Мод. физ. 1992;64:645. doi: 10.1103/RevModPhys.64.645. [CrossRef] [Google Scholar]
4. Джонс Р.А.Л. Мягкое конденсированное вещество. Издательство Оксфордского университета; Нью-Йорк, штат Нью-Йорк, США: 2002. [Google Scholar]
5. Дюрр А.С., Шрайбер Ф., Ритли К.А., Круппа В., Круг Дж., Дош Х., Струт Б. Быстрое огрубление при выращивании тонкой пленки органического полупроводника (диинденоперилена) Phys. Преподобный Летт. 2003;90:016104. doi: 10.1103/PhysRevLett.90.016104. [PubMed] [CrossRef] [Google Scholar]
6. Ауфдерхайде А., Брох К., Новак Дж., Хиндерхофер А., Нерво Р., Герлах А., Банерджи Р., Шрайбер Ф. Анизотропные корреляции, вызванные смешением в молекулярно-кристаллических системах. физ. Преподобный Летт. 2012;109:156102. doi: 10.1103/PhysRevLett. 109.156102. [PubMed] [CrossRef] [Google Scholar]
109.156102. [PubMed] [CrossRef] [Google Scholar]
7. Курта Р.П., Алтарелли М., Вартанянц И.А. Структурный анализ с помощью угловых взаимных корреляций интенсивности рентгеновского излучения. Доп. хим. физ. 2016;161:1. doi: 10.1002/97811192.ch2. [CrossRef] [Google Scholar]
8. Кам З. Определение макромолекулярной структуры в растворе с помощью пространственной корреляции флуктуаций рассеяния. Макромолекулы. 1977; 10: 927–934. doi: 10.1021/ma60059a009. [CrossRef] [Google Scholar]
9. Кам З. Реконструкция структуры по электронным микрофотографиям случайно ориентированных частиц. Дж. Теор. биол. 1980;82:15–39. doi: 10.1016/0022-5193(80)-0. [PubMed] [CrossRef] [Google Scholar]
10. Griffin W.G., Pusey P.N. Антикорреляции в свете, рассеянном несферическими частицами. физ. Преподобный Летт. 1979; 43: 1100–1104. doi: 10.1103/PhysRevLett.43.1100. [CrossRef] [Google Scholar]
11. Кларк Н.А., Акерсон Б.Дж., Херд А.Дж. Кросс-корреляционная спектроскопия флуктуаций интенсивности в применении к коллоидным суспензиям. физ. Преподобный Летт. 1983; 50:1459. doi: 10.1103/PhysRevLett.50.1459. [Перекрестная ссылка] [Академия Google]
физ. Преподобный Летт. 1983; 50:1459. doi: 10.1103/PhysRevLett.50.1459. [Перекрестная ссылка] [Академия Google]
12. Вохнер П., Гутт К., Аутенриет Т., Деммер Т., Бугаев В., Ортиз А.Д., Дури А., Зонтоне Ф., Грюбель Г., Дош Х. Анализ кросс-корреляции рентгеновских лучей раскрывает скрытое Локальные симметрии в неупорядоченной материи. проц. Натл. акад. науч. США. 2009;106:11511–11514. doi: 10.1073/pnas.07106. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
13. Шроер М.А., Гутт С., Грюбель Г. Характеристики угловых взаимных корреляций, изученные с помощью рассеяния света на двумерных микросферических пленках. физ. Ред. Е. 2014;90:012309. doi: 10.1103/PhysRevE.90.012309. [PubMed] [CrossRef] [Google Scholar]
14. Курта Р.П., Гродд Л., Микаелян Э., Горобцов О.Ю., Фратодди И., Вендитти И., Спринг М., Григорян С., Вартанянц И.А. Структурные свойства π-π-сопряженной сетки в тонких полимерных пленках, изученные с помощью рентгеноструктурного анализа. Дж. Физ. конф. сер. 2014;499:12021. doi: 10.1088/1742-6596/499/1/012021. [CrossRef] [Google Scholar]
Физ. конф. сер. 2014;499:12021. doi: 10.1088/1742-6596/499/1/012021. [CrossRef] [Google Scholar]
15. Курта Р.П., Гродд Л., Микаелян Э., Горобцов О.Ю., Залужный И.А., Фратодди И., Вендитти И., Руссо М.В., Спринг М., Вартанянц И.А. и др. Локальная структура полукристаллических пленок P3HT, исследованная с помощью нанофокусированного когерентного рентгеновского излучения. физ. хим. хим. физ. 2015;17:7404–7410. дои: 10.1039/C5CP00426H. [PubMed] [CrossRef] [Google Scholar]
16. Курта Р.П., Островский Б.И., Зингер А., Горобцов О.Ю., Шабалин А., Джигаев Д., Ефанов О.М., Зозуля А.В., Спринг М., Вартаньянц И.А. Рентгеновский кросс-корреляционный анализ жидкокристаллических мембран в окрестности фазового перехода гексатик-смектик. физ. Ред. Е. 2013; 88:044501. doi: 10.1103/PhysRevE.88.044501. [PubMed] [CrossRef] [Google Scholar]
17. Залужный И.А., Курта Р.П., Сульянова Е.А., Горобцов О.Ю., Шабалин А.Г., Зозуля А.В., Менушенков А.П., Спринг М., Крувчинский А., Гурекская Е. и др. Структурные исследования связи-ориентационного порядка и гексатик-смектического перехода в жидких кристаллах различного состава. Мягкая материя. 2017;13:3240–3252. дои: 10.1039/C7SM00343A. [PubMed] [CrossRef] [Google Scholar]
и др. Структурные исследования связи-ориентационного порядка и гексатик-смектического перехода в жидких кристаллах различного состава. Мягкая материя. 2017;13:3240–3252. дои: 10.1039/C7SM00343A. [PubMed] [CrossRef] [Google Scholar]
18. Залужный И.А., Курта Р.П., Андре А., Горобцов О.Ю., Роуз М., Скопинцев П., Беседин И., Зозуля А.В., Спринг М., Шрайбер Ф., и другие. Количественная угловая корреляция между атомной решеткой и сверхрешеткой нанокристаллов, собранных с помощью направленной связи. Нано Летт. 2017;17:3511–3517. doi: 10.1021/acs.nanolett.7b00584. [PubMed] [CrossRef] [Google Scholar]
19. Лемкюлер Ф., Шульц Ф., Шроер М.А., Френцель Л., Ланге Х., Грюбель Г. Гетерогенный локальный порядок в самособирающихся пленках наночастиц, обнаруженный с помощью рентгеновских лучей Взаимные корреляции. IUCrJ. 2018;5:354–360. doi: 10.1107/S2052252518005407. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
20. Де Же У.Х., Островский Б.И., Шалагинов А.Н. Строение и флуктуации смектических мембран. Преподобный Мод. физ. 2003; 75: 181–235. doi: 10.1103/RevModPhys.75.181. [CrossRef] [Google Scholar]
Преподобный Мод. физ. 2003; 75: 181–235. doi: 10.1103/RevModPhys.75.181. [CrossRef] [Google Scholar]
21. Stanley H.E. Введение в фазовые переходы и критические явления. Издательство Оксфордского университета; New York, NY, USA: 1987. [Google Scholar]
22. Клеман М., Лаврентович О.Д. Физика мягкого вещества: введение. Спрингер; Нью-Йорк, штат Нью-Йорк, США: 2003. [Google Scholar]
9.0004 23. Ландау Л.Д., Лифшиц Э.М. Статистическая физика. Пергамон; Нью-Йорк, штат Нью-Йорк, США: 1980. [Google Scholar]24. Френкель Д. В кн.: Жидкости, замерзание и стеклование. Хансен Дж.-П., Левеск Д., Зинн-Джастин Дж., редакторы. Elsevier Science Publishers BV; Амстердам, Неверленд: 1991. стр. 691–762. [Google Scholar]
25. Де Женн П.Г., Прост Дж. Физика жидких кристаллов. 2-е изд. Издательство Оксфордского университета; Нью-Йорк, штат Нью-Йорк, США: 1993. [Google Scholar]
26. Освальд П., Пьерански П. Смектические и столбчатые жидкие кристаллы. Группа Тейлор и Фрэнсис; Бока-Ратон, Флорида, США: 2006 г. [Google Scholar]
[Google Scholar]
27. Гальперин Б.И., Нельсон Д.Р. Теория двумерного плавления. физ. Преподобный Летт. 1978; 41: 121–124. doi: 10.1103/PhysRevLett.41.121. [CrossRef] [Google Scholar]
28. Нельсон Д.Р. Дефекты и геометрия в физике конденсированного состояния. Издательство Кембриджского университета; Кембридж, Великобритания: 2002. [Google Scholar]
29. Костерлиц Дж. М. Физика Костерлица–Таулесса: обзор ключевых проблем. Респ. прог. физ. 2016;79:026001. doi: 10.1088/0034-4885/79/2/026001. [PubMed] [CrossRef] [Академия Google]
30. Стейнхардт П.Дж., Нельсон Д.Р., Ронкетти М. Бонд-ориентационный порядок в жидкостях и стеклах. физ. Преподобный Б. 1983; 28: 784–805. doi: 10.1103/PhysRevB.28.784. [CrossRef] [Google Scholar]
31. Мартин А.В. Ориентационный порядок жидкостей и стекол через флуктуационная дифракция. IUCrJ. 2017; 4:24–36. doi: 10.1107/S2052252516016730. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
32. Strandburg K. J. Связь-ориентационный порядок в системах конденсированных сред. Спрингер-Верлаг; Нью-Йорк, штат Нью-Йорк, США: 1992. [Google Scholar]
J. Связь-ориентационный порядок в системах конденсированных сред. Спрингер-Верлаг; Нью-Йорк, штат Нью-Йорк, США: 1992. [Google Scholar]
33. Pindak R., Moncton D.E., Davey S.C., Goodby J.W. Рентгеновское исследование многослойной гексатической жидкокристаллической фазы B. физ. Преподобный Летт. 1981; 46: 1135–1138. doi: 10.1103/PhysRevLett.46.1135. [CrossRef] [Google Scholar]
34. Кейм П., Марет Г., фон Грюнберг Х. Х. Константа Франка в гексатической фазе. физ. Ред. Е. 2007; 75:031402. doi: 10.1103/PhysRevE.75.031402. [PubMed] [CrossRef] [Google Scholar]
35. Дойчлендер С., Хорн Т., Лёвен Х., Марет Г., Кейм П. Двумерное плавление в условиях закалочного беспорядка. физ. Преподобный Летт. 2013;111:098301. doi: 10.1103/PhysRevLett.111.098301. [PubMed] [CrossRef] [Google Scholar]
36. Дерзи А., Ковач А.З., Донко З., Хартманн П. О метастабильности гексатической фазы при плавлении двумерных заряженных твердых частиц. физ. Плазма. 2014;21:23706. doi: 10.1063/1.4866019. [CrossRef] [Google Scholar]
[CrossRef] [Google Scholar]
37. Капфер С.К., Краут В. Двумерное плавление: от жидкостно-гексатического сосуществования к непрерывным переходам. физ. Преподобный Летт. 2015;114:035702. doi: 10.1103/PhysRevLett.114.035702. [PubMed] [CrossRef] [Академия Google]
38. Курта Р.П., Алтарелли М., Вартанянц И.А. Рентгеновский кросс-корреляционный анализ неупорядоченных ансамблей частиц: возможности и ограничения. Доп. Конденс. Материя физ. 2013;2013:959835. doi: 10.1155/2013/959835. [CrossRef] [Google Scholar]. Ориентационный и позиционный порядок в наклонной гексатической жидкокристаллической фазе. физ. Преподобный Летт. 1986; 57: 98–101. doi: 10.1103/PhysRevLett.57.98. [PubMed] [CrossRef] [Google Scholar]
40. Ахарони А., Биржено Р.Дж., Брок Дж.Д., Литстер Дж.Д. Мультикритичность в гексатических жидких кристаллах. физ. Преподобный Летт. 1986; 57: 1012–1015. doi: 10.1103/PhysRevLett.57.1012. [PubMed] [CrossRef] [Google Scholar]
41. Брок Дж.Д., Но Д.Ю., Макклейн Б. Р., Литстер Дж.Д., Биргено Р.Дж., Ахарони А., Хорн П.М., Лян Дж.З. Шестнадцатеричный порядок в свободно подвешенных жидкокристаллических пленках. физ. B-Конденс. Иметь значение. 1989; 74: 197–213. doi: 10.1007/BF01307386. [Перекрестная ссылка] [Академия Google]
Р., Литстер Дж.Д., Биргено Р.Дж., Ахарони А., Хорн П.М., Лян Дж.З. Шестнадцатеричный порядок в свободно подвешенных жидкокристаллических пленках. физ. B-Конденс. Иметь значение. 1989; 74: 197–213. doi: 10.1007/BF01307386. [Перекрестная ссылка] [Академия Google]
42. Брок Дж. Д., Биржено Р. Дж., Литстер Д., Ахарони А. Шестнадцатеричный порядок в жидкокристаллических пленках. Контемп. физ. 1989; 30: 321–335. doi: 10.1080/001075183772. [CrossRef] [Google Scholar]
43. Sutton M., Mochrie S.G.J., Greytak T., Nagler S.E., Berman L.E., Held G.A., Stephenson G.B. Наблюдение спекла с помощью дифракции на когерентных рентгеновских лучах. Природа. 1991; 352: 608–610. doi: 10.1038/352608a0. [CrossRef] [Google Scholar]
44. Miao J., Charalambous P., Kirz J., Sayre D. Расширение методологии рентгеновской кристаллографии для получения изображений некристаллических образцов микрометрового размера. Природа. 1999;400:342–344. дои: 10.1038/22498. [CrossRef] [Google Scholar]
45. Робинсон И.К., Вартаньянц И.А., Уильямс Г.Дж., Пфайфер М.А., Питни Дж.А. Реконструкция формы нанокристаллов золота с помощью когерентной рентгеновской дифракции. физ. Преподобный Летт. 2001;87:195505. doi: 10.1103/PhysRevLett.87.195505. [PubMed] [CrossRef] [Google Scholar]
Робинсон И.К., Вартаньянц И.А., Уильямс Г.Дж., Пфайфер М.А., Питни Дж.А. Реконструкция формы нанокристаллов золота с помощью когерентной рентгеновской дифракции. физ. Преподобный Летт. 2001;87:195505. doi: 10.1103/PhysRevLett.87.195505. [PubMed] [CrossRef] [Google Scholar]
46. Роденбург Дж. М., Херст А. С., Каллис А. Г., Добсон Б. Р., Пфайффер Ф., Банк О., Дэвид С., Ефимов К., Джонсон И. Hard-X-Ray Безлинзовое изображение протяженных объектов. физ. Преподобный Летт. 2007;98:034801. doi: 10.1103/PhysRevLett.98.034801. [PubMed] [CrossRef] [Google Scholar]
47. Seiboth F., Schropp A., Scholz M., Wittwer F., Rödel C., Wünsche M., Ullsperger T., Nolte S., Rahomäki J., Парфенюкас К. и др. Идеальная фокусировка рентгеновских лучей за счет подбора корректирующих очков к аберрированной оптике. Нац. коммун. 2017;8:14623. doi: 10.1038/ncomms14623. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
48. Крюгер С.П., Нойбауэр Х., Бартельс М., Калбфляйш С., Гивекемейер К. , Уилбрандт П.Дж., Спрунг М., Салдитт Т. Суб- Ограничение 10-нм пучка рентгеновскими волноводами: проектирование, изготовление и характеристика оптических свойств. Дж. Синхротронное излучение. 2012;19: 227–236. doi: 10.1107/S09011051983. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
, Уилбрандт П.Дж., Спрунг М., Салдитт Т. Суб- Ограничение 10-нм пучка рентгеновскими волноводами: проектирование, изготовление и характеристика оптических свойств. Дж. Синхротронное излучение. 2012;19: 227–236. doi: 10.1107/S09011051983. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
49. Huang X., Yan H., Nazaretski E., Conley R., Bouet N., Zhou J., Lauer K., Li L. , Эом Д., Легнини Д. и др. Фокус жесткого рентгеновского излучения с длиной волны 11 нм из многослойной линзы Лауэ с большой апертурой. науч. 2013;3:3562. doi: 10.1038/srep03562. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
50. Альтарелли М., Курта Р.П., Вартанянц И.А. Рентгеновский кросс-корреляционный анализ и локальные симметрии неупорядоченных систем: общая теория. физ. Ред. Б. 2010; 82:104207. doi: 10.1103/PhysRevB.82.104207. Ошибка: 2012 , 86 , 179904. [CrossRef] [Google Scholar]
51. Курта Р.П., Альтарелли М., Веккерт Э., Вартанянц И. А. Применение рентгеновского кросс-корреляционного анализа к неупорядоченным двумерным системам. физ. Ред. Б. 2012; 85:184204. doi: 10.1103/PhysRevB.85.184204. [CrossRef] [Google Scholar]
А. Применение рентгеновского кросс-корреляционного анализа к неупорядоченным двумерным системам. физ. Ред. Б. 2012; 85:184204. doi: 10.1103/PhysRevB.85.184204. [CrossRef] [Google Scholar]
52. Baskin J.S., Zewail A.H. Ориентированные ансамбли в дифракции сверхбыстрых электронов. ХимФизХим. 2006; 7: 1562–1574. doi: 10.1002/cphc.200600133. [PubMed] [CrossRef] [Академия Google]
53. Педрини Б., Мензель А., Гизар-Сикайрос М., Гузенко В.А., Горелик С., Дэвид С., Паттерсон Б.Д., Абела Р. Двумерная структура на основе изображений случайного рассеяния рентгеновских лучей множеством частиц с использованием кросс- Корреляции. Нац. коммун. 2013;4:1647. doi: 10.1038/ncomms2622. [PubMed] [CrossRef] [Google Scholar]
54. Салдин Д.К., Пун Х.С., Шнеерсон В.Л., Хауэллс М., Чепмен Х.Н., Кириан Р.А., Шмидт К.Е., Спенс Дж.Ч. Помимо малоуглового рассеяния рентгеновских лучей: использование угловых корреляций. физ. Ред. Б. 2010; 81:174105. doi: 10.1103/PhysRevB.81.174105. [Перекрестная ссылка] [Академия Google]
55. Донателли Дж.Дж., Цварт П.Х., Сетиан Дж.А. Итеративное фазирование флуктуационного рассеяния рентгеновских лучей. проц. Натл. акад. науч. США. 2015;112:10286–10291. doi: 10.1073/pnas.1513738112. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
Донателли Дж.Дж., Цварт П.Х., Сетиан Дж.А. Итеративное фазирование флуктуационного рассеяния рентгеновских лучей. проц. Натл. акад. науч. США. 2015;112:10286–10291. doi: 10.1073/pnas.1513738112. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
56. Курта Р.П., Дроняк Р., Альтарелли М., Веккерт Э., Вартанянц И.А. Решение фазовой задачи когерентного рассеяния на неупорядоченной системе одинаковых частиц. New J. Phys. 2013;15:13059. doi: 10.1088/1367-2630/15/1/013059. [Перекрестная ссылка] [Академия Google]
57. Курта Р.П., Донателли Дж.Дж., Юн Ч.Х., Бернтсен П., Белецкий Дж., Даурер Б.Дж., ДеМирси Х., Фромм П., Хантке М.Ф., Майя Ф.Р.Н.К., и др. Корреляции в рассеянных рентгеновских лазерных импульсах выявляют наноразмерные структурные особенности вирусов. физ. Преподобный Летт. 2017;119:158102. doi: 10.1103/PhysRevLett.119.158102. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
58. Вестер П., Залужный И.А., Курта Р.П., Меллер К.Б., Биасин Э., Халдруп К. , Нильсен М.М., Вартанянц И.А. Сверхбыстрая структурная динамика фотореакций, наблюдаемая с помощью рентгеновского кросс-корреляционного анализа с временным разрешением. Структура Динам. 2019;6:24301. doi: 10.1063/1.5086374. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
, Нильсен М.М., Вартанянц И.А. Сверхбыстрая структурная динамика фотореакций, наблюдаемая с помощью рентгеновского кросс-корреляционного анализа с временным разрешением. Структура Динам. 2019;6:24301. doi: 10.1063/1.5086374. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
59. Курта Р.П., Вигарт А., Флюэрасу А., Мэдсен А. Флуктуационное рассеяние рентгеновских лучей от наностержней в растворе выявляет слабое температурно-зависимое ориентационное упорядочение. IUCrJ. 2019; 6: 635–648. doi: 10.1107/S205225251
99. [PMC free article] [PubMed] [CrossRef] [Google Scholar]60. Латычевская Т., Манчини Г.Ф., Карбоне Ф. Роль когерентности в кросс-корреляционном анализе дифракционных картин от двумерных плотных мономеров. Дисперсные системы. науч. Отчет 2015; 5:16573. doi: 10.1038/srep16573. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
61. Davey S.C., Budai J., Goodby J.W., Pindak R., Moncton D.E. Рентгенофазовое исследование фазового перехода гексатик-В в смектик-А в жидкокристаллических пленках. физ. Преподобный Летт. 1984; 53: 2129–2132. doi: 10.1103/PhysRevLett.53.2129. [CrossRef] [Google Scholar]
физ. Преподобный Летт. 1984; 53: 2129–2132. doi: 10.1103/PhysRevLett.53.2129. [CrossRef] [Google Scholar]
62. Эппли Г., Бруинсма Р. Шестнадцатеричный порядок и колебания плотности жидкости. физ. Преподобный Летт. 1984; 53: 2133–2136. doi: 10.1103/PhysRevLett.53.2133. [CrossRef] [Google Scholar]
63. Ахарони А., Кардар М. Дифракционные картины от тонких гексатических пленок. физ. Преподобный Летт. 1988;61:2855–2858. doi: 10.1103/PhysRevLett.61.2855. [PubMed] [CrossRef] [Google Scholar]
64. Залужный И.А., Курта Р.П., Менушенков А.П., Островский Б.И., Вартаньянц И.А. Анализ формы рентгеновских дифракционных пиков, происходящих от гексатической фазы жидкокристаллических пленок. Мол. Кристалл. жидкость Кристалл. 2017; 647: 169–178. doi: 10.1080/15421406.2017.1289582. [CrossRef] [Google Scholar]
65. Stoebe T., Huang C.C. Физические свойства тонких жидкокристаллических пленок без подложки. Междунар. Дж. Мод. физ. Б. 1995;9:2285–2319. doi: 10.1142/S0217979295000896. [CrossRef] [Google Scholar]
[CrossRef] [Google Scholar]
66. Пачуски М., Кардар М. Гармоники ориентационного порядка в жидких кристаллах. физ. Преподобный Летт. 1988;60:861. doi: 10.1103/PhysRevLett.60.861. [PubMed] [CrossRef] [Google Scholar]
67. Залужный И.А., Курта Р.П., Сульянова Е.А., Горобцов О.Ю., Шабалин А.Г., Зозуля А.В., Менушенков А.П., Спринг М., Островский Б.И., Вартанянц И.А. Рентгеновские исследования жидких кристаллов с сильно развитым связно-ориентационным порядком с пространственным разрешением. физ. Ред. Е. 2015;91:042506. doi: 10.1103/PhysRevE.91.042506. [PubMed] [CrossRef] [Google Scholar]
68. Noh D.Y., Brock J.D., Litster J.D., Birgeneau R.J., Goodby J.W. Жидкая, гексатическая и кристаллическая фазы в терефтал-бис-(4 92 101 n 92 102 )-алкиланилинах. физ. Преподобный Б. 1989; 40: 4920–4927. doi: 10.1103/PhysRevB.40.4920. [PubMed] [CrossRef] [Google Scholar]
69. Ван Рой Б., Денольф К., Питси Г., Тон Дж. Характеристика перехода смектик-А-гексатик-В в 65OBC с помощью адиабатической сканирующей калориметрии. Евро. физ. JE 2005; 16: 361–364. doi: 10.1140/epje/i2004-10091-3. [PubMed] [CrossRef] [Google Scholar]
Евро. физ. JE 2005; 16: 361–364. doi: 10.1140/epje/i2004-10091-3. [PubMed] [CrossRef] [Google Scholar]
70. Залужный И.А., Курта Р.П., Мухарамова Н., Ким Ю.Ю., Хуббутдинов Р.М., Джигаев Д., Лебедев В.В., Пикина Е.С., Кац Е.И., Кларк Н.А. и др. Доказательства смектико-гексатического перехода первого порядка и его близости к трикритической точке в смектических пленках. физ. Ред. Е. 2018; 98:052703. doi: 10.1103/PhysRevE.98.052703. [CrossRef] [Google Scholar]
71. Chou C.-F., Ho J.T., Hui S.W., Surendranath V. Масштабирование 6n-кратных параметров ориентационного порядка связи в гексатической жидкокристаллической тонкой пленке. физ. Преподобный Летт. 1996;76:4556–4559. doi: 10.1103/PhysRevLett.76.4556. [PubMed] [CrossRef] [Google Scholar]
72. Chou C.-F., Jin A.J., Hui S.W., Huang C.C., Ho J.T. Многоступенчатое плавление в двумерных гексатических жидкокристаллических пленках. Наука. 1998; 280:1424–1426. doi: 10.1126/science.280.5368.1424. [PubMed] [CrossRef] [Google Scholar]
73. Кац Е.И., Лебедев В.В., Пикина Е.С. Теория Ландау сосуществования смектик-А-гексатик-В в смектических пленках. физ. Ред. Е. 2019; 100:022705. doi: 10.1103/PhysRevE.100.022705. [PubMed] [CrossRef] [Академия Google]
Кац Е.И., Лебедев В.В., Пикина Е.С. Теория Ландау сосуществования смектик-А-гексатик-В в смектических пленках. физ. Ред. Е. 2019; 100:022705. doi: 10.1103/PhysRevE.100.022705. [PubMed] [CrossRef] [Академия Google]
74. Эгами Т., Биллиндж С.Дж.Л. Под пиками Брэгга: структурный анализ сложных материалов. Пергамон; Оксфорд, Великобритания: 2003. [Google Scholar]
75. Элс-Нильсен Дж., МакМорроу Д. Элементы современной рентгеновской физики. Джон Уайли и сыновья, ООО; Чичестер, Великобритания: 2011. [Google Scholar]
76. Залужный И.А., Курта Р.П., Менушенков А.П., Островский Б.И., Вартаньянц И.А. Прямая реконструкция двумерной парной функции распределения в частично упорядоченных системах с угловыми корреляциями. физ. Ред. Е. 2016;94:030701. doi: 10.1103/PhysRevE.94.030701. [PubMed] [CrossRef] [Google Scholar]
77. Xia Y., Gates B., Li Z.-Y. Подходы самосборки к трехмерным фотонным кристаллам. Доп. Матер. 2001; 13: 409–413. doi: 10.1002/1521-4095(200103)13:6<409::AID-ADMA409>3. 0.CO;2-C. [CrossRef] [Google Scholar]
0.CO;2-C. [CrossRef] [Google Scholar]
78. Yethiraj A., Thijssen JHJ, Wouterse A., van Blaaderen A. Индуцированные электрическим полем коллоидные монокристаллы большой площади для фотонных приложений. Доп. Матер. 2004;16:596–600. doi: 10.1002/adma.200306192. [CrossRef] [Google Scholar]
79. Бланко А., Хомски Э., Грабчак С., Ибисате М., Джон С., Леонард С.В., Лопес С., Месегер Ф., Мигес Х., Мондиа Дж.П. и др. др. Крупномасштабный синтез кремниевого фотонного кристалла с полной трехмерной запрещенной зоной около 1,5 мкм. Природа. 2000;405:437–440. doi: 10.1038/35013024. [PubMed] [CrossRef] [Google Scholar]
80. Alonso-Redondo E., Schmitt M., Urbach Z., Hui C.M., Sainidou R., Rembert P., Matyjaszewski K., Bockstaller M.R., Fytas G.A. Новый класс перестраиваемых гиперзвуковых фононных кристаллов на основе коллоидов, связанных полимерами. Нац. коммун. 2015;6:8309. doi: 10.1038/ncomms9309. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
81. Ян Ю., Гао Л. , Лопес Г. П., Йеллен Б. Б. Настраиваемая сборка коллоидных кристаллических сплавов с использованием жидкостей с магнитными наночастицами. АКС Нано. 2013;7:2705–2716. doi: 10.1021/nn400118e. [PubMed] [CrossRef] [Google Scholar]
, Лопес Г. П., Йеллен Б. Б. Настраиваемая сборка коллоидных кристаллических сплавов с использованием жидкостей с магнитными наночастицами. АКС Нано. 2013;7:2705–2716. doi: 10.1021/nn400118e. [PubMed] [CrossRef] [Google Scholar]
82. Демирёрс А.Ф., Бельтрамо П.Дж., Вутукури Х.Р. Коллоидные переключатели электрическими и магнитными полями. Приложение ACS Матер. Интерфейсы. 2017;9:17238–17244. doi: 10.1021/acsami.7b02619. [PubMed] [CrossRef] [Академия Google]
83. Liu A.C.Y., Tabor R.F., de Jonge M.D., Mudie S.T., Petersen T.C. Благоприятные локальные структуры в аморфных коллоидных упаковках, измеренные с помощью микропучковой рентгеновской дифракции. проц. Натл. акад. науч. США. 2017;114:10344–10349. doi: 10.1073/pnas.1707198114. [Статья PMC бесплатно] [PubMed] [CrossRef] [Google Scholar]
84. Шроер М.А., Гутт К., Лемкюлер Ф., Фишер Б., Штайнке И., Вестермайер Ф., Спрунг М., Грюбель Г. Нано -Лучевая рентгеновская микроскопия высушенных коллоидных пленок. Мягкая материя. 2015;11:5465–5472. дои: 10.1039/C5SM00609K. [PubMed] [CrossRef] [Google Scholar]
2015;11:5465–5472. дои: 10.1039/C5SM00609K. [PubMed] [CrossRef] [Google Scholar]
85. Лемкюлер Ф., Фишер Б., Мюллер Л., Рута Б., Грюбель Г. Структура за пределами парных корреляций: рентгеновская взаимная корреляция из коллоидных кристаллов. Дж. Заявл. Кристаллогр. 2016;49:2046–2052. doi: 10.1107/S1600576716017313. [PMC free article] [PubMed] [CrossRef] [Google Scholar]
86. Schroer M.A., Westermeier F., Lehmkühler F., Conrad H., Schavkan A., Zozulya A.V., Fischer B., Roseker W., Sprung М., Гутт С. и соавт. Суспензии коллоидных кристаллитов, изученные методом малоуглового рассеяния рентгеновских лучей под высоким давлением. хим. физ. 2016;144:084903. doi: 10.1063/1.4941563. [PubMed] [CrossRef] [Google Scholar]
87. Weidman M.C., Smilgies D.-M., Tisdale W.A. Кинетика самосборки нанокристаллических сверхрешеток, измеренная с помощью рассеяния рентгеновских лучей в реальном времени in situ . Нац. Матер. 2016;15:775–781. doi: 10.1038/nmat4600. [PubMed] [CrossRef] [Google Scholar]
88. Болес М.А., Энгель М., Талапин Д.В. Самосборка коллоидных нанокристаллов: от сложных структур к функциональным материалам. хим. 2016; 116:11220–11289. doi: 10.1021/acs.chemrev.6b00196. [PubMed] [CrossRef] [Google Scholar]
Болес М.А., Энгель М., Талапин Д.В. Самосборка коллоидных нанокристаллов: от сложных структур к функциональным материалам. хим. 2016; 116:11220–11289. doi: 10.1021/acs.chemrev.6b00196. [PubMed] [CrossRef] [Google Scholar]
89. Fan Z., Grünwald M. Ориентационный порядок в самособирающихся нанокристаллических сверхрешетках. Варенье. хим. соц. 2019; 141:1980–1988. doi: 10.1021/jacs.8b10752. [PubMed] [CrossRef] [Google Scholar]
90. Биан К., Чой Дж.Дж., Кошик А., Клэнси П., Смилгис Д.-М., Ханрат Т. Преобразования симметрии, обусловленные анизотропией формы, в полиморфах нанокристаллической сверхрешетки. АКС Нано. 2011;5:2815–2823. doi: 10.1021/nn103303q. [PubMed] [CrossRef] [Академия Google]
91. Ли Р., Биан К., Ханрат Т., Бассет В.А., Ван З. Расшифровка сверхрешетки и структуры интерфейса усеченного суперкристалла, собранного из нанокристаллов PbS, и связанных с ними сил взаимодействия. Варенье. хим. соц. 2014; 136:12047–12055. doi: 10.1021/ja5057032. [PubMed] [CrossRef] [Google Scholar]
92. Сонг Р.-К., Кельфен Х. Мезокристаллы — упорядоченные суперструктуры наночастиц. Доп. Матер. 2010; 22:1301–1330. doi: 10.1002/adma.2005. [PubMed] [CrossRef] [Академия Google]
Сонг Р.-К., Кельфен Х. Мезокристаллы — упорядоченные суперструктуры наночастиц. Доп. Матер. 2010; 22:1301–1330. doi: 10.1002/adma.2005. [PubMed] [CrossRef] [Академия Google]
93. Талапин Д.В., Ли Дж.-С., Коваленко М.В., Шевченко Е.В. Перспективы коллоидных нанокристаллов для электронных и оптоэлектронных приложений. хим. 2010; 110:389–458. doi: 10.1021/cr7k. [PubMed] [CrossRef] [Google Scholar]
94. Scheele M., Brütting W., Schreiber F. Связанные органо-неорганические наноструктуры (COIN) Phys. хим. хим. физ. 2015;17:97–111. doi: 10.1039/C4CP03094J. [PubMed] [CrossRef] [Google Scholar]
95. Бахриг Л., Хики С.Г., Эйхмюллер А. Мезокристаллические материалы и участие ориентированного прикрепления — обзор. CrystEngComm. 2014;16:9408–9424. doi: 10.1039/C4CE00882K. [CrossRef] [Google Scholar]
96. Вайдман М.С., Ягер К.Г., Тисдейл В.А. Поправка к межчастичным расстояниям и структурному упорядочению в сверхрешетчатых нанокристаллах PbS, подвергающихся лигандному обмену. хим. Матер. 2015; 27: 474–482. doi: 10.1021/см503626с. [CrossRef] [Google Scholar]
хим. Матер. 2015; 27: 474–482. doi: 10.1021/см503626с. [CrossRef] [Google Scholar]
97. Андре А., Жеребецкий Д., Ханифи Д., Хе Б., Хошху М.С., Янковски М., Шассе Т., Ван Л.-В., Шрайбер Ф., Саллео А. и др. На пути к проводящим мезокристаллическим сборкам: нанокристаллы PbS, сшитые дикарбоксилатом тетратиафульвалена. хим. Матер. 2015; 27:8105–8115. doi: 10.1021/acs.chemmater.5b03821. [Перекрестная ссылка] [Академия Google]
98. Диролл Б.Т., Ма Х., Ву Ю., Мюррей С.Б. Анизотропное растрескивание нанокристаллических сверхрешеток. Нано Летт. 2017;17:6501–6506. doi: 10.1021/acs.nanolett.7b03123. [PubMed] [CrossRef] [Google Scholar]
99. Мухарамова Н., Лапкин Д., Залужный И.А., Андре А., Лазарев С., Ким Ю.Ю., Спрунг М., Курта Р.П., Шрайбер Ф., Вартаньянц И.А., и другие. Выявление границ зерен и дефектообразования в нанокристаллических сверхрешетках методом нанодифракции. архив 201.02408 [PubMed] [Академия Google]
100. Боднарчук М.И., Шевченко Е.В., Талапин Д. В. Структурные дефекты в периодических и квазикристаллических бинарных нанокристаллических сверхрешетках. Варенье. хим. соц. 2011;133:20837–20849. дои: 10.1021/ja207154v. [PubMed] [CrossRef] [Google Scholar]
В. Структурные дефекты в периодических и квазикристаллических бинарных нанокристаллических сверхрешетках. Варенье. хим. соц. 2011;133:20837–20849. дои: 10.1021/ja207154v. [PubMed] [CrossRef] [Google Scholar]
101. Балс С., Горис Б., Лиз-Марзан Л.М., ван Тенделу Г. Трехмерная характеристика наночастиц благородных металлов и их сборок с помощью электронной томографии. Ангью. хим. Междунар. Эд. 2014;53:10600–10610. doi: 10.1002/anie.201401059. [PubMed] [CrossRef] [Академия Google]
102. Жеребецкий Д., Шееле М., Чжан Ю., Бронштейн Н., Томпсон С., Бритт Д., Салмерон М., Аливисатос П., Ван Л.-В. Гидроксилирование поверхности нанокристаллов PbS, пассивированных олеиновой кислотой. Наука. 2014; 344:1380–1384. doi: 10.1126/science.1252727. [PubMed] [CrossRef] [Google Scholar]
103. Novák J., Banerjee R., Kornowski A., Jankowski M., André A., Weller H., Schreiber F., Scheele M. Site-Specific Ligand Interactions Благоприятствуют тетрагональному искажению сверхрешеток нанокристаллов PbS. Приложение ACS Матер. Интерфейсы. 2016;8:22526–22533. doi: 10.1021/acsami.6b06989. [PubMed] [CrossRef] [Google Scholar]
Приложение ACS Матер. Интерфейсы. 2016;8:22526–22533. doi: 10.1021/acsami.6b06989. [PubMed] [CrossRef] [Google Scholar]
104. Саймон П., Бахриг Л., Бабурин И.А., Форманек П., Рёдер Ф., Зикманн Дж., Хикки С.Г., Эйхмюллер А., Лихте Х., Книп Р. и др. Взаимосвязь наночастиц внутри двумерных сверхрешеток тонких пленок PbS/олеиновая кислота. Доп. Матер. 2014;26:3042–3049. doi: 10.1002/adma.201305667. [PubMed] [CrossRef] [Google Scholar]
105. Choi J.J., Bealing C.R., Bian K., Hughes K.J., Zhang W., Smilgies D.-M., Hennig R.G., Engstrom J.R., Hanrath T. Управление нанокристаллической сверхрешеткой Симметрия и форма-анизотропные взаимодействия через переменное покрытие поверхности лиганда. Варенье. хим. соц. 2011; 133:3131–3138. doi: 10.1021/ja110454b. [PubMed] [CrossRef] [Академия Google]
106. Манчини Г.Ф., Латычевская Т., Пеннаккио Ф., Регера Дж., Стеллаччи Ф., Карбоне Ф. Динамика порядка/беспорядка в супракристалле наночастиц золота, покрытых додекантиолом, методом малоугловой дифракции сверхбыстрых электронов. Нано. лат. 2016;16:2705–2713. doi: 10.1021/acs.nanolett.6b00355. [PubMed] [CrossRef] [Google Scholar]
Нано. лат. 2016;16:2705–2713. doi: 10.1021/acs.nanolett.6b00355. [PubMed] [CrossRef] [Google Scholar]
107. Lorenz U., Møller K.B., Henriksen N.E. Об интерпретации анизотропных дифракционных картин с временным разрешением. New J. Phys. 2010;12:113022. doi: 10.1088/1367-2630/12/11/113022. [Перекрестная ссылка] [Академия Google]
108. Нильссон А., Шрек С., Перакис Ф., Петтерссон Л.Г.М. Зондирование воды рентгеновскими лазерами. Доп. физ. Х. 2016; 1: 226–245. doi: 10.1080/23746149.2016.1165630. [CrossRef] [Google Scholar]
109. Lee J.C.T., Chess J.J., Montoya S.A., Shi X., Tamura N., Mishra S.K., Fischer P., McMorran B.J., Sinha S.K., Fullerton E.E., et al. Синтез пар, связанных скирмионами, в тонких пленках Fe-Gd. заявл. физ. лат. 2016;109:22402. doi: 10.1063/1.4955462. [CrossRef] [Google Scholar]
110. Хаджимихаэль М., Заттерин Э., Фернандес-Пенья С., Лик С.Дж., Зубко П. Ориентация доменных стенок в сегнетоэлектрических сверхрешетках, исследованная с помощью синхротронной рентгеновской дифракции. физ. Преподобный Летт. 2018;120:037602. doi: 10.1103/PhysRevLett.120.037602. [PubMed] [CrossRef] [Академия Google]
физ. Преподобный Летт. 2018;120:037602. doi: 10.1103/PhysRevLett.120.037602. [PubMed] [CrossRef] [Академия Google]
111. Курта Р.П. Многоволновое резонансное флуктуационное рассеяние рентгеновских лучей. Дж. Физ. Летучая мышь. Мол. Опц. физ. 2016;49:165001. doi: 10.1088/0953-4075/49/16/165001. [CrossRef] [Google Scholar]
112. Liu A.C.Y., Neish M.J., Stokol G., Buckley G.A., Smillie L.A., de Jonge MD, Ott R.T., Kramer M.J., Bourgeois L. Систематическое картирование икосаэдрического ближнего порядка в Zr 36 Cu 64 Металлическое стекло. физ. Преподобный Летт. 2013;110:205505. doi: 10.1103/PhysRevLett.110.205505. [PubMed] [CrossRef] [Академия Google]
113. Liu A.C.Y., Tabor R.F., Bourgeois L., de Jonge M.D., Mudie S.T., Petersen T.C. Расчет прогнозируемых параметров ориентационного порядка связи для количественной оценки локальных симметрий на основе данных дифракции пропускания. физ. Преподобный Летт. 2016;116:205501. doi: 10.1103/PhysRevLett. 116.205501. [PubMed] [CrossRef] [Google Scholar]
116.205501. [PubMed] [CrossRef] [Google Scholar]
NIST и Intel получают критическое значение (измерения) с помощью рентгеновских лучей
Исследователи из Национального института стандартов и технологий (NIST) и Intel сообщили* об успешном использовании метода рассеяния рентгеновских лучей для точного измерения характеристик на кремниевом чипе с точностью до долей нанометра или ширины одного атома кремния.
Это достижение может сделать экспериментальную технологию, известную как CDSAXS (критическое размерное малоугловое рассеяние рентгеновских лучей), главным претендентом в гонке за разработку новых встроенных инструментов управления технологическим процессом для измерения исчезающе малых функций на компьютерных чипах следующего поколения.
«В полупроводниковой промышленности заканчиваются методы измерения, которые не разрушают все более мелкие наноструктуры следующего поколения», — говорит ученый-материаловед NIST Р. Джозеф Клайн. «Это, безусловно, самые маленькие наноструктуры сложной формы, характеризуемые CDSAXS. Результаты показывают, что CDSAXS обладает разрешением, отвечающим требованиям метрологии следующего поколения».
Результаты показывают, что CDSAXS обладает разрешением, отвечающим требованиям метрологии следующего поколения».
Поскольку размер линий, канавок, отверстий и других элементов на кремниевых срезах сокращается до одноразрядных нанометров, измерительные инструменты, давно используемые для контроля производства чипов, приближаются к пределу своих возможностей. Принимая во внимание растущую сложность конструкции микросхем — например, создание стековых транзисторов вместо плоских, сдвиг, начавшийся с введением Intel FinFET-транзисторов в 2011 году, — легко понять, почему производители полупроводников стремятся к улучшенным измерительным возможностям.
Исследователи NIST и Intel использовали CDSAXS для измерения размеров кремниевых пластин, изготовленных в исследовательских центрах Intel, с периодическим массивом асимметричных линий. Массив был сделан с помощью шагового четвертования, метода, который увеличивает в четыре раза количество соединительных линий в пространстве, которое обычно вмещает только одну. Сложные массивы линий были созданы с использованием нескольких этапов формирования рисунка, которые теперь производители чипов должны использовать для создания функций, выходящих за рамки возможностей существующего светового печатного оборудования. Повсюду получение точных измерений имеет решающее значение; несовпадения во время последовательного процесса формирования паттерна могут привести к систематическим ошибкам или дефектам чипа.
Сложные массивы линий были созданы с использованием нескольких этапов формирования рисунка, которые теперь производители чипов должны использовать для создания функций, выходящих за рамки возможностей существующего светового печатного оборудования. Повсюду получение точных измерений имеет решающее значение; несовпадения во время последовательного процесса формирования паттерна могут привести к систематическим ошибкам или дефектам чипа.
Недостатком, вызывающим особую озабоченность, и который находится в центре внимания исследования NIST-Intel, является ошибка шага, изменение расстояния от одного края строки до другого.
«Полупроводниковая промышленность не только уменьшила размеры продуктов, но мы также разработали все более сложные трехмерные структуры. Эти структуры становится очень трудно охарактеризовать неразрушающим методом с помощью обычного встроенного SEM [сканирующего электронного микроскопа]», — сказал Скотт. Лист, главный инженер исследовательской группы компонентов Intel. «Ранние результаты современных измерений CDSAXS NIST для этих структур нанометрового размера обеспечили очень полезное разрешение в атомном масштабе для их трехмерных профилей».
«Ранние результаты современных измерений CDSAXS NIST для этих структур нанометрового размера обеспечили очень полезное разрешение в атомном масштабе для их трехмерных профилей».
В изготовленном на заказ образце, изученном в ходе исследования, линии, напоминающие плавники акулы, имели ширину 12 нанометров. Расстояние между линиями отличалось очень незначительно — менее чем на 0,5 нанометра — от шага в 32 нанометра.
Измерения CDSAXS периодических ошибок основного тона — отклонения от 32 нанометров — имели точность в пределах 0,1 нанометра; и измерения формы линий были точными примерно до 0,2 нанометра.
С 2000 года NIST является пионером в применении малоуглового рассеяния рентгеновских лучей для удовлетворения все более требовательных измерительных потребностей полупроводниковой промышленности, которая на протяжении десятилетий удваивает плотность транзисторов на кристалле примерно каждые два года в соответствии с законом Мура. Современные передовые интегральные схемы умещают несколько миллиардов транзисторов на кусочке кремния размером меньше обычной почтовой марки.
Используемые в настоящее время инструменты размерной метрологии основаны на видимом и ультрафиолетовом свете с длинами волн, намного превышающими измеряемые элементы. Рентгеновские лучи, используемые в CDSAXS, имеют длину волны менее 0,1 нанометра, что намного меньше, чем размеры элементов будущих поколений компьютерных чипов. CDSAXS использует короткую длину волны рентгеновских лучей и их чувствительность к различной плотности электронов в материалах, на которые они попадают.
Бесконтактный неразрушающий метод не требует подготовки образцов и работает с тестовыми структурами, уже используемыми производителями полупроводников. CDSAXS, однако, не дает эквивалента рентгеновского снимка, например, сломанного запястья. Скорее, рентгеновские лучи, рассеянные электронами в наноструктуре, улавливаются детектором, предоставляя данные для обработки компьютерами для определения исходной формы.
Анализ сравнивает картину рассеянного рентгеновского излучения с тщательно разработанными моделями формы массивов наноструктурных элементов на поверхности. Эта процедура подгонки данных может пройти несколько миллионов циклов, прежде чем будет достигнуто удовлетворительное соответствие между смоделированными и измеренными моделями электронной плотности.
Эта процедура подгонки данных может пройти несколько миллионов циклов, прежде чем будет достигнуто удовлетворительное соответствие между смоделированными и измеренными моделями электронной плотности.
Вслед за другими исследованиями, демонстрирующими возможности CDSAXS для множества наноразмерных измерений, исследование NIST-Intel на сложных образцах, представляющих производство полупроводников следующего поколения, показывает, что CDSAXS может обеспечить желаемое размерное разрешение.
Результаты должны послужить дополнительным стимулом для продолжающихся усилий по разработке компактных источников рентгеновского излучения с интенсивностью, необходимой для встроенных CDSAXS на предприятиях по производству полупроводников. Исследование NIST-Intel, подтверждающее концепцию, было проведено в Усовершенствованном источнике фотонов (APS) в Аргоннской национальной лаборатории, длина окружности которого составляет 1104 метра (более 12 футбольных полей вокруг), и вмещает более 60 экспериментов одновременно. Предыдущие исследования CDSAXS проводились на APS или аналогичных экспериментальных установках, известных как синхротронные источники света.
Предыдущие исследования CDSAXS проводились на APS или аналогичных экспериментальных установках, известных как синхротронные источники света.
*Д.Ф. Воскресенье, С. Лист, Дж.С. Чавла и Р.Дж. Клайн, «Определение формы и периодичности наноструктур с помощью малоуглового рассеяния рентгеновских лучей», J. Appl. Кристалл. (2015). http://dx.doi.org/10.1107/S1600576715013369
Полупроводники и материалы
Рентгеновские лучи и поперечные сечения для измерения пустот
Автор:
Gordon O’Hara, Matthew Vandiver, Jonathan Crilly2 Flextronics Corporation 923 , Остин, Техас
Ник Бринхофф
North Star Imaging, Роджерс, Миннесота
Расшифровка
По мере того, как сложные электронные сборки становятся все быстрее и быстрее, мощность с сопутствующим тепловыделением, целостность сигнала и надежность становятся важнее, чем когда-либо.
Пустоты в паяных соединениях потенциально могут повлиять на все это. Из-за ценового давления на компании, производящие эти типы продуктов, важно иметь возможность правильно диагностировать и охарактеризовать образование пустот неразрушающим образом.
Правильная характеристика позволяет адекватно устранять неисправности и разрабатывать процессы, необходимые для сведения к минимуму или устранения образования пустот. Кроме того, в случаях анализа отказов можно использовать неразрушающий анализ пустот.
Разрешение рентгеновских инструментов продолжает расти вместе с программным обеспечением, необходимым для автоматизированного анализа. Использование этих инструментов позволило идентифицировать и измерить пустоты в паяных соединениях.
Программное обеспечениепозволило автоматически проверять паяные соединения, чтобы быстро идентифицировать и своевременно измерить до 100 % паяных соединений на компонент и на сборку.
Несмотря на то, что в эти инструменты было внесено много улучшений, небольшие пустоты и истинное положение этих пустот было трудно увидеть без фактического поперечного сечения.
Теперь, благодаря последним достижениям в области рентгеновских технологий, доступно 3D-изображение с полным высоким разрешением с использованием технологии Cat Scan. Технология Cat Scan позволяет создавать бесконечные поперечные срезы неразрушающим образом.
Технология Cat Scan позволяет создавать бесконечные поперечные срезы неразрушающим образом.
Первой целью этой работы было сопоставление наиболее распространенных рентгеновских технологий, используемых в электронной промышленности. Каждая технология была сопоставлена не только с новейшей технологией Cat Scan, но и с фактическими поперечными сечениями на различных образцах пустот.
Вторая цель этой работы заключалась в том, чтобы идентифицировать и охарактеризовать различные пустоты от входящих компонентов в процессе оплавления SMT. Поступающие компоненты, идентифицированные с пустотами припоя, подвергались различным профилям оплавления, чтобы определить, что происходит с ними по отношению к размеру и положению.
Изображения и измерения были сделаны до и после оплавления с использованием всех традиционных рентгеновских инструментов вместе с Cat Scan. После того, как все изображения были завершены; для сравнения были взяты фактические поперечные сечения. Кроме того, компоненты с поступающими пустотами подвергались оплавлению под вакуумом в попытке удалить пустоты перед сборкой 9. 0011
0011
Итак, какие выводы?
1. 3D AXI необходим для отсеивания значительного количества компонентов в качестве точек данных до дальнейшей характеристики.
2. Для полной характеристики процесса и компонентов, особенно в случае повышенной сложности, необходимо сочетание доступных технологий обнаружения пустот.
3. Конструкция печатной платы и компонентов, параметры профиля оплавления, а также химический состав могут влиять на рост и расположение пустот.
4. Изображение высокого разрешения Cat Scan позволяет проводить полный анализ компонентов до и после сборки неразрушающим образом.
И 5. Необходимо рассмотреть четкую совместную отраслевую спецификацию для создания лучшей связи между производством компонентов и сборкой и проверкой печатных плат.
Резюме
Совместный проект между Flextronics Inc. и North Star Imaging Inc. осуществляется для сопоставления текущего рентгеновского изображения и анализа поперечного сечения пустот BGA с современной компьютерной томографией высокого разрешения.
 Наша основная цель состоит в том, чтобы подтвердить измерения пустот, полученные с помощью неразрушающих методов визуализации, с физически измеренными измерениями пустот в поперечном сечении. Второстепенная цель состоит в том, чтобы охарактеризовать свойства пустот до и после оплавления.
Наша основная цель состоит в том, чтобы подтвердить измерения пустот, полученные с помощью неразрушающих методов визуализации, с физически измеренными измерениями пустот в поперечном сечении. Второстепенная цель состоит в том, чтобы охарактеризовать свойства пустот до и после оплавления.Типичное инспекционное оборудование AXI обеспечивает от одной до трех горизонтальных опорных плоскостей для измерения пустот BGA. КТ-сканирование обеспечивает полное трехмерное объемное представление пустоты BGA с учетом данных о размере, объеме и положении пустоты. Информация, которая может быть использована в проектах по анализу отказов и описанию процессов без физического разрушения печатной платы.
В исследовании используются пять устройств FCBGA диаметром 50,0 мм и пять устройств FCBGA диаметром 52,5 мм с известным мочеиспусканием. Мочеиспускание для каждого устройства было измерено на аппарате 3D AXI, внеосевом рентгеновском аппарате высокого разрешения 2D и системе CT-Scan. Затем устройства будут размещены и оплавлены на печатных платах. После оплавления все объемы мочеиспускания будут снова измерены с использованием каждой единицы оборудования. Кроме того, выбранные пустоты будут разрезаны, отполированы и измерены с помощью цифрового микроскопа с большим увеличением и сопоставлены с другими инструментами рентгеновской визуализации.
После оплавления все объемы мочеиспускания будут снова измерены с использованием каждой единицы оборудования. Кроме того, выбранные пустоты будут разрезаны, отполированы и измерены с помощью цифрового микроскопа с большим увеличением и сопоставлены с другими инструментами рентгеновской визуализации.
Выводы
3D AXI необходимо для отсеивания значительного количества компонентов в качестве точек данных перед дальнейшим определением характеристик.
Комбинация доступных технологий обнаружения пустот необходима для полной характеристики процесса и компонентов, особенно для повышенной сложности (т. е. переходные отверстия, более мелкий шаг и т. д.). рост и расположение пустот
Компьютерная томография высокого разрешения позволяет провести полный анализ компонентов до и после сборки неразрушающим образом.
В то время как IPC 7095B ввел таблицы для индикаторов пустых процессов и устранения неполадок, а JEDEC Std 217 содержит рекомендации по допустимым пустотам в компонентах (до оплавления), необходимо рассмотреть четкую совместную отраслевую спецификацию для создания лучшей связи между производством компонентов и сборкой печатных плат и Инспекция.
Первоначально опубликовано в материалах МПК
Аналитические аппроксимации для рентгеновских сечений III (Технический отчет)
Аналитические аппроксимации для рентгеновских сечений III (Технический отчет) | ОСТИ.GOVперейти к основному содержанию
- Полная запись
- Другое связанное исследование
Этот отчет обновляет нашу предыдущую работу, в которой были представлены аналитические аппроксимации сечений фотоэлектрического поглощения фотонов атомами и некогерентного рассеяния фотонов атомами. Такое представление удобно для использования в программируемых калькуляторах и в компьютерных программах для численной оценки этих сечений. Результаты применимы к атомам с атомными номерами от 1 до 100 и для энергий фотонов больше или равных 10 эВ. Фотоэлектрические сечения снова аппроксимируются четырехчленными полиномами от обратных степеней энергии фотона. Однако теперь интервалы подгонки больше, чем использовались ранее. Сечения некогерентного рассеяния основаны на соотношении Клейна-Нишины, но используют более простые приближенные уравнения для эффективной компьютерной оценки. Мы опишем схему усреднения для применения этих атомарных результатов к любому композиционному материалу. Коэффициенты подгонки включены в таблицы, а поперечные сечения показаны графически. 100 графиков, 1 вкладка.
Фотоэлектрические сечения снова аппроксимируются четырехчленными полиномами от обратных степеней энергии фотона. Однако теперь интервалы подгонки больше, чем использовались ранее. Сечения некогерентного рассеяния основаны на соотношении Клейна-Нишины, но используют более простые приближенные уравнения для эффективной компьютерной оценки. Мы опишем схему усреднения для применения этих атомарных результатов к любому композиционному материалу. Коэффициенты подгонки включены в таблицы, а поперечные сечения показаны графически. 100 графиков, 1 вкладка.
- Авторов:
- Биггс, Ф; Лайтхилл, Р.
- Дата публикации:
- Исследовательская организация:
- Sandia National Labs.
 , Альбукерке, Нью-Мексико (США)
, Альбукерке, Нью-Мексико (США)
- Идентификатор ОСТИ:
- 7124946
- Номер(а) отчета:
- ПЕСОК-87-0070
В НАЛИЧИИ: DE88015366
- Номер контракта Министерства энергетики:
- AC04-76DP00789
- Тип ресурса:
- Технический отчет
- Отношение ресурсов:
- Дополнительная информация: Части этого документа неразборчивы на микрофишах
- Страна публикации:
- США
- Язык:
- Английский
- Тема:
- 74 АТОМНАЯ И МОЛЕКУЛЯРНАЯ ФИЗИКА; ПОПЕРЕЧНЫЕ СЕЧЕНИЯ; КОМПЬЮТЕРНЫЕ РАСЧЕТЫ; ПОГЛОЩЕНИЕ; МЕТОДЫ РАСЧЕТА; ЭНЕРГЕТИЧЕСКАЯ ЗАВИСИМОСТЬ; ПЕРЕДАЧА ЭНЕРГИИ; УРАВНЕНИЯ; РАССЕЯНИЕ; ТАБЛИЦЫ; Х ИЗЛУЧЕНИЕ; ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ; ИОНИЗИРУЮЩЕЕ ИЗЛУЧЕНИЕ; ИЗЛУЧЕНИЕ; 640302 * — Атомная, молекулярная и химическая физика — атомные и молекулярные свойства и теория
Форматы цитирования
- MLA
- АПА
- Чикаго
- БибТекс
Биггс Ф. и Лайтхилл Р. Аналитические приближения для рентгеновских сечений III . США: Н. П., 1988.
Веб. дои: 10.2172/7124946.
и Лайтхилл Р. Аналитические приближения для рентгеновских сечений III . США: Н. П., 1988.
Веб. дои: 10.2172/7124946.
Копировать в буфер обмена
Биггс, Ф. и Лайтхилл, Р. Аналитические приближения для рентгеновских сечений III . Соединенные Штаты. https://doi.org/10.2172/7124946
Копировать в буфер обмена
Биггс Ф. и Лайтхилл Р. 1988.
«Аналитические приближения для рентгеновских сечений III». Соединенные Штаты. https://doi.org/10.2172/7124946. https://www.osti.gov/servlets/purl/7124946.
Копировать в буфер обмена
@статья{osti_7124946,
title = {Аналитические приближения для рентгеновских сечений III},
автор = {Биггс, Ф. и Лайтхилл, Р.},
и Лайтхилл, Р.},
abstractNote = {Этот отчет обновляет нашу предыдущую работу, в которой были представлены аналитические аппроксимации сечений фотоэлектрического поглощения фотонов атомами и некогерентного рассеяния фотонов атомами. Такое представление удобно для использования в программируемых калькуляторах и в компьютерных программах для численной оценки этих сечений. Результаты применимы к атомам с атомными номерами от 1 до 100 и для энергий фотонов больше или равных 10 эВ. Фотоэлектрические сечения снова аппроксимируются четырехчленными полиномами от обратных степеней энергии фотона. Однако теперь интервалы подгонки больше, чем использовались ранее. Сечения некогерентного рассеяния основаны на соотношении Клейна-Нишины, но используют более простые приближенные уравнения для эффективной компьютерной оценки. Мы опишем схему усреднения для применения этих атомарных результатов к любому композиционному материалу. Коэффициенты подгонки включены в таблицы, а поперечные сечения показаны графически. 100 графиков, 1 таб.},
100 графиков, 1 таб.},
дои = {10,2172/7124946},
URL-адрес = {https://www.osti.gov/biblio/7124946},
журнал = {},
номер =,
объем = ,
место = {США},
год = {1988},
месяц = {8}
}
Копировать в буфер обмена
Посмотреть технический отчет (9,77 МБ)
https://doi.org/10.2172/7124946
Экспорт метаданных
Сохранить в моей библиотеке
Вы должны войти в систему или создать учетную запись, чтобы сохранять документы в своей библиотеке.
Аналогичных записей в сборниках OSTI.GOV:
- Аналогичные записи
Методы корреляции — GISAXS
Традиционное рассеяние рентгеновских лучей основано на усреднении по ансамблю для получения надежного изображения с высоким отношением сигнал/шум. Например, данные рассеяния обычно усредняются за определенный период времени для накопления достаточной статистики. Для номинально изотропных образцов двумерное изображение детектора сворачивается (круговое среднее) в одномерную кривую. Однако это усреднение отбрасывает потенциально полезную информацию, содержащуюся в дисперсия рентгеновского сигнала.
Например, данные рассеяния обычно усредняются за определенный период времени для накопления достаточной статистики. Для номинально изотропных образцов двумерное изображение детектора сворачивается (круговое среднее) в одномерную кривую. Однако это усреднение отбрасывает потенциально полезную информацию, содержащуюся в дисперсия рентгеновского сигнала.
Множество новых методов вместо этого фокусируются на подчеркивании и измерении вариаций или флуктуаций сигнала рассеяния рентгеновских лучей (во времени, пространстве, угле и т. д.). Такой анализ может, наиболее очевидно, вернуть информацию о неоднородности. Однако тщательный корреляционный анализ может также извлечь тонкую информацию о структуре (например, мотивы локальной упаковки), которая обычно стирается при усреднении по ансамблю.
- 1 XCCA
- 2 Флуктуационное рассеяние
- 3 Дисперсионное рассеяние
- 4 XPCS
- 5 ссылок
- 5.1 XCCA
- 5.2 Реконструкция
- 5.
 3 Разреженные данные
3 Разреженные данные - 5.4 XFEL
- 5.5 Флуктуационное рассеяние
- 5.6 Коррелированное рассеяние рентгеновских лучей (CXS)
Анализ кросс-корреляции рентгеновских лучей ( XCCA ) представляет собой набор методов для анализа корреляций в наборах данных рассеяния рентгеновских лучей. В частности, анализ угловых корреляций в изображении 2D-детектора можно использовать для выделения структурной информации, которая была бы потеряна в обычной 1D-кривой с круговым усреднением. Таким образом, даже для номинально изотропных материалов (порошкообразный образец) из данных можно извлечь информацию о локальной симметрии (и, следовательно, о мотивах упаковки или элементарной ячейке).
Информация об угловой корреляции также может быть получена для реконструкции трехмерного обратного пространства по отдельным снимкам 2D-детектора. То есть методы XCCA можно использовать для совместного выравнивания кадров рассеяния, регистрируя их в трехмерном объеме рассеяния. Концептуально это похоже на отображение обратного пространства, но вместо прямой реконструкции обратного пространства путем слияния изображений это делается в статистическом смысле (поскольку относительное выравнивание кадров неизвестно).
Концептуально это похоже на отображение обратного пространства, но вместо прямой реконструкции обратного пространства путем слияния изображений это делается в статистическом смысле (поскольку относительное выравнивание кадров неизвестно).
Методы корреляции можно комбинировать с эффектами когерентного рассеяния для усиления сигнала рассеяния рентгеновских лучей от слабого образца (см. XAmp).
Флуктуационное рассеяние : TBD
Термин Дисперсное рассеяние использовался для описания методов, которые намеренно подчеркивают и анализируют вариации сигналов рентгеновского рассеяния.
- Анализ кольцевой зернистости (для определения количества зерен, их размера и распределения по размерам, кристалличности и т. д.)
- Ягер, К.Г.; Маевский, П.В. Метрики зернистости: надежная количественная оценка количества зерен по неравномерности рассеивающих колец Journal of Applied Crystallography 2014 , 47, 1855–1865. дои: 10.1107/S1600576714020822
- Неоднородность
- C.
 J. Gommes Малоугловое рассеяние и неоднородность, зависящая от масштаба J. Appl. Кристалл. 2016 , 49, 1162-1176. дои: 10.1107/S1600576716007810
J. Gommes Малоугловое рассеяние и неоднородность, зависящая от масштаба J. Appl. Кристалл. 2016 , 49, 1162-1176. дои: 10.1107/S1600576716007810
- C.
Рентгено-фотонная корреляционная спектроскопия (XPCS) измеряет временные колебания когерентных спеклов. Из реконструированной временной корреляционной функции можно сделать вывод о динамике системы.
XCCA
- Peter Wochner, Christian Gutt, Tina Autenrieth, Thomas Demmer, Volodymyr Bugaev, Alejandro Díaz Ortiz, Agnès Duri, Federico Zontone, Gerhard Grübel and Helmut Dosch Рентгеновский кросс-корреляционный анализ открывает скрытые локальные симметрии в неупорядоченном веществе Труды Национальной академии наук 2009 , 106 (28), 11511–11514. doi: 10.1073/pnas.07106
- Альтарелли М., Курта Р.П., Вартанянц И.А. Рентгеновский кросс-корреляционный анализ и локальные симметрии неупорядоченных систем: общая теория Phys. Rev. B. 2010 , 82, 104207.
 doi: 10.1103/PhysRevB.82.104207
doi: 10.1103/PhysRevB.82.104207 - Курта Р.П., Алтарелли М., Веккерт Э., Вартанянц И.А. Рентгеновский кросс-корреляционный анализ в приложении к неупорядоченным двумерным системам Phys. Ред. B 2012 , 85, 184204. doi: 10.1103/PhysRevB.85.184204
- Курта Р.П., Дроняк Р., Альтарелли М., Веккерт Э., Вартанянц И.А. Решение фазовой задачи для когерентного рассеяния на неупорядоченной системе одинаковых частиц New Journal of Physics 2013 , 15. doi: 10.1088/1367-2630/ 01.15.013059
- F. Lehmkühler, G. Grübel и C. Gutt Определение ориентационного порядка в модельных системах методами кросс-корреляции рентгеновских лучей J. Appl. Кристалл. 2014 , 47, 1315-1323. дои: 10.1107/S1600576714012424
- Лемкюлер, Ф.; Фишер, Б.; Мюллер, Л.; Рута Б.; Грюбель, Г. Структура за пределами парных корреляций: кросс-корреляция рентгеновских лучей из коллоидных кристаллов Journal of Applied Crystallography 2016 , 49, doi: 10.
 1107/S1600576716017313
1107/S1600576716017313 - Julien R. Lhermitte, Cheng Tian, Aaron Stein, Atikur Rahman, Yugang Zhang, Lutz Wiegart, Andreas Fluerasu, Oleg Gang, and Kevin G. Yager Надежные рентгеновские угловые корреляции для изучения мезоструктур J. Appl. Кристалл. 2017 , 50(3). дои: 10.1107/S1600576717003946
- Julien R. Lhermitte, Aaron Stein, Cheng Tian, Yugang Zhang, Lutz Wiegart, Andreas Fluerasu, Oleg Gang, and Kevin G. Yager Когерентное усиление рассеяния рентгеновских лучей от мезоструктур IUCrJ 2017 4(5 ) doi: 10.1107/S2052252517008107
- Феликс Лемкюлер, Флориан Шульц, Мартин А. Шроер, Лара Френцель, Хольгер Лангеб и Герхард Грюбель Гетерогенный локальный порядок в самособирающихся пленках наночастиц, обнаруженный с помощью кросс-корреляций рентгеновских лучей IUCrJ 2018 , 5 (3), 354-360. doi: 10.1107/S2052252518005407
Реконструкция
- Цви Кам Реконструкция структуры по электронным микрофотографиям случайно ориентированных частиц; Журнал теоретической биологии (20047 19451, 90).
 дои: 10.1016/0022-5193(80)-0
дои: 10.1016/0022-5193(80)-0 - Richard A. Kirian, Kevin E. Schmidt, Xiaoyu Wang, R. Bruce Doak, and John C. H. Spence Сигнал, шум и разрешение в коррелированных флуктуациях в моментальном малоугловом рентгеновском рассеянии Физ. Ред. E 2011 , 84, 011921. doi: 10.1103/PhysRevE.84.011921
- G. Chen, M.A. Modestino, B.K. Poon, A. Schirotzek, S. Marchesini, R.A. Segalman, A. Hexemer и P.H. Zwart Определение структуры гантелей из Au с платиновым покрытием с помощью флуктуационного рассеяния рентгеновских лучей J. Synchrotron Radiation 2012 , 19, 695-700. doi: 10.1107/S09012023801
Разреженные данные
- K Ayyer, HT Philipp, MW Tate, JL Wierman, V Elser, SM Gruner Определение кристаллографических интенсивностей по разреженным данным IUCrJ 2015 , 2 (1), 29–34. дои: 10.1107/S2052252514022313
- Вирман Дж.Л., Лан Т.И., Тейт М.В., Филипп Х.Т., Эльзер В., Грунер С.М. Кристаллическая структура белка по неориентированным одноосным разреженным рентгеновским данным IUCrJ 2016 , 3 (1), 43-50.
 doi: 10.1107/S2052252515018795
doi: 10.1107/S2052252515018795
XFEL
- Дерек Мендес, Гершель Уоткинс, Шэнлан Цяо, Кевин С. Рейнс, Томас Дж. Лейн, Гундольф Даниэль Шенк, Гарретт Нельсон, Гарретт Нельсон, Ганеш Тони Джоно, Яши Субраманян, Яши Субраманян, Кенсуке Субраманян Ратнер и Себастьян Дониач Угловые корреляции фотонов при дифракции растворов в лазере на свободных электронах кодируют молекулярную структуру IUCrJ 2016 , 3(6), 420-429. doi: 10.1107/S2052252516013956
Флуктуационное рассеяние
- Г. Чен, М. А. Модестино, Б. К. Пун, А. Широтцек, С. Маркесини, Р. А. Сегалман, А. Пексемер и П. Х. Цварткотуация с помощью определения структуры гантелей Рентгеновское рассеяние J. Synchrotron Rad. 2012 , 19, 695-700. дои: 10.1107/S09012023801
- Эрик Малмерберг, Шерил А. Керфельд и Петрус Х. Зварт Эксплуатационные свойства флуктуационных данных рентгеновского рассеяния IUCrJ 2015 , 2(3), 309-316. дои: 10.


 с
с