Закон Паскаля — для жидкостей и газов
Давление
Идущий по рыхлому снегу человек будет в него постоянно проваливаться. А вот на лыжах он сможет передвигаться по тому же самому снегу спокойно. Казалось бы, ничего не меняется — человек воздействует на снег с одинаковой силой и на лыжах, и без них.
Дело в том, что «проваливание» в снег характеризуется не только силой — оно также зависит от площади, на которую эта сила воздействует. Площадь поверхности лыжи в 20 раз больше площади поверхности подошвы, поэтому человек, стоя на лыжах, действует на каждый квадратный сантиметр с силой в 20 раз меньшей, чем без них.
Или, например, если вы будете с одинаковой силой втыкать кнопки в пробковую доску, легче войдет та кнопка, у которой более заостренный конец, так как его площадь меньше.
Резюмируем: результат действия силы зависит не только от ее модуля, направления и точки приложения, но и от площади поверхности, к которой эта сила приложена.
А теперь подтвердим этот вывод опытами, как настоящие физики.
Возьмем небольшую доску и вобьем гвозди в ее углы. Также возьмем емкость с песком и поставим конструкцию из доски и гвоздей в эту емкость. Сначала расположим конструкцию шляпками вниз и поставим на нее гирю. Конструкция не утонет в песке, а только чуть-чуть углубится в него.
Затем перевернем конструкцию так, чтобы шляпки гвоздей оказались сверху и также поставим на доску гирю. Теперь конструкция утонет в песке.
От того, какая сила действует на каждую единицу площади поверхности, зависит результат действия силы.
Во всех примерах мы говорили о действии силы, перпендикулярной поверхности. Чтобы охарактеризовать это действие, используется величина давление.
| Давление p = F/S p — давление [Па] F — сила [Н] S — площадь [м2] |
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой.
Запишитесь и участвуйте в розыгрыше 8 уроков
Как уменьшить или увеличить давление
Тяжелый гусеничный трактор производит давление на почву, равное 40–50 кПа. Мальчик массой 45 кг производит давление всего лишь в 3 раза меньше, чем такой трактор. Это связано с большой площадью гусениц трактора.
В зависимости от того, какое давление хотят получить, площадь опор уменьшают или увеличивают. Например, чтобы уменьшить давление здания на грунт, в процессе строительства увеличивают площадь нижней части фундамента.
Шины грузовых автомобилей делают значительно шире легковых автомобилей. Чтобы убедиться в этом, обратите внимание на колеса какой-нибудь большой фуры. Самые широкие шины можно увидеть на автомобилях, предназначенных для передвижения в пустыне. Тот же лайфхак используется в шасси самолетов.
Обратную зависимость тоже применяют, например, при создании лезвий колющих и режущих инструментов.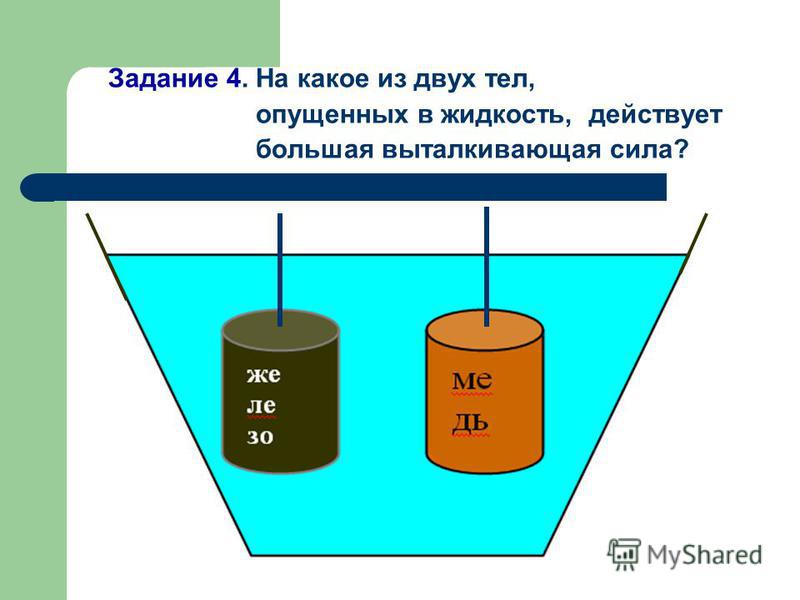
Острое лезвие имеет малую площадь, поэтому даже при небольшом нажатии создается большое давление.
Задачка раз
Книга лежит на столе. Масса книги равна 0,6 кг. Площадь ее соприкосновения со столом равна 0,08 м2. Определите давление книги на стол. В этой задаче g = 10 Н/кг.Решение
На стол будет давить сила, равная весу книги. Так как она покоится, ее вес будет равен силе тяжести. Следовательно:
p = mg/S = 0,6 × 10 / 0,08 = 75 Па
Ответ: давление книги на стол будет равно 75 Па.
Задачка два
Гусеничный трактор ДТ-75М массой 6 610 кг имеет опорную площадь обеих гусениц 1,4 м2. Определите давление этого трактора на почву. В этой задаче g = 10 Н/кг.
Решение:
p = mg/S = 6 610 × 10 / 1,4 = 47 214 Па = 47,2 кПа
Ответ: давление трактора на почву составляет 47,2 кПа.
Задачка три
Человек массой 80 кг с сумкой весом 100 Н стоит неподвижно на полу. Сила давления подошв его ботинок на пол равномерно распределена по площади 600 см2. Какое давление человек оказывает на пол? В этой задаче g = 10 Н/кг.
Решение
Масса человека: m = 80 кг.
Вес сумки, которую держит человек: Pc = 100 Н.
Площадь соприкосновения подошвы ботинок с полом: S = 600 см2.
600 см2 = 600 / 10 000 м2 = 0,06 м2
Давление — это отношение силы к площади, на которую она действует. В данном случае на площадь действует сила, равная сумме силы тяжести человека и веса сумки:
F = mg + Pс
Поэтому давление, оказываемое человеком с сумкой на пол, равно:
p = (mg + Pс) / S = (80 × 10 + 100) / 0,06 = 15 000 Па = 15 кПа
Ответ: давление человека с сумкой на пол равно 15 кПа.
Еще больше интересной практики — на элективном курсе по физике для 10 класса.
Определение закона Паскаля
Прежде чем переходить к формулировке закона, рассмотрим опыт с шаром Паскаля. Присоединим к трубе с поршнем полый шар со множеством небольших отверстий. Зальем в шар воду и будем давить на поршень. Давление в трубе вырастет и вода будет выливаться через отверстия, причем напор всех струй будет одинаковым. Такой же результат получится, если вместо воды в шарике будет газ.
Это работает только с жидкостями и газами. Дело в том, что молекулы жидких и газообразных веществ под давлением ведут себя совсем не так, как молекулы твердых тел. Если молекулы жидкости и газа движутся почти свободно, то молекулы твердых тел так не умеют. Они могут лишь колебаться, немного отклоняясь от исходного положения. Именно благодаря свободному передвижению молекулы газа и жидкости оказывают давление во всех направлениях.
Итак, мы подошли к формулировке закона Паскаля, и звучит она так:
Давление, производимое на жидкость или газ, передается в любую точку одинаково во всех направлениях.
Важный момент
У Земли есть атмосфера. Эта атмосфера создает давление, которое добавляется ко всем другим. То есть если мы давим рукой на стол, то давление, которое испытывает стол — это давление нашей руки плюс атмосферное.
Глава 9. Гидростатика
Для решения задач на гидростатику необходимо знать определения плотности и давления, уметь находить давление в покоящейся жидкости, возникающее благодаря притяжению этой жидкости к Земле (гидростатическое давление), а также находить силы, с которыми жидкости действуют на погруженные в них тела (силу Архимеда). Кратко сформулируем эти определения и законы.
Плотностью тела называется отношение
(9.1) |
где — масса тела, — его объем.
Очевидно, отношение (9.1) имеет смысл массы единицы объема тела. Если тело однородно, то плотность (9.1) является характеристикой не тела, а вещества, из которого оно состоит. Действительно, для тел, состоящих из одного и того же вещества масса пропорциональна объему, и отношение (9.1) одинаково у всех этих тел.
Для характеристики воздействия жидкости или газа на стенки сосудов вводят понятие давления жидкости или газа, которое определяется как отношение силы , действующей на элемент стенки сосуда со стороны жидкости или газа, к величине площади этого элемента :
(9.2) |
Важным свойством давления является то обстоятельство, что хотя оно и определяется через элемент площади стенки сосуда, от этого элемента давление (9.2) не зависит, а является характеристикой только жидкости или газа. Действительно, сила, действующая со стороны жидкости на элемент площади дна сосуда или стенки сосуда, пропорциональна площади этого элемента, и потому отношение (9.
2) от не зависит. Отметим, что хотя давление и определяется через векторную величину — силу, давление — величина не векторная. Как показывает опыт, отношение (9.2) не зависит не только от величины площадки , но и от ее ориентации в пространстве. Другими словами, жидкость, будучи сжатой, оказывает воздействие во всех направлениях. Последнее утверждение и говорит о невекторном характере давления и называется законом Паскаля.
В жидкости, находящейся в каком-либо сосуде в поле силы тяжести, благодаря ее притяжению к Земле, возникает давление. Это давление называется гидростатическим. Можно доказать, что гидростатическое давление жидкости не зависит от формы сосуда, в котором она находится, а зависит только от глубины. Гидростатическое давление жидкости плотности на глубине равно
(9.3) |
где — ускорение свободного падения. Если на поверхность жидкости действует атмосферный воздух, то давление жидкости на глубине будет складываться из атмосферного давления и гидростатического давления (9.
3).
Благодаря зависимости гидростатического давления жидкости от глубины возникает своеобразный эффект выталкивания тел, погруженных в жидкость, из этой жидкости. Действительно, в жидкости, находящейся в поле силы тяжести, возникает гидростатическое давление, и жидкость оказывает воздействие на поверхность тела, опущенного в жидкость. При этом силы, действующие на боковые поверхности тела, компенсируют друг друга. Однако из-за зависимости гидростатического давления от глубины, сила, действующая на более глубокую (нижнюю) поверхность тела, больше силы, действующей на верхнюю поверхность (см. рисунок), и на тело действует результирующая сила, направленная вертикально вверх. Эта сила называется выталкивающей силой или силой Архимеда. Можно доказать, что на тело, целиком погруженное в жидкость, действует выталкивающая сила
(9.4) |
где — плотность жидкости, — объем тела. Если тело погружено в жидкость не целиком, то выталкивающая сила также определяется формулой (9.
4), но вместо объема тела в нее входит объем погруженной в жидкость части тела.
С помощью формулы (9.4) можно установить условие плавания тел. Тело будет плавать, если сила Архимеда будет больше действующей на тело силы тяжести
где — плотность тела. Отсюда получаем, что тело плавает, если плотность жидкости больше плотности тела
(9.5) |
Рассмотрим теперь задачи.
В задаче 9.1.1 с использованием формулы (9.3) для гидростатического давления находим
(ответ — 4).
Поскольку высота уровней жидкости в сосудах (в задаче 9.1.2) и их плотности одинаковы, то давление жидкости около дна обоих сосудов одинаково (ответ 3).
В задаче 9.1.3 давление жидкости около дна сосудов одинаково (одинаковы плотности и уровень жидкостей), поэтому сила, действующая на дно, больше для того сосуда, площадь дна которого больше, а меньше для того, площадь дна которого меньше.
Поэтому (правильный ответ — 2).
Чтобы найти силу, действующую на небольшую поверхность внутри жидкости, нужно найти гидростатическое давление жидкости на той глубине, на которой находится рассматриваемая поверхность, и умножить это давление на площадь поверхности. Поэтому для крана из задачи 9.1.4 получаем
(ответ 4).
Бытовой насос (задача 9.1.5) поднимает воду благодаря создаваемому им избыточному давлению. Ясно, что вода в трубках насоса будет подниматься до тех пор, пока ее гидростатическое давление не компенсирует избыточное давление насоса. Поэтому насос сможет поднять воду на следующую высоту
где — избыточное давление, созданное насосом, — плотность воды, — ускорение свободного падения (правильный ответ — 3).
Поскольку бруски в задаче 9.1.6 изготовлены из одинакового материала, у них одинаковые плотности, и, следовательно, отношение их масс равно отношению их объемов.
А поскольку объем второго бруска вчетверо больше объема первого, то и его масса вчетверо больше массы первого, т.е. равна 40 г (ответ 3).
Пусть размер меньшего ребра бруска в задаче 9.1.7 — . Тогда размеры остальных сторон — и . Следовательно, площади граней бруска равны , и . Поэтому давления бруска на стол, когда он лежит на разных гранях, равны (начиная с наименьшего):
т.е. относятся друг к другу так же, как и длины сторон 1:2:3 (ответ 1).
В сообщающихся сосудах жидкость занимает такое положение, что ее давление в обоих коленах одинаково. Поэтому в задаче 9.1.8 имеем с использованием формулы для гидростатического давления
Отсюда находим
(правильный ответ — 4).
Поскольку плотность натрия 950 кг/м3 (задача 9.
1.9) меньше плотности воды 1000 кг/м3, то натрий плавает на поверхности воды (ответ 1).
На льдину (задача 9.1.10) действуют сила тяжести и сила Архимеда. Условие равновесия льдины дает
(1) |
где — плотность воды, — объем погруженной в воду части льдины, — ее масса. Поскольку, где — плотность льда, — объем льдины, из формулы (1) получаем
Отсюда находим, что отношение объема погруженной в воду части льдина к ее объему равно отношению плотностей льда и воды
(ответ 2). Таким образом, девять десятых частей плавающей льдины находятся под водой.
Поскольку тело в задаче 9.2.1 плавает в жидкости, выталкивающая сила Архимеда равна действующей на тело силе тяжести — 10 Н (ответ 1).
Весом тела называется сила, с которой тело действует на опору (сила реакции опоры). На тело, полностью погруженное в воду, действуют сила тяжести , выталкивающая сила Архимеда и сила реакции. Для силы реакции (веса тела) из условия равновесия тела имеем
где и — плотности жидкости и тела, — объем тела (обратим внимание читателя на то, что согласно этой формуле вес тела в жидкости уменьшается). Отсюда находим
(задача 9.2.2 — ответ 3).
Из условия равновесия коробки, плавающей на поверхности воды (задача 9.2.3), следует, что сила тяжести равна силе Архимеда , где — масса тела, — плотность воды, — объем погруженной части коробки, который можно выразить через площадь дна коробки и глубину его погружения в воду см3. Отсюда получаем для массы коробки = 500 г (ответ 2).
При решении задачи 9.2.4 школьники часто допускают ошибку, говоря, что выталкивающая сила равна нулю, так как шар, наполненный воздухом, находясь в воздухе, «всплывать» не будет. Последнее утверждение, конечно, правильно, а первое — нет. Шар, наполненный воздухом, не «всплывает» в воздухе не потому, что выталкивающая сила не действует, а потому, что она меньше силы тяжести. Выталкивающая сила действует на тело со стороны жидкости или газа и никак не может зависеть от того, что внутри этого тела, воздух или, напрмер, гелий, с которым шар всплывал бы. Для выталкивающей силы имеем согласно закону Архимеда Н (ответ 1).
На поплавок из задачи 9.2.5 действуют силы: тяжести , Архимеда , натяжения лески (см. рисунок). Используя стандартное выражение для силы Архимеда (9.4), получаем из условия равновесия поплавка
где — плотность воды, и — масса и объем поплавка. Выражая массу поплавка через его плотность и объем и учитывая, что по условию плотность воды вдвое больше плотности поплавка , получим 10 Н (ответ 1).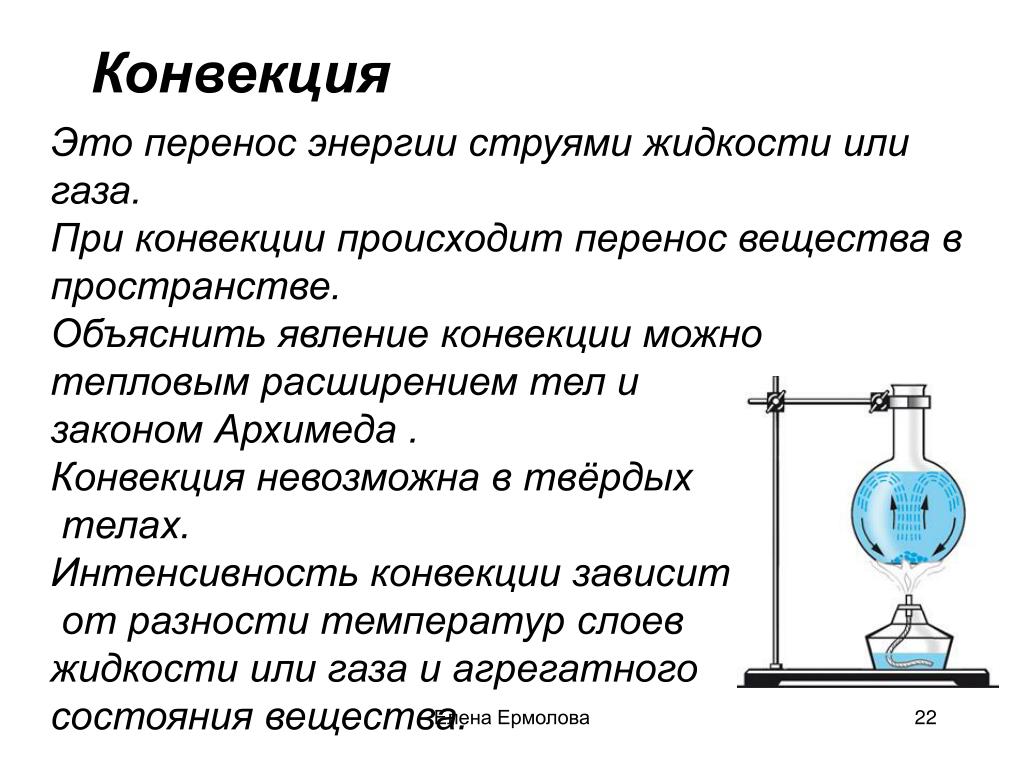
В задаче 9.2.6 умышленно дано много лишних данных. Поскольку и в воде, и в керосине мяч плавает, то архимедова сила и в том, и в другом случае уравновешивает силу тяжести мяча (ответ 2).
Несмотря на то, что тело в задаче 9.2.7 не касается дна и стенок сосуда, суммарная сила, действующая на левую чашку весов, увеличится. Действительно, при опускании тела в воду возникает сила Архимеда, действующая со стороны воды на тело, но при этом и тело действует на воду, причем эта сила направлена вертикально вниз и равна силе Архимеда. Чтобы весы остались в равновесии на правую чашку весов надо положить такой груз, сила тяжести которого равна этой силе, т.е. груз с массой , где — плотность воды, — объем тела. А поскольку плотность тела по условию вчетверо больше плотности воды, то (ответ 1).
Для нахождения давления жидкости, в которой плавают те или иные тела, существует следующий прием. Если мысленно удалить тело из жидкости и заполнить освободившееся место той же жидкостью, то силы, действующие со стороны жидкости на стенки сосуда не изменяться.
Действительно, на плавающее тело со стороны жидкости и со стороны тела на жидкость действует сила , где — плотность жидкости, — объем погруженной в жидкость части тела. Таким образом, тело действует на жидкость с той же силой, с которой на нее действовала бы жидкость, занимающая объем погруженной в воду части тела. Поэтому если вытащить тело из жидкости и заполнить освободившееся место жидкостью, то не меняется уровень жидкости, не меняются также все силы, действующие внутри жидкости. Поэтому если в жидкости плавает тело, то независимо от параметров этого тела (массы, плотности, объема), давление жидкости на глубине равно , причем отсчитывается от поверхности жидкости с плавающим в ней телом. Поэтому в задаче 9.2.8 надо найти, на сколько поднимется уровень воды в сосуде, а затем и связанное с этим повышением уровня избыточное гидростатическое давление около дна. Очевидно, что в цилиндрическом сосуде площадью сечения уровень воды поднимется на такую величину , что , где — объем погруженной в воду части тела.
Находя величину из условия равновесия тела и закона Архимеда, получим . Поэтому гидростатическое давление воды около дна вырастет на величину (ответ 1).
Из условия равновесия плавающего тела следует, что его масса равна массе воды в объеме погруженной части тела. . Поэтому суммарная масса воды и деревянного тела в одном ведре и суммарная масса воды и пенопластового тела в другом в задаче 9.2.9 равна массе воды в полном ведре, т.е. одинакова в обоих ведрах. Поэтому правильный ответ в этой задаче — 3.
Когда внутрь плиты из задачи 9.2.10 вставляют более плотное тело, возникает дополнительное гравитационное взаимодействие между жидкостью и плитой. Если до этого на каждый элемент жидкости действовала гравитационная сила, направленная вертикально вниз, то после этого возникает дополнительная сила, направленная к центру тела (см. рисунок, на котором нарисованы силы, действующие на выделенный элемент жидкости).
К каким последствиям для расположения жидкости на плите это приведет? Легко сообразить, что уровень жидкости в области над телом повысится. Действительно, поверхность жидкости всегда расположена перпендикулярно приложенным силам (иначе жидкость будет течь), поэтому она расположится так, как показано на рисунке. Другими словами, более массивное тело, вставленное внутрь плиты, благодаря дополнительному гравитационному взаимодействию «натянет» жидкость со всех сторон, и ее уровень над телом поднимется. Поэтому правильный ответ в задаче — 3.
Газ есть материя
Эта фокусная идея исследуется через:
- Противопоставление студенческих и научных взглядов
- Критические идеи обучения
- Преподавательская деятельность
Противопоставление студенческих и научных взглядов
Повседневный опыт студентов
У учащихся возникают особые проблемы с признанием существования газов как физического состояния материи, поскольку большинство газов невидимы.
Понятие «увидеть — значит поверить» очень важно для младших школьников и оказывает сильное влияние на их способность формировать понимание. Дополнительная сложность заключается в том, что в студенческом мире почти нет повседневных явлений цветных газов, которые можно было бы наблюдать.
Исследование: Stavy (1988)
Распространенное убеждение, поощряемое невидимостью газов, состоит в том, что они невесомы и не занимают места. Путаница может возникнуть, когда учащимся регулярно говорят, что контейнеры и банки, в которых ничего нет, пусты, но затем ожидается, что они поймут, что, хотя они пусты, на самом деле они содержат воздух.
Исследования: Russell, Longden & McGuigan (1991)
Третья проблема заключается в том, что слово газ при использовании в повседневном языке имеет другие значения, такие как природный газ и газ для кемпинга, которые не помогают учащимся сформировать свое понимание термина как классификации физическое состояние материи.
Эти вопросы также рассматриваются в основной идее
Знакомство с научным языком.
Научный взгляд
Термины «твердое тело», «жидкость» и «газ» представляют собой три простые, но полезные классификации состояний, в которых может находиться материя.
Это не единственные состояния материи, используемые учеными, и их использование не лишено проблем; например, как мы классифицируем такие вещества, как гель для волос, жир или майонез?
Эта проблема также рассматривается в фокусной идее Проблемы с классификацией.
Все газы имеют вес (1 литр воздуха в обычной комнате весит примерно 1 грамм). Большинство газов, с которыми сталкиваются учащиеся, бесцветны (например, воздух, водяной пар и кислород). Дым, туман и смог — это не окрашенные газы, а скорее мелкие частицы углерода или капельки воды, взвешенные в воздухе. Некоторые газы видны (например, двуокись азота и газообразный хлор), но учащиеся редко сталкиваются с ними.
Критические идеи обучения
- Помимо твердых и жидких тел, газы также являются физическим состоянием, в котором может находиться материя.
- Все газы имеют вес.
- В отличие от твердых и жидких тел, газы занимают всю емкость, в которой они находятся.
Исследуйте взаимосвязь между представлениями о газах и состояниями вещества в Карты развития концепции — (Сохранение материи, состояния материи)
На этом уровне уместно поощрять учащихся к пониманию того, что материя может быть классифицирована как твердое тело, жидкость или газ, и что эти термины описывают внешний вид веществ и как ведут себя вещества. Важно, чтобы газообразное состояние не игнорировалось при выполнении простых задач классификации.
Пока учащиеся закрепляют свое понимание этих терминов, не давайте им вещества, которые трудно классифицировать. Это станет очевидным для студентов, когда их понимание каждого состояния кристаллизуется, и они начнут осознавать, что границы иногда «нечеткие».
Эти вопросы также рассматриваются в основной идее Проблемы с классификацией.
Труднее убедить учащихся в том, что газы имеют вес, потому что для того, чтобы вес стал заметен, требуется много газа.
Некоторые учащиеся могут считать убедительной способность сильного ветра перемещать тяжелые предметы, но это не всегда помогает учащимся. Выдувание воздуха через соломинку, направленное на комок мятой бумаги, — это один из способов продемонстрировать, что что-то должно толкать бумагу, чтобы заставить ее двигаться, даже если этого не видно.
Ежедневный опыт, который является более сильным, — это изменение веса при наполнении газового баллона пропаном. Большие бутылки после наполнения явно тяжелее. На этом уровне неуместно обсуждать хранение пропана в виде жидкости под давлением или переход из жидкого состояния в газообразное при выпуске из баллона.
Учебные занятия
Открытие обсуждения путем обмена опытом и сбор доказательств и данных для анализа
Для простого упражнения по демонстрации движения газов по комнате сначала равномерно распределите учащихся по классу. Выпустите двухсекундный спрей из комнатного дезодоранта под давлением в одном углу комнаты.
Предложите учащимся поднять руки, как только они почувствуют запах, распространяющийся по комнате. Должно пройти совсем немного времени, прежде чем все ученики смогут почувствовать запах распространяющегося газа. Это движение газа будет быстрее в жаркий день. Предложите учащимся сыграть в игру «Найди и узнай запах», используя несколько аэрозольных баллончиков с дезодорантом для помещений.
Предложите открытую проблему для изучения в игровой форме и бросьте вызов некоторым существующим идеям
Чтобы побудить учащихся изучить идею о том, что газы занимают пространство, попросите их спланировать операцию по спасению пострадавшей подводной лодки. Учащиеся могут украсить простой прозрачный пластиковый стаканчик подводной лодкой, у которой заканчивается воздух для экипажа. Наполните эту чашку почти полностью водой и переверните ее так, чтобы она была в значительной степени над поверхностью, а ее край был внизу. С помощью другого прозрачного пластикового стаканчика предложите учащимся набрать воздух и перекачать его в поврежденную лодку, чтобы команда могла дышать.
Как они это сделают? Пусть по очереди переливают воздух из второго стакана в подводную лодку. Обсудите, как воздух занимает постоянное пространство и может быть заключен в чашу и позволить ему подниматься в чашку выше, выталкивая воду из пространства.
Прояснение и консолидация идей для/посредством сообщения другим
Предложите учащимся написать краткий рассказ о спасательной операции на подводной лодке. Попросите их нарисовать или нарисовать простые схемы чашек и показать, где они должны быть, чтобы выпустить захваченный воздух из чашки в подводную лодку. Обсудите, что чувствовала команда, когда они смогли вдохнуть свежий воздух, доставленный спасательной миссией.
Experimental Physics — Будет ли газ «весить» меньше, чем жидкость, если они имеют одинаковую массу?
Задавать вопрос
Спросил
Изменено 5 лет, 7 месяцев назад
Просмотрено 21k раз
$\begingroup$
Мысленный эксперимент: я приобрел две коробки одинаковых размеров и веса.
\circ\mathrm{C}$.
Я положил каждую коробку на простые электронные весы, чтобы измерить их вес. Неудивительно, что в коробке с водой оказалось $1\\mathrm{kg}$. А как насчет коробки с паром?
Мое предположение: электронные весы измеряют силу, действующую на объект, затем делят эту силу на $g$, чтобы получить массу объекта. Я думаю, что коробка с паром будет оказывать на весы меньшую силу, и поэтому весы сочтут, что ее масса меньше $1\\mathrm{kg}$.
- экспериментальная физика
- гидростатика
- вес
- газ
$\endgroup$
9
$\begingroup$
Прежде всего, невозможно иметь $1L$ жидкой воды в виде пара в контейнере $1L$. Жидкой и газообразной формам трудно занимать один и тот же объем. Молекулы газа будут так же близко друг к другу, как и в жидкой форме.
Однако, глядя на ваш последний абзац, можно сделать вывод, о чем вы на самом деле просите.
Я рассмотрю очень большую коробку вместо коробки за 1 литр долларов, чтобы ответить на этот вопрос.
Что измеряют весы?
Весы измеряют силу , прикладываемую к платформе весов испытуемым объектом.
Измерение веса жидкой воды
Рассмотрим гипотетическую ситуацию, когда вода существует только в жидкой форме. Давление пара отсутствует. Предположим, что коробка достаточно тяжелая, чтобы можно было пренебречь влиянием атмосферного давления.
Сила, действующая на коробку, определяется по формуле:
$$F = m_{box}g + m_{вода}g$$
На шкале будет отображаться $(m_{box} + m_{вода})g$.
Измерение веса газообразной воды
Газ внутри контейнера оказывает давление на стенки контейнера.
Давление на верхнюю часть контейнера = $P_{top}$
Давление на дно контейнера = $P_{top} + \rho gh$
Давление на верхнюю часть поможет уменьшить приложенную силу коробкой на платформе весов, а давление на дно поможет увеличить вес, прилагаемый коробкой.
Горизонтальные силы, приложенные газом к бокам коробки, аккуратно уравновешивают друг друга, давая результирующую горизонтальную силу $0N$.
Сила, действующая на весы со стороны ящика, определяется по формуле:
$$F = m_{box}g + (P_{нижний} — P_{верхний})A$$
$$F = m_{box} }g + (P_{top} + \rho gh — P_{top})A$$
$$F = m_{box}g + \rho ghA$$
$$V = Ah$$
$ $F = m_{box}g + (\rho V)g = m_{box}g + m_{gas}g$$
Если у вас есть такое же количество молекул в газообразном состоянии, как и в жидком состоянии , $m_{воды}$, полученной в предыдущем случае, равна $m_{газа}$, полученной в этом случае.
Весы будут показывать $(m_{коробка} + m_{вода})g$.
Если вы строго имели в виду $1L$ газа и $1L$ воды, то вода определенно будет весить больше, так как она плотнее, но этот вопрос был бы очень глупым, если бы это было так.
$\endgroup$
6
$\begingroup$
Сила, с которой коробка действует на весы, определяется разностью между силой, с которой газ действует вниз на дно коробки, и силой, с которой он действует вверх на верхнюю часть коробки.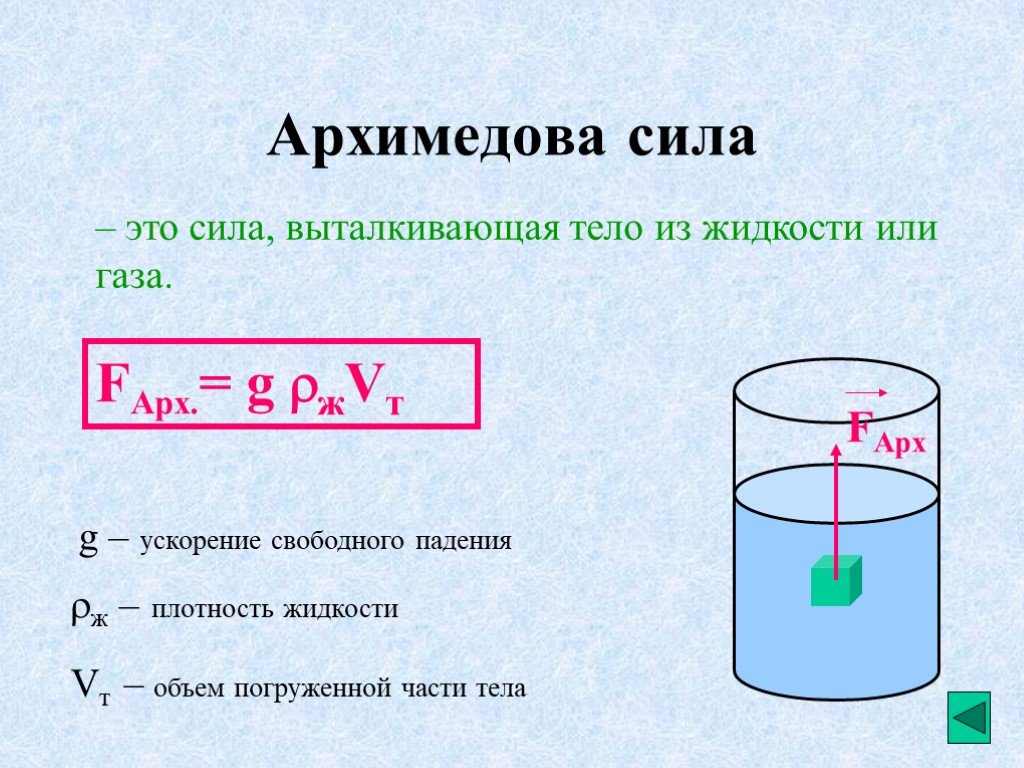
Обе силы можно записать как давление, умноженное на площадь $F = P S$, где $S$ — площадь верхней и нижней частей ящика. Разница в давлении просто определяется столбом газа внутри $P_{нижний}-P_{верхний}=\rho g h$, где $h$ — высота ящика. Затем:
\begin{equation} (\ text {сила на шкале}) = F _ {\ text {нижний}} — F _ {\ text {верхний}} = (P _ {\ text {нижний}} -P _ {\ text {верхний}}) S = \ rho ghS = \ rho g V = мг, \end{уравнение} равно весу газа , где $V=hS$ — объем, а $m=\rho V$ — масса.
Теперь, если вопрос: Что весит больше, литр жидкой воды или литр пара? Ответ, конечно, жидкость, потому что она имеет большую плотность.
Если вместо этого мы спросим, оказывает ли та же масса воды внутри коробки меньшую силу весов, ответ будет отрицательным, потому что сила, которую она оказывает, в точности равна ее весу, как показано выше.
$\endgroup$
9
$\begingroup$
Подводя итоги вопроса:
Начните с двух больших невесомых одинаковых коробок и $2 \text{кг}$ жидкой воды.
В каждую коробку насыпьте $1 \text{кг}$ воды. Нагрейте одну коробку так, чтобы ни одна молекула воды не покинула коробку, но вся вода превратилась в пар.
Затем сравните вес коробок, поставленных на весы.
Вес коробок действительно зависит от силы, давящей на весы вниз. Эта сила будет равняться весу ящика (ноль) плюс вес содержимого ящика за вычетом выталкивающей силы* воздуха, поднимающего ящик. Поскольку ящики одинаковые, выталкивающая сила будет одинаковой. А так как изначально в оба ящика пошла одна и та же масса воды, то и вес воды в ящиках будет одинаковым.
Однако ответ, какой ящик будет весить больше, зависит от того, что еще находится в каждом из ящиков:
Ничего:
Если бы у вас был вакуум, заполняющий оставшееся пространство, то не было бы дополнительной массы или веса добавлен. Таким образом, весы для камер с жидкой водой** и для камер с газообразной водой будут показывать 9,8 $ \text{N}$ минус выталкивающая сила*.
1 атм Воздух:
Если вы заполните оставшийся объем коробки воздухом при атмосферном давлении, то количество воздуха, которое вы добавите в каждую коробку, будет разным.
Жидкая вода займет меньше места в коробке, поэтому большая часть коробки будет заполнена воздухом. Таким образом, больше веса будет добавлено к ящику, в котором находится жидкая вода, и, таким образом, он будет весить больше.
N молей воздуха:
Если в каждую коробку добавить одинаковое количество молекул одного и того же типа, то массы останутся одинаковыми. Однако давление в ящике с газообразной водой будет намного выше из-за более высокой температуры.
*Плавающие ящики:
Интересно, что газообразная вода при той же температуре и давлении, что и газообразный воздух, будет менее плотной из-за более низкой молекулярной массы, чем азот или кислород. Это означает, что выталкивающая сила на самом деле будет больше, чем общий вес ящиков в трех сценариях; Только ящик с жидкой водой, заполненный воздухом, не мог просто уплыть, что очень затрудняло его размещение на весах.
Вероятно, эта плавучесть газов дает вам интуитивное представление о том, что равная масса будет весить меньше в виде газа, чем в виде жидкости.
**Фазы и вакуум:
В случае жидкой воды с вакуумом она мгновенно закипит и, в зависимости от температуры, может замерзнуть из-за низкого давления. Однако, как вы наблюдали за масштабом во время этих фазовых переходов, он оставался бы таким же, как вода кипит и замерзает, а затем замороженная вода в конечном итоге сублимируется до тех пор, пока в ней не останется только газообразная вода, как в другом ящике.
$\endgroup$
3
$\begingroup$
На это можно ответить очень просто: нет. Весить они будут одинаково.
Два ящика сделаны из одного и того же материала и занимают одинаковую общую площадь. Разница лишь во внутреннем расположении компонентов. То, что газ оказывает давление, ничего не значит — внутренние силы не могут воздействовать на коробку результирующей силой, поскольку это нарушило бы третий закон Ньютона.
Тогда видно, что это не имеет никакого значения для веса на весах. Масштабный вес состоит из двух вещей (при условии отсутствия ускоряющих рамок или других подобных странностей) — нисходящей силы тяжести на коробке плюс восходящей выталкивающей силы на коробку от окружающего воздуха. Оба в каждом случае совершенно одинаковы по постановке задачи (одинаковая масса и одинаковый объем воздуха, вытесняемый каждым контейнером). Так что есть нет разницы в измеренном весе . Нам даже не нужно заниматься математикой — для ответа на вопрос достаточно концептуального анализа.
РЕДАКТИРОВАТЬ: Это, конечно, только с учетом классической механики. Если бы наши весы могли быть произвольно чувствительными 90 154 и 90 155 , у нас было бы совершенно однородное гравитационное поле в 1 g, тогда в игру вступила бы теория относительности Эйнштейна, и она сказала бы, что паровая коробка будет весить немного на 90 154 больше 90 155 , из-за более высокого энергетического состояния, которое она имеет.
2}$, где $n$ — количество молей (не масса) воды, а $\Delta H_{\mathrm{vap}}$ теплота парообразования при температуре окружающей среды . На 1 кг воды это около 0,03 мкг. Местные колебания силы тяжести сделали бы это неуместным для весов.
$\endgroup$
0
$\begingroup$
Пропустить разницу между массой и силой. Они оба испытывают одинаковую гравитацию.
Да, литр воды равен 1 кг
Литр пара составляет примерно 1/1000 или примерно 1 г. Точнее 1,67 г (при 100С и 1 атм).
Если вы имеете в виду поместить 1 л воды в 1-литровую коробку и нагреть ее до 100°С или даже 200°С, то это тоже будет 1 кг. Но это будет НЕ пар. В коробке объемом 1 л ему некуда превратиться в пар. При 200С давление будет около 15 атм. Так что имейте прочную невесомую коробку.
Я думаю, что вы перепутали вопрос — я думаю, вы хотели спросить.
Масса 1 кг воды при 70 F и 1 атм и 1 кг пара при 212 F и 1 атм точно такая же.
Громкость будет существенно отличаться. Примерно в 1000 раз отличается.
Вес — это сила, и вес будет другим из-за плавучести. У меня сейчас нет времени прогонять цифры.
плотность воды 1 кг/л
плотность пара 0,0006 кг/л
Я думаю, что с плавучестью пар действительно уплывет, так как он менее плотный, чем воздух. Но я оставлю это для других.
$\endgroup$
0
$\begingroup$
На самом деле, если учесть релятивистские эффекты, ящик с паром будет весить больше, а не меньше, поскольку у него больше энергии и, следовательно, больше массы. Но игнорируя эти эффекты, оба ящика должны весить одинаково: у вас одинаковое количество молекул воды в каждом ящике , и гравитационное воздействие на каждую молекулу точно такое же.
$\endgroup$
1
$\begingroup$
Если оба ящика имеют одинаковый размер и вес, содержат одинаковую массу воды и одинаковую массу воздуха, то вес обоих ящиков будет одинаковым, а выталкивающая сила, действующая на ящики со стороны вытесняемого ими воздуха, будет быть таким же. При «при прочих равных условиях» две коробки будут весить одинаково, когда их кладут на электронные весы. Однако не все вещи равны. Ящик с паром значительно горячее ящика с водой. За счет этого термобокс будет нагревать чашу электронных весов, в результате чего воздух под чашей нагревается. Это создаст небольшую «подъемную силу», потому что горячий воздух менее плотный, чем воздух, который находится под чашей весов, когда взвешивается ящик с «водой». Предполагая высокую точность гипотетических электронных весов, это приведет к более низким показаниям веса для ящика с паром, чем для ящика с водой.
$\endgroup$
$\begingroup$
Вес пропорционален массе, конец истории, две коробки будут весить одинаково. Однако, чтобы удержать массу 1 кг пара в десятилитровом ящике, потребуется огромное давление. Объем идеального газа (который не является паром, но на мгновение пренебрегаем этим) составляет 22,4 литра на моль при нормальных условиях. Один моль воды весит 18 г, поэтому 1 кг пара будет иметь объем 1244 л при нормальных условиях. При 100°С громкость будет выше примерно в 373/29 раз.8 другими словами 1558 литров. Итак, вы хотите поместить это в 10-литровую коробку, что означает применение давления в 156 атмосфер, что составляет силу около 15,6 МПа, что эквивалентно 15,6 ньютонам на квадратный миллиметр. Вам понадобится технология типа кислородного баллона, которая будет весить огромное количество, что будет огромной нагрузкой на ваши точные весы.
Некоторые другие возражения, большое давление повысит точку кипения воды, поэтому вам нужно нагреть ее намного больше, чтобы она оставалась газообразной при таком огромном давлении.
В идеале вам нужно работать выше критической температуры воды, которая составляет 374 ° C, что приводит к соотношению давлений 647/29.8, что составляет 270 атмосфер, что удобно выше критического давления.
$\endgroup$
$\begingroup$
Ваш вопрос плохой. Настолько бедны, что мы можем дать целый ряд ответов.
Одна рука, две имеют одинаковую массу покоя, но у одной больше кинетическая энергия. Таким образом, его общая масса увеличилась на неизмеримую величину.
С другой стороны, пар, вероятно, выше в ящике, и сила тяжести выше от земли идет вниз. Таким образом, его вес уменьшается на неизмеримую величину.
Но вы заявили, что воздух был при 1 атм. Атм — единица давления; кипячение воды увеличит давление за счет более высокой температуры и за счет добавления атомов воды к количеству частиц газа. Таким образом, это означает, что ваша коробка должна была пропускать большое количество воздуха, чтобы поддерживать этот 1 атм, и, таким образом, вес снижается на измеримую величину.
На самом деле невозможно вскипятить 1 кг воды в 10-литровом ящике и поддерживать давление в 1 атм.
Если мы прочитаем ваши мысли и проигнорируем все эти проблемы, мы получим «твердый ящик содержит материю после фазового перехода, но вне зависимости от того, входит ли материя или выходит из нее, изменяется ли вес, измеряемый практическим изменением весов?» И ответ нет.
В целом, задавая вопрос по физике, лучше всего максимально точно описать серию событий, связанных с действиями людей или их доверенных лиц. Например:
Вы берете две жесткие большие коробки по 10 литров каждая. При комнатной температуре и нормальном давлении в каждый помещается 1 кг воды. Затем вы их запечатываете.
Затем вы нагреваете один из них до температуры выше 100 ° C и достаточно долго, чтобы вода внутри закипела. Ни из одной коробки ничего не вытекает.
Вы размещаете их в коммерческих масштабах с разумной точностью. Один весит больше другого?
Ответ на этот вопрос «нет».
$\endgroup$
0
$\begingroup$
Ваш вопрос невозможен (что теперь? То же количество воздуха плюс 1 кг водяного пара в том же объеме и давлении, что и 1 кг жидкости воды?). Вопрос также содержит собственный ответ: «Я приобрел две коробки одинаковых размеров и одинакового веса. … измерьте их соответствующие веса … как насчет коробки с паром?» Да, что насчет этого? Он имеет тот же вес, пост заканчивается здесь.
Хорошо, давайте предположим, что вы имели в виду что-то другое — возможно, массу, а не «вес»?
Но какой бы ни была ваша установка, ответ всегда очень прост: весы будут измерять гравитационную силу Земли, воздействующую на общую массу коробки 1 (т. е. упаковки плюс содержимое, включая весь газ), за вычетом выталкивающей силы коробка в атмосфере. Упаковка и плавучесть идентичны 2 для идентичных коробок, поэтому любая разница в «весе» (= сила на весах) должна быть связана с разницей в массе коробок.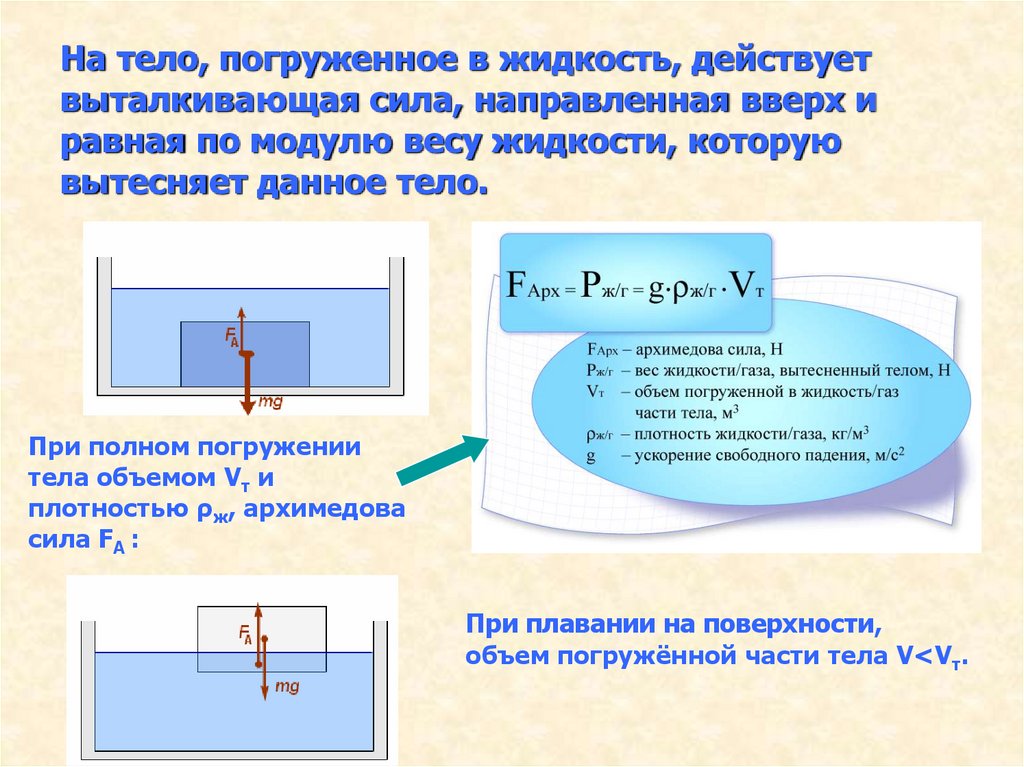
А теперь решите: что в коробках (газы, жидкости, твердые вещества)? Тогда у вас есть ответ.
1 Или, если хотите, гравитационная сила, с которой масса ящика действует на землю. Притяжение взаимно; просто землю это мало волнует.
2 Возможно, вас смущает плавучесть. В конце концов, мы, кажется, знаем, что объем, содержащий как можно меньше (горячий воздух, гелий, вакуум), испытывает подъем, который мы называем плавучестью, а тяжелые объекты, такие как камни или резервуары, этого не делают; а точка безубыточности наступает, когда плотность содержимого равна плотности воздуха. Но это только наше повседневное приближение: на самом деле все объектов, погруженных в газ или жидкость, обладают плавучестью; просто это не имеет отношения к нашему повседневному обращению с тяжелыми вещами. Величина плавучести зависит исключительно от объема тела (его водоизмещения). Это влияние перепадов давления между нижней и верхней сторонами на внешней стороне корпуса; то, что внутри, не имеет значения (и в мысленном эксперименте с идеальным «черным ящиком» непознаваемо).
Если бы содержимое ваших ящиков было неизвестно, и они имели бы одинаковую массу (и массовое распределение), они вели бы себя абсолютно одинаково во всех аспектах. Является ли содержимое жидкостью, паром или нейтронием, неизвестно и не имеет значения.
$\endgroup$
$\begingroup$
На самом деле все сводится к тому, что вы понимаете под словом «вес».
Если вы определяете вес с точки зрения силы, действующей на верхнюю часть весов, то вес наполненного гелием воздушного шара будет отрицательным. Масса того же воздушного шара положительна. Дело в том, что масса воздушного шара (кожи и содержимого) меньше, чем масса вытесненного воздуха, из-за чего воздушный шар поднимается вверх на ваших весах, а не толкается вниз. В этом случае единицами вашего результата являются ньютоны (или кгс), а не кг.
Вы получите аналогичный результат для пара (хотя вам понадобятся весы в комнате, наполненной воздухом с температурой выше 100°C, чтобы предотвратить быструю конденсацию пара).
Для идеального газа при любой температуре заданный объем содержит постоянное число молекул. (Общая формулировка такова: при стандартной температуре и давлении один моль газа занимает 22,4 литра). Молекулярная масса воды около 16, а воздуха около 30.
Но вы сказали «коробка», а не «воздушный шар». Если коробка является абсолютно жестким сосудом под давлением, она не будет расширяться и не позволит воде или пару сделать это. Поэтому сила, с которой ящик действует на весы, не изменится. Для любого реального сосуда под давлением он немного расширится, и «вес» немного изменится. (Не пытайтесь повторить это дома. Вода не превратится в пар, пока давление в коробке не станет очень высоким, а взрыв парового котла смертельно опасен).
Другое определение «взвешивания» означает определение массы объекта путем измерения силы, действующей на весы, и компенсации посторонних воздействий, таких как смещенная масса атмосферы и местные изменения силы тяжести. В соответствии с этим определением вопрос либо тавтологичен, либо касается обнаружения источников ошибки в действительной процедуре «взвешивания», исходя из предположения, что масса количества воды , а не изменяется при ее кипячении.
(ну, не значительно. Добавленное тепло сублимации имеет крошечную массу, согласно известному уравнению Эйнштейна).
Мы, вероятно, должны также отметить, что «взвешивание» обычно может относиться к определению цены вещества на весах, хотя это определение вряд ли может быть ответом на этот вопрос.
$\endgroup$
$\begingroup$
Сила, направленная вверх, одинакова для обоих ящиков (Архимед), как и сила, направленная вниз из-за массы ящиков. Но второй ящик не содержит такого же количества воздуха: ситуация во втором ящике достигается за счет нагревания ящика при комнатной температуре, содержащего один литр воды и воздуха при более низком давлении, чем 1 атмосфера (в конечном итоге при давлении 1 атмосфера при 100 градусах Цельсия), что подразумевает меньшую массу содержащегося воздуха. Если давление воздуха при 100 градусах Цельсия составляет 1 атмосферу, плотность воздуха меньше.
Объем, по которому распределяется воздух при 100 градусах Цельсия, увеличивается в меньший раз (с 9 литров до 10 литров), чем коэффициент, в который увеличивается температура (с 293 до 373 градусов по Кельвину).