Как найти диаметр цилиндра: Диаметр и высота цилиндра | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Как найти радиус основания цилиндра: формула через объем, площадь

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение радиуса цилиндра: формула и примеры

В данной публикации мы рассмотрим, как можно вычислить радиус цилиндра и разберем примеры решения задач для закрепления материала.

• Формулы вычисления радиуса цилиндра
  • 1. Через объем и высоту
  • 2. Через площадь боковой поверхности
  • 3. Через полную площадь поверхности
• Примеры задач

Формулы вычисления радиуса цилиндра

1. Через объем и высоту

Радиус цилиндра рассчитывается по формуле:

V – объем цилиндра; считается как произведение числа π на высоту фигуры на квадрат радиуса круга, являющего ее основанием.

V = πR²h

• R – радиус основания цилиндра, т.е. окружности;
• π – число, округленное значение которого равняется 3,14.

2. Через площадь боковой поверхности

Радиус цилиндра считается таким образом:

S_бок. – площадь боковой поверхности цилиндра; равна произведению длины окружности (2πR), являющейся основанием фигуры, на его высоту:

S = 2πRh

3. Через полную площадь поверхности

Радиус цилиндра равен:

Данная формула получена следующим образом:

S – полная площадь поверхности фигуры, равная:

S = 2πRh + 2πR² или S = 2πR(h + R)

Возьмем первое выражение. Если перенести S в правую часть, получим:

2πR² + 2πRh – S = 0

Можно заметить, что это квадратное уравнение вида ax² + bx + c = 0, где:

• a = 2π
• b = 2πh
• c = -S

R является корнем данного уравнения (

x). Подставив в стандартную формулу для расчета корней наши значения a, b и с получаем*:

* в нашем случае – только один положительный корень, т.к. радиус не может быть отрицательным.

Примеры задач

Задание 1
Высота цилиндра равняется 5 см, а объем – 141,3 см³. Вычислите его радиус.

Решение:
Воспользуемся соответствующей формулой, подставив в нее известные по условиям задачи значения:

Задание 2
Найдите радиус цилиндра, если площадь его боковой поверхности равна 175,84 см², а высота составляет 7 см.

Решение:
Применим формулу, в которой задействованы заданные величины:

Задание 3
Рассчитайте радиус цилиндра, если полная площадь его поверхности – 602,88 см

2, а высота – 10 см.

Решение:
Используем третью формулу для нахождения неизвестной величины:

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Как посчитать объем цилиндра — онлайн калькулятор

1. Главная
2. /
3. Математика
4. /
5. Геометрия
6. /
7. Как посчитать объем цилиндра

Чтобы посчитать объем цилиндра воспользуйтесь нашим удобным онлайн калькулятором:

Онлайн калькулятор

Найти чему равен объем цилиндра (V) можно зная (либо-либо):

• радиус r и высоту h цилиндра
• диаметр d и высоту h цилиндра
• площадь основания S_o и высоту h цилиндра
• площадь боковой поверхности S_b и высоту h цилиндра

Подставьте значения в соответствующие поля и получите результат.

Зная радиус r и высоту h

Чему равен объем цилиндра если его радиус

r = ,

а высота

h = ?

Ответ: V =

Чему равен объем цилиндра V если известны его радиус r и высота h?

Формула

V = π⋅r²⋅h

Пример

Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:

V = 3.14156 ⋅ 2² ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см³

Зная диаметр d и высоту h

Чему равен объем цилиндра если его диаметр

d = ,

а высота

h = ?

Ответ: V =

Чему равен объем цилиндра V если известны его диаметр d и высота h?

Формула

V = π⋅(^d/₂)²⋅h

Пример

Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:

V = 3. 14156 ⋅ (¹/₂)² ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см³

Зная площадь основания S

_o и высоту h

Чему равен объем цилиндра если площадь его основания

S_o = ,

а высота

h = ?

Ответ: V =

Чему равен объем цилиндра V если известны его площадь основания S_o и высота h?

Формула

V = S_o⋅h

Пример

Если цилиндр имеет высоту h = 10 см, а площадь его основания S_o = 5 см², то:

V = 10 ⋅ 5 = 50 см³

Зная площадь боковой поверхности S

_b и высоту h

Чему равен объем цилиндра если площадь его боковой поверхности

S_b = ,

а высота

h = ?

Ответ: V =

Чему равен объем цилиндра V если известны его площадь боковой поверхности S_b и высота h?

Формула

V = ^S_b2/_4πh

Пример

Если цилиндр имеет высоту h = 5 см, а площадь его боковой поверхности S_b = 30 см², то:

V = ³⁰²/ _{4 ⋅ 3. 14⋅ 5} = ⁹⁰⁰/_62.8 = 14.33 см³

См. также

Калькулятор круглого цилиндра

Форма круглого цилиндра

r = радиус
ч = высота
В = объем
L = площадь боковой поверхности

T = площадь верхней поверхности
B = площадь базовой поверхности
A = общая площадь поверхности
π = пи = 3,1415926535898
√ = квадратный корень

Калькулятор Использование

Этот онлайн-калькулятор рассчитает различные свойства цилиндра по двум известным значениям. Он также рассчитает эти свойства с точки зрения PI π. Это правильный круглый цилиндр, верхняя и нижняя поверхности которого параллельны, но его обычно называют «цилиндром».

Единицы: Обратите внимание, что единицы измерения показаны для удобства, но не влияют на расчеты. Единицы используются для указания порядка результатов, таких как футы, футы

2 или фут ³ . Например, если вы начинаете с мм и знаете r и h в мм, ваши расчеты дадут V в мм ³ , L в мм ² , T в мм ² , B в мм ² и A в мм ² .

Ниже приведены стандартные формулы для цилиндра. Расчеты основаны на алгебраических манипуляциях с этими стандартными формулами.

Формулы цилиндра через r и h:

• Рассчитать объем цилиндра:
  • В = πr ² ч
• Рассчитайте площадь боковой поверхности цилиндра (только кривизну снаружи)**:
  • Д = 2πrh
• Рассчитайте площадь верхней и нижней поверхности цилиндра (2 круги):
  • Т = В = πr ²
• Общая площадь поверхности закрытого цилиндра:
  • A = L + T + B = 2πrh + 2(πr ² ) = 2πr(h+r)

** Рассчитывается площадь только боковой поверхности наружной стенки цилиндра. Чтобы рассчитать общую площадь поверхности, вам нужно будет также рассчитать площадь верха и низа. Вы можете сделать это с помощью круговой калькулятор.

Расчеты цилиндров:

Используйте следующие дополнительные формулы вместе с формулами выше.

• По радиусу и высоте рассчитайте объем, площадь боковой поверхности и общую площадь поверхности.
  Вычислить V, L, A | Учитывая г, ч
  • используйте формулы выше
• По заданным радиусу и объему рассчитайте высоту, площадь боковой поверхности и общую площадь поверхности.
  Вычислить h, L, A | Учитывая г, В
  • ч = В / πr ²
• По заданным радиусу и площади боковой поверхности рассчитайте высоту, объем и общую площадь поверхности.
  Рассчитать h, V, A | Учитывая г, L
  • ч = л/2πr
• Зная высоту и площадь боковой поверхности, рассчитайте радиус, объем и общую площадь поверхности.
  Рассчитать r, V, A | Учитывая h, L
  • r = л/2πh
• Зная высоту и объем, рассчитайте радиус, площадь боковой поверхности и общую площадь поверхности.
  
  Вычислить r, L, A | Учитывая h, V
  • $r = √(В / πh)

Как найти объем цилиндра

Все математические ресурсы SAT

16 диагностических тестов 660 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 4 Следующая →

SAT Math Help » Геометрия » Твердая геометрия » Цилиндры » Как найти объем цилиндра

Объем цилиндра равен 36π. Если высота цилиндра равна 4, каков диаметр цилиндра?

Возможные ответы:

12

4

6

3

9

Правильный ответ:

6

Пояснение:

Объем цилиндра? V = πr ² ч.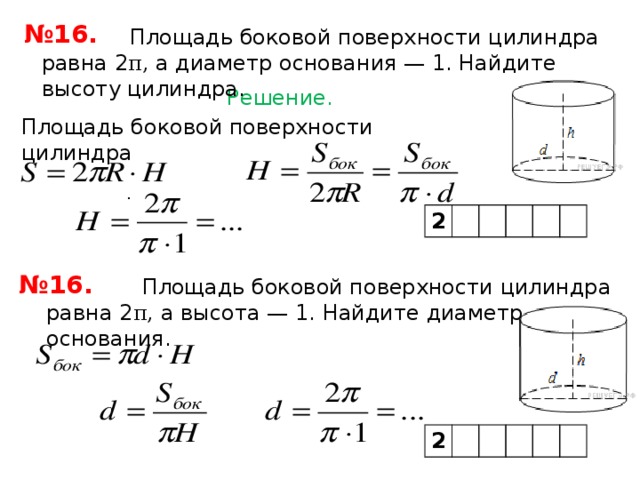

Переписанное в виде уравнения диаметра:

V = π(d/2) ² h = πd ² h/4

Sub in h и V: 36p = πd ² (4)/4 36p = πd ²

Таким образом, d = 6

Сообщить об ошибке

Цилиндр имеет высоту 5 дюймов и радиус 3 дюйма. Найдите площадь боковой поверхности цилиндра.

Возможные ответы:

8π

15π

30π

24π

45π

Правильный ответ:

30π

Объяснение:

LA = 2π(r)(h) = 2π(3)(5) = 30π

Сообщить об ошибке

Цилиндр имеет объем 20. Если радиус удвоится, каков новый объем?

Возможные ответы:

40

60

80

20

100

Правильный ответ:

80

Пояснение:

Уравнение объема цилиндра: πr ² ч. Когда радиус удваивается (r становится 2r), вы получаете π(2r) ² ч = 4πr ² ч. Таким образом, когда радиус удваивается, объем увеличивается в четыре раза, что дает новый объем 80.

Сообщить об ошибке

Высота цилиндра в три раза больше его радиуса. Если площадь боковой поверхности цилиндра равна 54π квадратных единиц, то каков его объем в кубических единицах?

Возможные ответы:

54π

27π

81π

9π

243π

Правильный Ответ:

8114

2. Пояснение:

Назовем r радиусом, а h высотой цилиндра. Нам говорят, что высота в три раза больше радиуса, что мы можем представить как h = 3r.

Нам также говорят, что площадь боковой поверхности равна 54π. Площадь боковой поверхности – это площадь поверхности, которая не включает основания. Формула площади боковой поверхности равна произведению длины окружности цилиндра на его высоту или 2πrh. Мы устанавливаем это равным 54π,

2πrh = 54π

Теперь подставим 3r вместо h.

2πr(3r) = 54π

6πr ² = 54π

Разделить на 6π

r ² = 9.

Извлечь квадратный корень

r = 3. 

h = 3r = 3(3) = 9.

Теперь, когда у нас есть радиус и высота цилиндра, мы можем найти его объем, который определяется как πr ² h.

В = πr ² ч

В = π(3) ² (9) = 81π

Ответ: 81π.

Сообщить об ошибке

Каков объем полого цилиндра с внутренним радиусом 2 см и внешним радиусом 4 см при высоте 5 см?

Возможные ответы:

20π CM ³

100π CM ³

.

60π см ³

Объяснение:

Объем определяется путем вычитания внутреннего цилиндра из внешнего цилиндра по формуле V = πr _из ² ч – πr _из ² ч. Площадь цилиндра с использованием внешнего радиуса составляет 80π см ³ , а полученное отверстие определяется объемом внутреннего радиуса, 20π см ³ . Разница между ними дает объем получившегося полого цилиндра, 60π см ³ .

Сообщить об ошибке

Каков объем прямого цилиндра с длиной окружности 25π дюймов и высотой 41,3 дюйма?

Possible Answers:

1032.5π in ³

3831.34π in ³

25812.5π in ³

6453.125π in ³

4813.33π in ³

Правильный ответ:

6453,125π в ³

Объяснение:

Формула объема прямого цилиндра: V = A * h, где A – площадь основания, или πr ² . Следовательно, общая формула объема цилиндра: V = πr ² ч.

 Во-первых, мы должны найти r, используя формулу для длины окружности (c = 2πr): 25π = 2πr; г = 12,5.

Исходя из этого, мы знаем, что объем нашего цилиндра должен быть: π*12,5 ² *41,3 = 6453,125π in ³

Сообщить об ошибке

В 8-дюймовом кубе высверлен цилиндр это. Цилиндр имеет радиус 2,5 дюйма. Каков примерно с точностью до сотых оставшийся объем куба?

Possible Answers:

391.33 in ³

354.92 in ³

157.08 in ³

203.34 in ³

462 in ³

Correct answer:

354,92 в ³

Пояснение:

Мы должны вычислить наши два объема и вычесть их. Объем куба очень прост: 8 * 8 * 8, или 512 в ³ .

Объем цилиндра рассчитывается путем умножения площади его основания на его высоту. Высота цилиндра 8 дюймов (высота куба, через который он просверливается). Следовательно, его объем равен πr ² h = π * 2,5 ² * 8 = 50π в ³

. или 354,92 в ³ .

Сообщить об ошибке

Из 12-дюймового деревянного куба высверлен цилиндр. Цилиндр имеет радиус 3,75 дюйма. Если плотность древесины 4 г/дюйм ³ , какова масса оставшейся древесины после высверливания цилиндра?

Possible Answers:

3193.33 g

3813.3 g

4921.4 g

4791.43 g

2594.11 g

Correct answer:

4791.43 g

Пояснение:

Мы должны вычислить наши два объема и вычесть их. После этого будем умножать на плотность.

Объем куба очень простой: 12 * 12 * 12, или 1728 в ³ .

Объем цилиндра рассчитывается путем умножения площади его основания на его высоту. Высота цилиндра 8 дюймов (высота куба, через который он просверливается). Следовательно, его объем равен πr ² h = π * 3,75 ² * 12 = 168,75π в ³ .

Объем, оставшийся в кубе после сверления, составляет: 1728 – 168,75π, или приблизительно 1728 – 530,1433125 = 1197,8566875 в ³ . Теперь умножьте это на 4, чтобы получить массу: (приблизительно) 479 1,43 г.

Сообщить об ошибке

Полая призма имеет основание 5 x 6 дюймов и высоту 10 дюймов. В призму помещена закрытая цилиндрическая банка. Затем оставшуюся часть призмы заполняют гелем вокруг цилиндра. Толщина банки незначительна. Его диаметр составляет 4 дюйма, а высота вдвое меньше призмы. Какой примерный объем геля необходим для заполнения призмы?

Возможные ответы:

249,73 ³

103,33 ³

237.17 in ³

187.73 in ³

203. 44 in ³

Correct answer:

237.17 in ³

Объяснение:

Общая форма нашей задачи:

Объем геля = Объем призмы – Объем банки

Объем призмы прост: 5 * 6 * 10 = 300 в ³

Объем банки найден. путем умножения площади круглого основания на высоту банки. Высота равна половине высоты призмы, или 10/2 = 5 дюймов. Площадь основания равна πr ² . Обратите внимание, что в подсказке указан диаметр. Следовательно, радиус равен 2, а не 4. Площадь основания равна: 2 ² π = 4 π . Таким образом, общий объем равен: 4 π * 5 = 20 π  в ³ .

Таким образом, объем геля составляет: 300 – 20 π или (приблизительно) 237,17 в ³ .

Сообщить об ошибке

Полая призма имеет основание 12 x 13 дюймов и высоту 42 дюйма. В призму помещена закрытая цилиндрическая банка. Затем оставшуюся часть призмы заполняют гелем, окружающим банку. Толщина банки незначительна. Его диаметр 9в , а его высота составляет одну четвертую высоты призмы. Банка имеет массу 1,5 г на ³ , а гель имеет массу 2,2 г на ³ . Какова примерная общая масса содержимого призмы?

Possible Answers:

13.95 kg

139.44 g

11.48 kg

973.44 g

15.22 kg

Correct answer:

13.95 kg

Пояснение:

Мы должны найти как объем банки, так и объем геля. Формула объема геля:

Объем геля = Объем призмы – Объем банки

Объем призмы прост: 12 * 13 * 42 = 6552 дюйма ³

Объем банки находится путем умножения площади круглого основания на высоту банка. Высота равна одной четвертой высоты призмы, или 42/4 = 10,5 дюйма.