Объём части цилиндра
Не откладывайте! ЗАГОВОРИТЕ на Английском!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2015-01-30
Объём части цилиндра. Здравствуйте, друзья! Для вас ещё одна статья с задачами про объём цилиндра. На момент написания этих строк данная группа задач исключена из открытого банка заданий ЕГЭ по математике, но они всегда туда могут «вернуться», и разумеется, их присутствие в составе заданий на самом экзамене вполне возможно. Это задачи на вычисление объёма части цилиндра. Задачки простенькие, решаются в 1-2 действия. Посмотрите, объём каких тел требуется найти:
*В условии задаются радиус основания, высота и угол сектора.
Если вы ещё не изучили статью, где речь шла об объёме части конуса, то посмотрите обязательно, здесь принцип решения тот же. Повторять его не буду. Напомню только формулу объёма цилиндра:
*Ещё можете посмотреть статью, в которой мы уже разобрали несколько заданий, связанных с объёмом цилиндра.
Также есть следующие формы тел, объём которых требуется найти, вот эскизы:
Процесс решения прост!
Рисунок Б. Тело состоит из цилиндра, на который как бы сверху поставили ещё полцилиндра. То есть чтобы найти объём такого тела, необходимо вычислить объёмы двух этих отдельных тел (цилиндра и полуцилиндра) и суммировать их.
Рисунок В. Тело представляет собой цилиндр, из которого как бы «вырезан» другой цилиндр. Для вычисления объёма тела достаточно найти объём «полного» цилиндра и затем из него вычесть объём пустого пространства (он тоже имеет форму цилиндра и объём вычисляется без труда). Рассмотрим задачи:
25739. Найдите объем V части цилиндра, изображённой на рисунке. В ответе укажите V/Пи.
Вычислим объём цилиндра:
Часть цилиндра построенного на секторе круга с углом в 900 составляет четвёртую часть от полного объёма:
Результат делим на Пи и записываем ответ.
Ответ: 9
25743.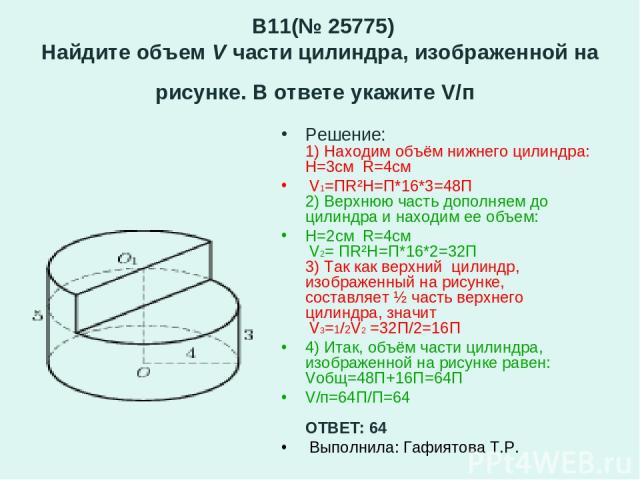 Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.
Вычислим объём цилиндра:
Часть цилиндра построенного на секторе круга с углом в 2700 (из трёхсот шестидесяти мы вычли девяносто) составляет три четвёртых от полного объёма:
Результат делим на Пи и записываем ответ.
Ответ: 15
27199. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.
Вычислим объём цилиндра:
Часть цилиндра построенного на секторе круга с углом в 3000 (из трёхсот шестидесяти мы вычли шестьдесят) составляет:
от полного объёма. Таким образом
Результат делим на Пи и записываем ответ.
Ответ: 937,5
25755. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.
Вычислим объём цилиндра:
Часть цилиндра построенного на секторе круга с углом в 600 составляет:
от полного объёма. Таким образом
Таким образом
Результат делим на Пи и записываем ответ.
Ответ: 112,5
25779. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.
Вычисляем объём цилиндра с радиусом равным 4 и высотой равной 3:
Вычисляем объём половины цилиндра с радиусом 4 и высотой равной 4 – 3 = 1
Объём тела будет равен:
Результат делим на Пи и записываем ответ.
Ответ: 56
25781. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.
Вычисляем объём цилиндра с радиусом равным 4 и высотой 5:
Вычисляем объём «вырезанного» цилиндра (пустой части) с радиусом 2 и высотой 5:
Объём тела будет равен:
Результат делим на Пи и записываем ответ.
Ответ: 60
27196. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.
Посмотреть решение
27197. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.
Посмотреть решение
27198. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.
Посмотреть решение
27200. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.
Посмотреть решение
27201. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.
Посмотреть решение
На этом всё! Успеха вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Стереометрия КОНУС ЦИЛИНДР | ЕГЭ-№2Объём
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
ЕГЭ Профиль №2.
 Цилиндр, конус, шар — math200.ru Skip to content
Цилиндр, конус, шар — math200.ru Skip to contentЕГЭ Профиль №2. Цилиндр, конус, шарadmin2022-08-28T09:32:48+03:00
Скачать файл в формате pdf.
ЕГЭ Профиль №2. Цилиндр, конус, шар
| Задача 1. В цилиндрический сосуд налили 2000 см3 воды. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в см3. Ответ ОТВЕТ: 1500. | |
| Задача 2. В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах. Ответ ОТВЕТ: 4. | |
Задача 3. Радиус основания цилиндра равен 2, высота равна 3. Ответ ОТВЕТ: 12. | |
| Задача 4. В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите в литрах. Ответ ОТВЕТ: 3. | |
| Задача 5. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой. Ответ ОТВЕТ: 1,125. | |
| Задача 6. Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра. Ответ ОТВЕТ: 6. | |
| Задача 7. Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра. Ответ ОТВЕТ: 2. | |
Задача 8.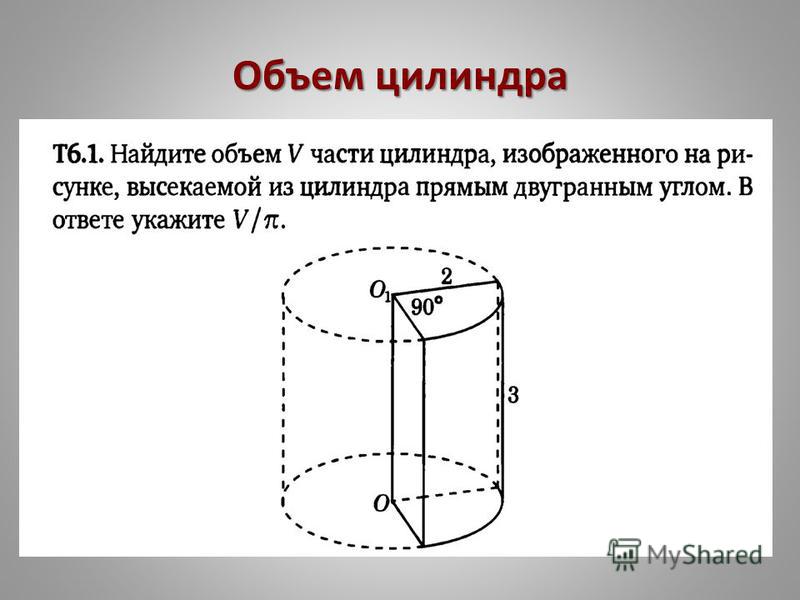 Площадь боковой поверхности цилиндра равна \(72\pi \), а диаметр основания — 9. Найдите высоту цилиндра. Площадь боковой поверхности цилиндра равна \(72\pi \), а диаметр основания — 9. Найдите высоту цилиндра.Ответ ОТВЕТ: 8. | |
| Задача 9. Площадь боковой поверхности цилиндра равна \(2\pi \), а высота — 1. Найдите диаметр основания. Ответ ОТВЕТ: 2. | |
| Задача 10. Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на \(\pi \). Ответ ОТВЕТ: 4. | |
| Задача 11. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите \(\frac{V}{\pi }\). Ответ ОТВЕТ: 45. | |
| Задача 12. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите \(\frac{V}{\pi }\). ОТВЕТ: 3,75. | |
Задача 13. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите \(\frac{V}{\pi }\). В ответе укажите \(\frac{V}{\pi }\).Ответ ОТВЕТ: 144. | |
| Задача 14. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите \(\frac{V}{\pi }\). Ответ ОТВЕТ: 937,5. | |
| Задача 15. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите \(\frac{V}{\pi }\). Ответ ОТВЕТ: 14. | |
| Задача 16. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите \(\frac{V}{\pi }\). Ответ ОТВЕТ: 105. | |
| Задача 17. Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса. Ответ ОТВЕТ: 2. | |
Задача 18. Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30o. В ответе укажите \(\frac{V}{\pi }\). В ответе укажите \(\frac{V}{\pi }\).Ответ ОТВЕТ: 1. | |
| Задача 19. Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 3 раза, а радиус основания останется прежним? Ответ ОТВЕТ: 3. | |
| Задача 20. Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 1,5 раза, а высота останется прежней? Ответ ОТВЕТ: 2,25. | |
| Задача 21. Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на \(\pi \) ОТВЕТ: 128. | |
| Задача 22. Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на \(\pi \). Ответ ОТВЕТ: 9. | |
Задача 23. Конус получается при вращении равнобедренного прямоугольного треугольника ABC вокруг катета, равного 6. Найдите его объем, деленный на \(\pi \). Найдите его объем, деленный на \(\pi \).Ответ ОТВЕТ: 72. | |
| Задача 24. Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на \(\pi \) Ответ ОТВЕТ: 16. | |
| Задача 25. Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса. Ответ ОТВЕТ: 3. | |
| Задача 26. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза, а радиус основания останется прежним? Ответ ОТВЕТ: 3. | |
| Задача 27. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 1,5 раза, а образующая останется прежней? Ответ ОТВЕТ: 1,5. | |
Задача 28. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.Ответ ОТВЕТ: 60. | |
| Задача 29. Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса. ОТВЕТ: 3. | |
| Задача 30. Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на \(\pi \) Ответ ОТВЕТ: 24. | |
| Задача 31. Найдите объем V части конуса, изображенной на рисунке. В ответе укажите \(\frac{V}{\pi }\). Ответ ОТВЕТ: 87,75. | |
Задача 32. Найдите объем V части конуса, изображенной на рисунке. В ответе укажите \(\frac{V}{\pi }\). Ответ ОТВЕТ: 243. | |
| Задача 33. Найдите объем V части конуса, изображенной на рисунке. В ответе укажите \(\frac{V}{\pi }\). Ответ ОТВЕТ: 216. | |
| Задача 34. Найдите объем V части конуса, изображенной на рисунке. В ответе укажите \(\frac{V}{\pi }\). Ответ ОТВЕТ: 607,5. | |
| Задача 35. Высота конуса равна 4, а диаметр основания — 6. Найдите образующую конуса. Ответ ОТВЕТ: 5. | |
| Задача 36. Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса. Ответ ОТВЕТ: 6. | |
| Задача 37. Диаметр основания конуса равен 6, а длина образующей — 5. Найдите высоту конуса. Ответ ОТВЕТ: 4. | |
Задача 38. В сосуде, имеющем форму конуса, уровень жидкости достигает \(\frac{1}{2}\) высоты. Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд? Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?ОТВЕТ: 490. | |
| Задача 39. Площадь основания конуса равна \(16\pi \), высота – 6. Найдите площадь осевого сечения конуса. Ответ ОТВЕТ: 24. | |
| Задача 40. Площадь основания конуса равна 18. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью. Ответ ОТВЕТ: 2. | |
| Задача 41. Высота конуса равна 8, а длина образующей – 10. Найдите площадь осевого сечения этого конуса. Ответ ОТВЕТ: 48. | |
| Задача 42. Диаметр основания конуса равен 12, а длина образующей – 10. Найдите площадь осевого сечения этого конуса. Ответ ОТВЕТ: 48. | |
Задача 43. Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза? Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза?Ответ ОТВЕТ: 4. | |
| Задача 44. Во сколько раз увеличится объем шара, если его радиус увеличить в три раза? Ответ ОТВЕТ: 27. | |
| Задача 45. Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов. Ответ ОТВЕТ: 12. | |
| Задача 46. Объем одного шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго? Ответ ОТВЕТ: 9. | |
| Задача 47. Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей. Ответ ОТВЕТ: 10. | |
Задача 48. Объем шара равен \(288\pi \). Найдите площадь его поверхности, деленную на \(\pi \). Ответ ОТВЕТ: 144. | |
| Задача 49. Площадь поверхности шара равна 12. Найдите площадь большого круга шара. Ответ ОТВЕТ: 3. | |
Реклама
Поддержать нас
Объем частично заполненного цилиндра с калькулятором
Объем частично заполненного цилиндра с калькулятором — Math Open ReferenceОткрытый справочник по математике
Главная Контакт О Тематический указатель
Определение: Форма, образованная при разрезании цилиндра плоскостью, параллельной сторонам цилиндра.
Попробуйте это Перетащите оранжевые точки, обратите внимание, как меняется громкость.
См. также: Объем цилиндра
Если мы возьмем горизонтальный цилиндр и разрежем его на две части разрезом, параллельным сторонам цилиндра, мы получим два горизонтальных сегмента цилиндра.
На рисунке выше нижний показан синим цветом. Другой — прозрачная часть сверху.
Если мы посмотрим на конец цилиндра, мы увидим, что это круг, разделенный на два круговых сегмента. Дополнительные сведения см. в разделе Определение сегмента окружности.
Всякий раз, когда у нас есть твердое тело, поперечное сечение которого одинаково по всей длине, мы всегда можем найти его объем, умножив площадь конца на его длину. Таким образом, в этом случае объем сегмента цилиндра равен площади сегмента круга, умноженной на длину.
Итак, по формуле объем горизонтального цилиндрического сегмента равен
Где
s = площадь сегмента окружности, образующего конец тела, и
l = длина цилиндра.
Площадь сегмента круга можно найти, используя его высоту и радиус круга.
См. Площадь сегмента круга при заданной высоте и радиусе.
Калькулятор
Используйте калькулятор ниже, чтобы рассчитать объем сегмента горизонтального цилиндра.
Он был настроен для практического случая, когда вы пытаетесь найти объем жидкости в цилиндрическом резервуаре. путем измерения глубины жидкости.
путем измерения глубины жидкости.
Для удобства он преобразует объем в жидкие меры, такие как галлоны и литры, если вы выберете нужные единицы измерения. Если вы не укажете единицы, объем будет в тех единицах, которые вы использовали для ввода размеров. Например, если вы использовали футов, тогда объем будет в кубических футах. Используйте одни и те же единицы измерения для всех трех входов.
| Единицы | Нет МетрическаяСША | |
| Диаметр цилиндра | ||
| Длина цилиндра | ||
| Глубина | ||
| Том |
| |
В виде формулы
объем = где:
R – радиус цилиндра.

D – это глубина.
L длина цилиндра Примечания :
- Результат функции cos -1 в формуле выражается в радианах.
- В формуле используется радиус цилиндра. Это половина его диаметра.
- Все входы должны быть в одних и тех же единицах измерения. Результат будет в этих кубических единицах. Так, например, если входные данные указаны в дюймах, результат будет в кубических дюймах. При необходимости результат должен быть преобразован в единицы объема жидкости, такие как галлоны.
Похожие темы
- Определение лица
- Определение края
- Том
- Определение и свойства куба
- Объем, заключенный в куб
- Площадь поверхности куба
- Определение и свойства пирамиды
- Косая и правая пирамиды
- Объем пирамиды
- Площадь поверхности пирамиды
- Цилиндр – определение и свойства
- Цилиндр относительно призмы
- Цилиндр как геометрическое место линии
- Наклонные цилиндры
- Объем цилиндра
- Объем частично заполненного цилиндра
- Площадь поверхности цилиндра
- Размер призмы
- Объем призмы
- Площадь поверхности призмы
- Объем сферы
- Площадь поверхности сферы
- Определение конуса
- Наклонный и правый конусы
- Объем конуса
- Площадь поверхности конуса
- Вывод формулы площади конуса
- Высота наклона конуса
- Конические профили — круг
- Конические профили — эллипс
- Икосаэдр (20 граней равностороннего треугольника)
(C) 2011 Copyright Math Open Reference.
Все права защищены
Объем цилиндра: определение, формула, примеры
Сталкиваетесь ли вы с трудностями при нахождении объема цилиндра, если его форма искажена? Задумывались ли вы над тем, как найти объем таких цилиндров? Это то, что вы узнаете через мгновение.
Объем цилиндра означает пространство внутри цилиндра, которое может вместить определенное количество материала. Проще говоря, способность цилиндра удерживать предмет — это его объем. Внутри пространства цилиндра вы можете удерживать любой из трех типов материи — твердое, жидкое или газообразное. Эту емкость можно наблюдать только в трехмерном цилиндре, т. е. вы не можете удержать ни жидкость, ни твердое тело, ни газ в двумерном цилиндре.
Совершенный трехмерный цилиндр имеет два конгруэнтных и параллельных одинаковых основания. Это известно как правильный круговой цилиндр. В прямом круговом цилиндре основания круглые, а каждый отрезок является частью боковой криволинейной поверхности, перпендикулярной основаниям. Вы могли видеть правильные круглые цилиндры в своей повседневной жизни. Формы банок, формы рулонов бумаги, прямое стекло и многое другое.
Вы могли видеть правильные круглые цилиндры в своей повседневной жизни. Формы банок, формы рулонов бумаги, прямое стекло и многое другое.
Однако, если форма стакана совершенно прямая, он будет называться правильным круглым цилиндром. Если форма нелинейна, то какой она будет?
Если две конгруэнтные и идентичные параллельные стороны каким-либо образом становятся непараллельными или искривляются, вы получите один из следующих цилиндров:
- Наклонный цилиндр – это цилиндр, стороны которого наклонены к основанию под углом, не равным равен прямому углу. Это будет форма искаженного стекла, о которой говорилось выше.
- Эллиптический цилиндр – это цилиндр, основания которого представляют собой эллипсы.
- Прямой круглый полый цилиндр. Имеет форму правильного круглого цилиндра. Однако в конце нет замкнутых кругов.
Найти объем цилиндра проще, чем вы думали. Если вам все еще интересно, как найти объем цилиндра, все, что вам нужно, это ведро с водой, весы и пустая плоская поверхность, на которую можно поставить ведро.
Если вам все еще интересно, как найти объем цилиндра, все, что вам нужно, это ведро с водой, весы и пустая плоская поверхность, на которую можно поставить ведро.
Поставьте ванну на плоскую пустую поверхность и начните наполнять ее водой. Вы должны убедиться, что вода заполнена до краев. Как только ванна наполнится водой, поместите цилиндр, объем которого вам нужно найти, внутрь ванны. Вы увидите, как вода начнет выходить из ванны.
Соберите выпавшую воду в стакан. Убедитесь, что вода не падает, пока вы делаете преобразование. Поставьте стакан на весы и запишите вес воды. Не забудьте вычесть вес стакана. Вы должны иметь только вес воды.
Согласно закону Архимеда, вес воды, падающей из ванны, будет равен весу цилиндра. Следовательно, вес полученной воды будет равен весу цилиндра. Вам может быть интересно, как найти объем цилиндра?
Согласно физике, если вы находитесь в помещении с комнатной температурой, вес будет равен объему. Это означает, что 1 кг будет эквивалентен 1 литру и так далее. Следовательно, вы получите объем цилиндра из объема воды.
Следовательно, вы получите объем цилиндра из объема воды.
Но что, если вы живете в холодном или жарком регионе? Тогда вам придется использовать другой метод.
Формула для нахождения объема цилиндраОбъем цилиндра можно найти с помощью формулы. Это универсально и может применяться независимо от вашего региона. Единицами объема являются кубические сантиметры, кубические дюймы или любые стандартные единицы с префиксом «кубический».
Объем цилиндра можно найти двумя способами. Это:
- Использование площади и высоты
- Использование размеров
- Нахождение объема цилиндров по площади и высоте есть не что иное, как произведение площади и высоты любой формы. Это правило справедливо для всех трехмерных фигур, известных в математике. Например, в кубоиде, если вы знаете площадь одной его стороны, а затем умножаете ее на высоту или ширину, то есть на оставшуюся сторону, вы получите объем.
В цилиндрах, V = площадь x высота
- Нахождение площади с известными размерами – Универсальная формула для нахождения объема цилиндра: π r 2 h, где значение π (пи) равно 3,14 или 22/7, r – радиус вершины или дно цилиндра, а h — высота.
 Используя формулу, можно найти объемы прямых круговых цилиндров и косых цилиндров.
Используя формулу, можно найти объемы прямых круговых цилиндров и косых цилиндров.
Однако для эллиптических цилиндров формула другая. Поскольку эллиптические цилиндры имеют разные радиусы, формула для нахождения их объемов имеет вид: V = π abh, где π = 22/7 или 3,14, a и b — радиусы основания эллиптического цилиндра, а h — высота .
Кроме того, формула также отличается для полых прямоугольных цилиндров. Объем полого прямоугольного цилиндра определяется формулой: V = π (R 2 – r 2 ) h , где R — внешний радиус круглого основания, r — внутренний радиус, а h — высота цилиндра.
Если вы ищете формулу площади поверхности цилиндра, то вот она: A = 2πr 2 + 2πrh , где r и h — радиус и высота цилиндра соответственно. Единицами площади поверхности будут квадратные единицы.
Шаги для расчета объема цилиндра Следуя приведенным ниже методам, вы можете найти объем цилиндра.
Шаг 1: Определите тип цилиндра, данный вам в вопросе или в реальной жизни.
Шаг 2: Когда у вас есть тип цилиндра, вам нужно выяснить формулу, по которой можно найти объем цилиндра.
Шаг 3: Теперь у вас есть и формула. Проверьте, какие размеры вам нужны, чтобы найти объем. Убедитесь, что все размеры имеют одинаковые единицы измерения.
Шаг 4: Разместите их на своих местах и рассчитайте объем.
Шаг 5: Сохраните единицы измерения после расчетного значения как «кубические единицы». Используйте соответствующую единицу измерения, такую как метр, сантиметр или любую другую, вместо слова единица измерения.
Примеры для нахождения объема цилиндра
Пример 1. Цилиндр имеет радиус 50 см и высоту 100 см. Как найти объем цилиндра?
Решение: Мы знаем, что объем цилиндра находится по формуле – π r 2 h, где r — радиус цилиндра, а h — высота.
Таким образом, подставив значения, получим
Пример 2: Как найти объем цилиндра, у которого один из радиусов равен 40 см, а другой — 60 см? Цилиндр имеет высоту 200 см.
Решение: Из приведенных данных видно, что цилиндр эллиптический, так как радиусы разные. Чтобы найти объем эллиптического цилиндра, используется формула V = π abh, где a и b — радиусы, а h — высота.
Следовательно, объем цилиндра = В = π abh
= π x 40 x 60 x 200 = 1507200 см 3 .
Пример 3: Как найти объем полого цилиндра изнутри и имеет внешний и внутренний радиусы единиц 6 и 8 соответственно? Высота этого полого цилиндра составляет 15 единиц.
Решение: Мы знаем, что формула объема полого цилиндра имеет вид V = π (R 2 – r 2 ) ч .
Следовательно, ставя значения, получаем,
V = π (R 2 – r 2 ) ч
= π (8 2 – 6 2 ) 15 = 1318,8 единиц 2 .
Пример 4: Однажды Алекс задался вопросом: «Как мне найти объем цилиндра, высота которого равна 6 дюймам, а радиус — 3 дюймам». Можете ли вы помочь ей найти объем этого цилиндра?
Ответ: Да, можно! Вы знаете формулу для нахождения объема цилиндра: V = π r 2 h.
Таким образом, подставив значения, вы получите V = π r 2 ч
= π x 3 2 x 6 = 169,56 в 3 .
Вы можете сказать Алексу, что объем цилиндра равен 169,56 в 3 .
Часто задаваемые вопросы – Часто задаваемые вопросы- Какова площадь криволинейной поверхности цилиндра?
Ответ) Площадь криволинейной поверхности цилиндра = 2πrh
2. Каков объем цилиндра?
Ответ) Объем цилиндра – это количество свободного места в нем. Его можно получить, умножив площадь основания на высоту. Объем цилиндра с радиусом основания «r» и высотой «h» равен V = πr2h.
3. Каков объем полого цилиндра?
Ответ) Измеряем два радиуса объема полого цилиндра, один для внутренней окружности, а другой для внешней окружности, образованной основанием полого цилиндра, и если «R» — внешний радиус, а «r» — внутренний радиус а «h» — высота, то объем полого цилиндра равен V = πh (R2 — r2).
