Как определить среднюю скорость: Как узнать среднюю скорость? — ответ на Uchi.ru

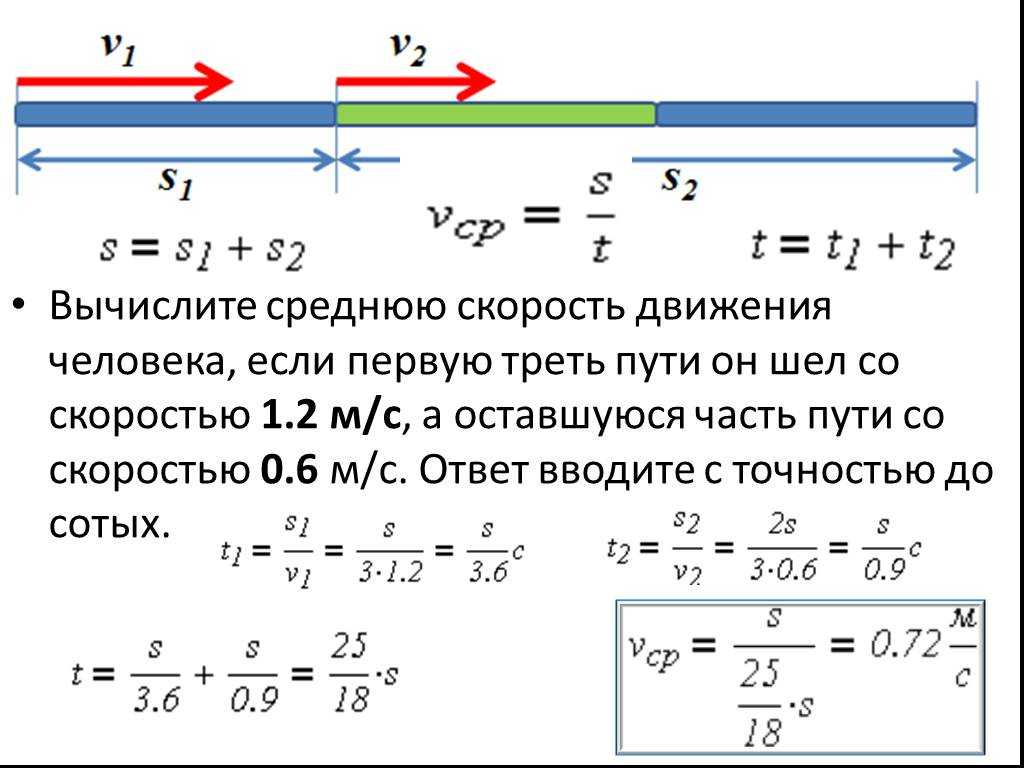
Неравномерное движение, мгновенная и средняя путевая скорость, перемещение. Графическое определение. Тест, упражнения

Физика->Кинематика->неравномерное движение->

Тестирование онлайн

• Неравномерное движение. Основные понятия

• Средняя скорость движения (средний уровень)

Виды неравномерного движения

Неравномерным считается движение с изменяющейся скоростью. Скорость может изменяться по направлению. Можно заключить, что любое движение НЕ по прямой траектории является неравномерным. Например, движение тела по окружности, движение тела брошенного вдаль и др.

Скорость может изменяться по численному значению. Такое движение тоже будет неравномерным. Особенный случай такого движения — равноускоренное движение.

Иногда встречается неравномерное движение, которое состоит из чередования различного вида движений, например, сначала автобус разгоняется (движение равноускоренное), потом какое-то время движется равномерно, а потом останавливается.

Мгновенная скорость

Охарактеризовать неравномерное движение можно лишь скоростью. Но скорость всегда изменяется! Поэтому можно говорить лишь о скорости в данное мгновение времени. Путешествуя на машине спидометр ежесекундно демонстрирует вам мгновенную скорость движения. Но время при этом надо уменьшить не до секунды, а рассматривать гораздо меньший промежуток времени!

Средняя скорость

Что же такое средняя скорость? Неверно думать, что необходимо сложить все мгновенные скорости и разделить на их количество. Это самое распространенное заблуждение о средней скорости! Средняя скорость — это весь путь разделить на затраченное время. И никакими другими способами она не определяется. Если рассмотреть движение автомобиля, можно оценить его средние скорости на первой половине пути, на второй, на всем пути. Средние скорости могут быть одинаковыми, а могут быть различными на этих участках.

У средних величин рисуют сверху горизонтальную черту.

Средняя скорость перемещения.

Средняя путевая скорость

Если движение тела не является прямолинейным, то пройденный телом путь будет больше, чем его перемещение. В этом случае средняя скорость перемещения отличается от средней путевой скорости. Путевая скорость — скаляр.

Главное запомнить

1) Определение и виды неравномерного движения;
2) Различие средней и мгновенной скоростей;
3) Правило нахождения средней скорости движения

Упражнения

Во время езды на автомобиле через каждую минуту снимались показания спидометра. Можно ли по этим данным определить среднюю скорость движения автомобиля?

Какую скорость переменного движения показывает спидометр автомобиля?

В каком случае мгновенная и средняя скорости равны между собой? Почему?

Скорость движения молотка при ударе равна 8м/с. Какая это скорость: средняя или мгновенная?

Поезд прошел путь между городами со скоростью 50км/ч. Какая это скорость: средняя или мгновенная?

*Два шарика начали одновременно и с одинаковой скоростью двигаться по поверхностям, имеющим форму, изображенную на рисунке. Как будут отличаться скорости и время движения шариков к моменту их прибытия в точку В? Силу трения не учитывать.

Неравномерное прямолинейное движение, средняя скорость, определение средней скорости движения тела

1. График скорости при неравномерном прямолинейном движении
2. Как найти путь и перемещение по графику скорости?
3. Средняя скорость и средняя путевая скорость
4. Задачи
5. Лабораторная работа №3. Определение средней скорости движения тела

п.1. График скорости при неравномерном прямолинейном движении

Прямолинейное и равномерное движение возможно лишь на участке пути.
Любое тело со временем меняет свою скорость, как по величине, так и по направлению.

Движение с переменной скоростью называют неравномерным.

Для описания неравномерного движения его можно разбить на участки, на которых скорость постоянна, и свести задачу к уже известному нам равномерному прямолинейному движению.

Например, пусть велосипедист добрался из города A в город B за 1 час. Первые полчаса он ехал со скоростью 9 км/ч, а потом проколол шину, и вторые полчаса шел пешком со скоростью 3 км/ч.
Направим ось ОХ также от A к B и получим значения проекций скоростей: $$ v_{x1}=9\ \text{км/ч},\ \ v_{x2}=3\ \text{км/ч} $$ Построим график скорости для этого случая:

Графиком скорости \(v_x=v_x(t)\) при неравномерном прямолинейном движении, которое можно разбить на участки с постоянной скоростью, является ломаная линия.

п.2. Как найти путь и перемещение по графику скорости?

Мы уже знаем, что путь равен площади прямоугольника, который образуется между отрезком графика скорости и отрезком \(\triangle t\) на оси \(t\) (см. §8 данного справочника).

В таком случае, путь велосипедиста в нашем примере:
\begin{gather*} s=v_{x1}\cdot \triangle t_1+v_{x2}\cdot \triangle t_2\\ s=9\cdot 0,5+3\cdot 0,5=4,5+1,5=6\ \text{(км)} \end{gather*} Сначала велосипедист проехал 4,5 км, а затем прошел 1,5 км.
Общий путь велосипедиста равен 6 км. Расстояние между городами 6 км.

Если принять город A за начало отсчета с \(x_0=0\), то координата велосипедиста в конце пути: $$ x_{к}=x_0+s=0+6=6\ \text{(км)} $$ Перемещение по оси ОХ: \(\triangle x=x_{к}-x_0=6\ \text{(км)}\).

Теперь рассмотрим другую ситуацию. Пусть велосипедист выехал из A в B и двигался со скоростью 9 км/ч в течение получаса. Но, после того как проколол шину, он развернулся и пошел пешком назад в A. Где будет находиться велосипедист через полчаса после разворота?
Снова направим ось ОХ от A к B и получим значения проекций скоростей: $$ v_{x1}=9\ \text{км/ч},\ \ v_{x2}=-3\ \text{км/ч} $$ Построим график скорости для этого случая:

Путь велосипедиста по-прежнему будет равен сумме площадей прямоугольников, которые образует ломаная \(v_x(t)\) с осью \(t\): \begin{gather*} x=v_{x1}\cdot \triangle t_1+|v_{x2}|\cdot\triangle t_2\\ s=9\cdot 0,5+3\cdot 0,5=4,5+1,5=6\ \text{(км)} \end{gather*}
Если мы учтем знак \(v_{x2}\) и уберем модуль, то получим величину перемещения по оси ОХ: \begin{gather*} \triangle x=v_{x1}\cdot \triangle t_1+v_{x2}\cdot \triangle t_2\\ \triangle x=9\cdot 0,5-3\cdot 0,5=4,5-1,5=3\ \text{(км)} \end{gather*} Сначала велосипедист проехал 4,5 км, а затем прошел 1,5 км в обратном направлении.
Конечная координата: $$ x_{к}=x_0+\triangle x=0+3=3\ \text{(км)} $$
Ответ на вопрос задачи найден. Через полчаса после разворота велосипедист будет находиться в точке D в 3 км от города A.

Пусть неравномерное прямолинейное движение разбито на \(n\) участков с постоянными скоростями. Каждому такому участку соответствует промежуток времени \(\triangle t_i\) и постоянная скорость \(v_{xi},\ i=\overline{1,n}\).
Тогда:
Весь пройденный путь равен сумме площадей прямоугольников на графике скорости: $$ s=|v_{x1}|\cdot\triangle t_1+|v_{x2}|\cdot\triangle t_2+…+|v_{xn}|\cdot\triangle t_n $$ Величина перемещения по оси ОХ равна сумме площадей прямоугольников с учетом знака: $$ \triangle x=v_{x1}\cdot\triangle t_1+v_{x2}\cdot\triangle t_2+…+v_{xn}\cdot\triangle t_n $$ Конечная координата равна: \(x_{к}=x_0+\triangle x\).

п.3. Средняя скорость и средняя путевая скорость

Средняя скорость на нескольких участках движения равна отношению общего перемещения к общему времени, затраченному на это перемещение: $$ \overrightarrow{v_{cp}}=\frac{\overrightarrow{r_1}+\overrightarrow{r_2}+. ..+\overrightarrow{r_n}}{t_1+t_2+…+t_n}=\frac{\overrightarrow{r}}{t} $$

Средняя путевая скорость на нескольких участках движения равна отношению общего пути к общему времени, затраченному на этот путь: $$ v_{cp.п}=\frac{s_1+s_2+…+s_n}{t_1+t_2+…+t_n}=\frac{s}{t} $$

Если тело все время движется в одном направлении, величина средней скорости равна средней путевой скорости, т.к. на каждом участке путь совпадает с модулем перемещения.
Если тело меняет направление движения, величина средней скорости меньше средней путевой скорости.

В нашем примере с велосипедистом, который все время двигался в одну сторону и дошел до города B, получаем: \begin{gather*} |\overrightarrow{v_{cp}}|=\frac{|\overrightarrow{r}|}{t}=\frac{\triangle x}{t}=\frac 61=6\ \text{(км/ч)}\\ v_{cp.п}=\frac st=\frac 61=6\ \text{(км/ч)} \end{gather*} Величина средней скорости равна средней путевой скорости.

А вот для случая, когда велосипедист развернулся и пошел обратно: \begin{gather*} |\overrightarrow{v_{cp}}|=\frac{|\overrightarrow{r}|}{t}=\frac{\triangle x}{t}=\frac 31=3\ \text{(км/ч)}\\ v_{cp. п}=\frac st=\frac 61=6\ \text{(км/ч)} \end{gather*} Величина средней скорости меньше средней путевой скорости.

п.4. Задачи

Задача 1. По графику скоростей найдите среднюю скорость и среднюю путевую скорость движения.

a)

Все движение можно разделить на три участка с постоянной скоростью:
\begin{gather*} \triangle t_1=3-0=3\ c,\ \ v_{x1}=5\ \text{м/с}\\ \triangle t_2=5-3=2\ c,\ \ v_{x2}=1\ \text{м/с}\\ \triangle t_3=7-5=2\ c,\ \ v_{x3}=2\ \text{м/с}\\ \end{gather*} Общий путь: \begin{gather*} s=|v_{x1}|\cdot \triangle t_1+|v_{x2}|\cdot \triangle t_2+|v_{x3}|\cdot \triangle t_3\\ s=5\cdot 3+1\cdot 2+2\cdot 2=21\ \text{(м)} \end{gather*} Все проекции скоростей положительны, тело двигалось в одном направлении, общее перемещение равно общему пути: \(\triangle x=s=21\) (м)
Общее время: \(t=\triangle t_1+\triangle t_2+\triangle t_3=3+2+2=7\) (с)

Величина средней скорости равна средней путевой скорости: $$ |\overrightarrow{v_{cp}}|=v_{cp.п}=\frac st=\frac{21}{7}=3\ \text{(м/с)} $$ Ответ: \(|\overrightarrow{v_{cp}}|=v_{cp. п}=3\ \text{(м/с)}\)

б)

Все движение можно разделить на три участка с постоянной скоростью:
\begin{gather*} \triangle t_1=3-0=3\ c,\ \ v_{x1}=5\ \text{м/с}\\ \triangle t_2=5-3=2\ c,\ \ v_{x2}=-2\ \text{м/с}\\ \triangle t_3=7-5=2\ c,\ \ v_{x3}=1\ \text{м/с}\\ \end{gather*} Общий путь: \begin{gather*} s=|v_{x1}|\cdot \triangle t_1+|v_{x2}|\cdot \triangle t_2+|v_{x3}|\cdot \triangle t_3\\ s=5\cdot 3+2\cdot 2+1\cdot 2=21\ \text{(м)} \end{gather*} Проекции скоростей имеют разные знаки, тело двигалось вперед и назад.
Общее перемещение будет меньше общего пути: \begin{gather*} \triangle x=v_{x1}\cdot \triangle t_1+v_{x2}\cdot \triangle t_2+v_{x3}\cdot \triangle t_3\\ \triangle x=5\cdot 3-2\cdot 2+1\cdot 2=13\ \text{(м)} \end{gather*} Общее время: \(t=\triangle t_1+\triangle t_2+\triangle t_3=3+2+2=7\) (c)

Величина средней скорости: $$ |\overrightarrow{v_{cp}}|=\frac{\triangle x}{t}=\frac{13}{7}\approx 1,86\ \text{(м/с)} $$ Средняя путевая скорость: $$ v_{cp.п}=\frac st=\frac{21}{7}=3\ \text{(м/с)} $$ Ответ: \(|\overrightarrow{v_{cp}}|\approx 1,86\ \text{(м/с)};\ \ v_{cp. п}=3\ \text{(м/с)}\)

Задача 2. Мотоциклист проехал расстояние между двумя пунктами со скоростью 40 км/ч. Потом увеличил скорость до 80 км/ч и проехал расстояние в два раза меньше. Найдите среднюю скорость мотоциклиста за все время движения.

Мотоциклист двигался все время в одном направлении, величина средней скорости равна средней путевой скорости: \(v_{cp}=\frac st\), где \(s\) — весь путь, \(t\) — все время.

Заполним таблицу:

	Скорость, км/ч	Время, ч	Расстояние, км
1й участок	40	\(\frac{2d}{40}=\frac{d}{20}\)	\(2d\)
2й участок	80	\(\frac{d}{80}\)	\(d\)
Сумма	—	\(t=\frac{d}{20}+\frac{d}{80}\)	\(s=2d+d=3d\)

Упростим сумму дробей: $$ t=\frac{d}{20}+\frac{d}{80}=\frac{4d+d}{80}=\frac{5d}{80}=\frac{d}{16} $$ Получаем: $$ v_{cp}=\frac st=\frac{3d}{d/16}=3\cdot 16=48\ \text{(км/ч)} $$
Ответ: 48 км/ч

Задача 3.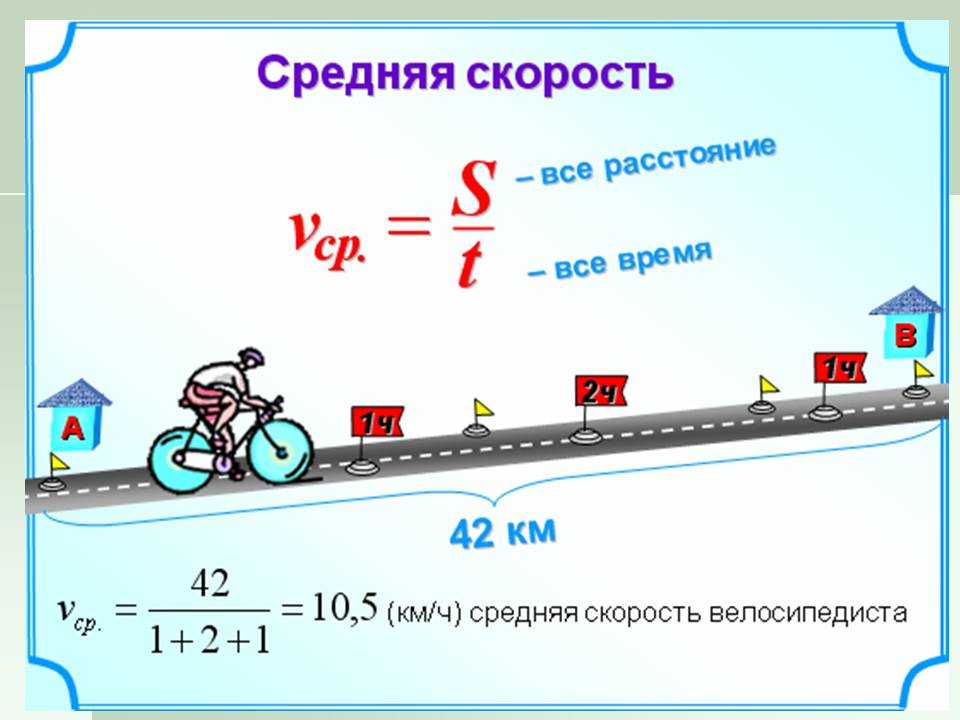 Автомобиль проехал первую половину пути по шоссе со скоростью 90 км/ч, а вторую половину – по грунтовой дороге со скоростью 30 км/ч. Найдите среднюю скорость автомобиля.

Величина средней скорости равна средней путевой скорости:

\(v_{cp}=\frac st\), где \(s\) — весь путь, \(t\) — все время.
Заполним таблицу:

	Скорость, км/ч	Время, ч	Расстояние, км
1й участок	90	\(\frac{s}{2\cdot 90}=\frac{s}{180}\)	\(\frac s2\)
2й участок	30	\(\frac{s}{2\cdot 30}=\frac{s}{60}\)	\(\frac s2\)
Сумма	—	\(t=\frac{s}{180}+\frac{s}{60}\)	\(s\)

Упростим сумму дробей: $$ t=\frac{s}{180}+\frac{s}{60}=\frac{s+3s}{180}=\frac{4s}{180}=\frac{s}{45} $$ Получаем: $$ v_{cp}=\frac st=\frac{s}{s/45}=45\ \text{(км/ч)} $$
Ответ: 45 км/ч

Задача 4*. Туристы прошли по маршруту со средней скоростью 32 км/ч. Маршрут был разделен на три участка, первый участок преодолевался пешком, второй – на автобусе, третий – на катере. Найдите скорость на каждом участке, если длины этих участков относятся как 1:4:45, а соответствующие интервалы времени как 4:1:20.

Величина средней скорости равна средней путевой скорости:
\(v_{cp}=\frac st\), где \(s\) — весь путь, \(t\) — все время.
Заполним таблицу:

	Скорость, км/ч	Время, ч	Расстояние, км
1й участок	\(\frac{d}{4t}\)	\(4t\)	\(d\)
2й участок	\(\frac{4d}{t}\)	\(t\)	\(4d\)
3й участок	\(\frac{45d}{20t}\)	\(20t\)	\(45d\)
Сумма	—	\(25t\)	\(50d\)

По условию средняя скорость: $$ v_{cp}=\frac st=\frac{50d}{25t}=2\cdot \frac dt=32\Rightarrow \frac dt=16 $$ Получаем: \begin{gather*} v_1=\frac{d}{4t}=\frac{16}{4}=4\ \text{(км/ч)}\\ v_2=\frac{4d}{t}=4\cdot 16=64\ \text{(км/ч)}\\ v_3=\frac{9d}{4t}=\frac{9}{4}\cdot 16=36\ \text{(км/ч)} \end{gather*}

Ответ: 4 км/ч, 64 км/ч и 36 км/ч

Задача 5*. Первую половину маршрута турист проехал на попутном автомобиле в 10 раз быстрее по сравнению с ходьбой пешком, а вторую половину – на попутном возу в 2 раза медленней. Сэкономил ли турист время на всем маршруте по сравнению с ходьбой пешком?

Пусть \(v\) — скорость туриста при ходьбе пешком.
Найдем среднюю путевую скорость \(v_{cp}\) и сравним ее со скоростью \(v\).
Если \(v_{cp}\gt v\), то турист выиграл время.
Заполним таблицу:

	Скорость, км/ч	Время, ч	Расстояние, км
1й участок	\(10v\)	\(\frac{s}{2\cdot 10v}=\frac{s}{20v}\)	\(\frac s2\)
2й участок	\(\frac{v}{2}\)	\(\frac{s}{2\cdot v/2}=\frac sv\)	\(\frac s2\)
Сумма	—	\(t=\frac{s}{20v}+\frac sv\)	\(s\)

Упростим сумму дробей: $$ t=\frac{s}{20v}+\frac sv=\frac sv\left(\frac{1}{20}+1\right)=\frac{21}{20}\cdot \frac sv $$ Средняя скорость: $$ v_{cp}=\frac{s}{\frac{21}{20}\cdot\frac sv}=\frac{20}{21}v\gt v $$Средняя скорость поездки оказалась меньше пешей скорости туриста.
Значит, он не выиграл по времени.
Ответ: нет

п.5. Лабораторная работа №3. Определение средней скорости движения тела

Цель работы
Научиться определять среднюю скорость движения тела по данным измерений на разных участках. Научиться вычислять абсолютные и относительные погрешности при подстановке данных измерений в формулы.

Теоретические сведения
В лабораторной работе изучается движение тела (шарика) по двум участкам (желобам) с различной скоростью.

Величина средней скорости при движении на двух участках определяется как средняя путевая скорость: $$ v_{cp}=\frac{s_1+s_2}{t_1+t_2} $$ где \(s_1\) и \(s_2\) – длина первого и второго участка; \(t_1\) и \(t_2\) — время движения по каждому из участков.

Длина участков измеряется с помощью мерной ленты с ценой деления \(\triangle=1\) см,
инструментальная погрешность равна: \(d=\frac{\triangle}{2}=0,5\) см
Абсолютная погрешность измерений при работе с мерной лентой равна инструментальной погрешности, поэтому: \(\triangle s_1=\triangle s_2=d=0,5\) см
Погрешность суммы двух длин: \(\triangle(s_1+s_2)= \triangle s_1+\triangle s_2=2d=1\) см

Измерение времени на каждом участке проводится в сериях их 5 измерений по методике, описанной в Лабораторной работе №2 (см. §4 данного справочника).
Погрешность суммы двух измерений: \(\triangle(t_1+t_2)=\triangle t_1+\triangle t_2\)

Относительная погрешность частного равна сумме относительных погрешностей делимого и делителя: $$ \delta_{v_{cp}}=\delta_{s_1+s_2}+\delta_{t_1+t_2} $$ Абсолютная погрешность определения средней скорости: $$ \triangle v_{cp}=v_{cp}\cdot \delta_{v_{cp}} $$

Приборы и материалы
Два желоба (не менее 1 м каждый), шарик, мерная лента, секундомер.

Ход работы
1. Ознакомьтесь с теоретической частью работы, выпишите необходимые формулы.
2. Соберите установку, как показано на рисунке. Установите один желоб под углом, другой – горизонтально, закрепите, поставьте в конце горизонтального участка упор. Подберите длину желобов и наклон так, чтобы движение по каждому участку было не менее 1 с.

3. Измерьте фактическую длину каждого участка движения в готовой установке с помощью мерной ленты.
4. Найдите относительную погрешность суммы двух длин \(\delta_{s_1+s_2}=\frac{\triangle(s_1+s_2)}{s_1+s_2}\)

5.  Проведите серии по 5 экспериментов для определения \(t_1\) и \(t_2\) с помощью секундомера.
6. Найдите \(\triangle t_1,\ \triangle t_2, \ \triangle(t_1+t_2),\ \delta_{t_1+t_2}\)
7. По результатам измерений и вычислений найдите \(v_{cp},\ \delta_{v_{cp}}\) и \(\triangle v_{cp}\).
8. Сделайте выводы о проделанной работе.

Результаты измерений и вычислений

1) Измерение длин
Цена деления мерной ленты \(\triangle =1\) см
Инструментальная погрешность мерной ленты \(d=\frac{\triangle}{2}=0,5\) см
Результаты измерений:
\(s_1=112\) cм
\(s_2=208\) cм
Сумма длин участков: \(s_1+s_2=112+208=320\) (см)
Абсолютная погрешность суммы: \(\triangle (s_1+s_2)=\triangle s_1+\triangle s_2=2d=1\) см
Относительная погрешность суммы: $$ \delta_{s_1+s_2}=\frac{\triangle (s_1+s_2)}{s_1+s_2}=\frac{1}{320}=0,3125% $$

2) Измерение времени
Цена деления секундомера \(\triangle =0,2\) с
Инструментальная погрешность секундомера \(d=\frac{\triangle}{2}=0,1\) с

Время движения по наклонному желобу

№ опыта	1	2	3	4	5	Сумма
\(t_1\) c	1,5	1,6	1,5	1,4	1,4	7,4
\(\triangle\) c	0,02	0,12	0,02	0,08	0,08	0,32

Найдем среднее время спуска с наклонного желоба: $$ t_1=\frac{1,5+1,6+1,5+1,4+1,4}{5}=\frac{7,4}{5}=1,48\ (c) $$ Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от \(t_1\): $$ \triangle_1=|1,5-1,48|=0,02;\ \triangle_2=|1,6-1,48|=1,02\ \text{и т.д.} $$ Среднее абсолютное отклонение: $$ \triangle_{cp}=\frac{0,02+0,12+0,02+0,08+0,08}{5}=\frac{0,32}{5}=0,064\ \text{c} $$ Среднее абсолютное отклонение меньше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ \triangle t_1=max\left\{d;\triangle_{cp}\right\}=max\left\{0,1;0,064\right\}=0,1\ \text{c} $$ Округляем полученное значение времени до десятых. \begin{gather*} t_1=(1,5\pm 0,1)\ \text{c}\\ \delta_{t_1}=\frac{0,1}{1,5}=\frac{1}{15}\approx 6,7\text{%} \end{gather*} Время движения по горизонтальному желобу

№ опыта	1	2	3	4	5	Сумма
\(t_2\) c	2,3	2,4	2,2	2,2	2,4	11,5
\(\triangle\) c	0	0,1	0,1	0,1	0,1	0,4

Найдем среднее время движения по горизонтали: $$ t_2=\frac{2,3+2,4+2,2+2,2+2,4}{5}=\frac{11,5}{5}=2,3\ (c) $$ Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от \(t_2\): $$ \triangle_1=|2,3-2,3|=0;\ \triangle_2=|2,4-2,3|=0,1\ \text{и т.д.} $$ Среднее абсолютное отклонение: $$ \triangle_{cp}=\frac{0+0,1+0,1+0,1+0,1}{5}=\frac{0,4}{5}=0,08\ \text{c} $$ Среднее абсолютное отклонение меньше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ \triangle t_2=max\left\{d;\triangle_{cp}\right\}=max\left\{0,1;0,08\right\}=0,1\ \text{c} $$ Получаем: \begin{gather*} t_2=(2,3\pm 0,1)\ \text{c}\\ \delta_{t_2}=\frac{0,1}{2,3}=\frac{1}{23}\approx 4,4\text{%} \end{gather*}

3) Расчет погрешности суммы интервалов времени
Сумма интервалов времени: $$ t_1+t_2=1,5+2,3=3,8\ \text{(c)} $$ Абсолютная погрешность суммы: $$ \triangle(t_1+t_2)=\triangle t_1+\triangle t_2=0,1+0,1=0,2\ \text{(c)} $$ Относительная погрешность суммы: $$ \delta_{t_1+t_2}=\frac{\triangle (t_1+t_2)}{t_1+t_2}=\frac{0,2}{3,8}=\frac{1}{19}\approx 5,3\text{%} $$

4) Расчет средней скорости $$ v_{cp}=\frac{s_1+s_2}{t_1+t_2}=\frac{320}{3,8}\approx 84,2\ \left(\frac{\text{см}}{\text{c}}\right) $$ Относительная ошибка частного: $$ \delta_{v_{cp}}=\delta_{s_1+s_2}+\delta_{t_1+t_2}=\frac{1}{320}+\frac{1}{19}\approx 0,003125+0,0526\approx 0,0557\approx 0,056=5,6\text{%} $$ (оставляем две значащие цифры).
Абсолютная ошибка: $$ v_{cp}=v_{cp}\cdot\delta_{v_{cp}}=84,2\cdot 0,056\approx 4,7\ \left(\frac{\text{см}}{\text{c}}\right) $$ Получаем: \begin{gather*} v_{cp}=(84,2\pm 4,7)\ \text{см/с}\\ \delta_{v_{cp}}=5,6\text{%} \end{gather*}

Выводы
На основании проделанной работы можно сделать следующие выводы.

Измерения длин проводились с помощью мерной ленты. Ошибка измерений равна инструментальной ошибке 0,5 см.
Измерения времени проводились с помощью секундомера. По результатам серий экспериментов ошибка была принята равной инструментальной 0,1 с.
Получена величина средней скорости: \begin{gather*} v_{cp}=(84,2\pm 4,7)\ \text{см/с}\\ \delta_{v_{cp}}=5,6\text{%} \end{gather*}

Рейтинг пользователей

за неделю

• за неделю
• один месяц
• три месяца

Помогай другим

Отвечай на вопросы и получай ценные призы каждую неделю

См. подробности

Различные методологии и задачи —

Средняя скорость является одной из основных функций, определяемых в движении. В этой статье мы узнаем, как найти среднюю скорость.

Основным методом определения средней скорости является деление суммы изменений положения объекта на общее время, затраченное этим объектом на завершение движения. Поскольку это векторная физическая величина, направление объекта также имеет важное значение при расчете средней скорости.

Далее мы изучим другие методы, как найти среднюю скорость, так как это основная тема поста.

Какова формула для средней скорости

Основная формула, используемая для расчета V _avg , включает в себя как перемещение во времени.

Общая используемая формула выглядит следующим образом:

Она используется при решении основных задач, связанных со средней скоростью.

V = S _f – S _I / T ₂ — T ₁

V = ΔS / ΔT

, где,

ΔS = Displaymed

. давайте посмотрим, как найти среднюю скорость с помощью расстояния и времени.
Как найти среднюю скорость по расстоянию и времени

Расстояние и время являются основными условиями, без которых невозможно найти среднюю скорость.

Прежде всего, мы должны рассчитать общую длину пути, по которому прошел объект, затем мы должны проверить продолжительность времени, затраченного на достижение пункта назначения. В дальнейшем, чтобы найти среднюю скорость этого движения, нам нужно использовать ранее вычисленные расстояние и время с помощью формулы.

Теперь давайте продолжим изучение, чтобы узнать больше о подходах к нахождению средней скорости.

Как найти среднюю скорость на интервале

Увидев важность расстояния и времени при расчете средней скорости. Теперь давайте, как вычислить его на интервале.

• Если вы вычисляете среднюю скорость на графике, то вы должны рассмотреть любые два интервала времени и расстояния, а затем узнать значения расстояния и времени и подставить их в формулу средней скорости.

                                                                V = S _f – S _i / t ₂ – t ₁

• В другом методе, если вы собираетесь использовать формулу напрямую, то вы должны знать начальную и конечную точки, чтобы она была легко для вас вычислить V _avg , вы даже можете рассмотреть некоторую часть интервала, чтобы найти V _avg Это происходит путем деления общего расстояния на общее время.

                                   V = общее расстояние/общее время     или

V = (V _f + V _i ) / 2

Теперь давайте рассмотрим метод расчета V _avg между двумя точками.

Средняя скорость между двумя точками

Среднюю скорость между двумя точками можно найти по простой формуле.

В общем случае мы знаем, что Vср тела равна среднему арифметическому начальной и конечной точек, приведенному ниже

Vср = [ Начальная скорость (i) + Конечная скорость (v)] / 2

Пришло время узнать, как найти V _avg на графике.

Как найти среднюю скорость на графике

Мы можем найти среднюю скорость с помощью графика перемещение-время.

• Здесь смещение будет по оси y, а время по оси x.
• Нанесите точки на оси и соедините их, чтобы создать область на графике.
• Затем найдите общую площадь на графике, взяв два интервала времени и расстояния.
• Измерение его вдоль линии графика и может быть рассчитана с использованием формулы

V _AVG = (V _I +V _F )/2.

Переменные, взятые на графике, имеют заметный характер, все факторы, такие как изменение положения (между начальной и конечной точками), характер графика, т. е. линейный он или нет.

При таком подходе мы можем рассчитать среднюю скорость по графику.

Как найти среднюю скорость на линейном графике

Линейный график иногда называют прямолинейным графиком.

Если мы хотим узнать среднюю скорость на линейном графике, то мы должны взять начальную и конечную скорости и разделить их на число 2. Это похоже на среднее значение, которое мы используем в математике для решения некоторых задач.

Теперь давайте узнаем условие для расчета средней скорости в нелинейном графике.

Как найти среднюю скорость на нелинейном графике

Нелинейный график также можно рассматривать как криволинейный график.

В нелинейном графике для расчета V _avg мы можем рассмотреть площадь под графиком, которая состоит из смещения (интегрировать ее), а затем разделить ее на время.

Таким образом, мы можем вычислить V _avg на нелинейном графике.

Средняя скорость Пример задачи

Приведенная ниже является одной из основных задач, которые могут быть решены с использованием подходов для расчета средней скорости.

Пример 1

Предположим, что человек едет на своей машине в какой-то пункт назначения, но в течение первых 15 с положение автомобиля меняется с x ₁  = 80 м на x ₂ = 100 м. Какова теперь средняя скорость автомобиля?

Решение: Начальная позиция равна x ₁ = 80M

Аналогично, конечная позиция составляет x ₂ = 100m

Изменение смещения автомобиля рассчитывается следующим образом:

Δx = X ₂ — x. ₁ = 100 м — 80 м = 20 м

ΔT = 15 с

Из формулы, которую мы имеем,

V = Δx / ΔT

V = 20/15

v= 1,33 м/с

Следовательно, средняя скорость автомобиля равна 1,33 м/с.

Из вышеприведенной задачи мы познакомились с еще одним подходом к нахождению средней скорости

Часто задаваемые вопросы | Часто задаваемые вопросы
Что такое средняя скорость?

Средняя скорость — важное явление в физике.

Это векторная величина, определяемая как ∆x, деленная на ∆t. Где ∆x означает перемещение, а ∆t говорит об общем времени, затраченном телом на совершение движения. Иногда это может быть положительным или отрицательным, все зависит от направления смещения. Обозначается с использованием единицы СИ м/с.

Чем средняя скорость отличается от других скоростей?

Обычно в физике встречаются два типа скоростей.

Два основных типа скоростей — это средние и мгновенные скорости. Как следует из их названия, среднее значение означает общую сумму скоростей каждого интервала, рассчитанную за общее время. Напротив, мгновенная скорость будет определять скорость в определенный период движения.

Чем средняя скорость отличается от мгновенной скорости в определенный интервал времени?

Если мы возьмем конкретный интервал времени, то будет разница в измерении средней и мгновенной скорости.

Основное отличие заключается в том, что для определенного периода интервала мгновенная скорость измеряется с учетом смещения и времени в определенной точке (s,t), а средняя скорость считается общим изменением положения со временем в определенное время. интервал.

Остается ли средняя скорость неизменной при движении?

Скорость не остается неизменной в конкретном движении, она продолжает меняться.

Мы изучили, что скорость является переменной величиной, зависящей от многих факторов. Он не остается постоянным, а продолжает изменять свое значение с помощью перемещения и времени этого объекта. Отсюда мы можем сказать, что средняя скорость не остается неизменной в движении.

Каковы два основных способа расчета средней скорости?

Существует множество приложений, с помощью которых мы можем легко измерить среднюю скорость.

Первый метод заключается в нахождении средней скорости путем взятия первой и конечной точек движения, вычитания их и последующего деления всего члена на 2.

Второй метод заключается в использовании формулы, известной как средняя скорость уравнение.

Уравнение средней скорости = V = (V _f + V _i )/2

• В = средняя скорость.
• V _f = конечная скорость.
• V _i = начальная скорость

Это простое уравнение для измерения средней скорости.

Как найти перемещение со средней скоростью?

Есть много способов найти перемещение в кинематике.

Один из них — найти перемещение с помощью формулы средней скорости, состоящей из изменения положения/перемещения. Поменяв местами члены формулы, мы можем использовать ее для расчета смещения.

Почему средняя скорость отличается от средней скорости?

Оба термина означают совершенно разные значения, когда мы изучаем их в физике.

Здесь мы знаем, что скорость является скаляром, а скорость является вектором, тогда основное различие заключается в физических величинах, которые измеряют значимость того, как их можно измерить.

Разница между средней скоростью и средней скоростью

Основная разница между этими двумя величинами приведена ниже,

• Средняя скорость говорит только о положении тела в движении, здесь надо заметить, что величина будет разной для каждого положения и нахождение скорости на любом временном интервале на длине пути делается с помощью средней скорость.
• Средняя скорость говорит о сохранении скорости на всем пути движения. Это сумма скоростей, рассчитанная с учетом общей длины пути и времени, и, поскольку это скаляр, мы не можем определить направление пути.

Как рассчитать среднюю скорость?

Академический

04.03.2023

В школе введено понятие средней скорости из стандарта 8 ^th или 9 ^th . Помимо этого, его также задают в количественных способностях или числовом разделе различных конкурсных экзаменов, таких как IBPS PO, IBPS Clerk, NDA, SSC CGL и т. Д. Однако, чтобы понять формулу средней скорости, студенты должны понимать понятие скорости и почему она не работает как обычная средняя.

Средняя скорость является важным компонентом в определении того, сколько времени потребуется, чтобы закончить путешествие. Средняя скорость — это метод, который вычисляет скорость движения и расстояние. Тот факт, что скорость меняется на протяжении всего пути, подчеркивает необходимость определения средней скорости. Существуют различные методы определения средней скорости объекта или транспортного средства.

Тем не менее, кажется, что тема достаточно проста для понимания, но почему-то правила ваших обычных средних значений не применяются. Поэтому термин «средний» становится запутанным.

В школьные годы мы выучили следующую формулу для среднего:

Среднее = (Сумма объектов)/(Количество объектов)

Однако средняя скорость не совпадает со средним значением всех скоростей. Итак, как нам это понять? Давайте взглянем.

Определение средней скорости 

В основном это сочетание двух слов и двух идей: «Средняя» и «Скорость». Среднее значение в основном получается из отдельных точек данных, а скорость — это в основном изменение положения.

Если вы можете рассчитать время движения и измерить расстояние, вы можете легко рассчитать среднюю скорость.

Проще говоря, Средняя скорость может быть определена как общее расстояние, пройденное объектом за определенный интервал времени. Это скалярная величина, что означает, что она не имеет направления. Он в основном представлен величиной.

Средней скоростью тела за период времени является его среднее значение. Так как скорость движущегося тела непостоянна и колеблется во времени, то требуется формула для средней скорости. Даже при изменении скорости можно использовать общее время и общее пройденное расстояние. Мы можем получить одно значение для описания полного движения, используя расчет средней скорости.

Знать формулу средней скорости 

Формула средней скорости равна общему расстоянию, пройденному объектом в вопросе, деленному на общее время, затраченное объектом на преодоление расстояния, т. е. общий период времени.

Формула средней скорости:

Если объект покрывает x1,x2,x3,x4……… t1,t2,t3,t4 … .. время соответственно, то:

Давайте разберемся с этим, используя задачу , предположим, что грузовик проезжает S ₁ миль/ч в момент времени t ₁ в пути и S ₂ миль/ч в момент времени t ₂ на обратном пути. Узнать среднюю скорость грузовика на протяжении всей поездки?

В этом случае не добавляйте 2 скорости, даже если время одинаковое. Это НЕ даст вам.

Давайте найдем ответ,

Общая средняя скорость = общее расстояние/общее время

т. е. средняя скорость

Мгновенная скорость:

остановиться, проехать некоторое время, разогнаться, затем притормозить на желтый сигнал светофора и остановиться.

Автомобиль движется с разной скоростью. Автомобиль не движется со скоростью 55 миль в час ни в один момент времени. Мили в час (mph). Это может быть 0 миль в час в один момент, 8 миль в час в следующий, 53 мили в час в следующий, 60 миль в час в следующий и, в конце концов, 5 миль в час, прежде чем вернуться к 0 миль в час.

Вы используете среднюю скорость всех дискретных событий, например, автомобиль проехал 5,5 миль за 6 минут, чтобы упростить измерения и добиться прогресса в физике или математике.

 


В ряде случаев нет необходимости знать формулу мгновенной скорости, v находит предел с изменениями во времени (мгновенный) и приближается к «0»:  

 

В течение временного события мгновенные скорости меняются. Оценить среднюю скорость намного проще и зачастую более информативно, чем вычислить мгновенную скорость.

Формула средней скорости в некоторых особых случаях за время t

₂ . Пройденные длины в периодах времени и рассчитываются как произведение S ₁ х t ₁ и S ₂ х t ₂ соответственно .

Случай 2: Когда ‘n’ различных скоростей, S ₁ , S ₂ , S ₃ ,… S _n ‘n ‘n, поставляются для разных периодов времени , t ₁ , t ₂ , t ₃ ,…t _n , формула средней скорости:

 

0015 1 , d ₂ ,….. d _n  покрываются в разный интервал времени t ₁ , t ₂ … t _n , соответственно:

2 Средняя скорость 

Чтобы определить среднюю скорость, необходимо знать общее расстояние, пройденное объектом, и общее время, затраченное объектом на преодоление пути.

Три части треугольника геометрически выровнены в правильных положениях:

Разделите общее расстояние на прошедшее время, чтобы получить среднюю скорость, с: D x t

Разделите общее расстояние на скорость, чтобы получить пройденное время, t: D x s

Умножьте скорость на продолжительность времени, чтобы получить расстояние, D: s x t

Например: Если вы хотите найти среднюю скорость автомобиля который преодолевает расстояние 82,6 км за 2 часа.

Поместите эти два числа в треугольник и получите 41,3 км в час.

Найти среднюю скорость

Например: Если вы хотите найти среднюю скорость автомобиля, преодолевающего расстояние 82,6 км за 2 часа.

Поместите эти два числа в треугольник и получите 41,3 км в час.

Найти общее расстояние

Чтобы найти общее расстояние, вы должны иметь скорость и время;

D= 41,3 км/ч x 2 часа

                 = 82,6 км

Решенные примеры средней скорости 1 час.

Найдите среднюю скорость автобуса.
• Раджат ехал 1 час со скоростью 50 миль в час и 3 часа со скоростью 60 миль в час, путешествуя из Дели в Гоа. Какова была его средняя скорость на всем пути?

Решение: Расстояние = скорость x время

Итак, расстояние, пройденное за один час = 50 x 1 = 50 миль.

Расстояние, пройденное за следующие 3 часа = 60 x 3 = 180 миль

Общее пройденное расстояние: 50+180 миль = 230 миль миль в час

Практические вопросы по средней скорости

 

1. Первые 4 часа поезд движется со скоростью 80 км/ч, следующие 3 часа — 110 км/ч. Найдите среднюю скорость поезда.
2. Лиса может пройти 0,6 мили за 36 секунд. Узнайте среднюю скорость лисы в милях в секунду, а также найдите скорость в милях в час (умножьте на 3600)

Решите вопросы на среднюю скорость, которые могут быть трудными для школьников, так как эта тема входит не только в предмет математики, но и в физику старших классов.