Как посчитать среднюю скорость автомобиля: Какова средняя скорость автомобиля , если за первые 3ч он проехал 80км , а следующие…

Как найти время, скорость и расстояние

Расстояние

Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.

Расстояние — это длина от одного пункта до другого.

• Например: расстояние от дома до школы 3 км, от Москвы до Петербурга 705 км.

Расстояние обозначается латинской буквой s.

Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).

Формула пути Чтобы найти расстояние, нужно умножить скорость на время движения: s = v × t

Бокс для отличной учёбы от Skysmart

Скачайте бокс, чтобы сделать учёбу проще и интереснее.

Узнайте про лайфхаки и игры, которые увлекут ребёнка учёбой. Закройте пробелы в знаниях с помощью игр и комиксов

Скорость

Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.

Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.

Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.

Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.

Формула скорости Чтобы найти скорость, нужно разделить путь на время: v = s : t

Показатели скорости чаще всего выражаются в м/сек или км/час.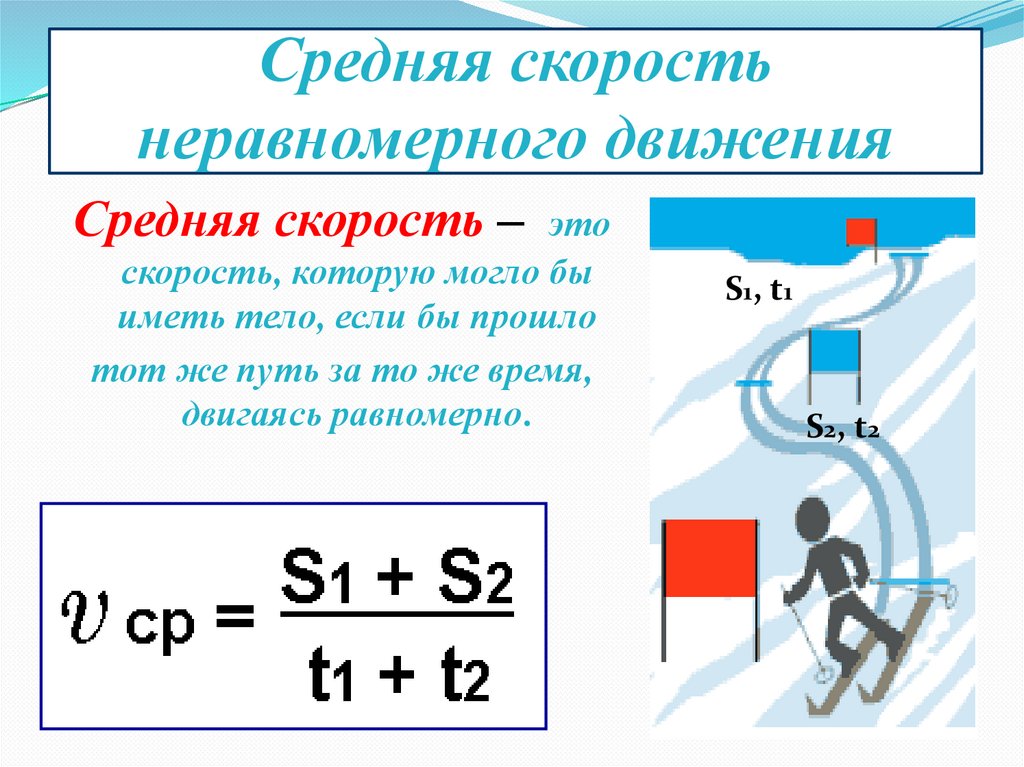

Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.

Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.

Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.

Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.

Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.

Время

Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.

Время — это продолжительность каких-то действий, событий.

• Например: от метро до дома — 10 минут, от дома до дачи — 2 часа.

Время движения обозначается латинской буквой t.

Чаще всего вам будут встречаться такие единицы времени, как секунды, минуты и часы.

Формула времени Чтобы найти время, нужно разделить расстояние на скорость: t = s : v

Эта формула пригодится, если нужно узнать, за какое время тело преодолеет то или иное расстояние.

Взаимосвязь скорости, времени, расстояния

Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.

Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.

Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес-браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?

Как рассуждаем:

Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров в минуту на 15 минут, мы определим расстояние от дома до магазина:

v = 50 м/мин

t = 15 мин

s = v × t = 50 × 15 = 750 (м)

Ответ: мы прошли 750 метров.

Если известно время и расстояние, то можно найти скорость: v = s : t.

Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние между двором и площадкой — 100 метров. Первый школьник добежал за 25 секунд, второй за 50 секунд. Кто добежал быстрее?

Как рассуждаем:

Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников — это расстояние, которое они пробегают за 1 секунду.

Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:

100 : 25 = 4

Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).

В нашей задаче расстояние дано в метрах, а время в секундах. Значит, будем измерять скорость в метрах в секунду (м/с).

100 м : 25 с = 4 м/с

Так мы узнали, что скорость движения первого школьника 4 метра в секунду.

Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:

100 : 50 = 2

Значит, скорость движения второго школьника составляет 2 метра в секунду.

Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.

4 (м/с) > 2 (м/с)

Скорость первого школьника больше. Значит, он добежал до спортивной площадки быстрее.

Ответ: первый школьник добежал быстрее.

Если известны скорость и расстояние, то можно найти время: t = s : v.

Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту.

За какое время мы дойдем до стадиона из школы?

Как рассуждаем:

Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?

Чтобы ответить на этот вопрос, нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое дойдем до стадиона:

s = 500 м

v = 100 м/мин

t = s : v = 500 : 100 = 5 (мин)

Ответ: от школы до стадиона мы дойдем за 5 минут.

Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.

Как найти скорость время и расстояние. Как вычислить среднюю скорость

С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах.

На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.

• через формулу нахождения мощности;
• через дифференциальные исчисления;
• по угловым параметрам и так далее.

В этой статье рассматривается самый простой способ с самой простой формулой — нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:

• v — скорость объекта,
• S — расстояние, которое пройдено или должно быть пройдено объектом,
• t — время, за которое пройдено или должно быть пройдено расстояние.

Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы , так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.

Теперь нужно подставить имеющиеся значения вместо буквенных символов:

v=100 км/1,5 ч=66,66 км/ч

Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.

Таким нехитрым способом можно найти скорость через время и расстояние.

А что делать , если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:

vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn — значения скоростей объекта на отдельных участках пути S, n — количество этих участков, vср — средняя скорость объекта на всем протяжении всего пути.

Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:

• vср=(S1+S2+…+Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
• S1, S2, Sn — отдельные неравномерные участки всего пути,
• t — общее время, за которое объект прошел все участки.

Можно записать использовать и такой вид вычислений:

• vср=S/(t1+t2+…+tn), где S — общее пройденное расстояние,
• t1, t2, tn — время прохождения отдельных участков расстояния S.

Но можно записать эту же формулу и в более точном варианте:

vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn — формулы вычисления скорости на каждом отдельном участке всего пути S.

Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей .

Другие способы вычисления

Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:

N=F*v*cos α , где N — механическая мощность,

v — скорость,

cos α — косинус угла между векторами силы и скорости.

Способы вычисления расстояния и времени

Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:

S=v*t, где v — понятно что такое,

S — расстояние, которое требуется найти,

t — время, за которое объект прошел это расстояние.

Таким образом вычисляется значение расстояния.

Или вычисляем значение времени , за которое пройдено расстояние:

t=S/v, где v — все та же скорость,

S — расстояние, пройденный путь,

t — время, значение которого в данном случае нужно найти.

Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.

Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.

И это еще не предел!

Видео

В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.

Все задачи, в которых присутствует движение объектов, их перемещение или вращение, так или иначе связаны со скоростью.

Данный термин характеризует перемещение объекта в пространстве за определенный отрезок времени – число единиц расстояния за единицу времени. Он является частым «гостем» как разделов математики, так и физики. Исходное тело может менять свое расположение как равномерно, так и с ускорением. В первом случае величина скорости статична и в ходе движения не меняется, во втором наоборот – увеличивается или уменьшается.

Как найти скорость – равномерное движение

Если скорость движения тела оставалась неизменной от начала перемещения и до окончания пути, то речь идет о перемещении с постоянным ускорением – равномерном движении. Оно может быть прямолинейным или же криволинейным. В первом случае траекторией перемещения тела является прямая.

Тогда V=S/t, где:

• V – искомая скорость,
• S – пройденное расстояние (общий путь),
• t – общее время движения.

Как найти скорость – ускорение постоянно

Если объект двигался с ускорением, то его скорость по мере движения менялась. В таком случае найти искомую величину поможет выражение:

V=V (нач) + at, где:

• V (нач) – первоначальная скорость движения объекта,
• a – ускорение тела,
• t – общее время пути.

Как найти скорость – неравномерное движение

В данном случае имеет место ситуация, когда разные участки пути тело проходило за разное время.
S(1) – за t(1),
S(2) – за t(2) и т.д.

На первом участке движение происходило в “темпе” V(1), на втором – V(2) и т.д.

Чтобы узнать скорость перемещения объекта на всем пути (ее среднее значение) воспользуйтесь выражением:

Как найти скорость – вращение объекта

В случае вращения речь идет об угловой скорости, определяющей угол, на который поворачивается элемент за единицу времени. Обозначается искомая величина символом ω (рад/с).

• ω = Δφ/Δt, где:

Δφ – пройденный угол (приращение угла),
Δt – прошедшее время (время движения – приращение времени).

• В случае, если вращение равномерное, искомая величина (ω) связана с таким понятием как период вращения – за какое время наш объект совершит 1 полный оборот. В таком случае:

ω = 2π/T, где:
π – константа ≈3,14,
T – период.

Или ω = 2πn, где:
π – константа ≈3,14,
n – частота обращения.

• При известной линейной скорости объекта для каждой точки на пути движения и радиусе окружности, по которой она перемещается, для нахождения скорости ω потребуется следующее выражение:

ω = V/R, где:
V – численное значение векторной величины (линейной скорости),
R – радиус траектории следования тела.

Как найти скорость – сближение и отдаление точек

В подобного рода задачах уместным будет использование терминов скорость сближения и скорость отдаления.

Если объекты направляются друг к другу, то скорость сближения (отдаления) будет следующей:
V (сближ) = V(1) + V(2), где V(1) и V(2) – скорости соответствующих объектов.

Если одно из тел догоняет другое, то V (сближ) = V(1) – V(2), V(1) больше V(2).

Как найти скорость – движение по водоему

Если события разворачиваются на воде, то к собственной скорости объекта (движение тела относительно воды) добавляется еще и скорость течения (т.е. движение воды относительно неподвижного берега). Как взаимосвязаны эти понятия?

В случае перемещения по течению V=V(собст) + V(теч).
Если против течения – V=V(собств) – V(теч.).

При прямолинейном равноускоренном движении тело

1. двигается вдоль условной прямой линии,
2. его скорость постепенно увеличивается или уменьшается,
3. за равные промежутки времени скорость меняется на равную величину.

Например, автомобиль из состояния покоя начинает двигаться по прямой дороге, и до скорости, скажем, в 72 км/ч он двигается равноускоренно. Когда заданная скорость достигнута, то авто движется без изменения скорости, т. е. равномерно. При равноускоренном движении его скорость возрастала от 0 до 72 км/ч. И пусть за каждую секунду движения скорость увеличивалась на 3,6 км/ч. Тогда время равноускоренного движения авто будет равно 20 секундам. Поскольку ускорение в СИ измеряется в метрах на секунду в квадрате, то надо ускорение 3,6 км/ч за секунду перевести в соответствующие единицы измерения. Оно будет равно (3,6 * 1000 м) / (3600 с * 1 с) = 1 м/с 2 .

Допустим, через какое-то время езды с постоянной скоростью автомобиль начал тормозить, чтобы остановиться. Движение при торможении тоже было равноускоренным (за равные промежутки времени скорость уменьшалась на одинаковую величину). В данном случае вектор ускорения будет противоположен вектору скорости. Можно сказать, что ускорение отрицательно.

Итак, если начальная скорость тела нулевая, то его скорость через время в t секунд будет равно произведению ускорения на это время:

При падении тела «работает» ускорение свободного падения, и скорость тела у самой поверхности земли будет определяться по формуле:

Если известна текущая скорость тела и время, которое понадобилось, чтобы развить такую скорость из состояния покоя, то можно определить ускорение (т. е. как быстро менялась скорость), разделив скорость на время:

Однако тело могло начать равноускоренное движение не из состояния покоя, а уже обладая какой-то скоростью (или ему придали начальную скорость). Допустим, вы бросаете камень с башни вертикально вниз с приложением силы. На такое тело действует ускорение свободного падения, равное 9,8 м/с 2 . Однако ваша сила придала камню еще скорости. Таким образом, конечная скорость (в момент касания земли) будет складываться из скорости, развившийся в результате ускорения и начальной скорости. Таким образом, конечная скорость будет находиться по формуле:

Однако, если камень бросали вверх. То начальная его скорость направлена вверх, а ускорение свободного падения вниз. То есть вектора скоростей направлены в противоположные стороны. В этом случае (а также при торможении) произведение ускорения на время надо вычитать из начальной скорости:

Получим из этих формул формулы ускорения. В случае ускорения:

at = v – v 0
a = (v – v 0)/t

В случае торможения:

at = v 0 – v
a = (v 0 – v)/t

В случае, когда тело равноускоренно останавливается, то в момент остановки его скорость равна 0. Тогда формула сокращается до такого вида:

Зная начальную скорость тела и ускорение торможения, определяется время, через которое тело остановится:

Теперь выведем формулы для пути, которое тело проходит при прямолинейном равноускоренном движении . Графиком зависимость скорости от времени при прямолинейном равномерном движении является отрезок, параллельный оси времени (обычно берется ось x). Путь при этом вычисляется как площадь прямоугольника под отрезком. То есть умножением скорости на время (s = vt). При прямолинейном равноускоренном движении графиком является прямая, но не параллельная оси времени. Эта прямая либо возрастает в случае ускорения, либо убывает в случае торможения. Однако путь также определяется как площадь фигуры под графиком.

При прямолинейном равноускоренном движении эта фигура представляет собой трапецию. Ее основаниями являются отрезок на оси y (скорость) и отрезок, соединяющий точку конца графика с ее проекцией на ось x. Боковыми сторонами являются сам график зависимости скорости от времени и его проекция на ось x (ось времени). Проекция на ось x — это не только боковая сторона, но еще и высота трапеции, т. к. перпендикулярна его основаниям.

Как известно, площадь трапеции равна полусумме оснований на высоту. Длина первого основания равна начальной скорости (v 0), длина второго основания равна конечной скорости (v), высота равна времени. Таким образом получаем:

s = ½ * (v 0 + v) * t

Выше была дана формула зависимости конечной скорости от начальной и ускорения (v = v 0 + at). Поэтому в формуле пути мы можем заменить v:

s = ½ * (v 0 + v 0 + at) * t = ½ * (2v 0 + at) * t = ½ * t * 2v 0 + ½ * t * at = v 0 t + 1/2at 2

Итак, пройденный путь определяется по формуле:

s = v 0 t + at 2 /2

(К данной формуле можно прийти, рассматривая не площадь трапеции, а суммируя площади прямоугольника и прямоугольного треугольника, на которые разбивается трапеция.)

Если тело начало двигаться равноускоренно из состояния покоя (v 0 = 0), то формула пути упрощается до s = at 2 /2.

Если вектор ускорения был противоположен скорости, то произведение at 2 /2 надо вычитать. Понятно, что при этом разность v 0 t и at 2 /2 не должна стать отрицательной. Когда она станет равной нулю, тело остановится. Будет найден путь торможения. Выше была приведена формула времени до полной остановки (t = v 0 /a). Если подставить в формулу пути значение t, то путь торможения приводится к такой формуле.

Равномерное движение, это вдвижение спостоянной скоростью. То есть другимим словами, тело за одинаковые промежутки времени должно проходить одинаковое расстояние. Например, если машина будет за каждый час своего пути проезжать расстояние в 50 километров, то такое движение будет являться равномерным.

Обычно равномерное движение очень редко можно встретить в реальной жизни. За примеры равномерного движения в природе, можно считать вращение Земли вокруг Солнца. Или например, конец секундной стрелки часов, тоже будет двигаться равномерно.

Расчет скорости при равномерном движении

Скорость тела при равномерном движении будет вычисляться по следующей формуле.

• Скорость = путь / время.

Если обозначить скорость движения буквой V, время движения буквой t, а путь пройденный телом буквой S, то получим следующую формулу.

• V=s/t.

Единица измерения скорости 1 м/с. То есть тело проходит расстояние в один метр, за время равное одной секунде.

Движения с переменной скоростью называется неравномерным движением. Чаще всего, все тела в природе двигаются именно неравномерно. Например, человек, когда куда-либо идет, двигается неравномерно, то есть его скорость в течении всего пути будет изменяться.

Расчет скорости при неравномерном движении

При неравномерном движении, скорость все время изменяется, и в этом случае говорят о средней скорости движения.

Средняя скорость неравномерного движения вычисляется по формуле

• Vcp=S/t.

Из формулы для определения скорости, мы можем получить и другие формулы, например, для расчета пройденного пути или времени, которое двигалось тело.

Расчет пути при равномерном движении

Чтобы определить путь, который прошло тело при равномерном движении, необходимо скорость движения тела умножить на время которое это тело двигалось.

• S=V*t.

То есть, зная скорость и время движения, мы всегда сможем найти путь.

Теперь, получим формулу для расчета времени движения, при известных: скорости движения и пройденном пути.

Расчет времени при равномерном движении

Для того чтобы определить время равномерного движения, необходимо путь пройденный телом, поделить на скорость, с которой это тело двигалось.

• t=S/V.

Полученные выше формулы будут справедливы, если тело совершало равномерное движение.

При расчете средней скорости неравномерного движения, полагают, что движение было равномерным. Исходя из этого, для вычисления по средней скорости неравномерного движения, пути или времени движения используют те же самые формулы, что и при равномерном движении.

Расчет пути при неравномерном движении

Получаем, что путь пройденный телом при неравномерном движении, равен произведению средней скорости на время которое тело двигалось.

• S=Vcp*t

Расчет времени при неравномерном движении

Время необходимое для прохождения некоторого пути при неравномерном движении, равняется частному от деления пути на среднюю скорость неравномерного движения.

• t=S/Vcp.

Графиком равномерного движения, в координатах S(t) будет являться прямая линия.

Скорость является функцией времени и определяется как абсолютной величиной, так и направлением. Часто в задачах по физике требуется найти начальную скорость (ее величину и направление), которой изучаемый объект обладал в нулевой момент времени. Для вычисления начальной скорости можно использовать различные уравнения. Основываясь на данных, приведенных в условии задачи, вы можете выбрать наиболее подходящую формулу, которая позволит легко получить искомый ответ.

Шаги

Нахождение начальной скорости по конечной скорости, ускорению и времени

1. При решении физической задачи необходимо знать, какая формула вам понадобится. Для этого первым делом следует записать все данные, приведенные в условии задачи. Если известны конечная скорость, ускорение и время, для определения начальной скорости удобно использовать следующее соотношение:

   • V i = V f — (a * t)
   • • V i — начальная скорость
     • V f — конечная скорость
     • a — ускорение
     • t — время
   • Обратите внимание, что это стандартная формула, используемая для вычисления начальной скорости.

2. Выписав все исходные данные и записав необходимое уравнение, можно подставить в него известные величины. Важно внимательно изучить условие задачи и аккуратно записывать каждый шаг при ее решении.

   • Если вы где-либо допустили ошибку, то легко сможете найти ее, просмотрев свои записи.

3. Решите уравнение. Подставив в формулу известные значения, воспользуйтесь стандартными преобразованиями для получения искомого результата. Если можно, используйте калькулятор, чтобы снизить вероятность просчетов при вычислениях.

   • Предположим, что объект, двигаясь на восток с ускорением 10 метров в секунду в квадрате в течение 12 секунд, разогнался до конечной скорости 200 метров в секунду. Необходимо найти начальную скорость объекта.
     • Запишем исходные данные:
     • V i = ?, V f = 200 м/с, a = 10 м/с 2 , t = 12 с
   • Умножим ускорение на время: a * t = 10 * 12 =120
   • Вычтем полученное значение из конечной скорости: V i = V f – (a * t) = 200 – 120 = 80 V i = 80 м/с на восток
   • м/с

   Нахождение начальной скорости по пройденному пути, времени и ускорению

   1. Используйте подходящую формулу. При решении какой-либо физической задачи необходимо выбрать соответствующее уравнение. Для этого первым делом следует записать все данные, приведенные в условии задачи. Если известны пройденное расстояние, время и ускорение, для определения начальной скорости можно использовать следующее соотношение:

      • В эту формулу входят следующие величины:
        • V i — начальная скорость
        • d — пройденное расстояние
        • a — ускорение
        • t — время

   2. Подставьте в формулу известные величины.

      • Допустив ошибку в решении, вы сможете без труда найти ее, просмотрев свои записи.

   3. Решите уравнение. Подставив в формулу известные значения, воспользуйтесь стандартными преобразованиями для нахождения ответа. Если возможно, используйте калькулятор, чтобы уменьшить вероятность просчетов при вычислениях.

      • Допустим, объект движется в западном направлении с ускорением 7 метров в секунду в квадрате в течение 30 секунд, пройдя при этом 150 метров. Необходимо вычислить его начальную скорость.
        • Запишем исходные данные:
        • V i = ?, d = 150 м, a = 7 м/с 2 , t = 30 с
      • Умножим ускорение на время: a * t = 7 * 30 = 210
      • Поделим произведение на два: (a * t) / 2 = 210 / 2 = 105
      • Поделим расстояние на время: d / t = 150 / 30 = 5
      • Вычтем первую величину из второй: V i = (d / t) — [(a * t) / 2] = 5 – 105 = -100 V i = -100 м/с в западном направлении
      • Запишите ответ в правильном виде. Необходимо указать единицы измерения, в нашем случае метры в секунду, или м/с , а также направление движения объекта. Если вы не укажете направление, ответ будет неполным, содержа лишь величину скорости без информации о том, в каком направлении движется объект.

   Нахождение начальной скорости по конечной скорости, ускорению и пройденному пути

   1. Используйте подходящее уравнение. Для решения физической задачи необходимо выбрать соответствующую формулу. Первым делом следует записать все начальные данные, указанные в условии задачи. Если известны конечная скорость, ускорение и пройденное расстояние, для определения начальной скорости удобно использовать следующее соотношение:

      • V i = √
      • Эта формула содержит следующие величины:
        • V i — начальная скорость
        • V f — конечная скорость
        • a — ускорение
        • d — пройденное расстояние

   2. Подставьте в формулу известные величины. После того, как вы выписали все исходные данные и записали необходимое уравнение, можно подставить в него известные величины. Важно внимательно изучить условие задачи и аккуратно записывать каждый шаг при ее решении.

      • Допустив где-либо ошибку, вы сможете без труда найти ее, просмотрев ход решения.

   3. Решите уравнение. Подставив в формулу известные значения, воспользуйтесь необходимыми преобразованиями для получения ответа. По возможности используйте калькулятор, чтобы уменьшить вероятность просчетов при вычислениях.

      • Предположим, объект движется в северном направлении с ускорением 5 метров в секунду в квадрате и, преодолев 10 метров, имеет конечную скорость 12 метров в секунду. Необходимо найти его начальную скорость.
        • Запишем исходные данные:
        • V i = ?, V f = 12 м/с, a = 5 м/с 2 , d = 10 м
      • Возведем в квадрат конечную скорость: V f 2 = 12 2 = 144
      • Умножим ускорение на пройденное расстояние и на 2: 2 * a * d = 2 * 5 * 10 = 100
      • Вычтем результат умножения из квадрата конечной скорости: V f 2 — (2 * a * d) = 144 – 100 = 44
      • Извлечем квадратный корень из полученного значения: = √ = √44 = 6,633 V i = 6,633 м/с в северном направлении
      • Запишите ответ в правильном виде. Необходимо указать единицы измерения, то есть метры в секунду, или м/с , а также направление движения объекта. Если вы не укажете направление, ответ будет неполным, содержа лишь величину скорости без информации о том, в каком направлении движется объект.

Как найти среднюю скорость (формула и примеры)

, написанный

Малкольм Маккинси

11 января 2023

Проверка по фактам

Пол Маззола

Средняя скорость. Средняя скорость

Средняя скорость. два слова: среднее значение, означающее среднее значение, полученное из множества отдельных точек данных, и скорость, означающая изменение положения. Вы можете рассчитать среднюю скорость для любого типа движения, если можете рассчитать время движения и измерить расстояние.

Формула средней скорости

Средняя скорость  это общее расстояние, пройденное для рассматриваемого объекта, деленное на общее время, затраченное на преодоление расстояния, общий период времени. Формула средней скорости:

Определение средней скорости и формула

Средняя скорость отличается от мгновенной скорости.

Мгновенная скорость

Средняя скорость учитывает совокупность событий, таких как ускорение автомобиля с места, ускорение, движение некоторое время, затем замедление на желтый сигнал светофора и, наконец, остановка.

Автомобиль движется с разной скоростью. В любой момент автомобиль не едет со скоростью 55 миль в час (миль в час). Это может быть 0 миль в час, затем 7 миль в час, затем 53 мили в час, затем 61 миля в час и, наконец, 3 мили в час, прежде чем вернуться к 0 милям в час.

Чтобы упростить измерения и добиться прогресса в решении задачи по физике или математике, вы берете среднюю скорость всех дискретных событий, говоря, что автомобиль проехал 5,5 миль  за 6 минут :

Все эти другие измерения в определенные моменты времени в путешествии мгновенные скорости . В большинстве случаев вам нужно , а не знать формулу мгновенной скорости, v , нахождение предела по мере того, как изменение во времени («момент») приближается к 0:

Мгновенные скорости колеблются в течение хронометрируемого события. Найти среднюю скорость far проще и, как правило, гораздо полезнее, чем вычислить мгновенную скорость.

Скалярные и векторные величины

Скорость есть скалярная величина . У него нет направления. Он имеет только размер, то есть величину или масштаб. Скалярные величины могут изменяться от 0 (без скорости) до бесконечно быстрой.

Векторная величина имеет размер и направление, как и движение самолета в небе. Скорость является векторной величиной.

Скорость, будучи скалярной величиной, никогда не может быть меньше 0. Средняя и мгновенная скорости всегда являются скалярными величинами, что означает, что вы всегда можете измерить их числом. Расстояние и время также являются скалярными величинами и также могут быть измерены числами.

Как рассчитать среднюю скорость

Чтобы рассчитать среднюю скорость объекта, вы должны знать общее расстояние, которое проходит объект, и общее время, затраченное на весь его путь.

Треугольник расстояние/скорость/время удобен для расчета этой и двух других скалярных величин (расстояние и время):

Скорость расстояние время треугольник и формулы

Три части треугольника математически расставлены в правильном положении:

1. Чтобы получить среднюю скорость, s , разделите общее расстояние на прошедшее время: Dt\frac{D}{t}tD​

2. Чтобы получить пройденное время, t , разделите общее расстояние на скорость: Ds\frac{D }{s}sD​

3. Чтобы получить расстояние, D , умножьте скорость на количество времени: s×ts\times ts×t

Допустим, вы хотите найти среднюю скорость Тихоокеанская афалина. Вам говорят, что он может пройти расстояние 89,7 км за 3 часа.

Подставьте эти два заданных числа в треугольник в их двух углах, чтобы получить:

Как рассчитать среднюю скорость

Если вы знаете две из трех переменных, расстояние, время и скорость, то вы можете использовать алгебру, чтобы найти то, что вы повторно отсутствует.

Если вам нужно общее время, вы должны иметь расстояние и скорость. Вы подставляете эти две скалярные величины в соответствующие части треугольника, чтобы получить:

Вычисление общего времени по средней скорости и расстоянию

Если вам нужно общее расстояние, вы должны знать скорость и время:

Расчет общего расстояния по средней скорости и времени

Средняя скорость особенно полезна, поскольку она учитывает реальность события, а не предполагает, что что-то или кто-то движется с постоянной скоростью.

Морская свинья могла начать медленно, ускориться, сделать паузу, чтобы поиграть, и продолжить. Этот трехпалый ленивец, возможно, остановился на мгновение, чтобы отдышаться, прежде чем поспешить дальше.

Возможно, вам придется делать многочисленные остановки при выгуле собаки, но во всех трех случаях вы можете легко рассчитать среднюю скорость, разделив общее пройденное расстояние на общее затраченное время.

Предостережение

Средняя скорость часто выводится из единиц расстояния или времени, которые должны быть преобразованы в другие единицы для окончательного ответа. Соблюдайте осторожность при этом.

Обычными преобразованиями являются умножение единиц в секунду на 60 или 3600, чтобы получить единицы в минуту и ​​единицы в час. Просто убедитесь, что ваш ответ дан в правильной единице времени.

Преобразование единиц измерения средней скорости

Если изменяется только одна единица измерения, вам нужно будет выполнить только одну математическую операцию (например, умножить секунды, чтобы получить минуты или часы). Если изменить две единицы (футы в секунду на мили в час), вы должны умножить и разделить (или умножить на десятичное значение).

Проблемы средней скорости

1. Тарпон (разновидность рыбы) может путешествовать 105 миль за 3 часа . Какова его средняя скорость?

2. Синий тунец может проплыть и преодолеть  286 миль за обычный учебный день 6,5 часов . Какова его средняя скорость, пока вы проводите свой день в классе?

3. Мировой рекорд по скорости бега назад (во время жонглирования!) принадлежит Джо Солтеру, который проехал 5280 футов дюйма 457 секунд . Какова была его средняя скорость в милях за час ? (умножить на 3600 и затем разделить на 5280 ; или умножить на 0,681818 )

4. Гепард может пройти 0,6 мили за 3 секунд. Какова средняя скорость гепарда в милях за секунду ? Как насчет скорости в милях за час ? (умножить на 3600 )

5. Косатка может двигаться со средней крейсерской скоростью 8 миль в час. Большая белая акула может преодолеть расстояние 35 миль за семь часов. Какова скорость большой белой акулы и какое животное плывет быстрее?

6. Самый быстрый человек в воде преодолел 22,9 метра за 10 секунд. Кальмар Гумбольдта может пройти 399,6 метра за 60 секунд . Вам нужно рассчитать среднюю скорость самого быстрого человека и кальмара Гумбольдта, чтобы узнать, кто кого может обогнать.

Мы знаем, что вы сначала сделаете работу, прежде чем проверять эти ответы, верно?

1. Рассчитайте среднюю скорость тарпона следующим образом: s=105miles3hourss=\frac{105miles}{3hours}s=3hours105miles​, что означает, что рыба может двигаться со средней скоростью 35 миль в час .

2. Формула голубого тунца будет выглядеть так: s = 286 миль 6,5 часов = \ frac {286 миль {6,5 часов} s = 6,5 часов 286 миль​, поэтому средняя скорость рыбы составляет 44 мили в час.

3. Joe Salter’s Cover 5,280 футов в 457 секунд , S = 5,280FEET457Secondss = \ FRAC {\ MathRM {5,280} FOT . Мы умножаем это на 3600 (количество секунд в часе), а затем делим на 5280 (футы в миле), чтобы получить среднюю скорость 7,87745 миль в час .

4. Формула для средней скорости гепарда будет:0021 0,01666 (повторяющееся десятичное число, поэтому мы аппроксимируем 0,01666 ) в милях за секунду , которые можно умножить на 3600 , чтобы получить среднюю скорость 60 миль/ч .

5. Косатка может двигаться со средней крейсерской скоростью 8 миль/ч , в то время как средняя скорость большой белой акулы s=35mi.7hours=5mph=\frac{35mi.}{7hours}=5mph=7hours35mi. ​ =5 миль в час. Косатка плавает быстрее.

6. Самый быстрый человек в воде плавал 22,9 метра в 10 секунд , поэтому средняя скорость s=22,9м10секунд=2,29метра/секунды=\frac{22,9м}{10секунд}=2,29метра/секунды=10секунд22,9м​=2,29метра/секунду. Кальмар Гумбольдта может пройти 399,6 метров за 60 секунд , поэтому s=399,6м60секунд=6,67м/сс=\frac{399,6м}{60секунд}=6,67м/сс=60секунд399,6м​=6,67м/с , значительно быстрее, чем самый быстрый пловец-человек. Будем надеяться, что вас никогда не преследовал кальмар Гумбольдта!

Как рассчитать среднюю скорость – TheMarketatdelval.com

Если вы хотите узнать среднюю скорость вашего , вы можете сделать несколько вещей. Один из них — использовать спидометр, если он есть в вашем автомобиле. Другой заключается в использовании устройства GPS. Наконец, вы можете использовать секундомер и измерять расстояние, пройденное вами за определенный период времени.

Наша способность рассчитывать время и расстояние в пути зависит от средней скорости, которая по сути является механизмом. Его можно рассчитать, разделив общее пройденное расстояние на общее время, затраченное на него. Формула для приведенного выше — S. Если S считается скоростью, D считается расстоянием, а T считается временем, D/T становится D/T. Посмотрев на период времени от точки А до точки Б и обратно во времени, вы можете рассчитать среднюю скорость человека. Если расстояние между А и В составляет 36 метров, рассчитывается средняя скорость человека. Как рассчитать среднее расстояние, пройденное частицей? В м/с можно указать (в м/с). Расстояние определяется как затраченное время, умноженное на скорость.

Анитья идет от А до Б в течение двух часов, преодолевая 8 миль. Средняя скорость в этом случае составляет 8 миль в час. Скорость рассчитывается путем умножения среднего значения на четыре. При изменении скорости формула, использованная в предыдущем разделе, изменяется. Самолету требуется 18 часов, чтобы перелететь из Соединенных Штатов в Малайзию, преодолев расстояние в девять тысяч миль.

Вы можете разделить сумму на два, сложив начальную и конечную скорости . В результате скорость усредняется.

Каждую скорость просто разделить на время, которое потребовалось, как показано на рисунке ниже: умножьте скорость на время, затраченное на достижение этой скорости, и разделите полученную сумму на время, затраченное на достижение этой скорости. Скорость: 90 км/ч за 2 часа, 80 км/ч за 1 час и 60 км/ч за 1,5 часа/час/час/час/час/час/час/час/час/час/час/час/час / час / час / час 1 = 350 км / 4,5 часа = 7 7,8 км/ч средней скорости (2+1).

Средняя скорость — это общее расстояние, пройденное объектом за заданный период. Иными словами, средняя скорость — это скалярная величина. Ему не хватает направления, и он представлен величиной.

Например, если задано пройденное расстояние в 250 миль и время в 5 часов, средняя скорость будет равна 50 милям в час (миль/ч).

Что такое средняя скорость и как она рассчитывается?

Фото: https://slideserve.com

Средняя скорость — это мера пройденного расстояния за время. Он рассчитывается путем деления пройденного пути на затраченное время.

Для тела средняя скорость равна сумме его дневной скорости и годовой скорости за данный период времени. Средняя скорость равна общему пройденному расстоянию, умноженному на общее время. Средняя скорость рассчитывается по следующей формуле. Средняя скорость = средняя. Пройденное расстояние выражается в километрах. Возьмем полный и общий частные случаи в случае формул средней скорости. Когда задано «n» различных скоростей или расстояний, формула средней скорости рассчитывается для каждой из них таким образом, чтобы скорости перемещались за одинаковое количество времени (**(t_1 = t.1)) Формула выглядит следующим образом: Средняя скорость .

Сэм едет со средней максимальной скоростью 45 км/ч. Сообщается, что поезд прибудет в пункт назначения за четыре часа со скоростью 80 миль в час. Формула средней скорости равна скорости среднего автомобиля. ( 90 4 + 110 3) (4) (4 + 3) В следующем примере число (650) обозначает (7). Расстояние 92,86 миль в час — это пройденное расстояние. Чтобы определить среднюю скорость объекта, умножьте скорость автомобиля на 43,57 м/с. Пройденное расстояние и затраченное время выражаются в имперских единицах. Формула времени будет преобразована в формулу средней скорости [Время =[/Время] для ее расчета. Среднее время прохождения дистанции Скорость движения Бегун преодолевает 100-метровый круг за 40 секунд. Эта формула показывает, что бегун может развивать максимальную скорость 2,5 метра в секунду.

Единицей измерения скорости в системе СИ является метр в секунду (м/с). Это также известно как метр на секунду в квадрате (м/с2). В системе СИ скорость света в вакууме составляет 299 792 458 метров в секунду.
В качестве еще одной единицы измерения скорости в системе СИ также используются километры в час (км/ч). При скорости 1000 метров в секунду это равно одному километру в час.

Значение средней скорости

Кроме того, важным фактором является скорость, с которой движется транспортное средство. Это также может помочь водителям опережать потоки машин, а также защитить пешеходов и велосипедистов от несчастных случаев.

Как найти среднюю скорость с учетом расстояния и времени?

Фото: https://studylib.net

Чтобы найти среднюю скорость , нужно знать пройденное расстояние и время, затраченное на это расстояние. Получив эти два значения, вы просто делите расстояние на время. Это даст вам среднюю скорость в метрах в секунду.

Как рассчитать среднюю скорость Физика

Фото: https://onlinemath5all.com

Есть несколько шагов в расчете средней скорости физики . Сначала определите пройденное расстояние. Во-вторых, определите время, затраченное на преодоление этого расстояния. Наконец, разделите расстояние на время. Полученное число и есть средняя скорость.

Расстояние, пройденное телом за определенный период времени, делится на среднюю скорость тела за этот период времени. В общем, формула средней скорости такова: я собираюсь поставить 2 в начале и 1 в конце. Давайте посмотрим, что такое скорость и скорость на самом деле. средняя скорость тела рассчитывается путем деления смещения тела за этот промежуток времени на его время. Формула расчета средней скорости: Средняя скорость = Средняя скорость. Общее расстояние, единица измерения. Все дело во времени. Чтобы узнать больше о скорости и скорости, загрузите приложение BYJU-INCLUDED. Приложение для обучения можно использовать для дополнения и улучшения навыков обучения.

Что такое средняя скорость в физическом примере?

Среднюю скорость можно рассчитать, разделив общее пройденное расстояние на интервал времени. Тот, кому требуется 40 минут, чтобы проехать 20 миль на север, а затем 20 миль на юг (чтобы прибыть в одно и то же место), имеет скорость 40 миль в минуту, разделенную на 40 минут, или 1 милю в минуту (60 миль в час).

Как рассчитать среднюю скорость

На уроке физики 11 мы изучаем движение и то, как объекты взаимодействуют друг с другом. Помимо изучения концепций средней и скорости, мы также занимаемся математикой. Средняя скорость рассчитывается путем деления общей длины пути пройденного пути на общий интервал времени движения. Мы можем рассчитать, как далеко объект прошел и сколько времени это заняло, используя его среднюю скорость.

Как рассчитать среднюю скорость в метрах в секунду

Чтобы рассчитать среднюю скорость в метрах в секунду, вам необходимо знать пройденное расстояние и время, затраченное на преодоление этого расстояния. Чтобы найти среднюю скорость, разделите расстояние на время.

Аналогичен миле в час, потому что это показатель скорости. Если вы измерите расстояние в метрах, а время в секундах, вы сможете быстро понять, насколько вы быстры. Точно так же вы можете определить скорость, разделив расстояние-время на скорость. Однако в некоторых случаях необходимо преобразовать другую единицу измерения, например мили или футы, в метры. Пройденное расстояние представлено осью Y в вертикальной плоскости. Расстояние можно рассчитать, найдя линию на графике и отметив, где она заканчивается. Расстояние рассчитывается путем вычитания значения y двух конечных точек линии из точки, в которой начинается линия (0,0).

Отсюда до моря 5280 футов. Чтобы определить скорость, умножьте миль в секунду на метры в секунду. Расстояние измеряется в метрах, с расстоянием 3,28084 фута. Разделите числитель на знаменатель, чтобы получить метры в минуту. Это отличный способ оценить скорость света в 299 792 458 м/с. Вычислите скорость по формуле скорость = расстояние/время. Поскольку скорость и скорость не имеют одной и той же формулы, их не следует путать. Продолжайте читать советы по преобразованию миль в час в метры в секунду. Считаете ли вы эту статью полезной?

Польза хорошего ночного сна Важность хорошего ночного сна

Как рассчитать среднюю скорость по графику

Наклон графика «расстояние-время» показывает скорость движения в пространстве. Другими словами, склон становится круче по мере того, как он движется быстрее.