Как узнать среднюю скорость автомобиля: Задачи на среднюю скорость — MathClub

Как найти среднюю скорость автомобиля формула. Как найти среднюю скорость

Механическим движением тела называется изменение его положения в пространстве относительно других тел с течением времени. При этом тела взаимодействуют по законам механики.

Раздел механики, описывающий геометрические свойства движения без учета причин, его вызывающих, называется кинематикой.

В более общем значении движением называется любое пространственное или временное изменение состояния физической системы. Например, можно говорить о движении волны в среде.

Относительность движения

Относительность — зависимость механического движения тела от системы отсчёта Не указав систему отсчёта, не имеет смысла говорить о движении.

Траектория материальной точки — линия в трёхмерном пространстве, представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве. Существенно, что понятие о траектории имеет физический смысл даже при отсутствии какого-либо по ней движения.

Кроме того, и при наличии движущегося по ней объекта, траектория сама по себе не может ничего дать в отношении причин движения, то есть о действующих силах.

Путь — длина участка траектории материальной точки, пройденного ею за определённое время.

Скорость (часто обозначается , от англ. velocity или фр. vitesse) — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта (например, угловая скорость). Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.

В науке используется также скорость в широком смысле, как быстрота изменения какой-либо величины (не обязательно радиус-вектора) в зависимости от другой (чаще изменения во времени, но также в пространстве или любой другой). Так, например, говорят о скорости изменения температуры, скорости химической реакции, групповой скорости, скорости соединения, угловой скорости и т.

д. Математически характеризуется производной функции.

Единицы измерения скорости

Метр в секунду, (м/с), производная единица системы СИ

Километр в час, (км/ч)

узел (морская миля в час)

Число Маха, 1 Мах равен скорости звука в данной среде; Max n в n раз быстрее.

Как единица, зависящая от конкретных условий среды, должна дополнительно определяться.

Скорость света в вакууме (обозначается c )

В современной механике движение тела подразделяется на виды, и существует следующая классификация видов движения тела :

Поступательное движение, при котором любая прямая линия, связанная с телом, остаётся при движении параллельной самой себе

Вращательное движение или вращение тела вокруг своей оси, считающейся неподвижной.

Сложное движение тела, состоящее из поступательного и вращательного движений.

Каждое из этих видов может быть неравномерным и равномерным (с не постоянной и постоянной скоростью соответственно).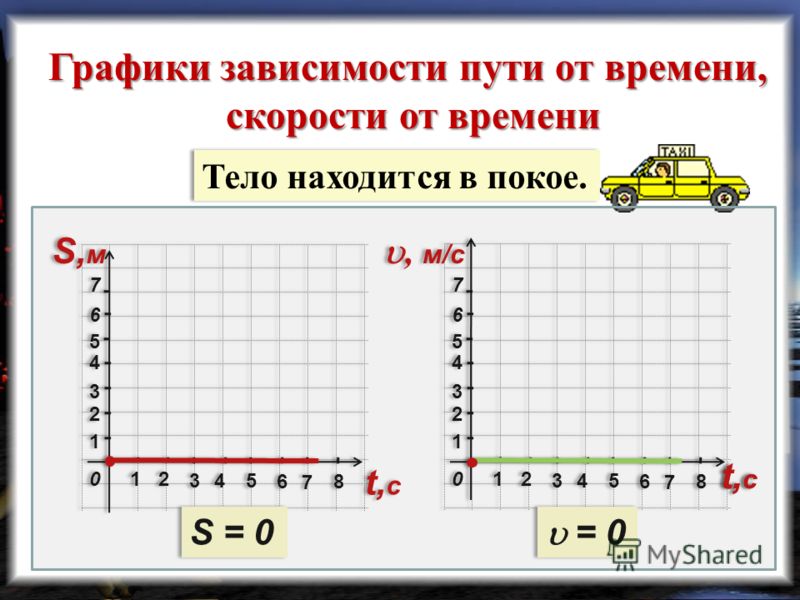

Средняя скорость неравномерного движения

Средняя путевая скорость — это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден:

Средняя путевая скорость, в отличие от мгновенной скорости не является векторной величиной.

Средняя скорость равна среднему арифметическому от скоростей тела во время движения только в том случае, когда тело двигалось с этими скоростями одинаковые промежутки времени.

В то же время если, например, половину пути автомобиль двигался со скоростью 180 км/ч, а вторую половину со скоростью 20 км/ч, то средняя скорость будет 36 км/ч. В примерах, подобных этому, средняя скорость равна среднему гармоническому всех скоростей на отдельных, равных между собой, участках пути.

Средняя скорость по перемещению

Можно также ввести среднюю скорость по перемещению, которая будет вектором, равным отношению перемещения ко времени, за которое оно совершено:

Средняя скорость, определённая таким образом, может равняться нулю даже в том случае, если точка (тело) реально двигалась (но в конце промежутка времени вернулась в исходное положение).

Если перемещение происходило по прямой (причём в одном направлении), то средняя путевая скорость равна модулю средней скорости по перемещению.

Прямолинейное равномерное движение – это движение, при котором тело (точка) за любые равные промежутки времени совершает одинаковые перемещения. Вектор скорости точки остаётся неизменным, а её перемещение есть произведение вектора скорости на время:

Если направить координатную ось вдоль прямой, по которой движется точка, то зависимость координаты точки от времени является линейной: , где — начальная координата точки, — проекция вектора скорости на координатную ось x.

Точка, рассматриваемая в инерциальной системе отсчёта, находится в состоянии равномерного прямолинейного движения, если равнодействующая всех сил, приложенных к точке, равна нулю.

Вращательное движение — вид механического движения. При вращательном движении абсолютно твердого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землей, ось вращения ротора генератора на электростанции неподвижна.

Характеристики вращения тела

При равномерном вращении (N оборотов в секунду),

Частота вращения — число оборотов тела в единицу времени,

Период вращения — время одного полного оборота. Период вращения T и его частота v связаны соотношением T = 1 / v.

Линейная скорость точки, находящейся на расстоянии R от оси вращения

,
Угловая скорость вращения тела.

Кинетическая энергия вращательного движения

Где I z — момент инерции тела относительно оси вращения. w — угловая скорость.

Гармонический осциллятор (в классической механике) — это система, которая при смещении из положения равновесия испытывает действие возвращающей силы, пропорциональной смещению.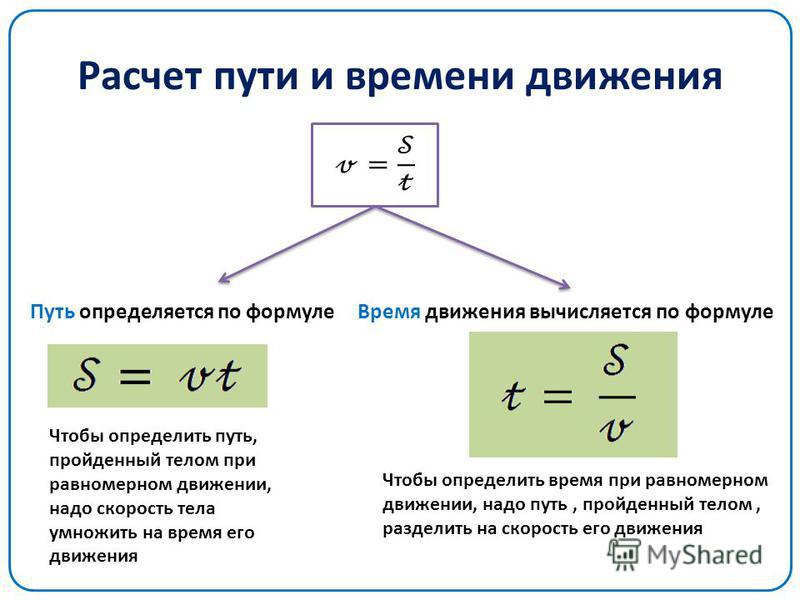

Если возвращающая сила — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.

Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором. Если трение не слишком велико, то система совершает почти периодическое движение — синусоидальные колебания с постоянной частотой и экспоненциально убывающей амплитудой. Частота свободных колебаний затухающего осциллятора оказывается несколько ниже, чем у аналогичного осциллятора без трения.

Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.

Механическими примерами гармонического осциллятора являются математический маятник (с малыми углами смещения), груз на пружине, торсионный маятник и акустические системы. Среди других аналогов гармонического осциллятора стоит выделить электрический гармонический осциллятор (см. LC-цепь).

Звук , в широком смысле — упругие волны, продольно распространяющиеся в среде и создающие в ней механические колебания; в узком смысле — субъективное восприятие этих колебаний специальными органами чувств животных или человека.

Как и любая волна, звук характеризуется амплитудой и спектром частот. Обычно человек слышит звуки, передаваемые по воздуху, в диапазоне частот от 16 Гц до 20 кГц. Звук ниже диапазона слышимости человека называют инфразвуком; выше: до 1 ГГц, — ультразвуком, более 1 ГГц — гиперзвуком. Среди слышимых звуков следует также особо выделить фонетические, речевые звуки и фонемы (из которых состоит устная речь) и музыкальные звуки (из которых состоит музыка).

Физические параметры звука

Колебательная скорость — величина, равная произведению амплитуды колебаний А частиц среды, через которую проходит периодическая звуковая волна, на угловую частоту w :

где В — адиабатическая сжимаемость среды; р — плотность.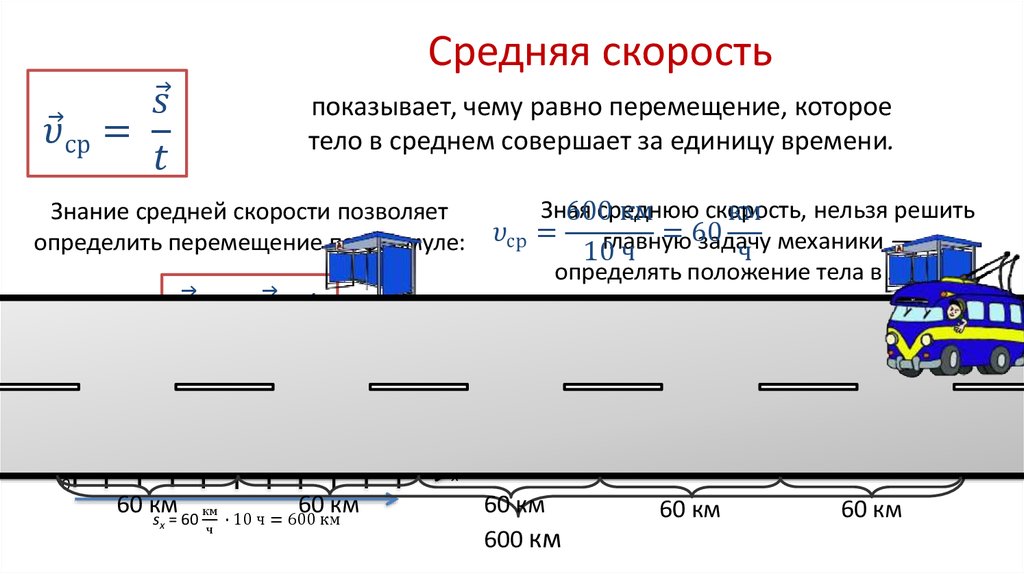

Как и световые волны, звуковые тоже могут отражаться, преломляться и т.д.

Если Вам понравилась эта страница, и Вам захотелось, чтобы Ваши друзья тоже её увидели, то выберите внизу значок социальной сети, где вы имеете свою страницу, и выразите своё мнение о содержании.

Ваши друзья и случайные посетители благодаря этому добавят Вам и моему сайту рейтинг

Все задачи, в которых присутствует движение объектов, их перемещение или вращение, так или иначе связаны со скоростью.

Данный термин характеризует перемещение объекта в пространстве за определенный отрезок времени – число единиц расстояния за единицу времени. Он является частым «гостем» как разделов математики, так и физики. Исходное тело может менять свое расположение как равномерно, так и с ускорением. В первом случае величина скорости статична и в ходе движения не меняется, во втором наоборот – увеличивается или уменьшается.

Как найти скорость – равномерное движение

Если скорость движения тела оставалась неизменной от начала перемещения и до окончания пути, то речь идет о перемещении с постоянным ускорением – равномерном движении. Оно может быть прямолинейным или же криволинейным. В первом случае траекторией перемещения тела является прямая.

Тогда V=S/t, где:

• V – искомая скорость,
• S – пройденное расстояние (общий путь),
• t – общее время движения.

Как найти скорость – ускорение постоянно

Если объект двигался с ускорением, то его скорость по мере движения менялась. В таком случае найти искомую величину поможет выражение:

V=V (нач) + at, где:

• V (нач) – первоначальная скорость движения объекта,
• a – ускорение тела,
• t – общее время пути.

Как найти скорость – неравномерное движение

В данном случае имеет место ситуация, когда разные участки пути тело проходило за разное время.
S(1) – за t(1),
S(2) – за t(2) и т.д.

На первом участке движение происходило в “темпе” V(1), на втором – V(2) и т.д.

Чтобы узнать скорость перемещения объекта на всем пути (ее среднее значение) воспользуйтесь выражением:

Как найти скорость – вращение объекта

В случае вращения речь идет об угловой скорости, определяющей угол, на который поворачивается элемент за единицу времени. Обозначается искомая величина символом ω (рад/с).

• ω = Δφ/Δt, где:

Δφ – пройденный угол (приращение угла),
Δt – прошедшее время (время движения – приращение времени).

• В случае, если вращение равномерное, искомая величина (ω) связана с таким понятием как период вращения – за какое время наш объект совершит 1 полный оборот. В таком случае:

ω = 2π/T, где:
π – константа ≈3,14,
T – период.

Или ω = 2πn, где:
π – константа ≈3,14,
n – частота обращения.

• При известной линейной скорости объекта для каждой точки на пути движения и радиусе окружности, по которой она перемещается, для нахождения скорости ω потребуется следующее выражение:

ω = V/R, где:
V – численное значение векторной величины (линейной скорости),
R – радиус траектории следования тела.

Как найти скорость – сближение и отдаление точек

В подобного рода задачах уместным будет использование терминов скорость сближения и скорость отдаления.

Если объекты направляются друг к другу, то скорость сближения (отдаления) будет следующей:
V (сближ) = V(1) + V(2), где V(1) и V(2) – скорости соответствующих объектов.

Если одно из тел догоняет другое, то V (сближ) = V(1) – V(2), V(1) больше V(2).

Как найти скорость – движение по водоему

Если события разворачиваются на воде, то к собственной скорости объекта (движение тела относительно воды) добавляется еще и скорость течения (т.е. движение воды относительно неподвижного берега). Как взаимосвязаны эти понятия?

В случае перемещения по течению V=V(собст) + V(теч).
Если против течения – V=V(собств) – V(теч.).

Помните, что скорость задается как численным значением, так и направлением. Скорость описывает быстроту изменения положения тела, а также направление, в котором движется это тело. Например, 100 м/с (на юг).

Найдите общее перемещение, то есть расстояние и направление между начальной и конечной точками пути. В качестве примера рассмотрим тело, движущееся с постоянной скоростью в одном направлении.

• Например, ракета была запущена в северном направлении и двигалась в течение 5 минут с постоянной скоростью 120 метров в минуту. Чтобы вычислить общее перемещение, воспользуйтесь формулой s = vt: (5 минут) (120 м/мин) = 600 м (на север) .
• Если в задаче дано постоянное ускорение, воспользуйтесь формулой s = vt + ½at 2 (в следующем разделе описывается упрощенный способ работы с постоянным ускорением).

Найдите общее время в пути. В нашем примере ракета перемещается в течение 5 минут. Среднюю скорость можно выразить в любых единицах измерения, но в международной системе единиц скорость измеряется в метрах в секунду (м/с). Конвертируйте минуты в секунды: (5 минут) х (60 секунд/минута) = 300 секунд .

• Если даже в научной задаче время дано в часах или других единицах измерения, лучше сначала вычислить скорость, а затем преобразовать ее в м/с.

Вычислите среднюю скорость. Если вы знаете значение перемещения и общее время в пути, вычислить среднюю скорость можно по формуле v ср = Δs/Δt. В нашем примере средняя скорость ракеты равна 600 м (на север) / (300 секунд) = 2 м/с (на север) .

• Не забудьте указать направление движения (например, «вперед» или «на север»).
• В формуле v ср = Δs/Δt символ «дельта» (Δ) означает «изменение величины», то есть Δs/Δt означает «изменение положения к изменению времени».
• Средняя скорость может быть записана как v ср или как v с горизонтальной чертой сверху.

Решение более сложных задач, например, если тело вращается или ускорение не является постоянным. В этих случаях средняя скорость по-прежнему вычисляется как отношение общего перемещения к общему времени. Не имеет значения, что происходит с телом между начальной и конечной точками пути. Вот несколько примеров задач с одинаковым общим перемещением и общим временем (а, следовательно, и одинаковой средней скоростью).

• Анна идет на запад со скоростью 1 м/с в течение 2 секунд, затем мгновенно ускоряется до 3 м/с и продолжает идти на запад в течение 2 секунд. Ее общее перемещение составляет (1 м/с)(2 с) + (3 м/с)(2 с) = 8 м (на запад). Общее время в пути: 2 с + 2 с = 4 с. Ее средняя скорость: 8 м / 4 с = 2 м/с (на запад) .
• Борис идет на запад со скоростью 5 м/с в течение 3 секунд, затем разворачивается и идет на восток со скоростью 7 м/с в течение 1 секунды. Мы можем рассматривать движение на восток как «отрицательное движение» на запад, поэтому общее перемещение равно (5 м/с)(3 с) + (-7 м/с)(1 с) = 8 метров. Общее время равно 4 с. Средняя скорость равна 8 м (на запад) / 4 с = 2 м/с (на запад) .
• Юля проходит 1 метр на север, затем проходит 8 метров на запад, а затем проходит 1 метр на юг. Общее время в пути составляет 4 секунды. Нарисуйте схему этого движения на бумаге, и вы увидите, что оно заканчивается в 8 метрах к западу от начальной точки, то есть общее перемещение равно 8 м. Общее время в пути составило 4 секунды. Средняя скорость равна 8 м (на запад) / 4 с = 2 м/с (на запад) .

Инструкция

Рассмотрим функцию f(x) = |x|. Для начала этой без знака модуля, то есть график функции g(x) = x. Этот график является прямой, проходящей через начало координат и угол между этой прямой и положительным направлением оси абсцисс составляет 45 градусов.

Так как модуль величина неотрицательная, то ту часть , которая находится ниже оси абсцисс необходимо зеркально отобразить относительно нее. Для функции g(x) = x получим, что график после такого отображения станет похож на V. Этот новый график и будет являться графической интерпретацией функции f(x) = |x|.

Видео по теме

Обратите внимание

График модуля функции никогда не будет находится в 3 и 4 четверти, так как модуль не может принимать отрицательных значений.

Полезный совет

Если в функции присутствуют несколько модулей, то их нужно раскрывать последовательно, а затем накладывать друг на друга. Результат и будет искомым графиком.

Источники:

• как построить график функции с модулями

Задачи на кинематику, в которых необходимо вычислить скорость , время или путь равномерно и прямолинейно движущихся тел, встречаются в школьном курсе алгебры и физики. Для их решения найдите в условии величины, которые можно между собой уравнять. Если в условии требуется определить время при известной скорости, воспользуйтесь следующей инструкцией.

Вам понадобится

• — ручка;
• — бумага для записей.

Инструкция

Самый простой случай – движение одного тела с заданной равномерной скорость ю. Известно расстояние, которое тело прошло. Найдите в пути: t = S/v, час, где S – расстояние, v – средняя скорость тела.

Второй — на встречное движение тел. Из пункта А в пункт В движется автомобиль со скорость ю 50 км/ч. Навстречу ему из пункта B одновременно выехал мопед со скорость ю 30 км/час. Расстояние между пунктами А и В 100 км. Требуется найти время , через которое они встретятся.

Обозначьте точку встречи К. Пусть расстояние АК, которое автомобиль, будет х км. Тогда путь мотоциклиста составит 100-х км. Из условия задачи следует, что время в пути у автомобиля и мопеда одинаково. Составьте уравнение: х/v = (S-x)/v’, где v, v’ – и мопеда. Подставив данные, решите уравнение: x = 62,5 км. Теперь время : t = 62,5/50 = 1,25 часа или 1 час 15 минут.

Третий пример – даны те же условия, но автомобиль выехал на 20 минут позже мопеда. Определить, времени в пути будет автомобиль до встречи с мопедом.

Составьте уравнение, аналогично предыдущему. Но в этом случае время мопеда в пути будет на 20 минут , чем у автомобиля. Для уравнивания частей, вычтите одну треть часа из правой части выражения: х/v = (S-x)/v’-1/3. Найдите х – 56,25. Вычислите время : t = 56,25/50 = 1,125 часа или 1 час 7 минут 30секунд.

Четвертый пример – задача на движение тел в одном направлении. Автомобиль и мопед с теми же скоростями двигаются из точки А. Известно, что автомобиль выехал на полчаса позже. Через какое время он догонит мопед?

В этом случае одинаковым будет расстояние, которое проехали транспортные средства. Пусть время в пути автомобиля будет x часов, тогда время в пути мопеда будет x+0,5 часов. У вас получилось уравнение: vx = v’(x+0,5). Решите уравнение, подставив значение , и найдите x – 0,75 часа или 45 минут.

Пятый пример – автомобиль и мопед с теми же скоростями двигаются в одном направлении, но мопед выехал из точки В, находящейся на расстоянии 10 км от точки А, на полчаса раньше. Вычислить, через какое время после старта автомобиль догонит мопед.

Расстояние, которое проехал автомобиль, на 10 км больше. Прибавьте эту разницу к пути мотоциклиста и уравняйте части выражения: vx = v’(x+0,5)-10. Подставив значения скорости и решив его, вы получите : t = 1,25 часа или 1 час 15 минут.

Источники:

• какая скорость машины времени

Инструкция

Рассчитайте среднюю тела, движущегося равномерно на протяжении участка пути. Такая скорость вычисляется проще всего, поскольку она не изменяется на всем отрезке движения и равняется средней . Можно это в виде : Vрд = Vср, где Vрд – скорость равномерного движения , а Vср – средняя скорость .

Вычислите среднюю скорость равнозамедленного (равноускоренного) движения на данном участке, для чего необходимо сложить начальную и конечную скорость . Разделите на два полученный результат, который и

Чтобы вычислить среднюю скорость, воспользуйтесь простой формулой: Скорость = Пройденный путь Время {\displaystyle {\text{Скорость}}={\frac {\text{Пройденный путь}}{\text{Время}}}} . Но в некоторых задачах даются два значения скорости — на разных участках пройденного пути или в различные промежутки времени. В этих случаях нужно пользоваться другими формулами для вычисления средней скорости. Навыки решения подобных задач могут пригодиться в реальной жизни, а сами задачи могут встретиться на экзаменах, поэтому запомните формулы и уясните принципы решения задач.

Шаги

По одному значению пути и одному значению времени

• длина пути, пройденного телом;
• время, за которое тело прошло этот путь.
• Например: автомобиль проехал 150 км за 3 ч. Найдите среднюю скорость автомобиля.

1. Формула: , где v {\displaystyle v} — средняя скорость, s {\displaystyle s} — пройденный путь, t {\displaystyle t} — время, за которое пройден путь.

   В формулу подставьте пройденный путь. Значение пути подставьте вместо s {\displaystyle s} .

   • В нашем примере автомобиль проехал 150 км. Формула запишется так: v = 150 t {\displaystyle v={\frac {150}{t}}} .

2. В формулу подставьте время. Значение времени подставьте вместо t {\displaystyle t} .

   • В нашем примере автомобиль ехал в течение 3 ч. Формула запишется так: .

3. Разделите путь на время. Вы найдете среднюю скорость (как правило, она измеряется в километрах в час).

4. Вычислите общий пройденный путь. Для этого сложите значения пройденных участков пути. В формулу подставьте общий пройденный путь (вместо s {\displaystyle s} ).

   • В нашем примере автомобиль проехал 150 км, 120 км и 70 км. Общий пройденный путь: .

5. T {\displaystyle t} ).

   • . Таким образом, формула запишется так: .
6. • В нашем примере:
     v = 340 6 {\displaystyle v={\frac {340}{6}}}

     Таким образом, если автомобиль проехал 150 км за 3 ч, 120 км за 2 ч, 70 км за 1 ч, то он двигался со средней скоростью 57 км/ч (округленно).

По нескольким значениям скоростей и нескольким значениям времени

1. Посмотрите на данные величины. Воспользуйтесь этим методом, если даны следующие величины:

   Запишите формулу для вычисления средней скорости. Формула: v = s t {\displaystyle v={\frac {s}{t}}} , где v {\displaystyle v} — средняя скорость, s {\displaystyle s} — общий пройденный путь, t {\displaystyle t} — общее время, за которое пройден путь.

2. Вычислите общий путь. Для этого умножьте каждую скорость на соответствующее время. Так вы найдете длину каждого участка пути. Чтобы вычислить общий путь, сложите значения пройденных участков пути. В формулу подставьте общий пройденный путь (вместо s {\displaystyle s} ).

   • Например:
     50 км/ч в течение 3 ч = 50 × 3 = 150 {\displaystyle 50\times 3=150} км
     60 км/ч в течение 2 ч = 60 × 2 = 120 {\displaystyle 60\times 2=120} км
     70 км/ч в течение 1 ч = 70 × 1 = 70 {\displaystyle 70\times 1=70} км
     Общий пройденный путь: 150 + 120 + 70 = 340 {\displaystyle 150+120+70=340} км. Таким образом, формула запишется так: v = 340 t {\displaystyle v={\frac {340}{t}}} .

3. Вычислите общее время в пути. Для этого сложите значения времени, за которые был пройден каждый участок пути. В формулу подставьте общее время (вместо t {\displaystyle t} ).

   • В нашем примере автомобиль ехал в течение 3 ч, 2 ч и 1 ч. Общее время в пути: 3 + 2 + 1 = 6 {\displaystyle 3+2+1=6} . Таким образом, формула запишется так: v = 340 6 {\displaystyle v={\frac {340}{6}}} .

4. Разделите общий путь на общее время. Вы найдете среднюю скорость.

   • В нашем примере:
     v = 340 6 {\displaystyle v={\frac {340}{6}}}
     v = 56 , 67 {\displaystyle v=56,67}
     Таким образом, если автомобиль двигался со скоростью 50 км/ч в течение 3 ч, со скоростью 60 км/ч в течение 2 ч, со скоростью 70 км/ч в течение 1 ч, то он двигался со средней скоростью 57 км/ч (округленно).

По двум значениям скоростей и двум одинаковым значениям времени

1. Посмотрите на данные величины. Воспользуйтесь этим методом, если даны следующие величины и условия:

   • два или несколько значений скоростей, с которыми двигалось тело;
   • тело двигалось с определенными скоростями в течение равных промежутков времени.
   • Например: автомобиль двигался со скоростью 40 км/ч в течение 2 ч и со скоростью 60 км/ч в течение других 2 ч. Найдите среднюю скорость автомобиля на всем протяжении пути.

2. Запишите формулу для вычисления средней скорости, если даны две скорости, с которыми тело движется в течение равных промежутков времени. Формула: v = a + b 2 {\displaystyle v={\frac {a+b}{2}}} , где v {\displaystyle v} — средняя скорость, a {\displaystyle a} — скорость тела в течение первого промежутка времени, b {\displaystyle b} — скорость тела в течение второго (такого же, как первый) промежутка времени.

   • В таких задачах значения промежутков времени не важны — главное, чтобы они были равны.
   • Если дано несколько значений скоростей и равные промежутки времени, перепишите формулу так: v = a + b + c 3 {\displaystyle v={\frac {a+b+c}{3}}} или v = a + b + c + d 4 {\displaystyle v={\frac {a+b+c+d}{4}}} . Если промежутки времени равны, сложите все значения скоростей и разделите их на количество таких значений.

3. В формулу подставьте значения скоростей. Неважно, какое значение подставить вместо a {\displaystyle a} , а какое — вместо b {\displaystyle b} .

   • Например, если первая скорость равна 40 км/ч, а вторая скорость равна 60 км/ч, формула запишется так: .

4. Сложите значения двух скоростей. Затем сумму разделите на два. Вы найдете среднюю скорость на всем протяжении пути.

   • Например:
     v = 40 + 60 2 {\displaystyle v={\frac {40+60}{2}}}
     v = 100 2 {\displaystyle v={\frac {100}{2}}}
     v = 50 {\displaystyle v=50}
     Таким образом, если автомобиль двигался со скоростью 40 км/ч в течение 2 ч и со скоростью 60 км/ч в течение других 2 ч, средняя скорость автомобиля на всем протяжении пути составила 50 км/ч.

Сметанный крем с желатином для торта – рецепт

Окунь морской красный рецепты приготовления

Как определить среднюю скорость автомобиля. По какой формуле рассчитывается средняя скорость

Инструкция

Рассмотрим функцию f(x) = |x|. Для начала этой без знака модуля, то есть график функции g(x) = x. Этот график является прямой, проходящей через начало координат и угол между этой прямой и положительным направлением оси абсцисс составляет 45 градусов.

Так как модуль величина неотрицательная, то ту часть , которая находится ниже оси абсцисс необходимо зеркально отобразить относительно нее. Для функции g(x) = x получим, что график после такого отображения станет похож на V. Этот новый график и будет являться графической интерпретацией функции f(x) = |x|.

Видео по теме

Обратите внимание

График модуля функции никогда не будет находится в 3 и 4 четверти, так как модуль не может принимать отрицательных значений.

Полезный совет

Если в функции присутствуют несколько модулей, то их нужно раскрывать последовательно, а затем накладывать друг на друга. Результат и будет искомым графиком.

Источники:

• как построить график функции с модулями

Задачи на кинематику, в которых необходимо вычислить скорость , время или путь равномерно и прямолинейно движущихся тел, встречаются в школьном курсе алгебры и физики. Для их решения найдите в условии величины, которые можно между собой уравнять. Если в условии требуется определить время при известной скорости, воспользуйтесь следующей инструкцией.

Вам понадобится

• — ручка;
• — бумага для записей.

Инструкция

Самый простой случай – движение одного тела с заданной равномерной скорость ю. Известно расстояние, которое тело прошло. Найдите в пути: t = S/v, час, где S – расстояние, v – средняя скорость тела.

Второй — на встречное движение тел. Из пункта А в пункт В движется автомобиль со скорость ю 50 км/ч. Навстречу ему из пункта B одновременно выехал мопед со скорость ю 30 км/час. Расстояние между пунктами А и В 100 км. Требуется найти время , через которое они встретятся.

Обозначьте точку встречи К. Пусть расстояние АК, которое автомобиль, будет х км. Тогда путь мотоциклиста составит 100-х км. Из условия задачи следует, что время в пути у автомобиля и мопеда одинаково. Составьте уравнение: х/v = (S-x)/v’, где v, v’ – и мопеда. Подставив данные, решите уравнение: x = 62,5 км. Теперь время : t = 62,5/50 = 1,25 часа или 1 час 15 минут.

Третий пример – даны те же условия, но автомобиль выехал на 20 минут позже мопеда. Определить, времени в пути будет автомобиль до встречи с мопедом.

Составьте уравнение, аналогично предыдущему. Но в этом случае время мопеда в пути будет на 20 минут , чем у автомобиля. Для уравнивания частей, вычтите одну треть часа из правой части выражения: х/v = (S-x)/v’-1/3. Найдите х – 56,25. Вычислите время : t = 56,25/50 = 1,125 часа или 1 час 7 минут 30секунд.

Четвертый пример – задача на движение тел в одном направлении. Автомобиль и мопед с теми же скоростями двигаются из точки А. Известно, что автомобиль выехал на полчаса позже. Через какое время он догонит мопед?

В этом случае одинаковым будет расстояние, которое проехали транспортные средства. Пусть время в пути автомобиля будет x часов, тогда время в пути мопеда будет x+0,5 часов. У вас получилось уравнение: vx = v’(x+0,5). Решите уравнение, подставив значение , и найдите x – 0,75 часа или 45 минут.

Пятый пример – автомобиль и мопед с теми же скоростями двигаются в одном направлении, но мопед выехал из точки В, находящейся на расстоянии 10 км от точки А, на полчаса раньше. Вычислить, через какое время после старта автомобиль догонит мопед.

Расстояние, которое проехал автомобиль, на 10 км больше. Прибавьте эту разницу к пути мотоциклиста и уравняйте части выражения: vx = v’(x+0,5)-10. Подставив значения скорости и решив его, вы получите : t = 1,25 часа или 1 час 15 минут.

Источники:

• какая скорость машины времени

Инструкция

Рассчитайте среднюю тела, движущегося равномерно на протяжении участка пути. Такая скорость вычисляется проще всего, поскольку она не изменяется на всем отрезке движения и равняется средней . Можно это в виде : Vрд = Vср, где Vрд – скорость равномерного движения , а Vср – средняя скорость .

Вычислите среднюю скорость равнозамедленного (равноускоренного) движения на данном участке, для чего необходимо сложить начальную и конечную скорость . Разделите на два полученный результат, который и

1. Материальная точка прошла половину окружности. Найти отношение средней путевой скорости к модулю средней векторной скорости.

Решение . Из определения средних значений путевой и векторной скоростей с учетом того, что путь, пройденный материальной точкой за время движенияt , равенR , а величина перемещения 2R , гдеR — радиус окружности, получим:

2. Автомобиль проехал первую треть пути со скоростью v 1 = 30 км/ч, а оставшуюся часть пути — со скоростью v 2 = 40 км/ч. Найти среднюю скорость на всем пройденном пути.

Решение . По определению =гдеS — путь, пройденный за времяt . Очевидно, что
Поэтому искомая средняя скорость равна

3. Студент проехал половину пути на велосипеде со скоростьюv 1 = 12 км/ч. Далее половину оставшегося времени он ехал со скоростьюv 2 = 10 км/ч, а оставшуюся часть пути шел пешком со скоростьюv 3 = 6 км/ч. Определить среднюю скорость движения студента на всем пути.

Решение . По определению
гдеS – путь, аt — время движения. Ясно, чтоt =t 1 +t 2 +t 3 . Здесь
— время движения на первой половине пути,t 2 – время движения на втором участке пути иt 3 — на третьем. По условию задачиt 2 =t 3 . Кроме того,S /2 =v 2 t 2 + v 3 t 3 = (v 2 +v 3)t 2 . Отсюда следует:

Подставив t 1 и t 2 +t 3 = 2t 2 в выражение для средней скорости, получим:

4. Расстояние между двумя станциями поезд прошел за времяt 1 = 30 мин. Разгон и торможение длилисьt 2 = 8 мин, а остальное время поезд двигался равномерно со скоростью v = 90 км/ч. Определить среднюю скорость поезда , считая, что при разгоне скорость увеличивалась с течением времени по линейному закону, а при торможении уменьшалась тоже по линейному закону.

Р

ешение . Построим график зависимости скорости поезда от времени (см. рис.). Этот график описывает трапецию с длинами оснований, равнымиt 1 иt 1 –t 2 и высотой, равной v. Площадь этой трапеции численно равна пути, пройденному поездом от начала движения до остановки. Поэтому средняя скорость равна:

Задачи и упражнения

1.1. Мяч упал с высотыh 1 = 4 м, отскочил от пола и был пойман на высотеh 2 = 1 м. Чему равен путьS и величина перемещения
?

1.2. Материальная точка переместилась на плоскости из точки с координатамиx 1 = 1 см иy 1 = 4cм в точку с координатамиx 2 = 5 см иy 2 = 1 см. Построить вектор перемещения и с помощью линейки определить модуль вектора перемещения и проекции вектора перемещения на осиx иy . Найти эти же величины аналитически и сравнить результаты.

1.3. Первую половину пути поезд шел со скоростью вn = 1,5 раза большей, чем вторую половину пути. Средняя скорость поезда на всем пути = 43,2 км/ч. Каковы скорости поезда на первой и второй половинах пути?

1.4. Первую половину времени своего движения велосипедист проехал со скоростью v 1 = 18 км/ч, а вторую половину времени — со скоростью v 2 = 12 км/ч. Определить среднюю скорость движения велосипедиста.

1.5. Движение двух автомобилей описывается уравнениями
и
, где все величины измеряются в системе СИ. Запишите закон изменения расстояния
между автомобилями от времени и найдите
через время
с. после начала движения.

Чтобы вычислить среднюю скорость, воспользуйтесь простой формулой: Скорость = Пройденный путь Время {\displaystyle {\text{Скорость}}={\frac {\text{Пройденный путь}}{\text{Время}}}} . Но в некоторых задачах даются два значения скорости — на разных участках пройденного пути или в различные промежутки времени. В этих случаях нужно пользоваться другими формулами для вычисления средней скорости. Навыки решения подобных задач могут пригодиться в реальной жизни, а сами задачи могут встретиться на экзаменах, поэтому запомните формулы и уясните принципы решения задач.

Шаги

По одному значению пути и одному значению времени

• длина пути, пройденного телом;
• время, за которое тело прошло этот путь.
• Например: автомобиль проехал 150 км за 3 ч. Найдите среднюю скорость автомобиля.

1. Формула: , где v {\displaystyle v} — средняя скорость, s {\displaystyle s} — пройденный путь, t {\displaystyle t} — время, за которое пройден путь.

   В формулу подставьте пройденный путь. Значение пути подставьте вместо s {\displaystyle s} .

   • В нашем примере автомобиль проехал 150 км. Формула запишется так: v = 150 t {\displaystyle v={\frac {150}{t}}} .

2. В формулу подставьте время. Значение времени подставьте вместо t {\displaystyle t} .

   • В нашем примере автомобиль ехал в течение 3 ч. Формула запишется так: .

3. Разделите путь на время. Вы найдете среднюю скорость (как правило, она измеряется в километрах в час).

4. Вычислите общий пройденный путь. Для этого сложите значения пройденных участков пути. В формулу подставьте общий пройденный путь (вместо s {\displaystyle s} ).

   • В нашем примере автомобиль проехал 150 км, 120 км и 70 км. Общий пройденный путь: .

5. T {\displaystyle t} ).

   • . Таким образом, формула запишется так: .
6. • В нашем примере:
     v = 340 6 {\displaystyle v={\frac {340}{6}}}

     Таким образом, если автомобиль проехал 150 км за 3 ч, 120 км за 2 ч, 70 км за 1 ч, то он двигался со средней скоростью 57 км/ч (округленно).

По нескольким значениям скоростей и нескольким значениям времени

1. Посмотрите на данные величины. Воспользуйтесь этим методом, если даны следующие величины:

   Запишите формулу для вычисления средней скорости. Формула: v = s t {\displaystyle v={\frac {s}{t}}} , где v {\displaystyle v} — средняя скорость, s {\displaystyle s} — общий пройденный путь, t {\displaystyle t} — общее время, за которое пройден путь.

2. Вычислите общий путь. Для этого умножьте каждую скорость на соответствующее время. Так вы найдете длину каждого участка пути. Чтобы вычислить общий путь, сложите значения пройденных участков пути. В формулу подставьте общий пройденный путь (вместо s {\displaystyle s} ).

   • Например:
     50 км/ч в течение 3 ч = 50 × 3 = 150 {\displaystyle 50\times 3=150} км
     60 км/ч в течение 2 ч = 60 × 2 = 120 {\displaystyle 60\times 2=120} км
     70 км/ч в течение 1 ч = 70 × 1 = 70 {\displaystyle 70\times 1=70} км
     Общий пройденный путь: 150 + 120 + 70 = 340 {\displaystyle 150+120+70=340} км. Таким образом, формула запишется так: v = 340 t {\displaystyle v={\frac {340}{t}}} .

3. Вычислите общее время в пути. Для этого сложите значения времени, за которые был пройден каждый участок пути. В формулу подставьте общее время (вместо t {\displaystyle t} ).

   • В нашем примере автомобиль ехал в течение 3 ч, 2 ч и 1 ч. Общее время в пути: 3 + 2 + 1 = 6 {\displaystyle 3+2+1=6} . Таким образом, формула запишется так: v = 340 6 {\displaystyle v={\frac {340}{6}}} .

4. Разделите общий путь на общее время. Вы найдете среднюю скорость.

   • В нашем примере:
     v = 340 6 {\displaystyle v={\frac {340}{6}}}
     v = 56 , 67 {\displaystyle v=56,67}
     Таким образом, если автомобиль двигался со скоростью 50 км/ч в течение 3 ч, со скоростью 60 км/ч в течение 2 ч, со скоростью 70 км/ч в течение 1 ч, то он двигался со средней скоростью 57 км/ч (округленно).

По двум значениям скоростей и двум одинаковым значениям времени

1. Посмотрите на данные величины. Воспользуйтесь этим методом, если даны следующие величины и условия:

   • два или несколько значений скоростей, с которыми двигалось тело;
   • тело двигалось с определенными скоростями в течение равных промежутков времени.
   • Например: автомобиль двигался со скоростью 40 км/ч в течение 2 ч и со скоростью 60 км/ч в течение других 2 ч. Найдите среднюю скорость автомобиля на всем протяжении пути.

2. Запишите формулу для вычисления средней скорости, если даны две скорости, с которыми тело движется в течение равных промежутков времени. Формула: v = a + b 2 {\displaystyle v={\frac {a+b}{2}}} , где v {\displaystyle v} — средняя скорость, a {\displaystyle a} — скорость тела в течение первого промежутка времени, b {\displaystyle b} — скорость тела в течение второго (такого же, как первый) промежутка времени.

   • В таких задачах значения промежутков времени не важны — главное, чтобы они были равны.
   • Если дано несколько значений скоростей и равные промежутки времени, перепишите формулу так: v = a + b + c 3 {\displaystyle v={\frac {a+b+c}{3}}} или v = a + b + c + d 4 {\displaystyle v={\frac {a+b+c+d}{4}}} . Если промежутки времени равны, сложите все значения скоростей и разделите их на количество таких значений.

3. В формулу подставьте значения скоростей. Неважно, какое значение подставить вместо a {\displaystyle a} , а какое — вместо b {\displaystyle b} .

   • Например, если первая скорость равна 40 км/ч, а вторая скорость равна 60 км/ч, формула запишется так: .

4. Сложите значения двух скоростей. Затем сумму разделите на два. Вы найдете среднюю скорость на всем протяжении пути.

   • Например:
     v = 40 + 60 2 {\displaystyle v={\frac {40+60}{2}}}
     v = 100 2 {\displaystyle v={\frac {100}{2}}}
     v = 50 {\displaystyle v=50}
     Таким образом, если автомобиль двигался со скоростью 40 км/ч в течение 2 ч и со скоростью 60 км/ч в течение других 2 ч, средняя скорость автомобиля на всем протяжении пути составила 50 км/ч.

Средней скоростью называется скорость, которая получается, если весь путь поделить на время, за которое объект преодолел этот путь. Формула средней скорости:

• V ср = S/t.
• S = S1 + S2 + S3 = v1*t1 + v2*t2 + v3*t3
• V ср = S/t = (v1*t1 + v2*t2 + v3*t3) / (t1 + t2 + t3)

Чтобы не путаться с часами и минутами, переводим все минуты в часы: 15 мин. = 0,4 час, 36 мин. = 0,6 час. Подставляем числовые значения в последнюю формулу:

• V ср = (20*0,4 + 0,5*6 + 0,6*15) / (0,4 + 0,5 + 0,6) = (8 + 3 + 9) / (0,4 + 0,5 + 0,6) = 20 / 1,5 = 13,3 км/час

Ответ: средняя скорость V ср = 13,3 км/час.

Как найти среднюю скорость движения с ускорением

Если скорость в начале движения отличается от скорости в его конце, такое движение называют ускоренным. Причём далеко не всегда тело действительно двигается всё быстрее и быстрее. Если движение замедляется, всё равно говорят, что оно движется с ускорением, только ускорение будет уже отрицательным.

Иными словами, если автомобиль, трогаясь с места, через секунду разогнался до скорости 10 м/сек, то его ускорение а равно 10 м в секунду за секунду а = 10 м/сек². Если в следующую секунду автомобиль остановился, то его ускорение тоже равно 10 м/сек², только уже со знаком минус: а = -10 м/сек².

Скорость движения с ускорением в конце временного отрезка вычисляется по формуле:

• V = V0 ± at,

где V0 — начальная скорость движения, a — ускорение, t — время, за которое наблюдалось данное ускорение. Плюс или минус в формуле ставится в зависимости от того, увеличивалась скорость или уменьшалась.

Средняя скорость за отрезок времени t вычисляется как среднее арифметическое начальной и конечной скорости:

• V ср = (V0 + V) / 2.

Находим среднюю скорость: задача

Шарик толкнули по ровной плоскости с начальной скоростью V0 = 5 м/сек. Через 5 сек. шарик остановился. Чему равны ускорение и средняя скорость?

Конечная скорость шарика V = 0 м/сек. Ускорение из первой формулы равно

• а = (V — V0)/ t = (0 — 5)/ 5 = — 1 м/сек².

Средняя скорость V ср = (V0 + V) / 2= 5 /2 = 2,5 м/сек.

Помните, что скорость задается как численным значением, так и направлением. Скорость описывает быстроту изменения положения тела, а также направление, в котором движется это тело. Например, 100 м/с (на юг).

7. Найдите общее перемещение, то есть расстояние и направление между начальной и конечной точками пути. В качестве примера рассмотрим тело, движущееся с постоянной скоростью в одном направлении.

   • Например, ракета была запущена в северном направлении и двигалась в течение 5 минут с постоянной скоростью 120 метров в минуту. Чтобы вычислить общее перемещение, воспользуйтесь формулой s = vt: (5 минут) (120 м/мин) = 600 м (на север) .
   • Если в задаче дано постоянное ускорение, воспользуйтесь формулой s = vt + ½at 2 (в следующем разделе описывается упрощенный способ работы с постоянным ускорением).

8. Найдите общее время в пути. В нашем примере ракета перемещается в течение 5 минут. Среднюю скорость можно выразить в любых единицах измерения, но в международной системе единиц скорость измеряется в метрах в секунду (м/с). Конвертируйте минуты в секунды: (5 минут) х (60 секунд/минута) = 300 секунд .

   • Если даже в научной задаче время дано в часах или других единицах измерения, лучше сначала вычислить скорость, а затем преобразовать ее в м/с.

9. Вычислите среднюю скорость. Если вы знаете значение перемещения и общее время в пути, вычислить среднюю скорость можно по формуле v ср = Δs/Δt. В нашем примере средняя скорость ракеты равна 600 м (на север) / (300 секунд) = 2 м/с (на север) .

   • Не забудьте указать направление движения (например, «вперед» или «на север»).
   • В формуле v ср = Δs/Δt символ «дельта» (Δ) означает «изменение величины», то есть Δs/Δt означает «изменение положения к изменению времени».
   • Средняя скорость может быть записана как v ср или как v с горизонтальной чертой сверху.

10. Решение более сложных задач, например, если тело вращается или ускорение не является постоянным. В этих случаях средняя скорость по-прежнему вычисляется как отношение общего перемещения к общему времени. Не имеет значения, что происходит с телом между начальной и конечной точками пути. Вот несколько примеров задач с одинаковым общим перемещением и общим временем (а, следовательно, и одинаковой средней скоростью).

    • Анна идет на запад со скоростью 1 м/с в течение 2 секунд, затем мгновенно ускоряется до 3 м/с и продолжает идти на запад в течение 2 секунд. Ее общее перемещение составляет (1 м/с)(2 с) + (3 м/с)(2 с) = 8 м (на запад). Общее время в пути: 2 с + 2 с = 4 с. Ее средняя скорость: 8 м / 4 с = 2 м/с (на запад) .
    • Борис идет на запад со скоростью 5 м/с в течение 3 секунд, затем разворачивается и идет на восток со скоростью 7 м/с в течение 1 секунды. Мы можем рассматривать движение на восток как «отрицательное движение» на запад, поэтому общее перемещение равно (5 м/с)(3 с) + (-7 м/с)(1 с) = 8 метров. Общее время равно 4 с. Средняя скорость равна 8 м (на запад) / 4 с = 2 м/с (на запад) .
    • Юля проходит 1 метр на север, затем проходит 8 метров на запад, а затем проходит 1 метр на юг. Общее время в пути составляет 4 секунды. Нарисуйте схему этого движения на бумаге, и вы увидите, что оно заканчивается в 8 метрах к западу от начальной точки, то есть общее перемещение равно 8 м. Общее время в пути составило 4 секунды. Средняя скорость равна 8 м (на запад) / 4 с = 2 м/с (на запад) .

Сметанный крем с желатином для торта – рецепт

Окунь морской красный рецепты приготовления

Вопрос Видео: Расчет средней скорости автомобиля

Стенограмма видео

Автомобиль движется из точки 𝐴 в точку 𝐷, как показано на диаграмме ниже. Автомобиль перемещается из 𝐴 в 𝐵 за 100 секунд, затем от 𝐵 до 𝐶 за 40 секунд, а затем от 𝐶 до 𝐷 за 60 секунд. Рассчитайте величину средняя скорость автомобиля.

Начнем с того, что вспомним, что средняя скорость 𝑣 объекта определяется формулой 𝑣 равно Δ𝑠, деленному на Δ𝑡, где объект имеет некоторое смещение Δ𝑠 за интервал времени Δ𝑡. Важно помнить, что перемещение автомобиля, Δ𝑠, это просто расстояние по прямой от его начального указать на его конечную точку. Так что хоть машина и ехала весь этот путь из точки 𝐴 в точку 𝐷, это не соответствует его смещение. Скорее, его смещение просто вдоль прямой линии, соединяющей точки 𝐴 и 𝐷, показанной здесь пунктиром линия.

Обратите внимание, что если бы мы использовали общее расстояние, которое автомобиль проехал от точки 𝐴 до 𝐵 до 𝐶, затем 𝐷, мы бы вычисляли его среднюю скорость, а не его среднюю скорость. Итак, чтобы ответить на этот вопрос правильно, мы должны быть осторожны, чтобы использовать объем автомобиля, а не общее пройденное расстояние.

Теперь пути автомобиля по первый и третий этапы его общего путешествия параллельны. Таким образом, если бы мы соединили все четыре точки от 𝐴 до 𝐷, мы бы сделали параллелограмм. Благодаря этому мы можем принять величина водоизмещения автомобиля составит 0,8 километра. Следовательно, мы знаем, что Δ𝑠 равно 0,8 км. Будет хорошей идеей преобразовать величина водоизмещения от километров до простых метров. Таким образом, мы закончим финал значение скорости в метрах в секунду. Мы знаем, что километр равен 1000 метров. Итак, 0,8 километра равно 800. метров. Итак, мы знаем, что Δ𝑠 равно 800. метров.

Далее, чтобы найти Δ𝑡, время интервал, нам просто нужно сложить общее время, которое понадобилось машине, чтобы добраться из точка 𝐴 к точке 𝐷. Время, затраченное на первый, вторая и третья части пути автомобиля составляли 100 секунд, 40 секунд и 60 секунд соответственно. Итак, складывая их вместе, находим что Δ𝑡 равно 200 секундам.

Теперь, когда у нас есть значения для Δ𝑠 и Δ𝑡, давайте подставим их в формулу скорости. Мы находим, что автомобиль в среднем скорость равна 800 метров разделить на 200 секунд. Наконец, оценивая это выражение, мы получаем результат четыре метра в секунду, и это наш окончательный отвечать. Мы обнаружили, что в среднем скорость автомобиля четыре метра в секунду.

Как определить среднюю скорость автомобиля. По какой формуле рассчитывается средняя скорость?

Инструкция

Рассмотрим функцию f(x) = |x|. Для начала это беззнаковый модуль, то есть график функции g(x) = x. Этот график представляет собой прямую линию, проходящую через начало координат, и угол между этой прямой линией и положительным направлением оси x составляет 45 градусов.

Поскольку модуль является неотрицательным значением, то часть, которая находится ниже оси x, должна быть отражена относительно него. Для функции g(x) = x получаем, что график после такого отображения станет подобным V. Этот новый график будет графической интерпретацией функции f(x) = |x|.

Видео по теме

примечание

График модуля функции никогда не будет находиться в 3-й и 4-й четвертях, так как модуль не может принимать отрицательных значений.

Полезный совет

Если в функции несколько модулей, то их нужно последовательно разворачивать, а потом накладывать друг на друга. В результате получится нужный график.

Источники:

• как построить график функции с модулями

Задачи по кинематике, в которых необходимо считать скорость , время или путь равномерно и прямолинейно движущихся тел, встречаются в школьном курсе алгебры и физики. Для их решения найдите в условии величины, которые можно уравнять между собой. Если условие требует определения времени с известной скоростью, используйте следующую инструкцию.

Вам понадобится

• — ручка;
• — бумага для заметок.

Инструкция

Простейший случай — движение одного тела с заданной равномерной скорость Ю. Путь, пройденный телом, известен. В пути находим: t = S/v, час, где S — расстояние, v — средняя скорость тела.

Второй — на встречное движение тел. Автомобиль движется из пункта А в пункт В со скоростью u 50 км/ч. В то же время мопед с развивает скорость до 30 км/ч. Расстояние между пунктами А и В равно 100 км. Хотел найти время , через которое они встречаются.

Обозначим точку встречи K. Пусть расстояние AK, на котором находится автомобиль, равно x км. Тогда путь мотоциклиста составит 100 км. Из условия задачи следует, что время в дороге машина и мопед одинаковые. Напишите уравнение: x/v = (S-x)/v’, где v, v’ — и мопед. Подставив данные, решить уравнение: x = 62,5 км. Теперь время : t = 62,5/50 = 1,25 часа или 1 час 15 минут.

Третий пример — даны те же условия, но машина уехала на 20 минут позже мопеда. Определить время в пути будет автомобиль до встречи с мопедом.

Напишите уравнение, подобное предыдущему. Но в данном случае время Поездка мопеда будет на 20 минут больше, чем у автомобиля. Чтобы уравнять части, вычтите одну треть часа из правой части выражения: x/v = (S-x)/v’-1/3. Найдите х — 56,25. Вычислите время : t = 56,25/50 = 1,125 часа или 1 час 7 минут 30 секунд.

Четвертый пример — задача о движении тел в одном направлении. Автомобиль и мопед движутся из точки А с одинаковой скоростью. Известно, что машина уехала через полчаса. Через что время догонит ли он мопед?

В этом случае расстояние, пройденное транспортными средствами, будет одинаковым. Пусть время машина проедет x часов, тогда время мопед проедет x+0,5 часа. У вас есть уравнение: vx = v'(x+0,5). Решите уравнение, подставив значение, и найдите x — 0,75 часа или 45 минут.

Пятый пример — автомобиль и мопед с одинаковыми скоростями движутся в одном направлении, но мопед выехал из пункта Б, расположенного на расстоянии 10 км от пункта А, на полчаса раньше. Рассчитать через что время после старта машина обгонит мопед.

Расстояние, пройденное автомобилем, на 10 км больше. Добавьте эту разницу к пути всадника и уравняйте части выражения: vx = v'(x+0,5)-10. Подставив значения скорости и решив ее, получим: t = 1,25 часа или 1 час 15 минут.

Источники:

• какова скорость машины времени

Инструкция

Вычислить среднее значение тела, движущегося равномерно по отрезку пути. Таких скорость вычислить проще всего, так как она не меняется на всем отрезке движений и равна средней. Он может быть в виде: Vrd = Vav, где Vrd — скорость равномерная движения , а Vav — средняя скорость .

Рассчитать среднюю скорость равномедленные (равномерно ускоренные) движения в этой области, для чего необходимо сложить начальную и конечную скорость . Разделите на два полученный результат, который равен

1. Материальная точка прошла половину окружности. Найти отношение средней путевой скорости к модулю средней векторной скорости.

Раствор . Из определения средних значений путевой и векторной скоростей с учетом того, что путь, пройденный материальной точкой при движении t , равен  R , а величина перемещения 2 Р , где Р — радиус окружности, получаем:

2. Первую треть пути автомобиль проехал со скоростью v 1 = 30 км/ч, а оставшуюся часть пути — со скоростью v 2 = 40 км/ч. Найдите среднюю скорость на всем пути.

Раствор . По определению = где S — пройденный путь за время t . Очевидно, что
Следовательно, искомая средняя скорость равна

3. Студент проехал половину пути на велосипеде со скоростью v 1 = 12 км/ч. Затем половину оставшегося времени он шел со скоростью v 2 = 10 км/ч, а оставшуюся часть пути шел со скоростью v 3 = 6 км/ч. Определить среднюю скорость студента на всем пути.

Раствор . По определению
, где S- путь, а t — время движения. Ясно, что т = т 1 + т 2 + т 3 . Здесь
— время в пути на первой половине пути, t 2 — время движения на втором участке пути и t 3 — на третьем. По заданию t 2 = t 3 . Кроме того, S /2=v2 t 2 + v3 t 3 = (v 2 +v 3) t 2. Отсюда следует:

t 3 = 2 t 2 в выражение для средней скорости получаем:

4. Расстояние между двумя станциями, пройденное поездом за время t 1 = 30 мин. Разгон и торможение продолжались t 2 = 8 мин, а в остальное время поезд двигался равномерно со скоростью v = 90 км/ч. Найти среднюю скорость поезда, считая, что при разгоне скорость возрастала со временем по линейному закону, а при торможении также уменьшалась по линейному закону.

Р

решение . Построим график зависимости скорости поезда от времени (см. рис.). Этот граф описывает трапецию с длинами оснований, равными t 1 и t 1 – t 2, и высотой, равной v. Площадь этой трапеции численно равна пути, пройденному поездом с начала движения до упора. Значит средняя скорость:

Задания и упражнения

1.1. Мяч упал с высоты ч 1 = 4 м, отскочил от пола и был пойман на высоте ч 2 = 1 м. Что такое путь S и величина смещения
?

1.2. Материальная точка переместилась на плоскости из точки с координатами х 1 = 1 см и у 1 = 4 см в точку с координатами х 2 = 5 см и у 2 = 1 см х и и . Аналитически найдите те же величины и сравните результаты.

1.3. Первую половину пути поезд шел со скоростью n = 1,5 раза большей, чем вторую половину пути. Средняя скорость поезда на всем пути = 43,2 км/ч. Каковы скорости поезда на первом и втором участках пути?

1. 4. Первую половину времени своего движения велосипедист проехал со скоростью v 1 = 18 км/ч, а вторую половину времени — со скоростью v 2 = 12 км/ч. Определить среднюю скорость велосипедиста.

1.5. Движение двух автомобилей описывается уравнениями
и
, где все величины измеряются в системе СИ. Запишите закон изменения расстояния
между автомобилями время от времени и найдите
через время
С. после начала движения.

Для расчета средней скорости используйте простую формулу: Скорость = Пройденное расстояние Время (\displaystyle (\text(Скорость))=(\frac (\text(Пройденное расстояние))(\text(Время)))) . Но в некоторых заданиях даются два значения скорости — на разных участках пройденного пути или в разные промежутки времени. В этих случаях нужно использовать другие формулы для расчета средней скорости. Навыки решения таких задач могут пригодиться в реальной жизни, а сами задачи могут встретиться на экзаменах, поэтому запоминайте формулы и разбирайтесь в принципах решения задач.

Шаги

Одно значение пути и одно значение времени

• длина пути, пройденного телом;
• время, которое потребовалось телу, чтобы пройти этот путь.
• Например: автомобиль проехал 150 км за 3 часа. Найдите среднюю скорость автомобиля.

1. Формула: где v (\displaystyle v)- средняя скорость, s (\displaystyle s)- пройденное расстояние, t (\displaystyle t)- время, затраченное на поездку.

   Подставьте пройденное расстояние в формулу. Замените значение пути на s (\displaystyle s).

   • В нашем примере машина проехала 150 км. Формула запишется так: v = 150 t (\displaystyle v=(\frac (150)(t))).

2. Подставьте время в формулу. Замените значение времени на t (\displaystyle t).

   • В нашем примере машина ехала 3 часа. Формула будет записана следующим образом:.

3. Разделить путь на время. Вы найдете среднюю скорость (обычно она измеряется в километрах в час).

4. Рассчитать общее пройденное расстояние. Для этого складываем значения пройденных участков пути. Подставьте в формулу общее пройденное расстояние (вместо s (\displaystyle s)).

   • В нашем примере машина проехала 150 км, 120 км и 70 км. Общее пройденное расстояние: .

5. Т (\displaystyle t)).

   • . Таким образом, формула будет записана как:.
6. • В нашем примере:
     v = 340 6 (\displaystyle v=(\frac (340)(6)))

     Таким образом, если автомобиль проехал 150 км за 3 часа, 120 км за 2 часа, 70 км за 1 час, то он двигался со средней скоростью 57 км/ч (округленно).

Несколько скоростей и несколько раз

1. Посмотрите на эти значения. Используйте этот метод, если даны следующие количества:

   Запишите формулу расчета средней скорости. Формула: v = s t (\displaystyle v=(\frac (s)(t))), где v (\displaystyle v)- средняя скорость, s (\displaystyle s)- общее пройденное расстояние, t (\displaystyle t ) — это общее время, затраченное на поездку.

2. Рассчитать общий путь. Для этого умножьте каждую скорость на соответствующее время. Это даст вам длину каждого участка пути. Чтобы рассчитать общий путь, сложите значения пройденных отрезков пути. Подставьте в формулу общее пройденное расстояние (вместо s (\displaystyle s)).

   • Например:
     50 км/ч за 3 часа = 50 × 3 = 150 (\displaystyle 50\times 3=150) км
     60 км/ч за 2 часа = 60 × 2 = 120 (\displaystyle 60\ умножить на 2=120) км
     70 км/ч за 1 час = 70 × 1 = 70 (\displaystyle 70\times 1=70) км
     Общее пройденное расстояние: 150 + 120 + 70 = 340 (\displaystyle 150+120+ 70=340) км. Таким образом, формула запишется так: v = 340 t (\displaystyle v=(\frac (340)(t))).

3. Рассчитать общее время в пути. Для этого складываем значения времени, за которое был пройден каждый участок пути. Подставьте общее время в формулу (вместо t (\displaystyle t)).

   • В нашем примере машина ехала 3 часа, 2 часа и 1 час. Общее время в пути: 3 + 2 + 1 = 6 (\displaystyle 3+2+1=6). Таким образом, формула запишется так: v = 340 6 (\displaystyle v=(\frac (340)(6))).

4. Разделите общее расстояние на общее время. Вы найдете среднюю скорость.

   • В нашем примере:
     v = 340 6 (\displaystyle v=(\frac (340)(6)))
     v = 56 , 67 (\displaystyle v=56,67)
     Таким образом, если автомобиль был двигался со скоростью 50 км/ч 3 часа, со скоростью 60 км/ч 2 часа, со скоростью 70 км/ч 1 час, затем двигался со средней скоростью 57 км/ч. (округленный).

На две скорости и два одинаковых времени

1. Посмотрите на эти значения. Используйте этот метод, если даны следующие количества и условия:

   • две или более скоростей, с которыми двигалось тело;
   • тело движется с определенной скоростью в течение равных промежутков времени.
   • Например: автомобиль ехал со скоростью 40 км/ч 2 часа и со скоростью 60 км/ч еще 2 часа. Найдите среднюю скорость автомобиля на всем пути.

2. Запишите формулу для расчета средней скорости при двух скоростях, с которыми тело движется в течение равных промежутков времени. Формула: v = a + b 2 (\displaystyle v=(\frac (a+b)(2))), где v (\displaystyle v)- средняя скорость, a (\displaystyle a)- скорость тела за первый промежуток времени, b (\displaystyle b)- скорость тела за второй (такой же, как и первый) промежуток времени.

   • В таких задачах значения временных интервалов не важны — главное, чтобы они были равны.
   • Для заданных скоростей и равных интервалов времени перепишите формулу следующим образом: v = a + b + c 3 (\displaystyle v=(\frac (a+b+c)(3))) или v = a + b + c + d 4 (\displaystyle v=(\frac (a+b+c+d)(4))). Если временные интервалы равны, сложите все значения скорости и разделите их на количество таких значений.

3. Подставляем значения скорости в формулу. Не имеет значения, какое значение подставлять вместо a (\displaystyle a), а какое вместо b (\displaystyle b).

   • Например, если первая скорость равна 40 км/ч, а вторая скорость равна 60 км/ч, формула будет выглядеть так: .

4. Сложите две скорости. Затем разделите сумму на два. Вы найдете среднюю скорость на всем пути.

   • Например:
     v = 40 + 60 2 (\displaystyle v=(\frac (40+60)(2)))
     v = 100 2 (\displaystyle v=(\frac (100)(2) ))
     v=50 (\displaystyle v=50)
     Таким образом, если автомобиль ехал 2 часа со скоростью 40 км/ч и еще 2 часа со скоростью 60 км/ч, то средняя скорость автомобиля за весь путь составлял 50 км/ч.

Средняя скорость — это скорость, которая получается, если весь путь разделить на время, в течение которого объект прошел этот путь. Формула средней скорости:

• В ср = S/t.
• S = S1 + S2 + S3 = v1*t1 + v2*t2 + v3*t3
• Vav = S/t = (v1*t1 + v2*t2 + v3*t3) / (t1 + t2 + t3)

Чтобы не путаться с часами и минутами, все минуты переводим в часы: 15 мин. = 0,4 часа 36 мин. = 0,6 часа. Подставляем числовые значения в последнюю формулу:

• В ср = (20 * 0,4 + 0,5 * 6 + 0,6 * 15) / (0,4 + 0,5 + 0,6) = (8 + 3 + 9) / (0,4 + 0,5 + 0,6) = 20 / 1,5 = 13,3 км/ч

Ответ: средняя скорость V ср = 13,3 км/ч.

Как найти среднюю скорость движения с ускорением

Если скорость в начале движения отличается от скорости в его конце, такое движение называется ускоренным. Более того, тело не всегда движется все быстрее и быстрее. Если движение замедляется, еще говорят, что оно движется с ускорением, только ускорение будет уже отрицательным.

Другими словами, если автомобиль, тронувшись с места, за секунду разогнался до скорости 10 м/с, то его ускорение равно 10 м в секунду за секунду а = 10 м/с². Если в следующую секунду автомобиль остановился, то его ускорение также равно 10 м/с², только со знаком минус: а = -10 м/с².

Скорость движения с ускорением в конце временного интервала вычисляется по формуле:

• V = V0 ± at,

где V0 — начальная скорость движения, a — ускорение, t — время, в течение которого наблюдалось это ускорение. Плюс или минус в формуле ставится в зависимости от того, увеличилась или уменьшилась скорость.

Средняя скорость за период времени t рассчитывается как среднее арифметическое начальной и конечной скоростей:

• Vav = (V0 + V) / 2.

Нахождение средней скорости: задача

Мяч толкают по плоской плоскости с начальной скоростью V0 = 5 м/с. Через 5 сек. мяч остановился. Какое ускорение и средняя скорость?

Конечная скорость мяча V = 0 м/с. Ускорение из первой формулы равно

• a = (V — V0) / t = (0 — 5) / 5 = — 1 м/с².

Средняя скорость V ср = (V0 + V) / 2 = 5 / 2 = 2,5 м/с.

Помните, что скорость задается как числовым значением, так и направлением. Скорость описывает скорость изменения положения тела, а также направление, в котором это тело движется. Например, 100 м/с (на юг).

7. Найдите полное перемещение, т. е. расстояние и направление между начальной и конечной точками пути. В качестве примера рассмотрим тело, движущееся с постоянной скоростью в одном направлении.

   • Например, ракета была запущена в северном направлении и двигалась в течение 5 минут с постоянной скоростью 120 метров в минуту. Для расчета полного смещения используйте формулу s = vt: (5 минут) (120 м/мин) = 600 м (север) .
   • Если в вашей задаче задано постоянное ускорение, используйте формулу s = vt + ½at 2 (в следующем разделе описан упрощенный способ работы с постоянным ускорением).

8. Найдите общее время в пути. В нашем примере ракета летит 5 минут. Средняя скорость может быть выражена в любых единицах измерения, но в международной системе единиц скорость измеряется в метрах в секунду (м/с). Преобразование минут в секунды: (5 минут) x (60 секунд/минуту) = 300 секунд .

   • Даже если в научной задаче время указано в часах или других единицах, лучше сначала вычислить скорость, а затем перевести ее в м/с.

9. Рассчитать среднюю скорость. Если известно значение смещения и общее время в пути, можно рассчитать среднюю скорость по формуле v av = Δs/Δt. В нашем примере средняя скорость ракеты 600 м (север) / (300 секунд) = 2 м/с (север) .

   • Обязательно укажите направление движения (например, «вперед» или «на север»).
   • В формуле vav = ∆s/∆t символ «дельта» (Δ) означает «изменение величины», то есть Δs/Δt означает «изменение положения на изменение времени».
   • Средняя скорость может быть записана как v avg или как v с горизонтальной чертой над ней.

10. Решение более сложных задач, например, если тело вращается или ускорение непостоянно. В этих случаях средняя скорость по-прежнему рассчитывается как отношение полного перемещения к общему времени. Неважно, что происходит с телом между начальной и конечной точками пути. Вот несколько примеров задач с одинаковым полным водоизмещением и полным временем (и, следовательно, с одной и той же средней скоростью).

    • Анна идет на запад со скоростью 1 м/с в течение 2 секунд, затем мгновенно ускоряется до 3 м/с и продолжает идти на запад в течение 2 секунд. Его полное перемещение равно (1 м/с)(2 с) + (3 м/с)(2 с) = 8 м (на запад). Общее время в пути: 2 с + 2 с = 4 с. Ее средняя скорость: 8 м / 4 с = 2 м/с (запад) .
    • Борис идет на запад со скоростью 5 м/с в течение 3 секунд, затем разворачивается и идет на восток со скоростью 7 м/с в течение 1 секунды. Мы можем думать о движении на восток как об «отрицательном движении» на запад, поэтому общее движение равно (5 м/с)(3 с) + (-7 м/с)(1 с) = 8 метров. Общее время 4 с. Средняя скорость 8 м (запад) / 4 с = 2 м/с (запад) .
    • Джулия проходит 1 метр на север, затем проходит 8 метров на запад, а затем проходит 1 метр на юг. Общее время в пути 4 секунды. Нарисуйте на бумаге схему этого движения, и вы увидите, что оно заканчивается в 8 метрах к западу от начальной точки, то есть общее движение составляет 8 м.