Идеальный газ — определение, свойства, условия
В жизни мы встречаем вещества в газообразном состоянии, когда чувствуем запахи. Запах очень легко распространяется, потому что газ не имеет ни формы, ни объема (занимает весь предоставленный объем) и состоит из хаотично движущихся молекул, расстояние между которыми больше, чем размеры молекул.
Агрегатных состояний точно три?
На самом деле есть еще четвертое — плазма. Звучит как что-то из научной фантастики, но это просто ионизированный газ — газ, в котором, помимо нейтральных частиц, есть еще и заряженные. Ионизаторы воздуха как раз строятся на принципе перехода из газообразного вещества в плазму.
Модель идеального газа
В физике есть такое понятие, как модель. Модель — это что-то идеализированное, она нужна в случаях, когда можно пренебречь некоторыми параметрами объекта или процесса.
Идеальный газ — это модель реального газа.
Важно знать
Модель идеального газа не может описать ситуацию, когда газ сжимают так сильно, что он конденсируется — переходит в жидкое состояние.
В повседневной жизни идеальный газ, конечно, не встречается. Но реальный газ может вести себя почти как идеальный. Такое случается, если среднее расстояние между молекулами во много раз больше их размеров, то есть если газ очень разреженный.
Свойства идеального газа
- Расстояние между молекулами значительно больше размеров молекул.
- Молекулы газа очень малы и представляют собой упругие шары.
- Силы притяжения между молекулами пренебрежимо малы.
- Молекулы взаимодействуют только при соударениях.
- Молекулы движутся хаотично.
- Молекулы движутся по законам Ньютона.
Среднеквадратичная скорость
Потенциальной энергией молекул газа пренебречь можно, а вот кинетической — никак нельзя. Потому что кинетическая энергия — это энергия движения, а мы не можем пренебрегать скоростью движения молекул.
На графике показано распределение Максвелла — то, как молекулы распределяются по скоростям. Судя по графику, большинство молекул движутся со средним значением скорости. Хотя есть и быстрые, и медленные молекулы, просто их значительно меньше.
Но наш газ идеальный, а в идеальном газе случаются чудеса. Одно из таких чудес — то, что все молекулы идеального газа двигаются с одинаковой скоростью. Эта скорость называется
Средняя квадратичная скорость v1, v2, vn — скорости разных молекул [м/с] N — количество молекул [-] |
Давление идеального газа
Молекулы газа беспорядочно движутся.
Во время движения они сталкиваются друг с другом, а также со стенками сосуда, в котором этот газ находится. Поскольку молекул много, ударов тоже много.
Например, в комнате, в которой вы сейчас находитесь, за одну секунду на каждый квадратный сантиметр молекулы воздуха наносят столько ударов, что их количество выражается двадцатитрехзначным числом.
Хотя сила удара отдельной молекулы мала, действие всех молекул на стенки сосуда приводит к значительному давлению. Представьте, что комар пытается толкать машину — она не сдвинется с места. Но если за работу возьмется пара сотен миллионов комаров, то машину получится сдвинуть.
Эксперимент
Чтобы смоделировать давление газа, возьмите песок и лист бумаги, зажатый между двумя книгами. Песчинки будут выступать в роли молекул газа, а лист — в роли сосуда, в котором этот газ находится. Когда вы начинаете сыпать песок на лист бумаги, бумага отклоняется под воздействием множества песчинок.
Так же и молекулы газа оказывают давление на стенки сосуда, в котором находятся.
Зависимость давления от других величин
Зависимость давления от объема
В механике есть формула давления, которая показывает, что давление прямо пропорционально силе и обратно пропорционально площади, на которую эта сила оказывается.
Давление p = F/S F — сила [Н] S — площадь [м2] |
То есть если наши двести миллионов комаров будут толкать легковую машину, они распределятся по меньшей площади, чем если бы толкали грузовой автомобиль, — просто потому, что легковушка меньше грузовика. Из формулы давления следует, что давление на легковой автомобиль будет больше из-за его меньшей площади.
Рассмотрим аналогичный пример с двумя сосудами разной площади.
Давление в левом сосуде будет больше, чем во втором, потому что его площадь меньше. А раз меньше площадь сосуда, то меньше и его объем. Значит, давление зависит от объема следующим образом: чем больше объем, тем меньше давление, и наоборот.
При этом зависимость будет не линейная, а примет вот такой вид (при условии, что температура постоянна):
Зависимость давления от объема называется законом Бойля-Мариотта. Она экспериментально проверяется с помощью такой установки:
Объем шприца увеличивают с помощью насоса, а манометр измеряет давление. Эксперимент показывает, что при увеличении объема давление действительно уменьшается.
Зависимость давления от температуры
Рассмотрим зависимость давления газа от температуры при условии неизменного объема определенной массы газа. Исследования в этой области впервые провел французский изобретатель Жак Шарль в XVIII веке.
В ходе эксперимента газ нагревали в большой колбе, соединенной с ртутным манометром в виде узкой изогнутой трубки. Незначительным увеличением объема колбы при нагревании можно пренебречь, как и столь же незначительным изменением объема при смещении ртути в узкой манометрической трубке. Таким образом, объем газа можно считать неизменным.
Подогревая воду в сосуде, окружающем колбу, ученый измерял температуру газа термометром, а давление — манометром.
Эксперимент показал, что давление газа увеличивается с увеличением температуры. Это связано с тем, что при нагревании молекулы газа движутся быстрее, из-за чего чаще ударяются о стенки сосуда.
С температурой все проще. Зависимость давления от температуры при постоянных объеме и массе будет линейной:
Эта зависимость называется законом Шарля в честь ученого, открывшего ее.
Основное уравнение МКТ
Основная задача молекулярно-кинетической теории газа заключается в том, чтобы установить соотношение между давлением газа и его микроскопическими параметрами: массой молекул, их средней скоростью и концентрацией.
В основе молекулярно-кинетической теории лежат три положения.
- Все вещества образованы из мельчайших частиц — молекул, которые состоят из атомов.
Молекулы химического вещества могут быть простыми и сложными, то есть состоять из одного или нескольких атомов. Молекулы и атомы представляют собой электрически нейтральные частицы. При определенных условиях молекулы и атомы могут приобретать дополнительный электрический заряд и превращаться в положительные или отрицательные ионы.
- Атомы и молекулы находятся в непрерывном хаотическом движении.
- Частицы взаимодействуют друг с другом силами, которые имеют электрическую природу. Гравитационное взаимодействие между частицами пренебрежимо мало.
Мы уже выяснили, что причина давления газа на стенки — это удары молекул.
Давление напрямую зависит от количества молекул — чем их больше, тем больше ударов о стенки и тем больше давление. А количество молекул в единице объема — это концентрация. Значит, давление газа зависит от концентрации.
Также давление пропорционально квадрату скорости, так как чем больше скорость молекулы, тем чаще она бьется о стенку сосуда. Расчеты показывают, что основное уравнение молекулярно-кинетической теории для идеального газа имеет следующий вид.
Основное уравнение МКТ p = nkT илиp — давление газа [Па] n — концентрация [м-3] T — температура газа [К] m0 — масса одной молекулы [кг] v — средняя квадратичная скорость [м/с] |
Коэффициент 1/3 обусловлен трехмерностью пространства: во время хаотического движения молекул все три направления равноправны.
Важный нюанс: средняя квадратичная скорость сама по себе не в квадрате! Ее формула указана выше, а в основном уравнении МКТ (да и не только в нем) она возведена в квадрат. Это значит, что формулу средней квадратичной скорости нужно подставлять не вместо v2, а вместо v— и потом уже возводить эту формулу в квадрат. Это часто провоцирует путаницу.
Мы знаем, что кинетическая энергия вычисляется по следующей формуле:
Кинетическая энергия Ек = mv2/2 Ек — кинетическая энергия [Дж] m — масса тела [кг] v — скорость [м/с] |
Для молекулы газа формула примет вид:
Средняя кинетическая энергия поступательного движения молекулы Ек = m0v2/2 Ек — средняя кинетическая энергия поступательного движения молекулы [Дж] m0 — масса молекулы [кг] v — скорость молекулы [м/с] |
Из этой формулы можно выразить m0v2 и подставить в основное уравнение МКТ.
Подставим и получим, что давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.
Основное уравнение МКТ p — давление газа [Па] n — концентрация [м-3] E — средняя кинетическая энергия поступательного движения молекулы [Дж] |
Хранение и транспортировка газов
Если нужно перевезти значительное количество газа из одного места в другое или если газ необходимо длительно хранить, его помещают в специальные прочные металлические сосуды. Из-за того, что при уменьшении объема увеличивается давление, газ можно закачать в небольшой баллон, но он должен быть очень прочным.
Сосуды, предназначенные для транспортировки газов, выдерживают высокие давления.
Поэтому с помощью специальных насосов (компрессоров) туда можно закачать значительные массы газа, которые в обычных условиях занимали бы в сотни раз больший объем.
Поскольку давление газов в баллонах даже при комнатной температуре очень велико, их ни в коем случае нельзя нагревать. Например, держать под прямыми лучами солнца или пытаться сделать в них отверстие — даже после использования.
Реальные и идеальные газы | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Газ — это состояние вещества, в котором оно не имеет собственной формы и заполняет весь предоставленный ему объем; его молекулы находятся в постоянном хаотическом движении и взаимодействуют лишь при столкновениях между собой и стенками сосуда, в котором они находятся.
По молекулярным представлениям, газы состоят из атомов или молекул, расстояние между которыми значительно превышает их размеры. Именно поэтому силы взаимодействия между молекулами газов практически отсутствуют, а следовательно, молекулы газов не удерживаются друг возле друга, а постоянно хаотически перемещаются.
Взаимодействие между ними фактически происходит лишь при кратковременных столкновениях.
При обычных условиях собственный объем молекул газа значительно меньше объема сосуда, в котором он находится. В связи с этим газы легко сжимаются. Они не имеют собственной формы и заполняют весь объем сосуда, в котором находятся.
Большинство уравнений и законов справедливы для идеального газа — упрощенной модели реальных газов. Прежде всего, это касается взаимодействия между молекулами — оно должно быть настолько малым, что им можно пренебречь. При таких условиях учитывается лишь кинетическая энергия молекул, поскольку потенциальная энергия их взаимодействия практически равна нулю.
Следующее ограничение касается размера молекул. Поскольку взаимодействие молекул идеального газа сводится лишь к кратковременным столкновениям, то размер молекул не влияет на давление и температуру газа.
Поэтому молекулы идеального газа можно считать материальными точками.
Идеальный газ — это модель газа, которая предусматривает пренебрежение размерами молекул и их взаимодействием; молекулы такого газа находятся в свободном беспорядочном движении, иногда сталкиваясь с другими молекулами или стенками сосуда, в котором они находятся. Материал с сайта http://worldofschool.ru
Реальные газы приобретают такие свойства при значительном разрежении, когда среднее расстояние между молекулами намного больше их размера. При таких условиях практически отсутствуют силы притяжения, а силы отталкивания действуют лишь при кратковременных столкновениях молекул между собой.
Молекулярно-кинетическая теория накладывает ряд ограничений на реальный газ, благодаря которым его можно считать идеальным. Это газ, размерами и взаимодействием молекул которого можно пренебречь.
На этой странице материал по темам:Реальные газы физика
Почему газы не имеют собственной формы и объема
Реальные газы шпаргалка
Объясните почему газы не имеют собственной формы и постоянного объема
Объясните , почему газ не имеет собственной формы и собственного объема
Объясните на основании молекулярно-кинетических представлений, почему газы не имеют собственной формы?
Дайте определение идеального газа.
Какие ограничения содержит модель реального газа в данном случае?При каких условиях свойства реальных газов приближаются к свойствам идеального газа?
Какие ограничения содержит модель реального газа в данном случае?Идеальные газы. Законы идеального газа. Уравнение Менделеева
1. Идеальным газом называется газ, в котором отсутствуют силы межмолекулярного взаимодействия. С достаточной степенью точности газы можно считать идеальными в тех случаях, когда рассматриваются их состояния, далекие от областей фазовых превращений.
2. Для идеальных газов справедливы следующие законы:
а) Закон Бойля — Mаpuomma: при неизменных температуре и массе произведение численных значений давления и объема газа постоянно:
pV = const
Графически этот закон в координатах РV изображается линией, называемой изотермой (рис.1).
б) Закон Гей-Люссака: при постоянном давлении объем данной массы газа прямо пропорционален его абсолютной температуре:
V = V0(1 + at)
где V — объем газа при температуре t, °С; V0 – его объем при 0°С.
Величина a называется температурным коэффициентом объемного расширения. Для всех газов a = (1/273°С–1). Следовательно,
V = V0(1 +(1/273)t)
Графически зависимость объема от температуры изображается прямой линией – изобарой (рис. 2). При очень низких температурах (близких к –273°С) закон Гей-Люссака не выполняется, поэтому сплошная линия на графике заменена пунктиром.
в) Закон Шарля: при постоянном объеме давление данной массы газа прямо пропорционально его абсолютной температуре:
p = p0(1+gt)
где р0 — давление газа при температуре t = 273,15 К.
Величина g называется температурным коэффициентом давления. Ее значение не зависит от природы газа; для всех газов = 1/273 °С–1. Таким образом,
p = p0(1 +(1/273)t)
Графическая зависимость давления от температуры изображается прямой линией – изохорой (Рис. 3).
г) Закон Авогадро: при одинаковых давлениях и одинаковых температурах и равных объемах различных идеальных газов содержится одинаковое число молекул; или, что то же самое: при одинаковых давлениях и одинаковых температурах грамм-молекулы различных идеальных газов занимают одинаковые объемы.
Так, например, при нормальных условиях (t = 0°C и p = 1 атм = 760 мм рт. ст.) грамм-молекулы всех идеальных газов занимают объем Vm = 22,414 л.· Число молекул, находящихся в 1 см3 идеального газа при нормальных условиях, называется числом Лошмидта; оно равно 2,687*1019> 1/см3
3. Уравнение состояния идеального газа имеет вид:
pVm = RT
где р, Vm и Т — давление, молярный объем и абсолютная температура газа, а R — универсальная газовая постоянная, численно равная работе, совершаемой 1 молем идеального газа при изобарном нагревании на один градус:
R = 8.31*103 Дж/(кмоль*град)
Для произвольной массы M газа объем составит V = (M/m)*Vm и уравнение состояния имеет вид:
pV = (M/m) RT
Это уравнение называется уравнением Менделеева — Клапейрона.
4. Из уравнения Менделеева — Клапейрона следует, чти число n0 молекул, содержащихся в единице объема идеального газа, равно
n0 = NA/Vm = p*NA /(R*T) = p/(kT)
где k = R/NA = 1/38*1023 Дж/град — постоянная Больцмана, NA — число Авогадро.
Идеальный газ — презентация онлайн
1. Идеальный газ – это модель в которой
Молекулы принимают за материальныеточки
Между молекулами нет сил
притяжения и отталкивания
Столкновения частиц между собой и со
стенками сосуда абсолютно упругие
• Размеры молекул малы по сравнению с расстояниями
между ними
• Число молекул очень велико
• Молекулы распределены по всему объему
равномерно
• Молекулы газа движутся хаотично, то есть в любом
направлении движется одинаковое число молекул
• Скорости молекул могут принимать любые
значения
• Силы взаимодействия проявляются только в
момент соударений. Соударения абсолютно
упругие.
• Для отдельно взятой молекулы справедливы законы
Ньютона
3. Реальный газ можно считать идеальным, если он сильно разрежен и хорошо нагрет
4. Скорости движения молекул
При одной и той же температуре всемолекулы одного газа движутся с
разными скоростями
Средняя скорость хаотического
движения молекул равна нулю:
ср
1 2 N
N
0
Средняя арифметическая скорость: 1 2 N
N
Средняя квадратичная скорость:
2
1
2
2
N
2
N
Микропараметры
(характеризуют одну молекулу)
Макропараметры
m0
ЕК
r0
р
m
V
T
p
п
(можно измерить приборами)
6.
В модели «идеальный газ» все молекулы движутся с одинаковыми скоростями равной средней квадратичной N3
N
6
— молекул
движется по
каждой оси.
— молекул
движутся
в одном
направлении вдоль
каждой оси
Все направления движения хаотического движения молекул
равновероятны:
2
х
2
у
2
z
7. Давление газа создается ударами молекул
• малые силы отдельных ударов складываются впостоянную силу давления
8. Основное уравнение МКТ
-связывает микро и макро параметры9. Изменение импульса молекул
11. Вывод основного уравнения МКТ
p x 2m0 xF1
t
t
1
Z n S x t
2
F F1 Z nS x t 2m0 x 1
1
2
2
p
nm0 x nm0
S
S
2
t S
3
12. Основное уравнение МКТ
12
p nm0
3
1
2
p
3
2
p nЕК
3
Тепловым равновесием называют такое
состояние, при котором все макроскопические
параметры сколь угодно долго остаются
неизменными.
Температура характеризует состояние
теплового равновесия системы тел: все тела
системы, находящиеся друг с другом в
тепловом равновесии, имеют одну и ту же
температуру.
Температура характеризуют степень нагретости тел
(холодное, теплое, горячее).
Можно предположить, что
при тепловом равновесии именно средние
кинетические энергии молекул всех газов
одинаковы
водород
кислород
2
2N
р nE
E
3
3V
гелий
16. Зависимость давления газа от температуры при V = const.
Зависимость давления газа от температурыпри V = const.
Уравнение процесса:
р nk t 273,15
17. ШКАЛА КЕЛЬВИНА
• Английский физик У. Кельвин в 1848 г.предложил использовать точку нулевого
давления газа для построения новой
температурной шкалы (шкала
Кельвина). В этой шкале единица
измерения температуры такая же, как и
в шкале Цельсия, но нулевая точка
сдвинута:
T = t + 273 [K]
р nkТ
2
p nЕК
3
3
Е К kT
2
19.
Температура – мера средней кинетической энергии молекул За абсолютный ноль принимаюттемпературу при которой
прекращается поступательное
движение молекул.
ΔТ = Δ t
Т = t + 273
— температура в энергетических единицах
kT
Т — абсолютная температура [K]
k — постоянная Больцмана, связывает
температуру в энергетических единицах
с температурой в Кельвинах
k 1,38 10
23
Дж
K
При одной и той же температуре
средние кинетические энергии
движения молекул всех газов равны
m0
3
ЕК kT
2
2
2
3kT
3k N AT
3RT
m0
M
M
R kNA
1,38 10
23
Дж
23
1
6 10 моль
К
Дж
R 8,31
моль К
Универсальная газовая постоянная
Нормальные условия
р0 = 100 кПа =
5
10
Т0 = 273 К
Па
25. Следствия:
Приодинаковых
давлениях
и
температурах концентрация молекул
у всех газов одинакова
2.
Для смеси газов давление равносумме парциальных давлений – закон
Дальтона
1.
р р1 р2 рN
26. Принцип опыта по определению скоростей молекул
Молекул много, ониочень малы.
Следовательно,
мишень не должна
быстро уехать. Как
сделать так, чтобы
мишень всё время
была перед стрелками,
но при этом место
попада-ния зависело
от скорости
«снаряда»?
27. Опыт Штерна,1920г.
3Опыт Штерна,1920г.
1.
2.
3.
4.
5.
4
Стеклянный колпак
Внешний цилиндр
Внутренний цилиндр
Щель
Металлическая нить
(платина)
6. Полая ось
7. Контактные
кольца
8. Слой серебра
СПРАВКА:
Коаксиальные
цилиндры имеют
общую ось.
5
Место попадания
самых быстрых
молекул
Распределение
молекул по
скоростям
Самые медленные
молекулы
28. Выведем формулу для средней скорости атомов
RА(R
2
n
s
B
R A)
R
B
s
29.
Объясните, а как действует эта установка? Щелиформируют
пучок.
Диски с прорезями
Объясните,
а как
действует
эта
сортируют молекулы по скоростям. Угол между
установка?
прорезями =α.
Через прорези проходят частицы со скоростями
υ+Δυ . Для того чтобы частица попала на
детектор, она должна успеть за время t =α/ω
пройти путь ℓ. υ=ℓ/t=ℓω/α
Идеальный газ. Основное уравнение молекулярно-кинетической теории.
Идеальный газ
Это несуществующая физическая модель газа, который состоит из большого числа молекул, размеры которых ничтожно малы по сравнению со средними расстояниями между ними. Молекулы такого газа можно считать материальными точками, это означает, что их вращательное и колебательное движения не принимаются во внимание. Движение молекул происходит без столкновений с другими молекулами, подчиняется законам Ньютона. Соударения молекул со стенками сосуда являются абсолютно упругими.
Параметры состояния газа
Давление, температура и объем — параметры состояния газа.
Или их называют макропараметрами. Температура — внешняя характеристика скоростей частиц газа. Давление — внешняя характеристика соударений со стенками, например, сосуда. Объем — место, куда заключены частицы газа. Газ занимает весь предоставленный ему объем. Существуют еще внешние параметры, например тела или поля, действующие на газ из вне.
Микропараметры (маленькие, внутренние характеристики) газа — это параметры, которые мы не можем оценить без специальных экспериментов, например, скорость и направление движения каждой молекулы газа.
Состояние термодинамической системы, когда все ее параметры при неизменных внешних условиях не изменяются со временем, называют равновесным.
Основное уравнение молекулярно-кинетической теории
Уравнение связывает микропараметры и макропараметры (давление, объем и температуру) идеального газа.
Рассмотрим идеальный газ, который находится в кубическом сосуде. Каждая молекула упруго сталкивается со стенкой сосуда, при этом изменятся ее импульс.
Столкновение всех молекул со стенкой на макроуровне ощущается как давление газа на сосуд. В формулах будут присутствовать средние значения, потому что какая-то молекула движется быстрее, какая-то помедленнее, для того, чтобы оценить примерную скорость, будем брать средние значения.
Основное уравнение мкт имеет вид
Средний квадрат скорости молекул
Средняя квадратичная скорость vкв молекул это квадратный корень из среднего квадрата скорости
Средняя кинетическая энергия молекул
Можно вывести формулы
Температура
Это макропараметр, который характеризует способность тел к теплопередаче. Если два тела разной температуры контактируют, то произойдет переход энергии или передача теплоты от более горячего к холодному. Установится тепловое равновесие, все части будут одинаковой температуры.
Температура характеризует интенсивность движения частиц, поэтому связана со средней кинетической энергией частиц. Из опыта известно, что средняя кинетическая энергия молекул не зависит от вида газа и определяется температурой.
Связь между температурами по шкале Цельсия и по шкале Кельвина
Основное уравнение молекулярно-кинетической теории (МКТ) с выводом
В статье рассмотрена модель идеального газа, приведено основное уравнение молекулярно-кинетической теории и его вывод.
Чтобы объяснить свойства материи в газообразном состоянии, в физике применяется модель идеального газа. Идеальный газ — разреженный, состоящий из одного типа атомов газ, частицы которого не взаимодействуют между собой. Помимо основных положений МКТ эта модель предполагает, что:
- молекулы имеют пренебрежимо малый объем в сравнении с объемом емкости
- при сближении частиц друг с другом и с границами емкости имеют место силы отталкивания
Основное уравнение молекулярно-кинетической теории
Физический смысл основного уравнения МКТ заключается в том, что давление идеального газа — это совокупность всех ударов молекул о стенки сосуда.
Это уравнение можно выразить через концентрацию частиц, их среднюю скорость и массу одной частицы:
p – давление молекул газа на границы емкости,
m0 – масса одной молекулы,
n — концентрация молекул, число частиц N в единице объема V;
v2 — средне квадратичная скорость молекул.
Вывод основного уравнения МКТ
Частицы идеального газа при соударениях с границами емкости ведут себя как упругие тела. Такое взаимодействие описывается согласно законам механики. При соприкосновении частицы с границей емкости проекция vx скоростного вектора на ось ОХ, проходящую под прямым углом к границе сосуда, меняет свой знак на противоположный, но сохраняется неизменной по модулю:
Поэтому после соударения частицы с границей емкости проекция импульса молекулы на ось ОХ меняется с mv1x = –mvx на mv2x = mvx.
Изменение импульса молекулы ΔP равняется удвоенному произведению массы молекулы на ее скорость:
Поскольку в каждом из шести основных направлений декартовой системы координат (вверх, вниз, вперед, назад, вправо, влево) движется одна шестая часть частиц N/6.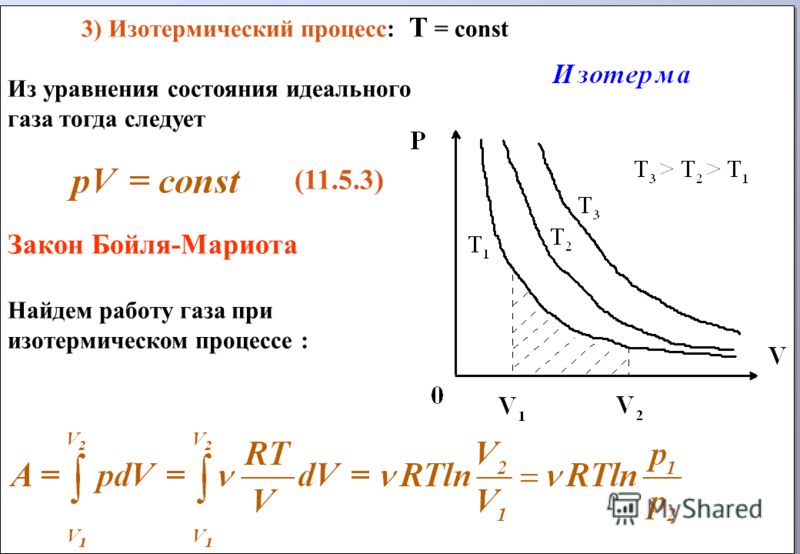
Тогда число частиц, которые сталкиваются с каждой стенкой за время Δt равно:
S – площадь этой стенки
n — концентрация частиц
Давление p равно отношению силы F к площади S, на которую действует эта сила:
Суммарная сила, с которой частицы давят на стенку равна отношению произведения числа этих частиц N и изменения импульса ΔP ко времени, в течение которого происходит давление:
Исходя из вышенаписанного получаем:
Тогда
Если заменить среднее значение кинетической энергии поступательного движения молекул — E:
и подставить эту формулу в основное уравнение МКТ, получим давление идеального газа:
Давление идеального газа равняется двум третям средней кинетической энергии поступательного движения молекул на единицу объема. При решении задач реальный газ можно считать идеальным газом, если он одноатомный и можно пренебречь взаимодействием между частицами.
Понравилась статья, расскажите о ней друзьям:
Скорее всего, Вам будет интересно:
Газы идеальные — Справочник химика 21
Если р взято в Па V — в м /кмоль, Т — в К, то значенне К — универсальной газовой постоянной — равно 8314,3 Дж/кмоль.) При более высоких давлениях или при температурах, меньших температуры конденсации, уравнение состояния идеального газа не применимо. Однако поведение реальных газов и паров может быть соотнесено с поведением газов идеальных с помощью фактора сжимаемости [c.150]Обобщая полученные результаты и опираясь на многочисленные расчеты, следует сказать, что, заменяя в некоторой области диаграммы реальный газ идеальным, у которого / у получаем значения КПД, удовлетворяющие нас по точности совпадения с действительными значениями. То обстоятельство, что при йу процессе сжатия i) o 4s. > огя в реальном рабочем веществе все будет наоборот, может быть препятствием к применению метода условных температур только при ky высокой сжимаемостью, средние значения показателя изоэнтропы ky, определенные по формулам (3.
47) и (3.48) для конечных интервалов давлений, становятся меньше единицы только в области, близкой к критической точке, и отличаются от нее не более чем на 2—4 %. При таких близких к единице значениях ky изоэнтропный и политропный КПД практически совпадают независимо от того, будет k , больше единицы или меньше ее. [c.123]Идеальная растворимость газа, т. е. растворимость его в идеальном растворе, может быть вычислена по закону Рауля—Генри (для Р = 1 атм), если считать приближенно газ идеальным при [c.223]
Упражнение 111,20. Считая газы идеальными, найдите равновесную концентрацию СО2 в реакции 2С0 — СО — С =0 при 1000° К и атмосферном давлении. Свободные энергии образования СО, Oj и С прп этой температуре равны соответственно —76 062, —138 078 и —2771 кал/моль. Покажите также, что если X — равновесная мольная доля Oj, то величина (1 — х)/х пропорциональна давлению. [c.59]
Законы идеальных газов. Идеальный газ характеризуется отсутствием межмолекулярного взаимодействия и исчезающе малым объемом молекул по сравнению с объемом, занимаемым газом.
Реальные газы и пары отклоняются от законов идеальных газов. Однако при относительно невысоких давлениях углеводородные [c.230]
В качестве примера найдем выражения для энтропии идеального газа. Идеальный газ —это единственная система, для которой в предыдущих главах были даны выражения i/.. и р. Согласно 118 [c.118]
В изолированной системе при 273,16 К 1 моль газа обратимо и изотермически расширяется от 1,01-10 до 1,01-10″ Па. Вычислите значения Q, А1У, АЯ, А5, АЛ и АО (считать газ идеальным) 1) для газа и для всей изолированной системы в целом 2) при свободном расширении газа (расширение в вакууме необратимо), для газа и для всей изолированной системы в целом. Результаты расчета представьте в виде таблицы. [c.92]
Для реакции, протекающей в газовой фазе, при условии, что газ идеальный [c.150]
На в отношении 1 2 не содержащая примесей) может быть получено 208 г углеводородов. Фактически, как показывает опыт практической работы, общий выход углеводородов, включая углеводородь Сз— С4, составляет 125—160 г/нм газа идеального состава.
Отсюда следует, что для получения 1 кг когазина нужно израсходовать 6+8 кг чистого синтез-газа. Так как реальный газ не является 100%-ным и содержит инертные прнмеси, то оказывается, что для установки мощностью 100 000 т суммарной продукции в год требуется в год около 800 млн. синтез-газа, или около 100 000 м /час. [c.80]
Коэффициент теплового расширения газов (идеальных) [c.452]
Если считать газ идеальным, то при 7 = 273,16 К, Р = 0,1 МПа и У=22,414 мл масса т равна молекулярной массе М газа. В тех же условиях масса 22,414 мл воздуха составляет 28,9 г, откуда относительная плотность газа или пара относительно воздуха равна [c.11]
Рассчитано из предположения, что газ идеальный. [c.380]
Если пренебречь изменением кинетической энергии, внешними утечками (т = т ) и считать, что газ идеальный (2 = = 1), то расчет упрощается. Так как в этом случае Ту.
[c.199]
Объем Уа определим из уравнения политропы расширения с показателем Пр (газ идеальный) [c.232]
Считая газы идеальными и пренебрегая мольными объемами жидкостей, имеем [c.195]
Известны различные приближенные способы выполнения поверочного расчета П1, 80]. В способе, предложенном автором, первоначально находят предварительные промежуточные давления, а затем их уточняют. Допустим, что у всех ступеней = I и Я,- = 1. При этом объемы газа, всасываемого по ступеням, равны Если газ идеальный [c.90]
Рнс. 3.2. Взаимное расположение линий некоторых характерных процессов для газов (идеальных) в системе координат р — V. [c.73]
Основные газовые законы выведены для идеального газа. Идеальным называется газ, находящийся в таком состоянии, при котором можно пренебречь силами межмолекулярного взаимодействия и собственным объемом его молекул. [c.14]
Балансы элементарных реакций позволяют рассчитать массовые расходы кислорода и количество продуктов реакции на единицу массы рассматриваемого элемента.
Знание удельных весов (плотностей) газов дает возможность перейти от массовых единиц к объемным. Расчет обычно проводится для нормальных условий (0° С и 760 мм рт. ст), объемы газов выражаются в нормальных кубометрах нм . Если считать газы идеальными, то удельные веса легко [c.13]
Таким образом, на основании опытов Гей-Люссака и Джоуля мы подошли к понятию о внутренней энергии идеального газа. При объяснении результатов этих опытов следует подчеркнуть особенности идеального газа. Идеальный газ отличается полной независимостью всех движущихся частиц друг от друга, что обусловлено отсутствием каких бы то ни было сил притяжения или отталкивания между ними. Поэтому для такой системы безразлично, в каком объеме она распределена. Запас энергии системы определяется суммой энергий движения частиц. Поэтому плотность идеального газа не играет роли, ибо энергия данной системы будет одна и та же для частиц, близко расположенных друг от друга (газ большой плотности), и для частиц, располагающихся на значительном рас— стоянии (разреженный газ с малой плотностью), так как между частицами нет взаимодействия.
Поэтому внутренняя энергия идеального газа не зависит от объема и давления. [c.32]
Рассмотрим в общем аиде влияние этих воздействий на скорость движения газа. Дпя простоты будем считать газ идеальным. Расход газа равен С = рюР. [c.202]
Рассчитать парциальное давление хлора, находящегося в равновесии с фосгеном 1при 600° К и общем давлении 1 атм, полагая, что газы идеальные. Ответ. 0,0475 атм. [c.176]
По аналогии с идеальным газом, идеальной резиной можно считать ту, у которой высокоэластичность обусловлена только изменением энтропии. Для идеальной резины, следовательно [c.116]
Понятие идеальный раствор ни в коем случае нельзя путать с понятием смесь идеальных газов . Идеальный раствор представляет собой гомогенную смесь реальных веществ, молекулы которых имеют конечный объем и взаимодействуют между собой. Но идеальный раствор является системой, в которой можно пренебречь различием межмолекулярных взаимодействий разных компонентов.
[c.62]
Здесь и далее под идеальным газом следует понимать газ идеального состава для синтеза по Фишеру — Тропшу, т. е. СО Нг = 1 2. — Яриж. ред. [c.131]
Считая газ идеальной системой, получаем константу скорости [c.298]
Если в исходном состоянии газы разделены сплошной перегородкой, то при ее удалении произойдет самопроизвольное смешение. При этом внутренняя энергия не изменится (газы идеальные), работы произведено не будет (внешние силы не действуют) и, следовательно, процесс не будет сопровождаться выделением или поглощением теплоты. [c.72]
Решение. Предположим, что поглощаемый газ идеальный. СО2 (А) растворяется в щелочи, диффундирует внутрь и в то же время реагирует с ионами гпдрокспла В) по уравнению реакции второго порядка = —кс сд- Описа- [c.169]
Необходимо отметить, что при обычных давлениях, не превышающих 5—Ю атм, ошибки в расчете фазового равновесия мало зависят от коэффициентов фугитивности, и, таким образом, точность вычисления вириальных коэффициентов определяется допустимыми ошибками расчета равновесия.
Тем не менее даже при низких давлениях лучше пользоваться приближенными значениями вторых вириальнчх коэффициентов, чем считать газ идеальным или применять правило Льюиса. [c.24]
Правильность полученных параметров может быть проверена непосредствеппой заменой реального газа идеальным. В результате такой замены эти четыре Г1араметра должны свестись к двум. Действительно, коэффициент сжимаемости идеального газа всегда равен единице, так что этот параметр из рассмотрения исключается. Число определяемое выражением (2.52), в числителе содержит квадрат скорости звука в точке приведения, которая для идеального газа определяется известным выражением = = кНТ. Отсюда следует, что для идеального газа число х есть не что иное как показатель изоэнтропы, т. е. у. = к. Безразмерная скорость звука а в идеальном газе равна отношению температуры газа в некоторой точке термодинамического процесса к его температуре в точке приведения [c.80]
При изотермическом процессе передача теплоты от одного тела к другому производится при постоянной температуре.
Если газ идеальный, то внутренняя энергия 1 моль газа не зависит ни от объема, который газ занимает, ни от давления, а зависит только от температуры. Отсюда при изотермическом процессе, когда У = сопз1, уравнение (1.10) имеет вид [c.23]На рис. 3.2 в системе координат р—v (где р — давление, V—удельный объем) показаны уравнения и взаимное расположение линий некоторых наиболее характерных процессов для газов (идеальных). Если Р1ачальное состояние газа определяется [c.73]
Peo, = pHj = 1 атм, т. e. ровщ == 4 атм (все газы идеальны), прореагировало бы по 1 молю СО и HjO, то в результате энергия Гиббса уменьшилась бы на 6,843 ккал. [c.62]
14.11: Реальные и идеальные газы
- Последнее обновление
- Сохранить как PDF
- Реальные и идеальные газы
- Резюме
- Авторы и авторства
Поведение молекулы во многом зависит от ее структуры.
\ text {o} \ text {C} \ right) \). Разница заключается в количестве межмолекулярного взаимодействия (сильные \ (\ ce {H} \) — связи для этанола, слабые силы Ван-дер-Ваальса для эфира).
Реальные и идеальные газы
Идеальный газ — это газ, который следует законам газа при любых условиях температуры и давления. Для этого газ должен полностью соответствовать кинетико-молекулярной теории. Частицы газа должны занимать нулевой объем, и они не должны проявлять никаких сил притяжения по отношению друг к другу.Поскольку ни одно из этих условий не может быть истинным, идеального газа не существует. Реальный газ — это газ, который не ведет себя в соответствии с предположениями кинетико-молекулярной теории. К счастью, в условиях температуры и давления, которые обычно встречаются в лаборатории, реальные газы имеют тенденцию вести себя очень похоже на идеальные газы.
В каких же условиях газы ведут себя наименее идеально? Когда газ находится под высоким давлением, его молекулы сближаются, так как пустое пространство между частицами уменьшается.
Уменьшение пустого пространства означает, что предположение о пренебрежимо малом объеме самих частиц менее верно. Когда газ охлаждается, уменьшение кинетической энергии частиц заставляет их замедляться. Если частицы движутся с меньшей скоростью, силы притяжения между ними более заметны. Другой способ взглянуть на это заключается в том, что продолжающееся охлаждение газа в конечном итоге превратит его в жидкость, и жидкость определенно больше не является идеальным газом (см. Жидкий азот на рисунке ниже).Таким образом, реальный газ больше всего отклоняется от идеального газа при низких температурах и высоких давлениях. Газы наиболее идеальны при высокой температуре и низком давлении.
На рисунке ниже показан график зависимости \ (\ frac {PV} {RT} \) от давления для \ (1 \: \ text {mol} \) газа при три разных температуры — \ (200 \: \ text {K} \), \ (500 \: \ text {K} \) и 1000 \: \ text {K} \).
Идеальный газ имел бы значение 1 для этого отношения при всех температурах и давлениях, а график был бы просто горизонтальной линией. Как видно, происходят отклонения от идеального газа. Когда давление начинает расти, силы притяжения приводят к тому, что объем газа становится меньше ожидаемого, и значение \ (\ frac {PV} {RT} \) падает ниже 1. Продолжающееся повышение давления приводит к увеличению объема газа. частицы становятся значительными, и значение \ (\ frac {PV} {RT} \) возрастает до значения больше 1. Обратите внимание, что величина отклонений от идеальности максимальна для газа при \ (200 \: \ text {K } \) и минимум для газа в \ (1000 \: \ text {K} \).
Идеальность газа также зависит от силы и типа сил межмолекулярного притяжения, существующих между частицами. Газы со слабыми силами притяжения более идеальны, чем с сильными силами притяжения.
При той же температуре и давлении неон более идеален, чем водяной пар, потому что атомы неона притягиваются только слабыми дисперсионными силами, в то время как молекулы водяного пара притягиваются относительно прочными водородными связями.Гелий — более идеальный газ, чем неон, потому что в нем меньшее количество электронов означает, что силы дисперсии гелия даже слабее, чем у неона.
Сводка
- Настоящий газ — это газ, который не ведет себя в соответствии с предположениями кинетико-молекулярной теории.
- Описаны свойства реальных газов и их отклонения от идеальности.
Авторы и авторство
Фонд CK-12 Шэрон Бьюик, Ричард Парсонс, Тереза Форсайт, Шонна Робинсон и Жан Дюпон.
Идеальное поведение | PNG 520: Фазовое поведение природного газа и конденсатных жидкостей
Идеальный газ — это воображаемый газ , который удовлетворяет следующим условиям:
- Незначительные взаимодействия между молекулами,
- Его молекулы не занимают объема (пренебрежимо малый молекулярный объем),
- Столкновения между молекулами совершенно упругие, то есть после столкновения энергия не теряется.
Мы признаем, что эта жидкость — мнимый , потому что, строго говоря, не существует идеальных газов.В любой жидкости все молекулы в той или иной степени притягиваются друг к другу. Однако приближение идеального работает лучше всего в некоторых предельных условиях, когда силы притяжения можно считать слабыми. Фактически, к идеальному поведению можно приблизиться с помощью реальных газов при низких давлениях, (близких к атмосферным) и высоких температурах, . Обратите внимание, что при низких давлениях и высоких температурах расстояние между любой парой молекул газа велико. Поскольку силы притяжения ослабевают с расстоянием, мы выбрали условие, при котором силами притяжения можно пренебречь.В заключение мы рассматриваем газовый идеал, когда каждая молекула ведет себя так, как если бы она была одна — молекулы настолько удалены друг от друга, что на них не влияет существование других молекул.
Поведение идеальных газов было исчерпывающе изучено и может быть подробно описано математическими соотношениями.
Для данной массы идеального газа объем обратно пропорционален давлению при постоянной температуре, то есть
vα1P (при постоянной температуре) Это уравнение не отображается должным образом из-за несовместимого браузера.Список совместимых браузеров см. В разделе «Технические требования в ориентации». (6.1)
Это соотношение известно как закон Бойля. Кроме того, объем прямо пропорционален температуре, если давление поддерживается постоянным, то есть
vαT (при постоянном давлении) Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации». (6,2)
Эти отношения известны как закон Чарльза. Комбинируя оба закона и признавая «R» (универсальная газовая постоянная) как константа пропорциональности, мы получаем очень знакомое уравнение:
Это представляет собой уравнение состояния (УРС) идеального газа. Числовые значения «R» зависят от используемой системы единиц: R10.731psia ft3lbmol R8.3144Joulegmole K1.9872calgmole K Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования» в разделе «Ориентация».Список совместимых браузеров см. В разделе «Технические требования в ориентации». Если мы построим диаграмму P-v для идеального газа при заданной температуре, мы получим изотерму, показанную на рисунке 6.2. Рисунок 6.2: Изотерма P-v для идеального газа Модель идеального газа предсказывает два ограничивающих поведения жидкости: во-первых, объем газа становится очень большим при очень низких давлениях v → ∞. Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации».as P → 0 Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации». , концепция, которая согласуется с тем, что мы знаем из нашего опыта в физическом мире). Во-вторых, v → ∞ Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации». as P → 0 Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации».(объем материи просто «исчезает», если давление достаточно велико: эту концепцию мы не были бы так готовы принять). Эти два поведения являются следствием предположений, сделанных в модели идеального газа. Идеальный газ определяется как жидкость, в которой объем молекул газа незначителен по сравнению с объемом, занимаемым газом. Считается, что такие идеальные газы подчиняются закону Бойля, закону Чарльза и закону идеального газа или уравнению идеального газа.Сначала мы обсуждаем идеальные газы, а затем реальные газы. Если M представляет собой молекулярную массу газа, а масса определенного количества газа составляет m , количество молей n определяется как (1,27) n = mM , где n — это число, которое представляет количество молей в данной массе. Например, молекулярная масса метана составляет 16,043. Следовательно, 50 фунтов метана будут содержать примерно 3 моля. Закон идеального газа, также называемый уравнением идеального газа, гласит, что давление, объем и температура газа связаны с числом молей следующим уравнением: (1.28) PV = nRT , где в единицах USCS P — Абсолютное давление, фунты на квадратный дюйм, абсолютное (psia) V — Объем газа, футы 3 n — Количество фунт-моль, как определено в уравнении. (1,27) R — Универсальная газовая постоянная, psia ft 3 / фунт · моль · ° R T — Абсолютная температура газа, ° R (° F + 460) Универсальная газовая постоянная R имеет значение 10.73 фунт / дюйм2 фут 3 / фунт · моль · ° R в единицах USCS. В единицах СИ уравнение идеального газа выглядит следующим образом: (1,29) PV = nRT , где P — Абсолютное давление, кПа V — Объем газа, м 3 n — Количество моль в кг, как определено в уравнении. (1,27) R — Универсальная газовая постоянная, кПа · м 3 / кг · моль · K T — Абсолютная температура газа, К (° C + 273) Универсальная газовая постоянная R имеет значение 8.314 Дж / моль · К в единицах СИ. Мы можем комбинировать Ур. (1.27) с формулой. (1.28) и выразите уравнение идеального газа следующим образом: (1.30) PV = mRTM Константа R одинакова для всех идеальных газов и поэтому называется универсальной газовой постоянной. Было обнаружено, что уравнение идеального газа верно только при низких давлениях, близких к атмосферному (14,7 фунтов на квадратный дюйм или 101 кПа). Поскольку газопроводы обычно работают при давлениях выше атмосферного, мы должны изменить формулу.(1.30), чтобы учесть влияние сжимаемости. Последнее учитывается с помощью термина, называемого коэффициентом сжимаемости или коэффициентом отклонения газа. Мы обсуждаем реальные газы и коэффициент сжимаемости под заголовком «Реальные газы». Следует отметить, что в уравнении идеального газа (уравнение [1.30]) давления и температуры должны быть в абсолютных единицах. Абсолютное давление определяется как манометрическое давление (измеренное манометром) плюс местное атмосферное давление в определенном месте.Следовательно, (1,31) Pabs = Pgauge + Patm Таким образом, если давление газа составляет 200 фунтов на квадратный дюйм (измеренное манометром), а атмосферное давление составляет 14,7 фунтов на квадратный дюйм, абсолютное давление газа составляет Pabs = 200 + 14,7 = 214,7 фунтов на квадратный дюйм Абсолютное давление выражается в фунтах на квадратный дюйм, а манометрическое давление — в фунтах на квадратный дюйм. Сумма манометрического давления, которая представляет собой местное атмосферное давление, также называется базовым давлением. В единицах СИ манометрическое давление 500 кПа равно 601 кПа абсолютному давлению, если базовое давление составляет 101 кПа.Давление в единицах USCS указывается в фунтах на квадратный дюйм (фунт / дюйм 2 ) или фунтах на квадратный дюйм. В единицах СИ давление выражается в килопаскалях (кПа), мегапаскалей (МПа) или барах. См. Приложение 1 для таблиц преобразования единиц. Абсолютная температура газа измеряется выше определенной точки. В единицах USCS абсолютная шкала температуры обозначается как градус Ранкина (° R) и получается добавлением константы 460 к температуре газа в ° F. В единицах СИ шкала абсолютной температуры обозначается как Кельвин (K).Абсолютная температура в К равна (° C + 273). Следовательно, (1,32) ° R = ° F + 460 (1,33) K = ° C + 273 Обратите внимание, что, в отличие от температур в градусах Ранкина (° R), нет символа градуса для абсолютной температуры в Кельвин (К). Идеальные газы также подчиняются законам Бойля и Чарльза. Закон Бойля связывает давление и объем данного количества газа при постоянной температуре. Постоянная температура называется изотермическим состоянием. Согласно закону Бойля, для данного количества газа в изотермических условиях давление обратно пропорционально объему.Другими словами, объем газа увеличится вдвое, если его давление упадет вдвое, и наоборот. Поскольку плотность и объем обратно пропорциональны, закон Бойля также означает, что давление прямо пропорционально плотности при постоянной температуре. Таким образом, заданное количество газа при фиксированной температуре удвоится по плотности, когда давление удвоится. Точно так же снижение давления на 10% приведет к уменьшению плотности на ту же величину. Закон Бойля можно выразить следующим образом: (1.34) P1P2 = V2V1 или P1V1 = P2V2 , где P 1 и V 1 — давление и объем газа при условии 1 и P 2 и V 2 — соответствующее значение при каком-либо другом условии 2, где температура такая же. Закон Чарльза гласит, что при постоянном давлении объем газа прямо пропорционален его температуре. Точно так же, если объем поддерживается постоянным, давление изменяется прямо пропорционально температуре, как показано следующими уравнениями: (1.35) V1V2 = T1T2 при постоянном давлении (1,36) P1P2 = T1T2 при постоянном объеме , где T 1 и V 1 — температура и объем газа при условии 1 и T 2 и V 2 — соответствующие значения при каком-то другом условии 2, где давление одинаково. Аналогично, при постоянном объеме T 1 и P 1 и T 2 и P 2 — это температура и давление газа в условиях 1 и 2, соответственно. Следовательно, согласно закону Чарльза для идеального газа при постоянном давлении объем будет изменяться в той же пропорции, что и его температура. Таким образом, повышение температуры на 20% приведет к увеличению объема на 20% до тех пор, пока давление не изменится. Точно так же, если объем остается постоянным, повышение температуры на 20% приведет к тому же проценту увеличения давления газа. Постоянное давление также известно как изобарическое состояние. Идеальный газ занимает объем резервуара 400 футов 3 при давлении 200 фунтов на квадратный дюйм и температуре 100 ° F. Каков объем газа при стандартных условиях 14,73 фунтов на кв. Дюйм и 60 ° F? Предположим, что атмосферное давление составляет 14,6 фунтов на квадратный дюйм. Если газ охлаждается до 80 ° F, какое давление газа? Начальные условия P1 = 200 + 14,6 = 214,6 фунтов на квадратный дюймV1 = 400 футов3T1 = 100 + 460 = 560 ° R Конечные условия P2 = 14,73 фунтов на квадратный дюйм V 2 подлежит расчету. T2 = 60 + 460 = 520 ° R Используя уравнение идеального газа (уравнение [1.30]), мы можем утверждать, что 214,6 × 400560 = 14,73 × V2520 V2 = 5411,3 футов3 Когда газ охлаждается до 80 ° F, необходимо определить конечные условия. T2 = 80 + 460 = 540 ° RV2 = 400 футов3 P 2 подлежит расчету. Начальные условия: P1 = 200 + 14,6 = 214,6 psia V1 = 400 футов3T1 = 100 + 460 = 560 ° R Видно, что объем газа постоянен (объем резервуара), а температура снижается со 100 ° F до 80 ° F.Следовательно, используя уравнение закона Чарльза (уравнение [1.36]), мы можем рассчитать конечное давление следующим образом: 214,6P2 = 560540 Решив для P 2 , мы получим P2 = 206,94 psia = 206,94−14,6 = 192,34 фунта на кв. Дюйм изб. идеальный газ , также называемый идеальный газ , газ, который по физическому поведению соответствует определенной идеализированной связи между давлением, объемом и температурой, называемой общим законом газа.Этот закон является обобщением, содержащим как закон Бойля, так и закон Чарльза как частные случаи и гласит, что для определенного количества газа произведение объема v и давления p пропорционально абсолютной температуре t ; то есть в форме уравнения: p v = k t , в котором k является константой. Такое соотношение для вещества называется его уравнением состояния, и его достаточно, чтобы описать его грубое поведение. Общий газовый закон может быть выведен из кинетической теории газов и основан на предположении, что (1) газ состоит из большого числа молекул, которые находятся в беспорядочном движении и подчиняются законам движения Ньютона; 2) объем молекул пренебрежимо мал по сравнению с объемом, занимаемым газом; и (3) никакие силы не действуют на молекулы, кроме как во время упругих столкновений пренебрежимо малой продолжительности. Подробнее по этой теме газ: Идеальный газ Уравнение состояния идеального газа может быть выведено путем расчета давления, вызванного молекулярными ударами о стенку контейнера.Внутренний … Хотя ни один газ не обладает такими свойствами, поведение реальных газов довольно точно описывается общим газовым законом при достаточно высоких температурах и низких давлениях, когда относительно большие расстояния между молекулами и их высокие скорости преодолевают любое взаимодействие. Газ не подчиняется уравнению, когда условия таковы, что газ или любой из составляющих его газов в смеси находится вблизи точки конденсации, температуры, при которой он сжижается. Общий газовый закон может быть записан в форме, применимой к любому газу, в соответствии с законом Авогадро, если константа, определяющая количество газа, выражена через количество молекул газа.Для этого в качестве единицы массы используется грамм-моль; т.е. молекулярная масса, выраженная в граммах. Уравнение состояния n грамм-моль идеального газа может быть записано как p v / t = n R , в котором R называется универсальной газовой постоянной. Эта константа была измерена для различных газов в почти идеальных условиях высоких температур и низких давлений, и было обнаружено, что она имеет одинаковое значение для всех газов: R = 8.314472 джоулей на моль-кельвин. К концу этого раздела вы сможете: До сих пор закон идеального газа, PV = nRT , применялся к множеству различных типов задач, начиная от стехиометрии реакции и задач эмпирических и молекулярных формул до определения плотности и молярной массы газа.Однако, как упоминалось в предыдущих модулях этой главы, поведение газа часто неидеально, а это означает, что наблюдаемые отношения между его давлением, объемом и температурой не точно описываются газовыми законами. В этом разделе рассматриваются причины этих отклонений от поведения идеального газа. Один из способов определения точности PV = nRT — это сравнение фактического объема 1 моля газа (его молярный объем V м ) с молярным объемом идеального газа при том же температура и давление.Это отношение называется коэффициентом сжимаемости (Z) с: [latex] \ text {Z} = \ frac {\ text {молярный объем газа при одном и том же} \; T \; \ text {and} \; P} {\ text {молярный объем идеального газа при одном и том же} \ ; T \; \ text {and} \; P} = (\ frac {PV_m} {RT}) _ {\ text {измерено}} [/ latex] Следовательно, идеальное поведение газа обозначается, когда это отношение равно 1, а любое отклонение от 1 указывает на неидеальное поведение. На рисунке 1 показаны графики Z в большом диапазоне давлений для нескольких обычных газов. Как видно из рисунка 1, закон идеального газа плохо описывает поведение газа при относительно высоких давлениях. Чтобы определить, почему это так, рассмотрите различия между свойствами реального газа и тем, что ожидается от гипотетического идеального газа. Частицы гипотетического идеального газа не имеют значительного объема и не притягиваются и не отталкиваются друг от друга.В общем, реальные газы приближаются к такому поведению при относительно низких давлениях и высоких температурах. Однако при высоких давлениях молекулы газа сжимаются ближе друг к другу, и количество пустого пространства между молекулами уменьшается. При этих более высоких давлениях объем самих молекул газа становится заметным по сравнению с общим объемом, занимаемым газом (рис. 2). Следовательно, газ становится менее сжимаемым при таких высоких давлениях, и хотя его объем продолжает уменьшаться с увеличением давления, это уменьшение не является пропорциональным , как предсказывается законом Бойля. При относительно низких давлениях молекулы газа практически не притягиваются друг к другу, потому что они (в среднем) так далеко друг от друга и ведут себя почти как частицы идеального газа. Однако при более высоких давлениях сила притяжения также перестает быть незначительной. Эта сила притягивает молекулы немного ближе друг к другу, немного уменьшая давление (если объем постоянный) или уменьшая объем (при постоянном давлении) (рис. 3).Это изменение более выражено при низких температурах, потому что молекулы имеют более низкий KE по сравнению с силами притяжения, и поэтому они менее эффективны в преодолении этого притяжения после столкновения друг с другом. Существует несколько различных уравнений, которые лучше описывают поведение газа, чем закон идеального газа. Первый и самый простой из них был разработан голландским ученым Йоханнесом ван дер Ваальсом в 1879 году. Уравнение Ван-дер-Ваальса улучшает закон идеального газа, добавляя два члена: один для учета объема молекул газа и другой для сил притяжения между ними. Константа a соответствует силе притяжения между молекулами определенного газа, а константа b соответствует размеру молекул конкретного газа.2} [/ latex], а «поправка» к объему — nb . Обратите внимание, что когда V относительно велико, а n относительно мало, оба этих поправочных члена становятся незначительными, и уравнение Ван-дер-Ваальса сводится к закону идеального газа, PV = nRT . Такое состояние соответствует газу, в котором относительно небольшое количество молекул занимает относительно большой объем, то есть газу при относительно низком давлении. Экспериментальные значения констант Ван-дер-Ваальса некоторых распространенных газов приведены в таблице 3. При низких давлениях поправка на межмолекулярное притяжение, a , более важна, чем поправка на молекулярный объем, b . При высоких давлениях и малых объемах поправка на объем молекул становится важной, потому что сами молекулы несжимаемы и составляют значительную часть от общего объема.При некотором промежуточном давлении две поправки оказывают противоположное влияние, и газ, кажется, следует соотношению, заданному формулой PV = nRT в небольшом диапазоне давлений. Такое поведение отражается в «провалах» на некоторых кривых сжимаемости, показанных на рисунке 1. Сила притяжения между молекулами изначально делает газ более сжимаемым, чем идеальный газ, по мере увеличения давления (Z уменьшается с увеличением P ). При очень высоких давлениях газ становится менее сжимаемым (Z увеличивается с P ), поскольку молекулы газа начинают занимать все более значительную долю от общего объема газа. Строго говоря, уравнение идеального газа хорошо работает, когда межмолекулярное притяжение между молекулами газа пренебрежимо мало, а сами молекулы газа не занимают заметной части всего объема. Этим критериям удовлетворяются условия при низком давлении и при высокой температуре. Говорят, что в таких условиях газ ведет себя идеально, а отклонения от газовых законов достаточно малы, чтобы ими можно было пренебречь — однако очень часто это не так. Сравнение закона идеального газа и уравнения Ван-дер-Ваальса (а) из закона идеального газа (б) из уравнения Ван-дер-Ваальса (c) Объясните причину (ы) разницы. Решение [латекс] P = \ frac {nRT} {V} = \ frac {3.2} [/ латекс] Это окончательно дает P = 32,4 атм. (c) Это не очень отличается от значения из закона идеального газа, потому что давление не очень высокое, а температура не очень низкая. Значение несколько отличается, потому что молекулы CO 2 действительно имеют некоторый объем и притяжение между молекулами, а закон идеального газа предполагает, что они не имеют объема или притяжения. Проверьте свои знания (а) из закона идеального газа (б) из уравнения Ван-дер-Ваальса (c) Объясните причину (ы) разницы. (а) 46,562 атм; б) 46,594 атм; (c) Уравнение Ван-дер-Ваальса учитывает объем самих молекул газа, а также межмолекулярные притяжения. Молекулы газа обладают конечным объемом и испытывают силы притяжения друг к другу.Следовательно, поведение газа не обязательно хорошо описывается законом идеального газа. В условиях низкого давления и высокой температуры этими факторами можно пренебречь, уравнение идеального газа является точным описанием поведения газа, и говорят, что газ демонстрирует идеальное поведение. Однако при более низких температурах и более высоких давлениях требуются поправки на молекулярный объем и молекулярное притяжение, чтобы учесть конечный размер молекулы и силы притяжения. Уравнение Ван-дер-Ваальса — это модифицированная версия закона идеального газа, которую можно использовать для объяснения неидеального поведения газов в этих условиях.2}) \ times (V — nb) = nRT [/ latex] (а) высокое давление, малый объем (б) высокая температура, низкое давление (в) низкая температура, высокое давление CO, CO 2 , H 2 , He, NH 3 , SF 6 ? (a) с использованием закона идеального газа (b) с использованием уравнения Ван-дер-Ваальса (c) Объясните причину разницы. (d) Определите, какая коррекция (для P или V) является доминирующей и почему. (a) Если бы XX вел себя как идеальный газ, как бы выглядел его график зависимости Z от P? (b) На протяжении большей части этой главы мы проводили расчеты, считая газы идеальными.Было ли это оправдано? (c) Как объем молекул газа влияет на Z? При каких условиях этот эффект невелик? Когда он большой? Объясните, используя соответствующую схему. (d) Как межмолекулярное притяжение влияет на значение Z? При каких условиях этот эффект невелик? Когда он большой? Объясните, используя соответствующую схему. (e) В целом, при каких температурных условиях вы ожидаете, что Z будет иметь наибольшие отклонения от Z для идеального газа? 1.Газы C, E и F 3. Поведение газа наиболее похоже на поведение идеального газа при условиях, указанных в (b). Молекулы имеют высокие скорости и перемещаются на большие расстояния между столкновениями; у них также более короткое время контакта, и взаимодействия менее вероятны. Отклонения возникают при условиях, описанных в (a) и (c). В условиях (а) некоторые газы могут сжижаться. В условиях (c) большинство газов сжижается. 5. SF 6 7. (a) Прямая горизонтальная линия в точке 1.0; (b) Когда реальные газы находятся при низких давлениях и высоких температурах, они ведут себя достаточно близко к идеальным газам, что их можно аппроксимировать как таковые, однако в некоторых случаях мы видим, что при высоком давлении и температуре приближение идеального газа нарушается и значительно отличается от давления, рассчитанного по уравнению идеального газа (c) Чем больше сжимаемость, тем большее значение имеет объем. При низких давлениях поправочный коэффициент для межмолекулярного притяжения более значителен, и влияние объема молекул газа на Z будет небольшим снижением сжимаемости.При более высоких давлениях влияние объема самих молекул газа на Z увеличит сжимаемость (см. Рисунок 1). (D) И снова при низких давлениях влияние межмолекулярного притяжения на Z будет более важным, чем поправочный коэффициент для объем самих молекул газа, хотя, возможно, все еще небольшой. При более высоких давлениях и низких температурах эффект межмолекулярного притяжения будет сильнее. См. Рисунок 1. (e) низкие температуры Соберите термины.Разделите каждое уравнение на давление P и разделите каждое уравнение на соответствующий мольный член: Настройте свою таблицу известных и неизвестных: Подставьте известные величины в уравнение закона Авогадро: Решите указанное выше уравнение для объема V 2 , умножив обе части уравнения на 16.0 моль: Обратите внимание, как объем и моль прямо пропорциональны. По мере увеличения количества молей газа увеличивался и объем газа. Закон о комбинированном газе Что произойдет, если ни одна из переменных для газа не будет постоянной (были изменены давление, объем, температура и моль газа)? Результатом стал бы Закон о комбинированном газе. Выведем этот закон. Приведите индексы давления, объема, молей и температуры, поскольку все они изменяются: Соберите термины.Разделите каждое уравнение на соответствующие моль и температурный член: Это уравнение очень полезно, поскольку оно содержит любые эмпирические зависимости закона газа, которые могут вам понадобиться. Если моль и температура остаются постоянными, то приведенное выше уравнение упрощается до закона Бойля. Если давление и количество молей остаются постоянными, тогда уравнение упрощается до закона Чарльза и т. Д. Если постоянными остаются только моли, подставьте известные давление, объем и температуру в приведенное выше уравнение и найдите неизвестную величину.Например, предположим, что у вас есть газ при давлении 15,0 атм, объемом 25,0 л и температуре 300 К. Каким будет объем газа при стандартной температуре и давлении? Стандартное давление составляет 1,00 атм, а стандартная температура составляет 0 o C (или 273 K) Настройте таблицу известных и неизвестных, как и раньше: Подставьте эти переменные в комбинированный газовый закон. Поскольку моль не изменилась, мольные члены выпали из уравнения: Решить объем, V 2 .Умножьте обе части уравнения на 273 K и разделите обе части уравнения на 1,00 атм: Другие уравнения, выведенные из закона идеального газа Подставьте это в закон идеального газа, и вы получите уравнение: Умножая обе части на молярную массу, MM, получаем: Это уравнение полезно для определения молярной массы газа из экспериментальных данных, где измеряются масса, давление, объем и температура газа. Теперь давайте разделим обе части приведенного выше выражения на объем, V: Поскольку мы знаем, что г / В — это плотность, D, давайте заменим г / В в приведенном выше уравнении на г / В: Это уравнение полезно для установления связи между давлением, плотностью и температурой газа так же, как и другие эмпирические законы газа, с которыми мы столкнулись. Реальные газы Обратите внимание на то, как «корректируются» значения давления и объема.Поскольку столкновения реальных газов неупругие, член n 2 a / V 2 корректирует взаимодействия этих частиц. Величина а является постоянной величиной и должна определяться экспериментально для каждого газа. Поскольку частицы реального газа имеют реальный объем, член nb корректирует исключенный объем. Значение b является постоянным и должно определяться экспериментально для каждого газа. Константы Ван-дер-Ваальса a и b для многих газов приведены в таблице CRC Handbook of Chemistry and Physics .Излишне говорить, что они будут даны вам, если вам потребуется решить проблему с помощью этого уравнения. На этом уровне можно легко решить только давление или температуру. Решение для объема нетривиально и включает решение кубического полиномиального уравнения. Давайте покажем, как уравнение Ван-дер-Ваальса перестраивается для определения давления. Начните с деления обеих частей уравнения на член объема, V — nb: Затем вычтите член межчастичного взаимодействия, n 2 a / V 2 из обеих частей уравнения: Используя закон реального газа, давайте найдем давление, равное 2.00 моль углекислого газа при 298 К в контейнере Подставляя все переменные в соответствующие члены уравнения, получаем давление: Сравните это с давлением, рассчитанным по закону идеального газа: На главную »Различия между» Идеальным газом и реальным газом — определение и 8 основных различий — обзор
Идеальные газы
Раствор
идеальный газ | химия и физика
9.6 Неидеальное поведение газа — Химия
Цели обучения
Газ a (L 2 атм / моль 2 ) b (л / моль) N 2 1,39 0,0391 О 2 1,36 0,0318 CO 2 3,59 0,0427 H 2 O 5,46 0.0305 He 0,0342 0,0237 CCl 4 20,4 0,1383 Таблица 3. Значения констант Ван-дер-Ваальса для некоторых распространенных газов Пример 1
Колба объемом 4,25 л содержит 3,46 моль CO 2 при 229 ° C. Рассчитайте давление этого образца CO 2 :
(a) Из закона идеального газа:
Колба на 560 мл содержит 21 штуку.3 г N 2 при 145 ° C. Рассчитайте давление N 2 : Ответ:
Химия: упражнения в конце главы
Глоссарий
Решения
газов.хтм
P 2 V 2 = n 2 RT 2
.
5,00 л. Константы Ван-дер-Ваальса для диоксида углерода равны: a = 3,592 л 2 . атм / моль 2 и b = 0,04267 л / моль. Идеальный газ и настоящий газ — определение и 8 основных различий
Создано с BioRender.com Определение реального газа
8 основных различий (идеальный газ и реальный газ)
Ссылки и источники Характеристики Идеальный газ Реальный газ Определение Идеальный газ — это теоретический газ, который подчиняется закону идеального газа, поскольку частицы газа не подвергаются межчастичным взаимодействиям. Настоящий газ — это неидеальный газ, который занимает пространство и не подчиняется закону идеального газа, поскольку частицы газа имеют тенденцию к межчастичному взаимодействию. Закон об идеальном газе Идеальные газы подчиняются закону идеального газа. Настоящие газы не подчиняются закону идеального газа. Межмолекулярное притяжение Между молекулами идеального газа нет межмолекулярного притяжения. Между молекулами реального газа существует межмолекулярное притяжение. Объем и масса Частицы идеального газа не имеют определенного объема и массы. Частицы реального газа имеют определенный объем и массу. Столкновения Столкновения между частицами газа совершенно упругие. Столкновения между частицами газа неупругие. Кинетическая энергия Кинетическая энергия частиц остается постоянной. Кинетическая энергия частиц изменяется при каждом столкновении. Влияние температуры и давления Идеальный газ может вести себя как настоящий газ при высоком давлении и низкой температуре. Настоящий газ может вести себя как идеальный газ при низком давлении и высокой температуре. Концепция Идеальный газ — это теоретическое понятие. Все газы — настоящие газы.
Категории Различия между, Физическая химия Теги Идеальный газ, Настоящий газ сообщение навигации .