PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
-
2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
-
3 Термодинамика и МКТ
- 3.1 МКТ
 2 Термодинамика
2 Термодинамика
-
4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
-
5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
-
5.
 3 Фотометрия
3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.6 СТО
-
6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
Ивантеевский филиал Московского политехнического университета: Сведения об образовательной организации
php_value «upload_max_filesize» «15M» php_value «post_max_size» «15M» php_value «memory_limit» «32M»
Размер:
AAA
Цвет: C C C
Изображения
Вкл.
Обычная версия сайта
День открытых дверей Версия для слабовидящих Версия для слабовидящих
-
О филиале
- Сведения об образовательном учреждении
- Педагогический совет
- Структура
- Руководство
- Преподаватели и сотрудники
- История
- Положение о филиале
- Библиотека
- Объявления
- Лицензии
- Приемная комиссия
- Видеогалерея
- Правовая информация
- Противодействие коррупции
- Противодействие терроризму и экстремизму
- Дополнительные сведения о деятельности филиала
- Охрана труда
- Контакты
-
Абитуриентам
- День открытых дверей
- Приемная комиссия
- Приемная кампания
- Документы и справки
- Специальности и направления
- Стоимость обучения
- Правила и условия приема
- Общежитие
- Студенческая жизнь
- Фотогалерея
-
Обучающимся
- Учебные материалы
- Расписание
- Информация об учебных группах
- Оплата обучения
- Документы и справки
- Студенческая жизнь
- Спортивная жизнь
- Социальная сфера
- Международная деятельность
- Иностранным студентам
- Доступная среда
- Горячая линия
-
Выпускникам
- График работы ГЭК
- Центр содействия занятости
- Дополнительное образование
- Банк вакансий
- Контакты
- Главная
- ›
- Сведения об образовательной организации
- ›
- Образование
- ›
- 23-02-03
arcgis desktop — Радиус кривизны для кривых сегментов дорог для всей дорожной сети
спросил
Изменено 7 лет, 10 месяцев назад
Просмотрено 7к раз
У меня есть шейп-файл дорожной сети для штата США, и я пытаюсь получить радиус кривизны сегментов дорог в этом шейп-файле.
Сегменты дороги варьируются от 0,2 мили до 5 или около того миль. Каждый сегмент имеет несколько поворотов, но меня интересуют только повороты, достаточно маленькие, чтобы заставить транспортное средство сделать разумный поворот. Это должно уменьшить количество интересующих кривых на сегмент максимум до 1 или 2, при этом многие сегменты вообще не имеют таких кривых. Я не определил максимальный радиус кривой (порог), который я хотел бы использовать.
Для сегментов только с 1 такой кривой я хотел бы получить значения этих кривых для этих сегментов, а для сегментов с более чем 1 подойдет среднее значение.
- arcgis-desktop
- геометрия
- кривизна
6
Кривизна (κ) двумерной кривой определяется как κ=dϕ/ds, где ϕ — тангенциальный угол, а s — длина дуги ( источник ).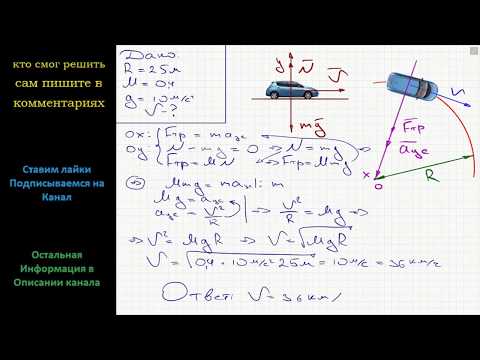 Чтобы избежать вычислений, эту производную можно аппроксимировать как общее изменение угла , деленное на общую длину кривой . Радиус кривизны (r) — это просто величина, обратная кривизне: r = 1/κ
Чтобы избежать вычислений, эту производную можно аппроксимировать как общее изменение угла , деленное на общую длину кривой . Радиус кривизны (r) — это просто величина, обратная кривизне: r = 1/κ
Эту математику можно использовать для расчета радиуса кривой в оцифрованной полилинии дороги, которая аппроксимируется несколькими сегментами линии. Процедура выглядит примерно так:
- Определите начальную и конечную точки кривой.
- Измерьте общее изменение угла и общей длины кривой от начала до конца.
- Посчитайте и сохраните радиус кривизны.
Однажды я написал скрипт, который перебирает вершины полилиний, вычисляя направление линии и изменение угла. В зависимости от изменения угла (поворот вправо? влево? не поворот?), он решает, является ли каждая точка
Существует несколько дополнительных шагов фильтрации для игнорирования очень малых изменений угла и других проблем, возникающих из-за артефактов оцифровки, а не реальной кривизны дороги. Если радиус находится в пределах определенного интересующего диапазона (для наших целей нас интересовало только r меньше 100 футов), он выводит его в новый шейп-файл. Даже при всем при этом он достаточно быстр и способен пробежать тысячи дорог. Результаты кажутся достаточно надежными, хотя я не проводил всестороннего анализа ошибок.
Если радиус находится в пределах определенного интересующего диапазона (для наших целей нас интересовало только r меньше 100 футов), он выводит его в новый шейп-файл. Даже при всем при этом он достаточно быстр и способен пробежать тысячи дорог. Результаты кажутся достаточно надежными, хотя я не проводил всестороннего анализа ошибок.
2
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
геометрия — Средний радиус кривизны множества точек на дороге?
спросил
Изменено 4 года, 2 месяца назад
Просмотрено 2к раз
$\begingroup$
У меня есть набор точек (широта, долгота) на серпантинной дороге. Как правильно рассчитать средний радиус кривизны дороги?
Даже без учета точек (широта, долгота), только на 2D-поверхности, предполагая, что есть много точек (xi, yi), которые могут быть частью 2D-дороги, как лучше всего рассчитать 1 — габаритная кривизна 2 — отдельные кривизны каждого из выпуклых/вогнутых участков.
Можно разделить, рассчитав точки перегиба, а затем можно использовать приведенную здесь формулу, но мне было интересно, есть ли другой лучший способ сделать это. Поскольку возможно иметь выпуклое сечение, которое очень сложно, и просто взятие 3 точек может не дать полной картины.
Поскольку возможно иметь выпуклое сечение, которое очень сложно, и просто взятие 3 точек может не дать полной картины.
- геометрия
- тригонометрия
- кривизна
- угол
- сплайн
$\endgroup$
4
$\begingroup$
Чтобы добиться этого, я бы использовал гладкую интерполирующую кривую с непрерывностью не менее $G_2$. Кубический сплайн является хорошим кандидатом.
Затем можно установить аналитическое выражение кривизны для каждого участка сплайна и построить график с произвольной выборкой. Вы, вероятно, захотите построить кривизну как функцию криволинейной абсциссы (уравнение внутренней кривой).
Вы можете получить криволинейные абсциссы путем численного интегрирования и в то же время интегрировать (абсолютную) кривизну, чтобы получить среднее значение.
$\endgroup$
$\begingroup$
Правильное определение кривизны гладкой кривой включает вторую производную.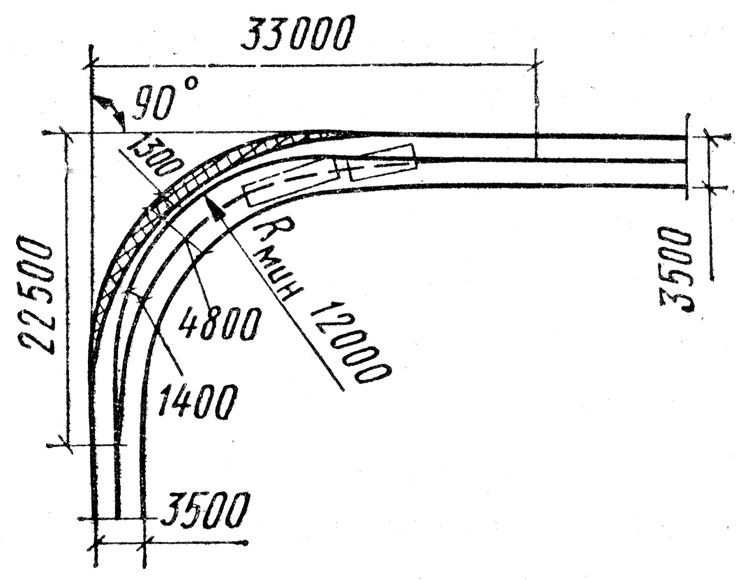

 2 Термодинамика
2 Термодинамика