Оптимальный коэффициент — избыток — воздух
Cтраница 1
Оптимальные коэффициенты избытка воздуха устанавливают при наладке парогенераторов. Способы поддержания его на заданном уровне различны. На больших парогенераторах применяют специальную систему автоматики, которая поддерживает определенную концентрацию кислорода в дымовых газах изменением подачи воздуха к горелкам. При этом контролируют и наличие химического недожога, по которому корректируется оптимальное значение избытка воздуха. [1]
Оптимальный коэффициент избытка воздуха определяется при тепловых испытаниях котлоагрегата. При эксплуатации воздух подают в соответствии с режимной картой, газоанализатор контролирует это соответствие и должен показывать значение СО2 с отклонениями 0 4 — 0 6 % от заданного. На котлах с производительностью пара 20 т / ч типа ДКВР-20-13 избыток воздуха целесообразно контролировать по содержанию кислорода О3 в уходящих газах, что увеличит точность определения коэффициента избытка воздуха.
За оптимальный коэффициент избытка воздуха принимается такой, при котором сумма потерь тепла с уходящими газами, от химической и механической неполноты горения и расход электроэнергии на тягу и дутье минимальны. [3]
За оптимальный коэффициент избытка воздуха принимается такой, при котором сумма потерь теплоты с уходящими газами, 01 лнмлческой и механической неполноты горения и расход элек-ур О — пещ1пг на тягу и дутье минимальны. [4]
Определение оптимального коэффициента избытка воздуха рекомендуется производить в два этапа. На первом этапе определяется ориентировочное значение оптимального коэффициента избытка воздуха. На втором этапе производится уточнение и окончательный выбор оптимального коэффициента избытка воздуха. Второй этап выполняется после проведения опытов по выбору оптимальной тонкости пыли и положения факела в топочной камере.
Определение оптимального коэффициента избытка воздуха в топке ( за первой ближайшей к топке поверхностью нагрева) проводится в продолжение опытов по выявлению оптимального положения факела в топке. [6]
Ориентировочное определение оптимального коэффициента избытка воздуха производится путем анализа продуктов горения с определением содержания RO2 и О2 на выходе из топочной камеры или за первой, ближайшей к топке поверхностью нагрева. [7]
Что называется оптимальным коэффициентом избытка воздуха и как он определяется. [8]
| Выбор тонкости пыли в зависимости от выхода летучих в топливе для топок с молотковыми мельницами. [9] |
Опыты проводятся при ориентировочно выбранном оптимальном коэффициенте избытка воздуха
Зависимость инжекционной способности единичного элемента смесителя блочной инжекциопной горелки от давления газа перед горелкой. а — при длине туннеля 100 мм и разрежении в топке 3 ( 1 и 2 ( 2 мм вод. ст.. б — при разрежении в топке 2 0 мм вод. ст. и длине туннеля 100 ( 7 и 135 мм ( г.
[11] а — при длине туннеля 100 мм и разрежении в топке 3 ( 1 и 2 ( 2 мм вод. ст.. б — при разрежении в топке 2 0 мм вод. ст. и длине туннеля 100 ( 7 и 135 мм ( г.
[11] |
Отсюда следует, что оптимальный коэффициент избытка воздуха на выходе из смесителя, равный 1 02 — 1 03, обеспечивается при разрежении в топке 2 0 мм вод. ст. и давлении газа перед смесителем больше 2000 мм вод ст., а оптимальной длиной туннеля следует считать 100 мм. [12]
При работе котлоагрегата с пониженными нагрузками оптимальный коэффициент избытка воздуха увеличивается. В связи с этим необходимо определять оптимальный коэффициент избытка воздуха для характерных нагрузок агрегата. Рекомендуется определять его для четырех нагрузок котлоагрегата: номинальной, 75 % и 50 % номинальной, а также минимальной, при которой топка еще работает устойчиво и происходит надежная циркуляция воды в котле. [13]
При работе котлоагрегата с пониженными нагрузками оптимальный коэффициент избытка воздуха увеличивается. В связи с этим необходимо определять оптимальный коэффициент избытка воздуха для характерных нагрузок агрегата. Рекомендуется определять его для четырех нагрузок котлоагрегата: номинальной, 75 % и 5СИ4 номинальной, а также минимальной, при КОТОРОЙ топка еш е работает устойчиво и происходит надежная циркуляции-воды в котле.
[14]
В связи с этим необходимо определять оптимальный коэффициент избытка воздуха для характерных нагрузок агрегата. Рекомендуется определять его для четырех нагрузок котлоагрегата: номинальной, 75 % и 5СИ4 номинальной, а также минимальной, при КОТОРОЙ топка еш е работает устойчиво и происходит надежная циркуляции-воды в котле.
[14]
Для каждой топки в печи существует оптимальный коэффициент избытка воздуха
 При неполном сгорании топлива увеличивается содержание СОз и уменьшается содержание О2, и — наоборот, незначительное содержание СО2 или высокое содержание кислорода О2 говорит об избытке воздуха.
[15]
При неполном сгорании топлива увеличивается содержание СОз и уменьшается содержание О2, и — наоборот, незначительное содержание СО2 или высокое содержание кислорода О2 говорит об избытке воздуха.
[15]Страницы: 1 2 3 4
Топливо для дизелей | Тепловые машины жд
Страница 23 из 33
Глава III
ДВИГАТЕЛИ ВЫСОКОГО СЖАТИЯ (ДИЗЕЛИ)
§ 8-9. Топливо для двигателей внутреннего сгорания
Правильный выбор вида и сорта топлива определяет экономичность и эксплуатационную долговечность двигателя.
В двигателях внутреннего сгорания может применяться газообразное, жидкое и твердое топливо. Оно должно обладать способностью сравнительно быстро перемешиваться с воздухом внутри цилиндра.
В продуктах сгорания не должно быть твердого остатка в виде золы или кокса, смолистых паров, а также агрессивных к металлу веществ.
Твердый остаток, попадая в смазку, усиливает износ цилиндров поршня и других деталей. Пары смолы, конденсируясь, осаждаются на клапанах и особенно на внутренних поверхностях выпускной системы. Даже незначительное количество смол способно уменьшить проходное сечение выпускного трубопровода.
Пары смолы, конденсируясь, осаждаются на клапанах и особенно на внутренних поверхностях выпускной системы. Даже незначительное количество смол способно уменьшить проходное сечение выпускного трубопровода.
Каменный уголь, дрова, торф используются только после их газификации в специальных устройствах — газогенераторах. Опыты сжигания твердого топлива в виде угольной пыли показали отрицательные результаты, так как зола и несгоревшие частицы пыли вызывали повышенный износ цилиндра и поршневой группы. Работа двигателя сопровождалась весьма высоким расходом смазки.
Для грузовых автомобилей, работающих вблизи газокомпрессорных станций, иногда применяется высокосжатый или сжиженный газ, содержащийся в баллонах, установленных под кузовом автомобиля.
Дизельное топливо — продукт переработки сырой нефти, в зависимости от фракционного состава оно подразделяется на ряд сортов или марок.

Для быстроходных двигателей вырабатываются четыре марки дизельного топлива: ДА (арктическое), ДЗ (зимнее), ДЛ (летнее), ДС (специальное). Такое топливо характеризуется весьма низкой вязкостью.
При использовании для двигателей топлива, имеющего высокую вязкость, его необходимо подогревать, чтобы обеспечить движение в топливопроводе и нормальную работу топливной аппаратуры. Температура подогрева равна 45—55° С.
Качество топлива определяют следующие показатели.
Зольность бензина и керосина должна быть равна нулю. Для всех видов топлива, используемых в дизелях, зольность допускается не больше 0,02—0,05%.
Содержание кокса в продуктах сгорания указывает на присутствие в жидком топливе смолистых веществ, которые из-за краткости времени сгорания переходят в кокс. Поэтому оценка величины смолистых веществ, имеющихся в топливе, производится так называемым коксовым числом. Коксовое число определяется путем нагревания пробы воздуха в тигле без доступа воздуха и выражается в процентах от первоначального веса пробы.

В топливе могут быть сернистые соединения и элементарная сера. Сернистые соединения вызывают коррозию топливных баков, топливопроводов и деталей топливной аппаратуры. Особенно активен сероводород, поэтому его присутствие в топливе не допускается.
При сгорании серы образуется сернистый ангидрид и серный ангидрид. В продуктах сгорания всегда имеется водяной пар, способный конденсироваться. При соединении влаги и сернистого ангидрида образуется сернистая кислота, соединение же серного ангидрида с водой дает серную кислоту. В результате сжигания сернистого топлива в цилиндре двигателя образуется преимущественно серная кислота. Попадание серной кислоты на стенки цилиндра, поршня и поршневых колец ускоряет их коррозию, а примешивание к смазочному маслу вызывает также коррозию шеек вала и подшипников. При этом в смазочном масле повышается величина смолистых веществ, что ускоряет засорение фильтров и уменьшает срок службы масла.

С увеличением содержания серы в топливе наблюдается повышенное отложение нагара на днище поршня и его кольцах, в выпускном тракте. Поэтому содержание серы в дизельном топливе строго ограничивается.
В качестве меры, снижающей отрицательное воздействие серы, к топливу и смазке добавляют специальные присадки, количество которых составляет около 0,7% веса топлива.
Основные характеристики топлива регламентируются ГОСТами, содержащими, в частности, следующие данные (табл. 8-1).
Таблица 8-1
§ 8-10. Теплота сгорания топлива и рабочей смеси.
Коэффициент избытка воздуха
Характеристикой, определяющей энергетическую ценность топлива, является его теплота сгорания Q, под которой понимают количество тепла, выделяющегося при сжигании 1 кг топлива.
Qн = 339 С + 1030 Н — 109 (От — S) кДж/кг.
 (8-11)
(8-11)Дизельное топливо состоит в среднем из углерода (86%), водорода (13%), серы (до 1%), кислорода (1,0-0,1%). Теплота сгорания QH = = 42 284 кДж/кг или QH = 10 200 ккал/кг.
На железнодорожном транспорте используются виды и сорта топлива, имеющие различную величину теплоты сгорания, поэтому при учете расхода топлива вводится так называемое условное топливо, имеющее теплоту сгорания 29 330 кДж/кг (7000 ккал/кг).
Отношение теплоты сгорания действительного топлива к теплоте сгорания условного топлива называется калорийным эквивалентом. Для дизельного топлива калорийный эквивалент равен 1,43.
В цилиндр двигателя подаются топливо и воздух, содержащий кислород, необходимый для сгорания топлива. Смесь воздуха и частиц топлива или его паров называется горючей смесью.
Количество требующегося воздуха и получающееся количество газов сгорания определяется по реакциям полного сгорания всех элементов, входящих в топливо (§ 4-5, 4-6, 4-7).
Для сгорания 1 кг жидкого топлива, имеющего С =86%, Н =13%, От = 1%, требуется воздуха Lo = 14,4 кг/кг.
Величина Lo называется теоретически необходимым количеством воздуха, так как получена в предположении, что процесс сгорания происходит при полном перемешивании топлива с воздухом, когда каждая частица топлива получает количество кислорода, достаточное для полного сгорания.
В действительности, к таким условиям приближается процесс смесеобразования у двигателей карбюраторных и газовых, использующих легко испаряющееся топливо, имеющих длительный период смесеобразования (такты всасывания и сжатия). Для дизелей с весьма кратким временем смесеобразования (0,0034-0,004 с) требуется вводить в цилиндр воздуха больше теоретически необходимого. Отношение количества воздуха, поступающего в цилиндр Lд, к теоретически необходимому называется коэффициентом избытка воздуха α.
У двигателей с воспламенением от сжатия коэффициент избытка воздуха 1,6—1,8 (в цилиндр подается доза топлива, соответствующая номинальной мощности двигателя).
Стационарные двигатели работают при постоянной частоте вращения коленчатого вала. При понижении мощности, снимаемой с вала, регулятор уменьшает количество топлива, поступающего в цилиндр. Однако количество воздуха, засасываемого в цилиндр, при любой мощности практически остается постоянным. Поэтому при уменьшении мощности, развиваемой двигателем, коэффициент избытка воздуха увеличивается.
При понижении мощности, снимаемой с вала, регулятор уменьшает количество топлива, поступающего в цилиндр. Однако количество воздуха, засасываемого в цилиндр, при любой мощности практически остается постоянным. Поэтому при уменьшении мощности, развиваемой двигателем, коэффициент избытка воздуха увеличивается.
Мощность тепловозного двигателя зависит от частоты вращения коленчатого вала и количества топлива, впрыскиваемого в цилиндр. Изменение частоты вращения очень мало влияет на количество воздуха, засасываемого в цилиндр. Поэтому в данном случае можно принять зависимость величины избытка воздуха только от количества топлива, поступающего в цилиндр. Наименьшее количество топлива подается в цилиндр на холостом ходу; по мере возрастания мощности, развиваемой двигателем, доза впрыскиваемого топлива увеличивается, поэтому коэффициент избытка воздуха уменьшается и при номинальной мощности достигает расчетной величины (рис. 8-16).
Рис. 8-16 Изменение коэффициента избытка воздуха в зависимости от нагрузки двигателя
При проектировании нового двигателя величина коэффициента α для номинального режима берется на основании опытных данных с учетом конструктивных особенностей двигателя и режима его эксплуатации. Коэффициент избытка воздуха для построенного двигателя определяется по анализу газов, забираемых из выпускных патрубков, или по расходу воздуха и топлива.
Коэффициент избытка воздуха для построенного двигателя определяется по анализу газов, забираемых из выпускных патрубков, или по расходу воздуха и топлива.
Горючая смесь, находящаяся в цилиндре при α=1, состоит из L0 кг воздуха и 1 кг топлива. Объемом жидкого топлива вследствие его малости по сравнению с объемом воздуха можно пренебречь. Тогда теплота горючей смеси Qcm при α= 1 и теплоте сгорания топлива QH
(8-12)
Для различных сортов дизельного топлива величины QH и Lo изменяются незначительно, поэтому QCM можно принять зависящей только от коэффициента избытка воздуха. Другие виды и сорта топлива имеют разную величину QH и Lo, вследствие этого теплота сгорания смеси получается разной и зависит от QH, Lo и а.
Поэтому некоторые топлива с меньшей теплотой сгорания образуют смеси с большей теплотой сгорания, например при а = 1 этиловый спирт имеет QH = 27 100 кДж/кг, Lo = 7 м®/кг, Qcm = 3866 кДж/кг; крекинг-бензин имеет QH = 43 000 кДж/кг, Lo = 11,5 м3/кг и Qcm= 3739 кДж/кг, т. е. на 3,3% меньше по сравнению с теплотой сгорания горючей смеси этилового спирта. Следовательно, мощность двигателя зависит от теплоты сгорания горючей смеси, а не топлива. Из формулы (8-12) следует, что с увеличением Lo теплота сгорания смеси уменьшается.
е. на 3,3% меньше по сравнению с теплотой сгорания горючей смеси этилового спирта. Следовательно, мощность двигателя зависит от теплоты сгорания горючей смеси, а не топлива. Из формулы (8-12) следует, что с увеличением Lo теплота сгорания смеси уменьшается.
- << Назад
- Вперёд >>
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 4 из 10Следующая ⇒ При образовании и сгорании горючей смеси на каждый килограмм топлива может расходоваться различное количество воздуха. То количество воздуха, которое действительно расходуется на сжигание 1 кг топлива, называется действительным количеством воздуха и обозначается буквой LД. Если теоретически необходимое количества воздуха — величина определенная для каждого сорта топлива, то действительное количество воздуха может иметь практически любую величину: 7, 10, 15, 70, 100 и т. д. килограммов воздуха на каждый килограмм сжигаемого топлива. Для оценки качества горючей смеси, образующейся и сгорающей в зоне сгорания, служит коэффициент избытка воздуха. Коэффициентом избытка воздуха называется отношение действительно поданного количества воздуха л теоретически необходимому; обозначается он греческой буквой α.
Это безразмерный коэффициент; он показывает, во сколько раз действительное количество воздуха, расходуемое на сгорание 1 кг топлива, больше или меньше теоретически необходимого количества воздуха. Топливо — воздушная смесь, составленная из 1 кг керосина и 15 кг воздуха, называется нормальной (теоретической) смесью. Коэффициент избытка воздуха для нее равен 1. Все знакомы с керосиновой осветительной лампой. Посмотрите, как происходит в ней сгорание керосина (рис. 22,положение А). Керосин по фитилю подается к горелке, где испаряется. Пары керосина перемешиваются с воздухом и сгорают в зоне горения, давая яркий факел пламени. Яркое устойчивое пламя и отсутствие копоти указывает, что в зону горения подается как раз столько воздуха, сколько его необходимо для полного сгорания керосина. В зоне горения’ образуется нормальная смесь с а=1 или немного обогащенная. Увеличим подачу керосина — вывернем фитиль, при этом пламя станет темным, начнет колебаться, появится копоть (рис. 2, положение Б). Почему? Потому, что подача воздуха осталась почти неизменной, так как размер стекла не изменился, а подача топлива увеличилась, и топливовоздушная смесь стала богатой топливом. При сгорании богатой смеси кислорода не хватает, чтобы сгорел весь керосин, поэтому часть керосина остается несгоревшей и улетает в виде дыма и копоти. Рис. 22 Горение бедной, нормальной и богатой смесей Топливовоздушная смесь, в которой на 1 кг керосина приходится воздуха меньше 15 кг, называется богатой смесью. Коэффициент избытка воздуха у богатой смеси меньше единицы: α < 1. Чем больше увеличивать подачу керосина в лампу, тем более богатой будет смесь. Что же случилось с горением? Количество воздуха, протекающего через лампу, осталось неизменным, а количество керосина, поступающего в зону горения, уменьшилось, горючая смесь стала бедной. Бедная смесь горит медленно, плохо поджигается (поэтому при разжигании лампы вывертывается фитиль). Таким образом, если в смеси на 1 кг керосина приходится воздуха больше 15 кг, то такая смесь называется бедной. В турбореактивном двигателе а зависимости от режима работы на каждый килограмм сгорающего керосина приходится от 50 до 90 кг воздуха. Следовательно, через двигатель протекает в 3 — 6раз больше воздуха, чем необходимо для полного сгорания топлива, подаваемого в камеры сгорания. По предложению инженера Базарова (1924 г.) воздух в камере сгорания разделяется на два потока, меньшая часть его направляется а зону горения и используется там для окисления топлива (для сгорания топлива). В зоне горения добиваются образования нормальной смеси, которая хорошо горит. Остальная, большая часть воздуха (вентиляционный или вторичный воздух) в горении не участвует, она служит только для охлаждения нагретых деталей двигателя и для “разбавления” продуктов сгорания, образующихся в зоне горения. КАМЕРА СГОРАНИЯ Камера сгорания — элемент ТРД, где происходит непрерывное образование и сгорание топливовоздушной смеси и повышение температуры газов. Камера сгорания является очень ответственным элементом двигателя. От ее устройства и осуществления процесса сгорания зависят экономичность двигателя, надежность работы и длительность эксплуатации как самой камеры сгорания, так и двигателя. Камера сгорания должна удовлетворять следующим требованиям: 1. Объем камеры сгорания должен обеспечивать возможно высокую теплонапряженность, т. е. камера должна иметь малый объем, что уменьшает ее размеры и вес. Под теплонапряженностью камеры сгорания понимают количество тепла, выделяющееся единице объема (1 м3) камеры в течение 1 часа. Ждя современных камер сгорания (середина 50-х) теплонапряженность достигает 150000000 кал/м3 в час. 2. Топливо в камере сгорания должно сгорать полностью, В современных камерах полнота сгорания достигает 97 — 98%. 3. При запуске двигателя на земле и в воздухе должно обеспечиваться надежное поджигание смеси. 4. Нагретые детали камеры сгорания должны хорошо охлаждаться, это обеспечивает их работу длительное время без дефектов (прогаров, коробления, трещин и нагара от действия пламени). 5. Камера сгорания должна иметь небольшое гидравлическое сопротивление движению воздушного потока (давление газов в камере сгорания должно уменьшаться незначительно). 6. В камере должно обеспечиваться устойчивое горение смеси, т.е. не должно быть колебаний, затухания и срывом пламени при всех режимах работы двигателя. 7. Горение должно заканчиваться в жаровой трубе. Факел пламени не должен доходить до лопаток газовой турбины во избежание перегрева и обгорания их. 8. Температура газового потока на выходе из камеры сгорания должна быть одинаковой по всему сечению, чтобы не получилось местного обгорания или оплавления сопловых лопаток турбины. На современных ТРД наибольшее распространении получили трубчатые камеры сгорания. Трубчатая камера сгорания (рис. 23) состоит из внутренней жаровой трубы и внешнего кожуха сгорловиной. Жаровая труба сварена из листов жаростойкого сплава. В передней части жаровой трубы приварены конус для забора первичного воздуха, диск и конус с отверстиями для прохода воздуха. В конусе помещается лопаточный завихритель — для придания потоку воздуха вращательного движения. Внутри завихрителя помещается форсунка, впрыскивающая топливо в завихренный поток воздуха; этим достигается хорошее перемешивание топлива с воздухом. На конической части жаровой трубы сделаны отверстия большого размера для подвода вторичного воздуха внутрь жаровой трубы. Жаровые трубы соединяются между собой соединительными патрубками, через которые передается пламя при запуске и выравнивается давление газов в соседних камерах сгорания. Рис. ⇐ Предыдущая12345678910Следующая ⇒ Читайте также: Организация работы процедурного кабинета Статус республик в составе РФ Понятие финансов, их функции и особенности Сущность демографической политии |
|||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 249; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176. |
Теоретически необходимое количество воздуха
Для полного сгорания 1 кг топлива необходимо израсходовать определенное количество воздуха. Если воздуха взять недостаточное количество, то будет происходить неполное сгорание топлива. Если воздуха взять больше, чем надо для полного сгорания 1 кг топлива, то продукты сгорания будут иметь более низкую температуру, чем при полном сгорании топлива, а реакция сгорания будет протекать медленно, вяло.
Теоретически необходимым количеством воздуха называется то наименьшее количество воздуха, которое необходимо израсходовать для полного сгорания 1 кг топлива.
Обозначается теоретически необходимое количество воздуха буквой L0.
Например, для полного сгорания 1кг .керосина (или бензина) необходимо израсходовать 14,7 кг воздуха. Поэтому для керосина считают теоретически необходимое количество воздуха равным:
При
образовании и сгорании горючей смеси
на каждый килограмм топлива может
расходоваться различное количество
воздуха. То количество воздуха, которое
действительно расходуется на сжигание
1 кг топлива,
называется действительным количеством
воздуха и обозначается буквой LД.
То количество воздуха, которое
действительно расходуется на сжигание
1 кг топлива,
называется действительным количеством
воздуха и обозначается буквой LД.
Если теоретически необходимое количества воздуха — величина определенная для каждого сорта топлива, то действительное количество воздуха может иметь практически любую величину: 7, 10, 15, 70, 100 и т. д. килограммов воздуха на каждый килограмм сжигаемого топлива.
Для оценки качества горючей смеси, образующейся и сгорающей в зоне сгорания, служит коэффициент избытка воздуха. Коэффициентом избытка воздуха называется отношение действительно поданного количества воздуха л теоретически необходимому; обозначается он греческой буквой α. (альфа).
Это
безразмерный коэффициент; он показывает,
во сколько раз действительное количество
воздуха, расходуемое на сгорание 1 кг топлива,
больше или меньше теоретически
необходимого количества воздуха.
Топливо — воздушная смесь, составленная из 1 кг керосина и 15 кг воздуха, называется нормальной (теоретической) смесью. Коэффициент избытка воздуха для нее равен 1.
Все знакомы с керосиновой осветительной лампой. Посмотрите, как происходит в ней сгорание керосина (рис. 22, положение А). Керосин по фитилю подается к горелке, где испаряется. Пары керосина перемешиваются с воздухом и сгорают в зоне горения, давая яркий факел пламени. Яркое устойчивое пламя и отсутствие копоти указывает, что в зону горения подается как раз столько воздуха, сколько его необходимо для полного сгорания керосина. В зоне горения’ образуется нормальная смесь с а=1 или немного обогащенная. В зоне горения камеры сгорания реактивного двигателя также стараются получить нормальную или немного обогащенную смесь — она хорошо загорается от электрической искры я устойчиво горит.
Увеличим
подачу керосина — вывернем фитиль, при
этом пламя станет темным, начнет
колебаться, появится копоть (рис. 2,
положение Б). Почему?
Потому, что подача воздуха осталась
почти неизменной, так как размер стекла
не изменился, а подача топлива увеличилась,
и топливовоздушная смесь стала
богатой топливом. При сгорании богатой
смеси кислорода не хватает, чтобы сгорел
весь керосин, поэтому часть керосина
остается несгоревшей и улетает в виде
дыма и копоти.
2,
положение Б). Почему?
Потому, что подача воздуха осталась
почти неизменной, так как размер стекла
не изменился, а подача топлива увеличилась,
и топливовоздушная смесь стала
богатой топливом. При сгорании богатой
смеси кислорода не хватает, чтобы сгорел
весь керосин, поэтому часть керосина
остается несгоревшей и улетает в виде
дыма и копоти.
Рис. 22 Горение бедной, нормальной и богатой смесей
Топливовоздушная смесь, в которой на 1 кг керосина приходится воздуха меньше 15 кг, называется богатой смесью. Коэффициент избытка воздуха у богатой смеси меньше единицы: α < 1.
Чем
больше увеличивать подачу керосина в
лампу, тем более богатой будет смесь.
Пламя начнет мигать, выделение копоти
увеличится — процесс горения керосина
будет идти неустойчиво, вяло, и при
сильном обогащении смеси пламя погаснет.
Для улучшения процесса сгорания смесь
надо
обеднить
-уменьшить подачу керосина. Будем
уменьшать, подачу топлива — ввертывать
фитиль. Пламя начнет переходить в
ярко-желтый цвет, это значит, что
топливовоздушная смесь имеет нормальный
состав, т. е. у нее α=1. При дальнейшем
ввертывании фитиля пламя лампы из
ярко-желтого будет переходить в синий,
голубой цвет, пламя начнет дрожать,
вспыхивать — процесс горения станет
неустойчивым (рис. 22, положение В).
Будем
уменьшать, подачу топлива — ввертывать
фитиль. Пламя начнет переходить в
ярко-желтый цвет, это значит, что
топливовоздушная смесь имеет нормальный
состав, т. е. у нее α=1. При дальнейшем
ввертывании фитиля пламя лампы из
ярко-желтого будет переходить в синий,
голубой цвет, пламя начнет дрожать,
вспыхивать — процесс горения станет
неустойчивым (рис. 22, положение В).
Что же случилось с горением? Количество воздуха, протекающего через лампу, осталось неизменным, а количество керосина, поступающего в зону горения, уменьшилось, горючая смесь стала бедной. Бедная смесь горит медленно, плохо поджигается (поэтому при разжигании лампы вывертывается фитиль).
Таким
образом, если в смеси на 1 кг керосина
приходится воздуха больше 15 кг, то
такая смесь называется бедной. Коэффициент
избытка воздуха в бедной смеси больше
единицы α > 1. Например, смесь,
состоящая из 1 кг керосина
и 20 кг воздуха,
будет бедной. При сгорании ее сгорит
весь керосин, но часть кислорода воздуха
останется неиспользованной. Продукты
сгорания бедной смеси гореть не могут.
Продукты
сгорания бедной смеси гореть не могут.
В турбореактивном двигателе а зависимости от режима работы на каждый килограмм сгорающего керосина приходится от 50 до 90 кг воздуха.
Следовательно, через двигатель протекает в 3 — 6 раз больше воздуха, чем необходимо для полного сгорания топлива, подаваемого в камеры сгорания. По предложению инженера Базарова (1924 г.) воздух в камере сгорания разделяется на два потока, меньшая часть его направляется а зону горения и используется там для окисления топлива (для сгорания топлива). В зоне горения добиваются образования нормальной смеси, которая хорошо горит. Остальная, большая часть воздуха (вентиляционный или вторичный воздух) в горении не участвует, она служит только для охлаждения нагретых деталей двигателя и для “разбавления” продуктов сгорания, образующихся в зоне горения.
Топливовоздушная смесь в бензиновом двигателе
Для работы двигателю с искровым зажиганием (SI) требуется топливовоздушная смесь с определенным соотношением количества воздуха и топлива (отношение воздух/топливо). Идеальное, теоретически полное сгорание топлива имеет место при отношении масс 14,7:1 (стехиометрическое отношение), т.е. для сгорания 1 кг топлива требуется 14,7 кг воздуха. Или: топливо объемом 1 л полностью сгорает в присутствии 9500 л воздуха.
Идеальное, теоретически полное сгорание топлива имеет место при отношении масс 14,7:1 (стехиометрическое отношение), т.е. для сгорания 1 кг топлива требуется 14,7 кг воздуха. Или: топливо объемом 1 л полностью сгорает в присутствии 9500 л воздуха.
Содержание
- Топливовоздушная смесь
- Коэффициент избытка воздуха λ
- Системы смесеобразования
Топливовоздушная смесь
Удельный расход топлива в значительной степени зависит от соотношения воздух/топливо (см. рис. «Влияние коэффициента избытка воздуха на удельный расход топлива и неравномерную работу двигателя при постоянной эффективной мощности» ). Для обеспечения действительно полного сгорания топлива требуется избыточное количество воздуха и, следовательно, как можно более низкий расход топлива. Однако здесь имеют место ограничения, зависящие от воспламеняемости и доступного времени сгорания смеси.
Также состав смеси влияет на эффективность снижения выбросов токсичных веществ с отработавшими газами. В настоящее время с этой целью используется трехкомпонентный каталитический нейтрализатор, который действует с максимальной производительностью при стехиометрическом соотношении воздух/топливо. Это может значительно снизить вероятность повреждения компонентов системы очистки отработавших газов. Поэтому современные двигатели, когда это позволяют условия работы, работают при стехиометрическом составе смеси.
В настоящее время с этой целью используется трехкомпонентный каталитический нейтрализатор, который действует с максимальной производительностью при стехиометрическом соотношении воздух/топливо. Это может значительно снизить вероятность повреждения компонентов системы очистки отработавших газов. Поэтому современные двигатели, когда это позволяют условия работы, работают при стехиометрическом составе смеси.
Для определенных условий работы двигателя требуется адаптация состава смеси. Так, изменение состава смеси требуется при пуске холодного двигателя. Отсюда следует, что системы смесеобразования должны обеспечивать работу двигателя в различных режимах.
Коэффициент избытка воздуха λ
В качестве показателя отличия фактического состава смеси от теоретически необходимого массового отношения (14,7:1) был выбран коэффициент избытка воздуха λ (лямбда). Коэффициент λ равен отношения массы подаваемого в двигатель воздуха к массе воздуха, необходимой для обеспечения стехиометрического состава смеси.
λ = 1: масса подаваемого в двигатель воздуха равна теоретически необходимой массе.
λ < 1: недостаток воздуха и, следовательно, богатая топливно-воздушная смесь. Максимальная выходная мощность двигателя имеет место при λ = 0,85 — 0,95.
λ > 1: имеет место избыток воздуха, т.е. смесь становится обедненной. При работе на бедной смеси эффективная мощность двигателя падает, при этом обеспечивается снижение расхода топлива. Максимально допустимое значение λ — «предел возникновения пропусков зажигания при обеднении смеси» в значительной степени зависит от конструкции двигателя и используемой системы смесеобразования. При использовании такой смеси она долго не воспламеняется, а процесс сгорания происходит с нарушениями, сопровождаемыми неравномерной работой двигателя.
На двигателях с искровым зажиганием (SI) и впрыском топлива во впускной трубопровод, при постоянной выходной мощности двигателя, минимальный расход топлива достигается в зависимости от двигателя при избытке воздуха 20 — 50 % (λ = 1,2 -1,5).
На рис. «Влияние коэффициента избытка воздуха на содержание токсичных веществ в отработанных газах» показаны зависимости удельного расхода топлива, а также содержания различных токсичных веществ в отработавших газах от коэффициента избытка воздуха (при постоянной выходной мощности двигателя). Из этих графиков видно, что нельзя выбрать идеальное значение коэффициента λ, при котором все рассматриваемые показатели были бы в максимальной степени приемлемы. Для двигателей с впрыском топлива во впускной трубопровод для обеспечения «оптимального» расхода топлива при «оптимальной» эффективной мощности приемлемым является значение λ в диапазоне 0,9-1,1.
В двигателях с прямым впрыском топлива и послойным распределением заряда смеси имеют место иные условия сгорания топлива, поэтому предел обеднения смеси наступает при значительно более высоких значениях λ. В диапазоне частичных нагрузок эти двигатели могут работать при значительно более высоком коэффициенте избытка воздуха (до λ = 4).
Для нормальной работы трехкомпонентного каталитического нейтрализатора необходимо точное соблюдение λ = 1 при нормальной рабочей температуре двигателя. Выполнение этого условия возможно при обеспечении точной дозировки массы поступающего воздуха, включая и возможные добавки.
Для получения оптимального процесса сгорания в двигателях с системой впрыска топлива во впускной трубопровод необходимо обеспечивать не только впрыск точного количества топлива, но и однородность топливовоздушной смеси, что достигается эффективным распылением топлива. Если эти условия не соблюдаются, во впускном трубопроводе или на стенках камеры сгорания образуются большие капли топлива, которые полностью не сгорают, что приводит к повышенным выбросам несгоревших углеводородов.
Системы смесеобразования
Системы впрыска топлива или карбюраторы служат для приготовления топливовоздушной смеси, наилучшим образом обеспечивающей эффективную работу двигателя в заданном режиме. Системы впрыска топлива, особенно их электронные версии, лучше приспособлены для получения оптимальных режимов. Они позволяют снизить расход топлива и повысить эффективную мощность двигателя. Все более строгие требования в отношении снижения токсичности отработавших газов заставили производителей автомобилей практически полностью отказаться от карбюраторных топливных систем и перейти на электронные системы впрыска топлива.
Системы впрыска топлива, особенно их электронные версии, лучше приспособлены для получения оптимальных режимов. Они позволяют снизить расход топлива и повысить эффективную мощность двигателя. Все более строгие требования в отношении снижения токсичности отработавших газов заставили производителей автомобилей практически полностью отказаться от карбюраторных топливных систем и перейти на электронные системы впрыска топлива.
До начала этого столетия в автомобильной промышленности практически исключительно использовались системы, в которых смесеобразование происходит вне камеры сгорания (система с впрыском топлива во впускной трубопровод, см. рис. «Схематическое изображение системы впрыска топлива» , а). В настоящее время все шире применяются системы с внутренним смесеобразованием, т.е. с прямым впрыском топлива в камеру сгорания (система прямого впрыска топлива для бензиновых двигателей, см. рис. «Схематическое изображение системы впрыска топлива» , Ь), позволяющие еще больше снизить расход топлива и повысить выходную мощность двигателя.
РЕКОМЕНДУЮ ЕЩЁ ПОЧИТАТЬ:
Пример HTML-страницы| Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика | ⇐ ПредыдущаяСтр 4 из 8Следующая ⇒ Минимальное количество воздуха, необходимое для полного сгорания единицы количества (кг, кмоль, м3) горючего вещества, называется теоретическим количеством воздуха (Vв0). При горении на пожарах расход воздуха отличается от теоретически необходимого. Определение количества воздуха и объема продуктов горения оказывается возможным на основании закона сохранения массы по уравнениям химических реакций. При составлении уравнений материального баланса процессов горения принято учитывать не только кислород, принимающий в реакции окисления, но и азот, входящий в состав воздуха:
C6H6 + 7,5O2 + 7,5×3,76N2 = 6CO2 + 28,2N2 + 3H2O
Если состав горючего дан в весовых процентах каждого элемента из расчета на 1 кг массы, то по балансу элементарных реакций можно рассчитывать массовые расходы кислорода и количество продуктов горения. Из уравнения: H2 + 0,5O2 + 0,5×3,76N2 = H2O + 0,5×3,76N2 можно записать: 2 кг Н2 сгорают в 0,5×3,76×22,4 м3 воздуха; 1 кг Н2 сгорают в 26,7 м3 воздуха.
Общая формула для расчета Vв0 будет иметь вид: м3/кг, где C, H, S и О – содержание элементов в горючем, % весовые. Если состав газообразного горючего дан в объемных процентах, то, помня закон Авогадро, что в равных объемах газов при одинаковых внешних условиях содержится одинаковое число молекул, по балансу отдельных реакций можно определить с учетом заданного объема каждого газа в 1 м3 смеси объемы воздуха, теоретически необходимые для полного сгорания каждого газа, а следовательно, и всей смеси. CH4 + 2O2 + 2×3,76N2 = CO2 + 2H2O + 2×3,76N2;
VВ0=(2O2 + 2×3,76N2) м3 на (I м3 CH4) = 2+2×3,76 = 9,52 м3 или на I м3 CH4 расходуется 2 м3 O2, тогда м3. Формула для расчета теоретически необходимого объема воздуха для полного сгорания 1 м3 газовой смеси имеет вид: м3/м3, где и — процентное содержание данного газа в 1 м3 газовой смеси, — число молей кислорода, необходимое для полного сгорания 1 моля 1-го горючего газа. Аналогичным образом получают и формулы для расчета объемов продуктов горения. Если aВ>1, то избыточное количество воздуха учитывается в продуктах горения: , м3.
Коэффициент избытка воздуха при неполном сгорании рассчитывается по формуле: ,
а при полном , где CO2, СО, СН4 и т.д. процентное содержание каждого газа в продуктах горения; О2 – процентное содержание кислорода в продуктах горения. Таким образом, объем воздуха, пошедший на горение, можно рассчитать, если известен состав горючего. При этом наиболее оптимальный способ расчета выбирается, исходя из способа выражения состава горючего материала. Можно решать и обратные задачи: исходя из состава продуктов горения определять количество сгоревшего вещества; находить коэффициент избытка воздуха.
Задача 1.Определить объем воздуха и продуктов горения при н.у., если при пожаре на складе сгорело 2 кг ацетона, а горение протекало при aВ=2. Решение.Из возможных способов решения задачи следует остановиться на расчете объема воздуха и продуктов горения по уравнению химической реакции, т.
(CH3)2CO+4O2+4×3,76N2=3CO2+3H2O+4×3,76N2.
Определив молекулярную массу горючего, можно, составив пропорцию, рассчитать и количество воздуха, необходимое для сгорания 2 кг ацетона, а также и объем продуктов горения. Молекулярная масса ацетона 58, для горения этого количества ацетона требуется 4+4×3,76 молей воздуха, или (4+4×3,76)×22,4 м3 воздуха, т.к. объем 1 кмоля воздуха при н.у. равен 22,4 м3, тогда на горение 2 кг ацетона теоретически необходимое количество воздуха рассчитывается из выражения:
м3.
Действительное количество воздуха с учетом коэффициента избытка воздуха aВ=2 рассчитывается по выражению: VВ=2×14,7=29,4 м3, а избыток воздуха: VВ-VВ0=29,4-14,7=14,7 м3. Объем продуктов горения также определяется по уравнению реакции: из 58 кг ацетона образуется 3×22,4 м3 углекислого газа, 3×22,4 м3 водяного пара, 4×3,76×22,4 м3 азота, расчетный объем продуктов горения на 2 кг ацетона находятся из выражения: м3.
С учетом избытка воздуха полный объем продуктов горения: VП.Г. = 16,25+14,7=30,95 м3. Примечание.Если температура в процессе горения была задана другой, то объем продуктов горения и воздуха рассчитывается с учетом объема, который занимает один кмоль газа при этой температуре: , где Po=101325 Па; Т0=273,15 К; заданные температура и давление. Задача 2.Определить объем воздуха и продуктов горения при сжигании 1 кг горючего вещества, имеющего элементный состав: С-40 %, Н-10 %, N-20%, золы-18 %, влаги-12 %; aВ=I (считать, что воздух и продукты горения находятся при н. Решение.Для решения задачи необходимо было бы записать балансы элементарных реакций горения углерода, водорода с учетом процентного содержания каждого элемента в 1 кг горючего, но есть уже готовые формулы, которыми можно воспользоваться, например, объем воздуха: м3/кг. Поскольку азот, влага и зола не горят, а S и О в веществе нет, уравнение принимает вид: м3/кг. Тогда объем воздуха, пошедший на горение, будет: м3/кг. Объем продуктов горения рассчитывается исходя из элементного состава горючего следующим образом. Из уравнений элементарных реакций известно, что объем углекислого газа при горении 1 кг углерода составляет 1,86 м3,сернистого газа из 1 кг серы – 0,7 м3 и т.д. Но в условии задачи углерода в горючем 40 %, что составляет 0,4 кг углерода, равно . В состав продуктов горения войдут азот, углекислый газ, водяной пар с учетом влаги из горючего вещества: м3/кг; м3/кг; м3/кг, м3/кг. Задача 3.Газовая смесь объемом 1 м3, состоящая из 20 % ацетилена, 40 % бутана, 20 % углекислого газа и 20 % кислорода сгорает с 30 %-м избытком воздуха. Вычислить объем воздуха, принимающего участие в горении, и объем продуктов горения, если процесс протекает при н.у. Решение.Записываем уравнения горения каждого газа: C2H2+2,5O2+2,5×3,76N2 = 2CO2+H2O+2,5×3,76N2; C4H10+6,502+6,5×3,76N2 = 4CO2+5HO2+6,5×3,76N2. Углекислый газ не горит, поэтому его надо учесть только в продуктах горения, когда будем вычислять их полный объем. Рассчитываем объем воздуха, теоретически необходимый для полного сгорания газовой смеси:
м3/м3.
Действительный объем воздуха находим, учитывая коэффициент избытка воздуха, равный 1,3: VВ = VВ0aВ=13,81×1,3=17,95 м3/м3. Избыток воздуха, который войдет в состав продуктов горения, будет: DVВ= VВ— VВ0=17,95-13,81=4,14 м3. В результате горения образовались углекислый газ и водяной пар. Из уравнения реакции видим, что при горении 1 м3 ацетилена образуется 2 м3 СО2 и 1 м3 Н2О, но в составе газовой смеси находится 0,2 м3 С2Н2, поэтому углекислого газа образуется при горении ацетилена лишь 2×0,2=0,4 м3, водяного пара 1×0,2=0,2 м3. Полный объем углекислого газа находим, учитывая количество его в горючей смеси: =2×0,2+4×0,4+0,2= =2,2 Аналогично рассчитываем объем водяного пара в продуктах горения:
м3. В состав продуктов горения войдет избыток воздуха 4,14 м3, который состоит из 4,14×0,21=0,87 м3 кислорода и 4,14×0,79=3,27 м3 азота. Тогда полный объем продуктов горения, учитывая, что в продуктах горения содержится углекислый газ, водяной пар, азот и кислород, находим следующим образом: м3. Примечание.Целесообразно определять раздельно в продуктах горения объемы азота и кислорода, а если потребуется, состав продуктов горения можно выразить в процентном соотношении. ⇐ Предыдущая12345678Следующая ⇒
Поиск по сайту: |
Топливо и сжигание
Топливо и сжигание
Большинство видов топлива содержат углерод и Водород и находятся в твердом, жидком или газообразном состоянии.
1.
Твердое топливо (уголь): состоит из влаги, летучих веществ, связанного углерода.
и пепел. Анализ указывает на основе массы относительные количества этих
составляющие. Окончательный анализ может быть дан на сухую основу.
Окончательный анализ может быть дан на сухую основу.
2. Жидкие виды топлива: большинство жидких видов топлива представляют собой смеси различных Углеводороды. Типичными примерами являются бензин, керосин, дизельное топливо и т. д. Обычно жидкое топливо рассматривается как отдельный углеводород по эмпирической формуле C x H y , даже если оно представляет собой смесь нескольких углеводороды.
3. Газообразное топливо: природный газ (в основном метан), угольный газ (смесь метан и водород) и т. д.
В большинстве процессам горения необходимый кислород не подается в виде чистого кислорода, а подается в виде воздуха. В воздухе содержится 21 моль % O 2 и 79 мольных % N 2 .
количество воздуха, обеспечивающее необходимое количество кислорода для полного
горение топлива называется стехиометрическим или теоретическим воздухом.
Количество воздуха сверх стехиометрического количества воздуха называется избыточным воздухом . Это обычно выражается в пересчете на стехиометрический состав воздуха в процентах избытка воздуха . Количество воздуха меньше стехиометрического называется недостатком воздуха .
коэффициенты к веществам, называемым стехиометрическими коэффициентами. Баланс атомов дает теоретическое количество воздуха как
C: = x
H: 2 =y
N 2 : =3.76*
O 2 :
And the total количество молей воздуха на 1 моль топлива становится
n воздуха =
Два важных
параметрами, часто используемыми для выражения соотношения топлива и воздуха, являются воздушно-топливные
соотношение (AF) и его обратное соотношение топливо-воздух (FA).
AF масса = м воздух / м топливо
АФ моль = n Air / n Fuel
Проблема:
Метан (CH 4 ) сжигается атмосферным воздухом. Анализ продуктов на сухую основу следующим образом:
CO 2 10,00%
o 2 2,37
CO 0,53
N 2 87,10
—————-
100,00%
Рассчитайте коэффициент воздуха-формирования и процент теоретического воздуха, и определить уравнение горения.
Решение:
Решение состоит из написание уравнения горения 100 кмоль сухих продуктов, вводя буквенные коэффициенты для неизвестных величин, а затем решение для них.
Из анализа продуктов, можно написать следующее уравнение, имея в виду, что это анализ на сухую основу.
Баланс по каждому из элементов будет позволяют решить для всех неизвестных коэффициентов:
Баланс азота: c = 87,1
Так как весь азот поступает с воздуха,
c / b =3,76 b=87,1/3,76=23,16
Баланс углерода: a = 10,00+0,53=10,53
Баланс водорода: d=2a=21,06
Баланс кислорода: все
были решены неизвестные коэффициенты, поэтому кислородный баланс
обеспечивает проверку правильности. Таким образом, b также может определяться кислородным
остаток средств.
Таким образом, b также может определяться кислородным
остаток средств.
b=10,00+0,53/2+2,37+21,06/2=23,16
подставляя эти значения для a,b,c и d имеем
Деление на 10,53 дает уравнение горения на кмоль топлива.
Соотношение воздух-топливо на моль основа
2,2+8,27=10,47 кмоль воздуха/кмоль топливо
Топливо-воздух в массе находится путем введения молекулярных масс.
AF=10,47*28,97/16,0=18,97 кг воздуха/кг топлива
Теоретическая воздушно-топливная соотношение находится путем записи уравнения горения для теоретического воздуха.
AF тео = (2+7,52)28,97/16,0=17,23 кг воздуха/кг топлива
Теоретический процент воздуха IS 18,97/17,23 = 110%
Проблема
Определенный уголь имеет после окончательного анализа в пересчете на сухую массу, % по массе:
Компонент | Проценты по массе |
Сера | 0,6 |
Водород | 5,7 |
Углерод | 79,2 |
Кислород | 10,0 |
Азот | 1,5 |
Ясень | 3,0 |
Этот уголь нужно сжечь
с 30% избытком воздуха. Рассчитайте соотношение воздух-топливо по массе.
Рассчитайте соотношение воздух-топливо по массе.
Решение:
Один из подходов к этой проблеме состоит в том, чтобы написать уравнение горения для каждого из горючих элементов на 100 кг топлива. Сначала находится молярный состав на 100 кг топлива.
кмоль S / 100 кг топлива = 0,6/32 = 0,02
кмоль H 2 / 100 кг топливо = 5,7/2 = 2,85
кмоль C / 100 кг топливо=79,2/12=6,60
кмоль O 2 / 100 кг топливо=10/32=0,31
кмоль N 2 / 100 кг топливо=1,5/28=0,05
Уравнения горения для теперь выписаны горючие элементы, что позволяет найти Теоретическая потребность в кислороде.
1 0 . требуется / 100 кг топлива
-0,31 кмоль O 2 в топлива / 100 кг топлива
7,73 кмоль O 2 от воздух / 100 кг топлива
AF тео = [7,73+7,73(3,76)]28,97/100=10,63 кг воздуха/кг топлива
При 30% избытке воздуха соотношение воздух-топливо
AF=1,3*10,63=13,82 кг воздуха/ кг топлива
Сколько воздуха требуется для полного сгорания?
РЕКЛАМА:
В следующей статье вы узнаете: Сколько воздуха требуется для полного сгорания?
Стехиометрическое соотношение воздух-топливо: Стехиометрическое соотношение воздух-топливо можно определить как отношение количества воздуха, необходимого для полного сгорания 1 кг топлива. Его также называют химически правильным соотношением воздух-топливо.
Его также называют химически правильным соотношением воздух-топливо.
Если сгорание завершено, то и тогда от данного топлива может быть получено только максимальное количество тепла. Теоретически точное количество необходимого кислорода можно рассчитать с помощью уравнений или с помощью формулы, полученной из приведенных выше уравнений, и это даст нам непосредственно теоретически необходимое количество кислорода, если мы знаем окончательный анализ топлива.
ОБЪЯВЛЕНИЯ:
Кислород для сжигания топлива должен быть получен из атмосферного воздуха, хотя в некоторых случаях определенное количество кислорода входит в состав топлива. Воздух представляет собой смесь кислорода, азота, небольшого количества углекислого газа и небольших следов редких газов, таких как неон, аргон, криптон и т. д.
Для всех практических целей мы предполагаем, что воздух состоит из 23% по массе кислорода, а остальные 77% составляют азот. Если считать по объему, воздух состоит из 21% кислорода и 79% азота. Зная количество кислорода, необходимое для сгорания топлива, мы можем определить количество воздуха, необходимое для полного сгорания одного кг топлива.
Зная количество кислорода, необходимое для сгорания топлива, мы можем определить количество воздуха, необходимое для полного сгорания одного кг топлива.
Возьмем 1 кг топлива, предельный анализ которого показывает, что углерод составляет C кг, водород H кг, кислород O кг и сера S кг.
1 кг углерода требует для полного сгорания 8/3 кг кислорода; следовательно, для C кг углерода потребуется C x 8/3 кг кислорода, что эквивалентно 2,66 C кг кислорода (с учетом до двух знаков после запятой).
ОБЪЯВЛЕНИЯ:
1 кг водорода требует 8 кг кислорода; следовательно, для H кг водорода требуется 8H кг кислорода.
1 кг серы требует 1 кг кислорода; поэтому S кг серы требует S кг кислорода.
Следовательно, количество кислорода, необходимое для сгорания 1 кг топлива, составляет:
(2,66С+8Н+Т) кг.
ОБЪЯВЛЕНИЯ:
Если топливо содержит O кг кислорода; то учитывается
∴ Кислород, необходимый из воздуха для полного сгорания топлива, будет (2,66C + 8H + S – O), что может быть записано как 2,66C + 8 (H – O/8) + S, термин в скобках известен как доступный водород. Таким образом, мы получаем формулу для определения минимального количества кислорода для полного сгорания твердого или жидкого топлива, предельный состав которой известен.
Таким образом, мы получаем формулу для определения минимального количества кислорода для полного сгорания твердого или жидкого топлива, предельный состав которой известен.
Формула может быть записана следующим образом:
Определение избытка воздуха:
Мы рассчитали минимальное количество воздуха, необходимое для полного сгорания одного кг топлива. На практике мы подаем воздуха больше, чем теоретическое минимальное количество, чтобы обеспечить полное сгорание топлива, потому что весь подаваемый воздух не вступает в тесный контакт с частицами топлива.
ОБЪЯВЛЕНИЙ:
Большое количество избыточного воздуха оказывает охлаждающее действие на процесс горения и представляет собой потери, и во избежание этого охлаждающего действия воздух перед поступлением в топку котла предварительно подогревается.
При естественной тяге избыток воздуха больше, чем при искусственной тяге. Общее количество подаваемого воздуха зависит от количества топлива, скорости сгорания, системы зажигания и интенсивности тяги. Избыток воздуха может приближаться к 100 %, но в современной практике используется от 25 до 50 %.
Избыток воздуха может приближаться к 100 %, но в современной практике используется от 25 до 50 %.
На избыток воздуха указывает CO 2 % в дымовых газах. Когда в котельной ланкаширского типа используется ручное сжигание с естественной тягой, 10-12% CO 2 в дымовых газах считается хорошей практикой. С механическими толкателями и искусственной тягой было бы вполне разумно ожидать от 12% до 15% CO 2 .
ОБЪЯВЛЕНИЯ:
В случае двигателя внутреннего сгорания весь воздух, всасываемый во время такта всасывания, не будет соприкасаться с частицами топлива; в результате подается избыточный воздух, который необходимо свести к минимуму, чтобы получить более конкретную производительность. Если подача воздуха в цилиндр двигателя составляет менее 15 %, то смесь воздуха и топлива в цилиндре называется богатой. Если подача воздуха превышает теоретический минимум более чем на 30 %, то смесь называют слабой смесью.
Пример:
Определить теоретическую массу воздуха, необходимого для полного сгорания 1 кг угля, анализ которого по массе дан следующим образом:
Углерод — 83%, водород — 5%; кислород – 2%;
Сера – 0,2%; остаток негорючий.
Решение:
Как известно, при окончательном анализе топлива определяется масса различных горючих элементов в топливе. В 1 кг топлива:
Углерод 0,83 кг, водород 0,05 кг, кислород 0,02 кг и сера 0,002 кг.
Минимальное количество воздуха, необходимое для полного сгорания 1 кг топлива, определяется по формуле:
Анализ дымовых газов по массе и объему:При сгорании топлива продуктами сгорания будут двуокись углерода, водяной пар, двуокись серы и азот воздуха. При подаче избыточного воздуха кислород также будет одной из составляющих анализа дымовых газов.
Для проведения анализа дымовых газов по массе определяют массу каждой составляющей отдельно и выражают каждую из них в процентах от общей массы. Когда массовый анализ дымовых газов известен, его можно преобразовать в объемный анализ с помощью гипотезы Авогадро (молекулярные массы всех газов при равных объемах).
Определение количества подаваемого воздуха на основе объемного анализа дымовых газов: Количество воздуха, подаваемого в топку котла, очень велико и не может быть измерено напрямую. Его косвенное измерение можно сделать, если мы знаем объемный анализ сухого дымового газа. Когда мы рассматриваем объемный анализ дымовых газов, мы учитываем окись углерода, двуокись углерода, кислород и азот, поскольку количество двуокиси серы незначительно, а водяной пар конденсируется.
Его косвенное измерение можно сделать, если мы знаем объемный анализ сухого дымового газа. Когда мы рассматриваем объемный анализ дымовых газов, мы учитываем окись углерода, двуокись углерода, кислород и азот, поскольку количество двуокиси серы незначительно, а водяной пар конденсируется.
Рассмотрим топливо, содержащее С% по весу углерода. Анализ сухих дымовых газов сжигания этого топлива показывает-
Мы знаем, что молекулярные массы газов являются относительными массами равных их объемов. Отсюда следует, что относительный вес данного относительного объема газов показан как:
Определение утечки воздуха в дымоходах котлов:
Давление в топке котла и различных газоходах ниже атмосферного при искусственной и естественной тяге; поэтому атмосферный воздух, скорее всего, просачивается в различные дымоходы через щели. Проведя анализ дымовых газов в двух точках, мы можем определить утечку воздуха между этими двумя контрольными точками. Величину подсоса воздуха можно определить по формуле.
Величину подсоса воздуха можно определить по формуле.
Определение количества воздуха, подаваемого на кг топлива:
Определение количества воздуха, подаваемого на кг топлива, по анализу дымовых газов при расчете по массе:
Пусть C будет % углерода в одном кг топлива, а вес газа указан ниже:
Химически правильное соотношение воздух-топливо:Минимальное количество воздуха, необходимое для полного сгорания одного м 3 газообразного топлива, которое рассчитывается как ниже-
I. Сжигание водорода:
II. Сгорание угарного газа:
III. Сжигание болотного газа:
Применяя полученную выше формулу, мы можем определить минимальное качество воздуха, необходимое для полного сгорания одного м 3 газообразного топлива. Зная процент избыточного подаваемого воздуха, мы можем узнать фактическое качество подаваемого воздуха для сжигания газообразного топлива.
Коэффициент избытка воздуха:
Количество воздуха, подаваемого сверх минимального количества воздуха, необходимого для полного сгорания. Это может быть выражено в процентах от избытка необходимого воздуха или с помощью коэффициента, известного как коэффициент избытка воздуха α.
Определение анализа дымовых газов по объему и массе в случае газообразного топлива:Когда объемный анализ газообразного топлива известен, мы можем легко определить объемный анализ сухого дымового газа. Когда известен объемный анализ, анализ по массе может быть получен с помощью метода. Иллюстрация взята для пояснения метода определения объемного анализа дымовых газов.
Пример :
Генераторный газ имеет следующий процентный состав по объему:
Н 2 – 15; СН 4 – 2; СО – 20; СО 2 – 6; О 2 = 3; № 2 – 54.
Для горения подается 50% избыток воздуха. Рассчитать объем воздуха, подаваемого на м 3 газа и провести анализ по объему сухих продуктов сгорания.
Рассчитать объем воздуха, подаваемого на м 3 газа и провести анализ по объему сухих продуктов сгорания.
Решение:
Количество кислорода, необходимое для полного сгорания водорода
= 0,5 х 0,15 = 0,075 м 3 .
Количество кислорода, необходимое для полного сгорания метана
= 2 х 0,02 = 0,04 м 3 .
Количество кислорода, необходимое для полного сгорания монооксида углерода
= 0,5 х 0,2 = 0,1 м 3 .
Определение количества подаваемого воздуха на м 3 Газ:Определение количества подаваемого воздуха на м 3 газа по сухому анализу дымовых газов в случае газообразного топлива:
Для определения количества подаваемого воздуха требуется анализ газа, а также анализ выхлопных газов. Из объемного анализа газа можно определить минимально необходимое количество воздуха, общий объем продуктов сгорания и образовавшегося водяного пара. Когда пар сконденсировался, можно рассчитать объем сухих продуктов сгорания. При анализе выхлопных газов пар конденсируется.
Когда пар сконденсировался, можно рассчитать объем сухих продуктов сгорания. При анализе выхлопных газов пар конденсируется.
Пусть V 1 м 3 — количество воздуха, подаваемого на 3 м газа сверх необходимого для полного сгорания, а V — объем сухих продуктов сгорания при подаче минимального количества воздуха.
∴ Суммарный объем фактических продуктов сгорания = (V 1 + V) м 3 .
Пусть O будет процентным содержанием кислорода (по объему), присутствующим в выхлопных газах, тогда избыточное количество воздуха, которое будет содержать этот объем кислорода, будет O/21 м 3 .
Когда известен избыток воздуха и известно минимальное необходимое количество воздуха, мы можем определить количество воздуха, подаваемого на 3 м газа.
Главная ›› Термодинамика ›› Топливо ›› Как ›› Определить количество воздуха, необходимого для горения
Введение Типичные вопросы, которые рассматриваются в этом разделе о горении: Ссылка на: апплет продуктов сгорания Воздух и топливо смешиваются в поршневом цилиндре, образуя реагенты горения. Равновесные продукты сгорания Если температура конечного продукта ниже 1000 K, продуктами являются CO2, h3O, N2, O2, CO и h3 с точными концентрациями в зависимости от температуры реакции и соотношения топливо/воздух. При высоком соотношении топливо/воздух не хватает кислорода для превращать весь углерод в топливе в двуокись углерода, что приводит к образованию монооксид углерода. При температуре выше 1000 К диссоциация
реакции в процессе горения
приведет к дополнительным видам, включая OH, NO, H и O. Определения Соотношение топливо/воздух
Коэффициент эквивалентности
Если коэффициент эквивалентности равен единице, горение стехиометрическое. Если он равен 1, сгорание богатое с неполным сгоранием. Топливо Шесть распространенных видов топлива:
C 3 H 8 Пропан C 2 H 5 OH Этанол С 8 Н 18 Октан
Н 2 Водород Раствор для молей CO на моль воздуха, v5 , равен предоставлено: 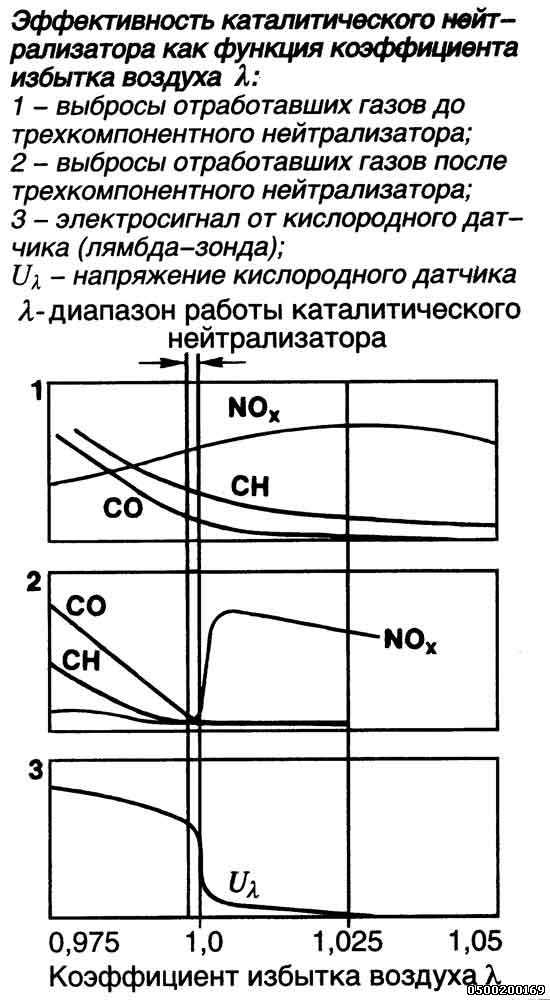 Решения для молярных коэффициентов продуктов Решения для молярных коэффициентов продуктов
 Следующий апплет является расширением параметров производительности двигателя. Апплет: Производительность двигателя Апплет параметров с типом топлива. Этот апплет сравнивает эффект типа топлива на производительность двигателя, а также включая эффекты передачи тепла. корреляция Вошни использовался коэффициент теплопередачи. На следующей странице обсуждается метод, используемый для определить Цинь. |
Модель с сосредоточенными параметрами для оценки релевантности избыточного воздуха в качестве индикатора обменных потоков между передающими и емкостными отсеками карстовых систем
Введение
Карстовые системы состоят из известняковых образований (карбонатных пород), часто осмысляемых через совместное наличие трех типов пористости: (i) межзерновая пористость, (ii) трещинная пористость и (iii) крупные и широкие каналы (Palmer, 1991). Относительные пропорции каждого типа пористости в карстовых водоносных горизонтах вызывают сильную пространственную изменчивость гидравлической проводимости (Jeannin, 2001) со значительными последствиями для кинетики потока (Ford and Williams, 2013). Это приводит к неоднородному полю проницаемости и нелинейному гидравлическому поведению. Дренаж в карстовых водоносных горизонтах представляет собой самоорганизующуюся структуру, ведущую к предпочтительному пути потока через сеть трубопроводов, встроенную либо в пористую матрицу, которая иногда является высокопроницаемой, либо в трещиноватую матрицу с низкой проницаемостью (Ford and Williams, 2013). Предпочтительные пути потока могут быть соединены с поверхностью через воронки или стоки, что обеспечивает быструю инфильтрацию поверхностных вод, что может повлиять на химический состав подземных вод (Aquilina et al., 2005), а также сопряжено с серьезным риском карстового загрязнения подземных вод (Hartmann). и др., 2021; Лукач Реберски и др., 2022).
Это приводит к неоднородному полю проницаемости и нелинейному гидравлическому поведению. Дренаж в карстовых водоносных горизонтах представляет собой самоорганизующуюся структуру, ведущую к предпочтительному пути потока через сеть трубопроводов, встроенную либо в пористую матрицу, которая иногда является высокопроницаемой, либо в трещиноватую матрицу с низкой проницаемостью (Ford and Williams, 2013). Предпочтительные пути потока могут быть соединены с поверхностью через воронки или стоки, что обеспечивает быструю инфильтрацию поверхностных вод, что может повлиять на химический состав подземных вод (Aquilina et al., 2005), а также сопряжено с серьезным риском карстового загрязнения подземных вод (Hartmann). и др., 2021; Лукач Реберски и др., 2022).
В то время как дренажная система контролирует перенос загрязняющих веществ внутри водоносного горизонта, матрица может накапливать загрязняющие вещества из-за бокового обмена между предпочтительным путем потока и окружающей матрицей. Таким образом, карстовые водоносные горизонты очень уязвимы из-за быстрого распространения загрязняющих веществ и их потенциального накопления в материнской породе с течением времени. Понимание и рассмотрение латерального обмена между этими двумя видами карстовой пористости, по-видимому, необходимы для надлежащего качественного (химическая уязвимость) и количественного (наличие ресурсов) управления ресурсами подземных вод карстового водоносного горизонта.
Понимание и рассмотрение латерального обмена между этими двумя видами карстовой пористости, по-видимому, необходимы для надлежащего качественного (химическая уязвимость) и количественного (наличие ресурсов) управления ресурсами подземных вод карстового водоносного горизонта.
Шоле и др. (2017) предложили совместную деконволюцию весеннего гидрографа и массового химографа для оценки латерального вклада с точки зрения потока и минерализации в карстовой системе с преобладанием водоводов. Исследование показывает, что поток слабоминерализованной воды может возникнуть из водовода в матрицу после крупных осадков в ненасыщенной зоне. Митрофан и др. (2015) также обратили внимание на вызванный паводком поток из карстового канала в окружающую матрицу, о чем свидетельствуют потоки хлоридов. Мартин и Дин (2001) показали, что водообмен из канала в матрицу может также иметь существенное значение в процессах карстификации из-за проникновения воды, недонасыщенной кальцитом, в матрицу. Численное моделирование также может дать представление о динамике латерального обмена (Bailly-Comte et al. , 2010; Reimann et al., 2011; Sivelle et al., 2019).; Даль Соглио и др., 2020 г.; Ширафкан и др., 2021). Вклад обмена от систем с медленным течением к системам с быстрым течением в трех карстовых водосборах, расположенных на юге Китая, оценивается между 64 и 87% (Zhang et al., 2017). В пределах мелового водоносного горизонта Норвиль (север Франции) потоки из материнской породы в водовод составляют примерно 10 % весеннего стока (Duran et al., 2020). В пределах сильно закарстованных водоразделов Багет и Алиу (Французские Пиренеи) годовой вклад матрицы в общий весенний сток составляет ~3% и может увеличиваться до 25% в периоды с малым количеством осадков (Sivelle et al., 2019).). Кроме того, при численном моделировании обменного потока могут быть полезны вспомогательные переменные, такие как температура (Berglund et al., 2020) или концентрация ионов Ca 2+ и Mg 2+ (Zhang et al., 2017) для калибровки модели. Другой подход заключается в анализе результатов моделирования вместе с физико-химическими свойствами, такими как электропроводность (Duran et al.
, 2010; Reimann et al., 2011; Sivelle et al., 2019).; Даль Соглио и др., 2020 г.; Ширафкан и др., 2021). Вклад обмена от систем с медленным течением к системам с быстрым течением в трех карстовых водосборах, расположенных на юге Китая, оценивается между 64 и 87% (Zhang et al., 2017). В пределах мелового водоносного горизонта Норвиль (север Франции) потоки из материнской породы в водовод составляют примерно 10 % весеннего стока (Duran et al., 2020). В пределах сильно закарстованных водоразделов Багет и Алиу (Французские Пиренеи) годовой вклад матрицы в общий весенний сток составляет ~3% и может увеличиваться до 25% в периоды с малым количеством осадков (Sivelle et al., 2019).). Кроме того, при численном моделировании обменного потока могут быть полезны вспомогательные переменные, такие как температура (Berglund et al., 2020) или концентрация ионов Ca 2+ и Mg 2+ (Zhang et al., 2017) для калибровки модели. Другой подход заключается в анализе результатов моделирования вместе с физико-химическими свойствами, такими как электропроводность (Duran et al. , 2020), чтобы лучше оценить физическое значение моделируемых внутренних потоков.
, 2020), чтобы лучше оценить физическое значение моделируемых внутренних потоков.
Среди них изучение растворенных благородных газов в недрах может представлять интерес для улучшения понимания динамики подземных вод в карстах за счет предоставления информации о пути течения и связях между компонентами водоносного горизонта. Исторически инертные газы использовались в качестве индикаторов окружающей среды для различных целей, таких как реконструкция палеоэкологических и палеоклиматических условий или определение зон питания (Heaton and Vogel, 19).81; Уилсон и Макнейл, 1997 г.; Эшбах-Хертиг и др., 2000; Питерс и др., 2002; Ингрэм и др., 2007 г.; Сано и др., 2017; Томонага и др., 2017 г.; Попп и др., 2021 г.; Шиллинг и др., 2022). В то время как равновесие растворимости атмосферных газов в основном контролируется температурой зоны пополнения, многие исследования показывают, что концентрации инертных газов в подземных водах часто отличаются от этих атмосферных равновесий и, по-видимому, модифицируются другим повсеместным явлением, называемым «избыток воздуха». Работа Holocher et al. (2002) удалось экспериментально показать, что образование избыточного воздуха можно объяснить полным или частичным растворением захваченных пузырьков воздуха под действием гидростатического давления (Heaton and Vogel, 19).81; Стьюте и Шлоссер, 2000 г.; Эшбах-Хертиг, 2004). Следовательно, избыток воздуха можно рассматривать как трассер, который может дать дополнительную полезную информацию о типе питания, то есть насыщенном или ненасыщенном, и амплитуде колебаний уровня грунтовых вод (Clark et al., 2005; Massmann and Sültenfuß, 2008; Schilling). и др., 2021). Избыток воздуха обычно выражается в виде объема при стандартных условиях температуры и давления (СТД), единицей измерения является см 3 СТД.кг -1 . Работа Перотен и др. (2021) показали на карсте Дюрзон с большой зоной аэрации (>200 м), что перенос воды по зоне аэрации вызывает небольшой избыток воздуха (+0,8 см 3 ст.ст.кг -1 ), который остается небольшим по сравнению с наблюдаемым у источника Дюрзон (+ 5,5 см 3 ст.
Работа Holocher et al. (2002) удалось экспериментально показать, что образование избыточного воздуха можно объяснить полным или частичным растворением захваченных пузырьков воздуха под действием гидростатического давления (Heaton and Vogel, 19).81; Стьюте и Шлоссер, 2000 г.; Эшбах-Хертиг, 2004). Следовательно, избыток воздуха можно рассматривать как трассер, который может дать дополнительную полезную информацию о типе питания, то есть насыщенном или ненасыщенном, и амплитуде колебаний уровня грунтовых вод (Clark et al., 2005; Massmann and Sültenfuß, 2008; Schilling). и др., 2021). Избыток воздуха обычно выражается в виде объема при стандартных условиях температуры и давления (СТД), единицей измерения является см 3 СТД.кг -1 . Работа Перотен и др. (2021) показали на карсте Дюрзон с большой зоной аэрации (>200 м), что перенос воды по зоне аэрации вызывает небольшой избыток воздуха (+0,8 см 3 ст.ст.кг -1 ), который остается небольшим по сравнению с наблюдаемым у источника Дюрзон (+ 5,5 см 3 ст. ст.кг -1 ), что свидетельствует о том, что избыток воздуха в основном формируется за счет вариаций уровень воды зоны насыщения этого карста.
ст.кг -1 ), что свидетельствует о том, что избыток воздуха в основном формируется за счет вариаций уровень воды зоны насыщения этого карста.
В этом исследовании мы исследовали актуальность использования ЭА для характеристики водообмена между трансмиссивными и емкостными отсеками в карстовой системе Дюрзона. Используя модель стока осадков с сосредоточенными параметрами, ЭА был смоделирован в предположении образования в емкостной части водоносного горизонта, когда происходит значительное пополнение, и путем добавления обменных потоков между трансмиссивной и емкостной частями карстовой системы Дюрзона. Сначала мы представляем геологический, гидрогеологический и метеорологический контекст исследуемой области. Затем описывается формирование ЭА, а также информация об условиях перезарядки, полученная в результате измерений концентрации инертных газов. Наконец, объясняется модель расхода дождевых осадков с сосредоточенными параметрами и способ учета EA в модели, прежде чем представить результаты калибровки, учитывающие как весенний расход, так и EA, и их значение с точки зрения параметрической неопределенности рассматриваемой модели расхода дождевых осадков с сосредоточенными параметрами.
Область исследования
Местная геология и гидрогеология
Карстовая система Дюрзона расположена в районе Гранд-Косс в Южном Центральном массиве (Франция) со средней высотой около 700 м над уровнем моря, варьируя от 500 до 900 м над уровнем моря ( Форес, 2016). Район исследования является частью природного регионального парка Гранд-Косс (PNRGC). Это один из исследовательских сайтов Французской национальной службы наблюдения H+ (http://hplus.ore.fr/), который является частью европейской инфраструктуры Elter (https://www.lter-europe.net/elter- Эсфри). Геология в этом районе состоит из юрских карстовых карбонатов: карбонатная серия Хеттанга отделена от серии карбонатов Доггера и Мальма мергелевой серией тоара, которая считается непроницаемым геологическим слоем (рис. 1). Мергелевые образования играют важную роль в гидрогеологическом функционировании гидрогеологической системы, разделяя два основных водоносных горизонта, которые представляют собой две упомянутые выше карбонатные толщи. Надвиг Госпиталет приводит мергель Лиас в контакт с водоносным горизонтом Доггер-Мальм и обеспечивает выход источника (рис. 1). Источник Дюрзона является единственным известным выходом одинарной карстовой системы, т. е. имплювий сложен только закарстованными породами и состоит из воклюзианского источника, т. е. сток организован ниже уровня источника (Марсо, 19).96). Родник расположен на высоте 533 м над уровнем моря и дренирует бассейн питания, площадь которого, оцененная по балансам массы, колеблется от 98 до 117 км 2 (Ricard, Bakalowicz, 1996; Tritz et al., 2011; Fores, 2016). ). Пространственные границы бассейна были определены на основе искусственных трассерных испытаний и геологических особенностей, накладывающих границу на границе раздела с непроницаемыми мергелями.
Надвиг Госпиталет приводит мергель Лиас в контакт с водоносным горизонтом Доггер-Мальм и обеспечивает выход источника (рис. 1). Источник Дюрзона является единственным известным выходом одинарной карстовой системы, т. е. имплювий сложен только закарстованными породами и состоит из воклюзианского источника, т. е. сток организован ниже уровня источника (Марсо, 19).96). Родник расположен на высоте 533 м над уровнем моря и дренирует бассейн питания, площадь которого, оцененная по балансам массы, колеблется от 98 до 117 км 2 (Ricard, Bakalowicz, 1996; Tritz et al., 2011; Fores, 2016). ). Пространственные границы бассейна были определены на основе искусственных трассерных испытаний и геологических особенностей, накладывающих границу на границе раздела с непроницаемыми мергелями.
Рисунок 1 . (Слева) Геологическая карта карстовой системы Дурзон (с изменениями из Fores, 2016 г.) (Справа) Схематический разрез источника Дурзон с проекцией различных точек отбора проб вдоль ненасыщенной зоны с гипотетическим положением воды уровень зоны насыщения (с изменениями из Pérotin et al. , 2021).
, 2021).
Система характеризуется зоной инфильтрации толщиной 200 м, и ни одна скважина на этой площади не достигает зоны насыщения. Поэтому только изменение весеннего расхода может дать необходимую информацию для гидродинамической характеристики зоны насыщения.
Климат
Район характеризуется средиземноморским климатом и влиянием океана. Годовое совокупное количество осадков колеблется от 929 до 1729 мм (2007–2019 гг.), При этом среднегодовое количество осадков составляет ~ 1180 мм, распределенных на ~ 92 дождливых дня в году (количество осадков > 1 мм.день -1 ). Средняя температура воздуха колеблется от 2,5°C зимой до 18°C летом, при среднегодовой температуре воздуха около 10°C. Среднегодовая потенциальная эвапотранспирация (ПЭТ), рассчитанная по формуле Пенмана-Монтейта (Penman, 1948) национальным метеорологическим агентством MétéoFrance на станции Кайлар, колеблется от 830 до 1020 мм (2007–2019 гг.) При среднегодовом ПЭТ примерно 927 мм. . Среднее значение ПЭТ менее 1 мм. сут -1 зимой и повышается примерно до 5 мм.день −1 в летний период. Осень характеризуется интенсивными дождливыми эпизодами, называемыми «севеноловыми эпизодами», когда кумулятивное количество осадков может достигать 286 мм в сутки −1 (17 сентября 2014 г.). Такие метеорологические явления в значительной степени способствуют пополнению водоносного горизонта и могут вызвать наводнения, динамика которых зависит от водного состояния водоносного горизонта. Например, выброс цевенола в 2014 г. произошел в конце длительного периода рецессии и привел к весеннему максимальному расходу всего 5 м 9 .0666 3 .s −1 у источника Дурзон. Следующий эпизод дождей, гораздо менее интенсивный, с максимальной интенсивностью осадков около 100 мм.сутки 90 666 -1 90 667 , вызвал максимальный весенний сток 16 м 90 666 3 90 667 .с 90 666 -1 90 667 (рис. 2).
сут -1 зимой и повышается примерно до 5 мм.день −1 в летний период. Осень характеризуется интенсивными дождливыми эпизодами, называемыми «севеноловыми эпизодами», когда кумулятивное количество осадков может достигать 286 мм в сутки −1 (17 сентября 2014 г.). Такие метеорологические явления в значительной степени способствуют пополнению водоносного горизонта и могут вызвать наводнения, динамика которых зависит от водного состояния водоносного горизонта. Например, выброс цевенола в 2014 г. произошел в конце длительного периода рецессии и привел к весеннему максимальному расходу всего 5 м 9 .0666 3 .s −1 у источника Дурзон. Следующий эпизод дождей, гораздо менее интенсивный, с максимальной интенсивностью осадков около 100 мм.сутки 90 666 -1 90 667 , вызвал максимальный весенний сток 16 м 90 666 3 90 667 .с 90 666 -1 90 667 (рис. 2).
Рисунок 2 . (Вверху) Временные ряды осадков (Pr) и эвапотранспирации (ET), измеренные на станции Кайлар, и временные ряды расхода, измеренные в источнике Дурзон, и отбор проб растворенных газов – (Внизу) Увеличение периода с 2014 по 2016 год.
Материалы и методы
Образование избытка воздуха
Избыток воздуха возникает в результате захвата пузырьков воздуха в пористой среде после значительного перезаряда. Гидростатическое давление, воздействующее затем на пузырьки воздуха, вызывает их растворение, вызывая приток воздуха больше, чем можно ожидать при равновесном обмене между воздухом и водой (Holocher et al., 2002; Aeschbach-Hertig, 2004; Klump et al., 2007). ). EA рассчитывали на основе концентраций Ne-Ar-N 2 , как N 2 не производится и не потребляется в значительных количествах на исследуемом участке (Heaton and Vogel, 1981; Plummer et al., 2004; Chatton, 2017). Благодаря процессу своего формирования ЭА может использоваться в качестве качественного индикатора изменения пьезометрического напора в водоносном горизонте.
Wilson и McNeill (1997) исследовали взаимосвязь между улавливанием пузырьков воздуха и литологией путем сравнения средних значений EA (рассчитанных на основе изотопов Ne) в пробах подземных вод из водоносных горизонтов, образовавшихся в известняках, песчаниках и гранитах.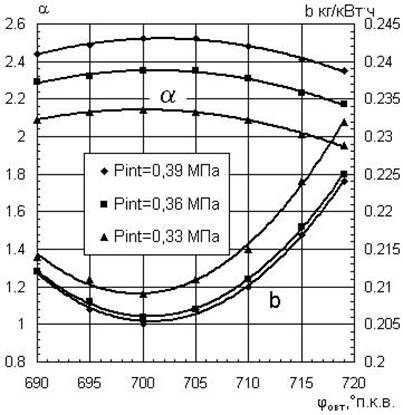 Образцы из гранитных водоносных горизонтов практически не имели ЭА, в то время как образцы из карбонатных водоносных горизонтов имели самые высокие значения ЭА (~1,0 см 3 STP.kg −1 ). Несколько авторов (Herzberg and Mazor, 1979; Heaton and Vogel, 1981; Mazor et al., 1983) сообщили о высоких значениях EA в карстовых водоносных горизонтах. Было предложено несколько концептуальных моделей для объяснения образования ЭА во время перезарядки. Согласно Хитону и Вогелю (1981), наличие пузырьков воздуха, захваченных под действием капиллярных сил в капиллярной кайме (в микроскопическом масштабе), могло бы объяснить образование ЭА. При инфильтрации поверхностных вод пузырьки воздуха переносятся на уровень зоны насыщения. Когда к захваченным пузырькам воздуха прикладывается достаточное гидростатическое давление, они растворяются в грунтовых водах. Герцберг и Мазор (1979), предположил, что высокопроницаемая трещиноватая природа большинства карстовых водоносных горизонтов часто связана с быстрой подпиткой, которая может быть ответственна за образование EA в макроскопическом масштабе.
Образцы из гранитных водоносных горизонтов практически не имели ЭА, в то время как образцы из карбонатных водоносных горизонтов имели самые высокие значения ЭА (~1,0 см 3 STP.kg −1 ). Несколько авторов (Herzberg and Mazor, 1979; Heaton and Vogel, 1981; Mazor et al., 1983) сообщили о высоких значениях EA в карстовых водоносных горизонтах. Было предложено несколько концептуальных моделей для объяснения образования ЭА во время перезарядки. Согласно Хитону и Вогелю (1981), наличие пузырьков воздуха, захваченных под действием капиллярных сил в капиллярной кайме (в микроскопическом масштабе), могло бы объяснить образование ЭА. При инфильтрации поверхностных вод пузырьки воздуха переносятся на уровень зоны насыщения. Когда к захваченным пузырькам воздуха прикладывается достаточное гидростатическое давление, они растворяются в грунтовых водах. Герцберг и Мазор (1979), предположил, что высокопроницаемая трещиноватая природа большинства карстовых водоносных горизонтов часто связана с быстрой подпиткой, которая может быть ответственна за образование EA в макроскопическом масштабе. Таким образом, карбонаты представляются подходящей литологией для образования EA, хотя физический процесс остается гипотетическим.
Таким образом, карбонаты представляются подходящей литологией для образования EA, хотя физический процесс остается гипотетическим.
Эшбах-Хертиг и др. (2002) предполагают, что изменения концентрации неона (и, следовательно, EA) могут быть показателем изменения пьезометрического напора в водоносном горизонте. Такое утверждение подтверждается многими другими исследованиями (Beyerle et al., 2003; Kulongoski et al., 2004; Ingram et al., 2007; Manning and Caine, 2007; Osenbrück et al., 2009).; Чжу и Кипфер, 2010). Холочер и др. (2002) экспериментально исследовали образование ЭА в квазинасыщенных пористых средах с использованием вертикальных столбов песка. При моделировании вариаций уровня воды наблюдалась корреляция между этими вариациями и измеренной ЭА. Затем ЭА изменялась от 0,14 до 1,62 см 90 666 3 90 667 стп.кг 90 666 -1 90 667 с максимальным изменением пьезометрического напора 1 м. Согласно Holocher et al. (2002), общее давление, оказываемое на захваченный воздух, является доминирующим параметром, определяющим общее количество растворенного воздуха в подземных водах. Таким образом, образование ЭА будет зависеть от количества захваченных пузырьков воздуха и от гидростатического давления, вызывающего их растворение. В некоторых карбонатных породах, таких как доломиты, пористая матрица является подходящей средой для улавливания пузырьков воздуха, учитывая межзерновую пористость и значительное и быстрое изменение пьезометрического напора с быстрым переходом от поверхности к зоне насыщения. Для простоты и во избежание чрезмерной параметризации в подходе к моделированию (см. раздел Включение избытка воздуха в модель с сосредоточенными параметрами) предполагается, что выделение избытка воздуха линейно связано с пьезометрическими флуктуациями.
Таким образом, образование ЭА будет зависеть от количества захваченных пузырьков воздуха и от гидростатического давления, вызывающего их растворение. В некоторых карбонатных породах, таких как доломиты, пористая матрица является подходящей средой для улавливания пузырьков воздуха, учитывая межзерновую пористость и значительное и быстрое изменение пьезометрического напора с быстрым переходом от поверхности к зоне насыщения. Для простоты и во избежание чрезмерной параметризации в подходе к моделированию (см. раздел Включение избытка воздуха в модель с сосредоточенными параметрами) предполагается, что выделение избытка воздуха линейно связано с пьезометрическими флуктуациями.
Оценка условий пополнения по температуре благородных газов и избытку воздуха
Температура пополнения подземных вод (NGT, температура благородных газов) и EA (Heaton and Vogel, 1981; Plummer et al., 2004; Chatton, 2017) можно оценить с использованием концентрации растворенных благородных газов (Ne, Ar) и азота (N 2 ). Последний является основным атмосферным газом, который, кроме того, может образовываться в результате биологических реакций, таких как денитрификация в бескислородных системах (Mariotti, 1986; Smith et al., 19).91; Блихер-Матизен и др., 1998). В карстовых системах редко наблюдаются бескислородные условия, особенно в безнапорном водоносном горизонте. Принимая во внимание карстовую систему Дюрзона, измеренное содержание растворенного кислорода всегда выше 7,6 мг·л -1 , что исключает наличие денитрификации. По этой причине предполагается, что концентрация растворенного N 2 остается стабильной в течение гидрологического цикла и использовалась для расчета как NGT, так и EA.
Последний является основным атмосферным газом, который, кроме того, может образовываться в результате биологических реакций, таких как денитрификация в бескислородных системах (Mariotti, 1986; Smith et al., 19).91; Блихер-Матизен и др., 1998). В карстовых системах редко наблюдаются бескислородные условия, особенно в безнапорном водоносном горизонте. Принимая во внимание карстовую систему Дюрзона, измеренное содержание растворенного кислорода всегда выше 7,6 мг·л -1 , что исключает наличие денитрификации. По этой причине предполагается, что концентрация растворенного N 2 остается стабильной в течение гидрологического цикла и использовалась для расчета как NGT, так и EA.
Оценки проводились с использованием концептуальной модели нефракционированного избытка воздуха (UA) путем полного растворения пузырьков воздуха в соответствии с методологией, описанной Aeschbach-Hertig and Solomon (2013). Эта модель не включает дегазацию или разделение газа. Уравнения модели, разработанные Эшбахом-Хертигом и Соломоном (2013), не подробно описаны в этой статье. Полная методология оценки EA представлена в предыдущих исследованиях (Pérotin, 2021; Pérotin et al., 2021). Средняя высота пополнения была установлена на уровне 700 м над уровнем моря. Изменчивость высоты изучаемой области вызывает < 1°C и 0,2 см 3 стп.кг −1 неопределенности параметров NGT и EA соответственно.
Полная методология оценки EA представлена в предыдущих исследованиях (Pérotin, 2021; Pérotin et al., 2021). Средняя высота пополнения была установлена на уровне 700 м над уровнем моря. Изменчивость высоты изучаемой области вызывает < 1°C и 0,2 см 3 стп.кг −1 неопределенности параметров NGT и EA соответственно.
Отбор проб и анализ
Пробы воды были отобраны на различных глубинах в пределах аэративной зоны исследуемого участка (см. Pérotin, 2021). Пробы Canalettes и Reynelles, взятые на глубине 5 и 9 м (691 и 685 м над уровнем моря соответственно), позволяют охарактеризовать эпикарстовую зону, а скважина глубиной 45 м (655 м над уровнем моря) позволяет охарактеризовать перенос воды в ненасыщенной зоне (Jasse). . Подземная река на глубине 120 м в ненасыщенной зоне (Бизе, 580 м над ур. м.) позволяет более комплексно охарактеризовать потоки в зоне аэрации, эта вздымающаяся подземная река расположена почти на 55 м выше уровня источника Дюрзон (535 м над уровнем моря).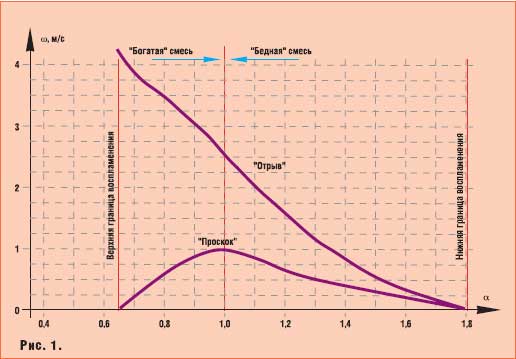 м над уровнем моря). Были проведены две кампании по отбору проб в условиях паводка и маловодья (март 2018 г. и сентябрь 2019 г.)., соответственно) для оценки сезонного гидрологического влияния на газопереносы. Были проведены две кампании по отбору проб в периоды половодья и маловодья (март 2018 г. и сентябрь 2019 г. соответственно) для характеристики характеристик растворенного газа в аэрационной зоне. Пробы растворенных газов были собраны в источнике Дурзон с 2009 по 2019 год с месячным шагом по времени между февралем 2010 года и ноябрем 2011 года.
м над уровнем моря). Были проведены две кампании по отбору проб в условиях паводка и маловодья (март 2018 г. и сентябрь 2019 г.)., соответственно) для оценки сезонного гидрологического влияния на газопереносы. Были проведены две кампании по отбору проб в периоды половодья и маловодья (март 2018 г. и сентябрь 2019 г. соответственно) для характеристики характеристик растворенного газа в аэрационной зоне. Пробы растворенных газов были собраны в источнике Дурзон с 2009 по 2019 год с месячным шагом по времени между февралем 2010 года и ноябрем 2011 года.
Растворенные в воде инертные газы были собраны в стеклянные бутылки емкостью 500 мл, закрытые резиновыми пробками и запечатанные металлическим кольцом. Небольшой погружной насос (Mini Twister 12 вольт, стандартный ПВХ — sdec-France) использовался для отбора проб воды пещеры Рейнель (9м) и мониторинг проводился на источнике Дюрзон. В пещере Каналеттес (глубина 5 м) потребовался перистальтический насос из-за очень малого количества воды в естественном бассейне. Отбор проб производится непосредственно в пещере, поэтому насос и резервуар с водой находились на одной высоте, чтобы избежать потери давления и, следовательно, декомпрессии в насосе. Применительно к скважине Яссе (глубина 45 м) использовался насос Grundfos MP1, а пробы растворенного газа отбирались под водой (непосредственно в скважине или в ведре) во избежание загрязнения воздуха после 3-кратного обновления воды. Для каждого образца отбирали по две-три повторности. Также с помощью портативного мультиметра HACH HQ40D регистрировали физико-химические параметры (температуру, рН, удельную электропроводность и растворенный кислород) для каждой пробы растворенного газа. Температура подземных вод в скважине Джассе измерялась с помощью CTD Diver, расположенного в скважине, а не после отбора проб.
Отбор проб производится непосредственно в пещере, поэтому насос и резервуар с водой находились на одной высоте, чтобы избежать потери давления и, следовательно, декомпрессии в насосе. Применительно к скважине Яссе (глубина 45 м) использовался насос Grundfos MP1, а пробы растворенного газа отбирались под водой (непосредственно в скважине или в ведре) во избежание загрязнения воздуха после 3-кратного обновления воды. Для каждого образца отбирали по две-три повторности. Также с помощью портативного мультиметра HACH HQ40D регистрировали физико-химические параметры (температуру, рН, удельную электропроводность и растворенный кислород) для каждой пробы растворенного газа. Температура подземных вод в скважине Джассе измерялась с помощью CTD Diver, расположенного в скважине, а не после отбора проб.
Растворенные газы (Ne, Ar, N 2 ) проб воды анализировали на аналитической платформе CONDATE Eau (Университет Ренна) методом газовой хроматографии. Газы Ne-Ar-N 2 экстрагировали парофазным методом (Sugisaki and Taki, 1987) и измеряли методом газовой хроматографии с использованием катарометрического детектора (μGC 3000 — SRA) с точностью 8% для Ne и 5 % для Ar и N 2 .
Подход к моделированию
Моделирование с сосредоточенными параметрами
Предлагаемая модель (рис. 3) рассматривает три отсека, каждый из которых соответствует физическому объекту (эпикарст, канал, матрица). Отсеки организованы в виде двухуровневой структуры: верхний уровень модельной структуры включает в себя отсек Е (эпикарст), а нижний уровень состоит из двух связанных между собой отсеков М (матрица) и С (кондуит). Как было предложено в предыдущем исследовании (Tritz et al., 2011), отсек E представляет собой почвенно-эпикарстовую подсистему и представляет собой зону перехвата, где часть полученных осадков Pr возвращается в атмосферу через скорость эвапотранспирации ET. Вода, содержащаяся в отсеке E, перетекает в нижний отсек M. В периоды высокого уровня воды часть воды, содержащейся в отсеке E, образует гистерезисный перелив Q hy (Tritz et al., 2011), достигая отсека С или пружина. Перераспределение потока для Q hy в отделение C или пружину параметризуется коэффициентом разделения X хай . В нижней части модельной конструкции обмен между отсеками M и C пропорционален разности уровней воды между двумя отсеками. Это позволяет воспроизвести взаимодействие матрицы и канала, что подтверждается прямыми наблюдениями в других карстовых системах (Bailly-Comte et al., 2010). Модель может быть реализована с помощью платформы моделирования KarstMod, разработанной в рамках сети карстовых обсерваторий SNO KARST (www.sokarst.org), инициированной французским институтом INSU/CNRS (Jourde et al., 2018). Модель основана на уравнениях баланса массы, данных Mazzilli et al. (2019), предполагая закон линейного выписки для каждого компартмента модели:
В нижней части модельной конструкции обмен между отсеками M и C пропорционален разности уровней воды между двумя отсеками. Это позволяет воспроизвести взаимодействие матрицы и канала, что подтверждается прямыми наблюдениями в других карстовых системах (Bailly-Comte et al., 2010). Модель может быть реализована с помощью платформы моделирования KarstMod, разработанной в рамках сети карстовых обсерваторий SNO KARST (www.sokarst.org), инициированной французским институтом INSU/CNRS (Jourde et al., 2018). Модель основана на уравнениях баланса массы, данных Mazzilli et al. (2019), предполагая закон линейного выписки для каждого компартмента модели:
dedt = pr — et — qem — qhy (1)
dmdt = qem — qmc (2)
dcdt = (xhy × qhy)+qmc — QCS (3)
, где:
QEM=kEM×hE(t)Lrefif E(t)>0, иначе QEM= 0 (4)
QMC=kMC × [hM(t) − hC(t)] Lref (5)
QCS=kCS ×hC(t)Lref (6)
Qhy=εhy × khy × (hE − EhyLref) (7)
где hE, hM и hC — уровни воды [мм] в отсеках Е, М и С соответственно k EM , k MC , k CS , k hy [мм. сут −1 ] – удельные расходные коэффициенты для расхода Q EM , Q MC 20 0,02 QCS 20 , и Q hy [мм.сут −1 ], соответственно, X hy [-] — коэффициент разделения, который разделяет потоки Q hy 9020 отсека непосредственно в отсеке к пружине, L № — единица длины [мм] и ε hy [-] — бинарный показатель активации гистерезисного разряда (Tritz et al., 2011).
сут −1 ] – удельные расходные коэффициенты для расхода Q EM , Q MC 20 0,02 QCS 20 , и Q hy [мм.сут −1 ], соответственно, X hy [-] — коэффициент разделения, который разделяет потоки Q hy 9020 отсека непосредственно в отсеке к пружине, L № — единица длины [мм] и ε hy [-] — бинарный показатель активации гистерезисного разряда (Tritz et al., 2011).
Рисунок 3 . Структура модели с сосредоточенными параметрами. Входные переменные выделены синим цветом, отсек и внутренние потоки выделены черным цветом, рабочая гипотеза для моделирования EA выделена зеленым цветом, а свободный параметр выделен красным. Информация о параметрах модели приведена в таблице 1.
Имитация пружинного разряда Q sim [m 3 .s −1 ] зависит от области подпитки, например: где Ra [км 2 ] — площадь питания водосбора, деленная на константу постоянства единицы для преобразования расхода воды на единицу поверхности [мм·день −1 ] в расход [м 3 . с −1 ] .
с −1 ] .
Включение избытка воздуха в модель с сосредоточенными параметрами
Включение ЭА в предлагаемую модель учитывает, что формирование ЭА в основном происходит в отсеке М в результате увеличения пьезометрического напора. Действительно, образование ЭА происходит за счет захвата пузырьков воздуха в пористой среде, которые растворяются при значительном увеличении гидростатического давления. В случае изучаемой карстовой системы относительно высокая пористость доломитовых образований позволяет рассматривать эту гипотезу. Для представления такого физического процесса в модели предполагается, что формирование ЭА в отсеке М пропорционально изменениям пьезометрического напора:
EAM*(t) = a×Δh(t) if Δh(t) > 0 else = 0 (9)
где EAM* (t) – концентрация ЭА [см 3 СТП.кг − 1 ] в отсеке М в момент времени t, являющийся результатом изменения пьезометрического напора Δ ч ( t ) в момент времени t в зависимости от коэффициента пропорциональности a . Если Δ h ( t ) отрицательно, формирование ЭА не происходит и ЭАМ* (t) = 0. Характеристика ЭА в отсеке М зависит от баланса масс между притоком из отсека Е и оттоком в отсек С:
Если Δ h ( t ) отрицательно, формирование ЭА не происходит и ЭАМ* (t) = 0. Характеристика ЭА в отсеке М зависит от баланса масс между притоком из отсека Е и оттоком в отсек С:
EAM(t+1)=hM(t)×EAM(t)+QEM(t)×EAE×Δt−QMC(t)×EAM(t)×ΔthM(t)+QEM(t)×Δt- QMC(t)×Δt + EAM*(t), если QMC(t)> 0 (10)
EAM(t+1)=hM(t)×EAM(t)+QEM(t)×EAE×Δt− QMC(t)×EAC(t)×ΔthM(t) + QEM(t)×Δt− QMC(t)×Δt + EAM*(t), если QMC(t) < 0 (11)
, где Q EM и Q MC [мм·день −1 ] — скорости внутреннего разряда на единицу площади поверхности, а EA E , EA M и EA C — концентрации EA [см 3 стп.кг -1 ] в отсеках Е, М и С соответственно, а Δt — единичный временной шаг модели [сутки].
Сигнатура EA в отсеке C зависит от баланса масс между притоком из C и оттоком к источнику.
EAC(t+1)=hC(t)×EAC(t)+QMC(t)×EAM×Δt+QhyEC(t)×EAE(t)×Δt-QCS(t)×EAC(t) × ΔthC(t)+QMC(t)×Δt+QhyEC(t)×Δt−QCS(t)×Δt если QMC(t)> 0 (12)
EAC(t+1)=hC(t)×EAC (t)+QMC(t)×EAC×Δt+QhyEC(t)×EAE(t)×Δt−QCS(t)×EAC(t)×ΔthC(t)+QMC(t)×Δt+QhyEC(t )×Δt − QCS(t)×Δt если QMC(t)< 0 (13)
где Q hyEC — расход на единицу площади поверхности из отсека E в C [мм.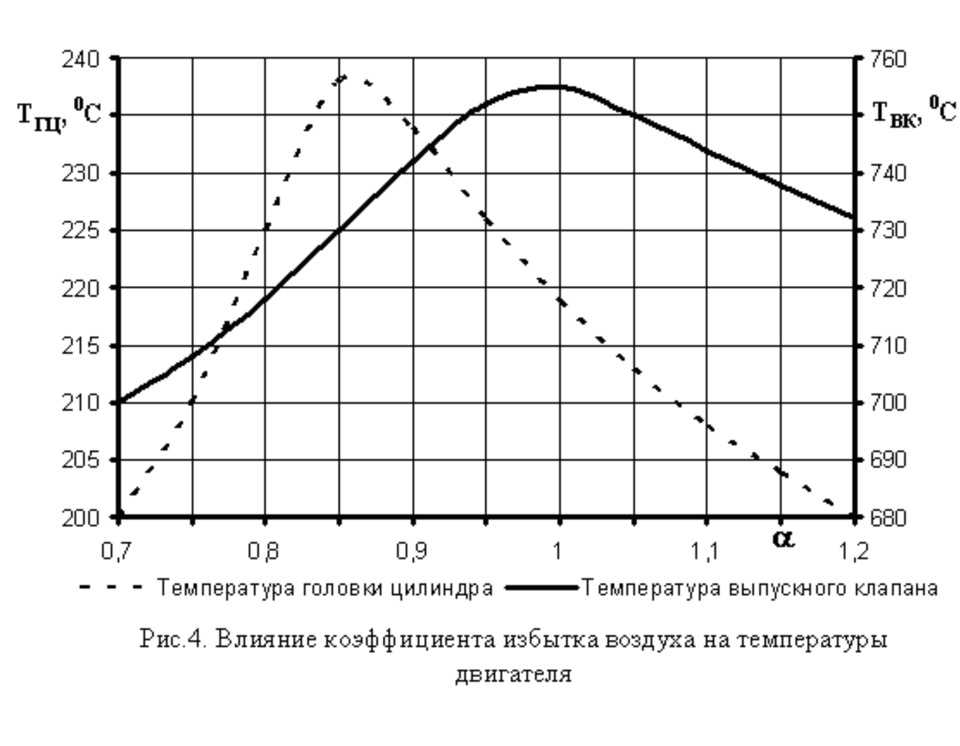 сут −1 ], Q CS — расход на единицу площади поверхности из отсека C в родник [мм.сут. -1 ].
сут −1 ], Q CS — расход на единицу площади поверхности из отсека C в родник [мм.сут. -1 ].
Сигнатура ЭА у родника зависит от баланса масс между истечением из отсека С и истечением из отсека Е непосредственно к роднику:
EAsim(t+1)=QCS(t)×EAC(t) + QhyES(t) ×EAE(t)QCS(t) + QhyES(t) (14)
, где Q hyES — слив из отсека Е на родник.
Калибровка модели
Предлагаемая модель ливневых стоков насчитывает 6 параметров (Таблица 1), а моделирование ЭА на источнике дает еще один параметр. Концептуальное представление формирования EA считается максимально простым, чтобы избежать чрезмерной параметризации и ограничить потенциальную параметрическую эквифинальность (Perrin et al., 2001). На основании прежних исследований область питания была определена как Ra = 116 км 2 . Модель реализована в среде Python (Summerfield, 2010), а оценка параметров выполнялась с использованием процедуры оптимизации роя частиц (PSO) (Eberhart and Kennedy, 19). 95), реализованный в пакете «pyswarm» (Lee, 2014). Кроме того, применяется выборка латинского гиперкуба (LHS) для учета параметрических неопределенностей и исследования распределения параметров в соответствии с критериями эффективности модели. Калибровка производится в течение 10 лет (с сентября 2009 г. по декабрь 2019 г.). Поскольку модель не предназначена для целей прогнозирования или экстраполяции изучаемых климатических условий, в этом исследовании не рассматривается период проверки. Калибровка производится с учетом широко используемой эффективности Нэша-Сатклиффа (NSE; Nash and Sutcliffe, 19).70) criterion on both spring discharge ( Q obs and Q sim ) and excess air ( EA obs and EA sim ) measurement at весна. Тогда целевая функция Φ состоит из взвешенной суммы:
95), реализованный в пакете «pyswarm» (Lee, 2014). Кроме того, применяется выборка латинского гиперкуба (LHS) для учета параметрических неопределенностей и исследования распределения параметров в соответствии с критериями эффективности модели. Калибровка производится в течение 10 лет (с сентября 2009 г. по декабрь 2019 г.). Поскольку модель не предназначена для целей прогнозирования или экстраполяции изучаемых климатических условий, в этом исследовании не рассматривается период проверки. Калибровка производится с учетом широко используемой эффективности Нэша-Сатклиффа (NSE; Nash and Sutcliffe, 19).70) criterion on both spring discharge ( Q obs and Q sim ) and excess air ( EA obs and EA sim ) measurement at весна. Тогда целевая функция Φ состоит из взвешенной суммы:
Φ=ω×NSE(Qsim)+(1-ω)×NSE(EAsim) (15)
, где ω изменяется от 0 до 1 для учета различных важность обоих Q obs и EA obs в процедуре калибровки.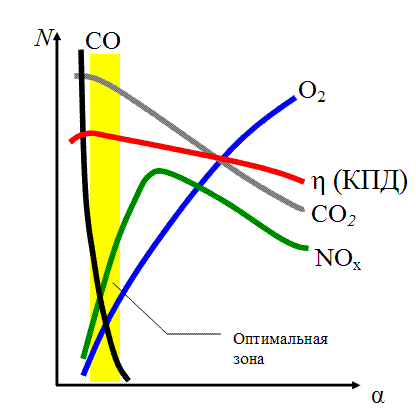 Следует отметить, что в период калибровки Q obs состоит из непрерывного суточного ряда (3760 наблюдений), тогда как временной ряд EA obs насчитывает 18 наблюдений в пределах 3 гидрологических циклов.
Следует отметить, что в период калибровки Q obs состоит из непрерывного суточного ряда (3760 наблюдений), тогда как временной ряд EA obs насчитывает 18 наблюдений в пределах 3 гидрологических циклов.
Результаты
Анализ измерений EA
EA источника Дюрзон показывает важные изменения во время гидрологического цикла. Самые низкие значения EA меньше 1 см 3 стп.кг −1 и наблюдались во время паводков с расходом от 3,9 до 5,4 м 3 .с −1 . Периоды спада характеризуются высокими значениями избытка воздуха до 11 см 3 ст.ст.кг -1 при весеннем стоке ниже 0,8 м 3 .с -1 . Измерения растворенного газа, проведенные в мелководной эпикарстовой зоне в периоды половодья, показывают, что EA низкая, около 0,5 см 90 666 3 90 667 ст. ст. кг-1 для Canalettes и Reynelles (Pérotin et al., 2021). Низкие значения измерены также для подземной реки Бизе (1,3 см 3 стп. кг-1), что позволяет более обобщенно квалифицировать характер потоков, протекающих в дренажной сети авадозной зоны. Измерение ЭА на разных глубинах ненасыщенной зоны над водосбором Дюрзона свидетельствует о том, что формирование ЭА, наряду с переносом воды в насыщенную зону, невелико (менее 2 см 3 стп.кг -1 ) и появляется недостаточны для объяснения значений ЭА, измеренных на источнике Дюрзон, где значения ЭА возрастают до 11 см 3 стп.кг −1 в маловодные периоды. По-видимому, наблюдается убывающая зависимость экспоненциального типа между измеренным значением EA и весенним расходом (рис. 4). В карстовых средах быстрое и значительное пополнение запасов с поверхности в зону насыщения может привести к изменению пьезометрического напора от нескольких метров до десятков метров в пределах зоны пропускания. Когда происходит такое пополнение, наблюдаются инверсии потока между основными элементами дренажа (т. е. пещерами, каналами, незасоренными трещинами) и окружающей пористой матрицей (Martin and Dean, 2001; Meyerhoff et al.
кг-1), что позволяет более обобщенно квалифицировать характер потоков, протекающих в дренажной сети авадозной зоны. Измерение ЭА на разных глубинах ненасыщенной зоны над водосбором Дюрзона свидетельствует о том, что формирование ЭА, наряду с переносом воды в насыщенную зону, невелико (менее 2 см 3 стп.кг -1 ) и появляется недостаточны для объяснения значений ЭА, измеренных на источнике Дюрзон, где значения ЭА возрастают до 11 см 3 стп.кг −1 в маловодные периоды. По-видимому, наблюдается убывающая зависимость экспоненциального типа между измеренным значением EA и весенним расходом (рис. 4). В карстовых средах быстрое и значительное пополнение запасов с поверхности в зону насыщения может привести к изменению пьезометрического напора от нескольких метров до десятков метров в пределах зоны пропускания. Когда происходит такое пополнение, наблюдаются инверсии потока между основными элементами дренажа (т. е. пещерами, каналами, незасоренными трещинами) и окружающей пористой матрицей (Martin and Dean, 2001; Meyerhoff et al. , 2012; Mitrofan et al., 2015). .
, 2012; Mitrofan et al., 2015). .
Таблица 1 . Описание параметров модели.
Рисунок 4 . Эволюция сигнатуры ЭА на источнике Дюрзон в зависимости от расхода источника. EA obs соответствуют измерениям EA на источнике Дурзон, а EA sim находится в доверительном интервале (CI) с долей 0,1% из 50 000 симуляций в пространстве параметров, выбранном с помощью Процедура Latin Hypercube Sampling (LHS).
Когда градиент давления индуцирует поток из основной дренажной сети в окружающую пористую матрицу, это способствует пополнению матрицы вблизи дренажных элементов (т. к увеличению гидростатического давления вслед за быстрыми потоками воды через основные дренажные сооружения в сторону зоны насыщения. Чем больше увеличение пьезометрического напора, тем больше гидростатическое давление, действующее на пузырьки воздуха, и, следовательно, выше образование ЭА. Предполагается, что такой процесс объясняет образование ЭА в пористой матрице при увеличении пьезометрического напора после перезарядки.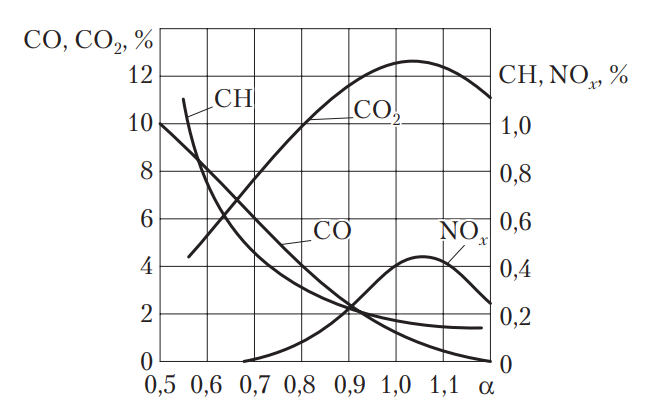 В периоды рецессии родниковый сток в основном снабжается подземными водами из материнской породы с незначительным стоком из водоводных сетей (Plagnes, 19).97). Такое поведение объясняет как высокие значения весеннего EA при низком весеннем расходе, так и уменьшающуюся экспоненциальную зависимость между измеренным EA и измеренным весенним расходом (рис. 4). В маловодные периоды основной вклад в сток родника вносит матрикс, поэтому значения ЭА у родника увеличиваются за счет поступления воды, характеризующейся более высокими значениями ЭА.
В периоды рецессии родниковый сток в основном снабжается подземными водами из материнской породы с незначительным стоком из водоводных сетей (Plagnes, 19).97). Такое поведение объясняет как высокие значения весеннего EA при низком весеннем расходе, так и уменьшающуюся экспоненциальную зависимость между измеренным EA и измеренным весенним расходом (рис. 4). В маловодные периоды основной вклад в сток родника вносит матрикс, поэтому значения ЭА у родника увеличиваются за счет поступления воды, характеризующейся более высокими значениями ЭА.
В периоды высокого стока (т. е. высокого пьезометрического уровня в зоне насыщения) родниковый сток в основном обеспечивается быстрым течением через основную дренажную сеть с поверхности в зону насыщения. В эти периоды измерения циркуляции воды через зону инфильтрации, по-видимому, указывают на то, что инфильтрационная вода имеет низкую характеристику ЭА (<1,3 см 3 стп.кг −1 ), и, таким образом, образование ЭА в подземных водах с быстрым течением. Это могло бы объяснить низкие значения EA, измеренные в источнике Дюрзон в периоды высокого стока, при условии отсутствия дегазации. Когда пьезометрический напор уменьшается в масштабе водоносного горизонта и в пределах карстовой дренажной сети, латеральный обмен с окружающей пористой матрицей меняется на противоположный, вызывая дренирование грунтовых вод, хранящихся в матрице, через дренажную сеть. Этот поток подземных вод из матрицы способствует сбросу в источнике и, таким образом, вызывает увеличение значений EA в источнике. Этот процесс формирования и переноса ЭА из недр в родник предполагает, что более низкие значения ЭА, измеренные в источнике, будут репрезентативными для значений ЭА эпикарстовых вод.
Это могло бы объяснить низкие значения EA, измеренные в источнике Дюрзон в периоды высокого стока, при условии отсутствия дегазации. Когда пьезометрический напор уменьшается в масштабе водоносного горизонта и в пределах карстовой дренажной сети, латеральный обмен с окружающей пористой матрицей меняется на противоположный, вызывая дренирование грунтовых вод, хранящихся в матрице, через дренажную сеть. Этот поток подземных вод из матрицы способствует сбросу в источнике и, таким образом, вызывает увеличение значений EA в источнике. Этот процесс формирования и переноса ЭА из недр в родник предполагает, что более низкие значения ЭА, измеренные в источнике, будут репрезентативными для значений ЭА эпикарстовых вод.
Кроме того, четыре измерения растворенного газа, выполненные на разных глубинах в пределах ненасыщенной зоны, показали, что EA колеблется от 0,5 до 1,2 см 3 STP.kg −1 (Pérotin et al., 2021). Этот диапазон изменчивости на один порядок меньше, чем вариация ЭА, измеренная у родника, где измерения показывают вариацию до 11 см 3 стп.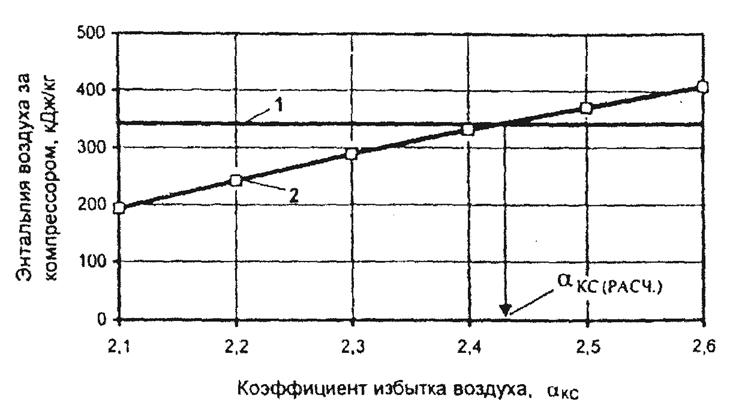 кг -1 . Для моделирующего подхода примем, что избыток воздуха воды в ненасыщенной зоне равен 0,9, т. е. промежуточное значение к измеренным в эпикарсте и на Бисе.
кг -1 . Для моделирующего подхода примем, что избыток воздуха воды в ненасыщенной зоне равен 0,9, т. е. промежуточное значение к измеренным в эпикарсте и на Бисе.
Совместное моделирование потока и ЭА
Модель откалибрована с учетом весеннего расхода и измерений ЭА (таблица 2). На рис. 5 показаны различные временные ряды, позволяющие анализировать внутреннее функционирование водоносного горизонта Дурзон. Периоды сосредоточены на 2010–2012 годах с более высокой плотностью измерений EA, хотя периоды калибровки длились до 2019 года (последнее измерение EA на источнике Дурзон). Калибровка модели показывает вполне удовлетворительное согласие с NSE( Q sim ) = 0,75 и NSE ( EA sim ) = 0,53. Смоделированный сток, по-видимому, воспроизводит крупное наводнение, но не воспроизводит некоторые незначительные наводнения, как в декабре 2011 г. и в период с мая по июнь 2012 г. Смоделированный весенний сток состоит из отсека непосредственно к роднику, что происходит, когда уровень воды в отсеке E превышает порог срабатывания E hy = 295,9 мм. Этот быстрый сток вносит основной вклад в весенний сток во время паводков, особенно после эпизодов со значительным накоплением осадков. Кроме того, часть перетока из отсека E способствует подпитке отсека C через потоки Q hyEC и составляет основную часть перетока из отсека E. Действительно, коэффициент перераспределения X hy равен оценивается в 0,84, что означает, что 84% из Q hy способствует пополнению отсека C, и эти 16% стекают непосредственно в родник и, таким образом, участвуют в наводнениях, наблюдаемых после сильных осадков. В остальное время года потоки из отсека C в родник Q CS обеспечивают базовый сток родника. Модель, по-видимому, завышает весенний сток в периоды рецессии. Сложное поведение потока в источнике Дюрзона, впервые объясненное рассмотрением гистерезисного поведения (Tritz et al., 2011), было лучше воспроизведено при рассмотрении бесконечной характеристической передаточной функции времени (Guinot et al.
Этот быстрый сток вносит основной вклад в весенний сток во время паводков, особенно после эпизодов со значительным накоплением осадков. Кроме того, часть перетока из отсека E способствует подпитке отсека C через потоки Q hyEC и составляет основную часть перетока из отсека E. Действительно, коэффициент перераспределения X hy равен оценивается в 0,84, что означает, что 84% из Q hy способствует пополнению отсека C, и эти 16% стекают непосредственно в родник и, таким образом, участвуют в наводнениях, наблюдаемых после сильных осадков. В остальное время года потоки из отсека C в родник Q CS обеспечивают базовый сток родника. Модель, по-видимому, завышает весенний сток в периоды рецессии. Сложное поведение потока в источнике Дюрзона, впервые объясненное рассмотрением гистерезисного поведения (Tritz et al., 2011), было лучше воспроизведено при рассмотрении бесконечной характеристической передаточной функции времени (Guinot et al. , 2015). Однако такая структура модели не позволяет моделировать формирование ЭА, а также обмены между емкостной и проницаемой частями водоносного горизонта, что позволяет учитывать задержку между подпиткой (формированием ЭА) и возрастанием весенних значений ЭА в периоды маловодья (рис. 4). .
, 2015). Однако такая структура модели не позволяет моделировать формирование ЭА, а также обмены между емкостной и проницаемой частями водоносного горизонта, что позволяет учитывать задержку между подпиткой (формированием ЭА) и возрастанием весенних значений ЭА в периоды маловодья (рис. 4). .
Таблица 2 . Пространство параметров и значения параметров, оцененных с помощью процедуры Particle Swarm Optimization (PSO), реализованной в пакете «pyswarm» (Lee, 2014) в соответствии с различными целевыми функциями.
Рисунок 5 . (i) Временные ряды осадков и потенциальной эвапотранспирации, (ii) наблюдаемые и смоделированные весенние расходы, (iii) наблюдаемые и смоделированные весенние временные ряды EA, (iv) временные ряды уровня воды в отсеках E, M и C. Периоды, отмеченные синим цветом цвет фона соответствует периодам, когда уровень воды в C больше, чем уровень воды в M, поэтому Q MC > 0 (отсек C питает отсек M). И наоборот, периоды, окрашенные оранжевым фоном, соответствуют периодам, когда отсек M кормится отсеком C.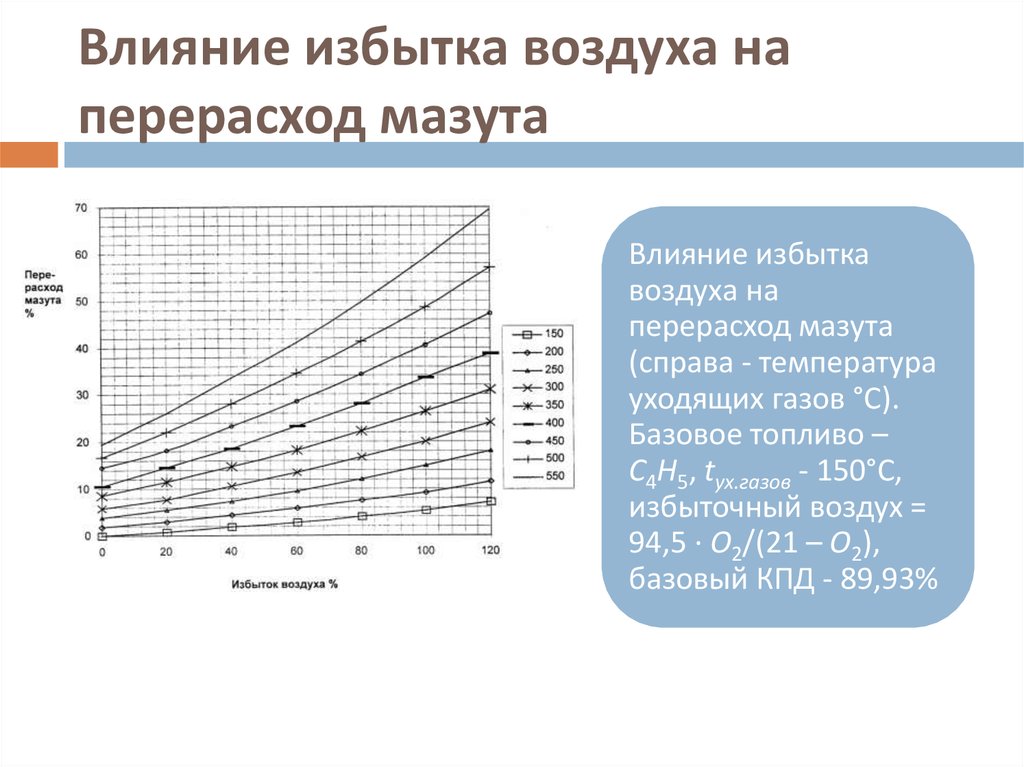
Несмотря на скудное временное разрешение временных рядов EA, весенняя вариация EA выглядит довольно хорошо воспроизведенной. Действительно, модель позволяет воспроизвести наблюдаемое весеннее снижение ЭА после выпадения осадков в марте и ноябре 2011 г. Это происходит одновременно с появлением Q hyES , что соответствует быстрому течению с поверхности к источнику без значительного образования ЭА и, таким образом, позволяет воспроизвести характеристику ЭА, наблюдаемую у источника, поскольку вода из отсека Е имеет низкую концентрацию ЭА, которая, по оценкам, составляет около = 0,9 см 3 стп.кг -1 (Pérotin et al., 2021). Учитывая разворот потока в марте 2011 г., весенний ЭА увеличивается после короткого периода, и хотя модель занижает сигнатуру весеннего ЭА, динамика воспроизведена достаточно хорошо.
Уровень воды в E (hE) демонстрирует значительную годовую изменчивость с полностью засушливыми периодами в конце лета. И наоборот, уровни воды в M (hM) и C (hC) плавно меняются, хотя в отсеке C наблюдается гораздо более динамичная реакция на подпитку. Предлагаемая модель учитывает, что ЭА может формироваться в отсеке М линейно с интенсивностью подпитки. Коэффициент оценивается равным 0,1, тогда модель считает, что интенсивность питания 1 мм.сут -1 даст EA 0,1 см 3 STP.kg -1 . Следует отметить, что максимальная интенсивность питания в отсеке М оценивается примерно в 3 мм.сут -1 , поэтому максимальное создание ЭА за одни сутки составляет 0,3 см 3 ст.ст.кг -1 . В предлагаемой модели ЭА, сформированный на временном шаге (здесь равный 1 дню), смешивается с запасом воды, имеющимся на рассматриваемом временном шаге, с его унаследованной сигнатурой ЭА (т.е. рассчитанной на предыдущем временном шаге). Численная модель рассматривает мгновенное идеальное смешивание, которое представляет собой довольно простую модель смешивания, но кажется разумной, учитывая плохое временное разрешение временных рядов EA, измеренных на выходе.
Предлагаемая модель учитывает, что ЭА может формироваться в отсеке М линейно с интенсивностью подпитки. Коэффициент оценивается равным 0,1, тогда модель считает, что интенсивность питания 1 мм.сут -1 даст EA 0,1 см 3 STP.kg -1 . Следует отметить, что максимальная интенсивность питания в отсеке М оценивается примерно в 3 мм.сут -1 , поэтому максимальное создание ЭА за одни сутки составляет 0,3 см 3 ст.ст.кг -1 . В предлагаемой модели ЭА, сформированный на временном шаге (здесь равный 1 дню), смешивается с запасом воды, имеющимся на рассматриваемом временном шаге, с его унаследованной сигнатурой ЭА (т.е. рассчитанной на предыдущем временном шаге). Численная модель рассматривает мгновенное идеальное смешивание, которое представляет собой довольно простую модель смешивания, но кажется разумной, учитывая плохое временное разрешение временных рядов EA, измеренных на выходе.
Параметрические неопределенности
Процедура LHS применяется для исследования пространства параметров с 50 000 симуляций, где для оценки доверительного интервала учитывается только 0,1% часть наилучшего значения Φ (рис. 6). Параметрические неопределенности приводят к значительным ошибкам прогнозирования. Действительно, доверительный интервал может охватывать широкий диапазон значений временных рядов весеннего стока. Например, для паводка в ноябре 2011 г. доверительный интервал (ДИ) охватывает диапазон пиковых значений от 4,5 до 11 м9.0666 3 .s −1 , для наблюдаемого весеннего стока около 8,5 м 3 .s −1 . Кроме того, некоторые симуляции не воспроизводят паводки умеренной амплитуды, например, в январе 2011 г. Принимая во внимание данные EA, измеренные на выходе, доверительный интервал показывает согласующуюся динамику с наблюдаемым временным рядом. Хотя параметрические неопределенности приводят к ошибкам прогнозирования, ошибки не меняют динамику смоделированных временных рядов. Кроме того, учитывая ранее обсуждавшийся эпизод в марте и ноябре 2011 г., все модели позволяют воспроизвести уменьшение EA, наблюдаемое на выходе.
6). Параметрические неопределенности приводят к значительным ошибкам прогнозирования. Действительно, доверительный интервал может охватывать широкий диапазон значений временных рядов весеннего стока. Например, для паводка в ноябре 2011 г. доверительный интервал (ДИ) охватывает диапазон пиковых значений от 4,5 до 11 м9.0666 3 .s −1 , для наблюдаемого весеннего стока около 8,5 м 3 .s −1 . Кроме того, некоторые симуляции не воспроизводят паводки умеренной амплитуды, например, в январе 2011 г. Принимая во внимание данные EA, измеренные на выходе, доверительный интервал показывает согласующуюся динамику с наблюдаемым временным рядом. Хотя параметрические неопределенности приводят к ошибкам прогнозирования, ошибки не меняют динамику смоделированных временных рядов. Кроме того, учитывая ранее обсуждавшийся эпизод в марте и ноябре 2011 г., все модели позволяют воспроизвести уменьшение EA, наблюдаемое на выходе.
Рисунок 6 .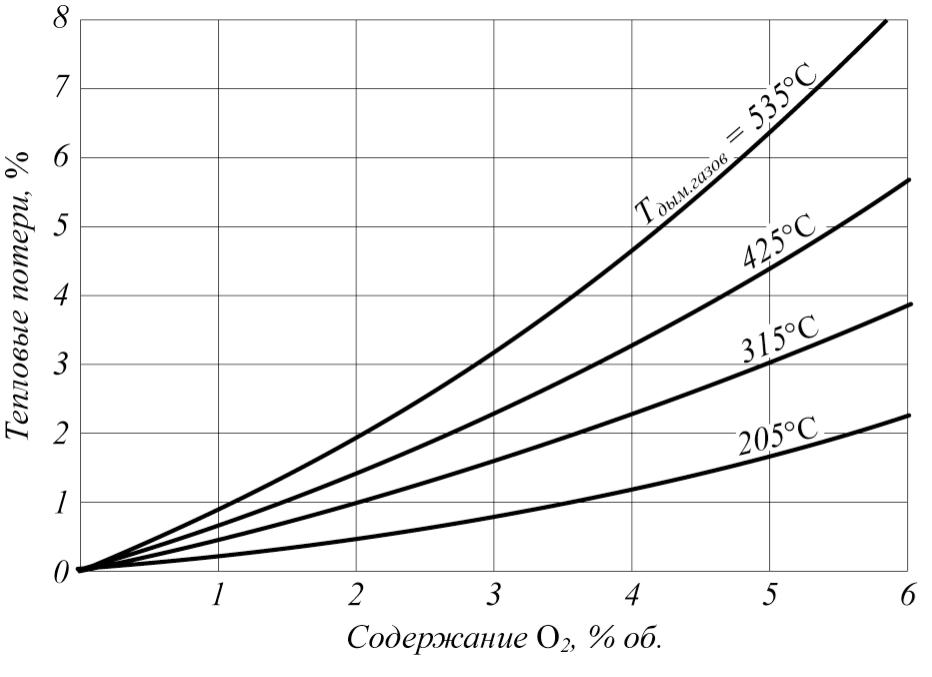 Наблюдаемые и смоделированные временные ряды в доверительном интервале (ДИ) с долей 0,1% из 50 000 симуляций в пространстве параметров, отобранных с помощью процедуры Latin Hypercube Sampling (LHS): (вверху) весенний выпуск Q и (внизу) весенний избыток воздуха EA . Q prob и EA prob состоит из средневзвешенного моделирования в доверительном интервале. Вес соответствует целевой функции Φ, например, чем меньше ошибки прогнозирования, тем выше вес.
Наблюдаемые и смоделированные временные ряды в доверительном интервале (ДИ) с долей 0,1% из 50 000 симуляций в пространстве параметров, отобранных с помощью процедуры Latin Hypercube Sampling (LHS): (вверху) весенний выпуск Q и (внизу) весенний избыток воздуха EA . Q prob и EA prob состоит из средневзвешенного моделирования в доверительном интервале. Вес соответствует целевой функции Φ, например, чем меньше ошибки прогнозирования, тем выше вес.
Такие результаты показывают, что построение модели стока дождевых осадков с учетом концепции формирования EA согласуется с моделированием весеннего EA, но может внести существенную погрешность в моделирование весеннего стока. Кроме того, параметрические неопределенности могут быть менее чувствительными с учетом временных рядов EA из-за низкого временного разрешения весенних временных рядов EA, доступных для оценки параметров.
Процедура LHS применяется с учетом трех Φ, поэтому при калибровке учитывается либо только напор пружины, и напор пружины, и пружинный EA, либо только пружинный EA. Соответственно, вес ω, на который влияет каждая калибровочная переменная (пружинный разряд и пружинный EA), изменяется, например, ω = [0, 0,5, 1]. На рис. 7 показаны графики рассеяния значений целевой функции (период калибровки) в зависимости от значений параметров и соответствующая оценка плотности ядра (KDE) для каждой целевой функции. KDE нормализован до 1 для облегчения сравнения распределения в соответствии с различными целевыми функциями. По всем параметрам модели можно наблюдать разные случаи относительно KDE:
Соответственно, вес ω, на который влияет каждая калибровочная переменная (пружинный разряд и пружинный EA), изменяется, например, ω = [0, 0,5, 1]. На рис. 7 показаны графики рассеяния значений целевой функции (период калибровки) в зависимости от значений параметров и соответствующая оценка плотности ядра (KDE) для каждой целевой функции. KDE нормализован до 1 для облегчения сравнения распределения в соответствии с различными целевыми функциями. По всем параметрам модели можно наблюдать разные случаи относительно KDE:
• KDE показывает различные распределения, если модель откалибрована в соответствии с пружинным разрядом или весенним EA, как это наблюдается для параметров k hy и k CS .
• KDE показывает близкое положение пика распределения, в то время как распределение имеет другую форму, как это наблюдается для параметров k EM , E hy , X hy и k MC . Учитывая k EM , KDE кажется бимодальным при учете только разряда пружины, в то время как KDE кажется унимодальным при рассмотрении пружинного EA для калибровки модели. Кроме того, KDE кажется центрированным около 4 × 10 −4 мм.сут −1 . Такие результаты также относятся к k MC , где разброс распределения, по-видимому, уменьшается при рассмотрении пружинного ЭА для оценки параметров, в то время как оптимальное значение находится между 7 и 9 × 10 -2 мм.день -1 .
Кроме того, KDE кажется центрированным около 4 × 10 −4 мм.сут −1 . Такие результаты также относятся к k MC , где разброс распределения, по-видимому, уменьшается при рассмотрении пружинного ЭА для оценки параметров, в то время как оптимальное значение находится между 7 и 9 × 10 -2 мм.день -1 .
Рисунок 7 . Оценка плотности ядра для каждого параметра модели в зависимости от целевой функции Φ. Здесь изменяется только вес, на который влияют переменные калибровки (либо весенний разряд, либо весеннее измерение EA).
Анализ распределения параметров показывает, что введение измерений ЭА родника может внести неопределенность в оценку параметров, определяющих непосредственно динамику потока у родника, то есть k hy и k CS . И наоборот, учет весеннего ЭА, по-видимому, уменьшает параметрическую неопределенность параметров, определяющих динамику внутри отсека М (представителя емкостной части водоносного горизонта), то есть k EM и k MC .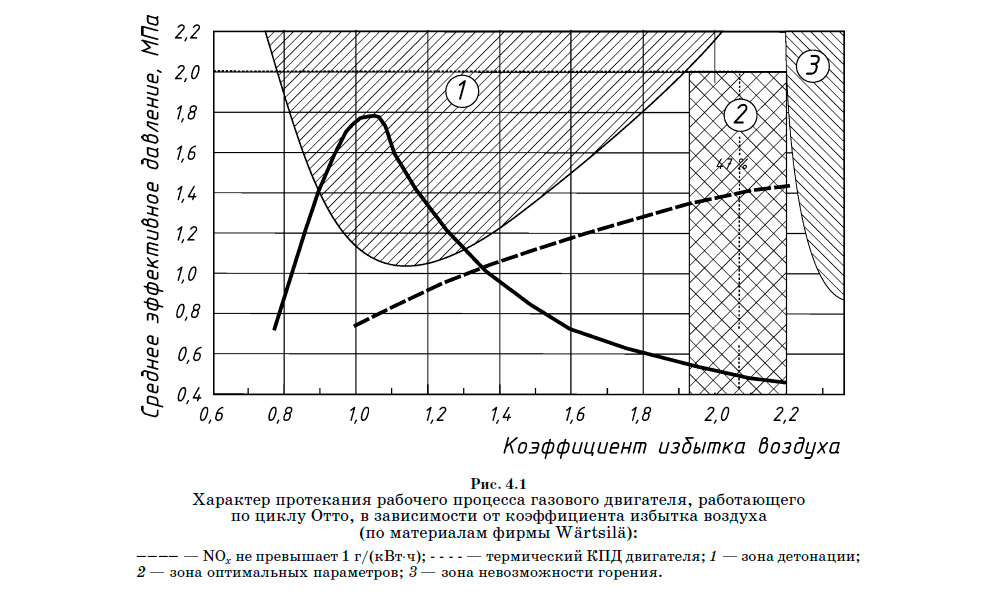 Такие результаты согласуются с рабочей гипотезой, поскольку предложенная модель стока дождевых осадков основана на концептуальном представлении о формировании ЭА в карстовых водоносных горизонтах.
Такие результаты согласуются с рабочей гипотезой, поскольку предложенная модель стока дождевых осадков основана на концептуальном представлении о формировании ЭА в карстовых водоносных горизонтах.
Обсуждение
Процедура оценки параметров, учитывающая только измерения ЭА на источнике, показывает, что смоделированные гидрографы по-прежнему воспроизводят основные компоненты поведения стока родника (рис. 8). Действительно, крупные паводки кажутся довольно хорошо воспроизводимыми, если рассматривать только весеннюю ЭО для оценки параметров. Тем не менее, некоторые паводки, такие как в январе 2010 г. и январе 2011 г., не воспроизводятся при рассмотрении весеннего ЭО только для оценки параметров, а воспроизводятся при учете только весеннего стока для оценки параметров. Предлагаемая модель расхода осадков имеет некоторые недостатки в моделировании весеннего гидрографа по сравнению со структурой модели, предложенной в предыдущих исследованиях (Tritz et al., 2011; Mazzilli et al.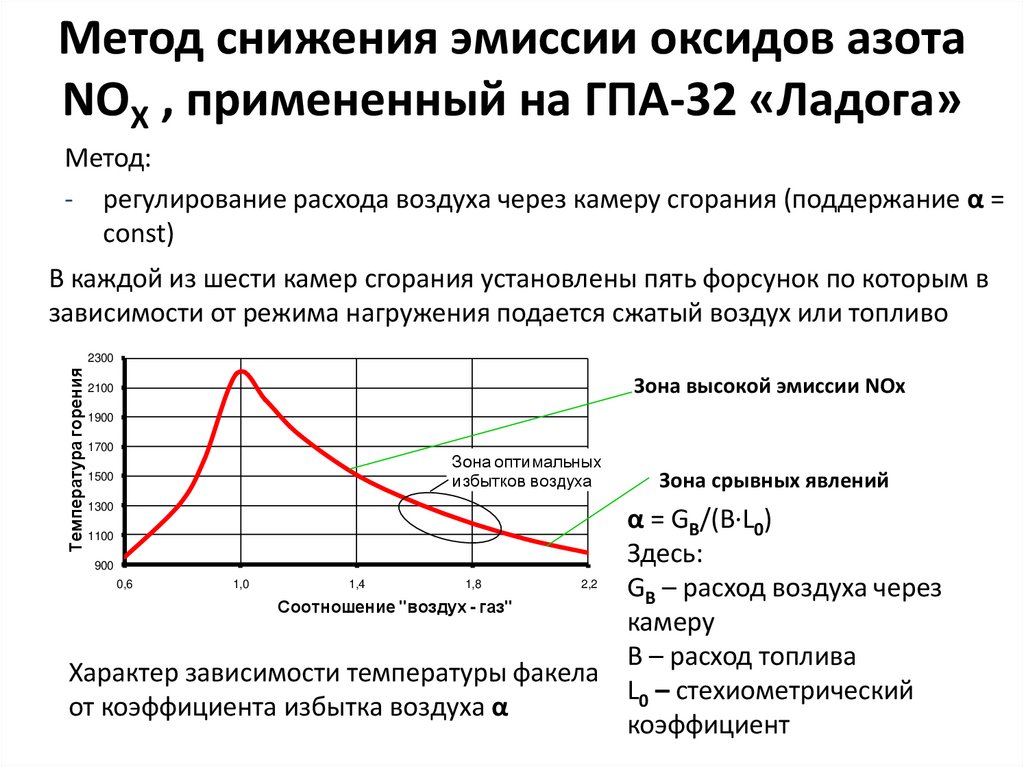 , 2012, 2013; Guinot et al., 2015). Однако предложенная модель позволяет воспроизвести динамику наблюдаемых весенних вариаций ЭА и дает согласованные весенние гидрографы. Такие результаты дают ответы на следующие вопросы:
, 2012, 2013; Guinot et al., 2015). Однако предложенная модель позволяет воспроизвести динамику наблюдаемых весенних вариаций ЭА и дает согласованные весенние гидрографы. Такие результаты дают ответы на следующие вопросы:
• Каково информационное содержание (т. е. ценность данных) дополнительных наблюдений, таких как весенний EA?
Рисунок 8 . Наблюдаемые и смоделированные временные ряды весенних расходов с учетом различных целевых функций.
В карстовой гидрологии модели стока осадков обычно калибруются только на основе наблюдений за весенним стоком. Однако несколько исследований проявили интерес к рассмотрению дополнительных наблюдений, таких как NO 3 и SO .4 концентраций (Hartmann et al., 2013) или электропроводности (Chang et al., 2021), особенно для определения реалистичных структур модели стока дождевых осадков. В карстовой системе Дурзон Mazzilli et al. (2013) попытались откалибровать модель водохранилища с дождевыми стоками с учетом наземных измерений силы тяжести. Результаты исследования показывают, что гравиметрические измерения не помогают лучше ограничить калибровку модели расхода осадков. Среди других причин таких результатов авторы ставят вопрос о репрезентативности данных. Другие исследования пытались включить пьезометрические изменения напора с противоречивыми результатами. Например, Сивель и Журд (2020) определили сложную взаимосвязь между временными рядами пьезометрических напоров и временными рядами весеннего стока в пределах водосбора родника Оэйяль (юг Франции) и поэтому не рассматривали изменение пьезометрического напора для калибровки модели дождевого стока. И наоборот, для карстовой системы Лез (юг Франции) учет изменения пьезометрического напора при оценке параметров, помимо расхода, позволил предложить экономную модель с лучшими характеристиками, чем предыдущие модели (Mazzilli et al., 2011; Cousquer and Jourde). , 2022). Кроме того, изменение пьезометрического напора, полученное на основе наземных измерений силы тяжести, может представлять интерес для калибровки модели стока дождевых осадков, но информативность таких данных может быть спорной с точки зрения пространственного рассмотрения, а также геометрии водоносного горизонта (Mazzilli et al.
Результаты исследования показывают, что гравиметрические измерения не помогают лучше ограничить калибровку модели расхода осадков. Среди других причин таких результатов авторы ставят вопрос о репрезентативности данных. Другие исследования пытались включить пьезометрические изменения напора с противоречивыми результатами. Например, Сивель и Журд (2020) определили сложную взаимосвязь между временными рядами пьезометрических напоров и временными рядами весеннего стока в пределах водосбора родника Оэйяль (юг Франции) и поэтому не рассматривали изменение пьезометрического напора для калибровки модели дождевого стока. И наоборот, для карстовой системы Лез (юг Франции) учет изменения пьезометрического напора при оценке параметров, помимо расхода, позволил предложить экономную модель с лучшими характеристиками, чем предыдущие модели (Mazzilli et al., 2011; Cousquer and Jourde). , 2022). Кроме того, изменение пьезометрического напора, полученное на основе наземных измерений силы тяжести, может представлять интерес для калибровки модели стока дождевых осадков, но информативность таких данных может быть спорной с точки зрения пространственного рассмотрения, а также геометрии водоносного горизонта (Mazzilli et al. , 2013).
, 2013).
В нашем исследовании мы попытались откалибровать предлагаемую модель расхода дождевых осадков с учетом весенних измерений ЭА, рассматриваемых как показатель процессов пополнения в масштабе водосбора. Тем не менее, лежащая в основе численного моделирования гипотеза рассматривает линейную зависимость между изменениями уровня воды в отсеке M (представителем емкостной функции водоносного горизонта) и формированием EA. Кроме того, в исследовании не учитываются наблюдаемые изменения пьезометрического напора, поскольку ни одна скважина на этом участке не достигает зоны насыщения. Таким образом, в результатах недостаточно информации для обсуждения физического реализма взаимосвязи между формированием ЭА и изменениями пьезометрического напора. Хотя некоторые эксперименты в лабораторном масштабе (Holocher et al., 2002) выявили некоторую связь между изменением пьезометрического напора и характеристикой ЭА на песчаных столбах, ни одно исследование не исследовало такую связь в естественных гидрогеологических системах, особенно в карстовых водоносных горизонтах. Как было предложено Перотином и соавт. (2021) « неизвестно, существует ли прямая связь между EA и интенсивностью пополнения запасов осадков ». Результаты настоящего исследования показывают, что учет линейной зависимости между EA и скоростью пополнения оказывается эффективным для воспроизведения изменений EA, наблюдаемых весной, с помощью модели расхода осадков.
Как было предложено Перотином и соавт. (2021) « неизвестно, существует ли прямая связь между EA и интенсивностью пополнения запасов осадков ». Результаты настоящего исследования показывают, что учет линейной зависимости между EA и скоростью пополнения оказывается эффективным для воспроизведения изменений EA, наблюдаемых весной, с помощью модели расхода осадков.
• Как выбрать подходящую структуру модели?
Было предложено несколько моделей расхода осадков для имитации родникового стока Дюрзона. Девиль и др. (2013) предложили двухуровневую модельную структуру, в которой верхний отсек (C1) подвергается воздействию осадков и эвапотранспирации, а нижний уровень (C2) принимает поток, когда содержание воды превышает порог активации в C1. Нижний отсек C2 обеспечивает пружинный разряд. Модель откалибрована в соответствии с наземными измерениями силы тяжести и показывает результаты, согласующиеся с наблюдениями. Проведен дополнительный анализ за более длительный период, который показывает, что сила тяжести сама по себе не может ограничивать модель стока дождевых осадков, поскольку измерение силы тяжести в этом районе кажется более чувствительным к медленному переносу (Fores et al. , 2017). Триц и др. (2011) предложили гистерезисную модель для лучшего учета как гистерезиса кривой всасывания в зоне почвы/эпикарста, так и влияния связности этой зоны, что позволяет быстро увеличить весенний сток в периоды важной подпитки. Авторы подчеркивают, что использование гистерезисной функции позволяет лучше воспроизводить пики первого паводка, которые дополняют наземные гравиметрические данные. Тем не менее, Mazzilli et al. (2013) показали, что информация, полученная с помощью силы тяжести, может не ограничивать оценку параметров модели стока дождевых осадков. Гино и др. (2015) представили передаточную функцию с бесконечным характерным временем, обеспечивающую удовлетворительные критерии эффективности с меньшим количеством параметров. В этом исследовании калибровка проводилась с учетом только весеннего стока, а калибровка не проводилась с учетом дополнительных наблюдений, таких как наземные гравиметрические или гидрохимические наблюдения.
, 2017). Триц и др. (2011) предложили гистерезисную модель для лучшего учета как гистерезиса кривой всасывания в зоне почвы/эпикарста, так и влияния связности этой зоны, что позволяет быстро увеличить весенний сток в периоды важной подпитки. Авторы подчеркивают, что использование гистерезисной функции позволяет лучше воспроизводить пики первого паводка, которые дополняют наземные гравиметрические данные. Тем не менее, Mazzilli et al. (2013) показали, что информация, полученная с помощью силы тяжести, может не ограничивать оценку параметров модели стока дождевых осадков. Гино и др. (2015) представили передаточную функцию с бесконечным характерным временем, обеспечивающую удовлетворительные критерии эффективности с меньшим количеством параметров. В этом исследовании калибровка проводилась с учетом только весеннего стока, а калибровка не проводилась с учетом дополнительных наблюдений, таких как наземные гравиметрические или гидрохимические наблюдения.
Настоящее исследование предлагает новую модель структуры карстовой системы Дюрзон. Структура модели основана на водообмене между емкостной и трансмиссивной частями карстового водоносного горизонта, который считается необходимым условием для объяснения весеннего изменения ЭА. Введение ЭА пружины в процедуру оценки параметров позволяет не только воспроизвести динамику разрядки пружины, но и уменьшить параметрические неопределенности, особенно для параметра, определяющего динамику опорожнения емкостных отсеков, а именно k EM и k MC . Наоборот, параметры, определяющие смоделированный весенний сток, а именно, k hy и k CS , кажутся не более ограниченными при рассмотрении EA в калибровке, и производительность модели для моделирования весенних гидрографов оказывается ниже, чем та, которая была получена в прежних исследования (Tritz et al., 2011; Mazzilli et al., 2013; Guinot et al., 2015).
Структура модели основана на водообмене между емкостной и трансмиссивной частями карстового водоносного горизонта, который считается необходимым условием для объяснения весеннего изменения ЭА. Введение ЭА пружины в процедуру оценки параметров позволяет не только воспроизвести динамику разрядки пружины, но и уменьшить параметрические неопределенности, особенно для параметра, определяющего динамику опорожнения емкостных отсеков, а именно k EM и k MC . Наоборот, параметры, определяющие смоделированный весенний сток, а именно, k hy и k CS , кажутся не более ограниченными при рассмотрении EA в калибровке, и производительность модели для моделирования весенних гидрографов оказывается ниже, чем та, которая была получена в прежних исследования (Tritz et al., 2011; Mazzilli et al., 2013; Guinot et al., 2015).
Заключение
В исследовании оценивается актуальность использования ЭА для характеристики взаимодействий между матрицей и каналом в карстовых системах с использованием модели ливневых стоков в сочетании с моделированием измерений ЭА на выходе из исследуемой системы. Основные результаты показывают, что учет измерения EA может уменьшить параметрическую неопределенность. Действительно, параметры, управляющие динамикой емкостного отсека (E и M), кажутся более ограниченными, когда, помимо родникового разряда, измерения EA на роднике рассматриваются как дополнительные наблюдения при калибровке модели. Кроме того, модель расхода осадков позволяет воспроизвести весенние гидрографы, даже если в целевой функции учитывается только EA, измеренная у источника. Такие результаты подтверждают, что вариации EA, измеренные весной, информативны в отношении внутренней динамики карстового водоносного горизонта Дюрзон.
Основные результаты показывают, что учет измерения EA может уменьшить параметрическую неопределенность. Действительно, параметры, управляющие динамикой емкостного отсека (E и M), кажутся более ограниченными, когда, помимо родникового разряда, измерения EA на роднике рассматриваются как дополнительные наблюдения при калибровке модели. Кроме того, модель расхода осадков позволяет воспроизвести весенние гидрографы, даже если в целевой функции учитывается только EA, измеренная у источника. Такие результаты подтверждают, что вариации EA, измеренные весной, информативны в отношении внутренней динамики карстового водоносного горизонта Дюрзон.
Наконец, предложенная численная модель позволяет обосновать концептуальную модель, предложенную для объяснения образования ЭА в карстовых водоносных горизонтах. Кроме того, исследование дает обнадеживающие результаты по использованию EA в качестве индикатора обмена потоками. Перспективы исследования могут включать следующее:
• Уточнение взаимосвязи между EA, измеренной в источнике, и пьезометрическими вариациями в зоне насыщения (что остается неизвестным для системы Дюрзона из-за отсутствия глубокого бурения),
• Объединение информационного содержания измерений EA в источнике с другими наблюдениями, такими как наземные измерения силы тяжести, электропроводности и температуры,
• Оценка как структурных, так и параметрических неопределенностей, связанных с различными типами доступных наблюдений за осадками. Калибровка модели расхода осадков,
Калибровка модели расхода осадков,
• Оценка чувствительности прогнозов модели расхода дождевых осадков к наблюдениям, а также оценка информационного содержания каждого типа наблюдений для калибровки модели расхода дождевых осадков,
• Разработка более надежных моделей стока осадков, предназначенных для карстовых водоносных горизонтов, с использованием гидрохимических наблюдений.
Заявление о доступности данных
Данные, проанализированные в этом исследовании, подпадают под действие следующих лицензий/ограничений: Данные предоставлены Региональным природным парком Гранд-Косс (PNRGC) и Французской национальной службой наблюдения H+. Запросы на доступ к этим наборам данных следует направлять на http://hplus.ore.fr/.
Вклад авторов
VS: концептуализация, методология, программное обеспечение, формальный анализ и написание — первоначальный вариант. LP: концептуализация, обработка данных, методология, формальный анализ и написание — первоначальный проект. BL: администрирование проекта, методология, надзор и написание — обзор и редактирование. VM: администрирование проекта, получение финансирования и надзор. VB-C: методология и руководство. CC: методология, контроль и написание — обзор и редактирование. HJ: концептуализация, методология и написание — обзор и редактирование. Все авторы внесли свой вклад в статью и одобрили представленную версию.
BL: администрирование проекта, методология, надзор и написание — обзор и редактирование. VM: администрирование проекта, получение финансирования и надзор. VB-C: методология и руководство. CC: методология, контроль и написание — обзор и редактирование. HJ: концептуализация, методология и написание — обзор и редактирование. Все авторы внесли свой вклад в статью и одобрили представленную версию.
Финансирование
Эта работа была выполнена при финансовой поддержке докторской программы региона Окситания и Французской геологической службы BRGM, которые выражают благодарность.
Благодарности
Авторы хотели бы поблагодарить инициативу Французской национальной службы наблюдений KARST (http://sokarst.org/) в INSU/CNRS, которая направлена на усиление распространения знаний и содействие междисциплинарным исследованиям карста. систем в национальном масштабе за их поддержку использования модели KarstMod. Авторы также благодарят Региональный природный парк Гранд-Косс (PNRGC) за предоставление данных о стоке, а также Французскую национальную службу наблюдений H+ (http://hplus. ore.fr/) за предоставление метеорологических данных по карстовой системе Дюрзон. . Французские национальные службы наблюдения KARST и H+ являются частью европейской инфраструктуры Elter (https://www.lter-europe.net/elter-esfri). Анализы растворенного газа были выполнены в рамках аналитической платформы CONDATE-EAU, которые также получили признание за обсуждения.
ore.fr/) за предоставление метеорологических данных по карстовой системе Дюрзон. . Французские национальные службы наблюдения KARST и H+ являются частью европейской инфраструктуры Elter (https://www.lter-europe.net/elter-esfri). Анализы растворенного газа были выполнены в рамках аналитической платформы CONDATE-EAU, которые также получили признание за обсуждения.
Конфликт интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.
Примечания издателя
Все требования, изложенные в этой статье, принадлежат исключительно авторам и не обязательно отражают претензии их дочерних организаций, издателя, редакторов и рецензентов. Любой продукт, который может быть оценен в этой статье, или претензии, которые могут быть сделаны его производителем, не гарантируются и не поддерживаются издателем.
Ссылки
Aeschbach-Hertig, W. (2004). «Избыток воздуха в грунтовых водах: проблемы и возможности». на ежегодном собрании GSA (Денвер).
(2004). «Избыток воздуха в грунтовых водах: проблемы и возможности». на ежегодном собрании GSA (Денвер).
Google Scholar
Эшбах-Хертиг В., Петерс Ф., Бейерле У. и Кипфер Р. (2000). Реконструкция палеотемпературы благородных газов в подземных водах с учетом уравновешивания с вовлеченным воздухом. Природа 405, 1040–1044. doi: 10.1038/35016542
PubMed Abstract | Полный текст перекрестной ссылки | Академия Google
Эшбах-Хертиг, В., и Соломон, Д.К. (2013). «Термометрия благородных газов в гидрологии подземных вод», в «Благородные газы как геохимические индикаторы достижений в изотопной геохимии» , изд. П. Бернард (Берлин, Гейдельберг: Springer Berlin Heidelberg), 81–122.
Google Scholar
Эшбах-Хертиг В., Штут М., Кларк Дж. Ф., Ройтер Р. Ф. и Шлоссер П. (2002). Запись палеотемпературы, полученная по растворенным благородным газам в подземных водах водоносного горизонта Аквиа (Мэриленд, США). Геохим. Космохим. Acta 66, 797–817. дои: 10.1016/S0016-7037(01)00804-3
дои: 10.1016/S0016-7037(01)00804-3
Полнотекстовая перекрестная ссылка | Google Scholar
Аквилина Л., Ладуш Б. и Дёрфлигер Н. (2005). Процессы питания в карстовых системах исследованы на основе корреляции химического и изотопного состава дождевых и родниковых вод. Заяв. Геохим. 20, 2189–2206. doi: 10.1016/j.apgeochem.2005.07.011
Полнотекстовая перекрестная ссылка | Google Scholar
Bailly-Comte, V., Martin, JB, Jourde, H., Screaton, E.J., Pistre, S., and Langston, A. (2010). Водообмен и передача давления между водоводами и матрицей и их влияние на гидродинамику двух карстовых водоносных горизонтов с опускающимися водотоками. J. Hydrol. 386, 55–66. doi: 10.1016/j.jhydrol.2010.03.005
Полнотекстовая перекрестная ссылка | Google Scholar
Берглунд Дж. Л., Торан Л. и Герман Э. К. (2020). Можно ли калибровать модели карстовых каналов? Двойной подход с использованием трассировки красителя и температуры. Подземные воды 58, 924–937. doi: 10.1111/gwat.12988
doi: 10.1111/gwat.12988
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Байерле У., Руиди Дж., Лойенбергер М., Эшбах-Хертиг В., Петерс Ф., Кипфер Р. и др. (2003). Доказательства периодов более влажного и прохладного климата в Сахеле между 6 и 40 тыс. лет назад получены из подземных вод. Геофиз. Рез. Письмо . 30, 1173–1177. дои: 10.1029/2002GL016310
Полнотекстовая перекрестная ссылка | Google Scholar
Блихер-Мэтисен Г., Маккарти Г. В. и Нильсен Л. П. (1998). Денитрификация и дегазация в подземных водах по растворенным диазоту и аргону. J. Hydrol. 208, 16–24. дои: 10.1016/S0022-1694(98)00142-5
Полнотекстовая перекрестная ссылка | Google Scholar
Чанг Ю., Хартманн А., Лю Л., Цзян Г. и Ву Дж. (2021). Идентификация более реалистичных модельных структур по наблюдениям за электропроводностью карстового источника. Водный ресурс. Рез . 57, e2020WR028587. дои: 10.1029/2020WR028587
Полнотекстовая перекрестная ссылка | Google Scholar
Чаттон, Э. (2017). Вклад растворенных газов в понимание гидробиогеохимической динамики подземных вод . Доступно в Интернете по адресу: http://www.theses.fr/2017REN1S131 (по состоянию на 2 февраля 2022 г.).
(2017). Вклад растворенных газов в понимание гидробиогеохимической динамики подземных вод . Доступно в Интернете по адресу: http://www.theses.fr/2017REN1S131 (по состоянию на 2 февраля 2022 г.).
Google Scholar
Шоле К., Шарлье Ж.-Б., Мусса Р., Стейнманн М. и Денимал С. (2017). Оценка боковых потоков и переноса растворенных веществ во время наводнений в карстовой системе с преобладанием водоводов с использованием обратной задачи для уравнения адвекции-диффузии. Гидр. Земля Сист. науч. 21, 3635–3653. doi: 10.5194/hess-21-3635-2017
Полнотекстовая перекрестная ссылка | Google Scholar
Кларк Дж. Ф., Хадсон Г. Б. и Ависар Д. (2005). Перенос газа под искусственными водоемами для подпитки: выводы из растворенных инертных газов и эксперимента по трассировке двойного газа (SF6 и 3He). Окружающая среда. науч. Технол. 39, 3939–3945. doi: 10.1021/es049053x
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Кускер, Ю.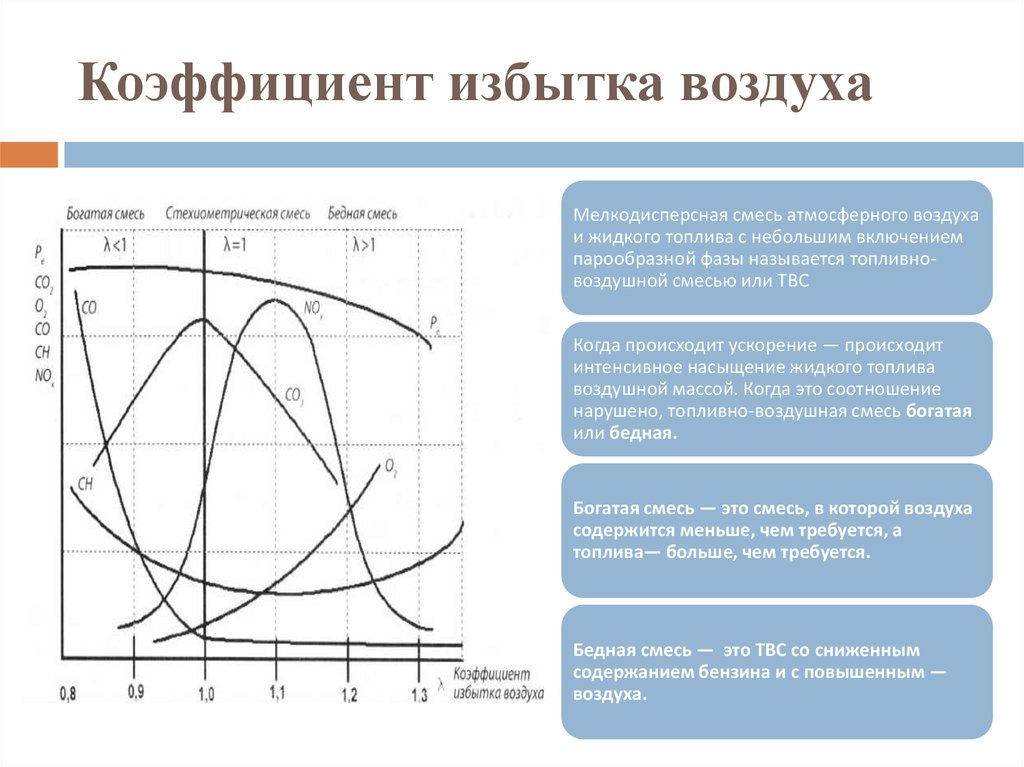 , и Журд, Х. (2022). Снижение неопределенности моделирования карстовых водоносных горизонтов с дополнительными гидрологическими наблюдениями для устойчивого управления ресурсами подземных вод. Дж. Гидрол . 612, 128130. doi: 10.1016/j.jhydrol.2022.128130
, и Журд, Х. (2022). Снижение неопределенности моделирования карстовых водоносных горизонтов с дополнительными гидрологическими наблюдениями для устойчивого управления ресурсами подземных вод. Дж. Гидрол . 612, 128130. doi: 10.1016/j.jhydrol.2022.128130
Полнотекстовая перекрестная ссылка | Google Scholar
Даль Сольо, Л., Данкиньи, К., Маццелли, Н., Эмбланч, К., и Массоннат, Г. (2020). Моделирование обмена матрицей и каналом как в эпикарсте, так и в зоне передачи карстовых систем. Вода 12, 3219. doi: 10.3390/w12113219
Полнотекстовая перекрестная ссылка | Google Scholar
Девиль С., Джейкоб Т., Шери Дж. и Шампольон К. (2013). О влиянии рельефа и строения маски на меняющуюся во времени силу тяжести, обусловленную местной гидрологией. Геофиз. Дж. Междунар. 192, 82–93. дои: 10.1093/gji/ggs007
Полнотекстовая перекрестная ссылка | Google Scholar
Дюран Л., Массей Н., Лекок Н., Фурнье М. и Лабат Д. (2020). Анализ многомасштабных гидродинамических процессов в карсте с помощью концептуального моделирования и подхода к декомпозиции сигналов. J. Hydrol. 583, 124625. doi: 10.1016/j.jhydrol.2020.124625
J. Hydrol. 583, 124625. doi: 10.1016/j.jhydrol.2020.124625
Полнотекстовая перекрестная ссылка | Google Scholar
Эберхарт Р. и Кеннеди Дж. (1995). «Оптимизация роя частиц», в Материалы Международной конференции IEEE по нейронным сетям (Citeseer) 1942–1948.
Google Scholar
Форд Д. и Уильямс П. (2013). Карстовая гидрогеология и геоморфология. Хобокен, Нью-Джерси: John Wiley & Sons .
Google Scholar
Форес, Б. (2016). Гравиметрия и система наблюдения за гидрологической моделью в карстовой среде: приложение в бассейне Дюрзона (Ларзак, Франция) . Доступно в Интернете по адресу: http://www.theses.fr/2016MONTT128 (по состоянию на 31 января 2022 г.).
Google Scholar
Форес Б., Шампольон К., Ле Муань Н., Байер Р. и Шери Дж. (2017). Оценка точности сверхпроводящего гравиметра iGrav для гидрологических моделей и идентификации карстовых гидрологических процессов. Геофиз. Дж. Междунар. 208, 269–280. дои: 10.1093/gji/ggw396
дои: 10.1093/gji/ggw396
Полнотекстовая перекрестная ссылка | Google Scholar
Гино В., Савеан М., Журд Х. и Неппель Л. (2015). Концептуальная модель осадков–стока с двухпараметрической бесконечной характеристической передаточной функцией времени. Гидр. Процесс. 29, 4756–4778. дои: 10.1002/hyp.10523
Полнотекстовая перекрестная ссылка | Google Scholar
Хартманн А., Ясечко С., Глисон Т., Вада Ю., Андрео Б., Барбер Дж. и др. (2021). Риск загрязнения подземных вод сильно недооценивается из-за быстрого поступления в водоносные горизонты. Проц. Нац. акад. науч. 118, е20244
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Хартманн А., Вагенер Т., Риммер А., Ланге Дж., Брильманн Х. и Вейлер М. (2013). Проверка реалистичности модельных структур для выявления процессов карстовой системы с использованием признаков качества и количества воды. Водный ресурс. Рез. 49, 3345–3358. дои: 10.1002/wrcr.20229
дои: 10.1002/wrcr.20229
Полнотекстовая перекрестная ссылка | Google Scholar
Хитон Т. Х. Э. и Фогель Дж. К. (1981). «Избыток воздуха» в подземных водах. J. Hydrol. 50, 201–216. дои: 10.1016/0022-1694(81)
-6
Полнотекстовая перекрестная ссылка | Google Scholar
Герцберг О. и Мазор Э. (1979). Гидрологические применения инертных газов и измерения температуры в системах подземных вод: примеры из Израиля. J. Hydrol. 41, 217–231. дои: 10.1016/0022-1694(79)
-5Полнотекстовая перекрестная ссылка | Google Scholar
Холочер Дж., Петерс Ф., Эшбах-Хертиг В., Хофер М., Бреннвальд М., Кинзельбах В. и др. (2002). Экспериментальные исследования образования избыточного воздуха в квазинасыщенных пористых средах. Геохим. Космохим. Acta 66, 4103–4117. дои: 10.1016/S0016-7037(02)00992-4
Полнотекстовая перекрестная ссылка | Google Scholar
Ингрэм, Р. Г. С., Хискок, К. М., и Деннис, П. Ф. (2007). Избыток воздуха в благородных газах применяется для определения условий пополнения запасов подземных вод. Окружающая среда. науч. Технол. 41, 1949–1955. doi: 10.1021/es061115r
Окружающая среда. науч. Технол. 41, 1949–1955. doi: 10.1021/es061115r
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Жаннин П.-Ю. (2001). Моделирование течения во фреатических и эпифреатических карстовых каналах в пещере Хёллох (Муотаталь, Швейцария). Водный ресурс. Рез. 37, 191–200. дои: 10.1029/2000WR
7Полнотекстовая перекрестная ссылка | Google Scholar
Журде Х., Массеи Н., Маццелли Н., Бине С., Батио-Гилье К., Лабат Д. и др. (2018). SNO KARST: французская сеть обсерваторий для междисциплинарного изучения процессов критической зоны в карстовых водоразделах и водоносных горизонтах. Зона Вадозе J. 17, 180094. doi: 10.2136/vzj2018.04.0094
Полнотекстовая перекрестная ссылка | Google Scholar
Кламп С., Томонага Ю., Кинцлер П., Кинзельбах В., Бауманн Т., Имбоден Д. М. и др. (2007). Полевые эксперименты позволяют по-новому взглянуть на газообмен и образование избыточного воздуха в природных пористых средах.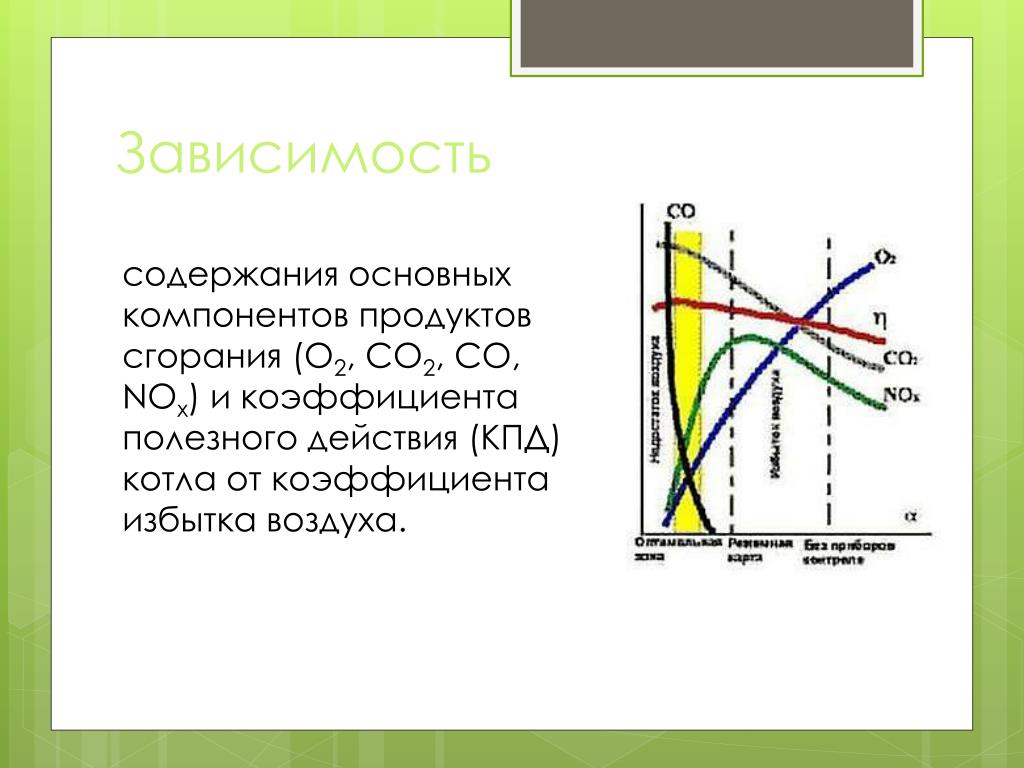 Геохим. Космохим. Acta 71, 1385–1397. doi: 10.1016/j.gca.2006.12.006
Геохим. Космохим. Acta 71, 1385–1397. doi: 10.1016/j.gca.2006.12.006
Полнотекстовая перекрестная ссылка | Google Scholar
Кулонгоски Дж. Т., Хилтон Д. Р. и Селаоло Э. Т. (2004). Изменчивость климата в Ботсване Калахари с позднего плейстоцена до наших дней. Геофиз. Рез. Письмо . 31. Дои: 10.1029/2003GL019238
Полнотекстовая перекрестная ссылка | Google Scholar
Ли, А. (2014). Pyswarm: оптимизация роя частиц (PSO) с поддержкой ограничений . Доступно в Интернете по адресу: https://github.com/tisimst/pyswarm (по состоянию на 27 мая 2021 г.).
Google Scholar
Лукач Реберски Дж., Терзич Дж., Морис Л. Д. и Лапворт Д. Дж. (2022). Возникающие органические загрязнители в карстовых подземных водах: оценка на глобальном уровне. J. Hydrol. 604, 127242. doi: 10.1016/j.jhydrol.2021.127242
Полнотекстовая перекрестная ссылка | Google Scholar
Мэннинг А. Х. и Кейн Дж. С. (2007). Инертные газы подземных вод, возраст и температурные сигнатуры в альпийском водоразделе: ценные инструменты для разработки концептуальной модели. Водный ресурс. Рез . 43. DOI: 10.1029/2006WR005349
Водный ресурс. Рез . 43. DOI: 10.1029/2006WR005349
Полнотекстовая перекрестная ссылка | Google Scholar
Мариотти, А. (1986). Денитрификация в подземных водах, принципы и методы идентификации сына: Une revue [Денитрификация в подземных водах, принципы и методы ее идентификации: обзор]. Дж. Гидрол . 88, 1–23. дои: 10.1016/0022-1694(86)-0
Полнотекстовая перекрестная ссылка | Google Scholar
Марсо, Б. (1996). Структура и функционирование новой зоны карста в части результатов экспериментов . Доступно в Интернете по адресу: http://www.theses.fr/1996PA112532 (по состоянию на 31 декабря 2019 г.).
Google Scholar
Мартин, Дж. Б., и Дин, Р. В. (2001). Обмен водой между трубопроводами и матрицей в водоносном горизонте Флориды. хим. геол. 179, 145–165. doi: 10.1016/S0009-2541(01)00320-5
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Массманн Г. и Зюльтенфусс Дж. (2008). Выявление процессов, влияющих на образование избыточного воздуха при естественной береговой фильтрации и управляемом питании водоносных горизонтов. J. Hydrol. 359, 235–246. doi: 10.1016/j.jhydrol.2008.07.004
Выявление процессов, влияющих на образование избыточного воздуха при естественной береговой фильтрации и управляемом питании водоносных горизонтов. J. Hydrol. 359, 235–246. doi: 10.1016/j.jhydrol.2008.07.004
Полнотекстовая перекрестная ссылка | Google Scholar
Мазор Э., ван Эвердинген Р. О. и Крауз Х. Р. (1983). Свидетельство геотермальной активности благородных газов в карстовой местности: скалистые горы, Канада. Геохим. Космохим. Acta 47, 1111–1115. дои: 10.1016/0016-7037(83)
-7Полнотекстовая перекрестная ссылка | Google Scholar
Mazzilli, N., Guinot, V., and Jourde, H. (2012). Анализ чувствительности калибровки концептуальной модели к систематической ошибке инициализации. Применение к моделям расхода карстовых источников. Доп. Вода Res. 42, 1–16. doi: 10.1016/j.advwatres.2012.03.020
Полнотекстовая перекрестная ссылка | Google Scholar
Mazzilli, N., Guinot, V., Jourde, H., Lecoq, N., Labat, D., Arfib, B. , et al. (2019). KarstMod: Платформа моделирования осадков — анализ стока и моделирование карстовых систем. Окружающая среда. Модель. Мягкий. 122, 103927. doi: 10.1016/j.envsoft.2017.03.015
, et al. (2019). KarstMod: Платформа моделирования осадков — анализ стока и моделирование карстовых систем. Окружающая среда. Модель. Мягкий. 122, 103927. doi: 10.1016/j.envsoft.2017.03.015
Полнотекстовая перекрестная ссылка | Google Scholar
Mazzilli, N., Jourde, H., Guinot, V., Bailly-Comte, V., and Fleury, P. (2011). Гидрологическое моделирование карстового водоносного горизонта при активном управлении подземными водами с использованием экономной концептуальной модели. в h3Karst (Безансон, Франция) 908:20 . Доступно в Интернете по адресу: https://hal.archives-ouvertes.fr/hal-01844603 (по состоянию на 27 апреля 2022 г.).
Google Scholar
Mazzilli, N., Jourde, H., Jacob, T., Guinot, V., Le Moigne, N., Boucher, M., et al. (2013). О включении наземных гравиметрических измерений в процесс калибровки глобальной модели резервуара с осадками и стоками: случай карстовой системы Дюрзона (Ларзак, юг Франции). Environ Earth Sci 68, 1631–1646. дои: 10.1007/s12665-012-1856-z
дои: 10.1007/s12665-012-1856-z
Полнотекстовая перекрестная ссылка | Google Scholar
Мейерхофф С. Б., Караулис М., Фибиг Ф., Максвелл Р. М., Ревил А., Мартин Дж. Б. и др. (2012). Визуализация различий проводимости канала и матрикса в карстовом водоносном горизонте с использованием удельного электрического сопротивления во времени. Геофиз. Рез. Письмо . 39, 2012GL053933. дои: 10.1029/2012GL053933
Полнотекстовая перекрестная ссылка | Google Scholar
Митрофан Х., Марин К. и Повар А. И. (2015). Возможные признаки водообмена между каналом и матрицей, обозначенные у карстового источника. Подземные воды 53, 113–122. doi: 10.1111/gwat.12292
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Нэш, Дж. Э., и Сатклифф, Дж. В. (1970). Прогнозирование речного стока с помощью концептуальных моделей, часть I — обсуждение принципов. J. Hydrol. 10, 282–290. дои: 10.1016/0022-1694(70)
-6Полнотекстовая перекрестная ссылка | Google Scholar
Озенбрюк К. , Штадлер С., Зюльтенфус Дж., Суков А. О. и Вайзе С. М. (2009). Влияние изменений пополнения на качество воды, о чем свидетельствует избыток воздуха в грунтовых водах Калахари, Ботсвана. Геохим. Космохим. Acta 73, 911–922. doi: 10.1016/j.gca.2008.11.006
, Штадлер С., Зюльтенфус Дж., Суков А. О. и Вайзе С. М. (2009). Влияние изменений пополнения на качество воды, о чем свидетельствует избыток воздуха в грунтовых водах Калахари, Ботсвана. Геохим. Космохим. Acta 73, 911–922. doi: 10.1016/j.gca.2008.11.006
Полнотекстовая перекрестная ссылка | Google Scholar
Палмер, А. Н. (1991). Происхождение и морфология известняковых пещер. Геол. соц. Являюсь. Бык . 103, 1–21.
Google Scholar
Петерс Ф., Эшбах-Хертиг В., Холочер Дж. и Кипфер Р. (2002). «Коррекция избытка воздуха в датировании подземных вод с помощью изотопов He». в geochimica et космохимика акта (pergamon-elsevier science ltd, бульвар, langford lane, kidlington), A587.
Google Scholar
Penman, HL (1948). Естественное испарение с открытой воды, голой почвы и травы. Проц. Р. Соц. Лонд. А. Мат. физ. Наука . 193, 120–145. doi: 10.1098/rspa.1948.0037
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Перотен, Л. (2021). Характеристика перезарядки и передачи карстовых водоносных горизонтов по принципу использования газа . Доступно в Интернете по адресу: https://tel.archives-ouvertes.fr/tel-03655132 (по состоянию на 6 мая 2022 г.).
(2021). Характеристика перезарядки и передачи карстовых водоносных горизонтов по принципу использования газа . Доступно в Интернете по адресу: https://tel.archives-ouvertes.fr/tel-03655132 (по состоянию на 6 мая 2022 г.).
Google Scholar
Перотен Л., де Монти В., Ладуш Б., Байи-Конт В., Лабаск Т., Верно В. и др. (2021). Перенос растворенных газов через мощную карстовую аэрационную зону – последствия для характеристики питания и определения возраста подземных вод в карстовых водоносных горизонтах. J. Hydrol. 601, 126576. doi: 10.1016/j.jhydrol.2021.126576
Полнотекстовая перекрестная ссылка | Google Scholar
Перрен К., Мишель К. и Андреасян В. (2001). Повышает ли большое количество параметров производительность модели? Сравнительная оценка общих моделей моделей водосбора на 429водосборы. J. Hydrol. 242, 275–301. дои: 10.1016/S0022-1694(00)00393-0
Полнотекстовая перекрестная ссылка | Google Scholar
Plagnes, V. (1997). Структура и функционирование карстовых водоносных горизонтов : характеристика геохимии вод . Доступно в Интернете по адресу: https://www.theses.fr/1997MON20193 (по состоянию на 3 марта 2022 г.).
(1997). Структура и функционирование карстовых водоносных горизонтов : характеристика геохимии вод . Доступно в Интернете по адресу: https://www.theses.fr/1997MON20193 (по состоянию на 3 марта 2022 г.).
Google Scholar
Пламмер Л. Н., Бузенберг Э. и Видман П. К. (2004). Применение растворенных N2 и Ar в подземных водах 908:20 . Рестон, Вирджиния: Геологическая служба США.
Реферат PubMed | Google Scholar
Попп А. Л., Пардо-Альварес А., Шиллинг О. С., Шайдеггер А., Муси С., Пил М. и др. (2021). Структура для распутывания переходного перемешивания грунтовых вод и времени прохождения. Водный ресурс. Рез. 57, e2020WR028362. дои: 10.1029/2020WR028362
Полнотекстовая перекрестная ссылка | Google Scholar
Reimann, T., Geyer, T., Shoemaker, WB, Liedl, R., and Sauter, M. (2011). Эффекты динамически изменяющейся насыщенности и связи матрикс-канал потока в карстовых водоносных горизонтах. Водный ресурс. Рез. 47. doi: 10. 1029/2011WR010446
1029/2011WR010446
Полнотекстовая перекрестная ссылка | Google Scholar
Рикард Дж. и Бакалович М. (1996). Разведка, благоустройство и охрана ресурсов в септентриональной воде Ларзак, Аверон (Франция) . Отчет R38953, BRGM, Орлеан.
Google Scholar
Сано Ю., Киношита Н., Кагошима Т., Такахата Н., Саката С., Токи Т. и др. (2017). Происхождение природного газа, богатого метаном, на границе сходящихся плит Западной части Тихого океана. Науч. Rep. 7, 15646. doi: 10.1038/s41598-017-15959-5
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Schilling, O.S., Parajuli, A., Tremblay Otis, C., Müller, T.U., Antolinez Quijano, W., Tremblay, Y., et al. (2021). Количественная оценка динамики пополнения подземных вод и процессов в зоне ненасыщения в водосборах с преобладанием снега с помощью анализа растворенного газа на месте. Водный ресурс. Рез. 57, e2020WR028479. дои: 10.1029/2020WR028479
Полнотекстовая перекрестная ссылка | Академия Google
Schilling, O. S., Partington, D.J., Doherty, J., Kipfer, R., Hunkeler, D., and Brunner, P. (2022). Обнаружение подземных палеоканалов с помощью модели подземных вод, наблюдений на основе трассеров и пространственно меняющейся предпочтительной калибровки пилотной точки анизотропии. Геофиз. Рез. лат. 49, e2022GL098944. дои: 10.1029/2022GL098944
S., Partington, D.J., Doherty, J., Kipfer, R., Hunkeler, D., and Brunner, P. (2022). Обнаружение подземных палеоканалов с помощью модели подземных вод, наблюдений на основе трассеров и пространственно меняющейся предпочтительной калибровки пилотной точки анизотропии. Геофиз. Рез. лат. 49, e2022GL098944. дои: 10.1029/2022GL098944
Полнотекстовая перекрестная ссылка | Google Scholar
Ширафкан М., Мохаммади З., Сивель В. и Лабат Д. (2021). Влияние обменного стока на гидрограф карстовых источников при различных режимах течения: подход синтетического моделирования. Вода 13, 1189. doi: 10.3390/w130
Полнотекстовая перекрестная ссылка | Google Scholar
Сивель В. и Журд Х. (2020). Методология оценки изменчивости ресурсов подземных вод в карстовых водосборах с редкими временными измерениями. Гидрогеол. J. 29, 137–157. doi: 10.1007/s10040-020-02239-2
Полнотекстовая перекрестная ссылка | Google Scholar
Сивель В., Лабат Д. , Маззилли Н., Массей Н. и Журд Х. (2019). Динамика обмена потоками между матрицей и водоводами в закарстованных водоразделах в различных временных масштабах. Вода 11, 569. doi: 10.3390/w11030569
, Маззилли Н., Массей Н. и Журд Х. (2019). Динамика обмена потоками между матрицей и водоводами в закарстованных водоразделах в различных временных масштабах. Вода 11, 569. doi: 10.3390/w11030569
Полнотекстовая перекрестная ссылка | Google Scholar
Smith, R.L., Howes, B.L., and Duff, JH (1991). Денитрификация в загрязненных нитратами подземных водах: возникновение в крутых вертикальных геохимических градиентах. Геохим. Космохим. Acta 55, 1815–1825 гг. дои: 10.1016/0016-7037(91)
-2
Полнотекстовая перекрестная ссылка | Google Scholar
Стьют М. и Шлоссер П. (2000). «Атмосферные благородные газы», в Индикаторы окружающей среды в подповерхностной гидрологии , ред. П. Г. Кук и А. Л. Герцег (Бостон, Массачусетс: Springer US), 349–377.
Google Scholar
Сугисаки Р. и Таки К. (1987). Упрощенные анализы He, Ne и Ar, растворенных в природных водах. Геохим. Дж. 21, 23–27. doi: 10.2343/geochemj.21.23
Полнотекстовая перекрестная ссылка | Google Scholar
Саммерфилд, М. (2010). Программирование на Python 3: полное введение в язык Python . Хобокен, Нью-Джерси: Addison-Wesley Professional.
(2010). Программирование на Python 3: полное введение в язык Python . Хобокен, Нью-Джерси: Addison-Wesley Professional.
Google Scholar
Томонага Ю., Марцокки Р., Пера С., Пфайфер Х.-Р., Кипфер Р., Декруи Л. и др. (2017). Использование данных по инертным газам и стабильным изотопам для определения происхождения и режимов течения подземных вод: приложение к базовому туннелю ceneri (Швейцария). J. Hydrol. 545, 395–409. doi: 10.1016/j.jhydrol.2016.11.043
Полнотекстовая перекрестная ссылка | Google Scholar
Триц С., Гино В. и Журд Х. (2011). Моделирование поведения водосбора карстовой системы с использованием нелинейной гистерезисной концептуальной модели. J. Hydrol. 397, 250–262. doi: 10.1016/j.jhydrol.2010.12.001
Полнотекстовая перекрестная ссылка | Google Scholar
Wilson, G.B., and McNeill, G.W. (1997). Температуры перезарядки благородных газов и составляющая избытка воздуха. Заяв. Геохим. 12, 747–762. дои: 10.1016/S0883-2927(97)00035-8
дои: 10.1016/S0883-2927(97)00035-8
Полнотекстовая перекрестная ссылка | Google Scholar
Чжан З., Чен Х. и Соулсби К. (2017). Концептуальное моделирование переноса воды и растворенных веществ в масштабе водосбора в системе двойного потока карстовой критической зоны. Гидр. Процесс. 31, 3421–3436. дои: 10.1002/hyp.11268
Полнотекстовая перекрестная ссылка | Google Scholar
Чжу, К., и Кипфер, Р. (2010). Сигнатуры благородных газов в виде импульсов высокой перезарядки и мигрирующего струйного течения в позднем плейстоцене над Черной Мезой, Аризона, США. Геология 38, 83–86. дои: 10.1130/G30369.1
Полнотекстовая перекрестная ссылка | Google Scholar
Соотношение воздух-топливо – x-engineer.org
Содержание
- Определение соотношения воздух-топливо
- Формула соотношения воздух-топливо
- Соотношение воздух-топливо для различных видов топлива
- Как рассчитывается стехиометрическое соотношение воздух-топливо
- Лямбда-соотношение воздух-топливо
- Соотношение воздух-топливо и мощность двигателя
- Калькулятор соотношения воздух-топливо
- Влияние соотношения воздух-топливо по выбросам двигателя
- Лямбда-регулирование сгорания с обратной связью
Определение соотношения воздух-топливо
Тепловые двигатели используют топливо и кислород (из воздуха) для производства энергии посредством сгорания. Для обеспечения процесса сгорания в камеру сгорания необходимо подавать определенное количество топлива и воздуха. А полное сгорание происходит, когда все топливо сгорает, в выхлопных газах не будет несгоревшего топлива.
Для обеспечения процесса сгорания в камеру сгорания необходимо подавать определенное количество топлива и воздуха. А полное сгорание происходит, когда все топливо сгорает, в выхлопных газах не будет несгоревшего топлива.
Соотношение воздух-топливо определяется как соотношение воздуха и топлива в смеси, приготовленной для сжигания. Например, если у нас есть смесь метана и воздуха с соотношением воздух-топливо 17,5, это означает, что в смеси у нас 17,5 кг воздуха и 1 кг метана.
Идеальное (теоретическое) соотношение воздух-топливо для полного сгорания , называется стехиометрическое соотношение воздух-топливо . Для бензинового (бензинового) двигателя стехиометрическое соотношение воздух-топливо составляет около 14,7: 1. Это значит, что для полного сгорания 1 кг топлива нам потребуется 14,7 кг воздуха. Возгорание возможно, даже если АТР отличается от стехиометрического. Для процесса сгорания в бензиновом двигателе минимальное значение AFR составляет около 6:1, а максимальное может достигать 20:1.
Когда соотношение воздух-топливо выше стехиометрического соотношения, смесь воздух-топливо называется постный . Когда соотношение воздух-топливо ниже стехиометрического соотношения, топливовоздушная смесь называется богатой . Например, для бензинового двигателя AFR 16,5:1 соответствует обедненной смеси, а 13,7:1 – богатой смеси.
Назад
Формула соотношения воздух-топливо
Применительно к двигателям внутреннего сгорания соотношение воздух-топливо (AF или AFR) определяется как соотношение между массой воздуха m a и массой топлива m f , используется двигателем при работе:
\[\bbox[#FFFF9D]{AFR = \frac{m_a}{m_f}} \tag{1}\]
Обратное соотношение называется топливно-воздушным соотношением (FA или FAR) и рассчитывается как:
\[FAR = \frac{m_f}{m_a} = \frac{1}{AFR} \tag{1}\]
Вернуться назад
Соотношение воздух-топливо для различных видов топлива
В таблице ниже мы можем см. стехиометрическое соотношение воздух-топливо для нескольких ископаемых видов топлива.
стехиометрическое соотношение воздух-топливо для нескольких ископаемых видов топлива.
| Топливо | Химическая формула | AFR |
| Methanol | CH 3 OH | 6.47:1 |
| Ethanol | C 2 H 5 OH | 9:1 |
| Butanol | C 4 H 9 OH | 11.2:1 |
| Diesel | C 12 H 23 | 14.5:1 |
| Gasoline | C 8 H 18 | 14.7:1 |
| Propane | C 3 H 8 | 15.67:1 |
| Methane | CH 4 | 17.19:1 |
| Hydrogen | H 2 | 34,3:1 |
Источник: wikipedia. org
org
Например, чтобы полностью сжечь 1 кг этанола, нам нужно 9 кг воздуха, а чтобы сжечь 1 кг дизельного топлива, нам нужно 14,5 кг воздуха.
Искровое зажигание (SI) Двигатели обычно работают на бензине (бензине) в качестве топлива. AFR двигателей SI колеблется в диапазоне от 12:1 (богатая смесь) до 20:1 (бедная смесь) в зависимости от режима работы двигателя (температура, частота вращения, нагрузка и т. д.). Современные двигатели внутреннего сгорания работают, насколько это возможно, в пределах стехиометрического AFR (в основном из-за доочистки газа). В таблице ниже вы можете увидеть пример AFR двигателя SI, функции частоты вращения двигателя и крутящего момента.
Изображение: Пример зависимости соотношения воздух-топливо (AFR) от частоты вращения и крутящего момента двигателя
Воспламенение от сжатия (CI) Двигатели обычно работают на дизельном топливе. Из-за характера процесса сгорания двигатели с системой внутреннего сгорания всегда работают на бедных смесях с AFR от 18: 1 до 70: 1. Основное различие по сравнению с двигателями SI заключается в том, что двигатели CI работают на стратифицированных (неоднородных) воздушно-топливных смесях, а SI работают на гомогенных смесях (в случае двигателей с распределенным впрыском).
Основное различие по сравнению с двигателями SI заключается в том, что двигатели CI работают на стратифицированных (неоднородных) воздушно-топливных смесях, а SI работают на гомогенных смесях (в случае двигателей с распределенным впрыском).
Приведенная выше таблица вводится в сценарий Scilab, после чего создается контурный график.
EngSpd_rpm_X = [500 1000 1500 2000 2500 3000 3500 4000 4500 5000 5500 6000 6500];
EngTq_Nm_Y = [10;20;30;40;50;60;70;80;90;100;110;120;130;140];
EngAFR_rat_Z = [14 14,7 16,4 17,5 19,8 19,8 18,8 18,1 18,1 18,1 18,1 18,1 18,1;
14 14,7 14,7 16,4 16,4 16,4 16,5 16,8 16,8 16,8 16,8 16,8 16,8;
14 14,7 14,7 14,7 14,7 14,7 14,7 15,7 15,7 15,3 14,9 14,9 14,9;
14,2 14,7 14,7 14,7 14,7 14,7 14,7 14,7 14,7 13,9 13,3 13,3 13,3;
14,7 14,7 14,7 14,7 14,7 14,7 14,7 14,7 14,7 14,5 12,912,9 12,9;
14,7 14,7 14,7 14,7 14,7 14,7 14,7 14,7 14,3 13,3 12,6 12,1 11,8;
14,7 14,7 14,7 14,7 14,7 14,7 14,7 14,7 13,6 12,9 12,2 11,8 11,3;
14,1 14,2 14,7 14,7 14,7 14,7 14,7 14,7 13,3 12,5 11,9 11,4 10,9;
13,4 13,4 13,8 14,3 14,3 14,7 14,7 13,6 13,1 12,2 11,5 11,1 10,7;
13,4 13,4 13,4 13,4 13,4 13,6 13,6 12,1 12,1 11,6 11,2 10,8 10,5;
13,4 13,4 13,4 13,4 13,1 13,1 13,1 11,8 11,8 11,2 10,7 10,5 10,3;
13,4 13,4 13,4 13,4 12,912,9 12,5 11,6 11,3 10,5 10,4 10,3 10,2;
13,4 13,4 13,4 13,4 12,9 12,9 12,5 11,6 11,3 10,5 10,4 10,3 10,2;
13,4 13,4 13,4 13,4 12,9 12,9 12,5 11,6 11,3 10,5 10,4 10,3 10,2];
контур(EngSpd_rpm_X,EngTq_Nm_Y,EngAFR_rat_Z',30)
сетка()
xlabel('Обороты двигателя [об/мин]')
ylabel('Момент двигателя [Нм]')
название('x-engineer. org')
org')
Выполнение приведенных выше инструкций Scilab создаст следующий контурный график:
Изображение: контурный график воздуха и топлива в Scilab
Назад
Как рассчитывается стехиометрическое соотношение воздух-топливо
Чтобы понять, как рассчитывается стехиометрическое соотношение воздух-топливо, нам нужно рассмотреть процесс сгорания топлива. Горение – это в основном химическая реакция (называемая окислением ), в которой топливо смешивается с кислородом и образуется двуокись углерода (CO 2 ), вода (H 2 O) и энергия (тепло). Учтите, что для того, чтобы произошла реакция окисления, нужна энергия активации (искра или высокая температура). Кроме того, чистая реакция сильно экзотермична (с выделением тепла).
\[\text{Топливо}+\text{Кислород}\xrightarrow[высокая \text{ } температура \text{ (CI)}]{искра \text{ (SI)}} \text{Углекислый газ} + \ text{Вода} + \text{Энергия}\]
Пример 1. Для лучшего понимания рассмотрим реакцию окисления метана . Это довольно распространенная химическая реакция, так как метан является основным компонентом природного газа (в пропорции около 94 %).
Для лучшего понимания рассмотрим реакцию окисления метана . Это довольно распространенная химическая реакция, так как метан является основным компонентом природного газа (в пропорции около 94 %).
Шаг 1 . Напишите химическую реакцию (окисление)
\[CH_4 + O_2 \rightarrow CO_2 + H_2O\]
Шаг 2 . Сбалансируйте уравнение
\[CH_4 + {\color{Red} 2} \cdot O_2 \rightarrow CO_2 +{\color{Red} 2} \cdot H_2O\]
Шаг 3 . Запишите стандартный атомный вес для каждого атома
\[ \begin{split}
\text{Водород} &= 1,008 \text{ а.е.м.}\\
\text{Углерод} &= 12,011 \text{ а.е.м.}\\
\text{Кислород} &= 15,999 \text{ а.е.м.}
\end{split} \]
Шаг 4 . Рассчитайте массу топлива, которое составляет 1 моль метана, состоящего из 1 атома углерода и 4 атомов водорода.
\[m_f =12,011 + 4 \cdot 1,008 = 16,043 \text{g}\]
Шаг 5 . Вычислите массу кислорода, состоящего из 2 молей, каждый из которых состоит из 2 атомов кислорода.
\[m_o =2 \cdot 15,999 \cdot 2= 63,996 \text{g}\]
Шаг 6 . Рассчитайте необходимую массу воздуха, содержащего расчетную массу кислорода, принимая во внимание, что воздух содержит около 21 % кислорода.
\[m_a = \frac{100}{21} \cdot m_o=\frac{100}{21} \cdot 63,996 = 304,743 \text{g}\]
Шаг 7 . Рассчитайте соотношение воздух-топливо, используя уравнение (1)
\[AFR = \frac{m_a}{m_f} = \frac{304,743}{16,043} = 18,995 \]
Расчетное значение AFR для метана не совсем соответствует указанному в литература. Разница может заключаться в том, что в нашем примере мы сделали несколько допущений (воздух содержит только 21 % кислорода, продукты сгорания – только углекислый газ и вода).
Пример 2. Тот же метод можно применить для сжигания бензина. Учитывая, что бензин состоит из изооктана (C 8 H 18 ), рассчитайте стехиометрическое соотношение воздух-топливо для бензина .
Шаг 1 . Напишите химическую реакцию (окисление)
\[C_{8}H_{18} + O_2 \rightarrow CO_2 + H_2O\]
Этап 2 . Сбалансируйте уравнение
\[C_{8}H_{18} + {\color{Red} {12,5}} \cdot O_2 \rightarrow {\color{Red} 8} \cdot CO_2 +{\color{Red} 9} \cdot H_2O\]
Шаг 3 . Запишите стандартный атомный вес для каждого атома
\[ \begin{split}
\text{Водород} &= 1,008 \text{ а.е.м.}\\
\text{Углерод} &= 12,011 \text{ а.е.м.}\\
\text{Кислород} &= 15,999 \text{ а.е.м.}
\end{split} \]
Шаг 4 . Рассчитайте массу топлива, которое составляет 1 моль изооктана, состоящего из 8 атомов углерода и 18 атомов водорода.
\[m_f =8 \cdot 12,011 + 18 \cdot 1,008 = 114,232 \text{g}\]
Шаг 5 . Вычислите массу кислорода, который состоит из 12,5 молей, каждый моль состоит из 2 атомов кислорода.
\[m_o =12,5 \cdot 15,999 \cdot 2= 399,975 \text{g}\]
Шаг 6 . Рассчитайте необходимую массу воздуха, содержащего расчетную массу кислорода, принимая во внимание, что воздух содержит около 21 % кислорода.
\[m_a = \frac{100}{21} \cdot m_o=\frac{100}{21} \cdot 399,975 = 1904,643 \text{g}\]
Шаг 7 . Рассчитайте соотношение воздух-топливо, используя уравнение (1)
\[AFR = \frac{m_a}{m_f} = \frac{1904,643}{114,232} = 16,673 \]
Опять же, расчетное стехиометрическое соотношение воздух-топливо для бензина равно несколько отличается от приведенного в литературе. Таким образом, результат приемлемый, так как мы сделали много допущений (бензин содержит только изооктан, воздух содержит только кислород в пропорции 21 %, единственные продукты сгорания – углекислый газ и вода, горение идеальное).
Назад
Лямбда соотношение воздух-топливо
Мы увидели, что такое и как рассчитать стехиометрическое (идеальное) соотношение воздух-топливо. В реальности двигатели внутреннего сгорания работают не именно с идеальным AFR, а с близкими к нему значениями. Таким образом, мы будем иметь идеальное и фактическое соотношение AFR воздух-топливо. Соотношение между фактическим соотношением воздух-топливо (AFR фактическое ) и идеальным/стехиометрическим соотношением воздух-топливо (AFR идеальное ) называется эквивалентным соотношением воздух-топливо 9.0482 или лямбда (λ).
\[\bbox[#FFFF9D]{\lambda = \frac{AFR_{actual}}{AFR_{ideal}}} \tag{3}\]
Например, идеальное соотношение воздух-топливо для бензина ( бензиновый) двигатель 14,7:1. Если фактическое/реальное значение AFR равно 13,5, коэффициент эквивалентности лямбда будет равен:
\[\lambda = \frac{13,5}{14,7} = 0,92\]
В зависимости от значения лямбда двигатель запускается с обедненной, стехиометрической или богатой воздушно-топливной смесью.
| Коэффициент эквивалентности | Тип воздушно-топливной смеси | Описание |
| λ < 1,00 | Богатое количество воздуха недостаточно для полного сгорания; после сгорания в выхлопных газах присутствует несгоревшее топливо | |
| λ = 1,00 | Стехиометрический (идеальный) | Масса воздуха точна для полного сгорания топлива; после сгорания нет избыточного кислорода в выхлопе и нет несгоревшего топлива |
| λ > 1,00 | Бедная | Кислорода больше, чем требуется для полного сжигания количества топлива; после сгорания в выхлопных газах присутствует избыток кислорода |
В зависимости от вида топлива (бензин или дизель) и типа впрыска (прямой или непрямой) двигатель внутреннего сгорания может работать на бедной, стехиометрической или богатой смеси топливные смеси.
Изображение: 3-цилиндровый бензиновый двигатель Ecoboost с непосредственным впрыском топлива (схема лямбда)
Кредит: Ford
Например, 3-цилиндровый двигатель Ford Ecoboost работает со стехиометрическим соотношением воздух-топливо на холостом ходу и средних оборотах двигателя и во всем диапазоне нагрузок, а также с обогащенной топливно-воздушной смесью на высоких оборотах и нагрузке. Причина, по которой он работает с обогащенной смесью при высоких оборотах двигателя и нагрузке, заключается в охлаждении двигателя . Дополнительное топливо (которое останется несгоревшим) впрыскивается для поглощения тепла (путем испарения), тем самым снижая температуру в камере сгорания.
Причина, по которой он работает с обогащенной смесью при высоких оборотах двигателя и нагрузке, заключается в охлаждении двигателя . Дополнительное топливо (которое останется несгоревшим) впрыскивается для поглощения тепла (путем испарения), тем самым снижая температуру в камере сгорания.
Изображение: Дизельный двигатель (лямбда-карта)
Авторы и права: wtz.de
Двигатель с воспламенением от сжатия (дизельный) работает все время на обедненной воздушно-топливной смеси , значение коэффициента эквивалентности (λ) зависит от рабочая точка (скорость и крутящий момент). Причиной этого является принцип работы дизеля: регулирование нагрузки не за счет массы воздуха (которого всегда в избытке), а за счет массы топлива (времени впрыска).
Помните, что коэффициент стехиометрического эквивалента (λ = 1,00) означает соотношение воздух-топливо 14,7:1 для бензиновых двигателей и 14,5:1 для дизельных двигателей.
Назад
Соотношение воздух-топливо и мощность двигателя
Мощность двигателя и расход топлива сильно зависят от соотношения воздух-топливо. Для бензинового двигателя наименьший расход топлива достигается при обедненной смеси AFR. Основная причина заключается в том, что кислорода достаточно для полного сжигания всего топлива, что выражается в механической работе. С другой стороны, максимальная мощность достигается при обогащении топливно-воздушных смесей. Как объяснялось ранее, подача большего количества топлива в цилиндр при высокой нагрузке и скорости двигателя охлаждает камеру сгорания (за счет испарения топлива и поглощения тепла), что позволяет двигателю развивать максимальный крутящий момент и, следовательно, максимальную мощность.
Для бензинового двигателя наименьший расход топлива достигается при обедненной смеси AFR. Основная причина заключается в том, что кислорода достаточно для полного сжигания всего топлива, что выражается в механической работе. С другой стороны, максимальная мощность достигается при обогащении топливно-воздушных смесей. Как объяснялось ранее, подача большего количества топлива в цилиндр при высокой нагрузке и скорости двигателя охлаждает камеру сгорания (за счет испарения топлива и поглощения тепла), что позволяет двигателю развивать максимальный крутящий момент и, следовательно, максимальную мощность.
Изображение: Функция мощности двигателя и расхода топлива от соотношения воздух-топливо (лямбда)
На рисунке выше видно, что мы не можем получить максимальную мощность двигателя и наименьший расход топлива при одном и том же соотношении воздух-топливо. Наименьший расход топлива (наилучшая экономия топлива) достигается при использовании бедных воздушно-топливных смесей с AFR 15,4: 1 и коэффициентом эквивалентности (λ) 1,05. Максимальная мощность двигателя достигается при обогащении топливно-воздушных смесей с AFR 12,6:1 и коэффициентом эквивалентности (λ) 0,86. При стехиометрической топливовоздушной смеси (λ = 1) существует компромисс между максимальной мощностью двигателя и минимальным расходом топлива.
Максимальная мощность двигателя достигается при обогащении топливно-воздушных смесей с AFR 12,6:1 и коэффициентом эквивалентности (λ) 0,86. При стехиометрической топливовоздушной смеси (λ = 1) существует компромисс между максимальной мощностью двигателя и минимальным расходом топлива.
Двигатели с воспламенением от сжатия (дизельные) всегда работают на бедных воздушно-топливных смесях (λ > 1,00). Большинство современных дизельных двигателей работают с λ между 1,65 и 1,10. Максимальная эффективность (наименьший расход топлива) достигается при λ = 1,65. Увеличение количества топлива выше этого значения (приблизительно к 1,10) приведет к увеличению количества сажи (несгоревших частиц топлива).
Р. Дуглас провел интересное исследование двухтактных двигателей. В своей докторской диссертации « Исследования замкнутого цикла двухтактного двигателя 93;
график (lmbd_g, eff_lmbd_g, ‘b’, ‘Ширина линии’, 2)
держать
график (lmbd_d, eff_lmbd_d, ‘r’, ‘Ширина линии’, 2)
сетка()
xlabel(‘$\лямбда\текст{[-]}$’)
ylabel(‘$\eta_{\lambda} \text{[-]}$’)
название(‘x-engineer. Выполнение приведенных выше инструкций Scilab выводит следующее графическое окно. Изображение: Функция полноты сгорания от коэффициента эквивалентности Как видите, двигатель с воспламенением от сжатия (дизельный) при стехиометрическом соотношении воздух-топливо имеет очень низкую полноту сгорания. Наилучшая полнота сгорания достигается при λ = 2,00 для дизельных двигателей и λ = 1,12 для двигателей с искровым зажиганием (бензиновых). Go back MethanolEthanolButanolDieselGasolinePropaneMethaneHydrogen Наблюдение : Эффективность сгорания рассчитывается только для дизельного топлива и бензина (бензин) с использованием уравнений (4) и (5). Назад Выбросы выхлопных газов двигателей внутреннего сгорания сильно зависят от соотношения воздух-топливо (коэффициент эквивалентности). Основные выбросы отработавших газов в ДВС приведены в таблице ниже. org’)
легенда(‘бензин’,’дизель’,4)
org’)
легенда(‘бензин’,’дизель’,4) Air fuel ratio calculator
m a [g] Fuel type λ [-] m f [g] η λ [%]  Для других видов топлива расчет полноты сгорания недоступен (NA).
Для других видов топлива расчет полноты сгорания недоступен (NA). Влияние соотношения воздух-топливо на выбросы двигателя


 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
 (альфа).
(альфа). В зоне горения камеры сгорания реактивного двигателя также стараются получить нормальную или немного обогащенную смесь — она хорошо загорается от электрической искры я устойчиво горит.
В зоне горения камеры сгорания реактивного двигателя также стараются получить нормальную или немного обогащенную смесь — она хорошо загорается от электрической искры я устойчиво горит. Пламя начнет мигать, выделение копоти увеличится — процесс горения керосина будет идти неустойчиво, вяло, и при сильном обогащении смеси пламя погаснет. Для улучшения процесса сгорания смесь надо обеднить -уменьшить подачу керосина. Будем уменьшать, подачу топлива — ввертывать фитиль. Пламя начнет переходить в ярко-желтый цвет, это значит, что топливовоздушная смесь имеет нормальный состав, т. е. у нее α=1. При дальнейшем ввертывании фитиля пламя лампы из ярко-желтого будет переходить в синий, голубой цвет, пламя начнет дрожать, вспыхивать — процесс горения станет неустойчивым (рис. 22, положение В).
Пламя начнет мигать, выделение копоти увеличится — процесс горения керосина будет идти неустойчиво, вяло, и при сильном обогащении смеси пламя погаснет. Для улучшения процесса сгорания смесь надо обеднить -уменьшить подачу керосина. Будем уменьшать, подачу топлива — ввертывать фитиль. Пламя начнет переходить в ярко-желтый цвет, это значит, что топливовоздушная смесь имеет нормальный состав, т. е. у нее α=1. При дальнейшем ввертывании фитиля пламя лампы из ярко-желтого будет переходить в синий, голубой цвет, пламя начнет дрожать, вспыхивать — процесс горения станет неустойчивым (рис. 22, положение В). Коэффициент избытка воздуха в бедной смеси больше единицы α > 1. Например, смесь, состоящая из 1 кг керосина и 20 кг воздуха, будет бедной. При сгорании ее сгорит весь керосин, но часть кислорода воздуха останется неиспользованной. Продукты сгорания бедной смеси гореть не могут.
Коэффициент избытка воздуха в бедной смеси больше единицы α > 1. Например, смесь, состоящая из 1 кг керосина и 20 кг воздуха, будет бедной. При сгорании ее сгорит весь керосин, но часть кислорода воздуха останется неиспользованной. Продукты сгорания бедной смеси гореть не могут.

 Они просты по конструкции, надежны о работе и удобны в эксплуатации — легко снимаются для осмотра, ремонта и замены без разборки двигатели.
Они просты по конструкции, надежны о работе и удобны в эксплуатации — легко снимаются для осмотра, ремонта и замены без разборки двигатели. 23. Трубчатая камера сгорания
23. Трубчатая камера сгорания 9.44.166 (0.007 с.)
9.44.166 (0.007 с.) Действительный расход воздуха на единицу горючего записывается как Vв=aVв0. Множитель a называется коэффициентом избытка воздуха. Разность между действительным и теоретически необходимым количеством воздуха DVв называется избытком воздуха.
Действительный расход воздуха на единицу горючего записывается как Vв=aVв0. Множитель a называется коэффициентом избытка воздуха. Разность между действительным и теоретически необходимым количеством воздуха DVв называется избытком воздуха. Знание плотности газов или объема 1-го кмоля (22,4 м3 при н.у.) позволяет перейти от массовых единиц к объемным:
Знание плотности газов или объема 1-го кмоля (22,4 м3 при н.у.) позволяет перейти от массовых единиц к объемным: Например, на горение 1 м3 метана объем воздуха находят из уравнения реакции горения:
Например, на горение 1 м3 метана объем воздуха находят из уравнения реакции горения:
 к. в условии задачи указана химическая формула горючего вещества (или ее можно записать по названию соединения). Следовательно, необходимо записать уравнение реакции горения ацетона в воздухе:
к. в условии задачи указана химическая формула горючего вещества (или ее можно записать по названию соединения). Следовательно, необходимо записать уравнение реакции горения ацетона в воздухе:
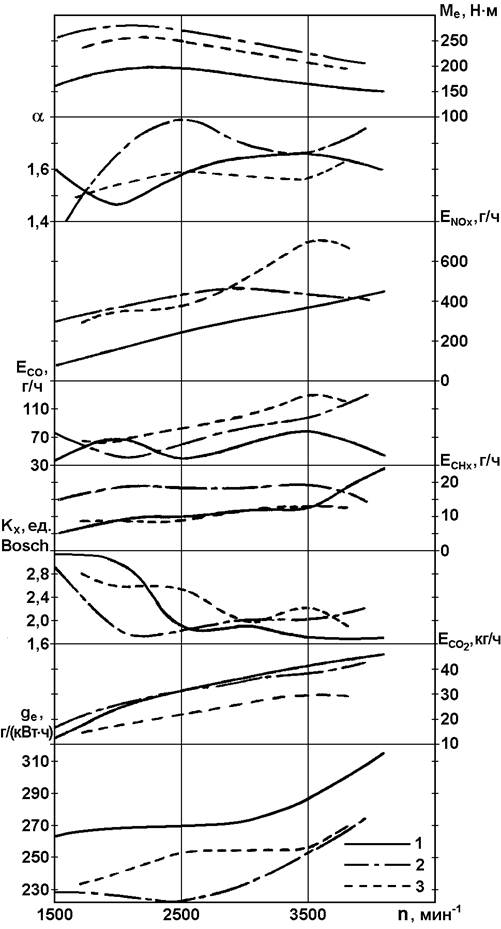 у.).
у.).

 Общий объем азота в продуктах горения V(N2)=2,5×3,76×0,2+6,5×3,76×0,4+3,27=14,93 м3.
Общий объем азота в продуктах горения V(N2)=2,5×3,76×0,2+6,5×3,76×0,4+3,27=14,93 м3. Если предположить, что все топливо будет израсходовано в ходе реакции, при температурах менее 1000 К,
химическая реакция может
написано как:
Если предположить, что все топливо будет израсходовано в ходе реакции, при температурах менее 1000 К,
химическая реакция может
написано как: В двигателе внутреннего сгорания NO образуется
в период горения при температурах реакции выше 2000 К. Скорость разложения
NO очень медленно действует при температурах ниже 2000 K, поэтому концентрация NO «замерзает» при концентрациях выше
равновесные значения при более низких температурах.
В двигателе внутреннего сгорания NO образуется
в период горения при температурах реакции выше 2000 К. Скорость разложения
NO очень медленно действует при температурах ниже 2000 K, поэтому концентрация NO «замерзает» при концентрациях выше
равновесные значения при более низких температурах.